Heterogeneity of cellular circadian clocks in intact plants and its correction under light-dark cycles

Cellular circadian clocks in a plant work in coordination under light-dark cycles by correcting heterogeneous traits between them.

Abstract

Recent advances in single-cell analysis have revealed the stochasticity and nongenetic heterogeneity inherent to cellular processes. However, our knowledge of the actual cellular behaviors in a living multicellular organism is still limited. By using a single-cell bioluminescence imaging technique on duckweed, Lemna gibba, we demonstrate that, under constant conditions, cells in the intact plant work as individual circadian clocks that oscillate with their own frequencies and respond independently to external stimuli. Quantitative analysis uncovered the heterogeneity and instability of cellular clocks and partial synchronization between neighboring cells. Furthermore, we found that cellular clocks in the plant body under light-dark cycles showed a centrifugal phase pattern in which the effect of cell-to-cell heterogeneity in period lengths was almost masked. The inherent heterogeneity in the properties of cellular clocks observed under constant conditions is corrected under light-dark cycles to coordinate the daily rhythms of the plant body. These findings provide a novel perspective of spatiotemporal architectures in the plant circadian system.

INTRODUCTION

To understand a multicellular organism as a dynamic system, it is essential to reveal the dynamics of cellular behaviors in the intact body because cellular processes fluctuate inherently and are altered by stochastic noise (1, 2). The circadian clock is the endogenous timing system based on self-sustained oscillations in individual cells synchronized (entrained) to day-night cycles through phase adjustment due to environmental cues (3). In many organisms, circadian synchronization contributes to survival (4). In eukaryotes, the core circadian oscillator is implemented as a gene regulatory network whose stochastic properties have been discussed (5–7). Recent bioluminescence imaging using mammalian cells revealed noisy circadian rhythms in isolated cells and nongenetic heterogeneity in the free-running period (FRP) among those cells (8). It is well known that tight coupling between neurons at the suprachiasmatic nucleus (SCN) allows such noisy and heterogeneous cellular clocks to generate a robust and synchronous rhythm and to relay reliable timing information to peripheral tissues so that free-running rhythms at the organismal level persist for more than a month (9–11). In contrast, the independence of cellular clocks has been demonstrated in plants. Previous studies that reported the intratissue desynchronization of circadian rhythms indicated the heterogeneity of cellular clocks and the weakness of cell-to-cell coupling in mature tissues (12–17). However, fundamental properties of the plant cellular clock, such as instability, heterogeneity, and the manner of cell-to-cell interaction, remain unclear because of the difficulty of monitoring circadian gene expression of individual cells in intact plants.

RESULTS

Experimental setup

To overcome this challenge, we developed a single-cell bioluminescence imaging system using a duckweed species, Lemna gibba, with a tiny, flat, floating body (Fig. 1A) (18). A circadian reporter, AtCCA1::LUC, was introduced mainly into mesophyll cells by particle bombardment. Plants were kept growing in a medium supplied with 1% sucrose before and after gene transfection to increase the luminescence signal. The luminescence from transfected cells that dispersed in the same frond (leaf-like structure) was monitored for more than a week under various light conditions: constant light (LL), constant dark (DD), and 12-hour light/12-hour dark cycle (LD) (fig. S1, A to C, and table S1). For each cellular rhythm, peak times (PTs) and trough times (TTs) were estimated by local curve fitting, and its period length was estimated by fast Fourier transform–nonlinear least squares (FFT-NLLS), a multicomponent cosine fit. In FFT-NLLS, the rhythmicity was assessed by a relative amplitude error (RAE) that increases from 0 to 1 as the rhythm nears insignificance (19). We selected cells that sustained rhythmicity throughout measurement and calculated their phases and amplitudes as functions of time (fig. S1, D to G, and Materials and Methods).

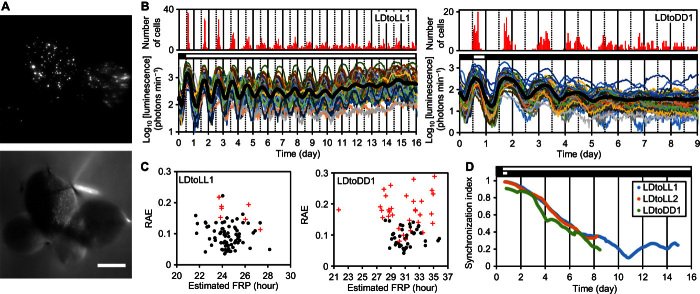
Fig. 1. Cellular rhythms were desynchronized after being released into constant conditions.

Plants grown under LL were subjected to particle bombardment and subsequently entrained in an LD cycle before starting bioluminescence monitoring. (A) Bioluminescence (top) and bright-field (bottom) images of a colony of L. gibba with four fronds. Scale bar, 2 mm. (B) Mean luminescence (black circles) and luminescence traces (other colored solid lines) of 85 cells in the frond (LDtoLL1, table S1) (left) and 73 cells in the frond (LDtoDD1, table S1) (right). The number of cells peaking at every hour is shown at the top. (C) FFT-NLLS analysis for cellular rhythms under LL (LDtoLL1, days 1 to 16) (left) or DD (LDtoDD1, days 1 to 9) (right). RAEs of rhythm-sustained cells (closed circles) and other cells that did not meet the criteria for circadian rhythms (red crosses) were plotted against estimated FRPs (see Materials and Methods). (D) Temporal changes in SIs during the three experiments. Open and black bars indicate light and dark conditions, respectively.

Cellular rhythms in intact plants were desynchronized under constant conditions

We first carried out release experiments and observed individual cellular circadian rhythms under LL and DD (Fig. 1B and movies S1 and S2). Before release, under LD, the luminescence of measured cells peaked synchronously (mean ± SD, 2.4 ± 1.5 hours after dawn; n = 240). This high synchrony of PTs gradually disappeared under both LL and DD (Fig. 1B). Rhythm sustainability differed under both conditions. Under LL, most cells sustained rhythms during the measurement, whereas under DD, cellular rhythms were severely damped and about half of the measured cells lost their rhythmicity by the end of measurement (Fig. 1B and fig. S2). The mean FRP of rhythm-sustained cells under DD was ~7 hours longer than those under LL (table S1). The FRPs of cells appeared to vary under both conditions (Fig. 1C and fig. S3). The cell-to-cell heterogeneity in FRPs was considered a major factor for the desynchronization of cellular rhythms. To quantitatively analyze the desynchronization process, we calculated the synchronization index (SI) at each time point from the phases of rhythm-sustained cells (16). SI takes on the value of 1 when rhythms are completely synchronized and decreases to 0 when rhythms are desynchronized. The SI at the time of release was near 1 and constantly decreased for more than a week under both LL and DD (Fig. 1D). For plants in an asynchronous state, patterns in the spatial distribution of circadian phases were unclear, suggesting that the circadian traits of cells varied uniformly within a frond (fig. S4).

Cellular rhythms were partially synchronized between neighboring cells

For further analysis of the circadian traits of cells in the asynchronous state, we examined plants that had not been entrained (Fig. 2A). The FRPs of cellular rhythms under LL were normally distributed (Kolmogorov-Smirnov, P = 0.88; n = 563; mean ± SD, 23.0 ± 1.6 hours) between 18.2 and 29.4 hours without apparent spatial patterns in the fronds (fig. S5). SIs of all monitored fronds stayed low throughout measurement (Fig. 2B), and their circadian phases showed no apparent spatial patterns (fig. S6). However, an analysis of the linkage between phase or FRP differences and cell-to-cell distances revealed that only cellular rhythms in the short range (<~0.5 mm) showed a tendency to synchronize (Fig. 2, C and D, and fig. S7). This indicated a phase-attractive interaction between neighboring cellular clocks.

Fig. 2. Asynchronous cellular rhythms under LL.

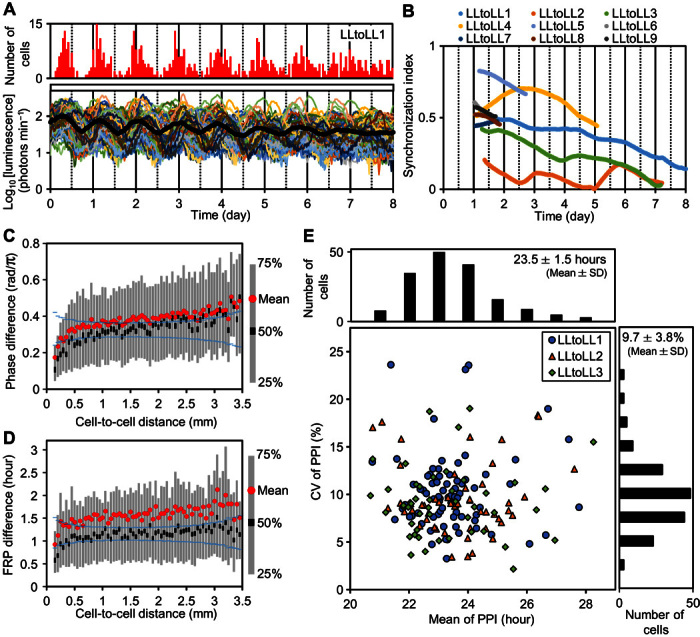
Plants grown under LL were subjected to particle bombardment and subsequently precultured under LL for 24 hours before starting bioluminescence monitoring. (A) Mean luminescence (black circles) and luminescence traces (other colored solid lines) of 89 cells in the frond (LLtoLL1, table S1). The number of cells peaking at every hour is shown at the top. (B) Temporal changes of SIs of nine experiments. (C) Relationship between phase differences between cellular rhythms and cell-to-cell distances. For all pairs of cellular rhythms in each experiment (LLtoLL1 to LLtoLL9, table S1), phase differences on day 1.5 and cell-to-cell distances were both calculated. Statistics (mean and quartiles) for the phase differences measured were plotted at every 0.05-mm interval of cell-to-cell distances. Blue symbols at each cell-to-cell distance interval represent 95% confidence limits of the median, assuming that samples in each interval have the same median value. The confidence limits were calculated on the basis of resampling (10,000 repeats) from all samples. (D) Relationship between FRP differences between cellular rhythms and cell-to-cell distances. The FRP of each cellular rhythm during each experiment (LLtoLL1 to LLtoLL9) was estimated by FFT-NLLS and analyzed in the same manner as in (C). (E) Plot of coefficient of variation (CV) of peak-to-peak intervals (PPIs) against the mean of PPIs and their histograms for three experiments (LLtoLL1 to LLtoLL3).

Cellular clocks in an asynchronous state run at their own FRPs

To capture the dynamics of the cellular rhythms in greater detail, we fitted an analysis of variance (ANOVA) model to the PPIs of the 8-day monitoring data (LLtoLL1 to LLtoLL3, table S1) (8). This model assumes that PPI_ij = τ_i + ε_ij, where τ_i is the normally distributed FRP of cell i, and ε_ij is the white Gaussian noise for cycle j of cell i. According tothe ANOVA table, the estimated SD of τ_i (1.11 hours) was smaller than that of ε_ij (2.45 hours). The cell-to-cell heterogeneity in FRPs was significant (ANOVA, P < 0.001; F = 2.43). This model could be used to explain the population-level dynamics of cellular clocks (fig. S8), suggesting that cellular clocks in the asynchronous state run at their own FRPs. Furthermore, this analysis indicated that the cycle-to-cycle variability is a non-negligible factor for understanding the spatiotemporal dynamics of cellular clocks. These evaluated values of the cell-to-cell heterogeneity and the cycle-to-cycle variability were comparable to those of cultured fibroblast cells of mouse (8). The CV of PPIs showed no clear correlations with FRPs (Fig. 2E and fig. S9A), suggesting that cycle-to-cycle variability occurred irrespective of the generation of cell-to-cell heterogeneity of FRPs. Note that neither FRP nor the CV of PPIs appeared to be correlated with the cellular luminescence intensity that reflected the amounts of DNA introduced (fig. S9, B and C) (18). This suggests that the observed cell-to-cell heterogeneity was unlikely to be due to the gene transfection procedure and the subsequent luminescence analyses.

Cellular clocks under LD formed a centrifugal pattern in contrast to their heterogeneity

Our single-cell–level analysis of plants under LL revealed the independence and heterogeneity of cellular clocks in a frond. We went on to investigate these properties under entrainment conditions by focusing on the relationship between FRP and locked phase (that is, PT after dawn) under LD because a positive correlation between them is a common feature of circadian rhythms (20–22). If the cellular rhythms in plants synchronized independently to LD cycles, their locked phases under LD are expected to reflect their FRPs with heterogeneity. To test this hypothesis, we monitored cellular rhythms in an asynchronous state under LL for 3 days, followed by five LD cycles (Fig. 3A and movie S3). Cellular rhythms at any phase under LL were synchronized to LD cycles within 2 days (Fig. 3A and fig. S10). However, luminescence traces in the first dark period differed dependently on their onset phases. To clarify the dependency, we sorted cellular rhythms into eight groups according to their last TTs before the first dark signal and then calculated the mean of PTs and TTs for each group (Fig. 3B and fig. S11). This analysis elucidated phase-dependent responses of individual cellular rhythms to the first dark signal. For example, a 3-hour phase difference between the following two groups: TT (57 to 60 hours) and TT (60 to 63 hours), resulted in opposing responses of the reporter activity in the darkness. The phase-dependent manner of these responses appeared to be interpreted through the idea of phase-response curve for entrainment (23). Thus, cellular clocks in the frond responded independently to the dark signal.

Fig. 3. Synchronization of cellular rhythms to LD cycles and the formation of a centrifugal pattern of their locked phases within a frond.

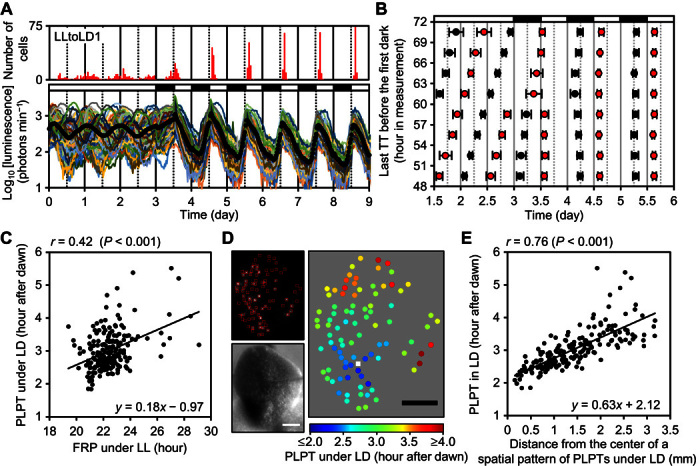
Plants grown under LL were subjected to particle bombardment and precultured under LL for 24 hours before starting bioluminescence monitoring. (A) Mean luminescence (black circles) and luminescence traces (other colored solid lines) of 90 cells in the frond (LLtoLD1, table S1). The number of cells peaking at every hour is shown at the top. (B) Cell-autonomous entrainment manner of cellular clocks. Time series of three experiments (LLtoLD1 to LLtoLD3, table S1) were sorted into eight groups according to the last TTs before the first dark signal. Each group has a 3-hour window. Means of PTs (red circles) and TTs (black circles) of each group were plotted (bar indicates SD). (C) Correlation between PLPTs under LD and FRPs under LL of three experiments (LLtoLD1 to LLtoLD3). (D) Bioluminescence image (upper left), bright-field image (bottom left), and spatial distribution of PLPTs (right) of the frond (LLtoLD1). PLPT is represented as the mean of PTs during days 5.5 to 8.5. The center of the spatial pattern was estimated by quadratic surface fitting and represented as a white square. Scale bars, 1 mm. (E) Correlation between PLPTs of cellular rhythms under LD and distances of cells from the center (LLtoLD1 to LLtoLD3). Open and black bars indicate light and dark conditions, respectively.

To investigate the relationship between FRP under LL and locked phase under LD, we estimated those of each cellular rhythm in the experiments described above (Fig. 3A). The FRP under LL was estimated by FFT-NLLS using data collected during the first 3 days of monitoring. This duration of monitoring appeared to be enough for the estimation of FRPs (fig. S12). The locked phase under LD was represented by phase-locked peak time (PLPT) and phase-locked trough time (PLTT). These indices were calculated as the means of PTs and TTs, respectively, during 3 days of LD (days 5.5 to 8.5). Both PLPTs and PLTTs varied significantly with >2-hour differences between cells in a frond (ANOVA, P < 0.001) (fig. S13). This indicated that individual cellular clocks in a frond were locked into different phases under LD. Furthermore, the PLPTs under LD positively correlated with FRPs under LL (r = 0.42, P < 0.001) (Fig. 3C), suggesting that the locked phases of individual cellular clocks reflect the heterogeneity of their FRPs. Although there was a significant correlation between PLPTs and FRPs, the correlation coefficient was relatively low, implying that some other factor is responsible for cell-to-cell variability in the locked phases. In three replicate experiments, PLPTs showed a spatial pattern in which the PLPTs near the center of a frond were advanced by ~2 hours compared with those in the peripheral region (Fig. 3D and fig. S14); the PLPTs correlated strongly with distances from the estimated center of the pattern (r = 0.76, P < 0.001) (Fig. 3E). Because there was no such spatial pattern in FRPs (fig. S15), the locked phase of each cellular clock depended on its position in a frond rather than its FRP. Thus, the effect of heterogeneous FRPs on cellular timing behaviors under LD was masked in the spatial pattern. Once formed, this pattern becomes stable. A similar pattern was observed after repeated LD cycles (fig. S16, A to C). Notably, a similar pattern was observed in the second PTs under LL following release from LD (fig. S16, D and E), confirming that the phases of cellular clocks under LD form a centrifugal pattern in a frond. We further confirmed that the daily rhythmic changes in the photosynthesis activity, a typical output of the circadian clock, followed a similar centrifugal pattern (fig. S17). To spatiotemporally evaluate photosynthesis activity in a frond, we monitored delayed fluorescence from chloroplasts that negatively reflects the photosynthesis activity (24). The delayed fluorescence of a frond was monitored under LD and then under LL. The first TTs of delayed fluorescence rhythms under LL showed a centrifugal pattern, suggesting that the circadian output followed the phase pattern of the circadian clock.

DISCUSSION

Our studies demonstrate that the plant circadian system consists of heterogeneous and unstable cellular clocks, similar to the mammalian system (8, 10). We determined that under constant conditions, cellular clocks in the intact plant behave as individual oscillators retaining their own FRPs, although there were indications of a weak phase-attractive interaction between neighboring cells. This is a striking difference from the mammalian circadian system in which peripheral clocks are synchronized to the SCN, which function as a central pacemaker (25). This weak cell-to-cell coupling is consistent with previous studies performed on other plants and may be a common feature of plant circadian systems (12–17). One explanation for why such a weak coupling has been maintained in the course of evolution is cell-autonomous entrainability; cellular clocks in plants independently responded to dark signals (Fig. 3B). This view is consistent with the idea that light-dark cues are more important than cell-to-cell coupling in maintaining synchrony of cellular clocks in plant leaves (16). However, our results indicate spatiotemporal regulation of an entrainment state at the whole-plant level; locked phases of cellular clocks depend on their positions in a frond under LD (Fig. 3, D and E). This suggests that plants under LD correct the heterogeneity of cellular clocks to generate coordinated daily rhythms. In this correction, phase-attractive interactions between cells may play a role in adjusting the variety of cellular locked phases that would reflect heterogeneous FRPs. Collectively, we suggest that the cell-to-cell interactions proposed in the past based on free-running experiments are an adaptive trait working under day-night cycles to coordinate cellular clocks (13–17).

In addition to cell-to-cell interactions, further mechanisms to form the centrifugal patterns in locked circadian phases of mesophyll cells close to the upper surface of the frond are needed. In the duckweed frond, veins branch near the center of the centrifugal pattern. In plants, it was proposed that veins affect the patterning of circadian phases in a leaf (13). The vein structure in a frond might contribute to the centrifugal patterns. Note that the shoot apical meristems (SAMs) of L. gibba are located at the base of the frond near the center of the centrifugal patterns. It was previously proposed that in Arabidopsis thaliana, a shoot apex (containing SAM) acts as a central pacemaker that is analogous to the SCN in mammals (17). In mice, the SCN exhibited advanced-phase relationships relative to peripheral tissues under LD (26). SAMs in L. gibba might affect the circadian phase of neighboring tissues and form the phase-advanced center in mesophyll tissue. Note that changes of endogenous sucrose content could shift the phase of the circadian clock (27). Daily rhythms of sugar production and consumption in the frond may be involved in the pattern formation that could be fed back to the regulation of these photosynthesis-related activities and also of clock-related genes.

For the observation of cellular circadian behavior, we used a bioluminescence reporter, AtCCA1::LUC, due to its high luminescence level with a high amplitude. This is a typical morning-phased reporter in plants, but circadian phenomena that were found using this reporter, such as the centrifugal pattern of circadian phases, might be reporter-specific phenomena. However, the delayed fluorescence rhythm showed a similar pattern in the frond under LD (fig. S17), suggesting that the circadian modulation of photosynthetic activity followed the centrifugal pattern. This also suggested that the centrifugal pattern could be found in a wide range of physiologies of at least the mesophyll tissue in the frond.

Here, using duckweed, we analyzed the plant circadian system at a single-cell level with a high time resolution and revealed the centrifugal pattern of circadian phases in a frond under LD. A previous study that used high-resolution bioluminescence imaging of Arabidopsis leaves also showed some spatial patterns of circadian phases under LD (16). This similarity of the morphologically and phylogenetically different species implies that the phase patterning under day-night conditions seems to be a common trait of the plant circadian system. The physiological roles of the centrifugal pattern of circadian phases are unknown, but the circadian modulation of the photosynthetic activity of duckweed plants also followed the same centrifugal pattern as that of AtCCA1::LUC luminescence rhythms under LD (fig. S17). This strongly suggests that the phase patterning in the frond under day-night conditions is physiologically important. Recently, it was shown that circadian systems, including phase determination of clock-controlled genes, are different between mesophyll and vascular tissues (28). Thus, the phase differences in the plant body appear to be well coordinated at various levels of plant structures. The physiological functions of circadian systems in plants should be reconsidered from the perspective of spatiotemporal architectures in the plant body.

MATERIALS AND METHODS

Plant materials and growth conditions

L. gibba strain p8L was maintained in NF medium with 1% sucrose under constant light conditions in a temperature-controlled room (25° ± 1°C) as previously described (29). The white light (~50 μE m⁻² s⁻¹) was supplied by fluorescent lamps (FLR40SEX-W/M/36-HG, NEC). Plants were grown on 60 ml of the medium in 200-ml Erlenmeyer flasks plugged with cotton. New stock cultures were made every week, and well-grown plants were used for experiments. For LD culture, an incubator (MIR-153, Panasonic Healthcare) was used. In this incubator, the white light (~50 μE m⁻² s⁻¹) was supplied by fluorescent lamps (FL20SS-W, Mitsubishi Electric), and the growth temperature was maintained at 25° ± 1°C. Under these LD conditions, new stock cultures were made every 2 weeks.

Luciferase reporter transfection by particle bombardment

The luciferase reporter gene pUC-AtCCA1:LUC⁺ (AtCCA1::LUC) was used as the circadian reporter (30). This construct was introduced into plants by particle bombardment, as described previously with minor modifications (18). Briefly, 0.48 mg of gold particles (1.0-μm diameter; Bio-Rad) was coated with 2 μg of plasmid DNA and introduced into L. gibba plants laid on a 60-mm polystyrene dish using a helium gun device (PDS-1000/He, Bio-Rad), according to the manufacturer’s instructions (vacuum, 27 mmHg; helium pressure, 450 psi). After particle bombardment, the 60-mm dish was filled with 8 ml of growth medium containing d-luciferin (0.5 mM potassium salt, Wako) and incubated under each experimental condition.

Experimental setup and bioluminescence monitoring

The single-cell bioluminescence imaging was carried out as described previously with minor modifications for long-term monitoring (18). The colony of L. gibba with the highest transfection efficiency was transferred to a 35-mm polystyrene dish with 5 ml of growth medium containing 0.5 mM d-luciferin. The 35-mm dish was set in a handmade cage built with a 60-mm dish to reduce evaporation of the growth medium. We constructed a motor-drive rotary table for providing uniform illumination to the plant from above. This table rotated to move the sample cage between the optical fibers and the electron multiplying charge-coupled device (EM-CCD) camera (ImagEM C9100-13, Hamamatsu Photonics) (fig. S1A). The optical fibers guided the white light (30 μE m⁻² s⁻¹) from a light-emitting diode device (RFB2-20SW, CCS Inc.). To reduce delayed autofluorescence from chloroplasts, a shortpass filter (SV630, Asahi Spectra) was fitted in the camera lens. By controlling this imaging system with a PC software (HOKAWO, Hamamatsu Photonics), the bioluminescence image was automatically captured every 30 min with either a 200-s or a 240-s exposure. Before image capture, we allowed a minimum of 60 s of dark period for autofluorescence decay. The bioluminescence intensity of each luminescent spot was measured as the integrated density of the region of interest (ROI; size, 6 × 6 pixels) (fig. S1B). Weak luminescent rhythms of cells that were located near high luminescent cells were manually excluded from further analysis. Image analysis and postprocessing were carried out with ImageJ (http://rsbweb.nih.gov/ij/).

Spatiotemporal analysis of delayed fluorescence

To analyze the timing regulation of photosynthetic activity, we monitored delayed fluorescence rhythms (24). The imaging system for delayed fluorescence was essentially identical to the bioluminescence imaging system described above but with the shortpass filter removed. The delayed fluorescence image was captured with a 30-s exposure 30 s after the light was switched off. The delayed fluorescence image was manually separated to ROIs (18 × 18 pixels) for spatiotemporal analysis of delayed fluorescence rhythms.

Time series analysis

R scripts were developed and run on R 3.1.1 (http://r-project.org/) for the time series analysis described below.

Removal of cosmic ray spikes. Some time series contained spike signals caused by cosmic rays. For these data, the luminescence intensity at the spike time was replaced by the mean intensity of the preceding and subsequent time points.

Fast Fourier transform–nonlinear least squares. The period of each luminescence rhythm was estimated by FFT-NLLS, a multicomponent cosine fit (19). In FFT-NLLS, the rhythm significance is estimated by an RAE that increases from 0 to 1 as the rhythm nears statistical insignificance. Because the basis of the FFT-NLLS is a cosine fitting without considering the time variations in amplitude, the RAE is strongly affected by the amplitude nonstationarity of the applied time series. Thus, the raw time series was transformed to have a mean of 0 and a constant variance as described in Izumo et al. (31). The time series was detrended by subtracting a 24-hour window moving average and then dividing it by the SD within each corresponding sliding 24-hour window. The time series obtained was analyzed subsequently by FFT-NLLS. Rhythms with a period of between 15 and 35 hours were taken similarly as those in the circadian range. The algorithm of FFT-NLLS was implemented as R scripts according to Zielinski et al. (19).

Peak and trough picking. Peaks and troughs in each bioluminescence rhythm were detected as follows. First, time series data were smoothed with the 8-hour moving average, and peak and trough positions were roughly identified as local maxima and minima, respectively. Precise positions of peaks and troughs were estimated by a local quadratic curve fitting for the smoothed time series with the 2-hour moving average (fig. S1D). The width of the local fitting area was set to 6 hours.

Calculating phase and amplitude as a function of time. To quantify the spatiotemporal dynamics of cellular circadian rhythms in a plant body, we introduced phase θ(t) and amplitude A(t) of the bioluminescence rhythms x(t) of each cell as follows

$$\mathrm{\theta }(\mathit{t})=2\mathrm{\pi }\frac{\mathit{t}-{\mathit{t}}_{\mathrm{P}}^{\mathit{k}}}{{\mathit{t}}_{\mathrm{P}}^{\mathit{k}+1}-{\mathit{t}}_{\mathrm{P}}^{\mathit{k}}}({\mathit{t}}_{\mathrm{P}}^{\mathit{k}}\le \mathit{t}<{\mathit{t}}_{\mathrm{P}}^{\mathit{k}+1},\mathit{k}=1\cdots {\mathit{N}}_{\mathrm{P}})$$

$$\mathit{A}(\mathit{t})=\frac{\mathit{U}(\mathit{t})-\mathit{L}(\mathit{t})}{\mathit{U}(\mathit{t})+\mathit{L}(\mathit{t})}$$

$$\mathit{U}(\mathit{t})=\{\begin{array}{c}{\mathit{x}}_{\mathrm{P}}^1(\mathit{t}<{\mathit{t}}_{\mathrm{P}}^{\mathit{k}}),\\ \frac{{\mathit{x}}_{\mathrm{P}}^{\mathit{k}+1}-{\mathit{x}}_{\mathrm{P}}^{\mathit{k}}}{{\mathit{t}}_{\mathrm{P}}^{\mathit{k}+1}-{\mathit{t}}_{\mathrm{P}}^{\mathit{k}}}\mathit{t}+\frac{{\mathit{x}}_{\mathrm{P}}^{\mathit{k}}{\mathit{t}}_{\mathrm{P}}^{\mathit{k}+1}-{\mathit{x}}_{\mathrm{P}}^{\mathit{k}+1}{\mathit{t}}_{\mathrm{P}}^{\mathit{k}}}{{\mathit{t}}_{\mathrm{P}}^{\mathit{k}+1}-{\mathit{t}}_{\mathrm{P}}^{\mathit{k}}}({\mathit{t}}_{\mathrm{P}}^{\mathit{k}}\le \mathit{t}<{\mathit{t}}_{\mathrm{P}}^{\mathit{k}+1},\mathit{k}=1\cdots {\mathit{N}}_{\mathrm{P}}),\\ {\mathit{x}}_{\mathrm{P}}^{{\mathit{N}}_{\mathrm{P}}}({\mathit{t}}_{\mathrm{P}}^{{\mathit{N}}_{\mathrm{P}}}\le \mathit{t})\end{array}$$

$$\mathit{L}(\mathit{t})=\{\begin{array}{c}{\mathit{x}}_{\mathrm{T}}^1(\mathit{t}<{\mathit{t}}_{\mathrm{T}}^{\mathit{k}}),\\ \frac{{\mathit{x}}_{\mathrm{T}}^{\mathit{k}+1}-{\mathit{x}}_{\mathrm{T}}^{\mathit{k}}}{{\mathit{t}}_{\mathrm{T}}^{\mathit{k}+1}-{\mathit{t}}_{\mathrm{T}}^{\mathit{k}}}\mathit{t}+\frac{{\mathit{x}}_{\mathrm{T}}^{\mathit{k}}{\mathit{t}}_{\mathrm{T}}^{\mathit{k}+1}-{\mathit{x}}_{\mathrm{T}}^{\mathit{k}+1}{\mathit{t}}_{\mathrm{T}}^{\mathit{k}}}{{\mathit{t}}_{\mathrm{T}}^{\mathit{k}+1}-{\mathit{t}}_{\mathrm{T}}^{\mathit{k}}}({\mathit{t}}_{\mathrm{T}}^{\mathit{k}}\le \mathit{t}<{\mathit{t}}_{\mathrm{T}}^{\mathit{k}+1},\mathit{k}=1\cdots {\mathit{N}}_{\mathrm{T}}),\\ {\mathit{x}}_{\mathrm{T}}^{{\mathit{N}}_{\mathrm{T}}}({\mathit{t}}_{\mathrm{T}}^{{\mathit{N}}_{\mathrm{T}}}\le \mathit{t})\end{array}$$

where t_P^k and t_T^k represent the occurrence time of the kth peak and the kth trough; x_P^k and x_T^k represent the bioluminescence intensity of the kth peak and the kth trough; N_P and N_T represent the total number of peaks and troughs; U(t) and L(t) represent the linear interpolation of peaks and troughs, respectively.

Determination of rhythm-sustained cells. Our peak and trough picking algorithm often estimated incorrect positions when applied to low luminescence or insignificant rhythms. To perform an accurate analysis of the spatiotemporal dynamics of cellular rhythms, unanalyzable data were excluded from further analysis. We developed an algorithm for determining the rhythm-sustained cells that showed circadian rhythms throughout monitoring as follows. First, we used RAE in FFT-NLLS analysis as an index of rhythmicity and judged those cells with an RAE of less than 0.15 as candidates for rhythm-sustained cells (candidate group 1). FFT-NLLS tends to give a high RAE score if the period of a rhythm shows instability, even if it has a high amplitude. We thus added those cells with an amplitude that stayed higher than 0.3 during monitoring to the candidate group 1 (candidate group 2). Next, we calculated the difference between the estimated period by FFT-NLLS and the mean of PPIs for each cell to check the consistency of the estimated peak numbers between them. In the candidate group 2, those cells for which the difference was less than 2.5 hours were chosen as rhythm-sustained cells.

Synchronization index

To address the synchrony between cellular rhythms within a plant body, the SI R(t), which is known as the order parameter in the Kuramoto model, was calculated at each time point as follows (32)

$$\mathit{R}(\mathit{t})\text{exp}(\mathit{i}\mathrm{\phi })=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathit{N}$}\right.{\displaystyle \sum _{\mathit{j}}}\text{exp}(\mathit{i}{\mathrm{\theta }}_{\mathit{j}}(\mathit{t}))$$

where θ_j(t) is the phase of the jth cell at time t, N is the number of cells, and φ is the mean phase of the population.

Creation of graphs and plots

Graphs and plots were created with R 3.1.1 or Excel (Microsoft Corporation). Quadric surface fitting for estimation of the center of spatial pattern was performed using nls function of R 3.1.1.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/7/e1600500/DC1

fig. S1. Outline of the quantitative analysis of cellular circadian rhythms.

fig. S2. Temporal changes in amplitudes of cellular luminescence rhythms after release into LL or DD from LD.

fig. S3. Results of FFT-NLLS analysis for cellular rhythms under LL.

fig. S4. Time evolution of the spatial distribution of cellular circadian phases after release into LL from LD.

fig. S5. Characteristics of asynchronous cellular rhythms under LL.

fig. S6. Time evolution of the spatial distribution of cellular circadian phases under LL.

fig. S7. Relationship between phase differences between cellular rhythms and cell-to-cell distances.

fig. S8. Population-level dynamics of cellular clocks explained by an ANOVA model.

fig. S9. Correlation between characteristic parameters for cellular bioluminescence rhythms under LL.

fig. S10. Cellular rhythms were synchronized to LD cycles within 2 days.

fig. S11. Cellular clocks respond to the first dark signal in a phase-dependent manner.

fig. S12. Correlation between FRPs during the first 3 days and during the subsequent 5 days.

fig. S13. Locked phases in LD were significantly different among cells in a frond.

fig. S14. Spatial distribution of PLPTs under LD.

fig. S15. FRPs of cellular clocks showed no clear spatial patterns as PLPTs did.

fig. S16. Spatial distribution of PLPTs after repeated LD cycles.

fig. S17. Spatial distribution of TTs of delayed fluorescence rhythms.

table S1. Summary of the quantitative analysis of cellular luminescence rhythms.

movie S1. Desynchronization of cellular luminescence rhythms on a frond under LL.

movie S2. Desynchronization and damping of cellular luminescence rhythms on a frond under DD.

movie S3. Asynchronous cellular luminescence rhythms on a frond under LL and their synchronization to LD cycles.

Reference (33)