Spatial regression with covariate measurement error: A semi-parametric approach

Summary

Spatial data have become increasingly common in epidemiology and public health research thanks to advances in GIS (Geographic Information Systems) technology. In health research, for example, it is common for epidemiologists to incorporate geographically indexed data into their studies. In practice, however, the spatially-defined covariates are often measured with error. Naive estimators of regression coefficients are attenuated if measurement error is ignored. Moreover, the classical measurement error theory is inapplicable in the context of spatial modelling because of the presence of spatial correlation among the observations. We propose a semi-parametric regression approach to obtain bias corrected estimates of regression parameters and derive their large sample properties. We evaluate the performance of the proposed method through simulation studies and illustrate using data on Ischemic Heart Disease (IHD). Both simulation and practical application demonstrate that the proposed method can be effective in practice.

1. Introduction

With the rapid growth of Geographic Information Systems (GIS), it is now common for epidemiologists to incorporate spatially indexed data into their studies (Elliott and Wartenberg, 2004). Analysis of such data, however, is complicated by correlations among neighbouring observations. Although there are well known statistical methods to adjust for spatial correlation, relatively little has been done in the context of spatial modelling when the covariate of interest is measured with error. In the case study that motivates this study, Australian researchers explored the relationship between the SEIFA index (an area-based measure of socio-economic status produced by the Australian Bureau of Statistics) and acute hospitalization for Ischemic Heart Disease (IHD) in New South Wales, Australia (Burden et al., 2005). Multivariate regression models suggest a significantly negative association between SEIFA and IHD, implying that heart disease rates increase with social disadvantages. However, the strength of association might be attenuated due to the fact that the SEIFA index is constructed using principal component analysis, therefore, is highly likely to be measured with error (Huque et al., 2014).

Many papers have appeared in the literature over the years on covariate measurement error in the context of independent data (Carroll et al., 2006; Fuller, 1987). However, relatively few have addressed the specific context of spatial modelling. Bernadinelli et al. (1997) and Xia and Carlin (1998) presented a spatiotemporal analysis of spatially correlated data with errors in covariates, in the context of disease mapping. They empirically studied several alternative measurement error models using a Gibbs algorithm. Li et al. (2009) derived asymptotic bias expressions for estimated regression coefficients in the context of a spatial linear mixed model. They showed that the regression estimates obtained from naive use of an error prone covariate are attenuated, while variance component estimates are inflated.

Recently, Huque et al. (2014) confirmed the findings of Li et al. (2009) and derived expressions for the bias when measurement error is ignored. They proposed two different strategies for obtaining consistent estimates: (i) correcting the estimate using an estimated attenuation factor; and (ii) using an appropriate transformation of the error prone covariate. They showed that both bias correction methods work reasonably well, however, the standard error is underestimated in the case when measurement error variances are estimated from the data. Moreover, their approach is fully parametric. Indeed, Ruppert et al. (2009) argued that penalized splines are the most effective method for correcting the covariate measurement error in case of independent data. So it is of natural interest to extent the spatial regression model with measurement error to a semi-parametric framework.

In this paper we propose a joint modelling approach to assess the relationship between a covariate with measurement error and a spatially correlated outcome in a semi-parametric regression context. Our approach contrasts with what is commonly assumed in the measurement error context, namely that some form of validation data are available. Underlying our approach is the critical assumption that the true, but unobserved covariate is smooth and that any random fluctuations from this smooth surface represent measurement error. This assumption makes our model identifiable by representing the unknown true covariate with a linear combination of spline basis functions (Yu and Ruppert, 2002; Xun et al., 2013). We use penalized least squares which makes the estimation of parameters and inference straightforward. We develop asymptotic theory for the estimated parameters and provide both model based and simulation based standard error estimates. Our simulation results reveal that the proposed method works well in obtaining consistent estimates of the true regression coefficient in the presence of measurement error. Our approach is computationally efficient and stable and can be implemented using standard nonlinear least squares software.

The structure of the paper is as follows: Section 2 describes our model formulation, estimation and inference procedures. Section 3 presents the data generation process and results from the simulation study. In section 4 we present an application of the proposed method to data on Ischemic Heart Disease (IHD). We conclude with general discussion in section 5. The Web Appendix (http:www.tibs.org/biometrics) gives detailed proofs, as needed.

2. Model

Suppose that X_i represents the true covariate of interest measured at geographical location, S_i ∈ ℝ², i = 1, …, n and suppose that X_i is related to an outcome Y_i, according to a spatial linear model:

$$Y_i={\beta }_0+{\beta }_1{X}_i+G_1\left(S_i\right)+{\mathit{∊}}_i,$$ (1)

where $\mathit{∊}={\left({\mathit{∊}}_1,\dots {\mathit{∊}}_n\right)}^T\sim N\left(0,{\sigma }_{\mathit{∊}}^2\right)$) and {G₁ (S_i): S_i ∈ ℝ² } is an unknown function that captures the spatial correlation, for now kept arbitrary. Further assume that ε_i and G₁(S_i) are independent of each other and of the true covariate X_i (Cressie, 1993). In practice, the outcome might also be related to other covariates and it is straight forward to extent model (1) to include these. However, for simplicity, we only consider a single covariate in model (1).

In the presence of measurement error, measurements on the true covariate X are not observed directly, instead an error contaminated version is available. Let W_i be the observed covariate for location S_i ∈ ℝ², i = 1, …, n, related to the true covariate X_i according to a classical measurement error model:

$$W_i=X_i+U_i,$$ (2)

where $U_i~N\left(0,{\sigma }_u^2\right)$. Note that in the case of independent data, a consistent estimate of the true regression coefficient β₁ can be obtained if either the measurement error variance is known or can be estimated using a validation data set on the true covariate (X) without measurement error (Carroll et al., 2006). However, in the spatial epidemiology setting such validation data are relatively rare. We develop an alternative approach assuming that the true covariate X is smooth and can be modelled by a second smooth function, G₂(S_i).

Many different choices of smoothers have been discussed in the literature, including locally-weighted running line smoothers (loess), Kernel smoothers or splines (Hastie and Tibshirani, 1990). In general, techniques based on regression splines are robust in approximating the true underling smooth functions and are relatively straight forward from a computational perspective, but have rigorous mathematical properties (Ruppert et al., 2003; Wood, 2006). In this paper we also adopt such a technique, specifically, cubic thin plate splines (Wood, 2006).

Within this framework, the unknown smooth functions, G_j(S_i), for j = 1, 2 are represented by linear combination of thin plate spline basis functions i.e., $G_j\left(S_i\right)=B_j^{\mathrm{T}}\left(S_i\right){\theta }_j$. Here B₁(S_i) and B₂(S_i) are two sets of thin plate splines basis functions with dimensions (q₁ + 3) × 1 and (q₂ + 3) × 1, respectively, where q₁ and q₂ are the corresponding number of knots and θ₁ and θ₂ are vectors of corresponding basis coefficients.

Under the above specifications model (1) and (2) can be rewritten as

$$Y_i=B_2^{\mathrm{T}}\left(S_i\right){\theta }_2{\beta }_1+B_1^{\mathrm{T}}\left(S_i\right){\theta }_1+{\mathit{∊}}_i;$$ (3)

$$W_i=B_2^{\mathrm{T}}\left(S_i\right){\theta }_2+U_i.$$ (4)

Since these equations are linear with respect to a set of unknown parameters, we use penalized least squares techniques for estimation (Yu and Ruppert, 2002; Xun et al., 2013). In this method, the data, (Y, W), are fitted to two different sets of spline basis functions B₁(S_i) and B₂(S_i) by least squares where parameters are estimated by minimizing the usual sum of squares plus roughness penalties. That is, we minimize

$$\mathit{J}\left(\beta ,{\theta }_1\right)=n^{-1}{\displaystyle {\sum }_{i=1}^n{\{Y_i-B_2^{\mathrm{T}}\left(S_i\right){\theta }_2{\beta }_1-B_1^{\mathrm{T}}\left(S_i\right){\theta }_1\}}^2+{\delta }_1{\theta }_1^{\mathrm{T}}{D}_1{\theta }_1;}$$ (5)

$$\mathit{J}\left({\theta }_2\right)=n^{-1}{\displaystyle {\sum }_{i=1}^n{\{W_i-B_2^{\mathrm{T}}\left(S_i\right){\theta }_2\}}^2+{\delta }_2{\theta }_2^{\mathrm{T}}{D}_2{\theta }_2,}$$ (6)

where the terms ${\delta }_1{\theta }_1^{\mathrm{T}}{D}_1{\theta }_1$ and ${\delta }_2{\theta }_2^{\mathrm{T}}{D}_2{\theta }_2$ are roughness penalties associated with models (3) and (4). These involve unknown regression coefficients θ_j, j=1,2, penalty parameters δ_j and penalty matrices D_j of dimension (q_j + 3) × (q_j + 3). The penalty matrices map the spline basis functions to the data whereas the penalty parameters control the amount of smoothing (Ruppert et al., 2003; Wood, 2006). Given knot locations $\{x_{j\left(i\right)}^{\ast }:1,2,\dots ,q_j\}$, penalty matrices have zeroes everywhere except in its lower right q_j × q_j block with $D_{j\left(ik\right)}={\Vert x_{j(i)}^{\ast }-x_{j(k)}^{\ast }\Vert }^2\log \Vert x_{j(i)}^{\ast }-x_{j(k)}^{\ast }\Vert$, for i, k≤q_j.

Note that the intercept term β₀ in the model (1) is set to 0 in (3), because it is not identifiable in the presence of a nonparametric function G₁(·). Even so, the parameters of these models are not completely identifiable without some additional assumptions outlined in the next section.

2.1 Identifiability

From the above models (3) and (4), it is evident that if B₁(·) ≡ B₂(·), then these models are not identifiable because in this case (3) becomes

$$Y_i=B_2^{\mathrm{T}}\left(S_i\right)\left({\theta }_2{\beta }_1+{\theta }_1\right)+{\mathit{∊}}_i.$$

Thus, we can identify only θ₂ and θ₂β₁ + θ₁, and cannot separate out β₁ and θ₁. To make these models identifiable, we assume that the asymptotic variability, Λ₁ and Λ₂ of two sets of basis functions B₁(.) and B₂(.), respectively, are different. The asymptotic variability Λ_j for j=1, 2, are the limiting values of Λ_nj, where

$${\mathrm{\Lambda }}_{nj}=\{n^{-1}{\displaystyle {\sum }_{i=1}^n{B}_j\left(S_j\right)B_j^{\mathrm{T}}\left(S_j\right)-{\delta }_j{D}_j{\}}^{-1}}.$$ (7)

In practice, this requirement can be easily achieved by ensuring that the numbers of knots q₁ and q₂ are unequal.

2.2 Parameter estimation

In addition to the assumption that Λ₁ ≠ Λ₂, we also assume that the penalty parameters are small relative to the sample size, i.e., n^1/2δ_j → 0 for j = 1, 2. This means that with large sample sizes, the estimated regression coefficients obtained using penalized least squares will be close to the OLS estimates. Thus minimizing the penalized sum of squares (6) and solving for θ₂, we have

$$\widehat{{\theta }_2}={\mathrm{\Lambda }}_{n2}{n}^{-1}{\displaystyle {\sum }_{i=1}^n{B}_2\left(S_i\right)W_i},$$ (8)

where Λ_n2 is defined in equation (7). A detailed derivation of $\widehat{{\theta }_2}$ along with it’s asymptotic distribution is given in Web Appendix A.1. Similarly, we can estimate θ₁ and β₁ by minimizing the corresponding penalized sum of squares (5). This yields (see the Web Appendix A.2 & A.3)

$$\widehat{{\theta }_1}=V_n-R_n\widehat{{\theta }_2}\widehat{{\beta }_1}$$ (9)

$$\widehat{{\beta }_1}=\frac{n^{-1}{\displaystyle {\sum }_{i=1}^n{Y}_i\{B_2^{\mathrm{T}}\left(S_i\right)-B_1^{\mathrm{T}}\left(S_i\right)}{R}_n\}\widehat{{\theta }_2}}{{\widehat{\theta }}_2^{\mathrm{T}}({\mathcal{T}}_n-R_n^{\mathrm{T}}{\mathrm{\Lambda }}_{n1}^{-1}{R}_n)\widehat{{\theta }_2}},$$ (10)

where

$$\begin{array}{l}{V}_n={\mathrm{\Lambda }}_{n1}{n}^{-1}{\displaystyle {\sum }_{i=1}^n{B}_1\left(S_i\right)Y_i};\\ R_n={\mathrm{\Lambda }}_{n1}{n}^{-1}{\displaystyle {\sum }_{i=1}^n{B}_1\left(S_i\right)Y_i{B}_2^{\mathrm{T}}\left(S_i\right)};\\ {\mathcal{T}}_n=n^{-1}{\displaystyle {\sum }_{i=1}^n{B}_2\left(S_i\right)B_2^{\mathrm{T}}\left(S_i\right)}.\end{array}$$

Although the above estimator of β₁ was estimated using pseudolikelihood, it is consistent for β₁. In the next section we will establish the asymptotic properties of the estimator.

2.3 Asymptotic Theory

Asymptotic theory for the estimators $\widehat{{\beta }_1}$ is based on treating the spatial locations S_i ∈ ℝ² as fixed constants. Following Yu and Ruppert (2002), if δ_j → 0 as n → ∞, then the bias also tends to 0 and consistency can be established. Asymptotic normality is established by the following theorem, whose proof appears in Web Appendix A.4.

THEOREM 1

Assume that the smoothing parameters are small relative to the sample size, i.e., n^1/2δ_j → 0, and the spatial correlation G₁(.) and unknown covariate X are correctly represented by a finite number of splines basis functions. Then the estimate of β₁ is consistent and asymptotically normally distributed with

$$n^{1/2}\left(\widehat{\beta 1}-\beta 1\right)\stackrel{d}{\to }N\left(0,{\sigma }^2\right),$$ (11)

where

$$\begin{array}{l}{\sigma }^2={\lim }_{n\to \infty }{n}^{-1}{\displaystyle {\sum }_{i=1}^n({\sigma }_{\mathit{∊}}^2{\mathcal{G}}_{ni}^2+{\sigma }_u^2{\mathcal{H}}_{ni}^2);}\\ {\mathcal{G}}_{ni}={\mathcal{D}}_{ni}{\left({\theta }_2^{\mathrm{T}}{\mathcal{C}}_n{\theta }_2\right)}^{-1};\\ {\mathcal{H}}_{ni}={\mathcal{A}}_n{\mathrm{\Lambda }}_{n2}{B}_2\left(S_i\right){\left({\theta }_2^{\mathrm{T}}{\mathcal{C}}_n{\theta }_2\right)}^{-1}-{\mathcal{A}}_n{\theta }_2{\mathcal{F}}_{ni}{\left({\theta }_2^{\mathrm{T}}{\mathcal{C}}_n{\theta }_2\right)}^{-2};\\ {\mathcal{A}}_n=n^{-1}{\displaystyle {\sum }_{i=1}^n\{G_2\left(S_i\right){\beta }_1+G_1\left(S_i\right)\}\{B_2\left(S_i\right)-R_n^{\mathrm{T}}}{B}_1\left(S_i\right){\}}^{\mathrm{T}}\mathrm{;}\\ {\mathcal{C}}_n={\mathcal{T}}_n-R_n^{\mathrm{T}}{\mathrm{\Lambda }}_{n1}^{-1}{R}_n;\\ {\mathcal{D}}_{ni}={\{B_2\left(S_i\right)-R_n^{\mathrm{T}}{B}_1\left(S_i\right)\}}^{\mathrm{T}}{\theta }_2;\\ {\mathcal{F}}_{ni}={\theta }_2^{\mathrm{T}}{\mathcal{C}}_2{\mathrm{\Lambda }}_{n2}{B}_2\left(S_i\right)+B_2^{\mathrm{T}}\left(S_i\right){\mathrm{\Lambda }}_{n2}{\mathcal{C}}_2{\theta }_2.\\ R_n={\mathrm{\Lambda }}_{n1}{n}^{-1}{\displaystyle {\sum }_{i=1}^n{B}_1\left(S_i\right)B_2^{\mathrm{T}}\left(S_i\right)};\\ {\mathcal{T}}_n=n^{-1}{\displaystyle {\sum }_{i=1}^n{B}_2\left(S_i\right)B_2^{\mathrm{T}}\left(S_i\right)}.\end{array}$$ (12)

Using this asymptotic expression we can also estimate the standard error of the estimated regression coefficient $\widehat{{\beta }_1}$ The next section will discuss two such options.

2.4 Estimating the standard error of $\widehat{{\beta }_1}$

We first consider a model based estimate of the standard error of $\widehat{{\beta }_1}$ using the asymptotic theorem discussed in the previous section and then suggest a more robust estimate of standard error using simulation.

2.4.1 Model based standard error

The model based standard errors of the estimated $\widehat{{\beta }_1}$ can be estimated by substituting corresponding consistent estimates of ${\sigma }_{\epsilon }^2$ and ${\sigma }_u^2$ (defined below) into expression (12). Specifically,

$$\begin{array}{l}{\widehat{\sigma }}_{\mathit{∊}}^2=\frac{{\displaystyle {\sum }_{i=1}^n{\{Y_i-B_2\left(S_i\right)\widehat{{\theta }_2}\widehat{{\beta }_2}-B_1\left(S_i\right)\widehat{{\theta }_1}\}}^2}}{n-2\text{trace}\left\{L_1\left({\delta }_1,{\delta }_2\right)\right\}+\text{trace}\left\{L_1\left({\delta }_1,{\delta }_2\right)L_1^{\mathrm{T}}\left({\delta }_1,{\delta }_2\right)\right\}}\\ {\widehat{\sigma }}_{\mathit{∊}}^2=\frac{{\displaystyle {\sum }_{i=1}^n{\{W_i-B_2\left(S_i\right)\widehat{{\theta }_2}\widehat{{\beta }_1}\}}^2}}{n-2\text{trace}\left\{L_2\left({\delta }_2\right)\right\}+\text{trace}\left\{L_2\left({\delta }_2\right)L_1^{\mathrm{T}}\left({\delta }_2\right)\right\}},\end{array}$$

where the denominators are the residual degrees of freedom associated with model (3) and model (4) with smoother matrices L₁(δ₁, δ₂) and L₂(δ₂), respectively (Ruppert et al., 2003). Define B_j = {B_j(S₁), …, B_j(S_n)}^T for j=1,2 and D_n = {D_n1, …, D_nn)}^T. Then the smoother matrices have the following expressions (see Web Appendix A.5)

$$L_1({\delta }_1,{\delta }_2)=n^{-1}\left\{{\mathit{D}}_n{\mathit{D}}_n^{\mathrm{T}}{({\widehat{\theta }}_2^{\mathrm{T}}{C}_n{\widehat{\theta }}_2)}^{-1}+{\mathit{B}}_1{\mathrm{\Lambda }}_{n1}{\mathit{B}}_1^{\mathrm{T}}\right\}$$ (13)

$$L_2({\delta }_2)=n^{-1}{\mathit{B}}_2{\mathrm{\Lambda }}_{n2}{\mathit{B}}_2^{\mathrm{T}}.$$ (14)

2.4.2 Simulated Standard error

From (10), the expression for ${\widehat{\beta }}_1$ can be written as (see the Web Appendix A.4)

$${\widehat{\beta }}_1=\frac{{\mathcal{A}}_n{\theta }_2+n^{-1}{\displaystyle {\sum }_{i=1}^n\{{\mathcal{A}}_n{\mathrm{\Lambda }}_{n2}{B}_2(S_i)U_i+{\mathcal{D}}_{ni}{\epsilon }_i\}}}{{\theta }_2^{\mathrm{T}}{\mathcal{C}}_n{\theta }_2+n^{-1}{\displaystyle {\sum }_{i=1}^n{\mathcal{F}}_{ni}{U}_i}}+o_p(n^{-1/2}),$$

where ε_i and U_i are the random errors defined in models (1) and (2). Since these quantities are not directly observed, we can estimate the variance of ${\widehat{\beta }}_1$ by a residual bootstrap (Carroll et al., 2006).

Let M be a fairly large number, say 100, and for b = 1, …, M, generate independent random samples ${\mathit{∊}}_{bi}~\text{Normal}(0,{\widehat{\sigma }}_{\mathit{∊}}^2)$ and $U_{bi}~\text{Normal}(0,{\widehat{\sigma }}_u^2)$ for i = 1, 2,…n. Define the b’th bootstrap estimates of β₁ as

$$\widehat{{\beta }_1^b}=\frac{{\widehat{\mathcal{A}}}_n\widehat{{\theta }_2}+n^{-1}{\displaystyle {\sum }_{i=1}^n\{{\widehat{\mathcal{A}}}_n{\mathrm{\Lambda }}_{n2}{B}_2(S_i)U_{bi}+{\widehat{\mathcal{D}}}_{ni}{\mathit{∊}}_{bi}\}}}{{\widehat{\theta }}_2^{\mathrm{T}}\widehat{{\mathcal{C}}_2}\widehat{{\theta }_2}+n^{-1}{\displaystyle {\sum }_{i=1}^n{\widehat{\mathcal{F}}}_{ni}{U}_{bi}}},$$

where ${\widehat{\mathcal{A}}}_n$, ${\widehat{\mathcal{D}}}_n$, ${\widehat{\mathcal{C}}}_n$ and ${\widehat{\mathcal{F}}}_{ni}$ can be estimated by substituting the appropriate quantities into expression (12). These estimated quantities preserve the underlying spatial structure. Therefore, the sample variance of ${\widehat{\beta }}_1^1,\dots ,{\widehat{\beta }}_1^M$ is a consistent estimate of the variance of ${\widehat{\beta }}_1$ (Efron and Tibshirani, 1993).

2.5 Smoothing parameter selection

Our main objective is to obtain a consistent estimate of the regression parameter β₁ such that it accounts for the measurement error in the covariate. However, selecting a suitable combination of the smoothing parameters (δ₁, δ₂) is a prerequisite to a good model fit. All discussion so far has assumed that these parameters are fixed and known.

To choose smoothing parameters that attempt to minimize the mean square error (prediction error), three common approaches have been discussed in the literature (Ruppert et al., 2003) (a) Generalized Cross Validation (GCV); (b) Mallow’s C_p; and (c) Akaike Information Criterion (AIC). Among these methods, minimization of GCV scores is more attractive because of being invariant and computationally efficient (Wood, 2006). We use the GCV criterion to estimate the smoothing parameters (δ₁, δ₂) in a two-step procedure (Wood, 2006). We first obtain an optimum value of δ₂ by minimizing the GCV score based on model (2) and then substitute this estimated value of δ₂ into (8) to obtain an estimate of θ₂. We then use these estimates of $\widehat{{\delta }_2}$ and $\widehat{{\theta }_2}$ in (13) to obtain an expression for the smoothing matrix, $L_1({\delta }_1,\widehat{{\delta }_2})$. Finally, we minimize the following GCV score associated with the outcome model to get an optimum value of δ₁:

$$\mathit{GCV}({\delta }_1)=\frac{n^{-1}{\displaystyle {\sum }_{i=1}^n{\{Y_i-\widehat{Y_i}\}}^2}}{{\{1-n^{-1}\text{trace}\{L_1({\delta }_1,\widehat{{\delta }_2})\left\}\right\}}^2},$$

where L₁ is defined in section 2.4.

3. Simulation study

In this section we discuss a simulation study designed to evaluate the finite sample properties of our proposed method in the presence of covariate measurement error in spatial linear regression.

3.1 Data generation

We simulate n sample locations randomly within a square, where n is the sample size. Specifically, the i^th random sample location S_i is generated by simulating two coordinates (e.g., latitude and longitude) from a Uniform[0,1] distribution. Given a set of simulated S_i’s, the unobserved true covariate X is generated using a bivariate bump function. Specifically, the bivariate bump function is generated using the product of two univariate bump functions generated separately for each co-ordinate. That is, for each coordinate, k, we generate $X_{ik}=\frac{1}{1+a_{ik}}+3e^{-50{(a_{ik}-0.3)}^2}+2e^{-25{(a_{ik}-0.7)}^2},$ k = 1, 2, where a_i1 and a_i2 are the first and second coordinates of simulated i^th sample location, respectively. The observed error contaminated versions, W, of the true covariate is generated by adding independent Gaussian noise with varying the measurement error variance ${\sigma }_U^2$ as 0, 0.25 and 0.50 to X. The contour plot associated with the true and error prone covariate is given in Figure 1.

Figure 1.

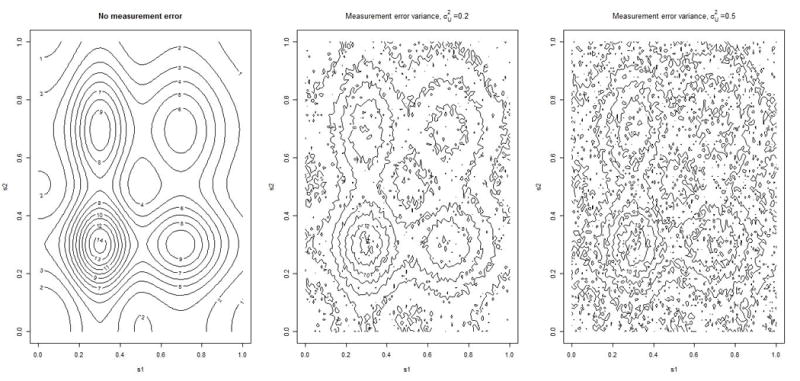
Contour plots of covariates (X and W) with different specification of measurement error variance

As shown in the Figure 1, presence of measurement error adds noises to the true distribution of the smooth covariate. As a result the underlying true covariate distribution becomes obscured for higher degrees of measurement error.

The smooth spatial surface, G₁(S_i), is generated to have a normal distribution with mean 0 and variance-covariance matrix ${\sigma }_{G_1}^2\mathit{R}$, where ${\sigma }_{G_1}^2=0.2$ and R has an exponential correlation structure with range parameter ${\tau }_{G_1}$ (Pinheiro and Bates, 2000). This implies that the correlation between two observations with distance h units apart is $\mathit{exp}\left(-h/{\tau }_{G_1}\right).$ We considered three different range parameters ( ${\tau }_{G_1}$= 0.1, 0.3 and 0.5) resulting in minimal, moderate and high correlation among the values of G₁’s.

Outcome data, Y, were then generated according to equation (1), with intercept and slope parameters are (β₀, β₁)^T = (1, 2)^T and the variance parameter for the independent residual error assumed to be 0.5. We used the nlme package (Pinheiro et al., 2013) in R to generate exponential spatial correlation for our simulated data and in model fitting. The R code for the simulation and implementation of the proposed method is available with this paper at the Biometrics website on Wiley Online Library.

3.2 Generating bi-variate splines basis functions

We now describe the steps used to fit our proposed semi-parametric model. We generated two sets of basis functions B₁(·) and B₂(·) using bivariate thin plate spline regression basis with 125 and 150 knots for response and covariate model, respectively. We choose thin plate splines because they are not sensitive to knot locations, perform reasonably well for a basis of any given lower rank, are computationally efficient and more importantly rotationally invariant (Wood, 2006; Ruppert et al., 2003). Unequal number of knots were chosen for B₁(·) and B₂(·) to make the model identifiable, (see Section 2.1). The number of knots for the response model (1) were analogous to the default number of knots [max{20,min(n/4,150)}] suggested by Ruppert et al. (2003). For the covariate model (2) we increased the default number of knots by 20%. Knot positions were automatically selected using the cluster separation method “clara” (Kaufman and Rousseeuw, 2005) in R (R Core Team, 2013).

Of course one could select the number of knots by another algorithm such as space filling algorithm (Nychka and Saltzman, 1998). However, implementation of this algorithm is computationally intensive. Nychka and Saltzman (1998, page-169) argued that the number of knots is flexible in the context of geo-spatial model and one needs to select large enough knots to accurately represent the underlying function while keeping the computational burden as low as possible. Furthermore, Ruppert (2002) suggest that given the GCV criteria, the number of knots is not crucial for penalized regression splines once it reaches a certain minimum value.

3.3 Simulation Results

The average of estimated regression coefficients along with their estimated standard errors based on 1000 simulation runs are presented in Table 1, assuming a sample size of 500 and varying the measurement error variance ${\sigma }_U^2$ between 0, 0.25 and 0.50. We estimated three different standard errors of the estimated regression coefficients, including, (i) empirical standard errors obtained by taking the standard deviation of the 1000 simulated regression coefficient estimates, (ii) the average of model based standard errors and (iii) the average of simulated standard errors defined in section (2.4). We considered three different range parameters ( ${\tau }_{G_1}$=0.1,0.3 and 0.5) to represent minimal, moderate and high level of spatial correlation in G₁(S_i). The first column of Table 1 specifies the range parameter used in that particular simulation. The next four columns list the estimated regression coefficient using ordinary least squares (OLS), linear mixed models with spatial correlation structure (LME), generalized additive models (GAM) and our proposed method when the true covariate is measured without error. The second and thirds sets of four columns also list estimates obtained using the above four methods (OLS, LME, GAM and proposed method) with measurement error variances 0.25 and 0.50, respectively. Except for our proposed method, all of these methods produce naive estimates of regression coefficient.

Table 1.

Simulation results using different combinations of range parameters and measurement error variance. Reported numbers are averaged over 1000 simulations with 500 observations per simulation.

Range* ( ${\tau }_{G_1}$)	No measurement error				Measurement error variance, ${\sigma }_u^2=0.25$				Measurement error variance, ${\sigma }_u^2=0.5$
	OLS	LME	GAM	Proposed	OLS	LME	GAM	Proposed	OLS	LME	GAM	Proposed
Estimated coefficient
0.1	2.001	2.001	2.002	1.991	1.928	1.439	1.332	2.066	1.858	1.274	0.986	2.034
0.3	1.999	1.999	1.999	1.988	1.927	1.574	1.327	2.096	1.858	1.343	0.987	2.036
0.5	2.001	2.001	2.001	1.991	1.926	1.599	1.312	2.064	1.857	1.389	0.999	2.035
Empirical standard error
0.1	0.029	0.028	0.040	0.029	0.032	0.609	0.216	0.056	0.035	0.751	0.216	0.069
0.3	0.035	0.030	0.030	0.032	0.036	0.554	0.211	0.045	0.038	0.730	0.219	0.058
0.5	0.031	0.027	0.026	0.029	0.035	0.543	0.223	0.051	0.039	0.712	0.210	0.052
Average of estimated standard errors
0.1	0.014	0.021	0.030	0.015	0.022	0.040	0.058	0.051	0.027	0.037	0.057	0.053
0.3	0.014	0.020	0.026	0.014	0.022	0.035	0.057	0.041	0.027	0.035	0.056	0.052
0.5	0.014	0.018	0.023	0.014	0.022	0.034	0.057	0.049	0.026	0.034	0.056	0.051
Average of simulated standard errors
0.1	—	—	—	0.015	—	—	—	0.050	—	—	—	0.068
0.3	—	—	—	0.014	—	—	—	0.041	—	—	—	0.052
0.5	—	—	—	0.014	—	—	—	0.049	—	—	—	0.051

${\tau }_{G_1}$: values of the range parameter following exponential correlation in G₁(s_i).

In the absence of measurement error, OLS, LME, GAM and our method all give similar answers. As the degree of measurement error increases, OLS, LME and GAM all exhibit bias, though the degree of bias varies. All naive standard error estimates ignoring covariate measurement error severely underestimate the empirical standard errors. In contrast, our proposed bias correction method performs well even if the degree of bias for generalized additive model with error prone covariate varies (range: 0.99–1.32) with the strength of the spatial correlation structure. Both model based and simulation based estimates of the standard error appear to be working well. In all cases, the average of the estimated measurement error variances are very similar to the true values (not shown in the table).

To evaluate the performance of the proposed method under small sample settings, we also conducted simulations with sample sizes of 250 and 100 assuming a measurement error variance ${\sigma }_U^2$ of 0.5. The results are given in Table 2.

Table 2.

Simulation results using different combinations of range parameters and sample sizes. Reported numbers are averaged over 1000 simulations with measurement error variance 0.5.

Range* ( ${\tau }_{G_1}$)	Sample size 250				Sample Size 100
	OLS	LME	GAM	Proposed	OLS	LME	GAM	Proposed
Estimated coefficient
0.1	1.860	1.511	0.976	1.952	1.859	1.831	1.037	1.947
0.3	1.861	1.495	0.975	1.951	1.859	1.824	1.045	1.948
0.5	1.860	1.522	0.980	1.950	1.860	1.831	1.036	1.949
Empirical standard error
0.1	0.045	0.536	0.217	0.046	0.066	0.088	0.344	0.069
0.3	0.047	0.541	0.207	0.048	0.067	0.099	0.349	0.072
0.5	0.046	0.530	0.209	0.046	0.066	0.095	0.342	0.068
Average of estimated standard errors
0.1	0.038	0.051	0.083	0.046	0.061	0.064	0.132	0.099
0.3	0.038	0.051	0.081	0.045	0.060	0.064	0.130	0.099
0.5	0.037	0.050	0.081	0.045	0.060	0.063	0.130	0.098
Average of simulated standard errors
0.1	—	—	—	0.046	—	—	—	0.101
0.3	—	—	—	0.046	—	—	—	0.101
0.5	—	—	—	0.045	—	—	—	0.099

${\tau }_{G_1}$: values of the range parameter following exponential correlation in G₁(s_i).

With the size of 250 samples our proposed method still provides reliable estimates of the true regression coefficient. However, with small sample sizes (say, n=100) the variance of estimated regression coefficients tends to be slightly inflated. To explore the impact of number of knots on our proposed method we conducted additional simulation study by varying the number of knots for covariate model as 130, 140 and 170 with measurement error 0.025, sample size of 500 and varying range parameters, where the number of knots for the residual error model was fixed as 125. The results are presented in the Web Table 1 in the supplementary materials available at the Biometrics website on Wiley Online Library. These results indicate that the proposed methods is robust for the selection of number of knots for covariates models.

4. Application

4.1 Analysis of Ischemic Heart Disease Data

We applied our proposed methodology to re-analyse data on Ischemic Heart Disease (IHD). One of the key objectives of the analysis is to assess the relationship between IHD rates and area level measures of socio-economic status. These data were collected from all hospitals in New South Wales, Australia between July 1, 1994 to June 30, 2002. A detailed description of the data has been given elsewhere (Burden et al., 2005). Briefly, patients who were admitted to the hospitals via the emergency room and discharged with IHD were defined as acute IHD cases. Data also includes patient age, gender and geographic location reported via postcode of residence. Data from 579 postcodes were included in the analysis. IHD event data were linked with the Census data which contains age and gender-specific population counts. SEIFA (Socio-Economic Indexes For Areas) scores and centroid co-ordinates (latitude and longitude) for each postcode were obtained from Australian Bureau of Statistics. We calculated age-sex adjusted standardized incidence ratios (SIR) by dividing the observed number of IHD cases by the age-sex adjusted expected number of IHD cases (Breslow and Day, 1987).

The results of our analysis are given in Table 3.

Table 3.

Analysis of Ischemic Heart Disease Data in NSW, Australia under different specification of measurement error

Methods	Estimates for SEIFA
	$\widehat{\beta }$	model based $\mathrm{se}(\widehat{\beta })$	Simulated $\mathrm{se}(\widehat{\beta })$
Ordinary Least Squares	−0.062	0.014	—
Generalized additive model	−0.145	0.014	—
Proposed semiparametric approach	−0.273	0.045	0.045
Huque et al. (2014) approach
Method I: Method of Moments	−0.377	0.041	—
Method II: Transformation of covariate	−0.278	0.015	—

The naive analysis ignoring spatial correlation, suggests a significant protective effect associated with higher SEIFA values ( ${\widehat{\beta }}_{\mathit{SEIFA}}=-0.062$, SE=0.014). Our proposed semi-parametric approach that account for measurement error in the covariates result in an estimated slope parameter β₁ of −0.273 with measurement error variance estimated as 0.52. We choose 145 knots to represent the spatial correlation in the outcome model and 180 knots to represent the covariate model. The model and simulation based standard errors were estimated as 0.045 and 0.045, respectively. Thus, accounting for the measurement error in the covariate reflects a high magnitude of protective effect of higher SEIFA scores on IHD rates, compared with naive analysis.

5. Discussion

In this paper, we develop a semi-parametric framework to obtain a consistent estimate of the true regression coefficients when covariates are measured with error in spatial regression modelling settings. Asymptotic theory establishes that our approach provides consistent, asymptotically normal estimates for the regression coefficient. The theory yields both model based and simulation based standard error estimates. Our empirical simulation results confirm that ignoring measurement error and conducting naive analysis using both generalized additive model and linear mixed model attenuates the estimated regression coefficient towards the null hypothesis of no effect. Our results also confirm the results of Huque et al. (2014) that the degree of measurement error bias depends on the assumed correlation structure. It is interesting that the bias appears to be least with OLS. This is likely because the covariate spatial structure and residual spatial structure compete to explain the variability in the response (Waller and Gotway, 2004). Our proposed semiparameteric bias correction method performs very well and provides comparable estimates of the regression parameters to the parametric methods described by Huque et al. (2014) when applied to Ischemic Heart Disease (IHD) data. Our approach is computationally efficient and stable because it involves direct estimation using least squares and can be implemented using standard nonlinear least squares software.

Although Huque et al. (2014) and Li et al. (2009) reported similar results for the bias associated with covariate measurement error in spatial regression settings, their approaches requires correct specification of the true covariate measurement error variance. In addition, Huque et al. (2014) reported under estimation of standard error when measurement error variances are estimated from the data. In contrast, our approach is robust because it neither assumes that the covariate measurement error is known nor depends on any particular kind of spatial correlation structure. Our method is analogous to the popular regression calibration method where we estimate the true underlying covariate following smoothing assumption and replace the error prone covariate with this estimate in the outcome model.

Measurement error theory makes it very clear that without some kind of information regarding the magnitude of measurement error, models will not be identifiable. Broadly speaking there are two possibilities: (i) measurement error varianace is known or can be estimated using some form of validation data (ii) assumptions are made regarding the nature of the measurement error process. By assuming that the true unobserved covariate is smooth, our paper is using the second approach. Because our approach is assumption based and not an empirical measurement error adjustment, our solution will not be robust to this particular assumption. Nevertheless, because we use a semi-parametric approach to quantifying the spatial correlation in our regression model, our approach should be more robust than parametric alternatives, such as those proposed by Huque et al. (2014). In practice, there will often be situations where it makes sense that spatially-defined covariates are smooth. Air pollution epidemiology might be a good example. In general, however, we recommend that our proposed method be used in the spirit of sensitivity analysis to assess the impact of measurement error.

One of the additional assumptions required by our approach is that the basis functions for the covariate and the spatial residual term are unequal. In practice, this can be achieved through ensuring more knots for the basis function representing covariate than the spatial residuals. This ensures estimation of variability in covariate in a smaller scale than the residual error. In many spatial epidemiology contexts, measurement error becomes an increasing concern at small scales because of limitations in measurement resources. As a result, the covariate measurement bias reduction relies in estimating variability in covariate at scale smaller than the residual error (Paciorek, 2010).

In our simulation, we have considered only a single covariate measured with error in a spatial linear mixed model with Gaussian error. It would be of interest to explore the effect of covariate measurement error in the presence of multiple covariates and also omitted covariates. Future work should also consider extensions of our formulation to the setting of spatial generalized linear mixed model with non-Gaussian outcomes. However, such explorations are beyond the scope of this present paper.

Our heart disease example demonstrated a substantial increase in the rates of IHD as the level of SEIFA measured at the postcode level decreased, with the magnitude of the effect increasing after adjustment for measurement error. Our results are consistent with broader literature suggesting a relationship between low socio-economic status and adverse health outcomes (see systematic review by Pickett and Pearl 2001).

Because the SEIFA Index is measured at a group level, it is tempting to think that Berkson measurement error theory should be in operation. However, this argument doesn’t apply since we are considering measurement error in a group level covariate applied at a group level analysis. It is also important to note that our results can only be interpreted at a group level. Interpretation at the individual level may result in ecological bias (Sheppard, 2003). While it might be ideal to use individual level data, in many research areas, group-level data are the only available source for analysis. Air pollution epidemiology provides a classic example, because individual measurements of air pollution studies are rarely collected, instead, they are estimated based on neighbourhood monitoring and other sources (Sheppard et al., 2012). Consequently, air pollution exposures are typically measured with error.

In spatial data settings, for example, in environmental epidemiology, with the increasing popularity of the semi parametric/multilevel models to account for the observed data correlations, it is important that practitioners be aware of the consequences of measurement error. Furthermore, it is useful to quantify its potential effect on the estimating exposure-outcome relationship. The approach presented in this paper provides one way of achieving this.