Abstract
Ribosomes—the primary macromolecular machines responsible for translating the genetic code into proteins—are complexes of precisely folded RNA and proteins. The ways in which their production and assembly are managed by the living cell is of deep biological importance. Here we extend a recent spatially resolved whole-cell model of ribosome biogenesis in a fixed volume1 to include the effects of growth, DNA replication, and cell division. All biological processes are described in terms of reaction-diffusion master equations and solved stochastically using the Lattice Microbes simulation software. In order to determine the replication parameters, we construct and analyze a series of Escherichia coli strains with fluorescently labeled genes distributed evenly throughout their chromosomes. By measuring these cells’ lengths and number of gene copies at the single-cell level, we could fit a statistical model of the initiation and duration of chromosome replication. We found that for our slow-growing (120 minute doubling time) E. coli cells, replication was initiated 42 minutes into the cell cycle and completed after an additional 42 minutes. While simulations of the biogenesis model produce the correct ribosome and mRNA counts over the cell cycle, the kinetic parameters for transcription and degradation are lower than anticipated from a recent analytical time dependent model of in vivo mRNA production. Describing expression in terms of a simple chemical master equation, we show that the discrepancies are due to the lack of non-ribosomal genes in the extended biogenesis model which effects the competition of mRNA for ribosome binding, and suggest corrections to parameters to be used in the whole-cell model when modeling expression of the entire transcriptome.
1 Introduction
In Escherichia coli, ribosomes account for approximately one fourth of the cellular dry mass and the majority of the total RNA2. It can be tempting, then, to think of the bacterial cell as a finely tuned machine for building ribosomes. Their ubiquity and high sequence conservation has made them an invaluable window into the process of evolution at the molecular level3–6, and their role in protein synthesis involves them (either directly or indirectly) in essentially every process within the cell.
Ribosome production has evolved to be tightly regulated by the cell. This is no small feat, considering that each 70S ribosome involves the coordinated transcription, translation, folding, and hierarchical assembly of three strands of rRNA and over four dozen proteins, all within the heterogeneous, crowded intracellular space. Starting as early as 1966, pioneering in vitro studies began to unravel some of the mechanistic details of this process7. Work on the 30S small subunit (SSU), which is largely responsible for recognizing and decoding mRNA, showed that assembly nucleates with the folding of the so called five-way junction in the 16S rRNA of the SSU (residues 27–45 and 394–554 in E. coli), and then proceeds through the hierarchical association of sets of ribosomal proteins, each progressively folding and stabilizing the rRNA's growing tertiary structure8–13. Interestingly, a number of in vitro studies have observed this process proceeding over timescales on the order of the cell cycle or longer8–10, while in vivo it can take just a few minutes14. Moreover, single cell-imaging studies on both slow- and fast-growing cells have also shown that complete ribosomes are not uniformly dispersed throughout the cytoplasm, but rather they tend to aggregate to the cell poles15–19. Understanding these phenomena requires a model with both a complete (or nearly-complete) kinetic description of the assembly process and fine spatial resolution.
Recently, Earnest et al.1 reported the first spatially resolved stochastic simulations of ribosome biogenesis for slow-growing E. coli. In that work, a model involving 251 different species (including the SSU, LSU, rRNA, 18 proteins that bind to it, the genes and mRNA that code for them, and over 140 possible intermediates in the SSU assembly) and approximately 1300 reactions for transcription, translation, and ribosome assembly were developed and parameterized along with diffusion constants for all species. The use of a stochastic simulation methodology was important for a number of reasons. First and foremost, gene expression has been shown to be highly variable from cell-to-cell; this is especially pronounced when the molecules involved are in low copy numbers20–22. Ribosomal RNA is transcribed from seven operons interspersed throughout the E. coli genome, and many of the intermediate structures along the assembly pathways can exist in very few copies due to the rapid binding of additional proteins1. Accurately modeling the random diffusive motions and reactions of the individual substrates allowed Earnest et al. not only to investigate the mean behavior of the assembly network, but also the inherent variability in it.
Although unprecedentedly complete, the model did not account for some of the most basic functions of the cell—namely, replication of the genome, cell division, and metabolism. Using mRNA distributions obtained from super-resolution imaging experiments, recent articles by Peterson et al. and Jones et al. showed that mRNA copy numbers exhibit a significant amount of variability simply by virtue of the fact that the genes that encode them are duplicated at some point during the cell cycle (which, in turn, depends on the genes’ positions on the chromosome)23,24. To quantitatively describe the replicative dynamics of the chromosome, we have generated a series of E. coli strains with gene loci labeled by a fluorescent repressor-operator system (FROS) distributed evenly around the chromosome. High-throughput imaging of these strains and identification and quantification of the gene copy number in each cell allows us to fit simple models of cell growth and genome replication to extract estimates for the timing of replication of each gene as a function of its position on the chromosome. We use these results to extend the ribosome biogenesis model to explicitly include cell growth, gene duplication, and division (henceforth referred to as the RBM, for ribosome biogenesis model). Although single-cell rRNA and ribosomal protein mRNA distributions are not available for direct comparison, a number of theoretical models of mRNA statistics—including some that account for gene duplication—have been proposed23,24, although, importantly, they do not explicitly account for mRNA–ribosome interactions. The transcription and mRNA degradation rates in the RBM differ from those generated by the theoretical model in fitting the simulated mRNA distributions. We ultimately attribute this discrepancy to the fact that the RBM does not account for competition from non-ribosomal gene expression (e.g. genes involved in metabolism, regulation, etc.) We derive a simple statistical model that accounts for messenger production, degradation, and interactions with the ribosomes (henceforth referred to as the SAM, for semi-analytical model) which we use to investigate the dependence of mRNA statistics on chromosome duplication as well as the expression of non-ribosomal genes within the cell.
2 Results and Discussion
2.1 Determining replication initiation timing and progression
To track the progress of replication in living cells, we constructed strains of E. coli where an array of 240 specific operators for tet repressor (TetR) was inserted chromosomally. The position of the tetO array was varied to evenly sample loci over the full genome (Figure 1b) at 14 positions. Expression of TetR-EYFP in trans from the plasmid pBH74 allows for the direct visualization of genomic loci and observation of operon counts to be gathered from populations of cells. These statistics can be combined with a model of cell replication to determine initiation time, replication time and quiescent phase time.
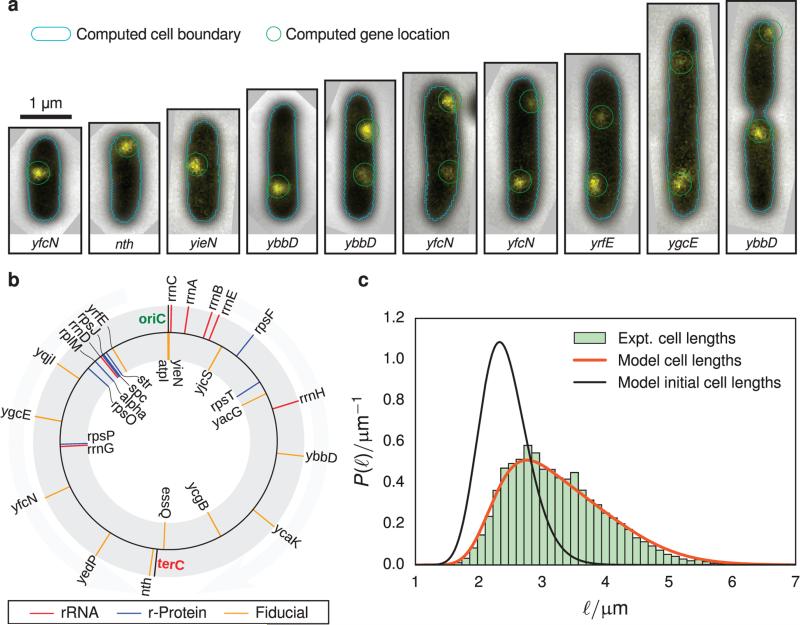
FIGURE 1.
(a) Composite phase-contrast and epifluorescence images of representative imaging data used to determine cell length and operon positioning. The cell boundaries (cyan) and operon locations (green) are determined computationally. Examples of rejected cells are presented in Figure S1 of the Supporting Information. (b) Diagram showing the position of labeled genes used to track DNA replication (fiducial, orange) and those involved in ribosome biogenesis (rRNA, red; ribosomal protein, blue). The black lines indicate the origin of replication (oriC) and the replication terminus (terC) (c) Abundance of cell lengths (green histogram) from imaging experiments are fitted to a simple exponential growth model (orange line, Equation 6) to estimate the average and variance of cell lengths after division (black line). Approximately 7600 cells are included in this histogram.
The strains were grown to exponential steady-state, doubling every 120 min. Approximately 1000 epifluorescence and phase-contrast images were taken of each of the 14 strains. The data processing procedure was automated such that the detection of cells in a frame, the measurement of length and width of each cell, and the counting of fluorescent peaks were all handled without human intervention (Figure 1a). This yielded ~7600 total cells with an average length of 3.2 μm and width of 0.7 μm.
To extract the cell cycle parameters from these data, we have developed a probabilistic model linking cell growth with DNA replication. We assume the following about the nature of cell growth and DNA replication. Cell volume is proportional to length since the width of cells do not vary significantly over their cell cycle25. Individual cells show variability in widths, however not more than 10% (see Figure S3 for the distribution of cell widths in the Supporting Information.) Cell lengths immediately prior to cell division, ℓ0, are distributed log-normally
| (1) |
with location parameter μlen0 and shape parameter σlen0. We base this assumption on experimental histograms of cell division lengths showing positive skewness25 and recent theoretical analysis showing that under the influence of Gaussian random noise in the cell division time, the cell division length distribution is log-normal.26. Since we are modeling E. coli with a mass doubling time of 120 min, we assume that only one round of replication occurs per cell cycle. We assume the duration of DNA replication, Trep, (i.e. the C period, Figure 2) is constant. Experimental measurements of the distribution of replication initiation times (i.e. duration of B period) over single cells is limited in the literature, however one study reports a broad distribution that could be approximated by a truncated normal distribution27. For the sake of simplicity and to allow for some variability we have assumed the DNA replication initiation times, trep, are distributed via a normal distribution truncated at zero:
| (2) |
where the normalization is
| (3) |
We assume that the cells expand in length exponentially following the growth law
| (4) |
where μtdiv is the mean division time. This assumption is supported by a great body of experimental evidence25,28–32. Finally, we assume that the cell length at birth and the replication initiation times are uncorrelated. There is evidence that the initiation time is correlated with the cell length at birth27, however including this effect would make analysis of the model significantly more difficult. Using an analytical form for the distribution of cell mass, m, of exponentially growing bacteria33,34,
| (5) |
and assuming that m ∝ ℓ, we derived the distribution of cell lengths,
| (6) |
by substituting Equation 1 into Equation 5 and normalizing the distribution over positive lengths.
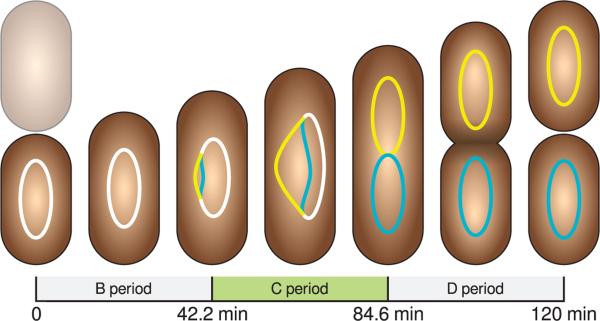
FIGURE 2.
A schematic of the replication time parameters extracted from experimental images in the context of a 120 minute doubling cell.
In order for our model to describe the relationship between the data we measure for each cell—its length, the identity of the labeled gene, and the number of copies of that gene—we must somehow theoretically connect the length of a cell with its gene copy number. To do this we use the cell age, tage—a latent variable of our model. We must first compute the distribution of cell ages conditioned on cell length. By performing a change of variables on Equation 1 using Equation 4, we are left with a normal distribution of cell ages, where the mean age is a function of the cell length,
| (7) |
and the standard deviation of the age is
| (8) |
To prevent negative ages, we truncate the distribution and renormalize:
| (9) |
where the normalization is
| (10) |
The joint–conditional distribution function of cell ages and replication times given length is
| (11) |
We consider a gene i to be copied if the age of the cell, tage, is greater than the DNA replication initiation time, trep, plus the time required to copy up to and including gene i. Written in terms of the relative replication fork position , we have that
| (12) |
when a cell has two copies of gene i. Here dist(x,y) refers to the distance between two genes along its replichore. Using the growth law, the distribution of lengths at cell division, the distribution of all cell lengths, and the replication time distribution, we can derive the probability to find a cell with length, ℓ, whose replication progress is further than ).
To compute the probability that a gene, i, has been replicated, we change variables to in Equation 11 and integrate over all less than χi
| (13) |
where
| (14) |
| (15) |
and
| (16) |
The probability to find a cell with length ℓ and n copies of gene i is then
| (17) |
Thus the likelihood function is
| (18) |
with
| (19) |
and the data for each cell is its length, ℓ, observed from the phase-contrast images, the copy number of the labeled gene, n, observed from the fluorescence data, and the identity of the labeled gene, i. Fitting Equation 18 to the data simultaneously determines the mean cell division length and its variance, the mean DNA replication initiation time and its variance, and the time necessary to replicate the full genome.
The model parameters were determined by maximizing the logarithm of Equation 18 over 7600 observed cells. To ensure that each operon contributed equally to the likelihood, we used the sum of the mean log-likelihood computed for each for each gene. We used a bounded, global optimization scheme, differential evolution35, to maximize the objective function. The lower bounds were set to 10−6 to prevent numerical divergence and the upper bounds were set to 10 μm and 4 for the cell division length location and scale parameters, and 240 min for the replication time parameters. Uncertainties in the parameters were computed via bootstrap, using 15000 resamplings of the data. A summary of the fitting parameters and their uncertainties are provided in Table I.
TABLE I.
Parameters derived from model fitting along with uncertainties computed from bootstrapping
| Symbol | Description | Value from fit (mean ± std) |
|---|---|---|
| μ len0 | Location parameter of cell lengths immediately prior to division | 4.772 ± 0.021 μm |
| σ len0 | Scale parameter of cell lengths immediately prior to division | 0.1560 ± 0.0050 |
| μ trep | Mean replication initiation time | 42.2 ± 3.0 min |
| σ trep | Standard deviation of replication initiation time | 22.1 ± 1.9 min |
| T rep | Replication duration (C period) | 42.4 ± 5.0 min |
| μ tdiv | Mean time between divisions | 120 mina |
| σ tdiv | Standard deviation of time between divisions | 12 minb |
From experiment
Assumed
The cell length distribution is well-described by the model (Figure 1c). The location parameter of the log-normal distribution describing the cell lengths prior to cell division is 4:772 ± 0:021 μm and the shape parameter of the distribution was 0:1560 ± 0:0050. These parameters converted to the arithmetic mean and standard deviation are 4:830 μm and 0:575 μm respectively, implying that new born cells are 2.415 μm long on average. These measurements can be compared to the division length reported for E. coli at a doubling time of 51 min reported by Taheri-Araghi et al.25 of 4:40±0:54 μm. The model predicts a mean replication initiation time of 42:2 ± 3:0 min (duration of B period) with a standard deviation of 22:1 ± 1:9 min, and a replication duration of 42:4±5:0 min. These results are reasonable in light of the experiments of Skarstad et al.36 who measured a B period of 34 min from E. coli B/r A doubling at 113 min and Adiciptaningrum et al.27 measured the B period distribution for E. coli with at 130 min doubling time and reported a broad distribution with a mean of 30 min and a standard deviation of 21 minutes. Michelsen37 reports a B period of 32 min and a C period of 52 min in E. coli K-12 MG1655 doubling at 137 min and shows that the C and D periods increases linearly with generation time when the doubling time is greater than 70 min, however these measurements tend to vary depending on the particular strain and the method of analysis.
Figure 3a shows the agreement of the experimental data to our model; fitting plots for all data are provided in the Supporting Information (Figure S4 and Figure S5). The model tends to underestimate the number of cells with two copies for genes near the origin and overestimates for genes near the terminus. However the peaks and dispersion in the model distributions reflects the experimental data well.
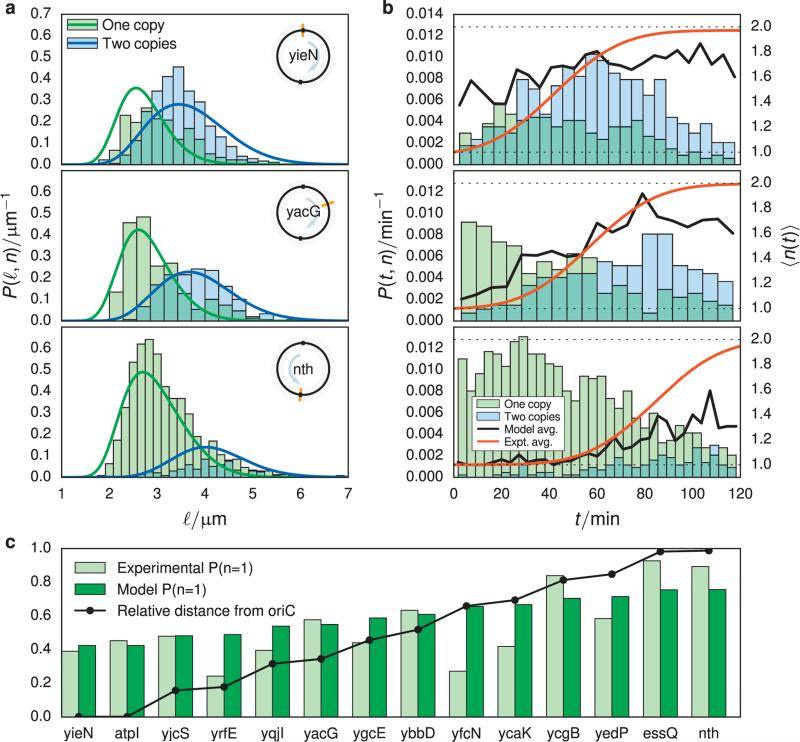
FIGURE 3.
(a) Fraction of cells found with one gene copy (green) and fraction predicted by the model (blue). The distance from the origin of replication to the gene, relative to the distance between oriC and terC along its arm of the chromosome is plotted in black. (b) Abundance of cells with length ℓ and either one (green histogram) or two (blue histogram) gene copies. The probability densities associated with these histograms predicted from the model Equation 17 are plotted as lines. (c) Abundance of cells with age and either one (green histogram) or two (blue histogram) gene copies for the same genes as shown in (a). The cumulative distribution function of gene replication times is plotted with a black line. Plots for all operons are available in the Supporting Information.
We also computed the probability of finding a cell with one copy of a gene. This was accomplished by considering an expression for the distribution of cell ages38,
| (20) |
and assuming that the individual cell division times are distributed normally with a standard deviation of 10% (σtdiv = 12min). The form for the distribution of the cell ages given the cell division time distribution is given where n is the colony growth rate. Assuming that the bulk mass doubling rate, ν, is approximately equal to the mean cell division rate, μtdiv, and evaluating the integral we have
| (21) |
with
| (22) |
The probability to find a cell that has not replicated its labeled gene is
| (23) |
where
| (24) |
follows directly from Equation 2. Rewritten in a form amenable to numerical integration,
| (25) |
with the constants
| (26) |
| (27) |
| (28) |
| (29) |
The probability to find a cell with one copy of each of the 14 genes is shown in Figure 3c, using the previously computed fitting parameters (Table I). Genes yrfE, yfcN, and ycaK show the worst agreement, neither following the model predictions nor the trend of the other experimental data, however the single copy fraction data for the remaining 11 genes follow the expected trend and are well-described by the model parameters.
As a final test of the fitting of our model parameters, our expression for the probability of finding a cell with a single gene copy was used to independently estimate the replication initiation timing, and the replication duration (see Section S2 of the Supporting Information). This somewhat less-sophisticated treatment yielded values of μtrep = 34:4 minutes, and Trep = 45:9 minutes. Importantly, although different in their approaches, both methods estimate similar C and D periods of around 40 minutes each.
It is remarkable that a reasonable measurement of the growth parameters can be made indirectly without monitoring individual cell lineages and labeling the replisome. Cell cycle control in bacteria is highly complex and not completely understood25,26,32,34,39–42. There have been at least three classes of cell growth models described in the literature: size-dependent division (“sizer”)34, time-dependent division (“timer”)41,42, and constant extension (“adder”)32,40 models, as well as more complicated mixed models25,26 have all been proposed. A major result of many of these works is the fact that the size of a cell before and after division is correlated. We are unable to account for this in our model since our experiments do not track individual cell lineages. Thus we use a simple model which ignores the correlations between generations.
2.2 Modeling the effects of DNA replication on ribosome biogenesis
We built upon our previous kinetic model of ribosome biogenesis in E. coli1 to construct the RBM, in order to investigate the effect of both gene duplication and changing volume due to cell growth. This model is simulated using Lattice Microbes43,44, a software package designed to simulate stochastic reaction-diffusion systems through sampling of the underlying reaction-diffusion master equation (RDME). The spatial domain of the problem is discretized onto a lattice, with each lattice site containing discrete particles. Particles diffuse between lattice sites according to diffusion constants that are local to each cellular region and specific for each species. A Gillespie type kinetic Monte Carlo simulation determines which reaction occurs at each lattice site and which particles diffuse to neighboring sites. Since this technique is highly parallelizable; it is implemented in CUDA to take advantage of NVIDIA GPUs, allowing for a complete cell cycle to be simulated in a single day.
The previous ribosome biogenesis model1 has between modified such that new ribosomal protein (r-protein) and rRNA operons (see Figure 1b for their loci) are added to the simulation at times reflecting their position in the genome using the parameters derived in Section 2.1, while dynamically growing the cell volume as the simulation progresses. Psuedocode describing the generation of the reduced assembly model (Algorithm 1), the dynamic construction of cell geometry (Algorithm 3), and the simulation procedure (Algorithm 2) is provided in the Supporting Information. The kinetic model of ribosome biogenesis includes seven ribosomal RNA operons which code for the 16S rRNA and nine operons coding for the 18 ribosomal proteins (r-protein), which along with the 16S rRNA, compose the 30S small subunit of the ribosome. Transcription of these operons is explicit in this model—the particles representing the operons are placed in the cell nucleoid region based on their genomic position and emit messenger RNA species at a constant rate, i.e. unregulated, constitutive expression. Translation of r-protein is explicit as well—the mRNA engage in a diffusive search in order to bind to the SSU. The resulting complex associates with the LSU to form a translating ribosome. R-protein are emitted from the translating ribosome in the order in which the r-protein genes appear in the transcript. Upon completion, the complex dissociates into free mRNA, LSU, and SSU species, allowing the cycle to begin anew. Newly translated r-protein diffuse away and associate to SSU assembly intermediates following the assembly network described in Earnest et al.1. A diagram of the assembly network is shown in Figure S8 of the Supporting Information. DNA replication is implemented by choosing a replication initiation time trep, from a normal distribution with mean μrep and variance σrep2. New operon copies are added to the simulation at times ti = trep + χiTrep which are taken directly from the experimental analysis in Section 2.1. The operon species are not subject to diffusion in our model, rather they are moved along the long axis of the cell such that they will be found in the same position in the daughter cells as in the mother cell at the start of the cell cycle (Figure 4b). This is a vast simplification of the dynamics of the chromosome, however it is the simplest approach given the lack of detailed time-dependent gene localization information available in the literature.
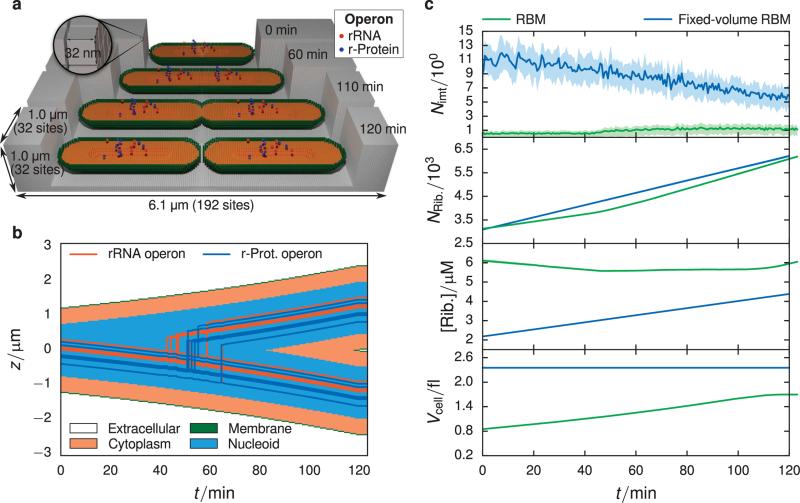
FIGURE 4.
(a) Schematic of geometry used in RBM simulations. The lattice is 32 × 32 × 192 sites in the x, y, and z directions respectively, with a lattice spacing of 32 nm. The simulation volume consists of 4 regions: (1) extracellular space (gray), (2) membrane (green), (3) cytoplasm (orange), and (4) nucleoid (not colored, found in center of cytoplasm). The initial length, 2.4 μm, and the width of the cell, 0.7 μm, were chosen from the previous experimental analysis (Section 2.1). The proportion of the nucleoid region to the cytoplasm is based on measurements of cryo-electron tomograms of slow-growing E. coli15. Operon species are placed within the nucleoid region based on their genomic loci and replicated at times computed from their genomic distance to the origin of replication. The position of the operon species is evolved in time such that the operons in the daughter cell are found in the same position as the operons in the mother cell. The cell volume grows constantly throughout the cell cycle at an exponential rate, where upon it divides into two daughter cells of length 2.4 μm. (b) Kymograph showing the evolution of spatial compartments and operon locations over one cell cycle. The jagged steps arise from the discreteness imposed by the 32 nm lattice. (c) Comparison between RBM (green) and fixed-volume RBM (blue) models using 16 replicates. Means are represented by solid lines and the interquartile range is given by the shaded area. There is an significantly lower average SSU intermediate count seen in the RBM compared to the fixed-volume RBM (top panel), which is a result of the changing cell volume. In the last three panels are plotted the absolute count of ribosomes (translating as well as dissociated), the absolute ribosome concentration, and the cell volume. The RBM produces ribosomes at approximately the same pace as volume expansion, leading to a constant ribosome concentration over the cell cycle.
We use μm from the modeling of the experimental data (Section 2.1) as the initial length of the cell and the mean cell width, 0.7 μm computed from the raw cell data, as the simulated cell's width. The cell grows to μlen0=4.7 μm over the course of its 120 minute cell cycle following the growth law, Equation 4. The new cell geometry, which includes the membrane, cytoplasm, and nucleoid cellular compartments, is computed using constructive solid geometry directly into the lattice data structure. The nucleoid compartment dimensions are chosen to match the proportions of nucleoid to cytoplasm observed in cryo-electron tomograms of slow-growing E. coli15 (available in Figure S7 of the Supporting Information). When the lattice changes, sites where particles were once forbidden are now allowed and the chemical species rapidly undergo diffusive relaxation to fill the empty space. During the constriction of the cell during division, particles in sites which were once cytoplasm can end up outside of the cell. This problem is mitigated by using the membrane compartment to direct outlying particles back into the cytoplasm. For all particles in the simulation, their transition rate from the membrane to the cytoplasm site type is set to the maximum diffusion rate, a2=4Δt, where a is the lattice constant, and Δt is the time step. Transitions from the cytoplasm into membrane sites are all set to zero. By changing the lattice slowly as well as using the membrane sites to redirect straying species, no particles are lost into the extracellular compartment.
Since the volume of the cell and number of gene copies change throughout this simulation, the original parameters used in Earnest et al.1 were slightly modified. The mRNA and rRNA transcription rates were scaled by a factor of 0.65 and 0.60, respectively, and the zeroth-order large subunit (LSU) birth rate was scaled by 2.1. The change in the transcription rates reflect the changing copy numbers, where as the change in the LSU birth rate is a consequence of the changing volume. These changes were executed in order to ensure the same particle copy numbers at the end of the cell cycle were reached as in the original simulations1 (fixed-volume RBM) to allow for a direct comparison which investigates the effect of cell growth and gene duplication. In order to compare the RBM on even footing with the fixed-volume RBM, the fixed-volume RBM was simulated again using the current development version of Lattice Microbes (version 2.3a) over 16 replicates.
Comparing the two models, the initial and final species counts are practically identical for all classes of particles with the exception of the SSU intermediates (see Figure 4c and Table III.) Here we see that the final intermediate count in the fixed-volume RBM is approximately a factor of five larger than the count seen in the RBM. The origin of this effect is due in part to the increased protein concentration at the start of the cell cycle in the RBM. Though the absolute protein numbers are approximately equal, the RBM volume is smaller than the constant cell volume over the full cell cycle. The fixed-volume RBM cell geometry is significantly greater than the RBM geometry since we had used dimensions of 4μm × 0.9μm in the original study1. However there appear to be other effects at play since the volume difference of 1.4× is not enough to account for the total difference.
TABLE III.
Initial and final particle counts from the RBM and fixed-volume RBM trajectories (mean±std).
| RBM counts |
fixed-volume RBM counts |
|||
|---|---|---|---|---|
| Particle Class | Initial | Final | Initial | Final |
| All ribosomes | 3125 ± 54 | 6191 ± 58 | 3094 ± 49 | 6208 ± 73 |
| Translating ribosomes | 545 ± 15 | 1088 ± 23 | 528 ± 18 | 1045 ± 26 |
| Dissociated ribosomes | 2580 ± 57 | 5103 ± 60 | 2566 ± 53 | 5163 ± 71 |
| SSU intermediates | 1.1 ± 1.4 | 1.2 ± 1.2 | 11.4 ± 3.5 | 5.8 ± 2.7 |
| Ribosomal proteins | 34000 ± 3500 | 69800 ± 4800 | 33200 ± 2700 | 66400 ± 4200 |
The changing volume due to cell growth causes particle concentrations to remain relatively constant throughout the cell cycle (Table IV). For example the ribosome concentration in the RBM spans 5.5–5.9 μM over the cell cycle, where as in the fixed-volume RBM the concentration spans 2.4–4.16 μM. However in the RBM the concentration tends to peak before and after cell division (Figure 4c). In the bottom panel of Figure 4c, the increase in volume slows down near the end of the cell cycle when the cell begins dividing. The ribosome number increases linearly over the whole cell cycle, however the growth of the cell volume can no longer keep the pace with ribosome production during this slowing, leading to an increase in ribosome concentration at the end of the cell cycle. When the cell finally divides, the protein concentration can now relax to the steady state concentration.
TABLE IV.
Initial and final concentrations from the RBM and fixed-volume RBM trajectories (mean±std).
| RBM concentrations [μM] |
fixed-volume RBM concentrations [μM] |
|||
|---|---|---|---|---|
| Particle Class | Initial | Final | Initial | Final |
| All ribosomes | 6.11 ± 0.10 | 6.055 ± 0.056 | 2.184 ± 0.034 | 4.382 ± 0.052 |
| Translating ribosomes | 1.065 ± 0.030 | 1.064 ± 0.023 | 0.373 ± 0.013 | 0.738 ± 0.018 |
| Dissociated ribosomes | 5.04 ± 0.110 | 4.991 ± 0.059 | 1.811 ± 0.038 | 3.644 ± 0.050 |
| SSU intermediates | 0.0022 ± 0.0028 | 0.0012 ± 0.0011 | 0.0081 ± 0.0024 | 0.0041 ± 0.0019 |
| Ribosomal proteins | 66.5 ± 6.9 | 68.2 ± 4.6 | 23.5 ± 1.9 | 46.9 ± 2.9 |
Though the majority of the chemical species in the RDME simulations show no spatial heterogeneity, e.g. r-protein (Figure 5, top), two classes of particles exhibit nonuniform distributions throughout the cell. Translating ribosomes, composed of an SSU particle, an LSU particle, and an mRNA, are partially excluded from the nucleoid region by imposing a bias in the transition rates between the nucleoid and cytoplasm compartments. The transition rate from the nucleoid region to the cytoplasm is four times greater than the reverse transition. These biased transition rates model the excluded volume effects arising from the folded chromosome which is not included in the simulation due to a restriction of the number of species allowed in the present version of Lattice Microbes. Heterogeneous distributions of ribosomes have been observed in single particle tracking experiments, which showed that the fully associated ribosome is partially excluded from the nucleoid17 region while the individual subunits are not19, as well as in cryo-electron tomography of slow-growing E. coli15 (see Figure S7 of the Supporting Information.) Since the fate of particles in these RDME simulations are determined by reaction and diffusion processes alone, biased transition rates are necessary to implement excluded-volume effects which arise due to intermolecular forces between particles. Though this is a simplistic approach, it is sufficient for the needs of this study.
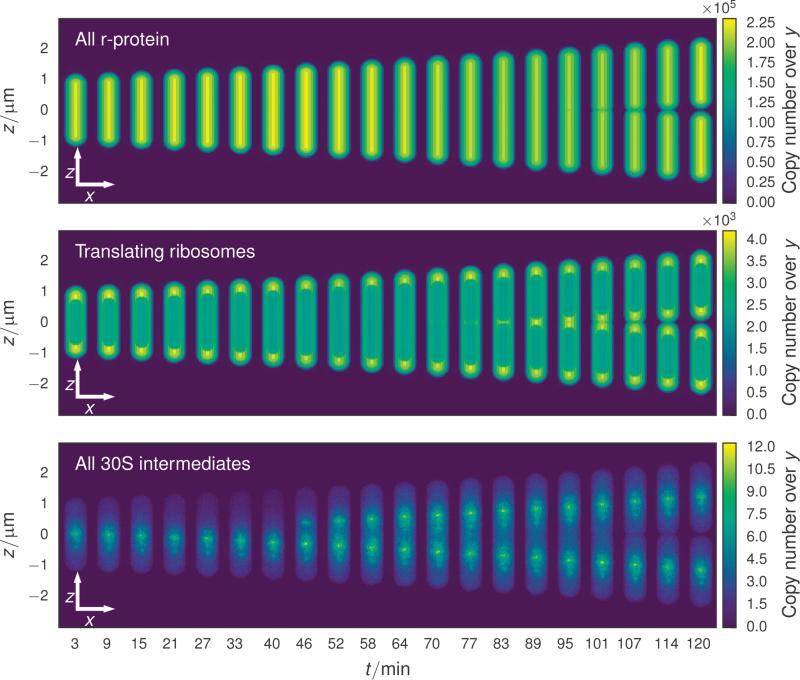
FIGURE 5.
xz copy number projections of cells at evenly spaced times throughout the cell cycle. The time evolution of the cell geometry is evident in this series of projections. Constriction begins approximately 100 minutes into the cell cycle through the constriction of the cell membrane. Ribosomal protein (top) diffuses rapidly through all compartments, leading to a distribution which mirrors the thickness of the cell at each (x, z) coordinate. The transition rates of translating ribosomes (middle) between the nucleoid and cytoplasm regions is biased to limit the number of ribosomes in the nucleoid, leading to localization of ribosomes to the cell poles and membrane. The most pronounced spacial heterogeneity is due to the SSU intermediates (bottom), where the earliest intermediates which result from the binding of primary proteins are found near the rRNA operon from which the 16S rRNA was transcribed.
The other particle class exhibiting a nonuniform spatial distribution are the SSU assembly intermediates (Figure 5 bottom). Ribosomes assemble in a well-defined binding order, where some proteins can only bind once other proteins are associated with the nascent subunit (see Figure S8 in the Supporting Information.) The earliest SSU intermediates, consisting of the primary and secondary binding proteins associated with the 5′ and central domains of the 16S rRNA1, are short lived and are found only within a few hundred nanometers of the site from which the rRNA was transcribed. Due to their short lifetime, their density tracks the position of the rRNA operon tightly. Later intermediates which are beginning to include tertiary binding proteins diffuse farther away from the originating rRNA operon until all memory of their birthplace is washed out.
2.3 Effects of DNA Replication and Translation on mRNA Statistics
As there are no experimental distributions available, computed distributions of the rRNAs and ribosomal protein operon mRNAs obtained from our simulations were compared to theoretical results from Peterson et al.24. The theory derived in Peterson et al. considers a constitutively expressed gene that is replicated during the cell cycle and includes the time-dependent messenger degradation. It was found that modeling the time-dependence was critical to capturing the correct shape and statistical features of the messenger distribution for highly expressed genes or genes with long half-life, both criteria which are met by the ribosomal protein operon genes. We found that the simulated RNA exhibited significantly higher expression and greater variability than the theory of Peterson et al. predicted. Attempts to fit the messenger distributions to theoretical distributions (see Figure 6 green lines; described in Section S3) yielded estimates of kt,eff and kd,eff (the messenger transcription and degradation rates, respectively) that differed systematically from the rates used in the RBM simulations—fit kt,eff values were approximately four times larger than those used in the RBM simulations while fit kd,eff values are about four times smaller (see Table V and Figure S9). We note, however, that the distributions based on the results of the theory24 do show better agreement than those of an earlier model of mRNA production that accounted for gene duplication, but neglected mRNA decay23. This is due to the high expression value of the mRNA and the long half-life of the messengers (8–12 min) both of which require the mRNA relaxation to be explicitly accounted for to capture the correct statistics24.
FIGURE 6.
Messenger distributions simulated in the ribosome biogenesis model (RBM; blue histogram) with fits from the theory of Peterson et al. (red curve)24. Fit parameters for the theory with mRNA relaxation can be found in Table V.
TABLE V.
Transcription (kt), degradation (kd), and messenger unbinding (ku) rate parameters for the ribosomal protein operon mRNA in the RBM (scaled from those in Earnest et al.1 as discussed in Section 2.2). Each value for the unbinding rates ku was estimated according to Equation S9. The last line gives the harmonic mean over all individual operon rate parameters. These mean values were used to make Figure S10b. Effective rate parameters (kt,eff, kd,eff) are from fitting the simulated messenger distributions with the theory of Peterson et al.24.
| Operon | kt (s−1) | kd (s−1) | ku (s−1) | kt,eff (s−1) | kd,eff (s−1) |
|---|---|---|---|---|---|
| alpha | 0.0047 | 8.363 × 10–4 | 0.0079 | 0.01813 | 0.00023 |
| rplM | 0.0030 | 1.197 × 10–3 | 0.0119 | 0.01431 | 0.00030 |
| rpsF | 0.0036 | 8.955 × 10–4 | 0.0103 | 0.01513 | 0.00027 |
| rpsJ | 0.0060 | 1.029 × 10–3 | 0.0059 | 0.02091 | 0.00022 |
| rpsO | 0.0045 | 1.238 × 10–3 | 0.0082 | 0.01810 | 0.00025 |
| rpsP | 0.0038 | 9.785 × 10–4 | 0.0092 | 0.02220 | 0.00037 |
| rpsT | 0.0027 | 1.144 × 10–3 | 0.0139 | 0.01519 | 0.00036 |
| spc | 0.0069 | 9.206 × 10–4 | 0.0055 | 0.02225 | 0.00020 |
| str | 0.0058 | 8.062 × 10–4 | 0.0063 | 0.02065 | 0.00022 |
| Mean | 0.0042 | 9.8359 × 10–4 | 0.0080 | ||
An important omission in the RBM, and the underlying reason for the disagreement we see with the results of Peterson et al.24, is that the simulated cells express only the genes involved in ribosome biogenesis. In reality, cells express a multitude of other mRNA and proteins in order to perform other cellular functions (e.g. metabolism and gene regulation, etc.) In order to investigate how these “missing” mRNA may affect our ribosomal mRNA statistics, we constructed a simple model of messenger production that accounts for both gene duplication and interactions with the cell's ribosomes (denoted SAM) consisting of the reactions
| (30) |
Here D(t) represents the gene copy number on the DNA; its time-dependence signifies that at some time tr (the replication time) it will double from one copy to two copies, and kt and kd are the transcription and degradation rate of the mRNA, respectively. Importantly, this model includes transitions of the messenger, m, into and out of a second state, n, which represents the ribosome-bound mRNA. The ribosome binding and unbinding rates are denoted kb and ku, respectively, and the binding rate is understood to be a function of the free ribosome concentration. The binding rate is kb = 4.2 × 108M−1s−1 while the unbinding constants can be estimated as described in Supporting Information Section S1.2 (also found in Table V). This model assumes (as do our simulations) that ribosome-bound messengers are protected from degradation.
A chemical master equation (CME) corresponding to Equation 30 (see Equation S1 in the Supporting Information) was used to derive a set of ODEs and boundary conditions that describe the mean and variance of m and n (see Equation S2 and Equation S3 in the Supporting Information). By assuming some number, c, of other genes whose mRNA compete for the available ribosomes, we estimated the equilibrium concentration of free ribosomes by solving the system numerically. Subsequent time-averaging over the cell cycle24 yielded values for the mean and variance of the modeled mRNA. We computed the mean and Fano factor for each of the ribosomal protein operons based on their respective rate parameters and gene doubling times (see Table V). When c = 8, which approximates the case of the RBM simulations (there are a total of 9 ribosomal protein operons in E. coli; messengers from 8 operons actively compete with the messengers from the operon of interest), we found that the resulting means from the SAM showed very good agreement with simulated RBM values, although the resulting Fano factors tended to be slightly overestimated (see Figure S10a, red and blue dots). However, when the value of c in the SAM was set closer to a biologically realistic value (on the order of 1000, assuming roughly 25% of the E. coli genome is actively expressed45), the resulting means and Fano factors essentially matched those predicted by Peterson et al.24 (see Section S4 and Figure S10a, green triangles and black “+” signs). These results underscore the need for including the expression of other non-ribosomal messengers in future RBM simulations.
Our analysis of the SAM indicates that when in the biologically realistic regime (c ~ 1000), messengers are generally not bound by ribosomes and their statistics can be described by the theory of Peterson et al. The question then arises: What is the expected mean count of messengers for each of the ribosomal protein operons and how should the RBM be modified when competing mRNAs are modeled? Using values from the CyberCell Database, which tabulates statistics describing an average E. coli cell46, we estimate that the total count of mRNAs to be between 3800 and 10000 in cells with our measured average length and width (3.2 μm and 0.715 μm, respectively; see Figure 1c and Figure S3). Using relative gene expression values from high-throughput sequencing data for E. coli47 we then estimate the mean mRNA counts for the ribosomal operons are between 20 and 120, which are in good agreement with the RBM values (55 and 145). In the biologically realistic regime for c the transcription and degradation kinetics used in the RBM give mean and noise values that are much lower than these estimates (Figure S10a green dots). This indicates that future applications of the RBM which include competing mRNAs will require transcription rate parameters that are about four times higher and degradation rate parameters that are about four times lower than in the current RBM to achieve mean mRNA counts that match experiments (as indicated by linear regression between fit and RBM rate parameters; see Figure S9). Using the theory of Peterson et al. we have estimated that the kt and kd values required for the ribosomal protein operons necessary to capture the correct mean messenger counts when modeling all competing mRNAs (see Table V).
3 Conclusions
In this article we performed fluorescence imaging studies at the single-cell level in order to estimate the timing and duration of DNA replication in slow-growing E. coli (doubling time of approximately 120 minutes). We described a simple analytical model describing growth and DNA replication in slow-growing E. coli (only one replication process per cell cycle) which does not require the explicit tracking of cell lineages and applied it to our single-cell studies. The B and C parameters determined by the model, 42.2 min and 42.4 min respectively, are reasonable when compared more direct measurements in bulk36,37 or in single cells25,27. These parameters were used to improve a recent spatially resolved, whole-cell model of ribosome biogenesis1 that involved the transcription and translation of the rRNA and ribosomal protein operons involved in production of the ribosomal 30S small subunit (SSU), as well as its assembly. This model was augmented through the use of the experimentally measured parameters to include the effects of cell growth and gene replication, the latter of which has been shown to significantly impact the copy number statistics of mRNA in models of gene regulation23,24. We found that the ribosomal protein operon messenger counts that emerged from our ribosome biogenesis model without regulation did not appear to be well-described by published theoretical models23,24. Specifically, the simulated messengers were expressed in greater numbers and with greater variability than the theory of Peterson et al. predicted. We found that this was associated with the low number of non-ribosomal genes in the RBM. By constructing a simple semi-analytical model (SAM) that accounts for varying numbers of non-ribosomal genes to be expressed, we showed that the mRNA statistics of a cell expressing realistic numbers of non-ribosomal genes should be close to those predicted by Peterson et al. This means that in order to recover the proper ribosomal messenger counts, future versions of the RBM that include other cellular networks like metabolism and regulation will also require adjustments to the ribosomal protein operon transcription and mRNA degradation parameters.
4 Materials and Methods
4.1 E. coli operon quantification
Strains and plasmids
All strains used in this study are derivatives of E. coli K-12 MG1655 Δlac48–50, in which the entire lac operon has been deleted from the N-terminus of lacI to the C-terminus of lacA using the method of Datsenko and Wanner51. Gene locations and numbers were determined using the fluorescent repressor operator system (FROS), where of the integration of an array of 240 operators for tet repressor, TetR, was performed at each of 14 loci at evenly spaced intervals around the chromosome using Landing Pad technology48–50,52,53.
Fluorescent repressor operator system
Gene locations were determined using the fluorescent repressor operator system (FROS) performed as described54. Integrations were made at each site consisting of an array of 240 operators for tet repressor, TetR, using Landing Pad technology. After growth to steady state as described below, 0.01% L-arabinose was added to each culture 1 hour before fixation to induce expression of TetR tagged with fluorescent EYFP in trans from the plasmid pBH7454. Cells were then fixed and processed as above.
Media and growth conditions
At the start of an experiment, a seed culture of each strain was inoculated from a glycerol stock into 2 ml Lysogeny Broth (LB) with appropriate antibiotics in 14 ml polypropylene round bottom tubes (Falcon) and allowed to grow to saturation in a 37 °C shaking water bath. This seed culture was then diluted 1000× into 3 ml of M63 minimal medium (100 mM KH2PO4, 15 mM (NH4)2SO4, 1.7 μM FeSO4, 1 mM MgSO4) + 0.5% glycerol in 20 mm diameter glass test tubes and allowed to grow with extremely vigorous shaking in a 37 °C water bath (New Brunswick Scientific model G76) until OD600 of the culture reached 0.5–0.6 as measured with a spectrophotometer (Bio-Rad SmartSpec 3000). These cultures were then used to inoculate another 25 ml baffled Erlenmeyer flasks of identical fresh medium pre-warmed to 37 °C at an initial density of OD600 = 0.005 and again grown with vigorous shaking in a 37 °C water bath. Samples were taken and the OD600 of the culture was measured at regular intervals to determine the doubling time of the culture. When the density of the culture reached OD600 = 0.2–0.4, the culture was harvested and fixed by the direct addition of an equal volume of freshly prepared and filtered 5% paraformaldehyde in phosphate buffered saline (PBS). The resulting solution was allowed to continue shaking at 37 °C for 10 minutes and was then placed on ice for 30 min. Cells were washed three times via centrifugation and resuspension in 1 ml filtered, ice-cold PBS. At the time of harvest, we estimate that the cultures had been growing in exponential steady-state for ~10 generations.
Microscopy
After preparation, samples were mounted on glass slides using 40% glycerol. Imaging was performed using a Nikon Eclipse TE2000U microscope with an Applied Scientific Instruments PZM-2000 automated stage utilizing Metamorph automation software. 1000 images per strain were collected using epifluorescent illumination with a 100× phase-contrast objective combined with a 4× telescope attachment using a Roper Scientific Cascade:512 camera.
4.2 Data analysis
Image analysis
All image analysis was performed in performed in the Jupyter environment55 using the SciPy Stack56 and scikit-image57. Following background subtraction of all phase-contrast images, a binary mask was computed from each frame using adaptive thresholding to identify potential cells. The potential cell regions from the phase-contrast images were then normalized to [0,1], where by a second binary mask of the cell was constructed from pixels with a normalized intensity less than 0.37. Cell lengths were measured from the arc length of a 5th degree polynomial fit to the cell mask in order to prevent measurement error due to cell curvature. Regions of YFP fluorescence were evaluated for suitability by computing the intensity histogram and only accepting regions with a skewness greater than 1. Locations of labeled operons were determined by finding the local maxima of the Gaussian filtered fluorescence image and accepting only peaks with values 1.45× greater than the median signal over the cell mask.
Model fitting
The gene replication model was fit to the experimental data by maximizing the objective function Equation 17, which was implemented in Cython58 for fast numerical optimization using differential evolution35 implemented in the SciPy library56. Uncertainty calculations using bootstrapping were performed on NCSA Blue Waters
4.3 Simulations
All simulations were performed using Lattice Microbes v2.3a on a local cluster consisting of three Cirrascale GB5600 Multi-GPU nodes, two equipped with 8 NVIDIA GeForce GTX TITAN X GPUs, and one equipped with 4 NVIDIA Tesla K80 GPUs. Analysis of simulation data was performed in the Jupyter environment55 using the SciPy Stack56.
Lattice Microbes 2.3a expands the capability of the GPU-based MPD-RDME algorithm43 by adding support for extended capacity lattices where sixteen different particles may occupy each lattice site. Previous versions allowed up to eight particles per site. When more particles occupy a lattice site than capacity allows, the extra particles are said to have “overflowed” and special handling is required to rectify the situation. A procedure on the CPU locates candidate neighboring lattice sites and moves the excess particles into them. This is costly, as the lattice must be copied to host memory and then back to the GPU after overflows are corrected. Additionally, a higher capacity lattice incurs a cost as well, as the diffusion and reaction operators must access a larger amount of memory to account for the greater number of particles. However, simulations that experience overflows on a frequent basis benefit from the greater capacity, as the cost of accessing more memory is offset by the savings gained from not needing to perform overflow handling.
RDME
Running a single replicate per GPU, the simulations completed 120 minutes of simulated time in 29 hours on the TITAN X nodes at a time step of 25 μs59. Cell growth and DNA replication was implemented using a custom RDME solver using pyLM60, whereby the lattice of site types was modified in situ every 2000 time steps. Initial species counts were taken from a chemical master equation based simulation of the growth ribosome biogenesis model at steady state. Operon placement was performed by estimating the position of a locus along the cell axis assuming that the chromosome is organized linearly. The operon position in the cross-sectional plane of the cells is distributed uniformly within the nucleoid region.
CME
Cell growth and DNA replication was implemented using a custom chemical master equation (CME) solver implemented using pyLM60. CME simulations of the SAM,
| (31) |
were used to validate the semi-analytic theory derived in this paper by varying the number of genes from 10 to 500 and the position of the gene between the oriC and terC in increments of 10%. In each simulation, c identical genes were produced. Each gene is associated with three species in the simulation, a gene (Di) that is transcribed to produce unbound messengers (mi) which can bind and unbind to a ribosome to become sequestered messengers (ni). The rates transcription, degradation, ribosome binding and unbinding rates (kt, kd, kb, and ku, respectively) were taken to be identical for each gene. Simulations of 100 replicate cells growing for 11 generations were performed to acquire convergent statistics. Each cell was seeded with identical initial conditions; therefore, the first generation was excluded when computing statistics (therefore, each average was over 100 replicate cells each growing for 10 generations). Each gene (Di) was replicated according to the fitted replication start (ts) and replication (Tr) times, and its position along the genome. Cell division was performed every tD = 120 minutes with cell components binomially distributed between daughter cells. Only a single daughter cell was followed after each cell division event. To allow comparison with theory a single set of rate were used for all genes, namely kt = 0.0042s−1, kb = 0.079s−1, ku = 0:008s−1 and kd = 9:84 × 10−4s−1.
Supplementary Material
TABLE II.
Summary of reactions and reaction rates used in the whole-cell model of ribosomal biogenesis. Parameters which differ between the RBM and fixed-volume RBM are provided for each with the fixed-volume RBM parameter in parenthesis. The complete assembly network is provided in Figure S8 of the Supporting Information, the complete list of all 1300 reactions is available in the Supporting Information of Earnest et al.1.
| Type | Reaction | Parameter values | Units | Compartments | |
|---|---|---|---|---|---|
| Assembly | Ii + Pj → Ii+1 (1° prot.) | 0.041 – 1.69 | μM–1 s–1 | cytoplasm, nucleoid | |
| Ii + Pj → Ii+1 (2° prot.) | 0.24 – 31. | μM–1 s–1 | cytoplasm, nucleoid | ||
| Ii + Pj → Ii+1 (3° prot.) | 0.025 – 1.75 | μM–1 s–1 | cytoplasm, nucleoid | ||
| Degradation | mRNAi → Ø | 1.0 × 10–3 – 1.4 × 10–3 | s–1 | cytoplasm, nucleoid | |
| Transcription | DNArrnX → DNArrnX + 16S | 0.037 (0.062) | s–1 | nucleoid | |
| DNAx → DNAx + mRNAx | 3.2 × 10–3 – 7.8 × 10–3 | s–1 | nucleoid | ||
| (4.9 × 10–3 – 0.012) | s–1 | ||||
| Translation | 1.0 × 102 | μM–1 s–1 | cytoplasm, nucleoid | ||
| 3.0 | μM–1 s–1 | cytoplasm, nucleoid | |||
| 0.019 – 0.27 | s–1 | cytoplasm, nucleoid | |||
| 0.015 | s–1 | cytoplasm, nucleoid | |||
| LSU birth | Ø → LSU | 6.5 × 10–4 (3.1 × 10–4) | 3.1 × 10–4 | cytoplasm, nucleoid | |
| Dimerization | uS6 + uS18 → uS6 : uS18 | 1.0 | μM–1 s–1 | cytoplasm, nucleoid | |
| uS6 : uS18 → uS6 + uS18 | 8.7 × 10–3 | s–1 | cytoplasm, nucleoid | ||
Acknowledgments
This work is supported by the National Science Foundation (NSF) grant MCB-1244570 (JAC, ZLS) and the NSF Center for the Physics of Living Cells grant PHY-1430124 (TME, TEK, ZLS), an NSF Graduate Research Fellowship grant DGE-1144245 (JRP), and the U.S. Department of Energy, Office of Science, Biological and Environmental Research as part of the Adaptive Biosystems Imaging Scientific Focus Area (TME). TEK is supported by an Alfred P. Sloan Foundation Research Fellowship in Physics (FG-2015-65532). This research is part of the Blue Waters sustained-petascale computing project, which is supported by the National Science Foundation (awards OCI-0725070 and ACI-1238993) and the state of Illinois. Blue Waters is a joint effort of the University of Illinois at Urbana-Champaign and its National Center for Supercomputing Applications. This work is supported in part by the National Institutes of Health grants 9 P41 GM104601-23 (MH, ZLS) and GM112659 (ZLS).
References
- 1.Earnest TM, Lai J, Chen K, Hallock MJ, Williamson JR, Luthey-Schulten Z. Biophys. J. 2015;109:1117–1135. doi: 10.1016/j.bpj.2015.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Valgepea K, Adamberg K, Seiman A, Vilu R. Mol. BioSys. 2013;9:2344. doi: 10.1039/c3mb70119k. [DOI] [PubMed] [Google Scholar]
- 3.Woese CR. Microbiol. Rev. 1987;51:221–271. doi: 10.1128/mr.51.2.221-271.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Woese CR, Kandler O, Wheelis ML. Proc. Natl. Acad. Sci. USA. 1990;87:4576–4579. doi: 10.1073/pnas.87.12.4576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Roberts E, Sethi A, Montoya J, Woese CR, Luthey-Schulten Z. Proc. Natl. Acad. Sci. USA. 2008;105:13953–13958. doi: 10.1073/pnas.0804861105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen K, Eargle J, Sarkar K, Gruebele M, Luthey-Schulten Z. 2010;99:3930–3940. doi: 10.1016/j.bpj.2010.09.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hosokawa K, Fujimura RK, Nomura M. Proc. Natl. Acad. Sci. USA. 1966;55:198–204. doi: 10.1073/pnas.55.1.198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bunner AE, Beck AH, Williamson JR. Proc. Natl. Acad. Sci. USA. 2010;107:5417–5422. doi: 10.1073/pnas.0912007107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mulder AM, Yoshioka C, Beck AH, Bunner AE, Milligan RA, Potter CS, Carragher B, Williamson JR. Science. 2010;330:673–677. doi: 10.1126/science.1193220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sashital DG, Greeman CA, Lyumkis D, Potter CS, Carragher B, Williamson JR. eLife. 2014:3. doi: 10.7554/eLife.04491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen K, Eargle J, Lai J, Kim H, Abeysirigunawardena S, Mayerle M, Woodson S, Ha T, Luthey-Schulten Z. J. Phys. Chem. B. 2012;116:6819–6831. doi: 10.1021/jp212614b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lai J, Chen K, Luthey-Schulten Z. J. Phys. Chem. B. 2013;117:13335–13345. doi: 10.1021/jp404106r. [DOI] [PubMed] [Google Scholar]
- 13.Kim H, Abeysirigunawarden SC, Chen K, Mayerle M, Ragunathan K, Luthey-Schulten Z, Ha T, Woodson SA. Nature. 2014;506:334–338. doi: 10.1038/nature13039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lindahl L. J. Mol. Biol. 1975:15–37. doi: 10.1016/0022-2836(75)90089-3. [DOI] [PubMed] [Google Scholar]
- 15.Roberts E, Magis A, Ortiz JO, Baumeister W, Luthey-Schulten Z. PLoS Comput. Biol. 2011;7:e1002010. doi: 10.1371/journal.pcbi.1002010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang W, Li G-W, Chen C, Xie XS, Zhuang X. Science. 2011;333:1445–1449. doi: 10.1126/science.1204697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bakshi S, Siryaporn A, Goulian M, Weisshaar JC. Mol. Microbiol. 2012;85:21–38. doi: 10.1111/j.1365-2958.2012.08081.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chai Q, Singh B, Peisker K, Metzendorf N, Ge X, Dasgupta S, Sanyal S. J. Biol. Chem. 2014;289:11342–11352. doi: 10.1074/jbc.M114.557348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sanamrad A, Persson F, Lundius EG, Fange D, Gynna AH, Elf J. Proc. Natl. Acad. Sci. USA. 2014;111:11413–11418. doi: 10.1073/pnas.1411558111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Swain PS, Elowitz MB, Siggia ED. Proc. Natl. Acad. Sci. USA. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Friedman N, Cai L, Xie XS. Phys. Rev. Lett. 2006:97. doi: 10.1103/PhysRevLett.97.168302. [DOI] [PubMed] [Google Scholar]
- 22.Shahrezaei V, Swain PS. Proc. Natl. Acad. Sci. USA. 2008;105:17256–17261. doi: 10.1073/pnas.0803850105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jones DL, Brewster RC, Phillips R. Science. 2014;346:1533–1536. doi: 10.1126/science.1255301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Peterson JR, Cole JA, Fei J, Ha T, Luthey-Schulten ZA. Proc. Natl. Acad. Sci. USA. 2015;112:15886–15891. doi: 10.1073/pnas.1516246112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Taheri-Araghi S, Bradde S, Sauls JT, Hill NS, Levin PA, Paulsson J, Vergassola M, Jun S. Curr. Biol. 2015;25:385–391. doi: 10.1016/j.cub.2014.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Amir A. Phys. Rev. Lett. 2014;112:208102. [Google Scholar]
- 27.Adiciptaningrum A, Osella M, Moolman MC, Lagomarsino MC, Tans SJ. Sci. Rep. 2015;5:18261. doi: 10.1038/srep18261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang P, Robert L, Pelletier J, Dang WL, Taddei F, Wright A, Jun S. Curr. Biol. 2010;20:1099–1103. doi: 10.1016/j.cub.2010.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mir M, Wang Z, Shen Z, Bednarz M, Bashir R, Golding I, Prasanth SG, Popescu G. Proc. Natl. Acad. Sci. USA. 2011;108:13124–13129. doi: 10.1073/pnas.1100506108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cooper S. Theor. Biol. Med. Model. 2006;3:1–15. doi: 10.1186/1742-4682-3-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Godin M, Delgado FF, Son S, Grover WH, Bryan AK, Tzur A, Jorgensen P, Payer K, Grossman AD, Kirschner MW, Manalis SR. Nat. Methods. 2010;7:387–390. doi: 10.1038/nmeth.1452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Campos M, Surovtsev IV, Kato S, Paintdakhi A, Beltran B, Ebmeier SE, Jacobs-Wagner C. Cell. 2014;159:1433–1446. doi: 10.1016/j.cell.2014.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Koch AL. J. Gen. Microbiol. 1966;45:409–417. [Google Scholar]
- 34.Koch AL, Schaechter M. J. Gen. Microbiol. 1962;29:435–454. doi: 10.1099/00221287-29-3-435. [DOI] [PubMed] [Google Scholar]
- 35.Storn R, Price K. J Global Optim. 1997;11:341–359. [Google Scholar]
- 36.Skarstad K, Steen HB, Boye E. J. Bacteriol. 1983;154:656–662. doi: 10.1128/jb.154.2.656-662.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Michelsen O. Microbiology. 2003;149:1001–1010. doi: 10.1099/mic.0.26058-0. [DOI] [PubMed] [Google Scholar]
- 38.Powell EO. J. Gen. Microbiol. 1956;15:492–511. doi: 10.1099/00221287-15-3-492. [DOI] [PubMed] [Google Scholar]
- 39.Osella M, Nugent E, Lagomarsino MC. Proc. Natl. Acad. Sci. USA. 2014;111:3431–3435. doi: 10.1073/pnas.1313715111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Soifer I, Robert L, Amir A. Curr. Biol. 2016;26:356–361. doi: 10.1016/j.cub.2015.11.067. [DOI] [PubMed] [Google Scholar]
- 41.Bates D, Kleckner N. Cell. 2005;121:899–911. doi: 10.1016/j.cell.2005.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bates D, Epstein J, Boye E, Fahrner K, Berg H, Kleckner N. Mol. Microbiol. 2005;57:380–391. doi: 10.1111/j.1365-2958.2005.04693.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Roberts E, Stone JE, Luthey-Schulten Z. J. Comp. Chem. 2013;34:245–255. doi: 10.1002/jcc.23130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hallock MJ, Stone JE, Roberts E, Fry C, Luthey-Schulten Z. Parall. Comp. 2014;40:86–99. doi: 10.1016/j.parco.2014.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Richmond CS, Glasner JD, Mau R, Jin H, Blattner FR. Nucl. Acids Res. 1999;27:3821–3835. doi: 10.1093/nar/27.19.3821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sundararaj S. Nucl. Acids Res. 2004;32:293D–295. doi: 10.1093/nar/gkh108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Li G-W, Burkhardt D, Gross C, Weissman JS. Cell. 2014;157:624–635. doi: 10.1016/j.cell.2014.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kuhlman TE, Cox EC. Nucl. Acids Res. 2010;38:e92–e92. doi: 10.1093/nar/gkp1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kuhlman TE, Cox EC. Mol. Sys. Biol. 2012:8. doi: 10.1038/msb.2012.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kuhlman TE, Cox EC. Phys. Rev. E. 2013:88. doi: 10.1103/PhysRevE.88.022701. [DOI] [PubMed] [Google Scholar]
- 51.Datsenko KA, Wanner BL. Proc. Natl. Acad. Sci. USA. 2000;97:6640–6645. doi: 10.1073/pnas.120163297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kuhlman TE, Cox EC. Bioeng. Bugs. 2010;1:298–301. doi: 10.4161/bbug.1.4.12386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tas H, Nguyen CT, Patel R, Kim NH, Kuhlman TE. PLOS ONE. 2015;10:e0136963. doi: 10.1371/journal.pone.0136963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Joshi MC, Bourniquel A, Fisher J, Ho BT, Magnan D, Kleckner N, Bates D. Proc. Natl. Acad. Sci. USA. 2011;108:2765–2770. doi: 10.1073/pnas.1019593108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Pérez F, Granger BE. Comput. Sci. Eng. 2007;9:21–29. [Google Scholar]
- 56.Jones E, Oliphant T, Peterson P, et al. [2016-03-18];SciPy: Open source scientific tools for Python. 2001 http://www.scipy.org/
- 57.van der Walt S, Schönberger JL, Nunez-Iglesias J, Boulogne F, Warner JD, Yager N, Gouillart E, Yu T. PeerJ. 2014;2:e453. doi: 10.7717/peerj.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Behnel S, Bradshaw R, Citro C, Dalcin L, Seljebotn D, Smith K. Comput. Sci. Eng. 2011;13:31–39. [Google Scholar]
- 59.Hallock MJ, Luthey-Schulten Z. Parallel and Distributed Processing Symposium Workshop (IPDPSW) IEEE International; 2016. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Peterson JR, Hallock MJ, Cole JA, Luthey-Schulten ZA. PyHPC 2013. Supercomputing; 2013. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.