Abstract
The evolution of life in our biosphere has been marked by several major innovations. Such major complexity shifts include the origin of cells, genetic codes or multicellularity to the emergence of non-genetic information, language or even consciousness. Understanding the nature and conditions for their rise and success is a major challenge for evolutionary biology. Along with data analysis, phylogenetic studies and dedicated experimental work, theoretical and computational studies are an essential part of this exploration. With the rise of synthetic biology, evolutionary robotics, artificial life and advanced simulations, novel perspectives to these problems have led to a rather interesting scenario, where not only the major transitions can be studied or even reproduced, but even new ones might be potentially identified. In both cases, transitions can be understood in terms of phase transitions, as defined in physics. Such mapping (if correct) would help in defining a general framework to establish a theory of major transitions, both natural and artificial. Here, we review some advances made at the crossroads between statistical physics, artificial life, synthetic biology and evolutionary robotics.
This article is part of the themed issue ‘The major synthetic evolutionary transitions’.
Keywords: major transitions, artificial life, synthetic biology, evolutionary robotics, phase transitions
1. Introduction: synthetic transitions
Looking backward to the unfolding of life on our planet, it is possible to identify several major qualitative changes that deeply marked evolutionary history. They have been labelled as the major evolutionary transitions (METs) owing to the fundamentally unique nature of the changes involved [1]. The emergence of life, the genetic code, complex cells, multicellular organisms and language are some of the best-known examples. They all involve a novel class of organization with high-order properties not reducible to the properties of the lower-scale units. The list of METs differs among authors [1–7], and in this paper we address a revised list of major transitions (MTs) incorporating different proposals. A first classification of METs would include (i) a loss of replicative potential by the units once belonging to a higher-order entity, (ii) a specialization of different units in different tasks, which requires a nonlinear mapping between genotype and phenotype, and (iii) changes in the ways information is processed and stored. But more importantly, we want to consider METs under the light of the theoretical, experimental and engineering perspectives involving the modelling, synthesis and imitation of living systems. For example, we can create a new multicellular system by engineering new cell–cell signals on single cells. Similarly, a proto-grammar can emerge in a group of interacting, evolvable robots. These are synthetic transitions that are not necessarily related to standard evolutionary paths, but they do involve ways to generate major innovations starting from simpler systems. We will use a general term to label this broad class of non-natural transitions: major synthetic transitions (MST). The study of MST provides a whole parallel approach to natural evolution and to the origin of innovations in complex systems, biological or artificial.
How similar are these two scenarios? Random events are known to play some role in evolutionary history [7–9] and they offer some clues to the origins (and likelihood) of some innovations. However, convergence seems also a widespread feature of evolved systems [10] as illustrated by the observation that some major innovations have emerged independently in different groups and often sharing surprisingly similar design principles. Such universal patterns could be a consequence of fundamental constraints beyond the specific nature of biological systems [11–13] and thus would be also inevitable in their synthetic counterparts. By understanding the role of constraints in both evolved and artificially generated innovations, we might achieve some understanding of the uniqueness of the known biology that we know [14].
Other important questions that can benefit from the analysis of MST are understanding why some transitions seem common, whereas others seem rather unique [7]. Are hard-to-obtain synthetic transitions connected to hard-to-evolve biological novelties? On the other hand, we might also ask if there are other MTs associated with the potentially different MST universe. What is their nature and why are they absent in the biological realm? No less important is the fact that MTs occur when a given set of preconditions is in place. Preconditions are relevant to our discussion because they imply the presence of a landscape of possibilities pervading the emergence of a major qualitative change. Moreover, there are remarkable commonalities shared by disparate systems. These universal traits are to be found in those principles stemming from the physics of complex systems [15,16], phase transitions [17,18] and the algorithmic logic of artificial life models [19,20]. In this context, it has been suggested that phase transitions [21,22] can help in understanding the patterns exhibited by METs. Because phase transitions are known to exhibit robust, universal laws [23,24], they will help understanding of the general nature of natural and artificial transitions, perhaps opening the construction of a general theory of what we can label as MTS.
2. Synthetic prebiotic chemistry
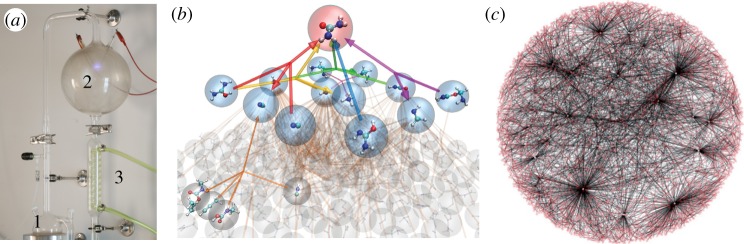
We start our list with a special problem: the presence of qualitative transitions in a pre-biological biosphere before true replicators emerged. We are thus closer to the domain of prebiotic systems chemistry [25] that defines the landscape of preconditions required for the rise of molecular replicators and genetic codes. The first attempts aiming for the creation and analysis of synthetic prebiotic systems were Stanley Miller's electric discharge experiments [26,27] that can be accurately simulated using molecular dynamics [28]. Miller's approach was simple and elegant: take a set of candidate molecules that were likely to be present in the primitive atmosphere and make it react under a constant energy source (figure 1a,b). The experiment generated amino acids (AAs) and other molecules, thus providing support to Oparin's conjecture that biochemical complexity can arise from purely chemical processes [30]. Further studies developed by the Catalan chemist Joan Oró showed that relevant building blocks of nucleic acids, such as adenine, could also emerge from using ammonium cyanide [31].
Figure 1.
Synthetic prebiotic chemistry. Miller's experiment (a) provided the first evidence for an abiotic scenario of generation of biologically relevant molecules (image courtesy of Adam Brown). The mixture is heated (1) receives electrical discharges (2) and is condensed in (3). (b) Many different molecules are generated, linked through a reaction network (adapted from [28]). The overall reaction network is similar to in silico networks of reactions in organic chemistry that can be obtained from databases, as shown in (c) where nodes are molecules and connections indicate possible reactions (adapted after [29]).
Because biochemical diversity of basic monomers pervades the development of true living entities, the synthetic soup created in these experiments provided the source of chemical variation to be exploited by further innovations. In general terms, a set of reactions can be described by a general reaction scheme
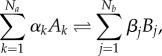 |
2.1 |
where αk, βj indicate stoichiometric coefficients associated with the Na substrates and Nb products of the reactions, indicated by Ak and Bj, respectively. However, too much chemical diversity can also make more difficult reacting molecules to find each other. The potential network of reactions rapidly explodes as shown in figure 1c, where only the 0.1% of organic molecules from a database is included [29]. In this context, the set of reactions shown in figure 1b is just a minimal subset of possible reactions, many of them leading to biologically irrelevant components. Two key questions in this context are (i) are there multiple molecular alternatives for a living biosphere emerging from the primitive soup, and (ii) what processes can drive the highly diverse molecular soup towards a non-random biochemistry?
The first question has been repeatedly addressed using a broad range of approximations and, strictly speaking, the answer is affirmative [32]. It is possible to obtain (or theoretically conceive) diverse and different types of organic molecules using solvents different from water and at extreme temperatures, with two universal limitations: the presence of non-equilibrium conditions and temperature intervals, allowing chemical bonds to form and break in reliable ways. In most of these alternative chemical scenarios, it is suggested that the candidate alternatives are feasible. However, feasible does not imply that the synthesis is likely to occur and—more importantly—what is needed to generate non-random mixtures of molecules.
To depart from chemical randomness, two classes of dynamical phenomena might have been relevant. One is connected to the chirality problem [33,34]. A characteristic pattern displayed by all biochemical species is a choice of one given configuration of molecular structures among the two possible (chiral) mirror forms (l and d): nucleic acids incorporate only d-ribose and d-deoxyribose, whereas proteins use l enantiomers of AAs. However, Miller-like experiments typically lead to a racemic mixture, where both types of handedness are equally represented. The rise of replicators capable of evolving Darwinian selection thus requires first solution of the problem of how to break this chemical symmetry. Evidence from chemical analysis of meteorites indicates that AAs display a slight asymmetry towards l forms. Because comets and asteroids might have been a major source of biomolecular precursors [35], a given asymmetry could bias handedness.
However, even if that is the case, the ideal scenario with a dominance of a single type of form requires an explanation. In this context, several models suggest that homochirality can spontaneously result from simple chemical reactions. The simplest model that accounted for this phenomenon included two types of chemicals, indicated by D and L and corresponding to the two forms [36,37]. They can react with an additional molecule A following the set of reactions
| 2.2 |
If we indicate by [D] and [L] the concentrations of the two forms, we can derive the equations describing the dynamics of this mixture and analyse them using linear stability.1 Let us indicate as ρ1 = [D] and ρ2 = [L] Assuming a constant population constraint (CPC) i.e. [D] + [L] = 1, we have
| 2.3 |
and
| 2.4 |
where the first two terms in the right-hand side correspond to the formation of molecules of each type and their conversion in A. The last terms introduce a dilution associated with an outflow. From the CPC, we have 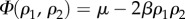 and it can be shown that
and it can be shown that
| 2.5 |
(a symmetric solution exists for [L]). The three equilibrium states are 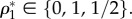 The first two are stable, homochiral states, whereas the third corresponds to an unstable racemic state. A symmetry breaking phenomenon takes place [17,18,22,23] where two alternative stable states ρ1 = 0, 1 are possible, both accessible from ρ1 = 1/2 through an amplification phenomenon. This can be seen using the so-called potential function Vβ(ρ1) defined from
The first two are stable, homochiral states, whereas the third corresponds to an unstable racemic state. A symmetry breaking phenomenon takes place [17,18,22,23] where two alternative stable states ρ1 = 0, 1 are possible, both accessible from ρ1 = 1/2 through an amplification phenomenon. This can be seen using the so-called potential function Vβ(ρ1) defined from
| 2.6 |
Here the potential2 is defined in such a way that its maxima and minima correspond to unstable and stable equilibria. This allows us to think of the potential as a mechanical system of balls rolling on a landscape towards the bottom of the valleys. The specific form of Vβ(ρ1) is shown in figure 2. Here, the (unstable) racemic mixture (D + L) and the two alternative (stable) homochiral configurations are displayed as empty and filled circles, respectively. Once we slightly deviate from the perfect racemic mixture, the ball rolls down towards one of the alternatives: the symmetry is broken towards a given chiral configuration [37–39].
Figure 2.
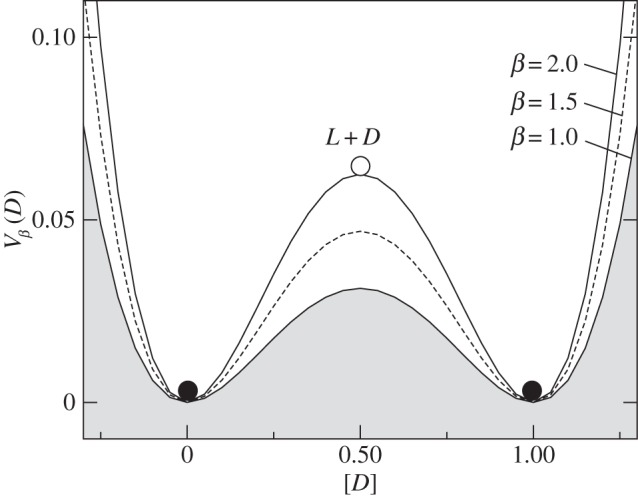
Symmetry breaking and the origin of homochirality. Using Frank's model (see text), the potential function 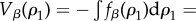
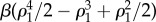 associated with the dynamics of a racemic mixture under the reaction set (1–3) is displayed (for different β). The unstable point (open circle) is associated with the ρ1 = 1/2 = ρ2 racemic mixture, which is unstable. Deviations from this symmetric state lead to either [D] = 0, [L] = 1 or a [D] = 1, [L] = 0 final state.
associated with the dynamics of a racemic mixture under the reaction set (1–3) is displayed (for different β). The unstable point (open circle) is associated with the ρ1 = 1/2 = ρ2 racemic mixture, which is unstable. Deviations from this symmetric state lead to either [D] = 0, [L] = 1 or a [D] = 1, [L] = 0 final state.
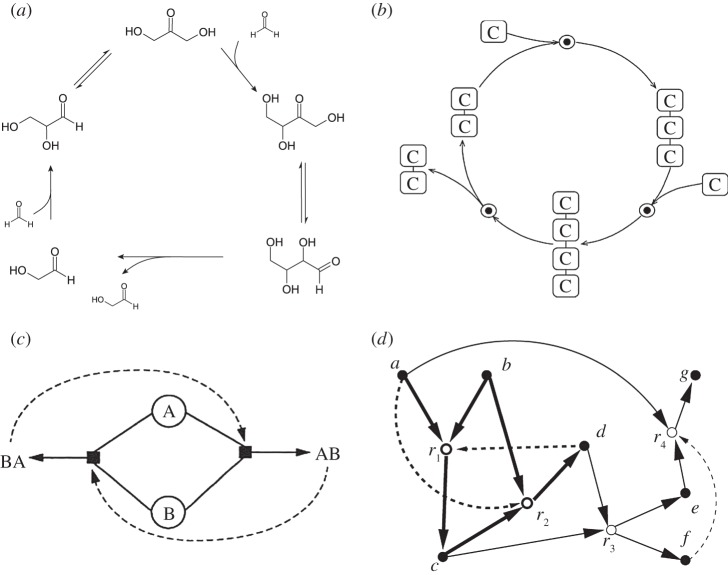
A different approach to the evolution of non-random sets of molecules is provided by autocatalytic sets (ACS, figure 3c,d) first proposed by Kauffman [40,41]. Here, in a rich chemical soup, closed loops of catalytic reactions can occur, leading to an ACS, defined as a set of molecules in which every member can be created catalytically by other entities within the set. An example (the only natural known example) is the formose reaction [42] (figure 3a,b). As discussed by Peretó ([43] and references cited therein) one of the fundamental questions that remains open is how the first autocatalytic cycles became incorporated into the chemistry of life. As pointed out by this author, one major goal of both models and synthetic approaches to prebiotic chemistry should address understanding how small networks involving inefficient reactions became large and dominated by efficient enzymes.
Figure 3.
Autocatalytic cycles. (a) The formose reaction involves the formation of sugars from formaldehyde. The overall reaction of the pathway above is of the form 2A + B → 2B, where A and B indicate formaldehyde and glycolaldehyde, respectively. As B cannot be created from A only, but the existence of B leads to more than one B, we say that B is an autocatalytic compound. A simplified picture of this cycle is shown in (b) where only the carbons are indicated. In (c), a two-member ACS is shown and in (d) a reaction network is shown including an ACS.
While waiting for further evidence from synthetic chemical networks, some relevant features of ACS are predicted by theoretical models, such as their potential for explosive growth. Consider an s-dimensional model with a set of s chemical species {x1, … , xs} such that 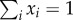 [44]. The model involves a set of coupled equations
[44]. The model involves a set of coupled equations
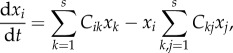 |
2.7 |
provided that xi, dxi/dt > 0. Here, 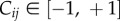 indicates the interaction strength between species i and j which can be cooperative (positive) or inhibitory (negative) and such that Ckk = 0. The model evolves exponentially (and inevitably) to a connected, diverse ACS. This type of phenomenon might have influenced the early evolution of RNA, as discussed in §3.
indicates the interaction strength between species i and j which can be cooperative (positive) or inhibitory (negative) and such that Ckk = 0. The model evolves exponentially (and inevitably) to a connected, diverse ACS. This type of phenomenon might have influenced the early evolution of RNA, as discussed in §3.
3. Synthetic molecular replicators
To address the problem of how self-replicating, information-carrying molecules emerged in the primitive biosphere implies considering the true nature of what separates chemistry from life. We know that the molecular logic of self-replication based on nucleic acids is the universal code of life. But is this the only possible logical scheme? Could it be based on different molecular supports? The earliest attempt that gave tentative answers to the previous questions was von Neumann's theory of minimal self-replicating machines [45]. Years ahead of molecular biology, von Neumann concluded that self-replicating machines should be composed of (i) a constructor, able to build a new system using the available raw materials, (ii) the instructions for the constructor, (iii) a duplicator which takes the instructions and duplicates them, and (iv) a controller required to guarantee a reliable process. This picture is surprisingly close to an algorithmic description of a biological replication event. More importantly, in our context, the agreement between this theoretical picture and reality suggests a universal logic of self-replication.
What kind of synthetic replicating systems can be constructed from biological and non-biological substrates? The first example of an experimental autocatalytic (figure 4a) set was obtained by von Kiedrowski. Using short nucleotide sequences that mutually catalyse each other's formation [46], other synthetic schemes have been proposed, including peptide ligation (figure 4b) systems [47] and several non-biological non-standard mechanisms [49], but also other mechanisms that even lead to exponential growth [48] despite lack of template-based replication (figure 4c). The synthetic alternatives to polymers indicate that other mechanisms can exist capable of generating large molecular structures. However, in general, they have also a very limited capacity of storing information, because the units included in their molecular assemblies tend to be homogeneous, thus preventing information growth. If a diverse polymer is a condition for any evolvable replicating system, potential candidates include RNA and RNA-based systems [50] because they can act both as catalysts and as templates, thus including both genetic information stored in a sequence and a phenotype derived from the catalytic properties of the molecule.
Figure 4.
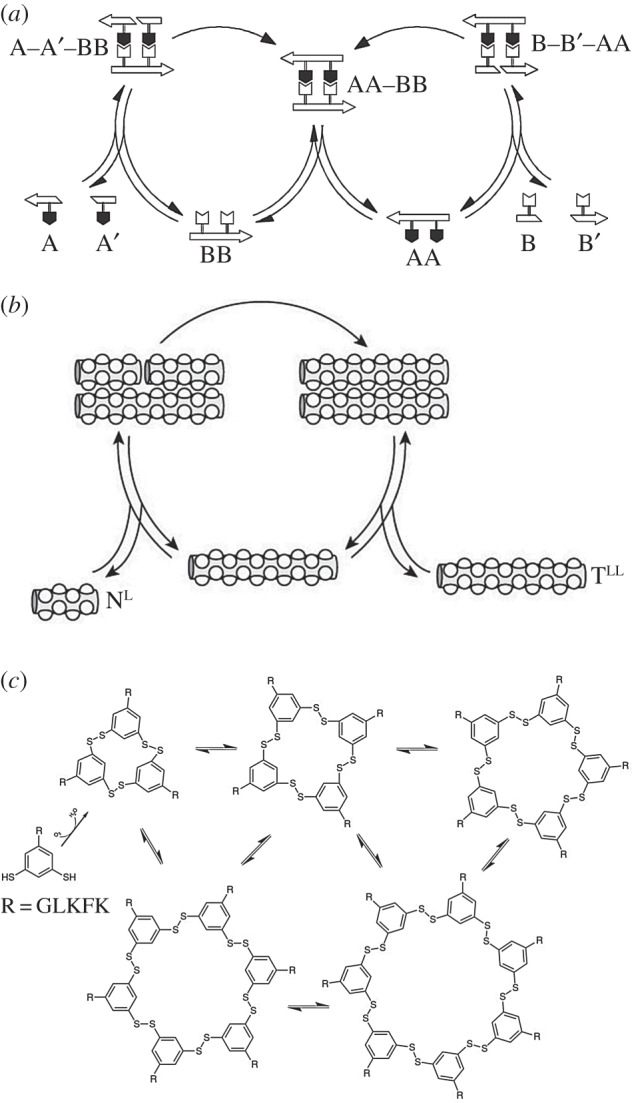
Synthetic molecular replicators: (a) von Kiedrowski's template-based replication (adapted from [46]); (b) Gadhiri's peptide ligation system (adapted from [47]). In (c), we show part of the replication mechanism presented in [48]. Here, a building block (R) containing two thiol functionalities leads to a mixture of growing cyclic structures. The hexamers self-assemble forming piled fibres that eventually break up. The number of fibres grows exponentially in time. Adapted from [48].
Many different experiments involving designed, simulated and evolved synthetic RNA molecules and ribozymes have revealed promising avenues as well as limitations. Interestingly, it was also shown that RNA molecules can cooperate [50] even forming ACS [51], thus supporting the picture of autocatalytic RNA networks. The presence of cooperative interactions might be a crucial component in defining the conditions for the success of early replicators in terms of phase transitions. In this context, artificial models of RNA networks provide us with evidence for a high probability of developing ACS under experimental conditions [52].
There is a very important reason to suggest that this class of RNA networks might have been a crucial condition for the growth of genetic information. Early theoretical arguments [53,54] indicated that there is a maximum length Lc associated with RNA chains that scales as the inverse of mutation rate μ (i.e. Lc ∼ 1/μ). Beyond this Lc, the system experiences a so-called error catastrophe, a phase transition where genetic information is lost. An elegant solution to this complexity limit was provided by the hypercycle, defined as a cyclic set of mutually enhancing catalytic components [55]. The hypercycle is a system in which autocatalytic replicators also heterocatalytically aid each other's replication, so that replication of each member is catalysed by at least one other member under second-order kinetics.3 A system of coupled reactions involving an RNA-based ACS (figure 5) was obtained by Vaidya et al. [51] showing that mixtures of RNA fragments self-assemble into self-replicating ribozymes through the emergence of evolvable catalytic cycles. The synthetic RNA system thus suggests that ACS could have been crucial to overcome some thresholds of survival and information storage.
Figure 5.
Experimental realization of a cooperative (ACS) cycle among ribozymes (adapted from Vaidya et al. [51]). Here, an intron ribozyme from Azoarcus can be broken into fragments that can covalently self-assemble by catalysing recombination reactions in an autocatalytic fashion.
A potential drawback of cooperative systems is that they can destabilize owing to the presence of parasites [56]. However, theoretical arguments indicate that compartments can strongly constrain their impact [57]. On the other hand, the appropriate nonlinear replication kinetics can also help a rapid expansion of replicators. To illustrate this idea, let us first consider a toy model [58] in which a set of replicators A cooperate and decay the following
| 3.1 |
If we use x = [A] to indicate the concentration of replicators, it is possible to show that
| 3.2 |
where a limiting value xmax = 1 has been introduced (this system exhibits three equilibrium points, namely x* = 0 or dead state, as well as two additional points)
| 3.3 |
The main result of this model is the existence of a discontinuous (first-order) phase transition separating the two possible phases. This is shown using the potential function associated with our system, namely
| 3.4 |
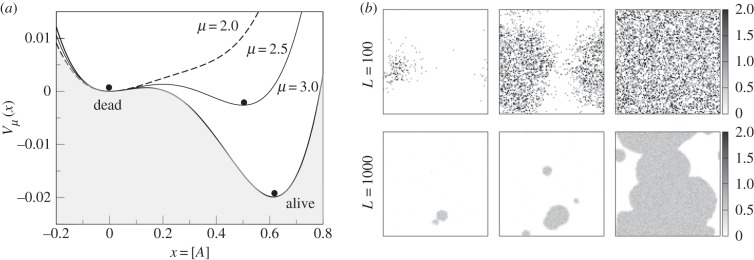
which is plotted in figure 6a. The minima defining the alive phase coexist with an alternative minimum where extinction is also an alternative possibility. When μ < μc = 2.25, a unique minimum is observable, associated with the extinction scenario (or dead phase), whereas for μ > μc, we will observe two minima, being the alive fixed point placed in a deeper valley.
Figure 6.
(a) Phase transition from death to living states. Using the simple model described in §3, a potential function shows the phase change that occurs once the cooperation parameter μ crosses a given threshold. (b) Phase transition in a synthetic RNA world with molecular cooperation on a two-dimensional space. Snapshots of the catalytic polymer concentration in the RNA polymerization model at the beginning (left), during (centre) and after (right) the transition from the dead state to the living state for different system sizes (L = 102, 103) and with local hopping rules. Adapted from Wu & Higgs [59].
A robust result leading to a phase transition from non-living to living was suggested by Wu & Higgs [59] by considering a spatially extended model of catalytic RNAs. The use of space is known to play a key role in stabilizing or even allowing some key replicator dynamics to occur. In the RNA system, two precursor molecules are available in the environment at concentrations F1 and F2. The RNA monomers, denoted by A, can be synthesized from F1. These monomers can react with F2 to produce activated monomers, A*. RNA polymers of length n are denoted An. An activated monomer can react with a polymer to extend its length. The transitions are now
| 3.5 |
and
| 3.6 |
Additionally, we also consider constant degradation rates for all molecules, which decay (or are removed) at a rate δ. The associated system of equations thus reads
| 3.7 |
| 3.8 |
| 3.9 |
where the total polymer concentration at all lengths is 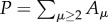 and the polymerization rate is given by r = r0 + kPn, with
and the polymerization rate is given by r = r0 + kPn, with 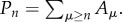 As occurs with the previous model, there is also a phase transition between a state with little or no polymerization and a ‘living’ state where the catalytic reactions lead to high polymer concentrations. If this is simulated using a discrete implementation, including stochastic fluctuations, a threshold of local concentrations must be crossed in order to switch to the living state. Once this occurs, the living state propagates through the entire space (figure 6b). The initial local transition can require a long time to occur, but the propagation is rather fast [59]. If we extrapolate this to the origin of life, this rapid spread might imply that early life just evolved once in our planet.4 In general, artificial models of spatially cooperative replicators with and without parasites reveal significant differences with respect to the mixed system [60–63].
As occurs with the previous model, there is also a phase transition between a state with little or no polymerization and a ‘living’ state where the catalytic reactions lead to high polymer concentrations. If this is simulated using a discrete implementation, including stochastic fluctuations, a threshold of local concentrations must be crossed in order to switch to the living state. Once this occurs, the living state propagates through the entire space (figure 6b). The initial local transition can require a long time to occur, but the propagation is rather fast [59]. If we extrapolate this to the origin of life, this rapid spread might imply that early life just evolved once in our planet.4 In general, artificial models of spatially cooperative replicators with and without parasites reveal significant differences with respect to the mixed system [60–63].
4. Synthetic genetics and xeno-codes
A crucial step towards a life-dominated planet required the establishment of a system able to expand and adapt under changing conditions. To such a goal, information and codes might have played a central role as a precondition for open-ended evolution. This requires the presence of both an alphabet and polymer strings as well as appropriate physical properties allowing the molecules to fold into compact structures. Molecular genetics grew along with information technology in the early 1950s. Many relevant terms, including coding and decoding, translation or transcription became adopted. A first glimpse of the possible nature of the molecular code of life was suggested by Erwin Schrödinger in 1944: the idea that an information-carrying molecule should be some class of aperiodic crystal [64].
An obvious question that has been raised by many different researchers is the uniqueness of the genetic code. All known organisms in our current biosphere share a common molecular synthetic genetic code [65] with very little variation in the mapping between codons and AAs summarized in figure 7a. What can happen if we scramble the letters of this diagram? Could different arrangements work as well as this one? The early days of decoding the genetic code soon revealed that the potential size n of codons should not exceed nor move below n = 3. Having 20 AAs as the building blocks of proteins and four nucleotides, small codons with n = 2 could only give 42 = 16 AAs, whereas for n = 3 we have 43 = 64 AAs and the genetic code would be able to account for the AA repertoire provided that some amount of degeneracy was present. Such degeneracy was known—from coding theory—to be a potential source of robustness, because errors in transmission can be compensated [66]. The uniqueness of the genetic code, along with some suboptimal traits, suggested that it might be a ‘frozen accident’ and thus opened the possibility for multiple alternative codes. Is DNA the only possible molecular option for our biosphere or just one among many?
Figure 7.
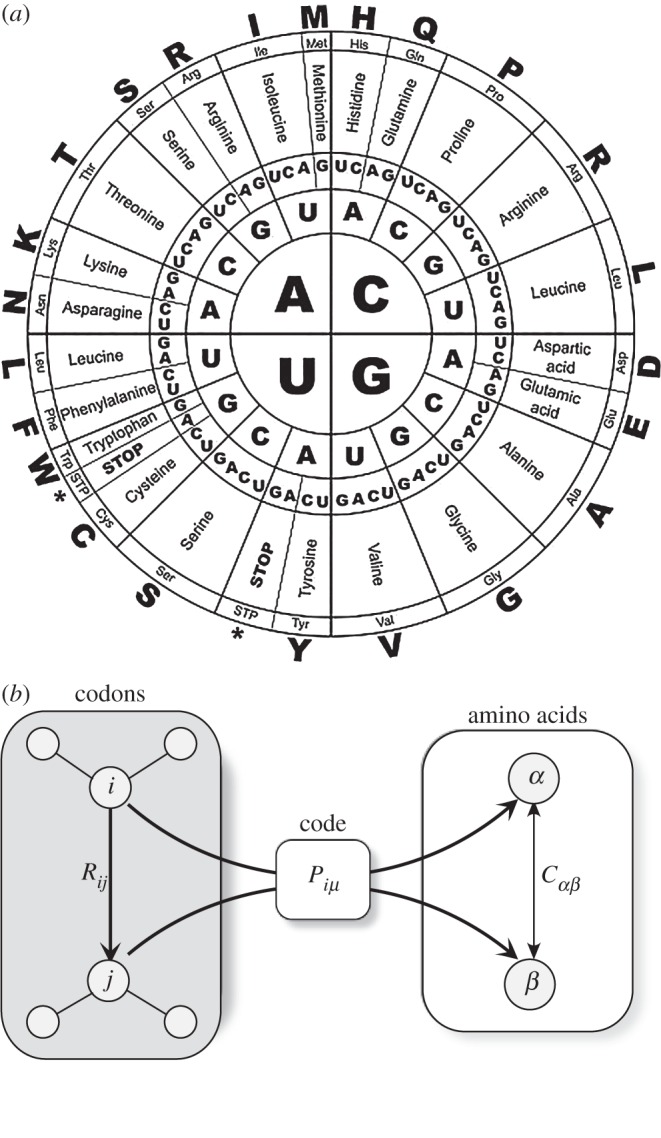
The universal character of the genetic code (a) and evidence for its optimality was obtained through an in silico analysis of millions of synthetic alternative codes, where the coding for amino acids (AAs) from the triplets defining codons has been randomly scrambled. (b) By treating the genetic code as a problem of information channels (b), we can find additional support for the optimality of the genetic code. Here, we indicate by Rij the probability of codon i being misread as codon j, whereas Piμ is the probability of codon i of encoding AAμ. The distance between AAs α and β is indicated as Cαβ.
Given the single-case scenario provided by all living forms in our biosphere, we need to consider ‘synthetic’ alternatives that can be reached either from computational models or through the experimental synthesis and analysis of new molecular codes. A systematic exploration of the space of possible codes based on n = 3 codons and their mapping into different potential AAs was performed [67,68]. Different genetic codes were randomly generated by partitioning the codon space into 21 non-overlapping sets and considering the impact of mutations on the efficiency of the code. Here, mutations to all codons were performed for each synthetic code and the change in AA hydrophobicity was determined. This property is connected to a very important feature of AAs (and proteins): how they interact with water. Hydrophobic AAs do not interact with water, whereas polar ones easily make contact with water. Different AAs have different hydrophobicities, and the analysis measured to what extent this parameter was changed by mutations. The sampled space included 106 alternative codes, much smaller than the potential 1018, but it nevertheless provides a strong argument in favour of the optimality of the natural code. In fact, when other biological and chemical constraints are considered, the possible repertoire shrinks to around 270 million alternative codes. When the frequency of codes against their efficiency (measured in terms of the error level) was obtained, it was found that the genetic code was the second best or, as the authors said ‘one in a million’. Here, we have a powerful case for optimality.
What are the conditions allowing a genetic code to arise? Are there here too phase transitions associated with the emergence of such codes? A model approach [69,70] developed by Tsvi Tlusty considers genetic codes as noisy information channels (figure 7b) with two sets associated with codons and AAs, respectively. An error-prone molecular reader (left) can sometimes lead to misreading of symbol i into symbol j, thus leading to a misread in the meaning space (right). The distance between the expected and actual outputs is also considered. Specifically, let us define three key quantities: (i) Piα, the probability that codon i = 1, … , Nc encodes the α = 1, … , Ns AA (thus we have 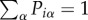 ); (ii)
); (ii) 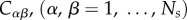 , i.e. the distance matrix separating two AAs (in terms of their hydrophobic properties); (iii) Rij the probability of misreading two symbols. We can then define the following three quantities. The first two provide a measure of the error load L and the code diversity D
, i.e. the distance matrix separating two AAs (in terms of their hydrophobic properties); (iii) Rij the probability of misreading two symbols. We can then define the following three quantities. The first two provide a measure of the error load L and the code diversity D
| 4.1 |
and
| 4.2 |
while the third weights the cost of the coding system, defined by
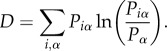 |
4.3 |
All these quantities can be obtained from the information channel description and allow a fitness function to be defined where code diversity is a positive entry whereas error load and cost introduce negative components. All the three constraints are combined by means of an energy function H to be maximized, namely H = −L + wDD − wcC with wD and wC being two parameters to be applied to many synthetic codes. The optimal code occurs at a phase transition point, where the mapping between codons and AAs moves from random (uniform) to non-random. Right at this point, the statistical regularities exhibited by the genetic code are recovered.
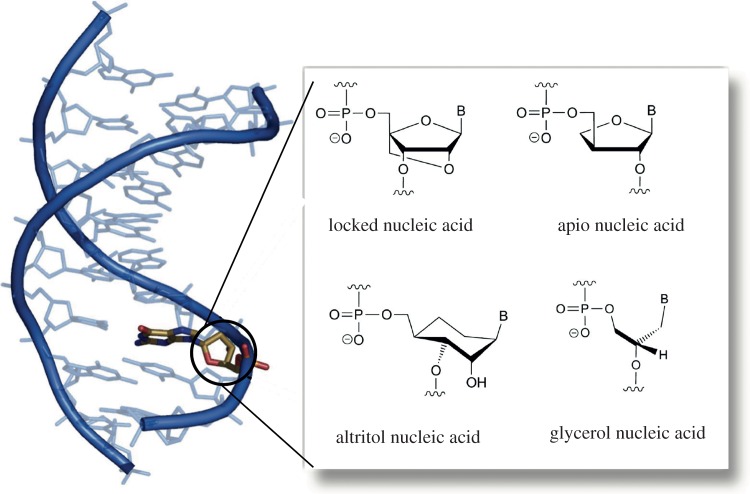
Beyond the in silico counterparts, synthetic biology offers the possibility of expanding the experimental repertoire defined by RNA and DNA. This can be done while including the potential for Darwinian evolution [71,72]. Moreover, orthogonal ribosomes have been synthetically evolved to decode quadruplet codons, thus allowing the encoding of unnatural AAs [73]. One particularly interesting path has been followed by designing, evolving and characterizing so-called XNAs [73] as well as synthetic catalysts (XNAzymes, see [74]) that allows one to speak of a synthetic genetics [75]. These studies have revealed XNA polymerase evolution, and the design allows alternative polymers to be used that can undergo Darwinian evolution. Examples of alternative backbones for a given XNA are shown in figure 8a,b. It is worth noting that the possibility of using glycerol and other simple molecules as an alternative backbone provides a valuable approach to the origin of the genetic code, because (as opposed to glycerol) ribose is a complicated sugar, less likely to be formed under prebiotic conditions [76]. The space occupied by the possible XNAs can be defined [72] where an idealized space of possible XNAs is constructed using three axes corresponding to sugar, base and backbone modifications, respectively. Most XNAs that have been studied so far (except peptide nucleic acid) lie on these axes. More divergent phenotypes should become accessible through a fuller exploration of the XNA space, that is, the replication and evolution of XNAs comprising a combination of modifications to base, sugar and backbone.
Figure 8.
The XNA alternatives for synthetic genetics. Several promising candidates have been designed and tested using a growing list of structurally diverse XNAs. The right panel shows several examples, each capable of undergoing Darwinian evolution.
5. Synthetic cells
An old saying of biology is that ‘every cell comes from another cell’. This statement connects us with our ancestral cellular origins through billions of years old tree-of-life forms. The cell is the most obvious minimal unit of life and its origin is one of the crucial steps towards our understanding of METs. Both synthetic and virtual protocells have been designed and explored in searching for the requirements needed to move through a whole cycle of growth, instability and division [77–80]. Cells might have been a precondition for an expansion of complex life. In particular, compartments might have been essential to escape from parasitic replicators and a powerful way of enclosing together the right reaction components at reasonable concentrations.
The challenge of creating an artificial cell has been addressed in both top-down and bottom-up approaches (figure 9). In the former, we start from existing genomes, because numerous genes are involved in cell–cell communication while others have been shown to be non-essential to cell functioning; it was earlier suggested that it would be possible to reduce genome complexity to a minimal set of N genes able to sustain metabolism and reproduction. Computational and theoretical arguments suggest that N ≈ 200–250 genes could define a minimal genome [81,82]; although the smallest synthetic cell has been obtained using N = 473 essential genes [83] the function of 149 of them is unknown.
Figure 9.
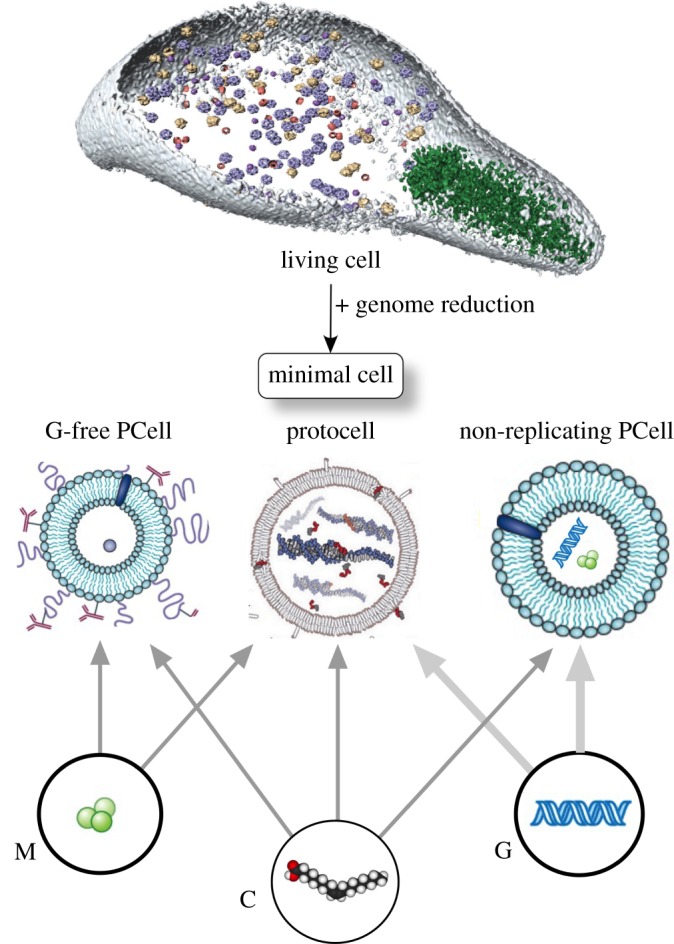
Pathways towards synthetic cells. Two major approaches to create an artificial cell involve either a top-down or a bottom-up approach. The first starts from a living, complex cell such as Mycoplasma sp. (top) and proceeds through genome reduction. The second makes use of a molecular toolkit from which different forms of assembly produce different types of artificial protocells.
The second, bottom-up approach is closer to chemistry and deals with the creation of protocells from the assembly of interacting chemical components [77]; it thus involves a major transition between non-living and living matter. In figure 9, we depict this as a combination of three potential ingredients, namely metabolism (M), compartment (C) and genetic information (G). They can be combined in different ways, including a complete protocell capable of self-maintenance and self-replication (M + C + G) but also information-free systems (M + C) or even non-replicating systems, where polymer self-replication might occur but not self-reproduction. The latter would correspond to a limit case involving liposome-like systems capable of self-maintenance but not self-reproduction. The crucial problem is how these three components (none of them defining life) need to cooperate among each other in order to lead to a self-replicating macromolecular entity.
Most models and implementations of protocells make use of either micelles or vesicles (figure 10a) as compartments. A canonical protocell model is provided by a so-called autopoietic system (figure 10b) where P and S stand for the membrane precursor and the surfactant molecules, respectively [79]. Here, P is transformed into S which is incorporated in the vesicle. If a vesicle Sk is made of k monomers, and assuming that monomers can degrade, we have
| 5.1 |
Figure 10.
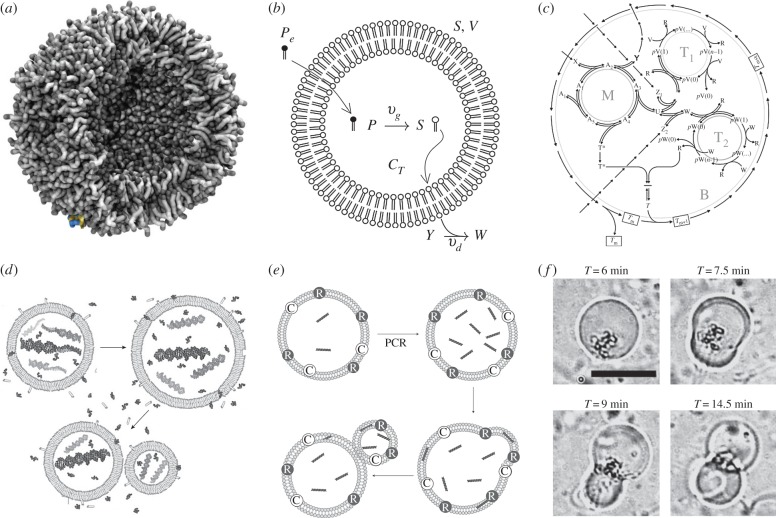
Synthetic protocells. (a) A common component of most protocells is a spherical vesicle involving a lipid bilayer. In (b), we show a minimal model of an autopoietic cell, where an external precursor P gets transformed into surfactant molecules S and can also degrade under the presence of a given Y, into a waste product W. Here, S,V and Vc stand for external surface, total and internal volumes, respectively. One version of Ganti's chemoton is shown in (c). Here, the metabolic cycle is indicated by M = {Aj} and zk are external resources. In this example, two types of templates, indicated by T1, T2, coexist in the same cell. Three different synthetic protocell cycles are shown in (d–f): (d) an RNA-based heterotrophic protocell [84]; (e) Kurihara et al.'s model [85] and (f) after [86].
The balance between growth and division determines the outcome of the protocell dynamics. If we indicate by vg and vd the rates of single events (figure 10b), then the vesicle would follow d[S]/dt = (vg − vd)[S] and its solution is thus
| 5.2 |
Three potential regimes are allowed by this kind of kinetics: (i) growth, when vg > vd, (ii) homeostasis, for vg = vd and (iii) collapse, when vg < vd [79]. Under this rather crude approximation, the system would be stable at criticality and capable of undergoing growth and division cycles provided that vg > vd.
Ganty's Chemoton model (figure 10c) provides an example of an explicit proposal for a protocell where several coupled cycles involving M + C + G are considered [80]. The model is spatially implicit and thus does not take into account the requirement for membrane instabilities: once a critical amount of material components have been accumulated, the model artificially splits the cell into two equal parts. The chemoton allows the study of different relevant problems related to the role played by template competition and error thresholds [87].
A major problem arises when dealing with an explicit implementation of the physics of compartments, particularly in relation to the instabilities required for replication to occur. While the process of vesicle or micelle formation has to do with a minimization of energy leading to a more or less symmetric structure, the growth-instability process involves an out-of-equilibrium procedure.5 To destabilize the system, the symmetry of the spherical configuration needs to be broken. In this context, the container and its coupling with metabolism and information define genotype–phenotype mapping [88,89].
The efforts aimed at creating an artificial cell must deal with different ways of triggering membrane instabilities leading to cell division. All these systems share a given environment where available membrane precursors are required to achieve a critical size. Current living systems share genetic control of cell division, but early stages in the evolution of protocells must have been dependent on the physical properties of membrane curvature. Theoretical models address this in two main ways. The first class uses a parameter ϕc (the so-called reduced surface6) defining the critical value associated with vesicle division. Here too, a phase transition scenario is present. A general condition for achieving a cell division cycle has been derived [90,91]. A simple example close to the autopoietic cell would be a self-reproducing enzymatic vesicle where the key reaction is given by
| 5.3 |
with E being, for example, an enzyme located inside the vesicle and n waste molecules being released. This model is a good approximation to some experimental set-ups using giant vesicles (GVs) that produce inside them, with the help of a catalyst, the main membrane component [92]. For this system, it can be shown that the critical balance obtained when
| 5.4 |
where rL = k[P]/NAV and ξ is the membrane permeability. Equation (5.3) provides a critical condition required to achieve cell division. Moreover, it introduces constraints between different components of the system and their couplings.
The second class of models gets closer to the physics of membrane instability by explicitly considering this factor as part of the process. Here, the use of the membrane energy is required.7
Mathematical and experimental investigations of vesicles show that phase transitions separate spherical from asymmetric vesicles associated with symmetry breaking [93]. The explicit energy associated with synthetic protocell growth has been introduced in different ways. These include pattern formation through Turing instabilities [94] or micelle-metabolism coupling in nanocells [95–97]. These artificial cell models suggests that instabilities can be easily generated provided that a given molecule gets asymmetrically distributed within the vesicle, thus creating spatial inhomogeneities. Alternatively, the packing of lipid molecules into a given spherical aggregate is strongly constrained by the shape of the surfactants. When a critical number of these molecules is reached, the aggregate is no longer stable.
Synthetic protocell reproduction has been experimentally investigated, using a diverse range of settings. None of them has been successful so far in showing a full, simple cell cycle following the growth-deformation-instability-division process. One candidate is a container (made of simple amphiphiles) that encloses oligonucleotides and uses a template copying mechanism that operates within the cell [84]. The interest of this system (figure 10d) is how prebiotically reasonable membrane compositions can be enough to provide a system capable of division driven by both internal and external forces. Other successful strategies have used different alternative ways of departing from the spherical symmetric compartment. An example of these synthetic systems (figure 10e) involved a GV-based model enclosing DNA molecules that are amplified through PCR [85]. In this system, membrane precursors are provided and the amplified DNA moves within the two lipid layers, triggering a local growth and budding process that ends in vesicle division. In another setting [86], the artificial cells contain RNA encoding a self-encoded RNA replicase that can be evolved over time. The artificial evolution experiments show that self-replication occurs (figure 10f) with the use of PCR and the input of a fresh translation system under vigorous mixing.
All these examples require the help of some extrinsic factors to trigger or facilitate instability. In that respect, synthetic versions of protocells suggest that the path towards spontaneous instability and division might be more difficult than expected. However, there is also another possibility: that the origin of protocells might have required such extrinsic factors to occur. In this context, very active research has also been done exploring the emergent properties associated with membranes [98]. One particularly important finding is the potential role played by vesicles as functional promoters and regulators of chemical reactions [99]. Moreover, synthetic vesicles can compete and interact in nonlinear ways providing further layers of complexity beyond simple compartments [100–102].
6. Synthetic multicellularity and organismality
Multicellularity has evolved multiple times through the history of our planet [103–105]. This transition has taken place in either increased aggregation and adhesion of cells (as occurs with myxobacteria and some slime moulds) or loss of cell separation after cell division (this includes bacteria and ciliates). Most classical models of the transition to multicellularity ignored physical interactions between cells within cell aggregates. In this context, these models [106] have been formulated in terms of a two-loci dynamical system where the transition implies an increase of cooperation among cells together with the regulation of conflict within the emerging organism. However, spatial structures create novel conditions that necessarily affect the fitness of the multicellular assemblies. Considering the embodied nature of these aggregates is not only required as an additional feature but also it can actually be crucial to understanding the transition itself. It is worth noting that the use of physical models of multicellularity reveals that even under very simplistic assumptions, complex forms easily emerge [107–112].
The transition to multicellularity required the presence of alternative cellular states along with stable, physical interactions among previously isolated cells [113–115]. Extant multicellular systems develop under tight controls of genetic networks [116,117]. Synthetic multicellular systems can be obtained in several ways, from non-clonal adhesion–differentiation processes to engineered consortia. In this context, developmental properties necessarily need to overcome thresholds of organization intimately connected to transition phenomena. It has been suggested that a small set of dynamical patterning modules (DPM) might have played a major role in the evolution of complex organisms. These DPM affect adhesion, diffusion, cross-inhibition or synchronization of cellular and tissue-level interactions through a set of key molecular actors [118]. In this context, artificially evolved multicellular aggregates [119], synthetic multicellular analogues [120] and their model counterparts [121–123] have shown potential for novel explorations of an old issue.
A successful strategy to create synthetic multicellular systems was put forward in a recent set of experiments [119] in which the authors sequentially subcultured Saccharomyces cerevisiae cells with the fastest sedimentation in order to force the selection of cooperating aggregates (figure 11). Remarkably, after just 60 selection rounds, the so-called snowflake phenotype appeared consistently in all cultures (figure 11b). These are roughly spherical clusters of cells formed not by aggregation but by defective separation of cells after division. It was found that clusters did not reproduce through events associated with single cells but instead involved a group-level set of events. This was achieved through a division of labour in the form of the active control of apoptosis, which caused the asymmetrical splitting of the cluster once it reached a threshold size [119].
Figure 11.
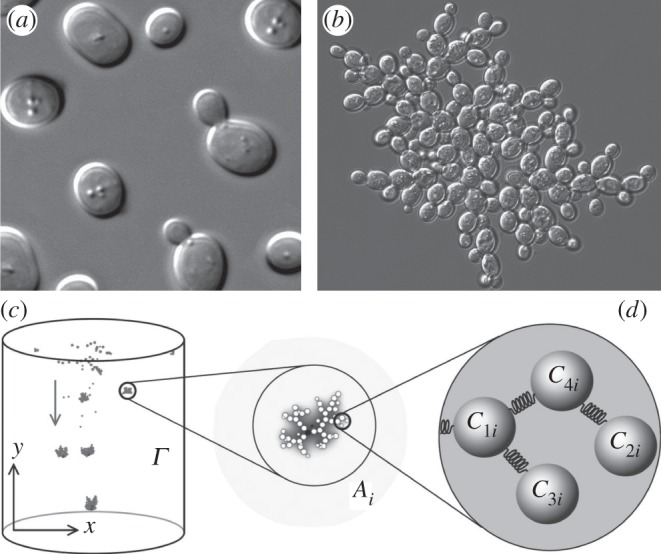
Synthetic evolved multicellularity. Using yeast strains (a) involving single-living cells (image from https://en.wikipedia.org/wiki/Yeast), it has been shown that selection favouring the formation of aggregates (b) leads to the emergence of multicellular systems (image courtesy of W. Ratcliff). This type of experiment can be easily modelled using embodied simulations (c) where wells are represented as physical objects that can adhere to each other.
To understand the origins of these multicellular structures, a simple model was developed [122] that was also used to test other potential scenarios for the rise of multicellular ensembles (figure 11c). Here, yeast cells and their interactions are simulated using a physical embodiment, with evolving adhesion rates. The model was able to reproduce the reported patterns in cluster size distributions and localized mortality. Moreover, the model suggests an alternative pathway to cell clusters and their fission based on a passive apoptotic effect of nutrient deprivation in cells at the centre of the aggregate.
An interesting observation in this area is the presence of a blurred zone at the boundaries separating some single-celled species from fully-fledged multicellular entities. Bacteria in particular exhibit multicellular traits [124], especially in the face of high-stress events [125,126]. Simple multicellular systems, such as Anabaena or myxobacteria are such examples of minimal multicellular organization [127,128] that can involve primitive developmental programmes. A minimal form of multicellularity comprises persister cells associated with cell subpopulations that can spontaneously switch back and forth among multiple resistant phenotypes, as a bet-hedging strategy [129,130]. Can this mechanism pre-date the transition to the first complex multicellular life forms? This is connected to the origins of what Queller and Strassman named organismality [131]. Specifically, it would be important to know whether primitive forms of cell adhesion and diffusion under selective conditions can lead to proto-organisms where division of labour is tied to spatial organization.
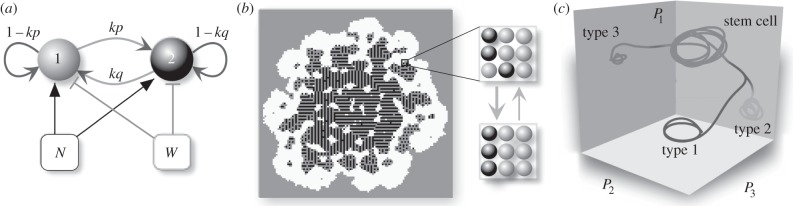
A minimal model has been proposed for the origins of proto-organisms [132] and is summarized in figure 12a–c. It includes (i) multistability, using a stochastic bistable phenotype, (ii) differential adhesion, and (iii) a selective environment involving both nutrients (N) and harmful (W) diffusible molecules. Cells are distributed over a two-dimensional lattice Ω. The two cell types need N to grow, whereas W causes increased cell death (figure 12a). Only cells of type 2 can degrade waste in the medium, at the expense of reducing their growth rates. Under appropriate metabolic trade-offs, it was shown [134] that evolution of undifferentiated multicellularity might pervade the coexistence of cell clusters. By adding adhesion, it can trigger the formation of proto-organisms (figure 12b,c). The result is the emergence of nested substructures and the creation of an internal environment. These results suggest very simple sets of pattern-forming rules can produce a rich, largely unknown landscape of structures predating the evolution of multicellular organisms [132,134]. Other types of similar proto-organisms have also been obtained by models involving dynamic differentiation under isologous diversification [133]. In this type of model, cell types are dynamical attractors in a high-dimensional landscape of expression (figure 12d).
Figure 12.
Emergence of in silico proto-organisms. A simple spatial model can lead to complex multicellular assemblies involving organismality. Using (a) a two-state model of cells with division of labour, a complex spatially organized system emerges (b) as a result of artificial evolution under a selective medium where both nutrients and waste are present (see [132]). The spatial dynamics is driven by a model of differential adhesion (c). A different class of model involves considering cells as complex networks whose phenotypes (P1, P2,…) are defined by attractors derived from stem cells [133].
Synthetic biology offers a unique opportunity for testing theories concerning the origin of multicellularity as well as the emergence of developmental programmes. Engineered cellular communication has already been achieved in different contexts, allowing the creation of novel cellular consortia [78,135,136]. By engineering unicellular systems, it is also possible to obtain novel forms of multicellular assemblies, able to carry out complex computations [137–139]. Finally, cell reprogramming and tissue niche engineering have shown the way to design synthetic tissues and organs [140,141] and explore synthetic development and its limits [142].
7. Synthetic symbiosis
Symbiosis refers to a scenario where once independent replicators come to live together in close association [143]. This association is typically tied to a physical interaction that often involves one partner embedded or in close contact within the other and the system experiences vertical transmission [144]. This close relationship can be parasitic or mutualistic. In the first case, one partner (the parasite) exploits the second, with no return from the former. Mutualism describes a mutually cooperative loop where both partners help each other.
What is the basis for the emergence and persistence of symbiosis? As with most of our previous examples, definitive answers might be difficult to obtain by studying natural systems. Instead, synthetic counterparts provide a powerful approach to the problem and several examples illustrate how to create de novo mutualisms. Synthetic biology has been successful in showing that different types of symbiotic relationships can be engineered in novel ways [145–149]. Different strategies have been followed, including: (i) design of auxotrophic interactions (figure 13a) creating a synthetic cooperative loop (a hypercycle) where each partner needs a molecular factor produced by the second [150] and (ii) transformation of plant pathogens into legume symbionts [154,155]. The experiment started from a designed chimeric strain of a plant pathogen carrying a symbiotic rhizobial plasmid from a plant endosymbiont (figure 13b). The initial strain evolved to a full endosymbiont after two key mutations allowing nodulation and plant cell infection. Here, niche engineering provides an additional approach to the problem, where two chosen non-cooperative species are made to coevolve under a forced exchange of carbon and nitrogen. The outcome of this experiment was a synthetic transition from free living life forms to obligate mutualists [151].
Figure 13.
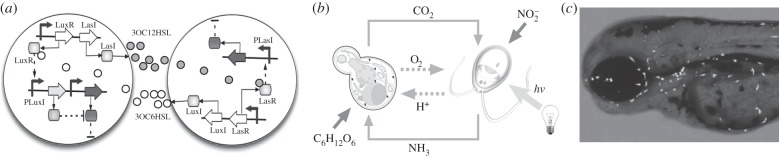
Synthetic symbiosis. (a) A cooperative synthetic system involving designed auxotrophic interactions [150]. (b) Synthetic mutualism resulting from niche engineering. Here, two species interact through a metabolic circuit based on carbon and nitrogen exchange. S. cerevisiae (left) metabolizes glucose (C6H12O6) releasing carbon dioxide (CO2), which is then assimilated photosynthetically by C. reinhardtii (right) to release oxygen (O2). On the other hand, C. reinhardtii metabolizes nitrite (NO2) and releases ammonia (NH3) as a nitrogen source for S. cerevisiae [151]. In (c), we display a microscope image of a chimaera zebra fish embryo containing living photosynthetic cells [152,153].
A last example is given by synthetic designed chimeric organisms (figure 13c). Here, photosynthetic microorganisms were injected into zebra fish embryos [152,153] as well as mammalian cells [152]. Such types of symbionts exist in nature and have been found in different phyla [156]. Here, the photobiont uses solar energy to provide reduced carbon as a source of energy to the metazoan host, which can provide nutrients in return. Successful invasion of mammalian cells (macrophages) by algae was improved by engineering the photosynthetic cells with invasins [152]. Interestingly, the algae remain alive and even reproduce while embryonic development takes place. This opens the possibility of future plant–vertebrate chimaeras where an additional engineering level would allow the production of useful metabolites other than oxygen [153,156].
The in silico approach to the emergence of symbiosis has also been successful and insightful, specially from computer models of evolving digital genomes [157]. The best-known example was given by Tom Ray's experiments with the Tierra model, based on a set of replicating and mutating computer programs competing for computer memory (the resource) [158]. After a first selection for shorter, faster replicating programs, shorter programs emerged, but were unable to replicate by themselves: parasites came to (digital) life. Similarly, in the long run, groups of slow-replicating programs were able to replicate faster by cooperating among themselves. Digital evolution supports the idea that the emergence of parasites might be an inevitable outcome of evolutionary dynamics [159,160]. One particular instance of man-made synthetic parasites is provided by the evolution of computer viruses (CVs). After their early appearance, CVs became more and more complex and diverse [161]. A crucial step in the historical development of CVs involved in the creation of internal sources of variability that mimicked natural mutations. Variability was thus an invention, and a rather intentional one, as opposed to the intrinsic, inevitable errors that constantly take place in living systems. Moreover, in contrast to the typically harmful effect of mutations on viral genomes, random changes in CVs have no impact on their viability: here no interactions are allowed to occur affecting functional traits. CVs eventually evolved towards more silent, apparently harmless designs based on their potential to ‘integrate’ themselves within the host machines, where they remain undetected [162,163].
8. Synthetic cognitive agents and swarms
The emergence of a special class of biological agents, the neural individuals [164] introduces a new layer of complexity: the rise of behavioural systems [165]. In this case, information transmission and processing is done within individuals. Here, behaviour can be defined in terms of patterns of interactions between individuals and their environment where the actions of the organism and its perceptions interact, eventually affecting future actions and perceptions. Here, we will consider two broad classes of synthetic cognitive systems and the key conditions for their emergence or synthesis: (i) individual cognitive agents and (ii) societies, i.e. large sets of interacting agents displaying colony-level behaviour. The latter are tied to the problem of how cooperative societies came about and how such swarm intelligence can be engineered. Walter's work in particular was the first systematic cybernetics approach aimed at creating robotic agents (figure 14a) [166–169], and using the term synthetic animals to refer to this class of automata capable of autonomous behaviour [170]. These simple autonomous robots were capable of some complex behavioural responses, including unexpected ones, as occurred when facing mirrors [168]. These and later [171] synthetic animals revealed an interesting (and largely unappreciated) feature, namely that the complexity of embodied agents was not just the result of their cognitive complexity, but of their interaction with the environment [172].
Figure 14.

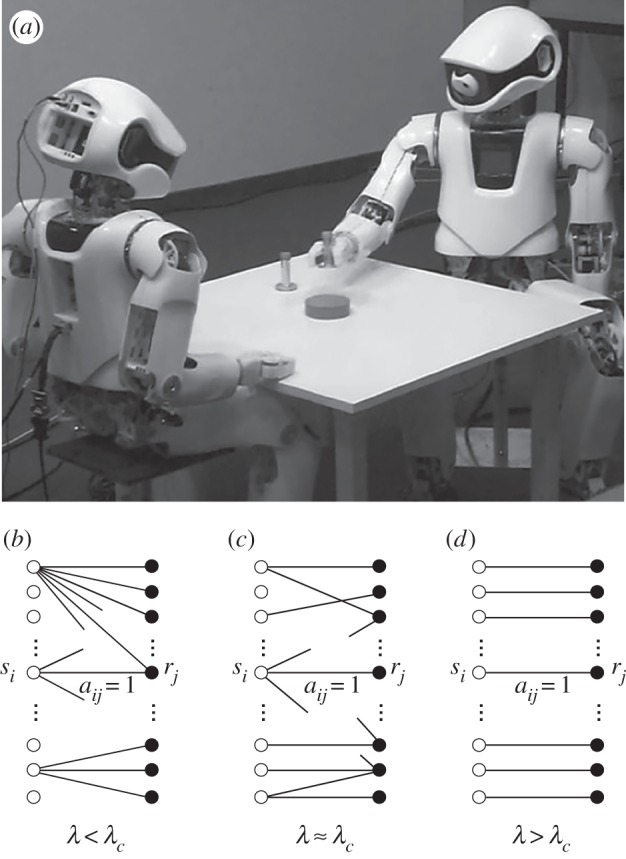
One of the first ‘synthetic animals' (a) was built by Grey Walter. It involved a simple wheeled robot with sensors and actuators and reacting to light in different ways. Mixed synthetic swarms have been created by communicating cockroaches and their robotic counterparts (b) in order to solve problems collectively. Robotic swarms (c) made of many small robots following simple rules of interaction, can self-organize using self-assembly rules.
One of the most active areas within robotics is grounded in a combination of designed and evolved agents [173–175]. Evolutionary robotics takes advantage of the search over parameter spaces by means of artificial Darwinian selection, which allows the synthesis of autonomous agents [174]. This field has clearly confirmed that behaviour is the emergent outcome of the interactions between the agent and its environment. The subsequent development of behaviour-based robotics has also been very useful as a pathway by which to approach relevant evolutionary questions [173]. An example is the transition from swimming to walking, which was required in the transition from sea to land. Inspired by the anatomy and behaviour of salamanders, a model of the central pattern generator of synchronized neurons controlling locomotion was used as a starting point for evolving its architecture and parameters to allow a switch to the walking gait of a tetrapod consistent with available information [176,177]. This is a powerful illustration of this field as an alternative path to uncover evolutionary innovations.
Collective intelligence and its potential synthetic counterparts need to be considered separately. The emergence of the superorganism requires crossing the so-called eusociality threshold, which involves overlapped generations, division of labour into reproductive and non-reproductive subsets and the maintenance of genetic relatedness [178,179]. Interestingly, Oster & Wilson [179] explicitly mention the potential relevance of phase transitions in understanding the organization of castes in social insects. What about the synthetic counterparts? Is it possible to evolve or engineer synthetic swarms? It has been pointed out that one precondition for the origin of societies of insects was a ‘get together’ rule that should operate after individuals are born. This is a key requirement in order to achieve a cohesive group. However, less importance has been given to the fact that, when such a step has been achieved, group responses resulting from phase transitions emerge too [18,180–182]. Here also, interactions among individuals can trigger system-level responses provided that critical thresholds are reached [18,181,183].
These transitions provide the group-level dynamics required to perform different types of tasks. A specially relevant example in our context is provided by an experiment that combined mixed societies of artificial and natural agents [184,185] including both real and robotic cockroaches (figure 14b) that have to perform a two-choice decision between two shelters. The robots were shown to modulate the collective decision process leading to a pattern that cannot occur in their absence. In other words, the artificial component of the mixture forces proper swarm behaviour to occur and test the hypothesis concerning the origins of swarm intelligence. Moreover, the use of robot swarms or simulated agents working on a given spatial domain provided insights into eusociality [186–189]. Novel ways of implementing large numbers of robotic swarms [190,191] capable of using self-assembly rules (figure 14c) have also been engineered.
Microbes are also capable of integrating sensory information, storing memories and displaying different levels of behavioural control [192–194]. They thus incorporate several relevant components required to build or design complex decision-making systems. In some cases, the ways microbial colonies respond to environmental challenges can be easily classified as a swarm intelligence problem [192]. Alternatively, many well-known examples of collective decision-making could be engineered using modified microorganisms [195] capable of implementing computational tasks with no known counterpart from the microbial world.
An interesting outcome of the study of natural, synthetic and robotic systems is the presence of seemingly universal decision-making rules of organization. Group responses displayed by ant colonies are based on so-called quorum sensing (QS) mechanisms [196] also displayed by microbial populations [197]. The QS rule, as well as other amplification mechanisms, pervades phase transitions between individual, disorganized behaviour (ants search individually) and colony order (collective search towards a given nutrient source). Here, a signal (a pheromone, for example) φ triggers its own production with constant rate μ and is proportional to the population density ρ. The signal is produced following a function f(φ) by individuals (present at a given density ρ) and decays at a rate δ [195]. The minimal model that captures this is: dφ/dt = fρ(φ) − δφ. A common form of f(φ) is a so-called Hill-like function8 namely
| 8.1 |
which gives small values for φ < θ and large values otherwise. Close to the threshold θ, it rapidly increases. The potential function now reads
| 8.2 |
and in figure 15, we show three examples for subcritical, critical (ρc = 0.5) and supercritical densities. For ρ < ρc we can see that the only stable state is the φ* = 0 point, as expected, but the shape of Vρ(φ) is clearly deforming as we approach ρc.
Figure 15.
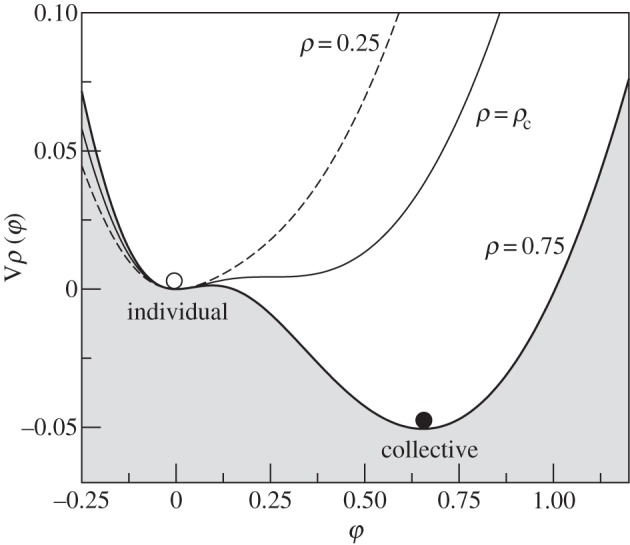
Phase transitions from individual to collective response through a QS mechanism, as described by Vp(φ). Here, the state of the system is described by a global field φ that is proportional to the system's activity. Here, we have fixed μ = 1, θ = 0.25 and δ = 1 (thus ρc = 0.5) and different values of ρ are used: ρ = 0.25, 0.5, 0.75.
Ant colonies have often been compared with brains and neural networks [198,199]. The analogy is approximate but useful, because it allows finding universal laws too. Both ant colonies and brains process, store and use information about their environments while monitoring internal colony states. However, ant colonies are made of agents in movement, thus defining a different state of matter compared with grey matter: insect colonies are fluid neural networks [200–202] and thus some of the crucial features of a standard neural network are not present in the swarm. Is the fluid state a constraint for developing more complex cognitive capacities? Are ‘solid’ and ‘fluid’ neural systems the only two solutions available? Future work might shed some light on the invention of eusociality [203] and the implications for defining universality classes of cognitive complexity.
9. Synthetic languages
The transition towards a complex language is a recent one and had an enormous relevance to human evolution. It is also a hard problem [204]. One of the obvious facts is the gap between the complexity of human language and any other known biological communication system. The gap is due to the presence of a grammar that allows the generation of recursive structures of potentially infinite complexity [1,205]. Another crucial observation concerns language acquisition in children. Around 2 years of age, the sequence of utterances babbling–one word–words is replaced by full sentences [206] and children develop grammatical competence, suggesting that this is an indication of an innate capacity of language [207,208]. Grammar effectively defines the mapping between linguistic forms and meanings. In its original formulation, Chomsky introduced the concept of universal grammar (UG) to describe the hardwired ‘linguistic theory’ that is shared by all human brains and allows children to search the (large) space of possible human grammars [209].
Two main avenues have been followed to study the transition to language using artificial systems. One involves theoretical and computational models including: (i) standard replicator equations [122,210]; (ii) information theoretic approaches [211,212]; (iii) statistical physics [213,214]; or (iv) the simulation of discrete agents [215,216]. The second class deals with physically embodied, robotic agents capable of sensing and tracking their environments while naming and sharing objects and actions [217–219]. In most of these artificial models, qualitative (phase) transitions are also at work.
Several transitions are involved in language complexity [220]. First, consider the evolutionary dynamics associated with the emergence of language coherence [221]. Let us assume that a set of possible rules 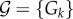 (with k = 1, … ,n). Each Gk can generate ‘valid’ messages. These have been identified as ‘grammars’ in previous studies [221], but the general approach can be applied to other features of language, including the inventory of shared words. Different Gs can have similar rules, and thus are capable of generating some common sentences. How can a search over a very large space
(with k = 1, … ,n). Each Gk can generate ‘valid’ messages. These have been identified as ‘grammars’ in previous studies [221], but the general approach can be applied to other features of language, including the inventory of shared words. Different Gs can have similar rules, and thus are capable of generating some common sentences. How can a search over a very large space 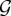 end in a common, shared grammar? We will define A = (aij), where aij indicates the similarity between Gi and Gj. If two individuals are communicating by means of two different grammars, the pay-off associated with this exchange will be F(Gi, Gj) = (aij + aji)/2 and the frequency of agents using the ith grammar follows a replicator–mutator equation
end in a common, shared grammar? We will define A = (aij), where aij indicates the similarity between Gi and Gj. If two individuals are communicating by means of two different grammars, the pay-off associated with this exchange will be F(Gi, Gj) = (aij + aji)/2 and the frequency of agents using the ith grammar follows a replicator–mutator equation
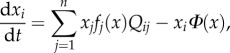 |
9.1 |
where 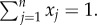 Moreover, we have
Moreover, we have 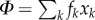 and the matrix Qij is the probability that an agent learning Gi from an individual ends using Gj instead. This introduces a noise in the model. If we assume the simplest, super-symmetric model where aij = a, and such that
and the matrix Qij is the probability that an agent learning Gi from an individual ends using Gj instead. This introduces a noise in the model. If we assume the simplest, super-symmetric model where aij = a, and such that 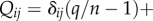
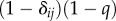 with δij = 1 if i = j and zero otherwise, here, q is a learning parameter and one solution is xi = x and
with δij = 1 if i = j and zero otherwise, here, q is a learning parameter and one solution is xi = x and 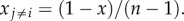 Assuming that
Assuming that 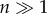 (a crude approximation, because x ∼ O(1/n) solutions are replaced by a zero) then the mean field equation follows
(a crude approximation, because x ∼ O(1/n) solutions are replaced by a zero) then the mean field equation follows
| 9.2 |
where η = (a + f0)(1 − q). This model involves a phase transition between a state associated with multiple coexisting grammars and one single, universally adopted one. The shape of the potential function is given by
| 9.3 |
and is shown in figure 16 for different values of the learning parameter q. As we can appreciate, there is a regime where many different grammars coexist (x* = 0), whereas after a threshold qc is reached, a stable state is given by a single dominant grammar for q > qc. In general terms, we can use this model to represent the emergence of language coherence within populations of communicating agents. As soon as the critical threshold is reached, a sudden jump to the single-language solution occurs.
Figure 16.
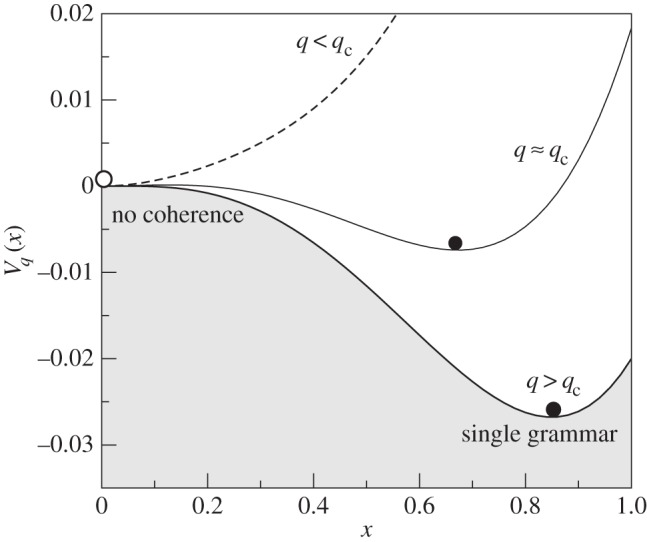
Phase transitions in grammar evolution. Here, the potential function Vq(x) is represented for three different q values of the leraning parameter, namely q = 0.5, 0.8, 0.9 which are below, close and beyond the critical value qc, respectively, separating multiple grammars (with a = 0.3 and f0 = 0) (here because  it corresponds to x = 0).
it corresponds to x = 0).
The previous strategy neither takes into account most structural and computational complexity of syntax nor the relevance of meaning [222]. An alternative approach to the problem incorporates a system capable of perception, programmed to label objects and actions. The use of embodied robotic agents (figure 17a,b) revealed several remarkable things. One is that embodiment is a key requirement to evolve complex communication [223]. Second, evolutionary experiments showed that, along with a lexicon, rudimentary forms of grammar also emerge [224] thus indicating that a grammatical network organization (figure 17b) should be expected also in artificially evolved languages. The complexity of the evolved networks of word interactions has been analysed by means of fluid construction grammars [225].
Figure 17.
Emergent synthetic languages. Using embodied robotic agents (a) a proto-grammar can emerge (image from the Neurocybernetics group at Osnabruck) that can be traced through the analysis of the underlying synthetic language network developed by the agents. A formal model of language (c) is described as an evolvable bipartite signal-object graph (b–d) whose topology depends on the specific trade-offs associated with the efforts of communicating agents, as described by equation (9.5) as weighted by a control parameter λ.
Finally, another avenue to synthetic languages is grounded in a statistical physics approach that seeks to explain some key universal traits such as Zipf's law, which establishes that the frequency of any word is inversely proportional to its rank [226]. Specifically, if we rank all the occurrences of words in a text from the most common word to the least common one, the probability p(si) that in a random trial we find the ith most common word Si (with i = 1, … , n) falls off as
| 9.4 |
with γ ≈ 1 and where Z is the normalization constant. This law indicates that most words are rare, whereas a few are very common, and this abundance is also connected with the frequency of connections between words within sentences [227]. Does Zipf's law define a universal feature of complex languages, natural and synthetic?
A toy model can be defined by considering a set of symbols S = {sk} and a set of objects of reference R = {rj} that are shared by a hearer and a speaker. A given toy language can be described by the graph that connects the two sets, as the one shown in figure 17b–d. Here, two efforts are defined, namely the one for the speaker, Ωs and one for the hearer, Ωh. Here, Ωs will be minimal using one or a few words to refer to all objects (figure 17b), whereas Ωh would be minimized if the speaker uses one signal (word) for each object (meaning), i.e. a one-to-one mapping (figure 17d). Clearly, minimal effort for one implies maximal effort for the second. A conjecture [228] suggested that language complexity might be a consequence of the simultaneous minimization of both efforts. This least effort principle was formalized using information theory [229]. One way of defining the global effort is to consider a linear (energy) function Ω(λ) to be minimized
| 9.5 |
with 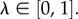 This parameter tunes the relative contribution of each effort. If p(si) is the probability of using si, the hearer's effort is defined by the entropy
This parameter tunes the relative contribution of each effort. If p(si) is the probability of using si, the hearer's effort is defined by the entropy
| 9.6 |
measuring symbol diversity. Similarly, the uncertainty of properly retrieving the right objects associated with each signal, gives
| 9.7 |
where p(rj|si) is the probability of associating the signal si to the reference object rj. It can be shown that minimal effort is achieved at H(S) = H(R|S) (when λc = 1/2) and that a phase transition occurs at this critical value (figure 17c). Zipf's law could be the outcome of criticality [229,230]. Indeed, the heterogeneous distribution of word use defined by Zipf's law seems to occur close to λc, where ambiguity is a key trait. The presence of ambiguity is a specially relevant property here, largely absent in embodied communicating agents, in order to avoid combinatorial explosions [231]. Because a heterogeneous distribution of words might automatically lead to an efficient navigation [227], the least effort scenario suggests a unified framework to account for some crucial features, including the roots of a proto-syntax [232].
10. Synthetic minds
The human brain experienced an accelerated expansion and differentiation through a series of events associated with successive additions of neural microcircuits [231]. Part of these processes deal with simple but key mechanisms that are common to humans and our ancestors. However, some circuits seem to incorporate distinctive traits that are related to our human condition [232]. The evolutionary dynamic of neural networks within complex brains has unfolded over millions of years, eventually allowing the rise of the human mind capable of symbolic thinking and self-awareness. Here, consciousness defines a special and specially puzzling property. It has been the focus of scholar efforts [233–235] and Darwin himself asked ‘How does consciousness commence?’ [236]. Despite its importance and implications for understanding general anaesthesia, coma or minimal consciousness, it remains an unsolved problem [237]. Different paths have been followed in search for the evolutionary origin of consciousness or even potential definitions or classes [238]. These include finding evolutionary homologies [239] and developing quantitative measures of neural correlates of consciousness [240]. In this context, it has been suggested that a parameter Φ can be defined that measures the capacity of a system to integrate information. Using a set of postulates under an information theory framework, Φ = 0 for non-conscious agents, whereas Φ > 0 otherwise, thus aiming at measuring consciousness levels [241], a relevant question is when and how did consciousness evolve? This necessarily requires the assumption that some kind of consciousness is present in some metazoans. As pointed out by Edelman [242], a scientific approach to this problem might ‘necessarily require the synthesis of artefacts’.
Can a machine be conscious? A crucial precursor to this question has to be found in Turing's classic paper ‘Computing machinery and intelligence’ [243]. Although not explicitly addressing the problem of consciousness, Turing was the first to explore the problem of how to detect (using natural language) intelligence in a machine. The pursuit of cognitively complex machines has pervaded many scientific and philosophical debates since the 1950s [244,245]. The field of artificial intelligence soon started to develop some systematic approaches based on the construction of ever more complex programmed machines, sometimes emulating cognitive tasks using neural networks but most of the time following an algorithmic approach. The field experienced a major shift because of the rise of new approaches to machine learning known as deep learning which are based on convolutional neural networks [246]. Beyond the impressive success of their practical implementation [247], these approaches have also raised relevant questions concerning the workings of natural and synthetic minds [248,249].
In previous sections, we have mentioned the importance of defining the preconditions for different major synthetic transitions. What would be the key conditions predating the emergence of consciousness [203,250,251]? Some advances within robotic agents suggest that key features of the problem might be achievable using the proper architectures. One especially interesting example is provided by robots capable of mirror recognition [252,253]. Because a self-aware robot would be more capable of dealing with novel situations, several studies have been focused towards developing robots involving internal self-models [254]. Here, the embodied nature of robotic agents and their capacity for visual recognition of their environment (figure 18a) has been the key to develop robots capable of passing the mirror test with high accuracy. By incorporating an internal model, artificial agents internally simulate their own actions and their sensory effects. In this way, they can achieve behavioural advantages, particularly if these can be generated by the robot itself [256]. These features provide the basis for the emergence of emotional states and what some authors name functional imagination, i.e. the manipulation of information that is not directly available to an agent's sensors [257]. Related work involves modelling the neural basis of mirror neuron systems [258] within artificial agents [255,259,260] and include explicit embodied modelling of interactions and the emergence of ritualized gestures (figure 18b). Such connections open novel avenues towards a synthetic ethology.
Figure 18.
Transitions to self-awareness. Robotic agents can be used (a) to explore the problem of mirror recognition (image provided by Luc Steels). When equipped with an internal representation of their internal states, they can pass the so-called mirror test. Modelling agent interactions (b,c) incorporating a mirror system in their architecture (d) allows developing behavioural patterns (adapted from [255]). (Online version in colour.)
Is the emergence of consciousness a phase transition phenomenon? Explicit suggestions of a tipping point [261] propose that once some brain complexity thresholds are overcome (but not below), consciousness might be inevitable. On the other hand, consciousness requires a neural substrate that provides a compromise between integration and segregation [240,262] and the right trade-off might need a brain poised at a critical (transition) point [263]. The transition might need specific architectural changes, as suggested by the re-entry hypothesis [264] incorporated within artificial systems as multiple positive loops [234,242]. It is interesting that research in this area also considers the potential repertoire of levels of consciousness in the anaesthetized brain [262,265] which reveal the presence of sharp transitions between aware and unconscious states.
As a final point, we also need to consider potential departures of synthetic minds (either evolved or designed) from real brains. This includes the fluid neural networks (virtual or natural) associated with collective intelligence systems [199,201]: would an ant colony or a termite nest have a Φ > 0 consciousness level? On the other hand, some artificial life models have shown how artificial agents evolve highly integrated ‘brains’ while evolving their complex environments [266]. But a major difference between artificial and biological candidates to a ‘mind’ is the potential of the former for gathering massive data from non-local sources [267]. Given the relevance played by embodiment in shaping minds [268,269], we should also expect major differences associated with the distributed nature of synthetic minds grounded in the use of non-local sources of information. Similarly, we should expect new classes of minds emerging in the future as a result of interactions between human and embodied communication robots equipped with learning and memory [270].
11. Synthetic ecosystems
As a final example in our hierarchy, let us consider the problem of designing and/or evolving synthetic ecosystems. Ecosystems are complex adaptive systems, and in many ways they can be described, under a systems approach, as far from equilibrium structures. Synthetic ecosystems include [271]: (i) those ecosystems that result from the evolution of communities under laboratory-constrained conditions; (ii) special species assemblies evolved in human-created environments that often display overabundance of extremophiles; and (iii) engineered communities of multiple interacting microbial organisms resulting from partial or total designed strains from synthetic biology techniques [272]. All these systems represent departures from their natural counterparts in several ways. Moreover, we can include in this list those synthetic ecosystems resulting from artificial life experiments [157,158,273,274] where a more or less sophisticated set of physical constraints are introduced along with evolvable genomes [275].
The canonical example of long-term evolution experiments using microorganisms is provided by Lenski's work with Escherichia coli, involving thousands of generations of population transfers [276]. Many other selection experiments have been shown to create novel adaptations not present in our current biosphere, such as the low-pressure conditions found in Mars [277]. A somewhat similar class of unintentional evolution experiments occurs in special contexts related to specific artificial environments, such as solar panels [278] or coffee machines [279]. Ecosystems adapted to these ‘alien’ conditions are dominated by extremophiles evolved under strong selection towards specific adaptations to—for example—high temperatures or caffeine abundance. These artificial ecosystems can be helpful not only to gain insights into the evolution of extreme communities, but also for ecosystems designed in future (see below).
The rise of synthetic biology allows us to create novel ecosystems where interacting species or their niches are engineered, with or without further artificial evolution. Understanding the patterns of organization of these communities is a much needed task, because no species within a given community live in isolation [272,280]. Examples of synthetic ecosystems include different microbial consortia in liquid or spatial environments involving different forms of communication [281–284]. These ecosystems will offer valuable information about the stability of artificial communities of interacting species, and this might be relevant for the engineering of the human microbiome and its alternative states [285,286] as well as in potential approaches to ecosystem bioengineering [287,288].
Because the microbiome seems to follow universal ecological patterns [289], these manipulations can shed some light on the resilience of future synthetic ecosystems resulting from the release of modified organisms. In this context, transitions between alternative states have been also recognized as a fundamental part of their robustness and fragility [290,291]. Here, some species, known as ecosystem engineers, play a crucial role in shaping the ecology and evolution of communities and their potential modification [292,293]. Finally, the possibility that learning can be incorporated as part of our understanding of evolution, particularly within the context of ecosystems [294,295], opens novel forms of thinking in evolutionary transitions and further levels of informational complexity to be designed or artificially evolved.
12. Discussion
What drives the emergence of major novelties in evolution? In this paper, we have explored the parallel path followed by artificial versions of those transitions that have been identified in the historical record of life. In some cases, the main difference involves the presence of developmental processes that are an inevitable part of biological complexity, but are absent in most artificial systems. An exception here are those based on synthetic biology and thus using cells and their interactions as part of the engineering toolkit. Development and constraints associated with genetic similarity and other features of real biology are largely absent in most artificial designs grounded in hardware but also in simulated scenarios, with some exceptions. Because development defines the mapping between genotype and phenotype in biological systems, it also incorporates a great deal of complexity that results from the contrived nature of evolution.
Some of the transitions that have repeatedly occurred in evolution have also been achieved in the artificial context, including multicellularity, symbiosis or different forms of cognitive complexity. In most cases, the basic logic is shared by the living and the designed systems, thus reflecting seemingly universal rules of organization. The universality has to be understood in terms of fundamental principles and minimal requirements, and in this context we suggest that phase transitions might be a specially relevant framework here. We have illustrated this in different case studies where simple models capture the nature of the transition, and where the qualitative nature of the change can be seen as an instance of a phase change not very different from those described by statistical physics models. This view has been defended within the context of origins of life studies [296], and future theoretical work will be needed to substantiate this conjecture, but it might also require rethinking of the framework of physical theories by incorporating the emergence of generative rules. This is especially important when we think of the nature of the rules allowing the open-ended nature of evolutionary change. In other words, novel ‘phases’ come with new properties but also with internal grammars that describe their computational complexity. Such a generalized theory is still missing.
Among the above-described examples, novel forms of communication or hybrid systems also illustrate the idea that synthetic transitions might incorporate qualitative features not present in biology. In most cases, the differences also arise owing to the lack of a natural selection process, where cost constraints and competition for resources should play a leading role. Molecular systems can display growth and replication processes not grounded in the standard template-based mechanism. Genetic codes with lower and higher combinatorial repertoires have been constructed and replicating protocells created by means of a mixture of growth-instability cycles and external triggers with no genetic control. Similarly, the non-local nature of information processing exhibited by robotic agents clearly departs from the limits imposed by the embedded neural system carried by every individual in the natural world. Similarly, the goal of creating self-aware machines typically ignores the social context and developmental path where natural minds arise. These examples not only stress the differences, but also suggest that in some cases (such as protocells or machine intelligence and consciousness) the path towards the transition might be more difficult to achieve—both the biological and the artificial contexts.
A final point to be made is that evolution, as pointed out by the French biologist Jacob [297] does not operate as an engineer. Evolution does not foresee the future and requires existing materials and rules to build new structures. Novelties thus necessarily arise through re-use and rewiring.9 The engineer is not (in principle) limited by such constraints, and can overcome the messy and often non-modular nature of biological circuits. However, it is not less true that, because of the contrived nature of evolution, biological structures often incorporate levels of robustness and integration that clearly depart from their artificial counterparts. The underlying landscape of evolved designs might contain properties that are not captured by the engineering-driven version where some simplifying assumptions are made. If that is the case, achieving some of the METs using synthetic paths might need to incorporate evolutionary dynamics as an essential part of the process.
Acknowledgements
This paper is dedicated to the memory of Harold Morowitz. I thank the members of the Complex Systems Laboratory for very stimulating and useful discussions as well as an anonymous referee for the reference on tinkering by Charles Darwin. I also thank all the participants of the Santa Fe Institute working group on Synthetic Major Transitions for their lively presentations and discussions.
Endnotes
For a one-dimensional system described by a single differential equation dx/dt = fµ(x), where x indicates the state of the given variable (a population, for example) and µ is a parameter or set of parameters. The potential equilibria are defined by those x* such that (dx/dt) at x* is zero (i.e. no changes occur) or, in other words, fµ(x*) = 0. For each fixed point, we determine the sign of the parameter 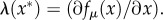 It can be shown that a stable (unstable) point x is such that λ < 0 (λ > 0).
It can be shown that a stable (unstable) point x is such that λ < 0 (λ > 0).
As defined, since we have dx/dt = f(x), the potential function is simply 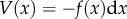 and it is easy to show that its maxima and minima correspond to the unstable and stable fixed points, i.e. those x* such that f(x*) = 0, following linear stability analysis.
and it is easy to show that its maxima and minima correspond to the unstable and stable fixed points, i.e. those x* such that f(x*) = 0, following linear stability analysis.
Although this definition poses some strong constraints on the potential candidates to a hypercyclic dynamics, the exact implementation might not be so relevant while looking for the generic (universal) properties of systems that include in their effective kinetics second-order terms.
The minimal model consistent with this set of reactions, as pointed out in [60] is 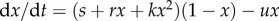 which again exhibits a potential function similar to the Fontanari–Ferreira model [58].
which again exhibits a potential function similar to the Fontanari–Ferreira model [58].
Micelle formation, for example, can be described as a cooperative reaction  where a closed system An composed of n monomers A1 is formed provided that a critical concentration x = [A1] is present. This cooperative behaviour is an important part of the self-organisation of micellar structures and indicates that, when a given concentration of monomers is exceeded, the system experiences a spontaneous transition towards macromolecular assemblies. These self-assembly properties are shared by a vast range of molecular candidates, both natural and artificial.
where a closed system An composed of n monomers A1 is formed provided that a critical concentration x = [A1] is present. This cooperative behaviour is an important part of the self-organisation of micellar structures and indicates that, when a given concentration of monomers is exceeded, the system experiences a spontaneous transition towards macromolecular assemblies. These self-assembly properties are shared by a vast range of molecular candidates, both natural and artificial.
This parameter is defined as 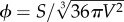 where S and V are the surface and volume of the vesicle, respectively. When ϕ = 1, we have a spherical, stable vesicle, whereas lower values lead to inflated vesicles (which can burst) and higher values favour deformed vesicles. A critical value is given at
where S and V are the surface and volume of the vesicle, respectively. When ϕ = 1, we have a spherical, stable vesicle, whereas lower values lead to inflated vesicles (which can burst) and higher values favour deformed vesicles. A critical value is given at 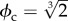 . A stable vesicle can be shown to exist within a domain
. A stable vesicle can be shown to exist within a domain 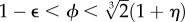 where
where 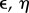 are measurable coefficients.
are measurable coefficients.
The energy associated with the bending of the vesicle is defined through the integral of the free energy on the surface. In its simplest form and considering low temperatures (i.e. thermal fluctuations are ignored) we have 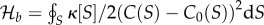 where
where 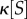 is the bending modulus and
is the bending modulus and  is the mean curvature of the vesicle surface at S. The result of the minimization of such energy function, i.e. the solutions of
is the mean curvature of the vesicle surface at S. The result of the minimization of such energy function, i.e. the solutions of 
The quadratic terms that appear in this Hill function are characteristic of some well-known regulatory controls associated with the presence of dimers as gene regulators. In other cases, saturation functions with similar shape are related to well-known threshold-like phenomena exhibited by physiological and neural systems.
Charles Darwin himself stated the presence of tinkering was part of the evolutionary process, see [298, p. 348].
Competing interests
I declare that I have no competing interests.
Funding
This work has been supported by an ERC Advanced grant no. 294294 from the EU seventh framework programme (SYNCOM), by the Botín Foundation, by Banco Santander through its Santander Universities Global Division, a MINECO FIS2015-67616 fellowship and by the Santa Fe Institute.
References
- 1.Maynard-Smith J, Szathmàry E. 1995. The major transitions in evolution. Oxford, UK: Oxford University Press. [Google Scholar]
- 2.Schuster P. 1996. How does complexity arise in evolution? Complexity 2, 22–30. ( 10.1002/(SICI)1099-0526(199609/10)2:1%3C22::AID-CPLX6%3E3.0.CO;2-H) [DOI] [Google Scholar]
- 3.Lane N. 2009. Life ascending: the ten great inventions of evolution. New York, NY: WW Norton. [Google Scholar]
- 4.Niklas KJ. 1997. The evolutionary biology of plants. Chicago, IL: University of Chicago Press. [Google Scholar]
- 5.Morowitz H. 2004. The emergence of everything. How the world became complex. Oxford, UK: Oxford University Press. [Google Scholar]
- 6.Koonin E. 2007. The biological big bang model for the major transitions in evolution. Biol. Direct 2, 21 ( 10.1186/1745-6150-2-21) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de Duve C. 2005. Singularities: landmarks on the pathways of life. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 8.Gould SJ. 1989. Wonderful life. New York, NY: Penguin. [Google Scholar]
- 9.Fontana W, Buss LW. 1994. What would be conserved if ‘the tape were played twice’? Proc. Natl Acad. Sci. USA 91, 757–761. ( 10.1073/pnas.91.2.757) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Conway Morris S. 2003. Life‘s solution: inevitable humans in a lonely universe Cambridge, UK: Cambridge University Press. [Google Scholar]
- 11.Alberch P. 1989. The logic of monsters. Geobios 22, 21–57. ( 10.1016/S0016-6995(89)80006-3) [DOI] [Google Scholar]
- 12.Goodwin BC. 1994. How the leopard changed its spots: the evolution of complexity. New York, NY: Charles Scribner and Sons. [Google Scholar]
- 13.Kauffman SA. 1993. The origins of order: self-organization and selection in evolution. Oxford, UK: Oxford University Press. [Google Scholar]
- 14.Barrow JD, Conway Morris S, Freeland SJ, Harper CL. 2008. Fitness of the cosmos for life. Biochemistry and fine tuning. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 15.Mitchell M. 2009. Complexity: a guided tour. Oxford, UK: Oxford University Press. [Google Scholar]
- 16.Solé RV, Goodwin BC. 2001. Signs of life: how complexity pervades biology. New York, NY: Basic Books. [Google Scholar]
- 17.Solé RV, Manrubia S, Luque B, Delgado J, Bascompte J. 1996. Phase transitions in complex systems. Complexity 1, 13–26. ( 10.1002/cplx.6130010405) [DOI] [Google Scholar]
- 18.Solé RV. 2011. Phase transitions. Princeton, NJ: Princeton University Press. [Google Scholar]
- 19.Langton CG. 1986. Studying artificial life with cellular automata. Physica D 22, 120–149. ( 10.1016/0167-2789(86)90237-x) [DOI] [Google Scholar]
- 20.Adami C. 1993. Artificial life. Cambridge, MA: MIT Press. [Google Scholar]
- 21.Szathmáry E. 2015. Toward major evolutionary transitions theory 2.0. Proc. Natl Acad. Sci. USA 112, 10 104–10 111. ( 10.1073/pnas.1421398112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Goldenfeld N, Woese C. 2011. Life is physics: evolution as a collective phenomenon far from equilibrium. Annu. Rev. Condensed Matter Phys. 2, 375–399. ( 10.1146/annurev-conmatphys-062910-140509) [DOI] [Google Scholar]
- 23.Stanley HE. 1987. Introduction to phase transitions and critical phenomena. Oxford, UK: Oxford University Press. [Google Scholar]
- 24.Stanley HE. 1999. Scaling, universality, and renormalization: three pillars of modern critical phenomena. Rev. Mod. Phys. 71, S358 ( 10.1103/RevModPhys.71.S358) [DOI] [Google Scholar]
- 25.Ruiz-Mirazo K, Briones C, de la Escosura A. 2013. Prebiotic systems chemistry: new perspectives for the origins of life. Chem. Rev. 114, 285–366. ( 10.1021/cr2004844) [DOI] [PubMed] [Google Scholar]
- 26.Miller SL. 1953. A production of amino acids under possible primitive Earth conditions. Science 117, 528–529. ( 10.1126/science.117.3046.528) [DOI] [PubMed] [Google Scholar]
- 27.Parker ET, Cleaves HJ., Dworkin JP, Glavin DP, Callahan M, Aubrey A, Lazcano A, Bada JL. 2011. Primordial synthesis of amines and amino acids in a 1958 Miller H2S-rich spark discharge experiment. Proc. Natl Acad. Sci. USA 108, 5526–5531. ( 10.1073/pnas.1019191108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang L-P, Titov A, McGibbon R, Liu F, Pande VS, Martinez TJ. 2014. Discovering chemistry with an ab initio nanoreactor. Nat. Chem. 6, 1044–1048. ( 10.1038/nchem.2099) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gothard CM, Soh S, Gothard NA, Kowalczyk B, Wei Y, Baytekin B, Grzybowski BA. 2011. Rewiring chemistry: algorithmic discovery and experimental validation of one-pot reactions in the network of organic chemistry. Angew. Chem. Int. Ed. Engl. 51, 7922–7927. ( 10.1002/anie.201202155) [DOI] [PubMed] [Google Scholar]
- 30.Oparin AI. 1952. The origin of life. New York, NY: Dover. [Google Scholar]
- 31.Oró J. 1960. Synthesis of adenine from ammonium cyanide. Biochem. Biophys. Res. Commun. 2, 407–412. ( 10.1016/0006-291X(60)90138-8) [DOI] [Google Scholar]
- 32.Benner SA, Ricardo A, Carrigan MA. 2004. Is there a common chemical model for life in the universe? Curr. Opin. Chem. Biol. 8, 672–689. ( 10.1016/j.cbpa.2004.10.003) [DOI] [PubMed] [Google Scholar]
- 33.Plasson R, Kondepudi DK, Bersini H, Commeyras A, Asakura K. 2007. Emergence of homochirality in far from equilibrium systems: mechanisms and role in prebiotic chemistry. Chirality 19, 589–600. ( 10.1002/chir.20440) [DOI] [PubMed] [Google Scholar]
- 34.Coveney PV, Swadling JB, Wattis JA, Greenwell HC. 2012. Theory, modelling and simulation in origins of life studies. Chem. Soc. Rev. 4, 5430–5446. ( 10.1039/c2cs35018a) [DOI] [PubMed] [Google Scholar]
- 35.Oró J. 1961. Comets and the formation of biochemical compounds on the primitive Earth. Nature 190, 389–390. ( 10.1038/190389a0) [DOI] [PubMed] [Google Scholar]
- 36.Frank FK. 1953. On spontaneous asymmetric synthesis. Biochim. Biophys. Acta 11, 459–463. ( 10.1016/0006-3002(53)90082-1) [DOI] [PubMed] [Google Scholar]
- 37.Blackmond DG. 2011. The origin of biological homochirality. Phil. Trans. R. Soc. B 366, 2878–2884. ( 10.1098/rstb.2011.0130) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hochberg D, Zorzano MP. 2006. Reaction-noise induced homochirality. Chem. Phys. Lett. 431, 185–189. ( 10.1016/j.cplett.2006.09.059) [DOI] [Google Scholar]
- 39.Brewer A, Davis AP. 2014. Chiral encoding may provide a simple solution to the origin of life. Nat. Chem. 6, 569–574. ( 10.1038/nchem.1981) [DOI] [PubMed] [Google Scholar]
- 40.Kauffman SA. 1986. Autocatalytic sets of proteins. J. Theor. Biol. 119, 1–24. ( 10.1016/S0022-5193(86)80047-9) [DOI] [PubMed] [Google Scholar]
- 41.Farmer JD, Kauffman SA, Packard NH. 1986. Autocatalytic replication of polymers. Physica D 22, 50–67. ( 10.1016/0167-2789(86)90233-2) [DOI] [Google Scholar]
- 42.Kim H-J, Ricardo A, Illangkoon HI, Kim MJ, Carrigan MA, Frye F, Benner SA. 2011. Synthesis of carbohydrates in mineral-guided prebiotic cycles. J. Am. Chem. Soc. 133, 9457–9468. ( 10.1021/ja201769f) [DOI] [PubMed] [Google Scholar]
- 43.Peretó J. 2012. Out of fuzzy chemistry: from prebiotic chemistry to metabolic networks. Chem. Soc. Rev. 41, 5394–5403. ( 10.1039/c2cs35054h) [DOI] [PubMed] [Google Scholar]
- 44.Jain S, Krishna S. 2001. A model for the emergence of cooperation, interdependence, and structure in evolving networks. Proc. Natl Acad. Sci. USA 98, 543–547. ( 10.1073/pnas.98.2.543) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Von Neumann J, Burks AW. 1966. Theory of self-reproducing automata. IEEE Trans. Neural Netw. 5, 3–14. [Google Scholar]
- 46.von Kiedrowski G. 1986. A self-replicating hexadeoxynucleotide. Angew. Chem. Int. Ed. Engl. 25, 932–935. ( 10.1002/anie.198609322) [DOI] [Google Scholar]
- 47.Lee DH, Granja JR, Martinez JA, Severin K, Ghadiri MR. 1996. A self-replicating peptide. Nature 382, 525–528. ( 10.1038/382525a0) [DOI] [PubMed] [Google Scholar]
- 48.Colomb-Delsuc M, Mattia E, Sadownik JW, Otto S. 2014. Exponential self-replication enabled through a fibre elongation/breakage mechanism. Nat. Commun. 6, 7427 ( 10.1038/ncomms8427) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tjivikua T, Ballester P, Rebek JA. 1990. Self-replicating system. J. Am. Chem. Soc. 112, 1249–1250. ( 10.1021/ja00159a057) [DOI] [Google Scholar]
- 50.Higgs PG, Lehman N. 2015. The RNA world: molecular cooperation at the origins of life. Nat. Rev. Genet. 16, 7–17. ( 10.1038/nrg3841) [DOI] [PubMed] [Google Scholar]
- 51.Vaidya N, Manapat ML, Chen IA, Xulvi-Brunet R, Hayden EJ, Lehman N. 2012. Spontaneous network formation among cooperative RNA replicators. Nature 491, 72–77. ( 10.1038/nature11549) [DOI] [PubMed] [Google Scholar]
- 52.Hordjik M, Steel M. 2013. A formal model of autocatalytic sets emerging in an RNA replicator system. J. Syst. Chem. 4, e3 ( 10.1186/1759-2208-4-3) [DOI] [Google Scholar]
- 53.Biebricher CK, Eigen M. 2005. The error threshold. Virus Res. 107, 117–127. ( 10.1016/j.virusres.2004.11.002) [DOI] [PubMed] [Google Scholar]
- 54.Eigen M, McCaskill J, Schuster P. 1988. Molecular quasi-species. J. Phys. Chem. 92, 6881–6891. ( 10.1021/j100335a010) [DOI] [Google Scholar]
- 55.Eigen M, Schuster P. 1979. The hypercycle: a principle of natural self-organization. Berlin, Germany: Springer. [DOI] [PubMed] [Google Scholar]
- 56.Smith JM. 1979. Hypercycles and the origin of life. Nature 280, 445–446. ( 10.1038/280445a0) [DOI] [PubMed] [Google Scholar]
- 57.Szathmáry E. 2006. The origin of replicators and reproducers. Phil. Trans. R. Soc. B 361, 1761–1776. ( 10.1098/rstb.2006.1912) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ferreira CP, Fontanari JF. 2002. Nonequilibrium phase transitions in a model for the origin of life. Phys. Rev. E 65, 021902 ( 10.1103/PhysRevE.65.021902) [DOI] [PubMed] [Google Scholar]
- 59.Wu M, Higgs PG. 2012. The origin of life is a spatially localized stochastic transition. Biol. Direct 7, 42 ( 10.1186/1745-6150-7-42) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sardanyes J, Solé R. 2006. Bifurcations and phase transitions in a spatially extended two-member hypercycle. J. Theor. Biol. 243, 468–482. ( 10.1016/j.jtbi.2006.07.014) [DOI] [PubMed] [Google Scholar]
- 61.Boerlijst MC, Hogeweg P. 1991. Spiral wave structure in pre-biotic evolution: hypercycles stable against parasites. Physica D 48, 17–28. ( 10.1016/0167-2789(91)90049-F) [DOI] [Google Scholar]
- 62.Cronhjort MB, Blomberg C. 1994. Hypercycles versus parasites in a two dimensional partial differential equations model. J. Theor. Biol 169, 31–49. ( 10.1006/jtbi.1994.1128) [DOI] [Google Scholar]
- 63.Attolini CSO, Stadler PF. 2006. Evolving towards the hypercycle: a spatial model of molecular evolution. Physica D 217, 134–141. ( 10.1016/j.physd.2006.03.015) [DOI] [Google Scholar]
- 64.Schrödinger E. 1952. What is life? Cambridge, UK: Cambridge University Press. [Google Scholar]
- 65.Koonin EV, Novozhilov AS. 2009. Origin and evolution of the genetic code: the universal enigma. IUBMB Life 61, 99–111. ( 10.1002/iub.146) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Cover TM, Thomas JA. 2001. Elements of information theory. New York, NY: John Wiley and Sons. [Google Scholar]
- 67.Freeland SJ, Hurst LD. 1998. The genetic code is one in a million. J. Mol. Evol. 47, 238–248. ( 10.1007/PL00006381) [DOI] [PubMed] [Google Scholar]
- 68.Knight RD, Freeland SJ, Landweber LF. 2001. Rewiring the keyboard: evolvability of the genetic code. Nat. Rev. Genet. 2, 49–58. ( 10.1038/35047500) [DOI] [PubMed] [Google Scholar]
- 69.Tlusty T. 2007. A model for the emergence of the genetic code as a transition in a noisy information channel. J. Theor. Biol. 249, 331–342. ( 10.1016/j.jtbi.2007.07.029) [DOI] [PubMed] [Google Scholar]
- 70.Tlusty T. 2010. A colorful origin for the genetic code: information theory, statistical mechanics and the emergence of molecular codes. Phys. Life Rev. 7, 362–376. ( 10.1016/j.plrev.2010.06.002) [DOI] [PubMed] [Google Scholar]
- 71.Pinheiro VB, et al. 2012. Synthetic genetic polymers capable of heredity and evolution. Science 336, 341–344. ( 10.1126/science.1217622) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Pinheiro VB, David L, Philipp H. 2013. Synthetic polymers and their potential as genetic materials. Bioessays 35, 113–122. ( 10.1002/bies.201200135) [DOI] [PubMed] [Google Scholar]
- 73.Neumann H, Wang K, Davis L, Garcia-Alai M, Chin JW. 2010. Encoding multiple unnatural amino acids via evolution of a quadruplet-decoding ribosome. Nature 464, 441–444. ( 10.1038/nature08817) [DOI] [PubMed] [Google Scholar]
- 74.Taylor AI, Pinheiro VB, Smola MJ, Morgunov AS, Peak-Chew S, Cozens C, Weeks KM, Herdewijn P, Holliger P. 2015. Catalysts from synthetic genetic polymers. Nature 518, 427–430. ( 10.1038/nature13982) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Chaput JC, Yu H, Zhang S. 2012. The emerging world of synthetic genetics. Chem. Biol. 19, 1360–1371. ( 10.1016/j.chembiol.2012.10.011) [DOI] [PubMed] [Google Scholar]
- 76.Deamer DW. 2011. First life. Berkeley, CA: University of California Press. [Google Scholar]
- 77.Rasmussen S, et al. (eds). 2008. Protocells: bridging nonliving and living matter. Cambridge, MA: MIT Press. [DOI] [PubMed] [Google Scholar]
- 78.Solé RV, Macia J, Munteanu A, Rodriguez-Caso C. 2007. Synthetic protocell biology: from reproduction to computation. Phil. Trans. R. Soc. B 362, 1727–1739. ( 10.1098/rstb.2007.2065) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Luisi PL. 2006. The emergence of life: from chemical origins to synthetic biology. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 80.Gánti T. 2003. The principles of life. Oxford, UK: Oxford University Press. [Google Scholar]
- 81.Mushegian AR, Koonin EV. 1996. A minimal gene set for cellular life derived by comparison of complete bacterial genomes. Proc. Natl Acad. Sci. USA 93, 10 268–10 273. ( 10.1073/pnas.93.19.10268) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Gabaldon T, Pereto J, Montero F, Gil R, Latorre A, Moya A. 2007. Structural analyses of a hypothetical minimal metabolism. Phil. Trans. R. Soc. B 362, 1751–1762. ( 10.1098/rstb.2007.2067) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Hutchison CA, et al. 2016. Design and synthesis of a minimal bacterial genome. Science 351, 1414–1425. ( 10.1126/science.aad6253) [DOI] [PubMed] [Google Scholar]
- 84.Mansy SS, Schrum JP, Krishnamurthy M, Tobé S, Treco DA, Szostak JW. 2008. Template-directed synthesis of a genetic polymer in a model protocell. Nature 454, 122–125. ( 10.1038/nature07018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kurihara K, Tamura M, Shohda KI, Toyota T, Suzuki K, Sugawara T. 2011. Self-reproduction of supramolecular giant vesicles combined with the amplification of encapsulated DNA. Nat. Chem. 3, 775–781. ( 10.1038/nchem.1127) [DOI] [PubMed] [Google Scholar]
- 86.Ichihashi N, Usui K, Kazuta Y, Sunami T, Matsuura T, Yomo T. 2013. Darwinian evolution in a translation-coupled RNA replication system within a cell-like compartment. Nat. Commun. 4, 2494 ( 10.1038/ncomms3494) [DOI] [PubMed] [Google Scholar]
- 87.Zachar I, Fedor A, Szathmáry E. 2011. Two different template replicators coexisting in the same protocell: stochastic simulation of an extended chemoton model. PLoS ONE 6, e21380 ( 10.1371/journal.pone.0021380) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Caschera F, Noireaux V. 2014. Integration of biological parts toward the synthesis of a minimal cell. Curr. Opin. Chem. Biol. 22, 85–91. ( 10.1016/j.cbpa.2014.09.028) [DOI] [PubMed] [Google Scholar]
- 89.Loakes D, Holliger P. 2009. Darwinian chemistry: towards the synthesis of a simple cell. Mol. Biosyst. 5, 686–694. ( 10.1039/b904024b) [DOI] [PubMed] [Google Scholar]
- 90.Mavelli F, Ruiz-Mirazo K. 2013. Theoretical conditions for the stationary reproduction of model protocells. Integr. Biol. 5, 324–341. ( 10.1039/C2IB20222K) [DOI] [PubMed] [Google Scholar]
- 91.Villani M, Filisetti A, Graudenzi A, Damiani C, Carletti T, Serra R. 2014. Growth and division in a dynamic protocell model. Life 4, 837–864. ( 10.3390/life4040837) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Takakura K, Toyota T, Sugawara T. 2003. A novel system of self-reproducing giant vesicles. J. Am. Chem. Soc. 125, 8134–8140. ( 10.1021/ja029379a) [DOI] [PubMed] [Google Scholar]
- 93.Svetina S. 2009. Vesicle budding and the origin of cellular life. Chem. Phys. Chem. 10, 2769–2776. ( 10.1002/cphc.200900577) [DOI] [PubMed] [Google Scholar]
- 94.Macía J, Solé R. 2007. Synthetic Turing protocells: vesicle self-reproduction through symmetry-breaking instabilities. Phil. Trans. R. Soc. B 362, 1821–1829. ( 10.1098/rstb.2007.2074) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Fellermann H, Solé R. 2007. Minimal model of self-replicating nanocells: a physically embodied information-free scenario. Phil. Trans. R. Soc. B 362, 1803–1811. ( 10.1098/rstb.2007.2072) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Solé R. 2009. Evolution and self-assembly of protocells. Int. J. Biochem. Cell. Biol. 41, 274–284. ( 10.1016/j.biocel.2008.10.004) [DOI] [PubMed] [Google Scholar]
- 97.Fellermann H, Rasmussen S, Ziock HJ, Solé RV. 2007. Life cycle of a minimal protocell: a dissipative particle dynamics study. Artif. Life 13, 319–345. ( 10.1162/artl.2007.13.4.319) [DOI] [PubMed] [Google Scholar]
- 98.Monnard PA, Walde P. 2015. Current ideas about prebiological compartmentalization. Life 5, 1239–1263. ( 10.3390/life5021239) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Walde P, Umakoshi H, Stano P, Mavelli F. 2014. Emergent properties arising from the assembly of amphiphiles. Artificial vesicle membranes as reaction promoters and regulators. Chem. Commun. 50, 10 177–10 197. ( 10.1039/C4CC02812K) [DOI] [PubMed] [Google Scholar]
- 100.Blain JC, Szostak JW. 2014. Progress toward synthetic cells. Annu. Rev. Biochem. 83, 615–640. ( 10.1146/annurev-biochem-080411-124036) [DOI] [PubMed] [Google Scholar]
- 101.Shirt-Ediss B, Ruiz-Mirazo K, Mavelli F, Solé R. 2014. Modelling lipid competition dynamics in heterogeneous protocell populations. Sci. Rep. 4, 5675 ( 10.1038/srep05675) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Shirt-Ediss B, Solé R, Ruiz-Mirazo K. 2015. Emergent chemical behavior in variable-volume protocells. Life 5, 181–211. ( 10.3390/life5010181) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Knoll AH. 2011. The multiple origins of complex multicellularity. Annu. Rev. Earth Planet. Sci. 39, 217–239. ( 10.1146/annurev.earth.031208.100209) [DOI] [Google Scholar]
- 104.Ruiz-Trillo I, Nedelcu AM (eds). 2015. Evolutionary transitions to multicellular life: principles and mechanisms. Berlin, Germany: Springer. [Google Scholar]
- 105.Bonner JT. 2001. First signals: the evolution of multicellular development. Princeton, NJ: Princeton University Press. [Google Scholar]
- 106.Michod RE, Roze D. 1997. Transitions in individuality. Proc. R. Soc. Lond. B 264, 853–857. ( 10.1098/rspb.1997.0119) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Hogeweg P. 2000. Evolving mechanisms of morphogenesis: on the interplay between differential adhesion and cell differentiation. J. Theor. Biol. 203, 317–333. ( 10.1006/jtbi.2000.1087) [DOI] [PubMed] [Google Scholar]
- 108.Coen E, Rolland-Lagan AG, Matthews M, Bangham JA, Prusinkiewicz P. 2004. The genetics of geometry. Proc. Natl Acad. Sci. USA 101, 4728–4735. ( 10.1073/pnas.0306308101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Cummings FW. 2001. The interaction of surface geometry with morphogens. J. Theor. Biol. 212, 303–313. ( 10.1006/jtbi.2001.2377) [DOI] [PubMed] [Google Scholar]
- 110.Doursat R, Sayama H, Michel O. 2013. A review of morphogenetic engineering. Nat. Comput. 12, 517–535. ( 10.1007/s11047-013-9398-1) [DOI] [Google Scholar]
- 111.Kaandorp JA, Blom JG, Verhoef J, Filatov M, Postma M, Müller WE. 2008. Modelling genetic regulation of growth and form in a branching sponge. Proc. R. Soc. B 275, 2569–2575. ( 10.1098/rspb.2008.0746) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Solé RV, Valverde S. 2013. Before the endless forms: embodied model of transition from single cells to aggregates to ecosystem engineering. PLoS ONE 8, e59664 ( 10.1371/journal.pone.0059664) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Michod RE, Viossat Y, Solari CA, Hurand M, Nedelcu AM. 2006. Life-history evolution and the origin of multicellularity. J. Theor. Biol. 239, 257–272. ( 10.1016/j.jtbi.2005.08.043) [DOI] [PubMed] [Google Scholar]
- 114.Rokas A. 2008. The origins of multicellularity and the early history of the genetic toolkit for animal development. Annu. Rev. Genet. 42, 235–251. ( 10.1146/annurev.genet.42.110807.091513) [DOI] [PubMed] [Google Scholar]
- 115.Forgacs G, Newman SA. 2005. Biological physics of the developing embryo. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 116.Carroll SB. 2001. Chance and necessity: the evolution of morphological complexity and diversity. Nature 409, 1102–1109. ( 10.1038/35059227) [DOI] [PubMed] [Google Scholar]
- 117.Erwin DH. 2009. Early origin of the bilaterian developmental toolkit. Phil. Trans. R. Soc. B 364, 2253–2261. ( 10.1098/rstb.2009.0038) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Newman SA, Bhat R. 2009. Dynamical patterning modules: a ‘pattern language’ for development and evolution of multicellular form. Int. J. Dev. Biol. 53, 693 ( 10.1387/ijdb.072481sn) [DOI] [PubMed] [Google Scholar]
- 119.Ratcliff WC, Denison RF, Borrello M, Travisano M. 2012. Experimental evolution of multicellularity. Proc. Natl Acad. Sci. USA 109, 1595–1600. ( 10.1073/pnas.1115323109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Maharbiz MM. 2012. Synthetic multicellularity. Trends Cell Biol. 22, 617–623. ( 10.1016/j.tcb.2012.09.002) [DOI] [PubMed] [Google Scholar]
- 121.Libby E, Rainey PB. 2013. A conceptual framework for the evolutionary origins of multicellularity. Phys. Biol. 10, 035001 ( 10.1088/1478-3975/10/3/035001) [DOI] [PubMed] [Google Scholar]
- 122.Duran-Nebreda S, Solé R. 2015. Emergence of multicellularity in a model of cell growth, death and aggregation under size-dependent selection. J. R. Soc. Interface 12, 20140982 ( 10.1098/rsif.2014.0982) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Libby E, Ratcliff W, Travisano M, Kerr B. 2014. Geometry shapes evolution of early multicellularity. PLoS Comput. Biol. 10, e1003803 ( 10.1371/journal.pcbi.1003803) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Shapiro JA and Dworkin M (eds). 1997. Bacteria as multicellular organisms. Oxford, UK: Oxford University Press. [Google Scholar]
- 125.Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. 2004. Bacterial persistence as a phenotypic switch. Science 305, 1622–1625. ( 10.1126/science.1099390) [DOI] [PubMed] [Google Scholar]
- 126.Lewis K. 2010. Persister cells. Annu. Rev. Microbiol. 64, 357–372. ( 10.1146/annurev.micro.112408.134306) [DOI] [PubMed] [Google Scholar]
- 127.Beaumont HJ, Gallie J, Kost C, Ferguson GC, Rainey PB. 2009. Experimental evolution of bet hedging. Nature 462, 90–93. ( 10.1038/nature08504) [DOI] [PubMed] [Google Scholar]
- 128.Wingreen NS, Levin SA. 2006. Cooperation among microorganisms. Proc. Natl Acad. Sci. USA 4, 1486–1488. ( 10.1371/journal.pbio.0040299) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Henderson IR, Owen P, Nataro JP. 1999. Molecular switches: the ON and OFF of bacterial phase variation. Mol. Microbiol. 33, 919–932. ( 10.1046/j.1365-2958.1999.01555.x) [DOI] [PubMed] [Google Scholar]
- 130.Veening JW, Smits WK, Kuipers OP. 2008. Bistability, epigenetics, and bet-hedging in bacteria. Annu. Rev. Microbiol. 62, 193–210. ( 10.1146/annurev.micro.62.081307.163002) [DOI] [PubMed] [Google Scholar]
- 131.Queller DC, Strassmann JE. 2009. Beyond society: the evolution of organismality. Phil. Trans. R. Soc. B 364, 3143–3155. ( 10.1098/rstb.2009.0095) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Duran-Nebreda S, Bonforti A, Montañez R, Valverde S, Solé R. 2015. Emergence of proto-organisms from bistable stochastic differentiation and adhesion. J. R. Soc. Interface 13, 20160108 ( 10.1098/rsif.2016.0108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Furusawa C, Kaneko K. 1998. Emergence of rules in cell society: differentiation, hierarchy, and stability. Bull. Math. Biol. 60, 659–687. ( 10.1006/bulm.1997.0034) [DOI] [PubMed] [Google Scholar]
- 134.Pfeiffer T, Bonhoeffer S. 2001. An evolutionary scenario for the transition to undifferentiated multicellularity. Proc. Natl Acad. Sci. USA 100, 1095–1098. ( 10.1073/pnas.0335420100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Benner SA, Sismour AM. 2005. Synthetic biology. Nat. Rev. Genet. 6, 533–543. ( 10.1038/nrg1637) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Cheng AA, Lu TK. 2012. Synthetic biology: an emerging engineering discipline. Annu. Rev. Biomed. Eng. 14, 155–178. ( 10.1146/annurev-bioeng-071811-150118) [DOI] [PubMed] [Google Scholar]
- 137.Regot S, et al. 2011. Distributed biological computation with multicellular engineered networks. Nature 469, 207–211. ( 10.1038/nature09679) [DOI] [PubMed] [Google Scholar]
- 138.Macía J, Posas F, Solé R. 2012. Distributed computation: the new wave of synthetic biology devices. Trends Biotech. 30, 342–349. ( 10.1016/j.tibtech.2012.03.006) [DOI] [PubMed] [Google Scholar]
- 139.Chuang JS. 2012. Engineering multicellular traits in synthetic microbial populations. Curr. Opin. Chem. Biol. 16, 370–378. ( 10.1016/j.cbpa.2012.04.002) [DOI] [PubMed] [Google Scholar]
- 140.Sasai Y. 2013. Cytosystems dynamics in self-organization of tissue architecture. Nature 493, 318–326. ( 10.1038/nature11859) [DOI] [PubMed] [Google Scholar]
- 141.Davies JA. 2008. Synthetic morphology: prospects for engineered, self-constructing anatomies. J. Anat. 212, 707–719. ( 10.1111/j.1469-7580.2008.00896.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Olle A, Duran-Nebreda S, Conde-Pueyo N, Montañez R, Solé R. 2016. A morphospace for synthetic organs and organoids: the possible and the actual. Integr. Biol. 8, 485–503. ( 10.1039/C5IB00324E) [DOI] [PubMed] [Google Scholar]
- 143.Margulis L, Fester R. 1991. Symbiosis as a source of evolutionary innovation: speciation and morphogenesis. Cambridge, MA: MIT Press. [PubMed] [Google Scholar]
- 144.Momeni B, Chen CC, Hillesland KL, Waite A, Shou W. 2011. Using artificial systems to explore the ecology and evolution of symbioses. Cell. Mol. Life Sci. 68, 1353–1368. ( 10.1007/s00018-011-0649-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Balagadde FK, Song H, Ozaki J, Collins CH, Barnet M, Arnold FH, Quake SR, You L. 2008. A synthetic Escherichia coli predator–prey ecosystem. Mol. Syst. Biol. 4, 187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Wintermute EH, Silver PA. 2010. Emergent cooperation in microbial metabolism. Mol. Syst. Biol. 6, 407 ( 10.1038/msb.2010.66) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Hosoda K, Suzuki S, Yamauchi Y, Shiroguchi Y, Kashiwagi A, Ono N, Mori K, Yomo T. 2011. Cooperative adaptation to establishment of a synthetic bacterial mutualism. PLoS ONE 6, e17105 ( 10.1371/journal.pone.0017105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Peisajovich SG. 2012. Evolutionary synthetic biology. ACS Synth. Biol. 1, 199–210. ( 10.1021/sb300012g) [DOI] [PubMed] [Google Scholar]
- 149.Celiker H, Gore J. 2013. Cellular cooperation: insights from microbes. Trends Cell Biol. 23, 9–15. ( 10.1016/j.tcb.2012.08.010) [DOI] [PubMed] [Google Scholar]
- 150.Shou W, Ram S, Vilar JM. 2007. Synthetic cooperation in engineered yeast populations. Proc. Natl Acad. Sci. USA 104, 1877–1882. ( 10.1073/pnas.0610575104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Hom EF, Murray AW. 2014. Niche engineering demonstrates a latent capacity for fungal–algal mutualism. Science 345, 94–98. ( 10.1126/science.1253320) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Agapakis CM, Niederholtmeyer H, Noche RR, Lieberman TD, Megason SG, Way JC, Silver PA. 2011. Towards a synthetic chloroplast. PLoS ONE 6, e18877 ( 10.1371/journal.pone.0018877) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Alvarez M, Reynaert N, Chávez MN, Aedo G, Araya F, Hopfner U, Fernández J, Allende ML, Egaña JT. 2015. Generation of viable plant–vertebrate chimeras. PLoS ONE 10, e0130295 ( 10.1371/journal.pone.0130295) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Kiers ET, et al. 2011. Reciprocal rewards stabilize cooperation in the mycrorrhizal symbiosis. Science 333, 880–882. ( 10.1126/science.1208473) [DOI] [PubMed] [Google Scholar]
- 155.Guan SH, et al. 2013. Experimental evolution of nodule intracellular infection in legume symbionts. ISME J. 7, 1367–1377. ( 10.1038/ismej.2013.24) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Reyes-Prieto A, Weber AP, Bhattacharya D. 2007. The origin and establishment of the plastid in algae and plants. Annu. Rev. Genet. 41, 147–168. ( 10.1146/annurev.genet.41.110306.130134) [DOI] [PubMed] [Google Scholar]
- 157.Ikegami T, Kaneko K. 1990. Computer symbiosis: emergence of symbiotic behavior through evolution. Physica D 42, 235–243. ( 10.1016/0167-2789(90)90077-3) [DOI] [Google Scholar]
- 158.Ray TS. 1991. An approach to the synthesis of life. In Artificial life II (eds Langton C, Taylor C, Farmer JD, Rasmussen S), pp. 371–408. Redwood City, CA: Addison-Wesley. [Google Scholar]
- 159.Koonin EV. 2011. The logic of chance: the nature and origin of biological evolution. Upper Saddle River, NJ: FT Press. [Google Scholar]
- 160.Hogeweg P, Takeuchi N. 2003. Multilevel selection in models of prebiotic evolution: compartments and spatial self-organization. Origins Life Evol. Biosphere 33, 375–403. ( 10.1023/A:1025754907141) [DOI] [PubMed] [Google Scholar]
- 161.Nachenberg C. 1997. Computer virus-coevolution. Commun. ACM 50, 46–51. ( 10.1145/242857.242869) [DOI] [Google Scholar]
- 162.Forrest S, Hofmeyr SA, Somayaji A. 1997. Computer immunology. Commun. ACM 40, 88–96. ( 10.1145/262793.262811) [DOI] [Google Scholar]
- 163.Forrest S, Beauchemin C. 2007. Computer immunology. Immunol. Rev 216, 176–197. ( 10.1111/j.1600-065X.2007.00499.x) [DOI] [PubMed] [Google Scholar]
- 164.Jablonka E, Lamb MJ. 2006. The evolution of information in the major transitions. J. Theor. Biol. 239, 236–246. ( 10.1016/j.jtbi.2005.08.038) [DOI] [PubMed] [Google Scholar]
- 165.Floreano D, Mattiussi C. 2008. Bio-inspired artificial intelligence: theories, methods, and technologies. Cambridge, MA: MIT Press. [Google Scholar]
- 166.Walter WG. 1950. An imitation of life. Sci. Am. 182, 42–45. ( 10.1038/scientificamerican0550-42) [DOI] [Google Scholar]
- 167.Walter WG. 1951. A machine that learns. Sci. Am. 185, 60–63. ( 10.1038/scientificamerican0851-60) [DOI] [Google Scholar]
- 168.Holland O. 1997. Grey Walter: the pioneer of real artificial life. In Proc. 5th Intl. Workshop Artif. Life, pp. 34–44. Cambridge, MA: MIT Press. [Google Scholar]
- 169.Wiener N. 1961. Cybernetics or control and communication in the animal and the machine. Cambridge, MA: MIT Press. [Google Scholar]
- 170.De Latil P. 1956. Thinking by machine: a study of cybernetics. New York, NY: Houghton Mifflin. [Google Scholar]
- 171.Braitenberg V. 1986. Vehicles: Experiments in synthetic psychology. Cambridge, MA: MIT Press. [Google Scholar]
- 172.Brooks RA. 1999. Cambrian intelligence: the early history of the new AI. Cambridge, MA: MIT Press. [Google Scholar]
- 173.Nolfi S, Floreano D. 2000. Evolutionary robotics: the biology, intelligence, and technology of self-organizing machines. Cambridge, MA: MIT Press. [Google Scholar]
- 174.Nolfi S, Floreano D. 2002. Synthesis of autonomous robots through evolution. Trends Cogn. Sci. 6, 31–37. ( 10.1016/S1364-6613(00)01812-X) [DOI] [PubMed] [Google Scholar]
- 175.Doncieux S, Bredeche N, Mouret J-B, Eiben G. 2015. Evolutionary robotics: what, why, and where to. Front. Robot. AI 2, a4 ( 10.3389/frobt.2015.00004) [DOI] [Google Scholar]
- 176.Ijspeert AJ, Crespi A, Ryczko D, Cabelguen JM. 2007. From swimming to walking with a salamander robot driven by a spinal cord model. Science 315, 1416–1420. ( 10.1126/science.1138353) [DOI] [PubMed] [Google Scholar]
- 177.Ijspeert AJ. 2008. Central pattern generators for locomotion control in animals and robots: a review. Neural Netw. 21, 642–653. ( 10.1016/j.neunet.2008.03.014) [DOI] [PubMed] [Google Scholar]
- 178.Hölldobler B, Wilson EO. 2009. The superorganism: the beauty, elegance, and strangeness of insect societies. New York, NY: WW Norton. [Google Scholar]
- 179.Oster GF, Wilson EO. 1978. Caste and ecology in the social insects. Princeton, NJ: Princeton University Press. [PubMed] [Google Scholar]
- 180.Gordon DM. 1996. The organization of work in social insect colonies. Nature 380, 121–124. ( 10.1038/380121a0) [DOI] [Google Scholar]
- 181.Sumpter DJ. 2010. Collective animal behavior. Princeton, NJ: Princeton University Press. [Google Scholar]
- 182.Garnier S, Gautrais J, Theraulaz G. 2007. The biological principles of swarm intelligence. Swarm Intel. 1, 3–31. ( 10.1007/s11721-007-0004-y) [DOI] [Google Scholar]
- 183.Detrain C, Deneubourg JL, Pasteels JM. 1999. Information processing in social insects. Berlin, Germany: Springer. [Google Scholar]
- 184.Halloy J, et al. 2007. Social integration of robots into groups of cockroaches to control self-organized choices. Science 318, 1155–1158. ( 10.1126/science.1144259) [DOI] [PubMed] [Google Scholar]
- 185.Krause J, Winfield AF, Deneubourg JL. 2011. Interactive robots in experimental biology. Trends Ecol. Evol. 26, 369–375. ( 10.1016/j.tree.2011.03.015) [DOI] [PubMed] [Google Scholar]
- 186.Amé JM, Halloy J, Rivault C, Detrain C, Deneubourg JL. 2006. Collegial decision making based on social amplification leads to optimal group formation. Proc. Natl Acad. Sci. USA 103, 5835–5840. ( 10.1073/pnas.0507877103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Mitri S, Wischmann S, Floreano D, Keller L. 2013. Using robots to understand social behaviour. Biol. Rev. 88, 31–39. ( 10.1111/j.1469-185X.2012.00236.x) [DOI] [PubMed] [Google Scholar]
- 188.Sahin E, Winfield A. 2008. Special issue on swarm robotics. Swarm Intell. 2, 69–72. ( 10.1007/s11721-008-0020-6) [DOI] [Google Scholar]
- 189.Hecker JP, Moses ME. 2015. Beyond pheromones: evolving error-tolerant, flexible, and scalable ant-inspired robot swarms. Swarm Intell. 9, 43–70. ( 10.1007/s11721-015-0104-z) [DOI] [Google Scholar]
- 190.Rubenstein M, Cornejo A, Nagpal R. 2014. Programmable self-assembly in a thousand-robot swarm. Science 345, 795–799. ( 10.1126/science.1254295) [DOI] [PubMed] [Google Scholar]
- 191.Werfel J, Petersen K, Nagpal R. 2014. Designing collective behavior in a termite-inspired robot construction team. Science 343, 754–758. ( 10.1126/science.1245842) [DOI] [PubMed] [Google Scholar]
- 192.Jacob EB, Becker I, Shapira Y, Levine H. 2004. Bacterial linguistic communication and social intelligence. Trends Microbiol. 12, 366–372. ( 10.1016/j.tim.2004.06.006) [DOI] [PubMed] [Google Scholar]
- 193.Lambert G, Kussell E. 2014. Memory and fitness optimization of bacteria under fluctuating environments. PLoS Genet. 10, e1004556 ( 10.1371/journal.pgen.1004556) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Vladimirov N, Sourjik V. 2009. Chemotaxis: how bacteria use memory. Biol. Chem. 390, 1097–1104. ( 10.1515/BC.2009.130) [DOI] [PubMed] [Google Scholar]
- 195.Solé R, Amor DR, Duran-Nebreda S, Conde-Pueyo N, Carbonell-Ballestero M, Montañez R et al. In press. Synthetic collective intelligence. Biosystems. ( 10.1016/j.biosystems.2016.01.002) [DOI] [PubMed] [Google Scholar]
- 196.Beekman M, Sumpter DJ, Ratnieks FL. 2001. Phase transition between disordered and ordered foraging in Pharaoh's ants. Proc. Natl Acad. Sci. USA 98, 9703–9706. ( 10.1073/pnas.161285298) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197.Atkinson S, Williams P. 2009. Quorum sensing and social networking in the microbial world. J. R. Soc. Interface 6, 20090203 ( 10.1098/rsif.2009.0203) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 198.Hofstadter DH. 1980. Gödel, Escher, Bach: an eternal golden braid. New York, NY: Basic Books. [Google Scholar]
- 199.Solé RV, Miramontes O, Goodwin BC. 1993. Oscillations and chaos in ant societies. J. Theor. Biol. 161, 343–357. ( 10.1006/jtbi.1993.1060) [DOI] [Google Scholar]
- 200.Boi S, Couzin ID, Del Buono N, Franks NR, Britton NF. 1999. Coupled oscillators and activity waves in ant colonies. Proc. R. Soc. Lond. B 266, 371–378. ( 10.1098/rspb.1999.0647) [DOI] [Google Scholar]
- 201.Solé RV, Miramontes O. 1995. Information at the edge of chaos in fluid neural networks. Physica D 80, 171–180. ( 10.1016/0167-2789(95)90075-6) [DOI] [Google Scholar]
- 202.Cole BJ, Cheshire D. 1996. Mobile cellular automata models of ant behavior: movement activity of Leptothorax allardycei. Am. Nat 148, 1–15. ( 10.1086/285908) [DOI] [Google Scholar]
- 203.Wilson EO. 2012. The social conquest of the Earth. New York, NY: WW Norton. [Google Scholar]
- 204.Hauser MD, Yang C, Berwick RC, Tattersall I, Ryan MJ, Watumull J, Chomsky N, Lewontin RC. 2014. The mystery of language evolution. Front. Psychol. 5, 401 ( 10.3389/fpsyg.2014.00401) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Számadó S, Szathmáry E. 2006. Selective scenarios for the emergence of natural language. Trends Ecol. Evol. 21, 555–561. ( 10.1016/j.tree.2006.06.021) [DOI] [PubMed] [Google Scholar]
- 206.Pinker S. 1994. The language instinct. New York, NY: William Morrow. [Google Scholar]
- 207.Deacon TW. 1998. The symbolic species: the co-evolution of language and the brain. New York, NY: WW Norton. [Google Scholar]
- 208.Hauser MD, Chomsky N, Fitch WT. 2002. The faculty of language: what is it, who has it, and how did it evolve? Science 298, 1569–1579. ( 10.1126/science.298.5598.1569) [DOI] [PubMed] [Google Scholar]
- 209.Nowak MA, Komarova NL, Niyogi P. 2002. Computational and evolutionary aspects of language. Nature 417, 611–617. ( 10.1038/nature00771) [DOI] [PubMed] [Google Scholar]
- 210.Niyogi P. 2006. The computational nature of language learning and evolution. Cambridge, MA: MIT Press. [Google Scholar]
- 211.Nowak MA, Krakauer DC, Dress A. 1999. An error limit for the evolution of language. Proc. R. Soc. Lond. B 266, 2131–2136. ( 10.1098/rspb.1999.0898) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212.Corominas-Murtra B, Fortuny J, Solé RV. 2011. Emergence of Zipf's law in the evolution of communication. Phys. Rev. E 83, 036115 ( 10.1103/PhysRevE.83.036115) [DOI] [PubMed] [Google Scholar]
- 213.Corominas-Murtra B, Valverde S, Solé R. 2009. The ontogeny of scale-free syntax networks: phase transitions in early language acquisition. Adv. Complex Syst. 12, 371–392. ( 10.1142/S0219525909002192) [DOI] [Google Scholar]
- 214.Kirby S. 2001. Spontaneous evolution of linguistic structure: an iterated learning model of the emergence of regularity and irregularity. Evol. Comput. IEEE Trans. Evol. Comput. 5, 102–110. ( 10.1109/4235.918430) [DOI] [Google Scholar]
- 215.Christiansen MH, Kirby S. 2003. Language evolution: consensus and controversies. Trends Cogn. Sci. 7, 300–307. ( 10.1016/S1364-6613(03)00136-0) [DOI] [PubMed] [Google Scholar]
- 216.Steels L. 2003. Evolving grounded communication for robots. Trends Cogn. Sci. 7, 308–312. ( 10.1016/S1364-6613(03)00129-3) [DOI] [PubMed] [Google Scholar]
- 217.Cangelosi A. 2010. Grounding language in action and perception: from cognitive agents to humanoid robots. Phys. Life Rev. 7, 139–151. ( 10.1016/j.plrev.2010.02.001) [DOI] [PubMed] [Google Scholar]
- 218.Nolfi S, Mirolli M (eds). 2009. Evolution of communication and language in embodied agents. Berlin, Germany: Springer. [Google Scholar]
- 219.Plotkin JB, Nowak MA. 2001. Major transitions in language evolution. Entropy 3, 227–246. ( 10.3390/e3040227) [DOI] [Google Scholar]
- 220.Komarova NL, Niyogi P, Nowak MA. 2001. The evolutionary dynamics of grammar acquisition. J. Theor. Biol. 209, 43–59. ( 10.1006/jtbi.2000.2240) [DOI] [PubMed] [Google Scholar]
- 221.Corominas-Murtra B, Fortuny J, Solé R. 2014. Towards a mathematical theory of meaningful communication. Sci. Rep. 4, 4587 ( 10.1038/srep04587) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 222.Steels L. 2015. The talking heads experiment. Berlin, Germany: Language Science Press. [Google Scholar]
- 223.Steels L. 1998. The origins of syntax in visually grounded robotic agents. Artif. Intell. 103, 133–156. ( 10.1016/S0004-3702(98)00066-6) [DOI] [Google Scholar]
- 224.Steels L. 2012. Computational issues in fluid construction grammar. Lecture Notes in Computer Science Berlin, Germany: Springer. [Google Scholar]
- 225.Ferrer-Cancho RF, Solé R. 2010. Two regimes in the frequency of words and the origins of complex lexicons: Zipf's law revisited. J. Q. Ling. 8, 165–173. ( 10.1076/jqul.8.3.165.4101) [DOI] [Google Scholar]
- 226.Ferrer-Cancho R, Solé R. 2001. The small world of human language. Proc. R. Soc. Lond. B 268, 2261–2265. ( 10.1098/rspb.2001.1800) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 227.Ferrer-Cancho R, Solé R. 2003. Least effort and the origins of scaling in human language. Proc. Natl Acad. Sci. USA 100, 788–791. ( 10.1073/pnas.0335980100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 228.Solé RV, Seoane LF. 2015. Ambiguity in language networks. Linguist. Rev. 32, 5–35. [Google Scholar]
- 229.Beuls K, Steels L. 2013. Agent-based models of strategies for the emergence and evolution of grammatical agreement. PLoS ONE 8, e58960 ( 10.1371/journal.pone.0058960) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 230.Solé R. 2005. Language: syntax for free? Nature 434, 289 ( 10.1038/434289a) [DOI] [PubMed] [Google Scholar]
- 231.Buckner RL, Krienen FM. 2013. The evolution of distributed association networks in the human brain. Trends Cogn. Sci. 17, 648–665. ( 10.1016/j.tics.2013.09.017) [DOI] [PubMed] [Google Scholar]
- 232.DeFelipe J. 2011. The evolution of the brain, the human nature of cortical circuits, and intellectual creativity. Front. Neuroanat. 5, 29 ( 10.3389/fnana.2011.00029) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 233.Dennett DC. 1993. Consciousness explained. New York, NY: Penguin. [Google Scholar]
- 234.Dehaene S. 2014. Consciousness and the brain: deciphering how the brain codes our thoughts. New York, NY: Penguin. [Google Scholar]
- 235.Koch C. 2004. The quest for consciousness. New York, NY: Roberts & Co. [Google Scholar]
- 236.Smith CUM. 2010. Darwin's unsolved problem: the place of consciousness in an evolutionary world. J. Hist. Neurosci. 19, 105–120. ( 10.1080/09647040903504781) [DOI] [PubMed] [Google Scholar]
- 237.Dehaene S, Kerszberg M, Changeux JP. 1998. A neuronal model of a global workspace in effortful cognitive tasks. Proc. Natl Acad. Sci. USA 95, 14 529–14 534. ( 10.1073/pnas.95.24.14529) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 238.Dennett DC. 2008. Kinds of minds: toward an understanding of consciousness. New York, NY: Basic Books. [Google Scholar]
- 239.Edelman DB, Baars BJ, Seth AK. 2005. Identifying hallmarks of consciousness in non-mammalian species. Conscious. Cogn. 14, 169–187. ( 10.1016/j.concog.2004.09.001) [DOI] [PubMed] [Google Scholar]
- 240.Edelman GM, Tononi G. 2000. A universe of consciousness: how matter becomes imagination. New York, NY: Basic Books. [Google Scholar]
- 241.Oizumi M, Albantakis L, Tononi G. 2014. From the phenomenology to the mechanisms of consciousness: integrated information theory 3.0. PLoS Comput. Biol. 10, e1003588 ( 10.1371/journal.pcbi.1003588) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242.Edelman G. 1992. Bright air, brilliant fire. New York, NY: Basic Books. [Google Scholar]
- 243.Turing AM. 1950. Computing machinery and intelligence. Mind 59, 433–460. ( 10.1093/mind/LIX.236.433) [DOI] [Google Scholar]
- 244.Pfeifer R, Scheier C. 2001. Understanding intelligence. Cambridge, MA: MIT Press. [Google Scholar]
- 245.Holland O. 2003. Machine consciousness. San Diego, CA: Imprint Academic. [Google Scholar]
- 246.Arel I, Rose DC, Karnowski TP. 2010. Deep machine learning-a new frontier in artificial intelligence research [research frontier]. Comput. Intell. Mag. IEEE 5, 13–18. ( 10.1109/MCI.2010.938364) [DOI] [Google Scholar]
- 247.LeCun Y, Bengio Y, Hinton G. 2015. Deep learning. Nature 521, 436–444. ( 10.1038/nature14539) [DOI] [PubMed] [Google Scholar]
- 248.Mnih V, et al. 2015. Human-level control through deep reinforcement learning. Nature 518, 529–533. ( 10.1038/nature14236) [DOI] [PubMed] [Google Scholar]
- 249.Koch C. 2015. Do androids dream? Sci. Am. Mind 26, 24–27. ( 10.1038/scientificamericanmind1115-24) [DOI] [Google Scholar]
- 250.Suddendorf T. 2013. The gap: the science of what separates us from other animals. New York, NY: Basic Books. [Google Scholar]
- 251.Huang GB. 2015. What are extreme learning machines? Filling the gap between Frank Rosenblatt's dream and John von Neumann's puzzle. Cogn. Comput. 7, 263–278. ( 10.1007/s12559-015-9333-0) [DOI] [Google Scholar]
- 252.Gold K, Scassellati B. 2007. A Bayesian robot that distinguishes ‘self’ from ‘other’. In Proc. 29thAnnual Meeting of the Cognitive Science Society, Nashville, TN, 1–4 August 2007, vol. 2, pp. 1027–1032. Red Hook, NY: Curran Associates.
- 253.Takeno J. 2012. Creation of a conscious robot: mirror image cognition and self-awareness. Boca Raton, FL: CRC Press. [Google Scholar]
- 254.Reggia JA. 2013. The rise of machine consciousness: studying consciousness with computational models. Neural Netw. 44, 112–131. ( 10.1016/j.neunet.2013.03.011) [DOI] [PubMed] [Google Scholar]
- 255.Arbib M, Varsha V, Gasser B. 2013. Dyadic brain modelling, mirror systems and the ontogenetic ritualization of ape gesture. Phil. Trans. R. Soc. B 369, 20130414 ( 10.1098/rstb.2013.0414) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 256.Gorbenko A, Popov V, Sheka A. 2012. Robot self-awareness: exploration of internal states. Appl. Math. Sci. 6, 675–688. [Google Scholar]
- 257.Marques HG, Holland O. 2009. Architectures for functional imagination. Neurocomputing 72, 743–759. ( 10.1016/j.neucom.2008.06.016) [DOI] [Google Scholar]
- 258.Gallese V, Goldman A. 1998. Mirror neurons and the simulation theory of mind-reading. Trends Cogn. Sci. 2, 493–501. ( 10.1016/S1364-6613(98)01262-5) [DOI] [PubMed] [Google Scholar]
- 259.Fellous JM, Arbib MA (eds). 2005. Who needs emotions? The brain meets the robot. Oxford, UK: Oxford University Press. [Google Scholar]
- 260.Floreano D, Ijspeert AJ, Schaal S. 2014. Robotics and neuroscience. Curr. Biol. 24, R910–R920. ( 10.1016/j.cub.2014.07.058) [DOI] [PubMed] [Google Scholar]
- 261.Buttazzo G. 2001. Artificial consciousness: Utopia or real possibility? Computer 34, 24–30. ( 10.1109/2.933500) [DOI] [Google Scholar]
- 262.Tononi G, Koch C. 2015. Consciousness: here, there and everywhere? Phil. Trans. R. Soc. B 370, 20140167 ( 10.1098/rstb.2014.0167) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 263.Chialvo DR. 2010. Emergent complex neural dynamics. Nat. Phys. 6, 744–750. ( 10.1038/nphys1803) [DOI] [Google Scholar]
- 264.Tononi G, Edelman GM. 1998. Consciousness and complexity. Science 282, 1846–1851. ( 10.1126/science.282.5395.1846) [DOI] [PubMed] [Google Scholar]
- 265.Alkire MT, Hudetz AG, Tononi G. 2008. Consciousness and anesthesia. Science 322, 876–880. ( 10.1126/science.1149213) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 266.Albantakis L, Hintze A, Koch C, Adami C, Tononi G. 2014. Evolution of integrated causal structures in animats exposed to environments of increasing complexity. PLoS Comput. Biol. 10, e1003966 ( 10.1371/journal.pcbi.1003966) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 267.Nourbakhsh IR. 2013. Robot futures. Cambridge, MA: MIT Press. [Google Scholar]
- 268.Damasio AR. 2006. Descartes’ error New York, NY: Random House. [Google Scholar]
- 269.Clark A. 1998. Being there: putting brain, body, and world together again. Cambridge, MA: MIT Press. [Google Scholar]
- 270.Solé R. In press. Rise of the humanbot. Front. Neurobot.
- 271.Escalante AE, Rebolleda-Gómez M, Benítez M, Travisano M. 2015. Ecological perspectives on synthetic biology: insights from microbial population biology. Front. Microbiol. 6, a143 ( 10.3389/fmicb.2015.00143) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 272.Mee MT, Wang HH. 2012. Engineering ecosystems and synthetic ecologies. Mol. Biosyst. 8, 2470–2483. ( 10.1039/c2mb25133g) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 273.Lenski RE, Ofria C, Pennock RT, Adami C. 2003. The evolutionary origin of complex features. Nature 423, 139–144. ( 10.1038/nature01568) [DOI] [PubMed] [Google Scholar]
- 274.Solé R, Valverde S. 2013. Macroevolution in silico: scales, constraints and universals. Palaeontology 56, 1327–1340. ( 10.1111/pala.12047) [DOI] [Google Scholar]
- 275.Elena SF, Lenski RE. 2003. Evolution experiments with microorganisms: the dynamics and genetic bases of adaptation. Nat. Rev. Genet. 4, 457–469. ( 10.1038/nrg1088) [DOI] [PubMed] [Google Scholar]
- 276.Wiser MJ, Ribeck N, Lenski RE. 2013. Long-term dynamics of adaptation in asexual populations. Science 342, 1364–1367. ( 10.1126/science.1243357) [DOI] [PubMed] [Google Scholar]
- 277.Nicholson WL, Krivushin K, Gilichinsky D, Schuerger AC. 2013. Growth of Carnobacterium spp. from permafrost under low pressure, temperature, and anoxic atmosphere has implications for Earth microbes on Mars. Proc. Natl Acad. Sci. USA 110, 666–671. ( 10.1073/pnas.1209793110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 278.Dorado-Morales P, Vilanova C, Pereto J, Codoner FM, Ramon D, Porcar M. In press. A highly diverse, desert-like microbial biocenosis on solar panels in a Mediterranean city. bioRxiv, 029660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 279.Vilanova C, Iglesias A, Porcar M. 2015. The coffee-machine bacteriome: biodiversity and colonisation of the wasted coffee tray leach. Sci. Rep. 5, 17163 ( 10.1038/srep17163) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 280.Wintermute EH, Silver PA. 2010. Dynamics in the mixed microbial concourse. Genes Dev. 24, 2603–2614. ( 10.1101/gad.1985210) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 281.Rainey PB, Travisano M. 1998. Adaptive radiation in a heterogeneous environment. Nature 394, 69–72. ( 10.1038/27900) [DOI] [PubMed] [Google Scholar]
- 282.Rainey PB, Buckling A, Kassen R, Travisano M. 2000. The emergence and maintenance of diversity: insights from experimental bacterial populations. Trends Ecol. Evol. 15, 243–247. ( 10.1016/S0169-5347(00)01871-1) [DOI] [PubMed] [Google Scholar]
- 283.Weber W, Daoud-El Baba M, Fussenegger M. 2007. Synthetic ecosystems based on airborne inter- and intrakingdom communication. Proc. Natl Acad. Sci. USA 104, 10 435–10 440. ( 10.1073/pnas.0701382104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 284.De Roy K, Marzorati M, Van den Abbeele P, Van de Wiele T, Boon N. 2014. Synthetic microbial ecosystems: an exciting tool to understand and apply microbial communities. Environ. Microbiol. 16, 1472–1481. ( 10.1111/1462-2920.12343) [DOI] [PubMed] [Google Scholar]
- 285.Cho I, Blaser MJ. 2012. The human microbiome: at the interface of health and disease. Nat. Rev. Genet. 13, 260–270. ( 10.3389/fnana.2011.00029) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 286.Pepper JW, Rosenfeld S. 2012. The emerging medical ecology of the human gut micro biome. Trends Ecol. Evol. 27, 381–384. ( 10.1016/j.tree.2012.03.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 287.Solé R. 2015. Bioengineering the biosphere? Ecol. Complex. 22, 40–49. ( 10.1016/j.ecocom.2015.01.005) [DOI] [Google Scholar]
- 288.Solé S, Montañez R, Duran Nebreda S. 2015. Synthetic circuit designs for earth terraformation. Biol. Direct. 10, 37 ( 10.1186/s13062-015-0064-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 289.O'Dwyer JP, Kembel SW, Sharpton TJ. 2015. Backbones of evolutionary history test biodiversity theory for microbes. Proc. Natl Acad. Sci. USA 112, 8356–8361. ( 10.1073/pnas.1419341112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 290.Scheffer M. 2009. Critical transitions in nature and society. Princeton, NJ: Princeton University Press. [Google Scholar]
- 291.Solé R. 2007. Scaling laws in the drier. Nature 449, 151–153. ( 10.1038/449151a) [DOI] [PubMed] [Google Scholar]
- 292.Jones CG, Lawton JM, Shachak M. 1994. Organisms as ecosystem engineers. Oikos 69, 373 ( 10.2307/3545850) [DOI] [Google Scholar]
- 293.Byers JE, Cuddington K, Jones CG, Talley TS, Hastings A, Lambrinos JG, Crooks JA, Wilson WG. 2006. Using ecosystem engineers to restore ecological systems. Trends Ecol. Evol. 21, 493–500. ( 10.1016/j.tree.2006.06.002) [DOI] [PubMed] [Google Scholar]
- 294.Watson R, Szathmáry E. 2016. How can evolution learn? Trends Ecol. Evol. 31, 147–157. ( 10.1016/j.tree.2015.11.009) [DOI] [PubMed] [Google Scholar]
- 295.Power DA, Watson R, Szathmáry E, Mills R, Powers ST, Doncaster CP, Czapp B. 2015. What can ecosystems learn? Expanding evolutionary ecology with learning theory. Biol. Direct. 10, 1–24. ( 10.1186/s13062-015-0094-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 296.Smith E, Morowitz H. 2016. The origin and nature of life on Earth: the emergence of the fourth geosphere. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 297.Jacob F. 1977. Evolution and tinkering. Science 196, 1161–1166. ( 10.1126/science.860134) [DOI] [PubMed] [Google Scholar]
- 298.Darwin C. 1862. The various contrivances by which British and foreign orchids are fertilized by insects. London, UK: John Murray. [PMC free article] [PubMed] [Google Scholar]