Parameterization of a disease progression simulation model for sequentially treated metastatic human epidermal growth factor receptor 2 positive breast cancer patients

Abstract

Background

The objective of this study is twofold: 1) to propose a simulation model for HER2+ metastatic breast cancer (mBC) which could further be used to assess the overall cost-effectiveness of the treatment sequences that would maximize survival of patients, and 2) to estimate transitional probabilities between treatment lines required to parameterize the simulation model, in the absence of individual patient data (IPD).

Methods

Individual patient data (IPD) were reconstructed for treatment lines composing four treatment sequences. Parametric models were tested to select the model that best fits the IPD. The transitional probability equations, used for disease progression modeling, were obtained by substituting the parameters of the general equation for transitional probabilities by the parameters estimated from fitted distributions.

Results

The log-logistic model best fitted the reconstructed data for progression-free and overall survival curves for each line of treatment. The shapes and scales of the log-logistic models were used to develop the transitional probability equations for the HER2+ mBC simulation model.

Key limitations: The estimation of the transitional probabilities depends heavily on the accuracy of the IPD reconstruction. Nonetheless, analytical and graphical tests can be performed to check the face validity of the reconstructed data. Additionally, sensitivity analyses can be conducted to test the impact of uncertainty surrounding the estimated parameters defining equations for transitional probabilities.

Conclusion

The results of this study can be used as input in model-based economic evaluations of sequential therapy for HER2+ mBC.

Introduction

Breast cancer is the second leading cause of cancer-related death among women globally¹. It is a heterogeneous disease comprising distinct molecular subtypes (luminal A and B, human epidermal growth factor receptor 2 [HER2] type, and triple negative/basal-like)². Globally 1.7 million breast cancer cases and 521,900 women’s deaths from breast cancer were estimated in 2012¹. Breast cancer accounts for approximately 25% of all cancer cases and 15% of all deaths among women¹.

Advances in our understanding of the molecular underpinnings of breast cancer have led to the availability of targeted systemic therapies which in turn have improved clinical outcomes. The elucidation of the human epithelial growth factor receptor (HER2/neu) pathway and its importance in the genesis of breast cancer, followed by the clinical development of effective HER2 targeted therapies, is one of the greatest recent successes in oncology. Treatment of HER2 positive metastatic breast cancer (mBC), which comprises about 20 to 25% of all mBC cases³, has rapidly evolved over the last decade⁴. There are four different HER2 targeted therapies that are FDA approved for use in the metastatic setting, which can be combined together or with chemotherapy. Different combinations in turn are used sequentially, being changed at the time of tumor progression. Consequently, there are different possible treatment sequences, which could be utilized for the treatment of metastatic HER2 positive breast cancer. The clinical benefits associated with these sequences, usually measured in terms of progression-free and overall survival times, are commonly assessed based on clinical trials investigating each line of treatment(s) separately. In order to assess the overall impact of sequential treatments on the progression of HER2+ mBC, it is important to estimate the likelihood values that a patient will either remain stable or progression-free (PF), transition from one treatment line to another or die. However, the estimation of such probabilities is usually complicated by the absence of individual patient data (IPD) corresponding to Kaplan–Meier curves published in clinical trials^5,6.

Therefore, the objective of the present study is twofold: (1) to propose a simulation model for HER2+ mBC which could further be used to assess the overall cost-effectiveness of the treatment sequences that would maximize survival of patients, and (2) to estimate transitional probabilities between treatment lines required to parameterize the simulation model, in the absence of individual patient data (IPD).

Methods

Identification of treatment sequences for HER2 positive metastatic breast cancer

The following criteria were adopted to identify HER2+ mBC treatment sequences that reflect current clinical practice: (1) only combinations supported by published phase III data and recommended in recent American Society of Clinical Oncology (ASCO) consensus guidelines were considered⁷; (2) earlier use of targeted anti-HER2 monoclonal antibody therapy is preferred to later use; (3) continuation of trastuzumab beyond first progression is beneficial; (4) combining drugs with non-overlapping toxicities is preferred to combinations with overlapping toxicities; and (5) capecitabine as the only commercially available oral chemotherapy is preferred to intravenous chemotherapy when data supports it, due to patient convenience. For each treatment sequence, data sources were identified through a literature review of the US National Library of Medicine’s PubMed. Key words used to develop the search strategy were ‘breast cancer’ coupled with ‘treatments’. The search was restricted to phase III trials. The identified treatment sequences are summarized in Table 1.

Table 1.

Treatment sequences for HER2-positive metastatic breast cancer.

Sequences	First line	Second line	Third line
1	Pertuzumab + trastuzumab + docetaxel	T-DM1	Capecitabine + lapatinib
2	Pertuzumab + trastuzumab + docetaxel	Trastuzumab + lapatinib	Trastuzumab + capecitabine
3	Trastuzumab + docetaxel	T-DM1	Trastuzumab + lapatinib
4	Trastuzumab + docetaxel	Trastuzumab + lapatinib	Trastuzumab + capecitabine

T-DM1: trastuzumab emtansine.

Disease progression simulation model overview for HER2+ mBC

The proposed disease progression simulation model was built upon: (1) the natural history of HER2+ mBC, (2) the impact of the identified HER2+ mBC treatment sequences on the likelihood of the occurrence of future outcomes including PFS, OS and serious adverse events, and (3) clinical expert opinions to ensure that the model reflects current clinical practice.

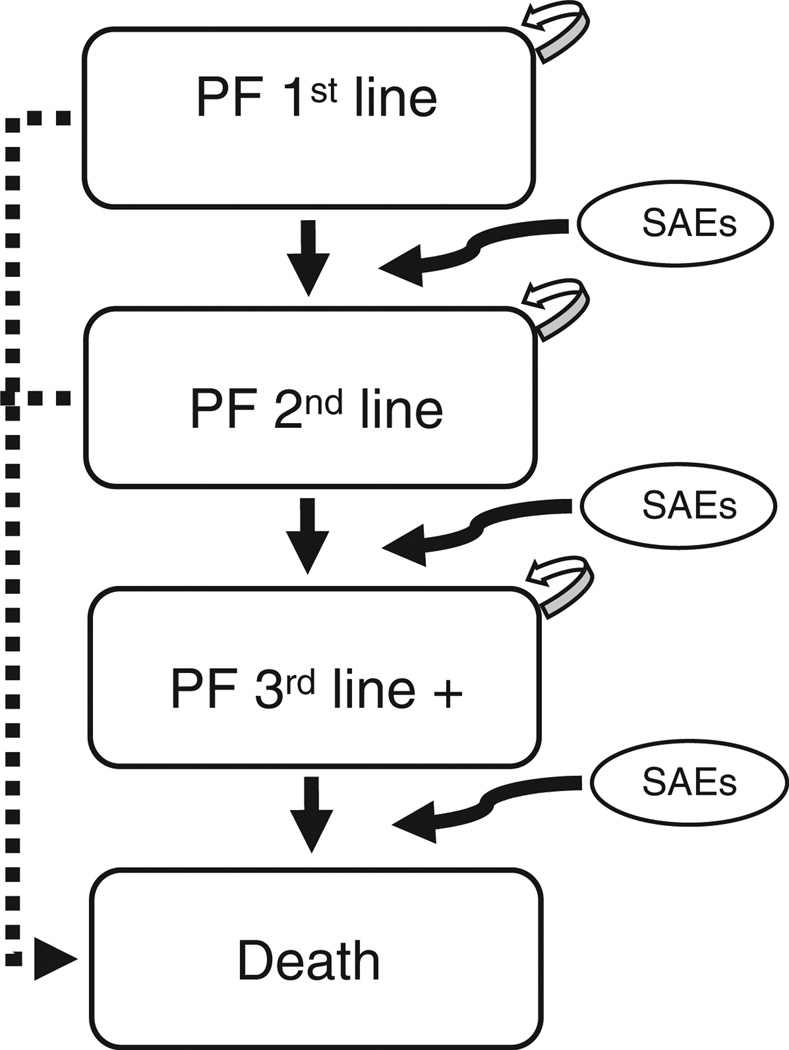
Figure 1 represents the disease progression simulation model for HER2+ mBC, where arrows represent possible transitions through four different health states: PF on first-line therapy (PF 1st line), PF on second-line therapy (PF 2nd line), PF on third-line therapy (PF 3rd line), and death. All HER2+ mBC patients enter the simulation model in the PF 1st line state. Upon treatment with a first-line therapy they may either remain in the stable state (see self-referential arrows in Figure 1) with or without serious adverse events, progress with or without serious adverse events or die, at the end of each simulation cycle. Patients who remain stable but experience serious adverse events or those who progress would discontinue their current line of therapy and be placed on the next treatment (e.g., a patient on second-line therapy who progresses would continue on to the third-line treatment option for that sequence); this occurs until all treatment options are exhausted.

Figure 1.

Disease progression in the simulation model (Markov). PF: progress-free; SAEs: serious adverse events; +: beyond.

The next section explains the approach used to parameterize the probability of transitioning through different health states considered in the disease progression simulation model for HER2+ mBC.

Estimation of transitional probabilities through different HER2+ mBC health states

The parameterization of the probabilities of transitioning through different health states of the HER2+ mBC simulation model builds upon the tutorial by Diaby et al.⁸. The approach consists of three steps: 1) reconstruction of IPD from the progression-free survival (PFS) and overall survival (OS) Kaplan–Meier (KM) curves of published clinical trials, 2) parametric distribution fitting to IPD, and 3) formulation of equations for the probability of staying progression free, dying, and transitioning from one treatment line to the next.

An initial step in the reconstruction of IPD consisted of the extraction of coordinates (censoring times [time variable on the x-axis] and failure events [failure variable on the y-axis]) from scanned KM curves of published clinical trials^9–13 (Table 2). To that end, the software WebPlotDigitizer (available at http://arohatgi.info/WebPlotDigitizer) was used to transform the pixels in scanned KM curves into x- and y-axis data values based on scaling values defined a priori. The resulting coordinates were checked for consistency with the fact that survival decreases over time. Then, a dataset containing a series of intervals matching the respective follow-up times of the published clinical trials, their upper and lower bounds in terms of the number of digitized points, and the number of individuals at risk for each interval was created. The final step involved the use of an algorithm to find numerical solutions to the inverted KM equations, based on the information available in the dataset created above^8,14. An approximation of the original censoring times and failure events with summary of survival data estimates were obtained. The IPD reconstruction was done using the R statistical package.

Table 2.

Clinical trials used for individual patient data reconstruction organized by treatment line.

Study (year)	Treatment(s)	Treatment line	Reference
Swain et al. (2013)	Pertuzumab + trastuzumab + docetaxel	First	9
Swain et al. (2013)	Trastuzumab + docetaxel	First	9
Verma et al. (2012)	T-DM1	Second	10
Blackwell et al. (2010)	Trastuzumab + lapatinib	Second	13
Geyer et al. (2006)	Capecitabine + lapatinib	Third	12
von Minckwitz et al.   (2009)	Trastuzumab + capecitabine	Third	11
Blackwell et al. (2010)	Trastuzumab + lapatinib	Third	13

T-DM1: trastuzumab emtansine.

Standard parametric statistical models (exponential, Weibull, Gompertz, log-logistic, log-normal, and gamma) were tested for suitability of fit to the reconstructed IPD for each line of treatment(s). The first step in the selection of the appropriate distribution(s) to fit to IPD consisted in graphically testing the proportional-hazards (PH) assumption to determine whether equations for the KM curves of the trials have to be estimated separately or not. The graphical assessment of the PH assumption consisted in comparing the log-cumulative hazard plots of the KM curves. The PH assumption was considered to hold when plots were parallel, or violated otherwise. Full consideration was given to parametric accelerated failure time (AFT) models since the PH assumption was violated.

The second step consisted in fitting individual parametric AFT models to reconstructed IPD using different regression models, for each treatment line(s). The selection of the best distribution fit was achieved using analytical (Akaike and Bayesian Information Criteria) and graphical (Cox–Snell residuals analysis) tools^15–17. The parameters defining each selected distribution (e.g. scale and shape of a Weibull distribution) were recorded for further use.

The equations for the probabilities of staying progression-free (Equation 1) and dying (Equation 2) for the simulation model were obtained by substituting the parameters of the general equation for transitional probabilities with the parameters estimated from distributions fitted to IPD, reconstructed respectively from the progression-free and overall survival KM curves. Finally, the sum of the probability of disease progression (Equation 3) and the probability of experiencing a serious adverse event while being in the progression-free state (Equation 4) was considered equivalent to the probability of moving from one treatment line to another (Equation 5). The probability of disease progression was derived by subtracting the sum of the probabilities of staying progression-free (Equation 1) and dying (Equation 2) from 1. Additionally, the probability of experiencing a serious adverse event while being in the progression-free state was the product of the probability of staying progression-free (Equation 1) and the probability of experiencing a serious adverse event (directly obtained from the published clinical trials used in this study).

Results

Individual patient data reconstruction

Four sequences of treatment were identified. Tables 1 and 2 show the identified treatment sequences and lines of treatment with their respective sources. IPD were reconstructed for each line of treatment using R statistical software. Table 3 summarizes median PFS and OS measures collected from the original clinical trials and corresponding estimates from reconstructed IPD. An internal validation of the IPD reconstruction process shows agreement with target data across PFS and OS, i.e. the reconstructed median PFS and OS compare very well to the original median PFS and OS published in clinical trials. In addition, a graphical test was done by plotting original and reconstructed KM curves for each treatment. The graphical tests showed that original and reconstructed KM curves superimpose very well (figures not shown). This confirms the face validity and accuracy of the IPD reconstruction process.

Table 3.

Summary measures collected from the original publications and their corresponding estimates obtained from the reconstructed individual patient data (IPD).

Treatment(s)	Median PFS		Median OS
	Original	Reconstructed	Original	Reconstructed
Pertuzumab + trastuzumab +   docetaxel	18.7 m	19.0 m	NE	NE
Trastuzumab + docetaxel	12.4 m	12.9 m	37.6 m	37.8 m
Capecitabine + lapatinib	5.9 m	27.7 w (6.4 m)*	NA	30.0 w
Trastuzumab + lapatinib	12.0 w	12.45 w	51.6 w	50.2 w
T-DM1	9.6 m	10.13 m	30.9 m	32.1 m
Trastuzumab + capecitabine	8.2 m	8.7 m	25.5 m	25.4 m

T-DM1: trastuzumab emtansine; PFS: progression-free survival; OS: overall survival; NE: not estimated; NA: not available; m: months; w: weeks.

^*Conversion from weeks to months using online converter (http://www.convertunits.com/from/weeks/to/months).

Parametric distribution fitting

Parametric distributions (exponential, Weibull, Gompertz, log--normal, log-logistic, and gamma) were fitted to the reconstructed data for each line of treatment. Based on the information criteria (Akaike Information Criterion [AIC] and Bayesian Information Criterion [BIC]) and a graphical analysis of the Cox–Snell residuals, the log-logistic model was found to be the best fit for the data. The shape and scale parameters of the log-logistic distribution that describe the PFS and OS KM curves are shown Table 4 for each treatment. The scale (λ) of the log-logistic distribution is parameterized as λ = exp(−x_jβ), with β being the vector of regression coefficients estimated from the regression analysis. The shape of the distribution (γ) was estimated from the regression conducted when fitting the log-logistic distribution to the data. The uncertainty surrounding the estimation of the PFS and OS shapes and scales are reflected in the confidence intervals presented in Table 4. Sensitivity analyses (deterministic and probabilistic) can therefore be conducted using these confidence intervals.

Table 4.

Shape and scale parameters of the parametric regression of the log-logistic model on the Kaplan–Meier data.

Therapy	PFS		OS
	Shape (γ)	Scale (λ)	Shape (γ)	Scale (λ)
Pertuzumab + trastuzumab +   docetaxel	0.6218719	0.052051	0.5436962	0.019241
Trastuzumab + docetaxel	0.5553811	0.074128	0.576501	0.024996
Capecitabine + lapatinib	0.5161625	0.03389	0.4647835	0.015981
Trastuzumab + lapatinib	0.5538419	0.082315	0.5882669	0.018985
T-DM1	0.6106105	0.104256	0.4743332	0.032557
Trastuzumab + capecitabine	0.0556305	0.115186	0.4513023	0.040966

PFS: progression-free survival; OS: overall survival; T-DM1: trastuzumab emtansine.

Equation for transitional probabilities

The general equation for transitional probabilities using a log-logistic distribution is presented in Equation 0⁸:

$$t_p(t_u)=1-\text{exp}\{{[\lambda (t-u)]}^{\left(\frac{1}{\gamma }\right)}-{(\lambda t)}^{\left(\frac{1}{\gamma }\right)}\}$$ (0)

where t_p is the transition probability, t_u the cycle for which the transition probability is estimated (t − u representing previous cycle), t representing the current cycle, λ and γ representing the scale and shape of the log-logistic model respectively.

Equations 1–5 can be generated for all therapy lines except that Equation 5 represents the probability of moving to the death state for the third line therapy.

$$t_p{(t_u)}_{\mathit{\text{Progression}}–\mathit{\text{free}}}=\text{exp}\{{[{\lambda }_{PFS}*(t-u)]}^{\left(\frac{1}{\gamma PFS}\right)}-{({\lambda }_{PFS}*t)}^{\left(\frac{1}{\gamma PFS}\right)}\}$$ (1)

where PFS stands for progression-free survival.

$$t_p{(t_u)}_{\mathit{\text{Death}}}1-\text{exp}\{{[{\lambda }_{OS}*(t-u)]}^{\left(\frac{1}{\gamma OS}\right)}-{({\lambda }_{OS}*t)}^{\left(\frac{1}{\gamma OS}\right)}\}$$ (2)

where OS stands for overall survival.

$$t_p{(t_u)}_{\mathit{\text{Progression}}}=1-[t_p{(t_u)}_{\mathit{\text{Progression}}-\mathit{\text{free}}}+t_p{(t_u)}_{\mathit{\text{Death}}}]$$ (3)

$$P{(t_u)}_{SAE/PFS}=[t_p{(t_u)}_{\mathit{\text{Progression}}-\mathit{\text{free}}}*P{(t_u)}_{SAE}]$$ (4)

where P(t_u)_PFS/SAE represents the probability of experiencing a serious adverse event conditional upon being progression free.

$$t_p{(t_u)}_{\mathit{\text{change}}\_Rx\_\mathit{\text{line}}}=[t_p{(t_u)}_{\mathit{\text{Progression}}}+P{(t_u)}_{SAE/PFS}]$$ (5)

For each line of treatment, the final transitional probabilities are obtained after replacing the parameters λ and γ by their respective PFS and OS values reported in Table 4.

Discussion

The concept of value in cancer care has become increasingly important in the move away from a fee for service model in the US. With respect to HER2+ breast cancer, there is a clear preferred treatment sequence, which is based on the definitive results of several well designed randomized trials. Our goal in this study was to: 1) propose a simulation model for HER2+ breast cancer which could accurately estimate the overall cost-effectiveness of the optimal or preferred treatment sequence, which is the sequence of HER2 targeted drugs that would maximize survival of patients, and 2) to estimate transitional probabilities between treatment lines that are used to parameterize the simulation model.

To our knowledge, this paper constitutes the first attempt to estimate the probability of transitioning through different health states of a disease progression simulation model for HER2+ mBC patients treated with sequential therapy, when only summary KM plots are available. The method used to attain this aim builds upon a previously published tutorial⁸. After the identification of four treatment sequences that reflect current clinical practice, IPD corresponding to KM plots of PFS and OS were reconstructed for each line of treatment. Afterwards, parametric distributions were fitted to the reconstructed IPD. For each line of treatment composing a sequence, the equations for transitional probabilities through HER2+ mBC states were parameterized using the shape and scale of the log-logistic distributions fitted to IPD. Note that the disease progression model underpinning the estimation of the transitional probabilities takes explicit account of serious adverse events.

The approach used in this study compares favorably with the one used by Walzer et al.¹⁸. These authors aimed at simulating and comparing progression-free survival among patients with non-squamous non-small-cell lung cancer treated with various sequential therapies. The parameterization of their simulation model was based on a Weibull distribution, which was done deterministically and probabilistically.

The application of the method presented in this paper is not without pitfalls. The accuracy in the reconstruction of IPD depends on the picture quality of the KM curves as presented in the original publications. The accuracy of the extraction of the coordinates of the KM curves also relies on the level of sophistication of the digitizing software used. Furthermore, missing information (such as the number of patients at risk, number of events) from published trials may impede the ability to reconstruct IPD.

It is uncommon to obtain IPD for transitional probabilities from a single clinical trial. These data are generally obtained from different trials, and therefore synthesizing existing evidence through meta-analyses is important. As such, IPD meta-analyses have become popular due to their ability to generate more comprehensive and accurate results when compared to meta-analyses that rely upon individual trials^19,20. Some of these advantages include the fact that IPD meta-analyses provide access to and analysis of original data, take into account patient characteristics, and allow standardization of the analyses across studies^20–22. Moreover, this type of analysis can be used to facilitate time-to-event analysis and ensure the quality of randomization and follow-up. Meta-analyses based on IPD also offer a practical way to conduct subgroup analyses and to better comply with the reporting of missing data^20,21. Even though meta-analyses based on IPD present several advantages, they are challenging to undertake. Some of these challenges include the time effort associated with data acquisition, data extraction and merging, the acquisition of appropriate tools and software to estimate and combine IPD as well as aggregating data^20,23,24. Similarly, indirect treatment comparison (ITC)/network meta-analysis, which provides strong evidence for differences in treatment effects between treatments that have not been directly compared in trials (head-to-head), have often been biased by cross-trial differences in patient characteristics^25,26. Therefore, indirect treatment comparisons can greatly benefit from using IPD instead of only aggregate data^27,28. That being said, appropriate statistical techniques need to be developed to ensure the successful conduct of ITC using IPD, a crucial step in estimating transitional probabilities when modeling disease progression for sequential therapies.

In this paper, the authors provided insights into the parameterization of a proposed HER2+ breast cancer simulation model, which can be used to compare sequential therapies. With no resource constraints sequence 1 is preferred, and there would be no reason to select the other sequences. However, it is worth noting that health care resources are constrained. As a result, the evaluation of the other sequences, using the proposed disease progression simulation model and the estimated equations for transitional probabilities, may offer some insight as to which sequence would be most cost-effective if sequence 1 were not feasible. We believe that the results of this study would appeal to third party payers, oncologists, and cancer centers/researchers and can be used to estimate the value for money associated with HER2 targeted treatment sequences.