A Survey of Colormaps in Visualization

Abstract

Colormaps are a vital method for users to gain insights into data in a visualization. With a good choice of colormaps, users are able to acquire information in the data more effectively and efficiently. In this survey, we attempt to provide readers with a comprehensive review of colormap generation techniques and provide readers a taxonomy which is helpful for finding appropriate techniques to use for their data and applications. Specifically, we first briefly introduce the basics of color spaces including color appearance models. In the core of our paper, we survey colormap generation techniques, including the latest advances in the field by grouping these techniques into four classes: procedural methods, user-study based methods, rule-based methods, and data-driven methods; we also include a section on methods that are beyond pure data comprehension purposes. We then classify colormapping techniques into a taxonomy for readers to quickly identify the appropriate techniques they might use. Furthermore, a representative set of visualization techniques that explicitly discuss the use of colormaps is reviewed and classified based on the nature of the data in these applications. Our paper is also intended to be a reference of colormap choices for readers when they are faced with similar data and/or tasks.

1 Introduction

COLOR vision is an important and fast channel for humans to acquire information. A colormap is a mapping from data values to colors that generates visual structures for the data [27]. Colormaps are commonly used in many domains in computer sciences, e.g., computer graphics, visualization, computer vision and image processing. In this paper, we focus on colormap generation techniques and applications in the visualization domain.

Colormaps play an important role in visualization as they are able to improve the efficiency and effectiveness of data perception and therefore allow more insights into the data. For example, colormaps are used in volume visualization as part of transfer functions [4]. However, to represent features of interest in a dataset, colormaps must be properly generated to allow correct and efficient comprehension. An ill-designed colormap may not provide insight into the data. Whereas a good colormap can provide the user with better understanding and identification of features in their data. Colormaps are not just data dependent but also depend on the undertaken task. Therefore, it is crucial for visualization designers and users to understand colormap generation techniques as well as the general rules for choosing appropriate colormaps for specific data.

Silva et al. [89] provide an excellent review of the topic of colormapping in visualization, in which they briefly review colormap papers and provide guidelines for using those techniques. An extended survey [90] from Silva et al. is more comprehensive. They summarize factors to be considered in colormapping, e.g., data types, tasks, spatial frequency, and audience, and survey techniques indicating different design guidelines. Furthermore, they introduce existing colormapping tools that help the design of colormaps. Reviews of colormapping techniques can also be found in the book by Ware [109], in which color theories, perception issues are discussed, and colormapping techniques are introduced as applications of these theories. Telea [93] introduces colormapping techniques from a data point-of-view. Likewise, Munzner [77] reviews and discusses general colormapping techniques including some recent advances. However, these book chapters are not comprehensive surveys and are intended for introducing visualization concepts. In contrast, we strive to provide readers a more comprehensive survey, a clear taxonomy that can be used for choosing the appropriate techniques for specific data and tasks as well as visualization application examples that explicitly discuss colormapping. Bergman et al. [10] made design rules to generate specific colormaps. We group colormapping techniques in the taxonomy which is similar to theirs, however, the intention is different, as our taxonomy is meant to map the surveyed publications. The contributions of our paper are as follows:

• First, we provide a comprehensive review of colormap generation techniques including the latest advances.

• Second, a taxonomy is created for these colormap generation papers. The taxonomy is intended to help readers quickly choose the right techniques and specific papers to refer to based on the type of data and tasks they are working on.

• Third, we classify representative visualization techniques that explicitly discuss the use of colormaps. Readers are encouraged to fit their applications into the classification and apply colormaps similar to those described in the cited application papers.

The remainder of the paper is arranged as follows: in Section 2, the basics of color spaces and color perceptual issues are briefly covered. Section 3 reviews techniques of colormap generation and summarizes these techniques in a taxonomy. Visualization applications that explicitly discuss the design of colormaps are reviewed in Section 4. Finally, conclusions are drawn in Section 6.

2 Color Spaces

Color spaces are used to quantitatively represent actual colors. Numerous color spaces are proposed, and in this section we briefly introduce the most commonly used spaces to provide some background knowledge.

2.1 Basic Color Spaces

Display devices utilize the combination of three channelsred, blue and green-to represent any color in an additive fashion [92]. Therefore, the combination naturally leads to the RGB color space, which is a cube where the coordinates represent the amount of red, green and blue channels, respectively. The cyan, magenta, yellow and black (CMYK) color space is used for printing devices due to the subtractive color nature of pigments [92].

However, these device-oriented color spaces are not easy to use. Ease of use is enhanced with cylindrical color spaces such as hue, saturation and value (HSV) and hue, saturation and lightness (HSL). Due to their convenience, HSV/HSL are utilized in color selection tools contained in many image editing tools (e.g., Adobe Photoshop, Microsoft Paint, etc.) as well as visualization applications (e.g., VisIt [30], Seg3D [33], etc.).

2.2 Perceptual Color Spaces

The basic color spaces may be easier to understand and interact with, but they have no connections with human color perception. Humans have two types of color receptors in the retina: cones and rods. The cones are sensitive to normal light levels and rods are sensitive to low light levels. The trichromacy theory states that humans perceive colors through three types of cones-S, M and L-named after their sensitivity to different wave lengths [111].

The commission internationale de l’Eclairage (CIE) proposes the first quantitative perceptual color space: CIEXYZ [91] in 1931. The CIEXYZ space is based on the CIE 1931 standard colorimetric observer and three color-matching functions x̄(λ), ȳ(λ) and z̄(λ), which are defined to approximate the three type of cones in the human retina for wavelength λ. These color-matching functions measure the chromatic response of the observer for different wavelengths. In practice, the transformed color space CIExyY is used for specifying colors. A projection of the CIExyY space onto the xy plane is called the CIE (x, y) chromaticity diagram, which is often utilized to visualize colors.

A major issue with the 1931 CIEXYZ color space is that it is not perceptually uniform. MacAdam [64] conducts color matching experiments for 25 locations in the CIE 1931 (x, y) chromaticity diagram to identify the color region around each location that cannot be distinguished by humans. The results are anisotropic ellipses (MacAdam ellipses [64]) of various radii for different regions in the color space. Colors inside each ellipse are perceived the same as the color at the center of the ellipse, and the contour of the ellipse shows the just noticeable differences (JND) in the color space. To make MacAdam ellipses more like circles, perceptually uniform color spaces are required.

The first perceptually uniform color space is proposed by Munsell [76]. Munsell forms an irregularly shaped discrete color space using three independent dimensions: hue, value and chroma. Munsell’s color space is created by experiments and measurements of human perception to figure out perceptually uniform colors. This color space is later commercialized [75] and is still very popular. However, this color space is discrete and the colors inside the space are quite limited.

CIE proposes two perceptually uniform color spaces, CIEL*a*b* (CIELab) and CIEL*u*v* (CIELuv), in 1976. Both color spaces are transformed from the CIEXYZ space to achieve perceptual uniformity. The CIELuv space is calculated from the CIEXYZ with a different transformation [34]. An important feature of both color spaces is that the distance between colors can be measured [34] since the color spaces are roughly uniform.

2.3 Human Color Perception Issues and Color Appearance Models

Color changes appearance under different viewing conditions and the color models discussed above cannot capture these changes. For example, simultaneous contrast effect, the background in which a stimulus is presented influences the apparent color of the stimulus (e.g., a gray stimulus appears brighter with a black background than with a white background [42]). With the Hunt effect, the perceived colorfulness for a constant chroma increases with luminance [42].

Researchers realize that color appearances cannot be modeled by only three variables. Therefore, color appearance models are proposed. Fairchild [42] provides a good comprehensive book on the topic. These models extend basic colorimetry (XYZ) to predict the appearance of stimuli (e.g., lightness, chroma, hue, etc.) in a variety of viewing conditions. Early works on the color appearance models include Hunt’s model [52], the model of Nayatani et al. [78] and RLAB [41]. These works converge as CIE takes the best of these models and proposes a simpler color appearance model CIECAM97s [35]. The CIECAM02 [74] model improves upon CIECAM97s and has become an industry standard for a color appearance model. The CIECAM02 model includes a chromatic adaption transform CIECAT02 and equations for computing appearance correlates of six terms: brightness, lightness, colorfulness, chroma, hue and saturation.

Fairchild and Johnson [43] extend the CIECAM02 model to the image color appearance model (iCAM). The iCAM framework is a robust image processing tool for color appearance, spatial vision effects (e.g., the simultaneous contrast effect), image differences and temporal effects. For technique details and the practical usages of the iCAM framework, readers are referred to [43], [70].

3 Color Map Design

In this section, major colormap design techniques are reviewed. Based on characteristics of these techniques, we divide them into four categories. The four categories are colormap generation techniques specifically focused on addressing data perception problems, namely procedural methods (Section 3.1), user-study-based methods (Section 3.2), rule-based methods (Section 3.3) and data-driven methods (Section 3.4. In addition, as seen in Section 3.5, we survey methods with focuses other than (or more than) data comprehension in which colormapping problems involved with aesthetics, energy saving and semantics are discussed. Then, we summarize these techniques and build a taxonomy for them in Section 3.7.

The most commonly used colormaps are 1D colormaps. 2D colormaps have been proposed for visualizing bivariate or multivariate data although they have to be used carefully as they can be difficult to interpret [24], [77]. An excellent survey of 2D static colormaps for multivariate data visualization is presented by Bernard et al. [11]. Examples of 2D colormaps can be found in [9], [18], [22], [24], [60], [81]. Here, our focus is on 1D colormap design techniques.

3.1 Procedural Colormap Generation

Numerous techniques have been proposed for the generation of a default colormap as an attempt to aid our understanding of most datasets. Robertson and O’Callaghan [82] use Trumbo’s [100] order and separation rules as rules to construct perceptual univariate and bivariate colormaps. They emphasize the importance of perceptual uniformity of colormaps and propose to utilize perceptually uniform color spaces, e.g. CIELab and CIELuv, to build colormaps. Specifically, they utilize the CIELuv space and strive to make uniform spacing between colors, e.g., they avoid high curvature turns in the color space to avoid distant colors on the color path to have very close distance in the color space. Both 1D and 2D colormaps are proposed in their work; however, there are no examples of data using colormaps.

Levkowitz and Herman [61] introduce their standards for a good colormap, namely order, colors should have perceptual orders in a colormap; uniformity and representative distance in which perceived color distances should match actual differences between the data they represent; and boundaries where colors should not create false perceived boundaries in data. Based on these standards, they propose a linear optimal colormap by maximizing the just noticeable differences JNDs between colors in the colormap. Specifically, they measure the sum of JNDs between neighboring colors in a black to white colormap in the CIELuv space. Next, the summed JNDs are maximized and linearized to make the distances of colors in the CIELuv as equal as possible. In an evaluation using medical scan images, they find that observers perform better with the linear optimal color scale than the previously advocated heated-object colormap, but both colormaps are inferior to a linearized grayscale colormap. They provide a twofold explanation of their results: first, perceived color changes due to a color’s surround are not taken into account and second, the CIELuv space is not adequate for modeling perceived uniformity. As such, they realize that depending on different circumstances, different colormaps are superior to others and therefore several candidate colormaps should be provided to the user. Some of the methods in Section 3.3 are based on this result. Pham [79] proposes a method that utilizes B-spline curves and surfaces to generate univariate, bivariate and trivariate colormaps. The author examines existing colormaps and argues that these methods rely on simple geometry in color spaces that restrain predefined color paths and are not good for perceptual reasons. Instead, the author proposes to use cubic B-spline curves and surfaces in the CIELuv space to design more flexible and perceptual colormaps.

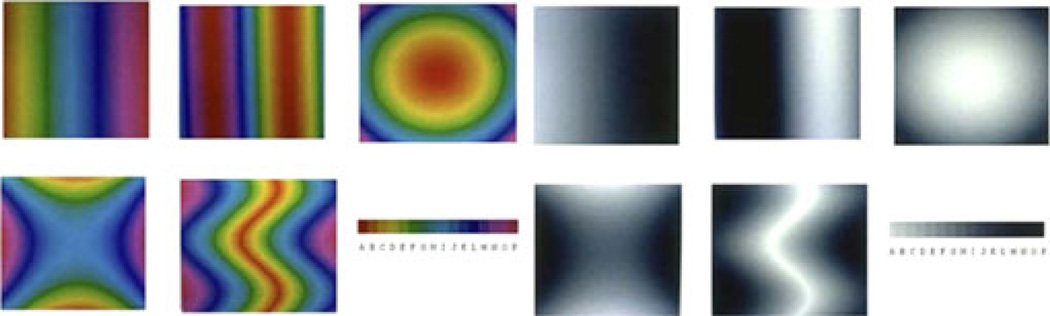
Ware [108], [109] points out that the nonuniformity of colormaps is a minor source of error compared to other human perceptual issues (Fig. 1).

Fig. 1.

Ware [108] concludes that a rainbow colormap is good for metric comprehension, while a grayscale colormap is good for shape comprehension. Copyright IEEE.

He proposes two goals for 1D colormaps: metric reading (metric comprehension), which enables users to accurately read absolute values in data, and form reading (form comprehension), which enables users to correctly perceive the shape. Further, he expects that a spectrum approximation colormap (rainbow) should be good for metric comprehension because humans can distinguish the multiple hues in such a map easily whereas a gray-scale colormap would be bad because of the simultaneous contrast effect. For form comprehension, Ware suggests that the opposite holds where a rainbow colormap is bad because it creates false color gradients that may be misleading whereas a gray scale colormap would be ideal because luminance is the most effective channel for shape perception. To test these hypotheses, Ware conducts user studies to confirm his assumptions. He also realizes it is possible for humans to switch their attention back and forth between hues and luminance. Therefore, he creates a lightness increasing spectrum approximation colormap, which makes a good trade-off between the metric comprehension task and the form comprehension task. This colormap is suggested as a good default colormap.

More recently, Moreland [73] proposes a diverging colormap that is a good compromise between metric comprehension and form comprehension and suggests it as a default colormap for scientific visualization. The diverging colormap is generated by interpolating a light blue color in the beginning with a color close to white in the center and a light red color at the end. The interpolation takes place in a so-called Msh color space, which is a spherical representation of the CIELab color space to make the color changes smoother. Examples comparing this new colormap to other colormaps, e.g., gray-scale, rainbow, heated body and isoluminant on both 2D images and 3D surfaces, show that the proposed colormap performs well in the example circumstances. This specific colormap is included in the visualization package ParaView [48] and has seen extensive use in visualization applications, as will be seen in Section 4, as the default mapping.

3.2 User-Study-based Colormap Generation

Some methods in the previous section utilize user studies to evaluate the effectiveness of proposed colormaps. Other methods, however, directly conduct user studies and learn colormaps from users.

Healey [45] proposes a systematic method for choosing effective colors that provide good discrimination between data values in discrete colormaps. The method first computes the maximum inscribed circle from an isoluminant slice in the CIELuv space and then chooses colors that are equally spaced around the circle, to ensure equal color distances between a color’s two nearest neighbors and a constant linear separation from other colors. Healey then conducts user studies to test the maximum number of colors that still provide good separation. Specifically, the author designs four user studies that test the response time for finding a target color with the presence of three, five, seven and nine colors, respectively. In each test, every color in the chosen colors is tested as a target and the response times for various sizes of stimuli with the absence and appearance of that color are recorded. From these studies, it can be shown that users have no difficulty with three and five colors but have significant difficulty with seven and nine colors. Healey also realizes color distance and linear separation are not enough to define colors that constantly produce good target identification. As such, he takes color category into account and segments the circumference of the maximum inscribed circle into 10 color categories identified by a previous method [46] rather than equally placed. To derive a maximum numbered color scheme, Healey studies one particular seven-color scheme that yields good response time. Based on further user studies of color similarities and response times, the seven-color scheme is optimized and a color selection scheme for these seven colors is proposed. The resulting colormap is then evaluated on a medical CT image where a small feature can be better perceived with the improved seven-color map compared to the original col-ormap as well as a gray-scale colormap.

With a properly designed user study, humans can easily determine the correct colors and luminance. Rogowitz et al. [83] propose a so-called the “Which Blair Project”, which is a user-study-based method to evaluate perceptual (increasing) luminance monotonicity of colormaps. It is desirable to have luminance monotonicity in a colormap as it preserves the perceptual ordering of data, and the higher the contrast in luminance in a colormap, the better that colormap represents absolute values in data. Rogowitz et al. let observers rate the naturalness of a gray-scale human face stimulus colored with a sequence of small segments of colors from eight commonly used colormaps. The rationale behind this test is that if a segment of colors preserves the relative brightness variation in the original face image, then this segment of colors is luminance monotonic. If all segments of colors in a colormap preserve the correct relative brightness variation, then this colormap is said to have luminance monotonicity. The user study results confirm the authors’ assumption of a positive correlation between the luminance monotonicity of colors and the naturalness of pseudo-colored face images. Also, in these tests, the degree of distortion from the natural looking image appears to be proportional to the distortion from luminance monotonicity. This work is successful because humans are very sensitive to luminance variations in human faces.

Kindlmann et al. [55] propose that the idea of Rogowitz et al. [83] can be further extended to create a perceptual colormap (Fig. 2). They propose to use a double face stimuli, which is a binary black and white face image and its black with white reversed copy placed side-by-side. Human brains can easily judge the “positive” face from the two faces. To match luminance, the authors replace the black with a certain shade of gray and the white with a certain color. Here, the users are given a series of double face stimuli of evenly increasing luminance in six major hues: red, cyan, magenta, yellow, green and blue. The users are asked to identify the luminance when the “positive” face turns from left to right for each hue. From this user study, the optimal luminance of each hue can be determined and used to create perceptual colormaps. Two colormaps are designed by interpolating the colors found in the user study: a perceptual isoluminant rainbow colormap and a monotonically luminance increasing colormap. A 2D image example is utilized to show the isoluminant colormap is helpful to aid data value comprehension. Thanks to the perceptual power of humans, the luminance matching is done very efficiently and accurately under the user study designed by the authors.

Fig. 2.

The double face image, (a), is used in the user studies by Kindlmann et al. [55]. The generated isoluminance colormap is shown in (b), whereas a luminance increasing colormap is shown in (c). Copyright IEEE.

3.3 Rule-Based Colormap Selection

Many accepted rules of human perception of colors are to be found in the field of psychology. These rules raise conflicting goals for colormaps [108], [109] and therefore researchers conclude that an attempt to find a default colormap that would work for all datasets may be infeasible. Instead, researchers utilize these rules to propose rule-based methods to generate colormaps for different data and tasks.

Trumbo [100] proposes four rules for color mapping bivariate statistical maps, namely, R1. order, R2. separation, R3. rows and columns and R4 diagonal. The first two rules apply to general colormapping problems and have become important principles for colormap research. According to R1. order, colors chosen to represent statistical variables should be perceived as preserving the order. R2. separation states that colors for important differences in statistical variables should be perceived as different. Rules R3 and R4 specifically deal with bivariate colormapping cases. Trumbo also provides examples of 1D and 2D colormaps that meet the rules he proposed.

Pizer and Zimmerman [80] argue that the gray scale colormaps have three weaknesses: 1) the eye is not sensitive to many distinct gray levels, 2) the eye has relatively low sensitivity to gray scale contrasts, which makes it difficult to visualize changes, and 3) the gray scale is 1D and cannot be used for encoding multivariate data. They claim that color has advantages for all these objectives, and describe four rules for colormapping: 1) sensitivity, the color has to be distinct, 2) naturalness of the color order, 3) the associability of nearby colors in the colormap, and 4) perceptual linearity. The authors then go on to evaluate colormaps applied to ultrasound imaging via user studies. From the study result, they conclude that the heated-object colormap is the map of choice for medical imaging, whereas grayscale colormap has poor sensitivity, the margenta colormap is somewhat garish, and the rainbow colormap is unnatural.

Bernard et al. [11] present a survey and task-based quality assessment of static 2D colormaps. The authors reimplement 2D colormaps in over 50 related works. Then, the 2D colormaps are grouped into two classes: static 2D colormaps and 2D colormaps intended for bivariate data-sets. The focus is on static 2D colormaps, and therefore, the authors exclude colormaps for bivariate datasets. A set of rules are formed where quality assessment measures are mapped on seven different analysis tasks. The authors calculate detailed quality information of every static 2D colormap across all quality assessment measures. From these results, suggestions, depending on the task, for the choice of 2D colormaps are included in the survey.

Bergman et al. [10] study the tasks of visualizations that utilize colormapping and build a taxonomy for colormaps for different tasks and data types. They follow the commonly accepted classification of data into four classes: nominal, discrete data that has nonordered tags; ordinal, discrete data with ordered tags; interval, continuous data where the differences between values are meaningful; and ratio, continuous data with all the properties of interval data and has absolute zero. In this paper [10], the authors specifically study the interval and ratio data and in an extended web-based version, they expand their rules to all four classes of data. They identify three tasks for colormaps in visualization: isomorphic, to faithfully represent form in data; segmentation, to show features in discrete colors; and highlighting, which focuses on certain areas with colors. Also, they emphasis the importance of spatial frequency in colormap design and classify data into low and high spatial frequency. For each combination of data type, visualization task and data spatial frequency, the authors make colormap design suggestions. Examples of colormaps designed following these rules are applied to both 2D and 3D data and compared against colormaps that do not follow these rules. Based on this taxonomy, a system called PRAVDA is implemented to aid visualization users. The PRAVDA system guides users to appropriate colormaps for given data types, tasks and spatial frequencies, and the system further allows users to interactively edit colormaps to better visualize their data. In a related paper, Rogowitz et al. [85] provide a more detailed explanation of their taxonomy and explain how a rainbow colormap can be misleading in visualizations. They summarize by stating that the rainbow colormap creates perceived contours that may not exist in the data, and that structures that fall within such false contours would not be represented. Finally, the yellow areas capture attention because of their high brightness and not because they are important.

The rainbow colormap provides excellent metric comprehension ability [108], [109] and creates aesthetically pleasing visualizations, and, more importantly, is accepted as the standard colormap by many domain users. As such, it is widely adopted by many visualization applications as the default colormap. However, the rainbow colormap has several important flaws that may lead to misinterpretation of the data. Although the shortcomings of the rainbow colormap have been studied and well documented in a number of papers (e.g., Ware [108], Rogowitz et al. [85]), visualization designers and users are generally not well aware of them. To raise the awareness of visualization researchers and users on this issue, papers specifically discussing how rainbow colormaps can be misleading have been published. Rogowitz and Treinish [84] illustrate the downsides of the rainbow colormap through examples of 2D and 3D data. They find that the rainbow colormap can hide small details in data and create artificial boundaries, which can greatly bias the perception of structures in data and further lead to misinterpretation of data. Their solution is to build perceptual colormaps with a focus on visualization tasks and the spatial frequency of the data. The PRAVDA system is recommended by the authors to achieve such colormaps, which are better than the rainbow colormap.

Borland and Taylor [16] list three aspects of how a rainbow colormap can be misleading using 2D synthetic data examples: has no perceptual order, hides details and creates sharp boundaries that are not in the data. Some suggestions are provided to create colormaps for different data types such as using a heated body colormap for high frequency ordinal data, isoluminant colormaps for 3D surface visualization and colors with equal bands along with iso-contours for continuous data visualization. The authors admit that there is not a single best default colormap, but several colormaps should be provided to users from which to choose. To educate readers about how widely the rainbow colormap is used in visualization despite studies repeatedly reporting its shortcomings, the authors further give the statistics of the appearance of the rainbow colormap in papers of visualization conferences from the years 2002 through 2007. The authors find an increasing number of studies using the rainbow colormap. Fortunately, visualization researchers have become aware of the choice of colormaps, and the visualization community has made significant improvements in carefully choosing appropriate colormaps according to the data and tasks, as will be seen in Section 4.

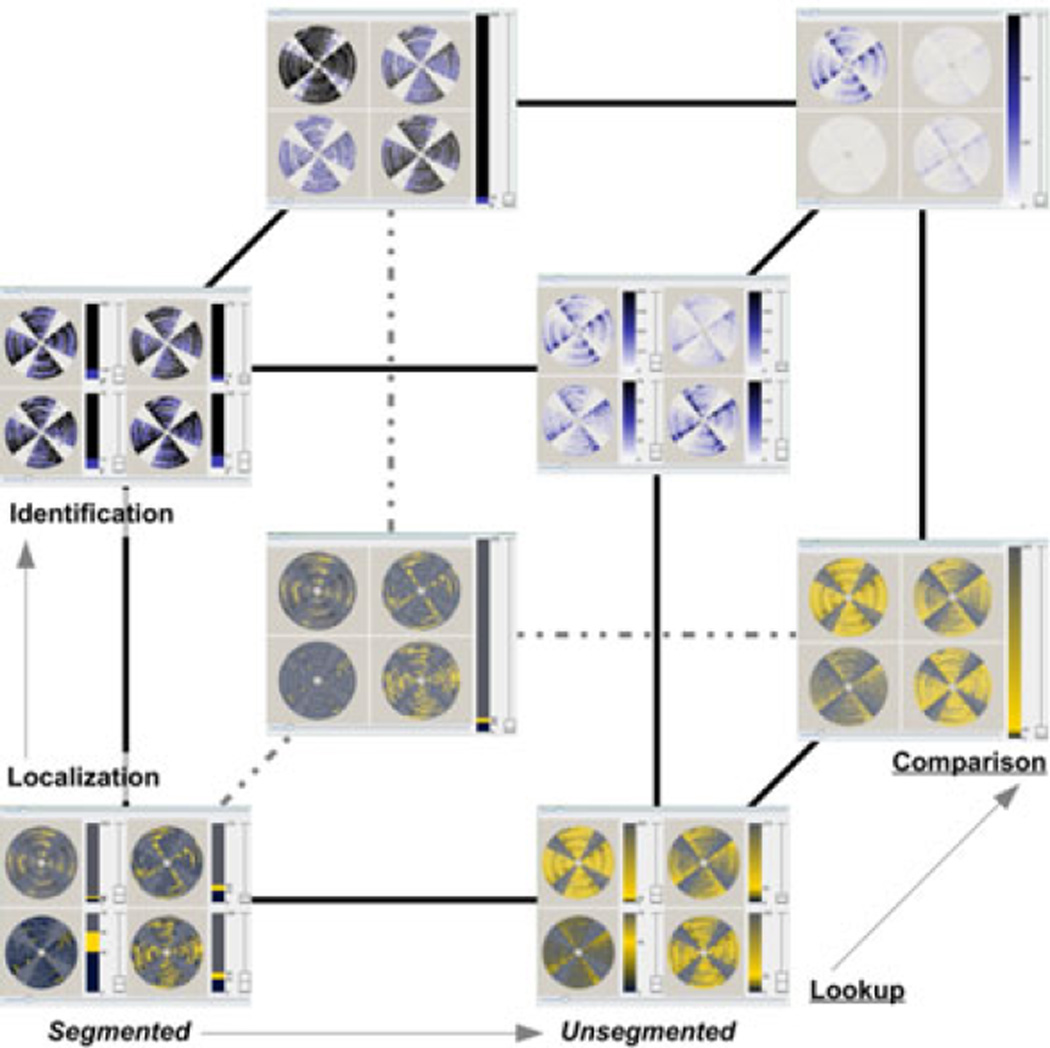
More comprehensive task-based colormap generation has been studied by researchers. Rheingans [81] realizes that there is no best colormap for all datasets. She summarizes existing univariate and bivariate colormaps and then proposes rules for choosing colormaps by considering several factors: the goals, the nature of the data, the intended audience, the whole visualization and cultural connotations. Tominski et al. [96] propose a more sophisticated and systematic task-driven colormapping technique considering the characteristics of the data, tasks and goals as well as the user (Fig. 3). Based on a formal hierarchical task typology [3], Tominski et al. choose different colormaps according to four tasks: lookup, comparison, identification and localization, and data characteristics. Histogram equalization and Box-Whisker plot adaption have been proposed to better adapt colormaps to data. Furthermore, interactive refinement methods for colormaps are provided to allow users to generate colormaps that better fit their own needs.

Fig. 3.

A task-color-cube proposed by Tominski et al. [96]. Copyright IEEE.

Brewer [22], [23], [24] proposes a set of perceptual discrete colormaps that can be grouped into four categories: qualitative, binary, sequential and diverging. The colormaps are carefully designed in a perceptual color space, namely HVC (Hue, Value and Chroma) color space, which is a Munsell-like [75] color space. Unlike the CIELab or CIE-Luv spaces, the HVC color space is a discrete colormap that can be easily converted into the RGB or the CMYK color spaces used by digital devices. In an earlier work, Brewer labels the Munsell color space with CMYK value combinations and utilizes the tagged color space to design quantitative colormaps [21]. In [23], Brewer proposes a systematic approach to generate all four categories of colormaps.

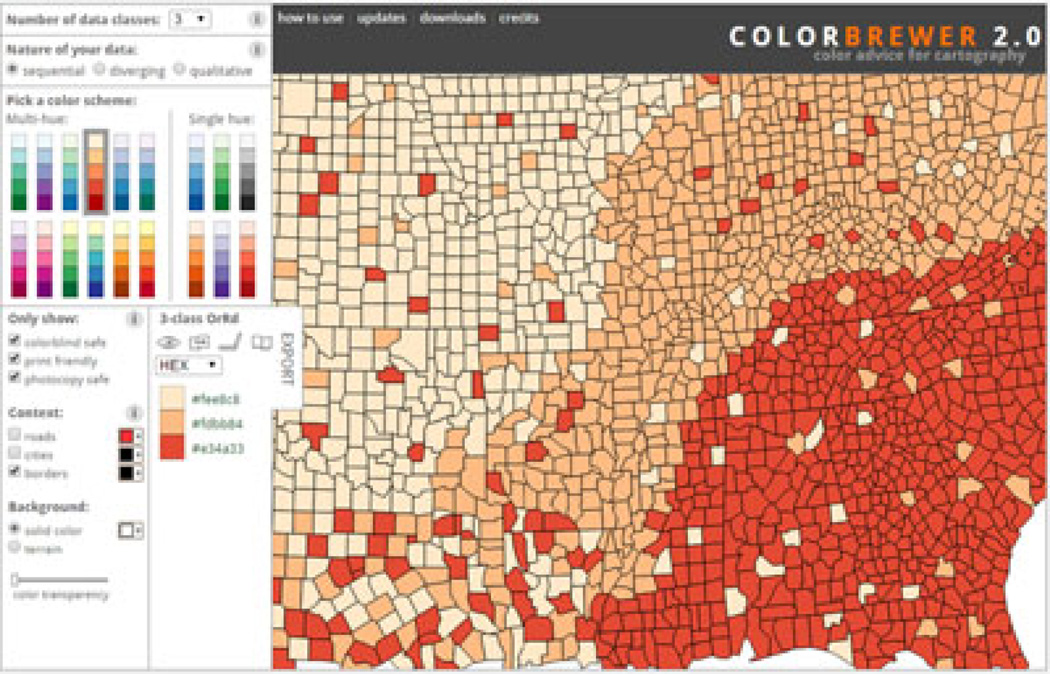
The specific color paths in the HVC color space are also proposed in [23]. In [22], Brewer proposes guidelines for colormaps for different datasets. Based on map data with different sociological statistics laid over it, the author summarizes good colormaps for different data and emphasizes that users should apply their knowledge of data to the colormapping process. She gives detailed hue, lightness and saturation usage advice for colormaps in different situations for univariate and bivariate maps. Specifically, she discusses qualitative, binary, sequential and diverging schemes for the univariate cases, whereas qualitative/ binary, qualitative/sequential, sequential/sequential, diverging/sequential, diverging/diverging and diverging/ binary are discussed for bivariate maps. Colormaps generated by Brewer may be better candidates for default colormaps compared to a rainbow colormap or a gray-scale colormap as Brewer pays much attention to reducing the simultaneous contrast effect for metric comprehension and enables good form comprehension at the same time. The method has been implemented in an online tool by Har-rower and Brewer [44] to facilitate colormap users (Fig. 4).

Fig. 4.

ColorBrewer [44] (http://colorbrewer2.org/) is an online application for choosing an appropriate colormap.

The tool suggests appropriate colormaps for a given number of data classes. The user can compare these colormaps on a US census data. Further, appropriate colormaps for CRT monitors, LCD displays, color printing and colorblindness are also suggested by the tool. Finally, the user can easily export colormaps and use them in their own applications either in their original discrete form or as interpolation nodes for continuous colormaps [73]. Because of the carefully designed colormaps and the easily accessible colormap tool, Brewer’s colormaps are now very popular in the visualization field as will be seen in Section 4.

Wijffelaars et al. [110] realize that the number of colormaps designed by Brewer is large but finite and the colormaps lack flexibility as they are manually designed. The authors therefore propose a more automated colormap generation method for single-hue and multihue sequential and diverging colormaps by Brewer’s definition. The method automatically generates paths from a set of intuitive parameters in a simplified displayable CIELuv color space with a customized distance function. An intuitive user interface is proposed that enables users to design colormaps that are similar to ones designed by experts. A user study has been conducted that shows the effectiveness of the method. Results from this method are close to those generated by Brewer.

The work of Zeileis et al. [112] is also inspired by the ColorBrewer tool [24], [44]. Here [112], the authors propose that colormaps fall into the three types suggested by Brewer, namely qualitative, sequential and diverging, for statistical maps. Instead of predefined discrete colormaps as in ColorBrewer, Zeileis et al. propose more general principles for constructing colormaps with paths in the perceptual HCL color space, which is derived from the CIELuv space. The authors show examples using the proposed colormaps and also discuss the implementation in statistical computing environments.

Some researchers study more specific rules of colormaps used in certain circumstances. Wang et al. [106] study the discrete colormap design for illustrative visualization. They summarize effective usage of colors from previous research and identify eight goals for colors in illustrative visualization. An equal-lightness path and an equal-hue path are computed in the hue, saturation and lightness space derived from the CIELab color space. They then propose methods to meet the eight rules based on the importance of objects determined by the user. Moreover, they study and propose methods to improve perception and to reduce false hues generated from color blending. Examples of both 2D and 3D visualizations are shown to demonstrate the effectiveness of their methods. Wang et al. further conduct a user study to evaluate the usefulness of their methods.

The methods above introduce rules for general colormap design. Borland and Huber [15] further discuss guidelines for designing effective colormaps for specific data and questions. They describe a collaborative process between a visualization designer and a domain expert designing highly tailored colormaps for three 2D scalar fields extracted from a unstructured 3D vector data each to answer a specific question that interests the domain expert. Interestingly, the colormaps they design are quite unorthodox and somewhat violate colormapping rules in visualization (e.g., not following perceptual ordering), but they adequately match the needs of domain experts. The important lesson here is that generic colormapping solutions are useful for providing first impressions to domain users but to achieve truly effective visualization, colormap design should be driven by the data and domain users’ knowledge of the data.

Real-world applications may require a combination of several tasks for colormaps. Mittelstädt et al. [71] propose a series of suggestions for combined tasks of colormapping. The authors point out that previous colormapping methods usually support only a single task, and exclude the visualization expert from the loop. The authors define requirements for analysis tasks and their combinations, form quality metrics for 1D colormaps to support these requirements, and also provide color-blind safe colormaps for each task combination. An interactive system, ColorCAT, is implemented to realize these rules. More importantly, this system integrates the visualization expert in the design of colormaps, and the authors argue that such complex combined tasks forbid automatic methods and interactivity is the key to address this issue.

3.4 Data-Driven Colormap Generation and Optimization

Most of above works discuss the generation of colormaps regardless of underlying data, although some works (e.g., [16], [85]) mention the importance of designing colormaps for specific data and [85], [96] provide interactive tools for that purpose. These general rules are problematic in many cases as interesting features are given inappropriate color ranges, and makes them hard to perceive and may interfere the first impression of the data, making further exploration and analysis difficult. In this section, automated methods that generate or optimize colormaps based on underlying data are surveyed.

3.4.1 Colormap Transformations

Schulze-Wollgast et al. [88] propose to extract statistical metadata from a dataset and automatically generate colormaps that map color ranges to the population of the data using linear, exponential or logarithmic mapping function. Eisemann et al. [40] introduce a simple interpolation scheme for colormap design that emphasizes outliers on 2D map visualizations. The authors compute the projection of data onto a diagonal axis spanned by the smallest and largest elements found in the data and use this projected value along with a user specified angle to interpolate nodes in colormaps. With a higher angle value, outliers are emphasized at the cost of reduced differences for other regions, whereas a lower angle value leads to better discrimination but loses absolute scale information.

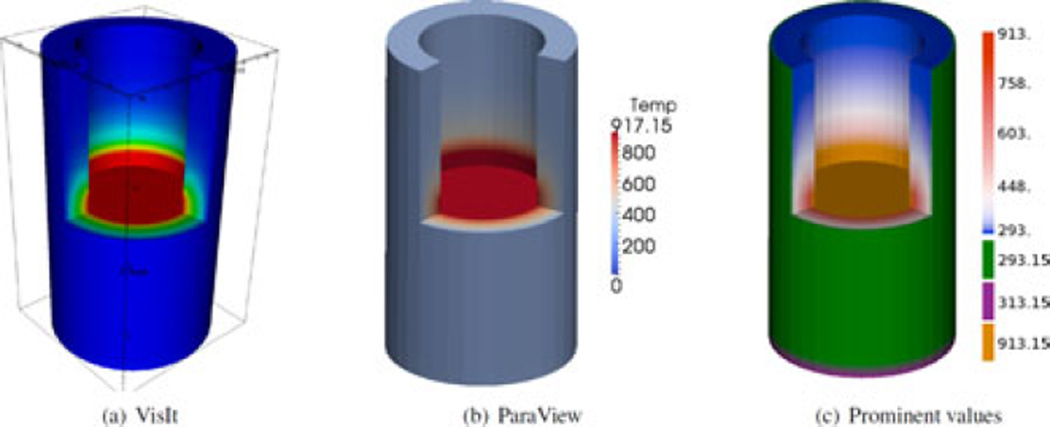
Thompson et al. [95] propose a technique to generate colormaps that essentially match the slope of colormaps to the underlying data by sampling volumetric data (Fig. 5). A proof is provided to show that the method gives a sufficient number of samples to capture important features in the volume. The key observation is that without matching the slope of the colormap to the data, small features are hard to perceive as they are surrounded by regions of a similar color, i.e., the simultaneous contrast effect. Both works extend the idea of Tominski et al. [96] in which they emphasize the importance of transforming the colormap to enhance the comprehension of forms in the data.

Fig. 5.

A comparison of volume renderings of a simulation dataset with colormaps from (a) VisIt, (b) ParaView, and (c) Thompson et al. [95]. Copyright IEEE.

A more in-depth and general analysis of colormap transformations is discussed in Bertini et al. [12]. The authors analyze shortcomings of previous density mapping techniques for continuous colormaps: 1) linear mapping, 2) density function mapping, and 3) histogram equalization. Two drawbacks are found with these techniques: increasing the number of density collisions and reducing the number and range of used color tones. The authors then propose a two-step mapping procedure that first splits the frequency distribution into intervals, and then assigns each interval a color scale value. Examples of 2D datasets demonstrate that the proposed method is able to show more density variations compared to previous methods. Furthermore, qualitative metrics, which are calculated in a case study, demonstrate the effectiveness of the method.

3.4.2 Discrete Colormaps for Particular Data Types

Wang and Kaufman [105] propose an importance-driven automatic colormap design technique for direct volume rendering. The user is able to specify the importance of each classified object in a volume rendered image and then an objective function is set up based on user-selected importance to assign colors to the objects to convey their importance. The objective function measures a rendered image, and takes object importance, separability, attentiveness of colors and distances of object colors as well as color harmony into consideration. An optimized objective function for colormapping along with an importance-based opacity mapping yields rendered images that improve the perception of important objects, as a user study shows.

Tennekes and de Jonge [94] propose a novel method for coloring tree-structured data. The method assigns each node in a tree with colors from the HCL (hue-chroma-luminance) color space. The colors satisfy three criteria for effective color perception: 1) all colors are unique, 2) the colors reflect the parent-child relationship, and 3) the colors encode the hierarchical depth. The method also allows parameter tuning to achieve better visualizations for specific datasets. A formal user study with 98 participants is conducted, and the study result demonstrates that Tree Colors enhances the understanding of hierarchical data visualization.

3.4.3 Perceptually-Based Optimization

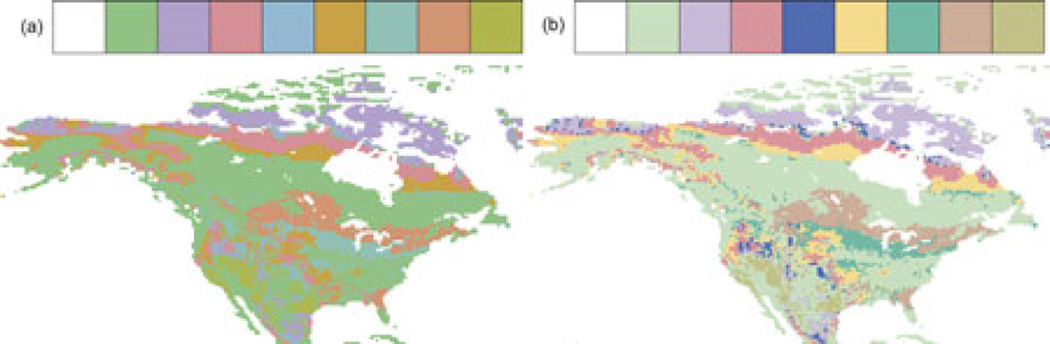
Lee et al. [58] propose an automated optimization method to improve categorical data perception on 2D map datasets (Fig. 6). Color appearance changes with different spatial context. This issue has been studied extensively as shown in Section 2. However, previous studies have not taken spatial information into account and therefore cannot address the color appearance issue. In [58], the authors define a point saliency measurement that computes the difference between the color of a pixel and the averaged color of its neighborhood in the CIELCH color space, which is a cylindrical representation of the CIELab space. Next, a class visibility metric is calculated as a weighted sum of point saliences of all pixels that belong to this class. Then, class visibilities of all classes are optimized in order to highlight classes that have smaller regions embedded in other classes. Specifically, an energy function that measures the sum of differences between the visibility of each class against the mean visibility of all classes is formulated and minimized using a GPU-based conjugate gradient method.

Fig. 6.

A categorical colormap, as shown in (a), results in a limited visibility of categorical differences on a map dataset. Lee et al. [58] propose a visibility optimization method that results in the colormap shown in (b), which provides much better contrasts in the data. Copyright IEEE.

Mittelstädt et al. [70] study the simultaneous contrast effect and propose methods for compensating such an effect. The idea is that, simultaneous contrast makes regions of the same color look different but by setting these regions with different colors, it is possible to make their perceived colors the same or very close. The methods they propose first compute the perceived image based on predictions of the simultaneous contrast effect using a customized color appearance model. Cost functions are set up to measure the differences between the perceived image and the original image. Cost functions are then optimized to minimize the differences between the perceived image and the original image. To better measure the color appearance, the authors extend the iCAM color appearance model [43] by modifying parameters. The authors identify two tasks for colormapping on 2D images, namely, the elementary task and the synoptic task, and formulate different cost functions to handle these tasks. They then utilize a weighted sum of cost functions to form a uniform cost function for different tasks. A heuristics-based approximation approach is designed for the optimization of cost functions. To examine the effectiveness of the method, the authors conduct two user studies. The study results suggest that the proposed compensation methods could improve the accuracy of metric comprehension in 1D colormapped data. Furthermore, applications on real data are examined and demonstrate the effectiveness of the method. Images are perceived significantly different by users. Therefore, Mittelstädt and Keim [72] further improve the performance of contrast compensation by introducing a personalized perception model. The method also improves over the original method in runtime, such that it runs interactively.

3.5 Beyond Data Comprehension

Researchers also focus on colormap design techniques for purposes beyond pure data comprehension.

3.5.1 Aesthetics

How to choose natural and visually pleasing color schemes for images is an important topic in computer graphics ( e.g., [36], [103]). It is also important in visualization as humans look at visually pleasing representations with more care, which may lead to more insights gained from a visualization.

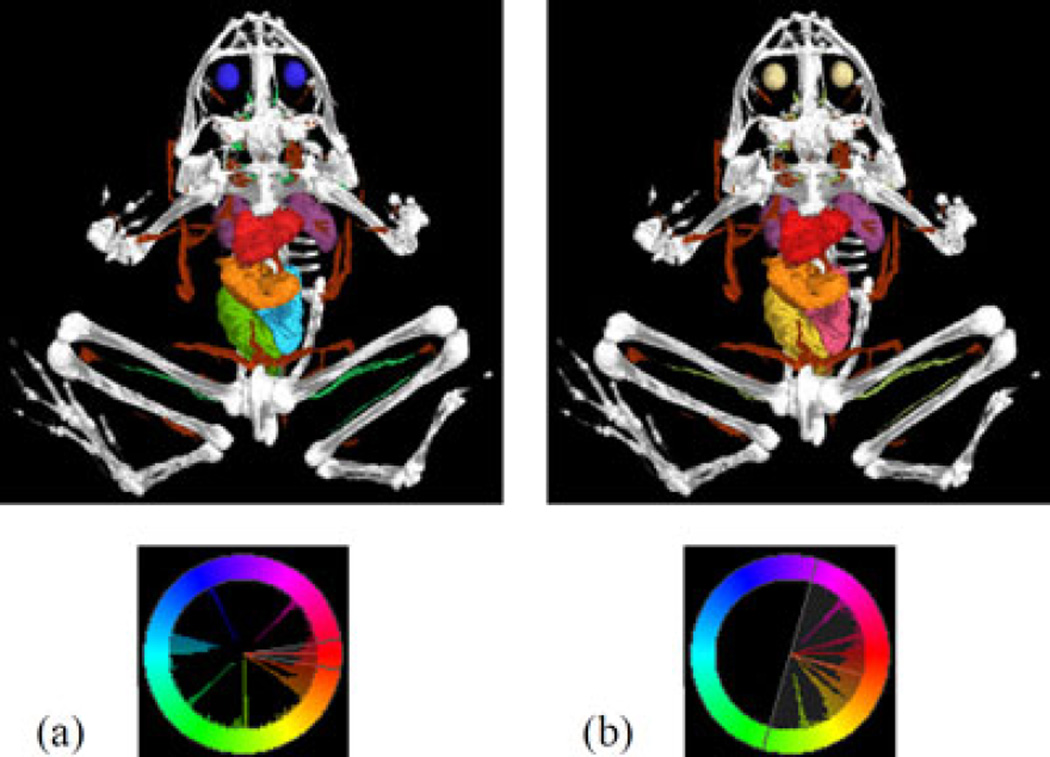
One application already being used in visualization is color harmonization proposed by Cohen Or et al. [36]. Cohen Or et al. [36] study the color harmonization theory and propose an optimization method to harmonize the colors used in an image. The resulting method is able to recolor an image into a harmonic scheme that looks natural and realistic. Wang and Muller [107] extend the work of [36] to preserve lightness in the harmonization scheme and apply it on volume visualization (Fig. 7). They propose to compute iso-lightness curves for hue slices in an HSV (hue, saturation and vividness) color space, which is transformed from the CIELab space. The colors change only on their corresponding iso-lightness curves when transformed into harmonic schemes. The lightness-preserved harmonic schemes allow better contrast for highlighting features that are important in the volume visualization. Wang and Kaufman [105] utilize color harmonization for assigning colors to 3D structures based on their importance. The aforementioned work of Wang et al. [106] also takes aesthetics into account in the design of discrete colormaps for categorical data. For example, they utilize vivid colors to focus attention on specific structures, and they use high-saturated colors for interior structures, whereas low-saturated colors for outside structures to make the interior structures stand out. Moreover, they study the color blending schemes to avoid opposing colors canceling each other, and propose optimization approaches to better preserve the ordering of overlapping structures.

Fig. 7.

The original volume rendering of a frog CT scan is shown to the left, whereas a harmonized version using [29] is shown to the right. Copyright IEEE.

3.5.2 Energy Awareness

Energy consumption is an increasingly important topic in computer science as a result of the demands for longer battery life for mobile devices, the lower energy cost of desktop computers as well as the increased environmental awareness of the whole society. For visualization, the need for lightweight methods to examine visualization results (e.g., physicians would like to use mobile devices to quickly check a patient’s CT scan) is growing and with the increasing computational power of mobile devices, many computationally intense visualization techniques have gone mobile [31], [113]. The display system of an electronic device is a major consumer of electricity, especially for the smart phones whose display is the biggest consumer of battery power [28]. Older displays (e.g., CRTs and LCDs) consume approximately constant energy for displaying any color. Emerging display techniques (e.g., OLED) allow variable energy consumption for different colors and researchers therefore have been striving for color mapping techniques that consume less energy without sacrificing the quality of perceived colors. Chuang et al. [32] propose two energy-aware colormap design techniques based on the CIELab space to reduce energy consumption of screen space variant energy displays for visualization applications. The first technique is based on the optimization of a set of discrete hues that is easily distinguishable as suggested by Healey [45]. The energy consumption of these colors are analyzed and an optimal scheme for minimizing energy is calculated. A second approach is based on constrained continuous optimization of color energy for lower overall color energy consumption. The authors compare their techniques to traditional color schemes (Color-Brewer [44] for 2D example) and typically achieve a 40 percent energy savings. Wang et al. [104] introduce energy-saving color schemes specifically for sequential data visualization on OLED screens. Color schemes are found by a multi-objective optimization approach that minimizes the power consumption of the whole display and maximizes a color perception distance term which measures the distance between the starting color and the ending color in the sequential colormap proposed by Wijffelaars et al. [110] in the CIELCH space. Experiments are performed to measure the energy consumptions of their proposed approach on colormaps from [44], applying a treemap visualization that results in a reduction of 17.2 percent of energy.

3.5.3 Semantics

Humans associate colors with semantics. If the visualization correctly matches the cultural background of visualization users, the resonance of colors and their semantics allow humans to gain insights more efficiently. In contrast, contrasting textual and color cues (e.g., use red color for the word ‘green’) greatly hampers understanding and humans take longer to understand; such an effect is called the Stroop effect [67]. Lin et al. [62] propose a method to select semantically resonant colors for data visualization. The idea is that given a set of colors and a set of categorical values, the method is able to assign the optimal color for each categorical value. Specifically, they first conduct web searches for categorical values (key words) in the data and compute an aggregate color histogram for each search result for analysis. A color probability for each color is then calculated based on the color histogram by measuring the conditional probability and the entropy. The color is then assigned for a categorical value based on an affinity score computed from the color probability. To validate the method, formal user studies are conducted and the results show that, first, with the resonant color, users are able to identify a category faster and, second, the color assignment result is close to crowd-sourced assignment results.

3.6 Color Vision Deficiency

Color vision deficiency (CVD) is the inability to distinguish certain shades of color or in more severe cases, see colors at all. The spectral response of each type of cone (S, M, and L) in the eye is defined by the specific type of photopigment it contains [66]. If a given photopigment changes its spectral response, it is called anomalous trichromacy. Dichromacy is caused by the absence of one of the photopigments. It can be further classified, for anomalous trichromacy and dichromacy respectively, into protanomaly, protanopia, or red-green weakness/blindness (less sensitive to red), which is caused by L cones, deuteranomaly, deuteranopia, or the second type of red-green weakness/blindness(less sensitive to green), which is caused by M cones, and tritanomaly, tritanopia, or blue-yellow weakness/blindness (S cones). Monochromacy, a much rarer deficiency, results from the existence of only a single kind of photopigment or no photopigment at all.

Approximately 7.9 percent of Caucasian men, 4.2 percent Asian men, and 2.6 percent African men, and 0.42 percent of Caucasian women, 0.58 percent Asian women, and 0.54 percent African women are affected with color vision deficiency of some kind, and their ability to carry out visualization tasks with colors may be compromised [66].

To improve visualization experience for people with CVD, Brettel et al. [20] propose a method to first simulate color perception dichromats for observers with normal vision. The method treats colors as vectors in a long-wavelength, middle-wavelength, and short-wavelength (LMS) space, and transforms color vectors from normal-vision gamut into gamut of color-vision deficiency based on previous physiological studies. The model is able to handle three types of vision deficiencies, protanopic, deuteranopic and tritanopic vision. Simulation results of a mosaic image are evaluated by a protanope and a deutranopic who both consider the simulations are close matches to their perceptions of the original image. Machado et al. [66] propose a physiologically-based model for simulating color perception. The model unifies normal color vision, anomalous trichromacy, and dichromacy in a robust framework. A controlled user experiment is conducted to demonstrate that the results created by the model closely matches the perception of people with color-vision deficiency. Furthermore, the method is equivalent or superior to current models for simulating anomalous trichromacy and dichromacy perceptions.

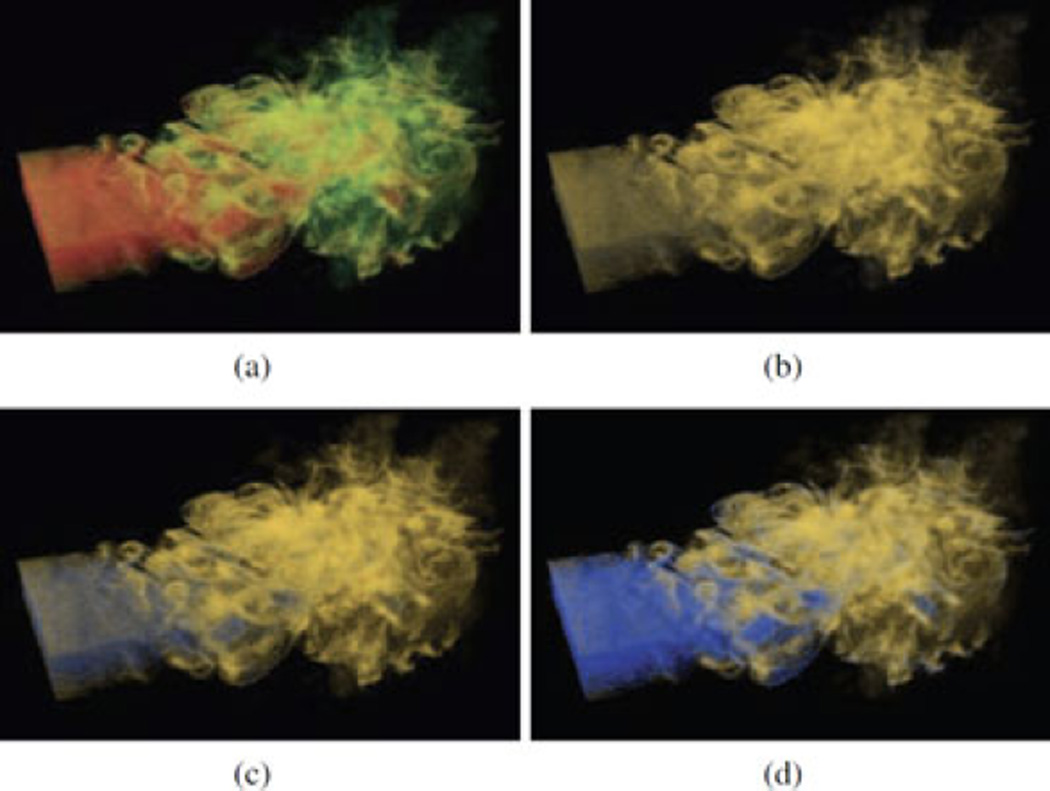
Based on these simulated CVD models, researchers have proposed methods to enhance visualizations for people with CVD. One approach is to recolor an image to improve color perception. An efficient method proposed by Kuhn et al. [56] automatically recolors an image to highlight important visual details that are unable to be noticed by dichromats (Fig. 8). The method preserves the naturalness of original colors as much as possible while increasing color contrast for better perception by dichromats. The method can be implemented on the GPU. The method is evaluated by paired-comparison with people with color-vision deficiencies and the effectiveness is validated. Machado and Oliveira [65] propose an automatic real-time image-recoloring technique that guarantees temporal coherence. The method has a computational cost that varies linearly with the number of image pixels. A comparison against state-of-the-art methods demonstrates that the proposed method has comparable quality, but is two orders of magnitude faster. Patterns are also utilized to encode color information for people with CVD. The method of Sajadi et al. [86] overlays a colormap with patterns, so that dichromats are able to better comprehend the values in the data, while original colors are preserved for normal trichromats. Two user studies are performed to validate the effectiveness of the method. From the studies, overlaid patterns not only help dichromats but also aid normal trichromats as an extra cue. The method is implemented easily on the GPU for real-time performance.

Fig. 8.

A volume rendering of a flame is shown in (a). Simulated views of protanopes for (b) original image, (c) result by image-recoloring technique by Kuhn et al. [15], (d) exaggerated color-contrast approach [15]. Copyright IEEE.

3.7 Summary of Methods

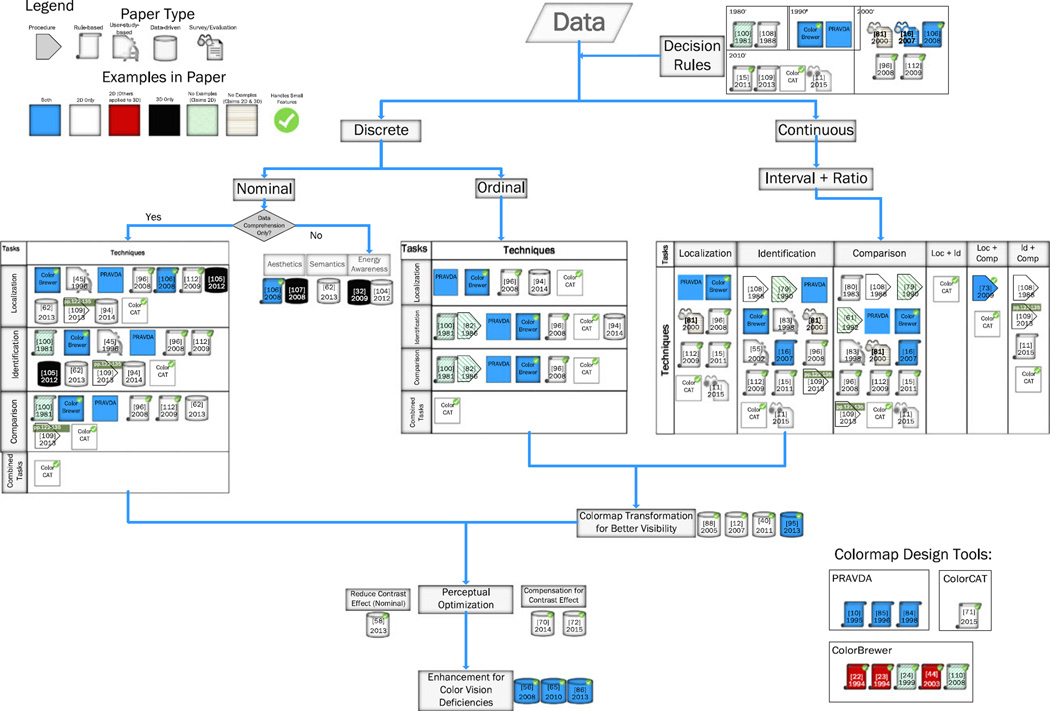
The colormap generation papers we have reviewed are classified into a taxonomy as shown in Fig. 9. In this graph, the papers are laid out in a taxonomy based on types of data and tasks. Visualization tasks have been systematically studied by Andrienkos [3], and more recently by Brehmer and Munzner [19]. Both focus on typologies that are able to describe complex visualization tasks using tasks decomposition and hierarchical decomposition and are good for design studies. However, the full task description is overly complex for our purpose, and therefore we specifically adopt the following tasks: localization, identification, comparison. These tasks have seen usage in colormapping work by Tominski et al. [96], and more recently by Mittelstädt et al. [71]. Mittelstädt et al. describe these three tasks: “localization is performed when the user wants to see where specific objects are located within the data. Identification is performed when the user browses or explores the data and reads values from color encoded objects on the screen.” A comparison task is used to compare multiple visual encoded objects, and to perceive and understand the relative and absolute differences. Ware [108], [109] refer the absolute comparison task as shape reading, whereas Bergman et al. [10] refer it as authenticity. Moreover, combined tasks [71] is where two or more of comparison, localization, or identification are used in a specific application. Each paper is represented by a tag whose shape and color determine the property of the paper. The shape of a tag indicates the class of the approach of that paper: chevron for procedural papers, scroll for rule-based papers, glasses with documents for survey papers, microscope and documents for user-study-based papers, and disk for data-driven techniques. The color and hatching of a tag represents the data examples: blue means that the paper handles both 2D and 3D data, white indicates 2D data only, black indicates 3D data only, dark red is used for 2D examples while others applied to 3D. Some papers do not have examples; nevertheless, we use green diagonal hatching to represent that the method is suggested for 2D data and brown horizontal hatching for methods that are suggested for both 2D and 3D data. Furthermore, we pay special attention to methods that handle small features, and use a check icon on the right top corner of the paper icon to indicate.

Fig. 9.

A taxonomy of colormap generation papers.

Except for the decision rules category, all leafs of the taxonomy represent papers that introduce new colormaps or colormap transformation/optimization techniques. Given a dataset, there are a number of papers on rules ([10], [15], [16], [22], [23], [44], [71], [81], [84], [85], [96], [100]). for determining which colormaps should be used.

In our taxonomy, the first step is to determine whether to visualize data with a discrete or continuous representation. For discrete representation, it is necessary to identify if the data is nominal or ordinal. For nominal data, if data comprehension is the only purpose, techniques can be found for different tasks. Some techniques exist for purpose beyond data comprehension, for example, aesthetics [106], [107], semantics [62], and energy awareness [32], [104].

If the data is visualized as continuous, there is usually not a distinction between interval and ratio data. For data comprehension purposes, combined tasks can be grouped as localization + identification, localization + comparison, and identification + comparison.

Colormap transformations [12], [40], [88], [95] can be performed to improve small feature perception. Perceptual optimization can be performed once the initial colormap is selected.

Care should be taken for people with color vision deficiencies, and several techniques [56], [65], [86] exist for enhancing colormaps for CVD.

4 Colormap Applications

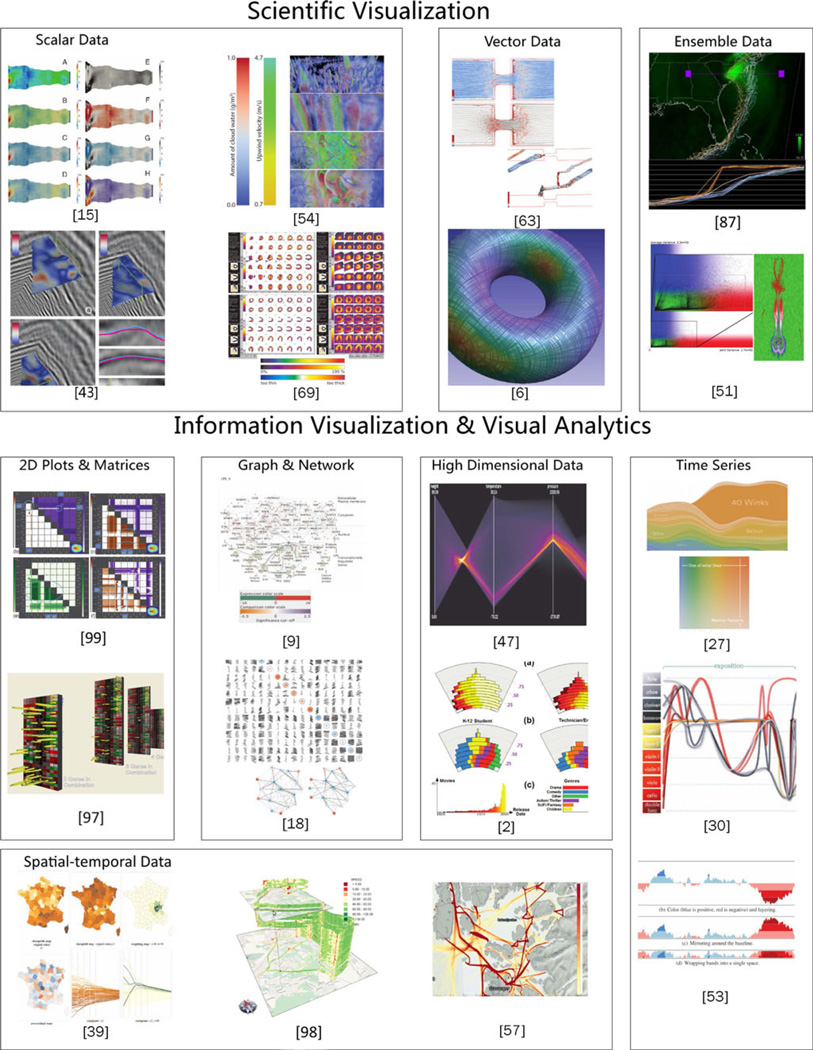
The applications of colormap are numerous in a wide spectrum of various communities. Here, we discuss a representative set of works in the visualization community that explicitly discuss how colormaps are created and used for specific applications. We place applications into the aforementioned tasks (Section 3.7), i.e., localization, identification, comparison, identification + localization, identification + comparison, localization + comparison, to analyze colormaps in each manuscript surveyed. Images from some of the works discussed below are summarized in Fig. 10.

Fig. 10.

Representative works in visualization that conduct good practices for colormapping. The works are classified based on the type of data they visualize. Copyright IEEE.

4.1 Scientific Visualization

Scientific visualization is the subarea in the visualization community that visualizes data that has spatial information in a physically meaningful sense. The most commonly visualized data for scientific visualization are 2D and 3D scalar field, 2D and 3D vector field and ensemble data from many simulation runs or from sensors over time.

4.1.1 Scalar Field Visualization

For scalar field data, there are one or more scalar values at a location. It is critical to set proper colormaps for the users to comprehend the data.

Many applications show 2D scalar field data with colormaps. Borkin et al. [14] evaluate different techniques on artery visualizations for heart disease diagnosis and specifically test the effectiveness of different colormaps, including the rainbow colormap and diverging colormaps from the ColorBrewer tool on 2D for the detection of low endothelial shear stress. The purposes of the colormaps are to localize and compare low endothelial shear stress regions. Malik et al. [68] design methods to visualize and compare different scalar fields of high-resolution industrial CT scans simultaneously with the rainbow colormap and utilize a black body colormap to visualize edges in the scans. They reason that the use of rainbow colormap is a result of the industrial convention and they customize the rainbow colormap to highlight small features of interest in the visualization. The rainbow colormap helps with the identification of multivariate data values in the multi-image view, and the black body colormap is utilized for the comparison of different regions in the edge view. Moreover, since all variables are drawn together, both colormaps are used for comparing different variables. Höllt et al. [49] utilize a diverging colormap to represent the magnitude of energy of a horizon finding algorithm on slices of seismic datasets. Such a blue-white-red colormap is typically used to localize regions with extreme scalar magnitudes in the petroleum industry. Zhou and Hansen [114] apply a ColorBrewer’s sequential color-map to show the confidence of feature boundaries of one or more attributes of volumetric datasets on 2D slices and allow the user to crop the colormap to highlight values of interest. Comparing and identifying computed confidence of different regions on feature boundaries are the tasks associated with the colormap.

Khlebnikov et al. [54] propose a noise-based multivariate volume visualization technique and utilize the diverging colormap proposed by Moreland to visualize one scalar field and customized sequential colormaps to visualize another attribute simultaneously. The diverging colormap is used to localize regions of interest of the first volume, whereas customized sequential/diverging colormaps are designed for identifying data values of the second volume, and can be distinguished from Moreland’s colormap as they are rendered together.

van der Zwan et al. [102] utilize ColorBrewer colormaps to visualize molecular surfaces with continuous abstraction as spheres, balls-and-sticks as well as ribbons with illustrative rendering. The colormap is applied to localize and identify different chemical elements for molecular spheres and front or back of ribbons, and the colormap also better suits cartoon rendering as it has a pastel look. Meyer-Spradow et al. [69] design a combined 2D scalar and 3D glyph visualization approach for multivariate single photon computed tomography (SPECT) with various multi-hue colormaps for efficient interactive detection of coronary artery disease. The reason to have several multihue colormaps is that values are shown on both surface and glyphs. All these colormaps can help with identification, while two of them also simultaneously fulfill the comparison task. Another color-map is designed for combined task of localization and identification for visualizing wall thickness.

4.1.2 Vector Field Visualization

Lipsa et al. [63] visualize both the irregular grid and path lines of 2D foam simulation data over multivariate 2D scalar fields with several diverging colormaps and a heat colormap. The diverging colormaps are utilized to help with localization and identification for averaged attribute values across all time steps, and for the path visualization of bubbles. The heat colormap, encoded by the number of time steps, is adopted for comparing attribute values. Noticeable is that Lipsa et al. design their colormaps specifically to highlight small features of interest. Bachthaler and Weiskopf [5] utilize an isoluminance colormap [55] with the same depth perception colors along with bump mapping to visualize line integral convolution on 3D surfaces. This colormap aids the identification of velocity magnitude values on 3D surfaces. Üffinger et al. [101] apply a white to green sequential colormap to show hyperbolicity of path surfaces and a white to blue sequential colormap for the finite-time Lyapunov exponent (FTLE) representation. These colormaps are used for the comparison of the vector field attributes.

4.1.3 Ensemble Visualization

Sanyal et al. [87] propose a tool for visualizing ensemble uncertainty of numerical weather simulation models with color-coded ribbons and spaghetti plots to show variances of simulation ensembles. To avoid the use of the rainbow colormap, a black to green colormap is applied to the background 2D scalar field, and Sanyal et al. apply a discrete colormap by combining three sequential colormaps from the ColorBrewer tool for rendering spaghetti plots. The colormaps are adopted for the comparison task within a spaghetti plots and across different simulation runs. Hummel et al. [51] design a 2D interactive colormap to separate the joint variance parameter space into similar, dissimilar and uncertain regions to visualize and explore an ensemble of 2D convection flows. The interactivity of the colormap enables the user to visualize specific values of interest. This 2D colormap is utilized for localization and identification at the same time. The user can localize regions of different joint variance classes(similar, dissimilar, and uncertain), and to identify the joint variance for each region.

4.2 Information Visualization

Information visualization deals with the visualization and analysis of data that does not have a physical location information. Since the field of information visualization includes large amount of various visualization techniques, we discuss only important categories of work.

4.2.1 2D Plots and Matrices

Bachthaler and Weiskopf [6] introduce the continuous scat-terplot with a sound mathematical model to map an n-D continuous data to an m-D density-based scatterplot, and an increasing luminance multihue colormap is utilized to show the scatterplot. The colormap is logarithmic to give more color ranges to a larger amount of samples. The colormap is used to identify the density value of a point in the scatterplot, and comparing regions of the plot. Torsney-Weir et al. [99] visualize the parameter space of image segmentation algorithms with sequential colormaps from the ColorBrewer tool. User interactions are supported for the colormaps to best visualize regions of interest. These colormaps aid the simultaneous localization and comparison for the matrix of scatterplots. Booshehrian et al. [13] propose a method for analysis of trade-offs, uncertainty and sensitivity in fisheries management decision-making. They design highly distinguishable colors for different scenarios as colored dots and plots. They also utilize discrete colormaps on contour plots to show isocontour interpolation for the simulation model. These discrete colormaps enable easy identification and localization of different scenarios. Correll et al. [37] explore collections of tagged text for literary scholarship using an isoluminant multihue colormap to show different genres (e.g., comedy, history and tragedy) for each tagged word in a literature, a histogram-based per-tag card view for each literature as well as a 2D dimensional reduced scatterplot for all literatures. To facilitate users who are familiar with existing tools, the rainbow colormap is also included as an option in the tool. The colormaps are intended for identification and localization of groups defined either by user, like genre, or by metadata such as composition year or author.

Lehmann et al. [59] apply a multihue colormap for scatterplot matrix and diverging colormaps for a set of visually abstracted scatterplots, which the authors compute from the original scatterplot. The diverging colormaps Lehmann et al. use are restricted to seven items as this is a good distinguishable color scheme suggested by Healey [45]. The multihue colormap is adopted for identifying items in the scatterplot matrix, whereas the diverging colormaps are utilized for identifying and localizing values in the visually abstracted scatterplots. With the help of color mapping, the proposed approach allows interactive navigation and selection to explore a large scatterplot matrix with more than 100 dimensions.

Tominski and Schumann [97] propose a visualization approach for gene combinations where they modify the conventional red-black-green colormap for genetics by adding saturation variations to represent the aggregated expression of a gene combination on matrices. With this colormap, the user can identify and localize gene expressions in different gene combinations.

4.2.2 Graphs

Barsky et al. [8] use both traditional and colorblind-friendly ColorBrewer colormaps for gene expression data overlay on the layout of graphs in a biological context to facilitate system biologists’ exploration and analysis of a biological system model. One colormap is used for localizing and identifying expression values of nodes in multiple conditions, whereas another colormap is used for comparing the differences between two conditions. Brandes and Nick [17] apply diverging colormaps for indegree of graph nodes and popularity measurement for a matrix representation of gestaltlines to analyze asymmetric relations in longitudinal social networks. A combined identification and localization task can be performed with the colormaps for the indegree of nodes.

4.2.3 High-Dimensional Visualization

Heinrich and Weiskopf [47] propose the continuous parallel coordinate plot, which is a density representation that reduces visual clutters for multivariate data, and they apply the same logarithmic increasing luminance multihue color-map as in [6] to visualize the fine details in the density of the plot. Dietzsch et al. [38] apply a multihue colormap and a diverging colormap to parallel coordinate plots and scatterplots to visualize and analyze high-dimensional gene expression data with statistics. The diverging colormap is used for localization, whereas the multihue colormap is intended for identification. Holten and van Wijk [50] evaluate cluster identification performance for different parallel coordinate plot variants and apply both a discrete multihue colormap and a rainbow colormap to show the cluster density values of each method. These colormaps are utilized for identification of density values of each cluster. Alsallakh et al. [1] propose a novel contingency wheel visualization colored by various types of colormaps, including diverging, qualitative and sequential colormaps for different metrics and incorporate the wheels with a star plot for visual analytics of large categorical data. The colormaps are applied to discrete data for a combined identification and localization task. Comparison can also be performed for different groups as the colors are distinct.

4.2.4 Time Series

Byron and Wattenberg [26] apply colormaps on different categories of items in a stream graph to visualize a time series. These colormaps are intended for identifying the category of a stream, and are designed with aesthetics in mind. Chan et al. [29] propose a visualization method for semantic structuring of a time series of the classical music score. To avoid false emotions invoked by misleading colors, they design a colormap based on colors of instruments to represent different groups of instruments in a layer braid visualization and the colormap is also interactive to allow customization. With the colormap, identification of different instrument groups can be easily done. The authors also take aesthetics into account for colormap design. Bruckner and Moller [25] apply a categorical ColorBrewer colormap to show cluster timelines of simulation sequences. Colors in the colormap are distinct, and therefore, users can easily identify the cluster number of an item and localize all items of a cluster. Javed et al. [53] apply a blue-white-red diverging colormap that is similar to Moreland’s colormap and a multihue colormap for a horizon graph and braided graph for visualizing multiple time series simultaneously. These colormaps are utilized for simultaneous identification and localization of items in horizon graphs or braided graphs.

4.2.5 Spatial-Temporal Data

Andrienko et al. [2] colorize self-organizing maps with ColorBrewer and customized colormaps for space-in-time and time-in-space visualizations to discover and explore high-level patterns of multivariate spatiotemporal data. The ColorBrewer colormaps are adopted for combined identification and localization task on the geospatial images, whereas the customized colormap is designed to identify cells of geospatial data and to distinguish from the ColorBrewer maps. In [7], Bak et al. use sequential colormaps on 2D sensor matrix and growth ring maps for analyzing spatiotemporal sensor logs. A sequential colormap is used for simultaneous identification and comparison for visualizing the sensor matrix. Multiple ColorBrewer sequential colormaps are adopted for identifying different ring maps. Dykes and Brunsdon [39] introduce geographically weighted maps and apply sequential and diverging colormaps on geographical views and scalograms to show statistics with spatial information to facilitate decision-making. These aid combined identification and localization of discrete map data for various statistics. Tominski et al. [98] propose a stacking-based visualization to show multivariate trajectory attribute data on geographical maps. Two discrete diverging colormaps from the ColorBrewer tool are applied to the trajectory attribute data as well as a star plot for analyzing trajectory behaviors. The colormaps are intended for combined identification and localization of a trajectory attribute, for example, speed. Lampe and Hauser [57] colorize their kernel density estimation-based visualizations with sequential colormaps similar to those from the ColorBrewer tool for visualizing streaming data of maritime vessel trajectories and air traffic in real-time on the GPU. The colormaps are used to compare different trajectory regions.

4.3 Summaries of Application Papers

Among the 33 papers in this section, 24 papers adopt colormaps designed by methods already proposed, 18 papers introduce original colormaps specifically designed for the applications and nine papers use both existing colormaps and original colormaps. By analyzing tasks associated with the colormaps, many applications utilize colormaps to carry out multiple tasks. They use multiple colormaps to cope with these tasks, 16 papers ([1], [2], [7], [14], [38], [39], [53], [54], [59], [63], [68], [69], [87], [98], [99], [101]) utilize more than one type of colormap for different data or tasks in their visualizations. Furthermore, many works, for example, [6], [8], [14], [37], [59], [69], require combined tasks to be performed with a single colormap. Also, aesthetics is an important goal for colormaps, and at least [26], [29] explicitly declare these as their goals.

In all 24 works adopting existing colormaps, 16 papers ([1], [2], [7], [8], [14], [17], [25], [38], [39], [53], [59], [87], [99], [102], [114]) apply colormaps from the ColorBrewer tool [44], three papers ([49], [54], [63]) utilize the colormap designed by Moreland [73], four papers ([1], [38], [63], [68]) use the black body or heat colormap, i.e., the black to red to yellow or white colormap, one paper [5] adopts the isoluminant multihue colormap proposed by Kindlmann et al. [55] and five papers utilize the rainbow colormap. For the 18 papers with originally designed colormaps, colormaps from [13], [101] are similar to the ColorBrewer colormaps, whereas [6], [47], [59], [69] utilize luminance increasing multihue colormaps, and [26], [29], [37], [54], [97] design multihue colormaps with the issues of standard rainbow colormap in mind.

Interestingly, five papers ([37], [50], [68], [69]) adopt the rainbow colormap. However, these are results of application domain conventions rather than arbitrary choice, e.g., Correll et al. [37] design a isoluminant multihue colormap but users of their tool prefer to have the option of the rainbow color-map as their familiarity with the colormap can contribute to gaining insight into their data. In another case, Borkin et al. [14] use the rainbow colormap in their user studies and report that the rainbow colormap reduces the time for finding features of interest but increases the error of misidentifying these features compared to a diverging colormap. Regardless, authors of these works are fully aware of the issues of rainbow colormaps and cite the rainbow colormap paper by Borland and Taylor [16]. Eleven papers ([1], [2], [8], [14], [29], [51], [63], [68], [98], [99], [110], [114]) allow users to edit colormaps to explore or highlight regions of interest in their data. Five papers ([6], [47], [51], [63], [68]) utilize colormaps specifically tailored to highlight small features in data. Moreover, two papers ([8], [59]) include colorblind-friendly colormaps in their applications.

5 Challenges in Colormap Research

From the taxonomy and the analysis of applications that explicitly discuss colormaps, we are able to identify several directions for future research of colormapping.

Perceptual issues in colormapping are very important as colors can change appearance due to its environment, and therefore, perceptual colormaps should take into consideration spatial information of the colorized data. While the simultaneous contrast effect has been recently studied [58], [70] many more effects need to be examined.

Multivariate colormaps are not widely used due to the limited number of colors human discern as well as the color appearance phenomena. However, visualizing multivariate data has become increasingly important with demands for high dimensional mappings which can highlight multivariate trends.

From a task point of view, as we can see in Section 4, most real-world visualization applications require multiple tasks to be conducted for different visualizations, and in many cases, combined tasks can utilize a single colormap. From a task point of view, as we can see in Section 4, most real-world visualization applications require multiple tasks to be conducted, and in many cases, combined tasks can utilize a single colormap. More metrics and tools should be proposed to fulfill other combined tasks.

There are many rules to guide users and there exist optimization methods to improve colormaps for the data. These methods typically require that the user has the knowledge of both the data and color perception principles which can be a problem for domain users who usually know only the former. Therefore, it is desirable to have an automatic, or semi-automatic, approach to intelligently determine the appropriate colormap for given data based on colormapping rules, and analysis of the data. Furthermore, this method should be able to learn from domain experts regarding what is relevant.

Aesthetics are important for all types of visualizations, but only few works have explicitly considered aesthetics as a goal. Aesthetics can sometimes conflict with colormapping rules and domain conventions. How to create aesthetically pleasing colormaps that still provide insight into data is an important research direction.

Semantics-driven colormapping may be able to improve the performance of users on tasks they carry out. Currently, only a recent work from Lin et al. [62] handles semantical nominal colormaps.

Several works [12], [40], [88], [95] have been proposed to utilize metadata for optimizing colormaps to better match color ranges to data distribution in scientific visualization. Other metadata could be utilized, such as spatial distribution of data values, and the connectivity of these spatial structures. Metadata with text information may also be used for semantic based colormapping.

6 Conclusions

In this paper, we survey papers related to colormaps in visualization. We classify colormap generation papers as: procedural, user-study based, rule based and data-driven. Our classification shows that with a deeper understanding of colors and data as well as the advent of more powerful computation resources, methods for colormap generation have evolved from procedurally designing a default color-map for all data to applying rules based on the nature of data and tasks, and then to more intelligent data-driven approaches as the state-of-the-art. We propose a taxonomy for the colormap generation papers as a decision tree that supports readers in finding papers which share similar types of data or tasks as in their applications. Fundamentals of color spaces including color appearance models are also briefly introduced in the paper.

We summarize papers that explicitly discuss the use of colormaps, and we analyze the tasks associated with the colormaps in these papers. Users can refer to papers which share similar types of data or tasks as in their applications accordingly. We identify some possible directions for future work. We believe our paper can be a valuable contribution to the visualization community and may inspire more investigations into the topic of colormapping.

Biographies

Liang Zhou received the BS degree in computer science from the Beijing Jiaotong University, China, in 2008, and the PhD degree in computing from the University of Utah, in 2014. He is currently a postdoc researcher at the Visualisierungsinstitut Universität Stuttgart (VISUS), Germany. His research interests include scientific visualization and visual analytics.

Charles D. Hansen received the PhD degree in computer science from the University of Utah, in 1987. He is a professor of computer science at the University of Utah and an associate director in the SCI Institute. From 1989 to 1997, he was a technical staff member in the Advanced Computing Laboratory (ACL), Los Alamos National Laboratory, where he formed and directed the visualization efforts in the ACL. He was a Bourse de Chateaubriand postdoc fellow at INRIA, Rocquencourt, France, in 1987 and 1988. His research interests include large-scale scientific visualization and computer graphics. He is a fellow of the IEEE.