Bayesian Penalized Spline Models for the Analysis of Spatio-Temporal Count Data

Abstract

In recent years, the availability of infectious disease counts in time and space has increased, and consequently there has been renewed interest in model formulation for such data. In this paper, we describe a model that was motivated by the need to analyze hand, foot and mouth disease (HFMD) surveillance data in China. The data are aggregated by geographical areas and by week, with the aims of the analysis being to gain insight into the space-time dynamics and to make short-term prediction to implement public health campaigns in those areas with a large predicted disease burden. The model we develop decomposes disease risk into marginal spatial and temporal components, and a space-time interaction piece. The latter is the crucial element, and we use a tensor product spline model with a Markov random field prior on the coefficients of the basis functions. The model can be formulated as a Gaussian Markov random field and so fast computation can be carried out using the integrated nested Laplace approximation (INLA) approach. A simulation study shows that the model can pick up complex space-time structure and our analysis of HFMD data in the central north region of China provides new insights into the dynamics of the disease.

1. Introduction

In recent years, the modeling of infectious disease data in space and time has gained increasing popularity. The aims of such modeling are many fold but gaining insights into space-time dynamics, which may give etiological insights, is a common objective. Modeling may also allow one to predict the potential effects of health interventions such as the introduction of vaccination. Many examples of such infectious disease data arise from government disease surveillance systems, and in many situations are in the form of spatially and temporally aggregated disease counts. In this paper, the motivating example was hand, foot and mouth disease (HFMD) surveillance data collected and monitored by the Chinese Center for Disease Control and Prevention. The dataset comprises weekly number of HFMD cases in 341 prefectures between 2009 and 2010. In this paper we develop a Bayesian space-time modeling framework for infectious disease count data, and achieve significant computational savings using the integrated nested Laplace approximation (INLA) technique. The goals of such modeling are to utilize the surveillance data to understand the space-time dynamics of the infectious disease outbreaks, and to provide predictions of future disease counts to aid in policy formation.

The literature on space-time models is ample, with many proposals based on disease mapping models. For example, in (1) and (2) the risk evolution over time is assumed to take a parametric form. A different approach is taken by (3) and (4), where the risks for every time period are modeled as time-independent spatial random effects with a time-specific precision parameter for the spatial variability. In the context of modeling multiple diseases, (5) proposes a temporally independent multivariate conditional autoregressive (MCAR) model for lung cancer mortality, with data on both males and females being studied. In (6), the authors propose a shared compartment model where the underlying risk for each disease is separated into a shared and a disease-specific component. Many of these space-time models were developed for non-infectious diseases such as cancers.

Disease mapping models developed for non-infectious diseases have been used, often for descriptive purposes, for infectious disease data, see for example, (7) for flu and (8) for meningococcal disease. In a series of papers (9; 10; 11; 12) a framework for the analysis of infectious disease surveillance counts has been developed. In its simplest form, the models can be viewed as Poisson branching process models with immigration, with mean risk being decomposed into an endemic component and an epidemic component. These models have been applied to a variety of diseases and have also used vaccination coverage as a covariate (13; 14). (15) modeled weekly counts of HFMD in prefectures of China using a similar negative binomial model with epidemic and endemic components. In a different approach, time series susceptible-infected-recovered (SIR) models have been developed (16; 17). The fitting of SIR models (and their variants) is challenging unless the populations under consideration are small, however, since the number of individuals in each of the compartments is imputed under the above Bayesian approach to inference (18). A variety of alternative approaches have been suggested for situations in which populations are not small, but all are computationally expensive (19; 20). Approximate Bayesian Computation (ABC) methods have been proposed as an alternative (21; 22).

In recent years, spline models have become increasingly popular in the space-time disease mapping setting, see for example (23). However, such models have mostly been applied to provide a flexible way of modeling the temporal trend, see for example (24). A notable exception is (25) who describes a broader class of regression spline models with spatial-temporal relative risks being modeled as spatially varying or randomly varying regression B-splines. (26) and (27) both consider space-time splines models, though do not include Markov random field (MRF) prior penalty terms, which is the cornerstone of the approach we describe in this paper. (28) compares a traditional space-time conditional autoregressive (CAR) model and a CAR-Pspline model in the context of small area predictions, with inference made using penalized quasi-likelihood (PQL).

In this paper, the approach we take to modeling the space-time spread of infectious disease data is to decompose the relative risk of disease into three components: a large-scale temporal trend, a large-scale spatial trend and a space-time interaction. The latter is the crucial element, and we use a tensor product B-spline model with a Markov random field (MRF) prior on the coefficients of the basis function. Such a model formulation allows the computation to be carried out using the integrated nested Laplace approximation (INLA) technique, resulting in significant computational savings when compared to a classical MCMC approach. Our approach therefore has the advantage of fast computation and easy implementation using R and existing packages.

The outline of this paper is as follows. We begin with a motivating example that concerns the China hand-foot-mouth (HFMD) surveillance data in Section 2. In Section 3 we describe the Bayesian spatial-temporal models that we propose. In Section 4, we demonstrate the performance of our proposed models via a simulation study. The simulated data is designed to mimic the epidemic center movements in space and time typically observed in infectious disease surveillance data. We return to the HFMD data in Section 5 and describe the results after applying the models to the dataset. We conclude the paper with a discussion in Section 6. The supplementary materials contain more technical details and additional supporting information.

2. Motivating Example

In this section, we provide details of the China HFMD surveillance data analyzed in this paper. HFMD is an acute contagious viral infection that has caused large-scale outbreaks in Asia during the past decade (29). It is caused by enterovirus pathogens and usually involves mild or moderate symptoms such as fever, oral ulcer or rashes on the hand and foot. HFMD is a disease often seen in children and in a small fraction of cases there is severe illness with neurological problems, and even death. Little is known about the etiology of the enterovirus, the factors associated with its spread, or an effective means of public health intervention. Therefore understanding the dynamics of HFMD patterns of spread can greatly benefit authorities charged with policy making to control this infectious disease.

Enterovirus-related HFMD, with the first large-scale epidemic outbreak in 2008 in China, has been included as one of the 39 notifiable infectious diseases in the Chinese Center for Disease Control and Prevention (CCDC) disease surveillance system. Each reported case from the CCDC surveillance system includes information on the person’s current home address, gender, age and the symptom onset date. Therefore, the disease surveillance system from China provides an extensive data resource for space-time modeling. More information about these data can be found in (15).

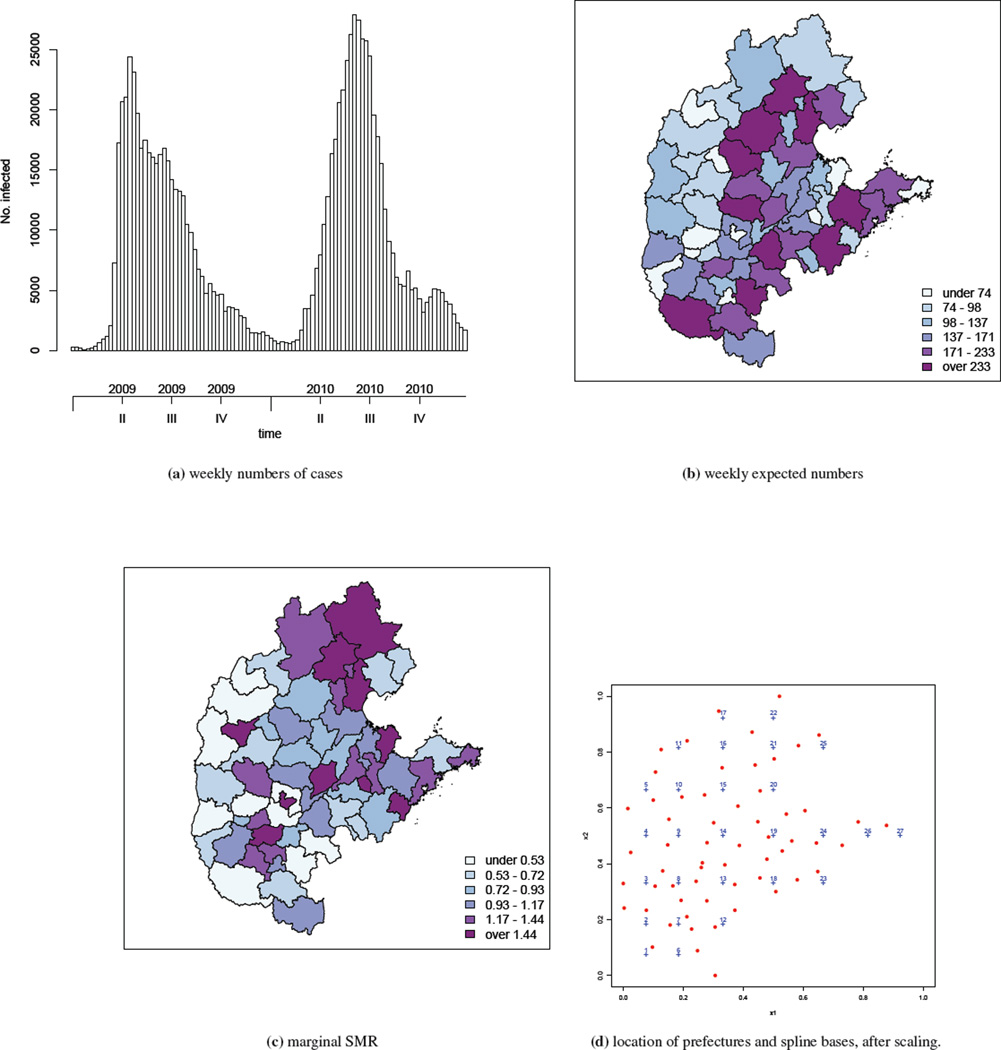
In this paper, we analyze data from the central north region of China from 2009 and 2010; this region is shown in relation to the whole of China in the supplementary materials. The central north region consists of 59 prefectures spread in five provinces and one direct-controlled municipality (i.e., Tianjin, Hebei, Henan, Shandong, Shanxi and Beijing). The total population in the region is estimated to be 318,022,505 in 2009/2010. Within the region, 418,949 and 478,238 HFMD cases were reported in 2009 and 2010, respectively. Here we aggregate the number of HFMD cases by week and by prefecture, see Figure 1(a). The temporal trend is clear: the epidemic starts around March, reaches its peak in May/June and gradually dies down towards the winter. This is the same pattern observed in both years, though the time that the epidemic reaches its peak seems to be later in 2010 than in 2009.

Figure 1.

Summaries of the central north region of China HFMD data from 2009–2010: (a) weekly numbers of cases, (b) weekly expected numbers, (c) marginal (across time) SMR, (d) centroids of prefectures (red dots) and location of spline bases (blue crosses), after scaling the study region.

Based on the population composition in each prefecture, we calculate weekly expected numbers of counts adjusting for age (with age bands 0–0.9, 1–2.9, 3–5.9, 6–9.9 and ≥10 years) and gender, using internal standardization (30). These expected numbers are shown in Figure 1(b), with a wide range from 18 to 364.We then calculate the marginal standardized morbidity ratios (SMRs) across time. These SMRs are the ratios of the total counts to the expected counts (adjusted for the confounders age and gender) over 2009–2010. A thematic map of the resulting SMRs is presented in Figure 1(c). Though subject to sampling variability, the spatial variation in the SMR is clearly seen in the map (an animation of the weekly log SMRs can be found at http://www.stat.brown.edu/cbauer/). However, the temporal pattern in the SMRs is unclear apart from a general south-to-north movement of the area with high SMRs. These initial examinations clearly suggest a model with spatial and temporal components is needed for analyzing the China HFMD data.

3. Methods

In this section, we describe the Bayesian spatial-temporal models that we propose. We start by describing the overall model framework, followed by details on each of the model components.

3.1. The Poisson Likelihood

Let Y_it denote the observed disease counts and E_it the expected counts, which account for the known confounders such as age and gender, in area i and in week t, i = 1, …, I; t = 1, …, T. In the HFMD example, the population is treated as constant at each time point so that E_it = E_i. The constant population is based on the assumption that the changes in population size over time are relatively small and so can be ignored. The expected count E_i is calculated using internal standardization, which takes into account of the differences in age-gender populations between areas.

The data model is a Poisson distribution with relative risk μ_it

$$Y_{\mathit{\text{it}}}|{\mu }_{\mathit{\text{it}}}~\text{Poisson}(E_i{\mu }_{\mathit{\text{it}}}).$$ (1)

Our overall strategy is to decompose the relative risk into the following components

$$\text{log}({\mu }_{\mathit{\text{it}}})=\alpha +{\mathit{z}}_{\mathit{\text{it}}}^T\mathit{\beta }+f_{\mathrm{S}}({\mathit{x}}_i)+f_{\mathrm{T}}(t)+f_{\mathrm{S}\mathrm{T}}({\mathit{x}}_i,t)$$ (2)

where α is the intercept, z_it is a vector of area-level covariates, and x_i = (x_1i, x_2i) is the centroid of area i. In this formulation, f_S(x_i) is the spatial trend, f_T(t) is the temporal trend and f_ST(x_i, t) is the spatial-temporal interaction. In a Bayesian framework, the spatial and temporal dependency is incorporated into the model through the prior. We now describe the priors used for the spatial trend, the temporal trend, and the spatial-temporal interaction in (2) respectively.

3.1.1. Temporal trend

The temporal component is modeled as the sum of a large-scale component, and noise terms with and without temporal structure

$$f_{\mathrm{T}}(t)={\mathit{x}}_t^T\mathit{\delta }+{\epsilon }_t+{\gamma }_t.$$

The large-scale component ${\mathit{x}}_t^T\mathit{\delta }$ can be modeled using parametric or semi-parametric models, which we have assumed can be represented via a linear basis. A popular example of the latter are spline models, see (24) and (25). As an alternative, seasonal variability in the data can be modeled via frequency domain models. For example, we can include a set of harmonic functions

$${\mathit{x}}_t^T\mathit{\delta }=\sum _{s=1}^S[a_s\text{ sin}({\omega }_{s}t)+b_s\text{ cos}({\omega }_{s}t)],\hspace{1em}s=1,\dots ,T/2$$ (3)

where S is the number of harmonics, δ = {a_s, b_s, s = 1, …, S} and ω_s are the Fourier frequencies with ω_s = 2πs/52 for weekly data. The row vector x_t is of length 2S with the sth pair of entries consisting of [sin(ω_st), cos(ω_st)]. The unstructured temporal term may be modeled as ${\epsilon }_t{~}_{iid}\mathrm{N}(0,{\tau }_{\epsilon }^{-1})$ while γ_t, which picks up short-term temporal structure, may be given a conditional autoregressive prior. In this paper we use a second-order random walk prior denoted as RW2. This model is a local stochastic smoothing model and may be represented as

$$p(\mathit{\gamma }|{\tau }_{\gamma })\propto \text{exp }[-\frac{{\tau }_{\gamma }}{2}{\mathit{\gamma }}^{\mathrm{T}}{\mathit{A}}_{\mathrm{T}}\mathit{\gamma }],$$

where the T × T matrix A_T is of rank T − 2 and has the form

$${\mathit{A}}_{\mathrm{T}}=\left[\begin{array}{ccccccccc}\hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -2\hfill & \hfill 5\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 1\hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill 1\hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill -4\hfill & \hfill 1\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -4\hfill & \hfill 5\hfill & \hfill -2\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill \end{array}\right],$$ (4)

with the blank spaces corresponding to zeros. We use τ through out the paper for the precision parameter, which is the inverse of the variance. The subscript of τ indicates the random variable with which the precision parameter is associated. Further technical details on this model, including the conditional mean and variance, are provided in the supplementary materials.

3.1.2. Spatial trend

The spatial trend is modeled as

$$f_{\mathrm{S}}({\mathit{x}}_i)={\beta }_1{x}_{1i}+{\beta }_2{x}_{2i}+{\upsilon }_i+u_i.$$ (5)

The covariates x_1i and x_2i represent the latitude and longitude of the centroid of area i and β₁ and β₂ are the associated coefficients. The unstructured spatial terms υ_i is assigned a $\mathrm{N}(0,{\tau }_{\upsilon }^{-1})$ prior, and the structured spatial term u_i is assigned an intrinsic conditional autoregressive (ICAR) prior. Hence, we are using the classic (31) convolution model. The joint distribution of the structured spatial term u_i is

$$\pi (\mathit{u}|{\tau }_u)\propto \text{exp }[-\frac{1}{2}{\mathit{u}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{S}}\mathit{u}],$$ (6)

where A_S has entries

$$A_{S_{ij}}=\{\begin{array}{cc}{m}_i\hfill & i=j,\hfill \\ -1\hfill & i~j,\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (7)

with i ~ j indicating that areas i and j are neighbors defined as areas sharing the same boundary, and m_i the number of neighbors for area i. Further details of the ICAR model are relegated to the supplementary materials.

3.1.3. Spatial-temporal interaction

Models with only spatial and temporal trends are usually insufficient for modeling the variation in temporal dynamics between regions, particularly for infectious diseases. Hence, the spatial-temporal interaction term we define is crucial, as this term captures the space-time dynamics of the infectious disease spread. In a disease mapping context, for example, (32) and (33), it has been suggested that a space-time interaction term could be constructed by combining the spatial random effects u and the temporal random effects γ. However, such a form contains a large number of random effects, IT to be exact, which is not a parsimonious representation. In addition, the interaction term adds great complexity to the model and makes the implementation for Bayesian inference, usually via Markov chain Monte Carlo (MCMC), very difficult for data with many areas and/or time points.

Motivated by (33), we propose an alternative approach to constructing the interaction term. We model the space-time interaction surface with a bivariate spline, and place a GMRF prior on the coefficients associated with the basis functions. Specifically, we assume

$$f_{\mathrm{S}\mathrm{T}}({\mathit{x}}_i,t)=\sum _{k=1}^K{b}_{kt}{B}_{ik},\hspace{1em}k=1,\dots ,K,$$ (8)

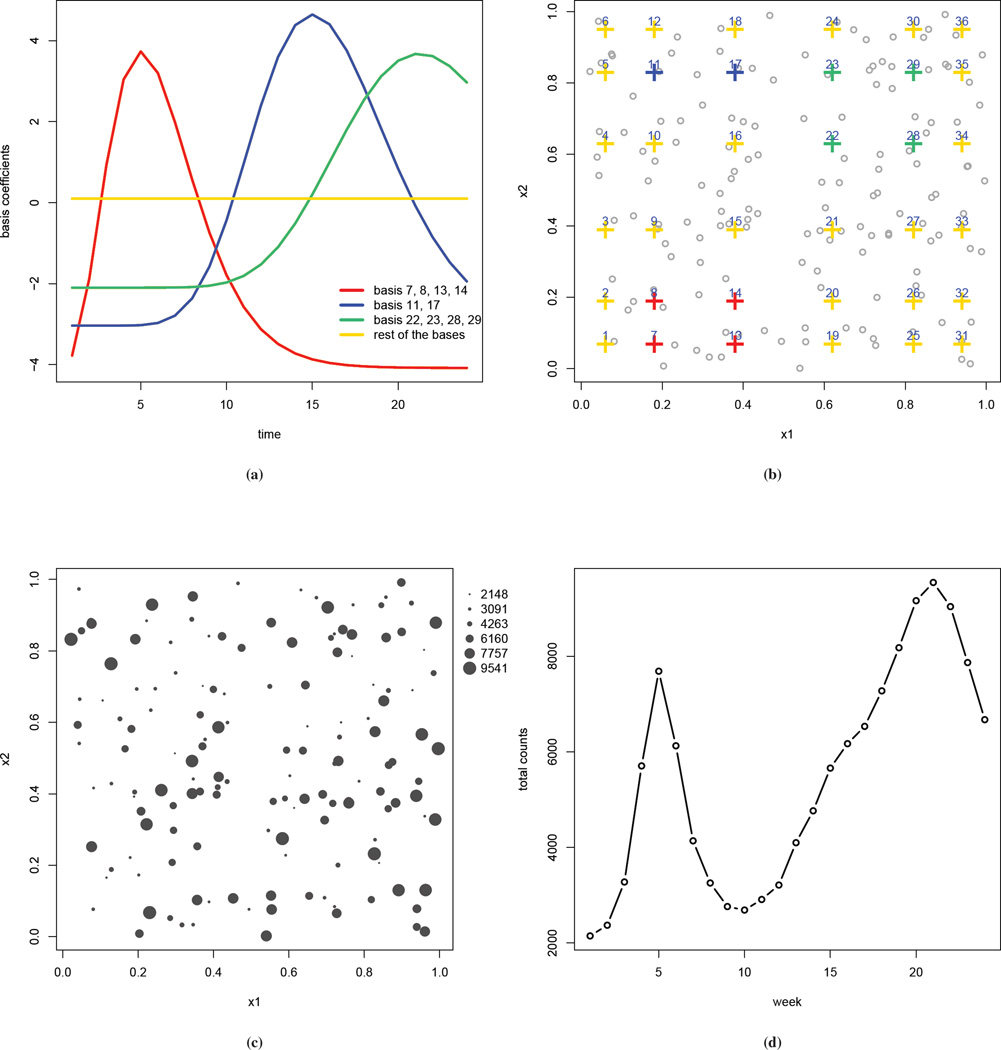
where B_ik is a tensor product of two univariate cubic B-spline functions, one in each spatial dimension, so that B_ik is a function of x_i. For notational convenience we index the bivariate basis functions by k. The number of basis functions K will typically be far less than the number of areas I, and so the number of latent random effects is reduced. Because these basis functions are constructed as a tensor product, they can be visualized as being laid out on a rectangular grid. Figure 2(b) presents such visualization using a simulated data set, for a total of 36 basis functions (6 for each spatial coordinate). The advantages of choosing a cubic B-spline include the computation efficiency and the relative insensitivity to the choice of basis numbers and locations (34; 35). More details of the tensor product basis functions can be found in the supplementary materials.

Figure 2.

Simulated Data: (a) true values of the basis functions b_kt versus time; (b) locations of the basis coefficients, color coded as in (a); the grey dots are the locations of the observed counts; (c) number of cases aggregated over time (with the size of the circles being proportional to the number of cases); (d) number of cases, aggregated over space, plotted by week.

The spatial-temporal structure of the interaction is imposed through the prior on the basis coefficients and can take one of the following four types, as with the disease mapping approach of (33)

Type I: A product of independent normal priors so that there is no spatial or temporal structure in the spline coefficients

$$\pi (\mathit{b}|{\tau }_b)\propto \text{exp }[-\frac{{\tau }_b}{2}\sum _{k=1}^K\sum _{t=1}^T{b}_{kt}^2].$$

This type of interaction assumes that, after accounting for spatial and temporal main effects, the residuals do not have structure in space and time. This model is the easiest to implement but the least appealing in a biological sense.

Type II: A second-order random walk (RW2) prior on the temporal structure with no spatial structure, so that we have a product of K temporal smoothing priors

$$\pi (\mathit{b}|{\tau }_b)\propto \text{exp }[-\frac{{\tau }_b}{2}\sum _{k=1}^K\sum _{t=3}^T{(b_{kt}-2b_{k,t-1}+b_{k,t-2})}^2].$$

Hence, the interactions have temporal structure but the bases are independent across space.

Type III: An ICAR prior in space but with no temporal structure, so that we have a product of T independent spatial models

$$\pi (\mathit{b}|{\tau }_b)\propto \text{exp }[-\frac{{\tau }_b}{2}\sum _{t=1}^T\sum _{k~k\prime }{(b_{kt}-b_{k\prime t})}^2].$$

The notation k ~ k′ indicates that bases k and k′ are first order neighbors, hence each interior basis has four neighbors. This model assumes that at time t, the bases that are close to each other are more likely to be similar, but across time the T sets are independent.

Type IV: A Kronecker product of RW2 and ICAR priors

$$\pi (\mathit{b}|{\tau }_b)\propto \text{exp }[-\frac{{\tau }_b}{2}\sum _{t=3}^T\sum _{k~k\prime }{\{(b_{kt}-2b_{k,t-1}+b_{k,t-2})-(b_{k\prime t}-2b_{k\prime ,t-1}+b_{k\prime ,t-2})\}}^2].$$

This model assumes that the basis coefficient b_kt at location x_k and at time t depends on those from the two previous time periods b_k,t−1 and b_k,t−2, as well as those from the neighboring basis x_k′, k′ ~ k. In addition, b_kt depends on those coefficients in the neighboring bases in the two previous time points, i.e. b_k′,t−1 and b_k′,t−2, for k′ ~ k. Therefore estimation of the coefficients borrows information in both space and time.

In addition to reducing the dimension of random effects, our proposed method has the advantage that, even with complicated structures, after writing (b₁₁, …, b_K1, b₁₂, …, b_K2, …, b_1T, …, b_KT)′ as b, all four types of interactions have a unified representation as GMRF models with the general form

$$\pi (\mathit{b}|{\tau }_b)\propto \text{exp }[-\frac{{\tau }_b}{2}{\mathit{b}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{S}\mathrm{T}}\mathit{b}].$$

The structure matrix A_ST of the spline coefficients is then the Kronecker product of the structure matrix for the space A_S and the temporal structure matrix A_T, i.e. A_ST = A_S ⊗ A_T. The supplementary materials give details on the form of A_ST for each interaction model. Such a representation also brings a flexibility to the modeling, as one can select different spatial and temporal structures, depending on the application.

One other advantage of our proposed models is in the computation. The GMRFs presentation of the spatial-temporal dynamics makes the computation far more convenient. In particular, this model can be fitted using the fast and flexible integrated nested Laplace approximation (INLA) technique (36). INLA has been demonstrated to provide accurate inference in a number of applications (36; 37; 38; 39; 40) and, compared to the more traditional MCMC method, is orders of magnitude faster for the model described above. In the supplementary materials we provide the WinBUGS code to implement our proposed models using MCMC, as well as the code that uses the R package INLA. We also show in the supplementary materials a numerical comparison between MCMC and INLA.

4. Simulation Study

4.1. Data Generation

In this section we describe a simulation study to investigate the performance of our proposed models. The key novelty of our proposed models lies upon the spatial-temporal interaction so we focus on assessing this aspect and fit the Poisson model (1), with the relative risk

$$\text{log}({\mu }_{\mathit{\text{it}}})=\alpha +f_{\mathrm{S}\mathrm{T}}({\mathit{x}}_i,t),$$ (9)

where f_ST is described by (8).

The study region is a unit square and we select two equal-distance inner knots in each spatial dimension to construct the tensor product cubic B-splines bases, so that K = 6² = 36.We assume T = 24 discrete observation times. The simulation is constructed to mimic the movements of epidemic centers over time. We first obtain fixed values of the spline basis coefficients b_kt, using gamma functions and one sine function of time t, and then use these b_kt to construct the underlying risk surface. The functions for obtaining the values of b_kt are treated as unknown at the analysis. Figure 2(a) plots these coefficients versus time with the curves being color coded by their locations, which are shown in panel (b). The values of the coefficients are chosen so that higher values are given to those in the bottom left corner at early weeks of the observation period, those in the top left corner at middle weeks, and those in the top right corner at later weeks. We choose the expected number of cases E_i to be between 5 and 50 and assume they are constant over the study period. The observed counts Y_it are then simulated at I = 150 randomly selected locations, which are indicated by the points in Figure 2(b). These point locations are used to represent areal centroids. The MRF prior is with respect to the bases, and so for the interaction term this is the only place that requires specification of a neighborhood structure. The simulated weekly counts Y_it range from 0 to 1063. In Figures 2(c) and (d) the number of cases over space and time are displayed. The aggregated counts in panel (c) show large spatial variation, ranging from 2148 to 9541. The weekly observed counts aggregated over space in panel (d) show two peaks, which is similar to that observed in the China HFMD data. The supplementary materials include more details on the simulation, such as the map of the realized E_i, and the bubble plots of the simulated number of cases at selected time points which give more details on how epidemic centers move over time.

4.2. Results of the simulation study

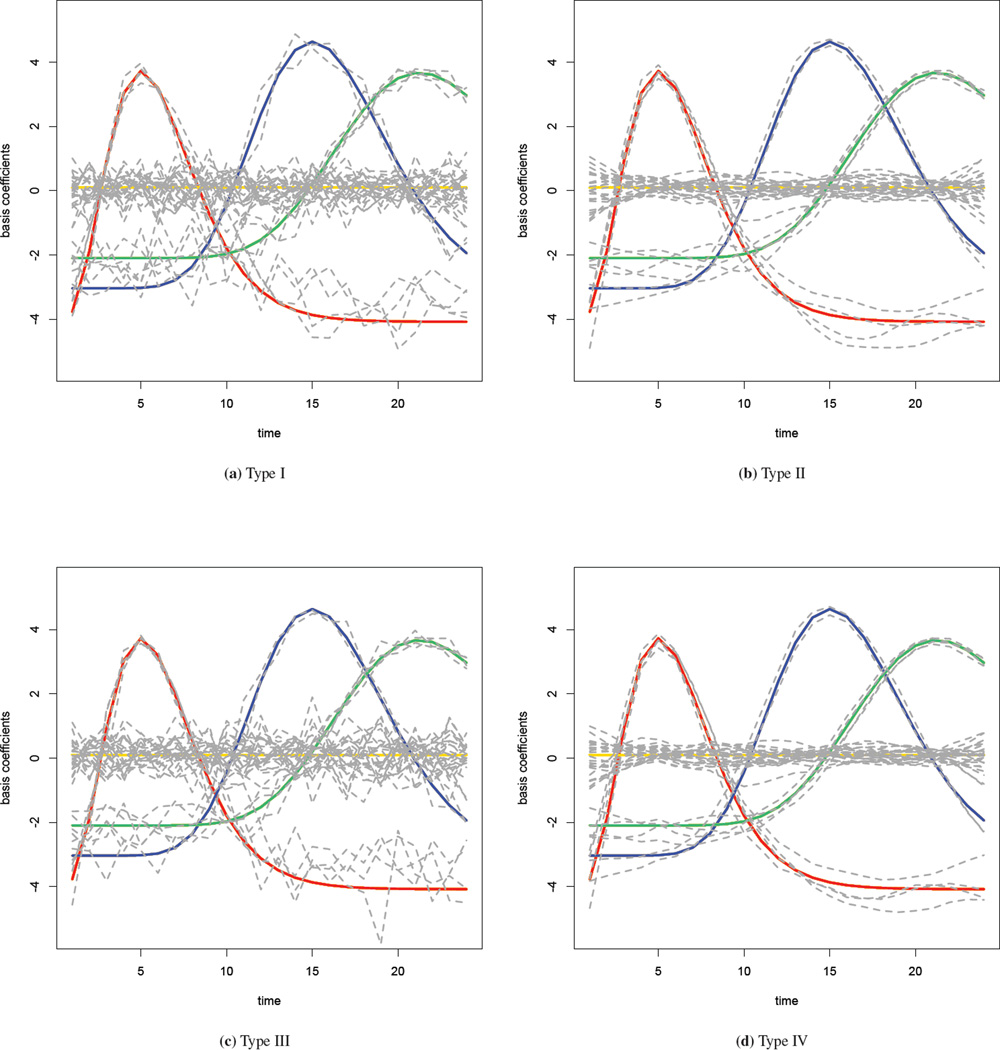
We fit the spatial-temporal interaction model (9) with the four interaction priors described in Section 3.1.3. A Gamma(1, 0.98) distribution is used as the prior for the precision parameter τ_b. Results of the parameter estimates are given in the supplementary materials, along with a sensitivity analysis with different priors for the precision parameter. Time series plots of the estimated basis coefficients are shown in Figure 3, with one for each interaction type. The true values of the coefficients are superimposed in the graph using the color scheme of Figure 2, and the grey lines denote the posterior median estimates. In the Type I interaction model where the coefficients have no spatial or temporal structure, the grey lines are very jagged and substantially deviate from the truth. In the Type II model where a RW2 model is used for the temporal structure in the interaction, the estimated coefficients are much smoother over time and closer to the truth. In the Type III model, the estimates are similar to those observed in the Type I model. Because the majority of the variation in the simulated data is temporal, smoothing across space alone cannot improve the estimation greatly. Finally, the Type IV model improves on the Type III fit and provides the estimates that are the closest to the true values. We now assess the model fits more formally.

Figure 3.

Estimated basis coefficients with four different priors in the simulation study: true values are colored as in Figure 2, while the grey lines are the estimates.

The overall measure of the model fit may be assessed using the conditional predictive ordinate (CPO) (41; 42) which represents a particular form of cross-validation measure. The CPO of observation it is

$$\mathrm{C}\mathrm{P}{\mathrm{O}}_{\mathit{\text{it}}}=\int \text{Pr}(y_{\mathit{\text{it}}}|{\mathit{y}}_{-\mathit{\text{it}},}\mathit{\theta })\pi (\mathit{\theta }|{\mathit{y}}_{-\mathit{\text{it}}})d\mathit{\theta }$$

where y_−it represent the data with observation y_it removed. We may calculate ${\sum }_{i=1}^I{\sum }_{t=1}^T\text{log }\mathrm{C}\mathrm{P}{\mathrm{O}}_{\mathit{\text{it}}}$ and models with larger values are preferred. (43) discuss how CPO values may be calculated efficiently with INLA, without the need to fit the model I × T times. For the simulated data, the sum of the log CPO values under the four types of interactions (scaled by the maximum, which is the Type II model) are: −429, 0, −106 and −20. The CPO values from the Type II and IV models are considerably higher than those from the Type I and III models, so that the former are preferred to the latter, which is not surprising given the strong temporal structure in the data.

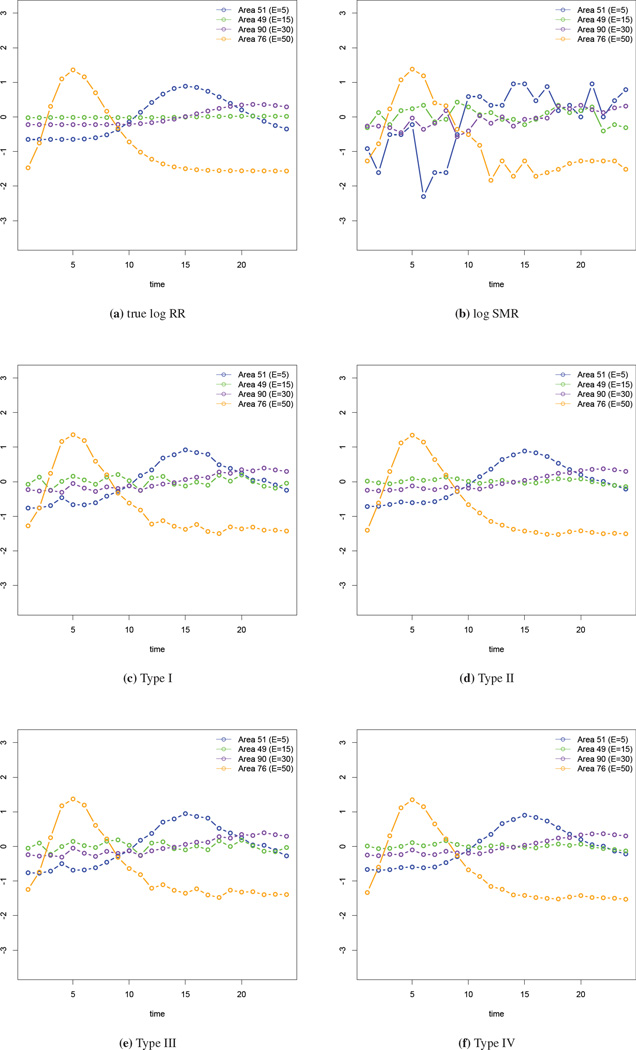
Examining the change of the spline coefficients provides some knowledge of the temporal trend in the risk. However, we would also like to obtain the estimated log relative risks at the observed locations. We select four areas with different expected numbers (E = 5, 15, 30, 50) and examine the model fits. In Figure 4(a) we give the true log relative risk for these four areas while in panel (b), we plot the log SMRs. It is clear that areas with lower expected numbers have larger variability in the log SMRs. In panels (c)–(f) we show the fits from the four types of interaction models. In these plots the estimated log relative risks using our models are clearly more accurate than the log SMRs. Informally comparing the four types of interaction models using these figures, the fits from the Type II and IV interaction models are closest to the truth.

Figure 4.

Comparison of the log relative risk in four selected areas.

Finally we examine the prediction performance of our proposed models. We take the data until time T^⋆ and predict the number of cases within q week ahead, i.e., y_it for t = T^⋆ + 1, …, T* + q. The prediction performance is evaluated using the mean squared error of prediction (MSEP) given by

$$\mathrm{M}\mathrm{S}\mathrm{E}\mathrm{P}=\frac{1}{Iq}\sum _{T^{\star }+1}^{T^{*}+q}\sum _{i=1}^I{({ŷ}_{\mathit{\text{it}}}-y_{\mathit{\text{it}}})}^2.$$ (10)

The results for q = 1 and q = 2, i.e. predicting 1 and 2 time periods ahead, are given in Table 1. We choose T* = 6 to give a minimum that has sufficient observed data for prediction. For each T^⋆ and q, the MSEP is reported for the Type I–IV models, with the smallest MSEP indicated in bold. Type II model predominately outperform the other types by giving the smaller MSEP, with 15 out of 18 weeks for q = 1 and 11 out of 17 weeks for q = 2. The Type IV model gives the smallest MSEP in all other weeks for q = 1 and three of the remaining weeks for q = 2. The predictions become worse for all models in weeks 19–22, which is the period in which the second epidemic peak occurs. This is somewhat unsurprising: without additional information of the disease etiology or drivers of the outbreaks, prediction of the time when an epidemic “kicks off” is generally very difficult in infectious diseases, particularly based on the surveillance data alone. Nevertheless, when the surveillance data is the only source to understand the space-time dynamics of the infectious disease process, including the temporal component is more crucial than the spatial one, which is emphasized by the better performance of the Type II and Type IV models.

Table 1.

The model is fitted to the simulated observations up until T^⋆, and predictions are made for q = 1 and q = 2 weeks ahead. For each T* and q, the mean squared error of prediction (MSEP) is reported for the Type I–IV models, with the smallest MSEP indicated in bold.

	q = 1				q = 2
T⋆	Type I	Type II	Type III	Type IV	Type I	Type II	Type III	Type IV
6	857	683	911	687	504	804	527	819
7	153	36	142	43	135	44	107	67
8	115	35	73	45	128	44	83	61
9	135	26	90	39	134	42	96	64
10	134	31	100	46	197	45	173	67
11	260	30	247	36	675	74	694	107
12	1088	71	1144	75	1649	91	1729	78
13	2209	781	2311	663	2688	6433	2823	5449
14	3170	395	3331	443	3086	2140	3263	2364
15	2998	336	3188	364	2619	1253	2820	1346
16	2237	201	2444	210	2578	473	2808	503
17	2918	82	3163	85	4258	149	4535	141
18	5595	193	5895	198	7501	1391	7831	1510
19	9411	361	9756	331	10917	2314	11275	2166
20	12424	426	12779	435	11451	2757	11792	2825
21	10474	784	10793	799	8845	2477	9131	2526
22	7216	173	7460	167	5582	471	5793	458
23	3954	120	4125	122	-	-	-	-

5. Application to HFMD Data in China

We now return to the HFMD data in the central north region of China over years 2009–2010. We assume the Poisson model (1) with μ_it given by (2). The study region is rescaled to a [0, 1] × [0, 1] square but retain the ratio [max(x_i2) − min(x_i2)]/[max(x_i1) − min(x_i1)]. We include the population density per square kilometer as a covariate, denoted as z_i, with this variable being normalized to have mean 0 and standard deviation 1. We manually remove those basis functions that lie outside of the study region. The locations of K = 16 bases used in the analysis are shown in Figure 1(d).

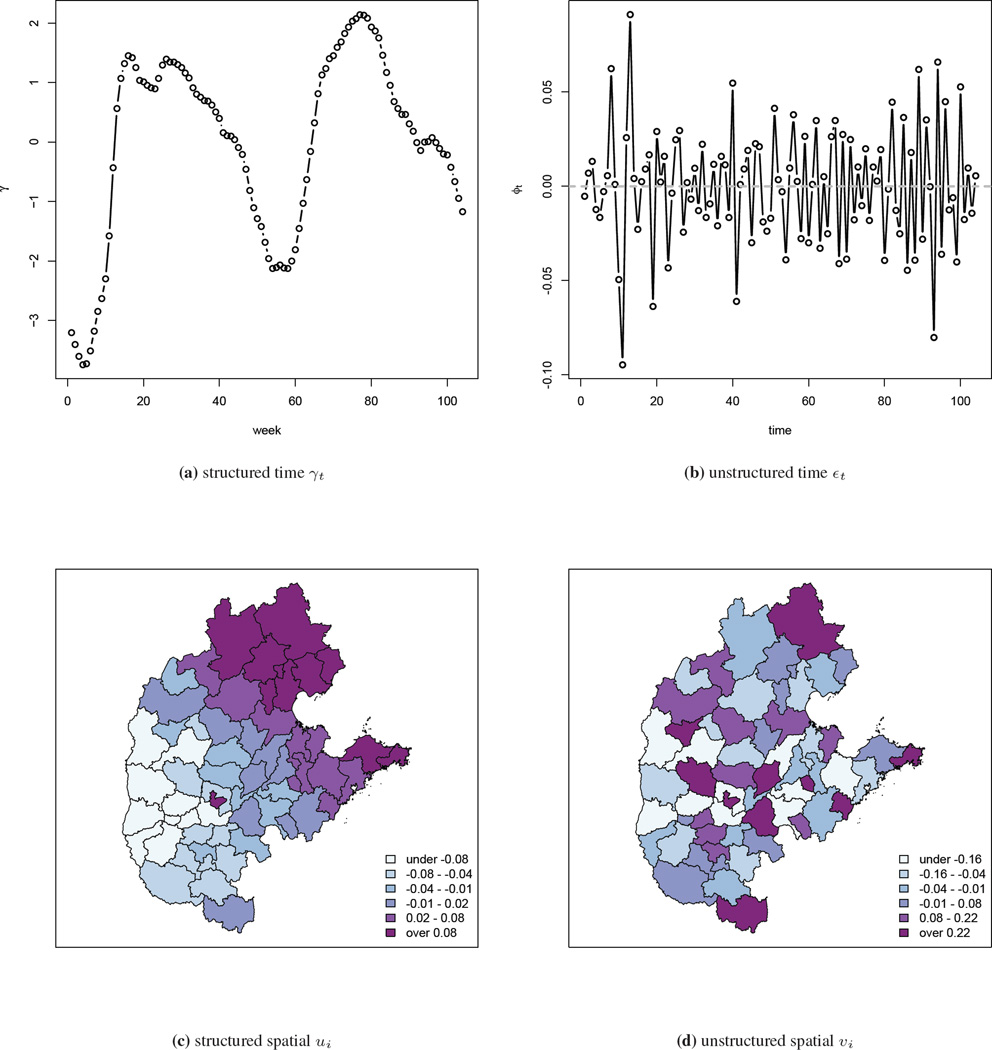
The model is implemented using INLA, and parameter point and interval estimates are presented in Table 2. The running time for the four models are 307, 501, 289 and 429 seconds, respectively, on a MacBook Pro with 2.6 GHz Intel Core i7 processor. In the Type I and III models, we find that population density has a significant positive association, which is consistent with the fecal-oral transmission route of HFMD since areas in which children are in closer proximity are likely to have greater rates of infection. Estimates of the structured and unstructured temporal components γ_t and ε_t are very similar in the four models, and therefore we only show the results from the Type IV interaction model in Figure 5. The overall temporal pattern that is common to all areas is captured in the structured temporal random effect γ and is shown in Figure 5(a). The unstructured temporal random effects ε_t, shown in Figure 5(b), reflects the residual temporal variability after accounting for the structured RW2 temporal effect γ_t. No clear pattern is observed and the range of the estimated ε_t is narrow (between −0.10 and 0.075). The estimated structured spatial random effect u_i ranges from −0.067 to 0.085, and the unstructured spatial random effect υ_i ranges from −1.1 to 0.95 so that the latter dominates. Maps of the median estimates are shown in Figure 5(c) and (d). These random effects are log relative risks of disease and so the spatial terms are not of great epidemiological significance. The sum of the log CPO values, again scaled by the Type II model, are: −7672, 0, −8075 and −3894, strongly suggesting the Type II model is most appropriate for the HFMD data.

Table 2.

Parameter estimates (median and 95% interval) from four types of interaction models, using weekly central north HFMD data in China 2009–2010.

Parameter	Type I	Type II	Type III	Type IV
α	−1.08 (−1.26, −0.88)	−0.97 (−1.45, −0.48)	−0.84 (−1.31, −0.37)	−0.96 (−1.45, −0.46)
β	0.30 (0.14, 0.45)	0.15 (−0.12, 0.41)	0.33 (0.13, 0.52)	0.16 (−0.11, 0.42)
σγ	0.15 (0.12, 0.20)	0.17 (0.13, 0.21)	0.15 (0.12, 0.19)	0.15 (0.12, 0.19)
σϕ	0.06 (0.04, 0.09)	0.06 (0.04, 0.09)	0.06 (0.04, 0.09)	0.06 (0.04, 0.09)
σu	0.13 (0.06, 0.46)	0.19 (0.06, 1.31)	0.13 (0.06, 0.50)	0.24 (0.07, 2.50)
συ	0.51(0.43, 0.63)	0.45 (0.36, 0.57)	0.51 (0.42, 0.63)	0.44 (0.35, 0.56)
σb	4.01(3.87, 4.16)	0.50 (0.47, 0.53)	8.09 (7.78, 8.42)	0.83 (0.79, 0.89)

Figure 5.

Estimated temporal component γ and ϕ, and spatial component u and υ from the Type IV interaction model with the China central north HFMD data.

An animation of the term $\hat{\alpha }+{\hat{\gamma }}_t+{\sum }_{k=1}^K{\hat{b}}_{kt}{B}_{ik}$ can be found at http://www.stat.brown.edu/cbauer/, which provides insight into the broad-scale space-time dynamics of HFMD. Compared to the log SMR maps, the movement of the epidemic center is much clearer as the regions with elevated relative risks are easier to identify. We see two local epidemics that start, respectively, in the north and south-west areas around week 22, and gradually move towards each other. This movement is not evident in the log SMR maps.

Next we take the first T^⋆ weeks of HFMD surveillance data and perform the q-week ahead prediction of total HFMD counts, by area. The performance of the prediction is again assessed via the MSEP in (10). For comparison the prediction is also carried out using the epidemic/endemic model of (9) implemented within the R surveillance package. Specifically, we use the form y_it|θ_it ~ Poisson(θ_it) with

$${\theta }_{\mathit{\text{it}}}={\lambda }_i^{\mathrm{A}\mathrm{R}}{y}_{i,t-1}+{\lambda }_i^{\mathrm{N}\mathrm{E}}\sum _{j\ne i}{w}_{ji}{y}_{j,t-1}+E_i{\lambda }_{\mathit{\text{it}}}^{\mathrm{E}\mathrm{N}}$$ (11)

where ${\lambda }_i^{\mathrm{A}\mathrm{R}}={\alpha }_0^{\mathrm{A}\mathrm{R}}+b_i^{\mathrm{A}\mathrm{R}}$ represents the autoregressive “self-area” component with random effects $b_i^{\mathrm{A}\mathrm{R}},{\lambda }_i^{\mathrm{N}\mathrm{E}}={\alpha }_0^{\mathrm{N}\mathrm{E}}+b_i^{\mathrm{N}\mathrm{E}}$ is an autoregressive “neighboring area” component (defined as sharing a common boundary) with random effects $b_i^{\mathrm{A}\mathrm{R}}$, and

$${\lambda }_{\mathit{it}}^{\mathrm{E}\mathrm{N}}={\alpha }_0^{\mathrm{E}\mathrm{N}}+b_i^{\mathrm{E}\mathrm{N}}+\beta z_i+\sum _{s=1}^S\left({\gamma }_s\text{ sin }\right[\frac{st}{52}2\pi ]+{\delta }_s\text{ sin }[\frac{st}{52}2\pi \left]\right)$$

is an endemic component with the random effects $b_i^{\mathrm{E}\mathrm{N}}$ and S = 1. All the random effects are assumed independently and normally distributed. Results with T* starting at week 90 are presented in Table 3. More comprehensive experiments with T* going back as early as week 34 can be found in the supplementary materials. We attempted analyses with T* smaller than 34 but the epidemic/endemic model encountered convergence issues. Compared to the epidemic/endemic model, out of the 14 weeks our models give smaller MSEP in 8 weeks for q = 1 and 7 weeks for q = 2. Among the four types of interaction models, the Type II and IV models give smaller MSEP in all weeks. Adding spatial structure can aid the prediction, as seen in the smaller MSEP in the Type III model as compared to the Type I model. However, since most of the variation in the data comes from the temporal trend, it is the temporal structure components included in the Type II and IV models that are most important for prediction.

Table 3.

Results of q-weeks ahead prediction using China central north weekly HFMD data from 2009 to 2010. The figures are MSEP, as given by 10 and are for the Type I–IV models, as well as the epidemic/endemic (epi/end) model 11. For each q, figures in bold are the row minimum MSEP.

	q = 1					q = 2
T⋆	Type I	Type II	Type III	Type IV	Epi/End model	Type I	Type II	Type III	Type IV	Epi/End model
90	6204 (0.93)	1563 (0.86)	4758 (1.00)	1421 (0.92)	1310	4837	1614	3711	1488	2736
91	3129 (0.88)	2492 (0.85)	2704 (0.95)	3263 (0.83)	873	2589	5453	2184	7263	1535
92	1702 (0.92)	947 (0.81)	1524 (0.97)	893 (0.85)	3900	2783	1111	2253	1087	3093
93	4161 (0.90)	1774 (0.80)	3523 (1.00)	1602 (0.80)	397	5255	3051	4510	2774	583
94	3576 (0.93)	1071 (0.83)	2993 (0.97)	984 (0.85)	1670	4495	1909	3768	1774	2716
95	5481 (0.86)	749 (0.83)	4288 (0.97)	755 (0.83)	1655	5693	1834	4755	1366	2174
96	5449 (0.88)	2058 (0.73)	5217 (0.98)	2216 (0.76)	1746	5321	3352	5468	3789	1811
97	5723 (0.88)	1643 (0.76)	4907 (0.97)	1630 (0.78)	992	4765	4118	4202	4135	1268
98	3940 (0.92)	1757 (0.76)	3569 (0.97)	1813 (0.78)	836	3473	2040	3110	2113	1017
99	3380 (0.88)	839 (0.66)	2895 (0.97)	849 (0.71)	927	2590	955	2237	971	1621
100	1390 (0.90)	727 (0.75)	1352 (0.95)	815 (0.76)	1121	1353	878	1244	1090	1843
101	853 (0.92)	600 (64)	831 (0.96)	573 (0.68)	1811	790	602	789	556	2106
102	744 (0.88)	507 (0.69)	729 (0.95)	509 (0.66)	841	773	529	756	538	1060
103	924 (0.88)	498 (0.68)	810 (0.90)	512 (0.66)	302	-	-	-	-	-

In addition to the q-week ahead prediction we also investigate the performance of our proposed models for cumulative prediction, where we take the first T* weeks of the observations and predict the total HFMD counts for the remaining weeks in 2009 and 2010, by area. As can be seen in Table 4, in all weeks, our models give better prediction than epi/end model, except in the last week, where the scenario reverts to the 1-week ahead prediction. The results suggest that our proposed models perform as well as the epidemic/endemic model for short-term prediction, and outperform the competing model when prediction is carried out over longer time period.

Table 4.

Results of cumulative prediction using China central north weekly HFMD data from 2009 to 2010. The figures are MSEP, as given by 10 and are for the Type I–IV models, as well as the epidemic/endemic (epi/end) model 11. For each q, figures in bold are row minimum MSEP.

T⋆	Type I	Type II	Type III	Type IV	Epi/End model
99	1527	1852	1372	1915	3514
100	1695	1086	1322	1590	3601
101	784	629	785	571	2679
102	773	529	756	538	1061
103	924	498	810	512	302

Residuals plots of these models can be found in the supplementary materials. There is still considerable variation in the residuals from all models and some systematic variability showing that not all of the signal is being adequately modeled.

6. Discussion and Future Work

In this paper we have described a model for space-time infectious disease count data. The model bridges the gap between disease mapping models for chronic diseases and the more traditional SIR type models that are difficult to fit when the populations are large and individual-level information such as time of infection is not available. A number of aspects deserve further discussion.

The choice of prior distributions on the random effects variances in the interaction models is challenging because of the conditional interpretation, which changes across the four model types. An obvious approach is to use simulation, in tandem with substantive knowledge on the range of relative risks. For example, we may believe that the 95% range of the residual relative risks is [0.1, 10], which means that the range of the spline contribution is ∑_k b_ktB_ik is [log(0.1), log(10)]. Experimentation with different prior choices via simulation can be carried out to achieve this aim. This is the approach that was taken to set the priors in our analysis, and the details can be found in the supplementary materials. From a practical point of view, our approach is computationally efficient since it is based on INLA. The improvement in computation time when compared with MCMC is considerable.

For the China central north HFMD data our model has allowed the following insights. In each year the epidemic moves from two centers, a major one in the south and a smaller one in the north. Population density is also seen to be an important aggregate level predictor, the credible intervals for the Type I and III models do not contain zero, but the intervals of the Type II and IV models contain zero, because the more flexible temporal model has absorbed some of the association with population density. This highlights the differences between models for prediction and those with which the identification of important covariates is sought. Without the etiology knowledge of the disease, prediction of future counts is difficult, in particular using the surveillance data alone. For HFMD disease, most of the variation in the surveillance data comes from the temporal trend. Hence, it is crucial to include the temporal structure in models for prediction.

The epidemic/endemic model is very appealing since it has autoregressive components, which allows aggregate level transmission to be estimated, and a good implementation. We would not suggest that our model be used as a replacement. Rather, we think the approaches are complimentary. The model we have described has the appealing feature of producing a smoothly time-varying relative risk surface and this can greatly help in gaining insight into the space-time dynamics.