Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jul 27;6:30508. doi: 10.1038/srep30508

Platelet activation risk index as a prognostic thrombosis indicator

K E Zlobina 1, G Th Guria 1,2,a
PMCID: PMC4962318  PMID: 27461235

Abstract

Platelet activation in blood flow under high, overcritical shear rates is initiated by Von Willebrand factor. Despite the large amount of experimental data that have been obtained, the value of the critical shear rate, above which von Willebrand factor starts to activate platelets, is still controversial. Here, we recommend a theoretical approach to elucidate how the critical blood shear rate is dependent on von Willebrand factor size. We derived a diagram of platelet activation according to the shear rate and von Willebrand factor multimer size. We succeeded in deriving an explicit formula for the dependence of the critical shear rate on von Willebrand factor molecule size. The platelet activation risk index was introduced. This index is dependent on the flow conditions, number of monomers in von Willebrand factor, and platelet sensitivity. Probable medical applications of the platelet activation risk index as a universal prognostic index are discussed.

In many cases, intravascular blood coagulation, followed by myocardial infarctions and strokes, is known to be the result of rapid increase in arterial pressure and relevant hemodynamic characteristics such as blood velocity and flow shear rate1,2. However, modern clinical tests are limited to predict thrombotic or bleeding risk because they measure clotting behavior under static (no flow) conditions3. Only first steps are made towards development of diagnostic methods and devices for measuring effects of hemodynamic forces that contribute to platelet function and thrombus formation4,5.

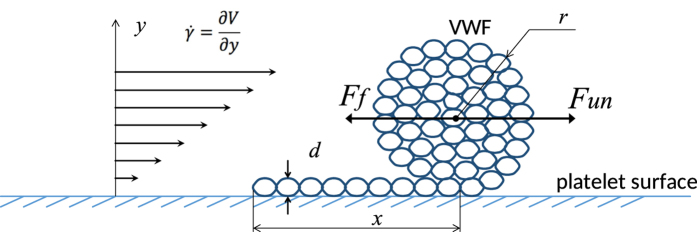
Von Willebrand factor (VWF) plays a central role in transmitting the dynamic effect of blood flow shear stress to intracellular platelet activation pathways6,7,8,9,10,11,12,13. VWF has a multimer structure, consisting of 2–80 monomers per multimer in the blood of healthy donors14,15. Each monomer contains an A1 domain that is capable of binding to the platelet receptor GP-Ib, thereby initiating platelet activation. VWF is present in blood in the globular form. Following an increase in shear rate, it unfolds into an elongated form, which has an increased binding ability16,17 (Fig. 1).

Figure 1. Partially unfolded VWF molecule globule in shear flow, r denotes the radius of the globular part, x is a length of the unfolded “tail”.

Figure 1

Open in a new tab

Diameter of a single chain of multimer is denoted as d. Blood shear rate is denoted as 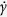Inline graphic. Ff is the folding force and Fun is the unfolding force.

It is known that platelet activation by VWF in a shear flow occurs only at high, overcritical shear rates. However, until recently, the value of the critical shear rate has been controversial, despite the presence of numerous experimental data8,12,17,18,19. It is well established7,8,20,21 that the value of the critical shear rate 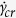Inline graphic is between 1000 sec−1 and 10000 sec−1.

The presence of large VWF multimers in blood causes thrombotic disorders18,22,23,24, while the decreased size of VWF multimers is known to be a factor in bleeding disorders25,26. The actual dependence of the critical shear rate value 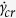Inline graphic on VWF molecule size has not yet been discussed.

Von Willebrand factor unfolding

A VWF multimer grafted onto a platelet surface in shear flow (Fig. 1) is exposed to at least two forces. The first force, Fun, is induced by the ongoing blood flow and unwinds the multimer from the globular to the stretched form17,27,28,29. The second force, Ff, is derived from the “effective surface tension,” which tends to wind the multimer into the most compact globular form. Both of these forces are dependent on the multimer size and its conformation.

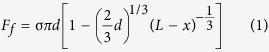graphic file with name srep30508-m3.jpg
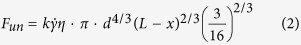graphic file with name srep30508-m4.jpg

where σ corresponds to the effective “surface tension”, d refers to the diameter of VWF monomeric subunits, L denotes the total length of the VWF molecule, x denotes the length of the “tail” (the unwound part of the molecule), 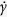Inline graphic is shear rate, η reflects the value of blood viscosity, k is a dimensionless proportionality coefficient.

A detailed mathematical model of VWF multimer folding-unfolding is presented in the Supplementary information. An analysis of the equilibrium conditions between the folding and unfolding forces revealed three states of VWF grafting on platelets:

• fully folded globular structure;

• partially folded globule with an unfolded “tail”;

• fully unfolded linear structure.

The existence and stability of each of these states are dependent on the VWF multimer size (n, monomers per multimer) and shear rate 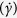Inline graphic. The parametric plane is presented in Fig. 2.

Figure 2. Parametric diagram of VWF folding-unfolding.

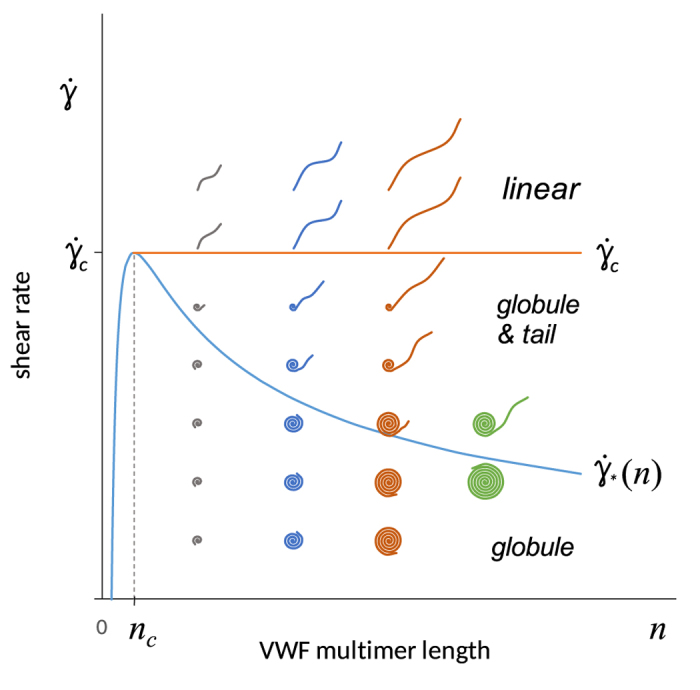
Figure 2

Open in a new tab

Three domains corresponding to a globule, to a globule with tail and to a linear state of VWF multimer are demonstrated. The relative size of VWF globular and linear parts is shown qualitatively in each domain.

The condition of the fully folded “globule” state is described by the inequality:

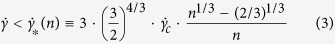graphic file with name srep30508-m7.jpg

(see the Supplementary information).

The curve 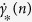Inline graphic reaches maximum at n = nc = 9/4. The model is hardly applicable to very short multimers. Further we discuss only the case n > nc.

The curve 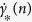Inline graphic monotonlically decreases, and the transition from a globule to a partially folded globule with a tail occurs at lower shear rates for larger multimers.

At any fixed value of n, a gradual increase in 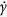Inline graphic is followed by several conformational changes in the VWF structure. This is demonstrated in the bifurcation diagram presented in Fig. 3, where u is the relative length of the unfolded VWF tail.

Figure 3. Bifurcation diagram of VWF multimer for n > nc.

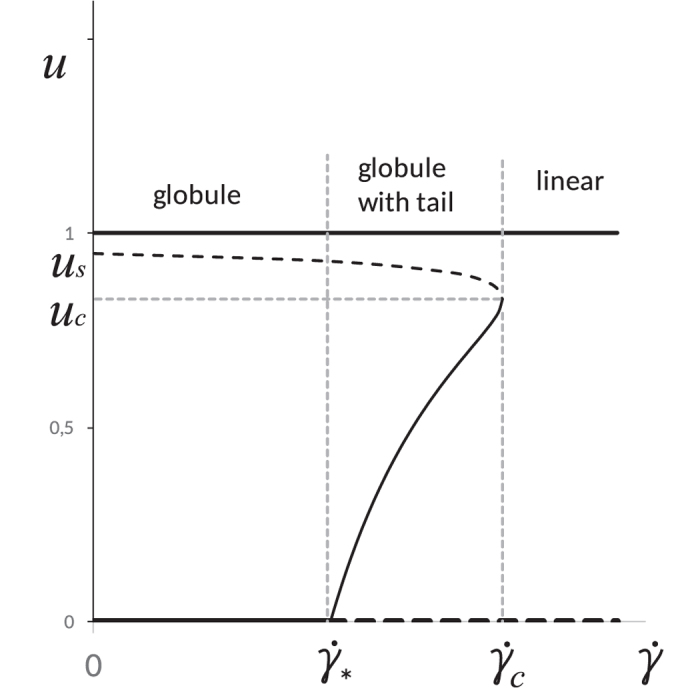
Figure 3

Open in a new tab

“u” denotes a relation of number of monomers in the unwound tail to the total number of monomers in VWF molecule (u = ntail/n ≡ x/(nd)). Branches relevant to stable stationary states are shown by solid line while branches relevant to unstable states – by dashed line.

At low shear rates 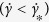Inline graphic, a VWF multimer is a fully folded globule. If the shear rate increases above 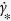Inline graphic, the multimer begins to unfold, becoming a globule with a tail. Further increases in the shear rate above 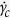Inline graphic, results in the unwinding of all VWF multimers regardless of their size.

Platelet activation

In this study, we assumed that only an unfolded VWF multimer exposing a sufficient amount of A1 domains can activate platelets via simultaneous binding to a group of GP-Ib receptors in an “accord” manner. In other words, we assumed the existence of “minimal platelet activation accord” (nA), i.e., a minimal amount of A1 domains on the unfolded part of VWF, which is sufficient for platelet activation.

In Fig. 4, a platelet activation diagram is presented. The area “U” corresponds to short VWF multimers containing less than the critical number of monomers per multimer, n < nA. VWF is unable to activate platelets.

Figure 4. Platelet activation diagram.

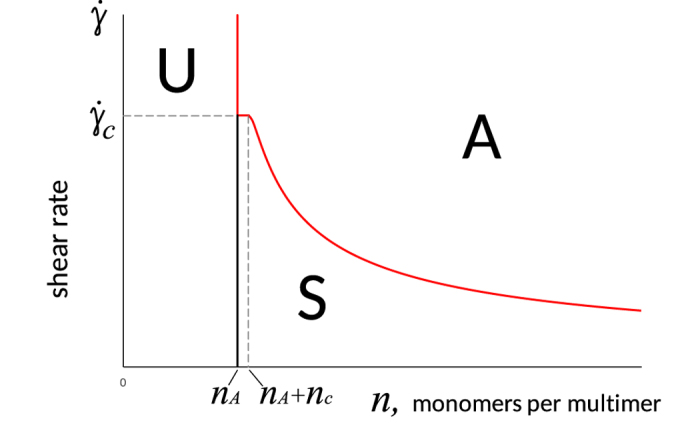
Figure 4

Open in a new tab

Solid lines divide the plane into three domains. Domain U corresponds to parameters at which platelets cannot be activated by VWF (n < nA). Domain A is relevant to parameters at which the length of the VWF tail is sufficient for platelets activation. Domain S refers to subcritical states (ntail < nA), but platelet may be eventually activated. The curve between domains “S” and “A” is described by Eq. (4).

Domains “S” and “A” correspond to larger VWF multimers, n > nA. In domain “A,” the unfolded part of the VWF multimer (i.e., the “tail” in the case of a “globule-with-tail” or the full multimer in the case of a fully unfolded multimer) contains more than nA monomers. In domain “S,” the number of monomers in the unfolded part of VWF is less than nA. In other words, domain “A” corresponds to the conditions required for platelet activation, while “S” domain corresponds to “subcritical” platelet activation and “U” corresponds to non-activation conditions.

The mathematical expression for the value of the critical shear rate 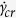Inline graphic sufficient for platelet activation has the form:

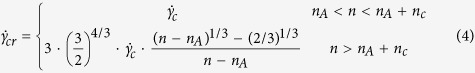graphic file with name srep30508-m15.jpg

(see the Supplementary information).

The necessary and sufficient condition for platelet activation, 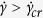Inline graphic, is equivalent to 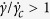Inline graphic for a small interval of VWF multimer sizes, 0 < n − nA < nc, and to:

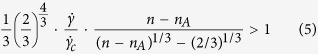graphic file with name srep30508-m18.jpg

for n − nA > nc. We denote the left part of this expression as the “platelet activation risk index” (PARI).

Taking in mind that in reality shear-induced platelet activation is governed by the value of shear stress (τ) rather than shear rate20 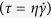Inline graphic for practical purposes, the following equation may be used instead of (5):

graphic file with name srep30508-m20.jpg

where Inline graphic and η is viscosity.

Discussion

To the best of our knowledge, the hypothesis that effective surface tension plays an important role in VWF folding-unfolding dynamics has not yet been analyzed. However, in polymer physics, a similar approach for the determination of the degree of polymer unwinding was developed at the end of the 20th century28,29.

By applying the approach developed by De Gennes28 and his colleagues29 to the VWF dynamics under shear stress conditions on the surface of platelets, we obtained for the first time the exact expression (4) for the dependence of the critical shear rate of platelet activation on VWF multimer size.

An essential assumption introduced in the present work concerns the concept of minimal platelet activation accord. This concept involves the clustering of GPIb receptors on the platelet surface in shear flow, which should enhance platelet interaction with VWF30. In this study, we propose that the clustering and cooperative action of platelet GPIb receptors occurred due to their binding to a sufficient amount of A1 domains on the VWF multimer.

Many researchers have observed that long VWF multimers activate platelets more easily while shorter molecules demonstrate a decreased ability to activate platelets or even a lack of ability18,22,23. Recently, it was shown that VWF multimers of less than 5500 kDa (22 monomeric units) cannot induce platelet activation23. Under the experimental conditions described, nA = 22. It is known that the ability of platelets to be activated by VWF varies among different platelet subpopulations31. The dependence of nA on various pharmaceuticals is of great interest.

VWF multimers are dispersed by size in blood. There is a wide range of hydrodynamic conditions in the blood circulation32. Thus, when trying to apply our results to real situations, instead of a specific representation point on the diagrams (Figs 2 and 4), corresponding representation clouds should be considered. The fraction of the representation cloud located in domain “A” on the platelet activation diagram (Fig. 4) should qualitatively reflect the integral intensity of platelet activation.

To easily quantify platelet activation, we introduced the PARI. If PARI < 1, platelets are not activated. If PARI > 1, platelets are activated by VWF. The PARI is dependent on VWF size (n), shear rate Inline graphic, and platelet sensitivity (nA). The value of Inline graphic may be calculated mathematically33 or directly determined (by MRI or ultrasonic data). The procedure used to determine the VWF size distribution is also known34.

There are several methods of regulating the value of PARI, including varying the arterial pressure and vessel geometry or controlling the distribution of VWF size, n.

VWF size is regulated by ADAMTS13, which cuts VWF into shorter multimer fragments33. An enhanced shortening of VWF multimers by ADAMTS13 is known as von Willebrand disease 2A25,26 (decreased platelet activation), and it corresponds to the shifting of representative points to the left in the platelet activation diagram (Fig. 4) and to a decreasing PARI.

The ADAMTS13-related increase in VWF length35 is known as thrombotic thrombocytopenic purpura and corresponds to a shifting of the representation cloud to the right in Fig. 4, resulting in easier platelet activation and a tendency toward thrombosis. Additionally, the value of the PARI is increased.

In this study, we found that the value of the critical shear rate of platelet activation is dependent on VWF multimer size. An integrative PARI was introduced. Correction of the PARI may be accomplished by the regulation of system hemodynamics, by a pharmacological change in platelet sensitivity, or by the regulation of VWF distribution by size. The PARI may be used as a universal prognostic index.

Additional Information

How to cite this article: Zlobina, K. E. and Guria, G. Th. Platelet activation risk index as a prognostic thrombosis indicator. Sci. Rep. 6, 30508; doi: 10.1038/srep30508 (2016).

Supplementary Material

Supplementary Information
srep30508-s1.pdf (631.1KB, pdf)

Acknowledgments

This work was supported by the Russian Scientific Foundation (grant #14-14-00990).

Footnotes

Author Contributions K.E.Z. and G.Th.G. wrote the main manuscript text and prepared Figures 1,2,3–4. All authors reviewed the manuscript.

References

  1. Bonow R., Mann D., Zipes D., Libby P. (ed.) Braunwald’s Heart Disease: A Textbook of Cardiovascular Medicine, 9th edition (Philadelphia: WB Saunders Company, 2011). [Google Scholar]
  2. Lown B. The Lost Art of Healing, 1 Reprint edition (Ballantine Books, 1999). [Google Scholar]
  3. Tynngard N., Lindahl T. L. & Ramstrom S. Assays of different aspects of haemostasis—what do they measure? Thromb. J. 13, 8 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Jain A. et al. A shear gradient-activated microfluidic device for automated monitoring of whole blood haemostasis and platelet function. Nat. Commun. 7, 10176 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Combariza M. E., Yu X., Nesbitt W. S., Mitchell A. & Tovar-Lopez F. J. Nonlinear dynamic modelling of platelet aggregation via microfluidic devices. IEEE Trans Biomed Eng. 62, 7, 1718–27 (2015). [DOI] [PubMed] [Google Scholar]
  6. Nesbitt W. S. et al. A shear gradient-dependent platelet aggregation mechanism drives thrombus formation. Nat Med 15(6), 665–673 (2009). [DOI] [PubMed] [Google Scholar]
  7. Kroll M. H., Hellums J. D., McIntire L. V., Schafer A. I. & Moake J. L. Platelets and shear stress. Blood 88, 1525–1541 (1996). [PubMed] [Google Scholar]
  8. Goto S., Ikeda Y., Saldívar E. & Ruggeri Z. M. Distinct mechanisms of platelet aggregation as a consequence of different shearing flow conditions. J Clin Invest. 101, 479–86 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ruggeri Z. M., Orje J. N., Habermann R., Federici A. B. & Reininger A. J. Activation-independent platelet adhesion and aggregation under elevated shear stress. Blood 108, 1903–1910 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Reininger A. J. Function of von Willebrand factor in haemostasis and thrombosis. Haemophilia 14 (Suppl. 5), 11–26 (2008). [DOI] [PubMed] [Google Scholar]
  11. Ruggeri Z. M. Platelet adhesion under flow. Microcirculation 16, 58–83 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Qiu Y., Ciciliano J., Myers D. R., Tran R. & Lam W. A. Platelets and physics: How platelets “feel” and respond to their mechanical microenvironment. Blood Rev. 29, 377–386 (2015). [DOI] [PubMed] [Google Scholar]
  13. Springer T. A. von Willebrand Factor, Jedi Knight of the Bloodstream. Blood Journal 124, 1412–1425 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Di Stasio E. & De Cristofaro R. The effect of shear stress on protein conformation: Physical forces operating on biochemical systems: The case of von Willebrand factor. Biophys Chem. 153, 1–8 (2010). [DOI] [PubMed] [Google Scholar]
  15. Bryckaert M., Rosa J.-P., Denis C. V. & Lenting P. J. Of von Willebrand factor and platelets. Cell. Mol. Life Sci. 72, 307–326 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Siedlecki C. A. et al. Shear-dependent changes in the three- dimensional structure of human von Willebrand factor. Blood 88, 2939–2950 (1996). [PubMed] [Google Scholar]
  17. Vergauwe R. M. A. et al. Shear-Stress-Induced Conformational Changes of von Willebrand Factor in a Water–Glycerol Mixture Observed with Single Molecule Microscopy. J. Phys. Chem. B 118, 5660–5669 (2014). [DOI] [PubMed] [Google Scholar]
  18. Moake J. L., Turner N. A., Stathopoulos N. A., Nolasco L. H. & Hellums J. D. Involvement of large plasma von Willebrand factor (vWF) multimers and unusually large vWF forms derived from endothelial cells in shear stress-induced platelet aggregation. J Clin Invest. 78, 1456–1461 (1986). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Schneider S. W. et al. Shear-induced unfolding triggers adhesion of von Willebrand factor fibers. PNAS 104, 7899–7903 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Shankaran H., Alexandridis P. & Neelamegham S. Aspects of hydrodynamic shear regulating shear-induced platelet activation and self-association of von Willebrand factor in suspension. Blood 101, 2637–2645 (2003). [DOI] [PubMed] [Google Scholar]
  21. Themistou E. et al. Application of fluorescence spectroscopy to quantify shear-induced protein conformation change. Biophysical Journal 97, 2567–2576 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Turner N. A. & Moake J. Assembly and activation of alternative complement components on endothelial cell-anchored ultra-large von Willebrand factor links complement and hemostasis-thrombosis. PLoS One 8, e59372 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Stockschlaeder M., Schneppenheim R. & Budde U. Update on von Willebrand factor multimers: focus on high- molecular-weight multimers and their role in hemostasis. Blood Coagul Fibrinolysis 25, 206–216 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Levy G. G. et al. Mutations in a member of the ADAMTS gene family cause thrombotic thrombocytopenic purpura. Nature 413, 488–494 (2001). [DOI] [PubMed] [Google Scholar]
  25. Sadler J. E. et al. Working Party on von Willebrand Disease Classification. Update on the pathophysiology and classification of von Willebrand disease: a report of the Subcommittee on von Willebrand Factor. J Thromb Haemost. 4, 2103–2114 (2006). [DOI] [PubMed] [Google Scholar]
  26. Gadisseur A. et al. Laboratory diagnosis and molecular classification of von Willebrand disease. Acta Haematol. 121, 71–84 (2009). [DOI] [PubMed] [Google Scholar]
  27. Kim J., Zhang C.-Z., Zhang X. & Springer T. A. A mechanically stabilized receptor–ligand flex-bond important in the vasculature. Nature 466, 992–997 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. De Gennes P. G. Kinetics of collapse for a flexible coil. J. Physique Lett. 46, 639–642 (1985). [Google Scholar]
  29. Buguin A. & Brochard-Wyart F. Unwinding of Globular Polymers under Strong Flows. Macromolecules 29, 4937–4943 (1996). [Google Scholar]
  30. Gitz E. et al. Platelet interaction with von Willebrand factor is enhanced by shear-induced clustering of glycoprotein Ib α. Haematologica 98(11), 1810–1818 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Michelson A. D. Platelets 3rd ed. (Academic Press, 2013). [Google Scholar]
  32. Caro C. G., Pedley T. J., Schroter R. C. & Seed W. A. The mechanics of the circulation (Oxford University Press, 1978). [Google Scholar]
  33. Rukhlenko O. S., Dudchenko O. A., Zlobina K. E. & Guria G. T. Mathematical Modeling of Intravascular Blood Coagulation under Wall Shear Stress. PLoS One 10, e0134028, 10.1371/journal.pone.0134028 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pruthi P. K. et al. Plasma von Willebrand factor multimer quantitative analysis by in-gel immunostaining and infrared fluorescent imaging. Thromb. Res. 126, 543–549 (2010). [DOI] [PubMed] [Google Scholar]
  35. Zheng X. L. ADAMTS13 and von Willebrand Factor in Thrombotic Thrombocytopenic Purpura. Annu. Rev. Med. 66, 211–25 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep30508-s1.pdf (631.1KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES