Flexible 2D Crystals of Polycyclic Aromatics Stabilized by Static Distortion Waves

Abstract

The epitaxy of many organic films on inorganic substrates can be classified within the framework of rigid lattices which helps to understand the origin of energy gain driving the epitaxy of the films. Yet, there are adsorbate–substrate combinations with distinct mutual orientations for which this classification fails and epitaxy cannot be explained within a rigid lattice concept. It has been proposed that tiny shifts in atomic positions away from ideal lattice points, so-called static distortion waves (SDWs), are responsible for the observed orientational epitaxy in such cases. Using low-energy electron diffraction and scanning tunneling microscopy, we provide direct experimental evidence for SDWs in organic adsorbate films, namely hexa-peri-hexabenzocoronene on graphite. They manifest as wave-like sub-Ångström molecular displacements away from an ideal adsorbate lattice which is incommensurate with graphite. By means of a density-functional-theory based model, we show that, due to the flexibility in the adsorbate layer, molecule–substrate energy is gained by straining the intermolecular bonds and that the resulting total energy is minimal for the observed domain orientation, constituting the orientational epitaxy. While structural relaxation at an interface is a common assumption, the combination of the precise determination of the incommensurate epitaxial relation, the direct observation of SDWs in real space, and their identification as the sole source of epitaxial energy gain constitutes a comprehensive proof of this effect.

Organic semiconductor materials are nowadays the basis for many types of devices such as light emitting diodes,^1,2 solar cells,³ or field effect transistors.⁴⁻⁶ While applications typically feature polycrystalline layers, from the scientific point of view highly ordered molecular films are especially interesting as they allow for an undisturbed insight into the physical properties of molecular layers and interfaces. At the same time, electronic device efficiencies may profit from well-ordered interfaces.^6,7 With the use of epitaxial film growth, the templating effect of a suitable crystalline substrate is exploited to grow such highly ordered films, and interestingly, molecular arrangements can form that do not naturally occur in the bulk material.⁸

The observed epitaxy of many, but not all, organic films on inorganic substrates can be classified by well-established rigid lattice concepts.⁹⁻¹² Therein, the total energy of a film of an organic material, growing under distinct orientations on top of a crystalline substrate, is minimized if both lattices share common sets of lattice lines.¹² In reciprocal space, this is tantamount to coincidences of reciprocal adsorbate and substrate lattice points. One also speaks of shared Fourier components or of lattices locking into registry. For inorganic films, usually commensurate epitaxy is reported, where the lattices match two-dimensionally leading to a finite number of different adsorption sites of the atoms belonging to the basis. In the case of soft organic films, more subtle modes of epitaxy exist besides the commensurate one. In these so-called point-on-line (POL) or line-on-line (LOL) epitaxy modes, the overlayer and the substrate share only one set of lattice lines,⁹⁻¹¹ which translates into a uniaxial coincidence of lattice points in reciprocal space.^10,11,13 The adsorption sites are all different but restricted to a set of substrate lattice lines.

On the one hand, already the existence of such a uniaxial coincidence of reciprocal lattice points can be shown to provide, in principle, an energetic gain for a rigid molecular domain as compared to that same domain rotated away to an arbitrary angle, i.e., an epitaxial energy gain.¹¹⁻¹³ On the other hand, in a sufficiently large rigid domain without any coincidences with reciprocal substrate lattice points, the great number of different adsorption sites leads to a total energy that is indifferent to rotation or translation of the domain.^11,12 Hence, no distinct and reproducible azimuthal orientation should be expected in such cases. Therefore, we strictly distinguish herein between structures with coincidences in reciprocal space and ones without any. We exclusively refer to the latter as “incommensurate” structures, thereby deviating from definitions of the term “incommensurate” which encompassed POL and LOL structures^14,15 and following more nuanced ones.^10,11

However, incommensurate adlayer–substrate combinations have been reported which feature reproducible orientations of the adlayer.¹⁶⁻¹⁹ Novaco and McTague suggested that so-called static distortion waves (SDWs) could be responsible for the observed epitaxial growth of incommensurate overlayers.²⁰⁻²³ Improving existing approaches,^24,25 the authors demonstrated theoretically that, if in an incommensurate noble gas overlayer on graphite each atom is assumed to relax laterally depending on the local interaction with the (rigid) substrate, these displacements can minimize the total energy for a seemingly arbitrary but in fact distinct orientation with respect to the substrate, without any coincidences of reciprocal lattice vectors. Due to the incommensurability, this growth mode consequently results in a deviation from strict translational symmetry in favor of an incommensurately modulated overlayer.

The properties of such relaxations are usually discussed based on the Frenkel–Kontorova model describing the intra–adlayer interaction by harmonic springs and the adlayer–substrate interaction by a sinusoidal function.^24,26−30 Some authors argue that in the case of a sufficiently strong interaction with the substrate, an incommensurate layer can relax into regions with almost perfect coincidence, separated by relatively small soliton-like domain walls with large misfit.^27,29,30

Even though incommensurate epitaxial systems could be explained reasonably well with the model of local relaxations, no direct experimental confirmation of SDWs in their crucial role for the orientational epitaxy of an incommensurate adlayer exists to date. Yet, in some studies, local distortions of an adlayer have been reported³⁰⁻³⁴ and in a few cases could be directly linked to the local interaction with the underlying substrate.^32,34 In a recently published indirect visualization of SDWs for the case of graphene on hexagonal boron nitride, a two-dimensional Young modulus was imaged and a difference of the graphene lattice constant within near-commensurate areas and soliton-like domain walls was reported.³⁰ Another study claims to have observed the Novaco–McTague mechanism in rotational modulations of rubrene on Bi(001).³¹ However, while all of these studies demonstrate that the adlayer structure can in fact respond locally to the underlying substrate, none of them rule out reciprocal lattice coincidences to evidence true incommensurability. Hence, the local distortions may arise due to varying adsorption sites but are not necessarily needed to understand the adlayer orientation, in contrast to the incommensurate case of Novaco and McTague where SDWs rule the epitaxy.

Here, we present a direct proof of SDWs as the source of the orientational epitaxy of incommensurate organic overlayers. The structure being discussed is a physisorbed monolayer of the organic molecule hexa-peri-hexabenzocoronene (HBC) on graphite, a system which was previously reported to be governed by simple commensurate epitaxy.^8,35−37 We elucidate why, on the one hand, this adsorbate–substrate combination is especially suited to detect SDWs, and why, on the other hand, we believe that SDWs in organic adsorbate layers are rather common yet difficult to be evidenced experimentally. The wave-like sub-Ångström displacements from a rigid reference grid are directly measured in both direction and size for more than 1,000 molecules using scanning tunneling microscopy (STM). With the help of low-energy electron diffraction (LEED) and a numerical model for the adsorption energy of realistically large and flexible molecular domains, we are able to exclude all rigid lattice concepts as sources for an epitaxial energy gain. Our calculations, which contain no free parameters, excellently reproduce all experimental results including the optimal orientation of the HBC domain. In consequence, we unambiguously identify the SDWs as the sole source of epitaxial energy gain, directly confirming the Novaco–McTague mechanism for orientational epitaxy. Moreover, our results prove that nanographene-type molecules and graphite do not automatically form commensurate structures, despite their apparent match in structure and symmetry.

Results and Discussion

LEED Measurements

Using LEED, STM, and numerical simulations, we characterize SDWs in monolayers of HBC on both epitaxial graphene (EG) on silicon carbide⁴⁰ and natural graphite (NG) substrates. There is no notable difference in the HBC growth on both substrate materials, as evidenced by LEED measurements on EG substrates discussed below, and on NG substrates (cf.Supporting Information). Hence, even though EG features a surface reconstruction⁴¹ due to the underlying silicon carbide,⁴¹ the HBC molecules arrange just like on natural graphite, in agreement with studies on another molecule adsorbed on the same substrates.⁴² While LEED measurements on EG exhibit a better diffraction quality compared to the buckled natural graphite, the surface reconstruction of EG makes STM measurements on adsorbed molecules more difficult to analyze. Therefore, we discuss LEED measurements on EG and STM measurements on NG.

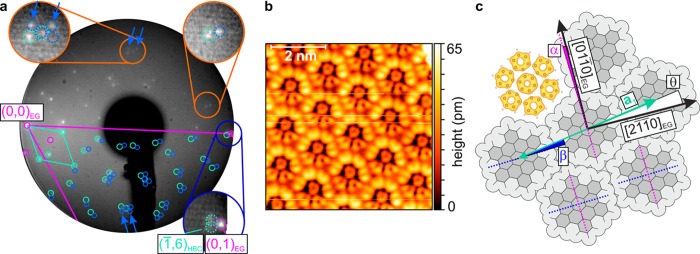
Figure 1a shows a LEED image of a monolayer of HBC on a tilted EG sample at room temperature that was corrected for imaging³⁸ and tilt distortions.³⁹ The beam energy was chosen such that both the specular beam near the left screen edge and a first diffraction order of graphite near the right edge are visible. Additional bright spots mainly in the left part of the image can be attributed to the HBC lattice (turquoise circles). However, the pattern displays features that are clearly inconsistent with commensurate epitaxy. In particular, the reciprocal HBC lattice does not coincide with the first order substrate spots. This can be seen exemplarily for the (1̅,6) diffraction order of HBC and one substrate spot in the dark blue zoom in Figure 1a, and is likewise true for equivalent ones. Further, some spots (blue circles) cannot be explained by the HBC lattice alone, but are consistent with multiple scattering^43,44 between HBC and EG and would not be present if the HBC lattice were commensurate. With LEEDLab, obtained from Scienta Omicron, we derive high-precision lattice data by fitting it to all evaluable reflections. The presence of the multiple scattering spots can be exploited to obtain precise values for the epitaxial relation because their positions depend sensitively on the relative scaling and shapes of both the HBC and the graphite lattices. Moreover, by using the multiple scattering description of the LEED pattern, we deliberately avoid the definition of large supercells to explain these additional spots, since the lattices are incommensurate, as will be evaluated later. The fit reveals for this room temperature (RT) structure a hexagonal HBC lattice with a lattice constant and a unit cell rotation θ between the first HBC lattice vector a₁ and [21̅1̅0]_EG which slightly but significantly differ from the reported commensurate values (cf.Table 1). The corresponding epitaxy matrix determined here defines the relation between the HBC lattice vectors and the graphite lattice vectors¹¹ and deviates from the matrix with strictly integer elements corresponding to the previously reported commensurate structure^35,36 (cf.Table 1 as well).

Figure 1.

(a) Room temperature LEED image (incident electron energy 38.0 eV, sample tilted by 15°, logarithmic contrast) of one HBC monolayer on epitaxial graphene (EG), corrected for imaging³⁸ and tilt distortions.³⁹ Dark blue zoom: the (1̅,6) HBC spot (turquoise) and its equivalents do not coincide with first order substrate spots (magenta), rendering the structure not commensurate. EG reconstruction spots (magenta as well) and multiple scattering between HBC and EG (blue) are needed to explain all spots (cf. orange zooms). The blue arrows mark the most intense multiple scattering spots in the simulated lattice and equivalent experimental locations in the upper half of the image. (b) STM image of a mirrored domain at 4.4 K with a sample bias of −3 V and a set point of 3 pA, corrected only for plane tilt. Predominantly, the HOMO is detected (cf. HOMO electron density via DFT in panel c). (c) Orientations from the STM and LEED measurements, where α = θ + β, with θ defined as the unit cell rotation.

Table 1. Comparison of Our Results with the Previously Reported Commensurate HBC Structure^a.

structure	epitaxy matrix	a [Å]	Γ [deg]	θ [deg]	temperature [K]	source
RT		14.01(8)	120.00(5)	–8.48(4)	300	LEED fit
LT		13.95(2)	120.00(3)	–8.66(2)	1.2	STM FFT fit
commensurate		13.70	120	–8.95	300/420	LEED (refs 35, 36)

^aAll lattice constants a are based on the epitaxy matrices relative to graphite with a lattice constant of 2.461 Å. Γ = ∠(a₁, a₂) is the unit cell opening angle and θ is the unit cell rotation (cf.Figure 1c). The commensurate matrix is equivalent to the commensurate structures reported in the cited references. Experimental uncertainties of the last significant digit are given in parentheses. The finite experimental accuracy does not imply a rationality of the matrix elements.

STM Measurements

To determine the actual molecular packing, we performed STM measurements on a monolayer of HBC on NG at low temperatures (LT). At small scan ranges and negative sample bias, the HBC molecules are imaged with submolecular contrast which can be predominantly attributed to the highest occupied molecular orbital (HOMO) and resembles the corresponding Clar formula^45,46 (Figure 1b). The simultaneous observation of both possible mirror domains allows for an accurate determination of the molecular rotation angle β = (5.1 ± 0.5)° (cf.Figure 1c) with a precision atypical for STM measurements (cf.Supporting Information). Judging from the STM data, the molecules lie flat or almost flat on the surface. An apparent deviation from a perfect D_6h symmetry is most likely tip-induced, as can be inferred from varying contrasts in Supplementary Figure 2b in the Supporting Information.

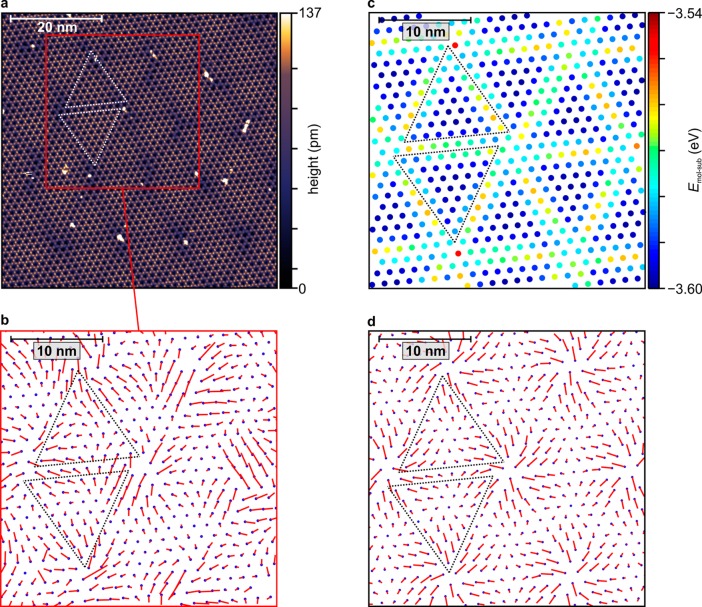
Complementary, large-scale STM measurements (Figure 2a) reveal molecularly resolved domains that are hundreds of nanometers wide, proving that the observed HBC growth mode is not merely a finite-size effect. In such images, the molecular centers appear dark at positive sample bias. Additionally, a two-dimensional Moiré pattern becomes visible in contrast-enhanced STM images, further confirming in real space that the HBC layer is indeed not commensurate. Moreover, it allows for a precise Fourier-based determination of the HBC lattice parameters (cf.Supporting Information) which are slightly altered to a smaller lattice constant and a different unit cell rotation θ upon cooling (LT structure, cf.Table 1). The Moiré pattern consists of hexagonally arranged triangular regions which often show a slight chiral behavior, best observable at their corners. The bright defects that are mainly located near the corners of these triangular regions are too small to be HBC molecules. We assume that, similar to a local surface reactivity,⁴⁷ these positions are especially prone to adsorption of rest gas molecules which might adsorb during the precooling of the samples to 80 K before the introduction into the STM.

Figure 2.

(a) STM image of 1 ML of HBC on NG, at 1.2 K with a sample bias of +3 V and a set point of 2 pA, corrected only for plane tilt, with a color scale adapted to enhance the subtle Moiré pattern, marked by dotted triangles as guides to the eye. (b) Reference lattice (blue dots) corresponding to the LT structure (cf.Table 1) and molecular displacements (red lines) determined from panel a, magnified by a factor of 15. (c) Molecular positions and calculated Moiré pattern in the molecule–substrate energy after relaxation. (d) Molecular starting positions and calculated displacements, magnified by a factor of 15 as well. Images b–d have the same lateral scale.

While there is an obvious long-range order in the HBC lattice that is also evident from the sharp frequencies in Fast Fourier Transforms (cf.Supporting Information), the bright-dark contrast of the Moiré pattern coincides with barely noticeable local deviations from a rigid hexagonal HBC lattice. These deviations follow a rather regular pattern which we visualize by applying an algorithm to our STM images that was originally developed to identify spot positions in LEED patterns with subpixel resolution.³⁸Figure 2b shows the numerically obtained rigid reference lattice that fits best all molecular positions, as well as the magnified local molecular displacement vectors from the reference lattice points to the actual molecular positions. Even though the molecular positions are somewhat disturbed by the bright point defects, the distribution of the molecular displacements is clearly not random. Rather, it resembles a smooth vector field as would be expected for static distortion waves: the displacements approximately follow the Moiré triangle edges and generally point away from the triangles’ corners. The average displacement is only 0.52 Å, while the resulting distribution of nearest-neighbor HBC bond lengths (cf.Supporting Information for the corresponding histogram) has a standard deviation of 0.28 Å. This amounts to only 3.7% and 2.0%, respectively, of the average nearest-neighbor distance.

Importantly, neither the Moiré pattern nor the pattern of displacements implies the presence of a periodic supercell or an assembly of many rigid commensurate patches separated by incommensurate domain walls. Rather, they may be interpreted as a continuous domain of HBC molecules whose positions are modulated with respect to an incommensurate reference lattice.

Evaluation of the Epitaxy Type

While the epitaxy between HBC and graphite is clearly not commensurate, other epitaxy types based on coincidences of reciprocal lattice vectors can as well be excluded as an explanation for the distinct orientation of the HBC lattice.^9,11 POL and LOL epitaxy types can be ruled out for symmetry reasons since both require a coincidence of reciprocal adsorbate and substrate lattice points in only a single direction. However, both the graphite and the HBC lattices exhibit truly 6-fold symmetry in LEED. Hence, any coincidence of reciprocal lattice points would have to repeat at multiples of 60°, therefore leading to coincidences in different directions which is only possible with either commensurate (ruled out already) or higher order commensurate (HOC) growth (i.e., all epitaxy matrix elements are rational numbers) producing a commensurate supercell.

While the noninteger epitaxy matrix above was derived with a state-of-the-art accuracy and produces no coincidences in reciprocal space within at least seven substrate diffraction orders for the LT structure, it inevitably contains a finite error margin that would allow one to define a very high-order HOC structure. However, the search for any arithmetically possible HOC structure is merely academic unless it is shown to provide an epitaxial energy gain that would favor the experimentally measured HBC domain orientation. As will be discussed next by means of our numerical model, it makes no difference in terms of adsorption energy whether the HBC layer exactly meets an HOC coincidence. Therefore, we refrain from applying such an unnecessary restriction of periodicity and aim to model a truly incommensurate HBC layer.

Modeling the Total Energy of an Incommensurate HBC Layer

To verify that the measured distortions indeed represent SDWs in an incommensurate layer and that the SDWs decisively minimize the system’s total energy, we developed a model to simulate the spatial relaxation of each molecule away from exact lattice points. The original Novaco–McTague theory requires calculated or experimental data for both the adsorbate–substrate interaction energies and the phonon dispersion in the adsorbate layer.²⁰ However, the phonon dispersion relations are usually not available for large aromatic molecules. Another inherent difficulty arises from the strong anisotropy of the molecule–molecule interaction and the dependence of the molecule–substrate interaction on the molecular orientation.

We resolve these issues by employing a simple energy gradient approach to optimize local molecular positions according to the interplay of local adsorption energies and nearest-neighbor interactions, relying on density functional theory (DFT) calculations for realistic interaction energies and on well-determined experimental parameters (cf.Methods and Supporting Information). In other words, the particles in our model are able to lower the total energy of the system by gaining more adlayer–substrate energy from adopting more advantageous positions on the substrate than they lose due to the straining of the intralayer bonds as a consequence of individual molecular displacements.

We believe that our approach is more sophisticated than pure symmetry considerations,⁴⁸ which cannot explain the orientation we observe for HBC on graphite, or the Frenkel-Kontorova model^24,26,27 which oversimplifies the intermolecular interaction of the HBC molecules as harmonic springs and does not account for the molecular orientation dependence of the molecule–substrate interaction. Our model does not impose restrictions in terms of periodicity. No boundary conditions are applied, and a realistically large domain with thousands of molecules can be simulated without the presence of any periodic arrangement with respect to the substrate. Moreover, we aim to not only calculate the energy gain due to local distortions, as was the goal of other simpler approaches including Novaco’s and McTague’s,^20−23,25 but also to simulate amplitudes and shapes of the SDWs to compare with our experiments. However, our algorithm resembles a quasi-static relaxation and is thus less complex and computationally less expensive than approaches which include dynamical processes.⁴⁹⁻⁵¹ Nevertheless, we will show that it adequately describes the local relaxation of a globally incommensurate layer and, most importantly, accurately predicts the optimal rotation angle of the HBC layer on graphite.

Resulting from such a calculation, Figure 2c,d shows cutouts of a structurally relaxed HBC domain of 10,981 molecules, with the starting configuration chosen to be the incommensurate reference lattice with the experimental LT lattice constant of a = 13.95 Å and rotation angles of θ = −8.66° and β = 5.1°. The latter is kept fixed during the relaxation. Each dot in Figure 2c marks the relaxed position of a molecule, while the corresponding molecule–substrate interaction energy at that position is color-coded. In Figure 2d, the calculated molecular displacements are depicted. The similarities between these calculated patterns and their experimental counterparts are striking, especially compared to the Moiré pattern without any relaxation which does not resemble the STM images (cf.Supporting Information). Even the apparent chirality of the triangular shapes in the Moiré patterns is reproduced. Yet, more importantly, the calculated mean displacement of 0.44 Å and the standard deviation of the nearest-neighbor distances of 0.29 Å (see Supporting Information for the corresponding histogram) are in excellent agreement with the experiment. As already implied by the cutouts in panels c and d of Figure 2, each triangle of the HBC domain looks slightly different from any other with respect to the color pattern or the pattern of displacements within, due to the incommensurability of the HBC reference lattice and the corresponding lack of strict periodicity.

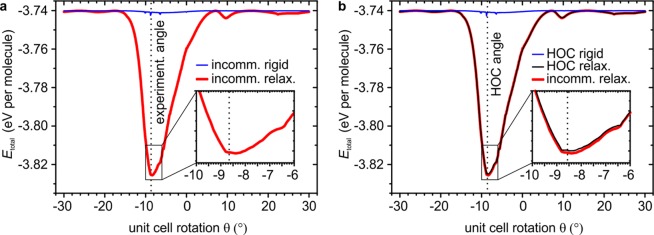
The red curve in Figure 3a is obtained by repeating the relaxation with the same LT lattice constant but with varying unit cell rotation θ as starting points (step width 0.1°) while keeping the molecular orientation within the unit cell (β) fixed. It confirms that the total energy is indeed minimal for a unit cell rotation θ = −8.5 ± 0.2°, matching our experiments very well and differing significantly from the commensurate value of −8.95°. We note that it does not correspond to any “magic angle” due to a coincidence of reciprocal lattice points but simply represents the orientation at which the molecules are able to gain the most energy in the molecule–substrate interaction before the intermolecular bonds counterbalance the relaxation. In this angular range, the molecule–substrate interaction features large gradients and the apparent Moiré period is especially long, allowing for larger displacements before strained nearest-neighbor bonds stop the relaxation. However, neither condition is fulfilled to its maximum, and the optimal angle can only be found by realistically describing the energy contributions and gradients. The fact that the experimental value of the unit cell rotation, together with the directions and the magnitudes of the molecular displacements constituting the SDWs, are reproduced so strikingly well evidences that the interaction energies are modeled realistically.

Figure 3.

(a) Total adsorption energy per molecule before (thin blue line) and after (thick red line) relaxation of an HBC domain with 10,981 molecules (diameter approximately 170 nm), initially separated by the experimental lattice constant of 13.95 Å, versus unit cell rotation θ of the starting configuration with respect to graphite. The global minimum of the red curve at −8.5 ± 0.2° is in excellent agreement with the rotation angle of −8.66 ± 0.02° determined experimentally (dotted vertical line). (b) A similar calculation, but with a lattice constant of 13.9552 Å that exactly produces an HOC coincidence at θ = −8.57° (dotted vertical line), being comparable but not identical to the measured LT structure. Importantly, without relaxation (thin blue line), the HOC structure does not produce any sizable epitaxial energy gain, which demonstrates that the lattice coincidence alone is not able to explain the experimentally found alignment. Vice versa, after relaxation (thin black line) no additional epitaxial energy gain at θ = −8.57° compared to the relaxed incommensurate structure from panel a (replotted here in red) is found for the HOC structure.

Compared to the total energy curve of the unrelaxed domain, i.e., of a rigid hexagonal HBC lattice with the experimental lattice constant (blue curve in Figure 3a), it is obvious that the SDWs alone provide a substantial average energy gain of 85 meV per molecule for the optimal domain orientation, while there is no discernible preferred orientation for the rigid domain as is expected in the incommensurate case. This readily explains why in all our experiments we observe a very reproducible domain orientation which is, together with the lack of reciprocal space coincidences in the simulated structure, a manifestation of orientational epitaxy as proposed by Novaco and McTague. The resulting SDW energy gain is also rather insensitive to different simulated domain sizes (cf.Supporting Information), in agreement with the concept of an incommensurate layer that is merely orientationally stabilized and in contrast to rigid lattice epitaxy energy minima that characteristically depend on the domain size.¹¹

While the blue curve in Figure 3a already demonstrates that there cannot be a significant epitaxial energy gain for any azimuthal orientation of a rigid HBC lattice with the experimental LT lattice constant, we emphasize that our results and conclusions neither depend on the “right choice” of the lattice constant nor on a deliberate avoidance of any exact HOC configuration. On the contrary, for the presented system, an HOC configuration both with and without SDWs is only a special case that does not lower the energy further when compared to the incommensurate case with and without SDWs. To show this, we choose lattice constants to exactly reproduce the smallest reasonable commensurate supercells close to either the experimental LT (cf.Figure 3b) or the RT structure (cf. Supplementary Figure 8b in the Supporting Information) at slightly different angles θ. The first unit cell vector of the hexagonal supercell close to the LT structure is a_1,super = 8a_1,HBC – 2a_2,HBC, while the one close to the RT structure is a_1,super = 6a_1,HBC – 2a_2,HBC.

First, in the rigid case (cf. respective blue curves in each figure), the HOC domains behave indeed like rigid incommensurate domains when rotated over the substrate: there is no meaningful energy minimum when the HOC condition is met or at any other angle, even for these smallest supercells discussed here. Since any larger supercell would only contain even more molecules, thereby flattening the blue curves even more, this supports our previous statement that rigid lattices cannot explain the observed orientational epitaxy, even in the presence of an HOC coincidence. Second, relaxing the molecular positions of the respective HOC configurations, and for all other angles θ (black curves in Figure 3b and Supplementary Figure 8b in the Supporting Information), results in curves being practically indistinguishable from the ones of the relaxed incommensurate structures (red curves). This demonstrates that the SDWs rule the energy curves and that there is no additional epitaxial energy gain when the HOC condition is met, as compared to the relaxed incommensurate layer. Hence, both with and without SDWs the HBC layer has no reason to prefer an HOC arrangement over an incommensurate one and the SDWs are the only source of epitaxial energy gain in this system.

Conclusions

From the lack of strict periodicity in both the large-scale STM images and the calculated Moiré pattern (cf.Figure 2c), together with the domain energy being indifferent to the existence of an HOC coincidence, we conclude that the HBC structure is indeed incommensurate with graphite within experimentally meaningful limits.

Therefore, in conclusion, we have shown that SDWs exist in an incommensurate monolayer of HBC on graphite by directly measuring the local relaxation with sub-Ångström resolution for every single molecule in a large STM image. More importantly, via supporting LEED measurements and theoretical modeling, we demonstrated that no rigid lattice concept can explain the observed orientational epitaxy and that the formation of the SDWs provides a substantial energy gain over a rigid structure at the domain orientation observed experimentally. Hence, we directly confirmed for a real system the stabilizing role of SDWs which enables the growth of epitaxial organic films in the absence of any coincidences, leading to an average epitaxial energy gain of as large as 85 meV per molecule in the film.

The occurrence of SDWs in the reported system is actually remarkable because aromatic hydrocarbons with D_6h symmetry such as HBC,³⁶ coronene³⁶ (both frequently dubbed nanographenes), and benzene⁵² have all been reported previously as commensurate on graphite. Owing to its symmetry and structure matching with graphite, it has been suggested or implied that an HBC molecule can be regarded simply as a small sheet of graphene,^8,53 and the stated commensurate growth³⁵⁻³⁷ or the assumption that the orientation of HBC molecules is determined exclusively by the graphite lattice³⁵ seemed natural. However, due to our improved measurement techniques, it becomes clear that HBC grows incommensurately, and that the orientation of the molecules with respect to graphite are a result of balanced intralayer and interlayer interactions, as already assumed earlier by others.³⁶ Hence, the presence of the hydrogen atoms at the circumference of the molecules cannot be neglected concerning structure formation.

The direct observation of SDWs leading to the above conclusions was feasible by using the advantageous properties of the reported system: (i) The disk-like shape of HBC in the STM images allowed for using the aforementioned spot finding algorithm to assign a meaningful position to each molecule in the STM images. (ii) The relatively soft intermolecular bonds produced displacements large enough for direct detection. And finally, (iii) the high symmetry of both substrate and adsorbate allowed for the safe and unambiguous exclusion of point-on-line and line-on-line epitaxy modes, reducing the complexity of the system.

Given the fact that high resolution data in combination with a spot finding algorithm and lattice fitting in distortion-corrected LEED patterns were all required to safely identify the incommensurability of HBC on graphite and to determine the epitaxial relation with sufficient accuracy for a numerical model, we suppose that incommensurate orientational epitaxy driven by SDWs might be far more common than has been assumed so far. Indeed, there are quite a few not fully understood epitaxial but incommensurate organic adlayer systems^17,19 which might be caused by similar local relaxations and may likewise be explainable by our approach. The only requirement for the prediction of the epitaxial orientation is a realistic model for the contributing energies to calculate the corresponding gradients. This potentially expands the range of molecule–substrate combinations for which well-ordered molecular layers can be understood, predicted, and achieved. Thereby, SDWs are also interesting from a technological point of view since well-ordered interfaces and films can lead to higher efficiencies of organic electronic devices.^6,7 Moreover, since local relaxation in the presence of matching lattice lines has been investigated before,^28,32 we anticipate that the respective roles of lattice epitaxy and local relaxation for the resulting epitaxy will be the focus of future research.

Methods

Materials

Epitaxial graphene (EG) is grown on a silicon carbide single crystal (SiC-4H(0001)) following a procedure from ref (40), producing few-layer graphene with thicknesses of two to three monolayers, estimated from X-ray photoelectron spectroscopy (XPS) measurements. The pristine SiC samples were purchased from Sterling Semiconductor.

The natural graphite (NG) crystals were purchased from Naturally Graphite, Michigan Technological University, and range in diameter between 3 and 5 mm. They are glued to molybdenum sample holders with PELCO High Temperature Carbon Paste (purchased from Plano), cleaved in air, and degassed in ultrahigh vacuum (UHV) at more than 800 K for several hours in order to evaporate any volatile components of the adhesive. The same samples are then recleaved in air and redegassed more gently at 600 K in UHV so as to ensure a contamination-free surface prior to any experiment.

Sample Production and Analysis

The molecules are evaporated in ultrahigh vacuum (5 × 10^–10 mbar base pressure) onto the room temperature samples at a rate of 0.1–0.2 monolayers/min, while thickness control is ensured via differential reflectance spectroscopy (DRS).⁵⁴ For the samples discussed here, the deposition is stopped after an optical monomer–dimer transition is observed in DRS, characterizing the beginning of the growth of the second monolayer. From this, the nominal thickness can be estimated to be 1.05 ± 0.05 monolayers.

Low-energy electron diffraction (LEED) is performed at room temperature with a dual microchannel plate (MCP) LEED from OCI Vacuum Microengineering, which has been distortion corrected and calibrated with LEEDCal, allowing us to fit geometrical lattices to all evaluable diffraction spots in any succeeding images with LEEDLab, both obtained from Scienta Omicron. The real space structure of our samples is probed with a low-temperature scanning tunneling microscope (STM) from SPECS Surface Nano Analysis using KolibriSensors in the STM-only mode.

Algorithm To Relax an Incommensurate Molecular Adlayer

If a molecular adlayer is incommensurate with the crystalline substrate, each molecule has a different adsorption site r_p and experiences an individual gradient in the molecule–substrate interaction energy ∇E_mol-sub(r_p). Since the intermolecular bonds in the adlayer are of finite stiffness, it is natural to assume that each molecule slightly moves into a more advantageous position by δ_p until the interaction with its neighboring molecules (expressed by E_mol-mol) stops that relaxation. The resulting directions and magnitudes of these molecular displacements from the ideal lattice points correspond to a balance between E_mol-sub and E_mol-mol.

On the basis of these facts, we aim to model both energy contributions on the first-principles level and then parametrize them in order to obtain local forces −∇E_mol-sub and −∇E_mol-mol on each molecule in a large domain consisting of about 11,000 molecules. Since the intermolecular interaction E_mol-mol is short-range, only the nearest-neighbor contribution is considered in order to keep numerical costs manageable. Additionally, the molecules are assumed to be flat-lying and retain their orientational angles throughout the energy minimization. The first assumption is consistent with our STM measurements, while the latter assumption can be rationalized by the steric hindrance preventing the molecules from significant rotations in densely packed domains. The total energy is minimized iteratively by allowing each molecule to take small steps along its (negative) individual total energy gradient until the total energy of the domain converges. The displacement δ_p^(s) of the p^th molecule in iteration step s and those of its nearest neighbors {δ_q} are used to refine the displacements in step s + 1: δ_p^(s+1) = δ_p – τ{∇_pE_mol-sub(r_p + δ_p^(s)) + ∑_q∇_pE_mol-mol(δ_p,δ_q^(s))}. The factor τ only affects the total number of iteration steps, if chosen small enough to reach convergence. The third term represents the sum over all nearest-neighbor interactions of molecule p. The algorithm outlined above was implemented in MATLAB.

Thermodynamically, this constitutes a minimization of the internal energy of the system, not its free energy. However, for our STM experiments at 1.2 K (cf.Figure 2a), entropy effects are expected to be negligible owing to the low temperature. Further, remarkably, even at 300 K the HBC epitaxy remains essentially unaltered (cf.Table 1). Therefore, we reason that the entropic influence is very small due to the substantial energy gain per molecule (cf.Figure 3) and the considerable domain sizes.

In the presented case of large aromatic molecules, the molecule–substrate interaction E_mol-sub(r,α) not only depends on the lateral position r of a molecule on the substrate but on its orientation α with respect to the substrate (cf.Figure 1c) as well. This complicates the model if different molecular orientations on the substrates are of interest, and standard procedures such as an expansion into a Fourier series⁵⁵ based on only a few values lose their advantages. Hence, we perform force-field calculations with the Merck molecular force field (mmff94)⁵⁶ using the grid technique⁵⁷ and scale the results using DFT calculations to overcome the known underestimation of the force-field energy corrugation of graphite.⁵⁸ The result is cross-checked with exemplary, additional DFT calculations (cf.Supporting Information).

In the force-field calculation, one HBC molecule (structurally optimized semiempirically with the PM7 parametrization⁵⁹) is translated and rotated over one unit cell of graphite to map E_mol-sub(r,α). The graphite has a thickness of 2 layers in bernal (AB) stacking to ensure a convergence of E_mol-sub. The lateral mapping resolution is 51 × 51 points; the angular resolution is 0.1°. For each configuration, the adsorption height was optimized. Therefore, a lateral displacement in the final relaxation algorithm automatically corresponds to an effective three-dimensional adjustment of the molecular position. Due to the relatively small adsorption height differences of less than 15 pm, this minor effect is neglected in the intermolecular interaction. The map E_mol-sub(r,α = 0°) contains both the lowest and the highest possible values of E_mol-sub, since they essentially correspond to AB and AA stackings of the HBC molecule on the top graphite layer, respectively. Hence, with DFT (see below), we calculate both configurations in order to offset and scale the map to match both extreme cases. The resulting scaling factor is 14.6, in agreement with other studies.⁵⁸ This rescaling is then applied to the maps for all angles α (cf.Supporting Information).

Density Functional Theory Calculations

Calculations of the ground-state electronic properties of the structures discussed in this paper, in particular the interaction energies E_mol-sub and E_mol-mol, were performed within the density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP).^60,61 The van-der-Waals (vdW) interaction is included based on a scheme originally proposed by Dion et al.(62) However, following Klimeš et al.,^63,64 we used the optB86b⁶⁵ exchange-energy part of the total energy in the generalized-gradient approximation (GGA).⁶⁶ The local part of the correlation energy is approximated within the local-density approximation (LDA). Details of the implementation can be found elsewhere.^63,64,67

Pseudopotentials for the core electrons and all-electron-like wave functions have been generated within the projector-augmented wave (PAW) method.⁶⁸ A kinetic energy cutoff of 500 eV was used in the plane-wave expansion of the wave functions of the valence electrons between the atoms. The k-space integrations only require the Γ point to obtain converged results.

A free HBC molecule is modeled within a 25 × 25 × 15 ų hexagonal unit cell and relaxed until the Hellmann–Feynman forces acting on the atoms are reduced below 1 meV/Å. For a single HBC molecule on the graphite surface, an 8 × 8 supercell of double-layer graphene is used, where the atoms in the substrate are kept fixed. The intermolecular interaction energies of a free-standing HBC layer are calculated for two cases: longitudinal and shear deformation of an intermolecular bond (see Supporting Information for details).

Additional Software

Gwyddion⁶⁹ was used for STM postmeasurement processing. The extraction of circular height profiles from STM images was conducted with ImageJ⁷⁰ and the Oval Profile Plot plugin.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b00935.

• HBC on natural graphite; determining the molecular orientation; Moiré pattern in real and reciprocal space; nearest-neighbor distance distributions; comparison of force-field and DFT calculations; parametrization of DFT calculations; nonrelaxed versus relaxed Moiré; domain size dependence and relaxation of room temperature structure (PDF)

Author Present Address

^⊥ Center for Advancing Electronics Dresden & Department of Chemistry and Food Chemistry, University of Technology Dresden, Mommsenstrasse 4, 01062 Dresden, Germany.

Author Contributions

M.M., R.F., and T.F. conceptualized the project. M.M. performed the STM and LEED measurements. M.M. and F.S. analyzed the experimental data. L.M. and F.B. implemented the DFT calculations. X.F. and K.M. synthesized the HBC molecules. M.M. and T.F. developed the relaxation model. M.M., S.C.B.M., R.F., and T.F. wrote the manuscript, and all authors discussed and commented on it.

The authors declare no competing financial interest.