Bayesian hierarchical modelling of continuous non‐negative longitudinal data with a spike at zero: An application to a study of birds visiting gardens in winter

Abstract

The development of methods for dealing with continuous data with a spike at zero has lagged behind those for overdispersed or zero‐inflated count data. We consider longitudinal ecological data corresponding to an annual average of 26 weekly maximum counts of birds, and are hence effectively continuous, bounded below by zero but also with a discrete mass at zero. We develop a Bayesian hierarchical Tweedie regression model that can directly accommodate the excess number of zeros common to this type of data, whilst accounting for both spatial and temporal correlation. Implementation of the model is conducted in a Markov chain Monte Carlo (MCMC) framework, using reversible jump MCMC to explore uncertainty across both parameter and model spaces. This regression modelling framework is very flexible and removes the need to make strong assumptions about mean‐variance relationships a priori. It can also directly account for the spike at zero, whilst being easily applicable to other types of data and other model formulations. Whilst a correlative study such as this cannot prove causation, our results suggest that an increase in an avian predator may have led to an overall decrease in the number of one of its prey species visiting garden feeding stations in the United Kingdom. This may reflect a change in behaviour of house sparrows to avoid feeding stations frequented by sparrowhawks, or a reduction in house sparrow population size as a result of sparrowhawk increase.

1. Introduction

Longitudinal studies aiming to monitor and explain trends in populations are common in the ecological sciences. Linear models are often used to analyse and explain the underlying dynamics of such populations of interest (e.g., Robinson et al., 2005; Newson et al., 2010). Relatedness between observations collected in space and time, however, is often not taken into account and linear mixed or hierarchical models that account for this are underused in ecology (Buckley et al., 2003). The fixed effects component can explain variation linked to measured covariates, whilst the random effects component accounts for additional variation that is specific to the grouping units, not explained by the fixed effects. Extensions and modifications to standard methods may be required if the data have unusual qualities, common examples of which are accounting for overdispersion (Richards, 1998) or zero‐inflated data (e.g., Martin et al., 2005) in discrete count problems. However, equivalent models for analysing continuous data with a spike at zero have developed at a much slower rate. Examples of scenarios where data are non‐negative continuous with a discrete mass at zero are frequent in the life sciences, particularly in ecology, so there is an obvious need for suitably flexible methods for dealing with this type of data. Generally, distributions that have support on the non‐negative real line are not able to account for spikes at zero. Several methods for modelling this type of data have been proposed, some of which model the zeros and positive observations through separate models (e.g., Shono, 2008; Foster and Bravington, 2012; Hvingel et al., 2012), whilst others use distributions that can directly account for the mass at zero, most commonly the Tweedie distributions (e.g., Smyth and Jørgensen, 2002; Candy, 2004; Shono, 2008; Foster and Bravington, 2012).

In this paper, we outline a Bayesian hierarchical model that uses the unified approach, and apply it to a long‐term ecological dataset of winter averaged maximum weekly counts of birds visiting UK gardens. By averaging within winters, the data are converted from a set of discrete counts to a single (effectively) continuous random variable, which for many of the species monitored through this survey, has a spike at zero (where no birds are observed). Being an average of counts, the data are bounded below by zero. In addition, some of the sites monitored are able to support very large numbers of birds leading to distributions that are also positively skewed. We account for environmental covariates through fixed and random site effects and for the spike at zero and skewness using the Tweedie distributions (Jørgensen, 1987), a highly flexible family of exponential dispersion models (EDMs). The Tweedie class of distributions contains the Poisson‐gamma distributions that are continuous and non‐negative with a spike at zero (Jørgensen, 1987; Smyth, 1996). The Tweedie distributions have been used predominately to model fisheries biomass data, but we are unaware of any previous use in the analysis of ecological data of the type discussed in this paper.

We adopt a Bayesian approach to obtain inference on the parameters of interest, where the covariates present in the model are unknown a priori. Reversible jump (RJ) MCMC is implemented to estimate posterior model probabilities, which allows us to discriminate quantitatively between covariates that are useful predictors of the observed trends in birds visiting gardens. When modelling population changes, frequently the question of how to estimate change in the first year arises. We let year 1 denote the first year in which a site i is monitored (therefore, the exact year will vary from site to site). In this context, previous analyses of population changes in relation to environmental covariates have reduced the dimension of the data in order to be able to model changes between years 1 and 2 (Thomson et al., 1998). The authors model the observed counts as a function of covariates, with the log abundance in the previous year included as an offset in the model. Typically, for such models, the data are modelled from year 2 onwards, with the first year of data used up in the offset, whilst any zero observations must also be discarded. Freeman and Newson (2008) reparameterised the model and use expected counts rather than observed counts, so that all the data can be used. The Bayesian framework offers a natural solution to dealing with this problem without the need to reduce the amount of data or to reparameterise, by using a data augmentation approach.

In Section 2, we introduce the dataset and the background to the application used in this paper, whilst Section 3 outlines the Tweedie regression model fitted to the application. In Section 4 we outline the specifics of the model implementation process, including algorithms to improve the efficiency of the MCMC algorithm. Section 5 presents the results of the application. Finally, Section 6 outlines the conclusions.

2. Monitoring changes in garden bird abundance: The Garden Bird Feeding Survey

The British Trust for Ornithology (BTO) carries out numerous surveys of varying scales on the numbers and distribution of birds across the United Kingdom. In this paper, we use data from their Garden Bird Feeding Survey (GBFS), which has been monitoring the number of birds visiting private garden feeding stations in the United Kingdom since the winter of 1970/71 (http://www.bto.org/volunteer‐surveys/gbfs). For the remainder of this paper, the year 1970 refers to the winter of 1970/71. The survey is conducted over 26 weeks each winter, spanning the months October to March inclusive and covering a representative range of garden types and geographic distribution across the United Kingdom (Fig. 1). There is no standardised amount of time over which each observation is conducted, however participants are asked to ensure consistency within sites. Of the 7483 averaged counts, 60% relate to an average over all 26 weekly maximum counts, and 93% of the average counts were averaged over at least 23. There was no obvious pattern in which weeks and sites were missed. The combination of relatively few missed counts and the lack of pattern should, therefore, introduce negligible bias to the results. Participants are asked to record the maximum number of each species of bird seen feeding from the provisioned food, or in the case of predators, feeding on the birds visiting the feeding station, in each of the 26 weeks. Given that there are up to 26 counts of each species at each site within a year, a very high level of computation would be required to analyse all the raw data, including the need for complex correlation structures. Chamberlain et al. (2009) avoid this problem by running independent analyses in weeks 1, 13, and 26, and then comparing the results for consistency. This, however, appears somewhat arbitrary and ignores most of the data collected. We therefore follow Bell et al. (2010) in taking an across‐winter average at each site, corresponding to the mean maximum count per site per year. These data are hence effectively continuous with zero as a lower bound, but show a marked peak at zero due in part to sites where the species is rare or difficult to observe. Very few of these zeros are likely to have been structural zeros, given the widespread distribution of the species, and the fact that only 16 sites had a zero mean count in every year that they were surveyed.

Figure 1.

Spatial distribution of surveyed sites across UK.

In this paper, we concentrate on one of the species of bird monitored under this survey, the house sparrow Passer domesticus, which is of particular concern having decreased by 47% in rural areas and approximately 60% in urban and suburban areas since the mid 1970s (Robinson et al., 2005). Figure 2b shows the decline of house sparrows at sites monitored by the GBFS between 1970 and 2010. Although house sparrows were recorded at 98% of sites monitored during this period, 10% of the annual average site counts were exactly zero. In addition some sites are capable of sustaining a much larger number of birds, and hence the distribution of averaged counts is strongly right‐skewed (Fig. 2a).

Figure 2.

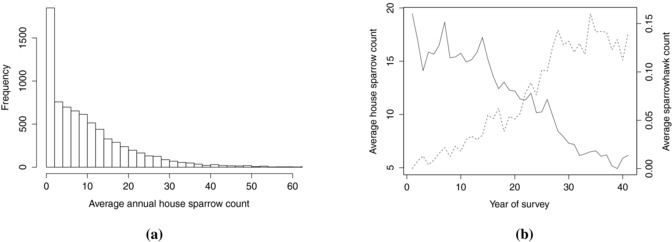
(a) Distribution of year‐by‐site averages of house sparrow counts from 1970–2010, clearly showing the problems of zero‐inflation and the right‐skewed nature of the positive observations. The histogram shows values only up to 60; there are an additional 36 observations above 60 with a maximum of 132.8. (b) Yearly averages of number of house sparrows (solid line) and sparrowhawks (broken line) observed across GBFS sites.

The long time period covered by this survey gives the best possible opportunity to test for evidence of effects of various environmental factors on the numbers of birds visiting the gardens. There is particular interest in whether changes in abundance and distribution of avian predators have had a negative impact on songbird populations (e.g., Bell et al., 2010; Newson et al., 2010), and hence the inclusion of the abundance of an avian predator as one of the covariates aims to test for evidence in favour of this hypothesis. In a similar time frame to the house sparrow's decline, the number of the Eurasian sparrowhawk Acipiter nisus (henceforth sparrowhawk), a predator of the house sparrow, has increased (Fig. 2b). This increase in abundance and also distribution relates to a re‐colonisation of mainly arable regions in eastern England, resulting from voluntary bans on organochlorine pesticides during the 1960s and 70s that had caused declines in the preceding decades (Newton, 1986). The collared dove Streptopelia decaocto has colonised the United Kingdom in a similar time frame to that of the sparrowhawk, however spreading from the east rather than the west (Marchant et al., 1990). Previous analyses have included it as a ‘pseudo‐predator’ covariate (Thomson et al., 1998; Newson et al., 2010) to test for spurious correlation that could arise coincidentally. We would not expect a strong negative relationship between house sparrows and collared doves on ecological grounds and hence if such an effect is found, any additional sparrowhawk effect could be called into question.

The year‐on‐year turnover of sites is fairly high with few sites spanning the full time period, although the number of sites monitored each year has remained fairly consistent. On average there is an 8% yearly drop‐out rate for the years 1970–2010. We include only sites with at least three years of consecutive monitoring, giving us a total of $n_{site}=727$ for the entire period (Fig. 1).

Chamberlain et al. (2009) and Bell et al. (2010) analysed the dataset to test for changes in house sparrow abundance at feeding stations in relation to sparrowhawk numbers and found contrasting results. Bell et al. (2010) found negative sparrowhawk effects on house sparrows but failed to account for additional environmental covariates in the model, whilst Chamberlain et al. (2009) found no significant effect. The latter's model did account for temperature and number of feeding units, but no additional factors. In this paper, we use a more extensive and flexible method to account for additional factors that may be expected to contribute to changes in house sparrow numbers.

3. The model

In this section, we outline the model used in this paper. Of particular interest here are Exponential Dispersion Models with a power mean‐variance relationship Var(Y)$=\varphi {\mu }^p$ for some index parameter p, as this mean‐variance relationship is commonly found in ecological processes (Taylor, 1961; Foster and Bravington, 2012). Following Jørgenson (1987, 1997) these are referred to as Tweedie distributions and exist for any real valued p outside the interval (0, 1). For values of p in the interval (1, 2), the Tweedie distribution has support on the non‐negative real line with a spike at zero, corresponding to the type of data shown in Fig. 2a.

Mathematically, let $y_{it}$ (henceforth mean sparrow count) denote the mean maximum number of house sparrows at site i in year t ($i=1,...,n_{site};t\in {\mathbf{t}}_i$), where ${\mathbf{t}}_i$ is the set of years in which observations are carried out at site i. Further, let ${\mathbf{x}}_i$ denote a vector of covariates that are time invariant and ${\mathbf{v}}_{it}$ a vector of time‐varying covariates for site i with associated regression parameter vectors $\beta$ and $\gamma ,$ respectively. If E$\left(y_{it}|{\mathbf{x}}_i,{\mathbf{v}}_{it},{\epsilon }_i\right)={\mu }_{it}$ is the expectation of the mean of weekly maxima then

$$y_{i,t}\sim Tw\left({\mu }_{it},\varphi ,p\right)$$ (1)

where Var$\left(y_{it}\right)=\varphi {\mu }_{it}^p$ and

$${\mu }_{it}={\mu }_{it-1}exp\left(\alpha +{\mathbf{x}}_i^{\top }\beta +{\mathbf{v}}_{it}^{\top }\gamma +{\epsilon }_i\right).$$ (2)

Equivalently,

$$log\left(\frac{{\mu }_{it}}{{\mu }_{it-1}}\right)=\alpha +{\mathbf{x}}_i^{\top }\beta +{\mathbf{v}}_{it}^{\top }\gamma +{\epsilon }_i.$$ (3)

The ${\epsilon }_i$ denote site random effects such that

$${\epsilon }_i\sim N\left(0,{\sigma }^2\right)\mathrm{for}i=1,...,n_{site},$$ (4)

where σ² denotes the random effect variance.

This model is able to account for the spike at zero as well as the right‐skewed continuous nature of the data as discussed above. Distributions of this form can also be written as a mixture of N gamma distributions, where N is a Poisson random variable, and have as such been referred to as Poisson‐gamma distributions (e.g., Dunn and Smyth, 2005). In the absence of covariates, the Poisson‐gamma formulation of the Tweedie distributions is directly equal to the Tweedie formulation outlined above (Foster and Bravington, 2012). However, the former assumes that the response variable being modelled can be split into groups or schools, and has as such been used for fisheries catch data (e.g., Shono, 2008; Foster and Bravington, 2012). As the data being modelled in this application relate to averaged counts, there is no intuitive interpretation of the data in this reparameterised form. Hence, in this paper we use the general form of the Tweedie distribution with parameters ($\mu ,\varphi ,p$).

We model the expected value in year t as a function of the expected value in year $t-1$ and the environmental covariates (Eq. (2)), requiring the specification of ${\mu }_{i0}$, the expected number of birds at site i in year zero, that is the year prior to data being collected at site i. The simplest method to deal with this is to replace the ${\mu }_{it}$ of Eq. (2) with the observed number of birds, $y_{it}$ (Thomson et al., 1998). This does, however, cause two problems. Firstly, it leads to a reduction in the amount of data available as the analysis can only start in the second year (with the first year used to start the recursive process off). Secondly, and of more concern, it cannot be used when zero observations occur as for any years after zero observations the expected count under the model remains at zero for the rest of the survey period, irrespective of covariate values, preventing the realistic possibility of site recolonisation. This causes an additional problem when using the Tweedie distributions as they are only defined for $\mu >0$. Freeman and Newson (2008) maintain the use of the expected values and reparameterise the model to a recursive form with the expected value in year 1 included as a fixed site‐dependent offset.

We follow the modelling approach of Freeman and Newson (2008) and specify the expected value in year t to be a function of the expected value in year $t-1$. However, using a Bayesian approach we extend the modelling process and treat ${\mu }_0$ as a vector of additional parameters to be estimated through MCMC simulation (Tanner and Wong, 1987). We adopt a data augmentation approach treating the ${\mu }_{i0}$ as unknown parameters to be estimated from the rest of the data by updating using the Metropolis–Hastings algorithm at every iteration. This methodology then allows zero observations and the first observation at each site to contribute to estimating the remaining regression parameters. This method can also be used when values of covariates are missing or for missing years of observations during the survey. The data augmented ${\mu }_{i0}$ are also used as the density‐dependence covariate for the initial year of observations, $v_{i10}$.

A common problem with repeated measure multilevel models such as this is the highly computationally intensive nature of the parameter estimation process, particularly when using MCMC methods (Browne et al., 2009). In particular, the constructed Markov chains are often highly correlated, leading to slow convergence and/or poor coverage of parameter space, usually leading to high Monte Carlo error. To improve the efficiency of the MCMC algorithm we use hierarchical centring (Gelfand et al., 1995), a reparameterisation algorithm developed for nested random effect models where the original parameters in the model are replaced with less correlated ones. The aim of this method is to remove correlation between the parameters associated with fixed effects in the linear predictor that are constant within random effect clusters and the zero‐mean random effects (Browne et al., 2009). This simple reparameterisation replaces the zero mean of the random effects from Eq. (4) with the sum of the site level fixed effects ‘pulled’ from the linear predictor. In particular, the common intercept α of Eq. (2) and the ${\mathbf{x}}_i$ are all covariates whose values are constant within random effect groups (the intercept is also constant across sites). We can therefore rewrite Eqs. (3) and (4) as

$$\begin{array}{c}\hfill log\left(\frac{{\mu }_{it}}{{\mu }_{it-1}}\right)={\mathbf{v}}_{it}^{\top }\gamma +{\epsilon }_i\end{array}$$

and

$$\begin{array}{c}\hfill {\epsilon }_i\sim N\left(\alpha +{\mathbf{x}}_i^{\top }\beta ,{\sigma }^2\right),i=1,...,n_{site,}\end{array}$$

respectively. Oedekoven et al. (2014) apply this reparameterisation method within RJMCMC, where it was found to improve model mixing and movement over model and parameter space.

This model specifies the change in log mean sparrow count as a linear function of the covariates, as previously used for example by Thomson et al. (1998) and Freeman and Newson (2008). The use of a change model removes any dependence on the initial size of the population and is concerned only with how that population changes over time. This reduces the chance of spurious correlations between the abundance of the predators and prey that may be driven by concurrent processes (Newson et al., 2010). The site random effect terms are included to account for additional variation between sites that is not explained by the fixed effects.

To test for evidence of effects of environmental factors on changes in house sparrow numbers, we include the following covariates in the model: northing ($x_{i1}$), easting ($x_{i2}$), level of urbanisation (rural = −1 and suburban/urban = 1) ($x_{i3}$), averaged sparrowhawk count ($v_{i2t}$), averaged collared dove count ($v_{i3t}$), and average number of days frost across the relevant months ($v_{i4t}$). Following Dennis and Taper (1987), we test for density dependence by including a year‐lagged measure of house sparrow abundance as an additional covariate ($v_{i1t-1}$). This Markov property, that the population at time t depends only on the population size at time $t-1$, is a general assumption that has been applicable in many ecological applications (Dennis and Taper, 1987; Thomson et al., 1998). The autoregressive structure has additionally be used in other longitudinal data analyses, such as to aid smoothing in state space modelling of population indices (Mazzetta et al., 2007) and hidden Markov models (e.g., Langrock, 2011). The temporal change in house sparrow abundance is not constant across the United Kingdom and hence the use of spatial variables in the model will correspond to general trends in populations that are not specific to the measured covariates. The ${\mathbf{x}}_i=\{x_{i1},x_{i2}\}$ covariates relate to spatial northing and easting values for the site respectively and are time independent. The ground frost covariate is an average number of days of ground frost obtained from the Met Office's UKCP09 gridded datasets (http://ukclimateprojections.metoffice.gov.uk/). These data are a measure of the number of days of ground frost for each 5 km square across the United Kingdom, interpolated from Met Office observation stations. Further details of the interpolation process can be found in Perry and Hollis (2005). The nearest monitoring point to each GBFS survey site was selected before averaging over the months of the survey (i.e., October to March inclusive) for each site and year in the GBFS dataset.

4. Model implementation

We adopt a Bayesian approach to obtain inference on the model parameters, exploring the posterior distribution of interest using a Markov chain Monte Carlo (MCMC) approach. Tweedie densities are calculated using the functions included in the R package fishMod. In order to improve the mixing of the parameters updated using the Metropolis–Hastings algorithm, pilot tuning was used to tune the variance of the proposal distributions independently for each parameter during the burn‐in phase. Gelman et al. (1996) suggest optimal acceptance probabilities of between 20% and 40% depending on the dimension of the target distribution. Acceptance probabilities between 10% and 80% in this application seemed to lead to optimal convergence and mixing. For further details of the MCMC algorithms used in the paper, see for example King et al. (2010) and the Supporting Information on the journal's website.

4.1. Prior and posterior distributions

Initial discussion with ecologists suggested that zero mean‐symmetric distributions would be sensible as priors for the regression parameters, particularly as there was no overall favour towards positive or negative parameter values. Zero‐mean normal distributions were chosen with variance ${\tau }^2={10}^{-2}$, as larger variances than this induced exponential growth or decay in the populations, which was known not to be the case for the population of interest. Hence, we place independent $N\left(0,{10}^{-2}\right)$ priors on α, ${\beta }_j$ and ${\gamma }_k$ (for $j=1,2,3$ and $k=2,...,4$). As in Dennis and Taper (1994), density dependence is formulated in such a way that we are only concerned with values of ${\gamma }_1\le 0$, hence a half normal prior is used for γ₁, the parameter associated with this covariate. A prior sensitivity analysis is also conducted to ensure this was not unduly affecting the results. As the data are continuous and non‐negative with a spike at zero, we expect p to be in the interval (1, 2). Outside of this we have no prior information on where in this interval p will lie, hence we use a Uniform distribution on this interval. Plotting Tweedie distributions with varying ϕ suggested that any values of ϕ greater than 5 generated distributions that were unrealistically constrained around zero. A uniform prior on the interval (0, 5) is therefore used. Again a prior sensitivity analysis is conducted to check this was not unduly restrictive.

The site random effects are assumed to follow a normal distribution and are constrained with a zero mean and common variance σ², upon which a conjugate inverse gamma prior is placed, that is ${\sigma }^2\sim {\Gamma }^{-1}\left({\alpha }_{\sigma },{\beta }_{\sigma }\right)$. For a non‐informative prior we specify ${\alpha }_{\sigma }={\beta }_{\sigma }={10}^{-3}$. Additionally, we must specify priors on the augmented data for the year 0. We use a flat prior on the ${\mu }_{i0}$, with upper bound 200 that is ${\mu }_{i0}\sim U\left[0,200\right]$. This upper bound was chosen to be greater than the maximum count that the ecologists would expect to be observed at a single site.

The joint posterior density can then be written as

$$\begin{array}{c}\hfill \pi (\theta ,\epsilon ,{\sigma }^2,{\mu }_0|\mathbf{y})\propto Tw\left(\mathbf{y}|\theta ,\epsilon ,{\sigma }^2,{\mu }_0\right)f\left(\epsilon \right|{\sigma }^2)p\left(\theta \right)p\left({\mu }_0\right)p\left({\sigma }^2\right)\end{array}$$

where $\theta$ is the set of fixed effect regression parameters and Tweedie distribution variance parameters, $Tw(.)$ the Tweedie likelihood expressed in Eq. (1), f(.) the normal distribution likelihood of Eq. (2) and p(.) the prior distributions. In a Bayesian framework inference about the parameters can be obtained from the individual marginal posterior densities. These densities require integration of the joint posterior density across all other parameters, which is not analytically possible in this case. Hence, we use an MCMC approach. We note that the posterior conditional distributions are not of standard form and hence we use a single update random walk Metropolis–Hastings algorithm to generate dependent samples from these distributions. The conjugate prior specified on the site random effect variance σ² allows a Gibbs step to be used for this parameter. The posterior conditional distribution for σ² is thus

$$\begin{array}{c}\hfill \pi \left({\sigma }^2\right|\epsilon )\sim {\Gamma }^{-1}\left(\frac{n_{site}}{2}+{\alpha }_{\sigma },\frac{{\displaystyle \sum _{i=1}^{n_{site}}{\epsilon }_i^2}}{2}+{\beta }_{\sigma }\right),\end{array}$$

where ${\alpha }_{\sigma }$ and ${\beta }_{\sigma }$ are the rate and shape parameters of the inverse gamma prior specified on σ² respectively.

4.2. Model discrimination and checking

Not all of the covariates included in the model are necessarily expected to affect changes in house sparrow numbers. We therefore use RJMCMC (Green, 1995), an extension of the Metropolis–Hastings algorithm that enables estimation of posterior model probabilities, to discriminate quantitatively between competing models. The algorithm used here considers only nested model moves where at each iteration, at most one covariate is either added or removed from the model, depending on its state at the current iteration (King et al., 2010). A priori model probabilities are considered to be equal, with the common intercept α of Eq. (2) always present. Predefined normal proposal distributions are used, with means and variances set equal to the posterior conditional means and variances calculated from an initial run of the MCMC algorithm in the saturated model. Again, see the Supporting Information for specific details of the algorithm. We then test the hypothesis ${\theta }_i=0$ versus ${\theta }_i\ne 0$ for each of the regression parameters (except for the intercept α) using Bayes factors.

To check for evidence of a lack of convergence, we use the Brooks–Gelman–Rubin (BGR) statistic, $\widehat{R}$ (Brooks and Gelman, 1998). Three chains were run independently with overdispersed starting values and then the width of the empirical 80% credible interval of the combined chains was compared with that of the corresponding mean within‐chain interval. Convergence is assumed when these are roughly equal, or equivalently $\widehat{R}\approx 1$.

In order to assess the goodness‐of‐fit of the model to the data, we calculate the posterior predictive Bayesian p‐value (Gelman and Meng, 1996) and the sampled posterior p‐value (Johnson 2004, 2007); the latter was found by Zhang (2014) to be superior in terms of computational expense, maximising power and correctly specifying type I errors. Bayesian p‐values close to 0.5 are indicative of a well fitting model. Both the deviance and Freeman–Tukey statistic are considered as the discrepancy statistic to allow for more than one possible model failure (Gelman et al., 2003, p. 172)

5. Results

Initially 20,000 iterations were conducted without the reversible jump algorithm in the saturated model. Posterior means and variances of the regression parameters obtained from this analysis were then used to advise sensible proposal parameters for the reversible jump step in future analyses. The full analysis including the reversible jump algorithm was then run for 20,000 iterations, with the first 5,000 iterations discarded as burn‐in. The BGR statistic for parameters always present in the model suggested that this was a very conservative choice given that $\widehat{R}$ converged on 1 within the first 1000 iterations (Fig. 3). The analysis was initially conducted in the saturated model only, that is all covariates present in the model. Additional chains were started in the intercept only model and saturated model with larger parameter values to investigate convergence. Summary statistics from the analysis are presented in Table 1. Posterior means, 95% highest posterior density intervals and Bayes factors were calculated empirically where appropriate. Bayes factors in this instance refer to the ratio of posterior odds to prior odds of ${\theta }_j\ne 0$ to ${\theta }_j=0$, where ${\theta }_j$ is the appropriate regression parameter. The prior odds here are simply equal to one as both models are equally likely a priori. A prior sensitivity analysis, the results of which can be found in the Appendix, was conducted to check for undue variation in results under alternate prior specifications.

Figure 3.

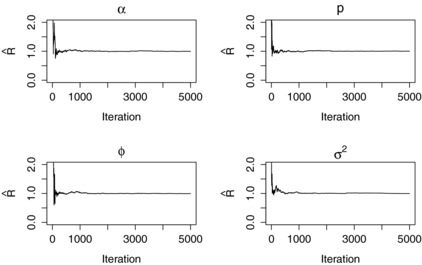
BGR statistic plots for parameters present across models obtained from three independent runs of the model with overdispersed starting values.

Table 1.

Posterior means and 95% highest posterior density intervals (HPDIs) (conditional on covariate being present in the model) and Bayes factors for model parameters. $\alpha ,\varphi ,p$ and σ² always in the model

Parameter	Covariate	Posterior mean	HPDI (95%)	Bayes factor
α	Intercept	−0.0773	(−0.0883, −0.0655)	NA
β1	Northing	−0.0109	(−0.0241, 0.0019)	0.257
β2	Easting	−0.0308	(−0.0436, −0.0186)	>100
β3	Sub/rur	−0.0164	(−0.0286, −0.0050)	2.760
γ1	Dens dep	−0.0002	(−0.0007, −0.0001)	0.002
γ2	Sparrowhawk	−0.0371	(−0.0454, −0.0302)	>100
γ3	Collared dove	−0.0004	(−0.0045, 0.0042)	0.023
γ4	Ground frost	0.0493	(0.0408, 0.0576)	>100
ϕ	−	0.7363	(0.7148, 0.7607)	NA
p	−	1.3651	(1.3542, 1.3758)	NA
σ2	−	0.0152	(0.0124, 0.0183)	NA

Model fit was assessed using Bayesian p‐values. Using both the deviance and Freeman–Tukey statistic as the discrepancy functions gave p‐values of 0.63 and 0.81, respectively using the posterior predictive p‐value and 0.87 and 0.42, respectively using the sampled posterior p‐value. Both of these test statistics measure overall fit of the model to the data, but the deviance tends to be more conservative as the Freeman–Tukey statistic scales down the differences between model and observed data. None of the p‐values, however, give any evidence to suggest a lack of fit of the model. Figure 4 shows a density plot of the expected values at each iteration of the analysis and the observed data. This plot once more gives no evidence to suggest a lack of fit of the model.

Figure 4.

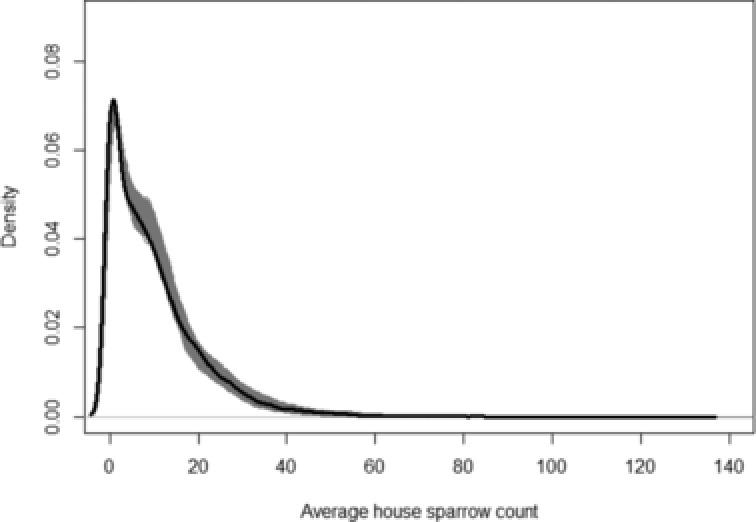
Density of observed data (thick line) plotted over expected values under the model for each iteration.

Kass and Raftery (1995) provide a scale for interpretation of Bayes factors (K), with $K>3$ giving positive support for one model over another. For the house sparrow application Bayes factors greater than 3 gave evidence to suggest a significant effect of that covariate on changes in mean house sparrow counts. The results give evidence to suggest that easting, sparrowhawk count and number of ground frost days affect the number of house sparrows visiting garden bird feeding stations in the United Kingdom, having Bayes factors greater than 3. In contrast, there was no evidence of an effect of northing, level or urbanisation, collared dove count or density dependence on house mean sparrow counts.

Aside from the effect of sparrowhawks on house sparrows, the findings of this analysis correlate well with known changes in house sparrow numbers. The new BTO atlas (Balmer et al., 2013, pp. 596–597) maps changes in distributions in breeding and winter abundance of birds in the United Kingdom. With regards to house sparrows, it is clear that they have fared particularly poorly in the east of the UK. While the higher presence of arable farming across eastern England may have contributed to the decline of house sparrow populations more widely within this region (Newton, 2004), it is suspected that different factors may be operating within urban habitats and that declines here may be linked to breeding success (Peach et al., 2008; Morrison et al., 2014). Given the differences in population change of house sparrows in rural and urban habitats outlined in Section 2, we would perhaps expect the parameter associated with this covariate to be significant. However, it may be that the differing severity of trends is better explained by underlying differences occurring concurrently at urban sites and modelled through the other fixed effects or the random site effects. Although the data analysed in this paper relate to winter abundance, Chamberlain et al. (2005) found c.97% correlation between winter abundance and equivalent breeding numbers for this species. A positive effect of days of ground frost is suggestive of an effect of more birds using garden feeding stations in colder weather, when food is scarcer or more difficult to access. This agrees with the analysis conducted by Chamberlain et al. (2005) who found negative associations of house sparrow abundance at feeders and temperature. Although a different covariate was used, there was a very strong negative correlation (−0.87) between days of ground frost and temperature for the sites and years analysed.

Under different prior specifications on the regression parameters, the results were largely consistent (see Appendix). Bayes factors were the statistics most susceptible to changes in the prior distributions specified, although under realistic priors no changes in interpretation were noted.

6. Concluding remarks

In this paper, we have outlined a highly flexible, unified method for analysing longitudinal hierarchical data that are continuous but with a spike at zero, extending the use of Tweedie distributions to incorporate serial temporal and spatial correlation. This is the first example we are aware of using this approach to longitudinal data using the Tweedie distributions. Shono (2008) modelled fisheries catch data collected across months and years by treating month and year as fixed effects, whilst Candy (2004) embedded Tweedie distributions into a GLMM framework with random effects. Our model extends the use of the Tweedie distributions to account for serial correlation through random site effects and the inclusion of the previous year's observation as a covariate. Other methods have been used to analyse this type of data that require two models to analyse the zero and positive observations separately. These methods, particularly the delta models, have been used extensively in the fisheries literature, but can often lead to difficulties in ensuring a multiplicative structure on the expected value (Foster and Bravington, 2012). This would be a more severe problem if sampling effort varied greatly between observations and an offset were required. Shono (2008) also found that a unified approach using the Poisson‐gamma distribution outperformed a delta log‐normal model in terms of prediction, where the delta log‐normal method models zero and positive observations through two separate sub‐models. Of the four models fitted by Foster and Bravington (2012), the results from their delta log‐normal model differed most from their other three unified methods. Modelling the zeros in this way also produces an often unnatural discontinuity at zero with abundance data (Ancelet et al., 2010).

The method developed in this paper unifies both groups of observations in a single family of distributions, namely the Tweedie distributions. Most previous analyses using a single distribution have reparameterised the Tweedie distributions as a Poisson‐gamma compound distribution (e.g., Smyth and Jørgensen, 2002; Shono, 2008; Foster and Bravington, 2012; Hvingel et al., 2012). This intuitively makes sense when dealing with biomass data, for example, when the total biomass can be separated into number of individuals (the Poisson part of the likelihood) and the average weight of each individual (the gamma part). The modelling of rainfall has similarly been conducted with this alternative reparameterisation (Dunn, 2004; Hasan and Dunn, 2010a, b). When the data relate to averaged counts, however, this reparameterisation does not have a natural interpretation.

Tweedie distributions of the general form have been less attractive due to the computational difficulty of estimating the value of p (Smyth and Jørgensen, 2002; Zhang, 2013). The estimation of this parameter is usually achieved using a profile likelihood (Smyth, 1996) or adjusted profile likelihood (Dunn and Smyth, 2005), whilst Foster and Bravington (2012) estimate it jointly with other parameters. Zhang (2013) used an MCMC algorithm in addition to several likelihood‐based inferential methods for evaluating linear mixed Tweedie models and found the MCMC method consistently produced the least biased estimates for both fixed effect and random effect parameters.

In general, the three parameters of the Tweedie distributions enable the fitting of a very flexible family of models and therefore offer the advantage of not requiring strong assumptions to be made about the distributional form a priori. Many standard distributions are special cases of the Tweedie family and can therefore be fitted within this framework. The flexibility of the Tweedie distributions means that this method is also applicable when the data are continuous, including when there is a spike at zero, or discrete. The use of both fixed and random effects allows abundance to be explained in relation to measured covariates as well as unmeasured site effects. The total variance can also be partitioned into variation within sites (fixed effects and σ²) as well as additional unexplained heterogeneity (through ${\mu }_{it},\varphi ,p$).

Long‐term survey data are becoming increasingly available as the power of citizen science studies is realised. These data are often collected at a higher temporal resolution than it is feasible to model directly, so by taking an average much of the information can be retained whilst ensuring computational feasibility. Ecological datasets rarely fit well with standard models and methods for analysing long‐term trends in these datasets that can effectively account for such deviations are needed. Although the model used in this analysis concerned longitudinal data, the methodology could be easily applied to other types of data. The distribution fitted in this paper was used specifically to address problems of non‐negative continuous data with excess zeros, equivalent to a value of p between 1 and 2. The fitting of the Tweedie distribution to data of this type is a unified approach, generating distributions with a power mean‐variance relationship that is common to ecological processes (Taylor, 1961; Foster and Bravington, 2012). Taylor's power law, that the variance is proportional to a fractional power of the mean, is exactly the relationship expressed under the Tweedie distributions.

The methodology used here extends those of Chamberlain et al. (2009) and Bell et al. (2010), taking into consideration additional environmental covariates and using a more flexible and extensive approach. The methodology uses a larger number of covariates to explain changes in house sparrow numbers than previous analyses of this dataset and the results give sensible suggestions as to factors that may be behind the severe declines observed in this species over the past four decades. The results of these analyses give strong evidence to suggest that garden feeding stations where the number of sparrowhawks has increased over the last 40 years have seen a reduction in the number of house sparrows visiting them. From this analysis alone, it is not possible to ascertain whether this reflects a change in behaviour of house sparrows to avoid garden feeding stations occupied by sparrowhawks, or a reduction in the overall house sparrow population as a result of an increase in sparrowhawk numbers.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Appendix 1.

1.1.

A.1. Prior sensitivity analysis

Posterior model probabilities (and hence Bayes factors) are known to be susceptible to the choice of prior distributions on model parameters (King et al., 2010, p. 170), referred to as Lindley's paradox. We therefore conduct a prior sensitivity analysis. Values of the prior variances specified on the regression parameters were altered as was the upper bound on the Tweedie dispersion parameter ϕ, and results are presented below (Table A1). The model specified previously was rerun with variances of one order of magnitude higher and lower than those specified in Section 4.1 and with a higher upper bound on the uniform prior specified on ϕ. There was no evidence of significant changes in parameter estimates under varying priors, however as expected Bayes factors increased when smaller prior variances were specified. This only changes inference for the urbanisation covariate, which becomes significant under the prior with the smallest variance. The Bayes factor for this parameter under the original prior specifications was only just below the threshold value. The smallest variance (${\tau }^2={10}^{-3}$), however, puts too much prior mass at values close to zero and is used for illustration purposes only.

Table A1.

Posterior means and marginal posterior probabilities for model parameters under alternative prior specifications. $\alpha ,\varphi ,p$ and σ² always in the model

Parameter	Covariate	${\tau }^2={10}^{-3}$		${\tau }^2={10}^{-1}$		$p\left(\varphi \right)=U[0,50]$
		Posterior	BF	Posterior	BF	Posterior	BF
		mean		mean		mean
α	Intercept	−0.0744	NA	−0.0783	NA	−0.0772	NA
β1	Northing	−0.0088	0.451	−0.0079	0.002	−0.0108	0.251
β2	Easting	−0.0297	>100	−0.0302	>100	−0.0309	>100
β3	Sub/rur	−0.0160	8.804	−0.0165	0.834	−0.0167	3.513
γ1	Dens dep	−0.0002	0.012	0.0000	0.000	−0.0002	0.008
γ2	Sparrowhawk	−0.0361	>100	−0.0361	>100	−0.0377	>100
γ3	Collared dove	−0.0008	1.091	0.0000	0.001	−0.0001	0.018
γ4	Ground frost	0.0487	>100	0.0490	>100	0.0502	>100
ϕ	−	0.7370	NA	0.7379	NA	0.7359	NA
p	−	1.3653	NA	1.3655	NA	1.3650	NA
σ2	−	0.0146	NA	0.0150	NA	0.0154	NA