Rapid genotype imputation from sequence without reference panels

Abstract

Inexpensive genotyping methods are essential for genetic studies requiring large sample sizes. In human studies, array-based microarrays and high-density haplotype reference panels allow efficient genotype imputation for this purpose. However, these resources are typically unavailable in non-human settings. Here we describe a method (STITCH) for imputation based only on sequencing read data, without requiring additional reference panels or array data. We demonstrate its applicability even in settings of extremely low sequencing coverage, by accurately imputing 5.7 million SNPs at a mean r² of 0.98 in 2,073 outbred laboratory mice (0.15X sequencing coverage). In a sample of 11,670 Han Chinese (1.7X), we achieve accuracy similar to alternative approaches that require a reference panel, demonstrating that this approach can work for genetically diverse populations. Our method enables straightforward progression from low-coverage sequence to imputed genotypes, overcoming barriers that at present restrict the application of genome-wide association study technology outside humans.

Introduction

Over the last decade, genome-wide association studies (GWAS) have detected thousands of loci associated with complex traits in the human genome.¹ Generally, these involve genotyping 0.5-1M SNPs on DNA genotyping microarrays, and then employing externally generated haplotype reference panels such as those provided by the HapMap² and the 1000 Genomes Project³ to infer genotypes at tens of millions of additional sites, employing algorithms for phasing⁴ and imputation^5–8.

In non-human species, large haplotype reference panels for fully genome-wide imputation are typically not available, and this fact has necessitated study designs incorporating high sample relatedness, and directed breeding, which can be leveraged to improve array-based genotype imputation^9–12. Moreover, inter-population differences within non-human species can further complicate genotyping array design and use. Arrays may work poorly when populations other than those used to design the chip are analyzed¹³, requiring the expensive development of either dense arrays, or many less dense, population specific arrays.

Given these issues, an attractive low-cost alternative to the use of arrays is to use low coverage next generation sequencing (LC-NGS) as a basis for imputation of complete genotypes¹⁴. Genotyping by LC-NGS could in principle be powerful: even at modest sequencing depth LC-NGS reads sample the majority of segregating sites, including those specific to the population of interest.

However, to date, there exist no published genotype imputation methods specifically designed to use LC-NGS without additionally using genotyping microarrays or a haplotype reference panel. While methods such as Beagle (version 4)⁷ and findhap (version 4)¹² can be applied in this setting, they are tailored to work best with reference panels, and array data, which provide a framework of high-confidence genotypes.

Furthermore, the read-based nature of NGS provides useful phasing information on nearby variants from a single (paired) read, which is likely to be especially powerful in species with high SNP densities. While some approaches have started to use phase informative reads when phasing multiple heterozygous SNPs⁴, there are additional benefits to a fully read based imputation framework. First, in the absence of reference haplotypes, phasing with reads may help to initialize the phasing procedure. Second, at high SNP density, it is inaccurate to treat genotypes from the same read as being independent, which may help mitigate the influence of incorrectly mapped reads, e.g. near an indel, a cluster of false positive SNPs will contribute only once to the model, and not multiple times.

Here, we describe a genotype imputation algorithm STITCH (Sequencing To Imputation Through Constructing Haplotypes) suitable for population samples in any species sequenced at low coverage without requiring a haplotype reference panel. The only requirement is a high-quality reference assembly for read-mapping. We demonstrate STITCH’s utility on two datasets, from two species: first a set of 2,073 Crl:CFW(SW)-US_PO8 (CFW) mice sequenced to 0.15X, and second a set of 11,670 Han Chinese samples sequenced to 1.7X¹⁵.

Results

Overview of model

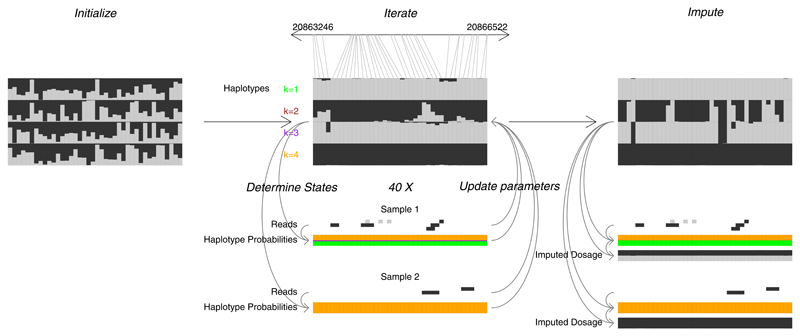
Our method, STITCH, models each chromosome in the population as a mosaic of K unknown founders or ancestral haplotypes. For fully outbred settings, these haplotypes can be thought of as informally capturing the set of distinct haplotypes within a region, so K may be large. We employ a hidden Markov model (HMM), whose parameters are sequentially updated using expectation maximization (EM), similar in spirit to the fastPHASE algorithm¹⁶. At each iteration of the EM, in the expectation step ancestral haplotype probabilities are generated for each sample, while in the maximization step ancestral haplotypes and other parameters are updated using sample haplotype membership. Both of these steps directly consider the underlying sequencing reads. An overview of the model used for imputation is presented in Figure 1.

Figure 1. Overview of STITCH.

After initializing various parameters (left), represented here by the ancestral haplotypes, 40 EM iterations are performed (middle). Each iteration involves i) determining hidden haplotype states (going down, left side) using current parameters and sample reads, and ii) parameter updates (going up, right side) using sample reads and haplotype probabilities (hidden states). Once the expectation-maximization iterations are completed, imputed genotypes are generated using the haplotype probabilities and ancestral haplotypes from the final iteration (right). This example uses real data from the CFW mice with K=4 founder haplotypes for approximately 3,000 base pairs on chromosome 19 containing 20 imputed SNPs. Each of the SNPs in the 4 reconstructed haplotypes are shown as a vertical bar split proportionally to the probability of emitting the reference (black) or alternate (grey). Sample reads are similarly coloured.

Computationally, the algorithm has a per-iteration time complexity linear in the number of samples and SNPs, and when run in its standard “diploid” mode, has quadratic time complexity in the number K of ancestral haplotypes. Because the ability to model large K is essential for STITCH to handle human and other large outbred populations, we developed an alternative mode, termed “pseudo-haploid”, with linear per-iteration time complexity in K. This is motivated by the observation that imputation in diploid individuals could be carried out with linear time complexity in K if the sequencing reads came with labels indicating their parental chromosomal origin (maternal, or paternal) – in other words, with phase information. In this setting, only reads mapping to the maternal chromosome would be required to impute mutations this chromosome carries, so the maternal and paternal chromosomes could be imputed separately. In the absence of such chromosome labels, in theory one could sample labels (e.g. by Gibbs sampling) for each read under our model. The relative contribution of a read to each chromosomes’ posterior likelihood would then depend on the probability it came from that chromosome. This sampling is in practice prohibitively computationally expensive. Therefore, in practice our pseudo-haploid makes several additional simplifying approximations (see the Supplementary Note for details, and discussion of other issues e.g. label-switching), to estimate, for every read, the probability it came from each chromosome. Given these probabilities, we can update the posterior ancestral haplotype probabilities for each chromosome separately, within the EM algorithm. This retains a common EM framework to both diploid and pseudo-haploid modes, thereby allowing the algorithm to switch between modes at any point. A full description of the diploid and pseudo-haploid modes is in the Methods and Supplementary Note, while guidance on parameter choice is in the Supplementary Note.

CFW outbred mice

We ran STITCH on low coverage sequence data (0.15X, paired end 100 base pair reads) from 2,073 outbred Crl:CFW(SW)-US_PO8 mice^17,18. These mice are thought to have descended from two outbred founders (i.e. K=4) about 100 generations ago. We imputed genotypes at 7.1 million single nucleotide polymorphic sites (SNPs) that either were polymorphic in the Mouse Genomes Project¹⁹ or passed VQSR²⁰ quality filtration¹⁷. Imputation accuracy was assessed in two ways – 44 mice genotyped on the Illumina MegaMUGA array (21,576 polymorphic SNPs) and four mice sequenced to 10X using an Illumina HiSeq. Correlations (r²) between genotypes and imputed dosages were calculated either per-site for the array or aggregated across all SNPs in a given frequency range for the high coverage sequencing data.

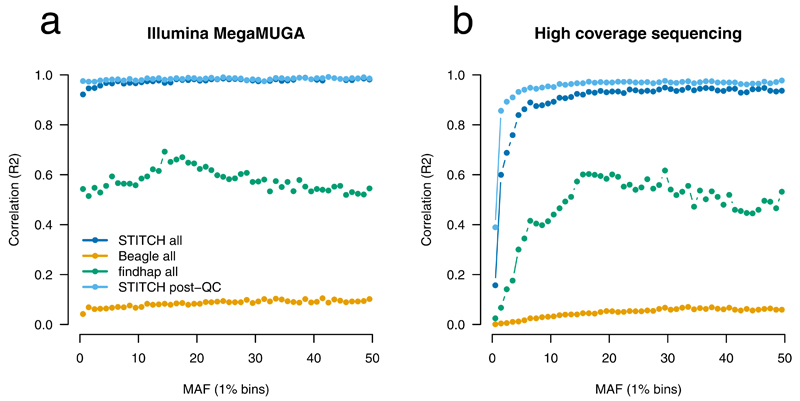
We compared results from STITCH (K=4, diploid mode) to Beagle and findhap run without a reference panel^7,12. Genotypes across all frequencies from STITCH correlated highly with the Illumina MegaMUGA array (Fig. 2a, r²=0.972) and 10X sequencing (Fig. 2b, r²=0.948) (Supplementary Table 1). Filtering with an imputation info score > 0.4 (Methods) and Hardy-Weinberg Equilibrium (HWE) p-value > 10⁻⁶ improved accuracy further, to r² of 0.981 and 0.974, with 5.72M SNPs (81%) retained. In general, imputation performance was good across all allele frequencies, except for a slight decrease at low frequency (<5%) SNPs (Fig. 2) that are expected to be challenging for low-coverage sequencing. Beagle under default conditions achieved r²’s of 0.080 and 0.219 compared to 10X sequencing and array without QC filtering, respectively, while findhap achieved 0.58 and 0.55 (Fig 2, Supplementary Table 1).

Figure 2. Performance of STITCH on CFW mice compared to external validation.

Validation dataset is the Illumina MegaMUGA array (a) and 10X Illumina sequencing (b). Results are shown for STITCH (K=4, diploid mode), Beagle (default) and findhap (maxlen=10000, minlen=100, steps=3, iters=4) genome-wide for n=2,073 mice featuring 7.07M SNPs before QC and 5.72M after QC. STITCH is run using K=4, diploid method, 40 iterations. Post-QC is SNPs with info>0.4 and HWE p-value > 1×10⁻⁶.

We performed additional analyses to explore parameter choices. We found that optimal results were achieved with K=4 for STITCH (Supplementary Table 2), as expected from the population’s ancestry. Results for Beagle did not differ appreciably when the number of iterations, window size, and model scale factor were changed, while the results reported above for findhap were the best observed when varying parameters of the method over a range of values suggested by the findhap documentation (Supplementary Table 2). Of the 3 methods, findhap was approximately 12 times faster than Beagle and 38 times faster than STITCH, although if parallelized by chromosome, imputation for all samples for any of the methods could be performed in less than 48 hours on a modest computational server. Ignoring phase information from reads in applying STITCH (i.e. treating each variant in a read as independent) reduced accuracy considerably, from r²=0.97 to 0.87 with the Illumina MegaMUGA array (Supplementary Table 2).

Converge study

To explore performance in human data, we ran STITCH on low coverage sequence data (1.7X, paired end 83 base pair reads) from 11,670 Han Chinese women¹⁵. Details of read mapping and variant calling are as detailed previously¹⁵. We used the first 10 Mbp of chromosome 20 to test the imputation algorithms and compared our predictions with genotypes from 72 individuals genotyped on the Illumina HumanOmniZhongHua-8 array and 9 individuals sequenced at 10X coverage¹⁵.

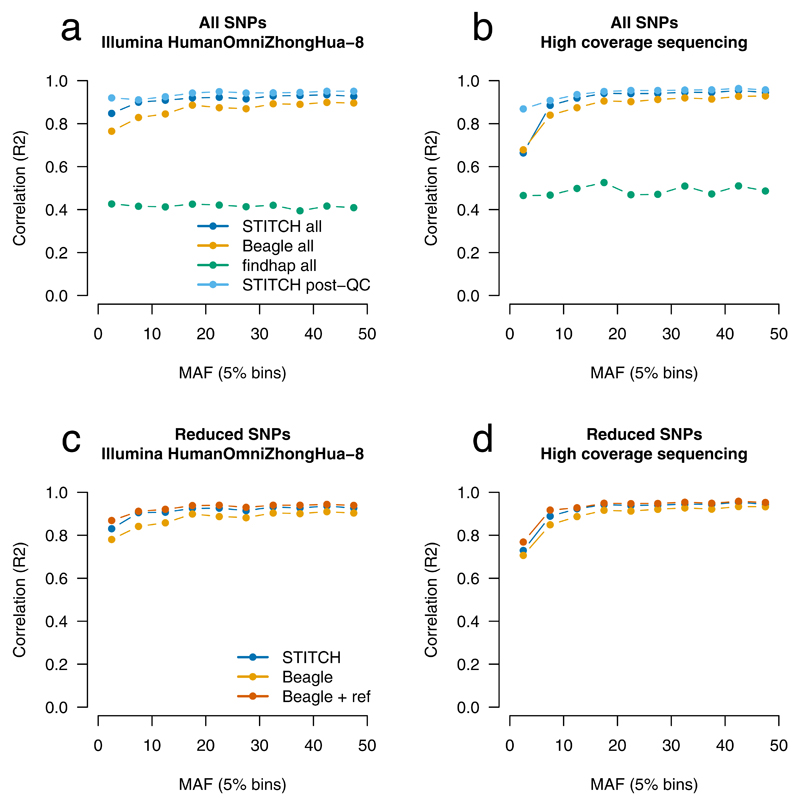
Following preliminary testing (Supplementary Table 3), we applied STITCH with K=40 “founder” haplotypes, with 40 rounds of updating to estimate parameters and perform imputation. The first 38 rounds were in the faster “pseudo-haploid” mode and the final 2 in the slower but more accurate “diploid” mode. STITCH achieved close correspondence to Illumina array results (Fig. 3A, r²=0.920, Supplementary Table 4) and 10X sequencing (Fig. 3B, r²=0.949), results that improved when SNPs were filtered (info > 0.4, HWE p-value > 10⁻⁶) (array r²=0.939, 10X r²=0.960). Accuracy declined for K < 40, and was marginally improved for K > 40. Running additional slower “diploid” mode iterations also improved accuracy only marginally, and fully diploid imputation became computationally prohibitive beyond K=30. Results were essentially unchanged when STITCH was run ignoring read information, reflecting the low SNP density in humans. Beagle without a reference panel achieved reduced r² values of 0.886 and 0.930 for sequencing and array without QC filtering, respectively, while the best parameter settings we identified for findhap achieved 0.414 and 0.550 (Fig 3, Supplementary Table 4).

Figure 3. Performance of STITCH on CONVERGE humans compared to external validation.

Validation dataset is the Illumina HumanOmniZhongHua-8 array (a, c) and 10X sequencing (b, d). Results are shown for STITCH (K=40, 38 pseudo-haploid iterations, 2 diploid iterations), Beagle (default (a,b), 3 iterations with reference panel (c,d)), and findhap (maxlen=50000, minlen=500, steps=3, iters=4) for the first 10 Mbp of chromosome 20 for n=11,670 Han Chinese samples, either for all SNPs (a,b), or for SNPs also present in the 1000 Genomes ASN reference panel (c,d). Post-QC is SNPs with info>0.4 and HWE p-value > 1×10⁻⁶.

We next compared STITCH to applying Beagle with additional reference panel information. In this setting, Beagle is modestly more accurate than STITCH, at the cost of run time (Fig. 3C, Fig. 3D, Supplementary Table 5, Supplementary Table 6). For example, Beagle achieved an r² of 0.943 versus 0.922 compared to the array for STITCH before SNP QC, although it took 7.3X as long.

We then repeated the imputation strategy for Beagle used in the original CONVERGE study¹⁵ of first imputing all sites without a reference panel, then imputing the subset of variants with a reference panel, and replacing SNPs in the former with the latter when they existed. We compared these results to those from STITCH, run without a reference panel on the entire set of SNPs. Results between these two strategies were essentially the same between STITCH and Beagle, (Supplementary Table 7) with STITCH achieving an r² of 0.972 (array) and Beagle 0.968 under the most stringent QC scenario, which retained 75% of common sites (>5% minor allele frequency). Results for STITCH were generated 5.3X faster than Beagle under this strategy.

Effect of sample size and coverage on imputation

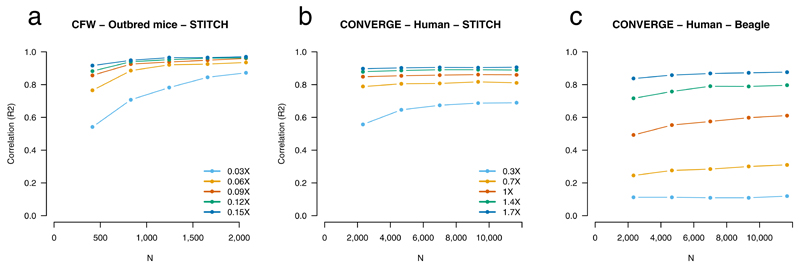
We next examined the consequences of altering sample size and sequence coverage (Fig. 4). For the CFW mice, for the full 0.15X coverage using STITCH, sample size above 500 has little impact on performance, while at down-sampled lower coverage, increasing sample size to 2,073 leads to substantially increased performance. Surprisingly, even at 0.06X for the full sample of 2,073 animals, results are only marginally poorer than using 0.15X. For the CONVERGE samples using STITCH, sample size has less of an influence across the range of sequencing coverages considered, although results did consistently improve with increasing sequencing depth. STITCH outperforms Beagle without a reference panel over the range of low coverages considered here (0.3-1.7X).

Figure 4. Effects of reduced sequence coverage.

Results are shown for CFW mice (a) and CONVERGE humans using STITCH (b) and Beagle run without a reference panel (c). Validation is using array data, with each value representing the average for common SNPs (allele frequency 5–95%), without correction for post-imputation QC. Downsampling of samples and reads, as shown in the legends, was performed at random, except that samples necessary for accuracy assessment were always retained. STITCH settings are the same as for the full CFW, CONVERGE datasets. Colours representing downsampling sequence depth are the same for STITCH and Beagle.

Effect of variant filtration on imputation performance

Methods of genotyping from next generation sequencing typically employ an initial step of variant filtration, to reject any newly discovered sites whose quality control metrics differ from those at known variant sites. One such method is the GATK Variant Quality Score Recalibrator²⁰. Since we developed STITCH to be applicable to populations in which a catalogue of variant sites was unavailable, we investigated whether prior variant filtration was necessary, or whether STITCH itself could be used to filter SNPs directly. We compared imputation at filtered variant sites in the CFW population, as defined using VQSR and known variable sites, to a two-step strategy where no prior variant catalogue is used. As a first step, all discovered sites in the sample are imputed without filtration. In the second step, only those variants that pass quality control (QC) filters from the first step are re-imputed. Results indicate this to be a viable strategy (Supplementary Table 8). For the one step strategy with variant filtration (the original study design), 152K SNPs on chromosome 19 were imputed, with 122K SNPs passing QC at an r² of 0.968. For the two-stage approach, 355K variants were imputed in the first round of imputation, with 136K passing QC. In the second round of imputation, these 136K were re-imputed, with 128K of them passing QC at an r² of 0.952. Overlap between the two approaches was 116K, with marginally better r² in the overlap from the two-step approach, with results specific to either set having lower r². These results indicate that prior knowledge of variable sites is not needed to impute accurately using STITCH.

Discussion

Inexpensive genotyping microarrays and imputation with large reference panels have made genome-wide association studies tractable in humans, but these resources are unavailable in many species, and are not ideal for human populations in parts of the world where appropriate reference populations have not yet been deeply sequenced. Our method alleviates this bottleneck, by imputing high quality genotypes directly from low coverage sequencing data. The method delivered highly accurate imputation at a depth of only 0.15X in the CFW mouse population. In a higher coverage situation of 1.7X in humans, STITCH performed similarly to a method using a reference panel, without requiring such a panel. This simplifies the imputation pipeline, and allows application in populations where no reference is available. We also introduce an approximation that achieves linear as opposed to quadratic time scaling with the number of founder haplotypes with very little loss of accuracy, making the method suitable for the analysis of very large and ancestrally complex populations.

Importantly, imputation results were better when using direct phase information, especially in the CFW mice, while the two-stage CFW imputation procedure showed that careful filtering of candidate SNPs based on prior variation is not essential. This can simplify the analysis, by alleviating the need for running separate SNP-filtering procedures, e.g. the VQSR²⁰.

The differences in imputation performance we observe in the mouse and human samples reflect their different genetic histories. Our method involves two alternating processes – reconstructing founder haplotypes, and determining in an individual sample which pair of founder haplotypes it is most similar to at each locus. Because the CFW mouse population was founded about 100 generations ago from just two progenitors, physical distances between haplotype switches are large, making it relatively easy to identify which of the small number of founder haplotypes an individual carries, even at low coverage. By contrast, in the CONVERGE Han Chinese population sample, haplotypic diversity is far greater, and consequently haplotypic switches occur much more frequently. This explains why imputation in humans is less accurate for a given level of sequence coverage and why increasing K – the modeled number of founder haplotypes – had little influence on performance in mice, but increased accuracy in humans. Because these datasets represent relatively extreme scenarios in terms of haplotypic diversity, we expect that STITCH will work well in intermediate settings, without haplotype reference panels.

Our method delivers the greatest accuracy improvements for populations with recent strong bottlenecks, such as those studied in agricultural or plant genomics^21,22,23. While poorer quality reference assemblies than those available for mice and humans will impact the performance of STITCH in other species, in future the decreasing cost of constructing high quality reference assemblies using single molecule long read technologies and optimal mapping techniques may mitigate this issue²⁴.

Although STITCH out-performed findhap for imputation using low-coverage sequencing data in the scenarios evaluated here, in cases where additional genotyping array data is also available, findhap may perform well. Specifically, if additional microarray data is available for a set of samples drawn from the same population as those sequenced at low coverage, findhap obtained comparable accuracy to our STITCH runs that used the read unaware option¹², and offers a speed advantage.

For human samples, at 1-1.5X sample coverage, STITCH accurately imputes all common variation, making it suitable for any population that lacks a reference panel, or one with an incomplete variant catalogue. We imagine that our method might be particularly appropriate for ethnic groups so far not subject to GWAS, population isolates, and for ancient humans, where low coverage sequencing is common.

Online methods

Overview and simulation under the model

Here we outline the model by describing how one would simulate (read) data from it, given knowledge of the underlying parameters. In the following section, we then more rigorously lay out how we infer parameters and perform inference of genotypes. We describe technical details of the EM procedure and parameter updating in the Supplementary Note.

We consider a population of individuals that can be approximated as having been founded G generations ago from K unknown ancestral founding haplotypes. Consider a haplotype from a single chromosomal region with T SNPs from a present day individual drawn from our model. A starting state (haplotype) k is chosen with probability π_k. Let d_t and p_t be the physical distance and average recombination rate between SNPs t and t+1, respectively. Therefore σ_t=d_tp_t is the recombination distance between SNPs t and t+1 in one generation, so in the G generations since founding the probability of recombination between these SNPs is 1−exp{−Gσ_t}.

Conditional on recombination locations, we sample an ancestral haplotype for each non-recombining interval. We allow genetic drift to play a sizeable role in the proportions of the ancestral haplotypes in each short genomic interval. As such, we model the probability of choosing ancestral haplotype k to the right (from SNP t+1), given a recombination between SNP t and SNP t+1 as α_t,k. This choice is made independently of the state at SNP t.

Finally, the reads are sampled conditional on the local haplotype background. Gene conversion, de novo mutation, read-mapping errors and other issues mean that not all chromosomes and reads descended from ancestral haplotype k will be an exact match to the ancestral sequence. We therefore model that for each read, for SNP t and ancestral haplotype k, that the alternate base will be drawn with probability θ_t,k, and the reference base with probability 1–θ_t,k. Inherent in this is the assumption that different reads are emitted from different samplings of θ_t,k; in reality there would be a simple sampling of θ_t,k for each haplotype, and reads sampled conditional on these real underlying bases. This assumption is necessary for computational reasons, and has reduced impact for low coverage sequencing data.

Consider sampling the r^th read, R_r. To do this, first choose read boundaries and determine u_r,j the set of indices of the SNPs in the read for j=1,…,J_r, where J_r is the number of SNPs in the r^th read R_r. Paired end reads can be easily accommodated in this way by allowing discontinuous u_r,j within read r. We make the assumption that recombinations are infrequent enough that reads have constant haplotype state over their length; as such, each read has a central SNP, call it c_r, and state membership over the read is drawn from the central SNP. Therefore, the underlying “real” bases for the sequencing read are sampled according to θ_t,k for t in u_r,j where k=k_t’ for t’=c_r. To sample “observed” bases, we sample b_r,j, the set of base qualities of the SNPs in the read – in practice these qualities are externally provided - and then sample observed bases s_r,j according to the real bases and the base qualities.

Expectation and hidden state determination

In the HMM, for the haploid model, let q_t be the hidden state at SNP t, i.e. q_t ∈ {1, …, K}. For the diploid model, let q_t=(k_t,1, k_t,2) be the hidden states at SNP t. Let λ={π,σ,α,θ} be the parameters of the model. The pseud-haploid model is described in the Supplementary Note.

Initial haploid state probabilities for the k=1,…,K different states are defined as π_k. Diploid initial state probabilities are taken by multiplying together haploid state probabilities.

For state transitions, with probability exp{−Gσ_t}, no recombination occurs between SNPs t and t+1, while with probability 1−exp{−Gσ_t}, a recombination occurs and a new state q_t+1 is chosen at SNP t according to α_t,k’ for k’=k_t+1. This gives the haploid transition matrix

$$P(q_{t+1}=k_{t+1}|q_t=k_t,\lambda )=\{\begin{array}{cc}{e}^{-G{\sigma }_t}+\left(1-e^{-G{\sigma }_t}\right){\alpha }_{t,k_{t+1}}& \text{if}{k}_{t+1}=k_t\\ \left(1-e^{-G{\sigma }_t}\right){\alpha }_{t,k_{t+1}}& \text{if}{k}_{t+1}\ne k_t\end{array}$$

Assuming independence between the two chromosomes then the diploid transition probability from state q_t=(k_t,1, k_t,2) at SNP t to q_t+1=(k_t+1,1, k_t+1,2) at SNP t+1 is:

$$\begin{array}{l}P\left(q_{t+1}=\left(k_{t+1,1},k_{t+1,2}\right)\text{|}{q}_t=\left(k_{t,1},k_{t,2}\right)\right)=\\ P\left(q_{t+1}=k_{t+1,1}\text{|}{q}_t=k_{t,1}\right)\times P\left(q_{t+1}=k_{t+1,2}\text{|}{q}_t=k_{t,2}\right)\end{array}$$

For the emission of reads, for read R_r, let c_r be the index of the most central SNP in that read, choosing at random when a read intersects exactly two SNPs. Reads that don’t intersect any SNPs are removed as they are uninformative. Consider the probability of an observation of a set of reads whose central SNP is t, or in other words O_t={R_r|c_r=t}. For SNP j in read R_r, s_r,j is the observed sequencingread (0 = reference, 1 = alternate), and b_r,j is the Phred scaled base quality, i.e. the log probability that the base is called erroneously, so let ε_r,j=10^(–b_r,j/10). Then, given the underlying (unobserved) genotype of this read at this SNP is g

$$P(s_{r,j}|g)=\{\begin{array}{cc}1-{\epsilon }_{r,j}& \text{if}{s}_{r,j}=g\\ \frac{1}{3}{\epsilon }_j& \text{if}{s}_{r,j}\ne g\end{array}$$

For convenience, set ${\varphi }_{r,j}^i=\underset{¯}{P(}{s}_{r,j}|g=i).$ We disregard sequenced bases which are not the reference or alternate base. Paired end reads are handled as the indices of the SNPs in the read u_r,j, are allowed to be discontinuous. Given there are J_r SNPs in read R_r, the probability of drawing read R_r from haplotype k is the product of the contribution of each SNP j=1,…,J_r in that read. For the j^th SNP, this probability is the probability the read contained the alternate base ${\varphi }_{r,j}^i$ times the probability θ_t,k for t=u_r,j that ancestral haplotype k emitted the alternate base, added to the equivalent probability for the reference base. Taken together, this yields

$$P(R_r|q_t=k,\lambda )={\displaystyle \prod _{j=1}^{J_r}({\theta }_{u_{r,j},k}{\varphi }_{r,j}^1+(1-{\theta }_{u_{r,j},k}){\varphi }_{r,j}^0))}.$$

Let O_t be the set of reads with central SNP t. In the haploid model, the probability of the observations at locus t is

$$P(O_t|q_t=k_t,\lambda )={\displaystyle \prod _{R_r\in O_t}P(R_r|q_t=k_t,\lambda )}$$

In the diploid model, each read is equally likely to come from either the maternal or paternal chromosome, giving

$$P(R_r|q_t=\left(k_{t,1},k_{t,2}\right),\lambda )=\frac{1}{2}P(R_r|q=k_{t,1},\lambda )+\frac{1}{2}P(R_r|q=k_{t,2},\lambda )$$

For every SNP t, the probability of the observations at that locus is

$$P(O_t|q_t=(k_{t,1},k_{t,2}),\lambda )={\displaystyle \prod _{R_r\in O_t}P(R_r|q_t=(k_{t,1},k_{t,2})},\lambda )$$

Finally, note that for SNPs which are not covered by reads, we set P(O_t|q_t=k_t,λ)=1 for all k_t.

CFW mouse sequencing

Full details on the Crl:CFW(SW)-US_PO8 (CFW) mice, including sample acquisition, age, sex and sequencing are provided elsewhere¹⁷. CFW mice are from a commercial outbred colony¹⁸. Sample pre-processing was done in accordance with best practice recommendations²⁰. Sequencing reads from low coverage samples were mapped to mm10 using bwa²⁵, remapped using Stampy²⁶, PCR duplicates were marked using Picard, files were merged using Picard, indel realignment was performed using the GATK²⁷, and base quality score recalibration was performed using the GATK. Variant calling was done using the GATK UnifiedGenotyper and filtered by the GATK VQSR, using as training data a set of variants from the Mouse Genomes Project¹⁹ and a sensitivity threshold of 80%. Sites in the training set which failed VQSR were nonetheless retained. In total, 7.07M SNPs were called on the autosomes and chromosome X. 4 mice were additionally sequenced at 10X. Genotypes for these mice were generated using the GATK UnifiedGenotyper using the genotype given alleles option. For comparisons with low coverage imputation, individual genotypes from the high coverage samples were set to missing if the read depth was less than 5 or more than 25, or if the genotype quality was less than 10.

CFW MegaMUGA Array Genotyping

48 of the 2,073 mice were sent to Neogen and genotyped using the Mega Mouse Universal Genotyping Array (MegaMUGA), an array built upon the Illumina Infinium platform with 77,808 SNPs (Neogen, Lincoln, Nebraska, USA). Genotype calling was performed by Neogen using GenCall.

After genotyping, recorded genders were compared to X and Y chromosome marker information, revealing no gender mismatches on the arrays. Samples were further compared to imputation and array QC metrics (call rate and 10% GC score); this revealed 4 of 48 samples had poorly performing array metrics. These 4 samples were subsequently removed from further analysis.

For the 77,808 SNPs for which we had genotypes, 144 were not mappable from mm9 to mm10 using liftOver, and out of the remaining sites, 29,694 intersected between imputation and MegaMUGA. Out of those, we removed sequentially for the following reasons: 17 for allele disagreements between sequencing and the array; 3,819 monomorphic array sites; 3,160 SNPs with an imputed SNP within 25 bp of the array target SNP (as off-target variation can affect microarray genotyping)¹³ ; 56 sites with an array Hardy-Weinberg Equilibrium p-value of less than 1 × 10⁻¹⁰. Subsequent comparisons between CFW imputed dosages and array genotypes were made for the remaining 21,576 sites.

Converge

Full details for the processing of the CONVERGE data, including low coverage, high coverage, Illumina array data, ethics committees and informed consent have been published elsewhere¹⁵. In brief, 11,670 low coverage (1.7X) Han Chinese samples were called using the GATK to yield a set of 20.5M variants. 9 samples were sequenced to 10X and used independently to call variants (5.9M). For our analysis, high coverage sample genotypes with a read depth of lower than 5, read depth greater than 25, or genotype quality of less than 10 were masked out. 72 samples were genotyped using the Illumina HumanOmniZhongHua-8 (v1.0B) BeadChip. Of the 21057 sites present on chromosome 20 on the array and used for imputation, we removed 292 sites with >5% missingness, 7642 sites with probes within 25bp of another site in the imputed dataset, and 0 sites with an array Hardy-Weinberg Equilibrium p-value of less than1×10⁻¹⁰. This left 13,123 sites used for assessing accuracy.

Beagle

For both the CFW and CONVERGE samples, Beagle version 4.0 (beagle.r1399.jar) was run using default parameters, unless otherwise noted⁷. Genotype likelihoods from VCF files were used as inputs. For the CONVERGE study, the 1000 Genomes Asian reference panel was used.

findhap

For both the CFW and CONVERGE samples, findhap version 4 was run with default parameters, unless otherwise noted¹². For both CFW and CONVERGE, allele depth information from VCF files was used to construct input files for findhap. Since pedigree information was not available for the CFW or CONVERGE study, input pedigree files were made with missing values for maternal and paternal inheritance. Results for CFW used maxhap=10000 and CONVERGE used maxhap=25000. Both methods used default options of overlap=10, lowdense=0.07, and errrate=0.01.

Correlation between dosages and validation

For the arrays, correlations (r²) are generated per-SNP between array genotypes and imputed dosages. When reported by frequency, values are averaged over all SNPs in that frequency bin; otherwise averaging is over all SNPs. For sequencing, correlations are between genotypes and imputed dosages across all samples. When reported by frequency, values are generated using only SNPs in that frequency bin, otherwise averaging is over all SNPs. When aggregating genotypes across sites, to remove an upward bias in correlations due to genotype encoding, dosages were recoded from the default of 0 as the reference allele and 1 the alternate allele to 0 for homozygous major allele and 1 homozygous for the minor allele.

Software

STITCH v1.0.0 was used for all analyses in this paper. STITCH is available from http://www.stats.ox.ac.uk/~myers/