Tradeoffs between dense and replicate sampling strategies for high throughput time series experiments

Abstract

An important experimental design question for high throughout time series studies is the number of replicates required for accurate reconstruction of the profiles. Due to budget and sample availability constraints, more replicates imply fewer time points and vice versa. We analyze the performance of dense and replicate sampling by developing a theoretical framework that focuses on a restricted yet expressive set of possible curves over a wide range of noise levels and by analyzing real expression data. For both the theoretical analysis and experimental data we observe that under reasonable noise levels, autocorrelations in the time series data allow dense sampling to better determine the correct levels of non-sampled points when compared to replicate sampling. A Java implementation of our framework can be used to determine the best replicate strategy given the expected noise. These results provide theoretical support to the large number of high throughput time series experiments that do not use replicates.

eTOC Blurb

Our study indicates that when facing budget or sample availability constraints researchers performing time series experiments should sample more time points rather than perform technical repeat experiments.

Introduction

High-throughput time-series experiments have been used to study several biological systems and processes, to measure readouts such as mRNA levels using RNA-Seq (Trapnell et al., 2012) and protein-DNA interactions using ChIP-Seq(Chang et al., 2013). Such studies are often designed with a defined start and end point and a selected number of time points to be sampled in between.

The more points that can be profiled between the start and end points, the more likely it is that the reconstructed trajectory for the data type being studied is accurate. However, in practice the number of time points that are used in a study is usually very small (Zinman et al., 2013). The main limiting factor for most experiments is budget. While technology has greatly improved over the last two decades, high-throughput sequencing studies still cost hundreds of dollars for a single experiment. This is a major issue for time series studies, especially those that need to profile multiple types of biological data (for example, mRNA, miRNAs and methylation levels) at each selected point. Another issue that can limit the number of experiments performed (and therefore the total number of time points that can be used) is biological sample availability. Thus, when designing such experiments, researchers often need to balance the overall goals of reconstructing the most accurate temporal representation of the data types being studied and the need to limit the number of experiments due to scarcity of resources.

Given these constraints, researchers designing high-throughput time-series studies must carefully consider the need for replicate experiments. On one hand, replicates are a hallmark of biological experiments (Cumming, Fidler, and Vaux, 2007), providing valuable information about measurement noise and reliability of the measured values. On the other hand, replicates further reduce the number of time points that can be profiled, leading to the possibility of missing key events between sampled points. When resource scarcity is an issue, even one replicate for each time point cuts the total number of points that can be profiled by half, and this can have a large impact on our ability to accurately reconstruct the trajectories of the biological data being profiled. Indeed, when examining the time-series datasets deposited in GEO, we observe that in many cases replicates have not been used in these studies (Zinman et al., 2013).

We aim to analyze the trade-offs between dense sampling (profiling more time points using one experiment per point) and replicate sampling (profiling fewer points, with more than one experiment for each point) in high throughput biological time series studies, and determine which strategy works best and under what circumstances.

The relative merit of replicates and their impact has been investigated previously for high throughput biological experiments, but this has been limited to static datasets (where no relationship is assumed between consecutive experiments that are not replicates), and not time series data. For example, (Mongan et al., 2008) analyzed the variation in a large number of replicate experiments of the same samples collected on different dates and determined that overall correlations between these experiments were high. Others have used replicate experiments for follow up analysis, for example, to identify differentially expressed (DE) genes (Tu, Stolovitzky, and Klein, 2002), and to improve the performance of clustering methods (Tjaden, 2006). However, while most methods for identifying differentially expressed genes in static experiments rely on replicates, most methods for the identification of differentially expressed genes in time-series studies do not assume replicates and instead rely on the overall trajectory of the genes (Kim J., Ogden, and Kim H., 2013; Bar-Joseph et al., 2003b; Ma, Zhong, and Liu, 2009).

Outside the realm of high-throughput biological datasets, the issue of replicate experiments in time series studies has been the focus of several statistical papers. For example, for epidemiological studies, tradeoffs were established between frequent measurements of a small number of patients and more infrequent measurements of a larger number of patients (Schmidt et al., 2010). Other examples include the analysis of sampling vs. replicates in speech processing (Listgarten et al., 2004) and early, theoretical work on reconstructing curves using parametric methods (Astrom, 1969). However, the major difference between high-throughput biological datasets and most prior work that studied these tradeoffs is the fact that in the biological experiments all genes must be sampled at the same time at each experiment. In other words, rather than trying to infer a single curve or profile for each experiment, we are actually inferring tens of thousands of curves simultaneously. Thus, methods for the analysis of such data should consider a much larger set of possible outcomes and examine the impact of the two possible strategies (using either dense or replicate sampling) in the context of such large number of potential curves.

To compare dense versus replicate sampling in the context of the complexity of high-throughput biological data, we establish a framework for both theoretical analysis and analysis of experimental (i.e. real) gene expression data. Several methods have been suggested and used for functional representation of high-throughput time series data such as gene expression profiles. These representations include splines (Bar-Joseph et al., 2003a), sinusoidal functions (Whitfield et al., 2002) Gaussian processes (Kalaitzis and Lawrence, 2011) and impulse models (Chechik et al, 2008) among others. Here we focus on piecewise linear curves (lines connecting the values at the measured points) which are by far the most popular for representing such profiles. While expression and other profiles are usually not piecewise linear, these curves canrepresent important types of biological responses (for example, gradual or single activation, cyclic behavior, increase and then return to baseline, etc.). Several popular analysis methods for time series expression data also assume such piecewise linear model(Ernst and Bar-Joseph, 2006; Ernst, Nau and Bar-Joseph, 2005). Thus, we believe that a theoretical analysis focused on piecewise linear functions provides a good balance between a realistic model for time series gene expression and our ability to rigorously compare different sampling strategies (which is easier to perform with these simple functions).

Overall, our results support the commonly used (though so far not justified) practice of reducing or eliminating replicate experiments in time-series high-throughput studies. For both the theoretical analysis when using reasonable noise levels and the biological data we analyzed, we see that profiles reconstructed using dense sampling are more accurate than those reconstructed based on dense sampling (i.e. they can better predict the levels of genes at intermediate time points that were not experimentally profiled). This indicates that autocorrelation can indeed be a useful feature when trying to reduce the impact of noise on the reconstructed curves. Our results can be used to determine the best strategy for using replicate experiments given the noise expected in the data.

Results

We perform both theoretical analysis and analysis of real data to test the impact of replicates on the ability to accurately characterize high throughput time series biological data. The main goal of our theoretical analysis (Experimental Procedures) is to develop a framework for computing the expected difference in the resulting error (defined as the difference between the true underlying curves and the estimated curves) between the two possible strategies we are considering. Unlike the analysis of real data, which is obviously restricted to a few sample datasets, the theoretical analysis methods we develop allows us to compute such errors for a very large, and generally representative, set of possible curves. While we constrain our analysis to piecewise linear profiles, these often represent the outcomes that researchers care about as mentioned above. Indeed, clustering methods based on such piecewise linear representation for time series data have been used in the past (Ernst and Bar-Joseph, 2006) indicating that they can represent an important subset of the possible trajectories.

Our comparisons focus on two possible strategies for sampling in time series data: Dense sampling, which performs a single expression experiment at each time point, and replicate sampling, which performs 2 or more (depending on the setting) such experiments at each of its time points. Since we assume a fixed budget (which means that the number of experiments both methods perform is the same), dense sampling is able to query more time points (using uniform sampling), but would have to pay a price in terms of accuracy at each point since no replicates are available.

To analyze the impact of replicates on the ability to accurately reconstruct the gene expression signal, we use a probabilistic model that computes the likelihood of reconstructing a specific profile under each of the strategies given a specific error level (Experimental Procedures). We use this to compare and evaluate the performance of the two strategies. This is done by computing the expected reconstruction error - difference between the true profile, which is based on sampled and non-sampled points, and the reconstructed profile, which is only based on the sampled points for the two strategies. The lower the error, the better the sampled points represent the full profile, which is the goal of the experiment. We repeat this process for different noise levels and different numbers of overall experiments.

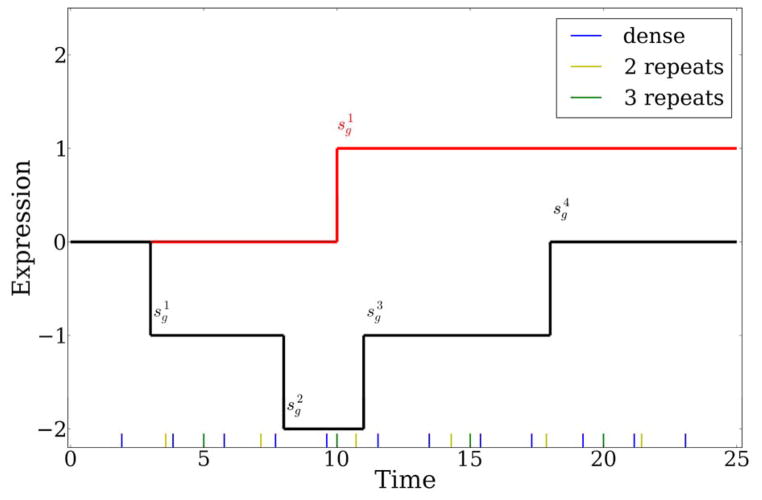
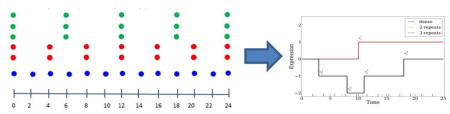
For the theoretical analysis, we assume that the time series is studied between [0, T_max] and that there are k transition points in each expression profile (Figure 1). The value at each transition point can change (up or down) by 1, where 1 represents a unit change in our model (for example, log fold change of 2). Note that while this assumption restricts the set of potential expression profiles, the possible set of resulting curves is still rich enough to define an important subset of expression trajectories. The transition points themselves are not restricted in terms of their temporal occurrence and so do not need to coincide with the measured time points. More importantly, by varying k, we can model (using a piecewise linear model) several realistic trajectories. Additionally, in many cases researchers are primarily interested in the transition points themselves (for example, the first time a gene becomes differentially expressed) and so such a model captures an important aspect of the goals of time series gene expression analysis.

Figure 1.

Examples of piecewise linear functions analyzed in this work. A step function (red) and a more complex transition function (black). Transition times are denoted by $S_i^g$. Blue, yellow, and green lines at the bottom represent the sampled points by Dense, Repeat₂ and Repeat₃ strategies respectively.

To test the difference between using a dense sampling (more time points profiled) vs. replicate sampling (fewer points, but the same number of experiments), we first used the theoretical framework discussed above to evaluate the expected performance of the two strategies then compared them using real gene expression profiles. For the theoretical analysis, we assumed that gene expression was measured between 0 and 50h (similar to real experiments, for example (Whitfield et al., 2002)). We use the term “Repeat_v” throughout the rest of the paper to represent a setting where we are using υ replicates for each time point and “Dense” to represent a setting where we are not using any replicates. In such settings, when we have a budget for x experiments, Dense performs x RNA-Seq (or microarray) experiments uniformly between 0 and 50h, whereas Repeat₂ and Repeat₃ perform 2 and 3 experiments at $\frac{x}{2}$ and $\frac{x}{3}$ uniformly sampled points, respectively. As mentioned above, we assume that noise in each measurement for each gene is Gaussian (mean 0, and standard deviation σ ranging between 0.1 and 1.5).

Detecting transition time for step functions

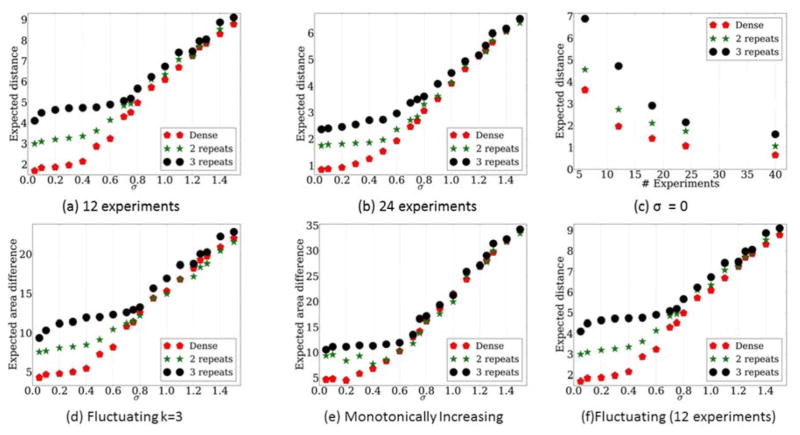
We first evaluated the performance for step functions. These functions can represent genes that start as inactive (0) and become active after a certain time point (1), where the goal is to determine the transition time (Experimental Procedures). For each of the noise levels we consider, we randomly selected 100 transition points and evaluated the performance of the two strategies for the resulting curves. For such profiles, Dense performs better for noise levels lower than 0.9 for both 12 and 24 experiments (Figure 2A,B). Note that because we assume that the difference between an active and non-active gene is 1, a standard deviation close to 1 is unlikely and so values less than 0.9 are more likely in practice. Indeed, for most gene expression experiments σ is much lower than 1 when analyzing log scale values (for example, close to 0.3 for (Blake et al., 2003)). For such values, Dense leads to lower reconstruction errors and is clearly much better than Repeat₂ and Repeat₃. We have also tested a larger number of experiments fixing the noise standard deviation at 0.3. As can be seen in Figure 2c, when the number of experiments increases beyond 24, the improvement seen for the dense strategy decreases. However, even for a very large number of experiments (40 over 50 hours with a single transition) Dense still outperforms Repeat₂ and Repeat₃ when using σ = 0.3.

Figure 2.

Comparison of expected error for both Dense and Repeat strategies. Fig. 2a–c: Comparison of the strategies for different number of experiments and noise levels. a) 12 experiments, b) 24 experiments, c) Different number of experiments for a fixed noise σ = 0.3. Fig. 2d–f: Comparison of sampling strategies for different noise levels over 12 experiments in terms of expected area difference. d) Fluctuating profile with 3 transitions, e) Monotonically increasing profile. f) Comparison of Dense and Repeat₂ and Repeat₃ strategies for recovering a profile for which the directions are unknown. The real data is generated from a fluctuating profile with 3 transitions, though these are not known in advance and so the likelihood function used to select the transition points and directions for both Dense and Repeat does not use this information. Results presented for different noise levels when performing 12 experiments.

Analysis of more complicated transition functions

Following the analysis of the step function scenario we analyzed more complex transition profiles including monotonically increasing and non-monotonic transitions (Figures 2d,2e) with 12 experiments. Specifically, we looked at a monotonically increasing function 0,1,2,3 representing a gene that is continuously up-regulated during the course of the study (common in response experiments, for example immune response (Teschendorff et al., 2007)) and at a 0, 1, 0, 1 representing a fluctuating gene (for example, for cases of cyclic activity such as cell cycle and circadian rhythms (Rund et al., 2011)). For these functions, we use the theoretical analysis above to compute the expected area difference between the true profile and the estimated profile for each of the methods (since the direction of the transitions are known, the differences are a function of inaccurate estimation of the transition time points). Dense outperforms Repeat₂ and Repeat₃ when the noise is low to moderate (Figure 2d,2e). However, even for high noise values we see that Repeat₂ and Repeat₃ do not improve upon Dense indicating that even when the noise levels cannot be completely determined, using Dense is at least going to lead to comparable results to the Repeat₂ and Repeat₃, and in most cases would outperform them.

For the most general type of our theoretical framework Dense outperforms Repeat₂ and Repeat₃ (Figure 2F) in noise levels up to 0.6 (which as mentioned above is much higher than often observed in practice). For this analysis, we fixed the number of transitions (in this case to 3) but do not assume that the directions are known. Thus, the analysis considers all possible 2³ transition profiles (Experimental Procedures). Results are more mixed for higher noise levels, though there does not seem be a noise level in which Repeat₂ and Repeat₃ strongly dominates Dense.

Analysis of real biological data

The analysis above used our theoretical framework to compare the Dense and Repeat strategies for various profiles and noise levels. While such analysis is informative since it applies to any measurements resulting from the setting being considered, it is also important to analyze real biological expression data to compare the two strategies. For this, we used a gene expression dataset that profiled 22769 genes in Anopheles Gambiae for 48 hours. The study had two settings, both with 13 experiments over the duration being studied: 12 hours light/12 hours dark (LD) switching and constant dark (DD). Experiments were performed every 4 hours with 2 replicates for each time point used. As usual, we computed the values in each time point as log fold changes to the values at time point 0. For both strategies, we performed the following analysis: Given a specific number of experiments (upper bounded by 13, the total number of points sampled), we sample time points uniformly between 12 and 60h for each strategy. We use the value of the closest time point if a time point is not measured in the original dataset. For Dense, we randomly select one of the replicates at each of the time points that are used, whereas both measurements are used for Repeat₂ (though the total number of time points used by Repeat₂ is half that of the ones used by Dense). Next, we fit interpolating splines for each gene and estimate the mean squared error (MSE) by comparing to median values obtained when using all sampled points. Note that in all experiments at least half the experiments are not used (even when sampling 13 points for Dense, it only uses 1 experiment for each time point) and so the test data is not fully used in the reconstruction even when using the largest number of points. We repeat this procedure 10000 times for Dense and Repeat₂ and report the mean error.

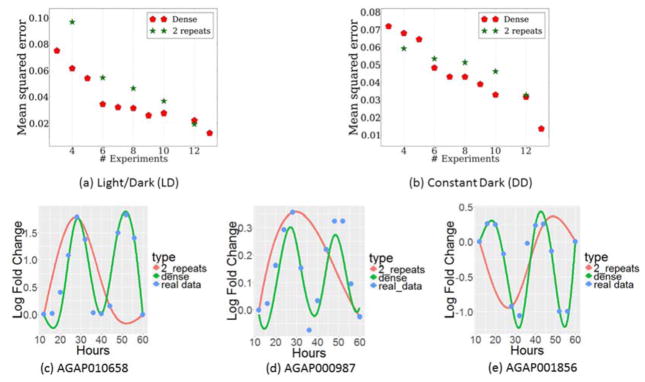
We find that Dense is better than Repeat₂ improving our ability to determine the correct expression levels at non sampled points in 9 of the 10 comparisons in which both strategies use the same number of points. Moreover, in some cases, Repeat₂ leads to errors that are 50% higher, on average, when compared to dense, for example when the budget only allows for 6–8 experiments in the LD setting (Figures 3a–3b). The performance difference between them decreases when the number of experiments increases. However, Dense is generally as good for all settings.

Figure 3.

Comparison of Dense and Repeat strategies for genes in Anopheles Gambiae. Fig. 3a–b: Comparison of strategies over all genes of Anopheles Gambiae by increasing number of experiments over a) LD data b) DD data. Fig. 3c–e: Comparison of the two strategies on individual genes by 8 experiments c) AGAP010658, d) AGAP000987, e) AGAP001856. The values used for the dense interpolation came from a single data point at times of 12,20,28,32,40,48,56, and 60 hours. The values used for the interpolation of Repeat₃ came from both data points at time of 12,28,44, and 60 hours.

The measured expression levels and the reconstructed profiles using both Dense and Repeat₂for three circadian genes are presented in Figure 3C–3E5. In this figure we allow both Dense and Repeat₂ to use 8 experiments. This figure helps explain the differences between the performance of the two methods While Dense correctly reconstructs the circadian profile of these genes, Repeat₂ is unable to correctly reconstruct these profiles since it only measures 4 of the time points. For example, for AGAP010658 and AGAP000987 which were identified in this study as cycling with LD (the key goal of this experiment), Dense indeed recovers the correct 2 cycles profile, while Repeat₂ completely misses the correct profile.

Comparisons using a subset of the genes

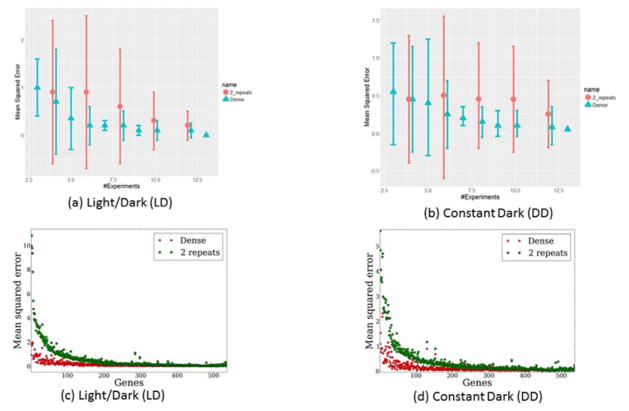
The above analysis examined performance over all genes profiled in the experiment. However, in most case researchers tend to focus on a much smaller subset of genes (often the most varying) and any strategy for designing experiments should be able to recover an accurate representation for these genes. To study the difference between the Dense and Repeat strategies for these key genes, we used 536 rhythmic genes identified as rhythmic using a cosine wave-fitting algorithm for both LD and DD conditions (Rund et al., 2011). We use a spline fitting procedure as discussed above. Dense performs better than Repeat₂ for this important subset, both quantitatively, leading to overall lower errors for non-sampled points, and qualitatively, enabling us to correctly identify cycling genes (Figure 4A,B).

Fig. 4.

Comparison of Dense and Repeat strategies for circadian genes. Fig. 4a–b: Comparison of strategies over all genes exhibiting circadian and diel rhythms by increasing number of microarrays over a) LD data, b) DD data. Std. dev. of the error is estimated over the considered genes. Fig. c–d: Comparison of strategies over all genes exhibiting circadian and diel rhythms where individual genes sorted by decreasing MSE difference between Dense and Repeat₂ when using 8 experiments over LD and DD data respectively. MSE is computed between spline interpolations for each strategy and left out data points.

Analysis of the gene specific performance differences for this smaller set of genes (as opposed to the average differences presented above) suggests that Dense performs better than Repeat₂for 468 (87%) and 523 (98%) out of the 536 rhythmic genes in the LD and DD datasets, respectively (Figure 4C,D). Even when increasing the number of experiments to 10, Dense still performs significantly better than Repeat₂ (p < 0.01, Wilcoxon rank-sum test). See also Figure S1, where we show similar results when using a piecewise linear fit rather than a spline fit for this data.

Discussion

While replicate experiments have been widely used in high-throughput analysis studies, they have been utilized to a much lesser extent when using the same technology to study time series data (Zinman et al., 2013). While it is hard to determine the exact causes for this practice, it is very likely that budget and sample quantity constraints have played a role. However, no systematic study examined the tradeoffs between more time points and more replicates for such studies.

Here we have tried to address this issue using a combined theoretical and analysis framework. Our theoretical models consider the impact of various noise levels on the ability of each of these strategies to correctly infer the underlying profile As we show, by analyzing a restricted yet expressive set of piecewise linear curves, for reasonable noise levels, dense sampling leads to better results than a strategy that profiles a smaller number of time points but a larger number of replicates per sample. We obtain similar results when analyzing real biological gene expression data for both the full set of genes being studied and a subset of the key genes identified in a specific study.

While we conclude that a dense sampling is beneficial when the number of experiments is limited by external constraints, we do not claim that replicates do not provide additional and valuable information.

If resource constraints do not exist, or if it is possible to increase the number of experiments performed, replicates are an important and useful strategy for identifying differentially expressed genes, for clustering and modeling their behavior, and for understanding measurement noise and reliability. However, while replicates can be very useful in dealing with measurement noise, if we assume that the data being studied can indeed be represented by a (smooth) continuous curve, which is often the case (Bar-Joseph et al., 2003b), then the autocorrelation between successive points can also provide information about the noise in the data (we do not expect large variations between these points). In such cases, more time points, even at the expense of fewer or no replicates, may prove to be a better strategy for reconstructing the dynamics of the type of data being studied.

While this study is mainly focused on developing a theoretical framework for considering the trade-offs between dense and replicate sampling of gene expression data, and on re-analysis of existing experimental data, the methods we developed can also be used by experimentalists when designing other high throughput time course experiments. Specifically, the Java program (provided as Data S1 and on the supporting website http://www.sb.cs.cmu.edu/repeats) allows researchers to input the total duration of their experiment, the total number of experiments that they can perform (given budget / sample constraints) and the expected noise (which, if unknown, can be determined by performing very few experiments for time point 0 (Bar-Joseph et al., 2003a)). Given these inputs we use the piecewise linear simulation framework to evaluate the expected curve reconstruction error when using dense and replicate sampling and the results are returned to the user.

Experimental Procedures

Likelihood-based Framework

We use a probabilistic model for our theoretical analysis. Such a model allows us to capture the uncertainty in the measurement replicates and the noise associated with high throughput biological data. We assume that the time series is studied between [0, T_max] and that there are k transition points in each expression profile (Figure 1). The value at each transition point can change (up or down) by 1, where 1 represents a unit change in our model (for example, log fold change of 2). The transition points are not restricted in terms of their temporal occurrence and so do not need to coincide with the measured time points. By varying k, we can model several realistic trajectories.

More formally, we use “Dense” to denote a dense sampling strategy and “Repeat_v” to denote a sampling strategy that uses υ replicates in each time point. Denote the observed data using Dense for a gene g by $D_g^d$ and for Repeat by $D_g^r$. Let T^d and T^r be the set of measured time points for each method respectively, and n_r be the number of experiments used for each time point in Repeat_nr. For a given budget B, we assume | T^d |= B and $\mid T^r\mid =\lceil \frac{B}{n_r}\rceil$. We assume that the true expression profile for a gene g is defined by transition times $S_g=\{s_g^1,\dots ,s_g^k\}$ and corresponding transition directions $C_g=\{c_g^1,\dots ,c_g^k\}$ where each $c_g^i\in \{-1,1\}$. The goal of an experiment (using either of the sampling methods) is to detect, as accurately as possible, these transition times and directions. Let $S_r=\{s_r^1,\dots ,s_r^k\}$ and $C_r=\{c_r^1,\dots ,c_r^k\}$ denote the points and directions estimated by Repeat_v. Similarly, let S_d and C_d denote the points and the directions estimated by Dense. We assume S_g, S_r, S_d to be sorted in increasing order, and define f_mis (S_g,C_g, S_r, C_r) to be the difference between the area of the true gene profile curve defined by S_g and C_g, and area of the estimated curve defined by S_r, C_r. We compare both strategies by f_mis.

General Likelihood Function

Given the experiment values and k (the required number of transitions), we next need to select the set of transition points and directions for each method S_d, C_d and S_r, C_r. For this, we use the maximum likelihood (ML) criterion. Let A^r be the set of all k -point subsets of T^r that are candidates for S_g, and Q = {1, −1}^k be the set of all possible transition directions for these points that are candidates for C_g. Each k-point subset $T^{\prime }=\{T_i^{\prime },i\in 1,\dots ,k\}\in A^r$ and a transition function C = {c_i,i∈1,…, k}∈Q partitions [0,T_max] into k+1 intervals $I^{\prime }=\{I_i^{\prime }=[T_i^{\prime },T_{i+1}^{\prime }),i\in 0,\dots ,k\}$ with corresponding values {v_i,i∈0, …, k} where $T_0^{\prime }=0,T_{k+1}^{\prime }=T_{max}$, and v_i+1 = v_i+c_i+1. Let $\mathrm{L}(T^{\prime },C\mid D_g^r)$ denote the probability of the observed values for Repeat_v conditioned on transition times T′ and directions C. Assuming independent Gaussian measurement noise, this likelihood can be formulated by:

$$\begin{array}{c}\mathrm{L}(T^{\prime },C\mid D_g^r)=p(D_g^r\mid T^{\prime },C)=\prod _{i=0}^k\prod _{t_a\le t_j^r<t_b,I_i^{\prime }=[t_a,t_b)}\prod _{z=1}^{n_r}p(d_{j:z}^r\mid v_i,\sigma )\\ =\prod _{i=0}^k\prod _{t_a\le t_j^r<t_b,I_i^{\prime }=[t_a,t_b)}\prod _{z=1}^{n_r}\frac{1}{\sigma \sqrt{2\pi }}{exp}^{-\frac{{(d_{j:z}^r-v_i)}^2}{2{\sigma }^2}}\end{array}$$

where $d_{j:z}^r\in D_g^r$ is the z’th replicate of j’th measured value, $t_j^r\in T^r$ is the set of time points for Repeat_nr, and $p(d_{j:z}^r\mid v_i,\sigma )$ is Gaussian probability of observing $d_{j:z}^r$ given mean v_i and standard deviation σ. To find the ML estimate for S_r and C_r, we set S_r, $C_r={\mathit{argmax}}_{T^{\prime }\in A^r,\overline{C}\in Q}p(D_g^r\mid T^{\prime },\overline{C})$. A similar analysis can be carried out to determine the ML estimate for S_d and C_d where we condition on observed values for each point in T^d and n_r = 1.

Analyzing a restricted set of profiles

While our goal is to evaluate the general likelihood function presented above, because of the combinatorial nature of the computation (over all selections of points and directions), it is impossible to compare the methods for completely unrestricted cases. We thus continue by discussing restriction on the general framework that on the one hand allow us to compute a closed form solution to the expected differences between the two methods in a reasonable (polynomial) time while at the same time capturing a relevant and biologically important subset of the potential expression profiles.

We start by considering step functions. Such functions allow only a single transition (for example, a gene that is only up or down regulated at some point during the experiment and stays in that level until the end). While step functions are clearly highly restricted, there are many cases where genes with a step function like behavior are of interest, for example when looking for differentially expressed genes in a response experiment. For such genes, the key question is to determine the timing of the step event (time of activation). We next discuss analysis that allows functions with a larger number of possible transitions assuming that we know the direction of each of these transitions. Finally we consider the most general case where both the location and direction of transitions are unknown.

For a step function, we only need to determine a single time point which leads to $s_r=s_r^1,s_d=s_d^1,s_g=s_g^1,c_r=c_r^1,c_d=c_d^1,c_g=c_g^1$. The likelihood function (1) becomes:

$$\mathrm{L}(s_r,c_r\mid D_g^r)=\prod _{t_j<s_r}\prod _{z=1}^{n_r}p(d_{i:z}^r\mid 0)\prod _{t_j\ge s_r}\prod _{z=1}^{n_r}p(d_{i:z}^r\mid c_r)$$ (2)

where c_r is the direction change (here an activation so c_r = 1). For a step function that transitions from 0 to 1 at time s_g, expected error is:

$$E(f_{\text{mis}})=\sum _{r_i^r\in T^r}p(s_r=t_i^r\mid c_r=1,s_g,c_g,{\sigma }^2)\underset{f_{\text{mis}}(s_g,c_g,t_i^r,c_r)}{\underbrace{((T_{max}-t_i^r)\mid c_g-c_r\mid +(t_i^r-s_g)\mid c_r\mid )}}$$ (3)

where $p(s_r=t_i^r\mid c_r,s_g,c_g,{\sigma }^2)$ is the probability of selecting the i’th time point that transitions into the value c_r = 1 conditioned on the actual step time, actual transition direction, and the noise in the measured data.

In order to select t_i as the step point, we need the likelihood defined by it and c_r = 1 to be higher than any other point and c_r. From here on, we drop the superscript r when referring to the sampled time points and values, and use the shorthand notation L(t_i,1) to denote $\mathrm{L}(t_i^r,1\mid D^r)$. Since transition direction is known:

$$p(s_r=t_i^r\mid c_r=1,s_g,c_g,{\sigma }^2)=p(\mathrm{L}(t_i,1)>\mathrm{L}(t_j,1),\forall j\ne i)$$ (4)

where L(t_i,1) is defined in Eq. 2. Computing p(L(t_i,1) > L(t_j,1), ∀j≠i) involves nested integrals over pairwise probabilities. Let S_i = {t₁,…, t_i−1} and M_i = {t_i+1, …,t_T} be the set of sorted time points that are smaller or larger than t_i respectively, and p(L(t_i, c_x) > L(t_j, c_y)) be the probability of likelihood defined by t_i and direction c_x being larger than the likelihood defined by t_j and c_y. For t_j ∈ S_i, both predicted curves have the same value up to t_j (0) as well as at and after t_i (1) since c_x = c_y = 1. Then, this pairwise probability p(L(t_i,1) > L(t_j,1)) can be expressed as in Eq. 5 in terms of the log-likelihood comparison:

$$\begin{array}{l}p(\mathrm{L}(t_i,1)>\mathrm{L}(t_j,1))=p(log(\mathrm{L}(t_i,1))-log(\mathrm{L}(t_j,1))>0)=p(-\frac{1}{2{\sigma }^2}(\sum _{m=j}^{i-1}\sum _{z=1}^{n_r}{(d_{m:z})}^2-\sum _{m=j}^{i-1}\sum _{z=1}^{n_r}{(d_{m:z}-1)}^2)>0)\\ =p(\sum _{m=j}^{i-1}\sum _{z=1}^{n_r}{d}_{m:z}\le n_r\frac{h}{2})=\mathrm{\Phi }(n_r\frac{h}{2},m_j^i,{\sigma }_j^i)\end{array}$$ (5)

where h is the number of measurements between t_j and t_i−1 including both time points and $\mathrm{\Phi }(n_r\frac{h}{2},m_j^i,{\sigma }_j^i)$ is the cdf of a Gaussian with mean $m_j^i$ and a standard deviation ${\sigma }_j^i$. Since we know s_g and c_g (the computation is conditioned on them) and we are dealing with a Gaussian, the sum of the observations is also a Gaussian with mean $m_j^i=n_r{\sum }_{m=j,t_m\ge s_g}^{i-1}1$ and standard deviation ${\sigma }_j^i=\sqrt{n_r{\sum }_{m=j}^{i-1}{\sigma }^2}$. Note that such analysis takes into account the number of replicates when computing the noise for each time point.

Repeating the pairwise comparison in Eq. 5 for all points in S_i and M_i returns set of distributions that need to be satisfied. For a step function, distributions returned by S_i and M_i are independent of each other, so the nested integral for Eq. 4 can be separated into two integrals each of which can be efficiently estimated by Gaussian quadrature or by MCMC (Press, 2007) (See Appendix for details).

Analyzing profiles with multiple transitions

Following the analysis of step functions, where we focused on identifying a single change point, we now consider the more general (though still not the most general) case where we know the number of transition points and the direction (for example, 0,1,2,1) but do not know the specific time points in which they occur. In this case, we estimate p(S_r = Tⁱ | C_r, S_g,C_g, σ²) for Tⁱ ∈ A^d in Eq. 3 which is defined as the probability of the likelihood defined by Tⁱ to be higher than the likelihood defined by any other k-subset.

In order to estimate this probability, we follow the approach used for the step function, and define the pairwise probability p(L(Tⁱ,C^r) > L(T^j,C^r)) as in:

$$p(\mathrm{L}(T^i,C^r)>\mathrm{L}(T^j,C^r))=p(\sum _{m=0}^k\sum _{\begin{array}{c}{t}_a\le t<t_b,\\ I_m^i=[t_a,t_b)\end{array}}\sum _{z=1}^{n_r}{(d_{t:z}-v_m^r)}^2-\sum _{n=0}^k\sum _{\begin{array}{c}{t}_a\le t<t_b,\\ I_n^j=[t_a,t_b)\end{array}}\sum _{z=1}^{n_r}{(d_{t:z}-v_n^r)}^2>0)$$ (6)

where Iⁱ and I^j are intervals defined by Tⁱ and T^j, and $v_{m+1}^r=v_m^r+c_{m+1}^r$ is the corresponding value of the m+2 ’th interval defined by transition directions C^r. For every k-subset Tⁱ, there are $\left(\begin{array}{c}T\\ k\end{array}\right)-1$ comparisons intersection of which define the integral boundaries for estimating Eq. 4. In contrast to the step functions in Section 0, we cannot separate the estimation of the nested integral in Eq. 4 into two parts since there is no total ordering and independence between variables. In this case, we estimate the integral by sampling over the domain. As with step functions, we evaluate the success of the Dense and Repeat strategies by determining the area between the true and estimated curves for each gene.

General Transition Functions

Finally, we arrive at the most general case where both the location and direction of transitions are unknown. Note that the number of transition k is an input for this computation, but since the goal of the modeling here is to determine how well Dense and Repeat strategies do, we can easily perform the computation on all relevant values of k to reach the conclusions we are interested in for a specific noise model (it is unlike that genes would have more than 5–6 transitions in most time series studies, in fact in most cases they have much fewer). For the case of k possible transitions, expected error becomes:

$$E(f_{\text{mis}})=\sum _{T^i\in A^r}\sum _{C^x\in Q}p(S_r=T^i,C_r=C^x\mid S_g,C_g,{\sigma }^2)f_{\text{mis}}(S_g,C_g,T^i,C_x)$$ (7)

where p(S_r = Tⁱ,C_r = C^x | S_g,C_g, σ²) is the probability of selecting k -point subset Tⁱ and set of transition directions $C^x=\{c_1^x,\dots ,c_k^x\}$ conditioned on the actual step time, actual transition direction, and the noise in the measured data. In Eq. 7, expectation is taken over all possible k -point subsets of T^r and all possible transition directions C^x of length k since we also do not know the transition directions. When estimating p(S_r = Tⁱ,C_r = C^x | S_g,C_g, σ²), we want the likelihood defined by Tⁱ and C^x to be higher than the likelihood defined by any other k -point subset T^j and k -length transition directions C^y pair. We follow the approach used for the step function, and define the pairwise probability p(L(Tⁱ,C^x) > L(T^j,C^y)) as in:

$$p(\mathrm{L}(T^i,C^x)>\mathrm{L}(T^j,C^y))=p(\sum _{m=0}^k\sum _{\begin{array}{c}{t}_a\le t<t_b,\\ I_m^i=[t_a,t_b)\end{array}}\sum _{z=1}^{n_r}{(d_{t:z}-v_m^x)}^2-\sum _{n=0}^k\sum _{\begin{array}{c}{t}_a\le t<t_b,\\ I_n^j=[t_a,t_b)\end{array}}\sum _{z=1}^{n_r}{(d_{t:z}-v_n^y)}^2>0)$$ (8)

where Iⁱ and I^j are intervals defined by Tⁱ and T^j, and $v_{m+1}^x=v_m^x+c_{m+1}^x,v_{m+1}^y$ are the corresponding values of the m + 2 ’th interval defined by transition directions C^x and C^y respectively. For every k -subset Tⁱ and C^x, there are $\left(\begin{array}{c}T\\ k\end{array}\right)2^k-1$ comparisons defining the integral boundaries in estimating Eq. 4. Similar to the discussion of known transition directions above, full ordering is not guaranteed between the variables, so the nested integral in Eq. 4 can again be estimated via sampling.

Highlight.

• Most High throughput time series studies do not contain technical repeats.

• Given limited budget, should we profile more repeat experiments or more time points?

• We develop a theoretical framework to address this question.

• Under reasonable assumptions more time points are the correct choice.