Resolution recovery for Compton camera using origin ensemble algorithm

Abstract

Purpose:

Compton cameras (CCs) use electronic collimation to reconstruct the images of activity distribution. Although this approach can greatly improve imaging efficiency, due to complex geometry of the CC principle, image reconstruction with the standard iterative algorithms, such as ordered subset expectation maximization (OSEM), can be very time-consuming, even more so if resolution recovery (RR) is implemented. We have previously shown that the origin ensemble (OE) algorithm can be used for the reconstruction of the CC data. Here we propose a method of extending our OE algorithm to include RR.

Methods:

To validate the proposed algorithm we used Monte Carlo simulations of a CC composed of multiple layers of pixelated CZT detectors and designed for imaging small animals. A series of CC acquisitions of small hot spheres and the Derenzo phantom placed in air were simulated. Images obtained from (a) the exact data, (b) blurred data but reconstructed without resolution recovery, and (c) blurred and reconstructed with resolution recovery were compared. Furthermore, the reconstructed contrast-to-background ratios were investigated using the phantom with nine spheres placed in a hot background.

Results:

Our simulations demonstrate that the proposed method allows for the recovery of the resolution loss that is due to imperfect accuracy of event detection. Additionally, tests of camera sensitivity corresponding to different detector configurations demonstrate that the proposed CC design has sensitivity comparable to PET. When the same number of events were considered, the computation time per iteration increased only by a factor of 2 when OE reconstruction with the resolution recovery correction was performed relative to the original OE algorithm. We estimate that the addition of resolution recovery to the OSEM would increase reconstruction times by 2–3 orders of magnitude per iteration.

Conclusions:

The results of our tests demonstrate the improvement of image resolution provided by the OE reconstructions with resolution recovery. The quality of images and their contrast are similar to those obtained from the OE reconstructions from scans simulated with perfect energy and spatial resolutions.

1. INTRODUCTION

Nuclear medicine (NM) imaging is well recognized for its capacity to investigate different body functions in vivo and at the molecular level. Unfortunately, current SPECT cameras with lead collimators suffer from low sensitivity and poor resolution. It is expected that NM imaging modalities that are based on the principles alternative to the standard SPECT will allow the users to overcome these limitations, potentially contributing to a significant progress in this field. One such modality is Compton camera (CC) which is able to image radiotracers’ distributions without the use of mechanical lead collimators.¹ Instead, CC employs the kinematics of Compton scattering and records time coincidences between the detected photons that Compton scatter in the first detector and are absorbed in the second. This type of detections of gamma photons, called electronic collimation, allows us to restrict the volume of possible source locations to half-conical surfaces. The parameters of these half-cones (direction, cone angle, and apex location) are defined by the locations and the deposited energies of the two detected events and can be calculated using the well-known Compton-scatter formula.²

Considering the physical principles of CC, it should exhibit high sensitivity and be able to image radiotracers without the artifacts related to collimator septal penetration, as no mechanical collimation is involved. However, one of the reasons why currently CC is not widely used in medical imaging is that the image resolution that can be achieved by the real-world systems based on electronic collimation is seriously limited by the finite energy and spatial resolutions of the available detectors, as well as by Doppler broadening.² Additional difficulty is related to the fact that CC imaging resolution is best when the distance between the imaged object and the first detector (scatterer) is small, while that between the scatterer and the second detector (absorber) is large. Such geometry, however, requires large detectors which may be very expensive; otherwise camera covers only small solid angle, which results in low sensitivity.

To summarize, the finite energy and spatial resolutions of the detectors create an inherent limit to the reconstructed image quality and resolution, which, in spite of a continuous search for detectors with improved characteristics, will always restrict the performance of the CC systems. At the same time, optimizing camera geometry in order to improve resolution may seriously deteriorate the CC sensitivity or dramatically increase the cost. Therefore, the image reconstruction algorithms, which could effectively compensate for these resolution-limiting effects, will be essential for the future clinical applications of CC.

Unfortunately, image reconstruction from the CC data is, in itself, a challenging problem. This is because, as already mentioned, the possible origins of the detected photons lie on the half-conical surfaces which are difficult to represent mathematically in the reconstruction algorithms. Several analytic and iterative algorithms have been proposed for the CC reconstruction.^3–6 However, to this date, little progress has been achieved in implementing any of the corrections that would be required for a successful high-resolution image reconstruction.^7,8 It was recently demonstrated⁹ that in the standard modeling of image resolution for CC using the shift-variant point spread functions (PSFs), the recalculation of the PSF model required computing times of the order of months. Investigators from Stanford implemented the ordered subset expectation maximization (OSEM) based model of resolution recovery (RR) for CC using the graphics processing unit (GPU) and this approach enabled them to achieve high speed of reconstructions (2.2 s/iteration for 50 000 Compton cones). Their preliminary results show that the method still requires improvements in terms of resulting image quality.¹⁰

Here we propose a different approach. In our previous publication,¹¹ we have already demonstrated that the origin ensemble (OE) algorithm is able to reconstruct the Compton camera images with the quality equivalent to the OSEM method but in much shorter time. The same approach was used by others¹² for reconstruction of the CC images in the beam range verification during proton therapy. The algorithm is based on the Markov Chain Monte Carlo method derived by Sitek¹³ (the theory behind the OE approach is discussed in Refs. ¹⁴ and ¹⁵). In this work, we present a new, substantially modified version of the OE algorithm which allows us to reconstruct CC images with resolution recovery option with little additional computational cost.

The performance of the new origin ensemble with resolution recovery (OE-RR) reconstruction algorithm was tested on the Monte Carlo simulated data using the CC camera design which could be used in small animal studies. Three different distances between the detectors were modeled resulting in substantial changes in both sensitivity and resolution of the system. Phantoms containing different configurations of small spheres filled with activity and placed in air and in the hot background were investigated. Our results show that in all modeled situations, the proposed OE-RR method effectively corrects for the image resolution losses caused by the finite energy and spatial resolutions of the detectors with only slightly increased processing time as compared to OE.

2. METHODS

2.A. Monte Carlo simulation of the CZT Compton camera

The performance of our new OE-RR reconstruction method with incorporated resolution recovery correction was tested using simulated Compton camera that can potentially be used in small animal imaging. The proposed camera employs CZT detectors and could be used for imaging the radioisotopes emitting single and multiple gamma rays using the CC mode, as well as the positron emitters using the PET mode. Consequently, when these two imaging modes are combined, our camera could perform simultaneous multitracer imaging studies.

Three different distance settings between the scatterer and the absorber were investigated, namely 30, 50, and 70 mm (Fig. 1). Although the configuration with 30 mm distance between the detectors increases the sensitivity of the system, the image resolution is sacrificed.² On the other hand, increasing this distance (up to 70 mm) while keeping unchanged the sizes of detectors, improves the spatial resolution but decreases sensitivity. Our hypothesis is that the new reconstruction method will be especially useful in the Compton camera configurations that are aimed at maximum sensitivities as it will allow us to compensate (at least partially) for the resolution losses while maintaining high sensitivity.

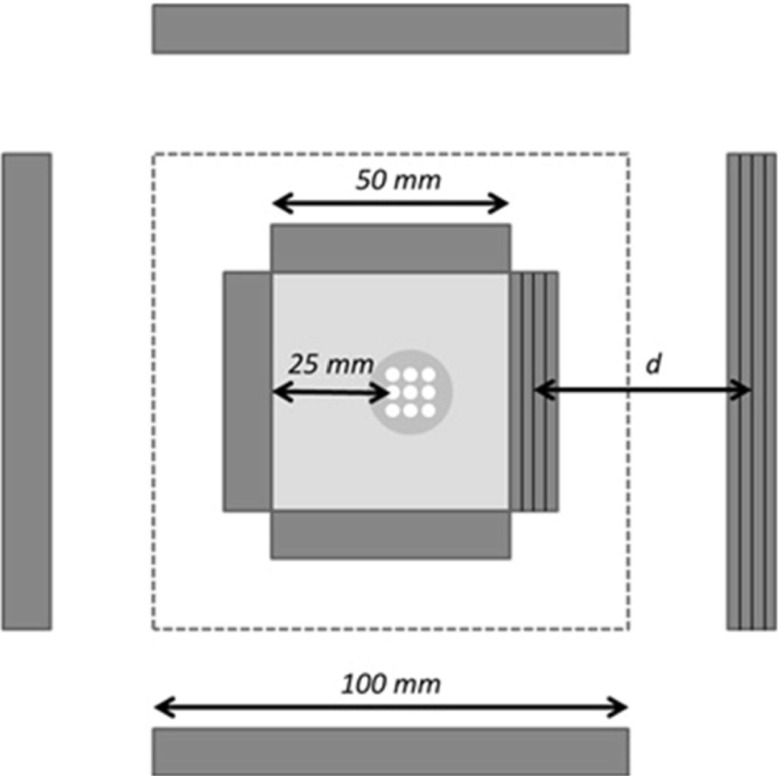
FIG. 1.

A small animal Compton camera simulated in this study. The dimensions of the CZT scatter detectors were 5 × 5 × 1 cm and the absorption detectors were 10 × 10 × 1 cm. The fifth pair of the CZT detectors was placed at the back of the field-of-view (FOV), as marked with dashed lines. Each detector panel consisted of four 2.5 mm thick layers (denoted by thick black lines on the right pair of detectors). Three different distances d between the scatter and absorption detectors (measured from the center to the center of the detectors) were investigated: 30, 50, and 70 mm. The phantom is positioned off-center inside the camera.

Taking into account the above considerations and using GATE (Ref. ¹⁶) Monte Carlo simulation tool, we created a Compton camera consisting of 1 cm thick-layered CZT detector blocks. Four pairs of scatter and absorber detectors were positioned as shown in Fig. 1, while the fifth detector pair was placed at the back of the system (as marked by a dashed line in Fig. 1). The dimensions of the scatter detectors were 5 × 5 × 1 cm and the absorption detectors were 10 × 10 × 1 cm. Each detector panel consisted of four 2.5 mm thick CZT layers (denoted in Fig. 1 by thick black lines on the right pair of detectors). As already mentioned, three camera geometries with distances between the scatter and absorption detectors (measured between centers of detector blocks) equal to 30, 50, and 70 mm were investigated. The distance between the front surfaces of the opposite scatter detectors (which defined the field-of-view of the system) was equal to 5 cm.

Although in real-life situations each photon can interact multiple times in each detector, for our tests of image reconstruction we selected only those photons that underwent a single Compton scatter in the scatterer and were fully absorbed (no additional Compton scatter) in the absorption detector. All other events were rejected. As events corresponding to photons that Compton scatter at angles close to 0° and 180° result in significantly degraded resolution,² we limited the scattering angles that were accepted in the analysis to those between 9° and 171°. The selection of photon scattering angles was done based on their deposited energies. In real-life situation, such selection will be more challenging due to the uncertainty in the experimentally measured energies.

We estimated the sensitivity values for detection of 511 keV single photons for the proposed Compton camera for the three detector configurations considered in our study. The sensitivity was defined as the ratio of the number of detected photons to the total number of emitted photons. The 511 keV energy was selected in order to allow for a direct comparison with PET or high energy SPECT cameras and to minimize Doppler effect. The point source positioned at the center of the camera emitting 10⁶ single 511 keV photons was used in the sensitivity determination.

Similarly, for our tests of the OE-RR algorithm developed in this work, objects emitting photons with the same 511 keV energy were simulated. The effects of attenuation and scatter in the objects themselves were ignored. During GATE Monte Carlo simulation, the exact deposited energies and the exact locations of photon interactions with the detectors were saved in the list-mode files. These data constitute datasets that we refer to as the “exact data” as they correspond to acquisitions with perfect energy and spatial resolutions.

To simulate a realistic acquisition, we assumed that all the CZT detectors were pixelated into detector elements of size 1 × 1 × 2.5 mm and with the relative energy resolution equal to Δ₅₁₁ = 3% FWHM at E₀ = 511 keV. We also assumed that the relative energy resolution at other energies was equal to ${\mathrm{\Delta }}_E=\sqrt{E_0/E{\mathrm{\Delta }}_{511}}$. Using these assumptions, the second “experimental” dataset was created. This second dataset reflected the energy and spatial resolutions of the modeled CZT detectors and was obtained by modifying the exact dataset as follows. Measured deposited energies were obtained as random samples from the normal distributions with the means equal to the true deposited energies and standard deviations equal to ${\sigma }_E={\mathrm{\Delta }}_{E}E/2.3548=\sqrt{E_{0}E{\mathrm{\Delta }}_{511}/2.3548}$. To model the limited spatial resolution, the exact locations of interactions were converted to the center of the corresponding detector element based on the assumed detector pixelization (1 × 1 × 2.5 mm detector elements). The effects of electronic and optical cross talk have been ignored (they have been shown to be negligible¹⁷).

2.B. The OE algorithm

According to the CC principle, in a system with detectors having perfect energy and spatial resolutions, each detected event (two coincident photon interactions detected in the scatterer and in the absorber, respectively) creates a half-conical surface which corresponds to all possible locations of the radioactive nucleus which emitted this photon (event origin).

In the first step, the OE algorithm assigns each event origin to a location randomly selected on its conical surface. In the subsequent Markov steps, the algorithm attempts to modify this location to a randomly chosen new location (voxel), again positioned on the conical surface corresponding to this particular event. The new event origin location can be accepted or rejected depending on the relative number of the other event origins in the voxels containing the new and the old locations. This is done one event at a time. Following this process, the number of event origins per voxel reaches steady state at which on average the number of events moving in and moving out of the voxel become the same. We successfully implemented this algorithm for the CC reconstructions in Ref. 11 and derived it from basic statistical principles in Ref. 14.

In the ideal case, the position of the apex, direction, and the opening angle (cone angle) of the half conical surface corresponding to each CC event used in the OE reconstruction are defined by the true deposited energies and the true locations of interactions of the photon in the two CC detectors. These energies and locations, however, are only known with the accuracy that is determined by the finite energy and spatial resolutions of the detectors. As a result, the conical surface which is created using the measured detectors’ outputs may not include the true event origin. This mismatch creates deterioration of the spatial resolution in the reconstructed image.

The new OE-RR algorithm that aims to correct for these effects is conceptually straightforward and follows the same principle as the “standard” OE algorithm. In the standard OE algorithm we position the event on the cone, this may be considered as a guess of the true location of the event. In the image space, this on-the-cone location is assigned to a particular voxel. Therefore, in simple terms, the OE algorithm^12–14 creates a series (a chain) of “guesses” of the numbers of emissions per voxel. In order to correct for the finite energy and spatial resolutions, in addition to guessing the position of the event origin on the half-cone, the true energies deposited per interaction and the true locations of the interactions within the detector elements (detector pixels) in which they were detected must also be “guessed.” If the OE-RR algorithm is properly designed (see Ref. 14 and Section E) these guesses are samples from the joint posterior distribution of the number of emissions per voxel, energies deposited per interaction, and locations of the interactions within the detector elements conditioned on the measured energies and the indices of detectors in which the interactions were detected. By averaging the sampled values of the number of emissions per voxel, the minimum-mean-square-error (MMSE) estimate of this number is obtained (effectively the true deposited energies and true locations of interactions within the detector elements are marginalized). Finally, the estimate of the voxel activity can be obtained by dividing the MMSE estimate of the number of emission per voxel by this voxel sensitivity. In this work, we assumed that the voxel sensitivity is uniform across the volume of interest.

Although in the present study, the effect of Doppler broadening was not included in the model, the correction for Doppler broadening can be implemented in a similar manner as corrections for the energy and spatial resolutions described in Secs. 2.C and 2.D.

2.C. Correction for finite energy resolution

In order to be able to “guess” the true deposited energy based on the energy that is actually measured, the posterior distribution of the true deposited energy is used. The energies of photons emitted by the radioisotopes used in medical imaging studies are always known; therefore we consider only the detection of photons with known initial energy E₀. The energies deposited in CC due to single Compton scattering in the first detector and due to photoabsorption in the second detector are E₁ and E₂, respectively, where E₁ + E₂ = E₀. The cone angle can be determined from

$${\displaystyle \theta =\text{acos}\left(1-\frac{511}{E_0}\frac{E_1}{E_2}\right)=\text{acos}\left(1-\frac{511}{E_0}\frac{E_1}{\left(E_0-E_1\right)}\right).}$$ (1)

Exact true deposited energies E₁ and E₂ are not known and only the measured ${\overline{E}}_1$ and ${\overline{E}}_2$ are available. Only one energy, E₁ or E₂, is necessary to determine the cone angle as shown by Eq. (1). Since in our design of CC both energies are measured, we combine these two measurements to provide a more precise estimation of E₁ which is sufficient to compute the cone angle θ [Eq. (1)]. The likelihoods $p_1\left({\overline{E}}_1\right|E_1)$ and $p_2\left({\overline{E}}_2\right|E_2)$ have Gaussian shapes centered around ${\overline{E}}_1$ and ${\overline{E}}_2$ and standard deviations σ_E1 and σ_E2, respectively. The Gaussian shape of the likelihood function is a consequence of the assumed Gaussian model of the energy resolution, where the measurement ${\overline{E}}_1$ is assumed to be derived from the Gaussian distribution with mean E₁ and standard deviation σ_E1. We further assume that we can approximate the standard deviations σ_E1 and σ_E2 by ${\sigma }_{{\overline{E}}_1}$ and ${\sigma }_{{\overline{E}}_2}$. The values of ${\sigma }_{{\overline{E}}_1}$ and ${\sigma }_{{\overline{E}}_2}$ are known since the deposited energies are measured, and because we assumed that the energy resolution is proportional to the deposited energy. The coefficient of proportionality between the sigma and the deposited energy is known (in our case 3% FWHM). Now, considering that the measurements of both energies are statistically independent, the combined likelihood $p({\overline{E}}_1,\hspace{0.17em}{\overline{E}}_2|E_1)$ is described by a normal distribution (see Appendix for derivation) with the mean μ and variance σ² where

$${\displaystyle \mu =\frac{{\overline{E}}_1{\sigma }_{{\overline{E}}_2}^2+(E_0-{\overline{E}}_2){\sigma }_{{\overline{E}}_1}^2}{{\sigma }_{{\overline{E}}_1}^2+{\sigma }_{{\overline{E}}_2}^2},}$$ (2)

$${\displaystyle {\sigma }^2=\frac{{\sigma }_{{\overline{E}}_1}^2{\sigma }_{{\overline{E}}_2}^2}{{\sigma }_{{\overline{E}}_1}^2+{\sigma }_{{\overline{E}}_2}^2}.}$$ (3)

The normal distribution defined by μ and σ² presented in Eqs. (2) and (3) is used in each Markov step of the OE algorithm to generate a sample of energy E₁ which subsequently is used to determine the cone angle using Eq. (1). The μ and σ² define the normal probability of observing ${\overline{E}}_1,{\overline{E}}_2$ when the true deposited energy in the first detector is E₁. By sampling E₁ from the likelihood function, we implicitly assume that the prior of E₁ is uniform and therefore the sampling is equivalent to sampling from the posterior $p\left(E_1\right|{\overline{E}}_1,{\overline{E}}_2)$.

2.D. Correction for finite spatial resolution

When implementing the correction for finite spatial resolution of the CC detectors, we considered our detectors to be pixelated in the x, y, and z directions. The sizes of these detector elements defined the detectors’ resolutions in each direction creating a “detector resolution voxel” (Fig. 2) which we also refer to as the detector element. The detector elements (pixels) in which the interactions occurred are identified as ${\overline{M}}_1$ and ${\overline{M}}_2$ for the scatterer and the absorber, respectively. To be consistent with the notation used previously for the energies, we use bar to indicate the measured values. We also define T₁ and T₂ at the true x, y, z locations of the interactions.

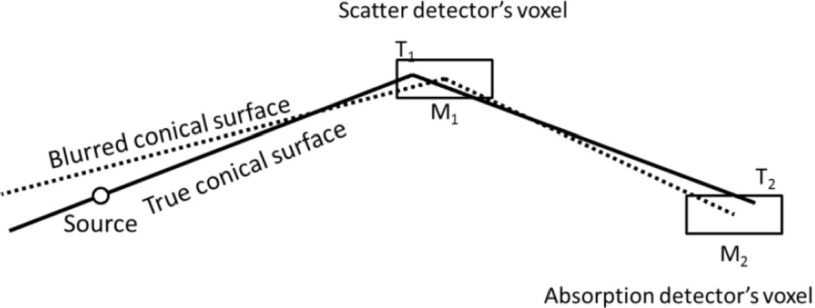
FIG. 2.

The schematic representation of the effects of finite intrinsic spatial resolution. T₁ and T₂ indicate the exact locations of photon interactions within each detector voxel. These are unknown therefore usually it is assumed that the interactions happen at the centers of the detector elements in both detectors (${\overline{M}}_1$ and ${\overline{M}}_2$). The conical surface indicated by the solid line corresponds to the true interaction locations. An incorrect assumption about the interaction locations will lead to the loss of spatial resolution.

When an event is considered by the OE algorithm, a new location of interaction within this 3D detector element is selected according to the appropriate photon-detection probability distribution.¹⁸ In our case, these distributions $p\left(T_1\right|{\overline{M}}_1)$ and $p\left(T_2\right|{\overline{M}}_2)$ are assumed to be uniform over the entire voxel volume, but other, more advanced, distributions more closely reflecting the physics and geometry of photons interactions within the detector material can be implemented. Unlike the correction for finite energy resolution where only one random number was generated to determine a sample from the normal distribution, the implementation of the correction for spatial resolution requires generation of six random numbers. Three random numbers are needed to simulate the detection uncertainty in the x, y, and z directions of the detector elements for each of the detectors.

2.E. Combined corrections for finite spatial and energy resolutions

The corrections described in Secs. 2.C and 2.D were combined in the new OE-RR algorithm to allow for the full modeling of the Compton camera resolution due to limited energy and spatial resolutions of the detectors. Assuming that for each detected event we measured the deposited energies ${\overline{E}}_1$ and ${\overline{E}}_2$ and identified detector elements ${\overline{M}}_1$ and ${\overline{M}}_2$, in the OE-RR reconstruction the following steps were executed:

• 1.For each detected event the initial cone direction and cone apex were determined by assuming the locations of interactions at the centers of detector elements in which they were recorded. The initial value (first guess) of the true energy deposited in the first detector was determined by assuming that it was equal to the measured value.²⁰ The cone angle was subsequently determined from this sampled values using Eq. (1). The cone direction, apex, and cone angle define the half-cone surfaces and in general are different for each event.
• 2.The initial locations (first guesses) of origins of all events were determined by stochastic assignment (random guess) of locations of each event origin on half-cone surfaces. Only a fraction of half-cone surface that was contained in the volume of interest (VOI). VOI corresponds to the volume where the object is located and which is considered for image reconstruction. In this work, the VOI was defined as the spherical volume with the diameter equal to the maximum image dimension.
• 3.Event n was randomly chosen and voxel i within VOI that contained the origin of this event was recorded.
• 4.The parameters of the new half cone corresponding to event n were stochastically determined by obtaining samples from the distributions of the locations of interactions in projection elements (Sec. 2.D) and deposited energies (Sec. 2.C).
• 5.Event n was randomly moved to a new location j on the half-cone surface determined in step 4 within VOI and voxel j which contained this new location was recorded.
• 6.A random number was generated. The new location of the event n was accepted if this random number (from a range [0,1]) was smaller than $\left(c_j+1\right){ϵ}_i/c_i{ϵ}_j$ where c_j and c_i were the numbers of event origins contained in voxels j and i before the move and ϵ_i and ϵ_j were these voxel sensitivities.
• 7.Repeated steps 3 to 6.

We refer to the processes described in steps 3 through 7 as a Markov move. Repetition of the Markov move N times corresponds to one iteration of the OE algorithm, where N is the total number of detected events.

The above algorithm reaches equilibrium when on average the number of events in each voxel remains constant i.e., events move in and out the voxels in Markov moves, but on average the number of event origins in each voxel remains the same. The initial number of iterations for which the algorithm reaches equilibrium is referred to as a burn-in period. Once the system reaches equilibrium, the numbers of events in each voxel c_i are recorded for this and for every subsequent iteration. At the end of the run, an average value ${\overline{c}}_i$ is determined for each voxel. This average voxel value, divided by this voxel sensitivity (in our case it was assumed uniform), constitutes the result of the algorithm. In general, the more events (coincident pairs of interactions in the scatterer and the absorber) are recorded, the more precise estimate of the expectation of the number of emitted events per voxel is obtained.

2.F. OSEM

In order to investigate the differences in processing times between the OE reconstruction with resolution modeling and the reconstructions that use more “traditional” iterative methods, we implemented the CC version of the OSEM algorithm with 16 subsets.¹⁹ The modeling of finite energy and spatial resolutions with the OSEM algorithm is computationally difficult as it requires integration over the thick conical surfaces (taking into account both uncertainties in the opening angle and cone orientation) at each forward projection and back projection. This means that at each step many more volume elements must be included in the system matrix than in the case when resolution is not modeled. No correction for the resolution recovery was included in our implementation of the OSEM algorithm due to the anticipated complexity of such task. However, based on the implemented forward projector and back projector operations, we estimated the time per iteration that would be required when the spatial and energy resolutions are modeled. Two different scenarios were considered in the estimation of the OSEM computing time. In the first one, we assumed additional 4 and in the second additional 8 sampling points per deposited energies and detector pixels. The assumed sampling scheme was selected ad hoc and is only used for an approximate estimation of the required computing times. Therefore, in order to create one forward projection 4 × 4 × 4 = 64 or 8 × 8 × 8 = 512 cone integrations would be used. This naïve algorithm provided a simple estimate of the computing time of an iterative algorithm with multiple sampling points.

2.G. Simulated phantom data

We simulated three three-dimensional (3D) phantoms composed of series of small spherical objects filled with radioisotope emitting 511 keV photons. No attenuation and Compton scatter in the phantoms were included in these simulations. For each phantom, three datasets were created for the three different Compton camera configurations considered in our study (30, 50, and 70 mm distance between the first and the second detector).

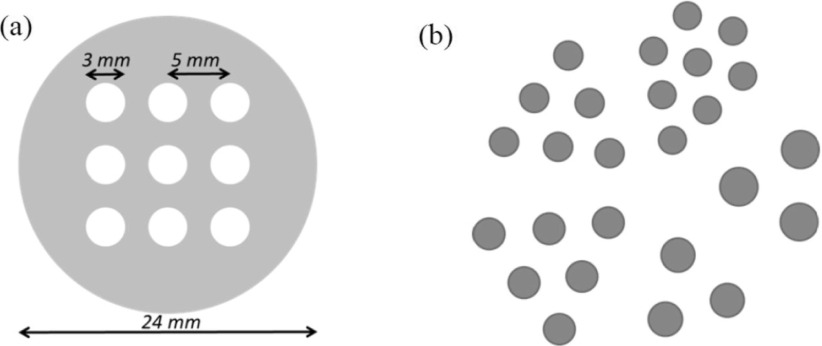
The first phantom consisted of nine small spheres of 3 mm diameter with a distance of 5 mm between their centers. The spheres were placed in air so no background was simulated. In the second phantom, the spheres were placed inside a thin cylinder containing activity (cylinder diameter was 24 mm and height 2 mm). The large cylinder thickness was selected low (less than the sphere diameter) in order to speed up the simulation. Only one of the central slices was used in the analysis. The ratio of activity concentrations between the spheres and the cylinder was 7:1.

In both simulated cases, the whole phantom with spheres was placed off-center (in the transaxial direction) between the detectors, with the left middle sphere positioned at the center of the FOV (see Fig. 1). Using this setup 1.4 × 10⁶ photons were detected in the no-background case and 3.2 × 10⁶ for the experiment with warm background in the phantom. The same numbers of detected photons were used in the simulations of CCs with different separation distances between the detectors. The exact values of the deposited energies and the locations of interactions were recorded (exact dataset).

The third phantom was comprised of 26 small spheres with diameters equal to 2.0, 2.25, 2.5, 2.75, and 3.0 mm placed in air. All spheres contained the same activity concentration and were arranged in the Derenzo pattern with distances between the spheres centers being equal to their diameters. No background or attenuating medium was modeled in this case and 8.7 × 10⁶ events were acquired (Fig. 3).

FIG. 3.

Two 3D phantom configurations that were used in our Monte Carlo simulations. (a) Nine spheres were imaged without (first phantom) and with warm background (second phantom). (b) Derenzo phantom with spheres ranging from 2 to 3 mm diameter (third phantom). In this case, the distances between the spheres were equal to two times their radii. No attenuating medium was simulated in any of these experiments.

2.H. Image reconstructions

The OE reconstructions were performed for: (1) the dataset with no resolution recovery (standard OE algorithm using measured energy and interaction locations corresponding to the centers of detector elements) and (2) for the dataset with resolution recovery (OE-RR). In order to provide a gold-standard reference, the reconstruction of the exact dataset was also performed using the standard OE algorithm. In all cases, a total of 10 000 iterations were used which is a very large number of iterations used to ensure the algorithm is in the equilibrium. As mentioned above, we define one iteration of the OE algorithm as the process in which all events are considered for the move (the number of guesses is equal to the number of events). For each reconstruction, the obtained numbers of event origins per voxel were averaged between 5100 and 10 000 iterations in steps of 100 iterations (total of 50 measurements) to obtain the estimate of the number of event origins per voxel. The first 5000 iterations were used as a burn-in period for the OE algorithm to reach the equilibrium.

Additionally, the third phantom was reconstructed using not only OE and OE-RR but also the OSEM algorithm. The OSEM algorithm was tested with a varying number of iterations. The average mean squared error (MSE) and the bias were calculated. As the average MSE and the bias reached the minimum value at ten iterations, it was taken as the optimal iteration number for the OSEM for both the exact dataset and the simulated data without resolution recovery (denoted by OSEM Exact and OSEM). All images were reconstructed into the 80 × 80 × 80 matrix with the voxel size of 0.5 mm. The images were post-filtered with the Gaussian filter with sigma of 0.75 voxels.

2.I. Data analysis

The images reconstructed using OE and OSEM from the exact datasets were compared to those obtained from the datasets corresponding to the detectors with realistic spatial and energy resolutions reconstructed using the OE and OE-RR algorithms. All displayed images were scaled to the common maximum. A Gaussian post reconstruction filter with sigma of 0.75 voxel was applied to remove excess noise.

Profiles were drawn through the center of the reconstructed images of the nine-sphere phantom to show the differences in the resolution achieved in these three cases. Since the OE algorithm operates directly on the counts, the images and the profiles were quantitative and expressed in the number of emissions detected per voxel.

Additionally, contrast-to-background ratios were estimated for the nine-sphere phantom with background. See Fig. 5 for the definition of the region of interest used for calculation of the contrast. Although all simulations were performed in 3D only a single 2D slice through the center of the spheres was analyzed.

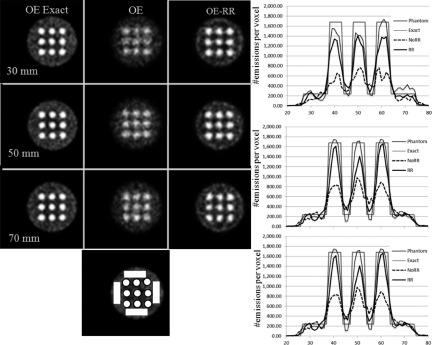
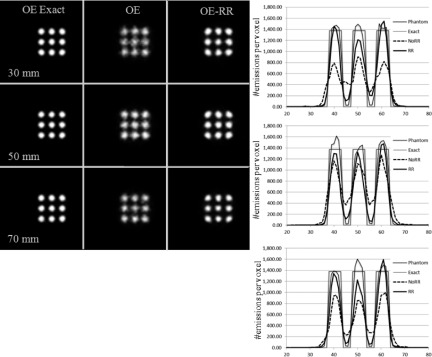
FIG. 5.

Center slice of the reconstructed images and the corresponding profiles of the nine-sphere phantom with warm background reconstructed using the OE and OE-RR algorithms. The first column presents images obtained from the exact data while the second column—from the data affected by resolution uncertainties and reconstructed with the OE without resolution recovery. The third column shows images obtained from the data affected by the resolution uncertainties but reconstructed using the OE-RR algorithm. Three different Compton camera configurations were investigated: with the distance between the scatterer (front detector) and the absorber (back detector) equal to 30 mm (first row), 50 mm (second row), 70 mm (third row). Profiles presented at the right part of the figure (top: 30 mm, middle: 50 mm, and bottom: 70 mm) were drawn horizontally through the three middle spheres. “Phantom” profile line corresponds to the true activity distribution, “Exact” profile was drawn through the images reconstructed from the exact data (i.e., simulated for detectors with perfect energy and spatial resolutions), and NoRR and RR profiles correspond to the data acquired with detectors with limited resolutions and reconstructed without and with resolution recovery option, respectively. The locations of ROI used for calculation of the contrast are shown in the picture displayed below the profiles.

3. RESULTS

The sensitivities corresponding to the three camera configurations were determined using the data simulated with the point source positioned in the center of the camera. The results summarized in Table I show that when the distance between the first and second detector increases from 30 to 70 mm, the sensitivity of the system decreased by more than a factor of 2. Considering the absolute values of the estimated sensitivities, these results also demonstrate that the proposed design for Compton camera will have good sensitivity, comparable to PET.

TABLE I.

Sensitivities for three investigated Compton camera configurations (Fig. 1) for detection of single photon emissions at 511 keV.

Distance between the scatter and absorption detectors (mm)	Sensitivity (%)
30	1.45
50	0.95
70	0.69

Figure 4 displays the reconstructed images of the nine-sphere phantom scanned in air (first phantom) using 30, 50, and 70 mm gap between the scatter and absorption detectors. Figure 5 shows similar images obtained from the second phantom (spheres with hot background). Corresponding profiles are displayed in the right column in both the figures.

FIG. 4.

Center slices of the reconstructed images and the corresponding profiles of the phantom containing nine spheres placed in air, reconstructed using the OE and OE-RR algorithms. The first column presents images obtained from the exact data while the second column from the data affected by resolution uncertainties; these images were reconstructed with OE without resolution recovery. The third column shows images obtained from the data affected by the resolution uncertainties but reconstructed using the OE-RR algorithm. Three different Compton camera configurations were investigated with changing distance between the scatterer (front detector) and the absorber (back detector): 30 mm (first row), 50 mm (second row), 70 mm (third row). The profiles presented in the right part of the figure (top: 30 mm, middle: 50 mm, and bottom: 70 mm) were drawn horizontally through the three middle spheres. “Phantom” profile corresponds to the true activity distribution, “Exact” profile was drawn through the images reconstructed from the exact data (i.e. simulated for detectors with perfect energy and spatial resolutions), and the NoRR and RR profiles correspond to the data acquired with detectors with limited resolutions and reconstructed without and with resolution recovery.

The images created from the exact data, assuming perfect energy and spatial resolution of all detectors (first column) show only small resolution degradation between studies performed with the camera having 70 and 30 mm distance between the detectors. However, the image resolution substantially deteriorated when the finite energy and spatial detector resolutions were included in the simulated model (second column in Figs. 4 and 5). The reconstructed images are particularly blurry for the case with 30 mm distance between the detectors for which the effects of the finite spatial resolution are more severe. Profiles drawn through the spheres show that both, the contrast and the quantitative accuracy of the reconstructed images, are severely affected by this blurring and that RR is able to improve the quality of reconstruction.

Analysis of the images presented in the third column of both figures confirms that by including the resolution recovery corrections in the OE algorithm we succeeded to greatly improve the quantitative accuracy of the reconstructions. In all cases, the image contrast is almost completely recovered, as compared with the images from the simulations in which both the deposited energy and the location of photon interactions were exactly known (first column in Figs. 4 and 5, respectively). It is important to point out, however, that the shapes of spheres in the images reconstructed with resolution recovery from the data affected by the resolution uncertainties are all slightly deformed. We speculate that this effect may be due to the square geometry of the simulated scanner. We plan to further investigate this effect in the future.

The contrast-to-background ratios for the nine-sphere phantom with background (Fig. 5) for the images obtained from exact data, blurred data but reconstructed without resolution recovery, and blurred and reconstructed with resolution recovery are summarized in Table II. The obtained values are consistent with the images presented in Figs. 4 and 5 and clearly demonstrate the improvement provided by the OE-RR reconstructions.

TABLE II.

Contrast ratios for the nine-sphere phantom with background. The true value of contrast in the phantom was equal to 7:1.

	Contrast ratio in the reconstructed images
Distance between the scatter and absorption detectors (mm)	Exact	No RR	RR
30	6.73	3.63	5.68
50	6.74	4.00	5.44
70	6.68	4.17	5.36

Figure 6 displays the images of the Derenzo phantom. Columns left to right show the images reconstructed by the OSEM from the exact data (exactly known energies and locations of interactions), OSEM without RR from blurred data, OE from exact data, and from blurred OE and OE-RR. While the quality of images reconstructed from the ideal data are very similar for both OSEM and OE algorithms, it is clear that when the data are created assuming realistic detector uncertainties, OE-RR very efficiently improves the image quality. Note, however, that in some cases the noise is amplified in the smallest sphere sector, which is an expected effect when RR is performed.

FIG. 6.

Images reconstructed with OE and OSEM from the Derenzo phantom placed in air. The first column presents the images obtained from the exact data using OSEM; second column—OSEM reconstruction without resolution recovery from the data affected by resolution uncertainties; third column—OE reconstruction from the exact data; fourth column—OE reconstruction from the data affected by the resolution uncertainties; fifth column—OE-RR reconstruction from the data affected by the resolution uncertainties. Three different Compton camera configurations were investigated based on the distance between the scatterer (front detector) and absorber (back detector): 30 mm (first row), 50 mm (second row), and 70 mm (third row). Images in all columns are scaled to the maximum value in OSEM Exact.

The reconstruction times are summarized in Table III. We predict that when resolution recovery is included in the OSEM algorithm, the reconstruction time would increase by a factor of 500 or more. This estimation was done assuming that OSEM was implemented using the naïve forward and back projection model with sampling by the ray-tracing of the conical surfaces.

TABLE III.

Time^a per 10 iterations for OSEM and 10 000 iterations for OE for the dataset with 8.7 × 10⁶ counts and image dimensions 80 × 80 × 80. Letters S + E4 indicate correction for the spatial and energy resolutions with four sampling points, S + E8 with eight sampling points.

OSEM (16 subsets)			OE
No RR	RR(S + E4)	RR(S + E8)	No RR	RR S + E
6920 s	176 400 0 sb (20 days)	282 960 00 sb (1 yr)	96 000 s	172 000 s

^aEstimates based on a single thread at Xeon 5504@2.0 GHz.

^bEstimates based on the number of assumed sampling points and the time needed for projection/backprojection operations, and the actual reconstructions were not performed.

On the other hand, the increase of the reconstruction time for the OE algorithm that is due to the use of the resolution recovery correction is not significant (compared to OSEM) as the reconstruction takes only about 80% longer to perform; in absolute units this time amounts to about 17 s/iteration for 10⁶ events.

Please note, however, that reconstructions using about 3–6 iterations of OSEM with 16 subsets per iteration and 2000–5000 iterations of the OE algorithm will produce roughly equivalent images in terms of resolution/noise, and we estimate that such images could be sufficient for many practical applications.

4. DISCUSSION AND CONCLUSIONS

A modification to the OE algorithm which allows us to perform resolution recovery for CC to compensate for the effects of finite spatial and energy resolutions of the detectors has been proposed and the initial evaluation performed. Our results are very encouraging and warrant further research. By modeling the probability distributions of the measured energy values and of the interaction locations in the scatter and absorption detectors, we were able to substantially improve the contrast recovery of the CC system. Further improvements may be possible when the accurate model of the interaction of photons with the detectors is incorporated into the reconstructions. Although we have not analyzed quantitatively the increase in noise levels related to OE-RR reconstructions, visual inspection of images of the second phantom with spheres placed in warm background (Fig. 5) suggests that this increase will not be substantial. More research is needed to thoroughly investigate the exact noise/resolution trade-off. We plan to perform such study in the future using more realistic phantoms and acquisitions that include the attenuation and scatter. Attenuation correction for the OE in single photon emitters (SPECT and CC) can be efficiently implemented by computing attenuation factors between voxels and possible detection locations of the first interaction on the scatterer. Modification of voxel sensitivities so they to take into account the attenuation is also needed. Once those factors are estimated their ratio can be taken into account in step 6 of the OE algorithm provided in Sec. 2.E. However, storing the matrix of these coefficients presents a challenge. We think that the solution would be to store the matrix corresponding to a coarse representation of the object and the projections space. Because attenuation is a smooth function, the coarse representation will likely be sufficient to describe it. In addition to modeling spatial and energy resolutions that were investigated in this study, we plan to expand our model to include the corrections for Doppler broadening and tail effect in the detected spectrum from CZT.

One of the limitations of current work is that we only provide single reconstructed images and this approach has a limited value. Ideally, we would like to perform the analysis of variances of reconstructed images and investigate these variances as a function of CC parameters, compare these variances to those obtained by iterative algorithms such as OSEM. In fact, the use of OE algorithm presents a unique opportunity to investigate the properties of reconstructed images as it is possible to compute Bayesian variance of the solution.^14,15 We showed that the time per iteration increased by a factor of 2 when the OE-RR was used, we have not, however, investigated the convergence to equilibrium of this algorithm which will likely be slower than the original OE. We plan to investigate these issues in the future.

We are convinced that the development of the reconstruction method which has an ability to perform resolution recovery is absolutely necessary for the CC to be acceptable for use in the medical applications. Such reconstructions can improve spatial resolution and contrast in the reconstructed images, even for systems in which resolution has been sacrificed in order to optimize sensitivity. This may allow CC to outperform current nuclear medicine imaging systems. In summary, the use of our OE-RR reconstruction method with resolution recovery in Compton camera may significantly improve the quality of images and lead to a widespread use of Compton imaging.

APPENDIX: DERIVATION OF LIKELIHOOD OF E₁

To derive Eqs. (2) and (3), we consider two measurements ${\overline{E}}_1$ and ${\overline{E}}_2$ which are modeled as drawn from normal distributions with means E₁ and E₂ and standard deviations σ₁ and σ₂. Assuming they are statistically independent, the joint probability of observing ${\overline{E}}_1$ and ${\overline{E}}_2$ is

$${\displaystyle p\left({\overline{E}}_1,{\overline{E}}_2|E_1,E_2\right)\propto e^{-\frac{{(E_1-{\overline{E}}_1)}^2}{2{\sigma }_1^2}}{e}^{-\frac{{(E_2-{\overline{E}}_2)}^2}{2{\sigma }_2^2}}.}$$

Because E₂ = E₀ − E₁,

$${\displaystyle p\left({\overline{E}}_1,{\overline{E}}_2|E_1\right)\propto e^{-\frac{{(E_1-{\overline{E}}_1)}^2}{2{\sigma }_1^2}}{e}^{-\frac{{(E_0-E_1-{\overline{E}}_2)}^2}{2{\sigma }_2^2}}.}$$

After rearranging the terms and pulling out some constant terms we obtain

$${\displaystyle p\left({\overline{E}}_1,{\overline{E}}_2|E_1\right)\propto exp-\frac{{\left(E_1-\frac{{\overline{E}}_1{\sigma }_2^2+(E_0-{\overline{E}}_2){\sigma }_1^2}{{\sigma }_1^2+\hspace{0.17em}{\sigma }_2^2}\right)}^2}{\frac{2{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+\hspace{0.17em}{\sigma }_2^2}}}$$

which defines the normal distribution with the mean and variance as given by Eqs. (2) and (3). The above is the likelihood function of true energy E₁ upon detection of energies ${\overline{E}}_1$ and ${\overline{E}}_2$. This likelihood is used to form the posterior of E₁ in the OE algorithm.

CONFLICT OF INTEREST DISCLOSURE

Dr. Andreyev and Dr. Sitek are currently employees of Philips. Dr. Ozsahin and Dr. Celler have no relevant conflicts of interest to disclose.