Correcting for Measurement Error in Time-Varying Covariates in Marginal Structural Models

Abstract

Unbiased estimation of causal parameters from marginal structural models (MSMs) requires a fundamental assumption of no unmeasured confounding. Unfortunately, the time-varying covariates used to obtain inverse probability weights are often error-prone. Although substantial measurement error in important confounders is known to undermine control of confounders in conventional unweighted regression models, this issue has received comparatively limited attention in the MSM literature. Here we propose a novel application of the simulation-extrapolation (SIMEX) procedure to address measurement error in time-varying covariates, and we compare 2 approaches. The direct approach to SIMEX-based correction targets outcome model parameters, while the indirect approach corrects the weights estimated using the exposure model. We assess the performance of the proposed methods in simulations under different clinically plausible assumptions. The simulations demonstrate that measurement errors in time-dependent covariates may induce substantial bias in MSM estimators of causal effects of time-varying exposures, and that both proposed SIMEX approaches yield practically unbiased estimates in scenarios featuring low-to-moderate degrees of error. We illustrate the proposed approach in a simple analysis of the relationship between sustained virological response and liver fibrosis progression among persons infected with hepatitis C virus, while accounting for measurement error in γ-glutamyltransferase, using data collected in the Canadian Co-infection Cohort Study from 2003 to 2014.

In longitudinal analyses of observational data, control of confounding is complicated whenever time-varying confounders are also intermediates on the causal pathway between the exposure and outcome. Adjustment for such covariates in standard regression models leads to biased estimators of exposure effects (1–3).

Marginal structural models (MSMs) represent an important improvement over conventional regression-based adjustment for time-varying covariates. The most common form of estimation for these models involves weighting by the inverse probability of exposure, or inverse probability weighting (IPW) (4). A fundamental assumption of MSMs is that there is no unmeasured confounding (1). In conventional, unweighted regression models, mismeasurement of confounders and mismodeling of functional forms in covariate-exposure relationships may undermine confounding adjustment (5–7). To date, the effect of measurement errors in confounders on inverse probability-weighted estimators has not been extensively studied (8, 9), even though MSMs are increasingly used in settings where measurement error is likely. For example, in analyses of human immunodeficiency virus (HIV) data, time-varying CD4⁺ cell counts are often used in IPW estimation (10). Like most laboratory measurements, CD4⁺ cell count is subject to high variability that is well-characterized following decades of use (11–13).

The behavior of exposure effect estimators in the context of misclassified or mismeasured confounders has received considerable attention in the literature. Greenland (14, 15) illustrated that adjustment for misclassified covariates impairs confounding control, and that nondifferential misclassification biases estimates in the direction of the crude exposure-outcome association. Ogburn and VanderWeele (16) demonstrated that adjusting for nondifferentially mismeasured ordinal covariates may increase bias—for example, if their effects differ qualitatively across exposure strata. In the context of IPW, covariate mismeasurement may result in over- or underestimation of the true parameters, and occasionally changes in the sign of their estimates (8). Overall, prior research suggests that the consequences of covariate mismeasurement may be unpredictable.

While most published IPW analyses do not implement modeling strategies to address measurement error, we note 2 important exceptions. To estimate the effect of HIV treatment on incident acquired immunodeficiency syndrome or death, Cole et al. (17) applied regression calibration to address exposure measurement error in a Cox MSM. McCaffrey et al. (9) suggested a propensity score-based approach to handle errors in covariates, relying partially on simulations, using the observed data to generate a weighting function. Their method performs well, but its implementation may be challenging for epidemiologists.

Here we consider a novel application of the simulation-extrapolation (SIMEX) procedure, originally proposed by Cook and Stefanski (18), to address measurement error in continuous time-varying covariates used for IPW. Our proposed adaptation of the SIMEX procedure to MSMs is straightforward and may be implemented with several statistical software packages. The method is both intuitive and easily explained. We validate the proposed approaches via simulation and conduct a simple analysis to illustrate a practical application.

SIMEX CORRECTION OF MEASUREMENT ERROR IN CONFOUNDING VARIABLES

Overview of the SIMEX procedure

Consider the classical measurement error model $L_{ij}{}^{\ast }=L_{ij}+{ϵ}_{ij},$ where $L_{ij}{}^{\ast }$ is the observed jth measure for individual i of covariate L_i, L_ij is the corresponding true value, and ϵ_ij represents a normally distributed mean-zero error term (19). Note that SIMEX procedures for Berkson error are also available (20, 21). For simplicity, we begin by describing the effect of a dichotomous exposure X in a single time interval:

$$Y={\beta }_0+{\beta }_{1}X.$$ (1)

Denote the target parameter by θ, where θ could be an average exposure effect or a vector of regression coefficients (β₀, β₁).

Given a regression model, the SIMEX procedure approximates the functional relationship between model parameters and the variance of measurement error using a 2-step simulation-based approach, assuming that the variance is known or accurately estimated (14). First, additional (“artificial”) random error is added to the original values of the error-prone covariate. The degree of artificial error is incremented over a set of user-defined multipliers λ. The number of λ values chosen need not be large, though Monte Carlo error is reduced as their quantity increases (18). For each value of λ, B data sets are simulated. The original regression model is refitted to each of B data sets to obtain ${\hat{\theta }}_b(\lambda ).$ Finally, the mean of the resulting parameter estimates is calculated: $\hat{\theta }(\lambda )=B^{-1}{\sum }_{b=1}^B{\hat{\theta }}_b(\lambda ).$ In the second step, $\hat{\theta }(\lambda )$ is regressed on λ, often assuming a quadratic relationship. Extrapolating the function back to the hypothetical case with no measurement error, which corresponds to λ = −1, yields the SIMEX estimate of the parameter of interest (19).

Proposed adaptation of SIMEX to MSMs

In equation 1, the exposure parameter is β₁, and the dependent variable Y represents the average difference between the counterfactuals Y^X=1 and Y^X=0, assuming all individuals had been exposed or not exposed, respectively. To obtain unbiased causal estimates of the effect of X while addressing confounding by L in equation 1, we may fit a weighted outcome model by inverting probabilities of exposure estimated from the following exposure model:

$$\text{logit}(P(X=1|L))={\alpha }_0+{\alpha }_{1}L.$$ (2)

We consider 2 alternative applications of the SIMEX procedure to address errors in L. Both approaches employ the same error variance information, but the approaches differ in the choice of which mean estimates are regressed on λ (see Web Table 1, available at http://aje.oxfordjournals.org/). The direct correction approach targets the estimated parameter β₁ in equation 1 while using naive weights obtained from the original, uncorrected exposure model. In denoting the SIMEX estimate for the bth (b = 1, …, B) data set as ${\hat{\beta }}_{1,b}(\lambda ),$ we obtain the direct SIMEX estimator by extrapolating the function ${\hat{\beta }}_1(\lambda )=B^{-1}{\sum }_{b=1}^B{\hat{\beta }}_{1,b}(\lambda )$ to λ = −1.

In the second approach, termed indirect correction, SIMEX is applied to the exposure model, and the IPW weights are corrected. Here, the correction is targeted at the estimated parameters α₀ and α₁ in equation 2; extrapolating ${\hat{\alpha }}_0(\lambda ),{\hat{\alpha }}_1(\lambda )$ to λ = −1 yields the SIMEX-corrected estimators for exposure model coefficients (Web Appendix 1). The outcome model is fitted using the SIMEX-corrected IPW weights. The indirect SIMEX procedure is easily implemented in most statistical environments. In contrast, no software packages support direct correction, as existing implementations were not designed for 2-stage estimation procedures.

SIMULATION STUDIES

In simulations, we assessed bias in naive MSMs, which do not correct for measurement error in a time-varying covariate, and the potential of the 2 SIMEX approaches to reduce the bias. We considered different combinations of relevant parameter values, and we simulated 300 data sets for each combination. We performed analyses in R, version 3.1.1 (R Development Core Team, Vienna, Austria), using our own SIMEX implementation (Web Appendix 2) and the R sprint package to efficiently apply the nonparametric bootstrap (22, 23). In all analyses, we specified 200 SIMEX replicates and used a quadratic function to perform the extrapolation. To account for clustering and the 2-stage estimation procedure, we obtained 95% confidence intervals for the exposure effect by means of the nonparametric bootstrap percentiles approach, using 1,000 bootstrap replicates for each parameter combination (24).

Methods

Single-time-interval simulation study: data generation

We first considered a single time interval setting to examine SIMEX performance in a simplified context. True (i.e., error-free) values of a continuous confounder L were generated from a uniform [−4, 4] distribution. A dichotomous exposure X, conditional on L, was then generated, assuming

$$p=\text{logi}{\text{t}}^{-1}({\alpha }_0+{\alpha }_{1}L)=(1+\exp (-{\alpha }_0-{\alpha }_{1}L){)}^{-1}.$$

We fixed α₀ at 0.25. To minimize the risk of positivity violations, we simulated exposure probabilities bounded between 0.1 and 0.9 by setting α₁ at 0.25, 0.50, or 0.75. The error-prone covariate L^* was generated by adding random error drawn from an N(0, σ_δ) distribution, with standard deviations σ_δ of 0.25, 0.75, and 1.25, representing scenarios with increasing measurement error.

The outcome, Y, was normally distributed with the expected value dependent on the exposure X and the “true” value of confounder L:

$$Y={\beta }_0+{\beta }_{1}X+{\beta }_{2}L+ϵ,$$

where ϵ ∼ N(0, 1). Figure 1A illustrates the data generation scheme using a directed acyclic graph. In all, we examined 27 simulated scenarios corresponding to various combinations of sample size (n = 100, n = 500, n = 1,000), measurement error magnitude (controlled by σ_δ), and strength of confounding due to L (controlled by β₁).

Figure 1.

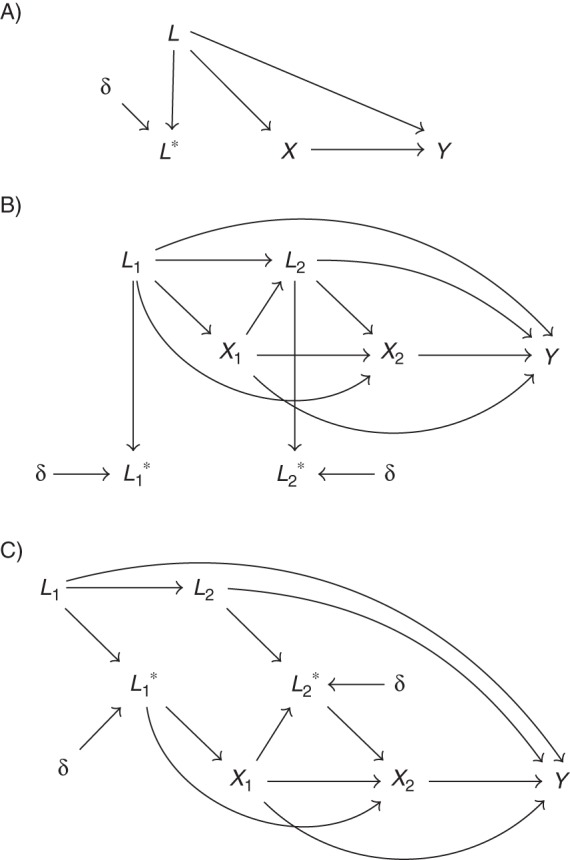
A) Data generation scenario for single-time-interval initial simulation studies, in which exposure is conditional on error-free covariate L. Measurement error is represented by δ. B) Data generation scenario for 2-interval simulation studies, in which exposure depends on error-free covariate L_j. Measurement error is represented by δ. C) Data generation scenario for secondary 2-interval simulation studies, in which exposure depends upon mismeasured covariate $L_j{}^{\ast }$. Measurement error is represented by δ.

Two-time-interval simulation study: data generation

Initial error-free values of a continuous covariate L₁ were drawn from a Uniform distribution with range −2 to 3. We generated first-interval exposure status X₁ from a Bernoulli distribution, conditional on L₁ with probability p = logit⁻¹(0.25 + α₁L₁), with α₁ equal to 0.50 or 0.75. The second-interval value of L was then generated from L₂ = 0.3L₁ + 1.25X₁ + ϵ, where ϵ ∼ N(0, 1). We generated second-interval exposure status X₂ given a Bernoulli distribution with probability p = logit⁻¹(0.25 + α₁L₂ – 1.25X₁). The outcome Y, at the second interval, was generated as

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{L}_1+{\beta }_4{L}_2+\eta ,$$

where η ∼ N(0, 1). Figure 1B depicts the 2-interval data generation scenario. Error-prone values of L_j (j = 1, 2) were obtained by adding random error, drawn from N(0, σ_δ), to the respective error-free values. We varied the strength of measurement error by specifying σ_δ to be 0.25 or 1.25.

Single-time-interval study: analysis

In each simulated data set, we fitted 2 alternative logistic models to predict exposure probabilities conditional on the error-free L or the mismeasured L^*. Inverting the predicted probabilities from each of these models generated weights, which were used to fit the 2 corresponding MSMs for a linear regression of Y on X. We compared the resulting regression coefficients to assess the influence of measurement error.

Secondary single-time-interval study: application of SIMEX-corrected MSMs to actual clinical data contaminated with additional error

Web Appendix 3 provides results for secondary simulations designed to more closely mimic real data and the example considered in the case study, in which we systematically increase error in a time-varying covariate using a clinical data set (Web Figure 1).

Two-time-interval simulation study: analysis

The 2-time-interval simulations were analyzed similarly to the single-time-interval study, using separate logistic models to respectively regress X₁ on L₁ and regress X₂ on X₁ and L₁. For the 2-time-interval MSMs, we stabilized the weights to reduce variance (1). Further details are available in Web Table 1.

Secondary 2-interval study: exposure status conditional on the mismeasured covariate

In our previous simulations, only the error-prone covariate was available to the analyst, while exposure was allocated using the true, error-free covariate. However, decisions to initiate, modify, or discontinue treatment may depend on the error-prone covariate, if no other relevant information is available to clinicians. In a sensitivity analysis, we assumed that exposure was conditional on the mismeasured covariate values of $L_1{}^{\ast }$ and $L_2{}^{\ast },$ as illustrated in Figure 1C. The simulated data were analyzed using the same methods as in the primary 2-interval study.

Sensitivity analysis: misspecification of measurement error variance

In our analyses of simulated data using the SIMEX procedure, we implicitly assumed that the measurement error variance is known precisely. In practice, this assumption may be violated to some degree. Consequently, we reanalyzed data in the 2-interval setting (Figure 1B), with α₁ = 0.50, to assess the influence of measurement error variance misspecification on SIMEX performance. We varied the ratio of specified measurement error variance to the true variance (used to generate L^*) across the range [0.25, 0.50, 0.75, 1.00, 1.25, 1.50, 1.75], with α₁ = 0.50 and all other parameters identical to those from the primary 2-interval simulations.

Comparative assessment of SIMEX performance

In Web Appendix 3, we present pairwise correlations for both SIMEX approaches and the naive MSM across all single-time-interval simulations (Web Figure 2) and consider the accuracy of the quadratic extrapolation in further simulations (Web Figure 3).

Simulation results

Single-time-interval study

Web Table 2 presents estimates from the naive MSM, which does not correct for measurement error, while Table 1 shows estimates from the 2 error-corrected SIMEX models.

Table 1.

Results From a Single-Time-Interval Simulation Study With 27 Scenarios (Rows) in Which Sample Size (N), the Magnitude of the Confounder L (α₁), and the Standard Deviation of Measurement Error σ_δ are Varied in Marginal Structural Models Including an Error-Free L and an Uncorrected Error-Prone L^*

α1, N, and Scenario	Error Deviation (σδ)	Model Using SIMEX-Corrected L*
		Direct Correction				Indirect Correction
		Bias (β1)	Relative MSEa	MCSE	95% Bootstrap Coverageb	Bias (β1)	Relative MSEa	MCSE	95% Bootstrap Coverageb
0.25
100
A	0.25	−0.006	1.000	0.219	0.950	−0.007	1.000	0.220	0.953
B	0.75	0.008	0.933	0.288	0.963	0.004	0.944	0.290	0.960
C	1.25	0.099	0.780	0.355	0.950	0.089	0.792	0.360	0.957
500
D	0.25	0.008	1.000	0.099	0.943	0.008	1.000	0.099	0.943
E	0.75	0.030	0.472	0.127	0.943	0.026	0.472	0.128	0.943
F	1.25	0.127	0.385	0.156	0.890	0.120	0.375	0.158	0.900
1,000
G	0.25	0.002	1.000	0.076	0.943	0.002	1.000	0.076	0.943
H	0.75	0.022	0.370	0.099	0.920	0.018	0.370	0.100	0.920
I	1.25	0.115	0.329	0.120	0.787	0.110	0.318	0.122	0.817
0.50
100
J	0.25	−0.005	1.016	0.251	0.963	−0.008	1.016	0.251	0.967
K	0.75	0.028	0.723	0.326	0.963	0.002	0.764	0.337	0.960
L	1.25	0.214	0.506	0.388	0.937	0.170	0.525	0.417	0.960
500
M	0.25	0.005	0.933	0.117	0.937	0.001	0.933	0.118	0.937
N	0.75	0.035	0.271	0.146	0.930	0.008	0.271	0.152	0.950
O	1.25	0.222	0.256	0.173	0.730	0.181	0.217	0.186	0.830
1,000
P	0.25	−0.003	0.875	0.085	0.917	−0.007	0.875	0.085	0.920
Q	0.75	0.025	0.178	0.111	0.907	−0.002	0.178	0.115	0.927
R	1.25	0.211	0.216	0.132	0.603	0.170	0.171	0.141	0.750
0.75
100
S	0.25	0.025	1.009	0.335	0.943	0.015	1.009	0.335	0.943
T	0.75	0.055	0.755	0.452	0.947	−0.013	0.792	0.467	0.967
U	1.25	0.327	0.479	0.499	0.890	0.220	0.486	0.559	0.930
500
V	0.25	−0.002	0.955	0.147	0.937	−0.015	1.000	0.148	0.943
W	0.75	0.025	0.245	0.190	0.920	−0.056	0.298	0.205	0.947
X	1.25	0.304	0.231	0.215	0.647	0.186	0.168	0.256	0.860
1,000
Y	0.25	0.000	0.833	0.102	0.937	−0.014	0.917	0.103	0.923
Z	0.75	0.026	0.139	0.135	0.920	−0.056	0.182	0.147	0.907
AA	1.25	0.302	0.199	0.155	0.443	0.184	0.116	0.183	0.787

Abbreviations: MCSE, Monte Carlo standard error; MSE, mean squared error; SIMEX, simulation-extrapolation.

^a MSEs are relative to those computed using a naive model including an error-prone L^* with an identical parameter set.

^b Bootstrap coverage was computed using the nonparametric bootstrap percentiles approach.

Bias in the naive estimators worsened systematically as measurement error increased (Web Table 2). For example, for a sample size of n = 1,000, with α₁ = 0.25, a 3-fold increase in σ_δ (from 0.25 to 0.75) resulted in a 7-fold increase in bias. The bias in the naive model grew as the strength of the association between the error-prone covariate L^* and exposure X increased. For n = 1,000 and σ_δ = 0.25, a 3-fold increase in α₁ (from 0.25 to 0.75) resulted in a 2-fold increase in bias. Due to bias, coverage was systematically low; the lowest coverage corresponded to settings with the highest σ_δ and stronger L-X associations.

Table 1 compares both SIMEX-based approaches. When measurement error was lowest (σ_δ = 0.25), SIMEX-corrected models yielded nearly unbiased estimates comparable to those from the error-free model (Web Table 2). For σ_δ = 0.75, median bias in β₁ was 99% and 88% lower for the indirect and direct SIMEX models, respectively, relative to the naive model. Due to a small degree of remaining bias, coverage rates were over 90% for both direct and indirect approaches, in contrast to poor coverage for the naive model (Table 1). Given high measurement error (σ_δ = 0.75), the indirect and direct SIMEX-corrected estimates were slightly biased, but they still reduced bias by 68% and 59% relative to the naive model estimates.

As anticipated, standard deviations of exposure effect estimates were slightly higher for both SIMEX-based models relative to naive estimates. The degree of variance inflation was minimal when the specified association between L and X was weakest (α₁ = 0.25). For α₁ = 0.50 and n = 1,000, average standard deviations were 23% greater for the indirect approach and 14% greater for the direct approach, in comparison with the naive model (data not shown). Given α₁ = 0.75, σ_δ = 1.25, and n = 1,000, mean standard deviations for the direct and indirect approaches were 28% and 50% greater than those for the naive model, respectively. However, mean squared errors (MSEs) for the SIMEX-corrected models were systematically lower than those for the naive model, reflecting a good trade-off in variance for bias, particularly when α₁ and σ_δ were largest (Table 1).

Given α₁ = 0.25, both SIMEX approaches produced highly comparable estimates across varying sample sizes and measurement error magnitudes. When the influence of L on X was stronger (α₁ = 0.50 or 0.75) and σ_δ = 1.25, the indirect SIMEX model (Table 1, right side) exhibited lower bias and MSE compared with the direct SIMEX model (Table 1, left side).

Both approaches yielded similar coverage for low-to-moderate confounding and smaller σ_δ. With increased N, coverage tended to decrease, as narrow intervals imply that even a relatively small bias results in suboptimal coverage. Coverage for the SIMEX-corrected models was noticeably poorer for higher levels of measurement error. Inadequate fit of the quadratic extrapolant is one possible explanation (25, 26). Kukush et al. (21) suggest that at larger error magnitudes, the naive ordinary likelihood estimator no longer conforms sufficiently to a quadratic relationship, and they propose alternative estimators to address this issue. An alternate hypothesis is that severe mismeasurement of L limits the amount of useful information available for adjustment using L^*. Overall, estimates from both SIMEX approaches remained practically unbiased and very similar for low-to-moderate degrees of measurement error. When measurement error was more extreme, the indirect SIMEX approach yielded better coverage, lower bias, and lower MSE.

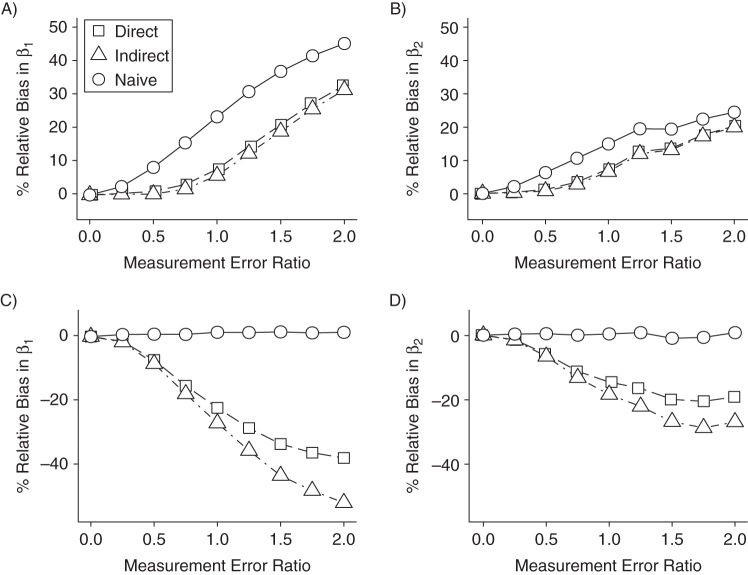
The 2-time-interval study

As in the 1-interval setting, SIMEX-corrected estimates were uniformly less biased and featured lower MSEs than the naive model (Table 2, panels A and B of Figure 2, and Web Table 3). Given higher measurement error and stronger confounding (scenario 4), the biases of direct and indirect SIMEX exposure effect estimates for the first interval were 56% and 71% smaller, respectively, than the bias from the naive model. In the second interval, biases in the direct and indirect estimates were 33% and 41% smaller, respectively.

Table 2.

Results^a From a 2-Time-Interval Simulation Study With 4 Scenarios (Rows) in Which the Magnitude of the Confounder L (α₁) and the Standard Deviation of Measurement Error σ_δ are Varied in Marginal Structural Models Including an Error-Free L and an Uncorrected Error-Prone L^*

α1 and Scenario	Error Deviation (σδ)	Model Using SIMEX-Corrected ${\mathit{L}}_{\mathbf{1}}{}^{\mathbf{\ast }}$, ${\mathit{L}}_{\mathbf{2}}{}^{\mathbf{\ast }}$
		Direct Correction							Indirect Correction
		Bias		Relative MSEb		MCSE		95% Bootstrap Coveragec	Bias		Relative MSEb		MCSE		95% Bootstrap Coveragec
		β1	β2	β1	β2	β1	β2	(β1, β2)	β1	β2	β1	β2	β1	β2	(β1, β2)
0.50
1	0.25	−0.003	0.009	1.000	1.000	0.097	0.107	0.923, 0.970	−0.006	0.007	1.000	1.000	0.097	0.107	0.927, 0.970
2	1.25	0.187	0.154	0.263	0.552	0.112	0.114	0.600, 0.760	0.158	0.145	0.218	0.507	0.118	0.117	0.717, 0.793
0.75
3	0.25	0.008	0.013	1.000	0.950	0.126	0.137	0.907, 0.933	−0.001	0.008	1.000	0.950	0.127	0.138	0.913, 0.933
4	1.25	0.249	0.213	0.240	0.565	0.127	0.141	0.527, 0.650	0.162	0.189	0.151	0.522	0.150	0.158	0.783, 0.720

Abbreviations: MCSE, Monte Carlo standard error; MSE, mean squared error; SIMEX, simulation-extrapolation.

^a A sample size of n = 1,000 was used for all simulations.

^b MSEs are relative to those computed using a naive model including an error-prone L^* with an identical parameter set.

^c Bootstrap coverage was computed using the nonparametric bootstrap percentiles approach.

Figure 2.

Relative bias in β₁ estimates from naive and simulation-extrapolation (SIMEX)-corrected marginal structural models in 2-interval simulation studies, given varying ratios of covariate measurement error to residual error in Y. Parts A and B correspond to data generated according to Figure 1B, and parts C and D correspond to data generated according to Figure 1C. The left- and right-hand plots (parts A and C and parts B and D, respectively) represent first- and second-interval exposure effect estimates, respectively.

Both SIMEX models exhibited nearly identical coverage for α₁ = [0.50 or 0.75] and σ_δ = 0.25 and improved coverage versus the naive model given σ_δ = 1.25. While coverage of the direct and indirect SIMEX-corrected intervals was as low as 53% and 78%, it was 0% for the naive model. In scenarios 1–3 from the primary study, where exposure depended on the error-free covariate, the two approaches produced nearly identical estimates. In scenario 4, given high measurement error and a strong L-X relationship, the indirect approach appeared more accurate (Table 2).

In contrast, in our secondary simulations, where exposure depended on error-prone covariates $L_j{}^{\ast }$, both SIMEX approaches introduced bias, which grew as measurement error increased (Figure 2, parts C and D), while the naive MSM yielded unbiased estimates with the lowest MSE. This finding was not surprising; Figure 1C illustrates that inclusion of $L_j{}^{\ast }$ in the exposure (weighting) model effectively blocks the causal path between X_j and $L_j{}^{\ast }$. Using IPW, we impose conditional independence between X_j and $L_j{}^{\ast }$ (27, 28).

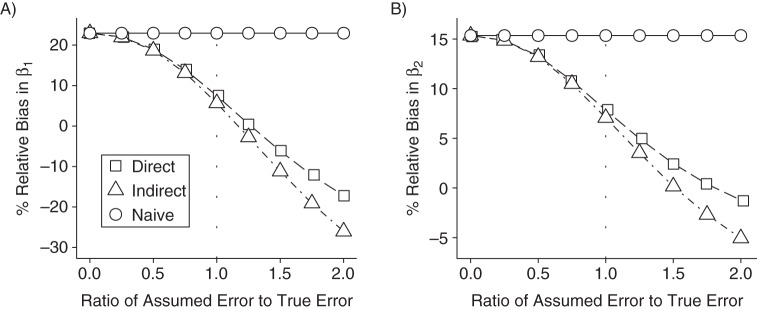
Figure 3 presents the results of a sensitivity analysis. It appears that when exposure depends on the error-free covariate, SIMEX-corrected estimates are less biased than the naive estimates, even when the variance of the error distribution is misspecified by as much as 50%.

Figure 3.

Influence of misspecification of measurement error variance on relative bias in exposure effect estimates from 2-interval simulations using naive, direct simulation-extrapolation (SIMEX)-corrected, and indirect SIMEX-corrected marginal structural models. A) first-interval estimates; B) second-interval estimates. The dotted line at X = 1.0 is used to indicate the scenario with correctly specified measurement error variance. Data were generated according to Figure 1B. Note that the axis scales differ between plots.

CASE STUDY: THE CANADIAN CO-INFECTION COHORT STUDY

To demonstrate an application of SIMEX-corrected MSMs, we analyzed data from the Canadian Co-infection Cohort Study (CCC). The CCC is an ongoing study of over 1,400 individuals coinfected with HIV and hepatitis C virus (HCV) (29). Persons aged 16 years or older may participate, given documented HIV infection (enzyme-linked immunosorbent assay confirmed by Western blot) and chronic HCV infection or laboratory evidence of HCV exposure (30). Study visits generally occur every 6 months (±1 month) and include a liver test profile. A key objective of the CCC is to explore predictors of liver disease progression among persons living with HIV/HCV. We analyzed data from a subset of 258 individuals treated for HCV, for whom at least 1 visit occurred after completing therapy (Web Figure 4, Web Table 4).

We investigated the relationship between HCV treatment and progression of liver disease. The exposure of interest was sustained virological response (SVR) to therapy, a clinically relevant measure of HCV treatment effectiveness and cure. Ghany et al. (31) define SVR as an undetectable HCV RNA result in a sensitive polymerase chain reaction assay at a specified number of weeks following discontinuation of therapy. We assessed SVR at 12 weeks posttherapy, which correlates well with SVR at 24 weeks and has recently been recommended as an endpoint for future HCV trials (32–34). The outcome variable was the aspartate aminotransferase:platelet ratio index (APRI), a continuous, noninvasive surrogate marker of liver fibrosis severity (35). APRI has been validated among persons coinfected with HIV and HCV (36, 37). We initially intended to conduct a 2-interval study but chose to consider a single time interval after identifying collinearity when modeling subsequent SVR measures.

The outcome model included the following covariates: female sex, age, duration of HCV infection, and HCV genotype. In the exposure model, we included continuous measures of current γ-glutamyltransferase (GGT) level, body mass index (weight (kg)/height (m)²), HIV viral load, and time since discontinuation of HCV therapy, as well as indicator variables for any reported alcohol consumption or injection drug use in the past 6 months and HIV therapy status. We applied both SIMEX approaches to correct measurement error in GGT. Although GGT is strongly correlated with APRI, recent research suggests that these measures reflect different disease features. Everhart and Wright (38) argue that GGT is associated with disease activity, while platelet counts (the denominator of APRI) capture disease severity; they further conclude that GGT may be more important prognostically than either aspartate aminotransferase or alanine aminotransferase for persons with advanced liver disease. In a more recent study, Mandorfer et al. (39) determined that GGT was an independent predictor of failure of HCV treatment to produce SVR. Note that the exposure variable represents a (biological) response, rather than a clinician-driven decision to modify or initiate treatment, and it is therefore affected by the error-free GGT value rather than the error-prone measurement available to the clinician. Our observation period began at the first study visit after completion of HCV therapy and concluded at the third posttherapy visit.

We use the following notation:

• $L_1{}^{\ast }=\text{lo}{\text{g}}_{10}(\text{GGT})$ at first (baseline) visit after completing HCV therapy.

• X₁ = 1 if SVR is attained between the first and second study visits; otherwise X₁ = 0.

• Y = log₁₀(APRI) at the third visit after completing HCV therapy.

Note that logarithmic transformation of the APRI score in a standard linear regression model produces estimates of the median APRI rather than the mean (40). Prior to analyses, we log-transformed $L_1{}^{\ast }$ values. For SIMEX, the standard deviation of the test error on $L_1{}^{\ast }$ was specified as 0.247, based on a recent systematic review (41). We addressed missing values in covariates using multiple imputation and the mice package in R (42). Because current HCV therapy may influence APRI measures, we censored individuals who reinitiated therapy, and we estimated inverse-probability-of-censoring weights for those who remained uncensored. We also censored persons with missing information on SVR status at the first or second study visit. To obtain estimates of the percent decrease in APRI reported below, we computed 1 − 10^β. Additional details on the analysis are available in Web Tables 5 and 6.

RESULTS

Estimates from the naive model (Table 3) ignoring measurement error in GGT suggested a 45% decrease in median APRI among persons attaining SVR, relative to those not experiencing SVR (β = −0.26, 95% confidence interval (CI): −0.40, −0.11).

Table 3.

Association Between a Sustained Virological Response to Hepatitis C Virus Treatment at 12 Weeks Posttherapy and Progression of Liver Disease, as Measured by the Aspartate Aminotransferase:Platelet Ratio Index, Canadian Co-Infection Cohort Study, 2003–2014

Variable	Model
	Naive MSMa		Direct SIMEX Correction		Indirect SIMEX Correction
	$\hat{\beta }$	95% CIb	$\hat{\beta }$	95% CI	$\hat{\beta }$	95% CI
SVR at third posttreatment visit	−0.26	−0.40, −0.11	−0.19	−0.38, −0.01	−0.17	−0.36, 0.01
Female sex	−0.09	−0.25, 0.09	−0.12	−0.32, 0.07	−0.08	−0.29, 0.10
Age, per 10 years	−0.07	−0.18, 0.03	−0.09	−0.21, 0.03	−0.08	−0.21, 0.04
Duration of HCV infection, per 10 years	0.03	−0.04, 0.09	0.02	−0.07, 0.11	0.03	−0.07, 0.12
HCV genotype of 2/3/4	0.00	−0.19, 0.19	0.02	−0.24, 0.28	−0.03	−0.26, 0.25

Abbreviations: CI, confidence interval; HCV, hepatitis C virus; MSM, marginal structural model; SIMEX, simulation-extrapolation; SVR, sustained virological response.

^a The naive MSM does not correct for measurement error in log₁₀(γ-glutamyltransferase).

^b All 95% CIs were computed by means of the nonparametric bootstrap percentiles approach.

The error-corrected models suggested a more modest relationship between SVR and APRI. The direct SIMEX-corrected model estimated a 35% decrease in median APRI relative to persons not experiencing SVR (β = −0.19, 95% CI: −0.38, −0.01). Similarly, the indirect SIMEX model estimated a 32% decrease in median APRI associated with SVR (β = −0.17, 95% CI: −0.36, 0.01). These results appear to support the hypothesis that successful treatment for HCV infection is associated with a meaningful improvement in liver health relative to persons who are treated but do not attain SVR.

DISCUSSION

We proposed, assessed, and validated 2 approaches to correcting measurement error in time-varying covariates in MSMs, by adapting Cook and Stefanski's SIMEX procedure (18) to this specific setting. Our simulation results suggest that both the direct and indirect SIMEX approaches largely reduce bias when exposure depends on the true value of mismeasured time-varying covariates. This finding is of practical importance, as indirect correction is supported in several statistical software packages (43, 44).

SIMEX-based estimators exhibited some bias with increasing measurement error variance and increasing strength of the covariate-outcome association; however, they provided uniformly better coverage than the naive estimators. We observed only minor differences between the 2 SIMEX approaches, which produced systematically more accurate estimators than those from the naive model. These findings and the easier implementation of the indirect approach suggest that the latter may be recommended for most applications.

Most estimators to which SIMEX has been applied do not have closed-form solutions, and therefore theoretical proofs are infeasible; this is true of our proposed SIMEX-based estimators also (45–48). Thus, we followed the previous literature by demonstrating performance by simulation, including the SIMEX-based estimators’ capacity to reduce bias under differing assumptions about the “true” data structure.

Our secondary simulations confirmed that ignoring measurement error was a reasonable choice if treatment assignment depended on the error-prone covariate; in this case, correcting for error introduced bias. However, MSMs are increasingly being used to estimate the causal effects of exposures that are neither treatments nor treatment decisions, where measurement error in time-varying covariates should be considered, and a reliable estimate of the error variance is available (49–51). The case study we have presented is one such example. Our findings support the application of measurement error models to time-varying covariates within this context.

We acknowledge several limitations of our study. MSMs are frequently applied to data collected over many points in time, including larger numbers of covariates, several of which may exhibit measurement errors. Due mostly to computational burden, the scenarios we examined were limited to a simplified 2-interval setting. However, the consistency of simulation results across a range of relevant parameters suggests that the potential advantages of SIMEX-corrected MSMs extend to multiple time points. Furthermore, practical application of the SIMEX procedure requires that the measurement error variance is known or can be estimated relatively well. We find it encouraging that sensitivity analyses demonstrated that a small degree of variance misspecification (<25%) did not markedly bias our corrected estimates, which remained less biased than the naive estimates even when we under- or overspecified the error variance by as much as 50%. This finding should be interpreted cautiously, as our investigations were limited to simple models fitted to simulated data (52).

Measurement error in time-varying covariates remains an important issue that must be carefully considered in any analysis. When the exposure of interest is based on the true (not mismeasured) covariate and the measurement error variance may be reasonably well estimated, the SIMEX procedure is a useful method with which to address error in time-varying covariates. Moreover, while several methods for measurement error correction exist, few are implemented in commonly used statistical packages; SIMEX is a notable exception. We have shown how analysts can take advantage of this approach to correct measurement error in time-varying covariates within the MSM framework.