Quantifying Nonnative Interactions in the Protein-Folding Free-Energy Landscape

Abstract

Protein folding is a central problem in biological physics. Energetic roughness is an important aspect that controls protein-folding stability and kinetics. The roughness is associated with conflicting interactions in the protein and is also known as frustration. Recent studies indicate that an addition of a small amount of energetic frustration may enhance folding speed for certain proteins. In this study, we have investigated the conditions under which frustration increases the folding rate. We used a C_α structure-based model to simulate a group of proteins. We found that the free-energy barrier at the transition state $\left(\Delta F\right)$ correlates with nonnative-contact variation $\left(\Delta A\right)$, and the simulated proteins are clustered according to their fold motifs. These findings are corroborated by the Clementi-Plotkin analytical model. As a consequence, the optimum frustration regime for protein folding can be predicted analytically.

Introduction

Understanding the underlying folding mechanism of a protein to its functional compact three-dimensional structure is one of the great challenges of modern science. Failure in the process of a protein to achieve the correct folded native state can cause a series of pathological conditions, like neurodegenerative disorders, including Alzheimer’s and Parkinson’s diseases (1). Over the last decades, the energy-landscape theory has been a consistent framework in revealing protein-folding mechanisms (1, 2, 3, 4, 5). This theory states that the energy landscape of globular proteins resembles a funnel of structures progressively folded en route to the native state with its bottleneck narrowed at the transition state between unfolded and folded ensembles (6, 7, 8, 9). The energy-landscape theory is successful in explaining, qualitatively and quantitatively, folding studies in theoretical (10, 11, 12, 13) as well as experimental (14, 15, 16, 17) investigations. Based on energy-surface theory, many computational models have been developed to predict folding mechanisms, rates, and stability parameters connected with experiments (9, 18, 19, 20, 21, 22).

The protein-folding energy surface is multidimensional, and it has a funnelled topography as a function of the reaction coordinate, usually described by the fraction of native contacts, Q. The funnel theory describes protein folding as an ensemble of conformations gradually diffusing from the unfolded state (lower Q), high entropic and energetic conformations at the top of the surface funnel, to the native state (higher Q), the lowest entropic and energetic state at its bottom (23, 24, 25, 26, 27, 28). Proteins are naturally designed through evolution, so that folding pathways toward the native state are not dominated by bumps due to local energetic traps (5, 29, 30, 31, 32, 33). Nature-designed sequences have the ability to fold completely on biological timescales.

To fold, the funnel energy slope must be steep enough to overcome the roughness and minimize local energetic trapping (13), or energetic frustration (21). Energetic frustration occurs due to the impossibility of satisfying all favorable energetic interactions simultaneously during folding events (34, 35, 36, 37), allowing the formation of nonnative contacts (pairs of residues not in contact at the native state). Kinetically foldable proteins are naturally selected throughout the evolution process so that the native state is minimally frustrated (34, 35, 36, 38, 39).

Clementi and Plotkin introduced a theoretical/analytical model that takes into account the effects of nonnative interactions on the folding rate and on the folding free-energy barrier (40). This model indicates that a nonzero amount of nonnative energy interaction may enhance protein folding rates. The theory for the folding speed limit upon the nonnative energetic frustration is well discussed in the literature (41, 42), and studies have been done on specific proteins regarding nonnative interactions (26, 43, 44, 45). In our previous article (46), using C_α structure-based models (SBMs) and homogeneous frustration, the maximum value of energetic frustration that can be added to the system to speed up folding rates was quantified. This maximum value was named the optimum energetic frustration $\left({ϵ}_{\text{f}}^{\text{opt}}\right)$ of each protein, and it was determined by analyzing the effect of the energetic frustration value $\left({ϵ}_{\text{NN}}\right)$ on free-energy barrier height and folding time. It was shown that not all proteins could have folding rates enhanced by including a small amount of frustration, i.e., ${ϵ}_{\text{f}}^{\text{opt}}$ is zero. However, for all of the other proteins, ${ϵ}_{\text{f}}^{\text{opt}}$ correlates with the free-energy barrier height (21) and the contact order parameter (47), clustering the proteins accordingly to their motif (48).

In this article, we seek the connection between the Clementi-Plotkin analytical model (40) and our previous computational results (46) through analysis of the underlying mechanism in nonnative-contact formation during folding. We show that the perturbed free-energy barrier variation $\left(\Delta \Delta F\right)$ depends on the nonnative energetic contact parameter $\left({ϵ}_{\text{NN}}\right)$, and on the nonnative-contact variation $\left(\Delta A\right)$, in the folding transition state $\left(Q^{\text{ts}}\right)$. These three quantities were calculated for a group of proteins using SBM simulations. The difference between the perturbed and nonperturbed SBM model, in both analytical and computational results, explains quantitatively the relevance of the nonnative-contact formation in the pretransition state for the maximal folding-speed-limit mechanisms. The former results of grouping the simulated proteins by their folding motif were also recovered.

Materials and Methods

In this study, a group of 15 proteins (46) was used to investigate the effect of nonnative interactions in the transition state. Proteins were simulated using molecular dynamics and a coarse-grained $C_{\alpha }$ SBM (12, 49). Despite the simplicity of this model, it can capture important characteristics of protein-folding mechanisms, as has been shown by computer simulations (9, 49, 50, 51). The agreement between experimental and computational folding rates using the SBM is remarkable, as has been shown by Chavez et al. (21).The simulation details are explained in the Supporting Material.

Effect of nonnative interactions on the free-energy barrier

Two order parameters are used by Clementi and Plotkin to map the folding process in their analytical model: the fraction of native contacts (Q) and the fraction of nonnative contacts (A) (40). These two order parameters are normalized between 0 and 1. The fraction of nonnative contacts depends on Q: the more native contacts are formed, the fewer nonnative interactions are allowed. The theoretical model does not allow nonnative contacts for $Q=1$. The native attraction is characterized by the mean attraction energy, ε (ε $<$ 0), and two energy scales are used to analyze the nonnative contribution: the mean energy of a nonnative interaction $\left({ϵ}_{\text{NN}}\right)$ and the energetic variance of nonnative interaction $\left(b^2\right)$. Nonnative interactions are designed to be weaker when compared to native interactions in a perturbative way. Expressions for thermal energy (E), free energy (F), and entropy (S) as a function of Q, A, and temperature (T) were normalized by the maximum number of contacts, M (Eqs. 7(a)–7(c) in (40)). The folding temperature of the model $\left(T_{\text{F}}^0\right)$ was defined as the temperature at which folded and unfolded states have the same probability. Thus, at $T_{\text{F}}^0$, $F\left(0,A\right)\approx F\left(\mathrm{1,0}\right)$ for ${ϵ}_{\text{NN}}=b^2=0$. If $A^{\ast }$ (Q) is the most probable value of A in a certain Q, the difference between the most probable value in the transition state, $A^{\ast }\left(Q^{\text{ts}}\right)$, and in the unfolded state, $A^{\ast }$ (0), is given by

$$\Delta A^{\ast }\left(Q^{\ne }\right)\equiv A^{\ast }\left(Q^{\text{ts}}\right)-A^{\ast }\left(0\right).$$ (1)

The variation in free energy between the unfolded and the transition states at $T_{\text{F}}^0$ is calculated. It is shown that the free-energy barrier height $\left(\Delta F\right)$ corresponds to the sum of the free-energy barrier between these states in the absence of nonnative forces $\left(\Delta F^0\right)$ plus a term referring to energetic frustration:

$$\frac{\Delta F}{T_{\text{F}}^0}=\frac{\Delta F^0}{T_{\text{F}}^0}+M\left(\frac{{ϵ}_{\text{NN}}}{T_{\text{F}}^0}-\frac{b^2}{2T_{\text{F}}^{02}}\right)\Delta A^{\ast }\left(Q^{\ne }\right).$$ (2)

Since ${ϵ}_{\text{NN}}$ always has negative values, Eq. 2 can be analyzed in two conditions. If $\Delta A^{\ast }\left(Q^{\ne }\right)>0$, more nonnative contacts are formed in the transition state than in the unfolded state, and the third term of Eq. 2 is negative, leading to a decrease in the free-energy barrier when compared with the barrier without nonnative interactions $\left(\Delta F<\Delta F^0\right)$. This condition implies an increase in the folding rate. On the other hand, for $\Delta A^{\ast }\left(Q^{\ne }\right)<0$, the opposite happens: nonnative interactions lead to an increase in the barrier, decreasing protein folding rates.

Nonnative-contact calculation

Nonnative contacts for the C_α SBM simulations were defined according to the following criteria:

• 1)Nonnative contacts cannot be listed in the first native-contact map generated from the protein native configuration (see the Supporting Material);
• 2)Nonnative contacts consist of any two nonbonded amino acid residues separated by at least four residues in the main chain and at a distance of up to 6 Å from each other;
• 3)Nonnative contacts cannot have a >30% probability of being found on folded structures $\left(Q>0.9\right)$, and if that is the case, these new contacts are included in the final native-contact list.

The difference in the number of nonnative contacts $\left(\Delta A\right)$ between the transition and the unfolded states is calculated by

$$\Delta A=\overline{A}\left(\text{TS}\right)-\overline{A}\left(\text{Unf}\right),$$ (3)

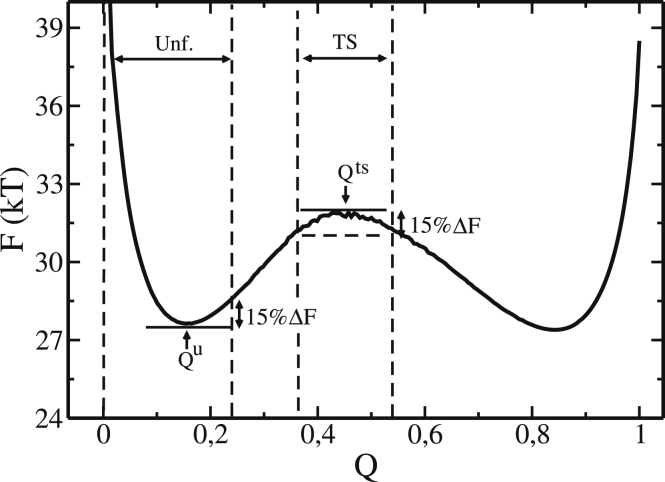
with $\overline{A}$ being the average of nonnative contacts formed in the transition state (TS) and in the unfolded state (Unf). The TS and the unfolded regions are defined using the free-energy profile as a function of the native contacts $\left(F\left(Q\right)\right)$ for the respective protein (Fig. 1). The unfolded region is defined as the region that involves all states from $Q=0$ to the configuration in which the protein reaches $15\text{\%}$ of barrier height $\left(\Delta F\right)$ after the unfolded minimum. On the other hand, the transition region is defined as the region that involves all states located inside the free-energy barrier and having a free energy $F\left(Q\right)\ge 85\text{\%Δ}F$. $\Delta F$ is calculated by the difference between the peak of the free-energy barrier $\left(F^{\ne }=F\left(Q^{\text{ts}}\right)\right)$ and its unfolded minimum $\left(F_{\text{unf}}=F\left(Q^{\text{u}}\right)\right)$, i.e., $\Delta F=F^{\ne }-F_{\text{unf}}$, as shown in Fig. 1. The values of $15\text{\%}$ and $85\text{\%}$, described above, were chosen because they delimit the unfolded and folded states and allow the presence of a pretransition region for all proteins studied in this work, including those with low free-energy barriers.

Figure 1.

Free-energy profile (F) as a function of the native-contact fraction (Q) at the folding temperature $\left(T_{\text{F}}\right)$ for a typical protein (Ubiquitin, PDB: 1UBQ). $Q^{\text{u}}$ is the native-contact fraction that corresponds to the first minimum in the unfolded state and $Q^{\text{ts}}$ corresponds to the transition state at the free energy barrier peak. The region between the first two vertical dashed lines is defined as the unfolded region (Unf). The region delimited by the third and fourth vertical dashed lines, which involves the free-energy barrier peak, is defined as the transition region (TS). $\Delta F$ is the variation in free energy between the unfolded and transition states $\left(\Delta F=F\left(Q^{\text{ts}}\right)-F\left(Q^{\text{u}}\right)\right)$.

Results and Discussion

Correlation between nonnative-contact variation and the free-energy barrier without energetic frustration

In accordance with the Clementi-Plotkin model (40) in Eq. 2, the change in folding rates is directly related to the difference in the number of nonnative contacts that are formed in the transition and unfolded states $\left(\Delta A\right)$. As described in the previous section, if $\Delta A$ is positive, the addition of an attractive interaction between nonnative contacts decreases the free-energy barrier and increases the folding rate. To test the correlation between the number of nonnative contacts and the height of the free-energy barrier without frustration $\left(\Delta F^0\right)$, the number of nonnative contacts formed during the folding process for 15 proteins was calculated (see Table 1).

Table 1.

Data Obtained for the 15 Proteins Studied and Sorted by $\Delta F^0$

Protein	PDB	Amino Acids	M	RCO	ΔF0 (kBT)	ΔA (× 10−3)
${\alpha }_{3}D$	2A3D	73	136	0.095	0.23	−5.44
PtABD	1BDC	60	102	0.086	0.36	−0.98
EnHD	1ENH	54	111	0.13	0.71	−9.81
IM9	1IMP	86	178	0.11	1.56	−4.44
HHCC	1HRC	104	246	0.11	1.79	−7.10
PtL	2PTL	60	136	0.18	2.13	2.05
ADA2h	1PBA	81	175	0.14	2.38	3.60
PtG	2K0P	56	139	0.17	2.95	4.17
CI2	1CIS	66	152	0.16	3.00	−1.25
SH3	1FMK	61	152	0.19	3.89	3.94
Ubiquitin	1UBQ	76	188	0.15	4.34	1.27
HPr	1HDN	85	222	0.18	5.06	1.30
CSPTm	1G6P	66	180	0.17	5.69	5.00
TWIg	1WIU	93	253	0.20	5.86	10.19
αAIT	2AIT	74	196	0.19	6.21	11.68

Data included in the table for the proteins shown are the Protein Data Bank (PDB) code, the number of amino acids, the number of native contacts (M), the relative contact order (RCO), the free-energy barrier without energetic frustration (ΔF⁰), and the variation in the fraction of nonnative contacts (ΔA).

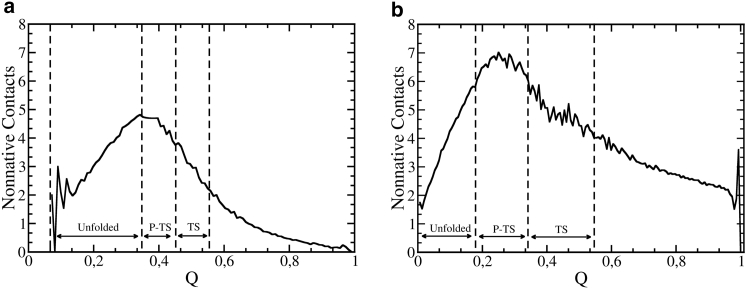
The average number of nonnative contacts formed during the folding process varies for each protein. For example, Fig. 2 shows the average number of nonnative contacts formed during the folding process for two proteins, EnHD (Fig. 2 a) and SH3 (Fig. 2 b). Fig. 2 shows that for both proteins, there is an increase in the formation of nonnative contacts up to the maximum value at the pretransition region (P-TS). After the maximum value, the number of nonnative contacts has a monotonic decrease. Beyond the small difference in the average number of nonnative contacts formed, these proteins can be differentiated by their values and signals of $\Delta A$. The protein EnHD, and also the proteins ${\alpha }_3$ D, PtABD, EnHD, HHCC, IM9, and CI2, formed more nonnative contacts on average in the unfolded than in the transition region, i.e., $\Delta A<0$. In this case, according to Eq. 2, it is expected that the addition of an energetic frustration in these proteins will be responsible for reducing the folding rates. On the other hand, for proteins PtL, ADA2h, PtG, SH3, Ubiquitin, HPr, TWIg, CSPTm, and αAIT, the formation of nonnative contacts in the transition state exceeds the number formed in the unfolded state, and therefore, $\Delta A>0$. $\Delta A$ values calculated for all 15 proteins are shown in Table 1.

Figure 2.

Average number of nonnative contacts $\left(\overline{A}\right)$ as a function of the native-contact fraction (Q) at the folding transition temperature $\left(T_{\text{F}}\right)$ for the proteins (a) EnHD and (b) SH3. Vertical dashed lines delimit the defined regions for the unfolded (Unf), transition (TS), and pretransition (P-TS) states. $\overline{A}$ reaches its maximum at the pretransition state for both cases.

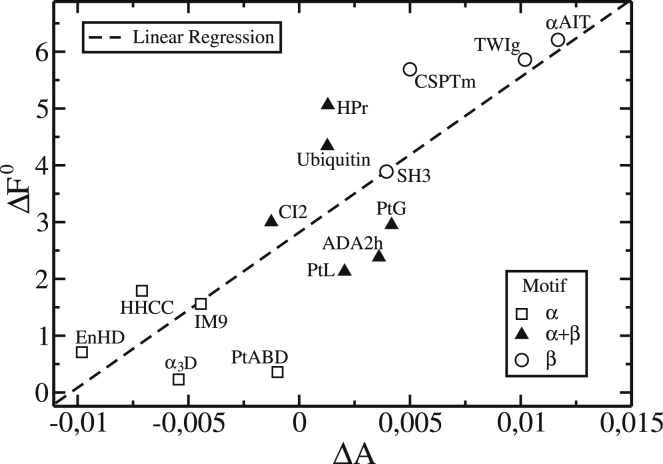
The correlation between the free-energy barrier height ($\Delta F^0$, in kT units), without the energetic frustration term, and the variation in the number of nonnative contacts $\left(\Delta A\right)$ for the 15 proteins studied are shown in Fig. 3. The free-energy barrier correlates with the nonnative-contact variation by a factor of 0.81 (linear correlation) and it clusters the simulated proteins by their fold motifs. This result shows a strong correlation between these two variables and indicates that α-helix proteins make, on average, fewer nonnative contacts in the transition state than in the unfolded state. The opposite effect happens with proteins with β-sheets. This result appears not to be dependent on the chain length. The positive linear correlation coefficient indicates that proteins with a low variation in nonnative contacts $\left(\Delta A\right)$ have a low free-energy barrier and that the free-energy barrier increases with the increase in variation of nonnative contacts.

Figure 3.

The free-energy barrier $\left(\Delta F^0\right)$ as a function of nonnative-contact-fraction variation $\left(\Delta A\right)$ for all proteins studied. Proteins are represented by their fold motif according to the SCOP database criterion (48): α (squares), β (circles), and $\alpha +\beta$ (triangles). The linear-fit correlation to the data is 0.81. $\Delta F^0$ is strongly correlated to $\Delta A$, and it clusters the simulated proteins by their motif in three distinct groups. The data were extracted from Table 1 using $\Delta F^0$ (without energetic frustration).

The product of $\Delta F^0$ by native contact order was found to be the best parameter to correlate with optimum frustration values, according to the principal-component analysis shown by Contessoto et al. (46). It will be seen that the $\Delta A$ values for each protein are also strongly correlated with relative contact order (RCO) × $\Delta F^0$, as can be seen in Fig. S1. The linear correlation of 0.84 between these parameters indicates that free-energy barrier height multiplied by the contact order is a good parameter for predicting the effect of the energetic frustration on these proteins, as was suggested in the earlier study (46). The $\Delta F^0$ and RCO values are shown in Table 1.

Comparing analytical and computational results

In this section, the $\Delta A$ values and the variation in the free-energy barrier $\left(\Delta \Delta F=\Delta F^{\text{frus}}-\Delta F^0\right)$ when the energetic frustration $\left({ϵ}_{\text{NN}}\right)$ is added to the C_α model are presented. The results were compared with those predicted by the Clementi-Plotkin model (Eq. 2) and the optimal energetic frustration from our previous study (46).

This study uses homogeneous energetic frustration with no sequence dependence. In our previous article (46), it was shown through principal-component analysis and partial least-squares analysis that the results seem to depend weakly on the frustration potential. In another study, a heterogeneous frustration potential was employed (9) in which energetic frustration was achieved by the addition of a random energy term characterized by a distribution width, b. An increase in folding temperature was observed for some values of $b^2$ and a decrease for high values. These results are analogous to the case of homogeneous frustration. More details regarding the potential used to add frustration to the C_α model can be seen in the Supporting Material. The ${ϵ}_{\text{NN}}$ values used were 0.05, 0.10, and 0.20.

Nonnative-contact formation with energetic frustration

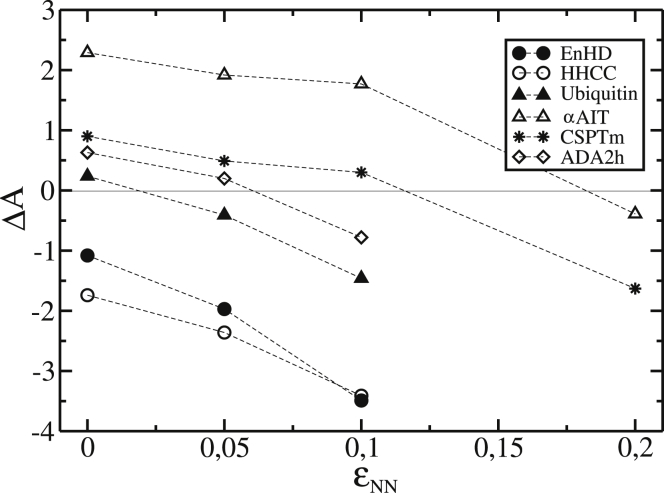
For all proteins studied here, an increase in the nonnative interaction leads to an increase in the formation of nonnative contacts during the folding process. This increase does not occur homogeneously in all ensembles; it becomes more evident in the unfolded and pretransition states. Therefore, depending on the value of ${ϵ}_{\text{NN}}$, a gradual increase in the amount of nonnative contacts is formed before the pretransition state and it can be higher than the average amount formed in the transition region. Thus, the gradual increase in the energetic frustration accounts for the reduction of $\Delta A$ values until it becomes negative, which, according to the Clementi-Plotkin model, makes the increase in frustration unfavorable to the folding process.

Fig. 4 shows the nonnative-contact variation $\left(\Delta A\right)$ as a function of the energetic frustration term $\left({ϵ}_{\text{NN}}\right)$ included in the simulation model. Each protein responds differently when a small quantity of frustration is added. Proteins formed exclusively by α-helixes, such as EnHD and HHCC, shown in Fig. 4, already had a negative value of $\Delta A$, even without the energetic frustration term, and continue to have more negative values of $\Delta A$ when ${ϵ}_{\text{NN}}$ is incremented. For $\alpha +\beta$ proteins, which had, initially, a positive value of $\Delta A$, an increase in the ${ϵ}_{\text{NN}}$ values causes a gradual change of their $\Delta A$ values and signals. Ubiquitin and ADA2h had their signals of $\Delta A$ inverted when the frustration term was 0.05 and 0.1, respectively. These values of ${ϵ}_{\text{NN}}$, which inverted the signal of $\Delta A$, correspond exactly to the optimal energetic frustration determined for these proteins by Contessoto et al. (46). Very similar behavior occurs with CSPTm and αAIT proteins formed mainly by β-sheets. Such proteins had their $\Delta A$ values decreased gradually, but only reached a negative value at larger degrees of frustration (${ϵ}_{\text{NN}}$ = 0.2). In all cases, when proteins formed more nonnative contacts in the unfolded state than in the transition state, ${ϵ}_{\text{NN}}$ was close to the optimal energetic frustration value determined previously (46). In this case, when proteins are in their optimum frustration degree, they are at the same regime as those proteins in which the increase of frustration slows folding.

Figure 4.

Variation in the formation of nonnative contacts $\left(\Delta A\right)$ according to the energetic frustration term $\left({ϵ}_{\text{NN}}\right)$ added in the simulation for six of our simulated proteins. Both axes are calculated at the respective folding temperature. The black line divides the positive and negative values of $\Delta A$. The dotted lines connecting the points are a visual guide. $\Delta A$ is the difference between the numbers of nonnative contacts formed in the transition region and the unfolded region.

The vast majority of proteins have an unfolded dimension that scales with the protein chain length. An increase in the formation of nonnative contacts in the unfolded region can occur when an attractive energetic frustration is added to the simulation, and more unfolded compact structures can be formed, as shown in Fig. 4. Compaction of unfolded structures has been identified and studied computationally and experimentally in some proteins (52, 53, 54, 55, 56). This compaction is associated with the formation of hydropobic cores or with the formation of medium/long-range contacts. These unfolded structural aspects seem to play an important role in the thermodynamics and kinetics of the folding process (52, 57).

Changes in the free-energy barrier height

To compare the variation of the simulated energetic barrier with and without the frustration term, a value of energetic frustration close to the optimal values already determined (46) was used; ${ϵ}_{\text{NN}}$ = 0.05 for α-helix proteins and Ubiquitin, ${ϵ}_{\text{NN}}$ = 0.1 for PtL, PtG, ADA2h, CI2, SH3, and HPr; and ${ϵ}_{\text{NN}}$ = 0.2 for CSPTm, αAIT, and TWIg.

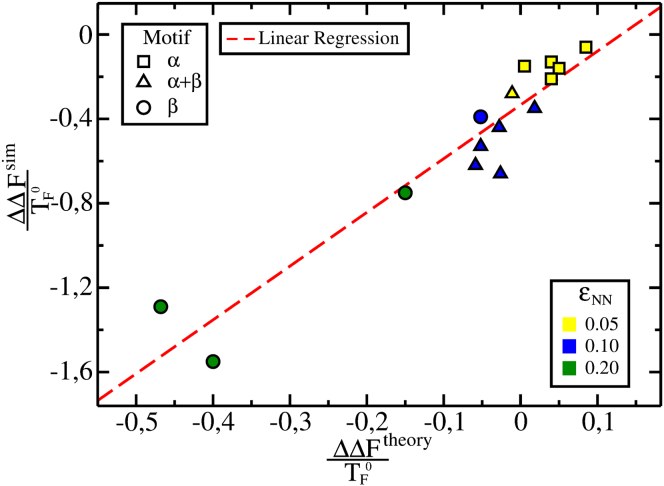
The comparison between the variation in the free-energy barrier height, $\Delta \Delta F^{\text{sim}}$, obtained by the simulations, and $\Delta \Delta F^{\text{theory}}$, given by Eq. 2, is shown in Fig. 5. $\Delta \Delta F^{\text{theory}}$ is calculated using the M, $T_{\text{f}}^0,$ and $\Delta A$ parameters calculated by simulation. Fig. 5 shows that the simulated results and the analytical model predictions are strongly correlated, with linear fit correlation 0.95. Thus, when the proteins are folded with a small degree of frustration close to their optimal value, the computational and the analytical result have the same behavior. Also, Fig. 5 shows the results clustered according to their folding motifs; β proteins have lower $\Delta \Delta F$ and high ${ϵ}_{\text{NN}}$, $\alpha +\beta$ proteins have intermediate $\Delta \Delta F$ and ${ϵ}_{\text{NN}}$, whereas α-proteins have high $\Delta \Delta F$ and low ${ϵ}_{\text{NN}}$, which is in agreement with the analytical model (Eq. 2) and the results from Fig. 3.

Figure 5.

Analytical and simulated free-energy barrier variations when energetic frustration is added $\left(\Delta \Delta F=\Delta F^{\text{frus}}-\Delta F^0\right)$. Each protein is represented by its respective motif according to the SCOP database criterion (48)—α (squares), β (circles), and $\alpha +\beta$ (triangles)—and colored by the energetic frustration $\left({ϵ}_{\text{NN}}\right)$ added to the simulation: 0.05, 0.1, and 0.2. Both axes are normalized by the respective folding temperature in the absence of ${ϵ}_{\text{NN}}$$\left(T_{\text{F}}^0\right)$. The dotted line is the linear regression of the two data sets. The values of $\Delta \Delta F^{\text{sim}}$ are obtained by simulation using the weighted histogram analysis method with Q (the fraction of native contacts) as an order parameter. The values of $\Delta \Delta F^{\text{theory}}$ are obtained using Eq. 2 as reference with $b=0$ and $\Delta A$ calculated by the simulation of each protein. The linear correlation to the data is 0.95. To see this figure in color, go online.

Conclusions

The difference in the number of nonnative contacts formed between the unfolded and the transition states showed a strong correlation with the height of the free-energy barrier, since proteins with a low free-energy barrier were those with fewer nonnative contacts formed in the transition state than in the unfolded state. In addition, the results suggest that proteins formed mainly by α-helix structures form more nonnative contacts in the unfolded state, in such a way that the ratio between the numbers of nonnative contacts formed in the transition state makes the energetic frustration unfavorable for them.

Energetic frustration, as it has been modeled in this study, proved to be responsible for increasing the formation of nonnative contacts, especially in the unfolded state. Frustration has also proved to reach a maximum threshold as the $\Delta A$ values is decreased, leading proteins to form fewer nonnative contacts in the transition state than in the unfolded state. The energetic frustration value, which changes the sign of $\Delta A$ for almost all proteins tested, was close to the optimal frustration determined previously by Contessoto et al. (46). This corroborates the results expected by the theory developed by Clementi and Plotkin and makes a connection with the former computational analysis. Despite all the approximations that were made for the simulation and the analytical models, both resulted in agreement in 95$\text{\%}$ of the cases, as can be seen in Fig. 5.

Although it appears to be controversial that the presence of nonnative contacts may favor the folding process, this can be explained mainly by the fact that when inserting an energetic frustration, we add an attractive interaction energy in the midst of the contacts, which according to the results obtained, leads to an increase in the nonnative collapse. The increase in the nonnative collapse may favor access to other structures, which may be responsible for bringing amino acids close to each other, which in turn favors the formation of native contacts, accelerating the kinetics of the process. One question that arises from these studies is about the nature of the changes and stabilizations observed when a nonnative potential is introduced. Such a stabilization may originate with entropic or enthalpic factors. In preliminary studies, we observed variations dependent on the protein motifs. Further studies should not only investigate different motifs, but also analyze such effects in terms of their dependence on the type of frustration used.

Author Contributions

P.R.M., J.C., and V.B.P.L. designed research. P.R.M. performed research. P.R.M. and V.G.C. contributed analytical tools. Data were analyzed by P.R.M., V.G.C., R.J.O., J.C., and V.B.P.L. All authors contributed to the manuscript writing.

Editor: Daniel Raleigh.

Supporting Citations

References (58, 59, 60, 61, 62, 63) appear in the Supporting Material.