Abstract
The stochastic behavior of single ion channels is most often described as an aggregated continuous-time Markov process with discrete states. For ligand-gated channels each state can represent a different conformation of the channel protein or a different number of bound ligands. Single-channel recordings show only whether the channel is open or shut: states of equal conductance are aggregated, so transitions between them have to be inferred indirectly. The requirement to filter noise from the raw signal further complicates the modeling process, as it limits the time resolution of the data. The consequence of the reduced bandwidth is that openings or shuttings that are shorter than the resolution cannot be observed; these are known as missed events. Postulated models fitted using filtered data must therefore explicitly account for missed events to avoid bias in the estimation of rate parameters and therefore assess parameter identifiability accurately. In this article, we present the first, to our knowledge, Bayesian modeling of ion-channels with exact missed events correction. Bayesian analysis represents uncertain knowledge of the true value of model parameters by considering these parameters as random variables. This allows us to gain a full appreciation of parameter identifiability and uncertainty when estimating values for model parameters. However, Bayesian inference is particularly challenging in this context as the correction for missed events increases the computational complexity of the model likelihood. Nonetheless, we successfully implemented a two-step Markov chain Monte Carlo method that we called “BICME”, which performs Bayesian inference in models of realistic complexity. The method is demonstrated on synthetic and real single-channel data from muscle nicotinic acetylcholine channels. We show that parameter uncertainty can be characterized more accurately than with maximum-likelihood methods. Our code for performing inference in these ion channel models is publicly available.
Introduction
Ligand-gated ion-channels are transmembrane proteins that enable fast cell-to-cell communication, which is crucial for the functioning of the nervous system and for the control of skeletal muscle. Conformational changes in the protein are induced by the binding of an agonist, such as a neurotransmitter, to the extracellular domain of the protein. These conformational changes lead to the opening of the gate of the channel pore within the protein, enabling the flow of ions down their electrochemical gradient. The resulting all-or-nothing current has an amplitude typically in the pA range at physiological membrane potential and ionic concentrations and can be recorded by patch-clamp techniques (1).
The conformational changes that occur during the gating process cannot be observed directly and therefore must be inferred from such recordings. These single-channel data are used to fit and assess mechanistic Markov models for description of the binding events and conformational changes that occur during channel activation. Such mechanistic mathematical models consist of components that may be directly interpreted as part of the system being modeled, allowing investigation of the underlying physical process.
Ion channels are unique among proteins in allowing the prolonged recording of single molecule activity at high temporal resolution. This in principle allows the fitting of models that are unusually detailed and relatively close to the physical reality of activation. For instance, in a ligand-gated ion channel, this reaction consists of the binding of several neurotransmitter molecules followed by conformational changes that eventually result in the channel opening. Fitting an appropriately parameterized model to estimate the rate constants for the different transitions allows us to establish the simplest model that adequately describes the observations and thus to probe the energy landscape of the channel. In turn, this is useful to compare with structural information and with molecular dynamics simulations of protein dynamics.
Single-channel records show only whether the channel is open or closed and realistic channel activation requires several closed and several open states. Ion-channel kinetics may be described mathematically using aggregated Markov models, because it is not possible to directly observe the conformational state of the protein, and their memoryless nature appears to match observed channel behavior. There are obvious difficulties, however. While temporal resolution can be very good for single-channel recordings, 10–30 μs at best, it still is not infinite, and this prevents the identification of shorter dwells of the channel in the open or closed states. These short dwells commonly occur in most ion-channels and, importantly, result in missing data, which we must account for in our modeling approach.
Recordings are usually idealized, that is, converted from digitized records to lists of intervals using various methods, such as time-course fitting, threshold crossing, and hidden Markov models to convert the recording to a putative sequence of open and closed intervals (2). Models of increasing complexity are fitted to these idealized data until a reasonable description of the channel behavior is obtained. Maximum-likelihood (ML) methods have been to date the most common inferential framework for estimating model parameters from single-channel data. This approach has been found to be useful in examining the activation of channels in the nicotinic superfamily (3, 4, 5, 6, 7). The main limitation of the ML approach, however, is that it is not straightforward to check the parameter nonidentifiability and the impact of parameter uncertainty. Parameter nonidentifiability can occur in two scenarios as outlined in Milescu et al. (8). First, there may exist a continuum of parameter values at the ML point such that estimated values of the model parameters cannot be constrained within a finite range. Second, there may exist multiple well constrained but discrete solutions that describe the observed data reasonably well. The first case, which we examine in this article, can be a particular problem for ion-channel models where the underlying structure of the physical process is not directly observable. The model may consequently be overparameterized and there may be great uncertainty in the parameter estimates. The ability to determine parameter identifiability and the impact of parameter uncertainty is vital for allowing physiologically meaningful conclusions to be drawn from a hypothesized ion-channel model, for example, when comparing the action of different channel agonists on a receptor, or when assessing the physical impact of mutations on channel behavior. Theoretical work has explored the maximum number of parameters that can be fitted to single-channel recordings (9) and investigated non-uniqueness of models (10), but these techniques are difficult to apply when fitting models to real experimental data. Assessing the impact of parameter uncertainty on model predictions also remains a challenging problem.
Our group used the approach pioneered by Colquhoun et al. (11, 12) to examine parameter identifiability by assessing standard errors and correlations derived using the empirical covariance matrix calculated at the ML estimate. Thus we verified the properties of the ML estimators for our main results on the nicotinic and glycine channel by extensive simulations (5, 12) showing our approach can reliably detect rate constants as fast as 130,000 s−1 for glycine channels (5). This technique has also robustly revealed intermediate conformational states in the nicotinic and glycine channels (7) and in the ELIC receptor in prokaryotes (13). Despite these successes (6, 7), there are limitations to the use of maximum-likelihood inference. In particular, checking the validity of model parameter estimates by fitting simulations remains an ad hoc laborious process.
There is increasing interest in Bayesian approaches in biophysics (14, 15) and in particular in single-channel analysis, e.g., Rosales (16), Calderhead et al. (17), and Siekmann et al. (18). In Bayesian methods, rate parameters are treated as random variables with a known prior probability distribution. This allows the assessment of parameter identifiability through the calculation of their posterior probability distributions. The uncertainty in these distributions may therefore be directly propagated through before examining uncertainty in the predictions of the model. Bayesian methods are more computationally expensive than ML estimation when the posterior probability distribution is not known analytically and so Markov chain Monte Carlo (MCMC) sampling schemes are required to facilitate Bayesian inference in such models. MCMC schemes are called “samplers” as they derive estimates of this density by defining probabilistic Markov processes that draw samples from such probability distributions.
However, to our knowledge, there is currently no Bayesian approach for ion-channel models that exactly corrects the model likelihood for the two important, inevitable technical constraints of the experimental data, namely the limited temporal resolution in the experimental record and the lack of knowledge about the number of channels in the experimental patch. This article addresses this shortfall thus:
-
1.
We propose a practical approach specially tailored for performing highly efficient Bayesian inference in ion-channel models using multiplicative Metropolis-within-Gibbs (MWG) and adaptive MCMC sampling in a package called BICME, available at https://github.com/miepstei/bicme.
-
2.
We examine how well our approach assesses parameter identifiability and parameter uncertainty using the obtained posterior distribution. We examine how uncertainty in parameter values affects the uncertainty in model predictions and we apply our approach to both synthetic and real experimental data for muscle nicotinic acetylcholine receptors.
-
3.
We correct the model likelihood for missed events and compare the results of MCMC methods with those from existing ML and Bayesian methods (12, 19).
Materials and Methods
Ion-channel stochastic framework
The analysis aims to infer a continuous-time Markov process from a discretely sampled signal that has been idealized by a time-course fitting procedure (2). Idealization deconvolves the channel signal from the filtered output. Within a continuous time framework we seek an expression for the probability of observing an open or shut interval of length t in the experimental recording. To calculate the likelihood, we need the probability density of the length of time for which the channel appears to be open (although it may contain missed brief shuttings) or shut. Using the notation of Colquhoun and Hawkes (20), we outline the derivation for the required probability as follows. Consider a continuous time finite-state Markov process S(t), t > 0, such that S(t) = i denotes that the process is in state i at time t. The state space, I, of this process represents the conformational states of the proposed mechanism. The possible transitions between states in this process are encoded and parameterized with a corresponding generator matrix Q, which contain the rates of transition between the conformational states of the mechanism. Each state in I is either open (set A), or closed (set F).
We begin by assuming that there is perfect resolution in the record. From Colquhoun and Hawkes (20), the Q matrix is partitioned into conformations that produce one of two conductance levels, such that partition QAA represents the transition rates between states that that are open and QAF represents the rates of transitions from open to shut states. Partitions QFF and QFA are denoted similarly for transitions within shut states and from shut states to open states, respectively. The initial goal is to derive a probability for observing an open (or closed) interval of length t given that we cannot directly observe transitions within each conductance class A or F. We can subsequently derive a likelihood for the idealized recording from the probabilities of these individual sojourns (11). Conditional on the process starting in an open state , the individual probabilities of the process remaining within the set of open states A for a sojourn t, and instantaneously transitioning to a shut state , are given by the elements of the matrix GAF(t) in Eq. 1 (20):
| (1) |
The overall probability of observing an opening of length t, where the process starts in any one of the open states and finishes in any one of the closed states, is given as
| (2) |
where the initial vector denotes the probabilities of a sojourn starting in any one of the hidden open states of the process, and the final column vector is a column of ones that sums up the probabilities of finishing in each shut state. The analogous probabilities for a closed sojourn are obtained by switching the partition labels A and F.
Accounting for missed events
Single-channel recordings have finite time resolution, and channel events shorter than the resolution time are not observed in the idealized record. With the continuous time framework outlined above, these unobserved transitions need to be accounted for within the likelihood, and we used the exact missed-events correction of Hawkes et al. (21, 22). The probability of observing an open interval of length t, in the presence of missed events, can be calculated by noting that t can be broken into three parts given the recording resolution time τ. The first part is the open interval of length , which may contain zero, one, or many shuttings of length that are undetected. This first element, , is known as the survivor function as it represents transitions from open states to closed states over a time , during which shut intervals of duration may occur but are not detected. The second component is the instantaneous transition from the open to the shut states, . The third component is a shut interval of length τ that must occur such that the open interval is brought to a close, which is simply . We denote these probabilities analogously to as (11):
| (3) |
Calculating the correction for missed events (Eq. 3) is much more involved than the ideal case (Eq. 1) as it requires calculating the convolution of open intervals with an unknown number of short shut intervals, each less than τ in length, over the period . The required convolution can be expressed as the following Laplace transform (11):
| (4) |
where is the Laplace transform of the matrix defined in Eq. 1, and represents the Laplace transform of a short sojourn in the shut states. A corresponding transform for observed shut intervals, , is found again by reversing the partitioning labels.
Although the Laplace transform in Eq. 4 is intuitively simple to understand, it must be inverted to provide expressions for probability densities of open and closed sojourns as a function of time. Fortunately, an exact inversion of the transform in Eq. 4 was found by Hawkes et al. (21) in the form of a piecewise solution in multiples of the resolution time, such that a different solution is obtained for , , and so on. The solution relies on evaluating a matrix polynomial of increasing order based on multiples of the resolution time, τ. While this calculation becomes numerically unstable for large t, we can employ an asymptotic form of the solution (found by Hawkes et al. (22)), which is accurate for periods of (11). Calculating the asymptotic solution in part relies on a numerical root-finding procedure that adds to the computational burden of evaluating the corrected likelihood.
Accounting for the number of channels in the patch
In general it is not known how many channels are present in the patch from which we are recording. Counting the number of channels simultaneously open provides only a minimum estimate. Our analysis therefore requires that records be broken up into stretches where it can be assumed almost certainly that the gating of a single-channel molecule is being observed, because the gating of multiple channels would be detectable. These stretches of open and shut times will be referred to as “groups”. At low concentrations, channel openings occur in groups termed as “bursts”, during which it is possible to assume that only a single channel is operating, because multiple channel openings during this interval would almost surely result in multiple conductance levels observable in the record. Bursts are separated by long shut times that are the expression of the time taken for the channel to rebind agonist and contain information on the binding steps in the mechanism. The record can be broken up into groups by choosing a time interval value, tcrit, on the basis of the dependence of the shut time distribution on the agonist concentration. Shut intervals longer than tcrit are deemed to separate the record into bursts. Effectively, the long shuttings can be only shortened by the presence of more than one channel in the patch. As a result, the analysis must take into account the fact that the real shut sojourn before the first opening of the burst is equal to or longer than tcrit. This is done by employing corrected initial vectors, known as “CHS vectors” (11), denoted . Their use has been shown to increase the precision of estimates of rate constants from low-concentration records (12). In contrast, a feature of channel activity at high concentrations is the presence of channel desensitization; long stretches of channel activity are separated by desensitized shuttings where there is no observed opening. Given that desensitized states are not typically incorporated in the model, these shuttings are excised from the record and are not used for fitting (12). The analysis uses the groups (clusters) of openings separated by the desensitized gaps. The open probability in the clusters is high enough to be sure that only a single molecule is active. In this instance, equilibrium vectors denoted are used to provide the probability of starting in any open state at the start of the group.
Accounting for an unknown number of channels in the patch requires an alteration to the likelihood calculation. At a given concentration of agonist, , time interval, tcrit, and resolution time, τ, the log-likelihood of the series of bursts or clusters may be defined as the sum of the log probabilities of N individual groups, each of varying length , observed in the record. The initial vector, is either the CHS vector or the equilibrium vector , depending on the agonist concentration in the experiments, as outlined above:
| (5) |
Equation 5 denotes the calculation of the corresponding log-likelihood over a series of recordings at different agonist concentrations, which may similarly be defined as the sum of the log-likelihood at each concentration. The code for this likelihood calculation is publicly available at https://github.com/DCPROGS/HJCFIT.
An introduction to Bayesian inference and MCMC sampling
Unknown parameters in the model are specified as random variables in the Bayesian framework (for further discussion, see Supporting Materials and Methods S1 and S2 in the Supporting Material). Bayes theorem for continuous variables can be stated as per Eq. 6 below:
| (6) |
which requires the specification of a prior probability distribution, , referred to as the “prior”, which captures what is known about the model rate constants before any data is observed. The combination of the model likelihood, as calculated in Eq. 5, and the prior , results in a posterior probability distribution, , referred to as the posterior, that may be calculated only pointwise up to a normalizing constant. This means an analytical description of the posterior as a normalized probability distribution is not available, but the posterior distribution of the rate constants can be estimated using MCMC sampling.
We now provide a basic outline of MCMC sampling. We define a separate discrete-time Markov chain, noting here that this is a different mathematical object from the aggregated Markov process defined previously, which was used to define the likelihood function. The aim of this Markov chain is to sample values from the posterior distribution and has the desirable property that its stationary distribution is the posterior distribution under estimation. The Markov chain is initialized at an initial set of parameters, , and the posterior probability density at this point is calculated. In each MCMC step, we define another probability distribution , known as the proposal distribution, to propose a new set of parameters, , given the current parameter values; for example, a Gaussian distribution with mean equal to the current parameters. The posterior probability density of the proposed parameters is then calculated, . The move is accepted according to the Metropolis-Hastings acceptance ratio (23), which means accepting the move with a probability given as
| (7) |
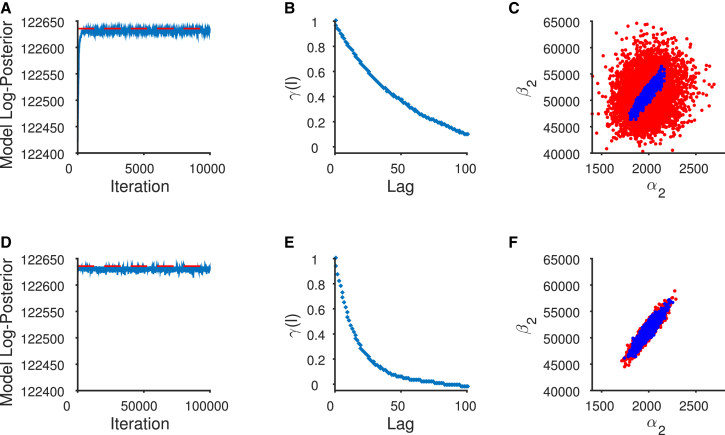
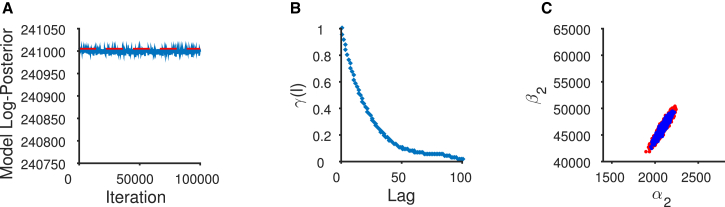
When the sampler uses a symmetric proposal distribution, Eq. 7 simplifies to , the minimum of 1 and the ratio of the values of the posterior distribution at and . If the move is accepted, we set the current parameters equal to the proposed parameters, , else we retain the current parameters. At each iteration, we record the current parameters as another sample from the posterior distribution. The Metropolis-Hastings ratio ensures that the samples we obtain are in fact distributed according to the posterior distribution. We note that there is an initial period during which the chain is converging to the correct distribution; this is known as the “burn-in” phase of the chain. These initial samples generated by our sampler are therefore typically discarded in subsequent analysis and an example of this convergence is shown in Fig. 3 A.
Figure 3.
Chain diagnostics for MWG and adaptive algorithms. (Top panel) MWG pilot sampler. (A) The sampler converges quickly to the posterior mode. (B) The pilot MCMC chain exhibits high levels of autocorrelation in the posterior samples of parameter . Autocorrelation within the sample is defined as correlation between values of at the nth iteration and the value at the n–lth iteration where l is the autocorrelation lag. (C) Five-thousand samples drawn from the posterior distribution show the strong pairwise correlation between the rate constants and . A similar correlation is observed using experimental repetition in Colquhoun et al. (12). The random-walk nature of the MWG sampler results in proposals (red points) away from the ridge of high posterior density, and this increases the number of rejected samples. The accepted samples are shown in blue. This is corrected by the adaptive MCMC sampler (bottom panel). (D) The chain is started at the posterior mode and continues to sample from it. (E) The level of autocorrelation of has been reduced as the sampler has learned the posterior correlation between and . (F) The proposals become much more efficient. This is seen in the substantial overlap between the 5000 accepted samples (blue) and the 5000 proposed samples (red). To see this figure in color, go online.
The main aims when choosing different MCMC samplers are 1) to maximize the speed of convergence of the chain and 2) to minimize the autocorrelations of the MCMC samples generated by the algorithm. The first can be assessed by plotting the parameters or the value of the log-posterior as the MCMC chain iterates and collects the parameter samples. The second can be assessed by calculating the autocorrelation lags of samples taken after the chain has converged. A commonly used metric of sampling efficiency that incorporates the autocorrelation of the samples is the effective sample size (ESS), which gives an indication of the number of equivalent independent samples drawn per sampling iteration or per unit of computational time. Optimizing an MCMC sampler often involves assessing different choices of proposal distribution . (For a brief introduction to Bayesian methods and MCMC sampling algorithms, please refer to the Supporting Materials and Methods S1 and S2; and for a full primer in the context of biophysics, see Hines (15).) We now outline a strategy that demonstrates an efficient sampling approach for evaluating the ion-channel model posterior distribution.
MCMC sampling of ion-channel models with missed events correction
We assume with all our examples that we know little about the values of our rate constants, so that all rate constants have uniform priors. Opening and closing rates and dissociation rates have a prior, , whereas association rates are limited by the theoretical rate of diffusion of the agonist, for which we use a prior of . It should be noted that these are the same bounds that are in place during a typical ML model fitting, but within the Bayesian framework they are specified as the prior probability distributions.
We propose a two-step MCMC sampling strategy that we present in BICME. First, we employ a pilot MCMC based on a MWG sampling scheme (24) to locate quickly the approximate mode of the posterior distribution (25). We then switch to an adaptive MCMC sampler (26), which learns a covariance matrix based on the empirical covariance between the model parameters at this mode. This relies on the assumption that the posterior distribution is unimodal. In fact analysis of single-channel records at a single concentration can result in bimodal distributions (12), although in practice the use of multiple concentrations for fitting often removes this second false mode (27). Nonetheless, a different starting position for the pilot MCMC sampler can be found by sampling initial parameters from the prior distribution to assess convergence to the same mode. Our two-step approach greatly speeds up the inference, because the second adaptive sampler would converge much more slowly during the initial transient phase of the Markov chain’s exploration of the parameter space.
The pilot MCMC chain (see Algorithm S1 in the Supporting Material) is based on a multiplicative MWG algorithm (24), which updates each parameter individually in log space with proposal distribution , where (Algorithm S1). The proposal distribution is scaled during the burn-in phase of the chain to account for varying parameter magnitudes. The benefit of this approach is that the multiplicative proposals in the original parameter space speed up convergence of the Markov chain compared to additive proposals. After convergence and location of the posterior mode, an adaptive MCMC algorithm (26) is employed (Algorithm S2). The second algorithm learns an appropriate covariance structure from the sample history of the chain in such a way that it still converges to the correct stationary distribution; see Haario et al. (28) for full details.
We consider the ESS (see S2 in the Supporting Material) of each sampler as a metric for sampling efficiency. For each sampling algorithm we can assess both the ESS generated per iteration and the ESS per second of runtime, giving an assessment of overall computational efficiency. In practice, it is the second measurement that is often more important, because it gives a direct measure of computational efficiency across algorithms, although this may be highly dependent on specific implementations in code.
Results
Bayesian inference with synthetic data
We initially evaluated our method by examining whether the dual MCMC sampling strategy we propose works on simulated data produced with a well-characterized ion-channel model. Simulated data at three different agonist concentrations were fitted simultaneously. The model we chose (shown in Fig. 1 with simulation rate constants in Table 1) was first proposed by Colquhoun and Sakmann in 1985 (29) to describe single-channel activity of the muscle nicotinic receptor, and was validated by other labs (30). Hatton et al. (3) investigated parameter identifiability when this model was used to fit muscle nicotinic data using ML inference (12). This makes it ideal to test whether Bayesian inference can also successfully identify the model parameters. In contrast to ML inference, we provide estimates of parameter uncertainty derived from the posterior distributions. We display how the uncertainty over the estimated parameters affects the predictions of the observable features of the data by drawing sets of parameters from the posterior distribution and assessing the corresponding variability of the predictions.
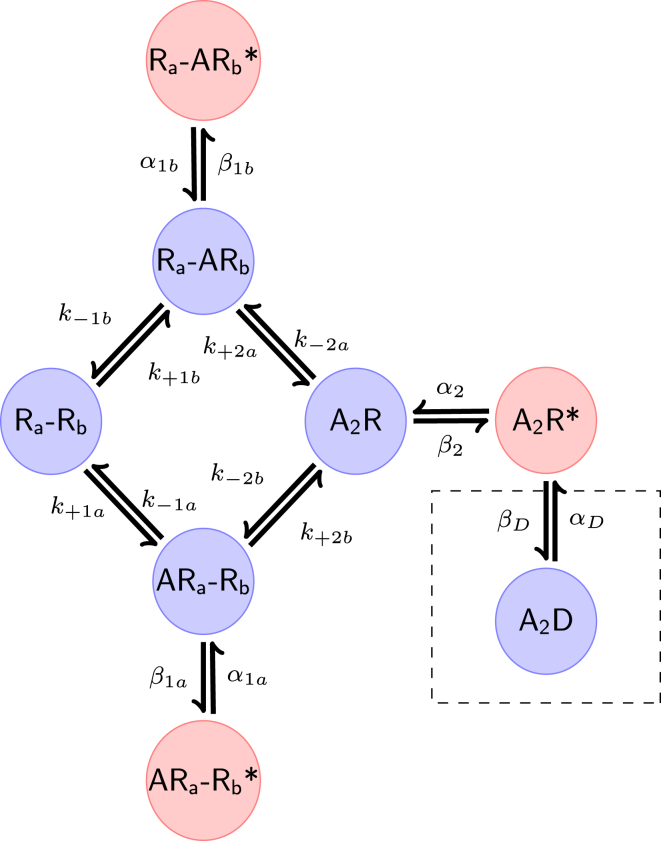
Figure 1.
Example model used for fitting. This seven-state model has previously been used for the analysis of parameter identifiability in acetylcholine receptor gating (3) with limited time resolution using maximum likelihood estimation (12). This model has three open states (in red) and four closed states (in blue) and two agonist binding sites A and B. The data are simulated assuming independent binding sites for the agonist. An additional eighth state inside the dashed box is used to simulate data at high concentrations (10 μM acetylcholine) but is not used for fitting. To see this figure in color, go online.
Table 1.
Parameter Values Used to Simulate Data from the Model in Fig. 1, Reproduced from Colquhoun et al. (12)
| Rate | Units | Value |
|---|---|---|
| s−1 | 2000 | |
| s−1 | 52,000 | |
| s−1 | 6000 | |
| s−1 | 50 | |
| s−1 | 50,000 | |
| s−1 | 150 | |
| s−1 | 5 | |
| s−1 | 1.4 | |
| s−1 | 1500 | |
| M−1 s−1 | 2.0 × 108 | |
| s−1 | 10,000 | |
| M−1 s−1 | 4.0 × 108 | |
| s−1 | 1500 | |
| M−1 s−1 | 2.0 × 108 | |
| s−1 | 10,000 | |
| M−1 s−1 | 4.0 × 108 |
The muscle nicotinic ion-channel model used for fitting (Fig. 1) has three open states, four closed states, and two binding sites, A and B. The dashed box contains a desensitized state used only to simulate high-concentration data (12). This state is not fitted. We assume that the binding sites are independent for this model, i.e., the presence of agonist bound to one site (e.g., site A) does not impact the rates of binding or unbinding of agonist at the other site (site B), and vice versa. As the channel is at steady state, we can assume that the principle of microscopic reversibility holds in the mechanism. This means that, for the mechanism with a cyclic component in Fig. 1, the product of the rate constants going clockwise around the cycle is equal to the product of the rate constants in the anti-clockwise direction (20). This allows an additional rate constant to be constrained (31). The assumption of independent binding sites, together with the assumption of microscopic reversibility in the cycle of the mechanism, reduces the number of rate constants to be estimated from 14 to 10, because, as in Colquhoun et al. (12), , , , and .
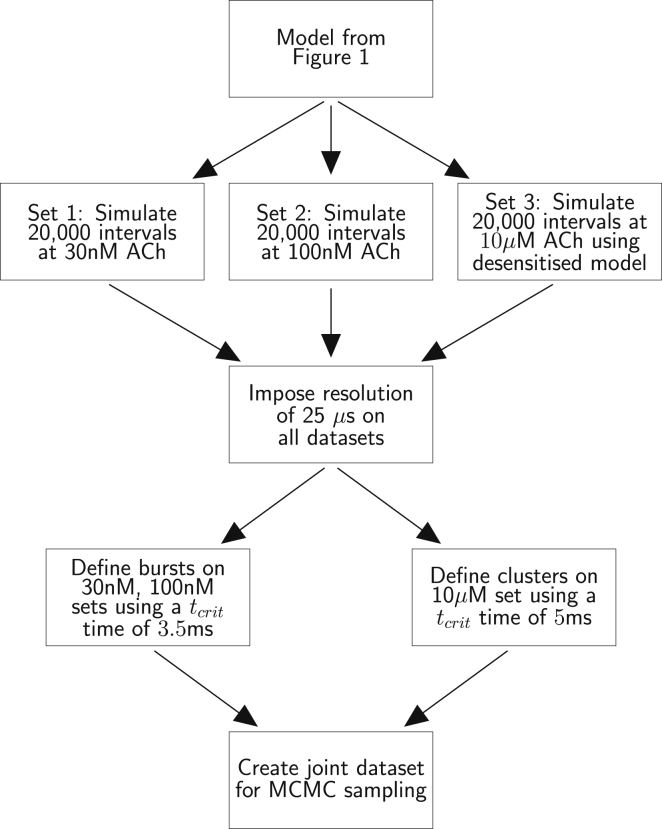
Our design for the experiments reproduce that in the previous ML identifiability study with this model (12), with respect to the number of events, concentration values, the tcrit times chosen to divide the records into groups, and the resolution imposed onto the raw records (25 μs). The same rate parameters were used to generate raw records (Table 1). Fig. 2 shows the workflow for the experiments. Two sets of intervals using low agonist concentrations of 30 and 100 nM were simulated from the basic seven-state model in Fig. 1. In addition, a set of intervals at a high agonist concentration (10 μM) was simulated from the same model that includes the additional desensitized state A2D. The additional state is attached to the doubly liganded opening A2R∗ with transition rate constants , and is represented by the dashed box in Fig. 1. It introduces into the simulated data long shut times that mimic the long silent periods that appear in real experiments at high acetylcholine concentrations. For each of the three agonist concentrations, 20,000 intervals were generated, reflecting the number of events that can be gathered in a typical single-channel experiment with the muscle nicotinic channel. The tcrit time was set at 3.5 ms for the low-concentration recordings and 5 ms for the high-concentration recording. This tcrit value is used to break up the resolved record into groups of openings that almost certainly all originate from the same individual channel. For the low concentrations, CHS vectors were used in the calculation of the likelihood (see Materials and Methods). We applied the two-step MCMC sampling approach, described in the Materials and Methods, to this synthetic data. For the initial pilot MWG chain, 10,000 samples were drawn from the posterior distribution, of which 5000 were discarded as burn-in samples. Subsequently, the adaptive MCMC was started at the posterior mode evaluated from the pilot chain output. One-hundred-thousand samples were then drawn from the posterior distribution using this second chain, and again half of these samples were discarded as burn-in, because the chain is initially learning the correlation structure of the posterior distribution and takes time to converge to the distribution of interest.
Figure 2.
An experimental workflow to perform MCMC sampling using the muscle nicotinic receptor in Fig. 1. Two low-concentration datasets (30 and 100 nM) are simulated and these records are separated into groups (bursts), to account for the lack of knowledge of the number of channels in the patch. A high-concentration recording is also separated into groups discarding the intervals where the channel is desensitized. See Materials and Methods for the definition of groups. The joint dataset comprising the groups for all three sets is then used for MCMC sampling. The first sampler (MWG) is used to locate the posterior mode. The adaptive sampler, started at the mode, learns the covariances of the posterior distribution and then draws samples for analysis.
Whenever we employ MCMC to draw samples from a distribution, it is important to examine diagnostics of the Markov chain to ensure its convergence. We initially consider some diagnostic plots of the pilot chain, the multiplicative MWG sampler (see Algorithm S1), used to locate the posterior mode. One such diagnostic is to examine visually how quickly the chain converges to the posterior distribution given its starting position. This can be done by observing how quickly the value of the log-posterior of the model approaches a stable, stationary time-series using a trace plot of how the log posterior value changes, with each set of sampled parameters, as the chain iterates. In Fig. 3 A, we observe the sampler converging quickly to the posterior mode after fewer than 500 iterations. A second possible metric involves calculating and plotting the autocorrelations of the samples drawn by the MCMC chain after it has converged. Although samples from the MCMC chain are invariably autocorrelated, we aim to deploy an MCMC chain that exhibits as little autocorrelation as possible. The autocorrelations of each series of parameter samples are considered a measure of the sampling efficiency of the chain. This is distinct from any correlations that may be observable between parameters in the posterior distribution. Higher levels of autocorrelation mean that the sampler takes a larger number of iterations to produce one independent sample from the posterior distribution. In such cases we say that our Markov chain mixes poorly. This is seen to be the case in our example with the MWG sampler, which displays very inefficient mixing after convergence. Although it was observed in Fig. 3 A that the MCMC chain converged to the posterior mode in ∼500 iterations, the proposal distribution was allowed to adjust according to the acceptance rate until 5000 samples had been drawn. We therefore still discard the first 5000 of the drawn samples under the assumption that these samples are drawn when the MCMC chain is still converging. We considered the next 5000 of samples to be drawn from the posterior distribution, and found that these 5000 samples exhibit high levels of autocorrelation (shown in Fig. 3 B for parameter ). This is shown by the persistence of the sample autocorrelation, even after the 100th lag. The reason behind this can be examined by illustrating the distribution of proposed points relative to those points that are accepted as samples. Fig. 3 C plots the 5000 posterior samples of and . This shows that many proposals (red points) are made in areas of lower posterior probability density, away from the ridge of high posterior density. The posterior density is formed by the accepted samples (in blue). The proposals clearly have an uncorrelated Gaussian shape, quite different from the correlated shape of the accepted parameter values. We can conclude from this graph that this algorithm learns the required proposal scales per parameter through adjusting the proposal variance, but cannot take into account the correlations between parameters in the posterior distribution. This results in inefficient sampling after convergence.
The mode of the posterior distribution represents the point of highest probability density in the posterior distribution and has been located using the MWG algorithm. However, we have shown that this sampler draws samples inefficiently once it has converged to this mode. This is why we use the second sampler, the adaptive MCMC algorithm (see Algorithm S2), which is started at the posterior mode obtained by the first sampler. The adaptive sampler learns the parameter correlation from the history of samples drawn by the chain and therefore, after the burn-in period, makes correlated proposals that are more likely to be accepted as new parameter samples in the Metropolis-Hastings acceptance step. This leads to a chain that exhibits a lower level of autocorrelation and thus needs to be run for a shorter number of iterations to produce the equivalent number of independent samples as the initial pilot MWG algorithm.
The bottom panel of Fig. 3 demonstrates the benefit of using this adaptive sampler initiated at the posterior mode (Fig. 3 D). This sampler learns the posterior correlations, and this reduces the autocorrelation of the resulting samples (shown again by plotting parameter in Fig. 3 E). Fig. 3 F demonstrates the improved efficiency of sampling using an adaptive Markov chain. This is shown by the tight overlap of the proposed parameter values (in red) with the samples that are actually accepted (in blue).
In Table 2 we compare the efficiency of the two samplers based on the ESS. This provides a measure of sampling efficiency per iteration and per unit of computational time, as defined in the Materials and Methods. The adaptive sampler is superior to the pilot MWG sampler, both in terms of equivalent independent samples per iteration and equivalent independent samples generated per min of computational time. This further validates the approach of using a two-step sampling technique—firstly, the MWG sampler to quickly locate the posterior mode and secondly, the adaptive sampler to sample more efficiently from the posterior distribution once this mode has been found. Although the adaptive sampler can be used in isolation, it takes longer to converge to the mode of the posterior. The run time (in minutes) for the two algorithms is also shown, and each sampler takes ∼1 h to complete on an Intel 2.5-GHz core i7 MacBook Pro (Intel, Mountain View, CA; Macintosh, http://www.apple.com/mac/) with 16 GB of RAM.
Table 2.
Effective Sample Sizes and Run Times for the Converged MWG Pilot and Adaptive Samplers for Distribution of the Parameter
| MWG | Adaptive | |
|---|---|---|
| Number of significant lags | 137 | 81 |
| ESS/sample | 0.01 | 0.03 |
| ESS/minute | 0.99 | 23.65 |
| Runtime, minutes | 57 | 64 |
Adaptive sampling is three times as efficient as the MWG sampler, in terms of samples per iteration (see second line). Furthermore, it is much more computationally efficient in terms of samples per min. The number of significant lags is the number of lags for which the autocorrelation coefficient is significantly greater than zero and so these lags are used in the calculation of the ESS estimates.
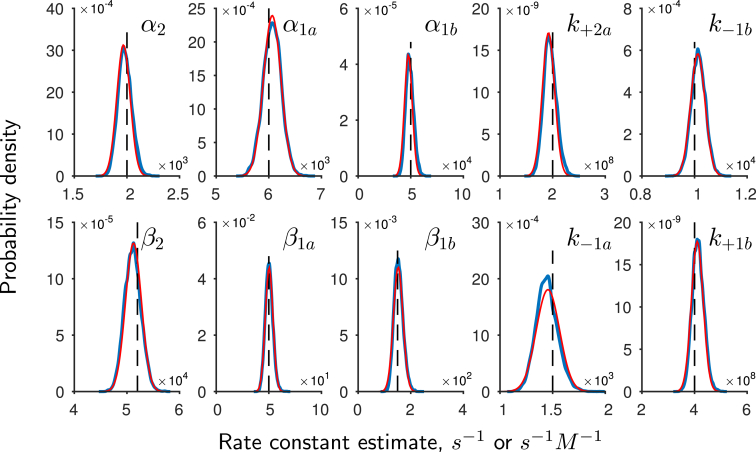
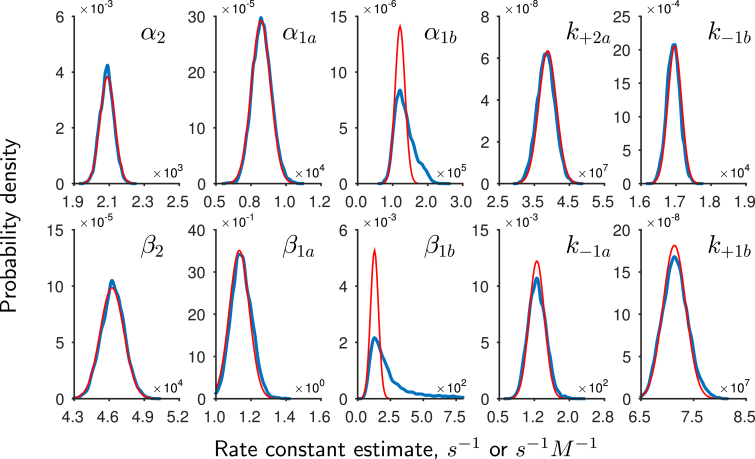
We now examine the posterior samples generated by the adaptive sampler. The individual posterior distributions for the 10 rate parameters, known as marginal distributions, are shown in Fig. 4 (in blue). The rate parameters used to generate the synthetic data are shown by the dashed black lines. The fact that each distribution is constrained and encloses the true rate constant demonstrates that the correct rate constants originally used to generate this data can be identified and recovered as in the original ML study (12). Next, we observe that the shape of the marginal distributions appears Gaussian. Given our choice of uniform priors (see Materials and Methods), we note that the location of the posterior mode has to be the same as the location of the ML estimates and therefore we can directly compare each marginal distribution to the Gaussian distribution that would be used to estimate asymptotic standard errors for parameter estimates in a maximum-likelihood estimation. We obtain estimates of the standard errors by inverting an estimate of the Hessian at the posterior mode. Comparing the shape of the error distributions (in red, Fig. 4) with the obtained marginal distributions for the parameters reveals that the shape of the posterior distributions are indeed approximately Gaussian. Hence in this case, similar conclusions would be drawn about parameter identifiability and uncertainty using Bayesian inference and ML.
Figure 4.
Marginal posterior distributions for model parameters obtained from synthetic data are shown in blue. The black vertical lines indicate the parameter values used to generate the data. The association rate constants and are in s−1 M−1 units, otherwise the units are s−1. The posterior parameter distributions enclose the rate constants and show that the Bayesian approach can recover the rate parameters used to generate the data. Plotted in red are Gaussian distributions obtained from the Hessian at the mode. This shows that the posterior distributions in this example are approximated well by Gaussian distributions. To see this figure in color, go online.
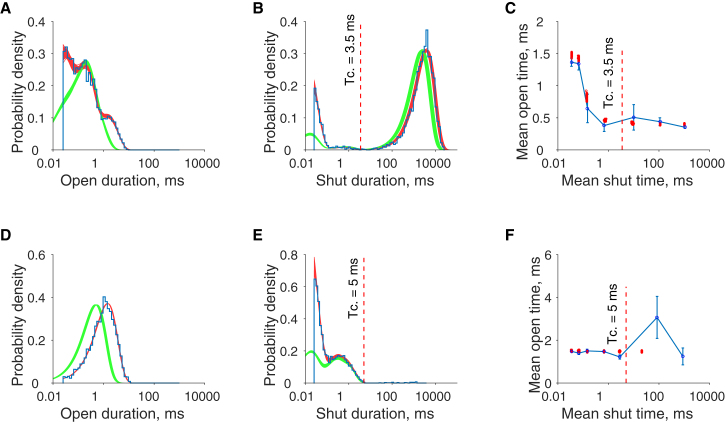
We can now illustrate the impact of the uncertainty in the estimated parameter posterior distribution on the uncertainty of model predictions, by taking samples from the posterior distribution and using them to simulate predictions of open and shut interval distributions and the correlation between the durations of adjacent open and shut intervals from the model. All predictions are corrected for missed events so that they can be compared directly to the observed data. One-hundred parameter samples were taken at random from the posterior distributions of the adaptive sampler (shown in Fig. 4). Predicted distributions were then calculated using these samples to assess how well they reproduce the observed data and how variable the model predictions are. These predictions are shown in Fig. 5.
Figure 5.
Predicted distributions of model behavior at low (30 nM, top panel) and high acetylcholine concentrations (10 μM, bottom panel). 100 samples taken at random from the posterior distributions of the model in Fig. 1, fitted to synthetic data, are used to calculate predictive open time distributions (A and D), shut time distributions (B and E), and correlations between adjacent closed-to-open sojourns (C and F). The open and shut time distributions show the predicted durations of intervals with the imposed resolution of 25 μs (red), and with perfect resolution (green), and are overlaid by the observed durations summarized as a histogram (blue). Open-shut correlations are examined by calculating the mean of the succeeding open interval against the mean of the preceding shut interval, conditional on range of preceding shut interval durations (11). Mean durations predicted by the model are denoted by red points. These are consistent with the conditional mean calculated from the observed experimental data (blue points with SD error bars, connected with a blue line). The shut range intervals used to calculate the conditional means are (0.025–0.05, 0.05–0.1, 0.1–0.2, 0.2–2, 2–20, 20–200, 200–2000) ms. The plots in (A), (B), (D), and (E) show that there is excellent agreement of the predictions from the fit with the time resolved open and shut distributions and that it becomes more precise as the agonist concentration increases. In practice, the shut distributions and correlations can be interpreted only up to the value of the tcrit interval (marked on the graph) as it is not known how many channels are in the patch. The model can also recover the correlations observed in the adjacent shut to open intervals up to the tcrit value. To see this figure in color, go online.
The variability in the predictive open time distributions, at low concentration (30 nM) and high concentration (10 μM), are shown in Fig. 5, A and D. As expected from previous identifiability analysis of the channel (12), the model fit is very good across all concentrations. This figure demonstrates that uncertainty in the model predictions decreases as the agonist concentration increases. This is apparent as the range of the curves evaluated from the parameter samples becomes narrower as the thickness of the superimposed predicted curves (red) is reduced. Note the higher variability in the prediction of short open times at low concentration. This is to be expected as low concentration records contain sparse information compared to high-concentration records, because they have fewer usable shut times due to the short tcrit required to separate the record into individual channel activations. They are nonetheless the predominant source of information on single-liganded openings in the model. At high concentrations, the record is rich with predominantly diliganded openings, and so this aspect of the channel is very accurately predicted. Shut time distributions (Fig. 5, B and E) are predicted well across both concentrations, because although we have treated the recordings so that there may be multiple channels in the patch, in reality we have simulated the data with only one channel. In practice, we would not be able to predict accurately the shut time distribution beyond tcrit. In all open and shut distributions, the impact of not taking missed events into account is illustrated by the difference between the green probability densities (which are the open or closed probability densities assuming perfect resolution calculated from Eq. 2) and the red densities (which correctly assume the finite recording resolution using Eq. 3). This illustrates the importance of applying the missed events correction in the open and closed probability density functions before comparing the model predictions to what is actually observed.
One of the key considerations of any proposed ion-channel model is the ability of the postulated model to reproduce the degree of correlations between adjacent open and shut intervals observed in experimental data. A feature of nicotinic muscle channel behavior is that at low concentrations there is a negative correlation between the length of the open interval and the length of the preceding shut interval. Predictions of such model correlations are shown alongside correlations observed in the empirical data in Fig. 5 C for low concentration and Fig. 5 F for high concentration. The model correctly recovers, with high accuracy, the negative correlation between the duration of shut intervals and the duration of the following open intervals observed at low concentrations, as does the original ML fit (12). At high concentrations, no correlation is predicted or observed. This is because diliganded openings are predominantly observed at this concentration. This represents only one kind of opening in the channel and so correlations are absent (32).
Sampling with experimental data results in a non-Gaussian posterior distribution
Real data from a nicotinic acetylcholine receptor (3) were used to test our MCMC approach. As with the simulated data, the experimental recordings were taken at three concentrations. A summary of these three datasets and their experimental conditions is described in Table 3.
Table 3.
Experimental Conditions and Summary Data for Real Acetylcholine Receptor Recordings from Hatton et al. (3)
| Set | ACh Concentration (μM) | Number of resolved intervals | tcrit (ms) | Number of groups | Use CHS vectors |
|---|---|---|---|---|---|
| 1 | 0.05 | 14,056 | 2 | 4134 | yes |
| 2 | 0.1 | 24,230 | 3.5 | 8471 | yes |
| 3 | 10 | 13,822 | 35 | 134 | no |
The resolution for all recordings was 25 μs. The table summarizes the number of resolved intervals in the experimental patch, the tcrit interval used to separate the resolved intervals into groups, the number of resulting individual groups (see Materials and Methods), and whether CHS vectors are required for initial openings in each group.
Similarly to the synthetic example, we begin our analysis by considering the diagnostic output from our MCMC sampler. The pilot MWG sampler successfully located the posterior mode, and at this stage we consider only the output of the adaptive sampler. Fig. 6 A shows how the adaptive chain samples starting from the posterior mode (Fig. 6 B) draw samples efficiently from the posterior distribution of , given the correlation between rate parameters and that was observed also in the synthetic example (Fig. 6 C). This demonstrates that our MCMC approach successfully samples from both real and synthetic data.
Figure 6.
Chain diagnostics for the adaptive algorithm with experimental data (compare to Figs. 3, D–F). (A) The adaptive chain is started at the posterior mode, as shown by the red horizontal dotted line. (B) The adaptive sampler produces efficient samples from parameter as it has learned the pairwise posterior correlation between and shown in (C). This is shown by the tight overlap with the proposed samples (red) and the accepted samples (blue) between the and parameters. To see this figure in color, go online.
Fig. 7 shows the marginal posterior distribution of the rate constants. Most rate constants are close in shape to a Gaussian distribution, and hence approximated well by the Hessian derived at the mode. However, that is not so for the faster monoliganded opening and shutting rates and those for the B binding site, and . For these rates, the posterior distributions are nonsymmetrical, and consequently their uncertainty is not directly captured well by the Gaussian error approximation used in a typical ML approach.
Figure 7.
Marginal posterior parameter distributions calculated using experimental data using adaptive MCMC are shown in blue. The Gaussian approximation obtained from the Hessian mode is shown in red. It is clearly seen that the posterior of parameters and exhibit non-Gaussian distributions. This uncertainty is more accurately captured by the Bayesian approach. The association rate constants and again are in s−1 M−1 units, otherwise the units are s−1. To see this figure in color, go online.
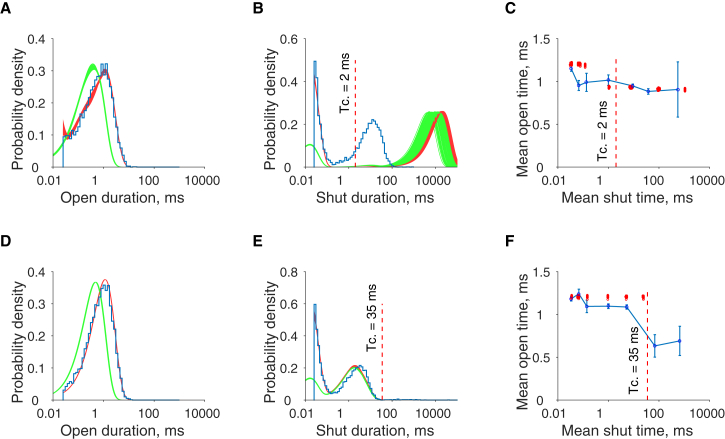
We can again assess the impact of parameter uncertainty on the predicted output of the model (Fig. 8). One-hundred samples were again taken at random from the posterior distribution in Fig. 7 and used to calculate summary distributions of open, closed, and conditional mean open times. Predictions of open time distributions again become more certain with increasing concentration, with the short openings at low concentration being most variably predicted (Fig. 8, A and D). Shut interval distributions at low concentration (Fig. 8 B) illustrate the ambiguity posed by not knowing how many channels are in the experimental patch. Although the short shut interval components are well predicted, longer shut interval durations are not, because the presence of many channels in the low-concentration experimental patches makes the observed lifetime in the long shut state appear to be shorter than it actually is. In practice, it is accepted that due to this limitation, only short shut events up to tcrit can be inferred reliably from the experimental data.
Figure 8.
Predicted distributions of model behavior at low (50 nM, top row) and high acetylcholine concentrations (10 μM, bottom row). One-hundred samples from the posterior distributions of the model (Fig. 1), fitted with real data, are used to calculate predicted distributions, analogous to those generated in Fig. 5. The predicted durations of intervals with the imposed resolution of 25 μs are again shown in red, and with perfect resolution in green. The predicted distributions of the model are less precise with this real dataset than for the synthetic dataset. The open time distributions (A and D) are still generally well predicted, but show variability near the resolution time. The long component of the low-concentration shut intervals (B) is poorly predicted as expected, as no information is available about the numbers of channels in the patch. This results in accurate inferences about the shut time distribution being restricted to the dwell times up to the tcrit interval. To see this figure in color, go online.
In determining the model prediction of the mean open time conditional on the preceding mean shut time, model predictions are fairly accurate across agonist concentrations (Fig. 8, C and F). The negative correlation with the preceding shut interval duration is reasonably accounted for by the model at low concentrations, although predictions of mean intervals after tcrit, indicated on each chart, for the experimental patch must be taken with caution given the unknown number of channels in the patch (3).
Inferential approaches should account accurately for the limitations of raw recordings
We have shown, using our synthetic example, that a model likelihood based on a continuous-time Markov model can recover rate constants used to generate datasets from a physiologically realistic model of a muscle nicotinic receptor. The key to the success of this approach is an accurate idealization of the noisy filtered record and the correction for missed events that arises from the filtering of the raw recordings, as described in Materials and Methods. In practice, the incomplete detection of opening and shut intervals is a very real problem for accurately inferring model parameters from single-channel recordings. Indeed, it was estimated in a real channel record that even with good resolution, as many as 88% of short shuttings may be missed (5).
An alternative practical Bayesian approach to single-channel analysis has recently been described in Siekmann et al. (18, 19). It has been claimed that this method can detect model overparameterization more robustly than a maximum-likelihood inferential method that provides an approximate correction for missed events (33). Broadly, the method of Siekmann et al. (19) relies on estimating a model likelihood from sampled points in the single-channel record. The model likelihood makes no probabilistic statement about the states of the channel between sampling points and it is claimed therefore that this method does not need to correct for missed events. It is therefore a natural step to compare our Bayesian method with missed-events correction with the Bayesian approach of Siekmann et al. (19), using datasets that have missed events incorporated into the channel record to mimic the effect of filtering the raw trace.
The method of Siekmann et al. (19) can briefly be defined as follows: raw sampling points are taken at time intervals from an experimental trace. These points are classed into open or closed observations in the trace by half-thresholding each sampling point. These are the data on which inference of the model rate constants is performed. Note that experimental noise and missed events may cause the classification of the open and closed points to be wrong.
The rate constants in the Q matrix are then used to calculate a Markov transition matrix that denotes the individual probabilities of moving from one state at the start of the sampling interval to another at the end of the sampling interval. This uses the whole Q matrix (as for macroscopic currents), and considers only the state of the system at the sampling points (20). There may be any number of transitions between the sampling points. A discrete likelihood for the entire record is then calculated using this transition matrix and the projections for each sampling point that restrict the entry and exit states of the process as defined by the thresholding. The likelihood is calculated using a forward algorithm commonly used to estimate likelihoods in discrete HMM models. This likelihood, in combination with a weakly informative prior distribution for the rate constants forms the posterior distribution that is sampled using an MCMC algorithm (19).
We reproduced the synthetic experiment from Siekmann et al. (19) in conditions of perfect resolution and after imposing progressively worse resolution to emulate the process by which filtering raw experimental traces results in missed events in the outputted signal. We did this to test empirically whether the analysis method from Siekmann et al. (19) and from this article are equivalent in retrieving the rate constants of the model.
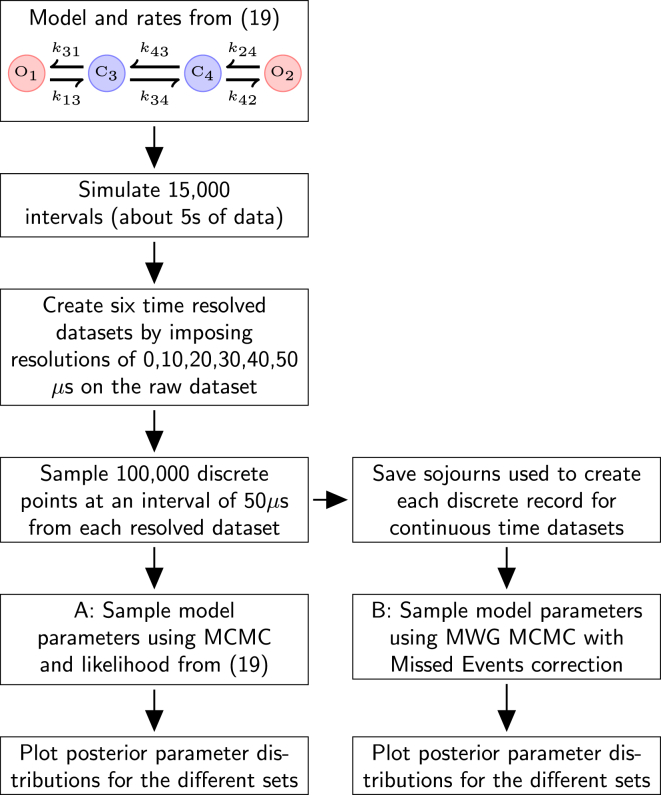
We have used the four-state ion-channel model and rates described in Siekmann et al. (19) (Fig. 9), to simulate 15,000 sojourns, assuming unrealistically that there is only one channel in the patch. This perfect resolution dataset, R, was sampled at 50 μs to produce 100,000 points, as in Siekmann et al. (19). The original sojourn intervals were also stored for comparison with the likelihood and sampler described in the Materials and Methods.
Figure 9.
Experimental workflow to examine the requirement for missed events correction. Raw data was initially simulated from the four-state ion-channel model and rates from Siekmann et al. (19). , , , , , and . Rates in s−1. To see this figure in color, go online.
This ideal, perfect resolution record R, was then subjected to increasing coarsening of time resolution. Separate additional datasets of continuous records were generated from R with time resolutions of 10, 20, 30, 40, and 50 μs. This concatenates intervals shorter than the resolution with the adjacent resolved intervals. This distorts the channel record to an increasing degree as the resolution time worsens and mimics the act of filtering in real experimental traces. Next, for each dataset, the data was again sampled at 50 μs to produce 100,000 discrete data points. Posterior parameter samples were generated using these datasets with the discrete likelihood MCMC algorithm and codebase (https://github.com/merlinthemagician/ahmm/) of Siekmann et al. (19). The continuous time sojourns for each dataset were then analyzed separately using the initial MWG pilot MCMC algorithm described in the Materials and Methods. Thus the performance of the two methods can be compared over with the same amount of information. The prior for the rate constants in both sets of experiments was the same as Siekmann et al. (19). Posterior distributions were estimated after both MCMC samplers had converged.
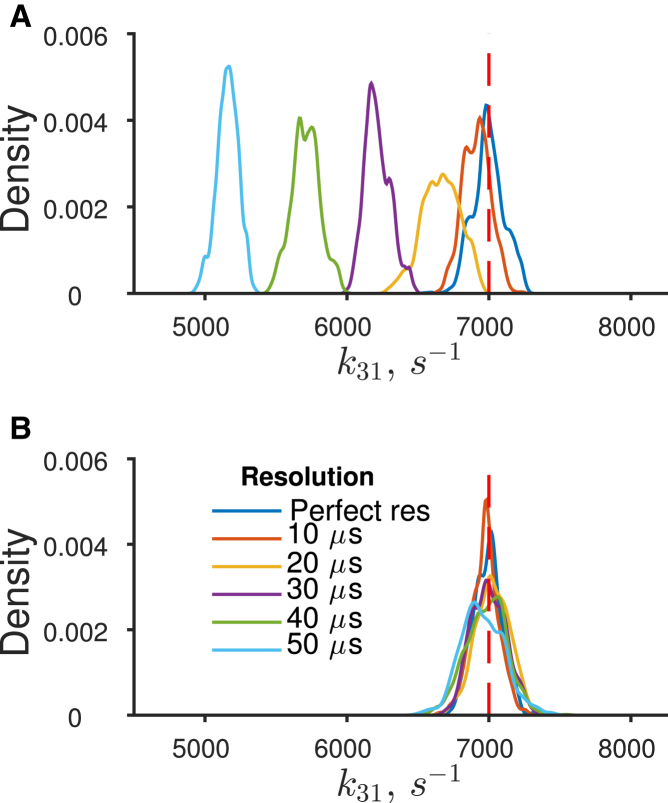
The posterior distributions from the Siekmann likelihood (19) and that from our method, which uses the likelihood of Colquhoun et al. (11), were examined at each resolution to establish whether they could recover the rate constant values that generated the initial dataset, R. The comparison for the faster rate k31 is shown in Fig. 10 A. It is clear that estimates obtained with the method of Siekmann et al. (19) become increasingly biased as the resolution worsens. Even with an optimistic resolution of 20 μs, the posterior distribution of rate constant k31 is biased away from the correct value (dashed red line). In contrast, the correct rate constant can still be recovered using our analysis (Fig. 10 B) even at the worst resolution (50 μs). It is interesting to note that even in these limited MCMC runs, the inference over the rate constant k31 in Fig. 10 B becomes less precise. This is seen by a broadening of the posterior, and would be expected despite the missed events correction, as more information is removed from the record.
Figure 10.
Simulation based on an example from Siekmann et al. (19) highlights the requirement for missed events correction. (A) Posterior distributions of rate constant k31 using the likelihood of Siekmann et al. (19) sampled from data with worsening resolution times imposed (0–50 μs). These distributions become more biased as the resolution worsens. (B) The same analysis with our likelihood (11) and Pilot MWG MCMC sampler. This true parameter value is shown as the red-dashed line on both charts. To see this figure in color, go online.
It is worth noting also that a rate constant value of 7000 s−1 is relatively slow for an ion channel. At a resolution of 50 μs, the fraction of events expected to be missed in this example is only 29% of openings and 16% of shuttings. It is to be anticipated that this problem will worsen with faster channels with their quicker rate constants.
Discussion
In the context of modern single molecule biophysics, the modeling of single ion-channels using Markov processes has a comparatively long history. Inferential techniques for rate parameters have progressed from the fit of exponential components to dwell-time distributions (29) to ML approaches that use the sequence of the observed signal (11, 33). Current full-likelihood approaches broadly consist of two alternative methods. The first involves fitting a continuous-time Markov process to a signal idealized from the raw, filtered data typically by the use of threshold crossing or by time course fitting idealization (2). Filtering of the original signal is needed to enable event detection, but events of short duration are absent in the filtered record and subsequent idealization. This requires an explicit correction for missed events, as the model likelihood makes probabilistic statements regarding the state of the process through time (Eq. 1). The most widely used modeling approaches employ ML estimation with a continuous time model with either an approximate (33) or an exact correction (11, 21, 22) in the likelihood for missed events.
A second approach using discrete hidden Markov models has been applied to extract information directly from the raw data, without the idealization step (34). HMMs often require the estimation of the distribution over hidden states at each sampling point during the likelihood calculation. Calculating the likelihood directly from raw recordings in practice can require implementing higher-order Markov models, to account for correlated experimental noise (35, 36), and this increases the computational complexity of calculating the model likelihood. More recent methods avoid this issue by classifying points as either open or closed (19). Maximum likelihood inference of rate constants in HMM models is often achieved by implementing bespoke Forward-Backward algorithms combined with Baum’s reestimation (37) or direct optimization (38). We note that likelihoods defined in this manner make no probabilistic statement about channel activity between sampling points, and it has been claimed that no missed events correction is necessary (18). However, we have demonstrated that even for a simple ion channel model with four hidden states, HMM approaches that do not account for the unavoidable consequences of filtering and experimental noise, for example by fixed rather than probabilistic classifications of sampling points into conductance classes, result in severely biased inferences when using realistically sampled data.
We must seek to evaluate the quality of our estimates whenever we infer parameter values from data. This should involve establishing as realistically as possible that they are unbiased, and measuring the extent of our uncertainty in their values. For single-channel modeling, this has been achieved in examples where ML point estimates were used by employing simulation (5, 12), although simulation can be a laborious approach. The use of Bayesian inference, where by definition we obtain the posterior distribution rather than point estimates of the parameters, is beneficial in making these checks efficient and systematic. Bayesian approaches to date have used MCMC sampling in combination with either the continuous time (39, 40) or discrete likelihoods (16, 18, 19) to compute posterior distributions. We have demonstrated in this article that the correction for missed events is still vitally important to recover the correct rate constants even in small model examples. We therefore investigated MCMC sampling approaches that use a model likelihood that both corrects exactly for missed events and takes into account the unknown numbers of channels in each experimental patch (11).
We have proposed a two-stage sampling approach for performing Bayesian inference in these computationally expensive models, and made the package BICME available to download as MATLAB code (The MathWorks, Natick, MA). The first step relies on a MWG pilot algorithm to efficiently locate the posterior mode. This is followed by an adaptive MCMC sampler, which learns the covariance structure of the joint posterior distribution to sample the posterior distributions more efficiently. With these tools we performed our Bayesian analysis on a physiologically realistic ion-channel model for a muscle nicotinic acetylcholine receptor. This model’s identifiability has previously been evaluated using ML estimation (12). The sampling approach was initially evaluated using synthetic data and demonstrates how parameter identifiability can be established and how uncertainty in model parameterization can help examine directly the uncertainty in model predictions. A subsequent application using experimental data confirms the proposed approach can implement Bayesian inference in these models by efficiently sampling from the resulting posterior distribution. We show that, with real data, some posterior distributions are non-Gaussian in shape.
As in a typical Bayesian analysis, we report the full posterior distributions of the rate parameters rather than point estimates. We do note, however, that for our choice of prior distribution, the point estimates of rate constants as defined by the posterior mode would be the same as those that would be found by ML estimation. In the example with synthetic data, the posterior distributions are close to Gaussian and their shape well approximated by a covariance matrix calculated at the ML estimate. This is not the case with experimental data. In this instance the Bayesian approach has the advantage in cases where the posterior distributions are nonsymmetrical, in which case the posterior distribution gives a more realistic estimate of the uncertainty in the parameter estimates than error estimates derived from ML estimation.
Our approach was specifically designed to sample effectively for higher-dimensional ion-channel models and will form the basis for future work examining candidate models with larger numbers of rate parameters. In such models it has been shown that robust model parameterization and comparison remains statistically challenging (7). In the latter case, this sampling method will help measure uncertainty in the competing mechanistic models through the estimation of marginal likelihoods, which will form the basis of future research.
Author Contributions
M.E. performed the research and contributed analytic tools; M.E., B.C., L.G.S., and M.A.G. designed the research; and M.E., B.C., and L.G.S. wrote the article.
Acknowledgments
The authors thank Dr. Remigijus Lape for extremely helpful advice, extensive discussions, and providing experimental data for the muscle nicotinic acetylcholine receptor from the original study of Hatton et al. (3). They also thank Professor David Colquhoun for helpful comments on the draft.
M.E. was funded by the CoMPLEx Doctoral Training Programme (2010–2014) at University College London and was funded by an Engineering and Physical Sciences Research Council Doctoral Prize Fellowship (2014–2015) at Imperial College.
Editor: Andrew Plested.
Footnotes
Supporting Materials and Methods are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30450-7.
Supporting Material
References
- 1.Hamill O.P., Marty A., Sigworth F.J. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 2.Colquhoun D., Sigworth F. Fitting and statistical analysis of single-channel records. In: Sakmann B., Neher E., editors. Single-Channel Recording. Springer; Boston, MA: 1995. pp. 483–587. [Google Scholar]
- 3.Hatton C.J., Shelley C., Colquhoun D. Properties of the human muscle nicotinic receptor, and of the slow-channel myasthenic syndrome mutant εL221F, inferred from maximum likelihood fits. J. Physiol. 2003;547:729–760. doi: 10.1113/jphysiol.2002.034173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mukhtasimova N., Lee W.Y., Sine S.M. Detection and trapping of intermediate states priming nicotinic receptor channel opening. Nature. 2009;459:451–454. doi: 10.1038/nature07923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Burzomato V., Beato M., Sivilotti L.G. Single-channel behavior of heteromeric α1β glycine receptors: an attempt to detect a conformational change before the channel opens. J. Neurosci. 2004;24:10924–10940. doi: 10.1523/JNEUROSCI.3424-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lape R., Colquhoun D., Sivilotti L.G. On the nature of partial agonism in the nicotinic receptor superfamily. Nature. 2008;454:722–727. doi: 10.1038/nature07139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lape R., Plested A.J., Sivilotti L.G. The α1K276E startle disease mutation reveals multiple intermediate states in the gating of glycine receptors. J. Neurosci. 2012;32:1336–1352. doi: 10.1523/JNEUROSCI.4346-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Milescu L.S., Akk G., Sachs F. Maximum likelihood estimation of ion channel kinetics from macroscopic currents. Biophys. J. 2005;88:2494–2515. doi: 10.1529/biophysj.104.053256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fredkin D., Montal M., Rice J.A. Identification of aggregated Markovian models: application to the nicotinic acetylcholine receptor. In: Cam L.L., Olshen R., editors. Vol. 1. Wadsworth; Belmont, CA: 1985. pp. 269–289. (Proceedings of the Berkeley Conference in Honor of Jerzy Neyman and Jack Kiefer). [Google Scholar]
- 10.Bruno W.J., Yang J., Pearson J.E. Using independent open-to-closed transitions to simplify aggregated Markov models of ion channel gating kinetics. Proc. Natl. Acad. Sci. USA. 2005;102:6326–6331. doi: 10.1073/pnas.0409110102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Colquhoun D., Hawkes A., Srodzinski K. Joint distributions of apparent open and shut times of single-ion channels and maximum likelihood fitting of mechanisms. Phil. Trans. R. Soc. Lond. A. 1996;354:2555–2590. [Google Scholar]
- 12.Colquhoun D., Hatton C.J., Hawkes A.G. The quality of maximum likelihood estimates of ion channel rate constants. J. Physiol. 2003;547:699–728. doi: 10.1113/jphysiol.2002.034165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marabelli A., Lape R., Sivilotti L. Mechanism of activation of the prokaryotic channel ELIC by propylamine: a single-channel study. J. Gen. Physiol. 2015;145:23–45. doi: 10.1085/jgp.201411234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hines K.E., Middendorf T.R., Aldrich R.W. Determination of parameter identifiability in nonlinear biophysical models: a Bayesian approach. J. Gen. Physiol. 2014;143:401–416. doi: 10.1085/jgp.201311116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hines K.E. A primer on Bayesian inference for biophysical systems. Biophys. J. 2015;108:2103–2113. doi: 10.1016/j.bpj.2015.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rosales R.A. MCMC for hidden Markov models incorporating aggregation of states and filtering. Bull. Math. Biol. 2004;66:1173–1199. doi: 10.1016/j.bulm.2003.12.001. [DOI] [PubMed] [Google Scholar]
- 17.Calderhead B., Epstein M., Girolami M. Bayesian approaches for mechanistic ion channel modeling. In: Schneider V., editor. In Silico Systems Biology. Humana Press; Totowa, NJ: 2013. pp. 247–272. [DOI] [PubMed] [Google Scholar]
- 18.Siekmann I., Wagner L.E., 2nd, Sneyd J. MCMC estimation of Markov models for ion channels. Biophys. J. 2011;100:1919–1929. doi: 10.1016/j.bpj.2011.02.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Siekmann I., Sneyd J., Crampin E.J. MCMC can detect nonidentifiable models. Biophys. J. 2012;103:2275–2286. doi: 10.1016/j.bpj.2012.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Colquhoun D., Hawkes A.G. On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1982;300:1–59. doi: 10.1098/rstb.1982.0156. [DOI] [PubMed] [Google Scholar]
- 21.Hawkes A.G., Jalali A., Colquhoun D. The distributions of the apparent open times and shut times in a single channel record when brief events cannot be detected. Philos. Trans. R. Soc. Lond. A. 1990;332:511–538. doi: 10.1098/rstb.1992.0116. [DOI] [PubMed] [Google Scholar]
- 22.Hawkes A.G., Jalali A., Colquhoun D. Asymptotic distributions of apparent open times and shut times in a single channel record allowing for the omission of brief events. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1992;337:383–404. doi: 10.1098/rstb.1992.0116. [DOI] [PubMed] [Google Scholar]
- 23.Metropolis N., Rosenbluth A., Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 24.Sherlock C., Fearnhead P., Roberts G. The random walk Metropolis: linking theory and practice through a case study. Stat. Sci. 2010;25:172–190. [Google Scholar]
- 25.Geyer C. Practical Markov chain Monte Carlo. Stat. Sci. 1992;7:473–483. [Google Scholar]
- 26.Roberts G., Rosenthal J. Examples of adaptive MCMC. J. Comput. Graph. Stat. 2009;18:349–367. [Google Scholar]
- 27.Ball F.G., Davies S.S., Sansom M.S. Single-channel data and missed events: analysis of a two-state Markov model. Proc. Biol. Sci. 1990;242:61–67. doi: 10.1098/rspb.1990.0104. [DOI] [PubMed] [Google Scholar]
- 28.Haario H., Saksman E., Tamminen J. An adaptive Metropolis algorithm. Bernoulli. 2001;7:223–242. [Google Scholar]
- 29.Colquhoun D., Sakmann B. Fast events in single-channel currents activated by acetylcholine and its analogues at the frog muscle end-plate. J. Physiol. 1985;369:501–557. doi: 10.1113/jphysiol.1985.sp015912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Milone M., Wang H.L., Engel A.G. Slow-channel myasthenic syndrome caused by enhanced activation, desensitization, and agonist binding affinity attributable to mutation in the M2 domain of the acetylcholine receptor α subunit. J. Neurosci. 1997;17:5651–5665. doi: 10.1523/JNEUROSCI.17-15-05651.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Colquhoun D., Dowsland K.A., Plested A.J. How to impose microscopic reversibility in complex reaction mechanisms. Biophys. J. 2004;86:3510–3518. doi: 10.1529/biophysj.103.038679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Colquhoun D., Hawkes A.G. A note on correlations in single ion channel records. Proc. R. Soc. Lond. B Biol. Sci. 1987;230:15–52. doi: 10.1098/rspb.1987.0008. [DOI] [PubMed] [Google Scholar]
- 33.Qin F., Auerbach A., Sachs F. Maximum likelihood estimation of aggregated Markov processes. Proc. Biol. Sci. 1997;264:375–383. doi: 10.1098/rspb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chung S.H., Moore J.B., Gage P.W. Characterization of single channel currents using digital signal processing techniques based on hidden Markov models. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1990;329:265–285. doi: 10.1098/rstb.1990.0170. [DOI] [PubMed] [Google Scholar]
- 35.Venkataramanan L., Walsh J., Sigworth F. Identification of hidden Markov models for ion channel currents. I. colored background noise. IEEE Trans. Signal Process. 1998;46:1901–1915. [Google Scholar]
- 36.Qin F., Auerbach A., Sachs F. Hidden Markov modeling for single channel kinetics with filtering and correlated noise. Biophys. J. 2000;79:1928–1944. doi: 10.1016/S0006-3495(00)76442-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Venkataramanan L., Sigworth F.J. Applying hidden Markov models to the analysis of single ion channel activity. Biophys. J. 2002;82:1930–1942. doi: 10.1016/S0006-3495(02)75542-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Qin F., Auerbach A., Sachs F. A direct optimization approach to hidden Markov modeling for single channel kinetics. Biophys. J. 2000;79:1915–1927. doi: 10.1016/S0006-3495(00)76441-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ball F., Cai Y., O’Hagan A. Bayesian inference for ion-channel gating mechanisms directly from single-channel recordings, using Markov chain Monte Carlo. Proc. R. Soc. A. 1999;455:2879–2932. [Google Scholar]
- 40.Gin E., Falcke M., Sneyd J. Markov chain Monte Carlo fitting of single-channel data from inositol trisphosphate receptors. J. Theor. Biol. 2009;257:460–474. doi: 10.1016/j.jtbi.2008.12.020. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.