How van der Waals interactions determine the unique properties of water

Significance

Despite its simple chemical formula, H₂O, water is a complex substance with a variety of unusual properties resulting from its ability to form hydrogen bonds. A famous example for the anomalous behavior of water is the fact that it exhibits a density maximum at 4 °C. Here, we unravel the density anomaly of water on the molecular level using a powerful ab initio-based simulation technique. We show that weak van der Waals forces crucially modulate the flexibility of the hydrogen bond network, giving rise to the density maximum in water and causing ice to be less dense than the liquid.

Abstract

Whereas the interactions between water molecules are dominated by strongly directional hydrogen bonds (HBs), it was recently proposed that relatively weak, isotropic van der Waals (vdW) forces are essential for understanding the properties of liquid water and ice. This insight was derived from ab initio computer simulations, which provide an unbiased description of water at the atomic level and yield information on the underlying molecular forces. However, the high computational cost of such simulations prevents the systematic investigation of the influence of vdW forces on the thermodynamic anomalies of water. Here, we develop efficient ab initio-quality neural network potentials and use them to demonstrate that vdW interactions are crucial for the formation of water’s density maximum and its negative volume of melting. Both phenomena can be explained by the flexibility of the HB network, which is the result of a delicate balance of weak vdW forces, causing, e.g., a pronounced expansion of the second solvation shell upon cooling that induces the density maximum.

Water is an exceptional liquid exhibiting several anomalies, of which the density maximum at 4 °C is the most prominent (1). Together with the negative volume of melting, it is responsible for the fact that water freezes from the top down and ice floats on water. The unusual behavior of water can be directly related to its ability to form hydrogen bonds (HBs) which are of strongly directional nature and determine the microscopic structure of water (2, 3). To investigate the anomalies of water at the molecular level, atomistic computer simulations have become an essential tool. Important contributions have been made by simulations using simple empirical water models (3–8).

Simulations based on ab initio molecular dynamics (AIMD) (9–11) allow determination of the properties of water with high predictive power and enable a detailed analysis of their underlying microscopic mechanisms. In contrast to empirical water models (5), which depend on experimental data resulting in a limited transferability, in AIMD the atomic forces that govern the molecular dynamics are obtained directly from quantum mechanics. Although this approach is in principle exact [in combination with methods that account for the quantum nature of the nuclei (12, 13)], ab initio simulations of condensed matter systems are feasible only if approximate but efficient methods such as density-functional theory (DFT) are used. Even then, however, simulations are restricted to short times and small systems. AIMD simulations have been used to a limited extent to investigate the phase behavior of water, for instance by estimating melting temperatures (14, 15) and vapor–liquid coexistence curves (16, 17). However, many fundamental thermodynamic properties of water have not been evaluated to date. To circumvent the limitations of on-the-fly AIMD, various efficient water potentials using data from ab initio calculations have been developed. For instance, existing water models have been reparametrized, based solely on forces from AIMD simulations (18) or using a combination of experimental and theoretical data (19). Other potentials use truncated many-body expansions of the water interaction energy, with parameters that are fitted to ab initio results for small water clusters (20–22). Recently, it was shown that a minimal water model with a coarse-grained electronic structure described by quantum Drude oscillators (23) (QDOs) is able to predict many thermodynamic properties of water (24).

Here, we present a series of analytic potentials which accurately represent the ab initio potential-energy surface of water and overcome the computational bottleneck of AIMD simulations, enabling assessment of the performance of different density functionals. The form of the potentials is not constructed using simplified physically motivated models, but instead consists of a set of highly flexible functions in the form of artificial neural networks (25, 26) trained to a broad range of condensed phase configurations. Using this powerful approach we carry out converged large-scale molecular dynamics simulations of water and clarify the significance of vdW interactions for the thermodynamic anomalies of water.

Results and Discussion

Neural Network Potentials.

We developed four neural networks potentials (NNPs) representing the revised Perdew–Burke–Ernzerhof (RPBE) (27) and Becke–Lee–Yang–Parr (BLYP) (28, 29) density functionals with and without vdW corrections using the D3 method (30). Whereas NNPs can in principle be trained to any reference method, the majority of AIMD simulations for water reported to date have used gradient-corrected (GGA) DFT, and RPBE and BLYP are two well-established density functionals within this class.

The parameter set of each NNP was obtained in an iterative procedure using energies and forces from periodic configurations of liquid and crystalline water under various conditions. Details concerning the functional form and the composition of the reference data set of the NNPs are given in SI Appendix. Root-mean-squared errors of energies and forces in the final NNP training sets are $\mathrm{\approx }$ 2 meV/H₂ O and $\approx$ 70 meV/Å, respectively, and the error for configurations not included in the training set is of comparable order. Such errors are well below the intrinsic uncertainties of the DFT calculations related to the exchange–correlation functional and comparable to the much smaller error due to the finite basis set size. The NNPs closely reproduce the properties of liquid and crystalline water obtained from DFT calculations (compare Fig. 1A and SI Appendix, Figs. S3 and S5) and are thus well suited for assessing the quality of the underlying reference method. The inability of GGA density functionals to describe vdW forces can be compensated by vdW correction schemes (30). Comparing simulations with and without correction then allows us to investigate the effect of vdW interactions on the properties of water.

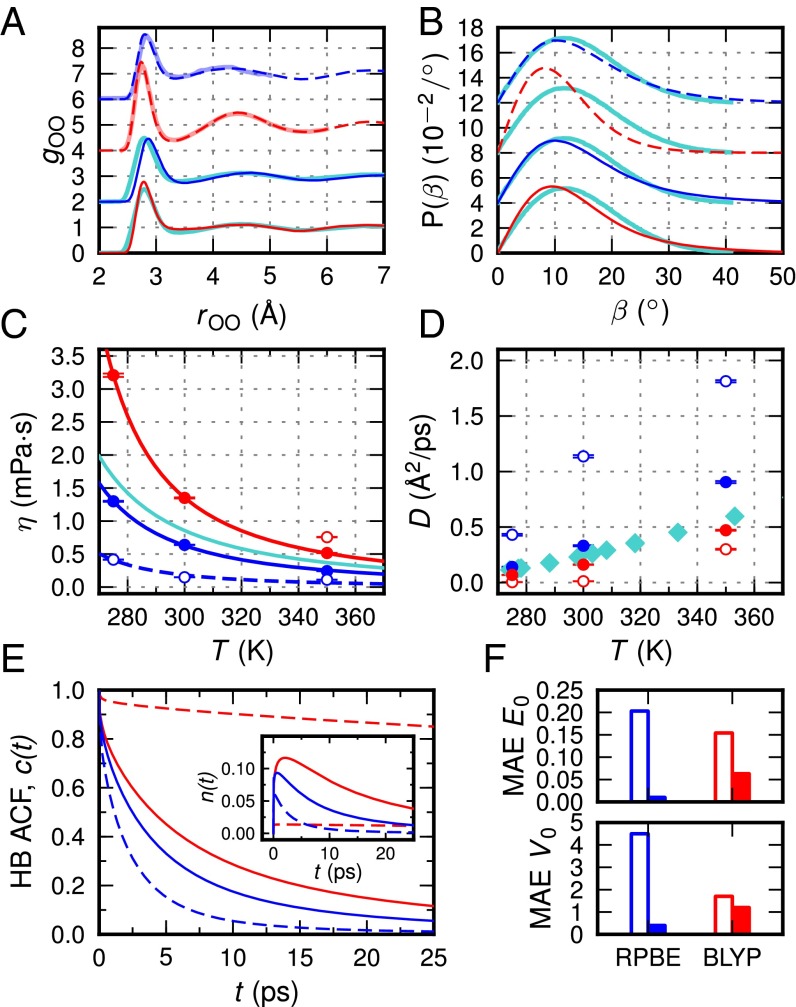
Fig. 1.

Static and dynamic properties of liquid and crystalline water. (A and B) Structure of water at T = 300 K obtained from NNP simulations based on RPBE (dark-blue lines) and BLYP (dark-red lines) density functionals with (solid lines) and without (dashed lines) vdW corrections, compared with data from AIMD (12, 31) (light-blue and red lines) and experimental results (32, 33) (cyan lines). (A) Oxygen–oxygen radial distribution functions ${\mathit{g}}_{\mathrm{OO}}$ and (B) probability density function P(β) of the HB angle $\beta =\angle {\text{H}}_{\text{D}}-{\text{O}}_{\text{D}}\mathrm{\cdots }{\text{O}}_{\text{A}}$. The curves are shifted for better visibility. (C and D) Viscosity η and diffusion coefficient D as function of temperature obtained from NNP simulations compared with experimental values (34, 35) (cyan line/cyan diamonds). Diffusion coefficients are corrected for finite size effects (compare SI Appendix, Fig. S4). Lines in C were obtained from a fit of the form: $\eta ={\left(T-T_0\right)}^{-b}$. (E) HB autocorrelation functions $c\left(t\right)$ and $n\left(t\right)$ (cf. ref. 36 and SI Appendix) obtained from NNP simulations at T = 300 K. (F) Mean absolute errors (MAEs) with respect to experiment of equilibrium lattice energies $E_0$ (in electronvolts per H₂O) and volumes $V_0$ (in cubic Ångstroms per ${\text{H}}_2$O) of seven ice phases computed at T $\mathrm{=}$ 0 K with NNPs based on plain (empty bars) and vdW-corrected (filled bars) density functionals. Energy vs. volume curves of all ice phases are reported in SI Appendix, Fig. S5.

The large impact of vdW forces on the properties of liquid and crystalline water as obtained from NNP simulations is illustrated in Fig. 1. vdW interactions soften the water structure, reducing deviations from the experimental curves, and significantly improve lattice energies and volumes of various ice polymorphs. The influence on the dynamic properties depends on the respective density functional. Whereas the BLYP-based simulations exhibit very low water mobility, the opposite behavior is observed for RPBE. Including vdW interactions improves both methods, resulting in a more realistic description of the dynamics of water. Similar conclusions have been drawn from AIMD simulations (37–43) and static DFT calculations (44, 45). However, the specific influence of vdW interactions on the thermodynamic anomalies of water is still unclear. To understand the atomistic origin of these fundamental properties, we have carried out large-scale NNP simulations to determine the density isobar of water and the melting temperature of ice Ih.

Density Isobars.

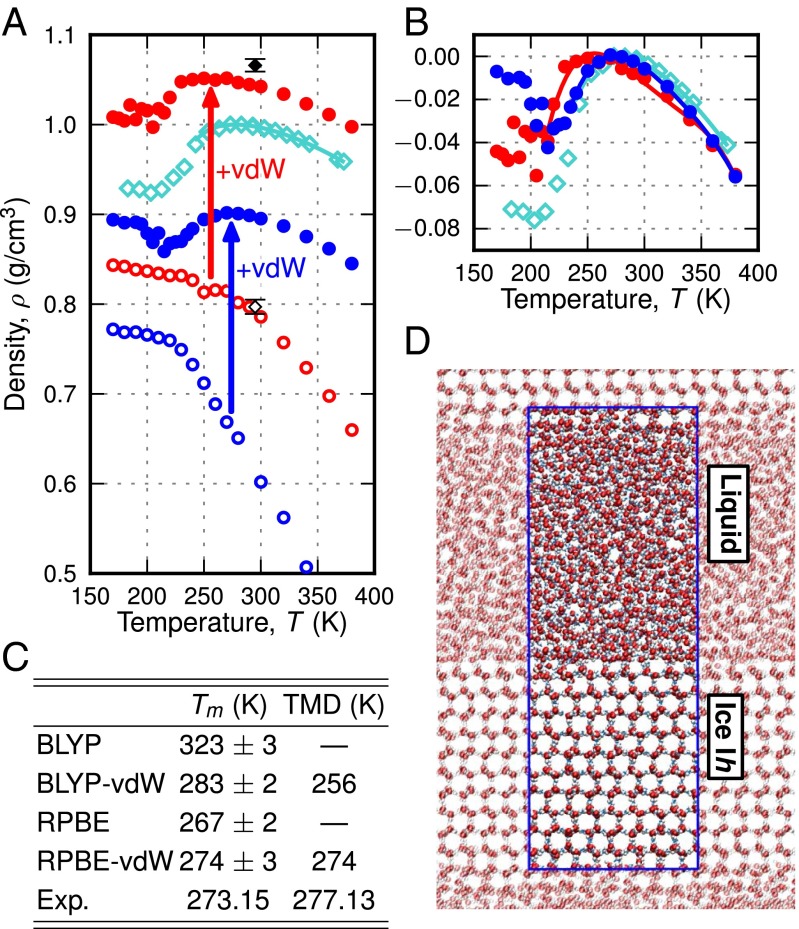
Fig. 2A compares density isobars down to the supercooled regime obtained from constant pressure simulations at P = 1 bar to experimental data for bulk and confined water (46). Simulations without vdW corrections show poor agreement with experiment: total densities are severely underestimated by 20–40%, no density maximum is observed, and the density increase upon cooling is too steep, resulting in strongly overestimated thermal expansivities at ambient conditions (compare SI Appendix, Table S4). In contrast, the inclusion of vdW forces leads to qualitatively correct results: both vdW-corrected potentials exhibit a density maximum, the shape of the isobars is in close agreement with experiment (compare Fig. 2B), and total densities are shifted to larger values [in agreement with AIMD simulations performed at a single state point (37, 39, 47)], reducing deviations from experiment to 5–10%. Moreover, a density minimum in the supercooled regime (at $\approx$ 200 K and $\approx$ 215 K for BLYP-vdW and RPBE-vdW, respectively) can be identified that is consistent with experimental measurements of water confined in silica pores (46) and simulations using empirical water models (7, 8). Comparable conclusions regarding the role of vdW forces in determining the density profile of water have been obtained from simulations with modified empirical water models: Truncating Lennard-Jones interactions resulted in reduced densities (15% lower compared with the full model) and the disappearance of the density maximum (48). Similar underestimated densities were found in simulations with the QDO water model, where the experimental value could be retained by increasing the strength of many-body dispersion (23).

Fig. 2.

Density isobars and melting temperature. (A) Density isobars at P = 1 bar obtained from NNP simulations based on the BLYP (red empty circles), BLYP-vdW (red filled circles), RPBE (blue empty circles), and RPBE-vdW (blue filled circles) density functionals. For comparison, experimental data for bulk (cyan line) and confined water (46) (cyan diamonds), and data from AIMD simulations with the vdW-corrected (black filled diamond) and uncorrected (black empty diamond) BLYP density functional (37) are also shown. (B) Densities relative to the density maximum. The density maxima for BLYP-vdW and RPBE-vdW were obtained from polynomial fits (red and blue lines) to the density isobars. (C) Melting temperature ($T_m$, errors were estimated by block averaging) and temperature of maximum density (TMD). Melting temperatures were corrected for deviations between the NNP and the DFT potential-energy surfaces (compare SI Appendix). (D) Snapshot of coexisting liquid water and ice Ih taken from the interface pinning simulation used to determine the melting temperature (the simulation cell is drawn in blue).

Melting Temperatures.

Exploiting the efficiency of NNPs, we have, for the first time to our knowledge, accurately computed the melting point of ice from first principles. Melting temperatures of ice Ih obtained using the interface pinning method (49) are listed in Fig. 2C. Whereas the melting point is overestimated by about 50 K in BLYP-based simulations, all other potentials (based on BLYP-vdW, RPBE, and RPBE-vdW) agree within 10 K with experiment. However, only when vdW interactions are accounted for, liquid water is denser than ice at coexistence (compare SI Appendix, Table S5) and the anomalous melting behavior that causes water to freeze from the top down can be reproduced. Estimates of the melting temperature of water obtained earlier from AIMD simulations using the BLYP density functional have been reported to be 360 K with (14) and 411 K without (15) vdW corrections. Whereas the lowering of the melting point of about 50 K with inclusion of vdW forces is consistent with our results, the previous reported melting temperatures are much higher [for plain BLYP these high melting temperatures have been inconsistent with the calculated boiling point, which was estimated to be about 350 K (16)]. This discrepancy may be attributed to the limited system size (192 molecules) and simulation time (15 ps) of the AIMD simulations and the fact that they have been carried out at the experimental density of 1 g/cm³ rather than at constant pressure. Whereas nuclear quantum effects (NQEs) not included here tend to weaken hydrogen bonds (50) and soften the structure of liquid water (12), they are unlikely to qualitatively change our findings for the thermodynamic properties of water. Melting temperatures are only weakly affected due to a competition between intra- and intermolecular NQEs (51–53). Further, simulations with ab initio-based potentials indicate that NQEs do not alter the location of the density maximum (54) and only marginally reduce the absolute water density (22, 54).

Water Neighbor Distribution.

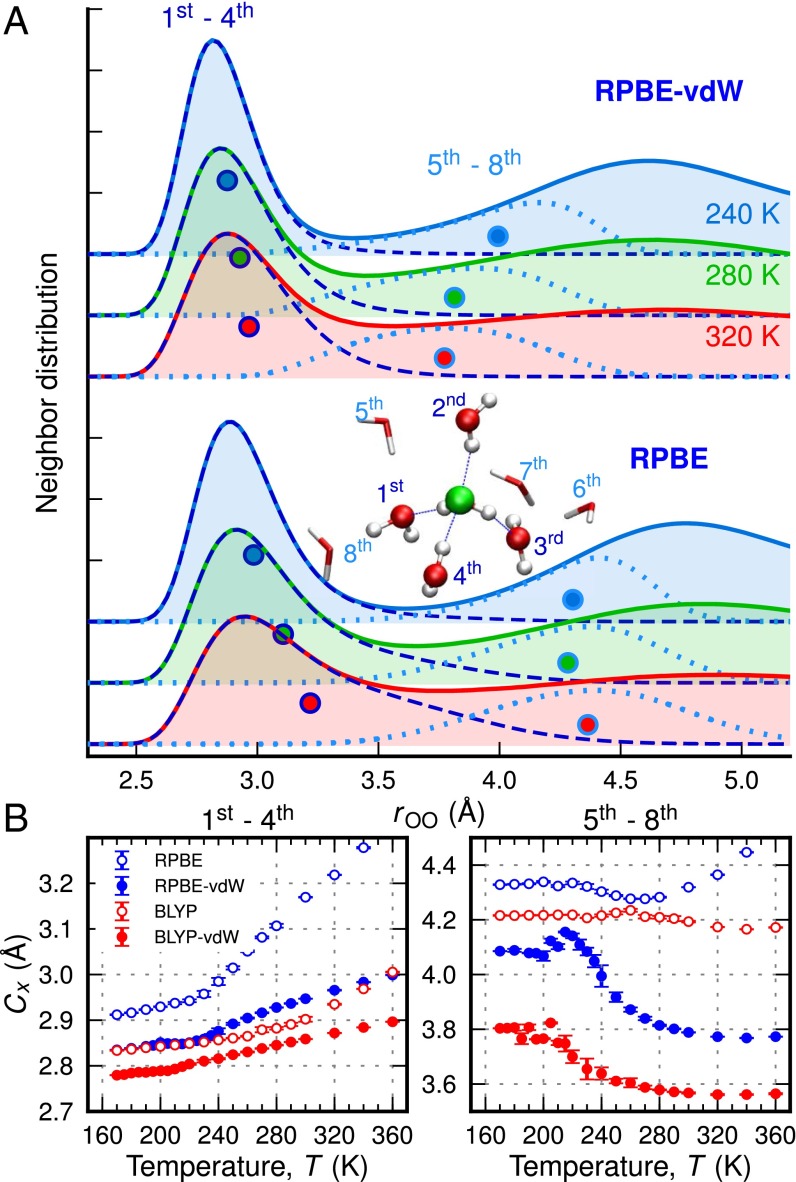
To identify the molecular origin of water’s complex density isobar (exhibiting both a maximum and minimum) we have analyzed the structure of water by decomposing (55) the oxygen–oxygen radial distribution function into contributions from first- and second-shell molecules (Fig. 3). At high temperatures, thermal fluctuations weaken HBs and lead to an increased distance to hydrogen-bonded molecules in the first solvation shell. At the same time, second-shell molecules are able to penetrate the first shell [becoming interstitial molecules (43, 55, 56)] and perturb the local tetrahedral water network. Upon cooling, the HB strength increases and the first shell approaches the central molecule (Fig. 3B, Left), causing a density increase. However, this effect is compensated by a reduced number of interstitial molecules resulting in a shift of the second shell to larger distances, thus lowering the density (Fig. 3B, Right) and inducing a density maximum. Decreasing the temperature further, the expansion of the second shell finally saturates and the density increases again after passing through a minimum in the supercooled regime. Simulations without vdW corrections do not feature a pronounced second-shell shift, which explains the monotonic density increase with decreasing temperature in this case.

Fig. 3.

Temperature dependence of water neighbor distribution. (A) Oxygen–oxygen radial distribution functions (solid lines) and decompositions into contributions from molecules in the first shell (first through fourth neighbors, dark-blue dashed lines) and part of the second shell (fifth through eighth neighbors, light-blue dotted lines) together with the centroid of the neighbor distribution (dark-blue and light-blue circles) for three different temperatures from simulations with (RPBE-vdW, Top) and without (RPBE, Bottom) vdW corrections. (B) Position of the neighbor distribution centroid $C_x$ as function of temperature. In general, with decreasing temperature a contraction of the first shell is observed (Left), whereas only in vdW-corrected simulations a maximum of the total density is found due to the expansion of the second shell (Right).

HB Analysis.

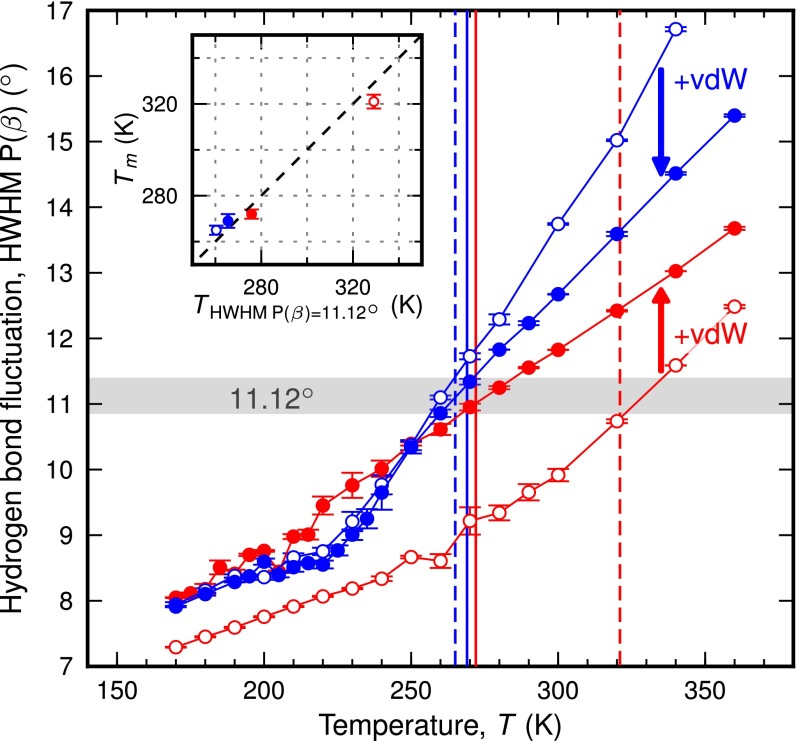
The absence of the density maximum in the simulations without vdW corrections can be understood by examining the strength of the HB network. In Fig. 4 we analyze the fluctuations in the HB angle β, a measure of the HB strength, as a function of temperature. The different magnitudes of HB fluctuations indicate that HBs in uncorrected simulations are either too strong (BLYP) or too weak (RPBE) to yield a density maximum. In BLYP-based simulations the tetrahedral water network is too rigid, so that even in the high-temperature regime second-shell molecules are not able to penetrate the first solvation shell and a shift of the second shell at lower temperatures is prevented. HBs in RPBE-based simulations, on the other hand, are very weak, as manifested by large fluctuations in β and large distances of first-shell molecules, so that the first and second solvation shells are both shifted to smaller distances upon cooling until at $\approx$ 260 K HBs are strong enough to slightly reduce the number of interstitial molecules. This effect leads to a strong contraction of the system, resulting in high thermal expansivities (compare SI Appendix, Table S4) with an almost 10-fold increase over the experimental value. These results are in line with the observations made for the dynamic properties of water shown in Fig. 1 C–E.

Fig. 4.

HB fluctuation and melting temperature. Fluctuation in the HB angle β, measured by computing the half width at half maximum (HWHM) of the distribution function P(β), as a function of temperature obtained from NNP simulations based on the BLYP (red empty circles), BLYP-vdW (red filled circles), RPBE (blue empty circles), and RPBE-vdW (blue filled circles) density functionals. The vertical lines denote the melting temperature of the respective potentials (solid lines, vdW-corrected potentials; dashed lines, uncorrected potentials). (Inset) Correlation between melting temperature $T_m$ and temperature of an HB fluctuation of 11.12°. The error bars of the melting temperatures were obtained by block averaging.

Interestingly, we find that the HB fluctuations evaluated for the liquid phase can be used as a measure for the melting temperature of ice Ih, $T_m$, in analogy to the Lindemann melting rule (57). For all NNPs used here, ice Ih melts when the HB fluctuations exceed a critical value of $\approx$ 11° (compare Fig. 4), which explains the different values for $T_m$ reported in Fig. 2C. To verify the correlation between HB strength and melting temperature, we performed simulations close to the melting temperature using a series of empirical water models. As shown in SI Appendix, Fig. S9, the critical fluctuation value at which melting occurs depends slightly on the class of water model. For models based on the 4-site transferable intermolecular potential (TIP4P) (5), a high degree of correlation is found at a critical value of $\approx$ 10°.

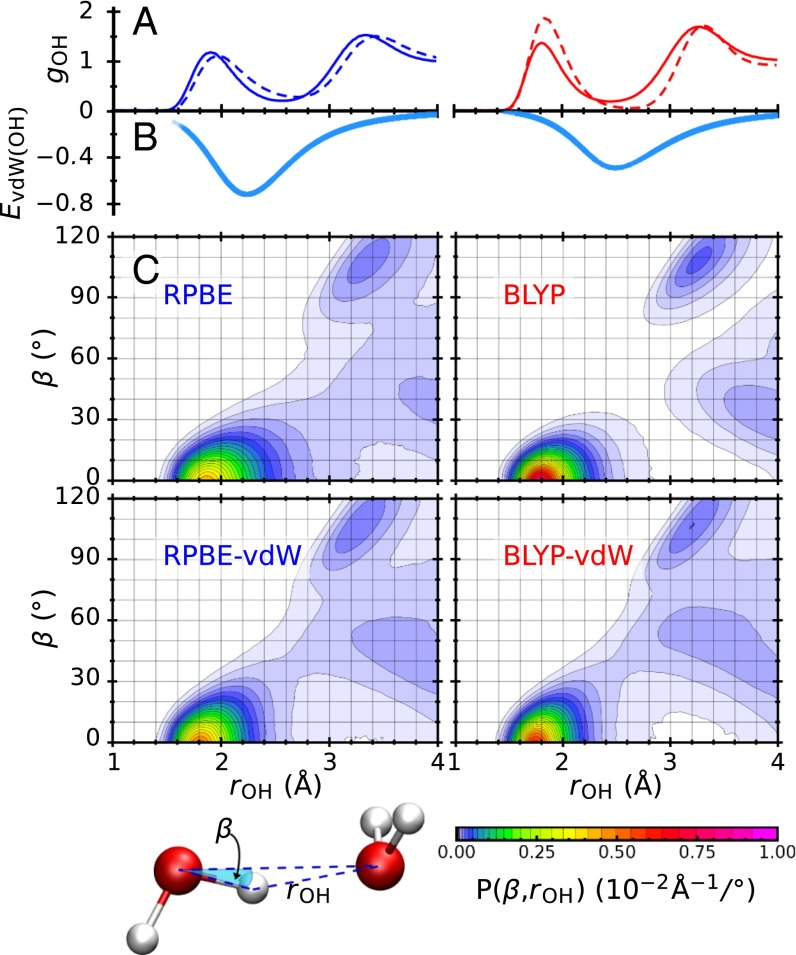
The fact that vdW corrections either weaken (BLYP) or strengthen (RPBE) HBs is related to the vdW correction terms which are different for the two density functionals (SI Appendix, Table S7). For RPBE, the vdW interactions between pairs of oxygen and hydrogen atoms (Fig. 5B, Left) have a deep minimum at short OH distances increasing the HB strength by reducing the probability of configurations with extended intermolecular OH distances (compare Fig. 5A, Left). In contrast, the BLYP vdW pair interaction (Fig. 5B, Right) is weaker and shifted to larger distances, inducing an increased population of extended HBs with reduced strength (Fig. 5A, Right). Similar observations can be made for vdW interactions between pairs of oxygen atoms, shown in SI Appendix, Fig. S10. Both effects are clearly visible in the probability density functions of HB angle and OH distance (Fig. 5C): HBs are very flexible in the case of RPBE and very stiff in the case of BLYP. Both vdW-corrected density functionals show similar distributions in between the uncorrected probability density functions.

Fig. 5.

Effect of vdW interactions on HB geometry. (A) Intermolecular oxygen–hydrogen radial distribution functions ${\mathit{g}}_{\text{OH}}$ from NNP simulations at 300 K based on the RPBE (Left) and BLYP (Right) density functionals with (solid lines) and without (dashed lines) vdW corrections. (B) vdW pair interaction energy $E_{\text{vdW}\left(\text{OH}\right)}$ (in units of $k_{\text{B}}T$, where $k_{\text{B}}T$ is Boltzmann's constant times temperature) between oxygen and hydrogen atoms as a functions of the pair distance $r_{\text{OH}}$ obtained from the NNP simulations. (C) Probability density function P(β,${\mathit{r}}_{\text{OH}}$) of the HB angle β and the oxygen–hydrogen distance $r_{\text{OH}}$.

Dielectric Properties.

We conclude by analyzing the influence of vdW interactions on the dielectric properties of liquid water. Calculating the dielectric constant from molecular dynamics (MD) simulations requires simulation times of several nanoseconds. Whereas rough estimates based on short AIMD trajectories have been made (58, 59), converged values have not been obtained to date. We have computed converged dielectric constants at 300 K by generating independent configurations in NNP simulations, which we then used to calculate molecular dipole moments from maximally localized Wannier functions (60) (SI Appendix). Whereas the dielectric constant is overestimated in simulations without vdW interactions (159.8 and 108.9 for BLYP and RPBE, respectively) compared with the experimental value of 78.4, the values improve if vdW forces are accounted for (106.2 and 95.2 for BLYP-vdW and RPBE-vdW, respectively) which is associated with a shift of the molecular dipole moment distributions to lower values (SI Appendix, Fig. S6A) in agreement with results from AIMD simulations (43).

Conclusions

In summary, we have shown that ab initio-based NNP simulations are able to correctly predict water’s density maximum and melting temperature provided that vdW forces are taken into account, highlighting the important role of these interactions in determining the properties of aqueous systems. Despite their rather weak and anisotropic nature, vdW forces crucially modulate the HB network and ensure the right level of flexibility that causes the anomalous behavior of water. These results demonstrate the predictive power of AIMD simulations compared with empirical water models [whose density maximum is usually underestimated if experimental density information is not explicitly included in the parametrization process (61)]. They further indicate that liquid water and ice can be accurately described already on the GGA level of theory if vdW corrections are considered without the need to include exact exchange in the form of computationally demanding hybrid density functionals. NNP simulations of water are thus a reliable and predictive tool which could also help investigate other important properties such as the existence of a liquid–liquid transition in water at supercooled conditions (4, 6). Unlike most water models, NNPs are capable of describing the making and breaking of chemical bonds, opening the possibility to study proton transfer and autoionization in the condensed phase.

Methods

MD simulations were performed with an extended version of the LAMMPS program (62) using four ab initio-based NNPs for water representing RPBE (27) and BLYP (28, 29) density functionals with and without vdW corrections using the D3 method (30). Parameter sets for all NNPs are publicly available (dx.doi.org/doi:10.6084/m9.figshare.1497907).

Distribution functions compared with previous AIMD results (Fig. 1A, top two curves) were computed in the canonical (NVT) ensemble at a density of 1 g/cm³, whereas for a comparison with experiment (Fig. 1A, bottom two curves and Fig. 1B) simulations were run in the isothermal–isobaric (NPT) ensemble (see below). Dynamic properties (Fig. 1 C–E) were obtained in the following way: For each NNP and temperature the equilibrium volume was determined by NPT simulations as described below. Then, simulations in the NVT ensemble were carried out for 1 ns using 512 water molecules and a time step of 0.5 fs. Thirty-two statistically independent sets of coordinates and velocities were extracted from each NVT trajectory and used as starting points for simulations in the microcanonical (NVE) ensemble with a simulation time of 200 ps per trajectory. After discarding the first 50 ps for the purpose of equilibration, viscosities and diffusion coefficients corrected for finite size effects were determined (see SI Appendix for details). HB kinetics were analyzed in terms of the Luzar–Chandler model (36) and computed with the GROMACS package (63, 64). The vibrational density of states (VDOS) spectrum shown in SI Appendix, Fig. S3 was computed from velocity autocorrelation functions obtained from 16 independent NVE simulations with a length of 20 ps using initial configurations from an NVT trajectory at 300 K.

Density isobars at 1 bar covering a temperature range from 380 to 170 K in steps of 5–20 K were obtained from MD simulations of 128 water molecules in the NPT ensemble with a time step of 0.5 fs and using the equations of motion of Shinoda et al. (65). As shown in SI Appendix, Fig. S7, simulation cells containing 128 molecules are sufficient to obtain converged density isobars. The simulation length at each single temperature was 2–20 ns (depending on temperature and convergence behavior), resulting in a total simulation time of more than 700 ns. Configurations from equilibrated simulations in the NVT ensemble were used as starting points for the NPT simulations at 380 K. Subsequently, simulations at lower temperatures were performed step by step by using the final configuration of the preceding simulation as initial configuration. The first halves of the trajectories served for equilibration and were not used for analyses. Density maxima and thermal expansivities at T = 25 °C were obtained from polynomial fits (fourth order for BLYP-vdW and RPBE-vdW, third order for BLYP and RPBE) to the density isobars.

Melting temperatures of ice Ih were computed using the interface pinning method (49, 66) (see SI Appendix for details). The densities of the liquid and the solid phase reported in SI Appendix, Table S5 were obtained from separate NPT simulations carried out at $T_m$ using 2,304 water molecules and simulation times of 1 ns (after equilibrating for 0.5 ns). To account for possible differences between the DFT and the NNP potential-energy surfaces, the melting temperatures were corrected using thermodynamic perturbation theory as described in SI Appendix. All correction terms have positive values which range from 2 to 11 K (SI Appendix, Table S6).