Abstract
Numerous processes across both the physical and biological sciences are driven by diffusion. Partial differential equations are a popular tool for modelling such phenomena deterministically, but it is often necessary to use stochastic models to accurately capture the behaviour of a system, especially when the number of diffusing particles is low. The stochastic models we consider in this paper are ‘compartment-based’: the domain is discretized into compartments, and particles can jump between these compartments. Volume-excluding effects (crowding) can be incorporated by blocking movement with some probability. Recent work has established the connection between fine- and coarse-grained models incorporating volume exclusion, but only for uniform lattices. In this paper, we consider non-uniform, hybrid lattices that incorporate both fine- and coarse-grained regions, and present two different approaches to describe the interface of the regions. We test both techniques in a range of scenarios to establish their accuracy, benchmarking against fine-grained models, and show that the hybrid models developed in this paper can be significantly faster to simulate than the fine-grained models in certain situations and are at least as fast otherwise.
Keywords: compartment-based modelling, hybrid modelling, diffusion, volume exclusion
1. Introduction
Diffusion can be modelled using a multitude of mathematical techniques. Partial differential equations (PDEs) are a popular choice, but are inappropriate where stochastic effects are significant [1]. Stochastic models of diffusion fall into two main categories: off-lattice models, where each particle's position lies on a continuum within the domain, and on-lattice, compartment-based models, where particles undergo a random walk on a lattice [2].
Volume exclusion (crowding) can be incorporated into compartment-based models by assigning a maximum particle capacity, m, to each compartment, where m varies linearly with the compartment's size. Attempted moves into any given compartment are blocked with some probability. Of particular interest is the case where this probability scales linearly with the compartment's current occupancy, such that the blocking probability is equal to zero when empty and to unity when full to capacity, m [3–5]. We describe such a model as ‘partially excluding’ or ‘coarse-grained’ when m > 1, and as ‘fully excluding’ or ‘fine-grained’ when m = 1. In one spatial dimension, the fully excluding model is an example of single-file diffusion, a class of model of particular relevance to biological processes such as the diffusion of αTAT1 within microtubules [6], the movement of flagellin in the formation of bacterial flagella [7] and the dispensing of proteins through in the nanochannels of drug delivery devices [8].
In a recent paper [9], we showed that the descriptions of a one-dimensional system given by fully and partially excluding models can be reconciled. Specifically, we demonstrated that the mean and variance of particle numbers within each partially excluding compartment of capacity m can be matched with the mean and variance of the total number of particles across the m corresponding contiguous fully excluding compartments.
Our previous work considered uniform lattices, where every compartment was of the same size and capacity. For some models, such as those of real biological systems, it may be necessary to incorporate events occurring across a wide range of spatial and temporal scales [10]. This means that it may be desirable to, for example, simulate the diffusion of particles with precision in a small spatial region of interest, such as the area around receptors on a cell membrane [11], or around an ion channel [12], while using less computationally intensive methods elsewhere on the domain. As a result, recent years have seen the development of multiple hybrid approaches for linking compartment-based models to off-lattice models of diffusion [13–15], off-lattice models to PDE models of diffusion [16] and PDE models to compartment models of diffusion [17–19]. To the best of our knowledge, however, there have been no attempts to develop a hybrid system interfacing volume-excluding compartment-based models at different scales.
In this paper, we consider how to interface a uniform region of partially excluding compartments with another uniform region of fully excluding compartments, and present two hybrid approaches capable of accurately simulating diffusion in such systems. Both approaches will be of value to researchers working on multi-scale systems, as they can speed up simulations while preserving precision where needed.
We begin by providing a short summary of our previous work on reconciling models of particle behaviour across spatial scales on uniformly partitioned lattices, before proceeding to consider hybrid models. The first hybrid method we present extends to diffusion on non-uniform lattices the previous results reconciling fully excluding and partially excluding systems. We use these results to present one simple and elegant means of connecting two uniformly partitioned regions of differing compartment capacity. The second hybrid method we present defines a small area between the fine and coarse regions of the domain, where particle behaviour exhibits some characteristics of both regions. We term this area a pseudo-compartment, and the modelling framework a pseudo-compartment method, by analogy to a recent paper using similar techniques to couple a PDE model to a compartment-based model [17].
To determine the accuracy of these hybrid approaches, we apply each one to three scenarios, comparing the correspondence of the means and variances of particle numbers in the hybrid system to the corresponding moments in non-hybrid fine- and coarse-grained systems, as well as to PDE solutions when appropriate. The first scenario confirms that the hybrid systems are capable of maintaining a uniform steady state. The second compares their accuracy in a simple case of particle spreading from an initially inhomogeneous particle distribution. In the third scenario, we examine a morphogen gradient formation system, incorporating particle decay and influx of particles at the left-hand boundary x = 0. Morphogen gradients are a common example of a multi-scale system in biology, as they incorporate both regions of low particle density where models with high spatial resolution are suitable, and regions of high particle density where such detailed modelling is computationally infeasible and unnecessary [20,21]. In all three cases, we observe that the mean and variance of particle numbers in each compartment of the hybrid models agree with those obtained from simulations run on uniform lattices.
Finally, we consider a simple multi-species scenario, where the simulated results of a partially excluding model fail to match those of a fully excluding model. We demonstrate that both hybrid systems are capable of matching the accuracy of the fully excluding model in this scenario, while requiring only between a third and a seventh of the computational time to simulate.
2. Random walks on uniform lattices
We consider a one-dimensional lattice-based random walk on 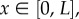 where each motile particle has length h. The length of the domain, L, is chosen such that L = Nh, where
where each motile particle has length h. The length of the domain, L, is chosen such that L = Nh, where 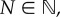 so that the domain can contain at most N particles. We impose a uniform lattice consisting of K compartments onto this domain, where choices of K are constrained by the requirement that m = L/(Kh) should be a positive integer. As a consequence, N = Km, and m describes the maximum number of particles that can reside in each of the K compartments, or their ‘capacity’. Diffusion may then be modelled as a series of jumps as particles move between neighbouring compartments; in the absence of volume exclusion, the jump rates between compartments scale inversely with the square of box lengths, i.e.
so that the domain can contain at most N particles. We impose a uniform lattice consisting of K compartments onto this domain, where choices of K are constrained by the requirement that m = L/(Kh) should be a positive integer. As a consequence, N = Km, and m describes the maximum number of particles that can reside in each of the K compartments, or their ‘capacity’. Diffusion may then be modelled as a series of jumps as particles move between neighbouring compartments; in the absence of volume exclusion, the jump rates between compartments scale inversely with the square of box lengths, i.e.
| 2.1 |
where D is the macroscale diffusivity of particles. The spatial resolution of the model can be varied by changing the compartment capacity, m, as illustrated in figure 1. We are particularly interested in the fine-grained limiting case m = 1, where each compartment contains at most one particle (fully excluding). We shall consider the fully excluding case to be ‘accurate’, in the sense that no assumptions are required to determine each particle's position within its compartment. We assume that the particles considered in this paper do not interact except through volume-excluding effects.
Figure 1.
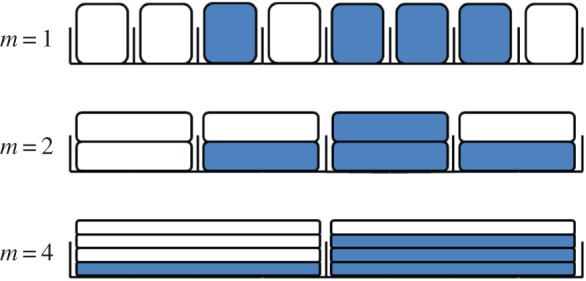
Shaded cells represent particles, and white cells unused capacity, within uniform compartments of different capacities. As m increases, the spatial resolution coarsens, but the descriptions given at these different scales can be reconciled. (Online version in colour.)
2.1. Volume exclusion
A common approach taken in the literature is to define the jump rates between compartments as the product of the non-excluding jump rate and a blocking probability
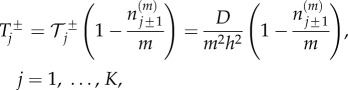 |
2.2 |
where 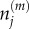 is the number of particles in compartment j when each compartment has capacity m [3]. The term in brackets incorporates volume exclusion by causing attempted jumps into a compartment to fail with a probability that scales linearly with the compartment occupancy. Other forms for the blocking probability could be chosen, but the resulting particle behaviours would not be conserved across spatial scales [9]. Imposing zero-flux boundary conditions so that the number of particles in the system is constant, the evolution of mean particle numbers in compartment 1 < j < K is given by
is the number of particles in compartment j when each compartment has capacity m [3]. The term in brackets incorporates volume exclusion by causing attempted jumps into a compartment to fail with a probability that scales linearly with the compartment occupancy. Other forms for the blocking probability could be chosen, but the resulting particle behaviours would not be conserved across spatial scales [9]. Imposing zero-flux boundary conditions so that the number of particles in the system is constant, the evolution of mean particle numbers in compartment 1 < j < K is given by
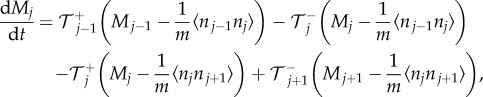 |
2.3 |
where  is used to denote expected values, and
is used to denote expected values, and 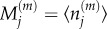 denotes the mean number of particles in the jth compartment of capacity m. Writing out the transition rates explicitly, the evolution of mean particle numbers in each compartment is given by
denotes the mean number of particles in the jth compartment of capacity m. Writing out the transition rates explicitly, the evolution of mean particle numbers in each compartment is given by
| 2.4 |
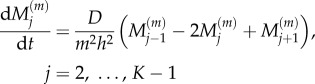 |
2.5 |
and
| 2.6 |
We refer to these as ‘mean master equations’, and note their linearity: this is a consequence of our choice of blocking probability, and would not be the case had we chosen otherwise [9]. Nonlinear terms will also occur when there is more than one species of particle present, or when there is directional bias in particle movement [22]. The absence of nonlinear terms in this macroscopic description does not imply that the individual particles are unconstrained by volume exclusion: a single-tagged particle can display density-dependent behaviour [6,22].
It is also possible to derive equations describing the evolution of the variance of 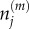 (variance master equations):
(variance master equations):
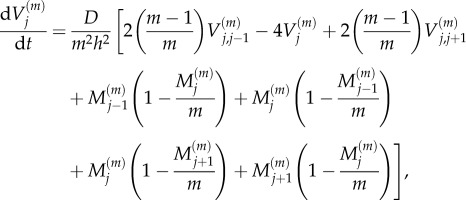 |
2.7 |
for 2 ≤ j ≤ K − 1, where 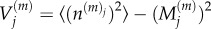 is the variance of particle numbers in compartment j, and
is the variance of particle numbers in compartment j, and 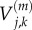 is the covariance of particle numbers in compartments j and k:
is the covariance of particle numbers in compartments j and k:
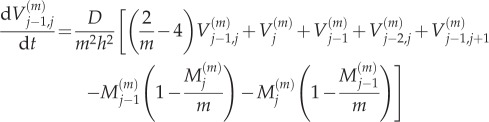 |
and
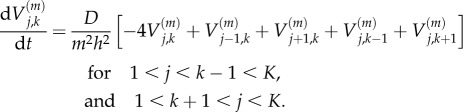 |
2.8 |
Similar expressions can be found for the variance and covariance terms involving the boundary compartments, j = 1, K. Note that, unlike the mean master equations, equations (2.7) and (2.8) contain m terms resulting from volume-excluding effects. As a result, mean particle numbers will evolve identically in volume-excluding and non-excluding models, but the variances and covariances of particle numbers will be different.
When comparing a fully excluding model (m = 1) to a partially excluding model (m > 1), we seek to show that the mean and variance of particle numbers in each compartment is conserved. In order to compare the results of the two models, we first consider the means and variances of the total number of particles residing in a group of m contiguous compartments with capacity one. We therefore define
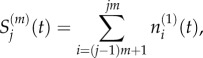 |
2.9 |
with 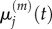 the mean of
the mean of 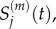 and
and 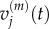 its variance.
its variance.
2.2. Moving between scales
We wish to establish the relationship between: (i) 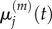 and
and 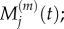 and (ii)
and (ii) 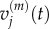 and
and 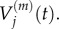 It is straightforward to show that, in both of these cases, the steady-state values match. To find the relationship between
It is straightforward to show that, in both of these cases, the steady-state values match. To find the relationship between 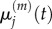 and
and 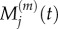 under transient conditions, we note
under transient conditions, we note
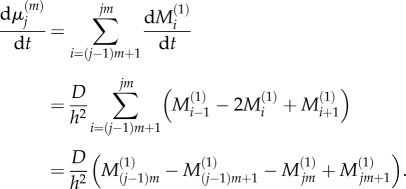 |
2.10 |
We compare this to the coarse-grained model, equation (2.5), which we re-state here for convenience:
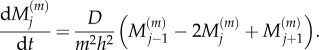 |
Under the assumption that particles in the coarse (m > 1) compartments are distributed, on average, following a linear interpolation between neighbouring coarse compartments. We therefore write
| 2.11 |
and
| 2.12 |
as shown in figure 2, with similar values for 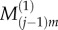 and
and 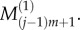 As a result, we have
As a result, we have
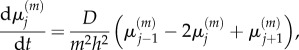 |
2.13 |
and evolution of the mean particle numbers in the coarse-grained system matches that of the accurate model. Analogous reasoning can be applied to match the evolution of the variance of particle numbers.
Figure 2.
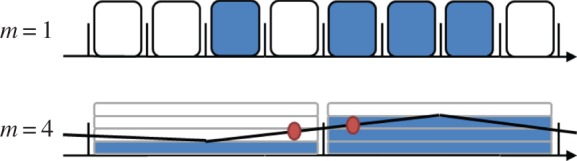
Schematic of the interpolation process for m = 4. (Online version in colour.)
3. Hybrid fully/partially excluding systems
Having reviewed the reasoning used to match descriptions of uniform lattices at different spatial scales, we proceed to outline two hybrid models using non-uniform lattices. In both cases, we justify the correspondence of mean particle numbers in each compartment of the hybrid model to the mean particle numbers in the accurate, m = 1 uniform lattice.
3.1. Voronoi method
Jump rates between compartments can be derived from the assumption of underlying Brownian motion of particles using first-passage time arguments (the method is outlined in the electronic supplementary material, appendix A) [23]. Particles are assumed to begin from a fixed point within their current compartment, the ‘residence point’, and are deemed to have jumped to a neighbouring compartment when they first reach that compartment's residence point. For a uniform lattice, these residence points are located at the centre of each compartment.
For a non-uniform lattice, we let the compartment residence points be at [x1, … ,xK] on the domain [0, L], then define Δxj = xj − xj−1, for 1 < j ≤ K. Compartment edges are then placed so as to be equidistant between neighbouring residence points, so that the jth compartment covers the interval 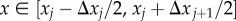 (an example is given in figure 3). Recall that the capacity of each compartment varies linearly with its length, and that the capacity of compartments on a uniform lattice is given by m = L/(Kh), that is, the compartment length divided by particle length, h. Similarly, we obtain capacities [m1, … ,mK] for the K Voronoi compartments by dividing their lengths by h, obtaining
(an example is given in figure 3). Recall that the capacity of each compartment varies linearly with its length, and that the capacity of compartments on a uniform lattice is given by m = L/(Kh), that is, the compartment length divided by particle length, h. Similarly, we obtain capacities [m1, … ,mK] for the K Voronoi compartments by dividing their lengths by h, obtaining
| 3.1 |
| 3.2 |
and
| 3.3 |
Figure 3.
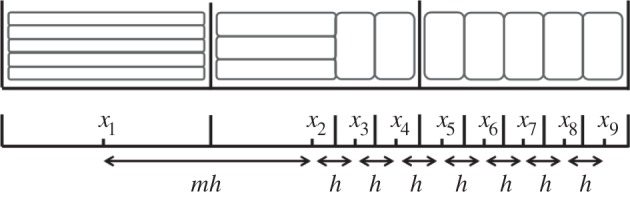
The locations of a Voronoi lattice's residence points are chosen (x1, … , x9), and then compartment edges are positioned equidistant between neighbouring residence points. This particular arrangement demonstrates how a compartment of capacity (m + 1)/2 can be used to interface regions where m > 1 with regions where m = 1. In this case, Δx2 = mh, and Δxj = h for j = 3, … , 9. When grouped, we would find 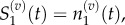
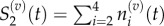 and
and 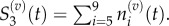
The positioning of residence points is restricted by a requirement that every compartment should have an integer-valued capacity. Inverting the conditional expected exit times obtained in the electronic supplementary material, appendix A, and factoring in the relative probabilities of moving left or right, the following transition rates for a particle in the jth compartment, in the absence of volume exclusion, can be obtained [23,24]:
| 3.4 |
| 3.5 |
Multiplying equations (3.4) and (3.5) by the jump blocking probability, 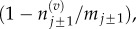 we arrive at the transition rates for a volume-excluding model:
we arrive at the transition rates for a volume-excluding model:
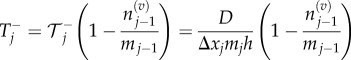 |
3.6 |
and
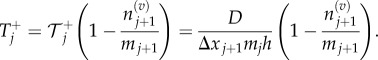 |
3.7 |
The following equation for the evolution of mean particle number can then be obtained:
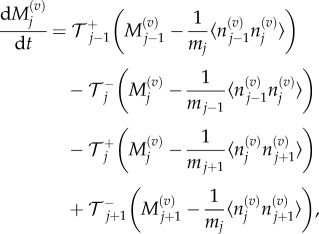 |
3.8 |
where we use 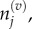
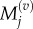 and
and 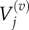 to denote the number, mean and variance, respectively, of particles in the jth Voronoi compartment. From the definitions of the transition rates given in equations (3.6) and (3.7), we note that
to denote the number, mean and variance, respectively, of particles in the jth Voronoi compartment. From the definitions of the transition rates given in equations (3.6) and (3.7), we note that 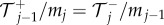 and
and 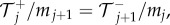 and hence equation (3.8) simplifies to
and hence equation (3.8) simplifies to
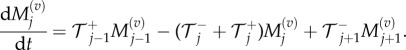 |
3.9 |
In the same way, we can obtain equations for the evolution of variances,
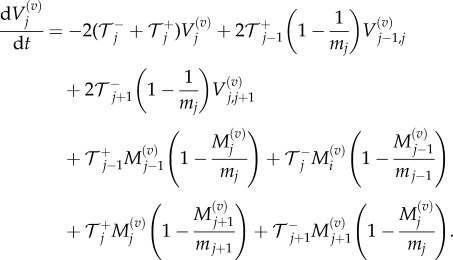 |
3.10 |
The derivations of both equation (3.8) and (3.10) are outlined in the electronic supplementary material, appendix B. In the previous section, we summarized previous work matching the behaviours of 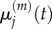 with
with 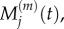 and of
and of 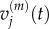 with
with 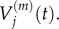 We now wish to show that particle behaviour is similarly conserved between scales when using a Voronoi partitioned lattice.
We now wish to show that particle behaviour is similarly conserved between scales when using a Voronoi partitioned lattice.
Suppose that the Voronoi lattice consists of p compartments of capacity m > 1 at the left of the domain, followed by a single compartment of capacity (m + 1)/2, and then the remainder of the domain is partitioned into fine compartments of capacity one (as illustrated in figure 3, for p = 1 and m = 5). To avoid non-integer compartment capacities, our choice of m must be odd-valued. Recall that, to aggregate compartments on a fully excluding uniform lattice, we wrote
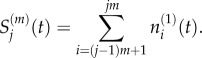 |
3.11 |
By analogy, we define 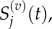 such that
such that
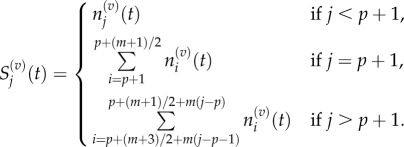 |
3.12 |
These groupings are illustrated in figure 3 for p = 1 and m = 5. As in the previous section, we write 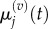 and
and 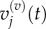 to denote the mean and variance of
to denote the mean and variance of 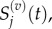 and seek to show a connection between: (i)
and seek to show a connection between: (i) 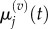 and
and 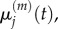 and (ii)
and (ii) 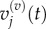 and
and 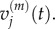 We can do this by examining the equation for the evolution of
We can do this by examining the equation for the evolution of 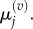 For j < p, we write
For j < p, we write
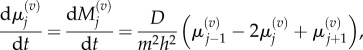 |
3.13 |
which clearly matches equation (2.13). For j > p + 1, a similar match can be obtained using the same linear interpolation applied in the previous section.
When j = p, p + 1 then we use equations (3.6) and (3.7) to obtain
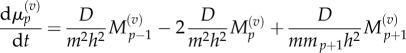 |
3.14 |
and
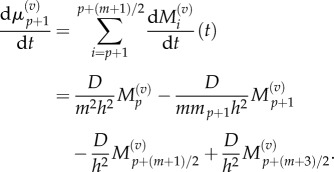 |
3.15 |
As before, we make the substitutions 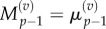 and
and 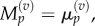 and interpolate values of
and interpolate values of 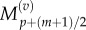 and
and 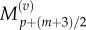 from
from 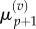 and
and 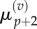 using equations (2.11) and (2.12). Finally, we observe that the residence point of the (p + 1)th Voronoi box coincides with the centre of the (p + 1)th aggregated box (as illustrated in figure 3), so the interpolated value for
using equations (2.11) and (2.12). Finally, we observe that the residence point of the (p + 1)th Voronoi box coincides with the centre of the (p + 1)th aggregated box (as illustrated in figure 3), so the interpolated value for 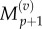 is simply
is simply
| 3.16 |
Substituting this into equations (3.14) and (3.15), we arrive at
| 3.17 |
and
| 3.18 |
so we can expect the values of μ(v) to match those of μ(m). Although we do not show them here, analogous treatments can be applied to match v(v) with v(m).
Voronoi partitioned lattices provide one method of interfacing two regions partitioned by uniform lattices of differing compartment capacities, but only for certain compartment capacity values. It is not possible, for example, to interface a region where m = 1 with a region where m = 2, as any intermediate sized compartment would have non-integer-valued capacity. In such situations, it is useful to have another hybrid method capable of interfacing the regions.
3.2. Pseudo-compartment method
Pseudo-compartment methods have previously been used to interface compartment-based models with PDE models. In such models, the domain consists of a region where diffusion is modelled using a discrete model, another region in which diffusion is modelled using a continuum PDE model, and a pseudo-compartment that combines both models. Specifically, although particle concentration in the pseudo-compartment is modelled in a spatially continuous manner using PDEs, discrete jump events between the pseudo-compartment and the neighbouring compartment-based region can take place, adjusting the particle concentration profile appropriately [17]. In this section, we discuss using similar ideas to interface one region of the domain, partitioned by a coarse lattice with compartment capacity m > 1, with another region, partitioned with a fine lattice where m = 1.
We assume, without loss of generality, that the coarse region is to the left-hand side of the domain, and that it consists of p compartments of capacity m > 1. The first m fully excluding compartments, i.e. those of index p + 1 through to p + m, are then said to collectively comprise the pseudo-compartment (this is illustrated for p = 1 and m = 5 in figure 4). Particles in compartments 1 through to p may attempt to jump to neighbouring compartments in this range with rate D/m2h2, while particles in compartments p + 1 through to K may attempt to jump to neighbouring compartments in this range with rate D/h2. In both cases, these jumps fail with blocking probability
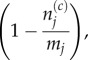 |
3.19 |
where j is the index of the destination compartment, and we use 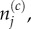 and later
and later 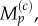 to denote, respectively, the number of particles and the mean number of particles in compartment j of the lattice.
to denote, respectively, the number of particles and the mean number of particles in compartment j of the lattice.
Figure 4.
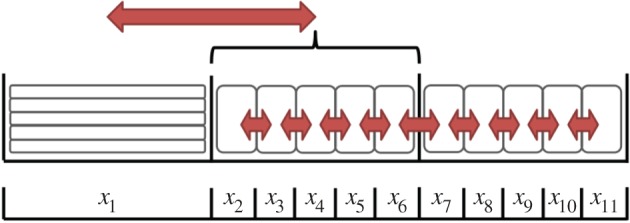
Pseudo-compartment method, with m = 5 and p = 1. The compartments of index 2 through to 6 form the pseudo-compartment. Particles in these compartments may attempt to jump to neighbouring compartments with rate D/h2, or into compartment 1 with propensity D/m2h2, subject to the standard blocking probability arising from volume exclusion. Particles in compartment 1 may jump into any unoccupied compartment with index 2 through to 6 with propensity D/mh2. When grouped, we have 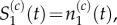
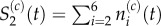 and
and 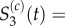
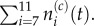 (Online version in colour.)
(Online version in colour.)
In addition, it is possible for a particle in compartment p to move into the pseudo-compartment with jump propensity D/m2h2. When this happens, one of the compartments that comprise the pseudo-compartment is selected uniformly at random, and if it is unoccupied a particle jumps into it from compartment p (if it is occupied then the jump is terminated). Equivalently, volume-excluding effects can be incorporated by multiplying the jump propensity by the fraction of compartments in the pseudo-compartment currently unoccupied, and selecting a destination from among the unoccupied compartments uniformly at random when a jump occurs.
Similarly, a particle residing within any part of the pseudo-compartment may jump into compartment p, with propensity
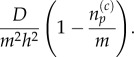 |
3.20 |
All of the possible particle jumps for an example lattice are illustrated by arrows in figure 4. Suppose that the pth compartment is the last partially excluding compartment, so that all compartments of index greater than p will be fully excluding. Within the coarse region, we write the usual equations for the evolution of mean particle number
| 3.21 |
and
| 3.22 |
The mean master equation for compartment p, the final partially excluding compartment, is modified to account for the incoming particles it can receive from all fully excluding compartments within the pseudo-compartment
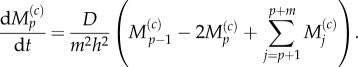 |
3.23 |
Similarly, the equations for mean particle number in the m fully excluding compartments comprising the pseudo-compartment region must also account for particles moving to, and arriving from, the partially excluding region, as well as for movement over the fully excluding lattice,
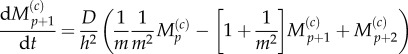 |
3.24 |
and
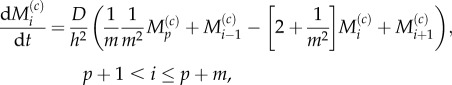 |
3.25 |
and, finally, beyond the pseudo-compartment, the evolution of mean particle number is described using the standard mean master equations with m = 1,
| 3.26 |
and
| 3.27 |
To compare the description of particle diffusion given by the pseudo-compartment model to the description given by the fully excluding model where m = 1 we must aggregate the compartments, writing
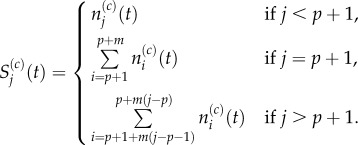 |
3.28 |
As before, we write 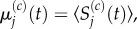 and seek to match
and seek to match 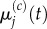 with
with 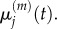 This is trivial for j < p and for j > p + 1, as these are sections of uniformly partitioned compartments where m > 1 and m = 1, respectively, and so the previously obtained results apply. When j = p, we use equation (3.23) to write
This is trivial for j < p and for j > p + 1, as these are sections of uniformly partitioned compartments where m > 1 and m = 1, respectively, and so the previously obtained results apply. When j = p, we use equation (3.23) to write
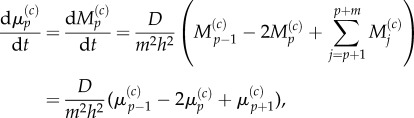 |
3.29 |
which is the expected form needed to match 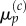 with
with 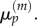 Similarly, for j = 1 we use equations (3.24) and (3.25) to write
Similarly, for j = 1 we use equations (3.24) and (3.25) to write
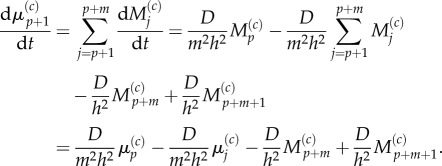 |
3.30 |
Interpolating values of 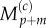 and
and 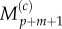 using equations (2.11) and (2.12), we finally arrive at
using equations (2.11) and (2.12), we finally arrive at
| 3.31 |
so we expect the values of 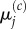 to match those of
to match those of 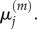
Having presented two hybrid methods for interfacing partially excluding with fully excluding regions, we now apply them both to a number of test systems to check their correspondence to the fully excluding model where m = 1.
4. Numerical investigations
In this section, we consider three single-species test cases: maintaining a uniform steady state in a purely diffusive system, particle redistribution from a non-uniform initial state and a morphogen gradient. For each case, we compare the following four different models:
(1) Uniform fully excluding (m = 1): 105 compartments of capacity one and length 0.2.
(2) Uniform partially excluding (m = 7): 15 compartments of capacity seven and length 1.4.
(3) Hybrid Voronoi: five compartments of capacity seven and length 1.4, one box of capacity four and length 0.8, and 66 compartments of capacity one and length 0.2.
(4) Hybrid pseudo-compartment: five compartments of capacity seven and length 1.4, and 70 of capacity one and length 0.2. The first seven fully excluding compartments form the pseudo-compartment.
In each case, we use these four models to obtain, respectively, numerical values for 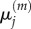 and
and 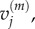 for
for 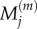 and
and 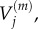 for
for 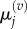 and
and 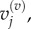 and for
and for 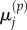 and
and 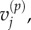 aggregating compartments from the finer grids into regions of capacity m = 7. In each case, we set h = 0.2, L = 21, and hence N = 105. We choose diffusion constant D = 2 for all test cases, and perform 50 000 realizations of each case over the time interval
aggregating compartments from the finer grids into regions of capacity m = 7. In each case, we set h = 0.2, L = 21, and hence N = 105. We choose diffusion constant D = 2 for all test cases, and perform 50 000 realizations of each case over the time interval 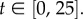
Because we consider the fully excluding model as ‘accurate’, in the sense that it specifies each particle's location precisely rather than making assumptions about its position within a larger compartment, a further 50 000 realizations of the fully excluding model were generated to provide an independent estimate for 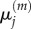 and
and 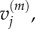 and these values were used as our comparison dataset. For the first two single-species test cases, it would also be possible to generate a comparison dataset by evaluating the master equations deterministically, but this would not be possible for the morphogen gradient test (the addition of particles to the first compartment with available capacity leads to a non-closed system of equations). In the interests of consistency, we have therefore generated all datasets by stochastic simulation, rather than using a mixture of approaches.
and these values were used as our comparison dataset. For the first two single-species test cases, it would also be possible to generate a comparison dataset by evaluating the master equations deterministically, but this would not be possible for the morphogen gradient test (the addition of particles to the first compartment with available capacity leads to a non-closed system of equations). In the interests of consistency, we have therefore generated all datasets by stochastic simulation, rather than using a mixture of approaches.
The agreement of the four models with the comparison dataset was then quantified using the histogram distance error (HDE) [25]:
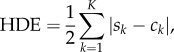 |
4.1 |
where Sk is the normalized value of the kth aggregated compartment of the model being considered, and ck is the normalized value of the kth aggregated compartment of the comparison dataset, such that
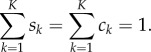 |
4.2 |
The HDE therefore returns values between zero and one, where zero corresponds to two identical datasets and one represents two completely distinct datasets. We note that the HDE is an example of an L1-norm, but that qualitatively similar results are observed when using L2-norms. Our conclusions are not affected by the choice of using an L1 or an L2-norm.
To generate realizations, we used an algorithm based on Gillespie's direct method [26], as described in the electronic supplementary material, appendix C. In each of the three test cases, we also record the time taken to simulate 50 000 realizations of each model. All simulations were performed using Matlab code, parallelized using parfor, on a four-core desktop computer using an AMD PhenomTM II X4 925 Processor.
4.1. Test case 1: maintaining a spatially uniform steady state
In this simplest test, for each realization we initialize 15 uniformly distributed particles over the lattice, let them diffuse freely, then record their final positions to ensure that they remain uniformly distributed. This is the most basic test and is performed to confirm that the hybrid interfaces do not interfere with a homogeneous particle distribution.
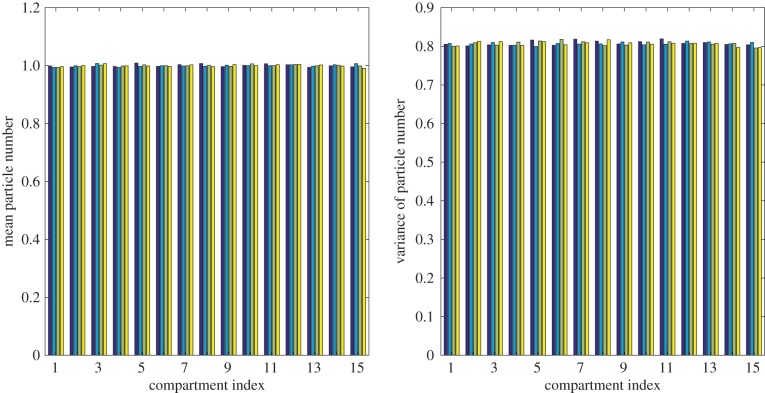
The mean and variance of particle numbers in each aggregated box at t = 25 are plotted in figure 5, showing good agreement between all four models. This agreement is quantified in table 1, where we observe that in each model, mean values deviate from the comparison data by less than 0.25%, and variance values deviate by less than 0.5%. Although we do not present the details here, it is also possible to demonstrate the steady-state agreement of all four models by analysing their mean and variance master equations.
Figure 5.
Results from 50 000 repeats of the uniform steady-state simulation at time t = 25. Fifteen particles were uniformly distributed at time t = 0 and then diffused until time t = 25. From left to right, each set of four bars shows results from the fully excluding (dark blue), partially excluding (light blue), Voronoi (green) and pseudo-compartment (yellow) models.
Table 1.
Details of uniform distribution simulation.
| model | mean HDE at t=25 | variance HDE at t=25 | time to simulate | acceleration relative to fully excluding |
|---|---|---|---|---|
| fully excluding | 0.0023 | 0.0046 | 28 741 s | — |
| partially excluding | 0.0022 | 0.0036 | 582 s | 49.4 times faster |
| Voronoi | 0.0020 | 0.0035 | 19 738 s | 1.5 times faster |
| pseudo-compartment | 0.0017 | 0.0033 | 26 361 s | 1.1 times faster |
We find that the hybrid models are faster to simulate than the fully excluding model. However, the decrease in computational time is modest, and we anticipate that significant computational savings will only be achieved when the majority of particle motion is concentrated in the partially excluding region. The case of maintaining a spatially uniform steady state is used in this paper solely to check the accuracy of the hybrid models, and hybrid modelling will not be helpful for such systems, unless the region partitioned with fully excluding compartments is small relative to the domain as a whole.
4.2. Test case 2: particle redistribution
The second test case examines the ability of our hybrid models to accommodate a net particle flux over the interface. Our initial state consists of 35 particles collected at the left of the domain. For the uniform fully excluding model, this means that the first 35 compartments are occupied. For all the other models, the first five compartments, each of capacity seven, are full to capacity.
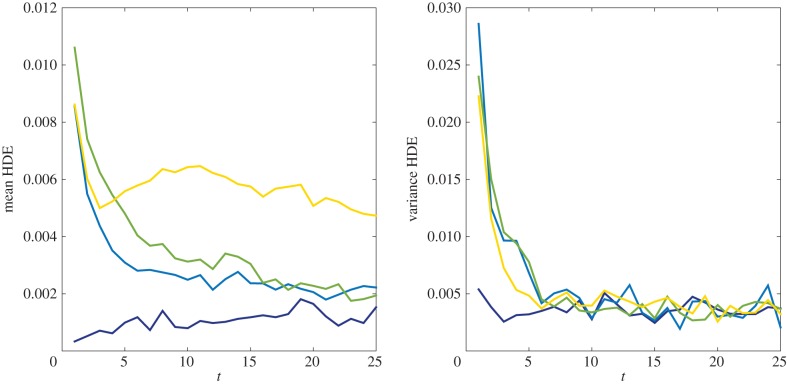
We compare the agreement of mean and variance values at t = 1, 2 ,3, … , 25 in figure 6. As anticipated, all four models perform well, although the Voronoi model performs somewhat better than the pseudo-compartment model. A possible explanation of this is that, with particle concentrations in the pseudo-compartment higher to the left and lower to the right, particles jumping into the pseudo-compartment from compartment p will disproportionately arrive in the more numerous vacant compartments to the right of the pseudo-compartment, slightly lengthening the average jump length. We note though that, even in this case of strongly asymmetric flux, the HDE remains below 0.008 throughout the simulation.
Figure 6.
HDE values for the mean and variance of the particle redistribution simulation results at discrete times t = 1, 2, … , 25. The four datasets in each figure correspond to the fully excluding (dark blue), partially excluding (light blue), Voronoi (green) and pseudo-compartment (yellow) models.
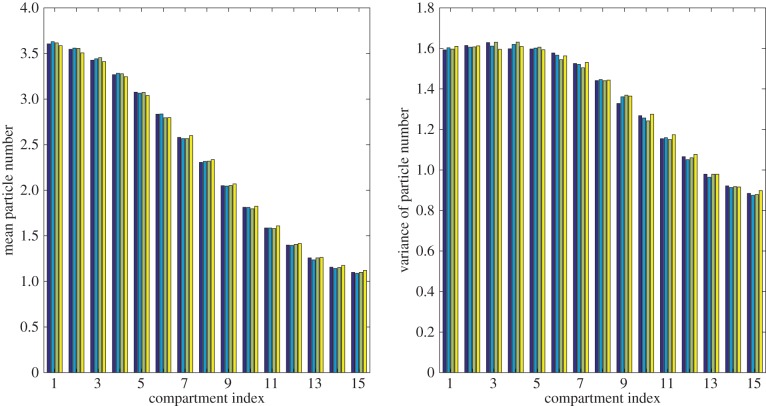
We also plot the means and variances of particle numbers at t = 25 in figure 7, and for consistency with the other test cases list the HDE values at time t = 25 in table 2. We also record the time taken to simulate each model in table 2, noting again that the hybrid models run faster than the fully excluding model, with the Voronoi model taking only half as much time to simulate. As with the spatially uniform steady state considered in the previous test, however, we would only expect significant time savings when the fully excluding region of the domain is relatively small; this case is presented primarily as a test of accuracy rather than to demonstrate significantly accelerated computation.
Figure 7.
Results from 50 000 repeats of the particle redistribution simulation at time t = 25. Thirty-five particles were initialized at the left of the domain at time t = 0. From left to right, each set of four bars shows results from the fully excluding (dark blue), partially excluding (light blue), Voronoi (green) and pseudo-compartment (yellow) models.
Table 2.
Details of particle redistribution simulation.
| model | mean HDE at t=25 | variance HDE at t=25 | time to simulate | acceleration relative to fully excluding |
|---|---|---|---|---|
| fully excluding | 0.0015 | 0.0037 | 40 775 s | — |
| partially excluding | 0.0022 | 0.0021 | 752 s | 54.2 times faster |
| Voronoi | 0.0019 | 0.0037 | 20 884 s | 2.0 times faster |
| pseudo-compartment | 0.0047 | 0.0032 | 31 330 s | 1.3 times faster |
4.3. Test case 3: morphogen gradient
In the final single-species test case, a simple morphogen gradient system is simulated. Starting from an empty initial state, particles enter the domain at the left-hand boundary with rate r1, while a zero-flux boundary condition is imposed at the right-hand boundary. As well as moving diffusively, particles decay with rate r2. In the absence of volume exclusion, a flux boundary condition can be implemented by adding or removing particles in the closest compartment to the boundary at a specified rate [27]. When volume exclusion is incorporated, however, it will sometimes be the case that the closest compartment to the boundary is already filled to capacity, in which case no more particles may be added to it. When this occurred in simulations, we added particles to the first compartment from the boundary with available capacity.
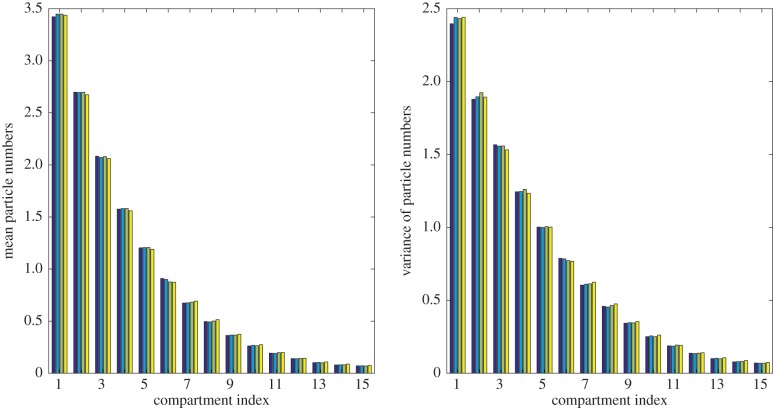
The means and variances of particles at time t = 25 are illustrated in figure 8, while HDE values and the computational time required to simulate each model are presented in table 3. In this case, the hybrid simulations are significantly faster than the equivalent fully excluding simulations. This is because the majority of particles are located in the first third of the domain, where the hybrid models use computationally efficient partially excluding compartments. Simulations of the Voronoi model ran more than four times faster than the fully excluding model, while simulations of the pseudo-compartment model ran more than three times faster than the fully excluding model.
Figure 8.
Results from 50 000 repeats of the morphogen gradient simulation at time t = 25. Particles are added to the system with rate r1 = 1 and are placed into the closest compartment to the left-hand boundary which is not full to capacity, while each particle may decay and be removed with rate r2 = 0.05. From left to right, each set of four bars shows results from the fully excluding (dark blue), partially excluding (light blue), Voronoi (green) and pseudo-compartment (yellow) models.
Table 3.
Details of morphogen gradient simulation.
| model | mean HDE at t=25 | variance HDE at t=25 | time to simulate | acceleration relative to fully excluding |
|---|---|---|---|---|
| fully excluding | 0.0015 | 0.0050 | 16 622 s | — |
| partially excluding | 0.0023 | 0.0060 | 385 s | 43.2 times faster |
| Voronoi | 0.0032 | 0.0059 | 3438 s | 4.8 times faster |
| pseudo-compartment | 0.0077 | 0.0105 | 4847 s | 3.4 times faster |
5. Application to a simple multi-species exclusion system
Having established the accuracy of the hybrid methodologies in the test cases of the previous section, we now apply them to a simple model system where the results of the partially excluding model deviate from those of the fully excluding model.
We consider a simple multi-species system containing two species of particle, A and B [22]. Neither species is reactive, and particles do not interact with each other except through volume exclusion effects. The initial state for the system consists of 21 particles of species A at the left of the domain, and 21 particles of species B at the right of the domain, as illustrated in figure 9 (so that for the fully excluding model, the first and last 21 compartments are occupied, and for the other models the first and last three compartments are filled to capacity). When simulated using a partially excluding model, this system will eventually reach a homogeneous steady state, with both A and B particles intermixed since the coarsened lattice description allows particles to move past each another. By contrast, the fully excluding model does not allow particles to pass one another, and hence the two species will remain separated. Our hybrid methods can improve the efficiency of simulations by modelling a small central region, where it is possible for the two species to meet, using a fully excluding lattice, while using a computationally efficient, partially excluding lattice elsewhere in the domain.
Figure 9.
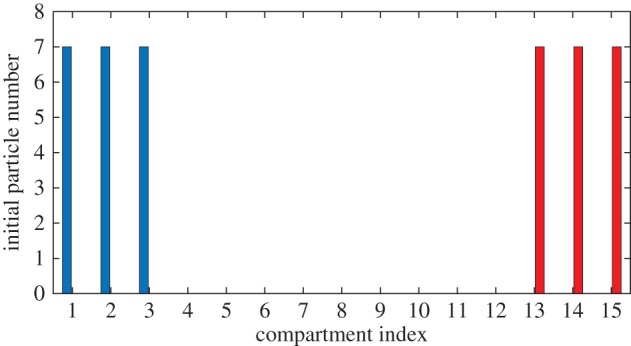
At time t = 0, 21 particles of species A (blue) are initialized at the left of the domain, and 21 particles of species B (red) are initialized at the right. (Online version in colour.)
Figures 10 and 11 illustrate how such regions can be arranged for Voronoi and pseudo-compartment models where m = 5, and how the interfaces can be shifted left or right to prevent particles of species A and B from passing one another. Shifting the interface imposes a small computational cost, but this is more than compensated for by the decreased number of jump events occurring due to the coarser lattice partitioning. This approach could be generalized to a model containing additional particle species by considering additional fully excluding regions between each species (assuming all particles of each species are initialized in distinct groups). In cases where multiple species are already mixed together at time t = 0, but preserving their ordering is important for the model, it may be necessary to employ a fully excluding model. Although it would not be necessary to prevent particle mixing in this way in a two- or three-dimensional model, it would still be possible to dynamically adjust the lattice in similar ways to save computational time where possible and preserve detailed modelling where necessary [28].
Figure 10.
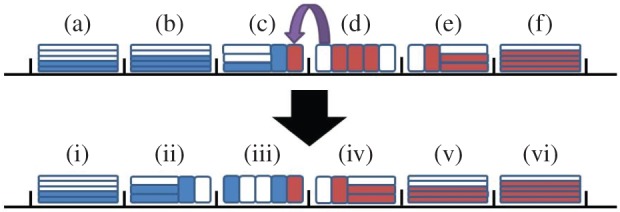
An illustration of an adaptive Voronoi domain partition. Particles of species A and B are shown in blue and red, respectively. The upper image shows the lattice before the hybrid region shifts left, where the areas marked (a), (b) and (f) are partially excluding, those marked (c) and (e) are a combination of fully excluding and partially excluding, and the one marked (d) is a section of fully excluding compartments. When a B particle enters box (c), the interface shifts left as illustrated in the lower image, where the areas marked (i), (v) and (vi) are partially excluding, those marked (ii) and (iv) are a combination of fully excluding and partially excluding, and the one marked (iii) is a section of fully excluding compartments. Where a partially excluding box is replaced with a finer partition (i.e. (b) and the left part of (c)), the particles within it are uniformly randomized across the compartments taking its place, weighted by the length of the destination compartments. When a section of compartments are replaced by a coarser partition (i.e. (e) and the right of (d)) the occupancy of the new compartments is found from the total number of particles across that section.
Figure 11.
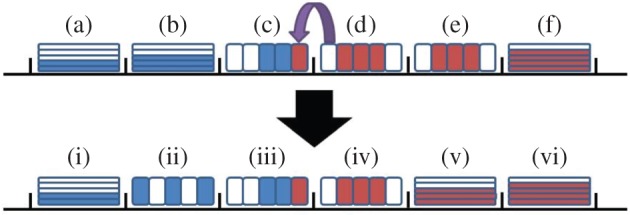
An illustration of an adaptive domain partition using the pseudo-compartment model. Particles of species A and B are shown in blue and red, respectively. The upper image shows the lattice before the hybrid region shifts left, where the areas marked (a), (b) and (f) are partially excluding, those marked (c) and (e) are pseudo-compartments, and the one marked (d) is a section of fully excluding compartments. When a B particle enters box (c), the interface shifts left as illustrated in the lower image, where the areas marked (i), (v) and (vi) are partially excluding, those marked (ii) and (iv) are pseudo-compartments, and the one marked (iii) is a section of fully excluding compartments. The positions of any particles in box (b) are uniformly randomized across (ii), while the occupancy of (v) is given by the total number of particles across (e).
We adopt the same values of N, h, L and D used in §4, and perform 50 000 realizations of each model over the time interval  For the Voronoi and pseudo-compartment models, we begin each realization with six compartments of capacity m = 7 at the left-hand side and at the right-hand side of the domain, with an intermediate region at the centre of the domain of the form illustrated in figures 10 and 11.
For the Voronoi and pseudo-compartment models, we begin each realization with six compartments of capacity m = 7 at the left-hand side and at the right-hand side of the domain, with an intermediate region at the centre of the domain of the form illustrated in figures 10 and 11.
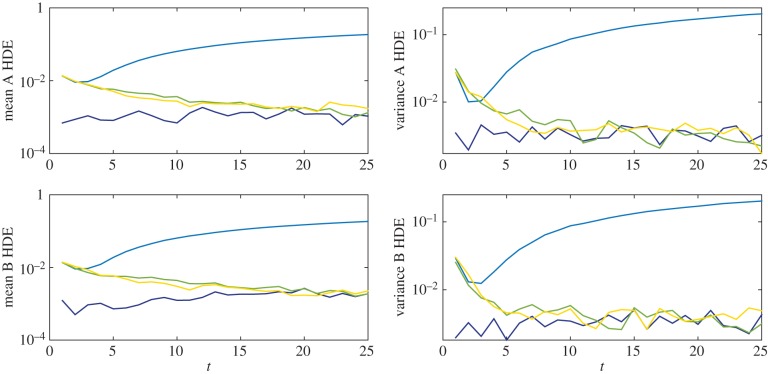
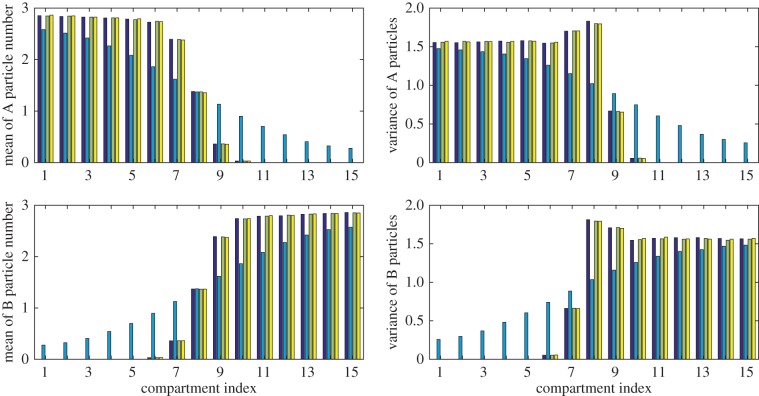
We compare mean and variance values at t = 1, 2, 3, … , 25, and plot the resulting HDEs in figure 12. As anticipated, the results generated using the partially excluding model deviate significantly from those generated using the fully excluding and hybrid models. This deviation is illustrated by plots of the means and variances of particle numbers at t = 25 in figure 13. The HDE values at time t = 25 are listed in table 4 together with the time taken to simulate each system. It can be seen that the Voronoi and pseudo-compartment models run 6.9 and 3.2 times faster, respectively, than the fully excluding system without losing accuracy.
Figure 12.
HDE values for the mean and variance of the multi-species simulation results at discrete times t = 1,2, … ,25. The growing deviation of the partially excluding model (plotted in light blue) from the other three models (fully excluding, Voronoi, and pseudo-compartment, plotted in dark blue, green and yellow, respectively) can be clearly seen in each case.
Figure 13.
Results from 50 000 repeats of the multi-species simulation at time t = 25. From left to right, each set of four bars shows results from the fully excluding (dark blue), partially excluding (light blue), Voronoi (green) and pseudo-compartment (yellow) models. The fully excluding and hybrid model results display strong agreement, but the results of the partially excluding model differ as this model cannot prevent the particles of differing type from moving past one another.
Table 4.
Details of multi-species simulation.
| model | mean HDE at t=25 (A/B) | variance HDE at t=25 (A/B) | time to simulate | acceleration relative to fully excluding |
|---|---|---|---|---|
| fully excluding | 0.0011/0.0019 | 0.0032/0.0043 | 53 663 s | — |
| partially excluding | 0.1853/0.1844 | 0.2034/0.2023 | 902 s | 59.5 times faster |
| Voronoi | 0.0013/0.0019 | 0.0022/0.0031 | 7722 s | 6.9 times faster |
| pseudo-compartment | 0.0017/0.0023 | 0.0017/0.0049 | 16 755 s | 3.2 times faster |
6. Discussion
In this paper, we have presented two methods for the simulation of volume-excluding compartment-based models on non-uniform lattices. We have presented analytical arguments for the agreement between aggregated mean particle distribution in the uniform partially excluding model with m > 1 and in both hybrid models (i.e. M(m) μ(v) and μ(p), respectively) with the aggregated mean particle distribution in the ‘accurate’ fully excluding model with m = 1 (μ(m)). Numerical investigations of three single-species test cases confirm that all four models agree on the mean and variance of particle numbers within each compartment. We have further presented a simple multi-species system, where the results of uniform partially excluding models deviate from those of the accurate fully excluding model, but the results of hybrid models match those of the fully excluding model and can be generated in a fraction of the time. This is a valuable development for researchers working with multi-scale diffusion systems, as it enables computationally efficient partially excluding compartments to be used where possible, while using fine-grained fully excluding compartments elsewhere in the domain when necessary. Time savings of nearly a factor of seven relative to the fully excluding model were observed for the Voronoi model when the test system was conducive to hybrid modelling, i.e. when the majority of particles spend most of the simulation within the coarse-grained region. The time savings in other situations could be even more significant. Partially excluding models are generally accurate and are consistently faster than both fully excluding and hybrid models, but the multi-species example in this section shows that they can be inadequate when fine spatial resolution is required in a region of the domain. In future work, we will consider two-dimensional hybrid models in greater detail, and discuss the implementation of reactions between particles in this framework.
Supplementary Material
Acknowledgements
The authors thank two anonymous reviewers for helpful comments on an earlier version of this manuscript.
Authors' contributions
All authors contributed to conceiving and designing the study, and to drafting the manuscript. P.R.T. wrote the computer code and ran the simulations. All authors approved the final manuscript.
Competing interests
We declare we have no competing interests.
Funding
P.R.T. gratefully acknowledges an EPSRC studentship through the University of Oxford's Systems Biology Doctoral Training Centre. M.J.S. acknowledges support from the Australian Research Council (FT130100148).
References
- 1.Spill F, Guerrero P, Alarcon T, Maini PK, Byrne H. 2015. Hybrid approaches for multiple-species stochastic reaction–diffusion models. J. Comput. Phys. 299, 429–445. ( 10.1016/j.jcp.2015.07.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Erban R, Chapman SJ. 2009. Stochastic modelling of reaction–diffusion processes: algorithms for bimolecular reactions. Phys. Biol. 6, 1–18. ( 10.1088/1478-3975/6/4/046001) [DOI] [PubMed] [Google Scholar]
- 3.Painter KJ, Hillen T. 2002. Volume-filling and quorum sensing in models for chemosensitive movement. Can. Appl. Math. Quart. 10, 501–543. [Google Scholar]
- 4.Anguige K, Schmeiser C. 2009. A one-dimensional model of cell diffusion and aggregation, incorporating volume filling and cell-to-cell adhesion. J. Math. Biol. 58, 395–427. ( 10.1007/s00285-008-0197-8) [DOI] [PubMed] [Google Scholar]
- 5.Khain E, Khasin M, Sander LM. 2014. Spontaneous formation of large clusters in a lattice gas above the critical point. Phys. Rev. E 90, 062702 ( 10.1103/PhysRevE.90.062702) [DOI] [PubMed] [Google Scholar]
- 6.Farrell SG, Brown AI, Rutenberg AD. 2015. Single file diffusion into a semi-infinite tube. Phys. Biol. 12, 064001 ( 10.1088/1478-3975/12/6/064001) [DOI] [PubMed] [Google Scholar]
- 7.Stern AS, Berg HC. 2013. Single-file diffusion of flagellin in flagellar filaments. Biophys. J. 105, 182–184. ( 10.1016/j.bpj.2013.05.030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang SY, Yang J, Kim E, Jeon G, Oh EJ, Choi KY, Hahn SK, Kim JK. 2010. Single-file diffusion of protein drugs through cylindrical nanochannels. ACS Nano 4, 3817–3822. ( 10.1021/nn100464u) [DOI] [PubMed] [Google Scholar]
- 9.Taylor PR, Yates CA, Simpson MJ, Baker RE. 2015. Reconciling transport models across scales: the role of volume exclusion. Phys. Rev. E 92, 040701. ( 10.1103/PhysRevE.92.040701) [DOI] [PubMed] [Google Scholar]
- 10.Walpole J, Papin JA, Peirce SM. 2013. Multiscale computational models of complex biological systems. Annu. Rev. Biomed. Eng. 15, 137–154. ( 10.1146/annurev-bioeng-071811-150104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Klann M, Ganguly A, Koeppl H. 2012. Hybrid spatial Gillespie and particle tracking simulation. Bioinformatics 28, 549–i555 ( 10.1093/bioinformatics/bts384) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Flegg MB, Rüdiger S, Erban R. 2014. Diffusive spatio-temporal noise in a first-passage time model for intracellular calcium release. J. Chem. Phys. 138, 154103 ( 10.1063/1.4796417) [DOI] [PubMed] [Google Scholar]
- 13.Flegg MB, Chapman SJ, Erban R. 2012. The two-regime method for optimizing stochastic reaction–diffusion simulations. J. R. Soc. Interface 9, 859–868. ( 10.1098/rsif.2011.0574) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Robinson M, Flegg MB, Erban R. 2014. Adaptive two-regime method: application to front propagation. J. Chem. Phys. 140, 124109 ( 10.1063/1.4868652) [DOI] [PubMed] [Google Scholar]
- 15.Flegg MB, Hellander S, Erban R. 2015. Convergence of methods for coupling of microscopic and mesoscopic reaction–diffusion simulations. J. Comput. Phys. 289, 1–17. ( 10.1016/j.jcp.2015.01.030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Franz B, Flegg MB, Chapman SJ, Erban R. 2013. Multiscale reaction–diffusion algorithms: PDE-assisted Brownian dynamics. SIAM J. Appl. Math. 73, 1224–1247. ( 10.1137/120882469) [DOI] [Google Scholar]
- 17.Yates CA, Flegg MB. 2015. The pseudo-compartment method for coupling partial differential equation and compartment-based models of diffusion. J. R. Soc. Interface 12, 141–155. ( 10.1098/rsif.2015.0141) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ferm L, Hellander A, Lötstedt P. 2010. An adaptive algorithm for simulation of stochastic reaction–diffusion processes. J. Comput. Phys. 229, 343–360. ( 10.1016/j.jcp.2009.09.030) [DOI] [Google Scholar]
- 19.Moro E. 2004. Hybrid method for simulating front propagation in reaction–diffusion systems. Phys. Rev. E 69, 060101. ( 10.1103/PhysRevE.69.060101) [DOI] [PubMed] [Google Scholar]
- 20.Bollenbach T, Kruse K, Pantazis P, González-Gaitán M, Jülicher F. 2005. Robust Formation of morphogen gradients. Phys. Rev. Lett. 94, 018103 ( 10.1103/PhysRevLett.94.018103) [DOI] [PubMed] [Google Scholar]
- 21.Tostevin F, ten Wolde PR, Howard M. 2007. Fundamental limits to position determination by concentration gradients. PLoS Comp. Biol. 3, e78 ( 10.1371/journal.pcbi.0030078) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Simpson MJ, Landman KA, Hughes BD. 2009. Multi-species simple exclusion processes. Physica A 388, 399–406. ( 10.1016/j.physa.2008.10.038) [DOI] [Google Scholar]
- 23.Yates CA, Baker RE, Erban R, Maini PK. 2012. Going from microscopic to macroscopic on nonuniform growing domains. Phys. Rev. E 86, 021921 ( 10.1103/PhysRevE.86.021921) [DOI] [PubMed] [Google Scholar]
- 24.Redner S. 2001. A guide to first-passage processes. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 25.Cao Y, Petzold L. 2006. Accuracy limitations and the measurement of errors in the stochastic simulation of chemically reacting systems. J. Comput. Phys. 212, 6–24. ( 10.1016/j.jcp.2005.06.012) [DOI] [Google Scholar]
- 26.Gillespie DT. 1977. Exact stochastic simulation of coupled chemical reactions. J. Chem. Phys. 81, 2340–2361. ( 10.1021/j100540a008) [DOI] [PubMed] [Google Scholar]
- 27.Taylor PR, Baker RE, Yates CA. 2015. Deriving appropriate boundary conditions, and accelerating position-jump simulations, of diffusion using non-local jumping. Phys. Biol. 12, 016006 ( 10.1088/1478-3975/12/1/016006) [DOI] [PubMed] [Google Scholar]
- 28.Bayati B, Chatelain P, Koumoutsakos P. 2011. Adaptive mesh refinement for stochastic reaction–diffusion processes. J. Comput. Phys. 230, 13–26. ( 10.1016/j.jcp.2010.08.035) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.