Control theory meets synthetic biology

Abstract

The past several years have witnessed an increased presence of control theoretic concepts in synthetic biology. This review presents an organized summary of how these control design concepts have been applied to tackle a variety of problems faced when building synthetic biomolecular circuits in living cells. In particular, we describe success stories that demonstrate how simple or more elaborate control design methods can be used to make the behaviour of synthetic genetic circuits within a single cell or across a cell population more reliable, predictable and robust to perturbations. The description especially highlights technical challenges that uniquely arise from the need to implement control designs within a new hardware setting, along with implemented or proposed solutions. Some engineering solutions employing complex feedback control schemes are also described, which, however, still require a deeper theoretical analysis of stability, performance and robustness properties. Overall, this paper should help synthetic biologists become familiar with feedback control concepts as they can be used in their application area. At the same time, it should provide some domain knowledge to control theorists who wish to enter the rising and exciting field of synthetic biology.

1. Introduction

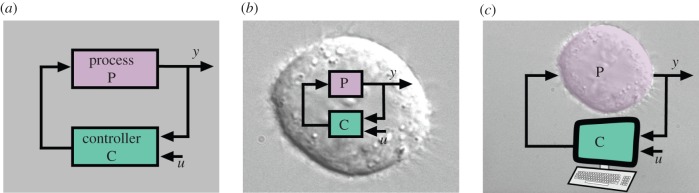
Control theory has arisen from the conceptualization and generalization of design strategies aimed at improving the stability, robustness and performance of physical systems in a number of applications, including mechanical devices, electrical/power networks, space and air systems, and chemical processes [1]. As shown in figure 1a, a closed loop feedback system involves a physical process to be controlled and a controller. In a classical negative feedback set-up, the controller measures the process output of interest y, compares it with a desired value u, and, based on the error between these two, computes the input to be applied to the process to ultimately decrease the discrepancy between y and u. Indeed, when the performance, reliability and robustness of certain hardware components cannot be improved further by better characterization or hardware design, negative feedback control is especially useful.

Figure 1.

Feedback control set-ups in synthetic biology. (a) General feedback control architecture where a controller measures an output y of interest of a process, compares it with a desired value u, and applies it as an input to the process. (b) In-cell feedback control implementation: the process and the controller are both ‘running’ in the cell and, as such, are implemented by biomolecular reactions. (c) In silico feedback control implementation: the process is the cell itself with all its molecular circuitry while the controller is implemented in a computer. (Microscopy image courtesy of Cell Image Library [2].)

A simple engineering example of negative feedback is the automatic cruise control of a vehicle, in which the process to be controlled is the vehicle, u is its desired speed (set by the driver) and y is its actual speed measured by a speedometer. An on-board controller computes the error u – y, and if this error is positive (y < u), throttle is applied to increase the propelling force applied to the vehicle by the engine, so that the speed y increases towards u. If the error is negative (y > u), then throttle (and/or brake) is used to decrease the propelling force, so that the speed y decreases towards u. As described, this feedback adjustment of the input (throttle or brake) requires minimal information about the process beyond the fact that more throttle increases the speed, whereas less throttle and/or brake decrease(s) the speed, and hence it tends to be robust to process uncertainty and disturbances, such as wind gusts. Realization of this negative feedback control system relies on the interconnection of highly modular, robust and accurate sensing, computing and actuating components (e.g. speedometer, on-board computer and engine, respectively). However, components that behave modularly and that are robust and accurate are especially hard to find in the field of synthetic biology, which we introduce next.

Synthetic biology is a nascent research area, in which biomolecular circuits are assembled in living cells with the final goal of controlling cellular behaviour for a variety of uses, from energy, to environment, to medicine [3]. However, partly owing to the nonlinearity, stochasticity, variability and lack of modularity in biomolecular processes, as reviewed in more detail in §§2, 4 and 5, realization of synthetic biomolecular circuits is often a lengthy and ad hoc process [4]. The past several years have witnessed an increased presence of control theoretic techniques and concepts in synthetic biology for tackling several of these problems, leading to promising results. However, the nature of biomolecular interactions has also posed unavoidable challenges to the implementation of negative feedback itself. Therefore, solving problems in synthetic biology using control theory requires much more than simply transplanting existing theories developed for engineering systems directly to a biomolecular setting.

Implementations of negative feedback design in synthetic biology fall into two different categories: in-cell feedback control and in silico feedback control, as illustrated in figure 1b,c. In-cell feedback control has both the process and the controller realized within the cell through biomolecular processes. It is more suitable for applications where cells need to function as autonomous programmed ‘machines’, such as in bioremediation where engineered bacteria can detect harmful compounds in the environment and target them for degradation, or in medical applications where engineered cells are injected into ill patients to target specific diseases. By contrast, in silico feedback control has the entire cell as the process to be controlled, while the controller is implemented in a computer. This may be suitable for applications where the cells to be controlled should be only minimally genetically modified, such as when controlling cell differentiation and de-differentiation (reprogramming). This paper reviews both set-ups, with more emphasis on in-cell feedback owing to the more extensive work that has been done in this setting.

Before delving into the review, we provide a short summary of synthetic biology in §2 and of the essence of feedback control in §3 to set the basis for the rest of the review. In-cell feedback control is reviewed in §§4–6. In §4, we focus on control designs created to improve the robustness of genetic circuits to a number of perturbations, including noise, and fluctuations in the genetic context. In §5, we illustrate how feedback control designs and implementations have been used to defeat loading problems appearing when connecting genetic modules to create larger systems. In §6, we discuss current implementations of cooperative feedback control to engineer multicell coordination for a number of applications. In silico feedback control is reviewed in §7, with a description of the main achievements and of the technical challenges that need to be overcome to make in silico feedback control practical.

2. Brief overview of synthetic biology and the role of control theory

Synthetic biology aims to engineer new living functionalities by creating, characterizing and assembling biological parts, devices and systems in living cells [5]. The ability to re-engineer living organisms has tremendous potential to address societal needs with a number of applications, ranging from energy, to environment, to medicine. Microbes can be engineered to convert biomass or light into biofuels [6], and the design of genetic control circuits provides a promising way to optimize microbial hosts to boost production [7]. Beyond typical energy usage on Earth, there is also a need for sustainable life support in space exploration missions, in which genetic circuitry that optimizes production is of paramount importance [8]. Bioremediation and biodegradation of harmful molecules in our water, soil or industrial facilities can also leverage synthetic biology technology by programming bacteria that seek out and degrade herbicides [9], or that sense environmental hazards such as heavy metals and signal them through visible output [10].

The potential to interface with human health in a way that traditional drugs cannot puts synthetic biology in a position to impact cancer treatment, microbiome engineering and regenerative medicine [11]. Engineered bacteria can be used to invade cancer cells or colonize tumours and, as a result, express a reporter for detection [12,13]. Similarly, engineered T cells (a type of the body's immune cells) can express special receptors that recognize molecules typical of cancer cells. With synthetic sensors, dynamic feedback control can be implemented through genetic circuits that eradicate cancer cells by regulating the secretion of killing agents [14]. The human microbiome, the vast community of microorganisms that reside on and in humans, maintains proper health by an actively regulated balance among the activities and amounts of its constituent microbes. The ability to engineer microbes to steer this balance back to a health state in microbiome-related diseases provides a powerful control mechanism that surpasses traditional antibiotic treatments, which are non-specific and can promote resistance [15]. Finally, synthetic biology could prove remarkably effective in regenerative medicine where some damaged tissues and organs are traditionally replaced by biomaterials to restore proper function. These and many more tissues could instead be replaced by patient-derived cells that have been reprogrammed through appropriate temporal and spatial control, avoiding innate immune responses [11,16].

2.1. From parts to modules

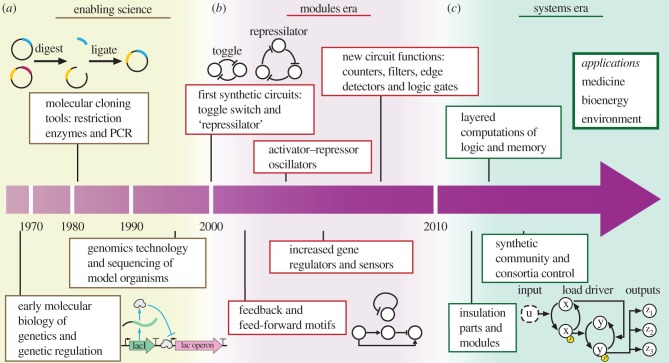
The roots of this emerging field may be traced back to two key Nobel Prize winning discoveries: the discovery of the lac operon's regulation in 1961 [17], shortly followed by the discovery of DNA restriction enzymes in 1969 [18] (figure 2a). The discovery that the rate of gene expression can be controlled by suitable proteins (transcription factors) enables genes to be viewed as (nonlinear) dynamical systems with inputs and outputs, where inputs and outputs are proteins. These parts can thus be assembled to form functional modules and larger systems. Technologically, restriction enzymes provided a way to assemble these circuits on DNA, because specific DNA sequences could be cut and then ligated into a new DNA sequence to create recombinant DNA [19]. A groundbreaking application of this technology was insulin production in engineered bacteria, Escherichia coli [20]. Further advances in genetics, including polymerase chain reaction (PCR) in 1985 [21] and automated DNA sequencing in 1986 [22], provided additional enabling technology to effectively engineer synthetic gene networks from a high-level functional specification to the corresponding coding DNA sequence in living cells. Although viewing genes as input/output systems that can be connected through transcription factors is a convenient abstraction for design, the reality is that the properties of these components are often altered by the DNA sequences of the genetic parts surrounding them. Dissecting this lack of modularity of basic parts and finding ways to mitigate it is a major research thrust in synthetic biology and remarkable progress has been made. This review is not concerned with modularity of basic parts, and a more detailed description of recent progress can be found elsewhere [23]. The first two forward-engineered genetic modules appeared in early 2000: the toggle switch and the ‘repressilator’ (figure 2b). The toggle switch uses two mutually repressing genes, effectively forming a positive feedback circuit, which leads to a bistable system that can switch between two possible states under suitable stimulation [24]. The toggle switch has been employed in several applications, such as in microbial kill switches for bacterial containment [25] and in detection/recording devices for living diagnostics [26]. The repressilator, instead, uses three genes mutually repressing each other in a loop, effectively forming a negative feedback system with substantial phase lag along the loop, leading to a genetic oscillator [27]. This circuit demonstrates that negative feedback systems with substantial phase lag may be used by Nature as mechanisms for time keeping. Other early works identified feedback and feed-forward motifs that can provide functions such as robustness to noise, improved temporal response and robustness to genetic context, as we detail in §4 [28–31]. For an extensive review of the early stages of synthetic biology and the many circuits that were built in the past several years, the reader is referred to [3,32].

Figure 2.

Condensed timeline of synthetic biology. (a) The development of synthetic biology is grounded on molecular biology, genetic engineering and genomics. (b) The early phases of synthetic biology were focusing mostly on forward engineering simple modules, such as switches and oscillators. (c) After the ‘era’ of modules, synthetic biology is heading towards the era of systems, in which modules will serve as functional units to create more complex and sophisticated systems with potential applications to energy, environment and medicine.

2.2. From modules to systems

As more parts and functional modules become available, larger systems can be assembled that accomplish sophisticated tasks such as those required to impact bioenergy, environment and medicine applications [32,33]. While initial results demonstrate the potential of assembling larger systems that perform non-trivial logic computations [34–37], substantial challenges need to be overcome to turn synthetic biology into a bottom-up engineering discipline where circuit modules are characterized in isolation and then assembled to create larger systems [4,38]. In particular, in a bottom-up design approach, a functional module, such as the repressilator or the toggle switch, should maintain its input/output behaviour as characterized in isolation unchanged upon connection with other modules. This modularity property is rarely satisfied by biomolecular systems [23]. Failure of modularity leads to a long and iterative design process where subsystems are re-characterized from scratch any time a new module is added, thus presenting a challenging obstacle to scaling up circuits' size. Control theory has especially played a key role in the design of insulation devices that ‘buffer’ modules from loading effects [39], as reviewed in detail in §5. Control theory is likely to play a central role also in ‘robustifying’ circuits’ behaviour to unwanted interactions with the cellular ‘chassis’, which range from the bacterium E. coli, to yeast Saccharomyces cerevisiae, to mammalian cells [40], to other bacteria like the gut bacterium Bacteroides thetaiotaomicron [41]. The host cell provides all the resources required for gene expression and protein modification, including RNA polymerase, ribosomes, amino acids, tRNA, proteases and ATP, which are all found in limited amounts. While, for small circuits, the added load by synthetic circuits on these resources may be sufficiently small and thus negligible, as the circuit size increases, these loads cannot be neglected any longer. These can cause harmful effects to cell physiology (toxicity) and may result in counterintuitive couplings among otherwise independent circuits [42–45]. Suitable engineering solutions to make a circuit's behaviour more robust to fluctuations in available resources and more generally to changes in the cellular context are highly desirable and the subject of intense research.

3. The essence of negative feedback

In this section, we review the benefits and trade-offs of negative feedback control, capitalizing on strategies that have been implemented in synthetic biology to address problems of relevance to the field.

3.1. Advantages of high-gain negative feedback systems

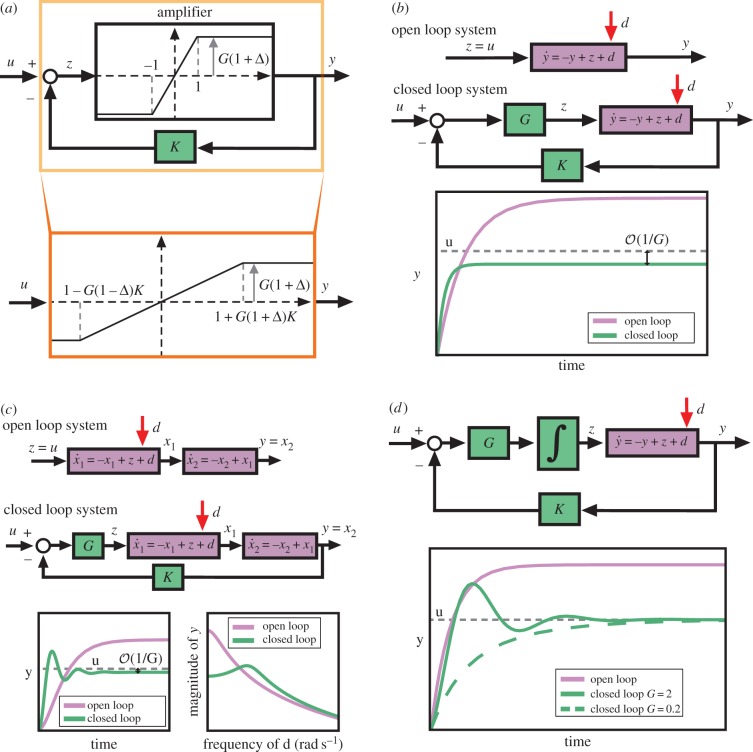
One of the early and highly celebrated applications of negative feedback addressed problems in the long-distance telephone line that in the early 1900s aimed to connect the west coast with the east coast in the USA. In particular, a pressing problem was the poor performance of the amplifiers that were connected in tandem along the telephone line to prevent signal attenuation. For example, a simplified representation of an amplifier in negative feedback set-up is illustrated in figure 3a. Within this representation, the output of the amplifier y represents a voltage signal whose value depends on an input voltage z to the amplifier. Owing to physical limitations, the input/output relationship of this amplifier is nonlinear. The linear regime is when −1 ≤ z ≤ 1, whereas the output saturates beyond this interval. Within the linear regime, the amplifier's input/output relationship is linear with slope G > 0 (y = Gz), which we will call here the amplifier's gain. The gain G is further subject to uncertainty Δ, owing, for example, to temperature changes and ageing. Therefore, even in the linear regime, the output will not be completely predictable. In the case of a genetic circuit, the input and output signals (z and y) are typically molecular counts/concentrations. For instance, z can be the concentration of a transcription factor regulating the production of a protein whose concentration is represented by y. The nonlinear input/output mapping of the amplifier may correspond to the dose–response curve of gene regulation, mathematically captured by the Hill function [46]. Gain G may represent the local slope of the Hill function, which is determined by the strength of the regulating transcription factors and cooperativity (see §4), and Δ may arise, for example, from uncertainties in biomolecular interactions when the circuit is placed in different host cells.

Figure 3.

The essence of negative feedback. (a) Negative feedback extends the linear regime of an amplifier and provides robustness to uncertainty. The top diagram shows the amplifier within a negative feedback loop. The bottom diagram shows the equivalent input/output mapping corresponding to the closed loop feedback system. The graph in the box shows the mapping (i.e. the dose–response curve) between the input (signal on incoming arrow) and the output (signal on outgoing arrow). (b) High-gain negative feedback attenuates disturbances and speeds up the temporal response. The purple block(s) represent the ordinary differential equation (ODE) that links the input (incoming arrow) to the output (outgoing arrow). For a desired constant value u, the open loop system's response is obtained by setting z = u and simulating the open loop system. The closed loop system response is obtained by simulating the closed loop system with K = 1 and G large. In this case, the steady-state error between y and the desired value u can be decreased by increasing G, that is, 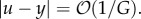(c) High-gain negative feedback can lead to oscillations and amplifies high-frequency disturbances. The open loop system is simulated as before by setting z = u. The closed loop system is simulated with G large and K = 1. The left-hand plot shows the time response of the system. The right-hand plot shows the frequency response of y to disturbance d. The horizontal axis represents the frequency ω of a periodic disturbance d(t) = sin(ωt) and the vertical axis shows the amplitude of the resulting y(t) signal. (d) Negative integral feedback completely rejects disturbances. The open loop system is as in panel (b) and simulated similarly. The closed loop system is simulated for two different values of G (as shown) and for K = 1. In all diagrams, the circle represents a summing junction: the outgoing arrow is a signal given by the weighted sum with the indicated signs of the signals on the incoming arrows. Also, we have used the shortened notation 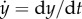. The simulation codes used to generate this figure are available in the electronic supplementary material.

Interestingly, once the amplifier is placed within a negative feedback set-up with feedback gain K > 0, which for a genetic circuit will represent, for example, the binding strength of a regulator with DNA operator sites, these two limitations practically disappear. Specifically, the linear regime of the input/output mapping of the closed loop system extends from [–1,1] for the ‘open loop’ amplifier to [−1−G(1 + Δ)K,1 + G(1 + Δ)K] for the closed loop system, which becomes larger with increased G. Further, the input/output relationship for the closed loop system in the linear regime becomes

This shows that the u-to-y amplification factor is decreased in the closed loop system, but it is approximately equal to 1/K for G sufficiently large, which is independent of the amplifier's uncertainty Δ. The net result is that negative feedback has turned a nonlinear, uncertain, high-gain device into an essentially linear system, whose input/output gain is robust to uncertainty. This discovery, by H. Black, enabled Bell Laboratories to overcome a major bottleneck affecting the transcontinental telephone line in the 1920s, and illustrates the pivotal role of negative feedback in overcoming limitations and shortcomings of available hardware components [47].

In the context of dynamical systems, negative feedback with high gain can often be used to attenuate the contribution of unknown disturbances d on the output of interest y (figure 3b). For synthetic biology applications, the output of interest can be, for example, the concentration of a fluorescence protein or any other molecule with physiological relevance. The disturbance can represent environmental perturbations, fluctuations in the system's parameters or noise. Within a high-gain negative feedback strategy, we set the input to the system z = G(u−Ky), which is proportional through a large amplification factor G to the error between the desired value of the output u and the measured output Ky. The system with this input is in a closed loop form (see diagram in figure 3b) and hence we will refer to it as the closed loop system. This is in contrast to the open loop system in which the input is pre-set as z = u and it is not adjusted based on the effect it has on y. As we will see in §§4 and 5, the amplification factor depends on the biomolecular mechanism chosen for the feedback. When transcriptional regulation is chosen for the feedback, G depends on the promoter and transcriptional regulator strengths, and it is not easily tunable (§4.1). When protein–protein interaction is chosen for the feedback, such as a phosphorylation cycle, the gain G can be easily increased by increasing the concentrations of suitable substrates and enzymes (§5).

Consider the first-order open loop process 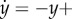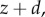which may describe, for example, the process of transcription with y the concentration of mRNA, z the concentration of a regulator and d a constant unknown disturbance, capturing, for example, additional unknown production rates. The result of applying high-gain negative feedback is twofold. First, while the open loop system has a steady-state value given by y = u + d, the closed loop system has a steady-state value given by y = (Gu + d)/(GK + 1). This value approaches u/K for large G; it is therefore independent of the disturbance d, and can be made equal to y by setting K = 1. Second, the time to reach steady state (typically measured by the earliest time the output y(t) is within 90% of the steady state) decreases as G increases, and thus the closed loop system is also faster. These results continue to hold if the disturbance and the desired output value vary with time, facts that can be shown using a variety of general tools, such as singular perturbation techniques [48,49].

3.2. Downsides of high-gain negative feedback systems

High-gain negative feedback relies on a sufficiently large amplification of the error between the system's output and the desired output to reduce the steady-state error owing to disturbances. However, this desirable property does not extend as easily to physical systems described by higher-order ordinary differential equations (ODEs), such as the second-order system depicted in figure 3c. This system may describe the sequential process of transcription and translation, in which x₁ may represent the concentration of mRNA and x₂ the concentration of protein [46], as we describe in greater detail in §4.1. In this case, increased amplification gain G may still result in a decreased steady-state error between the output y and its desired value u, thus attenuating the effect of disturbance d; however, the transient response can become oscillatory with increasing amplitude of oscillation as G increases. The frequency response of the system to disturbance d shown in figure 3c further shows that the closed loop system has less sensitivity than the open loop system to disturbance inputs at low frequency, but it has increased sensitivity to disturbances at high frequency when compared with the open loop system. This shows a fundamental trade-off in the design of any closed loop control system, also called the ‘water-bed’ effect [50], according to which a high-gain feedback control design that attenuates the effects of slow perturbations will result in potential amplification of high-frequency perturbations. Another potential concern in the implementation of high-gain feedback designs is the energetic requirement for the realization of such high gains. While, in electronics, this may not be a significant bottleneck, in the context of a biomolecular system it may translate into large protein amounts, with potential consequences for cell physiology (see §5).

3.3. Properties of integral negative feedback systems

More sophisticated control strategies can make a system robust to uncertainty without necessarily requiring large gains. These strategies thus avoid some of the above- described shortcomings. The simplest such control strategy, which we describe here, is integral feedback control [50]. Referring to figure 3d, the control input z of the physical process is set to be the integral of the error G(u − Ky). For the simple block diagram of this figure, the closed loop system equations are given by

3.1

which is a stable system for all positive G and K and admits y = u/K at steady state. Therefore, the output value at steady state is completely independent of the disturbance input d, and this disturbance rejection property is independent of the amplification gain G. This gain can therefore be picked to be small if the only interest is disturbance rejection. Lower gain G, however, will lead to a slower system while increased gain G will lead not only to a faster system but also to oscillations (figure 3d). If both disturbance rejection and speed of response are desirable, then a combination of proportional and integral feedback (PI control) is usually more appropriate. Other designs may incorporate a derivative action for enhanced stability, which however may have as an undesirable downside the amplification of high-frequency noise [50].

3.4. Feed-forward and positive feedback systems

Even though, in this review, the description of control strategies focuses on negative feedback systems, there are other types of control architectures that are possible depending on the design objective and on the problem definition. These include feed-forward controllers and positive feedback systems [50]. A feed-forward control system can be used to ‘cancel’ the effect of unwanted disturbances on an output of interest. Different from a feedback system, however, the control input is not adjusted based on the error between the output and its desired value, but it is pre-set based on perfect knowledge on how the disturbance affects the process. This control strategy is therefore viable only if the system's model is perfectly known and is not subject to perturbations. Combinations of feed-forward and negative feedback architectures are often used to obtain improved performance and robustness, and are present in several modern engineering applications [50]. In §4, we review an application of feed-forward control in synthetic biology to enable circuits' robustness to DNA plasmid variability. Positive feedback systems have been widely used in digital electronics to engineer oscillators, switches and hysteresis where the system output can take either of two stable values, and these are each kept unless a sufficiently large input stimulus is applied [51]. A detailed discussion of positive feedback is beyond the scope of this review and can be found elsewhere [46,52–55].

4. In-cell feedback and feed-forward control: modules

In-cell control mechanisms are well suited to enhance the performance and robustness of synthetic genetic circuits to a number of perturbations, including noise, parameter uncertainty, loading and fluctuations in available resources. Here, we review how control system designs improve robustness of protein levels to noise and to variability in the number of copies of plasmid on which a circuit is coded. We then discuss some of the major implementation challenges involved in the realization of high-gain negative feedback and integral feedback. We adopt the notation where, for a species x, we represent by x (italics) its concentration.

4.1. Negative feedback: robustness to noise, performance and trade-offs

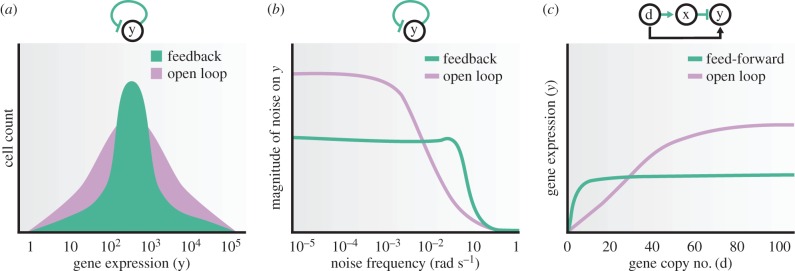
Stochasticity can not only substantially limit the precision at which the function of a circuit is executed [56], but also be exploited [57]. Substantial work is required to develop a design-oriented quantitative understanding of stochastic effects in order to attenuate them or leverage them, depending on the circuit's requirements. Because negative feedback tends to increase the robustness of a system's output to perturbations (figure 3b), a number of researchers have examined synthetic genetic implementation of negative feedback in order to assess its ability to reduce the stochastic variation of a protein concentration about its mean [28,58].

The simplest implementation of negative feedback on a protein of interest y is through negative transcriptional autoregulation as shown in figure 4a, in which y represses its production by binding to its own promoter to sequester it from RNA polymerase. A two-variable model of this circuit that captures the mRNA (m) and protein y dynamics is given by

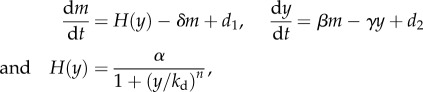in which H(y) is the Hill function, which models the effect of transcriptional repression by y, with n the cooperativity of y and k_d the dissociation constant of the binding. A smaller dissociation constant corresponds to stronger binding and thus to stronger repression. The larger the cooperativity n, the more switch-like is the Hill function. Parameters δ and γ are decay constants, and βm models the fact that protein production is proportional to the concentration of mRNA [46]. Here, d₁ and d₂ are additive perturbations capturing, for example, the effect of noise on the mRNA and protein dynamics. A simplified analysis of the effect of the negative feedback can be carried out by performing a linearization of H(y) near the steady state y_s, leading to H(y_s + y) ≈ b − ay with a,b > 0, and analysing the robustness of this system to noise when compared with the open loop system where we have H(y) = u. Referring to the diagram in figure 3b, we can set the parameters b = uG and a = KG, such that K = (a/b)u and the system with negative feedback will have amplification gain G. Inspecting the expression of G, we can determine how physically G can be increased. In particular, G can be increased by having both a and b sufficiently large. Because b = H(y_s), it can be increased by increasing α, that is, the promoter's strength; because −a is the slope of H(y) at the equilibrium point y_s, it can be increased (up to some limit) by decreasing k_d, that is, having a stronger repression, or by increasing the cooperativity n and suitably tuning k_d such that y_s falls exactly at the maximal slope of H(y). Therefore, physically increasing the gain G for a negative autoregulation implementation is non-trivial and severely limited. Nevertheless, there are measurable benefits of the closed loop system when compared with the open loop one.

Figure 4.

Enhancing robustness through feedback and feed-forward control. (a) Decreased variability of gene expression through negative autoregulation. (b) Negative autoregulation shifts noise to higher frequency. (c) Feed-forward circuits decrease the sensitivity of the output to input disturbances.

For a sensible comparison between the open loop and closed loop systems, it is important to set the parameters of the controller such that the steady state of the closed loop system is the same as that of the open loop system when the perturbations are not present and when the feedback gain G is sufficiently large. This can be obtained by setting K = δγ/β, leading to y_s = βu/(δγ). A standard measure of the noisiness of a signal is the coefficient of variation (CV), which is defined as the ratio between the standard deviation and the mean. For the above system, in which we use the linear approximation of H(y) and the fact that G is large, and we assume for simplicity that d₁ and d₂ are white noise processes, we can calculate the moments and hence also the CV leveraging the fact that the system is linear [46]. This leads to the two following expressions:

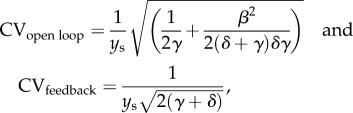which show that the system with high-gain feedback has a smaller CV than the open loop system, suggesting that under appropriate conditions the closed loop system is more robust to noise, as detailed by a number of theoretical works [59–62]. These theoretical predictions were confirmed experimentally by a genetic circuit implementation in E. coli of the negatively autoregulated gene [28]. In particular, in this paper, the authors computed the empirical probability distribution for both the closed loop and the open loop systems, resulting in the qualitative behaviour depicted in figure 4a, which shows reduced variability of protein level in the system with negative feedback.

Further, as illustrated in figure 3c, adding negative feedback around a system whose ODE model has order higher than 1 can give rise to oscillations and can lead to amplification of the response of the system to disturbances that have high-frequency content. The process of protein production involves a cascade of dynamical processes, including transcription, translation and protein folding [46]. It is expected that, just as shown in figure 3c, the water-bed effect may be observed wherein the noise spectrum of the output y shifts to high frequency in the closed loop system. This prediction was experimentally validated on a genetic autoregulation circuit in E. coli, in which the authors computed the experimental frequency response of both open loop and closed loop systems and which led to the qualitative plot shown in figure 4b [58].

Finally, figure 3b shows that the closed loop system is also sped up compared with the open loop system. Experiments performed on a negative autoregulation circuit in E. coli confirmed this finding, illustrating that negative feedback can be effectively used also as a mechanism to tune the temporal performance of genetic circuits [63].

4.2. Incoherent feed-forward control: robustness to genetic context

Synthetic genetic circuits are commonly coded on plasmids as this simplifies the assembly process compared with chromosomal integration, and allows higher expression levels, leading to easier detection of the proteins of interest. A major problem when implementing a synthetic genetic circuit on a plasmid is the variability in the copy number of the plasmid [64], which makes the levels of the expressed proteins also variable and thus poorly predictable. From a control systems point of view, the plasmid copy number is a ‘disturbance’ input d and the concentration of the protein of interest y is the output that ideally should be robust to changes in d. As such, it can be addressed by a number of potential designs, including negative feedback, integral feedback and feed-forward control. Negative feedback and feed-forward control were each implemented in [65] to tackle this problem. Here, we focus the description on the implemented feed-forward control and on its relationship with integral feedback.

The diagram of the incoherent feed-forward control scheme is shown in figure 4c. The plasmid copy number d directly ‘activates’ the protein it is expressing, because higher copy number leads to higher protein concentration. The control circuitry is implemented by expressing from the same plasmid an intermediate protein x (hence the positive arrow from d to x), which in turn represses the protein of interest (the negative arrow from x to y). This type of circuit topology is called an incoherent feed-forward loop and has been widely studied in the systems biology literature [66]. If the two forward branches are perfectly balanced, they cancel each other's action, and the net contribution from d to y is zero, leading to perfect disturbance rejection. In one of the genetic implementations proposed, protein x is a transcriptional repressor of protein y, leading to a simple model and steady state of the circuit given by

where k incorporates the dissociation constant of the binding of x to the promoter site controlling y. Hence, y will depend on d, unless δk/α is negligible compared with d as illustrated in the plot of figure 4c. This shows that the two branches need to exactly compensate each other in order for the disturbance to be perfectly rejected. Feed-forward architectures may thus be desirable, in general, to decrease the effect of a disturbance but not necessarily for perfectly rejecting it, for which integral feedback, when implementable, is better suited.

4.2.1. Relationship with integral feedback

Although a realistically implementable incoherent feed-forward control circuit such as this one does not reach perfect disturbance rejection, an ideal incoherent feed-forward control circuit in which k = 0, that is, the two branches are exactly compensating each other, reaches disturbance rejection, because 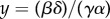is independent of d. In this case, it can be shown that the system contains a hidden feedback integral action, that is, there is a variable z such that 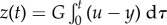or equivalently 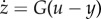with 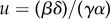[67]. Therefore, the ideal feed-forward control circuit is mathematically equivalent to an integral feedback controller. This fact is a consequence of a much more general principle from control theory called the internal model principle [50], which implies that if a system perfectly rejects (adapts to) a constant disturbance, then it must have a feedback integral action within it. From a practical implementation point of view, having k = 0 requires that the binding of protein x to promoter sites controlling y is irreversible, which is difficult to reach in practice, because even the strongest binding always has some non-zero probability of unbinding. This example illustrates some of the practical difficulties encountered when trying to reach perfect disturbance rejection with a feed-forward control circuit. It is not surprising that similar implementation challenges are encountered when seeking to implement an explicit feedback integral control as we detail in §4.3.

4.3. Implementations of negative feedback and their challenges

We review molecular mechanisms available for the implementation of negative feedback and discuss their physical constraints that make realization of feedback, especially integral, challenging.

4.3.1. Negative feedback implementations

In general, there are two different philosophies to implement negative feedback: inhibit the rate at which a protein is produced or enhance the rate at which it is degraded. Transcriptional regulation is of the first type (figure 5a): the output protein (y) binds with its own promoter (p) to inhibit transcription. This type of regulation has been widely used in the field of dynamic metabolic engineering to promote and/or ‘robustify’ biofuel production under changing environments [72–75]. In [76], Oyarzún & Stan provided detailed guidance on the selection of promoters and ribosome binding sites that reflects the trade-offs and constraints of transcriptional feedback for metabolic pathways. More broadly, feedback control has been extensively used in metabolic engineering, which is not the focus of this paper and an in-depth review can be found elsewhere [77].

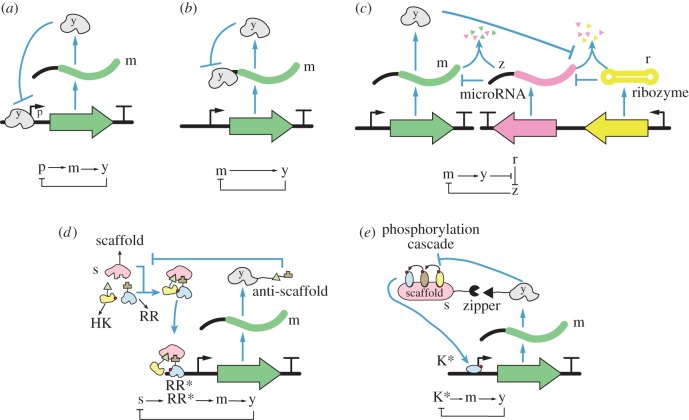
Figure 5.

Negative feedback implementation. (a) Transcriptional negative feedback by inhibition of protein transcription [46]. (b) Translational negative feedback by inhibition of protein translation [68]. (c) Translational negative feedback by increased mRNA degradation enabled by a microRNA (z) [69]. (d) Transcriptional negative feedback implemented through competitive binding with a scaffold protein s [70]. (e) Transcriptional negative feedback implemented by deactivation of transcriptional activator K* [71].

Recently, in addition to transcriptional regulation, the biological toolbox has significantly expanded. Negative feedback at the translation level (translational feedback), where the output protein inhibits its own translation without interfering with transcription, was theoretically found to be potentially superior to transcriptional repression at reducing stochasticity [78,79] in some scenarios, and at rejecting translational-level disturbances, such as fluctuations in ribosomes [80]. Translational feedback has been experimentally implemented in mammalian (HeLa) cells by using a ribosomal protein that tightly binds mRNA to block translation (figure 5b). Within a feedback architecture, this mechanism leads to a reduced level of the output protein y, which can be tuned by adjusting the binding strength [68]. A different approach to obtain translational feedback is through increased mRNA degradation, as experimentally tested in mammalian (HEK293) cells [69]. This negative feedback design (figure 5c) is realized by a non-coding microRNA (z) that binds and then degrades the protein y's own mRNA (m), and by a ribozyme (r) that cleaves the microRNA. The ribozyme is designed such that its cleavage rate decreases in the presence of the output protein y. Therefore, as y increases, z increases owing to the reduced ribozyme cleavage rate, thus reducing m and downregulating y, as a consequence.

Synthetic genetic negative feedback systems have been implemented also by sequestration of scaffold proteins (figure 5d). Scaffold proteins have specific interaction domains to assist the assembly of protein complexes or colocalization of signalling molecules [81]. In [70], the authors constructed a novel negative feedback loop in bacteria E. coli that enables input signal tracking, using a synthetic scaffold protein s and a two-component signalling system with scaffold-dependent phosphorylation (figure 5d). The two-component signalling system consists of a histidine kinase (HK) donating a phosphate to the response regulator (RR), transforming the RR into active RR*, which can activate transcription of output protein y. This two-component system is designed such that phosphotransfer occurs only when HK and RR are brought into close proximity by the scaffold protein s. The output protein y is a fusion of a fluorescence reporter and an anti-scaffold that sequesters free scaffold protein, leading overall to a negative feedback. Using the total amount of scaffold protein s as a reference input, Hsiao et al. [70] demonstrate that y can track the reference input concentration s (scaffold) over a range of input concentrations. The feedback gain can be tuned by relevant physical parameters, such as concentration of RR and phosphatase.

In [71], the authors created a new recruitment site on the Ste5 scaffold protein s with a leucine zipper (figure 5e). The new recruitment site recruits negative pathway modulator Msg5 (y), which is a phosphatase that dephosphorylates the pathway output K*. The negative feedback is created by the modulator y being expressed under the transcriptional control of K*. The strength of the negative feedback can be modulated by tuning the affinity of the matching leucine zipper, or the promoter strength of Msg5. The dynamics of the system with negative feedback displayed overshoot in the temporal response under continued stimulation. A similar feedback architecture finds application in modifying the T-cell receptor (TCR) signalling pathway in Jurkat T cells to precisely regulate the amplitude of T-cell activation [82]. This is practically important, because a challenge in adoptive T-cell therapy is to limit the over-activation of T cells that could lead to killing host cells or to life-threatening immune responses. The synthetic genetic negative feedback system of Wei et al. [82] addressed this challenge.

Less work is available on experimentally implementing a negative feedback where mRNA ‘inhibits’ its own transcription without interfering with translation. This type of mechanism has been discovered in Nature [72], where intron-based microRNAs in the human endothelial nitric oxide synthase gene can directly inhibit their own transcription. In synthetic biology, a potential implementation is by the CRISPR/Cas transcriptional repression system [83], where guide RNA recruits the Cas9 protein to block transcription.

4.3.2. Implementation challenges

The molecular mechanisms described so far can effectively be used to implement negative feedback control systems. However, it is unclear to what extent the gain G of the feedback controller can be increased and what consequences this may have on host cell physiology if increasing it requires increasing the concentrations of specific proteins. More work is required to investigate the potential trade-offs.

By contrast, the molecular mechanisms, if any, that may be used to implement an in-cell integral feedback controller are still the subject of intense investigation [84–87]. A major difficulty of implementing an explicit integral action is due to the unavoidable presence of dilution caused by cell growth [88]. In fact, for the concentration of a species z to be the pure integral of a signal s, we must have 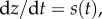but because z is subject to dilution within a growing and dividing cell, we will always have an added rate −δz, leading to 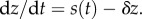Therefore, z(t) will not be the pure integral of s(t). Physically, if s were a constant production rate, then a pure integrator would want the concentration of z to grow to infinity according to z(t) = st. However, the presence of dilution always forces z(t) to saturate to a constant value given by s/δ. One may be tempted to think that, if s is large enough and z is kept at sufficiently low values, this issue may be overcome. Unfortunately, this is a misleading argument, because, within an integral control architecture, the objective is to make s(t) approach zero, at which point the integral variable z may be large to compensate for steady-state error and disturbances (refer to equation (3.1), where at steady state y = u/K and z = u/K − d). Even assuming that this is a non-issue, another significant difficulty is stability of the closed loop system as we illustrate next.

Briat et al. [85] proposed a novel feedback structure for biochemical reactions that can achieve perfect set-point regulation named ‘antithetic integral feedback’. Although the authors consider a stochastic model, the basic idea can be explained with the simplified deterministic model

4.1

where x represents the concentration of the output protein to be regulated, z₁ and z₂ are ‘controller species’, and u is a reference input (e.g. the desired x concentration). A change of variable z = z₁ − z₂ results in dz/dt = u − x, and therefore, as long as system (3.2) is stable, as t → ∞, we have dz/dt = u − x = 0, and the output tracking error x–u tends to 0 exactly. However, this system may be unstable. This technical problem is circumvented by the authors in [85] by studying its stochastic counterpart, and by mathematically showing that the mean of the stochastic output converges to the reference input for a large class of biomolecular systems with such structure. Most importantly, the stochastic model guarantees robust adaptation even in the presence of noise and at low molecule counts. Further experimental and theoretical studies are required to determine the performance and trade-offs of these types of integral controllers and how the issue of dilution may be overcome.

A component that is ubiquitous in any control system (proportional or integral) but difficult to realize biologically is a signal subtractor, used to find the error between the output y and reference input u in the standard feedback set-up (figure 3b–d). A recent study by Cosentino et al. [89] provides a set of biochemical reactions whose output can be approximated by the difference of the two inputs, given that a time-scale separation condition holds. In particular, the authors show that the negative feedback implemented using scaffold protein in [70] functions as an effective signal subtractor, leading to the observed tracking property under negative feedback.

Finally, cell-free systems, where circuits are studied in cell extracts in vitro, provide appealing testing platforms to accelerate synthetic circuits prototyping, and to deepen our understanding of natural systems [90,91] by removing issues such as cellular context dependence, noise and cell heterogeneity, and cell growth. Synthetic negative feedback loops, together with many other synthetic biology parts, such as the toggle switch and the repressilator, have been successfully reconstructed in cell-free systems [92,93]. Because experimental results have suggested that circuit performance in a cell-free system highly resembles its in-cell counterpart [91], cell-free systems can potentially serve as a rapid controller prototyping platform, similar to a wind tunnel for fluid dynamics, to investigate more sophisticated in vivo control strategies.

5. In-cell feedback control: from modules to systems

We recall that a fundamental property a circuit component is expected to have when we perform bottom-up design is modularity, that is, the input/output behaviour of the component should remain unchanged upon connection with other components. Failure of modularity forces a designer to re-engineer the entire system from scratch any time a new component is added, leading to an endless and combinatorial design process. In this section, we review engineering solutions that leverage high-gain negative feedback to enhance modularity.

5.1. The limits of modularity in genetic circuits

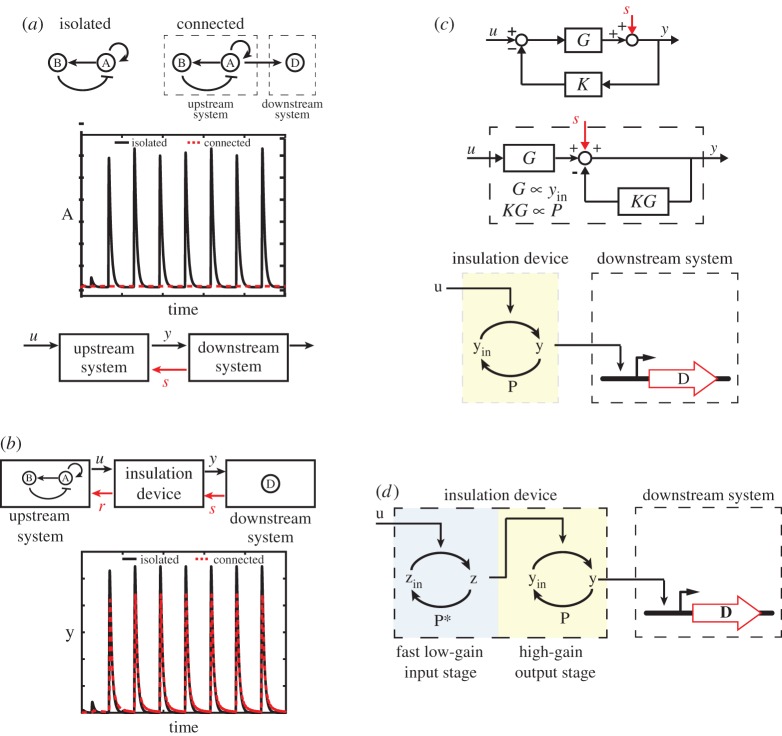
Although highly desirable, modularity is not a natural property of biomolecular systems, because the connection of an upstream system to a downstream one alters the state of the upstream component [94]. This fact is due to the physical process by which two components are connected: a connection implies that a communicating species of the upstream system binds to species of the downstream system, leading to new reaction rates that were not present when the upstream system was in isolation. These additional rates ‘load’ the communicating species and make it (temporarily) unavailable to the reactions of the upstream system, leading therefore to substantial changes in the upstream system's behaviour. This can be appreciated by considering as an illustration the connection of a genetic clock, such as that of [53], to downstream genetic targets that regulate, for example, the production of a fluorescent reporter used for characterization (figure 6a). While the isolated clock displays sustained oscillations, connection to the downstream reporter system quenches the oscillations. This phenomenon not only creates difficulties in measuring the clock's species for module characterization, but also more broadly prevents the clock's signal being sent to downstream systems, as desired, for example, in applications where downstream processes need to be synchronized [95]. A number of experimental studies on reconstituted protein systems, on genetic circuits in E. coli and in yeast, and on in vivo natural systems have characterized these effects of retroactivity [39,96–100]. Notable effects of retroactivity include the slowdown of the temporal response of the upstream system's communicating species and changes in the upstream system's steady-state input–output characteristics. These effects become more prominent as the concentration and/or affinity of downstream targets or substrates to which the communicating species binds increase.

Figure 6.

Improving modularity through feedback control. (a) Failure of modularity in genetic circuits. A synthetic genetic clock in isolation displays sustained oscillation (black, solid line), but, once it is connected to a downstream system, oscillations disappear (red, dashed line). Loading on the upstream system's transcription factor is formally modelled as a signal s called retroactivity, which affects as a disturbance the dynamics of the upstream system. (b) Insulation devices buffer from retroactivity. Insulation devices attenuate retroactivity to the output s and have small retroactivity to the input r; they can be placed as buffering elements between an upstream and a downstream system. (c) High-gain negative feedback to design insulation devices. High-gain negative feedback can be used to attenuate the effect of retroactivity s on the system's dynamics. A phosphorylation cycle where the output y results from u-mediated activation of inactive y_in and is converted back to y_in by a phosphatase P can implement the high-gain negative feedback design to attenuate s. Gain G can be increased by increased concentrations y_in and P. (d) Two-stage insulation device. This allows decoupling of the requirements of attenuating s from those of having small r. While the second stage is a high-gain feedback device as in (c), the first stage has low protein amounts (‘low-gain’) to have low retroactivity to the input r. It attenuates any load-induced slow down owing to large y_in by cycling at a fast rate compared with the speed of gene expression (time scale of input u). The simulation codes used to generate this figure are available in the electronic supplementary material.

In order to make the loading problem amenable to a solution that can leverage control systems tools, it was proposed to capture the additional reaction fluxes that appear any time a connection is performed as a signal s called retroactivity to the output (figure 6a). This signal can be viewed as a disturbance that alters the output of the upstream system once it is connected to a downstream one. For example, if y is a transcription factor expressed in the upstream system with rate H(u), and y binds downstream target sites p to form complex C according to 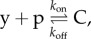we will have

in which s = 0 if the upstream system is in isolation (not connected to the downstream system). Accordingly, the problem of retroactivity mitigation can be viewed as the problem of engineering the system upstream of the load such that the effect of s on y is mitigated. This is a standard disturbance attenuation problem in the control theory sense as illustrated in §3. A system that is able to mitigate the effect of s on y also applies a small retroactivity (r), called retroactivity to the input, to its upstream system, called an insulation device. Hence, an insulation device could be placed between any upstream system (i.e. the clock) and a downstream load (i.e. the fluorescence reporter) such that the load is transferred to the insulation device and hence the upstream system signal is reliably transmitted to the downstream load (figure 6b).

5.2. Explicit high-gain negative feedback to design insulation devices

As described in §3, disturbance attenuation can be solved by the implementation of a high-gain negative feedback mechanism, as shown in a simplified block diagram in figure 6c. Basic block diagram algebra leads to

illustrating that as the gain G increases the contribution of s to y becomes negligible when compared with the contribution of u to y. The challenge is to implement this high-gain negative feedback mechanism through a biomolecular process that can realize sufficiently high gains. To address this question, it is useful to re-arrange the block diagram as illustrated in figure 6c. This indicates that we should realize a large input amplification G along with a similarly large negative feedback gain KG on the output where retroactivity acts. A number of ways have been proposed to implement such a mechanism within an insulation device [94]. One implementation that was experimentally realized and validated uses a covalent modification cycle as shown in figure 6c [101]. Here, the input amplification G is realized by having a sufficiently large reservoir of inactive protein y_in, which upon presentation of the input u is turned into the active output y. This output, in turn, is actively degraded with a rate proportional to the amount of phosphatase P, which converts y back to y_in. Therefore, we have and 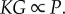It is worth highlighting that, because y_in and P are both large, the output y may be very small, yet it stays insensitive to large loads imparted by downstream targets. This high-gain futile cycle can effectively attenuate the retroactivity to the output in the presence of time-varying inputs u as illustrated in various modelling studies [94], in experiments on reconstituted systems [97], and in experiments on genetic circuits in E. coli [101].

5.3. Implicit high-gain negative feedback through time-scale separation

While the futile cycle of figure 6c provides a powerful and highly tunable way of attenuating the retroactivity to the output, it is subject to a stringent design trade-off. Attenuating retroactivity to the output s requires high gains as implemented through large substrate y_in and phosphatase P amounts. However, a large amount of substrate y_in imparts a significant load to the input kinase u that binds to it. Therefore, in this system, attenuating retroactivity to the output s potentially leads to increased retroactivity to the input r, which results in a load-induced slowdown of the input u. This trade-off has been mathematically characterized in [102] and experimentally demonstrated in [101].

To overcome this limitation and hence obtain an insulation device that could attenuate retroactivity to the output s while keeping a low retroactivity to the input r, a two-stage device was proposed as illustrated in figure 6d. The output cycle of the device is designed to be a high-gain negative feedback system just like the futile cycle described above, in which high gains are realized through large substrate and phosphatase amounts. The input cycle, by contrast, is designed to have lower amounts of substrate z_in and phosphatase P* such that the loading applied to the input u is small (small retroactivity to the input r). We can view it as a ‘low-gain’ stage in the sense that it is using low amounts of cycle proteins. Despite the low amount of cycle proteins, this cycle still effectively mitigates the load-induced slow down owing to large amounts of y_in binding to z if the input u evolves on the time scale of gene expression. In fact, load-induced delays occur at the faster time scale of the z-cycle (seconds) and are therefore negligible in the time scale of the input u (minutes to hours). This time-scale separation-based mechanism for insulation allows effective buffering of the genetic circuits from retroactivity by connecting them through fast signalling systems. This mechanism for retroactivity attenuation was implemented in yeast through a two-stage system in which the first stage is a phosphorylation cycle, and the second stage is a phosphotransfer system, resulting in almost complete retroactivity attenuation [39].

Mathematically, and under suitable stability conditions, this mechanism for disturbance attenuation is equivalent to high-gain negative feedback, wherein ‘high gains’ are implicitly realized through fast time scales [103,104]. This can be intuitively explained by considering the differential equation describing the rate of change of u and the faster rate of change of y

where 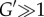quantifies that the time scale of y is much faster than that of u. If the y-subsystem is stable, and, for illustration purposes, we assume that u(t) is a small amplitude signal, we can use the linear approximation 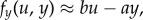with b,a > 0, so that 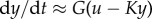with 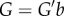and K = a/b. This is in the standard high-gain negative feedback form, but no explicit negative feedback was engineered. Because no explicit negative feedback needs to be engineered, these devices are substantially easier to implement through biomolecular core processes, where there are plenty of different time scales at which reactions occur. However, identifying the structures of signalling systems that qualify as insulation devices still requires more research.

6. In-cell feedback control: multicellular coordination

Our discussion of in-cell feedback control so far has focused solely on intracellular control, where feedback is implemented in each cell and cells function independent of each other. Many applications, however, require programming functions over space and these are enabled only by multicellular coordination. The ability to program spatial patterns of cells could potentially impact applications such as regenerative medicine that need coordinated self-organization of cells, for example in engineered stem cell organoids [105]. A number of works have demonstrated that, in principle, programmed cell coordination is possible, such as in dark–light edge detectors [106,107], spatial patterning [108–110], density-based gene activation [111] and microbial consortia [112], where multiple microbial populations interact to improve a product's yield.

In a multicellular coordination problem, although control action still takes place in individual cells through activation or repression of suitable genes, cells have access to the ensemble state of the entire population as obtained through diffusible signalling molecules. From a control theoretic perspective, this could be viewed as an example of cooperative control, where a large population of autonomous agents (cell) are interconnected through (cell–cell) communication, and the decision of each agent contributes to the collective behaviour of the population. Synthetic genetic cooperative feedback control systems have been built for a number of purposes. In the work by You et al. [113], a population control circuit autonomously maintains the density of E. coli at a desired level (figure 7). The rationale of this control system is as follows. Within each individual cell, LuxI is constitutively expressed to catalyse the synthesis of signalling molecule AHL, which can diffuse freely across the membrane. As the number of cells N increases, AHL concentration (A) increases, activating expression of a killer gene (E) in the circuit. The negative feedback system thus consists of (see red dashed line in figure 7). Experimental validation of the system shows robust regulation of cell density under various growth conditions. Furthermore, steady-state population size can be tuned through the AHL degradation rate constant, which plays a major role in the ‘cell–cell communication strength’. Multicellular feedback control has recently found its application to generate scale-invariant patterns in a bacterial population [109], where a core-ring fluorescence pattern is formed whose size preserves a constant ratio with the size of the population.

Figure 7.

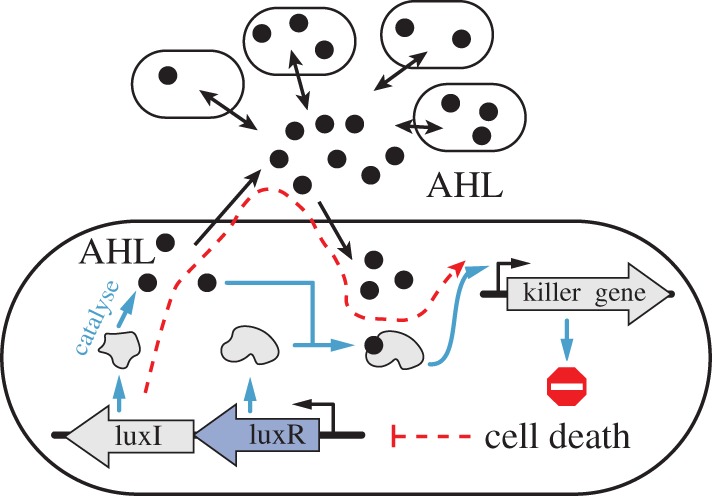
Coordinated population control system [113]. LuxI and LuxR are produced constitutively in each cell. LuxI catalyses the synthesis of small molecule AHL, which can diffuse freely across the membrane. As cell number grows, AHL concentration increases, binding with LuxR to activate a ‘killer gene’ to reduce cell count. Blue arrows indicate biochemical reactions, black arrows show the diffusion of AHL across the membrane, and dashed red arrows show the population control feedback loop.

In part owing to the mathematical difficulties of analysing large-scale, nonlinear multi-agent systems, the theoretical study of multicellular feedback control is challenging, and only limited results have been published. For example, Vignoni et al. [114] developed a mathematical model for a multicellular feedback control circuit, where AHL is involved in both negative autoregulation and cell–cell communication. The authors found, by analysing the model, that such a feedback system is stable, and can reduce variability of gene expression in the population. Were this theoretical result validated experimentally, multicellular control could be a powerful tool to complement existing in-cell control mechanisms, such as negative autoregulation, to reduce heterogeneity in gene expression and improve robustness to environmental perturbations. Additional theoretical and experimental research is required to understand the robustness, stability and performance of these systems.

7. In silico feedback control

Although the advances in implementing in-cell control systems to regulate cellular processes are remarkable, our ability to control processes tightly and robustly is often hindered by the genetic nature of living cells. Specifically, as discussed in §4.3, all control ‘algorithms’ must be implemented through biochemical core processes, which pose significant constraints to the level of sophistication that controllers can take. Furthermore, in-cell feedback controllers have to cope with a noisy and variable cellular environment, and thus the control signals themselves are corrupted by noise and uncertainty. Finally, there are some applications, such as the control of cell differentiation or de-differentiation (reprogramming), in which it may be desirable not to genetically and permanently modify the cells being controlled.

In silico control is an application of feedback control to synthetic biology, with the intention to complement in-cell control mechanisms to compensate for the aforementioned difficulties. An in silico feedback control system can be decomposed into four basic modules: measurement, control, actuation and the cellular processes to be controlled, that is, the plant (figure 1c). Using microscopy [115–117] or flow cytometry [118], a measurement module measures the reporter fluorescence intensity of either a cell population [115–118] or a single cell [116,117]. Measured data are then sent to a computer, where they are processed to infer the state of the cell (filtered), and sent as an input to the control algorithm to compute a desirable control input in silico. The control input is then actuated by applying external stimuli to the target cellular processes to be controlled. Major actuation methods include exposing the cell to light of a specific wavelength (optogenetics techniques) [116,118], changing osmotic pressure [117] or changing inducer concentration [115]. The feedback loop is closed when the cell responds to these stimuli through in-cell biomolecular reactions, which bring a change to the reporter fluorescence captured by the measurement module.

Existing studies [115–118] in this field differ most significantly in the control algorithm in silico, and in the cellular process to be controlled. For example, Toettcher et al. [116] and Menolascina et al. [115] applied a proportional–integral (PI) control algorithm. A PI controller requires minimal knowledge of the controlled process, and can eliminate any steady-state mismatch between measured and desired output (§3). In [116], protein–protein interaction processes form the plant to be controlled, and because these interactions have a characteristic time scale of seconds, a fast set-point tracking performance was observed. On the contrary, in [115], the process controlled is (cascaded) gene expression, which has a significant input/output lag resulting in a more difficult plant to control (see §3). However, constant and time-varying reference signal tracking were still successfully accomplished for a complicated synthetic network in yeast, which has five genes and feedback loops.

More sophisticated feedback control algorithms were implemented in [118] and [117]. In particular, the fluorescence measurements are sent through a Kalman filter to a model predictive controller (MPC) [50]. As a consequence, an accurate model of the cellular process to be controlled is required. The Kalman filter provides an optimal estimate of the state of the cell, which is then used by the predictive controller to compute an optimal control input that minimizes deviations between a desired and the future model-predicted output. In [118], fluorescence expression from an optogenetically controlled promoter is robustly regulated. The controlled cellular process in [117] includes a high-osmolarity glycerol signal cascade, which itself has an internal negative feedback loop that ensures adaptation. A system that can achieve adaptation is minimally responsive to control inputs, and is notoriously hard to control dynamically, especially using standard controllers such as the PI controller. With MPC, however, the authors in [117] were able to demonstrate robust and tight control of gene expressions to track both constant and time-varying references on both the population and the single cell level.

A current obstacle to the practical application of in silico control lies in the output measurement process. Most of the test circuits studied [115,117,118] involve control and measurement of the same protein, a fluorescence reporter. When the species to be controlled is not the fluorescent reporter itself, which is the case in most practical applications, an indirect measurement approach is required. For example, a gene-expression step can be added where a fluorescence reporter responds to changes in concentration of the species to be controlled. This type of strategy, however, will lead to delayed and noisy measurements, which are a major challenge for any feedback controller. While a simple PI controller may be unsuitable in this case, an advanced model-based controller, such as MPC, combined with estimators may be more promising. However, this requires a trustworthy model of the cellular processes to be controlled, which are typically subject to substantial noise and uncertainty. More research is required to understand how to overcome these challenges.

8. Summary

In this review, we have described some of the main achievements of feedback control designs in synthetic biology. Classical control designs have been extended or directly applied to make synthetic genetic circuits more reliable in the presence of noise, less sensitive to variability in the genetic context, more robust to loading and coordinated across many cells. We have also highlighted many open problems, especially those related to the stringent physical constraints that biomolecular hardware poses on in-cell feedback control implementations. These include resource limitations that restrict the extent to which gains can be increased in high-gain feedback designs; cell growth effects that, among others, make the implementation of exact integral feedback very challenging; and cell–cell heterogeneity that asks for coordinated control techniques, for which applicable theory is needed. In silico feedback control bypasses some of these difficulties, because the controller is implemented in a computer, but some challenges remain to make it a practical solution. Therefore, while the many successes of control design in synthetic biology show great promise for complementing and leveraging on-going efforts of parts characterization, discovery/invention and tuning, many unique challenges need to be overcome, which are likely to require new methods and theories.

Authors' contributions

D.D.V. generated the main ideas and coordinated the work. All authors wrote the manuscript. Y.Q. performed simulations. A.J.D. and Y.Q. created the figures.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by AFOSR grant no. FA9550-14-1-0060, ONR grant no. N000141310074, and an NSF Graduate Fellowship.