Orthogonalizing EM: A design-based least squares algorithm

Abstract

We introduce an efficient iterative algorithm, intended for various least squares problems, based on a design of experiments perspective. The algorithm, called orthogonalizing EM (OEM), works for ordinary least squares and can be easily extended to penalized least squares. The main idea of the procedure is to orthogonalize a design matrix by adding new rows and then solve the original problem by embedding the augmented design in a missing data framework. We establish several attractive theoretical properties concerning OEM. For the ordinary least squares with a singular regression matrix, an OEM sequence converges to the Moore-Penrose generalized inverse-based least squares estimator. For ordinary and penalized least squares with various penalties, it converges to a point having grouping coherence for fully aliased regression matrices. Convergence and the convergence rate of the algorithm are examined. Finally, we demonstrate that OEM is highly efficient for large-scale least squares and penalized least squares problems, and is considerably faster than competing methods when n is much larger than p. Supplementary materials for this article are available online.

1 INTRODUCTION

Observational data with massive sample size appear in an increasing multitude of fields. In a growing number of areas such as marketing, physics, computational biology, engineering, and web applications, data have tens of millions of observations or more. While much recent research has been devoted to high-dimensional data, in this paper we develop an experimental design method that targets big data. Our method is shown to have state-of-the-art performance for data with a large number of observations. We investigate the theoretical properties of our method and demonstrate its efficiency in the computation of standard statistical methods.

This project aims at developing a new data augmentation method for fitting ordinary and penalized least squares and in big data. Unlike approximate methods, OEM solves the least squares problem exactly. OEM starts with a trivial observation in fitting ordinary or penalized least squares with orthogonal matrices. If the design matrix is orthogonal, then the ordinary least squares problem has a closed-form solution without any matrix inversion. More importantly, this holds regardless of the sample size and in this sense, scales well for big data. But the hard truth is that most large observational data in practice do not have orthogonal design matrices. In this paper, we propose an experimental design method to circumvent this difficulty.

Consider a regression model 

$$\mathbf{y}=\mathit{X}\mathbf{\beta }+\mathbf{\epsilon },$$ (1)

where X = (x_ij) is an n × p regression matrix, y ∈ ℝⁿ is the response vector, β = (β₁, …, β_p)′ is the vector of regression coefficients, and ε is the vector of random errors with zero mean. The ordinary least squares (OLS) estimator of β is the solution to 

$$\underset{\mathbf{\beta }}{min}{\Vert \mathbf{y}-\mathit{X}\mathbf{\beta }\Vert }^2,$$ (2)

where ||·|| denotes the Euclidean norm. If X is a part of a known m × p orthogonal matrix 

$${\mathit{X}}_{\mathrm{c}}=\left(\begin{array}{c}\mathit{X}\\ \mathbf{\Delta }\end{array}\right),$$ (3)

where Δ is an (m−n)×p matrix, (2) can be efficiently computed by the Healy-Westmacott procedure (Healy and Westmacott 1956). Let 

$${\mathbf{y}}_{\mathrm{c}}={({\mathbf{y}}^{\prime },{\mathbf{y}}_{\text{miss}}^{\prime })}^{\prime }$$ (4)

be the vector of complete responses with missing data y_miss of m − n points. In each iteration, the procedure imputes the value of y_miss, and updates the OLS estimator for the complete data (X_c, y_c). This update involves no matrix inversion since X_c is (column) orthogonal. Dempster, Laird, and Rubin (1977) showed that this procedure is an EM algorithm.

The major limitation of the procedure is the assumption that X must be embedded in a pre-specified orthogonal matrix X_c. We propose a new algorithm, called orthogonalizing EM (OEM) algorithm, to remove this restriction and extend to other directions. The first step, called active orthogonization, orthogonalizes an arbitrary regression matrix by elaborately adding more rows. The second step imputes the responses of the new rows. The third step solves the OLS problem in (2) for the complete orthogonal design. The second and third steps iterate until convergence. The OEM procedure implicity adds rows and only requires the computation of the largest eigenvalue of X′X in order to achieve convergence.

For the OLS problem in (2), OEM works with an arbitrary regression matrix X. OEM can be extended to penalized least squares problems by adding penalties or constraints to β in (2). For penalized problems, the only difference in the OEM algorithm is the form of the solutions to the second and third steps. We demonstrate that OEM 

1. Is faster than competing methods when n ≫ p for ordinary and penalized least squares

2. Converges to the Moore-Penrose generalized inverse for rank-deficient matrices faster than standard methods for both when n > p and p > n

3. Computes solutions to penalization paths for multiple penalties efficiently

4. Results in estimates with grouping coherence, in that it yields the same coefficients for fully aliased columns in X

5. Converges faster for penalized least squares than ordinary least squares

The remainder of this paper will be presented as follows. Section 2 discusses the active orthogonalization procedure. Section 3 presents OEM for OLS. Section 4 extends OEM to penalized least squares. Section 5 provides convergence properties of OEM. Section 6 presents numerical examples to compare OEM with other algorithms for penalized least squares. Section 7 concludes with some discussion.

2 ACTIVE ORTHOGONALIZATION

For an arbitrary n × p matrix X in (1), we propose active orthogonalization to actively orthogonalize an arbitrary matrix by elaborately adding more rows. Let S be a p × p diagonal matrix 

$$\mathit{S}=\text{diag}(s_1,\dots ,s_p),$$ (5)

where s_j > 0 for j = 1, …, p. Consider the eigenvalue decomposition V′ΓV of S⁻¹X′XS⁻¹ (Wilkinson 1965), where V is an orthogonal matrix and Γ is a diagonal matrix whose diagonal elements, γ₁ ≥ ··· ≥ γ_p, are the nonnegative eigenvalues of S⁻¹X′XS⁻¹. For d ≥ γ₁, let 

$$t=\#\{j:{\gamma }_j=d,j=1,\dots ,p\}$$ (6)

denote the number of the γ_j equal d. For example, if d = γ₁ = γ₂ and γ₁ > γ_j for j = 3, …, p, then t = 2. If d > γ₁, then t = 0. Define 

$$\mathit{B}=\text{diag}(d-{\gamma }_{t+1},\dots ,d-{\gamma }_p)$$ (7)

and 

$$\mathbf{\Delta }={\mathit{B}}^{1/2}{\mathit{V}}_1\mathit{S},$$ (8)

where V₁ is the submatrix of V consisting of the last p − t rows. Put X and Δ row by row together to form a complete matrix X_c.

Lemma 1

The matrix X_c above is column orthogonal.

Lemma 1 indicates that at most p − t rows need to be added to make X orthogonal. The following lemma shows that p − t is actually the minimum value.

Lemma 2

Suppose that Δ is an l × p matrix satisfying X′X + Δ′Δ = diag(d₁, ···, d_p) with d₁, ···, d_p > 0. For any d > 0, let $\mathit{S}=\text{diag}(\sqrt{d_1/d},\dots ,\sqrt{d_p/d})$ and γ₁ ≥ ··· ≥ γ_p denote the eigenvalues of S⁻¹X′XS⁻¹. If d ≥ γ₁, then l ≥ p − t, where t = #{ j : γ_j = d, j = 1, …, p}.

We now consider the underlying geometry of active orthogonalization, which should provide intuition behind the OEM algorithm. For a vector x ∈ ℝ^m, let P_ωx denote its projection onto a subspace ω of ℝ^m. Lemma 1 implies that for the column vectors x₁, …, x_p ∈ ℝⁿ of X in (1), there exists a set of mutually orthogonal vectors x_c1, …, x_cp ∈ ℝ^n+p−t of X_c in (3) satisfying P_ℝⁿx_ci = x_i, for j = 1, …, p.

Remark 1

In (8) Δ has p − t rows, which does not rely on the number of rows in X. Lemmas 1 and 2 indicate that p − t rows need to be added to make X orthogonal.

Remark 2

The form of S in (5) can be chosen flexibly. One possibility is S = I_p with 

$${\mathit{X}}^{\prime }\mathit{X}+{\mathbf{\Delta }}^{\prime }\mathbf{\Delta }=d{\mathit{I}}_p$$ (9)

with d ≥ γ₁, and X_c is standardized such that the Euclidean norm of each column is d. Note that larger t corresponds to fewer rows needed, and t depends on S and d. We can use the optimal S and d that maximize the value of t. Clearly d = γ₁ leads to the maximum t for a given S, whereas the optimal S has no obvious form. From the algorithmic aspect, a more reasonable strategy is to select them that optimize the convergence rate of the proposed algorithm; see the appendix for details on the convergence rate. However, it adds extra computational burden to solve such optimization problems, and we usually use explicit form of S like S = I_p. For standardized X, another intuitive selection in (10) reduces to S = I_p.

The augmented rows Δ need not be computed explicitly. Instead, we can compute Δ′Δ, which has a simple form, dS² − X′X. As a direct result, only the largest eigenvalue of S⁻¹X′XS⁻¹ is required. Such a task can be very efficiently achieved using modern numerical linear algebra techniques.

Example 1

Suppose that X in (1) is orthogonal. Take d = γ₁ and

$$\mathit{S}=\text{diag}\left[{(\sum _{i=1}^n{x}_{i1}^2)}^{1/2},\dots ,{(\sum _{i=1}^n{x}_{ip}^2)}^{1/2}\right].$$ (10)

Note that S⁻¹X′XS⁻¹ is an identity matrix. Consequently, t = p, and Δ in (8) is empty, which indicates that active orthogonalization will not overshoot.

Example 2

Let

$$\mathit{X}=\left(\begin{array}{rrr}\hfill 0& \hfill 0& \hfill 3/2\\ \hfill -4/3& \hfill -2/3& \hfill 1/6\\ \hfill 2/3& \hfill 4/3& \hfill 1/6\\ \hfill -2/3& \hfill 2/3& \hfill -7/6\end{array}\right).$$

If S = I₃ and d = γ₁, then t = 2 and (8) gives $\mathbf{\Delta }=(-2/\sqrt{3},2/\sqrt{3},1/\sqrt{3})$.

See the Supplementary Materials for further examples.

3 OEM FOR ORDINARY LEAST SQUARES

We now develop OEM for the OLS problem in (2) when the regression matrix X has an arbitrary form. OEM converges to the solution even if the model is misspecified. In practice, standard linear model diagnostic procedures should be enacted. Active orthogonalization is first employed to obtain Δ in (8). If X_c is known (Healy and Westmacott 1956), then skip this step. For any initial estimator β⁽⁰⁾, the second step imputes y_miss in (4) with y_I = Δβ⁽⁰⁾. Let ${\mathbf{y}}_{\mathrm{c}}={({\mathbf{y}}^{\prime },{\mathbf{y}}_{\mathrm{I}}^{\prime })}^{\prime }$. The third step solves

$${\mathbf{\beta }}^{(1)}=\text{arg}\underset{\mathbf{\beta }}{\text{min}}{\Vert {\mathbf{y}}_{\mathrm{c}}-{\mathit{X}}_{\mathrm{c}}\mathbf{\beta }\Vert }^2.$$ (11)

Then, the second and third steps iterate for obtaining β⁽²⁾,β⁽³⁾, … until convergence. Define

$$\mathit{A}={\mathbf{\Delta }}^{\prime }\mathbf{\Delta }.$$ (12)

For X_c in (3), let (d₁, …, d_p) denote the diagonal elements of ${\mathit{X}}_{\mathrm{c}}^{\prime }{\mathit{X}}_{\mathrm{c}}$. For k = 0, 1, …, let 

$$\mathbf{u}={(u_1,\dots ,u_p)}^{\prime }={\mathit{X}}^{\prime }\mathbf{y}+\mathit{A}{\mathbf{\beta }}^{(k)},$$ (13)

and (11) becomes 

$${\mathbf{\beta }}^{(k+1)}=\text{arg}\underset{\mathbf{\beta }}{\text{min}}\sum _{j=1}^p(d_j{\beta }_j^2-2u_j{\beta }_j),$$ (14)

which is separable in the dimensions of β. Thus, (14) has a simple form 

$${\beta }_j^{(k+1)}=u_j/d_j,\text{for}j=1,\dots ,p,$$ (15)

which involves no matrix inversion. If X_c is constructed by active orthogonalization with S in (5), then $d_j={ds}_j^2$ in (15) for j = 1, …, p.

The above algorithm works for any S in (5). For simplicity, we fix S = I_p in the remaining part of this section; see Remark 2 for a discussion on selection of S. In practice, obtaining Δ in (8) may be computationally expensive. Instead, one can simply compute A = Δ′Δ and the diagonal entries d₁, …, d_p of ${\mathit{X}}_c^{\prime }{\mathit{X}}_{\mathrm{c}}$. For S = I_p, by (8), A = dI_p − X′X, where d is a number no less than the largest eigenvalue γ₁ of X′X. This essentially reduces OEM to finding a reasonable d, which can be accomplished efficiently. A possible choice is d = trace(X′X). Another choice is d = γ₁ to obtain the fastest convergence; see the appendix. We compute γ₁ by the Lanczos algorithm (Lanczos 1950) described in the Supplementary Materials.

Remark 3

When p > n, we ease the computational burden by replacting the p × p matrix X′X with the n × n matrix XX′ in the Lanczos method as the two matrices have identical non-zero eigenvalues.

When X has full column rank, the convergence results in Wu (1983) indicates that the OEM sequence given by (15) converges to the OLS estimator for any initial point β⁽⁰⁾. Next, we discuss the convergence property of OEM when X′X is singular, which covers the case of p > n. Let r denote the rank of X. For r < p, the singular value decomposition (Wilkinson 1965) of X is 

$$\mathit{X}={\mathit{U}}^{\prime }\left(\begin{array}{cc}{\mathbf{\Gamma }}_0^{1/2}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)\mathit{V},$$

where U is an n × n orthogonal matrix, V is a p × p orthogonal matrix, and Γ₀ is a diagonal matrix with diagonal elements γ₁ ≥ ··· ≥ γ_r which are the positive eigenvalues of X′X. Define 

$${\widehat{\mathbf{\beta }}}^{\ast }={({\mathit{X}}^{\prime }\mathit{X})}^{+}{\mathit{X}}^{\prime }\mathbf{y},$$ (16)

where ⁺ denotes the Moore-Penrose generalized inverse (Ben-Israel and Greville 2003).

Theorem 1

Suppose that X′X + Δ′Δ = γ₁I_p. If β⁽⁰⁾ lies in the linear space spanned by the first r columns of V′, then as k → ∞, for the OEM sequence {β^(k)} of the ordinary least squares, β^(k) → β̂^*.

In active orthogonalization, the condition X′X + Δ′Δ = γ₁I_p holds if d = γ₁ and S = I_p in (8). Using β⁽⁰⁾ = 0 satisfies the condition in Theorem 1.

The Moore-Penrose generalized inverse is widely used in statistics for a degenerated system. Theorem 1 indicates that OEM converges to β̂^* in (16) in this case. When r < p, the limiting vector β̂^* given by an OEM sequence has the following properties. First, it has the minimal Euclidean norm among the least squares estimators (X′X)⁻X′y (Ben-Israel and Greville 2003). Second, its model error has a simple form, E[(β̂^*−β)′(X′X)(β̂^*−β)]= rσ². Third, Xα = 0 implies α′β̂^* = 0 for any vector α. The third property indicates that β̂^* inherits the multicollinearity between the columns in X. This property is stronger than grouping coherence for penalized least squares in the appendix.

We now discuss the computational efficiency of OEM for computing β̂^* in (16) when X is degenerated. Recall that X′X and XX′ have the same nonzero eigenvalues. The computation of γ₁ in the OEM iterations by the Lanczos algorithm has complexity O(min{n, p}² max{n, p}). Since the complexity of the OEM iterations is O(np²), the whole computational complexity of OEM for computing β̂^* is O(np²). The singular value decomposition method computes (X′X)⁺ first by singular value decomposition to obtain β̂^*, and has computational complexity O(np² + p³). The OEM algorithm is superior to this method in terms of complexity for large p.

We conduct a simulation study to compare the speeds of OEM and the singular value decomposition-based least squares method for computing β̂^* in (16). The MATLAB function pinv is used in the singular value decomposition method as above. Generate all entries of X and y independently from the standard normal distribution. A new predictor calculated as the mean of all the covariates is added to degenerate the design matrix. Table 1 compares a simple MATLAB implementation of OEM and the singular value decomposition method in computing β̂^*. Both OEM and the singular value decomposition method give the same results. The results for p > n situations are similar to those of n > p and are included in the Supplementary Materials. Tables 1 and in Section C.1 in the Supplementary Materials indicate that OEM is faster than the singular value decomposition method for any combination of n and p, which is consistent with the above complexity analysis.

Table 1.

Average runtime (seconds) comparison between OEM and the SVD least squares method for n > p

n	p	OEM	SVD
50, 000	10	0.0433	0.0956
	50	0.2439	0.4098
	200	1.4156	4.9765
	1000	5.4165	45.3270
	5000	72.0630	442.3300

4 OEM FOR PENALIZED LEAST SQUARES

The OEM procedure can be easily extended to penalized least squares problems. Consider a penalized version of (1):

$$\underset{\mathbf{\beta }\in \mathrm{\Theta }}{min}\left[{\Vert \mathbf{y}-\mathit{X}\mathbf{\beta }\Vert }^2+P(\mathbf{\beta };\lambda )\right],$$ (17)

where β ∈ Θ, Θ is a subset of ℝ^p, P is a penalty function, and λ is the vector of tuning parameters. To apply the penalty P equally to all the variables, the regression matrix X is standardized so that

$$\sum _{i=1}^n{x}_{ij}^2=1,\text{for}j=1,\dots ,p.$$ (18)

Popular choices for P include ridge regression (Hoerl and Kennard 1970), the nonnegative garrote (Breiman 1995), the lasso (Tibshirani 1996), SCAD (Fan and Li 2001), and the MCP (Zhang 2010).

Suppose that Θ and P in (17) are decomposable as $\mathrm{\Theta }={\prod }_{j=1}^p{\mathrm{\Theta }}_j$ and $P(\mathbf{\beta };\lambda )={\sum }_{j=1}^p{P}_j({\beta }_j;\lambda )$. For the problem in (17), the first step of OEM is active orthogonalization, which computes Δ in (8). For any initial estimator β⁽⁰⁾, the second step imputes y_miss in (4) by y_I = Δβ⁽⁰⁾. Let ${\mathbf{y}}_{\mathrm{c}}={({\mathbf{y}}^{\prime },{\mathbf{y}}_{\mathrm{I}}^{\prime })}^{\prime }$. The third step solves

$${\mathbf{\beta }}^{(1)}=\text{arg}\underset{\mathbf{\beta }\in \mathrm{\Theta }}{\text{min}}\left[{\Vert {\mathbf{y}}_{\mathrm{c}}-{\mathit{X}}_{\mathrm{c}}\mathbf{\beta }\Vert }^2+P(\mathbf{\beta };\lambda )\right].$$

The second and third steps iterate to compute β^(k) for k = 1, 2, … until convergence. Similar to (14), we have an iterative formula 

$${\beta }_j^{(k+1)}=\text{arg}\underset{{\beta }_j\in {\mathrm{\Theta }}_j}{\text{min}}[d_j{\beta }_j^2-2u_j{\beta }_j+P_j({\beta }_j;\lambda )],\text{for}j=1,\dots ,p,$$ (19)

with u = (u₁, …, u_p)′ defined in (13). This shortcut as applied to the Lasso penalty (Tibshirani 1996) is as follows:

With Θ_j = ℝ, 

$$P_j({\beta }_j;\lambda )=2\lambda \mid {\beta }_j\mid ,$$ (20)

and (19) becomes

$${\beta }_j^{(k+1)}=\text{sign}(u_j){\left(\frac{\mid u_j\mid -\lambda }{d_j}\right)}_{+}.$$ (21)

Here, for a ∈ ℝ, (a)₊ denotes max{a, 0}. The formulas for further penalties are included in the Supplementary Materials.

OEM for (17) is also an EM algorithm. Let the observed data y follow the model in (1). Assume that the complete data ${\mathbf{y}}_{\mathrm{c}}={({\mathbf{y}}^{\prime },{\mathbf{y}}_{\text{miss}}^{\prime })}^{\prime }$ in (4) follows a regression model y_c = X_cβ + ε_c, where ε_c is from N(0, I_m). Let β̂ be a solution to (17) given by β̂ = argmax_β∈Θ L(β | y), and the penalized likelihood function L(β |y) is

$${(2\pi )}^{-n/2}exp\left(-\frac{1}{2}{\Vert \mathbf{y}-\mathit{X}\mathbf{\beta }\Vert }^2\right)exp\left[-\frac{1}{2}P(\mathbf{\beta };\lambda )\right].$$

Given β^(k), the second step of OEM for (17) is the E-step, 

$$\begin{array}{l}E[log\{L(\mathbf{\beta }\mid {\mathbf{y}}_{\mathrm{c}})\}\mid \mathbf{y},{\mathbf{\beta }}^{(k)}]=-C\{{\Vert \mathbf{y}-\mathit{X}\mathbf{\beta }\Vert }^2+E({\Vert {\mathbf{y}}_{\text{miss}}-\mathit{X}\mathbf{\beta }\Vert }^2\mid {\mathbf{\beta }}^{(k)})+P(\mathbf{\beta };\lambda )\}\\ =-C\{n+{\Vert \mathbf{y}-\mathit{X}\mathbf{\beta }\Vert }^2+{\Vert \mathbf{\Delta }{\mathbf{\beta }}^{(k)}-\mathbf{\Delta }\mathbf{\beta }\Vert }^2+P(\mathbf{\beta };\lambda )\}\end{array}$$

for some constant C > 0. Define

$$Q(\mathbf{\beta }\mid {\mathbf{\beta }}^{(k)})={\Vert \mathbf{y}-\mathit{X}\mathbf{\beta }\Vert }^2+{\Vert \mathbf{\Delta }{\mathbf{\beta }}^{(k)}-\mathbf{\Delta }\mathbf{\beta }\Vert }^2+P(\mathbf{\beta };\lambda ).$$ (22)

The third step of OEM is the M-step, 

$${\mathbf{\beta }}^{(k+1)}=\text{arg}\underset{\mathbf{\beta }\in \mathrm{\Theta }}{\text{min}}Q(\mathbf{\beta }\mid {\mathbf{\beta }}^{(k)}),$$ (23)

which is equivalent to (19) when Θ and P in (17) are decomposable.

Example 3

For the model in (1), let the complete matrix X_c be an orthogonal design from Xu (2009) with 4096 runs in 30 factors. Let X in (1) be the submatrix of X_c consisting of the first 3000 rows and let y be generated from (1) with σ = 1 and

$${\beta }_j={(-1)}^{j}exp[-2(j-1)/20]\text{for}j=1,\dots ,p.$$ (24)

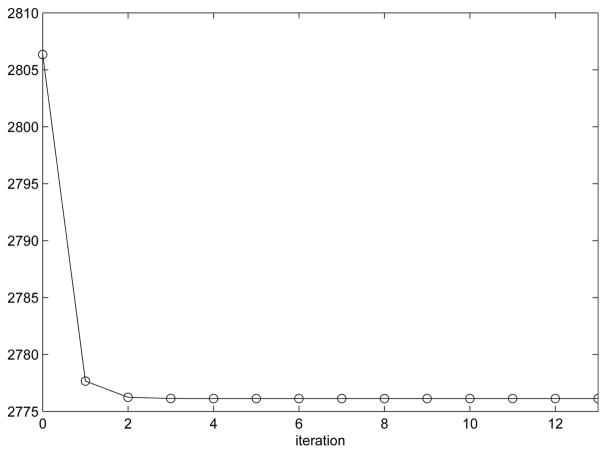
Here, let p = 30, n = 3000, and the response values for the last 1096 rows of X_c be missing. OEM is used to solve the SCAD problem with an initial value β⁽⁰⁾ = 0 and a stopping criterion when relative changes in all coefficients are less than 10⁻⁶. For λ = 1 and a = 3.7 in the SCAD penalty, defined in the Supplementary Materials, Figure 1 plots values of the objective function in (17) with the SCAD penalty of the OEM sequence against iteration numbers, where the convergence occurs at iteration 13, and the objective function significantly reduces after two iterations.

Figure 1.

Values of the objective function of an OEM sequence for the SCAD against iterations for Example 3.

5 CONVERGENCE OF THE OEM ALGORITHM

We now establish convergence properties of OEM with the general penalty in (17). We also give results to compare the convergence rates of OEM for OLS, the elastic-net, and the lasso. These convergence rate results show that for the same data set, OEM converges faster for penalized least squares than ordinary least squares. This provides a new theoretical comparison between these methods. The objective functions of existing EM convergence results like those in Wu (1983), Green (1990) and McLachlan and Krishnan (2008) are typically continuously differentiable. This condition does not hold for the objective function in (17) with the lasso and other penalties, and these existing results do not directly apply here.

For the model in (1), denote the objective function in (17) by 

$$l(\mathbf{\beta })={\Vert \mathbf{y}-\mathit{X}\mathbf{\beta }\Vert }^2+P(\mathbf{\beta };\lambda ),$$ (25)

which is defined on a subset Θ of ℝ^p. For penalties like the bridge, it is infeasible to perform the M-step in (23) directly. For this situation, following the generalized EM algorithm in Dempster, Laird, and Rubin (1977), we define the following generalized OEM algorithm 

$${\mathbf{\beta }}^{(k)}\to {\mathbf{\beta }}^{(k+1)}\in \mathcal{M}({\mathbf{\beta }}^{(k)}),$$ (26)

where β → ℳ(β) ⊂ Θ is a point-to-set map such that

$$Q(\mathbf{\varphi }\mid \mathbf{\beta })\le Q(\mathbf{\beta }\mid \mathbf{\beta }),\text{for}\text{all}\mathbf{\varphi }\in \mathcal{M}(\mathbf{\beta }).$$

Here, Q is given in (22). The OEM sequence defined by (23) is a special case of (26). For example, the generalized OEM algorithm can be used for the bridge penalty (Frank and Friedman 1993), where Θ_j = ℝ and 

$$P_j({\beta }_j;\lambda )=\lambda {\mid {\beta }_j\mid }^a$$ (27)

for some a ∈ (0, 1) in (17). Since the solution to (19) with the bridge penalty has no closed form, one may use one-dimensional search to compute ${\beta }_j^{(k+1)}$ that satisfies (26).

We make the following three assumptions throughout this section.

• Assumption 1. The parameter space Θ is a closed convex subset of ℝ^p.

• Assumption 2. For a fixed λ, the penalty P(β; λ) in (17) is continuous with respect to β ∈ Θ. 

• Assumption 3. The sequence {β^(k)} defined in (26) lies in a compact subset of ℝ^p.

Assumption 1 covers the case in which the sequence {β^(k)} may fall on the boundary of Θ (Nettleton 1999), like the nonnegative garrote (Breiman 1995) and the nonnegative lasso (Efron et al. 2004). The generalized OEM algorithms for the penalties discussed in Section 4 all satisfy Assumptions 1 and 2. By the monotonicity property of the generalized EM algorithm, Assumption 3 holds if we have the lower compact condition that {β ∈ Θ : l(β) ≤ C} is compact for any constant C. This condition is generally required in the convergence analysis of MM algorithms (Lange 1999), which are extensions of EM algorithms. It is obvious that the lower compact condition holds if l(β) → ∞ as ||β|| → ∞. Therefore, for SCAD and MCP, the lower compact condition holds if X has full column rank; for other penalties in Section 4, it holds for any X and y. The generalized OEM algorithm for the bridge penalty in (27) also satisfies the above assumptions.

Remark 4

When p is larger than n, the lower compact condition does not hold for SCAD or MCP. For this case, Assumption 3 also holds if there exists some k such that β^(k) lies in the set {β ∈ Θ : l(β) < inf ℒ}, where ℒ is the set of limit points of all {l(ϕ_n)} with ϕ_n ∈ Θ and ||ϕ_n|| → ∞ as n → ∞.

The objective functions in (17) with the lasso and other penalties are not continuously differentiable. A more general definition of stationary points is needed. We call β ∈ Θ a stationary point of l if

$$\underset{t\to 0_{+}}{liminf}\frac{l((1-t)\mathbf{\beta }+t\mathbf{\varphi })-l(\mathbf{\beta })}{t}\ge 0\text{for}\text{all}\mathbf{\varphi }\in \mathrm{\Theta }.$$

Let S denote the set of stationary points of l. By Assumption 2, ℳ is a closed point-to-set map (Zangwill 1969; Wu 1983). Analogous to Theorem 1 in Wu (1983) on the global convergence of the EM algorithm, we have the following result.

Theorem 2

Let {β^(k)} be a generalized OEM sequence generated by (26). Suppose that

$$l({\mathbf{\beta }}^{(k+1)})<l({\mathbf{\beta }}^{(k)})\text{for}\text{all}{\mathbf{\beta }}^{(k)}\in \mathrm{\Theta }\backslash S.$$ (28)

Then all limit points of {β^(k)} are elements of S and l(β^(k)) converges monotonically to l^* = l(β^*) for some β^* ∈ S.

Theorem 3

If β^* is a local minimum of Q(β | β^*), then β^* ∈ S.

This theorem follows from the fact that l(β) − Q(β | β^*) is differentiable and

$${\frac{\partial [l(\mathbf{\beta })-Q(\mathbf{\beta }|{\mathbf{\beta }}^{\ast })]}{\partial \mathbf{\beta }}|}_{\mathbf{\beta }={\mathbf{\beta }}^{\ast }}=0.$$

Remark 5

By Theorem 3, if β^(k) ∉ S, then β^(k) cannot be a local minimum of Q(β | β^(k)). Thus, there exists at least one point β^(k+1) ∈ ℳ(β^(k)) such that Q(β^(k+1) | β^(k)) < Q(β^(k) | β^(k)) and therefore satisfies the condition in (28). As a special case, an OEM sequence generated by (23) satisfies (28) in Theorem 2.

Next, we derive convergence results of a generalized OEM sequence {β^(k)} in (26), which, by Theorem 3, hold automatically for an OEM sequence. If the penalty function P(β; λ) is convex and l(β) has a unique minimum, Theorem 4 shows that {β^(k)} converges to the global minimum.

Theorem 4

For {β^(k)} defined in Theorem 2, suppose that l(β) in (25) is a convex function on Θ with a unique minimum β^* and that (28) holds for {β^(k)}. Then β^(k) → β^* as k → ∞.

Theorem 5 discusses the convergence of an OEM sequence {β^(k)} for more general penalties. For a ∈ ℝ, define S (a) = {ϕ ∈ S : l(ϕ) = a}. From Theorem 2, all limit points of an OEM sequence are in S (l^*), where l^* is the limit of l(β^(k)) in Theorem 2. Theorem 5 states that the limit point is unique under certain conditions.

Theorem 5

Let {β^(k)} be a generalized OEM sequence generated by (26) with Δ′Δ > 0. If (28) holds, then all limit points of {β^(k)} are in a connected and compact subset of S (l^*). In particular, if the set S (l^*) is discrete in that its only connected components are singletons, then β^(k) converges to some β^* in S (l^*) as k → ∞.

6 NUMERICAL ILLUSTRATIONS FOR SOLVING PENALIZED LEAST SQUARES

Many algorithms for solving the penalized least squares problem in (17) are available, including the LARS algorithm introduced in Efron, Hastie, Johnstone, and Tibshirani (2004) and the coordinate descent (CD) algorithm (Tseng 2001; Friedman, Hastie, Hofling and Tibshirani 2007; Wu and Lange 2008; Tseng and Yun 2009). The corresponding R packages include lars (Hastie and Efron 2011), and glmnet (Friedman, Hastie, and Tibshirani 2011). For nonconvex penalties in (17) like SCAD and MCP, existing algorithms for solving this optimization problem include local quadratic approximation (Fan and Li 2001; Hunter and Li 2005), local linear approximation (Zou and Li 2008), the CD algorithm (Breheny and Huang 2010; Mazumder, Friedman, and Hastie 2011) and the minimization by iterative soft thresholding algorithm (Schifano, Strawderman, and Wells 2010), among others. We demonstrate that in big data settings when n ≫ p, our OEM implementation vastly outperforms coordinate descent, as implemented in glmnet, which is considered one of the fastest algorithms for penalized regression problems. OEM is less efficient when p ≫ n. To mitigate this, computation can be vastly reduced via screening methods. Here we compare OEM with the CD, LARS, and glmnet algorithms for penalized least squares.

6.1 COMPARISONS WITH OTHER ALGORITHMS

We now compare the computational efficiency of OEM for penalized least squares problems with the coordinate descent (CD) algorithm. OEM is implemented in R with main code in C++. For fitting the lasso, we compare OEM and the R package glmnet, which uses Fortran for the main computation. For MCP, we compare OEM with a C implementation of the CD algorithm in the R package ncvreg and with a slightly different CD implementation in Fortran in the R package sparsenet.

We consider the situation when the sample size n is larger than the number of variables p. For the penalized problems, solutions for 100 tuning parameter values are computed for all methods. Three different covariance matrix structures for the predictor variables are compared. The first is the case where all the variables are independently generated from standard normal distribution, the second and third cases involve design matrices with a correlations structure 

$$\text{Cor}(X_i,X_j)={\rho }^{\mid i-j\mid }\text{for}i,j=1,\dots ,p,$$ (29)

where ρ = 0, 0.2, 0.8. The response is generated as a linear combination of the design matrix and the true model is y = Xβ + ε, where ε follows the normal distribution N(0, I_n), β is independent of ε and follows the normal distribution N(0, I_p).

To compare the performance of OEM, CD implemented in the ncvreg package (Breheny, et al 2011), and sparsenet (Mazumder, et al 2011) algorithms for nonconvex penalties, data are generated 10 times and the average runtime are shown in Table 3. The results indicate that OEM has advantages when the sample size is significantly larger than the number of variables especially for the independent design. All algorithms tend to require more fitting time when the correlations among the covariates increase. The results are similar for the SCAD penalty for OEM and CD and are not presented, but sparsenet lacks an implementation of SCAD. Table 2 in the Supplementary Materials shows that, for computing SCAD, the CD algorithm is faster and the computational gap gets wider when the ratio of p/n increases. This phenomenon also occurs for the lasso.

Table 3.

Average runtime (seconds) comparison between OEM and CD implemented in ncvreg and sparsenet for MCP when n is larger than p

p	n	OEM			CD			sparsenet
		ρ = 0	ρ = 0.2	ρ = 0.8	ρ = 0	ρ = 0.2	ρ = 0.8	ρ = 0	ρ = 0.2	ρ = 0.8
20	400	0.0015	0.0014	0.0024	0.0219	0.0225	0.0245	0.0054	0.0052	0.0054
	1000	0.0013	0.0014	0.0025	0.0539	0.0497	0.0539	0.0084	0.0085	0.0092
	2000	0.0013	0.0014	0.0025	0.0671	0.0929	0.1139	0.0143	0.0144	0.0165
50	1000	0.0033	0.0034	0.0082	0.1522	0.1548	0.1840	0.0178	0.0175	0.0201
	2500	0.0035	0.0037	0.0073	0.3397	0.3267	0.4330	0.0381	0.0382	0.0467
	5000	0.0043	0.0046	0.0083	0.6245	0.6328	0.9002	0.0748	0.0731	0.0888
100	2000	0.0099	0.0108	0.0229	0.8130	0.8037	0.9536	0.0629	0.0622	0.067
	5000	0.0124	0.0126	0.0232	1.7770	1.9665	2.4915	0.1437	0.1424	0.1594
	10000	0.0180	0.0181	0.0303	3.6344	3.8181	4.7047	0.2867	0.2754	0.3136

A close scrutiny of the two algorithms reveals that they take similar number of iterations but the computation of OEM required a one time computation of matrix multiplication X′X and the complexity of this process is O(np²), which dominates the algorithm especially when p is very large. This is the main drawback of the OEM algorithm.

An advantageous and unique property of the OEM algorithm is its ability to provide solutions for full tuning parameter paths for multiple penalties simultaneously with minimal relative added computation, especially as sample size increases. If in a particular application a comparison between many different penalties is required, OEM provides a way of computing them all at once. While many methods such as coordinate descent have been shown to be efficient in computing solutions to full penalization paths, this result is different in that OEM is efficient in the computation of solutions for full penalization paths for multiple penalties. To the best of our knowledge, no other algorithm possesses this property. A demonstration of this provided in Table 4. We compare the speed of OEM in computing a path of 100 tuning parameter values for the lasso penalty with that of OEM for paths of 100 tuning parameter values for each of the lasso, SCAD, and MCP penalties all at once.

Table 4.

Average runtime (seconds) comparison between OEM lasso and OEM lasso, SCAD, MCP

p	n	OEM Lasso	OEM Lasso, SCAD, MCP
200	1 × 104	0.0994	0.1552
	1 × 105	0.5646	0.6094
	1 × 106	5.6788	5.6909
	5 × 106	28.1284	28.2814

6.2 LARGE-SCALE PERFORMANCE

In many large scale applications, the regression matrix X cannot be fit into memory. Due to its structure, the OEM algorithm extends naturally to such problems. The key computational components of the OEM algorithm, A and X′y, can be computed in a block row-wise fashion, which removes the need to store the entirety of X in memory at once. Specifically, under this scheme, A is computed iteratively by partitioning X into manageable submatrices X_c: c = 1, …, C and computing ${\mathit{X}}^{\prime }\mathit{X}={\sum }_{c=1}^C{\mathit{X}}_c^{\prime }{\mathit{X}}_c$. X′y can be computed similarly. This allows OEM to scale naturally to settings where the number of observations is arbitrarily large. Methods based on CD do not naturally scale in this sense, as the entire coordinate gradient must be formed at each iteration.

In order to demonstrate the utility of OEM for extremely large-scale applications, a simulation with large sample sizes was conducted. For the dense matrix simulation, the data were simulated like in Table 2 with ρ = 0. As many applications such as text analysis result in regression matrices with mostly zero values, a sparse setting was investigated. In this setting the regression matrix X is much larger than in the dense simulation, but a majority of the values are 0. A was computed in blocks of size 10⁶ for the dense simulation and of size 10⁷ for the sparse simulation. Results are shown in Table 5.

Table 2.

Average runtime (seconds) comparison between OEM and glmnet for LASSO when n ≫ p

p	n	OEM			glmnet
		ρ = 0	ρ = 0.2	ρ = 0.8	ρ = 0	ρ = 0.2	ρ = 0.8
200	1 × 104	0.06	0.06	0.09	0.25	0.25	0.25
	1 × 105	0.46	0.46	0.49	2.81	2.81	2.80
	1 × 106	4.49	4.50	4.57	28.21	28.33	28.52
	1 × 107	45.86	45.77	46.34	325.25	325.57	330.37
1, 000	5 × 103	1.52	1.58	2.99	1.95	2.05	2.21
	1 × 104	1.61	1.60	2.72	3.92	4.01	4.57
	1 × 105	9.63	9.63	10.48	38.23	39.55	46.17
	1 × 106	92.97	92.75	93.38	382.21	386.71	461.81

Table 5.

Average runtime comparison (seconds) of OEM for various large-scale penalized and unpenalized least squares problems. All penalized models are fit for 100 values of the tuning parameter. Matrix Sparsity = 0 corresponds to a matrix with all nonzero values.

Matrix Sparsity	p	n	OLS	Lasso	MCP	Lasso, SCAD, MCP
0	100	1 × 108	140.140	140.141	140.140	140.143
		1 × 109	1, 394.577	1, 394.578	1, 394.578	1, 394.580
		1 × 1010	14, 267.520	14, 267.520	14, 267.520	14, 267.520
0	1, 000	1 × 107	946.168	946.266	946.265	946.463
		5 × 107	4, 625.954	4, 626.046	4, 626.045	4, 626.232
		1 × 108	9, 231.134	9, 231.223	9, 231.223	9, 231.405
0.999	10, 000	1 × 108	676.078	708.447	703.409	776.048
		5 × 108	3, 009.860	3, 047.521	3, 034.636	3, 098.680
		1 × 109	6, 119.103	6, 150.690	6, 144.003	6, 203.088
0.999	25, 000	1 × 108	2, 817.139	10, 584.220	3, 322.415	11, 924.730
		5 × 108	21, 630.780	22, 081.390	21, 866.760	22, 614.350
		1 × 109	40, 605.580	40, 952.200	40, 812.850	41, 382.630
0.995	10, 000	1 × 108	4, 221.646	4, 230.995	4, 321.926	4, 350.699
		5 × 108	20, 737.900	20, 732.570	20, 772.450	20, 789.470
		1 × 109	43, 202.950	43, 350.960	43, 313.470	43, 406.450

6.3 DATA ANALYSIS

Consider a dataset from US Census Bureau County and City Data Book 2007, United States Department of Commerce (2007). The response is population change in percentage. The 36 covariates are described in the Supplementary Materials. These variables are in percentage of population of the individual counties.

There are 2573 (counties) observations without missing observations. The linear regression model in (1) is used to fit the data. The solution paths for the lasso, SCAD and MCP fitted to the data set are given in the Supplementary Materials. The number of non-zero coefficients, cross validation residual sum of squares, AIC and BIC are presented in Table 6, where the tuning parameter λ is chose by BIC.

Table 6.

Lasso, SCAD and MCP results for the U.S. Census Bureau data

Penalty	Final Model				Runtime (s)
	Size	CV error	AIC	BIC	OEM	CD
LASSO	32	46.93	3.81	3.87	2.097	0.273
SCAD	28	47.12	3.81	3.87	1.783	3.454
MCP	23	47.17	3.82	3.88	1.433	3.032

The significant variables reveal that the population change is highly related to the living standards of the counties. Table 6 compares the fitted models from different penalized least squares problems. Note that MCP has the most sparse model with little sacrifice of CV error, AIC and BIC scores. LASSO has the model with smallest CV error but including nearly all the candidate predictors. In the example, the penalized models favor complex models with many nonzero coefficients and this reveals the fact that there are many factors that have profound influence on population change of counties in the US. In addition, the last two columns of Table 6 also give the runtime of fitting the 10-fold cross-validation to the data, where OEM is implemented in R with main code in C++, LASSO with CD from glmnet, and SCAD and MCP from ncvreg.

7 DISCUSSION

We have proposed a new algorithm called OEM for solving ordinary and penalized least squares problems for general data structures. We have showed that in order to actively orthogonalize a regression matrix X, one need not explicitly add new rows This can be avoided by a procedure that only requires the largest eigenvalue of X′X. For big data problems, we have demonstrated that OEM outperforms the competing methods and shows great potential in many modern large-scale applications. In addition to its numerical performance, OEM has several desirable theoretical properties, including convergence to the Moore-Penrose generalized inverse-based least squares estimator for singular regression matrices and convergence to a point having grouping coherence for the lasso, SCAD or MCP. For applications such as micro-array, one might be interested in extending the result to the small n and large p case, where OEM is generally slower than state-of-the-art algorithms. This suggests a new interface between optimization and statistics for penalized methods.

The algorithm can be sped up by using various methods from the EM literature (McLachlan and Krishnan 2008). A detailed discussion of this topic is included in the Supplementary Materials.