Hydrogen Peroxide Induced Cell Death: The Major Defences Relative Roles and Consequences in E. coli

Abstract

We recently developed a mathematical model for predicting reactive oxygen species (ROS) concentration and macromolecules oxidation in vivo. We constructed such a model using Escherichia coli as a model organism and a set of ordinary differential equations. In order to evaluate the major defences relative roles against hydrogen peroxide (H₂ O₂), we investigated the relative contributions of the various reactions to the dynamic system and searched for approximate analytical solutions for the explicit expression of changes in H₂ O₂ internal or external concentrations. Although the key actors in cell defence are enzymes and membrane, a detailed analysis shows that their involvement depends on the H₂ O₂ concentration level. Actually, the impact of the membrane upon the H₂ O₂ stress felt by the cell is greater when micromolar H₂ O₂ is present (9-fold less H₂ O₂ in the cell than out of the cell) than when millimolar H₂ O₂ is present (about 2-fold less H₂ O₂ in the cell than out of the cell). The ratio between maximal external H₂ O₂ and internal H₂ O₂ concentration also changes, reducing from 8 to 2 while external H₂ O₂ concentration increases from micromolar to millimolar. This non-linear behaviour mainly occurs because of the switch in the predominant scavenger from Ahp (Alkyl Hydroperoxide Reductase) to Cat (catalase). The phenomenon changes the internal H₂ O₂ maximal concentration, which surprisingly does not depend on cell density. The external H₂ O₂ half-life and the cumulative internal H₂ O₂ exposure do depend upon cell density. Based on these analyses and in order to introduce a concept of dose response relationship for H₂ O₂-induced cell death, we developed the concepts of “maximal internal H₂ O₂ concentration” and “cumulative internal H₂ O₂ concentration” (e.g. the total amount of H₂ O₂). We predict that cumulative internal H₂ O₂ concentration is responsible for the H₂ O₂-mediated death of bacterial cells.

Introduction

Oxygen is indisputably essential for life, but it can also impair cell ability to function normally or it can participate in its destruction ([1] and [2]) because of the generation of reactive oxygen species (ROS) like hydrogen peroxide (H₂ O₂), superoxide ($O_2^{•-}$) or hydroxyl radical (HO^•).

In order to better understand ROS dynamic within cells, we recently developed a mathematical model ([3]) for predicting reactive oxygen species (ROS) concentration and macromolecules oxidation invivo. This first study principally focuses on HO^• dynamic and its consequence on DNA whereas the current study will mainly focus on H₂ O₂ dynamic.

Escherichia coli was used as a model organism. In order to build our mathematical model we used data from a large number of articles dealing with enzymes or molecule concentrations (in E. coli, kinetic properties and chemical reaction rate constants). We were then able to propose a mathematical model based on a set of ordinary differential equations relating to fundamental principles of mass balance and reaction kinetics. It offers the possibility to simulate properly the experimental results obtained by biologists and therefore to understand the biological parameters involved in the observed phenomena.

The purpose of this study is to use our mathematical model in order to better understand H₂ O₂ mode of action on E. coli as a model organism.

In aerobic organisms, oxygen oxidizes redox enzymes, generating a flux of H₂ O₂ that can potentially damage the cell. For instance, Escherichia coli generates about 14 μM H₂ O₂ per second when it grows aerobically on glucose ([4]). In order to cope with H₂ O₂ stress, microbes typically contain multiple catalases and/or peroxidases. E. coli contains one Alkyl hydroperoxide reductase (Ahp) and two different catalases (Cat). Alkyl hydroperoxide reductase is the primary scavenger for endogenous H₂ O₂ in E. coli ([5]). Catalase contributes little when H₂ O₂ levels are low, but it becomes the most effective scavenger when H₂ O₂ levels are high ([5]). Moreover, membrane permeability is part of the global defence process against H₂ O₂ ([4]). However, to our knowledge, the question of their relative involvement remains unsolved especially with regard to the exogenous H₂ O₂ concentration.

Mechanisms involved in H₂ O₂ induced cell death were studied by Imlay and Linn ([6] and [7]) who showed that the exposure of E. coli to H₂ O₂ led to two different modes of killing. The first was observed at low H₂ O₂ concentration (1–3 mM H₂ O₂) and resulted from the DNA damage caused by HO^• ([7]). The second resulted from damage to unknown macromolecules, inflicted more directly, through H₂ O₂-mediated oxidation. However, and to our knowledge, the question of the relative involvement of the cumulative or the maximal H₂ O₂ dose involvement in this phenomenon remains unsolved. Dose response is a question often raised about radiative hazards. For instance Harrison et al. ([8]) indicated median survival times in rats following intravenous injection of polonium-210. The total alpha-particles-emitted numbers show that the cumulative dose and not the maximal dose is principally responsible for death.

Using our mathematical model, we first investigated the relative role of the different ways (principally Ahp, Cat and membrane) for cells to decrease and fight H₂ O₂ oxidative stress. Here we predict that their involvement depends on the H₂ O₂ stress level. Moreover and as observed for radiative hazards, we predict that cumulative internal H₂ O₂ concentration is responsible for the H₂ O₂-mediated death of bacterial cells.

Materials and Methods

The model assumes that all molecule concentrations are homogeneous in cells. We therefore describe the problem with a dynamic system of ordinary differential equations (ODE) instead of using a complex algorithm such as the Next-Sub-Volume Method. Indeed, one algorithm generally used to study the compartmentalization of molecules in microorganisms (for instance E. coli) is the Next-Sub-volume Method. It is a Gillespie-like ([9] and [10]) method approaching the spatial effects of diffusive phenomena and chemical reaction. According to the Next Sub-volume Method, the side length ℓ of the square sub-volumes has to satisfy the two inequalities

$$\begin{array}{c}\hfill R\ll \ell \text{and}{\tau }_{diff}=\frac{{\ell }^2}{6D}⪡{\tau }_{react}\hfill \\ \hfill \text{where}R\text{is the larger radius of a molecule of substrat}\hfill \\ \hfill \text{and}D\text{the diffusion constant of}{H}_2{O}_2\hfill \\ \hfill {\tau }_{diff}\text{represents the characteristic time of diffusion}\hfill \\ \hfill {\tau }_{react}\text{represents the characteristic time of reaction}\hfill \end{array}$$

The first inequality indicates that dissociation events can be properly defined within sub-volumes. The second criterion specifies that the time for any molecule to leave a sub-volume is much smaller than the shortest reaction time τ_min among the molecular species, so that all molecules are homogeneously distributed within the sub-volumes. For example, the 3D simulations are typically performed with ℓ = 0, 1 μm and the depth h = ℓ of the sub-volumes, which is many times larger than the average radius of a substrat even protein. Considering the H₂ O₂ molecule maximal number, the reaction initially follows a pseudo-first order kinetic with rate constant k′ = k[H₂ O₂] and the characteristic time of reaction is therefore τ = 1/k′. This time has to be compared to the characteristic time of diffusion of H₂ O₂: ${\tau }_{diff}=\frac{{\ell }^2}{6D}\approx {10}^{-6}$ s (with H₂ O₂ diffusion constant D = 2 10⁻⁹ m².s⁻¹). This comparison gives τ = 1/k′ = 1/k[H₂ O₂] ≫ 10⁻⁶ or [H₂ O₂] ≪ 10⁶/k. Even with very high rate constant such as 10⁶ M⁻¹s⁻¹, the inequality imposes [H₂ O₂] ≪ 1 M. In conclusion, while [H₂ O₂] ≪ 1 M, the diffusion within the cell is faster than the reaction rate and we do not need to consider compartmentalization.

$O_2^{•-}$ and H₂ O₂ are involved in many reactions. Of course we do not take all possible reactions into account, for instance, we do not consider the Haber-Weiss reaction, because our simulations showed no change with or without its consideration and moreover because the relevance of this reaction in vivo is questionable ([11] and [12]); actually adding the Haber-Weiss reaction, numerical simulations show that it is negligible whether H₂ O₂ concentration is under 0.1 mol⋅L⁻¹. Using published rate constants, we propose here some simplifications and approximations of the system achieved by neglecting the kinetically non-significant reaction. HO^• was studied in a previous article ([3]).

Superoxide kinetics

$O_2^{•-}$ is mainly involved in the following kinetically significant reactions:

Its production:

$$\begin{array}{c}\hfill metabolismproduction\stackrel{\phantom{(}{k}_1}{\underset{}{⟶}}{O}_2^{•-}\end{array}$$

Its dismutation by SOD (superoxide dismutase)

$$\begin{array}{c}\hfill O_2^{•-}+H^{+}\stackrel{\phantom{(}{k}_2}{\underset{SOD}{⟶}}\frac{1}{2}{H}_2{O}_2+\frac{1}{2}{O}_2\end{array}$$

These two reactions lead to the following ordinary differential equation (ODE) coming from the balance between production and dismutation by SOD:

$$\begin{array}{c}\hfill \frac{\mathrm{d}\left[O_2^{•-}\right]}{\mathrm{d}t}=k_1-k_2[SOD][O_2^{•-}]\end{array}$$

Internal hydrogen peroxide kinetics

H₂ O₂ appears significantly in the following reactions: Its productions:

$$\begin{array}{c}\hfill metabolismproduction\stackrel{\phantom{(}{k}_1^{\prime }}{\underset{}{⟶}}{H}_2{O}_2\end{array}$$

$$\begin{array}{c}\hfill O_2^{•-}+H^{+}\stackrel{\phantom{(}{k}_2}{\underset{SOD}{⟶}}\frac{1}{2}{H}_2{O}_2+\frac{1}{2}{O}_2\end{array}$$

Its dismutation by catalase (Cat) or Alkylhydroperoxidase (Ahp)

$$\begin{array}{c}\hfill H_2{O}_2\stackrel{\phantom{(}Cat}{\underset{}{⟶}}{H}_{2}O+\frac{1}{2}{O}_2\end{array}$$

$$\begin{array}{c}\hfill H_2{O}_2\stackrel{\phantom{(}Ahp}{\underset{}{⟶}}{H}_{2}O+\frac{1}{2}{O}_2\end{array}$$

Its diffusion across cell membrane

$$\begin{array}{c}\hfill H_2{O}_2\stackrel{\phantom{(}{k}_{diff}}{\underset{}{⟶}}{H}_2{O}_2{}_{out}\end{array}$$

k_diff has been calculated using the membrane permeability coefficient (P = 1.6 × 10⁻³ cm/s), the membrane surface area (A = 1.41 × 10⁻⁷ cm²) and cell volume (V = 3.2 × 10⁻¹⁵ L) given by Seaver and Imlay ([4]), therefore $k_{diff}=\frac{P\times S}{V}$.

The ODE becomes:

$$\begin{array}{ccc}\hfill \frac{\mathrm{d}\left[H_2{O}_2\right]}{\mathrm{d}t}& =& k_1^{\prime }\hfill \\ & & +\frac{1}{2}{k}_2\left[SOD\right]\left[O_2^{•-}\right]\hfill \\ & & -\frac{k_{cat}^{Ahp}\left[Ahp\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Ahp}}-\frac{k_{cat}^{Kat}\left[Cat\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Kat}}\hfill \\ & & -k_{diff}(\left[H_2{O}_2\right]-\left[H_2{O}_2\right]{}_{out})\hfill \end{array}$$

where H₂ O_2out corresponds to H₂ O₂ in the external habitat of the cell.

K_M ($K_M^{Kat}$ for catalase and $K_M^{Ahp}$ for alkylhydroperoxidase) is the Michaelis constant. k_cat ($k_{cat}^{Kat}$ for catalase and $k_{cat}^{Ahp}$ for alkylhydroperoxidase) is the turnover number, it represents the maximum number of molecules (here H₂ O₂) that an enzyme is able to convert into products per second.

External hydrogen peroxide

$$\begin{array}{c}\hfill \frac{\mathrm{d}{\left[H_2{O}_2\right]}_{out}}{\mathrm{d}t}=k_{diff}\frac{n·V_{in}}{V_{out}-n{V}_{in}}\left(\left[H_2{O}_2\right]-{\left[H_2{O}_2\right]}_{out}\right)\end{array}$$

The cell density is given by n. V_in represents the cell internal volume and V_out corresponds to the total volume. Of course, as microorganisms cannot take up more space than their medium, we have the inequality V_out−nV_in ≫ 0.

Cell density

For under 10 minutes experimental time (consistent with most of our simulation), cell density could be considered as a constant but for long time simulation we propose the logistic equation for cell growing function. The logistic equation (also called the Verhulst model) is a model of population growth first published by Pierre Verhulst ([13] and [14]). The continuous version of the Verhulst model is described by the following differential equation:

$$\begin{array}{c}\hfill \frac{\mathrm{d}n}{\mathrm{d}t}=r·n(1-\frac{n}{n_{max}})\end{array}$$

where r is the Malthusian parameter (rate of population growth) and n_max the maximum sustainable population. This differential equation gives an analytical solution:

$$\begin{array}{c}\hfill n\left(t\right)=\frac{n_0{e}^{rt}}{1+\frac{n_0}{n_{max}}(e^{rt}-1)}\end{array}$$

where n₀ is the initial density. This value depends on the experiment. We choose carrying capacity n_max = 5 × 10⁹ cell/mL. The maximal rate of growth usually shows that a growing bacterial population doubles at regular intervals near a characteristic time τ_d ≈ 20 minutes. Therefore n(t) expression also gives:

$$\begin{array}{c}\hfill n\left(t\right)=\frac{n_0{2}^{t/{\tau }_d}}{1+\frac{n_0}{n_{max}}(2^{t/{\tau }_d}-1)}\end{array}$$

where r = ln(2)/τ_d.

Nevertheless this characteristic time depends on cell history and stress. For example, even 0.2 mM of H₂ O₂ when added to a logarithmically growing E. coli population is enough to generate an immediate decrease in the number of viable cells. This phenomenon is transient and the original number of viable cells is recovered only about 40 minutes after the occurrence of the sub-lethal stress ([15]). This transient phenomenon is mirrored at the population level by a lag phase in which optical density remains almost constant for about 40 minutes. A fraction dies, and then the remaining bacteria resume growth so that the number of viable cells reaches the original number. For instance Chang et al. ([16]) also report a lag phase of about 40 minutes after an addition of 1.5 mM of H₂ O₂. In order to take into account this phenomenon we consider that τ_d → ∞ if t < 40 minutes so that n(t < 40 min) = constant after H₂ O₂ oxidative stress.

We were not concerned with stationary phase because no experiment carried out in this work reached the maximum sustainable population.

Kinetic constants

The kinetic constants used in this work are gathered in Table 1 according to Imlay and Fridovich ([17]) and Seaver and Imlay ([5] and [4]).

Table 1. Kinetic constants used to describe H₂ O₂ evolution.

Kinetic constants
k1	5.7 × 10−6 mol⋅L−1⋅s−1
k2[SOD]	2.8 × 104 s−1
k2	1.5 × 109 mol−1⋅L⋅s−1
Vin	3.2 × 10−15 L
$k_1^{\prime }$	12 × 10−6 mol⋅L−1⋅s−1
$k_{cat}^{Ahp}\left[Ahp\right]$	6.6 × 10−4 mol⋅L−1⋅s−1
$K_M^{Ahp}$	1.2 × 10−6 mol⋅L−1
$k_{cat}^{Kat}\left[Cat\right]$	4.9 × 10−1 mol⋅L−1⋅s−1
$K_M^{Kat}$	5.9 × 10−3 mol⋅L−1
kdiff	70 s−1

Numerical simulations

All numerical simulations were carried out using the MATLAB ODE solver ode15s for stiff differential equations. The multistep solver ode15s is a variable order solver based on the numerical differentiation formulas.

Results and Discussion

This section presents the analytical study of the dynamic system. This analysis will provide us with insight into the kinetic parameters significantly important for the dynamics of ROS.

Internal hydrogen peroxide

Without exogenous stress

In the wild-type strain, $O_2^{•-}$ equilibrium is rapidly reached. Indeed the characteristic time of $O_2^{•-}$ evolution is 1/k₂[SOD] ≈ 35 μs. Therefore we can consider $O_2^{•-}$ as a constant and we can assume that $\left[O_2^{•-}\right]\left(t\right)\approx {\left[O_2^{•-}\right]}_{\infty }$ (S1 File supporting information data for demonstration).

So in terms of changes to internal H₂ O₂ concentration, we approach

$k_1^{\prime }+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.k_2\left[SOD\right]\left[O_2^{•-}\right]\approx k_1^{\prime }+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.k_1$ because $\left[O_2^{•-}\right]\approx {\left[O_2^{•-}\right]}_{\infty }$ Let us call $k_1^{\prime }+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.k_1=k_{prod}$.

That is a first point, $O_2^{•-}$ dismutation by SOD involved nearly an increase of 25% in the endogenous H₂ O₂ production.

Moreover, in the absence of exogenous H₂ O₂, we can consider that:

$$\begin{array}{c}\hfill \left[H_2{O}_2\right]\ll K_M^{Ahp},K_M^{Cat}\end{array}$$

so the differential equation system can be simplified to a linear system:

$$\begin{array}{c}\hfill \frac{\mathrm{d}\left[H_2{O}_2\right]}{\mathrm{d}t}=k_{prod}-\left(\frac{k_{cat}^{Ahp}\left[Ahp\right]}{K_M^{Ahp}}+\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}\right)\left[H_2{O}_2\right]-k_{diff}\left(\left[H_2{O}_2\right]-{\left[H_2{O}_2\right]}_{out}\right)\end{array}$$

$$\begin{array}{c}\hfill \frac{\mathrm{d}{\left[H_2{O}_2\right]}_{out}}{\mathrm{d}t}=k_{diff}^{\prime }\left(\left[H_2{O}_2\right]-{\left[H_2{O}_2\right]}_{out}\right)\end{array}$$

with:

$$\begin{array}{c}\hfill k_{diff}^{\prime }=k_{diff}\frac{n·V_{in}}{V_{out}-n{V}_{in}}\end{array}$$

Let us call $\frac{k_{cat}^{Ahp}\left[Ahp\right]}{K_M^{Ahp}}+\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}=k_{enz}$, then the differential equation system can be written with a matrix structure:

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}\left[H_2{O}_2\right]\\ {\left[H_2{O}_2\right]}_{out}\end{array}\right)=\left(\begin{array}{c}{k}_{prod}\\ 0\end{array}\right)+\left(\begin{array}{cc}-\left(k_{enz}+k_{diff}\right)& k_{diff}\\ {k^{\prime }}_{diff}& -{k^{\prime }}_{diff}\end{array}\right)\left(\begin{array}{c}\left[H_2{O}_2\right]\\ {\left[H_2{O}_2\right]}_{out}\end{array}\right)\end{array}$$

The matrix eigenvalues are λ₁ > λ₂:

$$\begin{array}{c}\hfill {\lambda }_1=\frac{-\left(k_{enz}+k_{diff}+{k^{\prime }}_{diff}\right)+\sqrt{{\left(k_{enz}+k_{diff}+{k^{\prime }}_{diff}\right)}^2-4k_{enz}{k^{\prime }}_{diff}}}{2}<0\end{array}$$

$$\begin{array}{c}\hfill {\lambda }_2=\frac{-\left(k_{enz}+k_{diff}+{k^{\prime }}_{diff}\right)-\sqrt{{\left(k_{enz}+k_{diff}+{k^{\prime }}_{diff}\right)}^2-4k_{enz}{k^{\prime }}_{diff}}}{2}<0\end{array}$$

According to the value of the reaction rate constant, we can make the following approximation: ${\lambda }_1\approx -\frac{k_{enz}}{\left(k_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }$ and λ₂ ≈ −(k_enz + k_diff).

The full matrix V with columns corresponding to the eigenvectors is:

$$\begin{array}{c}\hfill V=\left(\begin{array}{cc}{k^{\prime }}_{diff}+{\lambda }_1& {k^{\prime }}_{diff}+{\lambda }_1\\ {k^{\prime }}_{diff}& {k^{\prime }}_{diff}\end{array}\right)\end{array}$$

The system becomes $\left(\begin{array}{c}\left[H_2{O}_2\right]\\ {\left[H_2{O}_2\right]}_{out}\end{array}\right)=V\left(\begin{array}{cc}A{e}^{{\lambda }_{1}t}& 0\\ 0& B{e}^{{\lambda }_{2}t}\end{array}\right)$

The resolution shows a bi-exponential expression:

$$\begin{array}{c}\hfill \left[H_2{O}_2\right]=\left({k^{\prime }}_{diff}+{\lambda }_1\right)A{e}^{{\lambda }_{1}t}+\left({k^{\prime }}_{diff}+{\lambda }_2\right)B{e}^{{\lambda }_{2}t}+\frac{k_{prod}}{k_{enz}}\end{array}$$ (1)

$$\begin{array}{c}\hfill {\left[H_2{O}_2\right]}_{out}=k_{diff}^{\prime }A{e}^{{\lambda }_{1}t}+k_{diff}^{\prime }B{e}^{{\lambda }_{2}t}+\frac{k_{prod}}{k_{enz}}\end{array}$$ (2)

with

$$\begin{array}{c}\hfill A=\frac{\left({\left[H_2{O}_2\right]}_0-\frac{k_{prod}}{k_{enz}}\right){k^{\prime }}_{diff}-\left({\left[H_2{O}_2\right]}_{out0}-\frac{k_{prod}}{k_{enz}}\right)\left({k^{\prime }}_{diff}+{\lambda }_2\right)}{\left({\lambda }_1-{\lambda }_2\right){k^{\prime }}_{diff}}\end{array}$$ (3)

$$\begin{array}{c}\hfill B=\frac{\left({\left[H_2{O}_2\right]}_0-\frac{k_{prod}}{k_{enz}}\right){k^{\prime }}_{diff}-\left({\left[H_2{O}_2\right]}_{out0}-\frac{k_{prod}}{k_{enz}}\right)\left({k^{\prime }}_{diff}+{\lambda }_1\right)}{\left({\lambda }_2-{\lambda }_1\right){k^{\prime }}_{diff}}\end{array}$$ (4)

In this first approach, [H₂ O₂]₀ = 0 and [H₂ O₂]_out0 = 0: initial concentrations are taken to be zero.

From the very beginning, $\left[H_2{O}_2\right]\approx \left({k^{\prime }}_{diff}+{\lambda }_1\right)A+\left({k^{\prime }}_{diff}+{\lambda }_2\right)B{e}^{{\lambda }_{2}t}+\frac{k_{prod}}{k_{enz}}$ as e^λ₁t ≈ 1 because |λ₁| ≈ 0.

Therefore $A\approx -\frac{k_{prod}}{k_{enz}{k^{\prime }}_{diff}}$ and $B=\frac{k_{prod}}{{\left(k_{enz}+k_{diff}\right)}^2}$

$$\begin{array}{c}\hfill k_{diff}^{\prime }+{\lambda }_1=k_{diff}^{\prime }-\frac{k_{enz}}{\left(k_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }=\frac{k_{diff}}{\left(k_{enz}+k_{diff}\right)}{k}_{diff}^{\prime };\end{array}$$

$$\begin{array}{c}\hfill k_{diff}^{\prime }+{\lambda }_2\approx -\left(k_{enz}+k_{diff}\right);\end{array}$$

In conclusion: $\left[H_2{O}_2\right]\approx \frac{k_{prod}}{k_{enz}+k_{diff}}\left(1-e^{-\left(k_{enz}+k_{diff}\right)t}\right)$

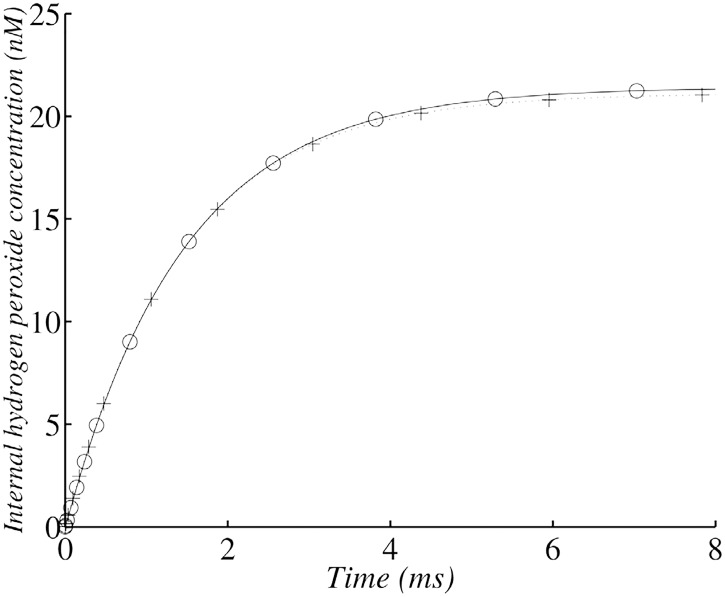
The first plateau (in Fig 1) corresponds to the compromise between production and consumption, but consumption now also depends on diffusion across cell membrane. Indeed, the value of this first plateau is approximately $\frac{k_{prod}}{k_{enz}+k_{diff}}$.

Fig 1. Changes in internal H₂ O₂ concentration in the wild-type strain with 10⁷ cells ml⁻¹.

(+) corresponds to the analytical solution of internal H₂ O₂ evolution according to the simplified system and (∘)) corresponds to the whole model solved with numerical methods.

The numerical values are ([4]):

$$\begin{array}{c}\hfill k_{enz}=633{\text{s}}^{-1}\text{with}\frac{k_{cat}^{Ahp}\left[Ahp\right]}{K_M^{Ahp}}=550{\text{s}}^{-1};\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}=83{\text{s}}^{-1};k_{diff}=70{\text{s}}^{-1}\end{array}$$

These values indicate that diffusion across the cell membrane accounts for approximately 10% of the H₂ O₂ eliminated, a level of activity close to that of Cat activity (≈12%). As previously reported ([5]), Ahp was identified as the principal scavenger (≈78%).

The first plateau concentration for H₂ O₂ is therefore $\frac{k_{prod}}{k_{enz}+k_{diff}}\approx 21$ nM.

For instance, in an Ahp(-) mutant without Cat induction, this concentration would be $\frac{k_{prod}}{\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}+k_{diff}}\approx 97$ nM.

After this transition step, we had e^λ₂t ≈ 0. The change in H₂ O₂ concentration therefore follows this equation:

$$\begin{array}{c}\hfill \left[H_2{O}_2\right]=\frac{k_{prod}}{k_{enz}}-\frac{k_{prod}}{k_{enz}}\frac{k_{diff}}{\left(k_{enz}+k_{diff}\right)}{e}^{{\lambda }_{1}t}\end{array}$$

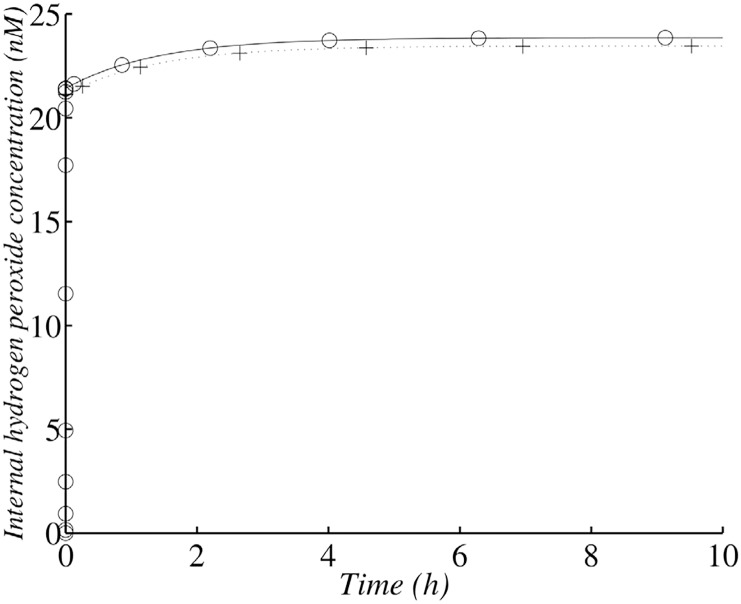
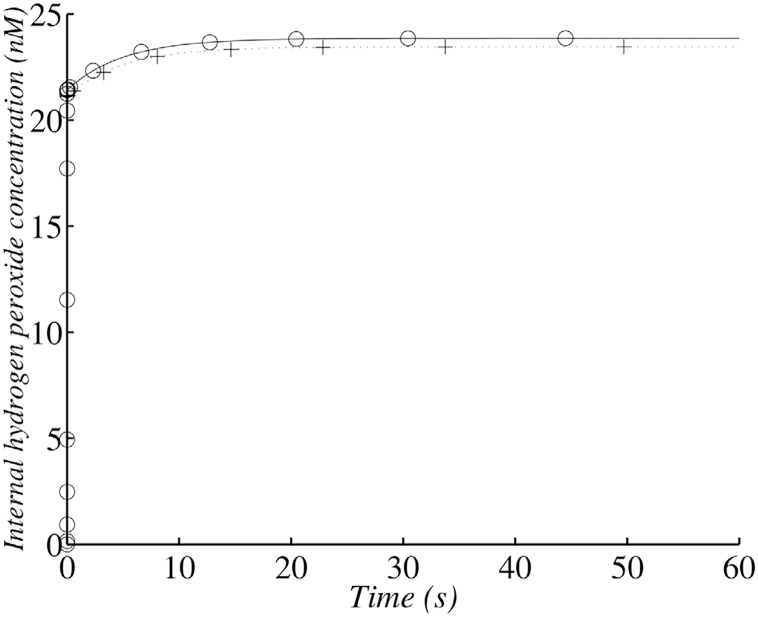
This second step is slower and depends on the number of cells, with the final steady-state concentration of H₂ O₂ reached more rapidly for denser cell populations (Figs 2 and 3).

Fig 2. Changes in internal H₂ O₂ concentration in the wild-type strain with 10⁶ cells ml⁻¹.

(+) corresponds to the analytical solution according to the simplified system and (∘)) corresponds to the whole model and a numerical solution.

Fig 3. Changes in H₂ O₂ concentration in the wild-type strain with 10⁹ cells ml⁻¹.

(+) corresponds to the analytical solution according to the simplified system and (∘)) corresponds to the whole model and a numerical solution.

The final steady-state value is ${\left[H_2{O}_2\right]}_{\infty }=\frac{k_{prod}}{k_{enz}}\approx 23.5$ nM and is not dependent on cell number. This value is close to that obtained by numerical simulation (23.9 nM) and to that proposed by Imlay (20 nM) ([4]).

For instance, in an Ahp(-) mutant without Cat induction, this value would be $\frac{k_{prod}{K}_M^{Kat}}{k_{cat}^{Kat}\left[Cat\right]}\approx 179$ nM (identical to the numerical simulation value and close to the value of 100 nM proposed by Seaver and Imlay ([4]).

This second step in the change in H₂ O₂ concentration depends on ${\lambda }_1\approx -\frac{k_{enz}}{\left(k_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }$, which depends on cell concentration via the $k_{diff}^{\prime }$.

The results are summarized in Table 2.

Table 2. H₂ O₂ steady-state concentration.

[H2 O2] (nmol L−1)	In this work	Seaver, Imlay [4]
Wild type	24	21
HPI+ HPII+ Ahp- (AhpCF(a))	179	100
HPI- HPII- Ahp+ (KatEKatG)	28	23

At steady state, the internal concentration is shown for cells in LB at 37°C.

(a) without induced HPI levels.

With exogenous stress

We propose linear approximations of Michaelis-Menten kinetics. Internal H₂ O₂ concentration approximately follows the law outlined below. Let us consider an experiment involving the addition of exogenous H₂ O₂. The initial ROS concentrations in the cell are taken to be the steady-state values obtained without exogenous H₂ O₂. The system requires modification as follows:

$$\begin{array}{ccc}\hfill \frac{\mathrm{d}\left[H_2{O}_2\right]}{\mathrm{d}t}& =& k_1^{\prime }+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.k_2\left[SOD\right]\left[O_2^{•-}\right]\hfill \\ & & -\frac{k_{cat}^{Ahp}\left[Ahp\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Ahp}}-\frac{k_{cat}^{Kat}\left[Cat\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Kat}}\hfill \\ & & -k_{diff}\left(\left[H_2{O}_2\right]-{\left[H_2{O}_2\right]}_{out}\right)\hfill \\ & & \\ \hfill \frac{\mathrm{d}{\left[H_2{O}_2\right]}_{out}}{\mathrm{d}t}& =& k_{diff}\frac{n·V_{in}}{V_{out}-n{V}_{in}}\left(\left[H_2{O}_2\right]-{\left[H_2{O}_2\right]}_{out}\right)\hfill \end{array}$$

As the system is nonlinear there is no analytical solution so with a view to solving the system, we had to compare the value obtained for the internal concentration of H₂ O₂ with the K_M values of Ahp and Cat to simplify the Michaelis-Menten expression. Moreover, cell behavior (and thus the dynamic system) depends on the comparison of internal H₂ O₂ concentration with the K_M values of Ahp and Cat. This comparison is essential to simplify the system into a linear one, which will then be solvable. This kind of study is frequently carried out and provides useful insight into the workings of systems. For example, Polynikis et al. ([18]) compared different modeling approaches (complete nonlinear model, simplified piecewise linear model etc.) for gene regulatory networks using Hill functions, a general form of the Michaelis-Menten equation.

To approximate the Michaelis-Menten hyperbole into a piecewise linear function, let us first examine the contribution of the two enzymes.

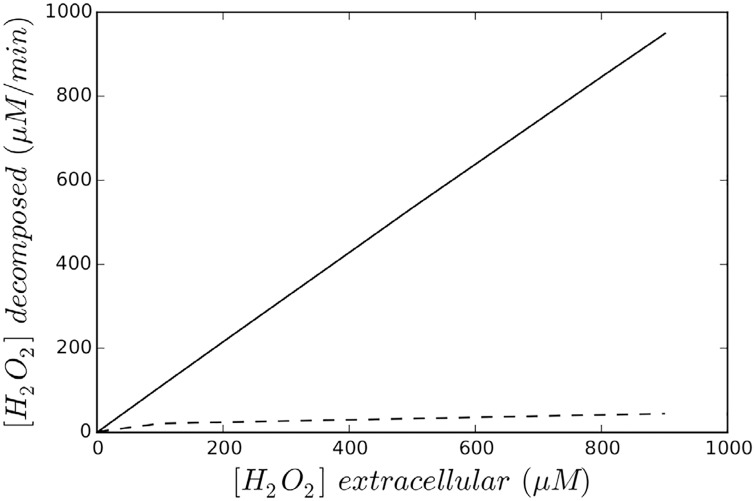
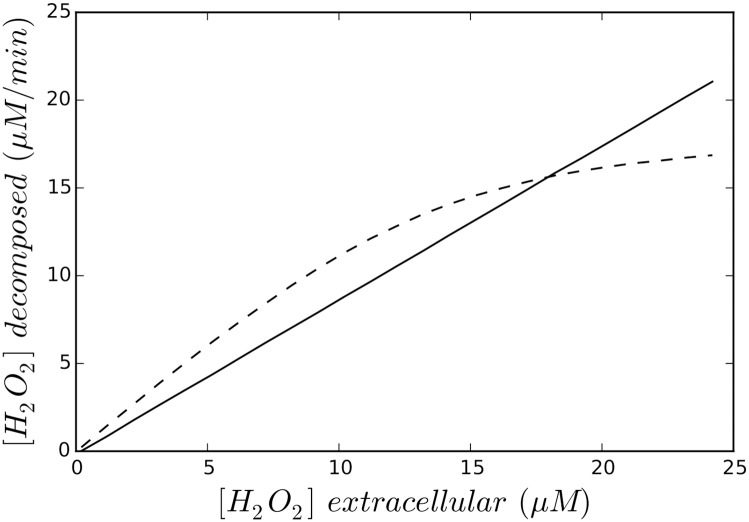
The rate (see Fig 4) followed the same pattern of change as that presented by Seaver and Imlay ([5]). Ahp was the leading scavenger in conditions of 17 μM exogenous H₂ O₂ (see intersection point in Fig 5).

Fig 4. Kinetics of exogenous H₂ O₂ decomposition for 1.5 × 10⁸ E. coli cells ml⁻¹.

The dotted line corresponds to the Cat(-) mutant and solid line corresponds to the Ahp (-) mutant.

Fig 5. Kinetics of exogenous H₂ O₂ decomposition for 1.5 × 10⁸ E. coli cells ml⁻¹.

The dotted line corresponds to the Cat(-) mutant and solid line corresponds to the Ahp (-) mutant (higher magnification for Fig 4).

We can consider that, in the presence of less than 10 μM H₂ O₂, Ahp activity is linear (Fig 5) and that Cat activity is linear at concentrations below 10 mM (due to its K_M value). At H₂ O₂ concentrations of more than 30 μM, Ahp activity is saturated.

According to the Michaelis-Menten equation, we should consider Ahp activity to be linear when $\left[H_2{O}_2\right]⪡K_M^{Ahp}\approx 1$ μM, but linearity was observed when [H₂ O₂]_out < 10 μM. It is unclear why there is a difference of one order of magnitude between exogenous [H₂ O₂]_out and internal [H₂ O₂] at the limit of linearity.

Such a difference was reported in another experiment presented by Seaver and Imlay ([4]) while studying H₂ O₂ fluxes.

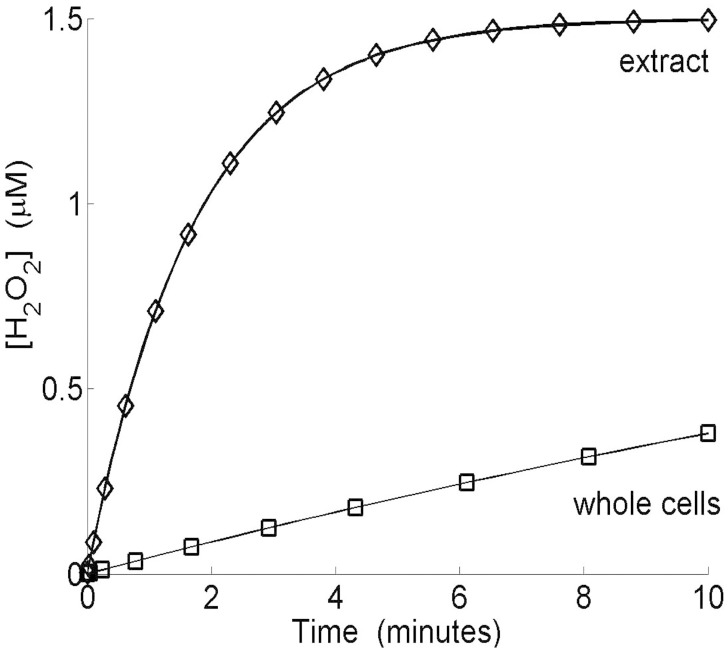
In this experiment, whole cells seemed to scavenge H₂ O₂ less efficiently than cell extracts. The cell membrane slows the entry of H₂ O₂, resulting in lower rates of decomposition. It also protects cells against high H₂ O₂ concentrations, by decreasing the maximum value of H₂ O₂ concentration. This phenomenon is described in more detail below. The simulation (Fig 6) for extract was modeled by eliminating membrane diffusion and the metabolism associated with ROS production. There is a perfect match between numerical simulation and the experimental results of Seaver and Imlay.

Fig 6. In silico, breakdown of exogenous H₂ O₂ by whole cells (Ahp(-) mutant) or cell extract. Simulation runs with 4 × 10⁶ cells ml⁻¹.

Moreover, Seaver and Imlay ([5]) observed that an Ahp(-) mutant contained seven times as much total Cat as wild-type cells. We therefore used the same ratio.

Two situations can be distinguished based on these previous observations.

In the first case, $\left[H_2{O}_2\right]⪡K_M^{Ahp}$ corresponds to [H₂ O₂]_out < 10 μM and to $\left[H_2{O}_2\right]⪡K_M^{Cat}$. The system approaches Michaelis-Menten terms as follows:

$$\begin{array}{ccc}\hfill \frac{k_{cat}^{Ahp}\left[Ahp\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Ahp}}+\frac{k_{cat}^{Kat}\left[Cat\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Kat}}& \approx & \frac{k_{cat}^{Ahp}[Ahp]}{K_M^{Ahp}}+\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}\left[H_2{O}_2\right]\hfill \\ & =& k_{enz}\left[H_2{O}_2\right]\hfill \end{array}$$

In the second case, if $\left[H_2{O}_2\right]\gg K_M^{Ahp}$, corresponding to [H₂ O₂]_out > 30 μM and to $\left[H_2{O}_2\right]⪡K_M^{Cat}$, then the system approaches Michaelis-Menten terms as follows:

$$\begin{array}{ccc}\hfill \frac{k_{cat}^{Ahp}\left[Ahp\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Ahp}}+\frac{k_{cat}^{Kat}\left[Cat\right]\left[H_2{O}_2\right]}{\left[H_2{O}_2\right]+K_M^{Kat}}& \approx & \left(k_{cat}^{Ahp}[Ahp]+\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}\right)[H_2{O}_2]\hfill \\ & =& k_{cat}^{Ahp}\left[Ahp\right]+k_{enz}^{\prime }\left[H_2{O}_2\right]\hfill \end{array}$$

where $\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}=k_{enz}^{\prime }$.

Then we examine Ahp activity with a micromolar exogenous H₂ O₂ concentration. In the first case ($\left[H_2{O}_2\right]⪡K_M^{Ahp}$ and $\left[H_2{O}_2\right]⪡K_M^{Cat}$), the differential equation system appears to be the same as that without exogenous H₂ O₂, but [H₂ O₂]_out ≠ 0. As ${\left[H_2{O}_2\right]}_0=\frac{k_{prod}}{k_{enz}}$, the constants A and B can be simplified as follows:

$$\begin{array}{c}\hfill A=\frac{-\left({\left[H_2{O}_2\right]}_{out0}-\frac{k_{prod}}{k_{enz}}\right)\left({k^{\prime }}_{diff}+{\lambda }_2\right)}{\left({\lambda }_1-{\lambda }_2\right){k^{\prime }}_{diff}}\end{array}$$

and

$$\begin{array}{c}\hfill B=\frac{-\left({\left[H_2{O}_2\right]}_{out0}-\frac{k_{prod}}{k_{enz}}\right)\left({k^{\prime }}_{diff}+{\lambda }_1\right)}{\left({\lambda }_2-{\lambda }_1\right){k^{\prime }}_{diff}}\end{array}$$

Moreover as ${\lambda }_1\approx -\frac{k_{enz}}{\left(k_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }$ and λ₂ ≈ −(k_enz + k_diff) with |λ₁| < <|λ₂| and |k′_diff| < <|λ₂|

$$\begin{array}{c}\hfill \left({k^{\prime }}_{diff}+{\lambda }_1\right)A\approx -\left({k^{\prime }}_{diff}+{\lambda }_2\right)\end{array}$$

$$\begin{array}{c}\hfill B\approx \left({\left[H_2{O}_2\right]}_{out0}-\frac{k_{prod}}{k_{enz}}\right)\frac{k_{diff}}{k_{diff}+k_{enz}}\end{array}$$

therefore:

$$\begin{array}{c}\hfill [H_2{O}_2]=\left({\left[H_2{O}_2\right]}_{out0}-\frac{k_{prod}}{k_{enz}}\right)\frac{k_{diff}}{k_{diff}+k_{enz}}\left(e^{{\lambda }_{1}t}-e^{{\lambda }_{2}t}\right)+\frac{k_{prod}}{k_{enz}}\end{array}$$

This bi-exponential function shows that changes in internal H₂ O₂ concentration follow two phases. There is a first phase, with a large rate constant −λ₂ ≈ k_enz + k_diff corresponding to the scavenging process, followed by a much slower second phase, with a low rate constant −λ₁ > 0 corresponding to the diffusion from the external H₂ O₂ into the cell. This second phase is faster for larger numbers of cells because $k_{diff}^{\prime }$ is highly dependent on cell concentration.

$-{\lambda }_1\approx \frac{k_{enz}}{\left(k_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }$ and as k_enz ≫ k_diff we can approach $-{\lambda }_1\approx k_{diff}^{\prime }$.

This function therefore reaches a maximum as $\frac{\mathrm{d}\left[H_2{O}_2\right]}{\mathrm{d}t}=0$ for:

$$\begin{array}{c}\hfill t_{max}=\frac{1}{{\lambda }_2-{\lambda }_1}ln\left(\frac{{\lambda }_1}{{\lambda }_2}\right)\approx \frac{1}{\left(k_{enz}+k_{diff}\right)}ln\left(\frac{{\left(k_{enz}+k_{diff}\right)}^2}{k_{enz}{k^{\prime }}_{diff}}\right)\end{array}$$

This time is weakly dependent on cell numbers. For example, t_max ≈ 18 ms with 10⁷ cells ml⁻¹ and 11 ms with 10⁹ cells ml⁻¹.

The maximum internal H₂ O₂ concentration is approximately:

$$\begin{array}{c}\hfill {\left[H_2{O}_2\right]}_{max}\approx \left({\left[H_2{O}_2\right]}_{out0}-\frac{k_{prod}}{k_{enz}}\right)\frac{k_{diff}}{k_{diff}+k_{enz}}+\frac{k_{prod}}{k_{enz}}\end{array}$$

and as ${\left[H_2{O}_2\right]}_{out0}\gg \frac{k_{prod}}{k_{enz}}={\left[H_2{O}_2\right]}_{\infty }$ which can be approached by:

$$\begin{array}{c}\hfill {\left[H_2{O}_2\right]}_{max}\approx \frac{k_{diff}{\left[H_2{O}_2\right]}_{out0}}{k_{diff}+k_{enz}}\end{array}$$

therefore

$$\begin{array}{c}\hfill \frac{{\left[H_2{O}_2\right]}_{max}}{{\left[H_2{O}_2\right]}_{out0}}\approx \frac{1}{1+k_{enz}/k_{diff}}\approx \frac{1}{9}\end{array}$$

The balance between the elimination processes in the value of the maximal internal H₂ O₂ concentration is due to:

$$\begin{array}{c}\hfill \frac{k_{cat}^{Ahp}\left[Ahp\right]}{K_M^{Ahp}\left(k_{enz}+k_{diff}\right)}\approx 78\%\text{to}\text{Ahp}\end{array}$$

$$\begin{array}{c}\hfill \frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}\left(k_{enz}+k_{diff}\right)}\approx 12\%\text{to}\text{Cat}\end{array}$$

and

$$\begin{array}{c}\hfill \frac{k_{diff}}{k_{enz}+k_{diff}}\approx 10\%\hfill \\ \hfill \text{to elimination by diffusion throughout cell membrane}\hfill \end{array}$$

The maximal value of internal H₂ O₂ concentration is almost one tenth the initial exogenous H₂ O₂ concentration. This phenomenon reflects the role of the cell membrane in limiting diffusion. The need to diffuse across the cell membrane limits the influx of exogenous H₂ O₂ and this process is highly effective at low exogenous H₂ O₂ concentrations. The difference of one order of magnitude between exogenous [H₂ O₂]_out and internal [H₂ O₂] arises because the membrane creates a rate-limiting step.

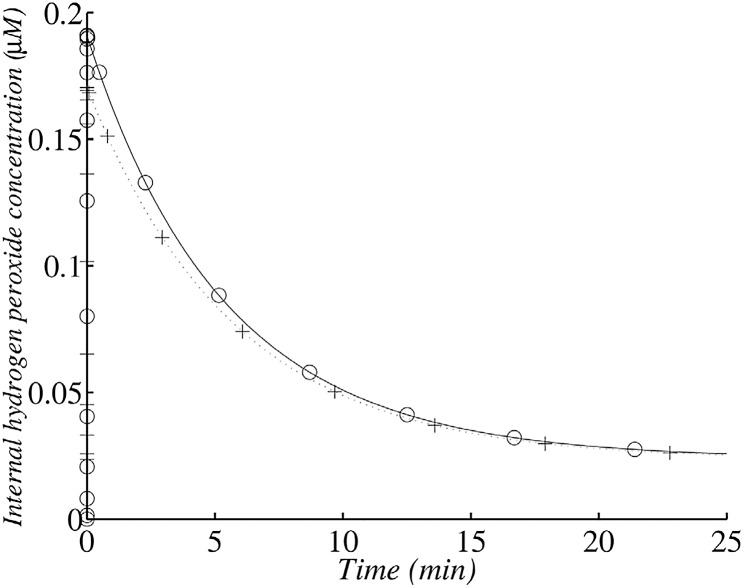
To illustrate this, we will investigate cell behaviour in the presence of 1.5 μM exogenous H₂ O₂.

After its peak value (Fig 7), internal H₂ O₂ concentration decreases because of scavenging, but diffusion across cell membrane is the process which limits the rate of H₂ O₂ disappearance, therefore H₂ O₂ decrease is slow. The membrane creates a rate-limiting step.

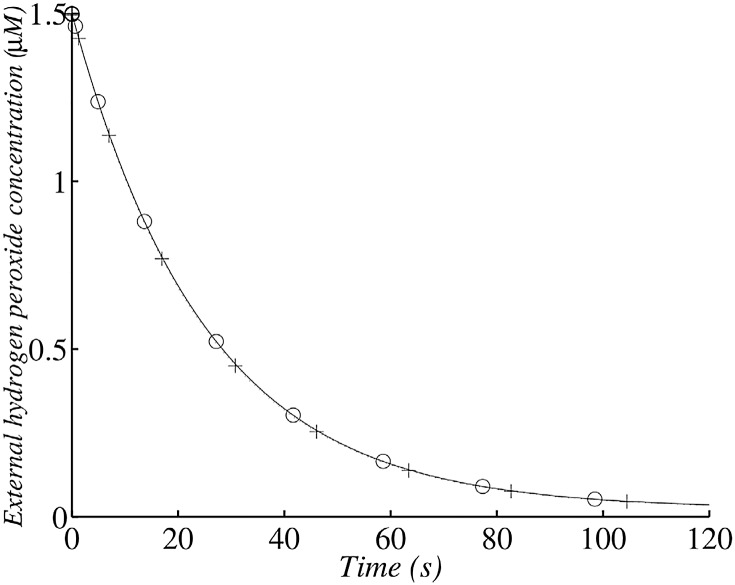
Fig 7. Changes in internal H₂ O₂ concentration in the wild type after the addition of 1.5 μM exogenous H₂ O₂ with 1.45 × 10⁷ cells ml⁻¹.

(+) corresponds to the analytical solution according to the simplified system and (∘) corresponds to the numerical solution of the whole model. The simulation was run with 1.45 × 10⁷ cells ml⁻¹ (corresponding to an OD₆₀₀ value of 0.1).

The maximal value is the approximate value of the first plateau proposed by Gonzalez-Flecha and Demple ([19]). It corresponds to the ratio of the rate of H₂ O₂ influx by diffusion to levels of scavenging and elimination by diffusion.

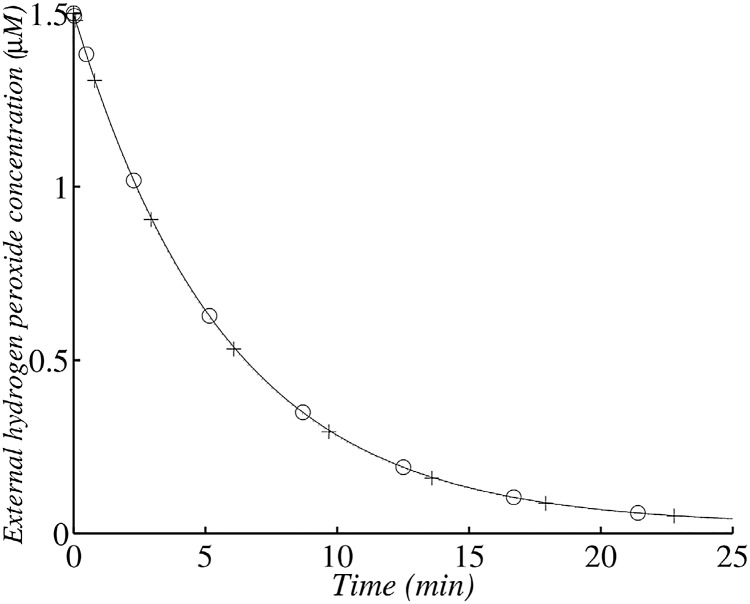
The experiments of Seaver and Imlay ([5]) showed that even non-induced cells scavenged micromolar concentrations of exogenous H₂ O₂ very quickly. For example, in a culture corresponding to 0.1 OD₆₈₀ unit (corresponding to around 1.5 × 10⁷ cells ml⁻¹), they found that the half time of H₂ O₂ in the medium was only 3.5 minutes, and that in a culture of 1.0 OD unit it was 20 s.

The exogenous H₂ O₂ concentration approximately follows the law outlined below:

$$\begin{array}{c}\hfill {\left[H_2{O}_2\right]}_{out}=\left({\left[H_2{O}_2\right]}_0-\frac{k_{prod}}{k_{enz}}\right)e^{{\lambda }_{1}t}+\frac{k_{prod}}{k_{enz}}\end{array}$$

where

$$\begin{array}{c}\hfill {\lambda }_1\approx -\frac{k_{enz}}{\left(k_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }\approx k_{diff}^{\prime }\end{array}$$

Its exponential decrease depends on the $k_{diff}^{\prime }$ rate constant, which is strongly dependent on cell numbers. The half-life of H₂ O₂ in the medium is approximately $t_{1/2}\approx \frac{ln2}{k_{diff}^{\prime }}$ and is a decreasing function of cell number. So, with an OD₆₈₀ of 0.1 (Fig 8) we find that t_1/2 ≈ 210 s (3.5 min) and with an OD₆₈₀ of 1 we find that t_1/2 ≈ 21 s (Fig 9). A comparison of the experimental data and the analytical results indicates that our model describes the change in H₂ O₂ correctly.

Fig 8. Changes in external H₂ O₂ concentration in the wild type after the addition of 1.5 μM exogenous H₂ O₂ with 1.45 × 10⁷ cells ml⁻¹.

(+) corresponds to the analytical solution according to the simplified system and (∘)) corresponds to the numerical solution of the whole model. The simulation was run with 1.45 × 10⁷ cells ml⁻¹ (corresponding to an OD₆₈₀ value of 0.1).

Fig 9. Changes in external H₂ O₂ concentration in the wild type after the addition of 1.5 μM exogenous H₂ O₂ with 2 × 10⁸ cells ml⁻¹.

(+) corresponds to the analytical solution according to the simplified system and (∘)) corresponds to the numerical solution of the whole model. The simulation was run with 2 × 10⁸ cells ml⁻¹ (corresponding to an OD₆₈₀ value of 0.1).

Finally we examine Ahp activitys, with a high H₂ O₂ concentration. In the second case, when $\left[H_2{O}_2\right]\gg K_M^{Ahp}$, corresponding to [H₂ O₂]_out > 30 μM, the differential equation system can be written with a matrix structure:

$$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}\left[H_2{O}_2\right]\\ {\left[H_2{O}_2\right]}_{out}\end{array}\right)=\left(\begin{array}{c}{k^{\prime }}_{prod}\\ 0\end{array}\right)+\left(\begin{array}{cc}-\left({k^{\prime }}_{enz}+k_{diff}\right)& k_{diff}\\ {k^{\prime }}_{diff}& -{k^{\prime }}_{diff}\end{array}\right)\left(\begin{array}{c}\left[H_2{O}_2\right]\\ {\left[H_2{O}_2\right]}_{out}\end{array}\right)\end{array}$$

where $k_{prod}^{\prime }=k_1^{\prime }+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.k_1-k_{cat}^{Ahp}\left[Ahp\right]$ is the usual production reduced by Ahp activity on saturation; and $k_{enz}^{\prime }=\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}$ (only Cat follows linear kinetics)

The study is similar to the previous one and internal H₂ O₂ concentration can be expressed as follows:

$$\begin{array}{c}\hfill [H_2{O}_2]=\left({\left[H_2{O}_2\right]}_{out0}-\frac{{k^{\prime }}_{prod}}{{k^{\prime }}_{enz}}\right)\frac{k_{diff}}{k_{diff}+{k^{\prime }}_{enz}}\left(e^{{{\lambda }^{\prime }}_{1}t}-e^{{{\lambda }^{\prime }}_{2}t}\right)+\frac{{k^{\prime }}_{prod}}{{k^{\prime }}_{enz}}\end{array}$$

with the eigenvalue ${\lambda }_1\approx -\frac{{k^{\prime }}_{enz}}{\left({k^{\prime }}_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }$ and λ₂ ≈ −(k′_enz + k_diff)

The maximum will be ${\left[H_2{O}_2\right]}_{max}\approx \frac{k_{diff}{\left[H_2{O}_2\right]}_{out0}}{k_{diff}+{k^{\prime }}_{enz}}$. With large concentrations of exogenous H₂ O₂, ${\left[H_2{O}_2\right]}_{max}\approx \frac{k_{diff}{\left[H_2{O}_2\right]}_{out0}}{k_{diff}+\frac{k_{cat}^{Kat}\left[Cat\right]}{K_M^{Kat}}}$. This corresponds to the ratio of the rate of H₂ O₂ influx by diffusion to its elimination by Cat or by diffusion only.

This expression shows that the ratio between the initial exogenous H₂ O₂ concentration and the maximal internal H₂ O₂ concentration in the cell is:

$$\begin{array}{c}\hfill \frac{{\left[H_2{O}_2\right]}_{max}}{{\left[H_2{O}_2\right]}_{out0}}\approx \frac{1}{1+\frac{k_{cat}^{Kat}\left[Cat\right]}{k_{diff}{K}_M^{Kat}}}\approx \frac{1}{2.2}(*)\end{array}$$

The contribution of each elimination process to the value of the maximal internal H₂ O₂ concentration is:

$$\begin{array}{c}\hfill \frac{{k^{\prime }}_{enz}}{{k^{\prime }}_{enz}+k_{diff}}\approx 55\%\text{to Cat}\hfill \\ \hfill \text{and}\frac{k_{diff}}{{k^{\prime }}_{enz}+k_{diff}}\approx 45\%\text{to elimination by diffusion across the cell membrane}\hfill \end{array}$$

We notice that: $\frac{{\left[H_2{O}_2\right]}_{max}}{{\left[H_2{O}_2\right]}_{out0}}$ is equal to the ratio of elimination by diffusion across the membrane to the sum diffusion and scavenging. Of course, without membrane this ratio will equal 1, so thanks to membrane, enzymes have to face less H₂ O₂. Moreover, at high exogenous H₂ O₂ concentrations, this ratio is quite different from the one (i.e. 1/9) obtained at low concentration.

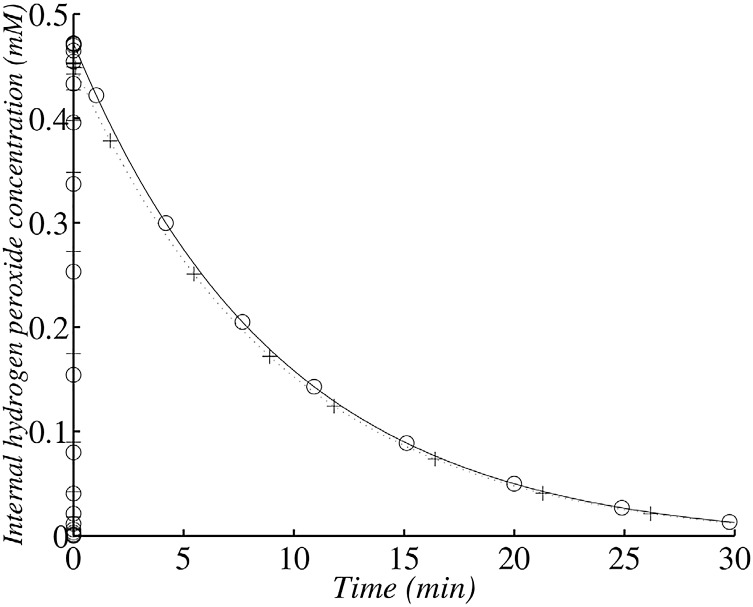
For instance, with an initial H₂ O₂ exogenous concentration [H₂ O₂]_out0 = 1 mM, we obtain [H₂ O₂]_max ≈ 0.45 mM (Fig 10). The maximal value is lower than the exogenous concentration because of diffusion and Cat activity, in this case Ahp is saturated and therefore plays a less important role.

Fig 10. Changes in internal H₂ O₂ concentration in the wild type after the addition of 1 mM exogenous H₂ O₂ with 1.45 × 10⁷ cells ml⁻¹.

(+) corresponds to the analytical solution according to the simplified system and (∘)) corresponds to the numerical solution of the whole model.

The exogenous H₂ O₂ concentration approximately follows the law outlined below:

$$\begin{array}{c}\hfill {\left[H_2{O}_2\right]}_{out}=\left({\left[H_2{O}_2\right]}_0-\frac{k_{prod}}{k_{enz}}\right)e^{{{\lambda }^{\prime }}_{1}t}+\frac{k_{prod}}{k_{enz}}\end{array}$$

where

$$\begin{array}{c}\hfill {\lambda }_1^{\prime }\approx -\frac{{k^{\prime }}_{enz}}{\left({k^{\prime }}_{enz}+k_{diff}\right)}{k}_{diff}^{\prime }\ne k_{diff}^{\prime }\end{array}$$

This exponential decrease depends on ${\lambda }_1^{\prime }$, which is a cell density function. The decrease rate of H₂ O₂ can be characterized by the half-time t_1/2. This time is approximately the same for internal and external concentration, as internal and external H₂ O₂ decrease are strongly linked. For instance, with an addition of 1 mM of exogenous H₂ O₂ and with a cell density of 1.45 × 10⁷ cells ml⁻¹, the half-live is approximately $t_{1/2}\approx \frac{ln1/2}{{\lambda }_1^{\prime }}\approx 6.5$ minutes, this results is consistent with Fig 10.

Moreover, as the exponential decrease in rate is dependent on ${\lambda }_1^{\prime }$, it ranges from zero when there is no scavenger (in a cat- mutant) to $k_{diff}^{\prime }$ when scavengers have a non-limiting rate constant (much higher than k_diff). Thus, a 10-fold induction of Cat (experimentally observed in an Ahp(-) mutant) should increase the rate of medium detoxification of high H₂ O₂ concentrations only with a ratio of:

$$\begin{array}{c}\hfill \frac{{{\lambda }^{\prime }}_{1,induction}}{{{\lambda }^{\prime }}_1}={\lambda }_1^{\prime }\approx \frac{10\left({k^{\prime }}_{enz}+k_{diff}\right)}{\left(10{k^{\prime }}_{enz}+k_{diff}\right)}\approx 1.7\end{array}$$

This result is consistent with the experimental data of Seaver and Imlay ([5]), who examined a doubling in efficiency when comparing the wild type and an Ahp(-) mutant.

It should also be noted that, in a Cat(-) mutant [H₂ O₂]_max ≈ [H₂ O₂]_out0 ≈ [H₂ O₂]₀ (according to equation *). The maximum internal H₂ O₂ concentration rapidly increases the exogenous H₂ O₂ concentration and, as there is no Cat, this value remains constant, resulting in the rapid death of the surviving bacteria. The only way to protect Cat(-) mutant cells against high exogenous H₂ O₂ concentrations is to add the wild type to the medium. This experiment has been reported by Ma and Eaton ([20]). This point will be examined in the following subsection.

Consequence of defence switch in the primary scavenger

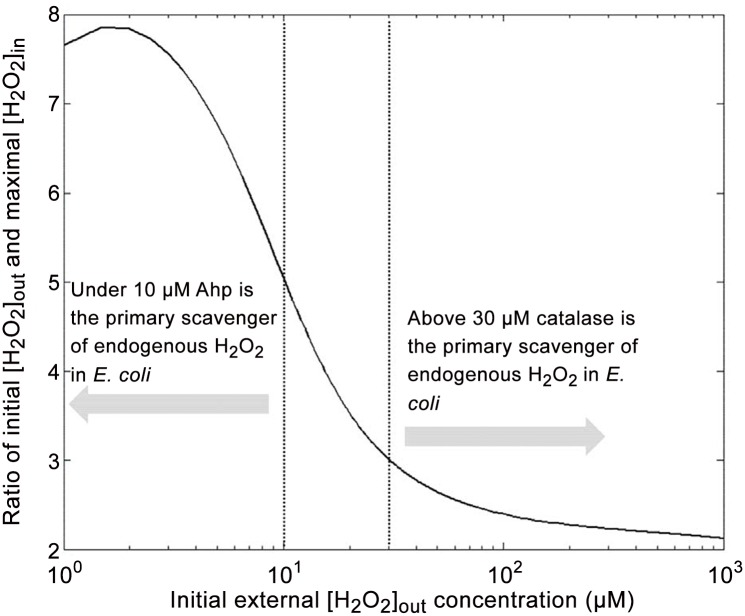
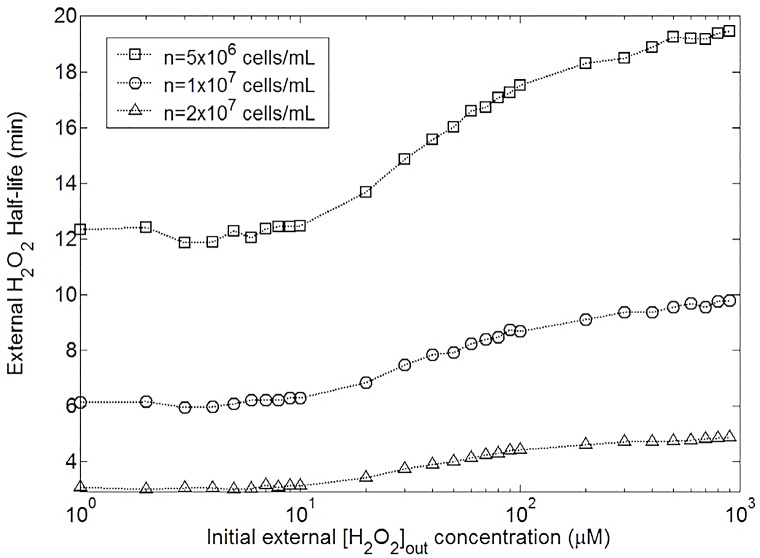
Fig 11 shows that increasing exogenous H₂ O₂ concentration involves the switch between the two primary scavengers. This switch has already been reported by Seaver and Imlay ([5]), but we show here another consequence. Actually this switch also triggers a change in the maximal internal H₂ O₂ concentration viewed by cell. We also find that this maximal internal concentration does not depend on the cell density. Nevertheless the temporal internal or external H₂ O₂ decrease strongly depends on cell density (as previously reported in Figs 7 and 8 or in the previous subsection). The switch between the two scavengers also occurs in Fig 12, actually it shows that H₂ O₂ half-life increases when shifting from Ahp to Cat while exogenous H₂ O₂ increases.

Fig 11. Changes in the ration between external initial H₂ O₂ concentration and internal maximal H₂ O₂ concentration in E. coli wild type.

The numerical solution presented in this graph was running according to the whole model without approximation.

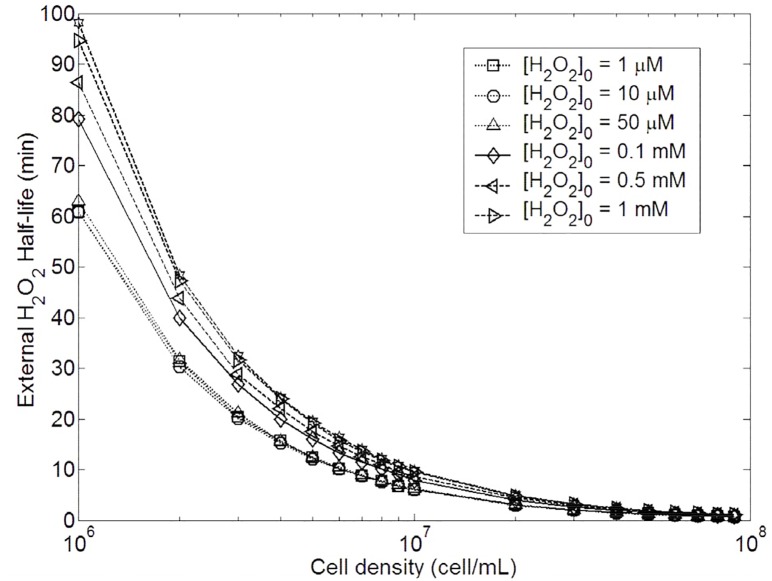
Fig 12. Changes in external H₂ O₂ half-life with different initial external H₂ O₂ concentrations and 3 different cell densities in E. coli wild type.

The numerical solution presented in this graph was running according to the whole model without approximation.

This switch involves non-linear behaviour in half-life external H₂ O₂ dependence. Once again, Ahp seems to be more efficient but it only concerns external H₂ O₂ concentration under 10 μM. Above 30 μM, Cat plays the major role. Unlike maximal internal H₂ O₂, half-life depends on cell density, and the more concentrated cells are, the faster medium detoxification occurs. Nevertheless, as reported in Fig 13, under 10 μM (Ahp is the primary scavenger) the half-life does almost not depend on the initial exogenous H₂ O₂ concentration. Above 50 μM, Cat is the primary scavenger and the half-life depends on the initial exogenous H₂ O₂ concentration.

Fig 13. Changes in external H₂ O₂ half-life with cell densities and with 7 different initial external H₂ O₂ concentrations in E. coli wild type.

The numerical solution presented in this graph was running according to the whole model without approximation.

Cumulative internal H₂ O₂ concentration, rather than maximum internal H₂ O₂ concentration, is involved in the H₂ O₂-mediated death of bacterial cells

We investigated whether the decrease in E. coli survival with increasing exogenous H₂ O₂ concentration was linked to theoretical maximum internal H₂ O₂ concentration or to the rate of decrease in internal H₂ O₂ concentration. Indeed, a steep decrease indicates the perception of a low mean internal H₂ O₂ concentration by the cell. We investigated this aspect by carrying out experiments in which only one of these two parameters was affected at any one time. We therefore reproduced in silico the experiments of Ma and Eaton on H₂ O₂-mediated killing by E. coli wild-type (Cat(+)) or Cat(-) strains alone or by cultures of E. coli containing similar numbers of Cat(+) and Cat(-) bacteria. Cat(-) cells from cultures of Cat(-) cells alone or from equal numbers of Cat(-) and Cat(+) cells had similar peak H₂ O₂ concentrations but different rates of decrease in internal H₂ O₂ concentration. This result led us to evaluate the involvement of these two parameters. Moreover, as these experiments were performed with diluted and concentrated cell cultures, giving similar peak H₂ O₂ concentrations but different rates of decrease in internal H₂ O₂ concentration, we also assessed the effect of these two parameters on cell death.

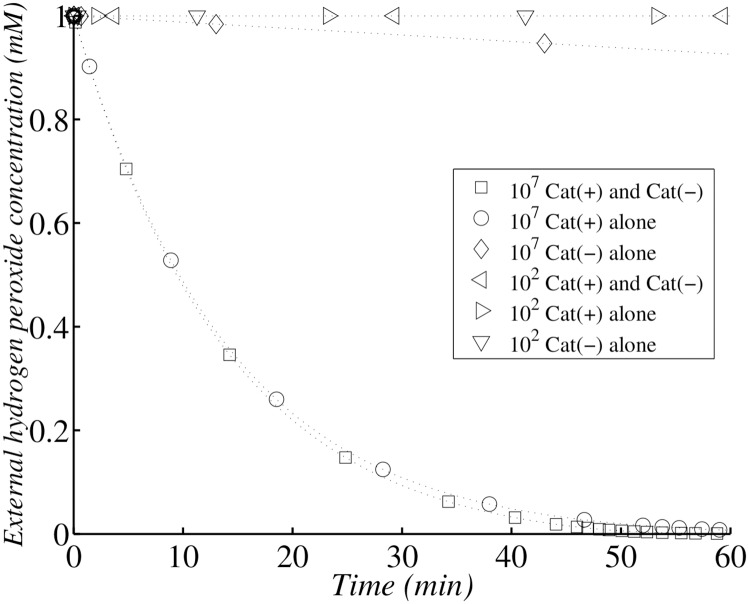
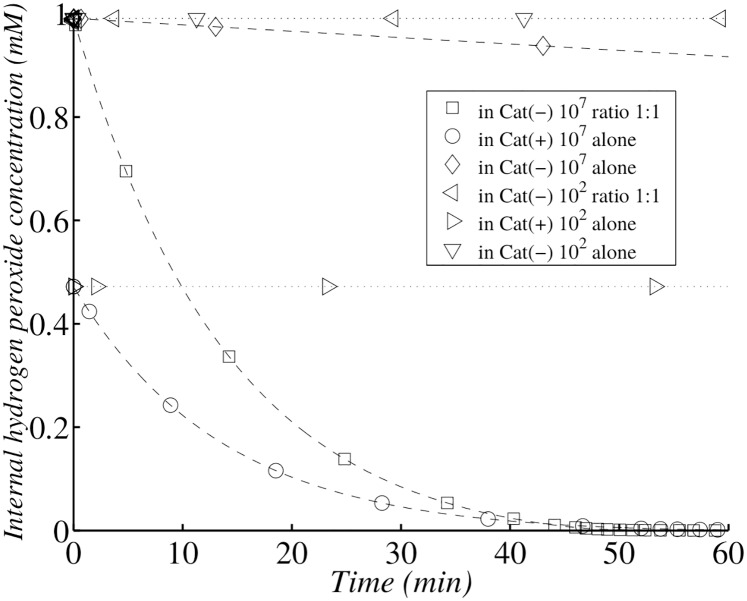
Simulations were performed with a dilute cell suspension (5 × 10² cells ml⁻¹, Figs 14 and 15) and a higher density of cells (10⁷ cells ml⁻¹). Dilute populations of Cat(-) cells were unable to decrease exogenous H₂ O₂ concentration. Dilute populations of Cat(+) cells were also unable to detoxify the medium (Fig 14), whereas the dense population of Cat(+) cells halved exogenous H₂ O₂ concentration within 10 minutes (Fig 14). In a Cat(-) mutant, the maximum internal concentration of H₂ O₂ was only 2.5 times higher than that in Cat(+) cells, but survival rates were similar for dilute populations of both Cat(-) and Cat(+) cells ([20]). As a conclusion, the maximum internal concentration of H₂ O₂ is not a biological significant factor determining survival rate. Each single cell of the separate Cat(-) and Cat(+) populations had a maximum internal H₂ O₂ concentration of about the same magnitude, but only cells from the high-density populations survived in the Eaton experiments. Survival rate was always high when medium detoxification was activated rapidly by a dense Cat(+) cell population. Thus, even Cat(-) E. coli can survive if they are mixed with Cat(+) cells able to detoxify the medium. We conclude that H₂ O₂ scavengers do not protect individual cells against bulk-phase H₂ O₂, because the maximum internal concentration of H₂ O₂ did not differ significantly between Cat(-) and Cat(+) cells. The major difference between these two types of cells concerned the rate of decrease in exogenous H₂ O₂ concentration and, consequently, the rate of decrease in internal H₂ O₂ concentration (Fig 15). We conclude that mean internal H₂ O₂ concentration has a significant impact on bacterial survival, whereas maximum internal H₂ O₂ concentration does not. So H₂ O₂ action can be compared to that of the radiative exposure. This means of action is the opposite of the one generally observed for drugs. For instance, the maximum amount of paracetamol for adults is 4 grams per day with a regular intake of 0.5 gram over 3 days, but a single intake of 10 grams can lead to liver failure ([21]).

Fig 14. Simulation of Ma and Eaton experiment following external hydrogen peroxide concentration.

Simulation of H₂ O₂ external concentration change with dilute (10² cells per ml) Cat(-) E. coli alone ($▿$) or Cat(+) E. coli alone (⊳) or admixed with an equal number of Cat(+), Cat(-) E. coli (⊲); and with concentrated (10⁷ cells per ml) Cat(-) E. coli alone (◇) or Cat(+) E. coli alone (∘) or admixed with an equal number of Cat(+), Cat(-) E. coli (▫). At zero time, H₂ O₂ was added to a final concentration of 1.0 mM, and the bacterial suspension was then incubated at 37°C.

Fig 15. Simulation of Ma and Eaton experiment following internal hydrogen peroxide concentration.

Simulation of H₂ O₂ internal concentration change with dilute (10² cells per ml) Cat(-) E. coli alone ($▿$) or Cat(+) E. coli alone (⊳) or admixed with equal numbers of Cat(+), Cat(-) E. coli (⊲); and with concentrated (10⁷ cells per ml) Cat(-) E. coli alone (◇) or Cat(+) E. coli alone (∘) or admixed with equal numbers of Cat(+), Cat(-) E. coli (▫). At zero time, H₂ O₂ was added to a final concentration of 1.0 mM, and the bacterial suspension was then incubated at 37°C.

Conclusions

In the absence of exogenous stress

An analysis of the most significant kinetic reactions confirmed that steady-state internal concentration H₂ O₂ results from the balance between its production and a combination of Ahp degradation (78%), Cat degradation (12%) and membrane permeability (10%)

With exogenous H₂ O₂ stress

Prediction of H₂ O₂ levels

Under conditions of exogenous H₂ O₂ stress, H₂ O₂ elimination is dependent on cell density. However, nothing is currently known about internal H₂ O₂ concentration during H₂ O₂ exposure. Under these conditions, internal H₂ O₂ concentration results mostly from influx due to diffusion across the cell membrane, because endogenous production is negligible. Moreover, the rate of diffusion into the cell is governed by membrane permeability. The internal concentration of H₂ O₂ must therefore be lower than the exogenous H₂ O₂ concentration. Consequently, exogenous H₂ O₂ stress leads to an increase in internal H₂ O₂ concentration until a maximum is reached. This peak is followed by a decrease in H₂ O₂ concentration, due to elimination by the cells. We aimed to identify the most significant parameters (kinetic constants and cell concentrations) accounting for the maximum internal H₂ O₂ concentration value reached and for the characteristic time points (time required to reach half the nearest steady–state concentration) during increases and decreases in internal H₂ O₂ concentration.

Surprisingly, based on our model, the maximal internal H₂ O₂ concentrations reached in individual cells was not dependent on cell density, suggesting that there is no population protection effect. This maximum, which is reached in a few milliseconds, and its characteristic timing, are dependent solely on exogenous H₂ O₂ concentration and the three routes of elimination of this radical (membrane permeability, Ahp and Cat scavenging).

For estimation of the maximal internal H₂ O₂ concentration, we needed to distinguish internal H₂ O₂ concentrations for which Ahp activity predominated from those for which Cat activity predominated. For initial exogenous H₂ O₂ concentrations below 10 μM, the maximal internal H₂ O₂ concentration was defined by the balance between the exogenous H₂ O₂ diffusion rate and the three routes of elimination. In these conditions, Ahp was responsible for about 78% of all the H₂ O₂ eliminated. The peak internal H₂ O₂ concentration was almost one tenth the concomitant exogenous H₂ O₂ concentration. At initial exogenous H₂ O₂ concentrations of more than 30 μM, the peak internal H₂ O₂ concentration was defined by the balance between the exogenous H₂ O₂ diffusion rate and the possible elimination routes (Ahp activity being negligible due to saturation). Thus, peak H₂ O₂ concentrations are determined not only by Cat activity (55%), but also by membrane permeability (45%). Surprisingly, at the peak internal H₂ O₂ concentration sensed by each cell, limited membrane permeability served as a passive defence against H₂ O₂, to a similar extent to Cat. In these conditions, internal H₂ O₂ concentration was only half the concomitant exogenous H₂ O₂ concentration.

We then showed that the rate of decrease in internal H₂ O₂ concentration and its characteristic timing were dependent principally on cell density and membrane permeability. This decrease was mediated not only by enzyme activity, but also by H₂ O₂ transport from the extracellular to the intracellular medium. The global kinetics of the decrease in internal H₂ O₂ concentration was determined by the slowest step in the process, diffusion across the membrane, which was limited by cell membrane permeability. Finally, similar conclusions were reported for exogenous H₂ O₂ concentration. The Imlay group has shown that the elimination rate for exogenous H₂ O₂ is much lower in intact cells than in cell extracts, indicating that diffusion across the cell membrane is the limiting process. This observation is consistent with what is known about the most significant kinetic parameters, including the major role played by the cell membrane. Indeed, diffusion across the cell membrane involves the bridging of a gap between internal and extracellular concentrations. This gap provides protection against the oxidizing extracellular medium, but it also decreases the efficiency with which E. coli can decrease the H₂ O₂ concentration of the extracellular medium (Fig 9). The kinetics of extracellular decomposition is almost exclusively diffusion-dependent and, therefore, very slow. As expected, the rate of H₂ O₂ disappearance (intra or extracellular) was greater at higher cell densities.

Instead of conducting real-world experiments, using simulations is generally cheaper, safer and sometimes more ethical. Simulations can also be conducted faster than experiments in real time. For instance, at the University of Pittsburgh School of Pharmacy, high-fidelity patient simulators are used in addition to therapeutics ([22]). Of course simulations have to be confronted with real experiments to test their robustness and to be improved. Our model is one step in a global modelling of the E. coli ROS dynamic.

“Remember that all models are wrong; the practical question is how wrong do they have to be to not be useful.”

— Box and Draper, Empirical Model-Building, p. 74

Supporting Information

S1 File. Superoxide kinetic and evolution.

(PDF)

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This work was supported by ANR (Agence National de la Recherchegrant) (ANR-12-BS07-0022 ROSAS). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.