Cross-scale integration of knowledge for predicting species ranges: a metamodeling framework

Abstract

Aim

Current interest in forecasting changes to species ranges have resulted in a multitude of approaches to species distribution models (SDMs). However, most approaches include only a small subset of the available information, and many ignore smaller-scale processes such as growth, fecundity, and dispersal. Furthermore, different approaches often produce divergent predictions with no simple method to reconcile them. Here, we present a flexible framework for integrating models at multiple scales using hierarchical Bayesian methods.

Location

Eastern North America (as an example).

Methods

Our framework builds a metamodel that is constrained by the results of multiple sub-models and provides probabilistic estimates of species presence. We applied our approach to a simulated dataset to demonstrate the integration of a correlative SDM with a theoretical model. In a second example, we built an integrated model combining the results of a physiological model with presence-absence data for sugar maple (Acer saccharum), an abundant tree native to eastern North America.

Results

For both examples, the integrated models successfully included information from all data sources and substantially improved the characterization of uncertainty. For the second example, the integrated model outperformed the source models with respect to uncertainty when modelling the present range of the species. When projecting into the future, the model provided a consensus view of two models that differed substantially in their predictions. Uncertainty was reduced where the models agreed and was greater where they diverged, providing a more realistic view of the state of knowledge than either source model.

Main conclusions

We conclude by discussing the potential applications of our method and its accessibility to applied ecologists. In ideal cases, our framework can be easily implemented using off-the-shelf software. The framework has wide potential for use in species distribution modelling and can drive better integration of multi-source and multi-scale data into ecological decision-making.

Introduction

Models of species range limits have wide applications, particularly in conservation biology where they can be used as decision-support tools in biodiversity management (Guisan et al., 2013). Due to large temporal and spatial scales as well as the complex and nonlinear nature of ecosystem dynamics, it is often impossible to construct experiments that adequately explore the processes generating species range limits (Wu & Loucks, 1995; Levin, 1998). Hence, range models are essential tools that have been applied to a large number of ecological subfields, including biogeography (Schurr et al., 2012), invasion biology (Catterall et al., 2012; Gallien et al., 2012), hybrid zone dynamics (Engler et al., 2013), and climate change impacts on species distributions (Blois et al., 2013; Thuiller et al., 2014b).

Despite the recognized potential of these models, it can be difficult to produce species distribution models (SDMs) with acceptable levels of precision and bias (Guisan et al., 2013). For mechanistic models, two important constraints can be problematic: (1) having the appropriate ecological theory needed to link data to modeling objectives, and (2) having sufficient data over a range of conditions to maintain coherence between the spatial and temporal scales of data and theory. In recent decades, however, modeling techniques have proliferated to take advantage of increased data availability. A growing body of theory, reflecting the diversity of processes generating species ranges, has also contributed to model diversification (Boulangeat et al., 2012). Of these model types, fine-scale mechanistic models often capture important ecological processes quite well, but may perform poorly when applied at the scale of species ranges. For instance, biotic interactions are usually not modeled mechanistically at regional or continental scales because they are poorly known or unrecorded, despite being considered a key determinant of range limits (Pigot & Tobias, 2013). In contrast to mechanistic models, more correlative approaches that statistically relate species occurrences to other variables have the advantage of indirectly accounting for underlying processes (Guisan & Zimmermann, 2000). However, their predictions rely on the stationarity of the relationships between occurrences and explanatory variables in time and space, implying that the selected variables are related to the processes limiting species ranges and that their correlations are constant for calibration and projection ranges in space and time (Dormann, 2007). Extrapolating beyond the scope of the original data (e.g., predicting ranges based on future climate) is therefore problematic, because nonlinear responses to novel combinations of explanatory variables cannot be accommodated in models that do not simulate the underlying processes.

Clearly, an approach is needed to unify the strength of different modeling approaches that can also incorporate multiple data sources. To this end, we present an application of hierarchical Bayesian methods that uses outputs from multiple models to inform the results of the final model. Techniques for multimodel inference have proliferated in recent years. For example, hybrid models that allow for combinations between mechanistic and phenomenological sub-models are commonly employed in SDMs (Gallien et al., 2010; Thuiller et al., 2013; Boulangeat et al., 2014). Within the hybrid framework, a correlative model might be used to account for abiotic variables limiting species distributions (Guisan & Thuiller, 2005), while a more mechanistic approach could include biotic interactions and space-time dynamics (Smolik et al., 2010). However, the link between different sub-models is based on assumptions about the scaling of ecological processes that are poorly known and difficult to test (Gallien et al., 2010), and as such uncertainties are approximated and their attribution to different sources is difficult to distinguish. An alternative to hybrid models is the direct combination of predictions, allowing models operating at the same spatio-temporal scales to be combined (e.g., model averaging, ensemble forecasting; Araújo & New, 2007). However, because uncertainty is approximated and may be poorly understood, it is not possible to evaluate the effects of convergent predictions on the total uncertainty of the outcomes, despite its potential importance in a prediction context.

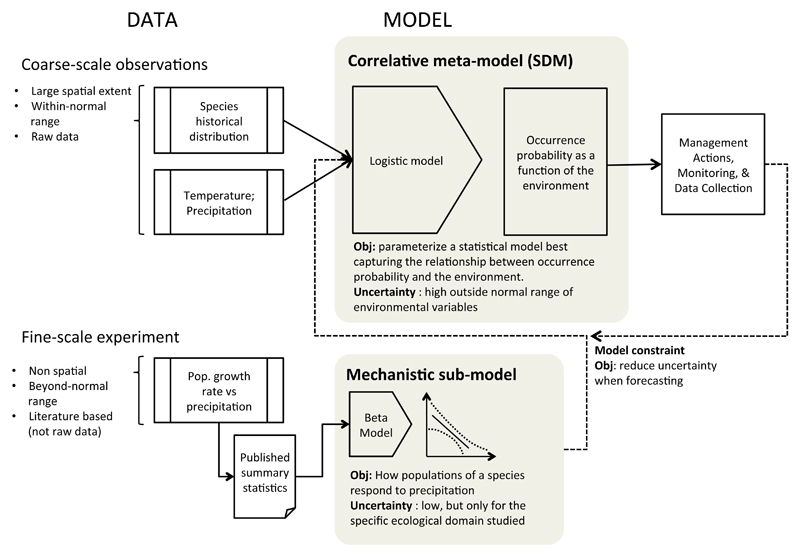
We propose an alternative to these approaches using a hierarchical Bayesian framework. This approach provides a number of advantages, including (1) the ability to incorporate multiple modes of inference (e.g., mechanistic, correlative models) (Van Oijen et al., 2005; Clark & Gelfand, 2006; Hobbs & Ogle, 2011; Hartig et al., 2012), (2) an easy mechanism to include multiple data sources at various scales (Levin, 1992; Peters et al., 2004), and (3) an intuitive and comprehensive reporting of uncertainty in model predictions that reflects variation at all levels of organization (Cressie et al., 2009; Hobbs & Ogle, 2011). Contrary to hybrid methods, the aim is not to link different sub-models into a single one, but to condition the predictions of a metamodel at the target scale (e.g., an entire species’ range) with information from independent sub-models at a variety of spatial scales, allowing for more flexibility regarding the type of information included. By integrating all available knowledge into a single prediction, our approach potentially mitigates the limitations inherent in each individual model, contributing to more robust predictions (Guisan & Thuiller, 2005; Araújo & Guisan, 2006). Moreover, a more comprehensive understanding of uncertainty can guide biodiversity management and prioritize future data collection by identifying parameters that contribute most to variance in the model predictions (McMahon et al., 2011).

We illustrate our framework with two examples. We begin with a hypothetical example, using simulated data, where we define the framework and demonstrate its application to multiple sources of information from different scales. In a second example, we apply the framework to combine presence-absence information with phenological data to improve uncertainty estimates and reduce bias when predicting changes to the range of sugar maple (Acer saccharum Marsh.), a widespread and dominant tree species from eastern North America, in response to climate change. We provide a more formal mathematical presentation in Appendix S1, along with complete code and data for both examples in Appendix S2.

Example 1: Adding experimental evidence for the fundamental niche to a species distribution model

The key idea of our approach is to formulate a metamodel that integrates data at the same ecological scale as the desired predictions, and to constrain the parameters of this model using the output of one or more sub-models. In this hypothetical example, we build a metamodel relating the distribution of an annual plant to coarse-scale climate with complementary information originating from a fine-scale experiment manipulating the precipitation regime. The metamodel attempts to capture the realized distribution of a species; as a correlative model, it implicitly captures the major physiological constraints and ecological processes constraining the distribution of the target species. However, for the purposes of forecasting, we would like to disentangle the fundamental response of a species to environmental variation from other processes in order to map the climatic envelope of where a species may be found in a natural setting. Thus, we use additional information on the physiological constraints affecting species distribution. Because these data are often collected at a finer scale than that of rangewide occurence data, we apply a simple scaling function, drawing on ecological theory, to compute the likelihood of a set of metamodel parameters given both the occurrence and the physiological data. See Appendix S1 for procedural details and scripts for executing the model.

We consider data collected from a species’ historical distribution, where the goal is to predict the distribution following a substantial reduction in precipitation. For the metamodel-scale data, we simulate a relatively high-quality presence-absence dataset covering a variety of ecological conditions, which we term X_M, where the subscripted M indicates that the data were collected at the same scale as the metamodel (Fig. 1). We desire to model the species’ distribution as a function of temperature, T_M, and precipitation, P_M. An initial version of the metamodel (θ_M) that has no constraints from other datasets will be referred to as the naive model. This naive model uses a simple logistic regression to estimate the probability of occurrence (ψ_N) as a function of second order effects of temperature and precipitation:

$$\begin{array}{lll}{\psi }_N\hfill & =\hfill & f\left({\theta }_M,T_M,P_M\right)\hfill \\ \hfill & =\hfill & p\left(X_M=1|{\theta }_M,T_M,P_M\right)\hfill \\ \hfill & =\hfill & {\text{logit}}^{-1}\left({\theta }_M{D}_M\right)\hfill \end{array}$$ (1)

where θ_M is the parameter vector of the model, D_M is the covariate matrix (i.e., T_M, P_M), and logit⁻¹ is the inverse of the logit function. We estimate parameters using a Metropolis-Hastings algorithm within a Markov Chain Monte Carlo (MCMC) method using the proportional form of Bayes’ theorem:

$$p\left({\theta }_M\hspace{0.17em}|\hspace{0.17em}{X}_M,T_M,P_M\right)\propto p\left(X_M\hspace{0.17em}|\hspace{0.17em}{\theta }_M,T_M,P_M\right)p\left({\theta }_M\right)$$ (2)

where p (X_M | θ_M, T_M, P_M) is often referred to as the likelihood of the data (X_M) given the model (θ_M), p(θ_M) is often referred to as the prior distribution of θ_M, and the goal of modeling is to estimate p(θ_M | X_M, T_M, P_M), the posterior distribution of θ_M, which gives the probability that θ_M takes particular values, given the observed data.

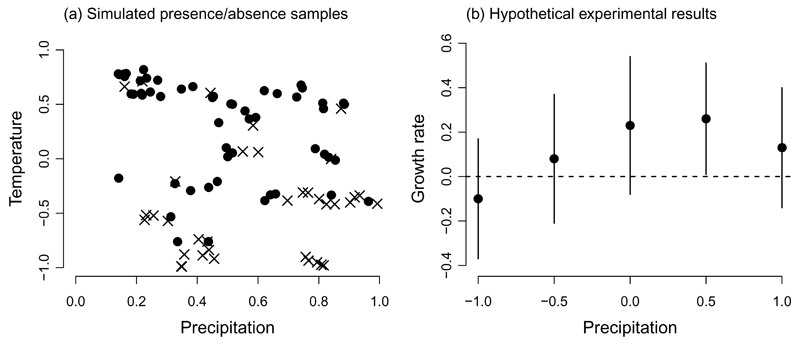
Figure 1.

Two simulated datasets used to illustrate the model integration framework. (a) Presences (circles) or absences (x’s) of the species in ecological space, where the range of precipitation values sampled was 0.1–1. (b) Growth rate (r) as a function of manipulations to the precipitation regime (whiskers show ± 1 SE), with a larger range for precipitation (i.e., -1.0–1.0). The dashed line shows the threshold above which the species net growth rate is positive (implying presence). Axis scales for temperature and precipitation are arbitrary, but note the different scales on the horizontal axes.

Thus far, we have considered only a single source of information to fit this model, and therefore the prior distribution p (θ_M) from Eq. 2 is uninformative. As a secondary source of information, we will consider an experiment relating the population growth rate of the plant to manipulations to the precipitation regime, with results (but no raw data) available from the literature (Fig. 1b). Furthermore, no information is available regarding the temperature regime for the experiment. Transplant experiments that evaluate performance beyond the range of a species are common and represent a plausible scenario for model integration (Hargreaves et al., 2014). According to niche theory (Holt, 2009), the fundamental niche corresponds to the set of environmental conditions where the per capita intrinsic growth rate r is positive. This concept gives us a reasonable model to fit a scaling function for our sub-model (Appendix S1). If we hypothesize that the errors from Figure 1b (σ_S) are normally distributed (where the S subscript indicates information pertaining to the submodel), then for an observation i, we can interpret the probability of presence (ψ_S,i) as the probability that the observed growth rate X_S,i is positive:

$${\psi }_{S,i}={\displaystyle {\int }_0^{\infty }N\left(X_{S,i},{\sigma }_{S,i}\right)}$$ (3)

where N is the normal density function. We can then estimate the posterior distribution for the sub-model by fitting the relationship between ψ_S and precipitation (P_S) using Bayesian beta regression (Ferrari & Cribari-Neto, 2004):

$$p\left({\theta }_S\hspace{0.17em}|\hspace{0.17em}{\psi }_S,P_S\right)\propto p\left({\psi }_S\hspace{0.17em}|\hspace{0.17em}{\theta }_S,P_S\right)p\left({\theta }_S\right)$$ (4)

Although the two datasets were collected at considerably different scales, we have sub-model predictions arising from a fine-scale experiment that are relevant at the scale of the metamodel (i.e., the probability of presence at a given precipitation regime). The scaling treats the fundamental niche as the only driver of species distribution, and only considers a single dimension of the niche. As such, it would be unwise to expect predictions from this model alone to resemble the actual distribution of the species; as a mechanistic model, it is simply too incomplete to predict distribution. However, the information from this sub-model, when applied as a constraint on the metamodel, can result in improved predictions that incorporate the information within each model.

We accomplish model integration by treating ψ_S, the posterior predictions of the submodel θ_S, as prior information about some of the parameters of θ_M (i.e., parameters related to precipitation), expanding Equation 2 to incorporate the new information from the sub-model:

$$\stackrel{\text{integrated}\hspace{0.17em}\text{posterior}}{\overbrace{p\left({\theta }_M\hspace{0.17em}|\hspace{0.17em}{X}_M,T_M,P_M,{\theta }_S,{\psi }_S\right)}}\propto \stackrel{\begin{array}{c}\text{new}\hspace{0.17em}\text{information}\\ \text{from}\hspace{0.17em}\text{sub-model}\end{array}}{\overbrace{p\left({\psi }_S\hspace{0.17em}|\hspace{0.17em}{\theta }_M,P_M\right)}}\stackrel{\begin{array}{c}\text{naive}\hspace{0.17em}\text{metamodel}\\ \text{posterior}\end{array}}{\overbrace{p\left(X_M\hspace{0.17em}|\hspace{0.17em}{\theta }_M,T_M,P_M\right)p\left({\theta }_M\right)}}\stackrel{\begin{array}{c}\text{prior}\hspace{0.17em}\text{for}\\ \text{sub-model}\end{array}}{\overbrace{p\left({\theta }_S\right)}}$$ (5)

As before, the metamodel θ_M can be used to predict probability of occurrence (ψ_I). However, these predictions now reflect the presence-absence data X_M as well as the information from θ_S, including all of the data sources used to produce this sub-model. Finally, we note the presence of marginal distributions for both models (i.e., p(θ_M) and p(θ_S)). These can be informative (e.g., incorporating further prior information or the predictions of additional sub-models), semi-informative (e.g., to provide greater weight to more informative models), or uninformative. For purposes of this example, we applied prior weights of 1 and 0.05 to the correlative and mechanistic models, respectively, reflecting the increased generality and much larger sample size of the correlative data. This procedure has the effect of increasing the variance of the model and prevents biasing the parameter estimation in favor of the mechanistic model.

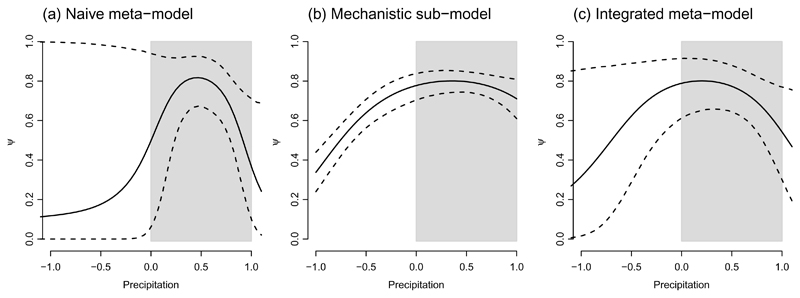
When comparing the three models (naive metamodel, mechanistic sub-model, and integrated metamodel), we observed extreme uncertainty in the first model when projecting beyond the range of the original data (Figs. 2a, 3a, 3b). The sub-model was highly precise with respect to precipitation, thus providing a fairly strong constraint when producing the integrated model (Fig 2b). The result was an integrated prediction that reflected the shapes of both models and showed considerably reduced uncertainty (Fig. 2). At the scale of the metamodel, considering both temperature and precipitation, we observed similar results, with reduced uncertainty in the predictions over the domain not covered by the presence-absence data (Fig. 3).

Figure 2.

Comparison of the naive model, mechanistic sub-model, and the integrated model showing the probability of presence (ψ) as a function of precipitation. Uncertainty is represented as dashed lines, showing the limits of 90% Bayesian credible intervals. The shaded region shows the calibration range for the naive model. (a) Naive model, using only presence-absence data. Uncertainty increases dramatically when attempting to project beyond the scope of the source data. (b) Mechanistic model, using observations of an experiment to infer probability of presence. (c) Integrated model, showing predictions that are intermediate between the two sub-models and uncertainty that is reduced compared to (a).

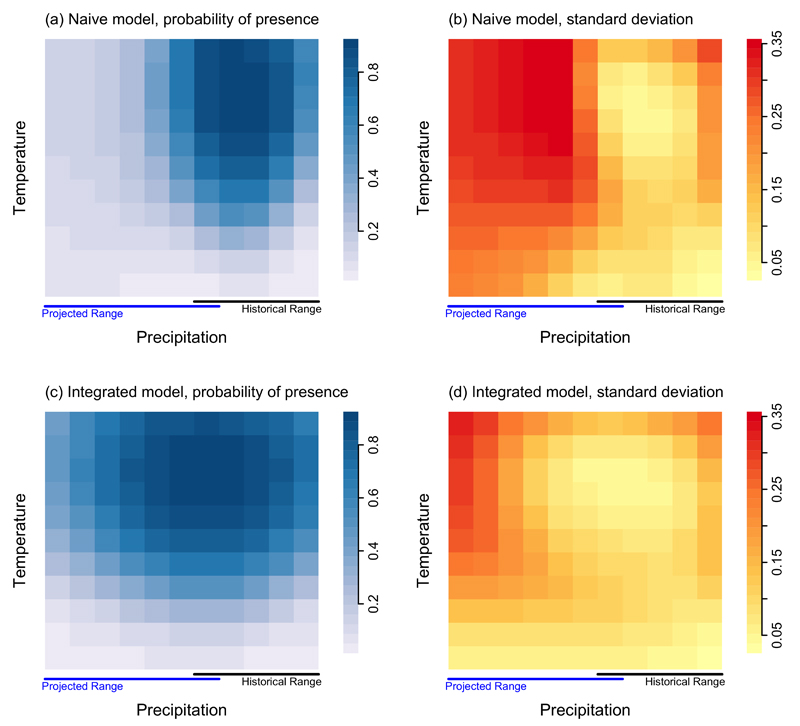
Figure 3.

Maps showing the predicted probability of presence (ψ; (a) and (c)) and the standard deviation of ψ ((b) and (d)) for the naive and integrated models. Historical (i.e., where presence-absence samples were available) and predicted future precipitation regimes are shown below the horizontal axes.

Example 2: Constraining an SDM using phenological information

For the second example, we consider the problem of forecasting a species’ potential distribution following climate change. There is considerable interest in comparing correlative and mechanistic projections with respect to climate change (Morin & Thuiller, 2009), and correctly characterizing uncertainty is a critical aspect of this problem (Cheaib et al., 2012). Despite being a relatively common application of SDMs (Guisan & Thuiller, 2005), projecting models parameterized with modern climate data to future climate scenarios remains problematic (Araújo & Guisan, 2006). We used our framework to constrain a climate-based SDM with information obtained from Phenofit, a mechanistic model that predicts a species’ probability of presence as a function of the suitability of the environment given the species’ phenology (Chuine & Beaubien, 2001; Morin & Thuiller, 2009). Here we describe briefly the dataset, methods, and the results of the analysis (see Appendix S1 for implementation details and Appendix S2 for data and scripts to reproduce the analysis).

We obtained climate variables, occurrence data, and Phenofit projections at 0.5-degree resolution for both the present and for 2100 for sugar maple, an economically and ecologically important species occurring in eastern North America (Morin & Thuiller, 2009). These data defined the metamodel scale. To these data, we added 4903 recorded presences and 21701 absences derived from permanent forest sample plots located in the United States and Canada (See Appendix S1 for a map of plot locations). We reserved 1/3 of this dataset for evaluation and used the remaining records to calibrate the models. We constructed the naive model by using a binomial generalized linear model (GLM) to relate the presence-absence dataset to three climate variables: the number of degree days (ddeg), mean annual precipitation (an_prcp), and the ratio of annual precipitation to potential evapotranspiration (pToPET). These variables were selected from an initial set of seven variables (see Appendix S1 and Morin & Thuiller, 2009, for details on the climate variables). We selected a GLM for its simplicity and interpretability because our focus was on demonstrating the framework, but more complex methods (e.g., generalized additive models) are compatible with the framework.

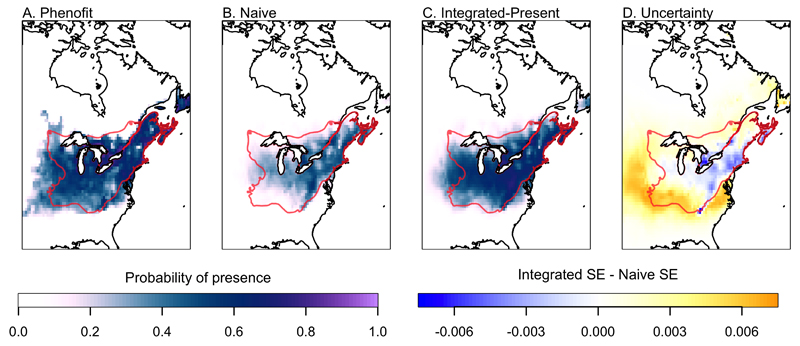
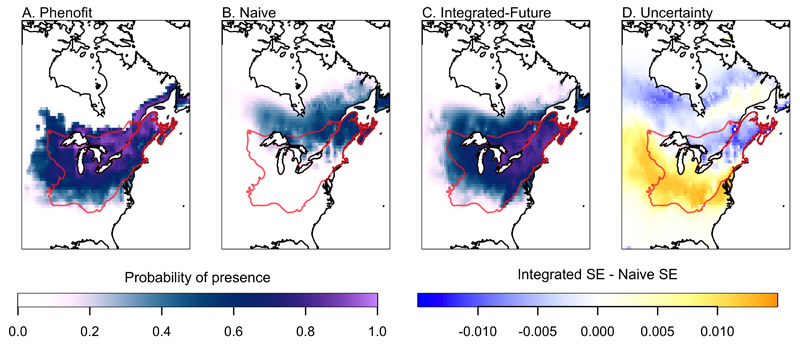
To perform the integration, we constrained the estimates of the naive model with the additional information from Phenofit while considering two different modeling objectives. The first is improving our model of the present range of the species. Using both datasets to develop a range model for the species has a number of advantages. Assuming we have chosen climate variables that well represent the constraints on the species, including Phenofit in our model is likely to reduce bias in our estimate of the fundamental niche. The posterior predictions of the model (that is, the probability of presence in geographic space) will incorporate uncertainty from all sources. This can provide a much more accurate estimate of the uncertainty of our predictions. Thus, for our first integration we combined the naive model with the Phenofit predictions for the present; we refer to this model as “Integrated-Present”. We also evaluated this model by constructing calibration curves and by computing the area under the receiver operating curve (AUC; see Appendix S1), which evaluates classification ability where 1 indicates perfect classification and 0.5 indicates no difference from a random model (Swets, 1988). The second modeling goal is to project changes to the range of sugar maple following climate change. Process-based and correlative models often differ substantially when projecting beyond the range of the original data (see Example 1). Thus, we obtained predictions for 2100 from Phenofit (Morin & Thuiller, 2009) and used them to condition the metamodel given the results of the naive model under future climate. This procedure provided a consensus view of the future range of the species; we refer to this model as “Integrated-Future.” In both cases, it was necessary to scale the Phenofit predictions, which were probabilistic, to make them compatible with the naive model, which was fit using occurrence data. We used a latent variable approach, which posits an unobserved “true” presence-absence dataset from which the Phenofit probabilities are derived. Similar to any other unknown parameter, we can generate a posterior distribution of this dataset by drawing samples during the MCMC procedure; thus, at each iteration, a dataset similar to the one used for the naive model was generated using the Phenofit probabilities (see Appendix S1 for a full statistical presentation of the model). This procedure expresses the information from Phenofit in a way that is compatible with the naive model, and also propagates the uncertainty in the Phenofit predictions. Additionally, it becomes possible to address future distribution via simulated future occurrences (which, by nature, are unobservable).

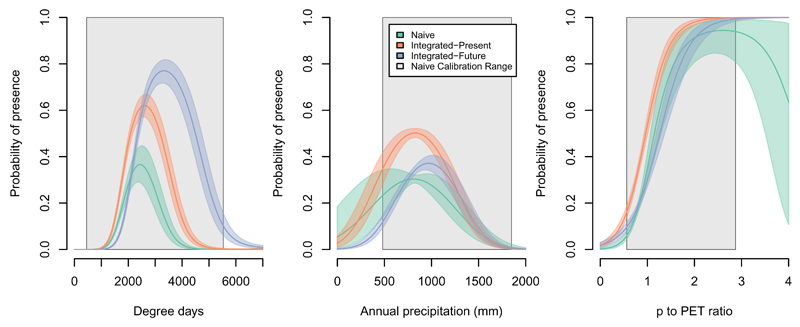
Model integration resulted in substantial reduction in posterior uncertainty in the parameters, and, for the Integrated-Future model, a large revision in the estimate of the response of sugar maple to temperature (i.e., variable ddeg) (Table 1, Fig. 4). When projecting beyond the calibration range for the naive model, the greater coverage provided by the integrated model produced substantial reductions in uncertainty (Fig. 4). When considering the present species distribution, the naive and Integrated-Present models made very similar predictions (Fig. 5). Furthermore, both models performed well when evaluated against reserved data, with median AUC values of 0.802 and 0.797 for the naive and integrated models, respectively (see Appendix S1). The small difference between the models indicates that both models adequately predict the probability of presence of sugar maple. The major advantage to integration is the improved understanding of uncertainty in the predictions, with greater uncertainty in southern portions of the range (Fig. 5). It is important to note that the naive model was the basis for the integrated model; thus the increased uncertainty present in the integrated model is not the result of a “worse” model, but rather should be viewed as a correction to overfitting in the naive model that incorporates uncertainty arising from the processes included in the metamodel. Phenofit predicts fitness based on how climate affects phenological timings, frost injury, reproduction, and survival (Chuine & Beaubien, 2001; Morin & Thuiller, 2009). Thus, climatic factors that ultimately limit species distribution might be quite different between the two source models, as illustrated by the differences in the potential future distributions predicted by Phenofit and the naive model.

Table 1.

Parameter estimates and 95% credible intervals for the naive model (i.e., a Binomial GLM relating sugar maple presence-absence data to climatic variables), and two integrated models combining the naive model and either the present or future predictions from the mechanistic model Phenofit. All models were fit on predictor variables standardized to mean=0 and unit variance, and all estimates are on the logit scale. Climate variables included the number of degree days (ddeg), mean annual precipitation (an_prcp), and the ratio of annual precipitation to potential evapotranspiration (pToPET). Area under the receiver operating curve (AUC) values measure model classification ability, with values of 0.5 indicating no improvement over random classification and 1 indicating perfect classification.

	Naive	Integrated-present	Integrated-future
intercept	-0.886 (-1.12, -0.66)	-0.103 (-0.23, 0.026)	-1.037 (-1.16,-0.92)
ddeg	2.904 (2.34, 3.45)	3.701 (3.37, 4.03)	6.431 (6.07, 6.79)
ddeg2	-6.697 (-7.04, 6.35)	-6.216 (-6.43,-6.00)	-5.241 (-5.43,-5.05)
ddeg3	1.669 (1.52, 1.79)	1.454 (1.37, 1.53)	0.893 (0.85, 0.94)
an_prcp	0.358 (-0.26, 1.02)	0.612 (0.28, 0.94)	1.412 (1.11, 1.71)
an_prcp2	-0.571 (-0.76,-0.40)	-0.848 (-0.95,-0.75)	-0.975 (-1.06,-0.90)
pToPET	2.960 (2.29, 3.61)	2.637 (2.28, 2.99)	2.093 (1.70, 2.48)
pToPET2	-0.557 (-0.74,-0.37)	-0.093 (-0.15,-0.03)	0.0064 (-0.070,-0.073)
AUC	0.802 (0.78,0.82)	0.797 (0.78,0.81)	–*

^*AUC is unavailable for the Integrated-future model because independent validation data are not available for future predictions.

Figure 4.

Response curves for each environmental variable for the three models. Predictions are broadly similar for the three models, with an increase the optimal temperature regime predicted by the Integrated-Future model (left panel). Integration reduced prediction uncertainty for all three variables, particularly for domains outside the naive calibration range. Single-variable predictions were computed with the other variables set to their medians. Uncertainty is represented by colored shaded regions showing 95% Bayesian credible intervals. The gray shaded region shows the calibration range for the naive model.

Figure 5.

Range predictions for present climate for Phenofit (A), the naive model (B), the Integrated-Present model (C), and the difference between posterior prediction standard errors (SE) of the Integrated-Present and Naive models (D; Integrated SE – Naive SE). Model predictions were quite similar, with reduced uncertainty where the models were in strongest agreement, and increased uncertainty near the range boundary where the models disagreed. For reference, the present range of the species is outlined in red (Little, 1971)

The Integrated-Future model presents a different interpretation of the response of sugar maple to warmer temperatures. The naive model predicted a substantial northward migration; in other words, the expectation under the naive model is that the present estimate of the realized niche (obtained using occurrence data) is an unbiased reflection of the fundamental niche; thus the species should track temperature northward as the climate warms. The Integrated-Future model, in contrast, predicted substantially more tolerance to warmer temperatures, reflecting similar predictions from Phenofit (Figs. 4, 6). This is because Phenofit estimates different aspects of the realized niche. Although both models predicted a northward range shift, the change under Phenofit was limited to approximately 200 km north of the present range limit of the species, compared with more than 900 km for the naive model. Phenofit also predicted little change in the southern range limit of the species, while the naive model projected loss of the species over much of the southern portion of the range (Fig. 6). The metamodel thus presents a consensus view of the niche of the species with respect to the macroclimatic variables included in the model (Fig. 5), incorporating the present range of the species (using the occurrence data) and information from Phenofit on what conditions will be tolerable in the future.

Figure 6.

Range predictions for future climate for Phenofit (A), the naive model (B), the Integrated-Future model (C), and the difference between posterior prediction standard errors (SE) of the Integrated-Future and Naive models (D; Integrated SE – Naive SE). The mechanistic sub-model Phenofit (A) predicted small shifts sugar maple range. In contrast, the naive model (B) projected a large northward change in suitable habitat. Model integration (C) produced predictions that were intermediate between the two models. Uncertainty decreased for the northern portion of the present range (red outline) where the models were in agreement, while it increased in the southern portion of the range where the models were in strong disagreement.

Discussion

Comparison with other methods

The methods provided here expand upon the motivation of hybrid models to develop more robust approaches for using ecological models for prediction while overcoming some limitations characteristic of other integrated approaches. In particular, it is often difficult in a hybrid model to identify parameters that can be used to connect different modeling frameworks and produce a meaningful response (Thuiller et al., 2013). The difficulty of including information from experimental studies or ecological processes at lower scales can be a possible drawback of hybrid models (Smolik et al., 2010; Thuiller et al., 2014a). Bayesian methods provide a natural framework for the incorporation of multiple sources of information, making them an attractive alternative to SDMs. Hierarchical models in particular have the potential to capture many of the intricacies necessary for implementing hybrid models (Latimer et al., 2006). Pagel & Schurr (2012) developed a hybrid approach to species distributions via a dynamic range model. Similar to our approach, their model integrated demographic information, abundance, and presence/absence data within a hierarchical Bayesian framework to predict species ranges. However, their approach explicitly links the modelled processes to occurrences/abundances via a detailed demographic model, requiring data that may not be available for many species. In contrast, our approach allows for the inclusion of less complete datasets because integration is performed via the separate predictions of each model (following the application of the scaling function where necessary). Because the metamodel is expressed as a series of conditional probabilities (see Appendix S1), this information can be included simply as long as the probability of the metamodel can be expressed mathematically. Furthermore, Bayesian methods produce posterior distributions of parameters and predictions rather than point estimates, allowing for a comprehensive understanding of the uncertainty. Finally, Bayesian methods inherently allow for feedbacks or interactions between sub-models, which may be a more realistic representation of ecological dynamics where many factors may simultaneously influence the system.

Our approach is a logical extension of other Bayesian approaches developed to deal with processes that occur at multiple scales while using several models simultaneously. In particular, it has certain similarities with Bayesian model averaging and Bayesian calibration of process-based models. Bayesian model averaging aims to combine several alternative models that operate at the same scale to obtain better predictions while taking into account parameter uncertainties (Hoeting et al., 1999). This is of particular interest in ecology, where the mechanisms underlying complex phenomena are often unknown (e.g., Link & Barker, 2006). Bayesian calibration of process-based models focuses on uncertainty of the parameter values, in this case the values of the parameters are calibrated by the model output (Van Oijen et al., 2005; Hartig et al., 2012). In contrast with these methods, our approach handles data and models operating at different hierarchical scales and uses process-based models to constrain the shape of the metamodel.

Advantages of Model Integration

Species distribution models are important tools that are increasingly used by land managers for science-based decision-making (Guisan et al., 2013). However, the possibility that diverse approaches will provide contrasting answers as a result of different assumptions and methodologies can create confusion and mistrust towards models, and some managers may be discouraged from incorporating their results in management plans. Integrated approaches have gained momentum in recent years, with integrative science being featured as a central theme for several science-based governmental organizations around the world (e.g., Bernier et al., 2013). Incorporating information from multiple sources, particularly with respect to uncertainty, fosters a connection between scientifically-generated knowledge and policy, and is therefore an important tool for adaptive management (Rehme et al., 2011, Fig. 7). Such approaches are needed in designing management plans for vulnerable species and ecosystems to avoid basing decisions on too-narrow subsets of the available information (Dawson et al., 2011). However, successful use of approaches such as ours will always remain dependent on an intimate understanding of the decision-making process, emphasizing the importance of close collaboration between modelers and practitioners at all stages of model development (Guisan et al., 2013).

Figure 7.

Sample workflow for applying the models presented in the first example in a management context. Critical steps include specifying the metamodel, identifying additional sources of information to be used as constraints on the metamodel, and using the integrated prediction for decision-making. As additional information becomes available from monitoring the results of management, this information can be incorporated in additional sub-models to further refine the metamodel.

Model uncertainty is another key factor affecting applicability of model outputs (Addison et al., 2013). One of the main strengths of our approach is that it allows for a transparent identification of uncertainties and how they propagate through the models. Transparency in uncertainty can be considered as a sort of sensitivity analysis, whereby the greatest sources of uncertainty can be detected and further research directed accordingly (e.g., Example 1, Figs. 1, 2). The new knowledge resulting from this research can then be readily incorporated into the metamodel and the model predictions updated to account for the new information. The ease of incorporating new knowledge to the modeling framework allows for a rapid adjustment of the predictions and the incorporation of the most recent available knowledge into management plans (Keith et al., 2011). Furthermore, the use of linked sub-models allows for clear specification of desired model outputs (via the specification of the metamodel) while easily retaining important ecological objectives (via careful specification of sub-models). Transparency in the model-building process must be accompanied by a clearly documented workflow. We suggest using the sub-models as a natural proxy for specifying specific objectives, and using this as the basis for developing workflows describing the process of model integration to ensure reproducibility and applicability (Fig. 7). Adaptive approaches such as the one presented here are often highlighted as a pressing need in order to develop strategies to promote ecosystems that are both feasible and resilient (Seastedt et al., 2008).

In many cases, both the data and theory needed to apply our approach already exist, and all that is needed is the development of sub-models and their integration into a metamodel. For example, climatic gradients may mediate competitive interactions (Kunstler et al., 2011), which means that simple correlative models that fail to account for competition may be wrong if the climate-competition association changes in the future. In North America, the US Forest Service maintains a long-term Forest Inventory Analysis database that could be utilized to parameterize a competition model. Such a model need not explicitly predict occurrence limits; rather it could be integrated with a larger-scale model to include information about competition in a distribution model. The phenological information needed to parameterize the sub-model for Example 2 is similarly available for a wide range of species (Morin & Thuiller, 2009). There are also a number of networks collecting high-quality data with good temporal and spatial coverage (e.g., the National Ecological Observatory Network; NEON, and Long-Term Ecological Research sites; LTER). There is great potential for these kinds of data to be used in fitting sub-models of the kind used in Example 1. In other cases, qualitative model comparison efforts have already been made (Morin & Thuiller, 2009; Cheaib et al., 2012). Our framework could be used post-hoc on the outputs of these models to quantify uncertainty resulting from model disagreement.

Challenges

Although our approach is highly flexible and can be applied in a number of situations, there are some challenges to successfully using the framework. Data quality and availability can present a significant constraint on the number and type of models that can be implemented in our framework. One obstacle is a lack of adequate and unbiased coverage of explanatory variables; exploratory analyses can be a significant aid in understanding how data coverage impacts resulting predictions (McKenney et al., 2002). Integration can solve these issues to some extent by using supplemental information (and conceptual advances) in additional sub-models where coverage is weak (e.g., Example 1, Figs. 2, 3). A strength of our approach is that it can be used without the full suite of data that would be required to run a fully mechanistic model. Given that the metamodel is correlative, it can be effectively implemented with, e.g., only presence-absence data, or, in the case where true absences are difficult to obtain, with presences and pseudo absences (provided sufficient care is used in interpreting the results of such a model). Consequently, any additional mechanistic data that become available will enhance predictions by constraining outputs of the metamodel.

Determining the functions to use to express the likelihood of the sub-models given the metamodel (i.e., Eq. 5) is a critical point. The challenge is three-fold: (1) determining which spatial and temporal scales (i.e. which processes), are to be considered, (2) selecting how to build a scale the sub-models to be consistent with the metamodels, and (3) understanding how error and uncertainty propagate from the sub-models to the metamodel. Although we argue that our proposed framework is able to easily deal with different scales and that the Bayesian framework allows for an efficient integration of uncertainty across all scales considered, the building of scaling functions is an object of investigation on its own. It is likely that the modeling process may include multiple functions operating at different scales when taking all known processes and models into account. Indeed, if species distributions are a function of, e.g. population growth rate (Guisan & Zimmermann, 2000), they will involve processes at the individual (e.g. competition) or cellular (e.g. photosynthesis) scales. Such very large differences in spatial scales would require more sophisticated upscaling methods than simple functions such as those we have used here. Our framework is still applicable whatever the chosen upscaling approach and is able to propagate uncertainties from sub-models to the metamodel. Indeed, if a sub-model provides poor information (due, for example, to cross-scale nonlinearities in the response to the environment), the resulting metamodel predictions may be worse than the pre-integration naive model. In general, we advise users of this framework to carefully consider the scaling in their models with respect to the biology of the organism studied, and to use prior model weights to downweight the scaled models when there is uncertainty about the applicability of a sub-model at the metamodel scale. For instance, in the first example, we applied a model weight to decrease the influence of the mechanistic model on the metamodel (while still retaining some information contained therein), recognizing that such a simplistic model may not scale well. Finally, as always when modelling ecological systems, we urge humility in the interpretation of model results and suggest the use of model evaluation and validation tools whenever possible. We provide additional discussion on the implementation of model weights in Appendix S1.

The implementation of the model itself can present an obstacle when model complexity increases. In many cases, off-the-shelf software can adequately express the model likelihoods with minimal programming, but more complicated models will require the development of custom programs. Developing such customized code requires careful model specification, understanding of applied Bayesian methods, and, in some cases, extensive programming. However, the flexibility of our approach and its transparency with respect to the propagation of uncertainty will often outweigh the implementation challenges.

Finally, this approach is not just a new methodological tool but a framework for forecasting species distributions which is fundamentally designed to make the link between modelers and practitioners while correctly estimating uncertainties and being updatable with new data and theoretical advances. A scientific approach such as presented here is particularly adapted to make a synthesis of available information and provide robust species distribution forecasts based on information known to be the best available scientific knowledge. It can incorporate large databases, valuing the efforts of data collection, and include models based on the latest theoretical advances, which is essential to decrease errors due to model specification (Austin, 2007). In addition, it provides practitioners and decision-makers with the best possible estimation of uncertainties, with direct applications to risk assessment or to guide the choice where investigating new research and accumulating new data. Finally, we argue that the adaptability of our approach is particularly appropriate in a world where collected data and theoretical knowledge are changing as quickly as climate and conservation practices must be adjusted accordingly.

Data Accessibility

All data, as well as all code required to repeat the analyses, have been uploaded as online supporting information in Appendix S2.

Biosketch

The Canada Research Chair in Biogeography and metacommunity ecology at the Université du Québec à Rimouski focuses on interactions between species distributions, community structure and ecosystem functioning. We apply principles of spatial ecology to a variety of organisms and systems, from bacteria to entire forests. We also use theoretical and simulation models to develop hypotheses and extend our work beyond the technical limitations of empirical studies. More information can be found at: http://chaire-eec.uqar.ca/