A distributed recurrent network contributes to temporally precise vocalizations

SUMMARY

How do forebrain and brainstem circuits interact to produce temporally precise and reproducible behaviors? Birdsong is an elaborate, temporally precise and stereotyped vocal behavior controlled by a network of forebrain and brainstem nuclei. An influential idea is that song premotor neurons in a forebrain nucleus (HVC) form a synaptic chain that dictates song timing in a top-down manner. Here we combine physiological, dynamical and computational methods to show that song timing is not generated solely by a mechanism localized to HVC but instead is the product of a distributed and recurrent synaptic network spanning the forebrain and brainstem, of which HVC is a component.

INTRODUCTION

Temporally precise and highly reproducible learned behaviors, such as those that characterize speech or musical performance, depend on both forebrain and brainstem circuitry. A major unresolved issue is how the forebrain interacts with “simpler” brainstem pattern generating networks to produce such complex, precise and reproducible behaviors. Birdsong, a learned form of vocal communication with parallels to human speech and music (Doupe and Kuhl, 1999; Fisher and Scharff, 2009; Lipkind et al., 2013), provides a powerful context in which to address this issue. Zebra finches sing highly stereotyped song motifs comprising sequences of single or multi-note syllables, and song timing is precisely reproducible at the note, syllable and motif level – features with timescales that range from milliseconds to seconds (Charlesworth et al., 2011; Chi and Margoliash, 2001; Glaze and Troyer, 2006; Ravbar et al., 2012). Studies in zebra finches and other songbirds have delineated a central circuit for song patterning that includes both forebrain and brainstem elements (Brainard and Doupe, 2013; Mooney, 2009; Schmidt and Wild, 2014), providing a powerful system for identifying the neural mechanisms that contribute to the precise temporal control of vocalization. Do forebrain components of this song circuit effectively commandeer and override brainstem pattern generating networks to enable singing, or do the forebrain and brainstem components interact in a more reciprocal manner? The answer to this question is likely to be broadly relevant to understanding how forebrain and brainstem circuits interact to produce a wide range of complex behaviors.

The forebrain song nucleus HVC is essential to singing (Nottebohm et al., 1976) and a certain class of HVC neurons that project to the song motor nucleus RA (i.e., HVC_RA cells) fire highly precise and temporally sparse bursts of action potentials, with different HVC_RA cells firing at different times in the motif (Hahnloser et al., 2002). An influential idea is that synaptically linked chains of HVC_RA cells form a neural clock that controls song timing, which has gained further support from the observation that focal, bilateral manipulation of HVC temperature by a few degrees Celsius slows or accelerates song timing without affecting either frequency or amplitude (Long and Fee, 2008). Nonetheless, the extent to which these timing signals arise from mechanisms local to HVC or from a more distributed brain network has remained controversial (Amador et al., 2013; Andalman et al., 2011; Goldin et al., 2013; Schmidt and Wild, 2014). Notably, song timing can be modulated non-uniformly when HVC is cooled (Andalman et al., 2011), and more extreme cooling of HVC can cause long syllables to break into shorter elements (Goldin et al., 2013), raising the possibility that other brain regions besides HVC are also involved in generating timing signals (Figure 1A). Indeed, HVC is part of a distributed and recurrent network that spans the forebrain and brainstem (Ashmore et al., 2008a; Schmidt et al., 2004). Focal microstimulation in a brainstem component of this network can disrupt song timing (Ashmore et al., 2005), and lesions placed in a thalamic nucleus (Uva) that relays activity from the brainstem to HVC permanently disrupts song (Coleman and Vu, 2005; Williams and Vicario, 1993), consistent with a distributed timing mechanism.

Figure 1. Conceptual models of song timing generation.

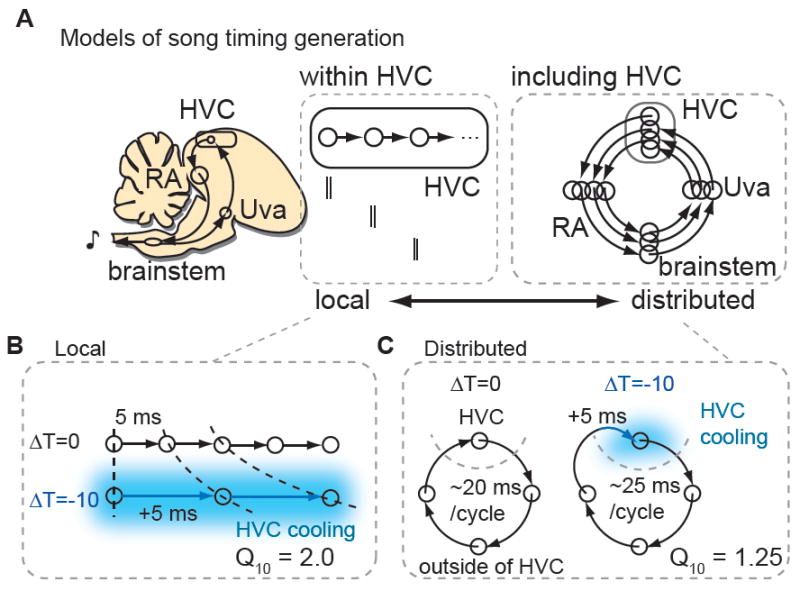
A, A localized model in which song timing is generated solely within HVC (left) contrasts with one in which song timing is generated by a recurrent, distributed including HVC and motor-thalamic loop (RA, brainstem vocal respiratory group and the thalamic song nucleus Uva (right). B, Predicted effect of HVC cooling on song timing employing a local mechanism. The physiological Q₁₀ (~2) and behavioral Q₁₀ are predicted to match. C, Predicted effect of HVC cooling on song timing for the distributed mechanism. The behavioral Q₁₀ will be much smaller than the physiological Q₁₀ measured for activity propagation in HVC.

Regardless of where timing signals are generated, one expectation is that temperature manipulations should affect the speed at which activity propagates through the relevant circuit in a manner that parallels the effects of temperature on song timing. In fact, focally cooling HVC exerts relatively weak effects on song timing, with song stretching or compressing ~3% with a change in temperature of 1 degree Celsius (°C) (Long and Fee 2008). To describe the temperature dependence of a biological process, Q₁₀ values - the ratio of time constant changes for a 10 °C change in temperature - are widely used (Hodgkin and Katz, 1949; Nobile et al., 1990; Sabatini and Regehr, 1996; Taylor, 1988). Using this convention, song stretches as a function of HVC temperature with a Q₁₀ ~1.3. In contrast, synaptic transmission and action potential generation times measured in a variety of systems have Q₁₀ values ~2 (Hodgkin and Katz, 1949; Nobile et al., 1990; Sabatini and Regehr, 1996; Soofi et al., 2014; Taylor, 1988). If song timing is controlled by synaptically coupled chains of HVC_RA neurons with conventional temperature dependencies then focal cooling of HVC should cause song to stretch with a Q₁₀ ~2, much greater than observed experimentally (Figure 1B). Conversely, if HVC is one of four or five nodes in a forebrain – brainstem song timing network, song timing would be predicted to stretch or compress ~20 - 25% for a 10°C change in HVC temperature (Q₁₀ ~ 1.20 - 1.25), similar to experimentally observed values (Figure 1A-C).

Here we focally manipulated the temperature of HVC and measured the temperature dependence of song and of activity propagation either local to HVC or across the distributed recurrent network in which HVC resides. We then measured song timing while focally manipulating the temperature of the thalamic component of the recurrent network. Finally, we performed network simulations and intracellular recordings in singing birds to determine whether HVC neurons display synaptic activity patterns expected of a distributed timing mechanism. Our findings support the idea that song timing is the product of a distributed, recurrent network, rather than a timing mechanism localized largely to HVC.

RESULTS

Temperature exerts different effects on local transmission in HVC and song timing

We bilaterally manipulated the temperature of HVC in adult male zebra finches with a custom miniature Peltier device inspired by recently published designs and confirmed that it was effective at cooling HVC across its entire dorsoventral extent (Figure 2A) (~500 μm from dura, Figure S1) (Long and Fee, 2008, Andalman et al., 2011). We quantified the dependence of the duration of several song features (motifs, syllables and gaps) on temperature changes in HVC (ΔT) using a Q₁₀ value, a standard measure of how the time constant of a process changes with temperature. We also confirmed that Q₁₀ values calculated for song timing and activity propagation (described below) are stable across the range of temperatures studied here, a necessary condition for using Q₁₀ to characterize the response of a system to temperature change (Table S1). Similar to previous reports, the durations of motifs, syllables and inter-syllable gaps were affected by temperature changes in HVC, stretching ~2.7% per degree Celsius decrease in temperature (Figure 2B-D; n = 3 birds; motifs, Q₁₀ = 1.25 ± 0.03, mean ± SEM; syllables and gaps, Q₁₀ = 1.27 ± 0.03) (Long and Fee, 2008, Andalman et al., 2011).

Figure 2. Temperature exerts markedly different effects on synaptic transmission in HVC and on song timing.

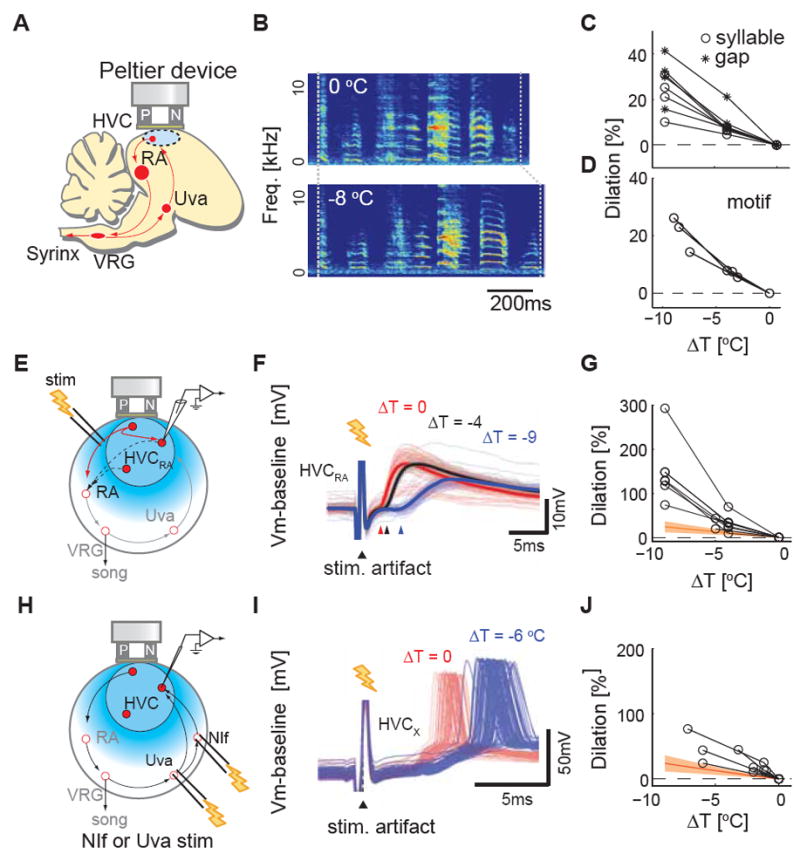
A, Schematic diagram of HVC surface cooling. B, A typical example of the effects of bilateral HVC cooling on song timing. C, Typical examples of temperature dependence of syllable and gap durations measured from one adult male zebra finch. Both syllables and gaps slow 20-40% per 10 °C (Q ₁₀ = 1.2-1.4). D, Motif, the typical syllable sequence sang by a zebra finch, also stretches to the similar extent (n = 3 birds, Q₁₀ = 1.25 ± 0.03). E, Schematic diagram of the experimental setup to measure local HVC_RA - HVC_RA interactions. F, An example of the effect of HVC surface cooling on synaptic transmission between HVC_RA cells (ΔT = 0 °C (red), ΔT = - 4 °C (black), ΔT = -9 °C (blue)). Thick solid lines are trial aver aged membrane potential trace, thin lines are individual traces; arrowheads mark average synaptic potential onsets at different temperatures. G, Cooling HVC slows synaptic transmission between HVC_RA neurons by 75-300% per 10 °C. Synaptic onset laten cies (n=9 HVC_RA): 2.9 ± 0.5 ms at ~40 °C versus 5.7 ± 0.6 ms at ~32 °C). Note the difference of y-axis scales in Figure 2C and 2F, 2I. H, Schematic diagram of the experimental setup to measure orthordomically evoked latencies. I, Examples of typical dilation effect of HVC surface cooling on the action potential responses to stimulation of HVC afferents (Uva, n = 6; NIf, n = 1). J, Manipulating HVC temperature increases action potential latencies (n = 3 HVC_RA, n = 4 HVC_X); 5.8 ± 0.8 ms at ~40 °C versus 8.6 ± 0.8 ms at ~3 2 °C, mean ± SEM. Orange hatched region represents the range of Q₁₀ of syllables and gaps; 1.27 ± 0.14 (mean ± SD).

We then measured the temperature dependence of synaptic transmission between HVC_RA neurons in urethane-anesthetized zebra finches. We made intracellular recordings from electrophysiologically identified HVC_RA neurons (Dutar et al., 1998; Mooney, 2000) and measured synaptic responses evoked in these cells by antidromically stimulating a subset of other HVC_RA neurons (i.e., antidromic action potentials invade local HVC_RA collaterals that form excitatory synapses on other HVC_RA cells as well as other HVC neurons)(Mooney and Prather, 2005). Using the same Peltier device employed for behavioral experiments (Figure 2E), we found that manipulating HVC temperature exerted a significantly greater effect on synaptic transmission between HVC_RA neurons than on song timing (Figure 2F, G; Q₁₀ = 2.5 ± 0.3; n = 9 HVC_RA neurons; P < 0.01). We also made whole cell voltage clamp measurements in brain slices prepared from adult male zebra finches and varied the bath temperature to further characterize the temperature dependence of monosynaptic transmission between HVC_RA neurons. Antidromic stimulation of HVC_RA axons near HVC’s caudal margin elicited short latency excitatory postsynaptic currents (EPSCs) in HVC_RA neurons, the onset times of which exhibited a temperature dependence significantly greater than that observed for song timing following surface cooling of HVC (Figure S2A-C; n = 10 cells, Q₁₀ = 1.91 ± 0.19, P < 0.001).

We note that a Q₁₀ value ~2 is consistent with the known temperature dependence of many features of neuronal excitability, including voltage-dependent calcium, sodium and potassium currents, synaptic transmission times in both vertebrates and invertebrates, and rhythms in oscillatory networks, measured across a wide range of physiological temperatures (Hodgkin and Katz, 1949; Nobile et al., 1990; Sabatini and Regehr, 1996; Soofi et al., 2014; Taylor, 1988). Indeed, in addition to synaptic transmission between HVC_RA neurons, voltage-dependent calcium currents in these cells are another biophysical feature hypothesized to contribute to activity propagation in local chain models of HVC (Long et al., 2010). Therefore, we made in vitro whole cell voltage clamp recordings from HVC_RA neurons to measure the rise times (i.e., onset to peak) of pharmacologically isolated voltage-dependent calcium currents. Varying the bath temperature revealed that the rise times of these currents display a classical temperature dependence, with a Q10 ~2.5 (Figure S2D-F, n = 8 cells, Q₁₀ = 2.51 ± 0.51). Synaptic transmission between other HVC neuron types, including interneurons and different types of projection neurons (PNs), could also contribute to or influence activity propagation through a chain local to HVC. Therefore, we used sharp intracellular electrodes to record from pairs of mono- and disynaptically coupled HVC_RA neurons, HVC_X neurons (an HVC PN type that innervates the striatopallidal region Area X), and HVC interneurons (HVC_INT). Recordings from a variety of synaptically connected neuron pairs revealed a temperature dependence of synaptic transmission in HVC with a Q₁₀ ~2.7 (Figure S2G-I, n = 10 pairs, Q₁₀ = 2.67 ± 0.31). Therefore, several features of the local HVC circuit likely to be important to activity propagation through a local chain exhibit temperature dependencies that are much greater than the dependence of song timing on HVC temperature.

We also investigated how focal cooling of HVC affected the orthodromic propagation of afferent activity to HVC, reasoning that synaptic transmission from these afferents should show a temperature dependence similar to that observed with antidromic stimulation of HVC_RA synapses. Indeed, focally cooling HVC while electrically stimulating either the telencephalic nucleus interface (NIf) or the thalamic nucleus Uva revealed that the latencies of synaptic and action potential responses recorded in either HVC_RA or HVC_X neurons showed a temperature dependence similar to that measured between HVC_RA cells (Figure 2H-J, Q₁₀ = 2.01 ± 0.22, n = 3 HVC_RA, n = 4 HVC_X neurons; synaptic data from one HVC_X cell is from NIf stimulation, and the other data are from Uva stimulation; the Q₁₀ values of orthodromic response latencies were not significantly different from Q₁₀ values of antidromic response latencies measured in vivo in the nine HVC_RA cells described previously, P = 0.57). In summary, focally manipulating HVC temperature reveals that propagation times between HVC_RA neurons and between HVC’s afferents and HVC PNs exhibit classical temperature-dependencies, which are markedly greater than the temperature dependence of song timing measured in response to focal cooling of HVC.

Transmission through the distributed recurrent network and song timing exhibit similar temperature dependencies

Given that manipulating HVC temperature exerts disparate effects on activity propagation within HVC and on song timing, we sought to test how focally manipulating the temperature of HVC affects activity propagation through the distributed recurrent forebrain – brainstem network that includes HVC as a component. This network links the right and left HVC through an ipsilateral efferent pathway to the brainstem vocal respiratory group (VRG) and through bilateral afferent pathways from the rostral VRG (rVRG) through the thalamic nucleus Uva and the telencephalic nucleus NIf to HVC (Figure 3A) (Ashmore et al., 2008b; Striedter and Vu, 1998). The bilateral symmetry of this circuit allowed us to measure activity propagation times through the entire recurrent network by unilaterally stimulating HVC and recording evoked synaptic responses in the contralateral HVC of anesthetized birds (Figure 3A). At normal brain temperatures under urethane anesthesia (~38 °C), the mean latencies fo r evoked synaptic and action potential onsets were consistent with a circuit involving ~4-5 synapses (synaptic latency; 18.5 ± 0.7 ms; action potential latency; 23.3 ± 2.3 ms; n = 7 HVC_RA neurons, n = 4 HVC_X neurons), and also consistent with prior measurements of interhemispheric conduction times (Ashmore et al., 2008a). Cooling HVC either bilaterally or unilaterally on the side of the recording delayed synaptic potential onsets and action potential latencies to a similar extent (Figure 3B, C, Figure S3; Q₁₀ SYN = 1.23 ± 0.05; Q₁₀ AP = 1.19 ± 0.06; P = 0.68, t-test). In contrast, unilaterally cooling the stimulated side did not affect activity propagation times through the recurrent network (Figure S3), indicating that the delays observed with bilateral cooling can be largely attributed to the temperature-dependent slowing of synaptic transmission within HVC on the side of the recording. Notably, bilateral cooling of HVC exerted nearly identical effects on activity propagation through the entire recurrent network and on song timing (Figure 3D, Q₁₀ values of network versus song, P = 0.6, t-test).

Figure 3. Temperature exerts highly similar effects on synaptic transmission through a distributed recurrent network and on song tempo.

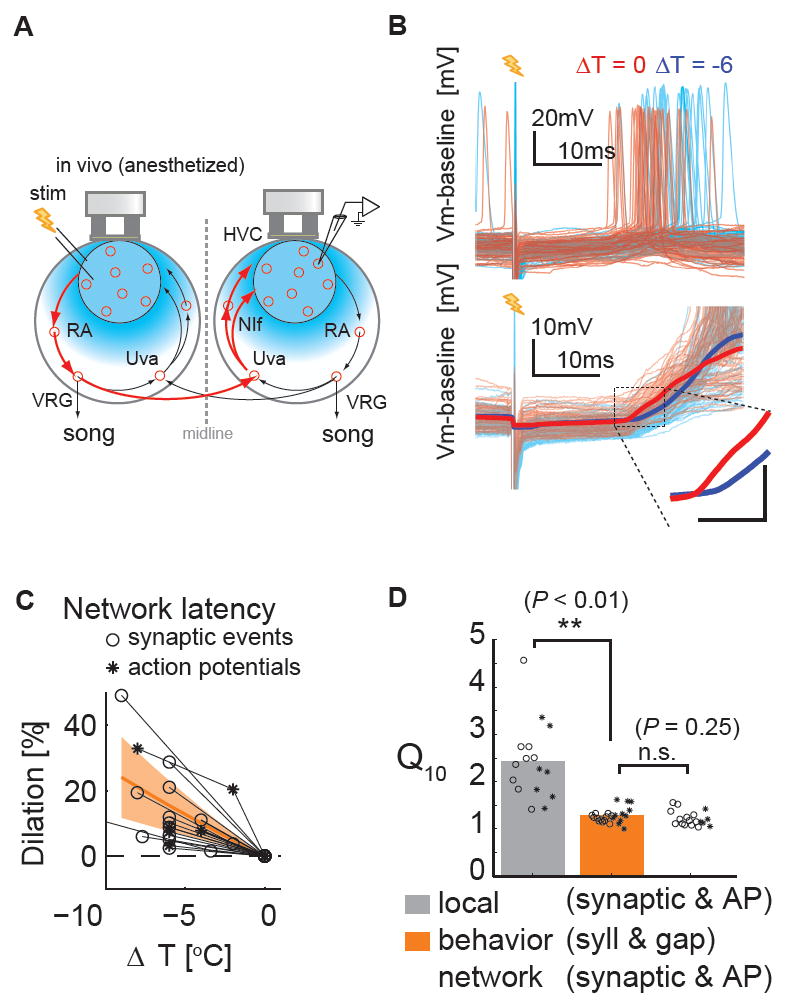
A, Schematic diagram of the experimental setup to measure recurrent network interactions. The minimum number of synapses mediating inter-hemispheric (red pathway) and intra-hemispheric HVC interactions (arrows enclosed within a single hemisphere) is the same (four). B, Typical examples of the effects of bilateral HVC surface cooling on the action potential (Top) and synaptic responses (Bottom) evoked in HVC by contralateral HVC stimulation. Scale bar in the inset is 5 ms × 5 mV. C, Manipulating HVC temperature bilaterally slows inter-hemispheric activity transmission. Synaptic latencies (circles): 18.5 ± 0.7 ms at ~38 °C versus 19.2 ± 0.6 ms at ~32 °C. Action p otential (AP) latencies (asterisks): 23.3 ± 2.3 ms at ~38 °C versus 25.6 ± 2.0 ms at 32 °C. (n= 8 HVC RA, n = 5 HVC_X neurons; n = 13 synaptic onsets, n = 5 APs). Orange hatched region; same as Figure 2C,F,I. Synaptic latencies (circles); action potentials latencies (asterisks). D, Q₁₀ values of song timing (syllables (circles); gaps (asterisks)) are significantly different from Q₁₀ values of HVC local interactions (P < 0.01), but not significantly different from Q₁₀ values of recurrent network interaction (P = 0.25). t-test, ** P < 0.01.

Cooling a thalamic node in the distributed recurrent network also slows song timing

An expected feature of a distributed model is that temperature manipulations at network nodes other than HVC should also affect song timing. One challenge to testing this idea is that manipulating temperature at one site in the zebra finch brain can also affect temperature at other sites. In fact, a prior study determined that manipulating temperature at the surface of HVC affects temperature in the song motor nucleus RA (Long and Fee, 2008), making it difficult to decouple the effects of temperature changes in HVC and RA on song timing. Therefore, we sought to manipulate temperature in a node in the recurrent network that was sufficiently distant from HVC to better decouple these temperature effects. We first measured temperature changes in several song nuclei in the recurrent network (HVC, RA, and Uva) during HVC surface cooling. We found that manipulating temperature at the surface of HVC exerted a moderate effect on temperature in RA but an almost negligible effect on temperature in Uva (< 3% of ΔT_HVC ; Figure 4A). Consequently, the effects on song timing resulting from surface cooling of HVC cannot be accounted for by indirect cooling of Uva.

Figure 4. Cooling the thalamic nucleus Uva slows song tempo in a manner consistent with a distributed timing mechanism.

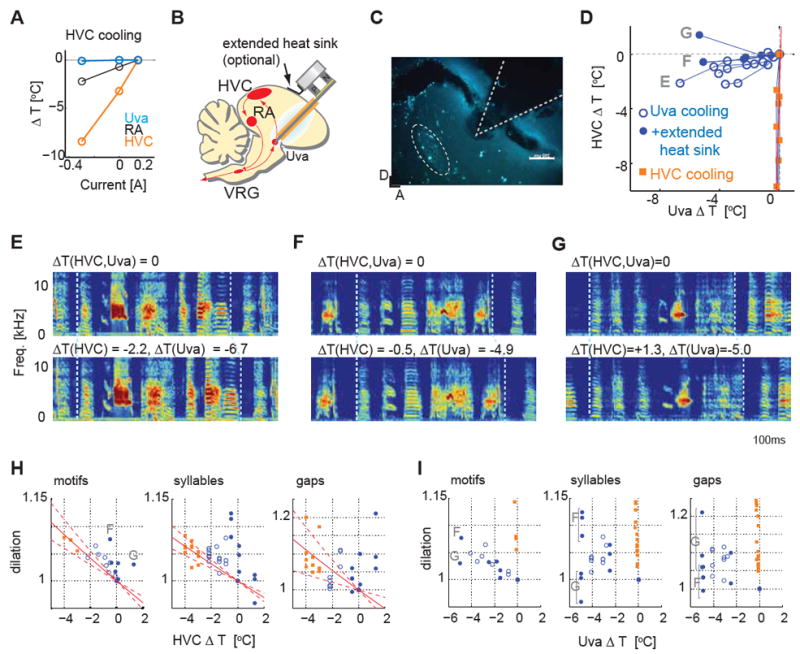
A, Effect of HVC cooling on other song nuclei; HVC cooling did not change Uva temperature. B, Schematic diagram of deep brain cooling targeting Uva. C, An example of a histological reconstruction of the probe tip position near Uva, labeled with retrograde tracer injection into HVC. D, Temperature changes measured in HVC and near Uva caused by Uva cooling (filled/open circles, with/without extended heat sink) and by HVC cooling (squares). E, Effect of cooling Uva bilaterally on song timing using the simple Peltier device. F, G, Two examples showing the effect on song timing of cooling Uva bilaterally using the modified Peltier device in which an extended heat sink offsets the cooling effects of the Uva cooling probe on HVC temperature. H, Dilation effects plotted as a function of ΔT(HVC). The dilation effects induced by Uva cooling largely fall outside of the range calculated from HVC cooling (red dashed lines: 1SD region). Same symbols are used as in D. I, Dilation effects plotted as a function of ΔT(Uva) showing that changes in Uva temperature also significantly affected song timing.

We then used a deep brain cooling probe (Aronov and Fee, 2011) implanted slightly dorsal to Uva (Figure 4B,C; Figure S4A, B) to establish that manipulating temperature in Uva strongly affected song timing (Figure 4D, E). Because the Uva cooling probe exerted a moderate effect on temperature in HVC in some birds (Figure 4D, open circles; n = 4 birds), we further modified the Peltier device to isolate the contribution of Uva on song timing. The modified Peltier device added an extended heat sink that was placed on the surface of the skull in between the shaft of the Uva cooling probe and HVC (Figure 4B, D; filled circles, n=3 animals, Figure S4C-E). In this modified Peltier device, the heat sink changes its temperature in the opposite direction from the cooling probe placed in Uva, therefore offsetting most or all of the cooling effect that the probe exerts on HVC. Using this modified probe in two birds, we still observed a clear slowing effect on song timing with Uva cooling even though the temperature of HVC was nearly unchanged (Figure 4F; -0.5 and -0.1 °C change in HVC; -4.9 an d -2.5°C change in Uva, respectively for each bird). In a third bird, the song still stretched slightly even though HVC temperature slightly increased when Uva was cooled (Figure 4G; Figure S4F; +1.3 °C in HVC, -5.0 °C in Uva). If HVC were the sole timekeeper, then this bird’s song should have compressed rather than stretched.

To observe the effect of Uva cooling on song timing, we plotted the song dilation effects as a function of HVC temperature (Figure 4H). If Uva cooling exerted no effect on song, song dilation values should fall within the confidence limit calculated from HVC cooling data. Behavioral data from Uva cooling experiments, especially those performed with the extended heatsink, fell largely outside of this range at all levels of song structure, including motifs, syllables, and inter-syllable gaps. This indicates that cooling Uva exerted a significant effect on song timing that cannot be explained by HVC temperature changes. To visualize the effect of Uva cooling from a different perspective, we also plotted the song dilation effects as a function of Uva temperature (Figure 4I). The distribution of dilation effects showed that song timing is influenced by Uva temperature.

To investigate the significance of the Uva temperature effect on song timing while simultaneously incorporating the effect of HVC temperature changes, we used a linear regression analysis. This analysis defines the plane that minimizes the error between the observed song dilation and the song dilation that is predicted given the temperature changes in Uva and HVC (Figure 5A). The regression coefficients represent the contribution of HVC and Uva temperature changes to changes in song timing. The Q₁₀ values calculated from these regression coefficients showed that both HVC and Uva contributed significantly to the timing of song motifs, syllables, and inter-syllable gaps (Motifs: Q₁₀(HVC) = 1.20 ± 0.04, Q₁₀(Uva) = 1.10 ± 0.02. Syllables: Q₁₀(HVC) = 1.17 ± 0.12, Q₁₀(Uva) = 1.09 ± 0.04. Gaps: Q₁₀(HVC) = 1.20 ± 0.11, Q₁₀(Uva) = 1.14 ± 0.07, mean ± 99 percentile range calculated from a bootstrapping method, see Methods for converting regression coefficients to Q10 values). The slope of the fitted plane is indicated by a vector in HVCΔT-UvaΔT space, with the direction of the vector indicating the relative contributions made by HVC and Uva to song timing (Figure 5B). This analysis supports the conclusion that temperature changes in Uva significantly affect all levels of song timing, including motifs, syllables and gaps (Figure 5C, p<0.01).

Figure 5. Linear regression analysis revealed significant contribution from Uva on song timing control.

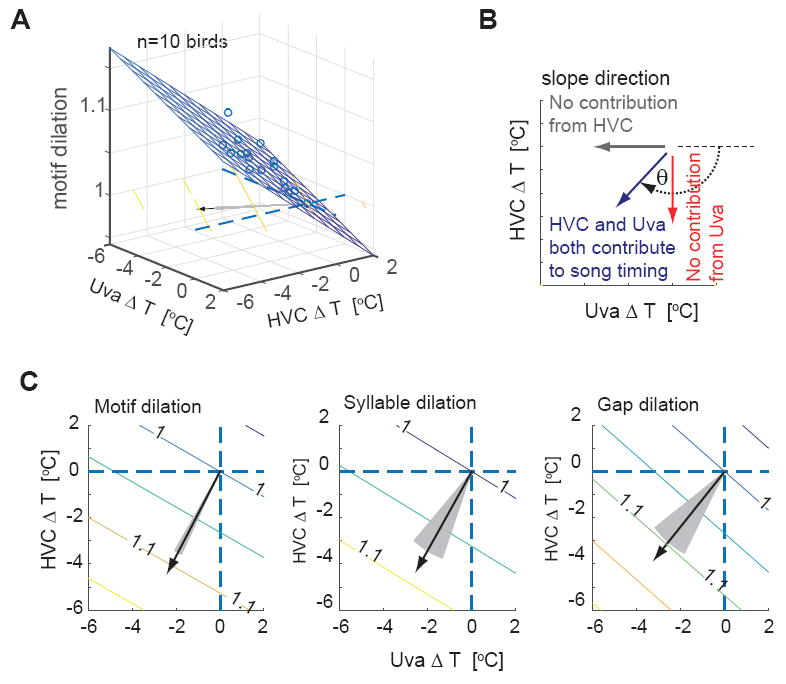
A, Linear regression analysis of the motif dilation. The slope of the regression plane is indicated by a vector (black arrow). B, The angle θ of the slope vector represents the contributions from HVC and Uva. C, The slope vectors for motif, syllables, and gaps, which are shown with equivalent lengths, were well separated from both the HVC and Uva axes (p<0.01), indicating that both HVC and Uva contribute significantly to song timing. (Motif: θ = -0.65 π ± 0.02, ratio (HVC/Uva contribution) = 1.90 ± 0.33; Syllable: θ = -0.67 π ± 0.09, ratio = 1.80 ± 1.05, Gap: θ = -0.70 π ± 0.07, ratio = 1.36 ± 0.71 (mean ± 3SD). The slope vectors were closer to the HVC temperature axis (vertical dashed line) than the Uva temperature axis (horizontal dashed line), suggesting that the contribution to song timing from HVC is relatively stronger than that from Uva. Gray shaded region; 2SD region calculated using a bootstrapping method.

One possibility is that cooling Uva reduces tonic drive to HVC neurons, diminishing their ability to participate in a local network process important to song timing. In fact, such a process has been invoked to explain the transient effects on song that accompany lesions made to another of HVC’s afferents, the telencephalic nucleus interface (NIf) (Naie and Hahnloser, 2011; Otchy et al., 2015). We believe that such a simple role for Uva is unlikely, because Uva lesions permanently disrupt song (Coleman and Vu, 2005), multiunit activity patterns in Uva of singing birds are not tonic (Williams and Vicario, 1993), and the modest changes in temperature (~5 °C) achieved with the implanted cooling probe are unlikely to inactivate Uva neurons. Nevertheless, to begin to explore this possibility, we made sharp intracellular recordings from electrophysiologically identified HVC_RA and HVC_X neurons in isoflurane anesthetized male zebra finches and measured their membrane potential activity while we reversibly cooled Uva (n = 10 cells from 3 birds in which behavioral cooling experiments were performed using the modified Peltier device with the extended heat sink). Reversibly cooling Uva to the same degree as achieved in behavioral experiments exerted no effect on the resting membrane potential of HVC PNs or on their spontaneous synaptic or action potential activity (Figure S5, P = 0.39, paired t-test). Although these experiments were performed in anesthetized birds, they support the idea that the effects of cooling Uva on song timing are not simply the result of removing tonic excitatory drive to HVC.

Distributed recurrent models predict synaptic correlations between HVC neurons

The finding that manipulating either HVC or Uva temperature could affect song timing provides empirical support for a distributed recurrent model for song timing, yet prior modeling efforts have focused on the idea that highly structured activity in HVC derives from local chain mechanisms. This raises the question of whether and how such structured activity in HVC could arise from a distributed and recurrently connected forebrain - brainstem circuit, and whether such a distributed model displays characteristic features that are similar to or distinct from those found in the simple class of local chain models proposed to account for sequential activity potential activity in HVC. To begin to address these issues, we constructed computational models of distributed and local chain networks that relied on minimal assumptions. Following experimental observations (Long et al., 2010, Hahnloser et al., 2002), we applied the following constraints to the models: i) ~50% of HVC_RA neurons generate action potentials during singing; ii) synaptic activity is non-zero outside of action potential timings; iii) the patterns of synaptic events and action potentials for a given HVC_RA neuron are temporally precise and reproducible between motifs (or runs of the network simulations).

We first simulated a distributed chain model in which sequential action potential activity repeatedly propagated through four groups of neurons, representing four nodes of the distributed forebrain-brainstem network that includes HVC (Figure 6A). For each group, a set of excitatory neurons was randomly selected to represent one time point in the song and these neurons were connected to neurons in the next group. The fourth group was connected to the first group, forming a circular chain structure. This process was repeated to generate a longer (100 layer) chain structure embedded in the recurrent distributed network, which was of sufficient length to generate ~500ms of activity, which is the duration of a typical zebra finch motif (see details in Methods). In addition to this long-range feedforward excitatory structure, both excitatory and inhibitory neurons were locally interconnected, which allowed the network to generate subthreshold synaptic activity in addition to precisely timed and temporally sparse action potential activity.

Figure 6. Simulations of local and distributed chain models can generate sparse sequential activity, but with different levels of correlated synaptic activity in HVC.

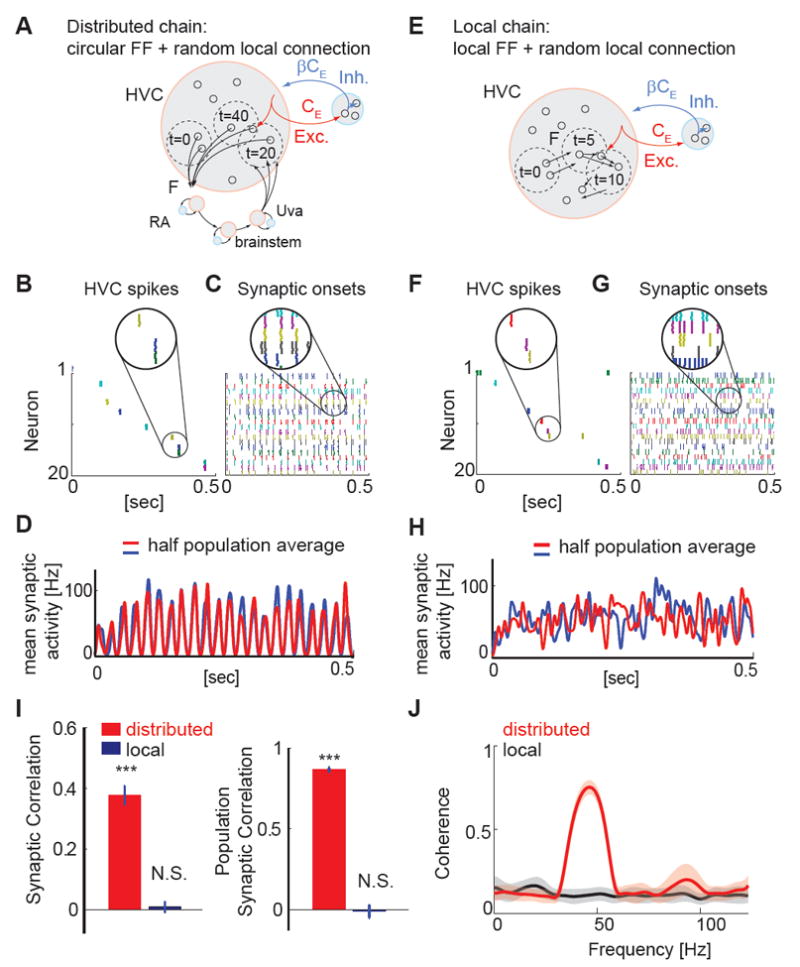
A, Schematic showing the structure of the distributed chain network: The excitatory neurons are grouped into four pools, representing HVC, RA, VRG, and Uva. Excitatory neurons form feedforward connections to the next group. The excitatory neurons and inhibitory neurons also form random recurrent connections within the group. F is the ratio of active neurons engaged in the chain of action potential activity. C_E (βC_E) is the number of presynaptic excitatory (inhibitory) neurons per single neuron in the form of random connections. B, C, Spike rastergrams (B) and synaptic onset rastergrams (C) of 20 randomly selected neurons, constructed from 5 runs of simulations. Only HVC neurons are shown. D, Population averaged synaptic onset activity calculated from half of the population (red, n=10) and from the other half of the population (blue, n=10). In the distributed chain model, the temporal profiles of population synaptic activity are highly similar. E, Local chain model: Groups of excitatory neurons form feedforward connections (FF) and excitatory and inhibitory neurons also form random recurrent connections. F, G, same as B, C. H, Population averaged synaptic onset activity calculated from each half of the randomly selected 20 neurons. In the local chain model, there is no obvious temporal structure common in the two groups of neurons. I, Left: Synaptic correlation (the correlation coefficient of the simulated synaptic onset patterns) of pairs of neurons revealed significant non-zero correlations in the distributed chain model (P < 0.001), but not in the local chain model (P = 0.66). Right: Population synaptic correlation (the correlation of population averaged synaptic event rates) of two randomly selected groups of neurons in either the distributed chain model (P < 0.001) or the local chain model (P = 0.73). Data were generated from the average of 5 realizations of networks, each containing 5 runs of simulations. t-test. J, Magnitude-squared coherence spectrum of the synaptic event rate calculated from pairs of simulated neurons (n = 10 cells). Neurons in the distributed chain model exhibited a clear peak around ~40 - 50 Hz reflecting the periodic occurrence of synaptic inputs at ~20 - 25 msec intervals. In contrast, a coherence analysis of neurons in the local chain model revealed no clear indication of periodicity within the 0 - 100 Hz range.

The overall population activity in the “HVC” group of this distributed chain model exhibited sequential activity patterns (Figure S6F). Randomly sampling 20 excitatory neurons from the HVC group revealed temporally sparse and sequential action potential activity (Figure 6B, Figure S6H). The synaptic activity underlying these sparse action potential bursts was frequent and reproducible within a cell from one motif to the next, as observed for HVC_RA neurons in singing zebra finches (Hahnloser et al., 2002; Hamaguchi et al., 2014; Long et al., 2010). Notably, synaptic onsets in different neurons tended to align closely (Figure 6C). In fact, the onset times of synaptic activity measured in pairs of neurons and the population-averaged synaptic activity both exhibited significantly positive correlations and a strong peak in the coherence spectrum was detectable at ~50 Hz, a feature that reflects the propagation time through the four nodes of the recurrent network (Figure 6D, I, J). These were consistent features of the distributed network model across the range of parameters where sequential activity propagated in a stable manner (Figure S6J,K).

We also explored whether the synaptic activity patterns evident in our recurrent distributed model were similar to those in the class of local chain models similar to those previously used to account for sequential activity propagation in HVC (Jin et al., 2007; Li and Greenside, 2006). To simulate the activity of a local chain (Figure 6D), we constructed a model consisting of excitatory neurons functionally organized in a feedforward chain network. A random set of excitatory neurons was selected to represent HVC_RA neurons and these neurons were connected to another set of randomly selected HVC_RA neurons to form a local chain structure. This process was repeated to form a chain network comprising 100 layers in total to generate ~500ms of activity, as with the distributed model. Furthermore, both excitatory and inhibitory neurons were sparsely interconnected, which allowed the network to generate subthreshold synaptic activity in addition to precisely timed and temporally sparse action potential activity. The incorporation of these sparse, random connections and the eligibility of individual neurons to participate in more than a single node in the chain distinguish this model from prior local network models of HVC, which focused on the stability of action potential burst propagation through a strictly feedforward network (Jin et al., 2007; Li and Greenside, 2006).

Similar to these strictly feedforward models, our local chain model displayed sequential action potential activity that propagated through groups of neurons in a stable manner (Figure 6E). Additionally, randomly sampling the membrane potential activity of 20 excitatory neurons in this network revealed that baseline synaptic activity was non-zero and within a cell was stereotyped between runs (Figure 6F, Figure S6D). However, unlike in the distributed chain model, no significant correlation was detected in the onset times of synaptic activity measured in pairs of neurons, or in the average synaptic activity measured in larger subpopulations of these cells (Figures 6H, I), and we also failed to detect a strong coherence peak in the range between 0 and 100 Hz (Figures 6J). A remaining possibility is that neurons in a local chain model will display higher synaptic correlation levels as the number of local presynaptic connections (C_E) is increased, because neurons in these more densely connected networks will have a higher probability of sharing presynaptic neurons. However, we found that changing the number of presynaptic neurons did not change the correlation level of local chain models (Figure S6I). These features were highly robust in the face of variations in network structure within the range of parameters where sequential activity propagates in a stable manner (Figure S6J,K). Therefore, synaptic activity is not correlated between neurons in the class of local chain models in which stable propagation of action potential activity is maintained by a uniform chain of excitatory neurons. Furthermore, while temporal non-uniformities in propagating activity in a local chain could lead to pair-wise correlations in synaptic events, such non-uniformities have yet to be demonstrated in local chain models of HVC circuitry.

In summary, both local and distributed models investigated here could generate sparse sequential action potential activity, but only the distributed model displayed high levels of correlated synaptic activity. This difference can be attributed in part to the difference in network structure of the two models. Although both models exhibit the same sequential action potential activity, HVC neurons in the distributed chain model receive transient synaptic inputs once every four propagation steps, while at other times synaptic inputs remain relatively silent. The temporal organization of active and silent phases of synaptic activity, which contrasts with the uniform action potential and synaptic activity of the local chain model, generates detectable membrane potential correlations and coherence peaks between HVC neurons.

HVC Neurons in Singing Zebra Finches Display Correlated Synaptic Activity

To determine whether synaptic activity patterns in HVC neurons display correlations like those of neurons in either distributed or local chain models, we made sequential sharp intracellular recordings from multiple HVC PNs in freely singing zebra finches (Figure 7A,B). We identified HVC_RA neurons using antidromic stimulation methods (Figure 7B, C) and identified HVC_X neurons by their characteristically higher spontaneous firing rates and the membrane potential hyperpolarizations that typify their singing-related activity patterns (Long et al., 2010, Hamaguchi et al., 2014) (Figure 7D). Consistent with previous studies (Hahnloser et al., 2002, Kozhevnikov and Fee, 2007), half (n = 12/24) of the HVC_RA neurons we recorded from generated action potentials at a precise time in the song, whereas the rest were non-spiking. Furthermore, different HVC_RA cells from the same bird generated bursts of action potentials at different times in the song such that, as a population, these bursts could be sequentially arrayed when aligned to the song motif (Figure 8A, B), as previously described (Hahnloser et al., 2002).

Figure 7. Examples of intracellular recordings of HVC PNs in singing birds.

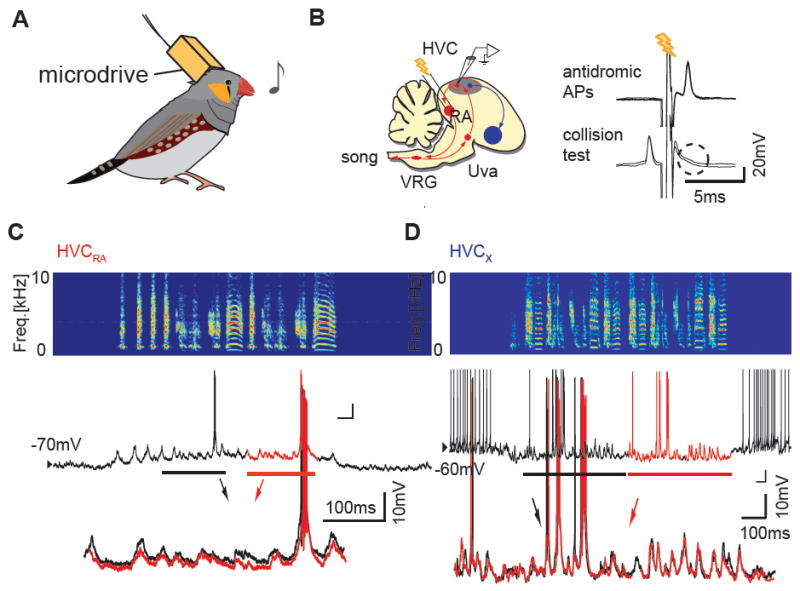
A, Schematic of sharp intracellular recordings in singing birds. B, Left: Schematic diagram of song motor pathway (red) and a part of the basal ganglia pathway (blue; Area X). Right: An example of antidromic identification of an HVC_RA neuron using a spike collision test. C, An example of synaptic and action potential activity of an identified HVC_RA neuron. Top: sonogram, Middle: membrane potential, Bottom: enlarged and overlaid membrane potential traces from two consecutive motifs reveal highly stereotyped synaptic activity. D, An example of synaptic and action potential activity of a putative HVC_X neuron recorded in another bird; overlaid membrane potential traces from two consecutive motifs also reveal stereotyped synaptic activity.

Figure 8. Correlated, high frequency synaptic activity underlies temporally sparse, sequential action potential patterns in HVC.

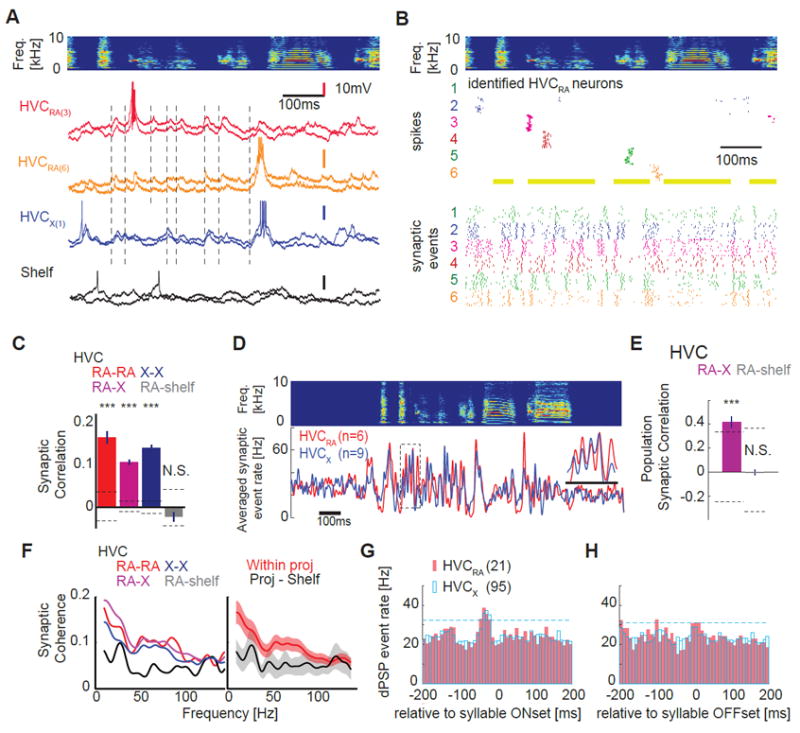
A, Top: sonogram of a single motif. Bottom: Examples of precisely timed membrane potential traces from different HVC PNs and a cell outside of HVC (HVC shelf) during singing; membrane potential records from two motif renditions are shown (light versus dark color), with different colors corresponding to different cells (HVC_RA (3) and HVC_RA (6) corresponds to cell #3 and #6 in Figure 8B). Occurrences of correlated synaptic onset timings are highlighted with vertical dashed lines. B, Motif-aligned sequential action potentials (middle) and synaptic onsets (bottom) in six identified HVC_RA neurons recorded from the same zebra finch; neurons with at least ten motif renditions are selected, with different colors depicting different neurons. C, Synaptic event timings between individual HVC projection neurons are all correlated (significantly non-zero); HVC_RA - HVC_RA pairs (red; Correlation Coefficient (CC) = 0.17 ± 0.04; n = 25 pairs, P < 0.001, t-test compared with shuffled data); HVC_X - HVC_X pairs (blue; CC = 0.11 ± 0.01; n = 177 pairs, P < 0.001); HVC_RA – HVC_X pairs (purple; CC = 0.14 ± 0.02; n = 137 pairs, t-test, P < 0.001). No significant difference was detected between different PN pairs (P > 0.15). No significant correlation in synaptic activity was detected between cell pairs involving HVC_RA cells and cells outside of HVC (Shelf, gray; CC = -0.02 ± 0.03; n = 15 pairs, P = 0.32). Dashed lines: 3SD from shuffled data. Error bars: SE. D, Averaged synaptic event rates obtained from the same bird showed striking similarity of input timings between two the projection neuron classes (HVC_RA and HVC_X cells). E, The temporal structure of synaptic input timings are highly similar in HVC_RA and HVC_X populations (purple; HVC_RA – HVC_X groups; n = 4 birds, CC = 0.41 ± 0.13, P < 0.001) but not in HVC_RA and Shelf populations (gray; HVC_RA – HVC shelf groups; n = 4 birds, CC = 0.01 ± 0.07, P = 0.95). Dashed lines: 3SD generated from shuffled data. F, Left: the magnitude-squared coherence spectrum calculated from pairs of HVC neurons (same color codes as in C) showed a broad peak ~ 50 Hz, which was not evident in HVC_RA - HVC shelf neuron pairs. Right: grouped average of magnitude-squared coherence calculated within HVC projection neurons (red) and between HVC projection neurons and HVC shelf neurons (black). G,H, Synaptic events precede sound onsets but not offsets in both HVC_RA and HVC_X cell types. dPSP peak at -37.6 ± 0.48 ms (n=21 HVC_RA), -33.1 ± 0.15 ms (n=95 HVC_X). Dashed lines are 2 SD of dPSP rate. A subset of HVC_X cell data was presented in [Hamaguchi and Mooney 2014].

In contrast to their temporally sparse and sequential action potential activity patterns, different HVC_RA cells from the same bird exhibited relatively high frequency (~30-60 Hz) and highly stereotyped patterns of depolarizing postsynaptic potentials (dPSPs), the timing of which was highly similar between pairs of HVC_RA cells (Figure 8A, B; see Figure S7A, B and Methods for dPSP detection methods). To quantify the similarity of this synaptic timing in different HVC PN pairs, we calculated the correlation coefficients of the trial-averaged dPSP rates (i.e., signal correlations) from pairs of PNs recorded in the same bird. This analysis revealed that singing-related synaptic activity patterns within pairs of HVC_RA neurons were significantly correlated (Figure 8C). Significant synaptic correlations were also detected between HVC_X neuron pairs and between pairs of HVC_RA and HVC_X neurons, but not between HVC_RA cells and neurons located just ventral to HVC, suggesting that the similar patterns of synaptic activity in HVC PNs did not reflect a non-specific, global synchronization of brain activity (Figure 8C). Moreover, the relative timing of synaptic inputs to individual HVC_RA and HVC_X cell pairs was not significantly biased from time lag zero (Figure S7C, D), confirming that our correlation coefficient analysis captured most of the correlational events in the system and suggestive of periodic alignment in global HVC activity. A similar correlation coefficient analysis at the HVC PN population level also revealed that synaptic input timings were significantly similar and correlated (Figure 8D, E). Further, a coherence analysis between pairs of HVC PNs revealed a peak ~50 Hz (Figure 8F), similar to the peak detected in the distributed recurrent network model, as well as a broad peak below 20 Hz indicative of slower temporal modulation of synaptic activity. Finally, dPSP onsets in HVC_RA and HVC_X neurons more frequently occurred slightly before syllable onsets but not around syllable offsets (Figure 8G,H), suggesting that respiratory activity associated with syllable onsets could drive correlated synaptic activity in populations of HVC neurons. Therefore, singing-related synaptic activity patterns in HVC display certain characteristics, including periodic signatures and possible respiratory elements, consistent with the known architecture of the recurrent forebrain-brainstem network in which HVC resides.

DISCUSSION

The forebrain song nucleus HVC plays a critical role in learned vocalizations through its indirect connections with brainstem vocal respiratory networks. The observations that HVC_RA neurons fire in a temporally precise and sparse manner during singing and that focal cooling of HVC stretches song have been cited as evidence of a localized mechanism that encodes song timing (Fee et al., 2004; Hahnloser et al., 2002; Long and Fee, 2008). Despite the simple beauty of this model, a variety of evidence suggests that song timing is the product of a more distributed mechanism that includes HVC as a component. For example, unilateral HVC cooling stretches only part of the song (Long and Fee, 2008), consistent with the idea that song timing is the product of coordinated bilateral HVC activity (Schmidt, 2003; Schmidt and Wild, 2014). Because the right and left HVC are not directly connected with each other, such bilateral coordination presumably depends on ascending bilateral projections from the brainstem rVRG to the thalamic nucleus Uva (Striedter and Vu, 1998), which is afferent to HVC (Nottebohm et al., 1982). Notably, microstimulation in the rVRG can interrupt singing (Ashmore et al., 2005) and lesions made in Uva severely disrupt temporal features of song (Coleman and Vu, 2005), suggesting that bottom up projections from the brainstem also play a role in song timing. Moreover, more extreme cooling of HVC in the canary causes longer syllables to break into smaller parts (Goldin et al., 2013), a phenomenon that cannot be accounted for by a top-down model of song control and that instead is most readily explained by reciprocal interactions between brainstem respiratory pattern generating networks and HVC (Alonso et al., 2015; Gibb et al., 2009).

We sought to further distinguish between localized versus distributed timing mechanisms by comparing the effects of manipulating HVC temperature on activity propagation either within HVC or through the recurrent network. We found that focal cooling of HVC exerts a three- to four-fold greater effect on activity propagation through the HVC_RA network than on song timing. (This disparity is a conservative estimate because HVC was cooled from its dorsal surface and temperature was measured from its ventral side, consequently the actual temperature changes in dorsal HVC were likely even more pronounced (Figure S4G).) These results indicate that a chain of synaptically linked HVC_RA neurons is unlikely to be the major source of timing signals for song motifs, syllables or intersyllable gaps. While measuring the temperature dependencies of all of the biophysical components of the HVC network is currently impractical, voltage-dependent calcium currents in HVC_RA neurons, which are implicated in singing-related bursting activity in these cells (Long et al., 2010), also exhibited a temperature dependence far in excess of the changes in song timing seen with surface cooling of HVC. Finally, we found that focally cooling HVC exerts similar effects on song timing and the activity propagation time through the recurrent network, consistent with the idea that focal cooling of HVC only modestly slows song timing because it affects only a small part of the timing network. Taken together, these findings support a distributed, recurrent network for song timing, and suggest that HVC local circuitry contributes less than half of the synaptic relays to activity propagation through this network.

The current findings do not exclude an important role for HVC local circuitry in vocal patterning. For example, recent experiments in Bengalese finches show that cooling HVC affects syllable transition probabilities (Yisi Zhang, 2015), suggesting that a mechanism local to HVC influences sequence transitions. The precise timing of action potential bursts in HVC PNs, which is determined by the balance of excitatory and inhibitory inputs onto these cells, is speculated to determine these sequence transitions. Because HVC PNs receive excitatory input from each other and inhibitory input from local interneurons (Kosche et al., 2015; Mooney and Prather, 2005), local circuitry can regulate the PN action potential timing (Rosen and Mooney, 2003) and thus could help regulate syllable transitions. Local excitatory and inhibitory interactions could provide additional nodes that contribute to song timing, which may account for why cooling HVC affects some syllables and gaps more than others (Figure 3D). Finally, the results of the regression analysis also suggest that HVC may contribute relatively more to song timing than does Uva (Figure 5C; see discussion below). Therefore, the song timing mechanism could involve regular and frequent interplay between recurrent network activity and activity propagation in HVC through short local chains of synaptically coupled PNs and interneurons.

We also directly tested the recurrent timing mechanism by cooling the thalamic nucleus Uva, which serves as a critical node in the recurrent network by its projections to HVC and its receipt of bilateral ascending projections from the rVRG and the midbrain dorsomedial intercollicular nucleus (the putative avian homologue of the lateral periaqueductal gray in mammals) (Ashmore et al., 2008b; Striedter and Vu, 1998). We found that cooling Uva stretches song, and used a modified Peltier device and linear regression analysis to determine that these behavioral effects could not be attributed to indirect cooling of HVC, lending further support to a distributed song timing mechanism. A previous study showed that cooling RA, which is downstream of HVC and is also part of the recurrent network, stretches song, but attributed these behavioral effects entirely to the temperature drop in HVC caused by the implanted cooling probes. However, in our hands, HVC surface cooling changes RA temperature (~30% of HVC), and RA cooling also affects HVC temperature (~30% of RA)(Long and Fee, 2008), making it difficult to correctly separate the behavioral effects of cooling either HVC or RA. In contrast, the asymmetric temperature coupling between HVC and Uva and a modified Peltier device enabled us to cool Uva without significantly lowering HVC temperature, revealing an “extra-HVC” effect of cooling Uva on song timing.

An analysis of the vocal effects elicited by focal cooling revealed that Uva’s contribution to song timing is significant, but less than that made by HVC. One explanation for this difference is that the temperature probe’s placement ventral to HVC led us to overestimate HVC’s contribution to song timing. Another possibility is that the actual chain length is longer than the minimum number of synapses necessary to form a circular network involving HVC and the brainstem. Additional links, such as a short local chain within HVC (+1), the VRG (PAm-RAm)-DM-Uva pathway (+2), and the Uva-NIf-HVC pathway (+1), could increase the total number of synapses in the chain to 7 or 8, which would account for a Q₁₀ ~ 1.13 with Uva cooling and a Q₁₀ ~ 1.25 with HVC cooling. A final consideration is that the cooling method used here is not highly focal. Consequently, surface cooling of HVC is likely to also cool other caudal telencephalic song nuclei (i.e., RA, NIf, and Avalanche), which could also play a role in song timing through their recurrent connections with HVC and/or their participation in the recurrent forebrain-brainstem network. That is, song timing is likely to be the product of activity not only in HVC and Uva, but also in other forebrain and brainstem nuclei.

A hallmark of HVC_RA cells is their remarkable capacity to fire action potentials in an ultra-sparse and sequential, clock-like manner during singing (Hahnloser et al., 2002; Lynch et al., 2016; Picardo et al., 2016). The simulation and intracellular recording methods used here suggest that this ultra-sparse action potential activity is generated from recurrent, high frequency (30-60 Hz) and synchronous synaptic inputs rather than simply from a local excitatory chain mechanism. In this model, the rapid propagation times through the recurrent network and the divergent patterns of connectivity from Uva to HVC give rise to correlated synaptic activity, while the specific patterns of convergence of thalamic afferents onto HVC_RA cells result in their ultra-sparse action potential activity. This requires a neural substrate that can reliably transmit action potential activity patterns over multiple synapses, as shown for cortico-basal ganglia pathways in the songbird (Hamaguchi and Mooney, 2012; Kimpo et al., 2003). A general point is that populations of neurons that each fire in a temporally sparse manner can be arrayed in a sequence without necessitating a local chain mechanism. In fact, sequential motor-related neural activity has been detected in several different brain regions of both birds and rodents (Goldberg and Fee, 2010; Harvey et al., 2012; Ito et al., 2015; Peters et al., 2014). Considering the widespread observation of sequential activity over regions of cortex, hippocampus, and basal ganglia, sequential activity patterns in these structures are likely to be the product of distributed mechanisms. Therefore, sequential activity in distributed networks may reflect a general solution to the control of sequential behaviors such as song, speech, and athletic activity.

EXPERIMENTAL PROCEDURES

Subjects

Male zebra finches (n = 41, > 90 days post hatch) were raised in our colony and used in temperature manipulation and intracellular recording experiments. All animal procedures were approved by Duke University Institutional Animal Care and Use Committee. Birds were housed in a sound proof chamber with ad libitum access to food and water.

Temperature manipulation using Peltier device

Custom-built miniature Peltier devices were built based on published techniques (Aronov and Fee, 2011; Long and Fee, 2008). The cooling probes were bilaterally placed over HVC (4.8 mm) or Uva (targeting the medial edge of Uva to avoid damage). For Uva cooling, polyimide tubing (MicroLumen, Inc. #315-I.5, O.D. 873 μm) was also attached to the probes as an insulator to enhance the heat delivery. In a subset of experiments, an extended heat sink was placed on the lower leaflet of the skull to limit temperature changes in HVC caused by the cooling probe implanted in Uva. The temperature change ΔT is defined as the relative difference from the physiologically normal brain temperature (~40 Celsius), which was maintained by running the Peltier device in the slightly warming direction to offset the cooling effect of placing the probe on the surface of the brain (Figure S1F, H). Song timing effects were measured as the relative changes from this “normal” temperature condition. See details of construction methods in Supplemental Experimental Procedures.

Intracellular recordings in singing birds

Intracellular recordings were made in six male zebra finches using the microdrive device we previously reported (Hamaguchi et al., 2014). HVC_RA neurons were identified by antidromic stimulation with a bipolar stimulating electrode (a pair of 75 μm diameter silver wires, ~500 μm apart, A-M systems, WA, USA) implanted in RA. HVC_X neurons were identified by their spontaneous, DC-evoked, and singing-related activity. In total, we recorded from n = 24 identified HVC_RA neurons and n = 82 HVC_X neurons. Recordings were attempted for approximately 7-21 days per bird. Signals were recorded and analyzed with in-house software written by KH in MATLAB (Mathworks). Synaptic onsets are detected by using an algorithm based on large deviations of dV/dt (Ankri et al., 1994)(see example traces in Figure S7A, B). See details in Supplemental Experimental Procedures.

Latency calculation in anesthetized birds

Synaptic latencies were calculated as the maximum of dV/dt within a detection window following the electrical stimulation. Action potential latencies were calculated as the median value of the action potential responses within the detection window. The detection window was set to 1 - 10 ms for local latency, 10 - 50 ms for network latency.

Syllable and gap duration analysis

Individual syllables were identified using a semi-automatic classification program described previously (Hamaguchi and Mooney, 2012). Then, gaps between the dominant syllable transitions were identified. For the cooling experiments, if the number of events (syllables or gaps) were less than 30 in any of the temperature conditions, we excluded such data from the analysis. We also restricted our analysis to gaps less than 120 ms to exclude long gaps that could occur between song bouts. Median values from each temperature condition were used for Q₁₀ analyses.

Q₁₀ analysis

Q₁₀ temperature coefficient is a measure of how a time constant changes per 10 Celsius change. Q₁₀ is defined as $Q_{\mathit{10}}={(\mathrm{L}\mathit{1}/\mathrm{L}\mathit{2})}^{(\frac{\mathit{10}}{\mathrm{T}\mathit{2}-\mathrm{T}\mathit{1}})}$, where L is the time constant (mean duration or mean latency) of the process and T is the temperature in Celsius degrees. For example, Q₁₀ = 2 indicates that the duration of a process becomes two times longer when the temperature declines 10 Celsius.

Slope analysis

We regressed the song dilation effect with the temperature changes in HVC and Uva, Dilation -1 = β₁ * HVCΔT + β₂ * UvaΔT.

The regression coefficients β₁ and β₂ represent the contributions of HVC and Uva respectively, and the direction of the slope vector. The angle θ of the vector is calculated as θ= tan^-1 (β₁/β₂). Q10 values reported in Figure 5 is calculated by 1+10 * β₁ for Q10(HVC), 1+10 * β₂ for Q10(Uva). The confidence intervals are calculated from a boot strapping method.

Computational Modeling

For simulations of local and distributed chain models, we used a leaky integrate-and-fire neuron model with an exponential decay current. Feedforward connectivity was generated by randomly selecting active neurons from the excitatory neuron population and connecting them in a feedforward manner. Random connections were also made between and among excitatory and inhibitory neurons. See Supplementary Experimental Procedures for more details.

Highlights.

Cooling HVC slows song timing much less than it slows activity propagation in HVC.

Cooling HVC exerts similar effects on song timing and recurrent network activity.

Synaptic activity in the HVC of singing birds displays a recurrent network signature.

Recurrent and local network simulations predict distinct synaptic activity patterns.