Examinations of the Chemical Step in Enzyme Catalysis

Abstract

Advances in computational and experimental methods in enzymology have aided comprehension of enzyme-catalyzed chemical reactions. The main difficulty in comparing computational findings to rate measurements is that the first examines a single energy barrier while the second frequently reflects a combination of many microscopic barriers. We present here intrinsic kinetic isotope effects and their temperature dependence as a useful experimental probe of a single chemical step in a complex kinetic cascade. Computational predictions are tested by this method for two model enzymes: dihydrofolate reductase (DHFR) and thymidylate synthase (TSase). The description highlights the significance of collaboration between experimentalists and theoreticians to develop a better understanding of enzyme-catalyzed chemical conversions.

Introduction

Empirical studies are invaluable in understanding many kinetic, mechanistic, and structural features of enzyme catalysis. However, many microscopic aspects of catalysis, such as transition state (TS) structures, reactive intermediate constituents, and dynamic effects, should also be examined by computational methods, which complement experiments and can provide atomistic insights. One of the main challenges in comparing experimental studies to calculations is ensuring that the two approaches actually examine the same phenomenon. When the experiments involve enzyme kinetics, this task is not trivial: most kinetic measurements reflect a complex combination of microscopic events, while most computations address a single event, such as a single energy barrier crossing.

Enzymes such as dihydrofolate reductase (DHFR) and thymidylate synthase (TSase) catalyze the breaking and formation of carbon-hydrogen bonds; several computational methods, including molecular dynamics (MD) and hybrid quantum mechanics/molecular mechanics (QM/MM), have been used in the study of these catalytic events. A partial list of such studies includes (Dametto, Antoniou, & Schwartz, 2012; S. Hammes-Schiffer & Benkovic, 2006; Klinman & Kohen, 2013; H. Liu & Warshel, 2007a; Luk et al., 2013; Rod, Radkiewicz, & Brooks, 2003; Thorpe & Brooks, 2004; Z. Wang, Ferrer, Moliner, & Kohen, 2013; K. F. Wong, Selzer, Benkovic, & Hammes-Schiffer, 2005). Each of these computational studies examined barrier-crossing for a specific H-transfer reaction, and predicted the involvement of several protein residues in facilitating C-H bond cleavage. A means of experimental examination of those predictions is the focus of this chapter. We describe several experimental probes of specific reactions’ barriers including measurements of rate constants, of their kinetic isotope effects (KIE), and their temperature dependence. The comparison of experimental observations with computational predictions of individual catalytic events is also discussed.

A KIE is the ratio of reaction rates for two substrates that differ only in their isotopic composition (isotopologues). Please note that this chapter refers only to primary (1°) KIEs, i.e., isotopic effects in which the isotope under study is part of the bond being cleaved or formed. When only the hydrogen on the C-H bond under study is isotopically labeled, KIEs offer an important means of probing activation of that bond. Isotopic labeling of the C-H that is cleaved in the reaction has little or no effect on other physical and chemical events along the catalytic cycle. This assumption follows that the C-H bond is not polarized and thus contributes little to the binding of large biological molecules, such as DHFR’s and TSase’s reactants.

While experimental measurements always yield an observed KIE (KIE_obs), the KIE for the bond cleavage per se is called the intrinsic KIE (KIE_int). By this definition KIE_int is free from kinetic complexities arising from the inclusion of other kinetic steps such as substrate binding, product release, or other chemical steps along the catalytic cascade that affect KIE_obs. Consequently, experimental evaluation of KIE_int (but not KIE_obs) can parallel the computational method in the sense that each examines a single chemical step.

We find that it is is possible to use KIE_int to examine predictions of high-level computations by exploiting the temperature dependence of KIE_int. This can be used to probe the nature of C-H bond cleavage and sub-nanosecond protein motions coupled to the C-H bond cleavage (Klinman & Kohen, 2013; Kohen, 2015b; D. Roston, Islam, Z., Kohen, A., 2014). An empirical interpretation of the temperature dependence of KIE_int is offered by “Activated Tunneling” models as described in the literature (Fan, Cembran, Ma, & Gao, 2013; Klinman, 2015; Klinman & Kohen, 2013; Kohen, 2015b; Layfield & Hammes-Schiffer, 2013; H. Liu & Warshel, 2007a, 2007b; Marcus, 2007; Nagel & Klinman, 2010; Jingzhi Pu, Gao, & Truhlar, 2006; Pudney et al., 2009; D. Roston, Islam, & Kohen, 2013). In the framework of these models small or no temperature dependence of KIE arise primarily from high frequency H-donor and H-acceptor distance (DAD) sampling, i.e., a narrow distribution of DADs. Temperature dependent KIE, on the other hand, stems from low-frequency DAD sampling (a broad distribution of DADs) at the transition state (TS). A high DAD sampling frequency indicates a well-organized TS, while a low DAD sampling frequency demonstrates a loose TS. A perturbation of the TS (for instance, through the mutation of a residue that affects the TS) alters the frequency of DAD sampling, and this manifests in an altered KIE temperature dependence. The temperature dependence of KIE_int, in other words, reflects the nature of a single bond cleavage step (within the complex kinetic cascade of an enzymatic reaction), which allows experimental comparisons to relevant computations.

That said, extracting the value of KIE_int from measured KIE_obs is a considerable challenge. While the Northrop method described below can be used with any KIE_obs (from single turnover, burst experiments, steady state parameters, etc.), we recommend measuring KIE_obs on the second order rate constant V/K competitively. The main advantage here is that only trace labeling with radioactive tritium (T) is needed in competitive experiments in which two isotopically-labeled substrates compete for the enzyme at the same pot. Most other methods would require close to 100% tritium in the bond to be cleaved, and close to no tritium in any other positions on the substrate, which is experimentally most challenging.

In the sections below we describe the process of extracting KIE_int from the observed value (KIE_obs) using the Northrop method then turn to examples of computational studies carried out on DHFR and TSase, followed by tests of these computational predictions with studies of temperature dependence of KIE_int. Finally, each case study includes the experimental procedure used to study a specific C-H bond activation.

Observed vs. Intrinsic KIE (KIE_obs vs. KIE_int)

Every experimental measurement of a KIE reflects a kinetically complex cascade rather than a single microscopic step. This kinetically complex chain of events may include binding and release of substrates and products, conformational changes associated with ligand binding or release, re-protonation of many enzymatic residues and the substrates, multiple chemical conversions within the reactive complex, etc. This problem is illustrated in Figure 1, and shows that steps other than the chemical step of interest (e.g., the C−H→C hydride transfer in the cases presented below) are partly rate-limiting for the different measurable kinetic parameters. This demonstrates how difficult it is to determine the rate constant or KIE_int on the intended chemical step per se, either from steady-state kinetics (e.g., k_cat or k_cat/K_M) or from pre-steady-state kinetics (e.g., single turnover or burst studies).

Figure 1.

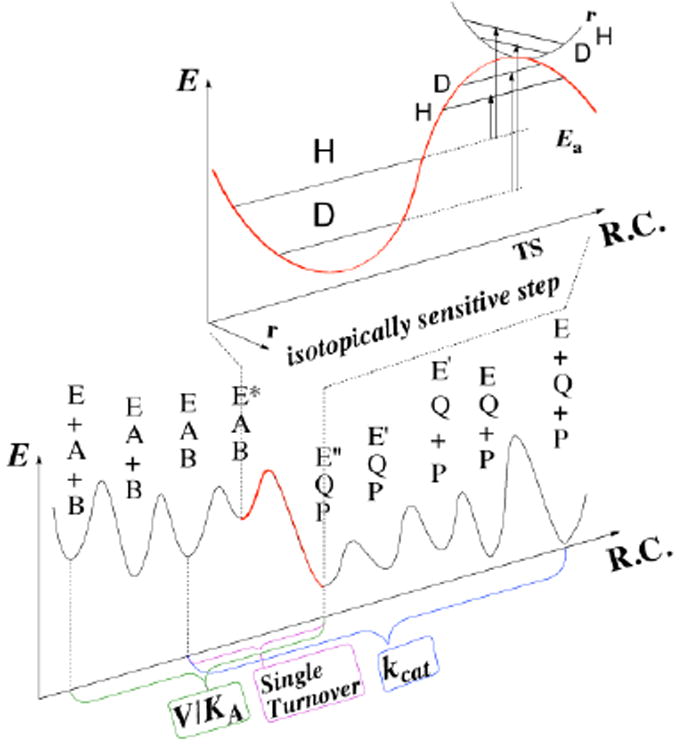
Relations between the chemical step (red) and measurable rate constants. Both steady-state parameters (e.g., k_cat/K_M (V/K) and k_cat) and pre-steady-state rates (e.g., single-turnover rate) involve several microscopic rate constants. The KIE_int reflects the nature of the chemical step, but assessing KIE_int from observed values is quite challenging (see text). Reproduced from ref (Kohen, 2015a) with permission from Faculty 1000.

The KIE_int in Figure 1 results from differences between the zero point energies (ZPE) of the ground state and the TS, and can be also affected by nuclear-quantum-mechanical tunneling (a phenomenon in which the atom is transferred under the classical energy barrier via its wave-like properties). These considerations are a matter of computational studies, but experimental information reflecting the cleavage of a single step is needed in order compare the two. The discrepancy between calculated and measured rates has led to some misunderstandings in the past: for example, the catalytic turnover rate, k_cat, is the uni-molecular rate constant representing the reciprocal of the time for a single enzymatic turnover (Cook & Cleland, 2007). However, since most enzymes did not evolve under saturating substrate concentrations, k_cat is often rate-limited by product release; thus comparing k_cat’s rates or KIEs with calculations examining merely the chemical step is not always meaningful.

The relations between the KIE_int of interest and the relevant measured KIE_obs and computational studies can be calculated per system. The mathematical expression for this relation always has a similar general form, although the specific expressions vary depending on the details of each system. For example, consider the following simple kinetic cascade, with only one irreversible chemical step and a single substrate:

$$\mathrm{E}+\mathrm{S}\underset{k_2}{\overset{k_1}{\rightleftharpoons }}\mathrm{ES}\stackrel{k_3}{\to }\mathrm{EP}\stackrel{k_4}{\to }\mathrm{E}+\mathrm{P}$$

Here the chemical step is the conversion of ES to EP, represented by the rate constant k₃. KIE_int = k_{3 light} / k_{3 heavy} or, in the case of H/D KIE, ^Dk₃ = k_3H/k_3D. As expressed in Eq. 1, the observed 1° KIE will be smaller than KIE_int by an amount that depends on commitment to catalysis. The KIE_obs on any steady-state rate constant is affected by commitments as follows (Cook & Cleland, 2007):

$${\mathrm{KIE}}_{\mathrm{obs}}=\frac{{\mathrm{KIE}}_{\mathrm{int}}+{\mathrm{C}}_{\mathrm{f}}+{\mathrm{C}}_{\mathrm{r}}·\mathrm{EIE}}{1+{\mathrm{C}}_{\mathrm{f}}+{\mathrm{C}}_{\mathrm{r}}}$$ (1)

where EIE is the equilibrium isotope effect. The forward commitment (C_f) is defined as the ratio of the isotopically-sensitive rate constant (k₃ in this case) in the forward direction to the net rate constant for the breakdown of the reactive ES complex into E and S (k₂ in this case). The reverse commitment (C_r) is the ratio of the isotopically-sensitive rate constant in the reverse direction (from EP to ES, zero in the current example) to the isotopically-insensitive net rate constant of the decomposition of the the EP complex to E and P (k₄). In cases where the chemistry is irreversible or cases where EIE = 1, Equation (1) simplifies to:

$${\mathrm{KIE}}_{\mathrm{obs}}=\frac{{\mathrm{KIE}}_{\mathrm{int}}+C}{1+C}$$ (2)

where C = C_f for irreversible reactions or C = C_f + C_r when EIE = 1. In cases where C is much smaller than KIE_int, KIE_obs is similar to KIE_int. KIE_int values can then be directly compared to a computed barrier crossing event, the assessment of which is the focus of this chapter.

The Northrop Method

There are several experimental methods that attempt to assess the nature of individual chemical steps: for instance, measurement of single-turnover rates as a function of pH (Fierke, Johnson, & Benkovic, 1987), or measurement of KIE_obs as function of substrate concentration (Hong, Maley, & Kohen, 2007). Measuring single-turnover rates can dramatically reduce the kinetic complexity by reducing the number of microscopic steps involved in the measurement, but as the initiation of the reaction involves substrate binding, and there is still a C > 0 that results from protonation changes and the conformational steps that follow that substrate binding, and of course from the chemical steps other than the one under study, in systems catalyzing sequential chemical conversions (e.g., see TSase below).

The Northrop method eliminates C by making use of measurements of KIE_obs for all three hydrogen isotopes (Northrop, 1991). The KIE_obs acquired for this method can be measured for single turnover rates, steady state rate constants, or other kinetically well-defined parameters. For example, for the simplified kinetic scheme presented above the expression for the second order rate constant (k_cat/K_M, denoted as V/K) is given by:

$${(V/K)}_i=\frac{k_1{k}_{3i}}{k_2+k_{3i}}$$ (3)

where i represents a given isotopologue, i.e., a substrate with hydrogen (H), deuterium (D) or tritium (T). For H-transfer reactions, since there are only three possible isotopologues, every KIE_obs has an isotope in common with one other, e.g., H/D KIE and H/T KIE share H as common isotope; H/D KIE and D/T KIE share D, and H/T KIE and D/T KIE share T as common isotope. All three combinations can be used, and each has different advantages and disadvantages as described in ref (Sen, Yahashiri, & Kohen, 2011). For each case, one must derive the Northrop equation so the commitment (C) for the shared isotope is moved to the denominator of the KIE_obs expression, and is the C for the shared isotope in each case. For H/T KIE and D/T KIE, where T is the common isotope, C for T must be the only commitment in each expression. In this case, one derives the reciprocal of KIE_obs on V/K for H/T, ^H(V/K)_T,obs:

$${}^H(V/K)_{T,\mathit{obs}}=\frac{{(\raisebox{1ex}{$V$}\!\left/ \!\raisebox{-1ex}{$K$}\right.)}_T}{{(\raisebox{1ex}{$V$}\!\left/ \!\raisebox{-1ex}{$K$}\right.)}_H}=\frac{\frac{k_1{k}_{3T}}{k_2+k_{3T}}}{\frac{k_1{k}_{3H}}{k_2+k_{3H}}}$$ (4)

where (V/K)_i is the rate for isotope i, and 1/KIE_obs for H/T is ^H(V/K)_{T, obs}.

$${}^H(V/K)_{T,\mathit{obs}}=\frac{k_{3T}{k}_2+k_{3T}{k}_{3H}}{k_{3H}{k}_2+k_{3H}{k}_{3T}}$$ (5)

Dividing the numerator and denominator by k_3H k₂ gives:

$${}^H(V/K)_{T,\mathit{obs}}=\frac{\left(\frac{k_{3T}}{k_{3H}}+\frac{k_{3T}}{k_2}\right)}{\left(1+\frac{k_{3T}}{k_2}\right)}$$ (6)

$${}^H(V/K)_{T,\mathit{obs}}=\frac{{}^H(k_3)_T+{\mathrm{C}}_{\mathrm{T}}}{1+{\mathrm{C}}_{\mathrm{T}}}$$ (7)

where C_T = k_3T/k₂ is the commitment for tritium (k_3T is the C-T bond cleavage rate in this simple example), ^H(k₃)_T = k_T /k_H is reciprocal of the intrinsic tritium KIE for isotopes H vs. T.

Similarly, the reciprocal of the KIE_obs on V/K for D vs. T is given by:

$${}^D(V/K)_{T,\mathit{obs}}=\frac{{}^D(k_3)_T+{\mathrm{C}}_{\mathrm{T}}}{1+{\mathrm{C}}_{\mathrm{T}}}$$ (8)

where ^D(k₃)_T = k_T /k_D is the reciprocal of the KIE_int for D/T. Subtracting 1 from both sides in Equations (7) and (8) gives:

$${}^H(V/K)_{T,\mathit{obs}}-1=\frac{{}^H(k_3)_T+{\mathrm{C}}_{\mathrm{T}}}{1+{\mathrm{C}}_{\mathrm{T}}}-1=\frac{{}^H(k_3)_T-1}{1+{\mathrm{C}}_{\mathrm{T}}}$$ (9)

$${}^D(V/K)_{T,\mathit{obs}}-1=\frac{{}^D(k_3)_T+{\mathrm{C}}_{\mathrm{T}}}{1+{\mathrm{C}}_{\mathrm{T}}}-1=\frac{{}^D(k_3)_T-1}{1+{\mathrm{C}}_{\mathrm{T}}}$$ (10)

Dividing Equation (9) by Equation (10) results in an expression with no commitment at all, no matter how complex the expression for C:

$$\frac{{}^H(V/K)_{T,\mathit{obs}}-1}{{}^D(V/K)_{T,\mathit{obs}}-1}=\frac{{}^H(k_3)_T-1}{{}^D(k_3)_T-1}$$ (11)

Equation 11 has two unknowns (the KIE_int for H/T and D/T), but no commitment (C). The Swain-Schaad relationship for the pairs of hydrogen isotope (between H/T and D/T) is given by (Swain, Stivers, Reuwer, & Schaad, 1958):

$$\frac{k_{\mathrm{H}}}{k_{\mathrm{T}}}={\left(\frac{k_{\mathrm{D}}}{k_{\mathrm{T}}}\right)}^{3.3}$$ (12)

where the value at the exponent (3.3) can be assessed by QM/MM calculations (like in the case of ecDHFR presented below), or calculated from basic principals as discussed below. Using the reciprocal of this relationship, the ^H(k₃)_T can be numerically determined from a pair of observed KIEs:

$$\frac{{}^T(V/K)_{H,\mathit{obs}}-1}{{}^T(V/K)_{D,\mathit{obs}}-1}=\frac{{}^H(k_3)_T-1}{{}^H(k_3)_T^{\frac{1}{3.3}}-1}$$ (13)

Further rearrangement of Eq. 13 leads to:

$$\frac{{}^T(V/K)_{H,\mathit{obs}}^{-1}-1}{{}^T(V/K)_{D,\mathit{obs}}^{-1}-1}=\frac{{}^T(k_3)_H^{-1}-1}{{}^T(k_3)_H^{\frac{-1}{3.3}}-1}$$ (14)

where ^T (V /K)_H,obs, ^T (V /K)_D,obs, and ^T(k₃)_H are observed H/T , observed D/T, and intrinsic H/T KIEs respectively. This equation only has one unknown, which is the KIE_int that represents KIE on only the bond cleavage event (k₃).

Thus KIE_int is extracted from its respective observed values using a numerical solution of Eq. 14. The equations were numerically solved for using a program that is freely available on our web site under tools: https://chem.uiowa.edu/kohen-research-group/calculation-intrinsic-isotope-effects.

Like any other experimental method, the Northrop method makes assumptions, and its associated assumptions have to be carefully tested for each system. Three assumptions are embedded in the Northrop method: 1) KIEs on binding or other kinetic steps (except the one under study) are insignificant; 2) Cr in Eq. 1 is close to zero or EIE is close to unity; and 3) the two KIE_int in Eq. 12 are related to each other, for example, via the Swain-Schaad exponent (SSE). The SSE can be calculated using QM/MM or assessed from $\mathit{SSE}=({\mu }_{C-H}^{-0.5}-{\mu }_{C-T}^{-0.5})/({\mu }_{C-D}^{-0.5}-{\mu }_{C-T}^{-0.5})$ (Swain et al., 1958), where μC_-i is the reduced mass for isotope i and carbon 12. At the high temperature limit (i.e., above 273 K), 1° SSE falls between 3.34 and 3.26, as the carbon’s mass in the C-H/D/T bond can vary between 12 and infinity, respectively (depending on its coupling to the rest of the heavy atoms). While at temperatures below 270 K SSE can vary, SSE is mostly temperature-independent in the range in which most biochemical experiments are conducted (Shelton, Hrovat, & Borden, 2007; Smedarchina & Siebrand, 2005). The value of SSE for specific systems can be calculated from QM/MM calculations with a tunneling correction (J. Pu, Ma, Gao, & Truhlar, 2005; J. Pu, Ma, Garcia-Viloca, et al., 2005), e.g., 3.3 for the enzyme DHFR.

A recent suggestion that there is another, “hidden” assumption in the Northrop method resulted from an false procedure in which C_T is calculated indirectly from ^T(V/K)_H and ^T(V/K)_D (Z. Wang, Antoniou, Schwartz, & Schramm, 2016), rather than from their reciprocals as used in the Northrop method (Eq. 14). The correct procedure described above (Eqs. 3-14) can be used for the complex kinetic scheme used in ref (Z. Wang et al., 2016) to calculate CT directly, without the use of any further assumptions.

Case study 1 – Thymidylate Synthase (TSase)

Thymidylate synthase (TSase) catalyzes the last committed step of the de novo synthesis of the DNA building block thymidylate (2’-deoxythymidine-5’-monophosphate, dTMP). It plays an essential role in regulating the balance of nucleotide pools and the replication of DNA, and thus is a major target for chemotherapeutic drugs (Carosati et al., 2012; Wilson, Danenberg, Johnston, Lenz, & Ladner, 2014). In the TSase-catalyzed production of thymidylate, the cofactor methylene tetrahydrofolate (CH₂H₄folate) sequentially provides a methylene and a hydride to the substrate dUMP (2’-deoxyuridine-5’-monophosphate). Following the formation of the ternary complex of TSase and its substrates, the catalyzed chemistry involves a series of bond cleavages and formations, including two C-H activations: a proton abstraction and a hydride transfer. In the conventionally proposed mechanism of E. coli TSase (Carreras & Santi, 1995; Finer-Moore, Santi, & Stroud, 2003; McMurry & Begley, 2016), a highly-conserved cysteine (C146) initiates the reaction by Michael addition at C6 of dUMP (step 1 in Scheme 1), forming an enolate. This enolate forms a methylene bridge with the pre-activated CH₂H₄folate iminium cation (step 2 and 3). Two H-transfers follow: (i) a proton abstraction from the C5 of dUMP (step 4), leading to the elimination of tetrahydrofolate (H₄folate) and the formation of an exocyclic methylene intermediate (step 4); and (ii) a hydride transfer from the C6 of the H₄folate to the C7 of the exocyclic methylene intermediate to produce the product dTMP (step 5). The traditionally proposed mechanism (left column in Scheme 1) was constructed from numerous experimental studies including X-ray crystallography (Stroud & Finer-Moore, 2003), kinetic isotope effects (Agrawal, Hong, Mihai, & Kohen, 2004; Spencer, Villafranca, & Appleman, 1997), steady-state kinetics, and mutagenesis (Carreras & Santi, 1995; Finer-Moore et al., 2003).

Scheme 1.

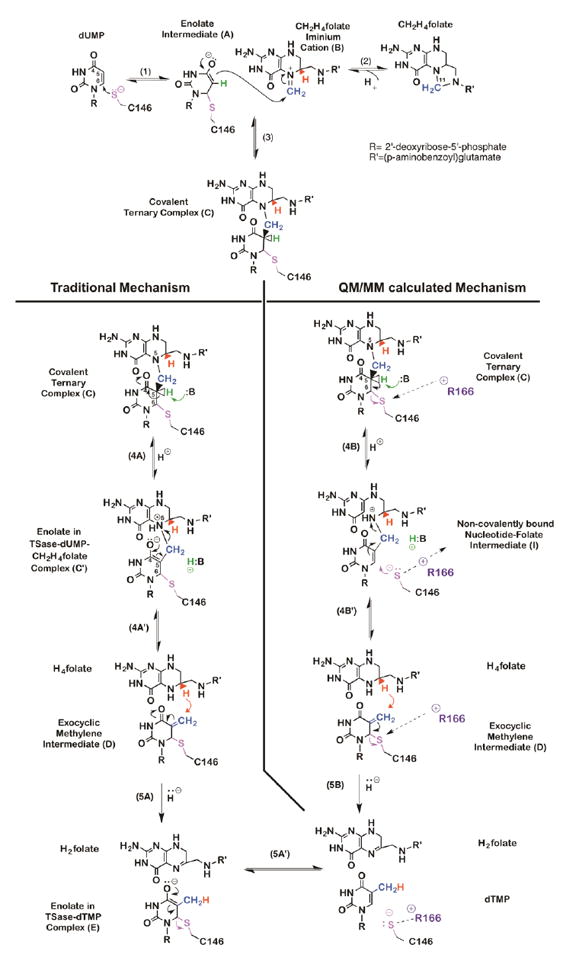
Chemical mechanism of TSase. Traditional (left panel) and QM/MM calculated (right panel) mechanisms for proton abstraction and hydride transfer.

The mechanism of TSase has also been investigated by hybrid quantum mechanics/molecular mechanics (QM/MM) calculations, which paint a slightly different picture (Kanaan et al., 2011; Kanaan, Marti, Moliner, & Kohen, 2007, 2009; Kanaan, Roca, Tunon, Marti, & Moliner, 2010; Z. Wang, Ferrer, et al., 2013) (right column in Scheme 1). One of the main differences between the two proposed mechanisms is in the hydride transfer step (step 5 in Scheme 1), which the traditional view (left colum) presents as a step-wise mechanism in which the hydride transfer precedes the elimination of enzymatic nucleophile C146 (step 5A and 5A’). The QM/MM calculations (right column), on the other hand, suggest a concerted process in which the transfer of hydride and the cleavage of the thio-ether bond happen together (step 5B). The difference in hydride transfer mechanisms is significant: the concerted mechanism involves the formation of a charged species (compound E in Scheme 1) while the other seems to bypass it, an important consideration for designing a transition state analogue. Key to the concerted mechanism’s favorability, according to calculations, is a highly conserved, positively charged residue R166 that moves closer to the thioether bond and promotes its cleavage at the transition state of the hydride transfer.

The QM/MM calculations also examined the mechanism of the proton abstraction from the C5 of dUMP in the ternary complex (compound C in Scheme 1) (Kanaan et al., 2007, 2009; Z. Wang, Ferrer, et al., 2013). The calculations suggest the formation of an intermediate that had not been proposed in the traditional mechanism. It was calculated that the removal of the C5 proton from intermediate C causes dissociation of the C146, leaving an intermediate in which the folate and the nucleotide are bound via a methylene bridge, but are not covalently bound to the enzyme (intermediate in Scheme 1)! If confirmed experimentally, this previously unrecognized intermediate might serve as a new target for antibiotic and chemotherapeutic drugs. In contrast to current drugs, which are either derivatives of pyrimidine or folate, this hypothetical new class of inhibitors could comprise part of the nucleotide and part of the folate.

These theoretical predictions were examined experimentally: The calculations predicted that as in the hydride transfer step R166 also plays a vital role in polarizing and cleaving the thio-ether bond during proton abstraction (Z. Wang, Ferrer, et al., 2013). A mutation at R166 should have altered the temperature dependence of KIE_int only if it was involved in TSs of H-transfers. KIE_obss for H/T and D/T were measured over a range of temperatures for the both the hydride transfer and the proton abstraction in WT and in a variant of R166 (R166K, the only active mutant of R166) (Agrawal, Hong, et al., 2004; Islam, Strutzenberg, Ghosh, & Kohen, 2015; Islam, Strutzenberg, Gurevic, & Kohen, 2014; Z. Wang & Kohen, 2010). KIE_ints were extracted from the KIE_obss using the Northrop method described above and plotted against the inverse of temperature (Figure 2).

Figure 2.

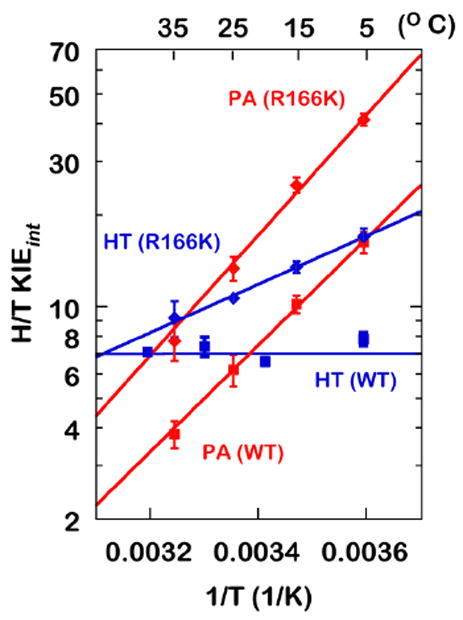
KIEints on the hydride transfer (blue) and the proton abstraction (red) for the WT (cubes) and R166K (diamonds). HT: Hydride Transfer, PA: Proton Abstraction. Reproduced from ref (Islam et al., 2015) with permission from ACS.

As is apparent in Figure 2, the mutation caused an increase in temperature dependence of KIE_int for both H-transfers. The KIE_int for the hydride transfer, which had been temperature-independent in the WT, became temperature-dependent in R166K, while the temperature dependence of the proton abstraction KIE increased in R166K (relative to WT). In addition, the mutation also increased the absolute magnitude of KIE_int for both H-transfers. Seen in the light of the activated tunneling model, the larger magnitudes and the steeper temperature dependence of KIEs in R166K suggest lower-frequency DAD sampling and a higher average DAD at the TS. Figure 3 illustrates the DAD sampling potential along the DAD coordinate.

Figure 3.

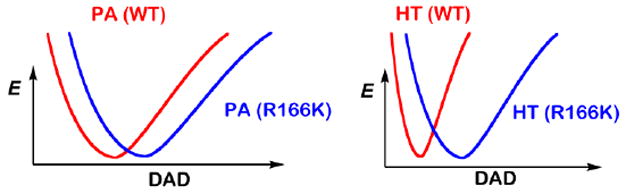
Schematic representations of PESs for the H-transfers along the DAD coordinate. Reproduced from ref (Islam et al., 2015) with permission from ACS.

A stiff potential energy surface (PES) represents a high DAD sampling frequency, suggesting a well-coordinated TS -- as is seen in the hydride transfer in WT ecTSase -- while a broad PES indicates a low DAD sampling frequency, demonstrating a loose TS, as can be seen in the proton abstraction in the wild type. The mutation at R166 caused the PES for the DAD to become wider for the both H-transfers, implying perturbation of the TSs. The mutation also caused a shift in the PESs’ minima, yielding larger DADs for both H-transfers.

These effects were attributed to R166’s being an indispensable part of the reaction’s TS for both the hydride transfer and the proton abstraction, in good agreement with the QM/MM calculations. Additionally, an observed normal secondary (2°) KIE on C6 of dUMP supported the concerted mechanism for the hydride transfer (Islam et al., 2014). As a control, mutation to several other residues closer to the reaction center were found to produce no or very minor changes in the temperature dependence of KIE_int (Abeysinghe & Kohen, 2015; Agrawal, Hong, et al., 2004; Z. Wang, Abeysinghe, Finer-Moore, Stroud, & Kohen, 2012).

In summary, examining chemical steps such as C-H bond activations in enzyme-catalyzed reactions is of contemporary interest. While computational approaches have advantages and the virtue of examining a single chemical step, experimental tools for such examinations are few. The temperature dependence of KIE_int probes the TS of a given chemical transfer, thereby offering a test of computational predictions. As an example, TSase has conventionally been thought to catalyze two sequential H-transfers in a complex cascade of physical and chemical steps; QM/MM calculations predicted new mechanisms for the both hydride transfer and the proton abstraction. In both cases the experimental findings, using KIE temperature dependence as a probe, offer strong support for the predictions made by QM/MM calculations. Not only was the role of a particular residue, R166, confirmed in both steps, but secondary KIEs (Islam et al., 2014) confirmed the concerted nature of the hydride transfer step proposed by QM/MM calculations.

The existence of the newly predicted intermediate (Z. Wang, Ferrer, et al., 2013) has not yet been directly demonstrated because the involvement of R166 in steps before and after that proposed intermediate is quite indirect. More experiments and computational studies are needed to further examine these proposals, such as QM/MM calculations and temperature dependence KIE_int measurements with TSase from other organisms, for isotopically labeled enzymes, and other studies that would further expose the nature of TSase catalysis.

Experimental section for TSase

[2-¹⁴C]dUMP (specific radioactivity of 52 Ci/mol) was purchased from Moravek Biochemicals. [5-³H]dUMP (15-30 Ci/mmol) and [³H]NaBH₄ (15Ci/mmol) were purchased from American Radiolabeled Chemicals. [2-³H]isopropanol was synthesized by reducing acetone using [³H]NaBH₄. . Isopropanol-d8 was purchased from Sigma-Aldrich.

Measurements of KIEs on the hydride transfer step

The upper panel in Scheme 2 shows the isotopic labeling pattern for the hydride-transfer KIE measurements, where the hydrogen at C6 of CH₂H₄folate (to be transferred at that step) was labeled as deuterium or tritium. The labeled (R)-[6-^xH]CH₂H₄folate ((^xH= D or T) was synthesized through a chemoenzymatic process described elsewhere (Agrawal, Mihai, & Kohen, 2004). The KIE measurements were performed in 100 mM Tris buffer (pH= 7.5), 2 mM TCEP, 1 mM EDTA and 7 mM HCHO. Both H/T and D/T KIE were measured competitively, yielding a KIE_obs on the second order rate constant (V/K)(Cook & Cleland, 2007).

Scheme 2.

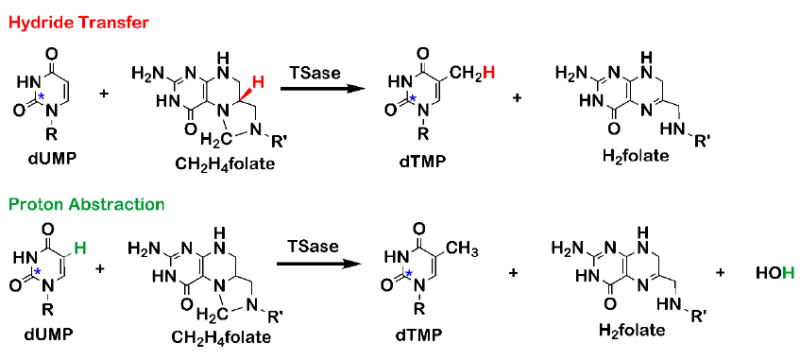
Isotopic labeling for measuring KIEs on the hydride transfer (top) and the proton abstraction (bottom). The hydride (red) and the proton (green) are the sites of isotopic labeling. The asterisks on dUMP represent remote ¹⁴C labeling to trace lighter isotopes.

In competitive KIE measurements, both the light and the heavy isotopologue are present in the same reaction mixture. Here, the ¹⁴C-labeled substrate ([2- ¹⁴C]dUMP) was used to trace the light isotope (H or D). For each reaction, trace (R)-[6-³H]CH₂H₄folate (about 2 million disintegrations per minute, Mdpm) in protiated or deuterated CH₂H₄folate for H/T or D/T KIE experiments, respectively, was mixed with ¹⁴C-labeled substrate [2- ¹⁴C]dUMP (~ 0.3 Mdpm) in a ratio of 6/1 (³H/¹⁴C) or higher. Since tritium radiation is weaker than ¹⁴C radiation, this ratio contributed to higher accuracies in the Liquid Scintillation Counting (LSC) analyses. Using unlabeled dUMP, the concentration of [2- ¹⁴C]dUMP was adjusted to 20% in excess over the total CH₂H₄folate in order to enable measurement of fractional conversion of dUMP to dTMP (f). Since high CH2H4folate concentration (~500 μM) was previously found to be inhibitory (Agrawal, Hong, et al., 2004; Z. Wang, Sapienza, et al., 2013), the chosen total concentration of dUMP was in the range of 100-400 μM so that with 20% in excess, CH₂H₄folate stayed below the inhibitory concentration. Aliquots of the reaction mixture were equilibrated to 5, 15, 25, and 35 °C and adjusted to pH 7.5. Prior to initiating the reaction by adding enzyme, two aliquots (t0) that served as controls were also taken and quenched (for consistency). At each temperature, the reaction was initiated with the addition of TSase, and six to eight aliquots of reaction mixture were removed and quenched at different time points (t) leading to fraction conversion between 20 and 80%. All aliquots were quenched with at least 5 times molar excess of 5-fluoro-dUMP, a nanomolar competitive inhibitor of TSase, over the substrate dUMP, and stored at -80 °C for further HPLC analysis. A solution of concentrated enzyme was added to the remaining reaction mixture and incubated further to reach the completion of the reaction, then divided into three aliquots that were quenched (for consistency) and served as infinite time points (t_∞). All of the aliquots (t0, t and t_∞) were subjected to RP HPLC analyses in which reactants and products were separated from each other and their radioactivity measured by LSC. The observed KIE for each time point was calculated using Equation 15, as mentioned in an earlier section:

$$\mathrm{KIE}=\frac{\mathrm{In}(1-f)}{\mathrm{In}[1-f(R_t/R_{\mathit{\infty }})]}$$ (15)

where f, R_t and R_∞ are the fractional conversion, the ratio of ³H/¹⁴C in the product, and the ratio of ³H/¹⁴C in the product at the infinity time points, respectively. R_∞ was averaged over the infinite time points. The fractional conversion f for all time points was calculated using the following equation:

$$f=\frac{[{}^{14}\mathrm{C}]\mathrm{dUMP}}{(100-\%\mathit{excess}\mathit{of}[{}^{14}\mathrm{C}]\mathrm{dUMP})([{}^{14}\mathrm{C}]\mathrm{dUMP})+[{}^{14}\mathrm{C}]\mathrm{dTMP})}$$ (16)

The exact excess of [2- ¹⁴C]dUMP over CH₂H₄folate was calculated from the infinite time points using following equation:

$$\%\mathit{excess}\mathit{of}[{}^{14}\mathrm{C}]\mathrm{dUMP}=\frac{[{}^{14}\mathrm{C}]\mathrm{dUMP}}{([{}^{14}\mathrm{C}]\mathrm{dUMP}+[{}^{14}\mathrm{C}]\mathrm{dTMP})}$$ (17)

Figure 4 shows a typical plot of KIE_obs versus fraction conversion (f). The fact that the observed KIEs are independent of fraction conversion serves as an important quality control, because most artifacts would lead to f-dependent KIE_obs. Each of the observed KIEs was averaged over at least five time points at each temperature. The KIE_ints were calculated using Eq 14.

Figure 4.

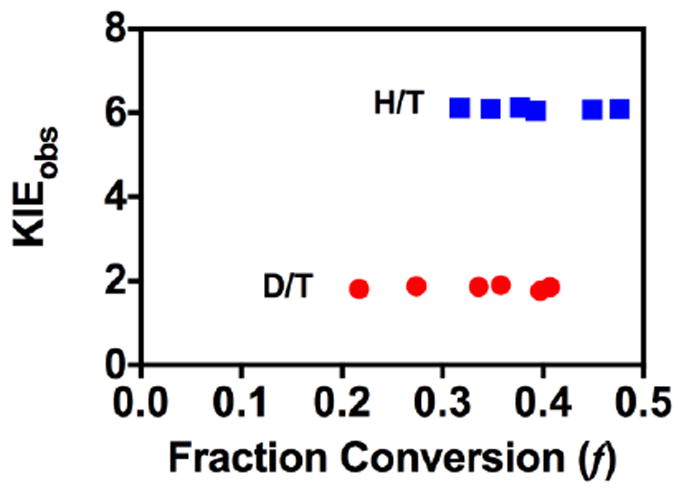
Observed H/T and D/T KIEs on hydride transfer for R166K at 35 °C.

Measurements of KIEs on the proton abstraction

The lower panel of Scheme 2 shows the isotopic labeling pattern for the proton-abstraction KIE measurements. Apart from different isotopic labeling, the experimental processes for the proton-abstraction KIEs are mostly identical to those of the hydride-transfer KIE measurements. Therefore, in this section, only the experimental procedures unique to hydride transfer are highlighted.

[2- ¹⁴C]dUMP and[5- ³H]dUMP were purchased from Moravek Biochemicals and American Radiolabeled Chemicals, respectively. [2- ¹⁴C, 5-²H]dUMP was synthesized following a published procedure (Wataya & Hayatsu, 1972).

To measure the isotope effects in the proton abstraction, trace [5- ³H]dUMP was mixed with [2- ¹⁴C]dUMP or [2- ¹⁴C, 5-²H]dUMP for H/T or D/T KIE measurements, respectively. The concentration of CH₂H₄folate was taken in excess to total dUMP concentration in order to obtain complete conversion of the labeled substrates.

It should be noted that the KIE_obs for proton abstraction is dependent on the concentration of CH2H4folate, as can be seen in Eqs. 2 and 18 (Ghosh, Islam, Krueger, Abeysinghe, & Kohen, 2015; Hong et al., 2007; Z. Wang & Kohen, 2010):

$$C_f=\frac{k_9}{k_5+\frac{k_2{k}_4}{k_2+k_3[{\mathrm{CH}}_2{\mathrm{H}}_4\mathrm{folate}]}}$$ (18)

where C_f is the forward commitment and k₉ denotes the proton abstraction step (Scheme 3).

Scheme 3.

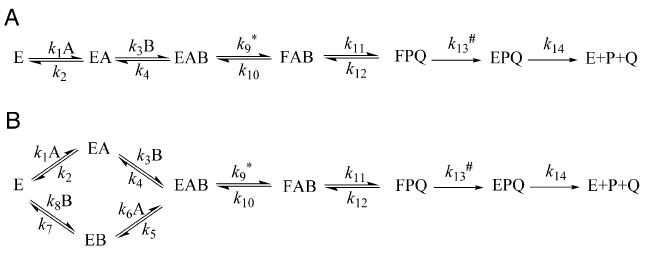
Ordered (A) and random (B) binding mechanisms for substrates dUMP (A) and CH₂H₄folate (B) for TSase. Asterisk (*) and number sign (#) represent the proton abstraction (k₉) and the hydride transfer (k₁₃), respectively.

In some cases, at high concentration of CH₂H₄folate KIE_obs goes to unity, which indicates a strictly-ordered binding mechanism with dUMP binding first (Panel A in Scheme 3), as can be seen in Eq. 19 (Ghosh et al., 2015; Hong et al., 2007; Z. Wang & Kohen, 2010):

$$C_f=\frac{k_9}{k_4}+\frac{k_3[{\mathrm{CH}}_2{\mathrm{H}}_4\mathrm{folate}]}{k_2{k}_4}$$ (19)

In Eq. 19 C_f goes to infinity at high concentrations of CH₂H₄folate, so KIE_obs goes to one (Eq. 1). For WT ecTSase an optimal concentration of CH₂H₄folate (3 μM) was chosen to yield large H/T and D/T KIE_obs with low errors (Z. Wang & Kohen, 2010). However, for many mutants (Abeysinghe & Kohen, 2015) including R166K (Islam et al., 2015) that follow a random binding mechanism, high concentrations of CH₂H₄folate yield large KIE_obs. The reaction mixture for the proton-abstraction KIE measurements contains 50 mM MgCl₂, which was added to reduce the commitment factor on this step (Z. Wang & Kohen) (Islam et al.). Note that the presence of MgCl₂ does not affect the intrinsic KIEs for the hydride transfer (Z. Wang, Sapienza, et al., 2013). The observed KIE was calculated using Eq. 15 while the fraction conversion was determined using the following equation:

$$f=\frac{[{}^{14}\mathrm{C}]\mathrm{dTMP}}{\left([{}^{14}\mathrm{C}]\mathrm{dUMP}+[{}^{14}\mathrm{C}]\mathrm{dTMP}\right)}$$ (20)

As in the hydride transfer, the absence of any trends in observed KIEs with fraction conversion (Figure 5) indicates that no significant artifact such as protium contamination distorts? the D/T KIEs. Though the proton abstraction is reversible, Eq. 14 for extracting intrinsic KIEs is still valid since the EIE was found to be close to unity for this step (Hong et al., 2007). Furthermore, the reverse commitment on the tritium is essentially zero since once released, the tritium is diluted into 110 M protiated water. Given all these assumptions, quality control (QC) is most important in this case, and our experience is that the most sensitive QC is f-independent KIE_int (Figure 5). Almost every deviation from the above assumptions leads to an f-dependent KIE_int.

Figure 5.

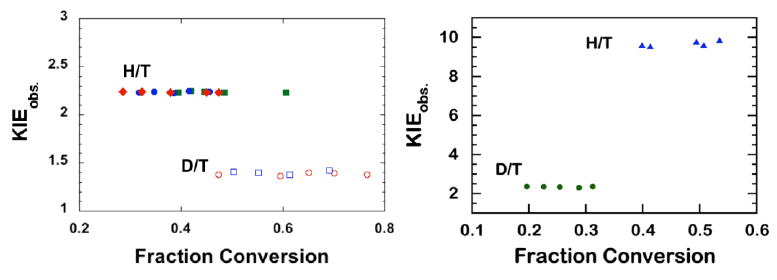
Examples of KIE_obs for the proton abstraction step for the WT ecTSase (left) (Z. Wang & Kohen, 2010) and its R166K mutant (right) (Islam et al., 2015). Reproduced from ref (Islam et al., 2015) with permission from ACS.

Case study 2 – Dihydrofolate Reductase (DHFR)

DHFR catalyzes the NADPH-dependent reduction of 7,8-dihydrofolate (H₂F) to 5,6,7,8-tetrahydrofolate (H₄F) through a stereospecific transfer of the pro-R hydrogen from NADPH to C6 of the si face of the pterin ring (Scheme 4) (S. Hammes-Schiffer & Benkovic, 2006). DHFR from E. coli (ecDHFR) is a common model system for various studies due to its small size, flexibility and the simple chemical transformation it catalyzes. The enzyme has served as a platform for many calculations and experimental studies, and the relationship between protein dynamics and its function has been examined by both theoreticians and experimentalists. A partial list of references includes (Arora & Brooks III, 2009; Bystroff & Kraut, 1991; Dametto et al., 2012; Fan et al., 2013; Fierke et al., 1987; Klinman & Kohen, 2013; H. Liu & Warshel, 2007b; Loveridge, Behiry, Guo, & Allemann, 2012; McElheny, Schnell, Lansing, Dyson, & Wright, 2005; Pauling, 1948; Singh, Abeysinghe, & Kohen, 2015; Singh, Francis, & Kohen, 2015; Singh, Morris, Tivanski, & Kohen, 2015a, 2015b; Z. Wang, Singh, Czekster, Kohen, & Schramm, 2014; Kim F. Wong, Watney, & Hammes-Schiffer, 2004). The focus of this section is to demonstrate a combination of different approaches to studying the DHFR-catalyzed reaction emphasizing the hydride transfer step, primarily through KIE experiments and hybrid quantum mechanical/molecular mechanics/molecular dynamics (QM/MM/MD) simulations. The current section emphasizes the interplay between experimental and computational approaches.

Scheme 4.

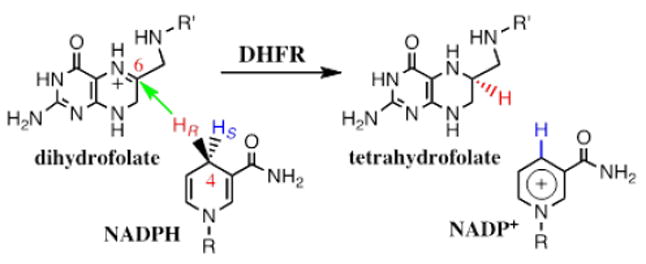
DHFR catalyzes the stereospecific transfer of the pro-R hydride of C4 of NADPH to C6 of protonated N5-DHF, producing THF and the oxidized cofactor NADP⁺. It is important for both measurements and computations that the hydride transfer (green arrow) takes place after DHF is already protonated (C. T. Liu, Francis, K., Layfield , J., Huang, X., Hammes-Schiffer, S., Kohen, A., Benkovic, S.J., 2014).

Computational vs. experimental studies

Network of coupled motions in DHFR

The concept of remote residues influencing events at the active site has been debated for several enzymes (Fraser et al., 2009; Ghanem, Li, Wing, & Schramm, 2008; Henzler-Wildman & Kern, 2007; Loria, Berlow, & Watt, 2008; Meadows, Tsang, & Klinman, 2014). Calculations by Brooks and Hammes-Schiffer independently predicted that a “network of dynamically coupled motions” was part of the reaction coordinate of the C-H→C hydride transfer in ecDHFR (S. Hammes-Schiffer & Benkovic, 2006; Radkiewicz & Brooks, 2000; Rod et al., 2003; K. F. Wong et al., 2005). These coupled motions denote thermal equilibrium; i.e., thermally-averaged conformational changes along the collective reaction-coordinate, producing configurations conducive to the hydride transfer reaction with the pre-protonated DHF (Scheme 4). A portion of this network of coupled motions in DHFR is illustrated in Figure 6.

Figure 6.

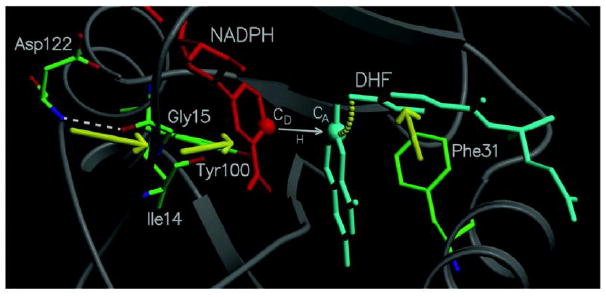
Diagram of a portion of the network of coupled promoting motions in ecDHFR. The yellow arrows and arc indicate the coupled promoting motions. From ref (Agarwal, Billeter, Rajagopalan, Benkovic, & Hammes-Schiffer, 2002) with permission from Proc. Natl. Acad. Sci.

The equilibrium motions produce configurations that promote hydride transfer through short DADs, a proper electrostatic environment for charge transfer, and correct orientation of the substrate and cofactor. Further insights into this network of coupled motion have been provided by calculations performed on mutants of DHFR. For example, G121V, one of the most intensively studied DHFR mutants, results in a 40-fold decrease in NADPH binding affinity and a 200-fold decrease in the single turnover rates, despite the fact that the mutation is located ~15 Å away from the active site (Boehr et al., 2013; Fan et al., 2013; H. Liu & Warshel, 2007a, 2007b; Mauldin, Sapienza, Petit, & Lee, 2012; Ohmae, Iriyama, Ichihara, & Gekko, 1998; Rajagopalan, Stefan, & Benkovic, 2002; Rod et al., 2003; Singh, Abeysinghe, et al., 2015; Singh, Sen, Francis, & Kohen, 2014; Swanwick, Shrimpton, & Allemann, 2004; Thorpe & Brooks, 2003, 2004; L. Wang, Tharp, Selzer, Benkovic, & Kohen, 2006). Simulations of G121V have resulted in a rate decrease that is consistent with experimental rate measurements and suggested that mutations may alter the network of coupled motions through nonlocal structural perturbations, raising the free energy barrier and reducing the reaction rate (Watney, Agarwal, & Hammes-Schiffer, 2003). These calculations have suggested that remote mutations far from the active site could bring subtle structural perturbations that affect the catalytic rate by altering the conformational sampling of the entire enzyme, leading to alterations in the network of coupled motions of the wild type enzyme. This concept provides an explanation for the experimentally observed non-additive rates (Rajagopalan et al., 2002): the introduction of a mutation modifies the thermal motions of the entire enzyme because the remote regions of the enzyme are coupled to each other through long-range electrostatics and extended hydrogen bonding networks (Kim F. Wong et al., 2004); in turn, altering the thermal motions of the enzyme affects the probability of the occurrence of sampling conformations conducive to the catalyzed chemical reaction, thereby influencing the free energy barrier and the rate. Other theoretical studies by Moliner, Allemann and co-workers on WT-DHFR and G121V also imply that mutation causes nonlocal structural effects that may lead to perturbation of the network of coupled motions (Luk et al., 2013).

The QM/MM/MD calculations predicted that distal residues M42, G121, and F125, as well as active-site residue I14, are part of the network in question (S. Hammes-Schiffer & Benkovic, 2006; Sharon Hammes-Schiffer & Watney, 2006; Rod et al., 2003; K. F. Wong et al., 2005; Kim F. Wong et al., 2004). Single turnover rates examined by Benkovic and co-workers on G121, M42, and their double mutants provided some support for these predictions (Rajagopalan et al., 2002). Intrinsic KIEs and their temperature dependence were examined experimentally to test for the presence of the predicted network and effects of mutants on that network. As is true of most wild-type enzymes, WT ecDHFR has a KIE_int that is temperature independent (Sikorski et al., 2004), indicating a narrow DAD distribution and an active site that is perfect for hydride transfer. The temperature dependence of KIE_int was measured for I14A and M42W, G121V, F125M, and W133F, as well as for their double mutants (Singh et al., 2014; L. Wang, Goodey, Benkovic, & Kohen, 2006a, 2006b; L. Wang, Tharp, et al., 2006). Synergy between single mutations was used to indicate that the tested residues “work together”, i.e., are part of a network of motions coupled or correlated with the hydride transfer step. “Synergy” in this context means that the sum of changes in single turnover rates or temperature dependence of KIE_int caused by single mutants is smaller than that caused by the relevant double mutant.

Figure 7 summarizes the temperature dependences of the intrinsic KIEs for remote single mutants, their double mutants, the single active site mutant, and a remote-active site double mutant. The synergistic effect of double-mutant KIEs is apparent in the non-additive values of the temperature dependence, i.e., ΔE_a, which is the difference between the energy of activations (E_a) of the two isotopes used per study. (Please note that for KIEs ΔE_a = ΔH^‡ because E_a = H^‡ - RT, and RT is the same for both isotopes.) Figure 8 summarizes the isotope effect on activation energy (ΔE_a) and the Arrhenius pre-exponential factors (A_light/A_heavy) for WT-ecDHFR and its mutants. Figure 8 also reveals that the effect of single distal mutation is similar to the effect of active site mutations I14V and I14A, while the effect of double distal mutation is similar to the effect of active site mutation I14G, suggesting similarities in the way those mutants affect DAD distribution at the active site.

Figure 7.

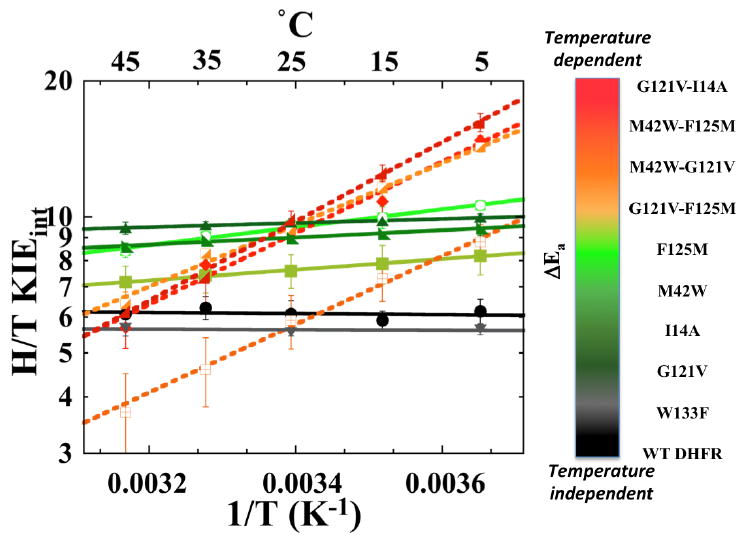
Comparison of Arrhenius plots of intrinsic H/T KIEs of WT DHFR and its mutants. The lines represent the non-linear regression to the Arrhenius equation and the error bars represent standard deviation.

Figure 8.

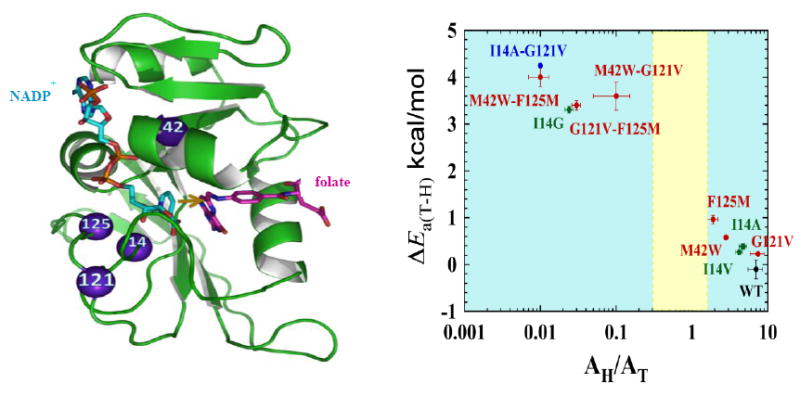
Roles of active site and distal residues on the DHFR-catalyzed reaction. Left panel: Structure of WT-ecDHFR (PDB Code 1RX2), with folate in magenta and NADP⁺ in light blue. A yellow arrow marks the hydride’s path from C4 of the nicotinamide to C6 of the folate, and the residues studied in ref (Singh et al., 2014) are marked as purple spheres. Right panel: Presentation of the temperature-dependence parameters of KIE_int for WT (black), distal (red), and active site I14 (green) mutants of DHFR, where error bars represent standard deviation. For each point, the ordinate is the isotope effect on activation energy (ΔE_a) and the abscissa is the isotope effect on the Arrhenius pre-exponential factor (A_H/A_T), both of which were determined from a non-linear regression of KIE_int to the Arrhenius equation. The yellow block represents the semi-classical range of the Arrhenius pre-exponential factor (0.3-1.7) (Kohen, 2006). Reprinted from ref. (Singh, Francis, et al., 2015) with permission from the American Chemical Society.

In summary, the influence of remote residues participating in a network of coupled motions on the catalyzed chemistry was validated for all the experimentally verified residues proposed by QM/MM simulations. Furthermore, W133F, the residue that had not been predicted by these calculations to be part of that network, did not seem to have an effect on hydride transfer. Because both the calculations and KIE_int examined the same single chemical step, the experimental findings can be compared directly to the computations that predicted that network. The findings thus validate calculations proposing that both remote and active-site residues constitute a network of coupled promoting motions correlated to the bond activation step (Singh, Francis, et al., 2015).

After the experimental findings for G121V and M42W were published (L. Wang, Goodey, et al., 2006a), Warshel and coworkers calculated the temperature dependences of KIE_int for these mutants and for the wild type using the empirical valence bond-quantum classical path method (EVB-QCP) (H. Liu & Warshel, 2007b). Those studies specifically explored the relationship between DAD and KIE_int at different temperatures. In good agreement with the empirical activated tunneling models mentioned above, Warshel’s calculations found a broader DAD distribution for steeper temperature dependence of KIEs (ΔE_a).

A very different computational study of ecDHFR used transition-path sampling (TPS) and examined the role of protein promoting vibrations (PPV) in ecDHFR catalysis (Dametto et al., 2012). This study found no such PPVs, which could be taken as contradictory to all the computational and experimental studies discussed above. However, the “network of coupled motions” along the reaction coordinate simulated by Hammes-Schiffer and others includes no non-statistical elements. The calculated PPVs, on the other hand, are non-statistical dynamic motions, so the apparent contradictions between the two methods likely reflect the fact that they examine very different phenomena. It seems that the experimental studies using KIE_int agree well with the first but did not test the second theoretical approach. Additionally, TPS calculatins of the human DHFR (hsDHFR) predicted significant PPVs, but KIE_int for both light and heavy hsDHFR where identical throughout the temperature range (Francis, Sapienza, Lee, & Kohen, 2016), falling to support the theoretical prediction. Similarly, in a different TPS study of liver alcohol dehydrogenase, it was predicted that the valine residues at position 203 and 207 facilitate enzyme catalysis as part of the PPV (Caratzoulas, Mincer, & Schwartz, 2002). However, no experimental evidence was found to support a role of V207 in the dynamics of catalysis (Yahashiri, Rubach, & Plapp, 2014).

Experimental section for DHFR

The cofactors [Ad-¹⁴C]-NADPH (50 mCi/mmol), (R)-[Ad-¹⁴C, 4-²H]-NADPH (50 mCi/mmol) and (R)-[4-³H]-NADPH (680 mCi/mmol) were synthesized according to previously published procedures (N. Agrawal & Kohen, 2003; Markham, Sikorski, & Kohen, 2004a, 2004b; McCracken, Wang, & Kohen, 2003; Sen et al., 2011; McCracken et al., 2003).

Competitive KIE measurements

For H/T 1° KIE, (R)-[4-³H]-NADPH and [Ad-¹⁴C]-NADPH were combined in a radioactivity ratio close to 5:1. Likewise, for D/T 1° KIE, (R)-[4-³H]-NADPH and (R)-[Ad-¹⁴C, 4-²H]-NADPH were combined in the same manner. Each mixture was co-purified on an analytical reverse phase HPLC column. The purified material was divided into aliquots containing 300,000 dpm of ¹⁴C and stored at -80 °C for short-term storage.

All measurements were done in MTEN (50 mM MES, 25 mM Tris, 25 mM ethanolamine and 100 mM NaCl) buffer at pH=9.0 over the temperature range of 5-45 °C. NADPH was added to the reaction mixture so that the final concentration was 4 μM, while dihydrofolate was added to a final concentration of 0.85 mM (~200-fold excess over NADPH). A pH electrode was calibrated at each temperature using standard buffers at the respective temperatures and used to check the pH of all reaction mixtures. For DHFR, the largest KIE_obs can be measured at pH 9.0, though KIE_obs at pH 8.0 and 7.0 have also been measured with good outcomes (C. T. Liu, Francis, K., Layfield , J., Huang, X., Hammes-Schiffer, S., Kohen, A., Benkovic, S.J., 2014). The reaction was initiated by addition of DHFR, and allowed to proceed until a fraction conversion of between 20-80% was reached, followed by quenching by adding an excess of methotrexate to a final concentration of 1.7 mM before storing in dry ice. Fraction conversions of 20-80% have been shown to produce minimal error when determining KIE_obs (Northrop, 1991). Samples were thawed and bubbled with oxygen before HPLC-LSC analysis to ensure complete oxidation of the product tetrahydrofolate. The samples were then separated by reverse phase HPLC and analyzed on a liquid scintillation counter (LSC). The KIE_obs was calculated using the following equation:

$$\mathrm{KIE}=\frac{\mathrm{In}(1-f)}{\mathrm{In}[1-f(R_t/R_{\mathit{\infty }})]}$$ (15)

where the fraction conversion (f) was determined from the ratio of ¹⁴C in the product and reactant, and R_t and R_∞ are the ratios of ³H/¹⁴C at a particular time point and at infinite time, respectively. Subsequently, KIE_int was extracted from its respective observed values using the Northrop method as explained in an earlier section. All quality controls were performed for DHFR as for TSase, as described under the experimental section for TSase.

Summary

In this chapter, we underscore the importance of examining the same chemical step, or microscopic event, in both calculations and experiments, and illustrate the necessity of such precise, parallel computational and experimental studies of DHFR and Tsase. The utility of intrinsic KIE as a probe for TS structures and their distribution is described. In the two case studies discussed above, the objective of the calculations is not only to explain experimental results but also to create experimentally testable predictions that permit the examination of the theory’s underlying rationale. The objective of the experimental work is to conduct measurements that afford the examination of the same phenomenon studied by the relevant calculations. In that context, we suggest that assessment of intrinsic KIE (KIE_int) from measured observed KIE (KIE_obs) is an important tool, and that in some cases the Northrop method can assist in that task. The two examples presented above started from predictions made by QQM/MM calculations (a newly proposed intermediate in TSase and a network of coupled motions in ecDHFR), and demonstrated how measurement of the temperature dependence of KIE_int supported theses predictions, then suggested further need for calculations and experimental studies.

We suggest that a collaborative blend of theoretical and experimental approaches is beneficial to resolving quandaries of theoretical models and experimental results. Collaborative approaches are likely to deepen our knowledge of enzyme mechanisms in general, as well as our knowledge of the role of protein motions in catalysis, allowing the development of more detailed and comprehensive models of enzyme catalysis. The expected gain is most significant: experimental findings that agree with computations lend reassurance to both methods; and exposing “hidden” features in enzyme mechanisms may lead to the identification of new targets for inhibitors and potential drugs.