Significance
Time-dependent network analysis is used to describe the structural dynamics underpinning electron transport in disordered aggregates of molecular materials, advancing understanding of how charges move through noncrystalline aggregates. Specifically, our methodology allows for the characterization of how collective, dynamic fluctuations in the 3N nuclear degrees of freedom of the disordered multimolecule aggregate impact the statistically averaged charge motion through that aggregate. Our results describe the characteristic timescales over which electron hopping competes with nuclear reorganization, providing insight into the fundamental timescales governing charge transport in disordered systems.
Keywords: organic semiconductors, charge transport, network analysis, dynamic disorder, molecular semiconductors
Abstract
Due to the nonperiodic nature of charge transport in disordered systems, generating insight into static charge transport networks, as well as analyzing the network dynamics, can be challenging. Here, we apply time-dependent network analysis to scrutinize the charge transport networks of two representative molecular semiconductors: a rigid n-type molecule, perylenediimide, and a flexible p-type molecule, . Simulations reveal the relevant timescale for local transfer integral decorrelation to be 100 fs, which is shown to be faster than that of a crystalline morphology of the same molecule. Using a simple graph metric, global network changes are observed over timescales competitive with charge carrier lifetimes. These insights demonstrate that static charge transport networks are qualitatively inadequate, whereas average networks often overestimate network connectivity. Finally, a simple methodology for tracking dynamic charge transport properties is proposed.
Computational tools using periodic boundary conditions are integral to understanding charge and excitation transport in crystalline semiconducting materials (1, 2). In noncrystalline systems, where Bloch’s theorem is inapplicable and inclusion of structural disorder is required for an accurate description of charge transport, comparable computational strategies are rare. Typically, one uses an approximate solution of the master equation with semiclassical rates derived from a combination of atomistic molecular dynamics (MD) and quantum chemistry. While this strategy has proven effective (3, 4), it possesses obvious deficiencies: it lacks both an explicit inclusion of structural dynamics and an understanding of the topology of charge transport networks.
Work in this group and others has proposed a view of charge transport based in network analysis (5–10). Network analysis represents a powerful means of analyzing structurally disordered charge transport networks, with the unique ability to place different mechanisms of charge transport on the same footing via the selection of a suitable graph metric. Recently, network views of charge transport in structurally disordered systems have provided useful insights: notably, the relationship between a molecule’s topology and the percolation threshold of its charge transport networks (5, 6), and that charge mobility can be independent of the global morphology, being primarily determined by local molecular packing (7).
Although a useful framework, previous applications of network analysis to structurally disordered charge transport networks have neglected the role of dynamic structural disorder: static snapshots of the charge transport network were used for the network analysis. Transport was assumed to occur on a charge transport network defined by time-independent site energies and electronic couplings. Whereas the static picture provides many insights into the nature of charge transport in soft materials, recent work has emerged indicating the importance of time-dependent fluctuations. Throughout the rest of this article we refer to these fluctuations as “dynamic disorder” (11–16).
In this work we use network analysis to examine the impact of dynamic disorder on charge transport networks of aggregates of two representative organic semiconducting molecules, perylenediimide (PDI, Fig. 1) (17) and (18). Although previous studies have examined the dynamics of local charge transfer couplings between two sites in great detail (11, 12), none has examined the dynamic evolution of the global network topology. Whereas conventional charge carrier mobility simulations would require either thousands of charge-hopping simulations at each time step, or a computationally intensive dynamic kinetic Monte Carlo algorithm (19), we use a simple graph metric (6) to significantly expedite the analysis.
Fig. 1.
(Top) Molecular structure of N,N′-Bis(1-pentylhexyl)perylene-3,4,9,10-tetracarboxylic diimide (PDI). (Bottom) Molecular structure of benzo[1,2-b:6,5-b′]dithiophene-dithieno-diketopyrrolopyrrole (). All side chains are 2-ethylhexyl.
We contend that qualitatively useful insights are derived by examining the dynamics of the charge transport network topology. Specifically, this contribution argues the following points: (i) The tools of network analysis provide a useful complement to conventional approaches for analyzing charge transport networks in structurally disordered environments over many timescales. (ii) The characteristic timescales of local intermolecular coupling correlations are 30 fs and 200 fs, which are assigned to effective intramolecular and intermolecular vibrational modes, respectively. (iii) Charge transport network topologies in disordered molecular semiconductors decorrelate on a timescale competitive with charge carrier lifetimes. (iv) Ordered morphologies maintain intermolecular coupling correlations longer than disordered morphologies. (v) Using the time-averaged network in charge transport overestimates the quality of charge transport networks by 20%; the average network does not predict the average of an ensemble of networks in a disordered system over relevant charge transport timescales.
Model and Methods
Network Analysis.
Because the primary focus of this contribution is on charge transport networks that are nonperiodic, we apply network analysis to characterize disordered multimolecule aggregates. We proceed by defining the time-dependent adjacency matrix of a graph representing the charge transport network. This network has edges (connections), , between vertices [PDI lowest unoccupied molecular orbital (LUMO)/ highest occupied molecular orbital (HOMO)]; the edges are defined as the absolute value of the intermolecular electronic coupling, , between relevant molecular orbitals (Eq. 1).
| [1] |
For an accurate treatment of charge transport in disordered systems, site-energy disorder must be taken into account (20). However, given that we are primarily concerned with intermolecular coupling-limited transport, we use a simple definition of the adjacency matrix using the intermolecular electronic coupling between molecular transport orbitals. For a complete treatment and experimental comparison, energetic disorder and reorganization energies must be taken into account (4, 21). It is our belief that the conclusions of this work are rendered most straightforwardly by using our simple definition of the adjacency matrix. Most formulations using energetic disorder will render the adjacency matrix nonsymmetric (hence the directed graph as opposed to an undirected graph), which significantly complicates the network analysis.
To visualize the three-dimensional charge transport networks of our materials, we consider an equivalent graph of the adjacency matrix defined in Eq. 1. A circular embedding of the adjacency matrix is used to visualize the time-dependent dynamics of representative MD trajectories characterizing PDI and charge transport networks.
The dynamics of the adjacency matrix are analyzed using both local and global approaches. The local characterization is chosen as a normalized time-correlation function (TCF), , for the absolute value of the intermolecular couplings between two PDI LUMOs/two HOMOs (Eqs. 2–5). For analysis, a value of = 0.0001 eV is chosen.
| [2] |
| [3] |
| [4] |
| [5] |
To quantify the global network topology, we examine a metric of the charge transport network known as the “Kirchhoff index” to understand whether fluctuations only cause minor perturbations to the overall network structure, or if they nontrivially modify the topology of the entire charge transport network. In previous work, the Kirchhoff index was used as a robust measure to quantify known differences in charge percolation properties in topologically distinct organic semiconducting molecules (6). It is simplest to think of the Kirchhoff index as a metric quantifying a statistically averaged random walk over the entire network (i.e., an average of mean first passage times). By computing the Kirchhoff index at various MD snapshots, we examine the dynamic nature of the disordered charge transport network. In addition to the time-dependent Kirchhoff index of the instantaneous graph (), we also compute the Kirchhoff index of the time-averaged graph () over the course of 20 ps.
Graph Parameterization with Atomistic Simulation.
To parameterize graphs characterizing the charge transport networks of PDI/, we randomly deposit 64/100 molecules (Fig. 1) into MD simulation boxes with periodic boundary conditions using a modified atomistic optimized potentials for liquid simulations all atom (OPLS-AA) 2009 (22) force field (SI Appendix). The simulation box is then subjected to a series of minimizations, compressions, thermal annealing, and equilibrations ( 30 ns) to assemble a simulation box of the appropriate density (SI Appendix), upon which a 20-ps sampling run is performed in the microcanonical (NVE) ensemble. For crystalline simulations, the unit cell of is repeated into a 5 × 5 × 2 structure, relaxed using the OPLS-AA 2009 force-field, and run for 20 ps to generate a trajectory of the crystalline system’s structural dynamics for comparison with the disordered morphology. The longer timescale evolution of the noncrystalline PDI morphology is simulated using an identical procedure, except using 150 ns of annealing and sampling. Given the inability of atomistic MD to adequately sample kinetically trapped, experimentally relevant morphologies over the timescale of the MD simulation, our noncrystalline morphologies are very likely stuck in high-energy configurations. We assume that these disordered morphologies represent useful models upon which to analyze time-dependent structural fluctuations in noncrystalline charge transport networks.
To analyze the properties of the time-dependent networks, we output MD geometries every 10 fs of the 20-ps NVE trajectories, and use semiempirical extended Hückel (5) theory to compute transfer integrals between all nearest-neighbor ( 2 nm) molecules in the system, creating a time-dependent Hamiltonian of the aggregate. Given that PDI is used as an electron accepting/transporting material (17, 23), we use the LUMO of each PDI molecule as the relevant localized charge transport state. Analogously, we use the relevant HOMO–HOMO couplings for . This information is used to generate an adjacency matrix of a graph representing the charge transport network (5, 6).
Results
Visualizing Dynamics of Aggregate Charge Transport Networks.
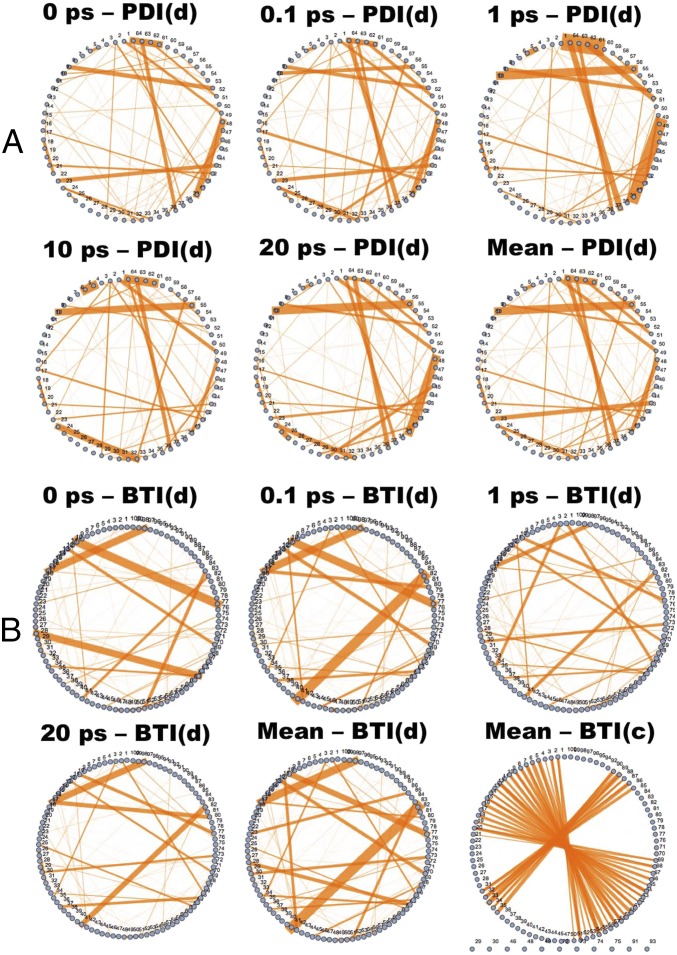
To visualize charge transport network dynamics of the molecular aggregates, we plot the time-dependent graph of the adjacency matrix corresponding to a single trajectory using a circular embedding. Fig. 2A shows five different time intervals (0, 0.1, 1, 10, and 20 ps) for PDI, as well as the time-averaged graph, whereas Fig. 2B shows similar intervals plus the time-averaged crystalline network for . Each numbered vertex on the circumference of each graph represents a charge transport state [PDI LUMO/ HOMO] of the system (note that the only spatial information contained in this graph is implicitly signified by the magnitude of the edge weights). The edge width between each numbered vertex corresponds linearly to the value of the adjacency matrix between those sites.
Fig. 2.
(A) Graph representations of the adjacency matrix of PDI (Eq. 1) at different times (0, 0.1, 1, 10, and 20 ps) using a circular embedding. A visualization of the time-averaged adjacency matrix is also provided. PDI(d) denotes a disordered morphology. (B) Graph representations of the adjacency matrix of (0, 0.1, 1, and 20 ps). A visualization of the time-averaged adjacency matrix for the disordered [BTI(d)] and crystalline [BDT(c)] morphologies is provided. Numbered vertices on the outer rim of the circle characterize PDI LUMOs of a 64-molecule bulk system. Orange lines between numbered vertices represent intermolecular electronic couplings between molecular orbitals, with line widths linearly proportional to the magnitude of intermolecular couplings.
Examination of Fig. 2 provides clear evidence that large fluctuations in transfer integrals are observed over short timescales; by 1 ps, many connections between states have increased significantly, and some have almost completely disappeared. This result is in contrast to the common assumption of a static charge transport network when computing mobilities via a master equation approach (24) in highly ordered crystalline, polymeric systems. Operating under the assumption that charge transport in noncrystalline organic semiconductors occurs in the perturbative limit, the timescales of significant changes in the intermolecular coupling appear to be competitive with the rates derived from a Marcus-like approach. This consideration warrants a reevaluation of the dominant mechanism of charge transport, as suggested by other authors (11, 12, 14, 16).
Examination of longer timescales in Fig. 2 demonstrates that by 10 and 20 ps, the charge transport network has substantially evolved. However, an inspection of the graphs in Fig. 2 provides evidence for connections between molecules which are maintained throughout the duration of the simulation. These dominant pathways are most apparent when compared with the time-averaged “mean” graph in Fig. 2. Whereas certain pathways are maintained throughout the simulation, we note how different the individual snapshots can appear compared with the mean graph. Importantly, the mean graph is more connected than any individual snapshot. It is to be emphasized that the time-dependent graphs presented in Fig. 2 are the results of single trajectories, although the nature of the dynamics should be universal across trajectories.
The circularly embedded graph also provides insight into the overall connectivity of the network structure of a crystalline system, allowing one to straightforwardly compare both crystalline and disordered charge transport networks. In Fig. 2B this type of visualization provides the useful insight that despite being highly ordered, the crystalline network possesses a significant number of molecular sites that are disconnected from the charge transport network. This is in contrast to the disordered system, which in most cases demonstrates the properties of a strongly connected graph (all vertices are reachable from all other vertices). The question of whether crystalline or disordered systems exhibit better charge transport depends on many details not captured by our simple model, but our approach demonstrates that a disordered aggregate can be in some sense “better connected” than a crystalline one.
Timescales of Local Intermolecular Coupling Decorrelation.
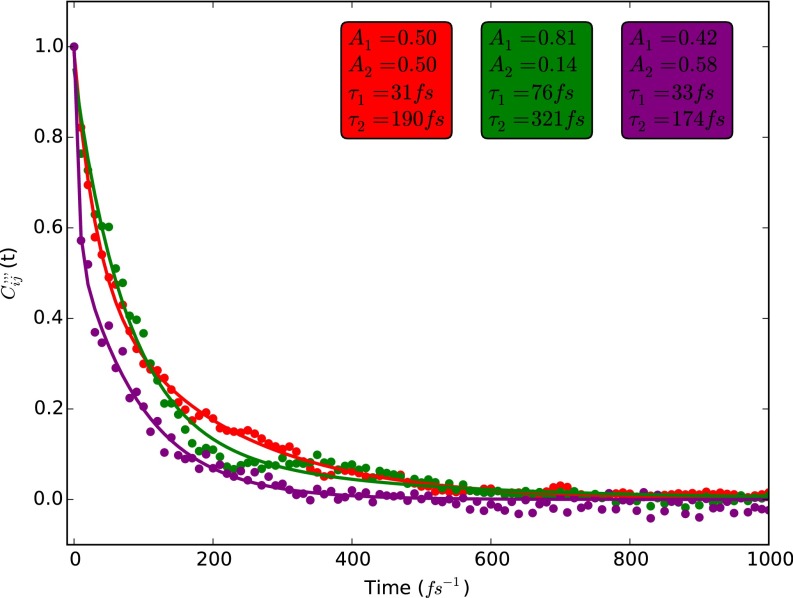
Whereas the graphical nature of Fig. 2 is inherently qualitative, we now explicitly quantify the timescale of electronic coupling decorrelation between pairs of molecules; what is the timescale behind fluctuations in the edge weights of Fig. 2? We plot the normalized TCFs of Eq. 5 for disordered PDI, disordered , and crystalline in Fig. 3. From Fig. 3 it is clear that the characteristic decay time of local site correlations is in agreement with the results derived from the visual inspection of the previous section (Fig. 2). In the specific case of PDI, when fit to a single-exponential decay, the TCF of Fig. 3 fits poorly with a time constant of 100 fs. When fit to a function containing two exponential decays, the TCF fit is greatly improved (Fig. 3). In this case, the fit corresponds to a near-50/50 split between an 30-fs and an 170-fs decay component. This result is in excellent agreement with both the results of the previous section, as well as with previous local TCFs computed for other conjugated systems (11). We note that the normalized TCF displayed in Fig. 3 has been scaled according to the value of . It bears mentioning that the average value of is 0.6.
Fig. 3.
Averaged, normalized TCF for intermolecular electronic couplings in disordered PDI (red), disordered (purple), and crystalline (green). Results are averaged over 20-ps trajectories with time intervals of 10 fs. Filled circles represent computational data whereas solid lines represented two-exponential fits. Color-coded legend represents two-exponential fits to the forms provided in SI Appendix.
Some caution must be taken in assigning physical meaning to the timescales of electronic coupling decorrelation. However, given the general assumption of independent local (intramolecular) and nonlocal (intermolecular) vibrational couplings in model Hamiltonians for charge transport (25), and the fact that the ubiquitous C=C vinyl stretching mode corresponds to a timescale of 30–50 fs (26), we feel that a qualitative assignment of these modes is valid. Consequently, we assign the 30-fs component to a single, effective local vibrational mode likely dominated by the C=C stretch, and the 200-fs component to a single effective nonlocal vibrational mode, which is likely some form of global libration of the PDI and molecules. To confirm this assignment, the two-exponential fit was subtracted off of the raw PDI data, and the resulting oscillations were Fourier transformed to project out the underlying molecular frequencies mediating the coupling (SI Appendix), with the strongest peaks corresponding to characteristic timescales of 200 fs and 60–75 fs.
Whereas the specific example of PDI’s electron transport network represents only a single molecular example, the hole transport networks of present additional insights. First, the rigidity of the PDI π-electron system relative to that of manifests in a slower decay of the TCF; this is in agreement with intuition, as the more flexible backbone should allow larger structural distortions, leading to faster decorrelation of the TCF. Second, both electron and hole transport networks possess similar dynamic behavior, suggesting that the decorrelation time constant can be assumed to be roughly constant regardless of the specific molecular orbital character of the charge transport network, especially in modeling considerations. Third is the comparison of the dynamics of the electronic coupling in crystalline and disordered . It is apparent from Fig. 3 that the timescale of coupling decorrelation is extended in the crystalline system relative to the disordered one. This is likely due to the increased homogeneity of the local environment leading to a narrower distribution of intermolecular vibrational modes, and is supported by the TCF of crystalline exhibiting more noticeable oscillatory structure during its decay than that of the disordered system. This result is vital for a careful understanding and modeling of charge transport in these systems, as the local crystal structure appears to impact decorrelation times of intermolecular coupling correlations.
Dynamic Fluctuations of Charge Pathways in Molecular Aggregates.
To rapidly characterize the dynamics of the entire charge transport network we use the Kirchhoff index as a metric of charge transport network connectivity (6). By computing the Kirchhoff index for 20-ps trajectories of distinct morphologies, we examine the real-time dynamics of the charge transport network topology. This information provides complementary information to the local TCF: if a single connection decorrelates [], then charge transfer between two sites could be mitigated, but if the rest of the network remains connected, the impact on global network properties could be minimal. However, if small fluctuations in numerous intersite couplings occur, it is possible that the dominant charge transport pathways could significantly rearrange, and the topology of the charge transport network could change.
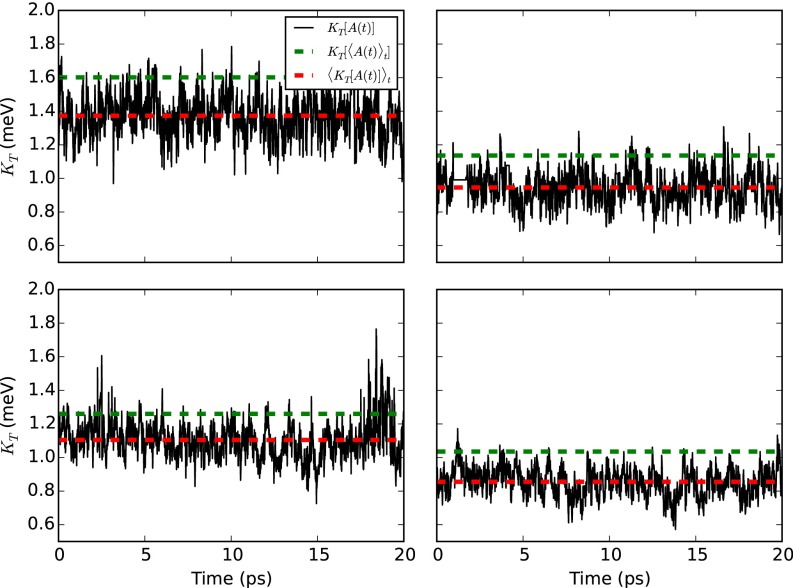
In Fig. 4 we display the time-dependent Kirchhoff index of 20-ps trajectories for four disordered PDI morphologies. In addition to the time-dependent Kirchhoff index, we plot the Kirchhoff index of the time-averaged graph and the average value of the time-dependent Kirchhoff index as horizontal dashed lines. The simulations of Fig. 4 show rapid fluctuations in the value of which agree with the timescales of the local TCF exponential decay constants ( 100 fs). Specifically, the value of is observed in some cases to fluctuate by nearly 50% of its average value over a timescale of 1 ps. These timescales are quantitatively confirmed by examining a TCF of the spectral norm, averaged over all trajectories (SI Appendix). These facts are indicative of not only significant changes in local site correlations, but also in the rapid rearrangement of the dominant pathways for charge transport on an ultrafast timescale. Moreover, the results of Fig. 4 demonstrate that the time-averaged graph overestimates transport by compared with the charge transport network described by the actual MD trajectory.*
Fig. 4.
Time-dependent data for the Kirchhoff index of four distinct trajectories. Black lines represent the instantaneous value of the Kirchhoff index. Dashed green and red lines represent the value of the Kirchhoff index of the time-averaged adjacency matrix and the average value of the instantaneous Kirchhoff index, respectively.
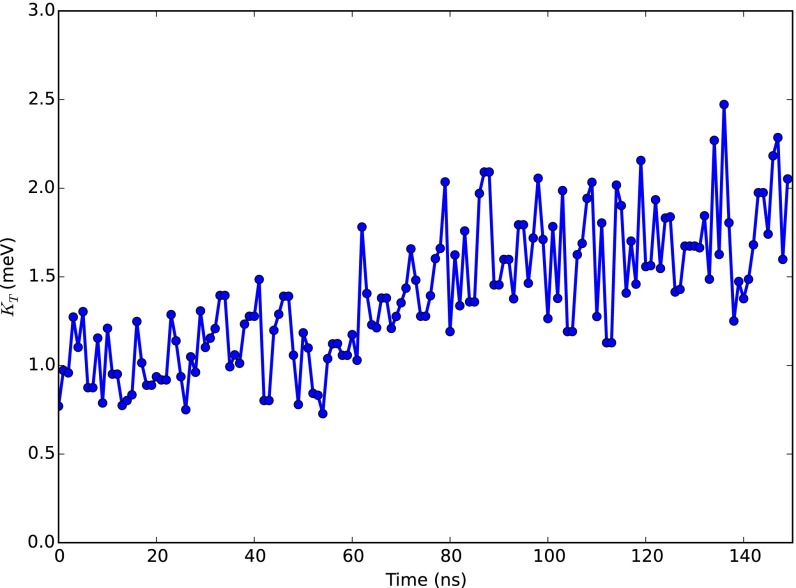
Whereas the fluctuations of the charge transport network topology on short ( 20 ps) timescales are relatively mitigated, an examination of Fig. 5 demonstrates that over timescales longer than intramolecular fluctuations, but shorter than charge carrier lifetimes, much larger rearrangements of the charge transport network topology can occur. The results of Fig. 5 clearly show that over the timescale of 150 ns, thermal fluctuations lead to structural rearrangements that rewire the disordered network topology considerably, as evidenced by the slow increase in the value of the Kirchhoff index as a function of time. In such situations, an average network approach that simply averages the mean-squared coupling between sites will overestimate the connectivity of the network and misrepresent dynamic transport over this network.
Fig. 5.
Time-dependent data for the Kirchhoff index of a 150-ns trajectory of PDI in the NPT ensemble. Here, 0–50 ns corresponds to heating at 550 K, 50–100 ns corresponds to linear cooling from 550 to 300 K, and 100–150 ns corresponds to simulation at 300 K.
Discussion
The Validity of the Static Network Assumption for Molecular Materials.
The previous results suggest that the dynamics of charge transport networks in disordered soft matter are not accurately characterized by a static network topology. Given the rapid timescale of intramolecular vibrations (30 fs) corresponding to the C=C vinyl stretching mode, and previous conclusions that intersite couplings of organic crystals possess SDs of a similar order-of-magnitude as the mean (3, 12), this result is not overly surprising. Whereas these facts may appear somewhat obvious, it is still common to use a single snapshot of the charge transport network to generate a directed graph for charge mobility simulations (24). Such an approximation may be more appropriate in crystalline materials at low temperature, where a combination of spatial restrictions of the equilibrium crystal geometry and decreased thermal energy could reduce large-amplitude thermal motions, as suggested in the results of crystalline (Fig. 3). Recent experimental work has suggested means of reducing dynamic disorder in crystalline systems (15) along these lines, although we suspect the validity of the static network approximation in modeling is still untenable.
Previous work (24, 27) on the structural dynamics of crystalline polymeric materials provides perspective on these conclusions. In these works, transfer integrals between charge transport states were centered around 1 eV, indicating a dominance of intrachain transport. This led to the assumption that escape times were significantly faster than transfer integral decorrelation times, supporting a static network picture. However, the rapid rate of transfer integral decorrelation times in our work is in good agreement with results from the same authors (approximately hundreds of femtoseconds) for intramolecular transport in a polymer where side-chain vibrational damping of dihedral motion was not present (27), leading the authors to adopt a picture using time-averaged transfer integrals. In the specific case of intermolecular dominated transport in disordered materials considered in this article, the dominant role of zero-point energy in intramolecular vibrational modes (3) and the lack of explicit vibrational damping of the π-electron system suggest that dynamic disorder should strongly influence the majority of molecular materials.
The synthesis of current results with previous literature indicates that in organic semiconducting molecules, the assumption of a static charge transport network is likely untenable. To accurately incorporate dynamic disorder into future charge transport calculations, semiclassical dynamics or dynamic kinetic Monte Carlo may be useful (19, 28), although the issues with these methods have been described in a recent review (16).
The Validity of the Average Network Assumption for Molecular Materials.
Although a static network approach is unviable, it is less clear if the utilization of an average network picture is appropriate. The results of Fig. 3 indicate that the value of the long-time intermolecular electronic coupling relative to the maximum is on average 0.6. While this result is a consequence of the definition of the adjacency matrix using the absolute value of the coupling, it has important implications for the master-equation approach to simulating charge carrier mobilities. In nearly all semiclassical rate theories, the rate of charge transfer depends on the ensemble-averaged value of the transfer integral squared. However, this approximation is only reasonable if the network over which transport is occurring is relatively static in its topology. In cases where a molecular translation or rotation during a simulation creates/eliminates a connection between molecules, averaging over the entire simulation time will overestimate the connectivity of the charge transport network. We note that previous works have observed an increase in the average mobility upon time-averaging couplings, (10, 27, 29) which may point to this effect.
To further explore the influence of the average network assumption, we examine the values of presented in Fig. 4. In all cases, the Kirchhoff index of the average graph is larger than the time-averaged Kirchhoff index of many independent graphs, supporting our claim that time averaging artificially increases the connectivity of the charge transport network. Additionally, whereas average graph approaches roughly characterize the overall mobility, the actual pathways taken by charges throughout the dynamically evolving network should be dramatically different, because at one time a charge could see a dominant pathway leading in one spatial direction out of the simulation box, whereas hundreds of picoseconds later the dominant charge transport pathway could lead in a completely different spatial direction. To put simply: averaging over structural fluctuations that do not occur in a simple harmonic well should result in artificially increased charge transport network connectivity. Such problems will particularly manifest in noncrystalline systems, where the structure is not a global minimum, and significant structural reorganization of the network can occur over charge carrier lifetimes (microseconds).
Given the ability of PDI and molecules to strongly couple in only a single spatial direction (orthogonal to the π-electron system) (5, 6), the electronic coupling between two molecules is not robust to molecular rotations, whereas in spherical molecules (fullerenes) average couplings should be large regardless of the relative rotational orientation between molecules. Consequently, average network approximations may be more appropriate in systems where molecular topology leads to charge transport networks that are robust to changes in molecular orientation, such as fullerenes (5). However, in the majority of cases where noncrystalline organic semiconductors consist of planar π-electron systems capable of coupling in only a single spatial direction (like PDI), these considerations warrant an approach which explicitly incorporates dynamic disorder.
Optimizing Morphologies for Transport in Noncrystalline Materials.
In brief, we propose a potential application of this combination of techniques to rapidly identify nonequilibrium molecular morphologies with desirable charge transport properties, as well as to dynamically monitor the charge transport network topology. In the case of the 150-ns trajectory of Fig. 5, even over the relatively short timescale of 150 ns, there is a noticeable drift in the average value of . This is a feature qualitatively observed in many trajectories by the authors. Some of this effect is likely due to box contraction after the 0–50-ns cooling phase, although it is clear that the morphology is very slowly evolving to a more conductive state even after all of the annealing phases have completed at 100 ns. We posit that such time-dependent tracking of is a useful way of evolving noncrystalline morphologies toward nonequilibrium states with desirable charge transport properties. By running MD trajectories (or Monte Carlo moves), one can check the value of at regular intervals. If the value of increases during the evolution, that trajectory can be kept. If the value of decreases, that trajectory can be canceled, and a new trajectory can be derived from the other trajectories leading to higher values of . This is in spirit very similar to a previous schematic by Nelson et al. (3), although it would be significantly expedited given the lack of explicit charge carrier mobility simulations.
Conclusion
We have analyzed the dynamic charge transport networks of two molecular semiconductors using a combination of atomistic MD, semiempirical electronic structure theory, and network analysis. Using a circular embedding, we have visualized the charge transport networks, providing insight into the topological proximity between charge transport states in a nonperiodic geometry. We have tracked the time dependence of a useful graph metric, the Kirchhoff index, characterizing the “resistance” of entire molecular aggregates, with the notable conclusion that the utilization of a time-averaged graph, especially in systems with nontrivial fluctuations, overestimates the connectivity of the charge transport network by 20%. All of these results demonstrate that a simulation approach incorporating dynamic disorder is warranted for an accurate treatment of charge transport in disordered molecular semiconductors, and that the traditional static and average pictures are often inadequate. Finally, we propose a simple approach to identifying nonequilibrium morphologies with advantageous charge transport properties using network analysis.
Supplementary Material
Acknowledgments
The authors thank Brett Savoie and Kevin Kohlstedt for useful discussion. We thank the US Department of Energy-Basic Energy Sciences Argonne-Northwestern Solar Energy Research Center, an Energy Frontier Research Center (Award DE-SC0001059), for funding this project.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. J.-L.B. is a Guest Editor invited by the Editorial Board.
*Whereas the Kirchhoff index has been only qualitatively associated with experimental charge mobilities in previous work (6), in SI Appendix we provide explicit kinetic Monte Carlo simulations that demonstrate a strictly monotonically increasing relationship between the zero-field charge carrier mobility and the Kirchhoff index, cementing the use of the Kirchhoff index as a meaningful qualitative metric for charge mobilities in disordered systems.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1601915113/-/DCSupplemental.
References
- 1.Chan MKY, Ceder G. Efficient band gap prediction for solids. Phys Rev Lett. 2010;105(19):196403. doi: 10.1103/PhysRevLett.105.196403. [DOI] [PubMed] [Google Scholar]
- 2.Tanabe T, Kozawa Y, Oyamal Y. Self-energy operators and exchange-correlation potential in semiconductors. Phys Rev B. 1988;37(17):10159–10175. doi: 10.1103/physrevb.37.10159. [DOI] [PubMed] [Google Scholar]
- 3.Nelson J, Kwiatkowski JJ, Kirkpatrick J, Frost JM. Modeling charge transport in organic photovoltaic materials. Acc Chem Res. 2009;42(11):1768–1778. doi: 10.1021/ar900119f. [DOI] [PubMed] [Google Scholar]
- 4.Rühle V, et al. Microscopic simulations of charge transport in disordered organic semiconductors. J Chem Theory Comput. 2011;7(10):3335–3345. doi: 10.1021/ct200388s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Savoie BM, et al. Mesoscale molecular network formation in amorphous organic materials. Proc Natl Acad Sci USA. 2014;111(28):10055–10060. doi: 10.1073/pnas.1409514111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jackson NE, Savoie BM, Chen LX, Ratner MA. A simple index for characterizing charge transport in molecular materials. J Phys Chem Lett. 2015;6(6):1018–1021. doi: 10.1021/acs.jpclett.5b00135. [DOI] [PubMed] [Google Scholar]
- 7.Rühle V, Kirkpatrick J, Andrienko D. A multiscale description of charge transport in conjugated oligomers. J Chem Phys. 2010;132(13):134103. doi: 10.1063/1.3352568. [DOI] [PubMed] [Google Scholar]
- 8.Baumeier B, Stenzel O, Poelking C, Andrienko D, Schmidt V. Stochastic modeling of molecular charge transport networks. Phys Rev B. 2012;86(18):184202. [Google Scholar]
- 9.Vehoff T, Baumeier B, Troisi A, Andrienko D. Charge transport in organic crystals: Role of disorder and topological connectivity. J Am Chem Soc. 2010;132(33):11702–11708. doi: 10.1021/ja104380c. [DOI] [PubMed] [Google Scholar]
- 10.Vehoff T, et al. Charge transport in self-assembled semiconducting organic layers: Role of dynamic and static disorder. J Phys Chem C. 2010;114(23):10592–10597. [Google Scholar]
- 11.Beratan DN, et al. Steering electrons on moving pathways. Acc Chem Res. 2009;42(10):1669–1678. doi: 10.1021/ar900123t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Troisi A, Orlandi G. Dynamics of the intermolecular transfer integral in crystalline organic semiconductors. J Phys Chem A. 2006;110(11):4065–4070. doi: 10.1021/jp055432g. [DOI] [PubMed] [Google Scholar]
- 13.Troisi A. Charge transport in high mobility molecular semiconductors: Classical models and new theories. Chem Soc Rev. 2011;40(5):2347–2358. doi: 10.1039/c0cs00198h. [DOI] [PubMed] [Google Scholar]
- 14.Aragó J, Troisi A. Dynamics of the excitonic coupling in organic crystals. Phys Rev Lett. 2015;114(2):026402. doi: 10.1103/PhysRevLett.114.026402. [DOI] [PubMed] [Google Scholar]
- 15.Illig S, et al. Reducing dynamic disorder in small-molecule organic semiconductors by suppressing large-amplitude thermal motions. Nat Commun. 2016;22(7):10736. doi: 10.1038/ncomms10736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fratini S, Mayou D, Ciuchi S. The transient localization scenario for charge transport in crystalline organic materials. Adv Funct Mater. 2016;26(14):2292–2315. [Google Scholar]
- 17.Huang C, Barlow S, Marder SR. Perylene-3,4,9,10-tetracarboxylic acid diimides: Synthesis, physical properties, and use in organic electronics. J Org Chem. 2011;76(8):2386–2407. doi: 10.1021/jo2001963. [DOI] [PubMed] [Google Scholar]
- 18.Harschneck T, et al. Substantial photovoltaic response and morphology tuning in benzo[1,2-b:6,5-b′]dithiophene (bBDT) molecular donors. Chem Commun (Camb) 2014;50(31):4099–4101. doi: 10.1039/c3cc49620a. [DOI] [PubMed] [Google Scholar]
- 19.Prados A, Brey JJ, Sanchez-Rey B. A dynamical Monte Carlo algorithm for master equations with time-dependent transition rates. J Stat Phys. 1997;89(3-4):709–734. [Google Scholar]
- 20.Bassler H. Charge transport in disordered organic photoconductors: A Monte Carlo simulation study. Phys Status Solidi, B Basic Res. 1993;175(1):15–56. [Google Scholar]
- 21.Barbara PF, Meyer TJ, Ratner MA. Contemporary issues in electron transfer research. J Phys Chem. 1996;100(31):13148–13168. [Google Scholar]
- 22.Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc. 1996;118(15):11225–11236. [Google Scholar]
- 23.Kozma E, Catellani M. Perylene divides based materials for organic solar cells. Dyes Pigments. 2013;98(1):160–179. [Google Scholar]
- 24.Poelking C, Andrienko D. Effect of polymorphism, regioregularity and paracrystallinity on charge transport in poly(3-hexylthiophene) [P3HT] nanofibers. Macromolecules. 2013;46(22):8941–8956. [Google Scholar]
- 25.Coropceanu V, et al. Charge transport in organic semiconductors. Chem Rev. 2007;107(4):926–952. doi: 10.1021/cr050140x. [DOI] [PubMed] [Google Scholar]
- 26.Spano FC. The spectral signatures of Frenkel polarons in H- and J-aggregates. Acc Chem Res. 2010;43(3):429–439. doi: 10.1021/ar900233v. [DOI] [PubMed] [Google Scholar]
- 27.Poelking C, et al. Characterization of charge-carrier transport in semicrystalline polymers: Electronic couplings, site energies, and charge-carrier dynamics in poly(bithiophene-alt-thienothiophene) J Phys Chem C. 2013;117(4):1633–1640. [Google Scholar]
- 28.Tamura H, Tsukada M, Ishii H, Kobayash N, Hirose K. Roles of intramolecular and intermolecular electron-phonon coupling on the formation and transport of large polarons in organic semiconductors. Phys Rev B. 2012;86(3):2–5. [Google Scholar]
- 29.Olivier Y, et al. Theoretical characterization of the structural and hole transport dynamics in liquid-crystalline phthalocyanine stacks. J Phys Chem B. 2009;113(43):14102–14111. doi: 10.1021/jp9061169. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.