Antibiotic resistance: a physicist’s view

Abstract

The problem of antibiotic resistance poses challenges across many disciplines. One such challenge is to understand the fundamental science of how antibiotics work, and how resistance to them can emerge. This is an area where physicists can make important contributions. Here, we highlight cases where this is already happening, and suggest directions for further physics involvement in antimicrobial research.

The emergence and spread of bacterial infections that are resistant to antibiotic treatment, combined with the lack of development of new antibiotics, pose a global health problem that is now well recognised^1–5. Tackling antimicrobial resistance (AMR) requires coordinated, cross-disciplinary effort: relevant themes include clinical medicine, microbiology, diagnostics, drug discovery, epidemiology, evolutionary biology, global public health policy, veterinary science and agriculture. What role can physicists play in this spectrum of activities? Some of these themes obviously require physics tools, for example to aid the development of new experimental methods and devices. We argue here that a ‘physics-inspired’ approach to basic science also has a prominent role to play in the effort to tackle AMR.

For a new, antibiotic-resistant, infectious bacterial strain to become a clinical problem, three events must occur. First, an individual pathogenic bacterium must acquire resistance to the antibiotic in question. This could happen via a spontaneous mutation in one of its genes, which might for example render a target protein less susceptible to the antibiotic by modification of the antibiotic binding site. Alternatively, the pathogenic bacterium could gain a gene encoding antibiotic resistance via horizontal transfer of DNA from a different bacterial strain. Second, the newly resistant bacterium must proliferate such that its resistance-encoding gene spreads in the local bacterial population and cannot be wiped out through random fluctuations in the number of organisms carrying this gene. Third, the resistant strain must spread beyond the local bacterial population where it originated, until it infects a significant number of humans and becomes clinically relevant. These events occur on widely varying length and time scales, from those of molecules (e.g. a mutational event in a DNA strand) to those of macroscopic objects (bacterial biofilms, host animals, or even whole ecosystems), and they involve processes that relate directly to the realms of soft matter, chemical and statistical physics.

On the molecular level, physical scientists are already contributing to our understanding of how antibiotics bind to their cellular targets, using both computer simulations and novel imaging techniques^6–8. At the level of a bacterial cell, questions arise as to whether an antibiotic kills, or inhibits, a bacterial cell, via direct inhibition of its target (e.g. the cell wall synthesis machinery for beta-lactam antibiotics or the protein synthesis machinery for macrolide antibiotics), or via other, downstream effects^9–11. Here, physicists can contribute by developing simple models for how the complex network of reactions that constitutes bacterial physiology response to the antibiotic-induced stress^12,13. At the level of a bacterial population, physical interactions between cells and their environment shape the self-assembly of spatially-structured bacterial conglomerates such as biofilms that form on medical implants¹⁴. From a physics point of view, the interplay between biological phenomena such as growth and physical phenomena such as chemical diffusion and physical forces provides many interesting questions. For example, biofilms are often surrounded by a secreted polymer matrix whose physical properties (e.g. viscosity) may affect how the biofilm assembles and how it responds to drug treatment¹⁵. Moreoever nutrient and drug gradients can emerge in biofilms due to the interplay between growth and chemical transport; these can affect biofilm structure^16–18 and potentially also the rate of evolution of resistant bacteria^19–21. Other population-level phenomena of interest to physicists include stochastic differences in the behaviour of individual cells, caused by noise in gene expression²², which can have drastic consequences for the response of the population to antibiotic treatment²³.

“A physics-like” approach thus has a role to play in many aspects of AMR if we define such approach as a belief that biological processes can be explained by a combination of simple, yet quantitative experiments and mathematical modelling. In the remainder of this article, we highlight three areas where such physics-like approaches are already proving successful, and we also comment on promising directions for future research.

Pathways to resistance

An active area of current research focuses on how antibiotic resistance evolves “de novo”, i.e. by genetic mutation in bacterial strains that are not initially resistant (as opposed to via gene transfer from an already resistant strain). Typically, the process of resistance evolution involves not just one genetic mutation but a sequence of mutations. This mutational “pathway to resistance” is one of many possible sequences of mutations in a hugely multidimensional space made up of all the possible genetic variants (genotypes) of the organism (Fig. 1A). To understand how resistance evolves we must therefore understand the structure of this “resistance landscape”.

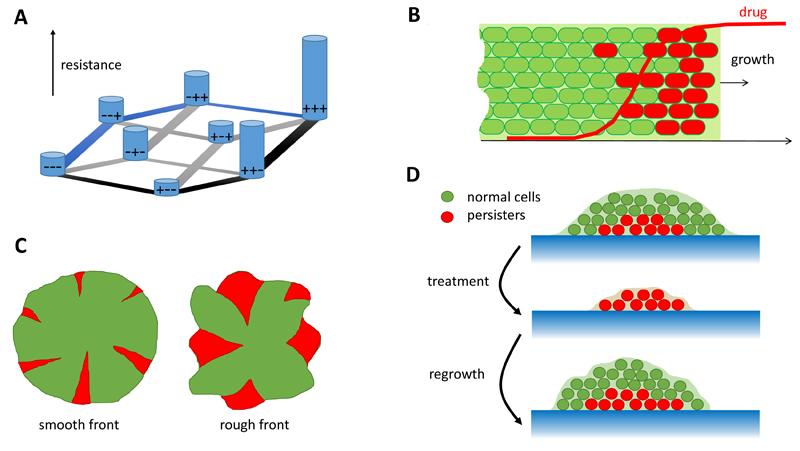
Figure 1.

(A) Example of a resistance landscape with three mutations. “+”/“−” denote the presence/absence of a particular mutation, hence the sensitive strain is represented by − − − and the most-resistant mutant strain by + + +. The level of resistance is indicated by the height of the bars, and permitted mutations are marked by gray lines. The mutant + + + can be reached by many paths, for example (− − −) → (− − +)→(− + +) → (+ + +) along which resistance increases monotonously (blue lines), or (− − −) → (+ − −) → (+ + −) → (+ + +) which has a “valley” at + − − (black lines). (B) Evolution in the presence of an antibiotic gradient for an expanding population. The fate of mutant red cells depends on whether they arise in the “bulk” or at the front of the population wave. In the first case there is no selective pressure due to low drug concentration and the mutant does not spread. However, if the mutant arises at the front, it benefits from the access to nutrients/higher growth rate, and it spreads quickly. (C) If resistant cells arise in microbial colonies, they form spatial “sectors”. The number and the size of such sectors depends on the roughness of the colony’s frontier, which in turn is affected by physical interactions between the cells and their environment. (D) A microbial population often contains “persister” cells which grow slowly but are resistant to drugs. If the population is treated with antibiotics, persisters can survive the treatment, switch back to the growing state and cause regrowth.

Two alternative models represent extreme limits of the resistance landscape. In the first model, the level of resistance changes randomly with each mutation (known as a “maximally rugged”, or “House of Cards” landscape²⁴), while in the second, mutations are additive, such that the total resistance is the sum of the contributions of the various mutations that a bacterium has acquired (this corresponds to a smooth fitness landscape). Using a statistical physics approach, an analysis of measured resistance landscapes for several different antibiotics suggests that these landscapes are neither fully random nor fully additive, but that they can be approximated by a “rough Mount Fuji” model, which essentially corresponds to a superposition of the rugged and smooth models^25,26. Further computer modelling²⁷ has shown that the pathways followed by evolution on such landscapes are most predictable in intermediate-size populations (Nμ² ≪ 1 ≪ Nμ, where N is the population size and μ is the mutation probability) whereas the evolution of resistance is predicted to be less reproducible in either very small or very large populations.

The predictability of the evolution of resistance has recently been tested experimentally by growing bacteria in antibiotic under constant selective pressure, using a “morbidostat”^28,29. This is a device in which the population density and growth rate of a bacterial population are constantly monitored, and the dosage of antibiotic to which it is subjected is adjusted to maintain (on average) a fixed growth rate. Thus, as the population evolves resistance, the antibiotic dosage increases. By sequencing the DNA of bacteria sampled from the morbidostat as the population evolves, qualitative differences in the pathways by which resistance to different drugs emerges have been revealed. In particular, the evolution of resistance to the antibiotic trimethoprim has been found to be rather reproducible, occurring by a well-defined and universal sequence of mutations, but the evolution of resistance to the antibiotics chloramphenicol and doxycycline was found to show a less predictable pattern, occurring via different sequences of mutations in replicate experiments²⁸.

Another “simple yet smart” experimental design has led to a different insight into the pathways leading to antibiotic resistance evolution. Here, bacteria are subjected to repeated brief exposures to antibiotic, alternating with periods of growth without antibiotic³⁰. Remarkably the bacteria become tolerant to the antibiotic by matching the duration of their “lag time”, or the dormancy period before they start to grow when exposed to fresh nutrient medium, to the duration of antibiotic exposure³⁰. This is an important finding because it suggests that tolerance to antibiotic exposure can be achieved much more easily than full resistance, by tinkering with the cell’s existing gene regulatory components, and that this may be a first step in the pathway to full resistance. Thus, to fully understand the pathways by which bacteria become resistant to antibiotics, we may need to study not just genetic mutations but also phenotypic changes that arise via gene regulation^31–33.

Evolution in spatially structured environments

Most studies of antibiotic resistance evolution assume that it happens in a well-mixed, spatially homogeneous environment. However, in infections, as well as more widely in the natural environment, bacterial populations are often highly spatially structured. For example, in biofilm infections bacteria deep within the biofilm are likely to experience quite different local concentrations of nutrients and, possibly, of antibiotic, compared with bacteria on the outside of the biofilm. Indeed, confocal microscopy images of lab-grown biofilms exposed to antibiotics show that some antibiotics act selectively on cells on the outside of the biofilm, while others selectively kill those on the inside³⁴. Could the spatial gradients of antibiotic that arise during treatment of infections influence the evolution of antibiotic resistance?

Experimental and theoretical physicists have recently addressed this topic by investigating the growth and evolution of bacterial populations in the presence of controlled spatial gradients of antibiotic. In particular, Zhang et al constructed a microfluidic device which allowed antibiotic gradients to be imposed across a spatially expanding bacterial population¹⁹. In this device, the evolution of E. coli bacteria which were resistant to the antibiotic ciprofloxacin occurred much more rapidly in the presence of an antibiotic gradient than in a uniform concentration of antibiotic. This work inspired the development of several theoretical models in which an expanding bacterial population invades a one-dimensional habitat containing a gradient of antibiotic^20,21 (Fig. 1B). These models suggest that the presence of an antibiotic gradient can accelerate the evolution of resistance because mutants that emerge at the tip of the expanding population wave are exposed to high antibiotic concentrations, for which they have a strong selective advantage, and because of the low population density at the tip of the population wave, they do not have to compete with less resistant genotypes. However this is not always the case; too steep a gradient can actually slow down the evolution of resistance, and the process also depends on the rate of bacterial migration²⁰ and the mutational pathway to resistance²¹.

Other important recent work shows that, even in the absence of an antibiotic gradient, evolution can work very differently in a spatially structured population compared to a spatially well-mixed one. Using colonies of bacteria and yeast cells growing on the surface of a semi-solid agar gel, Hallatschek et al, and others, showed that population fluctuations at the front of an expanding microbial colony can lead to some cell lineages randomly spreading in the population while others die out^35–38. In these experiments, spreading lineages are strikingly visualised as sectors of differently-coloured fluorescent cells (Fig. 1C). Further work investigating the probability of fixation of mutants in these expanding populations suggests that the roughness of the growing front plays a crucial role³⁹. However, much more work is needed before we can translate these principles into a full understanding of how the spatial structure of a bacterial population, for example in a biofilm infection, links to its propensity to generate and fix harmful antibiotic-resistant mutants.

Response of individual cells to antibiotics

Over the past decades, physicists have played a leading role in establishing the existence, and importance, of variation between individual cells within bacterial populations^40–42. This phenotypic heterogeneity arises from stochasticity in the molecular processes involved in gene expression, modulated by the networks of interactions between proteins and genes that regulate gene expression. From the perspective of antibiotic resistance, a particularly important example of phenotypic heterogeneity is the existence within bacterial populations of a subpopulation of “persister cells” which can survive antibiotic treatment (Fig. 1D). Classic experiments using microfluidic devices by Balaban et al visualised E. coli cells switching into and out of the non-growing persister state²³; yet the molecular mechanisms controlling this switch are still the topic of active research^43–46.

Evidence is also now emerging that bacterial population heterogeneity in the response to antibiotics may be a more general phenomenon. Several different theoretical models for the effects of antibiotics on bacterial growth predict the existence of bistable regimes, in which some cells in the population show fast growth while others grow only very slowly, if at all^12,47. The models suggest that this growth bistability can have a number of origins, including the interplay between bacterial growth and drug dilution⁴⁷ and an irreversible “annihilation” reaction between an antibiotic and its target¹². Joint experimental and theoretical work has also shown that growth bistability can arise from the partitioning of cellular resources between growth and production of proteins leading to antibiotic resistance⁴⁸. Whether, and how, these bistable growth regimes are related to the persister phenomenon, remains unclear. From the clinical point of view, we would also like to understand which drugs produce a heterogeneous response and how this impacts both on treatment strategies and on the evolution of resistance.

From an experimental point of view, investigations of bacterial phenotypic heterogeneity often rely on microfluidic technology which combines physical, chemical, and engineering knowledge to image and manipulate individual bacterial cells. Devices such as the “mother machine”⁴⁹ allow the proliferation of individual cells to be tracked under constant conditions over long times in the microscope, and these devices are beginning to reveal interesting information about the response to antibiotics⁵⁰. Another recently-developed microfluidic technique, Microscopy Assisted Cell Screening, provides a way to rapidly image thousands of cells immediately after sampling them from a growth device⁵¹. This approach can be used, for example, to measure population heterogeneity in processes like DNA damage, which involve small numbers of molecules per cell.

Perspective

The topics discussed above highlight important contributions that are being made by physicists to our understanding of antibiotic action and to AMR. We believe that this is just the beginning. Many questions remain to be addressed about how bacteria respond (and become resistant) to antibiotics, and physicists have an important role to play in this effort. As a first example, it is imperative to gain better understanding of how bacterial cells interact mechanically with one another and with their environment. Mechanical interactions appear to be very important in bacterial self-assembly^52–55, yet our limited knowledge of these interactions prevents us from building accurate models of how spatially structured infections like bacterial biofilms form. As a second example, horizontal gene transfer – the transmission of genes encoding antibiotic resistance between (potentially) unrelated bacteria by direct transfer of DNA – is very important in clinically relevant antibiotic-resistant infections, and has also been studied in a “physics” context in abstract, mathematical models^56–61, although so far without consideration of the mechanics of bacterial interactions. It would be very interesting to investigate how physical factors such as the forces existing between adjacent bacterial cells in a colony or biofilm affect the rate of gene transfer⁶².

We also believe that AMR can provide a rich source of more abstract problems in areas of physics from non-equilibrium statistical mechanics to soft matter physics and fluid mechanics. For example, the growth of bacterial biofilms shows a non-equilibrium phase transition (or fingering instability) between rough and smooth modes of interface growth¹⁶. Other examples include random walk models inspired by the dynamics of mutant sectors in expanding bacterial populations^35,36, and stochastic differential equation models to describe the emergence of waves of resistant mutants in an antibiotic gradient²¹. Physics models that are inspired by AMR may also be transferable to other biological fields - for example the evolution of bacterial antibiotic resistance has important analogies with the evolution of drug resistance in cancer tumours⁶³, while models for the dynamics of bacterial and viral infections also have many similarities.

Finally, we believe that an important goal of future research in AMR, by physicists and others, must be to make a link between the findings of simple laboratory experiments and theoretical models, and what happens in real infections, in clinical settings⁶⁴. Existing areas of progress in this direction include using observations on how antibiotics interact with the physiology of bacterial cells to suggest more effective clinical treatment strategies^12,65,66, using systematic measurements of thousands of bacterial growth curves, combined with simple theoretical models, to predict the clinical effectiveness of multi-drug therapies^67,68, and tracking mutational pathways in in vivo infections⁶⁹. Future challenges will include understanding the role of spatially structured infections in the evolution of clinical antibiotic resistance and the impact of bacterial population heterogeneity on clinical responses to treatment.

Conclusion

Achieving a better understanding of how antibiotic resistance emerges and spreads could help us to design strategies to prevent this from happening, for both current and future antibiotics. This is a goal to which physicists can contribute, not just by developing new machines and software tools, but also by designing simple yet insightful experimental and theoretical models to test basic principles. This work should not be carried out in isolation, but in coordination with the broad spectrum of other efforts that are being made to tackle the problem of antibiotic resistance. To make this possible, however, support is needed in the form of funding. This requires a breakdown of traditional discipline barriers. Indeed, for the breakthroughs highlighted in this article it is not relevant to ask “is it physics”? or “is it biology”, but simply “is it ground-breaking science”? It also requires a breakdown of national barriers, to allow the most talented scientists, within what is still a rather small international field, to work productively together without restrictions imposed by funding regulations.