Computational investigation of cold denaturation in the Trp-cage miniprotein

Significance

The ubiquity of cold denaturation in globular proteins has broad implications for developing preservation strategies for biological materials and understanding the evolution of freeze-tolerant organisms. Because cold denaturation conditions typically lie below water’s freezing point, direct experimental investigation of this phenomenon is often frustrated by ice formation in the surrounding solvent. Coarse-grained lattice and off-lattice models have provided significant insight into protein cold denaturation, but they lack the structural resolution to fully elucidate the molecular mechanism involved in this process. We perform extensive replica exchange molecular dynamics simulations (324 μs total) to conduct a fully atomistic computational study of cold unfolding of an α-helical protein.

Abstract

The functional native states of globular proteins become unstable at low temperatures, resulting in cold unfolding and impairment of normal biological function. Fundamental understanding of this phenomenon is essential to rationalizing the evolution of freeze-tolerant organisms and developing improved strategies for long-term preservation of biological materials. We present fully atomistic simulations of cold denaturation of an α-helical protein, the widely studied Trp-cage miniprotein. In contrast to the significant destabilization of the folded structure at high temperatures, Trp-cage cold denatures at 210 K into a compact, partially folded state; major elements of the secondary structure, including the α-helix, are conserved, but the salt bridge between aspartic acid and arginine is lost. The stability of Trp-cage’s α-helix at low temperatures suggests a possible evolutionary explanation for the prevalence of such structures in antifreeze peptides produced by cold-weather species, such as Arctic char. Although the 3₁₀-helix is observed at cold conditions, its position is shifted toward Trp-cage’s C-terminus. This shift is accompanied by intrusion of water into Trp-cage’s interior and the hydration of buried hydrophobic residues. However, our calculations also show that the dominant contribution to the favorable energetics of low-temperature unfolding of Trp-cage comes from the hydration of hydrophilic residues.

The functional native states of globular proteins that are stable near physiological conditions become labile when changes in temperature, pressure, and solvent composition alter their environment. The partial or complete unfolding of secondary and tertiary structure associated with this loss of stability can strongly affect protein behavior, leading to significantly impaired biological function (1, 2). Denaturation upon heating is a ubiquitous and well-studied phenomenon in which proteins gain configurational entropy and unfold as a result of increased kinetic energy. By contrast, the mechanisms responsible for pressure-induced unfolding, and for denaturation of globular proteins at low temperatures, remain incompletely understood (3–5).

Fundamental understanding of cold denaturation is important due to its ecological implications and relevance to industrial processing of proteins and biological materials. Freeze-tolerant organisms such as the Arctic char, for example, thrive in subfreezing habitats where cold denaturation can occur (6). Biopharmaceuticals are also exposed to cold conditions that can result in denaturation when they are lyophilized into freeze-dried solids to prolong their shelf life (7, 8). Natural cryoprotectants such as sugars and polyols stabilize proteins against denaturation in cold-weather species (6), and similar compounds have been used to mitigate the damaging effects of freeze-drying in pharmaceutical formulations (7, 9).

Cold denaturation was first reported by Hopkins in 1930 (10). Brandts (11) subsequently observed that the Gibbs free-energy change upon denaturation of the globular protein chymotrypsinogen exhibits a parabolic shape as a function of temperature, suggesting that unfolding can occur at both hot and cold conditions. Although similar parabolic free-energy curves have been reported for other globular proteins (3), direct observation of cold denaturation in experiment is often frustrated by freezing of the solvent because the low-temperature unfolding conditions usually lie below water’s freezing point (4, 5). Experimental investigations have therefore involved proteins that cold-denature above the freezing point of water (5, 12, 13), or systems whose thermophysical properties are altered by chemical denaturants (14, 15), freezing-point depressants (16), or pressurization (4). Alternatively, cold denaturation has been studied in deeply supercooled samples, stabilized by confining the protein in emulsified water droplets (17, 18) or by encapsulation in reverse micelles (19).

Numerous theoretical and computational investigations using coarse-grained models have been performed to understand cold denaturation (20–30). Such studies suggest that globular proteins denature at low temperatures due to destabilization of the folded structure as a result of hydration of hydrophobic residues in their core (21, 22, 24–26). However, such coarse-grained models have a limited ability to describe protein–water interactions realistically, highlighting the need for atomic-level understanding of this phenomenon. Furthermore, some recent studies have challenged this view, arguing that increased hydration of hydrophilic groups may also play a significant role in cold denaturation (27).

Here, we report results from a fully atomistic computational study of cold denaturation of a protein with an α-helix. Using replica exchange molecular dynamics (REMD), we examine the stability of the 20-residue Trp-cage miniprotein (31) at temperatures down to 210 K. Despite Trp-cage’s small size, it has a cooperatively folded tertiary structure with features similar to those found in larger globular proteins, including a hydrophobic core with a “caged” tryptophan amino acid residue, multiple secondary domains (an N-terminal α-helix, a 3₁₀-helix, and a C-terminal polyproline II segment), and a salt bridge between oppositely charged residues D9 and R16; its fast folding kinetics (∼4 μs) (32) make it an ideal model protein system for use in fundamental computational studies (32–38). Our simulations show that Trp-cage cold unfolds into a compact structure, increasing the exposure of both hydrophilic and hydrophobic residues to the surrounding solvent. We observe that intrusion of water into Trp-cage’s hydrophobic core is facilitated by disruption of the salt bridge and a shift in the position of the 3₁₀-helix. Despite shifting position, however, the α- and 3₁₀-helices remain stable under cold conditions, suggesting a possible explanation for the prevalence of helical structures in antifreeze peptides (39, 40).

Cold Denaturation Thermodynamics

In contrast with experiment, ice formation does not impede computational investigations of cold denaturation because crystallization is a rare event on the time scales accessible with simulation (41). Accordingly, simulations allow atomic-level investigation of systems in which folding and unfolding events are appreciably faster than ice nucleation. Cold denaturation is still challenging to simulate, however, because the solvent viscosity increases rapidly as the temperature drops below water’s freezing point (42), resulting in sluggish dynamics that frustrate sampling. As a result, previous studies have only examined the stability of Trp-cage at temperatures above 280 K. Yang et al. (43) recently demonstrated that such sampling challenges can be overcome by using REMD to investigate the folding behavior of a beta-hairpin structured miniprotein (MrH1) down to 240 K. We apply this same approach to study the stability of Trp-cage over the range 210–496.5 K, at ambient pressure.

Trajectories from the 4.5-µs REMD simulations of Trp-cage were analyzed using the two-state model of Anson (44) to compute changes in thermodynamic properties upon unfolding at each temperature (Fig. 1). The Gibbs free-energy change (ΔG) of unfolding was calculated using

$$\mathrm{\Delta }G=G_U-G_F=-RT\hspace{0.17em}\text{ln}\left(\frac{1-x}{x}\right),$$ [1]

where x is the fraction of folded proteins (37) or, equivalently, the probability of observing the single Trp-cage unit in a folded state. Determination of x requires defining a metric to distinguish between folded and unfolded structures. We used the rmsd of the α-carbons on Trp-cage (Cα rmsd) from a fully folded reference structure obtained from NMR data (31). Based on our analysis of this quantity at ambient conditions (Fig. S1), we define the folded state as the ensemble of configurations with a Cα rmsd value less than 0.3 nm. The enthalpy change (ΔH) was computed by directly averaging the instantaneous values of H over configurations belonging to the folded and unfolded states, respectively. The entropy of unfolding (ΔS) was calculated from ΔG and ΔH using the thermodynamic relationship ΔS = (ΔH − ΔG)/T.

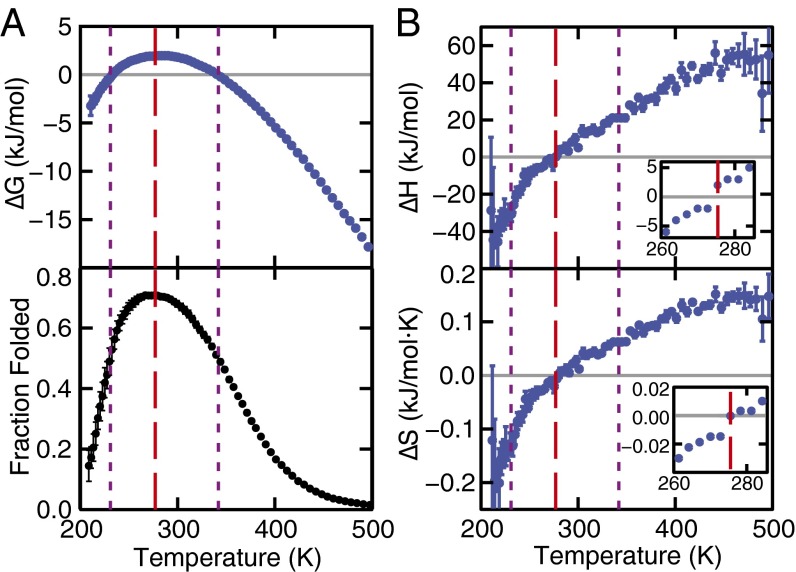
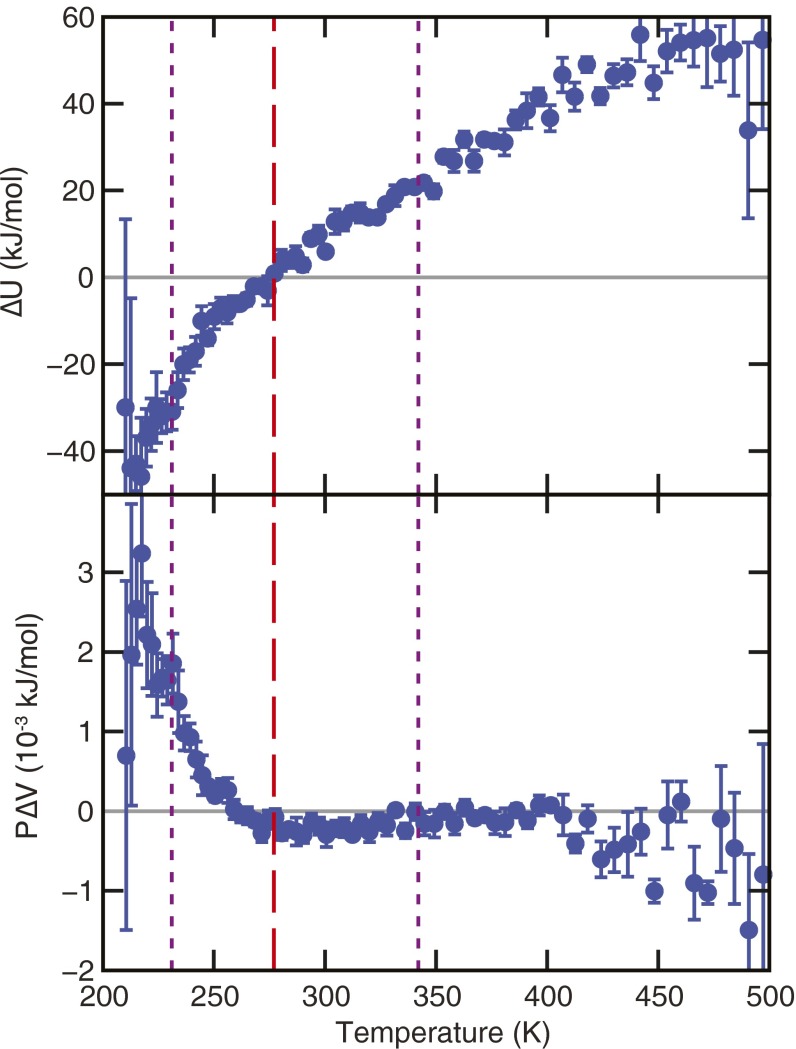
Fig. 1.

(A) The unfolding free-energy change (Upper) and the fraction of folded proteins (Lower) as a function of temperature. (B) The corresponding enthalpy and entropy changes. The temperature at which the fold fraction is a maximum is 277 K (red dashed line), and the melting and cold unfolding temperatures (x = 0.5, purple dotted lines) are located at 231 K and 342 K, respectively. Error bars are explicitly shown or are smaller than the symbols. See Materials and Methods for error calculation.

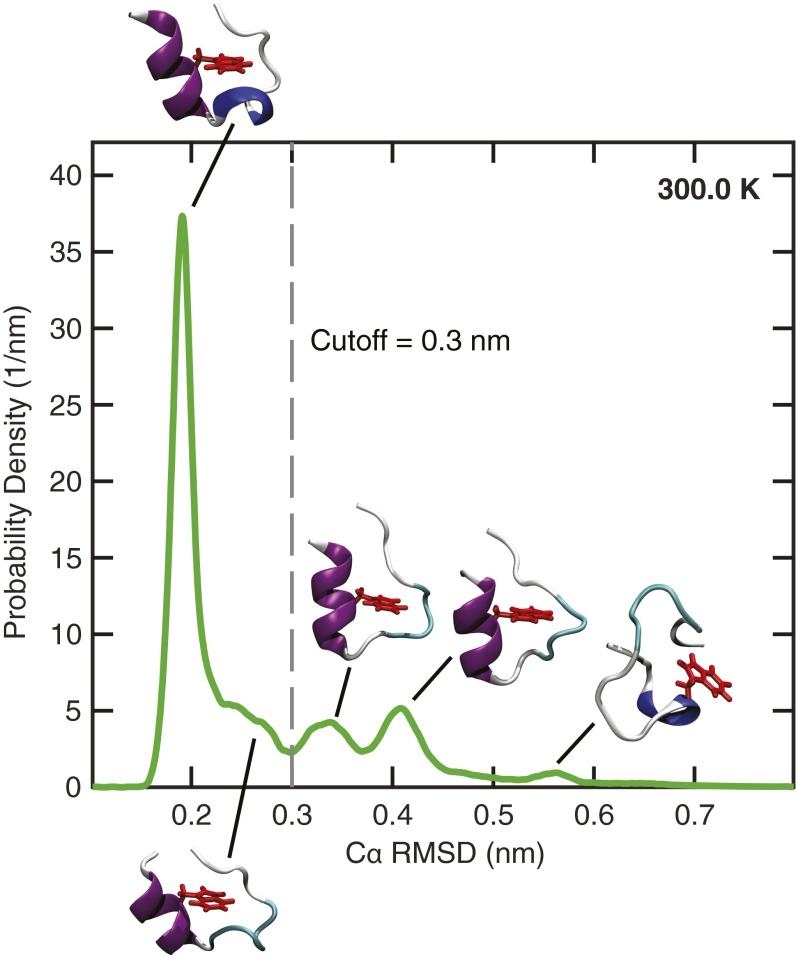
Fig. S1.

Probability distribution of the Cα rmsd at 300 K. A cut-off of 0.3 nm was chosen to distinguish between the folded and unfolded configurations. The protein structures show representative configurations at the peaks of the probability distribution. Trp-cage’s α-helix, 3₁₀-helix, and aromatic side chain on residue W6 are rendered in purple, blue, and red, respectively.

The parabolic shape of ΔG as a function of temperature (Fig. 1A) is characteristic of globular proteins that thermally unfold and cold denature (3, 11). The largest value of ΔG (2.1 kJ/mol) is observed at 277 K, where the folded fraction reaches its maximum. This estimate is in agreement with experimental studies of Trp-cage that report values of ΔG $\approx$ 3 kJ/mol near ambient conditions (45). Experimental studies of globular proteins also report ΔG values ranging from 1 kJ/mol for small peptides similar in size to Trp-cage to 20 kJ/mol for proteins with ∼100 residues (12, 46). In contrast, ΔG at ambient conditions ranges from 20 to 60 kJ/mol for larger proteins (46). The comparatively small value of ΔG for Trp-cage is a result of its small size and the absence of strong cooperative effects between amino acids that stabilize larger proteins. The fact that ΔG at the temperature of maximum stability is very similar to $RT$ (2.4 kJ/mol) indicates that in Trp-cage one observes a dynamic equilibrium of folded and unfolded states.

The stability of Trp-cage’s folded state decreases dramatically at temperatures above and below 277 K. Unfolding becomes favorable as the folded fraction drops below 0.5 and ΔG becomes negative. This threshold is crossed at 342 and 231 K, which are the nominal melting and cold unfolding temperatures, respectively. Our simulations predict a higher melting temperature (342 K) than the experimental value (315 K) (31), but they capture well the qualitative temperature dependence of Trp-cage’s stability. The computed change in heat capacity upon unfolding, ΔC_p, is 0.28 kJ/(mol K) at 298 K, in good agreement with the experimental value of 0.3 kJ/(mol K) (45). It was computed using the thermodynamic equation

$$\mathrm{\Delta }{C}_P=T{\left(\frac{\partial \mathrm{\Delta }S}{\partial T}\right)}_P.$$ [2]

The thermodynamic relationships

$$\mathrm{\Delta }S=-{\left(\frac{\partial \mathrm{\Delta }G}{\partial T}\right)}_P\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\mathrm{\Delta }H={\left(\frac{\partial \mathrm{\Delta }G/T}{\partial 1/T}\right)}_P$$ [3]

imply (Fig. 1B) that hot denaturation is endothermic with positive entropy change (ΔH, ΔS > 0), and cold unfolding is exothermic with negative entropy change (ΔH, ΔS < 0) (47).

Stability and Structure of Cold-Unfolded States

Coarse-grained computational models have captured the principal thermodynamic signatures of hot and cold denaturation (28). Fully atomistic simulations can offer additional insight, however, by providing a detailed microscopic description. To this end, we have characterized the effects of hot and cold denaturation on Trp-cage’s structure. Changes in Trp-cage’s overall structure were monitored by computing Cα rmsd; the evolution of its α-helix domain encompassing residues 2–8 was characterized independently by computing the rmsd of the backbone atoms in these residues with respect to those in an ideal helical reference structure (α-helix rmsd). The free-energy surface associated with these two order parameters (Fig. 2A) was computed at 210, 300, and 496.5 K using

$$\frac{G}{RT}=-\text{ln}\left(p\right)+C,$$ [4]

where R is the gas constant, p is a histogram approximation to the configuration density, and C is a normalization constant.

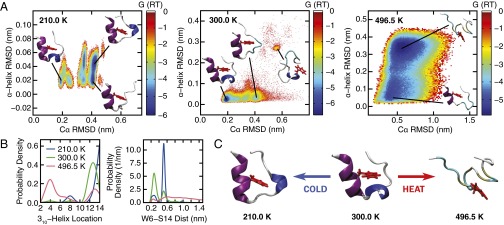
Fig. 2.

(A) The free-energy surface (reported in units of RT) associated with the order parameters Cα rmsd and α-helix rmsd at 210, 300, and 496.5 K. The protein structures show representative configurations for selected basins identified on the free-energy surface. (B) Probability distribution of the location of Trp-cage’s three-residue-long 3₁₀-helix structure (Left). The number reported on the abscissa denotes the residue on which the 3₁₀-helix is centered. The discrete distributions are represented using a continuous spline function for visual clarity. The most probable location of Trp-cage’s 3₁₀-helix shifts from residue 12–14 as the Trp-cage cold denatures. (Right) Distance between residues W6 and S14. As the Trp-cage cold denatures at 210 K, the separation between W6 and S14 widens. (C) Representative protein configurations from the most populated states at 210, 300, and 496.5 K. Trp-cage’s α-helix, 3₁₀-helix, and aromatic side chain on residue W6 are rendered in purple, blue, and red, respectively.

The free-energy surface at 496.5 K shows that Trp-cage’s heat-denatured state becomes stable with respect to the folded structure (Fig. 2A). This state is distinguished from the folded protein by the absence of well-defined secondary and tertiary structure, except for the α-helix, which remains partially folded in a large subset of the accessible configurations. The increase in Trp-cage’s radius of gyration and solvent-accessible surface area (Fig. S2) suggests that its structure unravels significantly at high temperatures. By contrast, cold unfolding at 210 K results in a denatured structure that is relatively compact (Fig. 2A). The cold-denatured state also conserves Trp-cage’s α-helix, which becomes more stable at cold temperatures, as evidenced by the disappearance of the structure where the α-helix is not present (α-helix rmsd >0.25 nm at 300 K). The free-energy surfaces also show that cold denatured-like states are already present at 300 K (Cα rmsd $\approx$ 0.3–0.45 nm). These states become increasingly populated as the temperature is lowered until they dominate the free-energy landscape (Fig. 2A and Fig. S2).

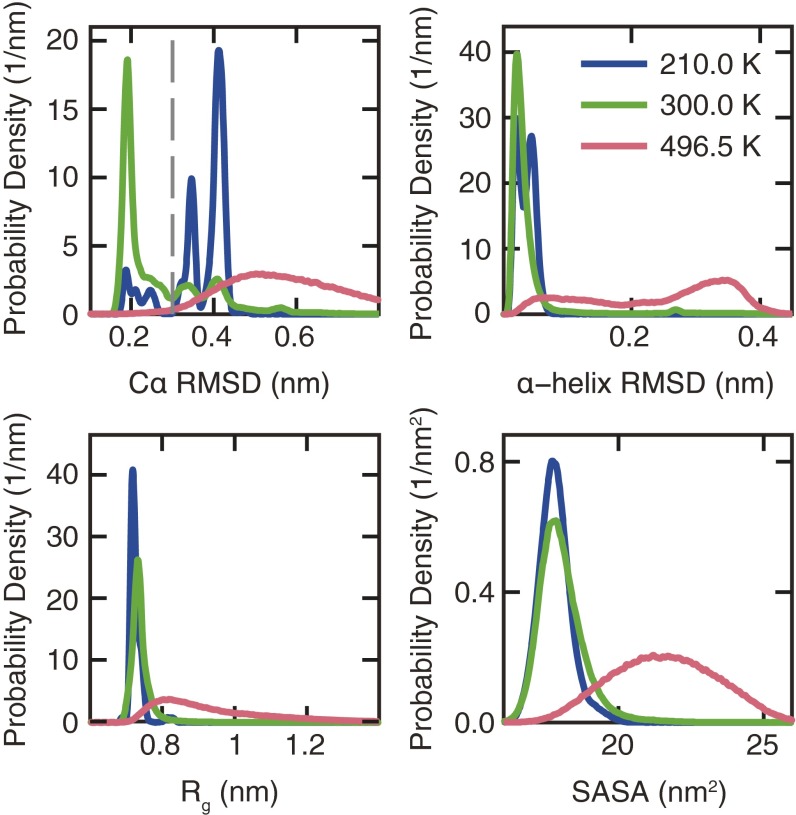
Fig. S2.

Probability distribution of Cα rmsd, α-helix rmsd, R_g, and SASA. The gray dashed line shows the cut-off value of the Cα rmsd (0.3 nm) that was used to define the folded state.

Secondary structure analysis using the STRIDE algorithm (48) reveals that the center of the three-residue-long 3₁₀-helix on Trp-cage positioned at P12 in the folded structure (Fig. 2B) shifts to S14 at cold conditions. This shift is accompanied by an increase in the distance between residues W6 and S14 (Fig. 2B), which reside in Trp-cage’s hydrophobic core and on its C-terminus, respectively. W6 and S14 are in close proximity in the folded structure, because of its U-shape. The increased separation at low temperatures therefore suggests a widening of Trp-cage’s U-shape and possible exposure of its hydrophobic core to the surrounding solvent. Such structural changes are indeed observed upon visual examination of representative configurations from the most populated state at each temperature (Fig. 2C). Configurations illustrate that hot denaturation causes significant destabilization of Trp-cage’s secondary and tertiary structures, whereas cold denaturation results in a compact, partially unfolded structure with a 3₁₀-helix that is slightly shifted from its position at ambient conditions. Recent REMD simulations of the β-hairpin miniprotein MrH1 also report a cold denatured state with compact backbone structure (43). Hence, cold denaturation in Trp-cage can be viewed as partial unfolding, rather than a nearly complete structural unraveling, as observed at high temperatures.

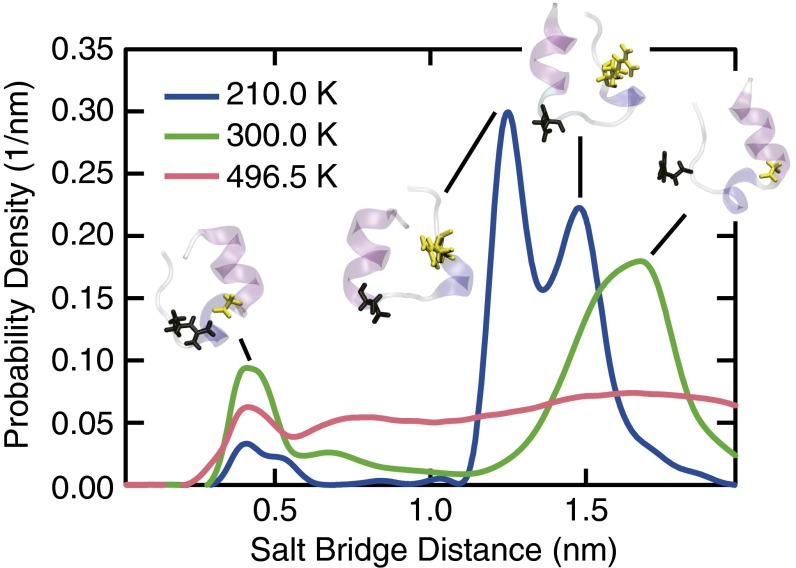
Strong electrostatic interactions between oppositely charged residues D9 and R16 on Trp-cage stabilize the folded structure. Computational studies have shown that the formation a salt bridge between these residues can expedite the folding kinetics of Trp-cage (32, 49). To the best of our knowledge, however, the effects of cold conditions on salt bridge stability have not been studied. We investigated the behavior of the Trp-cage’s salt bridge by monitoring the distance between oxygen and nitrogen atoms on the side chains of residues D9 and R16, respectively. The D9–R16 distance distribution shows that the salt bridge forms when the two residues are separated by less than ∼0.5 nm (Fig. 3). Although the salt bridge is metastable at all conditions examined, it loses stability upon heating or cooling the system. This effect is particularly pronounced upon cooling, as evidenced by the fact that states in which the salt bridge is intact become significantly less populated at low temperatures. The reduced stability of the salt bridge shows that the relative importance of attractive electrostatic interactions decreases at low temperature.

Fig. 3.

Probability distribution of the distance between salt bridge-forming residues D9 and R16. The protein structures show representative configurations from the two most populated states, highlighting the position of the two salt bridge-forming residues (D9, black; R16, yellow).

Hydration of Trp-Cage

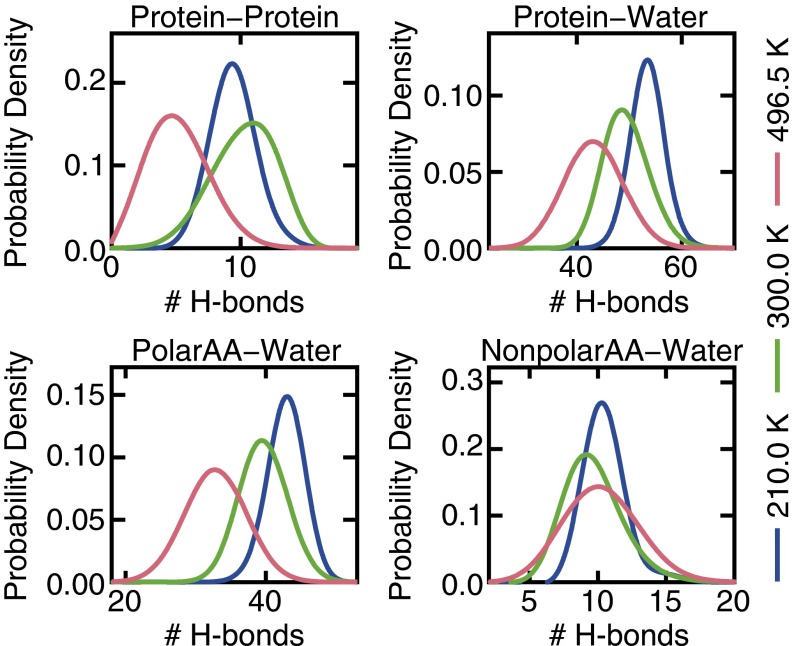
Unlike thermal denaturation, cold unfolding is an exothermic process that occurs despite an unfavorable change in entropy. Because of Trp-cage’s small size, the contribution to ΔH arising from the volume change of unfolding is negligible at ambient pressure (Fig. S3); it therefore changes in the configurational energy (ΔU) because of structural rearrangements in the protein and surrounding solvent that drive cold denaturation. Although unfolding results in less favorable intramolecular protein–protein interactions, this effect is offset at low temperatures by an appreciable increase in the strength of protein–water interactions. Intramolecular H-bonds formed within Trp-cage’s folded structure at 300 K are disrupted at both high and low temperatures (Fig. 4). The extent of disruption, however, is much more significant at high temperature, consistent with the fact that elements of Trp-cage’s secondary and tertiary structure are conserved in the cold-unfolded state. By contrast, protein–water H-bonds are affected differently by hot and cold conditions (Fig. 4): their number decreases at high temperature and increases upon cooling. The formation of 4.6 additional H-bonds on average during cold denaturation (i.e., at 210 K with respect to 300 K) (Fig. 4) aids in stabilizing the unfolded state. By computing the interaction energy between the protein and H-bonded water molecules, we estimate that the strength of a typical protein–water H-bond is approximately −7 kJ/mol for the models considered here, which is within the typical range found in biological systems (2–24 kJ/mol) (50, 51). The formation of H-bonds upon lowering the temperature from 300 to 210 K therefore decreases the configurational energy by ∼32 kJ/mol. This value is comparable to the −34 kJ/mol change in the enthalpy of unfolding observed between 300 and 210 K, suggesting that H-bond formation is largely responsible for the exothermic nature of the cold unfolding processes. Furthermore, we find that on average only 1.3 of the 4.6 H-bonds formed during cold unfolding are between water and hydrophobic nonpolar residues on Trp-cage; the remaining H-bonds are associated with increased hydration of hydrophilic polar residues. In agreement with recent arguments by Ben-Naim (27), our results therefore indicate that hydration of hydrophilic residues is the dominant contribution to the favorable enthalpy of unfolding.

Fig. S3.

Changes in the internal energy (Upper) and pressure volume (Lower) as the Trp-cage unfolds. The temperature of the maximum fraction folded is at 277 K (red dashed line), and the hot and cold melting temperatures (purple, dotted lines) are located at 231 K and 342 K, respectively.

Fig. 4.

(Upper) Probability distribution of the number of protein–protein and protein–water H-bonds. (Lower) Probability distribution of the number of H-bonds formed between water and polar amino acids (PolarAA), and between water and nonpolar amino acids (NonpolarAA) in Trp-cage.

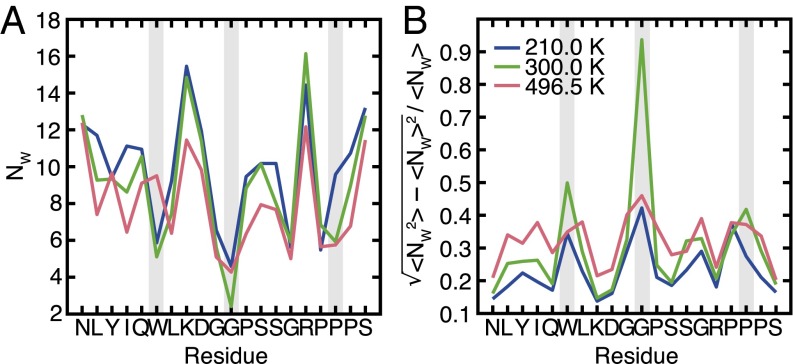
Theoretical studies of coarse-grained models have suggested that the protein structure is destabilized during cold denaturation by the exposure of the buried hydrophobic groups to water (21, 22, 24–26, 43). Although our findings suggest that hydrophobic hydration is not the dominant driving force for cold unfolding, we investigated this process further by computing the number of water molecules surrounding each residue (Fig. 5A) to examine changes in the local hydration state of Trp-cage. A water molecule was considered to be near a residue if the water’s oxygen was found to be within 0.4 nm of any atoms on the residue. Even in the folded configurations, the residues in the hydrophobic core, such as W6 and G11, are hydrated by a few water molecules, in agreement with previous calculations (35). The number of surrounding water molecules is found to increase near most residues as temperature decreases, and there is no clear trend suggesting a selective increase in hydration of polar vs. nonpolar residues. A more appropriate hydrophobicity metric, especially in a heterogeneous system such as a protein, is the magnitude of local solvent density fluctuations (52–55). This local compressibility quantifies the softness of the protein–water interface. Analysis of normalized water density fluctuations for Trp-cage shows a reduction in effective hydrophobicity upon cooling from 300 to 210 K (Fig. 5B). The most pronounced decrease is observed at W6, G11, and P18—nonpolar residues that are part of Trp-cage’s hydrophobic core. This behavior is consistent with the viewpoint that cold unfolding is accompanied by the hydration of buried nonpolar residues, leading to a reduction in their effective hydrophobicity at low temperatures (21, 22, 24–26, 43). Thus, hydrophobic hydration, though not the dominant effect energetically (at least not in Trp-cage), is responsible for the increase in the overall “hardness” of the protein–water interface upon cooling. We also see that “local” residue-level hydrophobicity depends not only on the nature of the residue but also, importantly, on its environment.

Fig. 5.

(A) Average number of water molecules within 0.4 nm of each residue. (B) Normalized fluctuation in the number of water molecules near each residue, a measure of residue effective hydrophobicity. The gray bars highlight the location of residues W6, G11, and P18, which exhibit a significant reduction in their effective hydrophobicity upon cooling to 210 K.

Conclusions

We have presented a fully atomistic simulation of cold unfolding of an α-helical protein. The free energy of unfolding has a parabolic temperature dependence, similar to that reported for larger globular proteins that undergo both heat and cold denaturation. In contrast to endothermic denaturation at high temperature, cold unfolding is enthalpically driven. The cold-denatured states are populated by compact, partially folded structures in which the salt bridge is destabilized and Trp-cage’s 3₁₀-helix is shifted slightly from its position at 300 K. Furthermore, the stability of Trp-cage’s α-helix increases at low temperatures, suggesting a possible evolutionary explanation for the prevalence of these structures in antifreeze peptides produced by freeze-tolerant organisms such as Arctic char. This finding may also have implications for understanding changes in protein stability during freeze-drying. The negative enthalpy change associated with cold unfolding of Trp-cage results from increased protein hydration, with the most significant contributions coming from additional H-bonds formed between water and polar residues. Although hydrophobic hydration is not the dominant driving force for cold unfolding of Trp-cage, analysis of water density fluctuations shows that the effective hydrophobicity of nonpolar residues is reduced at low temperatures. Our findings are therefore consistent with the prevailing hypothesis that cold unfolding involves hydrophobic hydration of buried core residues, but they suggest that hydration of polar residues must be considered in thermodynamic analysis of this process. The importance of polar groups in considering the hydrophobic effect was also noted in the case of chemical denaturation (56). Finally, we have demonstrated that REMD can be used to overcome sampling challenges associated with studying protein stability at temperatures as low as 210 K. We anticipate that improved sampling algorithms and increases in computational power will facilitate the study of cold denaturation of larger globular proteins and enable the calculation of full $P,T$ stability diagrams, which cannot be easily obtained by experiment.

Materials and Methods

The NMR structure of Trp-cage was taken from the Research Collaboratory for Structural Bioinformatics (RCSB) Protein Data Bank (PDB ID code 1L2Y) (31) and hydrated with 2,910 water molecules in a cubic box of 89.08 nm³ in volume. Electroneutrality of the system was achieved by adding a chloride ion (−1 e) to the system to counter the +1 e charge on Trp-cage at neutral pH. REMD simulations (57) were then performed using GROMACS (58, 59) to sample Trp-cage’s folded and unfolded states at 72 temperatures ranging from 210 to 496.5 K at 1 bar. Exchanges between neighboring replicas were attempted every 2 ps, and the distribution of replica temperatures was chosen to achieve a 15–25% acceptance rate for exchanges between adjacent states. This scheme resulted in an average round-trip time of ∼400 ns. Convergence of the REMD simulations was checked by performing independent sets of calculations that were initialized from a folded and a thermally unfolded Trp-cage structure, respectively. Analysis of the trajectories showed that the two REMD simulations converged after ∼500 ns (Fig. S4). Simulations initiated from the unfolded structure were for run 4.5 μs per replica (324 μs of simulation time total), and the last 3 μs of each trajectory was used for analysis.

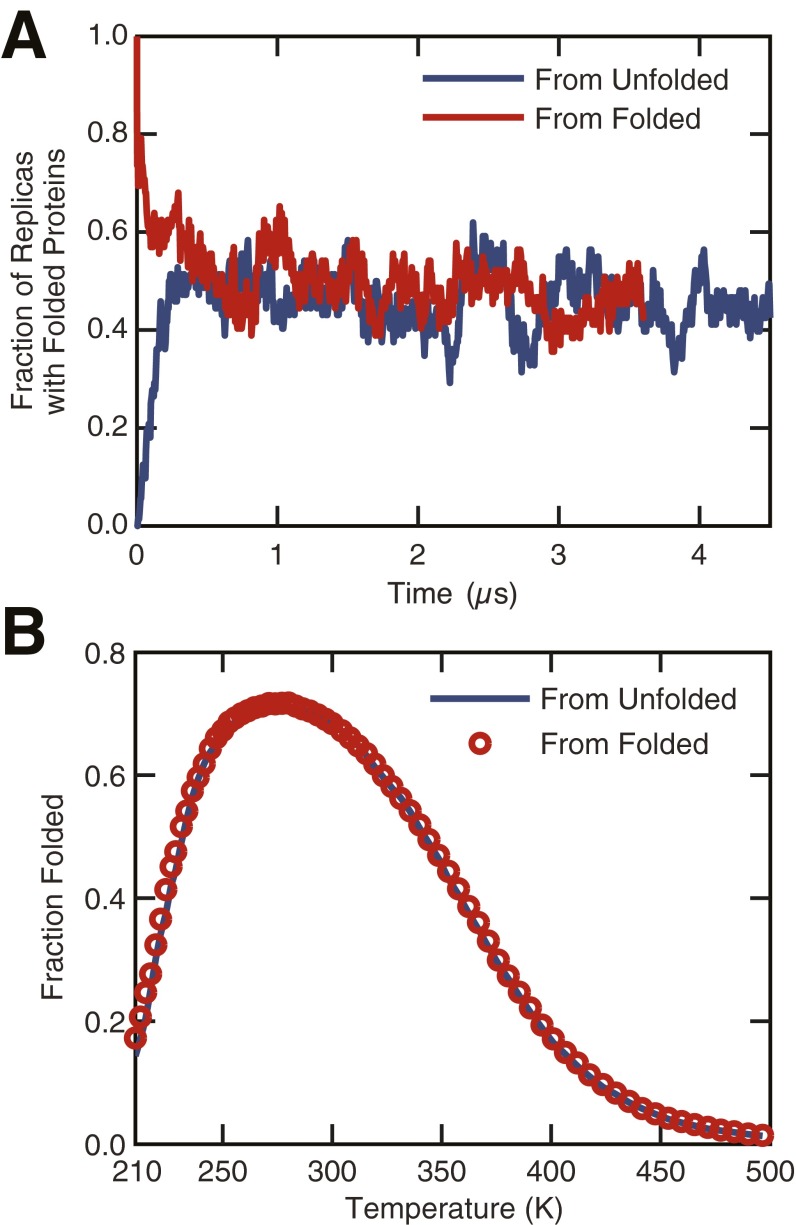
Fig. S4.

Fraction of folded proteins computed from two independent sets of REMD simulations. The first set of REMD simulations was initialized from a thermally unfolded Trp-cage structure, whereas a configuration from the folded state was used to initiate the second set. (A) The fraction of replicas with folded proteins computed as a function of time shows convergence of the two REMD simulations after ∼0.5 µs. (B) The fraction folded distributions computed from the REMD simulations after discarding the first 1.5 µs of each trajectory are indistinguishable, thus confirming that equilibrium has been reached.

The REMD simulations were carried out in the isothermal–isobaric ensemble using the leap-frog algorithm with a 2-fs time step to integrate the equations of motion. The temperature and pressure of the system were maintained using a Nosé–Hoover thermostat (60, 61) (0.2-ps time constant) and a Parrinello–Rahman barostat (62, 63) (2-ps time constant), respectively. A cut-off of 1 nm was used to truncate short-range interactions, and standard long-range dispersion corrections were applied to the energy and pressure. Long-range contributions to the electrostatic interactions were treated using the smooth-particle mesh Ewald method (64). Protein and water molecules were modeled using Amber03w (65, 66) and the TIP4P/2005 (67) force field, respectively. This force field combination was selected because it yields excellent agreement with experiment in terms of predicting Trp-cage’s folding kinetics and intermediate states (32). During the REMD simulations, the rigid structure of the TIP4P/2005 water molecules was maintained using SETTLE (68). To facilitate the use of a 2-fs time step, holonomic bond length constraints were also applied to Trp-cage using the linear constraint solver algorithm (LINCS) (69, 70).

Analysis of the REMD simulations was carried out using the utilities distributed with GROMACS (58, 59). Hydrogen bonds were identified using standard geometric criteria, in which a bond is considered to have formed if the donor–acceptor distance is less than 0.35 nm and the acceptor–donor-hydrogen angle is less than 30° (71). We considered OH and NH groups as donors, and nitrogen and oxygen atoms as acceptors. Images of Trp-cage’s structure were rendered using the Visual Molecular Dynamics package (72). The standard errors were estimated using block-averaging analysis (73), where the trajectory was divided into five blocks.

SI Materials and Methods

Thermodynamic and Structural Analysis.

Thermodynamic analysis of the REMD simulations using a two-state population model required defining an appropriate order parameter to distinguish between Trp-cage’s folded and unfolded states. We used the rmsd of the α-carbons on Trp-cage (Cα rmsd) from a fully folded reference structure. The Cα rmsd distribution at 300 K (Fig. S1) exhibits a gap at ∼0.3 nm that separates the peaks associated with Trp-cage’s stable and metastable states, respectively. Consequently, structures with Cα rmsd values less than 0.3 nm were considered to belong to the ensemble of folded configurations for the purpose of our analysis.

Structural characterization of Trp-cage at 210, 300, and 496.5 K was performed to investigate the effects of hot and cold denaturation on protein structure (Fig. S2). The large values of the order parameters Cα rmsd and α-helix rmsd observed at 496.5 K signify that Trp-cage is thermally denatured. The thermally denatured state also has a large radius of gyration (R_g) and solvent accessible surface area (SASA), indicating that Trp-cage is an extended conformation that does not conserve its folded secondary and tertiary structure. In the case of cold denaturation, however, the SASA, R_g, and α-helix rmsd distributions remain similar to those observed at 300 K, suggesting the unfolded state is characterized by compact conformations that conserve the α-helix.

Trp-cage’s parabolic free-energy curve suggests that cold denaturation is an enthalpically driven process. The dominant contribution to the enthalpy of unfolding (ΔH = ΔU + PΔV) is the internal energy change (ΔU) resulting from rearrangements in the protein’s structure and surrounding solvent (Fig. S3). By contrast, the pressure-volume term (PΔV) is negligible because of the small volume change of unfolding.

Convergence of REMD Simulations.

Convergence of the REMD calculations was checked by performing two independent sets of simulations. The first set of simulations was initialized from an unfolded Trp-cage configuration, whereas the second set was initiated using a folded protein structure. The unfolded structure was prepared by thermally unfolding the folded Trp-cage for 50 ns at 500 K using NVT molecular dynamics. The REMD simulations initialized with the folded and unfolded configurations were run for 3.8 and 4.5 µs, respectively. The fraction of replicas with folded proteins estimated from the two REMD simulations was observed to converge after ∼0.5 µs (Fig. S4A). We also computed the distribution of fraction of folded proteins (Fig. S4B) as a function of temperature, after discarding the data from the first 1.5 µs from each REMD trajectory to account for the transient equilibration period. The two distributions are indistinguishable, suggesting that the REMD simulations were fully equilibrated after 1.5 µs. Consequently, only the last 3.0 µs of the REMD trajectories initiated from the unfolded Trp-cage configuration were used for the analysis presented in the study.