Significance
Some freshwater snail species are intermediate hosts in the life cycle of parasites causing human schistosomiasis, a neglected water-based disease (treatable but debilitating and poverty-reinforcing) affecting about 150 million people yearly in sub-Saharan Africa alone. Snail abundance is thus often the target of epidemiological control measures of schistosomiasis incidence. Our work studies the ecology of host snails through field campaigns and theoretical models within natural/artificial water habitats across Burkina Faso’s highly seasonal climatic zones. Snail abundance is shown to depend on hydrological controls and to obey density-dependent demographic evolution. Statistical methods based on model averaging yield reliable snail abundance projections. Quantitative predictions on epidemiological effects of water resources development, risk mapping, and the allocation of control measures appear within reach.
Keywords: freshwater snails, water-based disease, infection controls, environmental monitoring
Abstract
We report about field and theoretical studies on the ecology of the aquatic snails (Bulinus spp. and Biomphalaria pfeifferi) that serve as obligate intermediate hosts in the complex life cycle of the parasites causing human schistosomiasis. Snail abundance fosters disease transmission, and thus the dynamics of snail populations are critically important for schistosomiasis modeling and control. Here, we single out hydrological drivers and density dependence (or lack of it) of ecological growth rates of local snail populations by contrasting novel ecological and environmental data with various models of host demography. Specifically, we study various natural and man-made habitats across Burkina Faso’s highly seasonal climatic zones. Demographic models are ranked through formal model comparison and structural risk minimization. The latter allows us to evaluate the suitability of population models while clarifying the relevant covariates that explain empirical observations of snail abundance under the actual climatic forcings experienced by the various field sites. Our results link quantitatively hydrological drivers to distinct population dynamics through specific density feedbacks, and show that statistical methods based on model averaging provide reliable snail abundance projections. The consistency of our ranking results suggests the use of ad hoc models of snail demography depending on habitat type (e.g., natural vs. man-made) and hydrological characteristics (e.g., ephemeral vs. permanent). Implications for risk mapping and space-time allocation of control measures in schistosomiasis-endemic contexts are discussed.
Schistosomiasis is a neglected water-based tropical disease causing an estimated 150 million people in need of treatment in sub-Saharan Africa today (1). The life cycle of the parasite, helminth worms of the genus Schistosoma, involves two hosts and two water-motile larval phases. The first larval stage, miracidium, reaches the environment through human feces or urine and seeks out aquatic snails of the Planorbidae family to infect. Within snails, the parasite matures and multiplies into the second larval stage, cercaria, which infects humans through skin penetration during water contact (2).
Retrospective analyses have suggested a notable disease-curbing role of local snail abundance management (3). Snail control measures include ecosystem management via natural predators (4–7) or timely spraying of molluscicides. Intervention effectiveness depends on ecological context and control methods (e.g., frequency and duration of molluscicide application), especially in seasonal climates (3). Insight into the population dynamics of the snails acting as intermediate hosts is therefore necessary to acquire an understanding of the ecology of the disease (8) and to minimize transmission through action aimed at snail population control (9).
Negative density feedbacks (sensu ref. 10) have been at the heart of a debate (11, 12) on whether or not they must be seen as a key ecological process for the demography of the intermediate hosts of schistosomes. Density feedbacks have been alternatively accounted for (6, 13, 14) or ignored (15, 16) in spatially implicit mathematical models of schistosomiasis transmission that include snail demography. Ecological approaches have also highlighted the role of environmental forcings in limiting snail abundance, including water temperature for Bulinus globosus in permanent streams in Zimbabwe (17) and water level fluctuations for Oncomelania hupensis (the intermediate host of Schistosoma japonicum) in irrigation canals in China (18). The population dynamics of B. globosus have been labeled as “density vague” (17), suggesting that, under natural conditions, snail abundance is controlled by adverse environmental conditions preventing crowding levels at which negative density feedbacks are appreciable. Occasionally, however, crowding was observed to occur in particularly favorable environments (6). Notably, a large body of literature exists on statistical methods for density feedback detection (19–22).
Schistosomiasis is endemic in Burkina Faso and, in general, in sub-Saharan Africa (23). Recent advances in worm burden reduction using targeted preventive chemotherapy and mass drug administration campaigns have refocused national public health objectives from morbidity control to disease elimination (24–26). This strategic shift will require the implementation of control measures tailored to the local socioecological conditions that support transmission, including water resources development (27). Possible controls include antihelminthic drugs; snail population management; public health education; and improved access to safe water, sanitation, and hygiene (28, 29). Both urogenital and intestinal schistosomiasis forms coexist in Burkina Faso, caused by Schistosoma haematobium and Schistosoma mansoni, respectively (23). The intermediate hosts of the parasite species (Bulinus spp. for the former and Biomphalaria pfeifferi for the latter) have been observed in various types of natural and man-made habitats, either permanent or ephemeral (Materials and Methods and SI Appendix). To our knowledge, only two field studies (30, 31) have addressed the ecology of snail hosts in Burkina Faso, and both highlighted notable seasonal abundance fluctuations of Bulinus spp. (SI Appendix). This seasonality is in contrast to current assumptions of spatially explicit models of schistosomiasis transmission that neglect the dynamics of local snail abundance, which are typically assumed to be constant and treated as a parameter (32, 33). Notably, the existing field studies focused on two sites in similar climatic zones and did not address quantitatively the underlying ecological processes driving population dynamics, particularly density effects and drivers borne out of external environmental forcings.
Here, we use formal model selection (34), specifically structural risk minimization (SRM) and other information criteria (Materials and Methods), to investigate the role, the relative importance, and the links between density feedbacks and environmental forcings and the fluctuating abundances of the intermediate hosts of schistosomiasis. Several population models are contrasted against field data gathered across different habitats (SI Appendix) chosen as representative of a broad range of conditions for endemic schistosomiasis throughout sub-Saharan Africa. SRM allows us to rank theoretical models of population dynamics, thus clarifying the relevant covariates that explain empirical observations of snail abundance at the various sites under actual climatic forcings. As a result, we identify statistical methods based on model averaging capable of providing reliable local snail abundance projections, whose implications, like sensible generalizations of current spatially explicit epidemiological models, we discuss also in view of schistosomiasis control.
Results
Burkina Faso experiences pronounced seasonal climatic fluctuations along a South/North gradient (SI Appendix). Seasonality, in turn, greatly affects the suitability of snail aquatic habitats (35). Rainfall occurs mainly during the rainy season (July–October), with little or no rain falling during the rest of the year (Fig. 1 and SI Appendix). Temperatures reach 45–50 °C in the dry season (36).
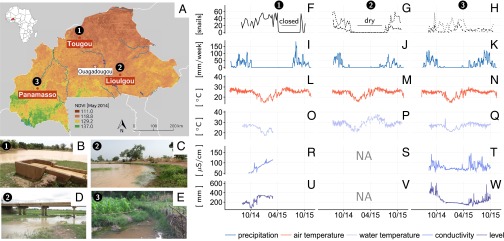
Fig. 1.
Ecological and environmental field data. (A) Situation map of the field sites (black dots) chosen along the South/North climatic gradient in Burkina Faso, here highlighted by values of the normalized difference vegetation index (source in SI Appendix), and the state capital (Ouagadougou). (B–E) Illustrations of the ephemeral or permanent habitats chosen for snail sampling in the experimental sites of Tougou, Lioulgou, and Panamasso. (F–W) Ecological and environmental data time series. Weekly snail relative abundance data are given per species and habitat: Bulinus spp. in a canal in Tougou (solid line) (F) and in a pond (short dashed line) and a stream (long dashed line) in Lioulgou (G) and B. pfeifferi (dashed line) and Bulinus spp. (dotted line) in a stream in Panamasso (H). Periods during which the habitat dried out are indicated for Lioulgou and Tougou (canal closed for operational reasons). Their respective environmental data are given in columnar format. Environmental data consist of weekly cumulative precipitation (I–K) and daily averages of air temperature (L–N), water temperature (O–Q), conductivity (R–T), and water depth (U–W). Graphs containing the term “NA” indicate ephemeral habitats (S and V). Details on sampling and environmental monitoring methods are given in the SI Appendix.
Abundance data show that snail populations in different climatic zones and habitats present distinct seasonal patterns (Fig. 1 F–H). Of the three villages in which we performed our field study (Fig. 1A), only Panamasso harbored the intermediate host of intestinal schistosomiasis (B. pfeifferi), whereas Bulinus spp. were found at all sites. Large populations were observed in the irrigation canal in Tougou during normal irrigation operation conditions (Fig. 1F). In the ephemeral habitats of Lioulgou, snails were absent during most of the year, from December to July, and population peaked toward the end of the rainy season between September and October (Fig. 1G). Opposite fluctuations were observed in the permanent stream of Panamasso for both B. pfeifferi and Bulinus spp., for which the maximum abundance was observed in the middle of the dry season between January and March. Such annual fluctuations are consistent with the ones observed in the historical data in both a temporary pond and a man-made reservoir experiencing climatic conditions similar to the ones in Lioulgou (30, 31).
According to our model selection (Fig. 2 and Materials and Methods), density feedbacks were detected across all species and habitats, although operating at different strengths depending on habitat type, environmental/hydrological conditions, and specific snail species. A strong density feedback (i.e., the Ricker model; discussed in Materials and Methods) was consistently selected only for Bulinus spp. in the ephemeral stream (Fig. 2C). Weaker density feedbacks (i.e., the Gompertz model, discussed in Materials and Methods) were selected for Bulinus spp. in the irrigation canal (Fig. 2A), the temporary pond (Fig. 2B), and the perennial stream (for both Bulinus spp. and B. pfeifferi; Fig. 2 D and E). The strength of density feedbacks also varied across species and habitats in the weak group (SI Appendix), that is, in decreasing order: Bulinus spp. per canal B. pfeifferi per stream Bulinus spp. per stream Bulinus spp. per pond. Density feedback results were fairly consistent for all species for all of the best 100 models, although the model ranked first by SRM (Materials and Methods) for Bulinus spp. in the temporary pond corresponds to a random walk model (Materials and Methods). This result could be due to the apparent lack of autocorrelation in the time series of population increments (tested using the Box–Ljung statistics, P value ), although a clear pattern of population fluctuation emerges. Results obtained using alternative selection criteria generally agreed with the SRM criterion regarding the presence of density feedback in all habitats (SI Appendix). Analysis of the historical temporary pond data further supports our results, although the limited amount of environmental data probably biased the prominent ratings of random walk models (SI Appendix).
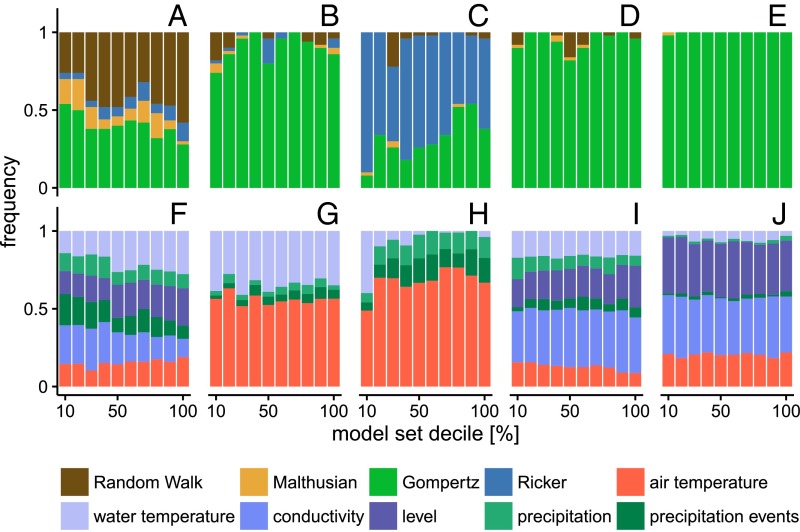
Fig. 2.
Density feedbacks, environmental covariates, and snail population dynamics. The strength of density feedbacks (A–E) and of measured environmental covariate features (F–J) is given in terms of the frequency of appearance in the 500 best-selected models, summarized by decile (decile 10 corresponds to the top 10% of model outcomes). Results are shown in columnar format for Bulinus spp. in the irrigation canal (A–F), in the temporary pond (B–G), and in the ephemeral stream (C–H), and for B. pfeifferi (D–I) and Bulinus spp. (E–J) in the perennial stream.
Environmental covariates were also found to play different roles in different settings. The importance of exogenous forcing in host population dynamics was quantified in terms of the frequency of occurrence of the monitored covariate types in the features of the 500 best regression models (Fig. 2 and SI Appendix). Physical and chemical characteristics of the water (including temperature and conductivity) were most important for snail species in both perennial habitats: Bulinus spp. in the irrigation canal (Fig. 2F) and Bulinus spp. and B. pfeifferi in the perennial stream (Fig. 2 I and J). In both ephemeral habitats (pond and stream; Fig. 2 G and H), Bulinus spp. were mostly conditioned by the variations in air and water temperatures, and much less by precipitation. Water level and conductivity were singled out as important determinants in the perennial stream for both B. pfeifferi and, to an even greater extent, Bulinus spp. (Fig. 2 I and J). This pattern is in contrast to the snail dynamics in the irrigation canal, a permanent snail habitat. Water temperature did not appear frequently in selected models in the perennial stream habitat for either genera, in terms of average values or measures of variability. Precipitation (either cumulative or event-based) seldom appeared in the top 500 models for Bulinus spp., and in a slightly larger proportion for B. pfeifferi. Finally, air temperature average and fluctuations were dominant in models for both ephemeral habitats, whereas they were only marginally present in the permanent habitats. Inclusion of lags in both the density feedback and the environmental features (Materials and Methods) was also varied among snail species and habitats, shedding additional light on the biology of snail development on which they possibly intervene (SI Appendix). Interestingly, a significant density feedback was singled out only during the week preceding the snail sampling date for the Ricker and Gompertz models. This short lag points toward increased death rates due to crowding rather than reduced reproduction, as suggested also by laboratory experiments (12). Environmental covariates had significant effects at different time lags for different habitats and species. Most of the effects were shown at short time lags (1–2 wk) in the ephemeral habitats (pond and stream), at intermediate lags (2–3 wk) in the irrigation canal, and at longer lags (3–4 wk) in the perennial stream. Indeed, water temperature effects were frequently observed at short lags for Bulinus spp. in the temporary pond (1 wk preceding sampling) and at longer lags in the irrigation canal and the perennial stream (3–4 wk). Similarly, water conductivity was mainly selected at a lag of 3 or 4 wk for both genera in the perennial stream, indicating a connection with the reproduction/development phases of the snail hosts. Water level fluctuations affected B. pfeifferi at short lags (1 wk) and affected Bulinus spp. at longer lags (3–4 wk) (SI Appendix), a figure suggesting differential susceptibility to hydrological conditions. In the models where they were selected, precipitation events were only singled out at short time lags in both temporary habitats and perennial streams.
The use of SRM (Materials and Methods) allows the selection of models suitable for predictions. Their predictive power was generally found to be consistent with model ranking (Materials and Methods and SI Appendix), thus confirming the ability of the SRM criterion to select for adequate levels of ecological complexity and supporting its use as a ranking tool. The SRM rank was therefore used for choosing the subset of all tested models to include in the jackknife model average (JMA) (SI Appendix). Of the models that were investigated in each site, the best 500 in terms of SRM were averaged to evaluate the prediction capacity of the model set. JMA captured both the trend and local variabilities of the snail abundance time series across habitats (Fig. 3), although it included only a fraction of the 500 best SRM-ranked models for each species and habitat (SI Appendix). The population dynamics in the canal during the time period were accurately reproduced, particularly the population peak observed in November. Within ephemeral habitats, the JMA reproduced well the seasonal variations of snail abundance, with the initial population burst at the beginning of the wet season, a first peak in July, and a second peak in October. Snail dynamics in the perennial stream were well predicted for Bulinus spp., with a population reduction during the rainy season from June onward and high abundance in March through April. For B. pfeifferi, the prediction of seasonal variation was slightly worse, with the March peak not as marked as in the field data. Remarkably, for both species, single models overshoot the prediction of snail abundance in August and July because of the strong variability in the environmental covariates, especially water level and conductivity, whereas the JMA offers reliable out-of-sample predictive ability. It is to be noted that the JMA performed remarkably well on historical data (at biweekly intervals) despite the lack of continuous environmental measurements (SI Appendix). These results are encouraging toward the extension of our approach to settings where scarce environmental and ecological data are available.
Fig. 3.
Observed and predicted snail abundances. Abundance (dots), LOO-CV prediction of the 500 best models (gray lines, increasing transparency indicating lower SRM performance), and JMA of the set (red line) are given for Bulinus spp. in the irrigation canal (A), the temporary pond (B), and the ephemeral stream (C), and for B. pfeifferi (D) and Bulinus spp. (E) in the perennial stream. Average predictions in the case of partial model averages due to missing data are also shown (dash-dotted red line; SI Appendix).
Discussion
Our study on the ecology of the intermediate hosts of schistosomes highlights the key role of hydrological drivers on parasite transmission dynamics. Our findings have direct implications on the design of effective disease control programs. In fact, the improved understanding of snail ecology implied by the prediction of their population abundances can directly refine spatially explicit disease transmission models by relaxing the key assumptions of stationary snail populations (32, 33). By providing empirical and theoretical evidence for discriminating ecological processes across climatic zones and habitat types, our ecohydrological framework accounts for the relevant environmental drivers, especially the kinds of climatic seasonality and habitat ephemerality typical of the Sahelian ecotone.
Our study encompasses multiple intermediate host species, habitats, and climatic zones through their individual roles and mutual interactions in affecting snail population fluctuations. In particular, we show how snail abundances fluctuate during the dry and rainy seasons, with opposite phases in the ephemeral habitats in the north and the perennial habitats in the south of Burkina Faso. Climatic conditions obviously determine the ephemerality of surface waters, resulting in the periodic disappearance of suitable habitats for Schistosoma’s intermediate hosts during the dry season (note that seasonality is survived through aestivation by Bulinus spp. but possibly not by Biomphalaria spp.). Population abundances peaked during the rainy season (July–September), as observed in Lioulgou (in both the stream and the pond) and in the historic ecological data for the country at large (SI Appendix). On the other hand, the perennial stream in the Sudanian climatic region (Panamasso) presented opposite abundance fluctuations (for both Bulinus spp. and B. pfeifferi) with peaks during the dry season (March–April) and low population levels during the rainy season. This observation has nontrivial consequences on the determinants of snail abundance and denies the feasibility of all-purpose stationary and homogeneous reference population sizes being used in large-scale disease pattern identification. Formal methods (e.g., 37) are available to quantify the impact of seasonality in snail fluctuations on disease persistence and prevalence, which will extend directly existing, spatially explicit approaches to the geography of the disease (32, 33). Population fluctuations in the perennial habitat of the south appeared to be in synchrony with snail abundance in the man-made reservoir located in the Sudano-Sahelian center of the country where early ecological studies took place (SI Appendix). The phase shift between the different types of habitats (permanent vs. ephemeral and natural vs. man-made) in the different seasonal climates of the country could have profound consequences on the logistics of national programs for schistosomiasis control due to the regional climatic conditions (38). Throughout the historical data (SI Appendix), Bulinus spp. displayed a double annual peak in the temporary pond, whereas the reservoir showed snail presence during longer periods. Such results provide insight into the potential impact of water resources development in the seasonal climate of Burkina Faso on the sustained transmission of schistosomiasis. In fact, the presence of small reservoirs can extend the period of the year in which intermediate hosts are present in the water points used for daily socioeconomic activities, with a peak of Bulinus spp. abundance in man-made habitats that occurs as the temporary ponds dry out. Moreover, the annual peak in man-made reservoirs was similar to the one observed in the perennial stream of Panamasso except for the disappearance of the snail population during aestivation (April and June; SI Appendix).
Ecological modeling suggests that snail population dynamics are determined by habitat type and hydrological conditions, and that quantitative relationships rule such dependence. Negative density feedbacks were detected in all habitats. The strongest feedback was found in the ephemeral streams, whereas weaker effects were found, in decreasing order of intensity, in the irrigation canal, the perennial stream, and the temporary pond. In the light of our results, the debate about snail demographic determinants (11, 12) is still germane today, particularly in countries presenting strong climatic seasonality. In Burkina Faso, our model identification process supports the view (12) that negative density feedback is necessary to explain seasonal bursts and decay of snail populations. Our evidence does not support the hypothesis of density-vague dynamics because some form of density dependence was always detected in our field observations. Hydrological conditions that characterize the dry and rainy seasons were found to be fundamental controls for all studied habitats and species. For instance, the variabilities in water level, conductivity, and temperature were singled out for both Bulinus spp. and B. pfeifferi in the perennial stream in the Sudanian climate of Panamasso and in the irrigation canal in the Sahelian village of Tougou. As a matter of fact, measuring conductivity proved valuable because it is not only an important determinant of snail growth rates (30) but also a viable proxy of stream discharge in running waters (39). Fluctuations of air and water temperatures are indicators of the transition between dry and rainy seasons (thus also signaling habitat contraction/expansion), which stands out as the main control of Bulinus spp. in the ephemeral habitats of Lioulgou (both stream and pond).
Statistical methods based on model averaging are shown to provide reliable snail abundance projections. The consistency of our results for a large set of best-ranking models suggests the use of specific models of snail demography depending on habitat type (e.g., natural vs. man-made) and hydrological characteristics (e.g., ephemeral vs. permanent). Ecohydrological approaches thus prove necessary to encompass the determinants of the abundance of the intermediate hosts of schistosomiasis adequately, and as a consequence of the entire life cycle of the parasite. Notably, the approach we propose could be relevant to other vector-borne diseases driven by environmental factors and ecological feedbacks. Predicting snail abundance fluctuations and their spatial heterogeneity is of prime interest for space-time modeling of schistosomiasis transmission and for timely application of mollusc control measures or optimization of preventive chemotherapy (27). Extension and upscaling of our approach would be possible through the use of remotely sensed data on the hydrological drivers of snail abundance (SI Appendix), in the perspective of providing predictions of the effectiveness of control interventions. Our approach complements ecological range inference methods [e.g., maximum entropy modeling (40)], and transmission suitability indices incorporating snail biology (41) in assessing seasonal variations of snail abundance and their hydrological controls, yielding potential insight on the impacts of climate change on schistosomiasis transmission at regional scales (33, 42).
Our results stress the importance of tailoring snail control measures to local ecological conditions, and provide a framework for forecasting snail population fluctuations based on habitat type and dominant hydrological controls. Dam constructions and expansions of water resources development infrastructure like irrigation canals, pursued to meet increasing demand and shrinking supply in sub-Saharan Africa, raise concerns about increased incidences of schistosomiasis (43, 44). Our quantitative representation of the related dynamics of the parasite’s intermediate hosts upgrades risk control and disease modeling capabilities, ultimately leading to what could be a minimal set of information required to forecast with confidence likely effects of interventions or control measures on the prevalence of schistosomiasis.
Materials and Methods
Field Sites.
A detailed account of the choice of experimental sites and their characteristics is given in the SI Appendix. Three villages were chosen along a South–North transect where the precipitation gradients characterize well the range of climates of the country. Four sampling locations were selected to cover the range of habitats harboring snail hosts, including an irrigation canal, a temporary pond, one ephemeral stream, and one permanent stream.
Ecological and Environmental Data, Field Protocols.
Representative host species of both urinary and intestinal parasites were sampled over 15 mo in our four sampling sites. Snail demographic data consisted of relative abundance counts between May through July 2014 and October 2015. A time-based snail sampling technique was used analogously to the ones previously used in similar malacological studies ( 6, 7, 30). Along with snail sampling, a network of wireless micrometeorological stations was installed in each village, allowing for the continuous monitoring of microclimatic and hydrological parameters, including air temperature, water level, conductivity and temperature, and precipitation (36). Details are given in the SI Appendix. Processed ecological and environmental data are available as Datasets S1 and S2 and have been deposited in the Knowledge Network for Biocomplexity Data Repository (doi:10.5063/F1F769HM).
Population Dynamics Modeling.
Snail population dynamics are simulated by discrete-time demographic models inclusive of extrinsic environmental forcing. Specifically, if denotes the abundance of the snail population in a given habitat at sampling time t, the simplest demographic model reads where λ corresponds to the finite instantaneous growth rate of the population between two sampling dates. The Ricker version of the Malthusian formulation incorporates density feedbacks in the form where b is a parameter that sets the feedback’s strength (45). The Ricker model reads where is the natural logarithm and Decreased recruitment and/or increased death rates at high population densities occur for . Exogenous forcing of environmental covariates, their lags, and lagged effects of abundance (46) can be accounted for by:
where and are the weights of the lagged population abundances and the environmental covariate features, taken at nonnegative integer time lags and are the maximum lags allowed for abundance and covariates). Lagged covariate features were taken in all possible combinations for a given maximum number m. Lagged abundance effects were only considered one at a time or all at once. Product interactions of the type were not considered. Similarly, a second class of models that incorporate density feedbacks is the Gompertz scheme (47), where the feedback is taken as a function of the logarithm of population abundance, rather than abundance itself (SI Appendix). Note that therein, the logarithmic dependence of the rate of increase on abundance implies a milder density feedback process. The relevant demographic processes were also assumed to be subject to multiplicative log-normal white noise, resulting in additive Gaussian noise when using logarithms of snail abundance. A null random walk model was also considered (SI Appendix). Model results were tested against all time series. The number of tested models is determined by the possible combinations between environmental covariates, density feedbacks, and their lags (a full account of the tested model structures is given in the SI Appendix).
Model Selection and Abundance Predictions.
Statistical tools for the detection of density feedbacks have been extensively studied, for example, through hypothesis testing with bootstrapping (19) or information-theoretical methods such as the Akaike information criterion (AIC) (48). Recently, SRM has been proposed as a viable alternative tool for ecological model selection (34). SRM does not depend on specific assumptions about the nature of the joint probability distribution of process and measurement errors and yields improved density feedback recognition capabilities compared with the widely used compensated AIC (22, 34). Within the SRM framework, the selection criterion corresponds to the choice of the model structure and parameter set that minimize the empirical upper bound of the true structural risk (R), given by:
where are the estimated model residuals associated with the vector of optimal parameter estimates for a given model structure k is the number of parameters, q is the total number of observations, and p is an index of complexity known as the Vapnik–Chervonenski (VC)-dimension, conveniently equal to in the case of linear models. The denominator is kept if strictly positive (34) (SI Appendix). To assess the actual predictive ability of the models retained by the SRM criterion, we performed a leave-one-out cross-validation (LOO-CV) consisting of sequentially removing one data point, refitting the models to the rest of the data, and predicting the values of the ignored observation. The LOO-CV residuals, resulting from this process are used to assess the predictive capacity of each model based on the mean squared cross-validation error (21), The is an unbiased estimator of the true expected model mean square error, thus providing a way of comparing models using MSECV ratios. Candidate models are combined using LOO-CV to obtain an optimal average model for predictions by minimizing the weighted sum of the cross-validation residuals of the retained set of models (49), resulting in the so-called JMA (SI Appendix). Given the large number of tested models, the technique was applied to a subset of the models retained using the SRM criterion (SI Appendix). The same modeling framework was used to validate the results with the available historical ecological data in Burkina Faso gathered from the literature (SI Appendix).
Supplementary Material
Acknowledgments
We thank Prof. Giulio De Leo and Dr. Susanne H. Sokolow (Stanford University) for their support in the design of snail sampling protocols. We also thank Prof. Jean-Noel Poda (University of Ouagadougou) for insightful discussions and Mohammed Bagayan for supporting our field campaigns. This work greatly benefited from the efforts of the field technicians: Isso Sawadogo in Tougou, Albert Kabore in Lioulgou, and Martin Sanou in Panamasso. We thank the Institut International d’Ingenieurie de l’Eau et de l’Environnement (2iE) in Ouagadougou for logistical support and for facilitating the use of its Microbiology and Biotechnology Laboratory. Special thanks are due to Jean-Marc Froehlich, the Project Manager, for his relentless support. This work was supported by the École Polytechnique Fédérale de Lausanne (EPFL) through the use of the facilities of its Scientific IT and Application Support Center. Funds provided by the Swiss Agency for Development and Cooperation, 2iE partie scientifique, through “Projet 3E Afrique, Burkina Faso” are gratefully acknowledged.
Footnotes
The authors declare no conflict of interest.
Data deposition: The data reported in this paper have been deposited in the Knowledge Network for Biocomplexity Data Repository, https://knb.ecoinformatics.org (doi:10.5063/F1F769HM).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1602251113/-/DCSupplemental.
References
- 1.Lai YS, et al. Spatial distribution of schistosomiasis and treatment needs in sub-Saharan Africa: A systematic review and geostatistical analysis. Lancet Infect Dis. 2015;15(8):927–940. doi: 10.1016/S1473-3099(15)00066-3. [DOI] [PubMed] [Google Scholar]
- 2.Rollinson D, et al. The Biology of Schistosomes from Genes to Latrines. Academic; Washington, DC: 1987. [Google Scholar]
- 3.King CH, Sutherland LJ, Bertsch D. Systematic review and meta-analysis of the impact of chemical-based mollusciciding for control of Schistosoma mansoni and S. haematobium transmission. PLoS Negl Trop Dis. 2015;9(12):e0004290. doi: 10.1371/journal.pntd.0004290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Michelson EH. Studies on the biological control of schistosome-baring snails; predators and parasites of fresh-water mollusca: A review of the literature. Parasitology. 1957;47(3-4):413–426. doi: 10.1017/s0031182000022101. [DOI] [PubMed] [Google Scholar]
- 5.Sokolow SH, Lafferty KD, Kuris AM. Regulation of laboratory populations of snails (Biomphalaria and Bulinus spp.) by river prawns, Macrobrachium spp. (Decapoda, Palaemonidae): Implications for control of schistosomiasis. Acta Trop. 2014;132:64–74. doi: 10.1016/j.actatropica.2013.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sokolow SH, et al. Reduced transmission of human schistosomiasis after restoration of a native river prawn that preys on the snail intermediate host. Proc Natl Acad Sci USA. 2015;112(31):9650–9655. doi: 10.1073/pnas.1502651112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Swartz SJ, De Leo GA, Wood CL, Sokolow SH. Infection with schistosome parasites in snails leads to increased predation by prawns: Implications for human schistosomiasis control. J Exp Biol. 2015;218(Pt 24):3962–3967. doi: 10.1242/jeb.129221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Plowright RK, Sokolow SH, Gorman ME, Daszak P, Foley JE. Causal inference in disease ecology: Investigating ecological drivers of disease emergence. Front Ecol Environ. 2008;6(8):420–429. [Google Scholar]
- 9.Sturrock RF. Current concepts of snail control. Mem Inst Oswaldo Cruz. 1995;90(2):241–248. doi: 10.1590/s0074-02761995000200020. [DOI] [PubMed] [Google Scholar]
- 10.Herrando-Pérez S, Delean S, Brook BW, Bradshaw CJA. Density dependence: An ecological Tower of Babel. Oecologia. 2012;170(3):585–603. doi: 10.1007/s00442-012-2347-3. [DOI] [PubMed] [Google Scholar]
- 11.Shiff CJ. Studies of Bulnius (physopsis) globosus in Rhodesia. II. Factors influencing the relationship between age and growth. Ann Trop Med Parasitol. 1964;58:106–115. [PubMed] [Google Scholar]
- 12.Jobin WR, Michelson EH. Mathematical simulation of an aquatic snail population. Bull World Health Organ. 1967;37(4):657–664. [PMC free article] [PubMed] [Google Scholar]
- 13.Feng Z, Eppert A, Milner FA, Minchella DJ. Estimation of parameters governing the transmission dynamics of schistosomes. Appl Math Lett. 2004;17(10):1105–1112. [Google Scholar]
- 14.Ciddio M, Mari L, Gatto M, Rinaldo A, Casagrandi R. The temporal patterns of disease severity and prevalence in schistosomiasis. Chaos. 2015;25(3):036405. doi: 10.1063/1.4908202. [DOI] [PubMed] [Google Scholar]
- 15.Liang S, et al. Environmental effects on parasitic disease transmission exemplified by schistosomiasis in western China. Proc Natl Acad Sci USA. 2007;104(17):7110–7115. doi: 10.1073/pnas.0701878104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chiyaka ET, Garira W. Mathematical analysis of the transmission dynamics of schistosomiasis in the human-snail. J Biol Syst. 2009;17(3):397–423. [Google Scholar]
- 17.Woolhouse ME, Chandiwana SK. Population dynamics model for Bulinus globosus, intermediate host for Schistosoma haematobium, in river habitats. Acta Trop. 1990;47(3):151–160. doi: 10.1016/0001-706x(90)90021-q. [DOI] [PubMed] [Google Scholar]
- 18.Remais J, Hubbard A, Zisong W, Spear RC. Weather-driven dynamics of an intermediate host: Mechanistic and statistical population modelling of Oncomelania hupensis. J Appl Ecol. 2007;44(4):781–791. [Google Scholar]
- 19.Dennis B, Taper ML. Density dependence in time series observations of natural populations: Estimation and testing. Ecol Monogr. 1994;64(2):205–224. [Google Scholar]
- 20.Andreasen V, Pugliese A. Pathogen coexistence induced by density-dependent host mortality. J Theor Biol. 1995;177(2):159–165. [PubMed] [Google Scholar]
- 21.Turchin P. Complex Population Dynamics: A Theoretical/Empirical Synthesis. Vol 35 Princeton Univ Press; Princeton: 2003. [Google Scholar]
- 22.Brook BW, Bradshaw CJA. Strength of evidence for density dependence in abundance time series of 1198 species. Ecology. 2006;87(6):1445–1451. doi: 10.1890/0012-9658(2006)87[1445:soefdd]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 23.Poda JN, Traoré A, Sondo BK. L’endémie bilharzienne au Burkina Faso. Bull Soc Pathol Exot. 2004;97(1):47–52. French. [PubMed] [Google Scholar]
- 24.Koukounari A, et al. Schistosoma haematobium infection and morbidity before and after large-scale administration of praziquantel in Burkina Faso. J Infect Dis. 2007;196(5):659–669. doi: 10.1086/520515. [DOI] [PubMed] [Google Scholar]
- 25.WHO . Schistosomiasis: Progress Report 2001-2011, Strategic Plan 2012-2020. Technical Report. World Health Organization; Geneva: 2013. [Google Scholar]
- 26.Ouedraogo H, et al. Schistosomiasis in school-age children in Burkina Faso after a decade of preventive chemotherapy. Bull World Health Organ. 2016;94(1):37–45. doi: 10.2471/BLT.15.161885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Utzinger J, N’goran EK, Caffrey CR, Keiser J. From innovation to application: Social-ecological context, diagnostics, drugs and integrated control of schistosomiasis. Acta Trop. 2011;120(Suppl 1):S121–S137. doi: 10.1016/j.actatropica.2010.08.020. [DOI] [PubMed] [Google Scholar]
- 28.Zhou XN, Bergquist R, Tanner M. Elimination of tropical disease through surveillance and response. Infect Dis Poverty. 2013;2(1):1–5. doi: 10.1186/2049-9957-2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gurarie D, et al. Modelling control of Schistosoma haematobium infection: Predictions of the long-term impact of mass drug administration in Africa. Parasit Vectors. 2015;8(1):529. doi: 10.1186/s13071-015-1144-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Poda J, Sellin B, Swadago L. Dynamique des populations de Bulinus senegalensis Müller 1781 dans une mare temporaire située dans une zone climatique nord-soudanienne au Burkina Faso. Rev Elev Med Vet Pays Trop. 1994;47(4):375–378. French. [Google Scholar]
- 31.Poda J, Sawadogo L, Sellin B, Sanogo S. Dynamique des populations de Bulinus truncatus rohlfsi Clessin, 1886, dans le barrage de Dyoro en zone nord soudanienne du Burkina Faso. Agronomie Africaine. 1996;8(1):61–68. French. [Google Scholar]
- 32.Gurarie D, Seto EYW. Connectivity sustains disease transmission in environments with low potential for endemicity: Modelling schistosomiasis with hydrologic and social connectivities. J R Soc Interface. 2009;6(35):495–508. doi: 10.1098/rsif.2008.0265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Perez-Saez J, et al. A theoretical analysis of the geography of schistosomiasis in Burkina Faso highlights the roles of human mobility and water resources development in disease transmission. PLoS Negl Trop Dis. 2015;9(10):e0004127. doi: 10.1371/journal.pntd.0004127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Corani G, Gatto M. Structural risk minimization: A robust method for density-dependence detection and model selection. Ecography. 2007;30(3):400–416. [Google Scholar]
- 35.Poda J. 1996. Distribution spatiale des hôtes intermediaires des schistosomes au Burkina Faso: Facteurs influençant la dynamique des populations de Bulinus truncatus rohlfsi (Classin, 1886) et de Bulinus senegalensis (Muller, 1781). PhD thesis (Université de Ouagadougou, Ouagadougou, Burkina Faso). French.
- 36.Mande T, et al. Suppressed convective rainfall by agricultural expansion in southeastern Burkina Faso. Water Resour Res. 2015;51(7):5521–5530. [Google Scholar]
- 37.Mari L, et al. Floquet theory for seasonal environmental forcing of spatially explicit waterborne epidemics. Theor Ecol. 2014;7(4):351–365. [Google Scholar]
- 38.Cecchi P, Meunier-Nikiema A, Moiroux N, Sanou B, Bougaire F. 2007 Why an Atlas of Lakes and Reservoirs in Burkina Faso? Technical Report iii (Small Reservoirs Project, Accra, Ghana). Available at www.smallreservoirs.org/full/toolkit/docs/IIa%2002%20Faso%20MAB_ML.pdf.
- 39.Weijs SV, Mutzner R, Parlange MB. Could electrical conductivity replace water level in rating curves for alpine streams? Water Resour Res. 2013;49(1):343–351. [Google Scholar]
- 40.Stensgaard AS, et al. Large-scale determinants of intestinal schistosomiasis and intermediate host snail distribution across Africa: Does climate matter? Acta Trop. 2013;128(2):378–390. doi: 10.1016/j.actatropica.2011.11.010. [DOI] [PubMed] [Google Scholar]
- 41.Walz Y, et al. Modeling and validation of environmental suitability for schistosomiasis transmission using remote sensing. PLoS Negl Trop Dis. 2015;9(11):e0004217. doi: 10.1371/journal.pntd.0004217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Simoonga C, et al. Remote sensing, geographical information system and spatial analysis for schistosomiasis epidemiology and ecology in Africa. Parasitology. 2009;136(13):1683–1693. doi: 10.1017/S0031182009006222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Barbier B, Yacouba H, Maïga AH, Mahé G, Paturel JE. Le retour des grands investissements hydrauliques en Afrique de l’Ouest: Les perspectives et les enjeux. Géocarrefour. 2009;84(1):31–41. French. [Google Scholar]
- 44.Steinmann P, Keiser J, Bos R, Tanner M, Utzinger J. Schistosomiasis and water resources development: Systematic review, meta-analysis, and estimates of people at risk. Lancet Infect Dis. 2006;6(7):411–425. doi: 10.1016/S1473-3099(06)70521-7. [DOI] [PubMed] [Google Scholar]
- 45.Ricker WE. Stock and recruitment. J Fish Res Board Can. 1954;11(5):559–623. [Google Scholar]
- 46.Turchin P. Rarity of density dependence or population regulation with lags? Nature. 1990;344(6267):660–663. [Google Scholar]
- 47.Gamito S. Growth models and their use in ecological modelling: An application to a fish population. Ecol Modell. 1998;113(1):83–94. [Google Scholar]
- 48.Johnson JB, Omland KS. Model selection in ecology and evolution. Trends Ecol Evol. 2004;19(2):101–108. doi: 10.1016/j.tree.2003.10.013. [DOI] [PubMed] [Google Scholar]
- 49.Hansen BE, Racine JS. Jackknife model averaging. J Econom. 2012;167(1):38–46. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.