Marginal Mean Models for Zero-Inflated Count Data

Summary

Zero-inflated regression models have emerged as a popular tool within the parametric framework to characterize count data with excess zeros. Despite their increasing popularity, much of the literature on real applications of these models has centered around the latent class formulation where the mean response of the so-called at-risk or susceptible population and the susceptibility probability are both related to covariates. While this formulation in some instances provides an interesting representation of the data, it often fails to produce easily interpretable covariate effects on the overall mean response. In this paper, we propose two approaches that circumvent this limitation. The first approach consists of estimating the effect of covariates on the overall mean from the assumed latent class models, while the second approach formulates a model that directly relates the overall mean to covariates. Our results are illustrated by extensive numerical simulations and an application to an oral health study on low income African-American children, where the overall mean model is used to evaluate the effect of sugar consumption on caries indices.

1. Introduction

Zero-inflated (ZI) regression models, which view data as being generated from a mixture of a point mass at zero and a non-degenerate distribution, have become a popular and interesting tool within the parametric framework to analyze count data with excessive zeros. Well known applications of these models include the works of Mullahy (1986), Farewell and Sprott (1988), Lambert (1992), Ridout et al. (1998), Böhning et al. (1999), Hall (2000), Gilthorpe et al. (2009) and references therein. Despite their increasing popularity, most of the generic applications of ZI models in statistical practice focus primarily on regression models that relate the mean response of the so-called at-risk or susceptible population and the susceptibility probability to covariates. Although this latent class formulation in some settings provides a versatile and useful representation of the data, the implied parameterization may fail to provide a clear answer to the question of evaluating the covariate effects on the marginal mean response. By marginal mean, we refer to the overall mean obtained by averaging the latent mean response across the distribution of the susceptibility status, regardless of covariates. This mean, even when there is a sizeable frequency of zeros in the data, is often the target of inference in many clinical trials and observational studies especially when non-susceptibility is scientifically obscured or implausible. And for this reason, many analyses involving ZI models tend to misinterpret the covariate effects on the mean of the susceptible population as effects on the overall mean (Preisser et al., 2012).

The work proposed in this paper is motivated by data generated from a unique oral health study on low-income inner city African-American children under the age of six and their main caregivers residing in Detroit, Michigan. Our primary interest for these data is to evaluate the effect of sugar intake on caries indices in primary dentition, possibly adjusting for important confounders such as age. The dental caries literature has consistently indicated that sugar consumption remains an important modifiable risk factor for dental caries prevention, although its effect is not as strong as it used to be in the pre-fluoride era (Burt and Pai, 2001; Tellez et al.; 2006; and Anderson et al., 2009). Evaluating this effect for medically underserved children, who are prone to extensive caries and excessive sugar consumption, would be helpful in formulating a tailored dental caries prevention policy. Because caries susceptibility may not be fully observed, focusing this evaluation on children presumed susceptible to caries would be obscured from a policy formulation standpoint.

The literature has been fairly silent about the usefulness of ZI regression models in evaluating the overall covariate effects on the marginal mean response. An important contribution was recently made by Albert et al. (2011) who proposed, in the context of binary exposures, the so-called average predicted value (APV) by integrating out the confounding variables from the model-predicted response for each subject. This approach is interesting but has some limitations. Although the APV operates on the marginal mean, which is often of primary interest, the involved numerical integration can be computationally very intensive for moderate to high dimensional confounding variables even when these confounders do not interact with the exposure variable. And most importantly, its extension to continuous exposures, such as sugar intake in our motivating data example, in not trivial. To address these limitations, these authors also proposed an approach for evaluating the exposure effect on the marginal mean by relating the susceptibility probability to covariates using the log link function. This approach which they referred to as the log – log approach has the key advantage that it provides a direct interpretation of the effects of covariates on the marginal mean response. A limitation, however, is that the log link may lead to unstable computations and inconsistent estimates, owing to the obvious constraints imposed on probabilities.

In this article, we propose two strategies for evaluating the effect of covariates on the marginal mean response, which merely use the heterogeneity implied by the ZI models as a device to account for extra zeros in the data. The first approach derives the covariate effect on the overall mean response from the estimates of the models relating the latent mean response and the class membership probability to covariates. The second strategy, which we refer to as the direct approach, consists of formulating a regression model that relates the marginal mean response to covariates. Under this model formulation, the regression model relating the latent mean to covariates is implied by the assumed models for the class membership probability and the marginal mean. This second approach generalizes the marginalized zero-inflated Poisson regression model recently proposed by Long et al. (2014) to any count data with excess zeros. Although this extension may appear conceptually modest, the estimation may require additional programming efforts beyond those encountered in ZI Poisson models.

In Section 2, we give a brief description of ZI models and give details on the derived and the direct methods to estimate the overall effects of covariates on the marginal mean response. We conduct simulation studies to evaluate the finite sample performance of these methods and illustrate their practical utility using data from the Detroit oral health study in Section 3. We conclude with some remarks and discussions in Section 4.

2. The method

Suppose we randomly select a sample of n independent subjects with response counts Y_i, i = 1, …, n, from a population which can be well represented by a ZI model. Under this model, the population is viewed as a mixture of susceptible and non-susceptible subjects, but the susceptibility status S_i, taking value 1 if subject i is susceptible to the event of interest and 0 otherwise, is not fully observed. For each subject i, this heterogeneity manifests itself through the probability mass function (pmf) of Y_i, assuming a covariate W_i,

$$\text{Pr}({\mathrm{Y}}_i=y|{\mathrm{W}}_i)=(1-{\pi }_i){\delta }_{0y}+{\pi }_i{f}_i(y|{\mathrm{W}}_i).$$

Here y is an observable count, π_i = Pr(S_i = 1|W_i) is the susceptibility or the at-risk probability, δ_0y is the kronecker's function taking value 1 if y = 0 and 0 otherwise, and f_i(y|W_i) = Pr(Y_i = y|S_i = 1; W_i) is the pmf for a susceptible subject indexed, possibly, by a finite dimensional parameter. Letting μ_i = E(Y_i|S_i = 1; W_i) be the mean response for a susceptible subject, the marginal mean response E(Y_i|W_i) is obtained by averaging the latent mean response E(Y_i|S_i; W_i) = S_iμ_i over the distribution of S_i, yielding E(Y_i|W_i) = π_iμ_i.

In real applications of ZI models, μ_i and π_i are related to, potentially different, subsets of W_i through regression models coupled with conventional link functions (Lambert, 1992 and Gilthorpe et al., 2009). Parameter estimates from these regression models often have the so-called latent class interpretation, and in some settings can also be interpretable vis-a-vis the marginal mean. This is especially true when π_i is constant or varies with covariates that are not of interest. In general, however, the interpretation of covariate effects on the marginal mean using individual regression models for μ_i and π_i is often not trivial, especially when these terms contain the exposure of interest. This limitation may preclude direct use of the latent class model formulation in practical settings.

In this paper, we aim at evaluating the effects of covariates on the overall mean E(Y_i|W_i), representing the target of inference. We propose two strategies, which rely on the trivial relation E(Y_i|W_i) = π_iμ_i, to achieve this aim. The first approach provides estimates of covariate effects on the overall mean from individual estimates of μ_i and π_i under the latent model formulation. In contrast, the second approach models directly the marginal mean E(Y_i|W_i) and the mixing weight π_i as a linear function of known covariates, but a regression model relating the latent mean μ_i to covariates is not directly specified but implied by the trivial relation ${\mu }_i=\mathrm{E}({\mathrm{Y}}_i|{\mathrm{W}}_i){\pi }_i^{-1}$. The core of estimation for these methods is based on the following joint pmf for observed outcomes y = (y₁, …, y_n) given covariates w = (w₁, …, w_n)

$$\mathcal{l}(\mathrm{y};\mathrm{w})=\prod _{i=1}^n{\{1-{\pi }_i+{\pi }_i{f}_i(y_i|w_i)\}}^{{\delta }_{0y_i}}{\{{\pi }_i{f}_i(y_i|w_i)\}}^{1-{\delta }_{0y_i}}.$$ (1)

With a proper specification of f_i(y_i|w_i), the estimation then proceeds by maximizing, preferably on the log scale, this joint pmf viewed as a function of finite dimensional parameters.

2.1 Derived marginal models

Suppose that the following regression models relating the latent mean and the at-risk probability to covariates using standard link functions are entertained,

$$log\{\mathrm{E}({\mathrm{Y}}_i|{\mathrm{S}}_i=1;{\mathrm{W}}_i)\}={\alpha }^{\prime }{\mathrm{V}}_i,\text{logit}\{\text{Pr}({\mathrm{S}}_i=1|{\mathrm{W}}_i)\}=\gamma \prime {\mathrm{Z}}_i,$$ (2)

where V_i = (1, v_1i, …, v_r−1,i)′ and Z_i = (1, z_1i, …, z_q−1,i)′ are respectively an r × 1 vector and a q × 1 vector and subsets of W_i, α and γ are the associated vector of unknown regression coefficients. Vectors V_i and Z_i may share common components, and because there are subsets of W_i, the basic regression models in (2) assume that the effects of some components of W_i on these latent quantities may be zeros. The log and logit link functions are also assumed but any monotone function should be applicable in principle.

Assume that the maximum likelihood estimates (MLEs) α̂ and γ̂ of α and γ are obtained by maximizing the joint pmf in (1). To derive the overall effect of covariates on the marginal mean response from these estimates of the conventional models in (2), suppose for example that there exists an unspecified column vector X_i of dimension p related to the marginal mean as follows,

$$log\{\mathrm{E}({\mathrm{Y}}_i|{\mathrm{W}}_i)\}=\beta \prime {\mathrm{X}}_i,$$ (3)

where β is the unknown parameter vector. Unlike the model formulation in (2) where V_i and Z_i are directly observable, the specification of X_i under the mean regression model in (3) is somewhat dictated by the working regression models for μ_i and π_i. This then necessitates X_i to be expressed in terms of covariates V_i and Z_i, at least approximately. A simple algebraic calculation shows that the relation between the marginal mean E(Y_i|W_i), the latent mean μ_i, and the at-risk probability π_i given the respective working regression models, can be expressed as

$$exp\{\beta \prime {\mathrm{X}}_i\}=exp\{\alpha \prime {\mathrm{V}}_i-log\{1+exp\{-\gamma \prime {\mathrm{Z}}_i\}\}\}.$$

Because α′V_i is linear in parameters, a simple approach for selecting X_i would be to linearize g_γ(Z_i) = log{1 + exp{−γ′Z_i}} in the parameters, using a Taylor expansion of g_γ(Z_i) around E(Z_i). As an example, the second order Taylor expansion

$$g_{\gamma }({\mathrm{Z}}_i)=g_{\gamma }(\mathrm{E}({\mathrm{Z}}_i))+h_i^{\prime }\mathrm{\nabla }{g}_{\gamma }(\mathrm{E}({\mathrm{Z}}_i))+\frac{1}{2}{h}_i^{\prime }{\mathrm{\nabla }}^2{g}_{\gamma }(\mathrm{E}({\mathrm{Z}}_i))h_i+0_p({\Vert h_i\Vert }^2)$$

where h_i = Z_i − E(Z_i), ∇g(.) and ∇²g_γ(.) are the gradient and Hessian matrix, would include in X_i all unique elements in V_i, and the first order (linear) and second order (quadratic and interaction) terms of Z_i. A first order Taylor approximation of g_γ(Z_i) around E(Z_i) would only include the unique elements in V_i and Z_i for the choice of X_i. Naturally if Z_i only contains one dummy 0 – 1 covariate, the Taylor approximation is not necessary.

With X_i specified, we focus on estimating β. We adopt the following notation. Let m_i(α, γ) denote the marginal mean on the log scale, log{π_i(γ)μ_i(α)}, where π_i(γ) and μ_i(α) highlight the dependence of μ_i and π_i on α and γ, and let X = (X₁, …, X_n)′ and m(α, γ) = (m₁ (α, γ), …, m_n(α, γ))′ respectively be a matrix and a column vector of dimensions n × p and n. Under the working independence assumption of elements of m(α̂, γ̂), a consistent estimate β̂_der of the unknown β, obtained by minimizing the sum of square deviations (Xβ−m(α̂,γ̂))′(Xβ − m(α̂, γ̂)), is

$${\widehat{\beta }}_{\mathit{\text{der}}}={(\mathbf{X}\prime \mathbf{X})}^{-1}\mathbf{X}\prime \mathbf{m}(\widehat{\alpha },\widehat{\gamma }),$$

with associated variance-covariance matrix cov(β̂_der) = (X′X)⁻¹ X′cov{m(α̂, γ̂)}X(X′X)⁻¹, where cov{m(α̂, γ̂)} = cov{m_i(α̂, γ̂), m_j(α̂, γ̂)}_{i,j ∈ {1, …, n}}. The matrix cov{m(α̂, γ̂)} can be approximated using the delta method or any resampling (including the bootstrap) technique. Details of these calculations for the delta method are given in the Appendix.

2.2 Direct Marginal Models

We formulate a ZI regression model that directly relates the marginal mean E(Y_i|W_i), the desired target of inference, to covariates. We consider the marginal mean model,

$$log\{\mathrm{E}({\mathrm{Y}}_i|{\mathrm{W}}_i)\}=\beta \prime {\mathrm{X}}_i,$$

where X_i = (1, x_1i, …, x_p−1,i)′ is a p × 1 vector and a subset of W_i, and β is a vector of unknown regression coefficients that directly captures the effects of covariates on the overall mean. It is worth noting that, unlike the model formulation in (3) where X_i is dictated by the working models of μ_i and π_i, here X_i represents the vector of covariates that are directly observable. To describe heterogeneity in the population, we assume that the unobserved latent variable S_i is a Bernoulli process with success probability π_i = Pr(S_i = 1|W_i) related to Z_i = (1, z_1i, …, z_q−1,i)′, a subset of W_i, as follows,

$$\text{logit}\{\text{Pr}({\mathrm{S}}_i=1|{\mathrm{W}}_i)\}=\gamma \prime {\mathrm{Z}}_i,$$

where γ is a vector of unknown regression coefficients. In the current model formulation, η_i = log{E(Y_i|S_i = 1;W_i)} describing the mean response for a susceptible subject is not directly modeled as a linear function of covariates as in (2) but is related to covariates through the trivial relation $exp\{{\eta }_i\}=\mathrm{E}({\mathrm{Y}}_i|{\mathrm{W}}_i){\pi }_i^{-1}$. Estimates of β, γ and other finite dimensional parameters defining f_i(.) can be obtained by maximizing the joint pmf in (1) viewed as a function of parameters. We denote by β̂_dir the MLE of β.

We refer to this formulation as the marginal log-logit zero-inflated regression model for count data. This marginal regression model is conceptually similar to the formulation proposed by Heagerty (1999) in the context of logistic regression models with random effects. In the current formulation, the unobserved class membership represents this author's random effects terms to model the within-subject association. The marginalized pattern-mixture model for informative missing data proposed by Wilkins and Fitzmaurice (2007) also shares some similarities with this model formulation. However, unlike in this model where the latent means are averaged across unobserved variables, their marginalized model is averaged over observed missing data patterns. As stated in Section 1, this model is a generalization of the marginalized zero-inflated Poisson regression model recently proposed by Long et al. (2014). It is generally applicable to any ZI regression model for which the associated non-degenerate function f_i(.) is a smooth function that decays rapidly at infinity with some degree of uniformity (see for example Preisser et al, 2015).

2.3 The relative merit of the derived and direct marginal models

For any of the marginally specified mean models, β is interpreted as contrasting the log mean for subgroups defined by measured covariates. In addition to this marginal interpretation of covariate effects, an appealing and interesting feature of the derived approach is that it also allows a latent class interpretation (through α) of covariate effects. This is scientifically valuable in situations where the scientist is not only interested in conducting inferences on variables that affect the mean response for subjects at risk but also variables that affect the overall mean response. The direct approach, however, focuses primarily on the marginal mean E(Y_i|W_i), while treating the latent components E(Y_i|S_i = 1; W_i) and Pr(S_i = 1|W_i) which describe how heterogeneity arises in the data as nuisance. But from a technical standpoint, because the parameters in this approach are directly estimated from a likelihood, β̂_dir will enjoy well known desirable asymptotic properties associated with MLE, compared to β̂_der obtained through the unweighted least squares method. Finally, it is worth mentioning that the degree of accuracy of the derived approach depends primarily on the order of the Taylor expansion. This may constitute a trade-off between the ease of interpretation and the degree of approximation of the derived marginal mean $exp\{{\widehat{\beta }}_{\mathit{\text{der}}}^{\prime }{\mathrm{X}}_i\}$ to the fitted mean π_i (γ̂)μ_i(α̂) from the fitted latent class regression models for π_i and μ_i.

3. Numerical studies

3.1 Simulation studies

We conduct a numerical study to evaluate the finite sample performance of estimated covariates effects on the marginal mean using both the derived and the direct approaches. The results of this evaluation are then compared to those of the APV approach of Albert et al. (2011), which we briefly describe. Suppose that v_1i is a binary exposure taking value 1 if subject i is exposed and 0 otherwise, and v_2i a potential confounder. The APV method compares the overall means of a subject under exposed and unexposed conditions with the confounder integrated out. And because it relies on the integrated mean, we will focus our investigation on the behavior of the estimate of the mean ratio for binary exposures

$$\text{MR}=\frac{\mathrm{E}({\mathrm{Y}}_i|v_{1i}=1)}{\mathrm{E}({\mathrm{Y}}_i|v_{1i}=0)},$$

where E(Y_i|v_1i) = ∫_v2i E(Y_i|v_1i, v_2i)dF(v_2i), v_1i is deterministic (v_1i = 1, i ≤ [n/2]; v_1i = 0, i > [n/2]) and v_2i is generated from a standard normal distribution F. Two data generating schemes based on ZINB models are considered. Given covariates v_1i and v_2i, Y_i is generated first with the latent mean model log{μ_i} = 1.5–0.5v_1i–0.1v_2i, and second with the marginal mean model log{E(Y_i|v_1i, v_2i)} = 1.5 – 0.5v_1i – 0.1v_2i. Both schemes set the dispersion parameter κ to 0.5 and relate π_i, to covariates using the model logit{π_i} = 1.5–0.5v_1i–0.2v_2i. Throughout our simulations, we compute the estimate of the MR using the derived approach and the direct approach, and the APV. Specifically, the APV and the derived estimates are computed using the working regression models log{μ_i} = α₀ + α₁v_1i + α₂v_2i and logit{π_i} = γ₀ + γ₁v_1i + γ₂v_2i. The MR estimate from the marginal log-logit model (direct approach) was obtained using the working model log{E(Y_i|v_1i, v_2i)} = β₀ + β₁v_1i + β₂v_2i. Estimates of the true MR are exp{β̂_1,der} and exp{β̂_1,dir}, respectively for the derived and the direct method. But the APV estimate is computed by integrating out the confounder v_2i from the fitted marginal mean π_i(γ̂)μ_i(α̂) predicted from individual models of π_i and μ_i. The three estimation methods of the mean ratio are compared according to the estimated mean ratio (EMR), the relative bias (RB) in percentage, the mean squared error (MSE), and the 95% coverage probability (CP) of Wald confidence intervals of the true mean ratio. Finally, all simulations are replicated 1,000 times and for sample sizes varying from 50 to 1000.

Results in Table 1 show that the three estimation methods work extremely well in finite samples with average estimates of the mean ratio virtually identical to their true values and relative bias below 5%. Moreover, the associated MSEs also decrease with increasing sample sizes leading to the conjecture that the invoked estimates are consistent. The derived estimation approach based on β̂_der has 95% coverage probabilities of confidence intervals higher than the nominal level, resulting from larger standard errors. And this behavior does not appear to change with increasing sample sizes. This phenomenon is also apparent in the analysis of early childhood indices in Section 3.2, where the parameter estimates from the derived mean model appear to be more variable than those from the direct method. This loss of precision under working independence assumptions is not uncommon and has been previously reported in the literature (Fitzmaurice, 1995).

Table 1. Simulation results for the mean ratio (exposed vs unexposed), using the APV and the derived mean estimation from a latent (conventional) log-logit model, and the direct mean estimation from a marginal log-logit working model, with data generated from ZINB models.

		Latent log-logit working model									Marginal log-logit working model
		APV estimation				Derived marginal mean estimation					Direct marginal mean estimation
True MR	n∓	EMR	RB(%)	MSE	CP(%)	EMR	RB(%)	MSE	CP(%)	AIC	EMR	RB(%)	MSE	CP(%)	AIC
Data generated from a ZINB model with a latent mean
0.543	100	0.547	0.743	0.017	92.7	0.545	0.314	0.019	99.8	434.14	0.548	0.915	0.018	92.6	434.17
	200	0.547	0.740	0.008	94.8	0.546	0.452	0.008	98.6	863.40	0.547	0.675	0.008	95.1	863.44
	400	0.546	0.546	0.005	92.1	0.545	0.281	0.005	99.9	1716.61	0.546	0.480	0.005	93.4	1716.68
	1000	0.545	0.301	0.002	94.2	0.543	0.024	0.002	>99.9	4285.21	0.544	0.224	0.002	95.3	4285.30
Data generated from a ZINB model with a marginal mean
0.607	100	0.625	3.086	0.021	94.7	0.625	3.071	0.045	96.7	475.74	0.626	3.281	0.021	94.7	475.72
	200	0.614	1.288	0.011	93.1	0.613	1.003	0.011	99.9	945.35	0.614	1.192	0.011	93.3	945.35
	400	0.609	0.435	0.005	94.7	0.608	0.254	0.005	>99.9	1883.04	0.608	0.395	0.005	94.5	1883.00
	1000	0.608	0.228	0.002	95.6	0.607	0.055	0.002	>99.9	4704.47	0.607	0.146	0.002	95.6	4704.40

^∓n/2 is sample size per group

A simulation study was also conducted for situations where the APV can not be computed, for example when the exposure of interest v_1i has infinitely many strata or is continuous. For such cases, the probability of observing a specific exposure profile is zero rendering the APV computationally unfeasible. Table 2 shows that both the derived and the direct estimation approaches give satisfactory results for the mean ratio MR = E(Y_i|v_1i + 1)/E(Y_i|v_1i) for one unit increase of the exposure generated from a standard normal distribution. These methods provide a decent estimation of the mean ratio in settings where the APV method can not be performed. Additional simulations to study the performances of the derived and direct estimation approaches when a second order Taylor expansion is assumed are given in Web supplementary materials.

Table 2. Simulation results for the mean ratio (one unit increase in continuous exposure), for the derived mean estimation from a latent (conventional) log-logit model, and the direct mean estimation from a marginal log-logit working model, with data generated from ZINB models.

		Latent log-logit working model Derived marginal mean estimation					Marginal log-logit working model Direct marginal mean estimation
True MR	n	EMR	RB(%)	MSE	CP(%)	AIC	EMR	RB(%)	MSE	CP(%)	AIC
Data generated from a ZINB model with a marginally specified mean
0.607	50	0.592	-2.38	0.014	97.4	162.16	0.620	2.22	0.012	94.3	162.29
	100	0.592	-2.41	0.007	98.5	317.52	0.612	0.94	0.005	93.4	317.34
	200	0.592	-2.32	0.003	99.3	625.57	0.606	-0.05	0.003	94.6	625.31
	500	0.594	-2.10	0.001	98.8	1559.95	0.605	-0.30	0.001	94.6	1559.14
	1000	0.595	-1.88	0.0007	98.7	3110.13	0.606	-0.11	0.0005	93.6	3108.68

3.2 Analysis of dental caries indices in primary dentition

We apply the proposed methods to dental caries data generated from the Detroit study aimed at identifying the social, familial, biological, and neighborhood determinants of dental caries and periodontal disease among low-income African American children and their caregivers (Sohn et al., 2007 and Ismail et al., 2011). Our chief focus in this article is to evaluate the effect of the daily amount of sugar intake (DASI), measured in grams per day, on early childhood caries, taking into account potential confounders. We are particularly interested in answering the following scientific question: do inner city African American children with higher levels of sugar intake experience greater caries severity relative to those with lower levels of intake in the modern age of fluoride exposure? The outcome of interest is the so-called dmfs (number of decayed, missing and filled tooth surfaces) index representing the cumulative severity of tooth decay for each surveyed child. This index has well-documented shortcomings but continues to be instrumental in evaluating and comparing the risks of dental caries across population groups (Lewsey and Thomson, 2004). Additional pertinent covariates include the child's age, the caregiver's employment status and oral health practices (measured by the personal hygiene performance-PHP index with lower scores being desirable, described by Podshadley and Haley, 1968).

The data set contains 874 children of which 427 (48.86%) have no caries, resulting in a sizeable frequency of zero dmfs counts. Following earlier analyses of caries indices in this inner city children population, a traditional zero-inflated negative binomial (ZINB) regression model is considered to accommodate excessive zeros and overdispersion due to some children having large caries indices (Todem et al., 2012 and Cao et al., 2014). Specifically, we postulate that the distribution of dmfs caries index, which we denote by Y_i, for a susceptible child i is a negative binomial model with mean μ_i and dispersion parameter κ > 0. And that the latent mean μ_i and the membership probability π_i are related to covariates as follows,

$$\{\begin{array}{l}log\{{\mu }_i\}={\alpha }_0+{\alpha }_1{\text{Unempl}}_i+{\alpha }_2{\text{Age}}_i+{\alpha }_3{\text{SI}}_i+{\alpha }_4{\text{PHP}}_i+{\alpha }_5{\text{Age}}_i{\text{SI}}_i,\hfill \\ \text{logit}\{{\pi }_i\}={\gamma }_0+{\gamma }_1{\text{Unempl}}_i+{\gamma }_2{\text{Age}}_i+{\gamma }_3{\text{SI}}_i+{\gamma }_4{\text{Age}}_i{\text{SI}}_i.\hfill \end{array}$$ (4)

For each child i, Unempl_i is the caregiver's employment status recoded to binary (Unempl_i = 1 if unemployed and 0 otherwise); Age_i is the child's age (standardized); SI_i is the child's sugar intake (standardized version of DASI); and php_i is the caregiver's PHP index (standardized).

Using the parameter estimates of the latent regression models in (4), and assuming a first order Taylor expansion of log{π_i} around the mean of its covariates, we indirectly estimate the overall effects of covariates on the marginal mean π_iμ_i, using the model

$$log\{{\pi }_i{\mu }_i\}={\beta }_0+{\beta }_1{\text{Unempl}}_i+{\beta }_2{\text{Age}}_i+{\beta }_3{\text{SI}}_i+{\beta }_4{\text{PHP}}_i+{\beta }_5{\text{Age}}_i{\text{SI}}_i.$$ (5)

Because the Taylor expansion only invokes linear terms of covariates in π_i, which are a subset of covariates in μ_i, the marginal mean model in (5) has the same covariates as the working model for the latent mean μ_i. In addition to the indirect approach, we also estimate the covariate effects on the overall mean using the marginal log-logit regression model coupled with the maximum likelihood estimation. This approach directly specifies a regression model for the overall mean π_iμ_i using the same covariates as in model (5). It also assumes a regression model for π_i similar to the formulation in (4).

Table 3 presents the MLEs and inference results for the parameters of the latent mean regression model in (4), as well as those of the derived and direct covariate effects from the marginal mean in (5). Both the derived and the direct approaches produce similar estimates and inferences, with the effect of sugar intake on average caries indices being significant at 5% nominal level. This effect, however, fails to reach significance on both the mean caries of the at-risk group and the susceptibility probability, after controlling for caregivers' employment and oral hygiene practices. This analysis constitutes an excellent example where the classical formulation of zero-inflated count regression models fails to capture the overall effect of covariates in contrast with the models that relate the overall mean to covariates. This finding is reminiscent of the statement by Preisser et al. (2012) who argued that misinterpreting the covariate effects on the mean of the susceptible subpopulation as the covariate effects on the overall may lead to the incorrect conclusion that covariate effects are not significant and thus can be grossly misleading.

Table 3. Parameter estimates, standard errors (SE) and p-values for the zero-inflated Negative Binomial model under the latent formulation (with derived overall effects) and the marginal log-logit model with direct overall effects.

	Latent log-logit model with derived overall effects on marginal∓			Marginal log-logit model (direct overall effects)
Effects	Estimate	SE	p-value	Estimate	SE	p-value
Mean
Intercept	1.915 (1.084)	0.098 (0.121)	< 10−4 (< 10−4)	1.278	0.104	< 10−4
Unemployed	0.175 (0.397)	0.105 (0.003)	0.096 (0.295)	0.295	0.110	0.007
Age	0.268 (0.974)	0.071 (0.093)	< 10−3 (< 10−4)	0.700	0.077	< 10−4
SI	0.056 (0.265)	0.074 (0.085)	0.450 (0.002)	0.266	0.081	0.001
PHP	0.136 (0.109)	0.049 (0.050)	0.006 (0.029)	0.128	0.049	0.009
Age*SI	-0.057 (-0.347)	0.077 (0.091)	0.460 (< 10−3)	-0.258	0.081	0.001
Susceptibility probability
Intercept	0.331	0.213	0.120	0.228	0.193	0.250
Unemployed	0.497	0.232	0.032	0.572	0.210	0.006
Age	1.817	0.254	< 10−4	1.635	0.208	< 10−4
SI	0.200	0.160	0.211	0.241	0.142	0.090
Age*SI	-0.254	0.211	0.229	-0.238	0.182	0.191
Dispersion log(κ)
Intercept	-0.005	0.115	0.965	-0.015	0.114	0.895
Summary statistics
Max logL		-1872.4			-1877.5
AIC		3768.8			3779.0

^∓Parameter estimates and inferences for the derived overall effects on the marginal mean under the latent log-logit model are in parentheses.

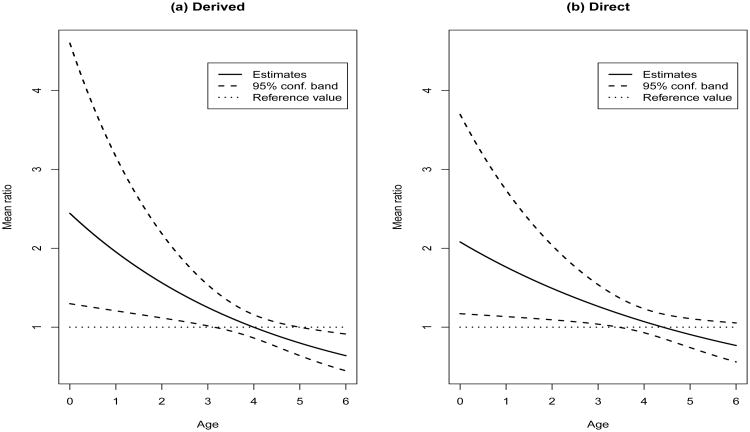
Children with high sugar intakes appear to exhibit worst caries indices on average although the size of the effect tends to diminish with age. In Figure 1, we plot the estimates of the ratios of mean caries indices for each unit increase in SI (standardized version of DASI) as a function of Age (years) and corresponding 95% joint confidence band, for the derived and the direct estimation approach, holding the caregivers' employment and oral hygiene practices constant. Note that each unit increase in the standardized version of sugar intake (DASI ‒ 126.47)/102.31, corresponds to an increase of about 229g sugar intake per day, which is substantial in view of the observed data. Nonetheless, the dramatic effect of sugar intake for this nominal increment is seen in infants under the age of 1 who can see their average caries indices multiplied by as much as 2. After age 3 years, however, the effect of sugar intake vanishes and fails to reach the significance level. This analysis shows that the study population clearly has different levels of vulnerability to dental caries from exposure to sugar intake. Such information is critical for designing targeted and age-specific oral health policies pertaining to dental caries in this inner city children population.

Figure 1. Estimates of mean ratio for each unit increase in DASI (standardized version) as a function of the child's age in years and corresponding 95% joint confidence band, for the derived estimation approach (a), and the direct estimation approach (b).

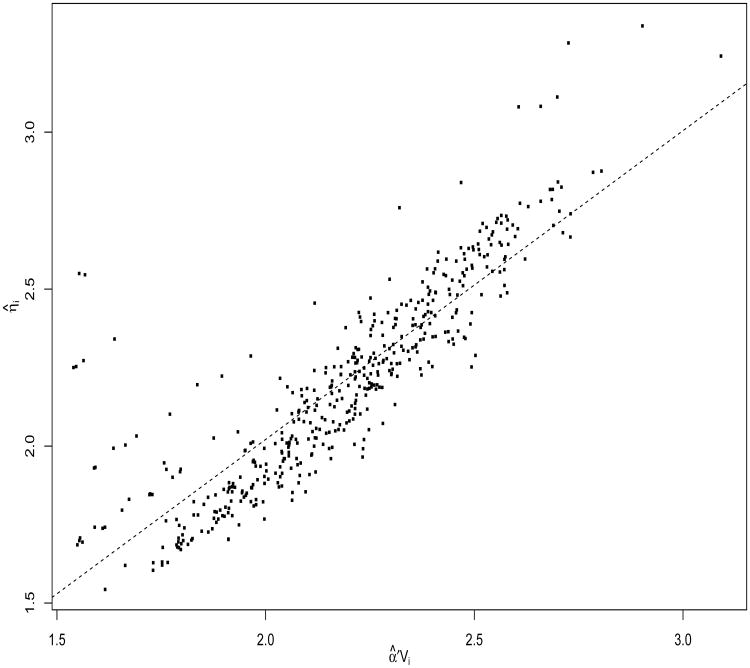
To study the agreement between the two fitted models, we plot in Figure 2 α̂′V_i, with V_i = (1, Unempl_i, Age_i, SI_i, PHP_i, Age_iSI_i)′, the estimates of the linear predictors of μ_i against η̂_i from the marginally specified model, only for susceptible subjects as predicted by these models. Susceptible children to caries are classified as such when they have a higher posterior probability $\text{Pr}({\mathrm{S}}_i=1|{\mathrm{Y}}_i=y_i;{\mathrm{V}}_i)={\left\{\frac{{\pi }_i\text{Pr}({\mathrm{Y}}_i=0|{\mathrm{S}}_i=1;{\mathrm{V}}_i)}{{\pi }_i\text{Pr}({\mathrm{Y}}_i=0|{\mathrm{S}}_i=1;{\mathrm{V}}_i)+1-{\pi }_i}\right\}}^{{\delta }_{0y_i}}$, where y_i is the observed caries index. An estimate of the susceptibility status is Ŝ_i = 1 if $\widehat{\text{Pr}}({\mathrm{S}}_i=1|{\mathrm{Y}}_i=y_i;{\mathrm{V}}_i)>0.5$, with children with observed nonzero dmfs indices being naturally classified as being at risk. These estimates generated from the two working models were almost identical with 465 among 874 children being classified as being at risk. The R² statistic for this plot is 0.72 representing the variation in η̂_i explained by covariates of μ_i in model (4). This level of correlation is consistent with inferential results obtained under the derived and direct approaches, which are virtually identical (Table 3). Additional analysis was conducted to evaluate whether a second order Taylor expansion of log{π_i} around the mean of its covariates, would lead to significant effects of higher order terms of covariates on the average caries indices. Table W.3 (Web supplementary materials) shows that except age, no significant effect of quadratic terms and other higher order interactions on the average caries indices were found.

Figure 2. Plot of η̂_i from the marginal log-logit model against the linear predictors α̂′V_i from the latent log-logit model, for predicted susceptible children (Ŝ_i = 1).

Table 4 presents the results of goodness-of-fit statistics for the two fitted models and those of competing formulations. Models that accommodate zero-inflation and overdispersion appear to give a better representation for these caries indices. Specifically, the ZINB coupled with the marginal and the latent means provides superior fit according to the AIC and BIC criteria. Although the latent mean and the marginal mean both have the same specification in terms of covariates and link functions, the latent mean model appears to provide a better fit to the data under the same mixing probability model.

Table 4. Goodness-of-fit statistics for alternative models fit to dental caries indices in young children.

Model	# parameters	-2 logLik	AIC	BIC
Homogeneous model
Poisson	6	8574.8	8586.8	8615.5
Beta Binomial	7	3787.4	3801.4	3834.8
Negative Binomial	7	3980.2	3994.2	4027.6
ZI model with latent mean
Poisson	11	5873.4	5895.4	5947.9
Beta Binomial	12	3749.1	3773.1	3830.4
Negative Binomial	12	3744.8	3768.8	3826.1
ZI model with marginal mean∓
Poisson	11	5901.4	5923.4	5975.9
Beta Binomial	12	3780.7	3804.7	3862.0
Negative Binomial	12	3755.0	3779.0	3836.3

^∓Marginal log-logit model

4. Discussion

This paper has extended the literature by developing two methods which relate the overall mean response to covariates but use the heterogeneity implied by the ZI models as a device to account for extra zeros. These methods are particularly useful when the overall mean response is the target of inference and the latent class parameterization based on the characterization of the population into the at-risk and not at-risk subgroups is scientifically implausible. As argued by Mwalili et al. (2007), the marginal distribution resulting from ZI models for count data does not always imply that there is an underlying classification of the at-risk and not at-risk population, and that the marginal distribution model may well provide a reasonable representation of data from a homogeneous population. In the Detroit study, it is unclear why some of the minority low-income children would be considered immune to dental caries.

From a practical standpoint, these methods can be implemented in commercial software with minimal programming effort. They can also be readily extended to latent class models with more than two classes. Consider a mixture population with J latent classes with a pmf function of the form $\text{Pr}({\mathrm{Y}}_i=y|{\mathrm{W}}_i)={\sum }_{j=0}^{J-1}\text{Pr}({\mathrm{S}}_i=j|{\mathrm{W}}_i)\text{Pr}({\mathrm{Y}}_i=y|{\mathrm{S}}_i=j;{\mathrm{W}}_i)$, where W_i is the vector of covariates and S_i represents the class membership for subject i. Using the trivial expression $\mathrm{E}({\mathrm{Y}}_i|{\mathrm{W}}_i)={\sum }_{j=0}^{J-1}\text{Pr}({\mathrm{S}}_i=j|{\mathrm{W}}_i)\mathrm{E}({\mathrm{Y}}_i|{\mathrm{S}}_i=j;{\mathrm{W}}_i)$, the overall covariate effect on the marginal mean E(Y_i|W_i) can be indirectly estimated from MLEs of the basic regression models relating the latent class means E(Y_i|S_i = j;W_i) and the latent class membership probabilities Pr(S_i = j|W_i) to covariates. A marginally specified mixture model can also be formulated by directly relating the marginal mean E(Y_i|W_i) to covariates and formulating regression models for the latent class membership probabilities Pr(S_i = j|W_i) and all but one latent means E(Y_i|S_i = j; W_i). This extension has wide applications not only to discrete data but also to continuous data in which case the probability mass functions are replaced by density functions.

The proposed methods have some limitations. The derived estimation approach by relying on the working independence assumption of elements of m(α̂, γ̂), is apt to yield less precise estimates β̂_der. A simple approach to circumvent this limitation might be to estimate β by minimizing the sum of the weighted square deviations (Xβ − m(α̂, γ̂))′ D̂⁻¹ (Xβ − m(α̂, γ̂)) with D = cov{m(α̂, γ̂)}, in which case β̂_der = (X′D̂⁻¹X)⁻¹X′D̂⁻¹m(α̂, γ̂), and cov(β̂_der) = (X′D̂⁻¹X)⁻¹. This approach, however, can be computationally demanding as it requires inverting D̂, a high dimensional matrix of order n × n.

Another limitation of our methodology is that the marginal mean is assumed to be linearly related to covariates through the log link function, which may be subject to misspecification. Although the methodology is readily applicable to any known link function, the linearity assumption may provide a poor approximation of the true function relating continuous covariates to the marginal mean. Given that the true underlying relationship between the mean response and covariates is usually unknown to the analyst, a general approach that does not specify a priori the form of this relationship appears to be the most robust analytic strategy. Smoothing techniques such as generalized additive models and spline models can then be used to reliably estimate the underlying relationship between the marginal mean and covariates (see, for example, Hastie and Tibshirani, 1986; Xue et al., 2004; Lam et al., 2006; Lui et al., 2012). This extension and other generalizations of the methodology are outside of the scope of this paper and may be the subject of further research.

Appendix: Calculation of cov{m(α̂, γ̂)}

Using a first order Taylor expansion of m_i(α̂, γ̂) around {α, γ}, we have,

$$m_i(\widehat{\alpha },\widehat{\gamma })=m_i(\alpha ,\gamma )+(\widehat{\alpha }-\alpha )\prime {\dot{m}}_{i,\alpha }+(\widehat{\gamma }-\gamma )\prime {\dot{m}}_{i,\gamma }+o_p(1)$$

where m˙_i,α = ∂m_i (α, γ)/∂α and m˙_i,γ = ∂m_i(α, γ)/∂γ.

Using the delta method, we have for i, j = 1, …, n,

$$\text{cov}\{m_i(\widehat{\alpha },\widehat{\gamma }),m_j(\widehat{\alpha },\widehat{\gamma })\}=({\dot{m}}_{i,\alpha },{\dot{m}}_{i,\gamma })\text{cov}(\widehat{\alpha },\widehat{\gamma })({\dot{m}}_{j,\alpha },{\dot{m}}_{j,\gamma })\prime ,$$

where m˙_{u, α} = V_u and m˙_u,γ = (1 − π_u(γ))Z_u with π_u(γ) = {1 + exp{−γZ_u}}⁻¹, u = 1, …, n. Applied at α̂ and γ̂, m˙_u,α and m˙_u,γ take values V_u and (1 − π_u(γ̂))Z_u, respectively.