How Good Are Statistical Models at Approximating Complex Fitness Landscapes?

Abstract

Fitness landscapes determine the course of adaptation by constraining and shaping evolutionary trajectories. Knowledge of the structure of a fitness landscape can thus predict evolutionary outcomes. Empirical fitness landscapes, however, have so far only offered limited insight into real-world questions, as the high dimensionality of sequence spaces makes it impossible to exhaustively measure the fitness of all variants of biologically meaningful sequences. We must therefore revert to statistical descriptions of fitness landscapes that are based on a sparse sample of fitness measurements. It remains unclear, however, how much data are required for such statistical descriptions to be useful. Here, we assess the ability of regression models accounting for single and pairwise mutations to correctly approximate a complex quasi-empirical fitness landscape. We compare approximations based on various sampling regimes of an RNA landscape and find that the sampling regime strongly influences the quality of the regression. On the one hand it is generally impossible to generate sufficient samples to achieve a good approximation of the complete fitness landscape, and on the other hand systematic sampling schemes can only provide a good description of the immediate neighborhood of a sequence of interest. Nevertheless, we obtain a remarkably good and unbiased fit to the local landscape when using sequences from a population that has evolved under strong selection. Thus, current statistical methods can provide a good approximation to the landscape of naturally evolving populations.

Introduction

In essence, a fitness landscape is a mapping from genotypes to fitness values, which are usually linked to the reproductive success of a genotype. The landscape formed by the fitness values of all possible genotypes provides information on which mutations are beneficial to an individual in a population. This knowledge can then in theory be used to predict how a population may evolve and adapt to its environment.

In reality, measuring real biological fitness landscapes is difficult. Due to the high dimensionality of genotype space it is only possible to exhaustively measure the fitness values of all variants when the sequence length of the genotypes is extremely short (Warren et al. 2006; Badis et al. 2009; Rowe et al. 2010; and Jiménez et al. 2013). Thus, for biologically relevant sequences we are restricted to either a very sparse sampling of the sequence space (Sanjuán et al. 2004b; Rokyta et al. 2005 , 2008; Kassen and Bataillon 2006; Domingo-Calap et al. 2009; Melamed et al. 2013; Acevedo et al. 2014; Bank et al. 2015; Payen C, et al. unpublished data) or to concentrating on only a few important loci and sampling all possible combinations of mutations at these loci (Weinreich et al. 2006; Lozovsky et al. 2009; Chou et al. 2011; Khan et al. 2011; Tan et al. 2011; Schenk et al. 2013; Podgornaia and Laub 2015). In addition to the difficulties associated with sampling a sufficient number of biologically relevant sequences to cover a significant proportion of the sequence space, quantifying the fitness of a genotype is also problematic and difficult to measure accurately (Elena and Lenski 2003; Sanjuán et al. 2004b; Betancourt and Bollback 2006; Bull et al. 2011).

The consequence is that although the fitness landscape metaphor has been used to describe the evolution of populations for a long time (see Wright [1932]), we still know very little about what real biological fitness landscapes look like. Since we can only explore a tiny fraction of the complete sequence space, our knowledge of real fitness landscapes is necessarily restricted to the subspace spanned by those sequences that we have sampled. One strategy to overcome this problem is to obtain a coarse sampling of the sequence space and then fit a statistical model to the sampled data (Hinkley et al. 2011; Ferguson et al. 2013; Otwinowski and Nemenman 2013; Romero et al. 2013; Bank et al. 2015; Hart and Ferguson 2015; Seifert et al. 2015). By using the model to predict fitness values of unsampled sequences, we can gain insight into the structure of the fitness landscape and predict the evolutionary dynamics of the system. It is unclear, however, to what degree such statistical models can accurately predict the fitness values of unobserved biologically relevant sequences and whether or not such a model can be used to inform us about how sequences will evolve. It has also been suggested that the biases introduced by such models may influence conclusions (Otwinowski and Plotkin 2014).

The accuracy of a statistical description of a fitness landscape depends not only on the correctness of the model used, but crucially also on the completeness of the data used to train the model. When faced with a small landscape it is possible to sample densely within that landscape, such that a random sample of sequences will contain enough information to describe all of the interactions present within the landscape. Such small landscapes, however, are only of limited biological relevance. For landscapes spanned by longer sequence lengths a random sampling will never be dense enough to gain a complete description of the fitness landscape. As such, the choice of which sequences to sample is unclear. However, in most instances we are not interested in the fitness landscape spanned by the complete sequence space, but only in particular types of sequences or in the neighborhood around a sequence of interest. Furthermore, most of the theoretically possible sequences will be lethal or have a very low fitness in the fitness landscape, making it improbable that they will ever be observed. Our aim is to explore the degree to which we can rely on the approximations made by statistical models within a realistic setting and to quantify the effect of different sampling strategies on the quality of the prediction and the types of inferences that can be made.

Since we lack a complete real fitness landscape, we must resort to simulated fitness landscapes to test the validity of such a statistical approach. One possibility is to use mathematical abstractions of fitness landscapes, such as random field models or tuneably rugged models such as the NK model (Kauffman and Weinberger 1989). In these models the fitness is a deterministic function of the genotype. This makes it possible to easily compute the fitness of any genotype and thus compare the statistical prediction to the “true” fitness value (Otwinowski and Plotkin 2014). These landscapes, however, are purely theoretical constructs, and finding a biologically meaningful interpretation of the fitness function of the genotype is challenging.

Quasi-empirical RNA fitness landscapes (Schuster et al. 1994; Fontana and Schuster 1998), offer a convenient middle-ground between empirical and theoretical fitness landscapes that has been used to reveal interesting clues about the properties of real fitness landscapes (Schuster et al. 1994; Huynen et al. 1996; Fontana and Schuster 1998; Ancel and Fontana 2000; van Nimwegen et al. 1999; Cowperthwaite et al. 2005, 2006; Sanjuán et al. 2006). RNA secondary structure is currently the only known system where it is possible to compute a genotype to phenotype map, as it is straightforward to computationally determine the secondary structure of an RNA molecule (Doudna 2000).

Although it is clear that the fitness of an RNA molecule does not depend solely on its secondary structure, using a biologically inspired fitness function arguably results in a more realistic fitness landscape. Since the size and strength of mutations depend on the RNA folding model, there is also no need to define them a priori. Similarly, the extent and form of epistatic effects depend on the RNA sequences and do not need to be explicitly defined. Moreover, these landscapes are correlated (the fitness of a sequence provides some information on the fitness of its neighbors) (Kryazhimskiy et al. 2009), while maintaining a certain level of inherent ruggedness, which is more similar to real fitness landscapes than random field models.

We use quasi-empirical RNA fitness landscapes to evaluate the ability of a simple regression model to accurately represent a complex fitness landscape and to assess how the sampling regime affects the quality of the approximation. We use a linear model accounting for the effects of independent single mutations (main effects), as well as a quadratic model that additionally includes the combined effects of pairs of mutations (epistatic interactions). The model implementation we use is a generalized kernel ridge regression (GKRR) originally developed to predict the in vitro replicative fitness of HIV-1 (Hinkley et al. 2011).

Results

Quasi-Empirical RNA Fitness Landscape

Noncoding RNAs perform essential functions within cells, primarily mediated by the three-dimensional conformation of the molecule (Doudna 2000). While the tertiary structures of RNA sequences are difficult to determine, secondary structures can be easily and relatively accurately computed through energy minimization (Zuker and Stiegler 1981; Zuker 1989). Although secondary structure is not directly linked to the function of a molecule, it can be used to approximate parts of the tertiary structure (Doudna 2000). Furthermore, whereas the sequence space of noncoding RNAs is highly neutral (as many sequences result in the same structure [Doudna 2000]) secondary structures are often highly conserved within sequence families (Doudna 2000). Hence, sequences with conserved secondary structures are likely to also have a conserved function, regardless of their sequence similarity. We use this idea to compute quasi-empirical RNA fitness landscapes, where the fitness of a sequence is based on the similarity of its secondary structure to an ideal target structure, which is assumed to fulfill a hypothetical function that is highly dependent on its structural conformation.

We use the minimum free energy (MFE) structure of a real, functional RNA sequence as the target structure. The human U3 snoRNA (Marz and Stadler 2009; Marz et al. 2011), downloaded from Rfam (Griffiths-Jones et al. 2005), is used as a focal genotype to generate the fitness landscape used in the following sections. This is a noncoding box C/D RNA of 217 nt, making it long enough to form nontrivial structures and for its fitness landscape to be both complex and biologically relevant. We use a real sequence to ensure that the fitness landscape is generated around a sequence with a biological function. The fitness of a candidate sequence is the average selective value of all the structures in the suboptimal ensemble of a sequence (containing all structures with free energies within a bounded distance from the minimal free energy structure). The fitness function is detailed in the Materials and Methods section and is similar to that used in Cowperthwaite and Meyers (2007) and Cowperthwaite et al. (2005, 2006). The resulting fitness landscape is continuous, exhibits a high degree of semineutrality, and places sequences under a strong selective pressure to have similar structures as the target structure while maintaining high stabilities.

Finally, we note that the sequence used to generate the target structure is not necessarily the fittest sequence in the landscape. This is because fitness is calculated on the suboptimal ensemble of a sequence and it is often the case that other sequences in its neighborhood have more stable ensembles.

Statistical Model

We make the assumption that the fitness of a sequence can be written as the product of independent contributions (multiplicative fitness), where each contribution is either due to the presence of a specific allele at a given locus (main effects) or interactions between loci (pairwise or higher-order effects). This is a reasonable assumption for the quasi-empirical RNA fitness landscape we use, where fitness depends on which bases are paired or unpaired and every additional mismatch affects the fitness in a multiplicative way (see Materials and Methods). To perfectly reproduce the fitness landscape, a regression model will need to contain terms for all independent contributions and each of the contributions will need to appear at least once within the training set. While this may be feasible for simple additive landscapes and even for landscapes containing only pairwise or ternary interactions between loci, the number of sequences required to fulfill this condition for landscapes with higher-order interactions makes it impractical for even moderate sequence lengths (unless interactions are restricted to only a few loci and we have a priori information about where these loci are).

The quasi-empirical RNA fitness landscape described above is composed of sequences containing 217 nt each. Even if the landscape contains only main effects and pairwise interactions, it is unlikely that a random sampling will contain enough information to reconstruct the entire landscape. Nevertheless, we expect epistatic effects to be important in RNA secondary structures and we anticipate the presence of higher-order interactions. In particular, a quadratic model trained on the independent fitness effects of all single and pairwise mutations will most likely fail to predict the fitness of sequences with higher numbers of mutations if higher-order interactions contribute to sequence fitness. We tested this prediction and found that a quadratic model trained on the two-mutational neighborhood of a sequence loses most of its predictive power when introducing more than two additional mutations (see supplementary notes and fig. S1, Supplementary Material online). It is therefore apparent that higher-order interactions are present within the landscape and do play an important role in determining sequence fitness.

We expect such a loss of the predictive power to occur for any model that has a lower order than the actual landscape. As in the case here, when dealing with real fitness landscapes, we generally do not know the highest-order of interactions present in the landscape and it is usually impossible to derive a model that definitely has a higher order than the fitness landscape. However, it is possible to train a simple model containing only lower-order interactions on sequences containing higher numbers of mutations and rely on the statistical model to infer the best way of representing complex higher-order interactions as combinations of lower-order effects. In some cases, it is even possible for a simple model to explain all or nearly all of the variance in a complex landscape (Poelwijk FJ, Krishna V, Ranganathan R, unpublished data). Here, we restrict ourselves to linear (first order) and quadratic (second order) models. Even so, we cannot easily sample enough sequences to result in a well-specified problem for the quadratic model (377,147 parameters), and therefore resort to a GKRR scheme to guard against overfitting (see Materials and Methods for model specifics).

Sampling Regimes

As explained above we can neither rely on a random sampling of the landscape nor on sampling only the independent contributions represented in the regression model. We therefore investigate nonrandom sampling regimes that restrict the sequence space to increase the information content within the training sets. We use three different sampling regimes and also compare them to an unbiased random sampling of the complete fitness landscape (hereafter Random).

Two types of sampling regimes were used to explore the local neighborhood around a sequence of interest (here the focal genotype of the fitness landscape). Random Neighborhood is a uniform random sampling within eight or less mutations from the focal genotype, while Complete Subset is an exhaustive sampling of all sequence variants, provided that all mutations occur on eight a priori selected loci. Finally, the Evolved sampling regime represents a set of highly adapted sequences drawn from a population evolving under selective pressures. This is not unlike sequences one might sample from a real population evolving under strong evolutionary constraints. In such data sets most sequences have a high fitness and similar phenotypes, even if the sequences themselves are distant from each other. Since most of the possible sequence variants have a very low fitness, allowing only high-fitness genotypes also has the effect of restricting the sequence space. The sampling regimes are detailed in the Materials and Methods section.

From each sampling regime we draw 65,000 sequences, except for Complete Subset, which is composed of all 65,536 possible sequences in this sampling regime. Data set sizes were chosen to be similar to those used in Hinkley et al. (2011). For Complete Subset we chose the number of mutable loci to result in a similarly sized data set. We characterize the distribution of fitness effects (DFEs) and the amount and type of epistasis present within each of the data sets by drawing 100 random sequences from each data set and sampling all single and double mutants of each sequence. We further characterize the ruggedness of the different subsets of the fitness landscape spanned by the data sets by looking at the number of unique local fitness peaks reached by a simple hill-climbing algorithm starting from 5,000 randomly drawn sequences within each data set. The data sets are summarized in figures 1 and 2 and supplementary table S1, Supplementary Material online.

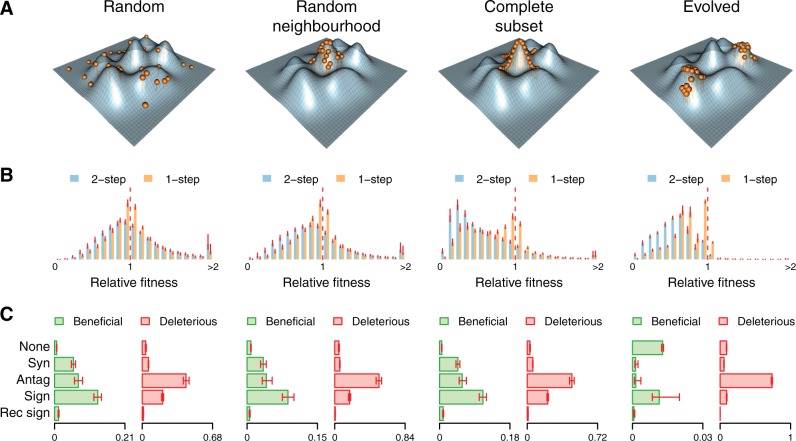
Fig. 1.

The four sampling regimes that were used to explore the quasi-empirical RNA fitness landscape. (A) Illustration of how the populations were sampled relative to an imaginary fitness landscape. (B) The DFEs for all single and double mutants of 100 sequences sampled at random from the four sampling regimes. Each bar represents the mean value for the respective bin in the histograms of fitness effects across the 100 sequences. Error bars represent the 95% confidence intervals of the means estimated from 1,000 bootstrap replicates. (C) The prevalence of different types of epistasis among all beneficial and deleterious mutants of 100 sequences sampled at random from the four sampling regimes. Interactions were considered to be nonepistatic (None) if the combined relative fitness effect of two mutations was within 0.0001 of the expected fitness under independence. For beneficial (deleterious) mutations synergistic magnitude epistasis, Syn, is defined as the double mutant being more (less) fit than expected under independence. Similarly, antagonistic magnitude epistasis, Antag, is defined as the double mutant being less (more) fit than expected. Thus, synergistic (antagonistic) magnitude epistasis occurs when the combined effect is bigger (smaller) than expected under no epistasis. Sign epistasis, Sign, occurs when a beneficial and a deleterious single mutant results in a beneficial or deleterious double mutant. Reciprocal sign epistasis, Rec sign, is defined as two beneficial (deleterious) single mutants resulting in a deleterious (beneficial) double mutant. Each bar represents the mean value for the respective bin in the histograms of pairwise epistatic effects across the 100 sequences. Error bars represent the 95% confidence intervals of the means estimated from 1,000 bootstrap replicates.

Fig. 2.

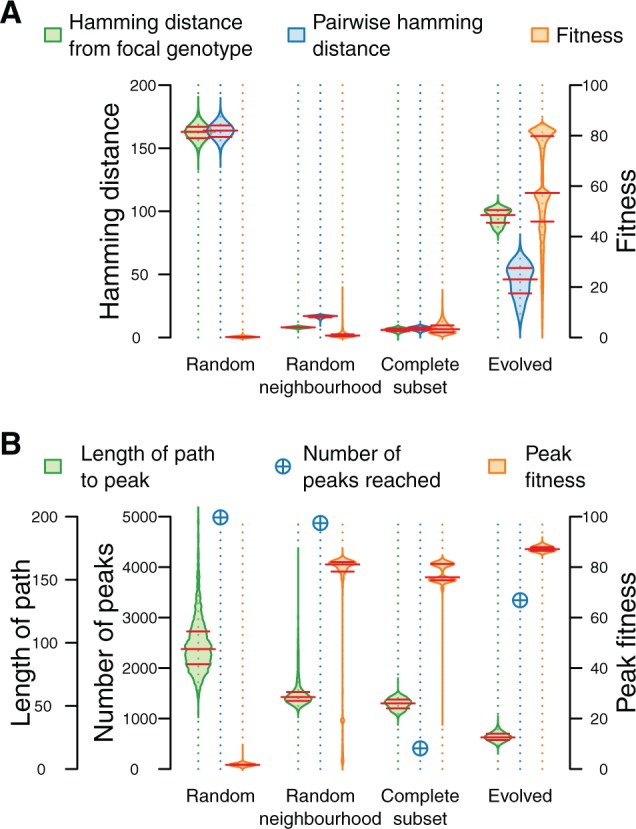
(A) Statistics of the data sets drawn under different sampling regimes. Each data set contains 65,000 sequences, except for Complete Subset, which contains 65,536 sequences. Distributions of sequences with regard to Hamming distance to the focal genotype, pairwise Hamming distance between sequences and sequence fitness are shown. Red lines indicate medians and interquartile ranges. (B) Statistics of local fitness peaks reached by a hill-climbing algorithm started from 5,000 random sequences drawn from each of the data sets. Distribution of path length to local fitness peaks, number of unique peaks reached, and distribution of peak fitness are shown. Red lines indicate medians and interquartile ranges. At each step the hill-climbing algorithm moves to the fittest neighbor of a sequence until no fitness increase is possible (i.e., a local fitness peak has been reached).

It is clear that the different sampling regimes result in different mutational neighborhoods. Both randomly sampled data sets (Random and Random Neighborhood) appear to have nearly symmetric distributions of beneficial and deleterious mutations, albeit with a substantial amount of highly beneficial mutations (fig. 1B). The second mutation shifts the distribution to the left (more deleterious), considerably decreases the amount of neutral and nearly neutral mutations, but actually increases the amount of strongly beneficial mutations. The presence of plenty of accessible high-effect beneficial mutations indicates that the majority of sequences in these data sets are not very well adapted. In contrast, Complete Subset and Evolved have far more deleterious mutations in their two-mutational neighborhoods, indicating that the sequences in these data sets generally have higher fitness than in the randomly sampled data sets (fig. 1B). Once again, the second mutation shifts the distributions to the left and decreases the amount of nearly neutral mutations more than any other type of mutation. However, there are still some beneficial mutations available in both data sets, with Complete Subset showing more room for adaptation than Evolved.

Regarding the role of epistasis in determining the fitness of double mutants, we note that the majority of double mutations are not additive and that reciprocal sign epistasis (two deleterious mutations resulting in a beneficial mutation or vice versa) is very rare (fig. 1C). Fitness reversals brought on by sign epistasis are responsible for most of the beneficial mutants observed (a beneficial and a deleterious mutation resulting in a beneficial mutation). This effect is especially pronounced for Evolved, because the chance of any two randomly selected single mutations both being beneficial is very low in this regime. Among deleterious double mutants antagonistic epistasis is responsible for the observed fitness in most cases, which in the case of deleterious mutations means that the double mutant is fitter than expected from the fitnesses of both single mutants. Finally, we note that the breakdowns of the different types of epistatic effects present are qualitatively similar in all data sets except for Evolved.

Sequences in Random and Complete Subset are on average as far away from each other as from the focal genotype (fig. 2A). Sequences in Random Neighborhood are on average further away from each other than from the focal genotype, as the focal genotype is in the middle of the set of viable sequences and nearly all sequences in this data set lie on the edge of the neighborhood (at a Hamming distance of 8 bp from the focal genotype). This is due to the exponential increase in the number of viable sequences with every added mutation. In Evolved, neutral drift resulted in sequences being far away from the focal genotype. While selection maintains a population that is on average closer to each other than to the focal genotype, this data set still shows the highest degree of sequence variation. Nonetheless, sequences in Evolved are in general much fitter than sequences in the other data sets. This indicates a high degree of neutrality within the RNA folding landscape, making it possible for very different genotypes to attain a high fitness. We note that nearly all randomly sampled sequences, and the majority of sequences in Complete Subset have a low fitness, showing that while the landscape is highly neutral, only a few mutations are sufficient to significantly decrease the fitness of a sequence.

With the exception of Random, the majority of sequences in the other data sets are within the basin of attraction of very high-fitness peaks (fig. 2B). Nevertheless, sequences in Evolved generally find higher fitness peaks in a smaller number of steps. While both randomly sampled data sets are almost maximally rugged, Evolved shows substantially less ruggedness and Complete Subset is in a much smoother part of the landscape. Because sequences in Complete Subset differ from each other on only eight loci, this has the effect of significantly decreasing the number of peaks that can be reached from these sequences.

Effect of Different Sampling Regimes on Predictive Power

We assessed the predictive power (measured as fraction of deviance explained) for both the linear and quadratic models based on 6-fold cross-validation by randomly dividing data sets into training sets of 60,000 sequences and test sets of 5,000 sequences (5,536 sequences for Complete Subset). The results are summarized in figure 3A. We further verified that the training sets contain enough sequences, such that increasing the training set size does not improve the predictive power (supplementary figs. S3 and S4, Supplementary Material online).

Fig. 3.

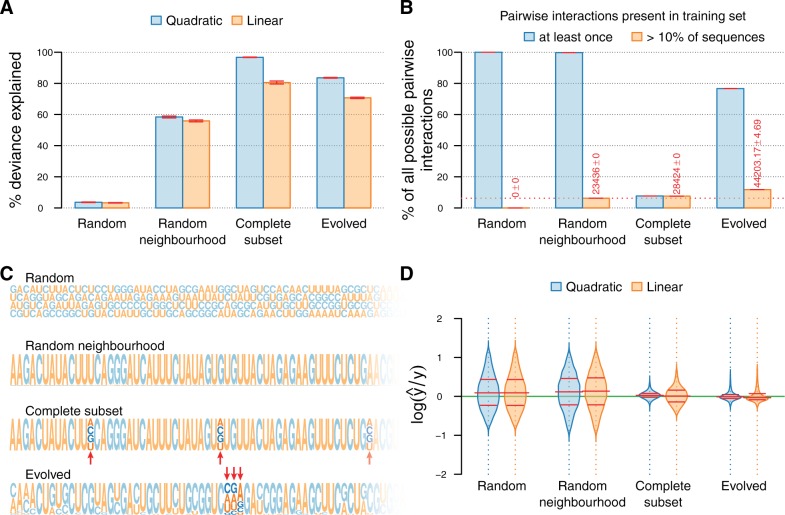
The effect of the sampling regime on the ability to approximate subsets of the fitness landscape. Four data sets were sampled from the same quasi-empirical RNA fitness landscape using different sampling regimes. Each data set contains 65,000 sequences (65,536 for Complete Subset) and was randomly split into training and test sets of 60,000 and 5,000 sequences (5,536 for Complete Subset), respectively. Six-fold cross-validation was used to assess the predictive power and biases of linear and quadratic models on the simulated data sets. (A) The percentage of deviance explained by the linear and quadratic models. Error bars indicate the standard error of the mean across the cross-validated replicates. (B) The percentage of all possible pairwise interactions represented at least once (blue) and in more than 10% of sequences (orange) in the training sets of the different data sets. Error bars indicate the standard error of the mean across the cross-validated replicates. Pairs below the dotted red line are exactly those pairs of mutations occurring in the focal genotype (orange bars only). Note that these are the only pairs of mutations present in more than 10% of the sequences in the Random Neighborhood training sets. (C) Illustration of the sequence diversity in the different data sets using sequence logos (extending over a fraction of the genome). The heights of nucleotides are proportional to the probability of alleles at each locus in the data set. The sequence logo for Random contains no information, whereas the sequence logo for Random Neighborhood simply reflects the focal genotype. For Complete Subset and Evolved, mutable loci are easily distinguishable and indicated by red arrows in the figure. Sequence logos were created using the RWebLogo wrapper for WebLogo 3 (Crooks et al. 2004; Wagih, 2014). (D) The distributions of the 95% confidence intervals of the logarithm of the ratio between the predicted and true fitnesses for models fit on different data sets with the linear and quadratic models. The figure shows only the distributions of one of the cross-validated replicates. The red lines indicate the median and the interquartile range.

We first verified our prediction that it is generally impossible for either model to explain any of the variation when trained on randomly sampled sequences (fig. 3A, Random). Next, we investigated the local neighborhood around a sequence of interest and found that within the restricted sequence space it is possible to sample densely enough to allow a quadratic model (and even a linear model) to reconstruct a fairly good approximation of the local landscape. The fit is much better for Complete Subset than for Random Neighborhood, although no sequence in either data set is more than eight mutations from the focal genotype. Only allowing mutations on eight preselected loci dramatically reduces the dimensionality and results in a much more restricted sequence landscape that encapsulates most of the possible variation within the training set (60,000 of 65,536 possible sequences). Furthermore, although the training sets for Complete Subset contain only a fraction of all possible pairs of epistatic interactions, all of the pairs in the training set appear in more than 10% of sequences (fig. 3B). By contrast, sequences in Random Neighborhood may have mutations at any locus, resulting in a much bigger landscape. Training sets for Random Neighborhood may contain every possible pair of interactions, but the only pairs present in more than 10% of sequences are exactly those pairs trivially present in the focal genotype. Thus, no pair of mutations co-occurs frequently enough in Random Neighborhood to accurately assess the interactions between pairs of loci independent of the genetic background. This explains why a quadratic model shows little improvement over a linear model for Random Neighborhood, and underlines the importance of seeing mutations (and combinations of mutations) within different contexts.

In order to investigate whether or not the predictive power on Complete Subset is strongly dependent on which loci are chosen to be mutable, we trained linear and quadratic models on ten replicate data sets, each of which have eight randomly selected mutable loci. While the predictive power does vary between replicates (supplementary fig. S5, Supplementary Material online), in almost all cases the models achieve a very good predictive power that is comparable to those reported in figure 3A.

On Evolved, both models achieve a surprisingly high predictive power, especially when considering that the variation in sequence space is much larger and that sequences are in general further away from the focal genotype (and each other) than in Random Neighborhood and Complete Subset (fig. 2A). Furthermore, adding pairwise epistatic effects to the model substantially improved the fit (fig. 3A). Selection acts to conserve loci important to fitness, and both the important loci and the favored alleles can easily be read off from the sequence logo of the data set (fig. 3C). In contrast, the sequence logos for Random and Random Neighborhood contain no information on loci important to the sequence fitness, since mutations are randomly distributed throughout the sequences. In Random Neighborhood the sequence logo only contains information on the consensus sequence, which is equal to the focal genotype. This is because each sequence can contain a maximum of only eight mutations, randomly distributed among all loci. Hence, no single mutation is represented frequently enough across the data set to be visible in the logo. The sequence logo for Complete Subset clearly identifies the variable loci, but does not contain any information on which alleles are important at these loci, since all alleles appear equally frequently within the data set. Since selection conserves exactly those loci important to the sequence fitness the same pairs of mutations regularly appear within the training set in different genetic backgrounds. The result is that not only do the training sets for Evolved contain a far higher proportion of all possible pairs of mutations than Complete Subset, but also contain more pairs that are present in more than 10% of all sequences (fig. 3B). Thus, it is possible for the quadratic model to infer which pairs of mutations are important to sequence fitness regardless of the context the mutations appear in.

In order to illuminate the effect of neutral drift on the quality of the prediction, we evolved the population from which Evolved was sampled past the last sample in the data set. Since the population had already reached a quasi-steady state prior to sampling Evolved (see Materials and Methods and supplementary fig. S2, Supplementary Material online), neutral drift plays the dominant role in further evolution. We used the model trained on Evolved to predict the fitness of sequences in subsequent generations (supplementary fig. S10, Supplementary Material online). It can be seen that while the prediction is initially still very good, after 600 generations the quadratic model loses most of its predictive power (supplementary fig. S10B, Supplementary Material online). This is due to the population accumulating mutations and drifitng away from the sequences in the training set (supplementary fig. S10A, Supplementary Material online). The linear model appears to be more robust to neutral drift (supplementary fig. S10C, Supplementary Material online). This is due to the prediction from the linear model only relying on main effects (single mutations) and not on epistatic effects between loci (pairwise mutations). Thus, the linkage between loci used by the quadratic model to predict fitness is destroyed faster by neutral drift. Interestingly, the decline in predictive power is not monotonic, as neutral drift sometimes moves the population back to a part of the landscape that the model approximates well. (This only happened within the first 1,000 generations, after that the population had accumulated too many mutations to return to the same area of the sequence landscape that the model was trained on).

Effect of Different Sampling Regimes on Prediction Bias

The quality of the prediction depends not only on the amount of variance explained, but also on the biases introduced. We use the distribution of the logarithm of the ratio between the predicted and true fitnesses to assess the bias of the prediction (fig. 3D). We further considered the distributions of the relative and mean scaled residuals, which both show qualitatively similar results (supplementary figs. S6 and S7, Supplementary Material online).

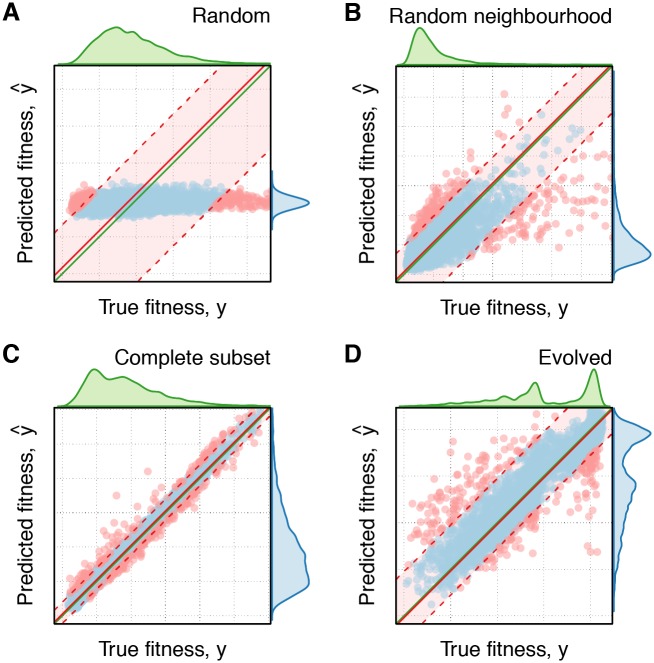
Although Random Neighborhood has a far higher predictive power than Random, the size of the residuals of both randomly sampled data sets have similarly wide distributions for the linear and quadratic models (fig. 3D). Furthermore, in both data sets the medians of the distributions are above 0, indicating a propensity for overestimating the fitness. Since most sequences in these data sets have low fitness, a systematic bias to overestimate low-fitnesses would result in the observed bias in the distributions. This is backed up by a strong correlation between the true fitness and the residual size, which further predicts a tendency to underestimate high fitnesses (supplementary fig. S8, Supplementary Material online). Finally, although Random Neighborhood clearly does a better job at predicting sequence fitness on average, the scatterplots of predicted against true fitnesses reveal that it fares less well for high-fitness sequences, with a bias toward underestimating their fitnesses (fig. 4A and B, supplementary S9A and B, Supplementary Material online).

Fig. 4.

Scatterplots of predicted against true fitness for the different data sets using a quadratic model. The distributions at the top and right of plots indicate, respectively, the distributions of true and predicted fitnesses. The solid green line indicates a perfect prediction. The shaded red area contains 95% of the points. The solid red line indicates the median bias in the residuals.

Complete Subset and Evolved both have smaller relative residual sizes and show more centered and peaked distributions, accompanied with a decrease in correlation between the true fitness and residual size when adding epistatic effects (fig. 3D and supplementary fig. S8, Supplementary Material online). Evolved has a slightly wider distribution of residuals than Complete Subset and appears to show a slight bias for overestimating the fitness (fig. 4C and D), however the overall distribution of its residuals is more peaked, especially for a quadratic model (fig. 3D). The slight bias observed in the median of the distribution for the linear model on Evolved is due to this model overestimating the fitness of extremely high-fitness sequences (supplementary fig. S9D, Supplementary Material online). This bias is much smaller when using a quadratic model (figs. 3D and 4D).

Effect of Different Sampling Regimes on Predicting the Local Structure of the Fitness Landscape

The DFE of all neighbors of a sequence influences its evolvability and plays an important role in determining the trajectories that evolution will follow. Even if a statistical model cannot predict the fitness of individual unseen sequences it may still be informative on the DFE around unseen sequences. Conversely, a model that accurately predicts the fitness of unseen sequences is of limited use if it cannot be used to gain knowledge about the DFE around sequences.

Both the quadratic and linear models are able to reconstruct qualitatively similar DFEs on Random Neighborhood and Evolved for both single and double mutants (supplementary figs. S11–S14, Supplementary Material online). However, there are discrepancies, with both models underestimating the amount of highly deleterious mutations and overestimating the amount of beneficial mutations. On Random Neighborhood there is also a tendency to overestimate the amount of mildly deleterious mutations. We also note that neither model manages to capture the highly beneficial mutations in Random Neighborhood.

The complete failure of both models to reconstruct DFEs for Random and Complete Subset is to be expected. In the case of Random, the sequences are too far apart to be informative and thus there is no information to train the model on. While both models do a good job at predicting the fitness of unseen sequences sampled from Complete Subset they cannot be used to extrapolate to sequence neighborhoods. A model trained on Complete Subset implicitly assumes that all mutations at the 209 invariable loci are neutral, because such mutations are never seen within the training set. This has the result that the DFE is predicted to consist almost entirely of neutral mutations (supplementary figs. S11–S14, Supplementary Material online). Thus, the model is uninformative about the relative fitness of most of a sequence’s neighbors and cannot be used to examine the DFE of a sequence or its evolvability.

Regarding the amount and type of pairwise epistatic effects present in the different sampling regimes the quadratic model is somewhat informative on Random Neighborhood and Evolved, however the results are mixed and the model clearly does not recover the correct distributions (supplementary figs. S15 and S16, Supplementary Material online). On Random the quadratic model essentially reduces to an additive linear model. This is due to no pairs of mutations appearing with any frequency in the training set, making it impossible for the model to accurately describe the pairwise effects of mutations. Similarly, the model highly underestimates the amount of epistasis on Complete Subset. Once again, this is due to using a model trained on a data set with variation on only eight-loci to infer epistatic effects on all 217 loci.

Effect of Sampling Density on Predictive Power

The previous section shows that it is possible to infer the local structure of a fitness landscape. In this section, we investigate how much we can increase the size of the local landscape before the prediction from a simple model breaks down. This is achieved by training and testing quadratic and linear models on data sets consisting of sequences uniformly sampled within increasing Hamming distances of the focal genotype. Each data set contains 65,000 sequences and eight data sets sampled from 2 to 100 mutations of the focal genotype were used (supplementary table S2, Supplementary Material online). As before, we assess the predictive power by 6-fold cross-validation on random divisions of data sets into 60,000 training sequences and 5,000 test sequences. For both linear and quadratic models the results are similar and shown in figure 5 and supplementary figure S17, Supplementary Material online, respectively. The results for Complete Subset and Evolved from the previous section are also plotted for comparison.

Fig. 5.

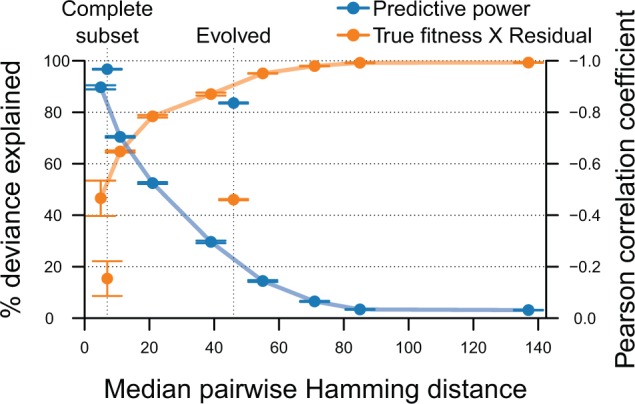
Effect of the sampling density on the ability of a quadratic model to approximate a fitness landscape from randomly sampled sequences. Data sets are composed of 65,000 sequences randomly sampled within successively higher Hamming distances from the focal genotype. Data sets were randomly split into training and test sets of 60,000 and 5,000 sequences, respectively, and 6-fold cross-validation was used to assess the predictive power and biases of a quadratic model on the simulated data sets. Data points are the mean predictive power (blue) and correlation between true fitnesses and residuals (orange) among replicates. Error bars indicate the standard error of the mean. For comparison Complete Subset and Evolved (shown in figs. 3 and 4) are also shown.

The predictive power is strongly correlated to the landscape size and decreases rapidly as the number of allowed mutations are increased. Similarly, we see that as the predictive power decreases the correlation between the true fitness and residual size increases. For randomly sampled sequences it is only possible to attain a high predictive power if the median Hamming distance between sequences in the training set is less than 20 mutations, equal to roughly 90% sequence conservation in the data set. Note that the median Hamming distance between sequences is only slightly smaller than the maximum Hamming distance between sequences. This is because most of the randomly sampled sequences contain the maximum number of allowed mutations, since landscape size grows exponentially with the number of allowed mutations. We further see that at median Hamming distances greater than 80 no prediction is possible. Thus, only on the smallest landscapes used here is it possible for a random sampling of 60,000 sequences to attain a dense enough sampling to produce a good fit.

In the smallest landscape examined here all sequences are within 1 or 2 mutations from the focal genotype. The prediction on this landscape is still worse than on Complete Subset, even though sequences in Complete Subset are more diverse and can have up to eight mutations. This is because the sequence landscape is more restricted in Complete Subset, since mutations are not randomly scattered throughout the genome. Furthermore, Evolved has a much higher predictive power than randomly sampled data sets of the same sequence diversity. This is most likely due to restricting the sequence landscape to high-fitness sequences in Evolved, and because it is not possible to infer which loci or alleles are important for sequence fitness from randomly sampled sequences.

Discussion

We assess the usefulness of regression models accounting for main effects and pairwise interactions between loci to approximate complex fitness landscapes, here represented by quasi-empirical RNA fitness landscapes. Our results show that achieving a high enough sampling density is crucial in order to obtain a good description of a fitness landscape. The curse of dimensionality ensures that it is not possible to sample densely enough to allow a simple model to accurately predict the fitness of any sequence in realistic fitness landscapes. However, while it is impossible to provide a good approximation of a complete fitness landscape in all but the simplest cases it is still possible to obtain an accurate representation of local regions of the fitness landscape by restricting the space sampled for the training set. But, since no model can predict the fitness of sequences that fall too far outside of the variation in its training set, the composition of the training set is extremely important. Care should be taken to select sequences that restrict the sequence space to those sequences, we are interested in and also to select sequences that elucidate epistatic interactions between loci.

We investigated three different sampling regimes restricting the fitness landscape to the local mutational neighborhood of a sequence (Random Neighborhood), the local mutational neighborhood of a sequence with the added restriction of mutations only occurring on a subset of predefined loci (Complete Subset), and the subspace of highly fit sequences (Evolved). Although the best overall prediction is achieved on Complete Subset, such a model only accounts for mutations on predefined loci and has no power to extrapolate to sequences with mutations on other loci. A model trained on a random sampling of the local neighborhood of a sequence results in a fairly good predictive capacity, along with providing some information about the structure of the fitness landscape. However, such a model also suffers from systematic biases in predicting the fitness as well as the DFE. Moreover, it cannot take advantage of epistatic terms in the model due to the low sampling density. Finally, a model trained on Evolved, which contains a highly divergent set of high-fitness sequences evolving under strong selective pressures, has a very high predictive capacity while maintaining a mostly unbiased prediction and providing some insight into the adaptability of sequences.

The sequence length we used was chosen to produce a fitness landscape of comparable size and complexity to real landscapes. Although a shorter sequence length would have allowed us to explore a greater fraction of the landscape, this would not serve our purpose, as we are specifically interested in landscapes where a dense sampling of the sequence space is impossible. For instance, Otwinowski and Plotkin (2014) employed a landscape composed of sequences of length 20, with two alleles per locus, resulting in a quadratic model with 211 parameters. In contrast, the quadratic model for the landscape, we use here contains 377,147 parameters (sequences of length 217, with four alleles per locus, see supplementary notes, Supplementary Material online, for more details). However, this is still much smaller than the landscapes we observe in practice. The fitness landscape of the HIV-1 protease and reverse-transcriptase genes, investigated by Hinkley et al. (2011), contains mutations at more than twice as many loci, which yields a quadratic model with more than a million parameters. But even this landscape still reflects only some 10% of the HIV-1 genome, which is many orders of magnitude smaller than eukaryotic genomes. Although our quasi-empirical landscape is still far smaller than many real fitness landscapes, we expect that it provides a much more realistic setting for testing statistical models and sampling strategies than have previously been explored. In particular, it allows us to explore a landscape with complex higher-order interactions that is too big to sample densely.

We chose a fitness function to be consistent with previous investigations into the properties of correlated fitness landscapes (Cowperthwaite et al. 2005, 2006; Cowperthwaite and Meyers 2007). We also performed additional experiments using different formulations of the selective value of a structure and also using a simplified fitness function which quantifies fitness based only on the selective value of the MFE structure (defined in Cowperthwaite and Meyers [2007] and also used in Otwinowski and Plotkin [2014]). However, this fitness function is undesirable because it is not continuous and has a very high degree of neutrality. Nonetheless, we observed similar results for different formulations of the selective value and for the simplified fitness function (not shown), showing that our results are robust to the particular fitness function used. Alternative model systems are also available, such as the protein-folding landscapes used by Lobkovsky et al. (2011). These models use similar ideas to quantify sequence fitness, which suggests that results would also be qualitatively similar.

In reality, many real fitness landscapes are highly restricted, since the vast majority of genotypes in real systems are nonfunctional or have a very low fitness (Sanjuán et al. 2004b; Poelwijk et al. 2007; Lobkovsky et al. 2011; Romero et al. 2013). Although our fitness landscape does not define any inaccessible sequences, we found that even when the sequence space is highly restricted the majority of all randomly sampled sequences are of a very low fitness. Within our quasi-empirical RNA fitness landscape these low-fitness sequences are effectively equivalent to nonfunctional sequences and would never be observed in practice. Hence, it may be tempting to train a model on only high-fitness sequences, such as the models we trained on our evolved data sets.

The dynamics observed in our evolved data sets are similar to those observed in real populations evolving under strong selective pressure and show similar DFEs (Sanjuán et al. 2004a; Barrick et al. 2009; Acevedo et al. 2014; Bank et al. 2015). Furthermore, as in real populations there is a preponderance of antagonistic epistasis and compensatory mutations among, respectively, deleterious and beneficial double mutants. Low-fitness sequences are not represented in the evolved data sets, which restricts the landscape and leads to a smoother landscape that is more readily approximated by smooth regression models. This has also been shown for data sets sampled from natural populations, especially if most of the mutations represented within the data set are beneficial (Kouyos et al. 2012; Szendro, Schenk, et al. 2013). Such a sampling regime leads to a biased view of the fitness landscape (which is almost certainly more rugged), and a dearth of information about low-fitness sequences.

Since we generally do not have a priori information on which sequences are nonfunctional and which are not, it becomes impossible to extrapolate to sequences which have never been observed in a real population using a model that was only trained on high-fitness sequences. The model will most probably predict a high-fitness for such sequences, although a sequence that has never been observed in practice has an overwhelming probability of being nonfunctional. However, if we are only interested in predicting the fitness of sequence variants sampled from naturally evolving populations, we are unlikely to sample any low-fitness or lethal sequences and we do not necessarily need to include any low-fitness sequences in the training set. Similarly, if neutral drift plays a dominant role unseen sequences may be very different from the sequences used to train the model and make accurate predictions impossible. Such a data set also provides information on the loci important for sequence fitness and on which of them are epistatically linked, making it possible for a quadratic model to obtain a much better predictive capacity than a linear model. Lastly, although we do not recommend using such a model to investigate the trajectories followed by populations evolving on a fitness landscape, it is surprising that a model trained only on high-fitness sequences appears at least qualitatively as good as a model trained on Random Neighborhood at approximating the DFE around a sequence.

If our purpose is to predict evolutionary outcomes or to describe the local structure of a fitness landscape, it is essential to also include low-fitness sequences in the training set. Excluding such sequences will lead to the model predicting evolutionary trajectories that stray into forbidden territory. Current efforts in this direction have focused on exhaustive sampling of a few loci (Weinreich et al. 2006; Lozovsky et al. 2009; Chou et al. 2011; Khan et al. 2011; Tan et al. 2011; Schenk et al. 2013; Szendro, Schenk, et al. 2013), such as in our Complete Subset data set, or in estimating the independent fitness contributions of all single or pairwise mutations of a model sequence (or the fitness effects of genes and pairs of genes) (Tong et al. 2004; Costanzo et al. 2010; Melamed et al. 2013; Acevedo et al. 2014; Al-Mawsawi et al. 2014; Bank et al. 2015; Payen C, et al. unpublished data). For realistic sequence lengths, this either restricts the degrees of freedom or limits us to the immediate sequence neighborhood around a sequence.

We have shown that extrapolating more than a few mutations from independent contributions is bound to fail in landscapes with higher-order interactions. In agreement with our simulated fitness landscape, the importance of higher-order interactions have also been observed on empirical fitness landscapes (Szendro, Schenk, et al. 2013). Similarly, a model that is locally combinatorially complete on a few loci (such as Complete Subset) has no power to extrapolate to variation in other loci. In many cases mutations at certain loci are known to confer large fitness advantages and mutations are rarely observed at other loci. In these cases a combinatorially complete subset offers an advantage over other sampling regimes, provided that mutations occur on few enough loci to make sampling such a data set tractable. However, care should be taken not to use such a model to extrapolate to sequences with mutations on loci that were assumed to be invariable. It should be remembered that selection and mutation acts on the whole sequence and not only on certain loci (Franke et al. 2011). Therefore, in the general case, where there is no knowledge about the loci where mutations can and cannot occur, such a model will not be useful to predict evolutionary outcomes. Thus, while models trained on these data sets provide a good description of the structure in the immediate neighborhood of a sequence and are useful in cases where we have prior information, they have limited power in predicting evolutionary trajectories in the absence of additional information.

Based on the above caveats, in the absence of a priori information, a dense random sampling around the sequence of interest (as in our Random Neighborhood data set) appears to be the only reliable option for obtaining an overview of the landscape structure in a larger neighborhood around a sequence and predicting evolutionary outcomes. However, the size of the sampled subset of the landscape increases exponentially with every added mutation and the model quickly loses predictive power. We found that in order for such a model to have a reasonable predictive power any two sequences in the data set should not differ in more than 10% of their loci. More worryingly, such a model is not able to take advantage of epistatic terms at even very low sequence divergences. In fact, because the size of the sequence neighborhood grows exponentially with each added mutation, it becomes unlikely to observe the same pairwise interactions multiple times in randomly sampled sequences. For higher-order interactions this probability decreases even more, making the use of more complicated models futile. Thus, if we are interested in obtaining a good description of the local structure of the fitness landscape around a sequence of interest within a large and complex landscape, increasing the model complexity leads to only modest gains in the predictive power of the model. This stems mostly from the inability of the model to extract sufficient information from a randomly sampled data set for even comparatively small local neighborhoods around a sequence of interest.

Care should be taken when interpreting the coefficients of the fitted regression model. The landscape contains higher-order interactions between loci, and the model approximates these interactions using combinations of lower-order interactions. Besides obscuring the physical interpretation of coefficients, this also makes it difficult to predict the absence of higher order interactions in a fitness landscape, as the amount of variance explained by the regression model saturates with increasing regression order before the maximum order of the landscape is reached (Poelwijk FJ, Krishna V, Ranganathan R, unpublished data). Furthermore, the quadratic model gives equal weights to both main effects and epistatic interactions, but epistatic interactions greatly outnumber the main effects, thus it is expected that the model overestimates the role of epistasis (Kouyos et al. 2012). Therefore, while the coefficients of the fitted model provide clues on which loci are epistatically linked, we should remain careful of further interpretations. Thus, the usefulness of the models we investigated is largely restricted to predicting the fitness of unseen sequences.

The regression model we use suffers from three sets of biases. We have already described the bias introduced by our inability to sample a data set that contains enough information to infer all interactions between loci. We have also shown the presence of higher-order interactions within the landscape, resulting in a model misspecification. Finally, we use a penalized regression scheme that increases the predictive power at the expense of bias. Although we could have used a more complicated statistical model in order to reduce the degree of misspecification, it is clear that we will never be able to define a perfectly specified model for any real fitness landscape, and even if we could we would still be unable to sample enough sequences to uniquely specify each independent parameter. Thus, while a more complex model would in theory be able to produce a better fit, in practice the sampling bias makes it unlikely that we will be able to sample densely enough to take advantage of the added model complexity. Moreover, deliberately introducing bias to increase the predictive power is standard practice for situations where the number of parameters greatly exceeds the number of datapoints and is necessary to prevent overfitting. This is the case for even the quadratic model and increasing the model complexity would only necessitate an even larger bias-variance trade-off.

The biases above have been investigated by Otwinowski and Plotkin (2014), although they did not investigate sampling bias in detail and only investigated smaller, more tractable landscapes. These biases are all important and should not be ignored. However, we argue that in a realistic setting they are unavoidable. Thus, if we wish to apply a statistical approach to describe real fitness landscapes, sparse sampling, and model misspecification are realities we have to deal with.

Our results are admittedly difficult to generalize. The space of all possible fitness landscapes is vast and it is impossible to cover this space sufficiently, either through simulated models or through sampling empirical data. The landscape we use serves only as an example of a fitness landscape, with sequences of biologically relevant lengths and complex higher-order interactions between loci. Nonetheless, we have shown that on restricted subsets of complex landscapes of a realistic size, with realistic sequence lengths, a simple regression model can still be informative. This is even more remarkable when considering the simplicity of the models we used in comparison to the complexity of the problem. Thus, we are of the opinion that statistical models, such as the penalized regression model investigated here, are a useful tool for exploring complex fitness landscapes and should not be dismissed as hopelessly underpowered and biased.

Materials and Methods

Fitness of RNA Sequences

The fitness of a sequence is defined as a weighted average of the similarity of the secondary structures in its suboptimal ensemble to an ideal target structure. The suboptimal ensemble of a sequence is composed of the lowest free energy structures within a bounded distance from the MFE structure. Thus, fitness is dependent on both the thermodynamic stability and the shapes of the most likely secondary structures of a sequence. This fitness function is similar function we use is similar to the plastic fitness function defined in Cowperthwaite and Meyers (2007) and Cowperthwaite et al. (2005, 2006).

ViennaRNA 1.8.5 (Hofacker et al. 1994; Hofacker 2009) is used to compute the secondary structures in the suboptimal ensemble of sequences through energy minimization (Zuker and Stiegler 1981; Zuker 1989; McCaskill 1990; Wuchty et al. 1999). The algorithm is relatively accurate for determining the structures of short sequences, but it does not incorporate pseudoknots and other noncanonical structures. We ignore energy barriers between structures and assume that a molecule equilibrates between all structures in the suboptimal ensemble with the amount of time spent in a particular conformation. The Boltzmann probabilities of structures are used as weights, which corresponds to the probability of observing a structure within the suboptimal ensemble.

The selective value of a secondary structure, σ, is given by,

$$f(\sigma )=\frac{1}{\alpha +{(d(\sigma ,\tau )/L)}^{\beta }},$$ (1)

where $d(\sigma ,\tau )$ measures the structural distance between σ and the target structure, τ, calculated as the number of basepairs that need to be opened or closed in order to convert σ into τ. L is set equal to the sequence length. The fitness of a sequence, s, is then given by,

$$y(s)={\displaystyle \sum _{\sigma \in {\mathcal{G}}_{\mathrm{ϵ}}(s)}f}(\sigma )p_{\sigma },$$ (2)

where ${\mathcal{G}}_{\mathrm{ϵ}}(s)$ is the ensemble of all structures within ϵkT from the MFE structure of s, where k is the Boltzmann constant and T is the temperature. The Boltzmann probability of observing structure σ within ${\mathcal{G}}_{\mathrm{ϵ}}(s)$ is represented by $p_{\sigma }$. We set ϵ = 5 which corresponds to roughly 3 kcal/mol at $37°\text{C}$. For the selective value of a structure we use $\alpha =0.01$ and β = 1 in all calculations, which results in fitness values between $\approx 0$ and 100.

Realistically, no sequence will achieve a fitness of 100, since that would require its suboptimal ensemble consisting of only the target structure. Furthermore, the fitness function is continuous, since no two sequences have the same suboptimal ensembles. However, the fitness landscape still exhibits a large degree of semineutrality. This is because there are far fewer secondary structures (phenotypes) than sequences (genotypes) and thus multiple sequences can have suboptimal ensembles dominated by the same structures (Doudna 2000), resulting in two completely different sequences having very similar fitnesses.

The hyperbolic decaying function we used to calculate the selective values of secondary structures models a regime of strong selection, where the deleterious effect of mutations is multiplicative, resulting in a superlinear decrease in fitness with added mutations. The particular decaying function used does not quantitatively change the results (own observations and [Fontana and Schuster 1998]), hence we chose a hyperbolic function with the same coefficients used in Fontana and Schuster (1998), Ancel and Fontana (2000), and Cowperthwaite et al. (2005, 2006). We used the basepair distance between structures, instead of the Hamming distance between the parenthetical representations of secondary structures (used in Cowperthwaite and Meyers [2007], Cowperthwaite et al. [2005, 2006]) as it is a more realistic measure at practically no extra cost.

Generalized Kernel Ridge Regression

The model described here was previously developed for predicting the fitness of HIV-1 strains from their amino acid sequences (Hinkley et al. 2011). However, it is readily adaptable to any type of genetic data, the only requirements being knowledge of the loci where mutations occur and all possible alleles at each locus. Sequence data are encoded as a binary string, s, which is fit to its corresponding fitness, y(s), according to the following model,

$$\log (y(s))=I+{\displaystyle \sum _{ij}{m}_{ij}}{s}_{ij}+{\displaystyle \sum _{ijkl}{\mathrm{ϵ}}_{ij;kl}}{s}_{ij}{s}_{kl},$$ (3)

where s_ij = 1 denotes the presence of allele j at position i and s_ij = 0 its absence. In the model, I is the intercept, m_ij are the main effects and ${\mathrm{ϵ}}_{ij;kl}$ the pairwise epistatic effects. Main effects represent the individual contributions of each allele to the fitness of a sequence, whereas epistatic effects represent the effect of an allele at one locus in combination with an allele at another locus. We distinguish between two models: the full quadratic model above, and the linear model. All ${\mathrm{ϵ}}_{ij;kl}$ terms are set to 0 in the linear model, thus this model only fits main effects and ignores all epistatic interactions. Although higher order terms such as three-way interactions can easily be included in the model, Hinkley et al. (2011) found that doing so did not significantly improve the predictive power for HIV.

The number of estimated parameters will generally greatly exceed the number of data points, such that standard approaches to fit the model cannot be used. Here, we use a kernelized ridge regression to overcome the problem of reliable parameter estimation without overfitting. Ridge regression adds a regularization parameter, λ, to penalize large coefficients, unless they contribute substantially to the fit. Kernelizing ridge regression makes the computation more efficient when there are more parameters than data points. Finally, the method is generalized into a weighted kernel ridge regression with iterative reweighting to account for nonnormal error structures (Nelder and Wedderburn 1972). The resulting GKRR method is described in detail in Hinkley et al. (2011).

Model Fitting

The ability of GKRR to accurately predict the fitness of sequences is measured as the fraction of the deviance explained by the model. The deviance measures the deviation from a perfect model and is a standard measure for generalized models with nonnormal error structures (Nelder and Wedderburn 1972). In the case of normal error structures, the deviance of a standard linear regression is equal to the coefficient of determination, R². The formula for calculating the deviance is given in the supplementary notes, Supplementary Material online and in Hinkley et al. (2011).

In order to fit the model we first find the optimal regularization parameter, λ, by fitting the model to subsets of the training set, before training the model using the optimal λ on the complete training set. This is done by randomly drawing six sets of 20,000 sequences from the training set. The model is then trained on 15,000 of the sequences in each subset and evaluated on the remaining 5,000 sequences. This is done for 57 candidate regularization parameters, spanning the space of likely values in a nonuniform manner. We select the largest λ such that the fraction of deviance explained is within one standard error of the mean from the best prediction. This λ is then used to train the model on the full training data.

Uniformly Sampled Data Sets

The dense data set ${\mathcal{D}}_k$ contains every possible sequence of length n that can be reached within k or less mutations from a sequence of interest (the focal genotype). It follows that ${\mathcal{D}}_0$ contains only the focal genotype, ${\mathcal{D}}_1$ contains $3n+1$ sequences and in general ${\mathcal{D}}_k$ contains ${\displaystyle \sum _{i=0}^k\left(\begin{array}{c}n\\ i\end{array}\right)}{3}^i$ sequences. Finally, for k = n, ${\mathcal{D}}_n$ is the complete sequence space and therefore contains all sequence variants of length n ($4^n$ sequences). Dense data sets with k > 2 are only of a manageable size for very short sequences. To produce data sets with more mutations at biologically meaningful sequence lengths we employ two types of sparse samplings of the local landscape.

Random neighborhood data sets represent a uniform sampling of all sequences around the focal genotype. Formally, the random neighborhood data set ${\mathcal{R}}_k$ is formed by uniformly sampling sequences from ${\mathcal{D}}_k$. As k is increased, ${\mathcal{R}}_k$ becomes an exponentially sparser sampling if the number of sequences sampled is kept constant.

Complete subsets are formed by sparsely sampling from the complete sequence space in a systematic fashion. This is achieved by limiting the degrees of freedom.

The complete subset ${\mathcal{C}}_k$ is constructed by selecting k loci randomly and then adding all the sequences with every possible combination of mutations in those k loci, while keeping the other n – k loci fixed. Hence, ${\mathcal{C}}_k$ contains $4^k$ sequences. Effectively, this results in a low-dimensional embedding of the high-dimensional sequence space.

Evolved Data Sets

Evolved data sets represent a sample of sequences from a population evolving under strong selective pressures. These data sets are similar to the ones used in Huynen et al. (1996), Fontana and Schuster (1998), van Nimwegen et al. (1999), Ancel and Fontana (2000), Wilke and Christoph (2001), and Cowperthwaite et al. (2005, 2006). We use a modified version of the RNAvolver program (Cowperthwaite et al. 2006) to obtain evolved data sets. The program evolves a stochastic asexually reproducing haploid population of a fixed size for a specified number of discrete generations. At every generation sequences from the previous generation are chosen to replicate at a rate proportional to their fitness and then subjected to a round of mutation. The number of sequences in the population is kept constant and the same sequence can have multiple copies within the population.

The dynamics of an evolving population is governed by the mutation rate, μ, the population size, N, and genetic constraints imposed by the fitness landscape (Szendro, Franke, et al. 2013). In particular, if $N\mu \ll 1$, the mutation supply rate is too small to allow for more than one mutant to arise at a time. In this scenario, populations are restricted to evolving on uphill trajectories and cannot cross fitness valleys (Szendro, Franke, et al. 2013; de Visser and Krug 2014). Increasing the mutation supply rate leads to the appearance of double mutants and a more diverse population that is able to robustly adapt to rugged landscapes. If the mutation rate is too high, selection ceases to play a role and genetic drift dominates.

It is impractical to evolve a population with enough unique sequences for our data sets. Thus, we set N to 1,000 and μ to ${10}^{-3}$, which leads to a population that is dominated by a couple of very fit sequences while containing a substantial diversity of less fit sequences. Under these parameter settings the mean population fitness initially increases rapidly before slowing down and eventually reaching a quasi-steady state after a few thousand generations (supplementary fig. S2, Supplementary Material online). Because of the large amount of semineutrality in the fitness landscape, the population drifts randomly through sequence space, while selecting for structures that are similar to the target. We evolved an initial monomorphic population for 20,000 generations and sampled unique sequences every 50 generations after discarding the first 10,000 generations. The initial monomorphic population is composed of the fittest sequence selected from a random sampling of 100 sequences, where all sequences are 20 mutations from the focal genotype.

Supplementary Material

Supplementary notes, tables S1 and S2, and figures S1–S17 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).