Wide-field quantitative imaging of tissue microstructure using sub-diffuse spatial frequency domain imaging

Abstract

Localized measurements of scattering in biological tissue provide sensitivity to microstructural morphology but have limited utility to wide-field applications, such as surgical guidance. This study introduces sub-diffusive spatial frequency domain imaging (sd-SFDI), which uses high spatial frequency illumination to achieve wide-field sampling of localized reflectances. Model-based inversion recovers macroscopic variations in the reduced scattering coefficient $\left({\mu }_{\text{s}}^{\prime }\right)$ and the phase function backscatter parameter (γ). Measurements in optical phantoms show quantitative imaging of user-tuned phase-function-based contrast with accurate decoupling of parameters that define both the density and the size-scale distribution of scatterers. Measurements of fresh ex vivo breast tissue samples revealed, for the first time, unique clustering of sub-diffusive scattering properties for different tissue types. The results support that sd-SFDI provides maps of microscopic structural biomarkers that cannot be obtained with diffuse wide-field imaging and characterizes spatial variations not resolved by point-based optical sampling.

1. INTRODUCTION

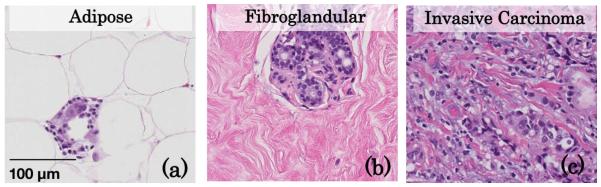
Measurements of light scattering are known to be sensitive to the composition and orientation of cells, intracellular constituents, and the extracellular matrix [1]. A variety of optical imaging techniques have been developed to sample tissue over a variety of length scales, each providing sensitivities to different structural features within biological tissue. Diffuse wide-field imaging of tissue exploits a signal dominated by multiply scattered light where the remission at each pixel is representative of an average of long and tortuous photon path lengths covering relatively large volumes (cubic millimeters to cubic centimeters). Optical measurement geometries based on small fiber optics or confocal setups have been designed to sample reflectance remissions within highly localized volumes of tissue (cubic micrometers to cubic milli-meters). Reflectance remissions that are collected near the source location are dominated by low-ordered scattered photons, which are sensitive to both the frequency of scattering events and the anisotropic character of the scatterers [2–6]. Under these conditions, the light-transport regime has been termed sub-diffuse. Previous work has characterized the interconnectedness of the tissue ultrastructure evaluated using microscopic approaches and the distribution of scattering structures that defines light scattering in the local tissue microenvironment [7–10]. Histology, shown in Fig. 1 for adipose, fibroglandular, and invasive breast tissue, is the “gold standard” for assessing tissue morphology in a clinical setting. With hematoxylin and eosin (H&E) stained histology sections, a pathologist interprets the types and organization of nuclei, cells, and extracellular components that comprise the tissue in order to make a diagnosis. Techniques such as scanning transmission electron microscopy allow the resolution of smaller structures, including organelles within and fibrous components outside of the cell. The density, composition, and size-scale dimension of these biological structures combine to determine the spatial distribution of refractive index fluctuations on length scales ranging from tens of nanometers to tens of micometers [11], which is the source of light scattering in tissue. These parameters define the angular probability of scattering events, given as the scattering phase function, with trade-offs between larger scatterers, which are on the size scale of the wavelength of light and preferentially scatter in a forward direction, and Rayleigh-type scatterers, which are smaller than the wavelength of light and scatter isotropically. Because histology and electron microscopy are both destructive to tissue and time consuming to evaluate, light scattering as a means to assess the microscopic character of tissue morphology in vivo, rapidly and over large tissue volumes, is of considerable interest.

Fig. 1.

Representative histology slides of human breast (a) adipose, (b) fibroglandular, and (c) invasive carcinoma tissues illustrating their unique density, size-scale distribution, and organization of biological features.

Fiber-optic methods that sample localized elastically scattered remissions near the source location are sensitive to the composition and morphology of biological tissue [12–14]. Advanced optical approaches have been developed that use low-coherence interferometry to either resolve the angular remission of light [15,16] from tissue or sample interference-based amplification of reflectance signals [17,18]. Such methods are capable of resolving fine details of the tissue micro-architecture, including the fractal dimension or correlation distance of cellular features [19] or the correlation length of the microscopic mass-density distribution [20], and hold promise for the diagnosis of pathologies such as cancer [21] by returning information usually reserved for destructive tissue analysis methods. However, point-based assessments of reflectance (including both non-coherent and low-coherent) do not characterize tissue heterogeneity over macroscopic length scales. While approaches to raster-scan localized-sampling methods are able to identify pathology and possibly guide clinical decisions during surgeries [22], they are time consuming when applied over large areas of tissue and may not be practical. Polarization imaging is one method that is reported to be sensitive to clinically relevant spatial variations in tissue microstructure [23], but it has yet to gain wide clinical acceptance.

This study focuses on a novel alternative that applies subdiffusive spatial frequency domain imaging (sd-SFDI) to achieve localized reflectance sampling over a wide field of view quickly. It extends previous microscopy work reported by Neil et al. [24], which acquired sub-diffractive signals without raster scanning by using structured illumination. Recently, our group showed that macroscopic imaging based on structured light with a high-frequency photon density wave, whose periodicity was finer than the length scale of diffuse photon propagation, resulted in sub-diffusive signal localization in a wide-field geometry. A spectroscopic [25] and multi-frequency [26] interpretation of high spatial frequency reflectance provided sensitivity to, and quantified images of, sub-diffuse scattering parameters, including the reduced scattering coefficient, ${\mu }_s^{\prime }$, and a phase function parameter, $\gamma =\frac{(1-g_2)}{(1-g_1)}$, that characterizes the backscatter likelihood of the medium and is expressed as a weighted ratio of the first two Legendre moments of the scattering phase function, g1 and g2 [3,27]. The current study applies sd-SFDI to validate wide-field quantitative images of the sub-diffusive scattering parameters in phantoms containing user-tuned phase functions and then applies the approach to image fresh ex vivo tissue samples. The resulting sub-diffusive parameter maps show clear discrimination of tissue types based on scattering parameters that reflect their microstructural differences.

2. METHODS

A. Sub-Diffusive Spatial Frequency Domain Imaging: Basic Concept

By spatially modulating the intensity of light incident on a turbid medium, the effective penetration depth of the resulting photon density wave can be altered by the fineness of the intensity pattern. Even though this technique is well known and has been used for diffuse spectroscopic imaging in a variety of applications [28,29], sub-diffusive imaging at high-spatial frequencies has only recently been explored [26,30]. While low spatial frequency photon density waves are described by isotropic scattering and are preserved [1–2] mm into the tissue on average, as the spatial frequency is increased, the photon density waves penetrate less deeply into the tissue. Here, the forward and backward propagation is influenced by the scattering anisotropy and yields a sub-surface fluence pattern that is preserved only to sub-millimeter depths of penetration. Diffuse reflectance can be completely described by the absorption and isotropic scattering of photons through μ_a and ${\mu }_s^{\prime }$, respectively. However, sub-diffusive reflectance collected within one-mean free path of propagation is sensitive to not only the frequency of scattering events, but also the relative likelihood that the scattering is large angled [2,3], which is quantified with phase-function parameter, γ. A first-order approximation to conceptualizing γ is the ratio of relative contributions of large to small scatters [27]. Previous work has reported γ values in tissue in the range of [1.3–2.2] [−] [12,14,26,31], with smaller values representative of scatterers that are smaller than the wavelength of scattered light and larger values representative of scatterers approaching the same length scale as the wavelength of light. While γ has been shown to be linearly proportional to the fractal dimension of scatterers in a turbid medium, a deterministic link between the two parameters is complicated by other physical parameters that influence the exact form of the scattering phase function [27]; therefore, a concise description of γ may best be as a metric proportional to the length scale of biological scattering features. Quantification of these parameters through a model inversion yields a complete description of the sub-diffusive reflectance and may offer biomarkers for discriminating between tissue types.

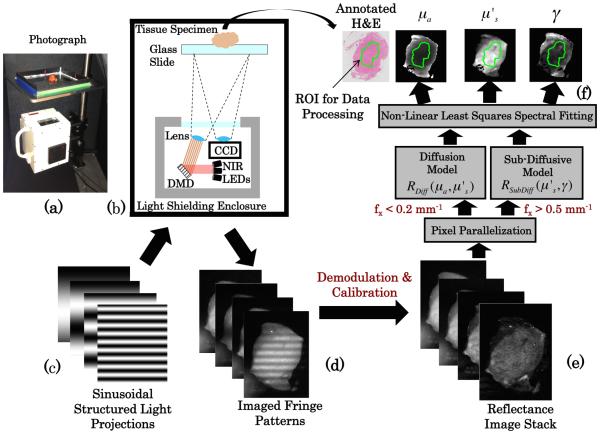
Details of sd-SFDI acquisition and analysis appear in Supplement 1. In brief, sd-SFDI was performed using spatial frequencies over the range of f_x = [0 − 0.2; 0.5 − 0.9] mm⁻¹ in steps of 0.05 mm⁻¹ with source LEDs centered about [658,730,850] nm. Demodulated reflectance images were calibrated and fit to a combined model of diffuse and sub-diffuse reflectance on a pixel-by-pixel basis, returning spatial maps of ${\mu }_s^{\prime }$, γ, and μ_a at each measured wavelength. Here ${\mu }_s^{\prime }$ was assumed to follow a power law, ${\mu }_s^{\prime }\left(\lambda \right)=A{\left(\frac{\lambda }{800\text{nm}}\right)}^{-B}$, in which A is the scatter amplitude and corresponds directly to ${\mu }_s^{\prime }$(800 nm), B is the spectral scattering power, and γ(λ) was fitted as a free parameter at each wavelength. Figure 2 illustrates the workflow of acquiring, analyzing, and spatially co-registering optical parameter maps with ex vivo tissue samples.

Fig. 2.

(a) Photograph of sub-diffusive spatial frequency domain imaging system and (b) diagram of major system components. Sinusoidal intensity patterns (c) are sent to the digital micromirror device and projected on the tissue, with the remitted fringe pattern imaged (d). The stack of fringe patterns over multiple spatial frequencies and wavelengths were demodulated and calibrated to a reference standard yielding a reflectance map stack (e), which was then used to calculate optical property maps (f ).

B. Phantom Imaging of Fractal Distribution of Mie Scatterers

Polystyrene spheres are a well-characterized scattering standard. Previous work demonstrated that proper selection of the fractal dimension, D_f, of the distribution of diameters yielded biologically relevant scattering phase functions [32], where the frequency of scatter sizes, C , follows a fractal distribution as a function of the particle diameter, d , defined as C(d) ∝ d ^−Df . As the fractal dimension increases, the phase function becomes more isotropic with a relative increase in Rayleigh scatterers that are much smaller than the wavelength of light. Conversely, as the fractal dimension decreases, the phase function becomes more forward peaked with an increase in larger Mie scatterers. Phantoms were constructed with physiologically relevant fractal dimension in the range of D_f = [3.6 − 4.85] [−]. In brief, D_f has a pronounced effect on the spectral power of ${\mu }_s^{\prime }$, as defined for models considering both discrete scatterers [8] and continuous random media [33], and introduces spectrally invariant differences in γ. Chamot et al. investigated γ in the context of a distribution of spherical particles [27] and showed, both theoretically and experimentally, that γ is proportional to the D_f of spheres.

Three sets of aqueous phantoms were prepared using mixtures of ten discrete diameter spheres, d = [0.099; 0.14; 0.21; 0.39; 0.5; 0.8; 0.96; 4.5; 10; 20] μm and n = 1.56 (Polysciences Inc., Warrington, Pennsylvania and Bangs Laboratories, Fishers, Indiana). The first set contained six phantoms, each with a different fractal dimension, D_f = [3.6:0.25:4.85], where the volume fraction of polystyrene spheres in each solution was adjusted to result in a matching reduced scattering coefficient at a selected wavelength, such that ${\mu }_s^{\prime }$(658 nm)= [1.2] mm⁻¹. The second set contained nine phantoms with three selected fractal dimensions, D_f = [3.6; 4.1; 4.6], each prepared with the volume fraction of spheres adjusted to yield three values of ${\mu }_s^{\prime }$(658 nm)= [1.2; 1.8; 2.4] mm⁻¹. The third phantom set contained nine phantoms with coupled variation of D_f = [3.6; 4.1; 4.6] and the absorption coefficient, which was varied by adding incremental amounts of Evans Blue dye to achieve μ_a(658 nm)= [0.02 − 0.18] mm⁻¹ such that the ratio $\frac{{\mu }_s^{\prime }}{{\mu }_a}$ ranged from 5.6 to 50 at 658 nm. The first phantom set was evaluated to establish the sensitivity of high-spatial frequency reflectance imaging to the uniquely tuned phase functions in each phantom and to test whether the model inversion accurately quantified the sub-diffuse scattering parameters (i.e., ${\mu }_s^{\prime }$ and γ). The second phantom set was imaged to demonstrate the separability of ${\mu }_s^{\prime }$ and γ in phantoms with differences in both the number density of scatterers and the scattering phase functions within the same image. The third phantom set was used to confirm the accuracy of scattering parameters in the presence of absorption-based attenuation. For all phantom images reported, a 1 cm circular region of interest is presented, as the optical properties are spatially homogeneous, and also to eliminate pixels close to the well wall that are influenced by boundary effects.

Additionally, solid agarose phantoms with a step-change in scatter contrast (i.e., both scatter density and scatter size) were constructed to estimate the spatial resolution and sensitivity to heterogeneously distributed optical scatter parameters. Details regarding the fabrication of these phantoms can be found in Supplement 1.

C. Ex Vivo Human Breast Tissue Imaging and Histological Analysis

To demonstrate the ability of sd-SFDI to differentiate tissue morphologies, optical scatter parameter maps of surgically excised human breast tissue were compared to spatially co-registered histopathologic diagnoses. The study, approved by the Dartmouth-Hitchcock Medical Center (DHMC) Institutional Review Board for the protection of human subjects, included 22 breast tissue specimens from 17 patients undergoing elective and consented breast surgeries at DHMC. After excision and margin inking, specimens were sent to the Department of Pathology and “bread loafed” according to standard-of-care protocol. Upon gross inspection of the loafed specimen, excess tissue that was not needed to make a pathologic diagnosis was evaluated. Specifically, excess tissue conforming to a standardized gross diagnosis of fibroglandular, adipose, benign fibroadenoma, or invasive carcinoma (both lobular and ductal) was cut to a size of approximately 25 mm × 25 mm × 5 mm and immediately imaged. The totals for each tissue type sampled are as follows: adipose (3 patients, 3 specimens, 5785 pixels), fibrolandular (8 patients, 10 specimens, 19391 pixels), benign fibroadenoma (3 patients, 4 specimens, 10459 pixels), and invasive carcinoma (5 patients, 5 specimens, 6984 pixels).

All tissue samples were imaged with sd-SFDI as in Fig. 2, with samples placed on a glass slide and imaged in an inverted geometry to minimize surface curvature and height variations. Additionally, the distance between the glass slide and optical system was fixed to ensure that the projected sinusoid was the correct spatial frequency and in focus. Spatial frequency imaging of the tissue samples required ≈2 min to complete. Additionally, a select set of specimens were also imaged with a dark-field reflectance microscope, the details of which are described in Supplement 1. Following optical imaging, the tissue samples underwent standard histological processing, including formalin fixation and H&E staining. The prepared tissue sections were evaluated by an expert pathologist (W.A.W.), who outlined final diagnoses over digital scans of the entire section. These annotated digital histology sections were readily co-registered to the optical scattering maps with simple rigid transformations and were used to create binary masks for pixel-based clustering analysis. Pixels near the boundary of the tissue were excluded from the clustering analysis, as shown in Fig. 2(f), to avoid boundary artifacts. All of the breast specimens included in the clustering analysis were uniformly comprised of a single breast tissue type in order to capture differences between well-defined tissue morphologies. However, one localized invasive cancer surrounded by adipose and fibrous tissue was analyzed to demonstrate the application of the method to a heterogeneous tissue specimen.

3. RESULTS AND DISCUSSION

A. Optical Parameter Recovery in Phantoms

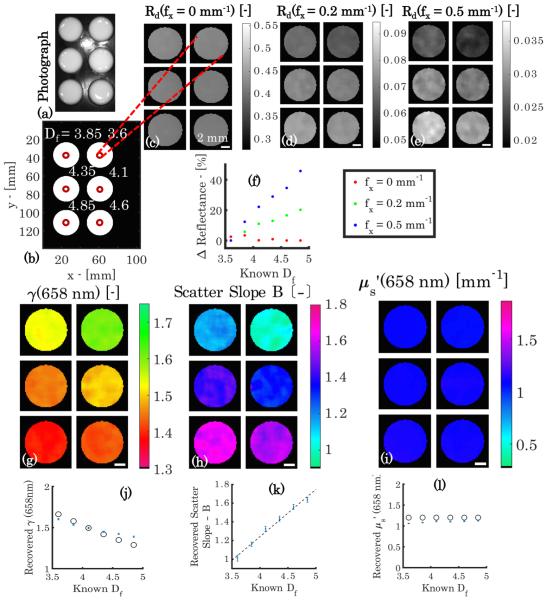
The data in Fig. 3 demonstrate contrast obtained with wide-field sd-SFDI from the scattering phase function. Here, each phantom contains a matched absorption and reduced scattering coefficient at λ = 658 nm, but a unique fractal distribution of scatterers, and therefore, a unique γ and scatter slope B. In Fig. 3(a), a photograph of the phantom set shows the individual phantoms to be indistinguishable under white light. Similarly, diffuse reflectance at f _x = 0 mm⁻¹, shown in Fig. 3(c), provides little contrast between the unique fractal distributions, which are annotated in panel Fig. 3(b). However, as the spatial frequency increases to f _x = 0.2 mm⁻¹ and 0.5 mm⁻¹ in Figs. 3(d) and 3(e), respectively, contrast appears in the calibrated reflectance, arising purely from sub-diffusive remissions, which are sensitive to the underlying particle size-scale distribution. This relationship between reflectance and fractal dimension of the distribution is shown to be linear in Fig. 3(f), with the magnitude of the proportionality increasing as the spatial frequency increases. At f _x = 0.5 mm⁻¹, a 40% change in reflectance occurs that is due to the relative differences in large-angle backscattering in each unique phase function. These changes in reflectance are quantified with the model inversion to yield optical property maps of γ, scatter slope B, and ${\mu }_s^{\prime }$ shown in Figs. 3(g)–3(i). The reduced scatter coefficient, describing isotropic diffusion, is constant throughout the phantoms, while both γ and the scatter slope show a strong dependence on the varied particle size distributions. Figures 3(j) and 3(l) show that the absolute values of the scattering parameters obtained with the model inversion, which are represented by the blue error bars, agree with those determined from the Mie theory, represented by the black circles. Interestingly, Figs. 3(j) and 3(k) also show a strong negative linear relationship between the fractal dimension versus γ, and a strong positive linear relationship between the fractal dimension versus scatter slope, respectively, as γ and scatter slope both describe the relative ratio of large to small scatterers.

Fig. 3.

Phantoms with ${\mu }_s^{\prime }$ held constant with γ variation. (a) Photograph, (b) annotated D_f , and (c)–(e) demodulated reflectance images at λ = 658 nm and f _x = [0; 0.2; 0.5] mm . (f ) Normalized plot of percentage change in reflectance versus D_f for each spatial frequency. Recovered maps of γ(658 nm), scatter slope B, and ${\mu }_s^{\prime }$(658 nm) are shown in (g), (h), and (i), respectively. Below are plots of recovered optical property values versus D_f in (j), (k), and (l), where the blue error bars represent recovered mean values ± one standard deviation, the black circles represent the Mie theory-predicted γ(658 nm) and ${\mu }_s^{\prime }$(658 nm) values, and the black dotted line represents a regression of scatter slope B versus D_f (r = 0.993). Scale bar is 2 mm.

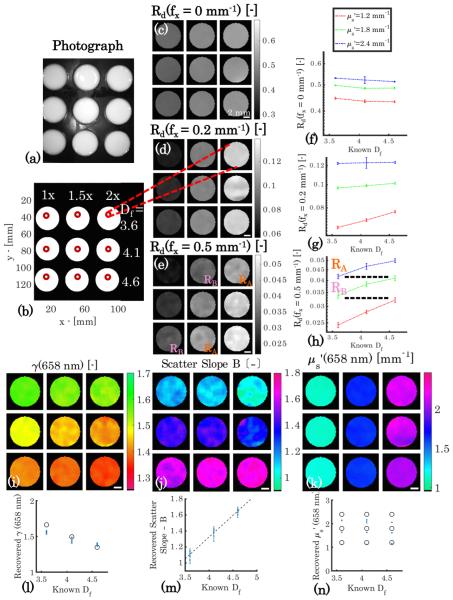
The data in Fig. 4 show that sd-SFDI is capable of distinguishing the relative density of scatterers from their size-scale distribution. The phantoms appear similar under white light illumination in Fig. 4(a) for the combinations of ${\mu }_s^{\prime }$ and D_f specified in Fig. 4(b). The diffuse reflectance images sampled at f _x = [0; 0.2; 0.5] mm⁻¹ shown in Figs. 4(c)–4(e) provide contrast along each column that arises from a 2-fold increase in particle concentration, and spatial frequency-dependent contrast in D_f is evident along each row. Reflectance maps of the phantoms are shown in panels (c)–(e), while the reflectance intensities quantified per fractal dimension are plotted in the accompanying panels, (f )–(h). Inspection of the reflectance data at f _x = 0.2 mm⁻¹ shows a contrast between the ${\mu }_s^{\prime }$ values in each column in the image in panel (d) and a ${\mu }_s^{\prime }$-dependent proportionality between the reflectance intensity and D_f in (g), with measurements of the lowest scattering coefficient resulting in the highest sensitivity to changes in the scattering phase function. The reflectance images at f _x = 0.5 mm⁻¹, shown in Figs. 4(e) and 4(h), again provide contrast between the columns, but now in the fully sub-diffusive regime, contrast occurs along every column that arises from the change in particle size-scale distribution, as shown in Fig. 4(h). Here, the reflectance intensity becomes non-unique for coupled variations of the concentration and distribution of particles sizes when sampled in the sub-diffusive regime. This phenomenon is highlighted by the orange and pink reflectance indicators R_A and R_B in Figs. 4(e) and 4(h), which show similar reflectance values for pairs of different combinations of ${\mu }_s^{\prime }$ and D_f . However, by applying the multi-spatial frequency inversion, differences in γ, the scatter slope, and ${\mu }_s^{\prime }$ are readily distinguished, as shown in Figs. 4(i)–4(k), respectively. The maps of both γ and the scatter slope show clear stratification along the rows related to the varied fractal dimension, while column-wise stratification with changing particle concentration appears in the map of ${\mu }_s^{\prime }$. As shown in Figs. 4(l) and 4(n), the absolute value of the parameters is in agreement with the Mie theory values, represented by blue error bars and black circles, respectively. A third tissue-simulating phantom experiment was performed with coupled variation in D_f and μ_a for constant ${\mu }_s^{\prime }$; imaging data are presented in Supplement 1 and show that both ${\mu }_s^{\prime }$ and γ are accurately recovered in the presence of a strong optical absorber.

Fig. 4.

Phantoms with coupled ${\mu }_s^{\prime }$ and γ variation. (a) Photograph, (b) annotation of ${\mu }_s^{\prime }$ and D_f values. Panels (c)–(e) show reflectance images at λ = 658 nm and f _x = [0; 0.2; 0.5] mm⁻¹ , while panels (f )–(h) show absolute values of reflectance versus D_f at each level of ${\mu }_s^{\prime }$ for each spatial frequency. The dashed lines in (h) correspond to areas within (e) and highlight the non-uniqueness of the reflectance intensity with respect to combinations of ${\mu }_s^{\prime }$ and γ. Panels (i),(j), and (k) show recovered γ(658 nm), scatter slope B, and ${\mu }_s^{\prime }$(658 nm) maps. Below are corresponding plots of recovered optical property values versus D_f in (l), (m), and (n), where the blue error bars represent recovered mean values ± one standard deviation, the black circles represent the Mie theory predicted γ(658 nm) and ${\mu }_s^{\prime }$(658 nm) values, and the black dotted line represents a regression of scatter slope B versus D_f (r = 0.983). Scale bar is 2 mm.

While Figs. 3 and 4 present recovered values for ${\mu }_s^{\prime }$ and γ at λ = 658 nm, optical scatter parameters were also recovered at λ = 730 and 850 nm. Mean absolute residuals, defined as $(100\%\frac{\mid \text{recovered}-\text{true}\mid }{\text{true}})$ where recovered is the experimental optical property value and true is the value obtained with the Mie theory, were calculated and averaged over all wavelengths. Similarly, Pearson product coefficients were calculated for the varied optical properties and averaged over all wavelengths. A summary of these parameters is included in Table 1, which shows all residuals <12%, with the exception of ${\mu }_s^{\prime }$ for the μ_a , γ variation experiment, and all correlation coefficients, r > 0.95. However, the authors would like to note that with the value of ${\mu }_s^{\prime }$ for the μ_a , γ variation experiment, the mean residual is heavily weighted by the 850 nm wavelength, where ${\mu }_s^{\prime }$ ≈ 0.5 mm⁻¹, but at 658 and 730 nm, the absolute residual ≈10%. It is important to note that the uncertainties in the recovered optical parameters reported in Figs. 3(j)–3(l) and Figs. 4(l)–4(n) represent a lower limit of scatter contrast that can accurately be resolved at an interface between scatterer (or tissue) types. Furthermore, analysis of the edge response function and line spread function for recovered maps of ${\mu }_s^{\prime }$ and γ in heterogeneous optical phantoms yielded estimates of spatial resolution and sensitivity. Details are provided in Supplement 1; in brief, ${\mu }_s^{\prime }$ and γ were accurately recovered with a resolution of ≈2 mm (i.e., 10 pixels) and ≈0.8 mm (i.e., 4 pixels), respectively.

Table 1.

Summary of Aggregate Residuals and Correlation Coefficients for Phantom Experiments

Phantom Set		❬residual❭ [%]	❬r❭[–]
${\mu }_s^{\prime }$ constant	${\mu }_s^{\prime }$	❬11.8 ± 9.2❭	n/a
γ variation	γ	❬3.9 ± 2.8❭	❬0.996 ± 0.003❭
${\mu }_s^{\prime }$ variation	${\mu }_s^{\prime }$	❬10.2 ± 7.8❭	❬0.997 ± 0.0003❭
γ variation	${\mu }_s^{\prime }$	❬4.5 ± 2.6❭	❬0.964 ± 0.01❭
μa variation	${\mu }_s^{\prime }$	❬23.8 ± 20.4❭	n/a
γ variation	γ	❬5.1 ±3.4❭	❬0.954 ± 0.052❭

B. Spatial Analysis of Breast Tissue Optical Properties

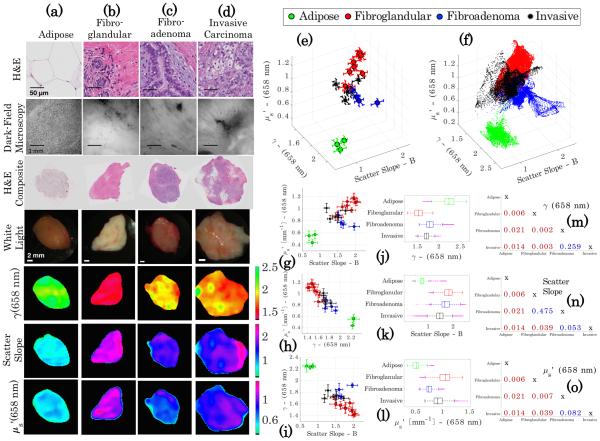
While phantom results demonstrate the technical accuracy of sd-SFDI and offer insights into the foundations of the optical signal, the composition of biological tissue has important differences from phantoms, especially at the microscopic level. Therefore, scatter parameter maps of freshly resected human breast tissue were co-registered to histopathologic diagnoses to demonstrate the potential of sub-diffusive scattering parameters to discriminate between microscopic morphologies of different tissue types. These data and comparisons are summarized in Fig. 5. Four ubiquitous breast tissue morphologies were considered: adipose, fibroglandular, benign fibroadenoma, and invasive carcinoma, corresponding to the columns in Fig. 5. Rows I and II contain “microscopic imaging” data and present representative high-magnification H&E and representative dark-field microscopy images from each tissue type. Rows III–VII include “macroscopic imaging” data and show co-registered H&E and white light images and optical parameter maps from a representative case for each tissue type.

Fig. 5.

Clustering of optical scatter parameters of homogeneous breast tissue of known diagnoses of (a) adipose, (b) fibroglandular, (c) benign fibroadenoma, and (d) invasive carcinoma. The first row of images shows high-magnification H&E stained histology slides of a representative area of each tissue type, and below is a corresponding representative dark-field microscopy image in the second row. In the third row, a scanned co-registered composite histology slide appears with a white-light photograph (below in the following row). The final three rows contain the three optical scatter parameter maps, γ [−], scatter slope B [−], and ${\mu }_s^{\prime }$[mm⁻¹]. Three-dimensional clustering plots are shown for the means ± one standard deviation and for all pixels for each specimen in (e) and (f ). (g)–(i) Show two-dimensional clustering of the specimen means ± one standard deviation for each pair of optical scatter parameters. (j)–(l) Show box and whisker plots for all points used in the cluster analysis for each scatter parameter. (m)–(o) Show two-sample Kolmogorov–Smirnov p-values for each pairwise combination of tissue diagnoses with each scatter parameter as the tested distribution.

An inspection of the microscopic imaging data reveals differences in microscopic morphology between tissue types. Figure 5, row I presents high-magnification histology sections for each tissue, revealing the relative proportions of fibrous stroma (appearing pink), nuclei density (appearing purple), and fat (appearing white due to clearing during processing). The adipose tissue in Fig. 5(a) is almost completely comprised of adipocytes with large lipid vacuoles on the size scale >25 μm, creating a tissue that is markedly forward scattering. The fibroglandular tissue in Fig. 5(b) appears to be largely comprised of stromal collagen, as shown by the overwhelming pink color in the H&E composite, with some fat and also functional, organized, yet sparse cellularity appearing in the high-magnification H&E. Although collagen fibers are relatively weak scatterers with a diameter of only a few micrometers, collagen fibrils are (≈20 nm–70 nm) in diameter with striations (< 100 nm) and act as Rayleigh scatters [34]. A fibroadenoma, shown in Fig. 5(c), is characterized by the benign proliferation of stromal collagen around the functional epithelium, which in turn compresses and expands the cellular epithelium. The invasive carcinoma, shown in Fig. 5(d), is characterized by uncontrolled growth of the epithelium, with very high nuclear density and an increase in the nuclear-to-cytoplasmic ratio and mitochondrial density. The size scale of both nuclei (≈5 μm) and mitochrondia (≈1 μm) characterizes them as weak, large scatterers.

Figure 5, row II contains dark-field microscopy reflectance images from fresh tissue samples, which show back-scattered light intensity from structural features. The dark-field images in row II were acquired on a slightly larger length scale from the high-magnification H&E images in row I. Dark-field images provide a unique scatter-based contrast from thick tissue samples and show clear differences in the microarchitecture of adipose with the more densely packed tissues. The effects of multiple scattering confound the resolution of many of the ultrastructural features in the fresh, thick tissue sample that is provided by the H&E analysis.

The panels in Fig. 5, row III show scanned composite sections of the histology that provide a description of the relative distribution of structural features on the millimeter-centimeter length scale. Figure 5, row IV contains white-light photographs of each tissue type, with adipose tissue exhibiting a markedly yellow color, while the other more fibrous tissues appear as various shades of white and red. Figure 5, rows V–VII present γ(658 nm), scatter slope B, and ${\mu }_s^{\prime }$(658 nm) for each tissue type, respectively. A quick inspection of these images shows differences between the tissue samples. The adipose tissue has a pronounced high γ and low ${\mu }_s^{\prime }$, which is consistent with large cells and lipid vacuoles that dominate light transport as large (forward) scatterers. Conversely, fibroglandular tissue presents a low γ and a high ${\mu }_s^{\prime }$, which is associated with a denser tissue composed of fibrils and striations with rapid and dense fluctuations in the refractive index that contribute meaningfully to Rayleigh-like scattering. A comparative inspection of the parameter maps of the fibroadenoma and invasive carcinoma with fibroglandular tissue show a reduced γ and an increased scatter slope, suggestive of a relative increase in larger scatterers. Additionally, both the glandular tissue and invasive carcinoma show an increased ${\mu }_s^{\prime }$ compared with fibroadenoma, which is descriptive of the density of scattering structures within each tissue type.

Figure 5(e) presents a cluster plot with the three axes specified as γ(658 nm), scatter slope B, and ${\mu }_s^{\prime }$(658 nm), for the means of each specimen with three-dimensional error bars representing one standard deviation, while Fig. 5(f) displays all pixels over all the specimens. Four distinct clusters appear, despite noticeable overlap in the cluster visualization. In Figs. 5(g)–5(i), scatter plots of specimen-based means with two-dimensional error bars are shown for each pair of scattering parameters. To quantitatively assess separation between tissue diagnoses, box and whisker plots are reported in Figs. 5(j)–5(l) for each optical scatter parameter. For the adipose tissue, the inter-quartile range (IQR) is fully separated from all tissue types for all three parameters. For γ(658 nm) in Fig. 5(j), the IQRs of the fibroglandular and invasive carcinoma are completely separated by their unique structure size-scale distributions; however, for the invasive carcinoma and fibroadenoma, significant overlap occurs. In Fig. 5(k), the IQRs for the scatter slope of the invasive carcinoma, fibroadenoma, and fibroglandular overlap, but for ${\mu }_s^{\prime }$ in Fig. 5(l), the fibroadenoma has noticeable separation from the invasive carcinoma and fibroglandular, which overlap due to their similar high densities. For further quantification, two-sample Kolmogorov– Smirnov non-parametric distribution tests were performed on the means of the specimens between each tissue type. P-values are tabulated in Figs. 5(m)–5(o) for all three scatter parameters, with a red color indicating a significant p-value at the α < 0.05 level. Differences in the distributions of γ(658 nm) were statistically significant for all tissue type pairings, except for invasive carcinoma compared with fibroadenoma, which did not yield a significant difference in distributions for all scattering parameters; however, the results may be due in part to the small sample size in this initial study.

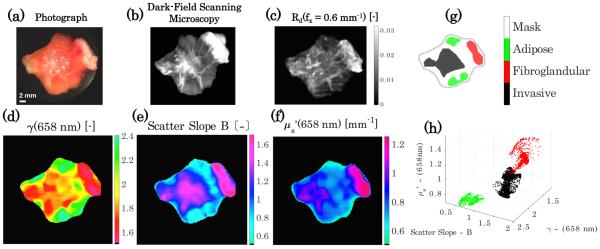
The data presented in Fig. 5 represent individual samples of selected tissue types. A more clinically relevant situation is the measurement of tissue samples that contain multiple tissue types. Figure 6(a) shows a photograph of freshly excised cancerous breast tissue, with surrounding fat and normal fibrous tissue. In Figs. 6(b) and 6(c), scanning dark-field microscopy and a calibrated reflectance image at f _x = 0.6 mm⁻¹ with no median filtering are shown, respectively. The improved spatial resolution of scatter-based features offered by the dark-field microscopy compared with the sub-diffusive reflectance has a trade-off with increased the acquisition time; it is important to note that improved sd-SFDI resolution could be achieved with optimized projection and imaging magnification and CCD sensitivity. Figures 6(d)–6(f) shows maps of the optical scatter parameters γ(658 nm), scatter slope B, and ${\mu }_s^{\prime }$(658 nm), respectively. Histology-guided regions of interest appear in Fig. 6(g), where spatial variations in tissue type exist, which stratify into the three distinct clusters shown in Fig. 6(h). These data demonstrate the ability to rapidly assess whole-tissue specimens through sub-diffusive imaging, where point-source or microscopic-based tissue interrogation methods would have to randomly sample a large number of locations to achieve similar robustness. Moreover, these data motivate a sampling strategy that uses multiple length-scale imaging for evaluation of malignancy within clinical tissue samples; such an approach would use sub-diffuse imaging to return a wide-field map of micro-structural parameters that may identify regions of interest, either for more detailed interrogation via microscopic imaging, or for guided selection of biopsy locations to obtain a definitive histological confirmation.

Fig. 6.

Spatial contexualization of scattering parameters for heterogeneous breast tissue. (a) Photograph of tissue, (b) dark field scanning microscopy, and (c) sub-diffusive calibrated reflectance image with f _x = 0.6 mm⁻¹ with no median filtering. (d)–(f ) Show scatter optical property maps of γ [−], scatter slope B [−], and ${\mu }_s^{\prime }$[mm⁻¹], respectively. (g) Regions of interest corresponding to areas of localized tissue diagnoses and (h) clustering of the scatter properties for each tissue diagnosis.

One promising clinical application for sd-SFDI is intraoperative tumor margin assessment for breast-conserving surgery, with sensitivity to the tissue composition at sub-millimeter levels that can be rapidly mapped over large fields of view. This wide-field imaging may be complementary to highly sensitive point-evaluation approaches (e.g., using Raman [35] or optical-coherence tomography [36]) by guiding the sampling locations within the surgical field. The envisioned embodiment of this approach may be as a back-bench setup to image excised tissue samples during surgery. Alternatively, an embodiment to image a surgical resection bed in vivo would be enabled by approaches to correct for height variations and boundary artifacts in the imaged field; profile-based corrections for height variations have been proposed for diffuse-SFDI [37] but have not yet been developed for the sub-diffusive regime and are an area of ongoing investigation.

4. CONCLUSIONS

This study presents the use of sub-diffuse spatial frequency domain imaging to differentiate between tissue types based on microscopic-level morphological differences. The approach samples tissue rapidly, on the scale of minutes, and acquires large fields of view, on the scale of square centimeters. The measurements in optical phantoms show, for the first time, validation of the ability to detect and quantitate phase-function-based contrast from a wide-field imaging technique, with accurate decoupling of parameters that define both the density and the size-scale distribution of scatterers. Data from a small clinical pilot study indicate that the complete set of sub-diffuse optical scattering parameter maps appears to distinguish between various breast tissue morphologies in both homogeneous and heterogeneous freshly resected human breast tissue samples. This study imaged extracted clinical tissue samples through a glass plate to mitigate height variations in the imaged field; future work will need to consider the appropriateness of profile-correction algorithms in the sub-diffusive regime to image tissues in vivo in a non-contact manner. The data presented in this paper show that sd-SFDI provides wide-field maps of scattering parameters that are usually reserved for microscopic evaluations.