Abstract
Purpose
A new acquisition and reconstruction method called T2 Shuffling is presented for volumetric fast spin-echo (3D FSE) imaging. T2 Shuffling reduces blurring and recovers many images at multiple T2 contrasts from a single acquisition at clinically feasible scan times (6 to 7 minutes).
Theory and Methods
The parallel imaging forward model is modified to account for temporal signal relaxation during the echo train. Scan efficiency is improved by acquiring data during the transient signal decay and by increasing echo train lengths without loss in SNR. By (1) randomly shuffling the phase encode view ordering, (2) constraining the temporal signal evolution to a low-dimensional subspace, and (3) promoting spatio-temporal correlations through locally low rank regularization, a time series of virtual echo time images is recovered from a single scan. A convex formulation is presented that is robust to partial voluming and RF field inhomogeneity.
Results
Retrospective under-sampling and in vivo scans confirm the increase in sharpness afforded by T2 Shuffling. Multiple image contrasts are recovered and used to highlight pathology in pediatric patients. A proof-of-principle method is integrated into a clinical musculoskeletal imaging workflow.
Conclusion
The proposed T2 Shuffling method improves the diagnostic utility of 3D FSE by reducing blurring and producing multiple image contrasts from a single scan.
Keywords: Fast spin-echo (FSE), T2 imaging, compressed sensing, multi-contrast
Introduction
Fast spin-echo (FSE) sequences are commonly used for MR imaging because of the ability to prescribe various image contrasts at target scan times in a flexible manner (1). Most clinical musculoskeletal protocols separately acquire 2D FSE images at multiple orthogonal planes, and repeat the set of scans for different image contrasts. Altogether, the full exam time is lengthy and the 2D images suffer from relatively thick slices with large gaps, which can obscure pathology (2–4). Volumetric (3D) FSE is an attractive alternative to 2D FSE because it provides isotropic resolution and the images can be reformatted in arbitrary orientations to evaluate pathology (1). However, long echo trains are required to maintain scan efficiency, leading to blurring due to T2 decay (3, 5, 6). Parallel imaging in tandem with variable flip angle modulation (e.g. CUBE, SPACE, VISTA) can reduce this effect by shortening echo trains and reducing the signal decay during the echo train, but blurring often persists, limiting diagnostic utility. Recent applications of compressed sensing to 3D FSE (4, 7, 8) have also shown promise in alleviating the tradeoff between scan time and blurring.
Cartesian 3D FSE scans acquire multiple k-space samples, i.e. an echo train, in each radiofrequency (RF) excitation. The speed of the acquisition depends primarily on the pulse repetition time (TR), the echo train length (ETL), and the spatial acceleration factor. Conventional reconstruction neglects the echo train time progression between acquired phase encodes and produces a single image. Since the signal decays during the echo train, blurring artifacts corrupt the final image, leading to loss in apparent resolution.
Several approaches to deblurring first estimate T2 and next deconvolve the echo train signal evolution based on this estimate (9–11). These methods are sensitive to errors in the T2 estimate, and can amplify noise in the deconvolution (high pass filtering) step. Other approaches exploit the Hermitian symmetry property of k-space to reduce the effect of T2 decay (12, 13), but are sensitive to phase errors that invalidate the Hermitian symmetry. The above methods do not fundamentally change the signal decay behavior, and instead aim to correct it with post-processing.
Many approaches aim to directly recover tissue parameters from under-sampled data through a model-based, non-linear optimization (14–17). These approaches often use radial sampling to leverage incoherence in the acquired signal and improve the conditioning of the reconstruction. Nonetheless, the reconstructions must cope with added complexity in the non-linear forward model and are sensitive to model mismatch, e.g. due to partial voluming. Other works first impose subspace constraints through principal component analysis (PCA) (18–22) and dictionary learning (23, 24) to linearize the parametric forward model and enforce spatial sparsity on the basis images. The linearization is attractive because it lends itself to a convex formulation and PCA can be applied to training signals that account for stimulated echoes and imperfect slice profiles. Data-driven variants (25, 26) can also be used to build robustness to motion (27) and other non-ideal imaging considerations. The linear subspace constraint is robust to partial voluming and implicitly accounts for multi-compartmental models, as linear combinations of signal evolutions remain in the subspace. However, the approximation error from PCA and other basis expansions may lead to biased parameter estimates and the parametric fitting step must still explicitly account for imaging non-idealities such as partial voluming and RF-field inhomogeneity. Parametric estimation is further complicated by the subtle dependence of tissue relaxation on pulse sequence design (28). Recently, pattern matching methods (29, 30) have shown promise at deriving tissue and system parameters. These methods employ pixel-wise matching of unknown signal evolutions to a database of simulated signals. However, they often neglect data fidelity in the reconstruction formulation. The addition of a data fidelity term (31) remains a topic of ongoing exploration.
In this work we present a subspace-constrained method called T2 Shuffling, first described in (32), that simultaneously recovers many images at multiple contrasts with increased sharpness from a single acquisition that is no longer than a conventional 3D scan. T2 Shuffling reduces the blurring due to long echo trains as well as the need to perform separate scans at target echo times (TEs) for each image contrast. The acquisition accounts for the echo train time progression, and the reconstruction combines recent advances in parallel imaging and compressed sensing in a software framework designed for a clinical workflow. Specifically, we build off of previous subspace (18–21) and low rank (33–36) modeling methods to reduce the degrees of freedom in the reconstruction. In contrast to the subspace-based parametric methods, we do not explicitly estimate parameter maps, and instead use the linear subspace constraint as a flexible approach to deblurring and recovering tissue dynamics. The method thus maintains the implicit robustness to imaging non-idealities present in other subspace-constrained approaches. Also, rather than regularizing in the parametric dimension, low-rank constraints are imposed directly on the subspace.
By accounting for signal decay, we are also able to improve scan efficiency and acquire more data in each TR. The wait time between the end of the echo train and the start of the next TR has been previously used to jointly produce a proton-density and a T2-weighted image from a single 3D FSE scan (37); here we take this observation one step further and recover an image at each TE along the signal evolution curve. The authors in (38) and (39) have demonstrated a similar principle through the use of a radial acquisition with a view-sharing reconstruction for T1-weighted imaging. Here we demonstrate the feasibility of T2 Shuffling with simulation and in vivo exams, and describe its use in a clinical environment.
Theory
A model-based description for FSE acquisition is that the observed signal is a linear mixture of a proton-density image and a temporal signal evolution function:
| (1) |
Here, y(t) is the acquired signal at time t, ρ(r) is the complex proton-density image at voxel r, and k(t) is the k-space trajectory. This model is easily extended to multiple receive coils in a straightforward manner. The temporal signal evolution function ft(·) depends on several factors, including tissue relaxation and the refocusing flip angle schedule. For a constant 180 degree flip angle train, a simple and common model used for FSE imaging is the mono-exponential decay. In this model, each voxel position r decays with T2(r) during the echo train and recovers with T1(r) after the echo train over a repetition time TR according to
| (2) |
where T is the ETL and Ts is the echo spacing. In practice, each voxel will contain a distribution of relaxation values. In conventional FSE image reconstruction, the time progression is ignored and an inverse Fourier transform is applied to Eq. (1), implicitly assuming that ft(·) does not change over time. For example, it is often assumed that ft(r) ≈ fTE(r) for all t, where TE is the (fixed) echo time when the center of k-space is acquired (1). To appreciate the impact of this approximation, we can express ft(·) in terms of k-space position using the relationship , where G is the gradient amplitude vector. For the special case of mono-exponential decay and neglecting the positional dependence of relaxation, we have
| (3) |
Because the k-space weighting in Eq. (3) is convolved in image space with the proton-density image, the approximation impacts the apparent tissue contrast and leads to blurring due to T2 decay during the acquisition (5, 6). Since relaxation depends on position, each voxel will undergo a different degree of blurring (11).
In this work we account for the temporal aspect of the acquisition and maintain the Fourier relationship through a lifting procedure (40). We do not assume a mono-exponential decay, and instead allow arbitrary signal evolutions formed by a distribution of T2 values. Consider a FSE experiment in which T echoes are acquired each TR with echo spacing Ts. Let
| (4) |
be the magnetization at the ith echo time and the rth voxel, and define the signal evolution at voxel r as
| (5) |
We call xi the virtual echo time image at the ith virtual echo time and x the time series of images. We extend the forward model to the time series of images:
| (6) |
| (7) |
The encoding matrix E operates on each virtual echo time image independently. Each image xi is point-wise multiplied by the coil sensitivity maps (S) and Fourier transformed (F). The data are then masked (P) according to the acquired phase encodes at each virtual TE and represented in k-t space by y. Figure 1 depicts the forward model for the time-series of images. Figure 1b shows the sampling operator corresponding to a center-out phase encode ordering, which is commonly used for proton-density FSE (6). In conventional 3D FSE, the acquired data are collapsed into a single k-space matrix, which in our case is equivalent to summing along the time dimension. By representing the data in the lifted k-t space, the model supports arbitrary sampling and is not restricted to a center-out view ordering. Figure 1c shows a randomly shuffled sampling procedure that leads to a better posed inverse problem (41), as discussed in the sequel.
Figure 1.
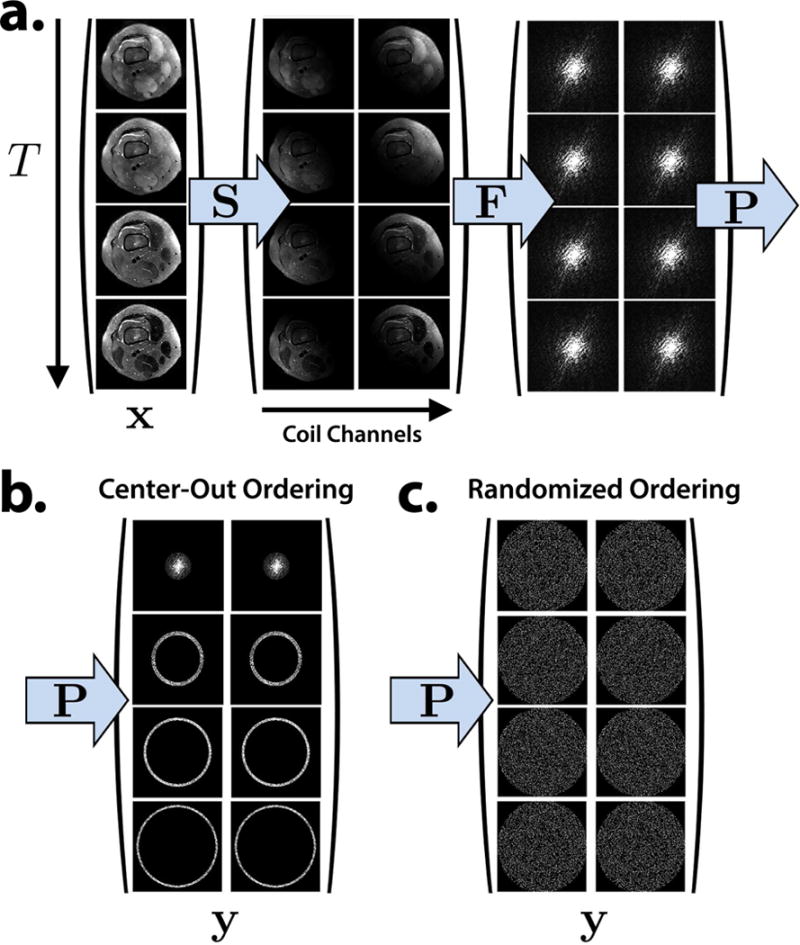
The forward model is extended to a time series of images at T virtual echo times. a. Each virtual echo time image is point-wise multiplied by the sensitivity maps, Fourier transformed, and sampled. b. A center-out view ordering used in conventional proton-density 3D FSE imaging. c. A randomly shuffled view ordering suitable for T2 Shuffling.
Since the ambient dimension of the unknown images is LT, where L is the number of voxels, a naive well-posed reconstruction in the lifted space requires T times the number of observations compared to a standard 3D FSE reconstruction. To overcome this limitation, structure in the data is exploited to reduce dimensionality. This is achieved in two ways: first, the temporal signal evolution is modeled and represented by a low-dimensional subspace; second, the sampling problem is formulated based on ideas from compressed sensing (42). These two approaches significantly reduce the dimensionality to a regime where the equivalent of a single 3D FSE acquisition can be used to reconstruct the full time series of images.
Temporal Subspace
The signal evolutions observed in a FSE experiment are functions of both the tissue parameters (T1, T2) and the flip angles in the echo train. Other factors such as B1 inhomogeneity will also influence the signal evolution (30). Using these parameters, signal evolutions can be generated with Bloch simulation and the Extended Phase Graph (EPG) algorithm (5, 30). In the case of a constant flip angle schedule, there also exist analytical solutions (16, 43). Figure 2 shows example signal evolutions using the variable flip angle modulation scheme described in (6). The signal evolutions corresponding to different tissues follow similar trends despite differing in relaxation parameters. It is this correlation that makes parameter mapping a difficult problem. However, the correlation implies that the signal evolutions of different tissues form a low-dimensional subspace.
Figure 2.
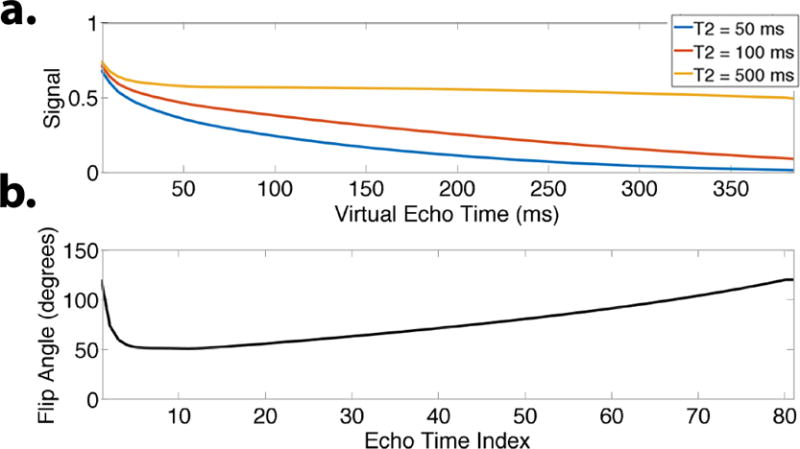
a. Simulated signal evolutions during an echo train using variable refocusing flip angles shown in (b) (T1 = 1000 ms). For T2 = 500 ms, the signal is nearly constant after the initial 20 ms, and will lead to minimal blurring in the image. For T2 = 100 ms and below, the signal decays throughout the echo train. Despite the different temporal profiles, the signal curves are highly correlated.
Consider an ensemble of N spins sampled at T echo times, . Each column in X represents the signal evolution of a spin with a particular (T1, T2) pair. Let be an orthonormal temporal basis, i.e.
| (8) |
We wish to design and a K–dimensional subspace, ΦK = span{φ1,…,φK}, such that
| (9) |
where ε is a modeling error tolerance. The choice of norm in Eq. (9) will affect the chosen subspace. If the Frobenius norm is used, then this metric captures the sum-of-squares error in the fit. If a max-column norm is used, then the tolerance can be interpreted as the worst-case error on any signal evolution. By choosing the ensemble X to match the distribution of (T1, T2) values in the tissue of interest, a suitable subspace that minimizes the Frobenius norm can be generated using PCA (19, 20, 44).
In conventional 3D FSE, variable refocusing flip angles are used to reduce the rate of decay for a particular range of T2 values (1, 5, 6). This leads to less intrinsic blurring in the final image. The choice of refocusing flip angles for the echo trains has a significant impact on the signal evolution, and thus the temporal subspace design. Since the model in Eq. (7) accounts for the temporal signal, it may no longer be necessary to design the flip angle train to reduce signal decay. Instead, other metrics such as SNR and CNR could be used as flip angle design criteria. Nonetheless, in this work we use the flip angle modulation scheme described in (6).
Using the subspace ΦK, we have
| (10) |
| (11) |
| (12) |
| (13) |
where are the K temporal basis coefficients that describe the time series of images. Neglecting model error, we also have
| (14) |
The reconstruction problem can now be posed in terms of α:
| (15) |
After solving for α, the unique time series is computed by projecting through the basis using Eq. (14). The subspace constraint significantly reduces the dimensionality of the unknown variable in the optimization problem. Rather than resolving each image voxel at T ≈ 80 time points, it is sufficient to represent each voxel with K ≈ 4 coefficients (19, 21).
A locally low rank (LLR) regularization functional is used to further reduce sample complexity (33–36, 45). LLR regularization is implemented in a manner similar to the approach described in (33). The operator Rr extracts a block from each temporal coefficient image centered around voxel r and reshapes each block into a column of a matrix.1 The nuclear norm is applied to each matrix with regularization parameter λ and the result is summed. LLR regularization exploits spatial correlations in the temporal image coefficients, providing substantial dimensionality reduction beyond the capabilities of joint wavelet regularization or finite differences (21, 32, 44, 46). In effect, LLR constrains local image patches into a smaller space within the subspace ΦK, which compresses the representation to fewer than K coefficients per voxel.
As discussed in the Appendix, a consequence of the subspace constraint Eq. (14) for a fully sampled, linear reconstruction is that the noise in the system does not depend on the ETL, even if the signal evolutions fully decay. This is because noise outside the subspace is removed through the projection operation, i.e. the final noise standard deviation is , where σ is the noise standard deviation of a conventional 3D FSE acquisition that neglects the time progression (47). Thus a linear reconstruction leads to a fixed reduction in SNR, as indicated by Eq. (32). Although we do not analyze the case for under-sampled acquisitions, we use the result as a heuristic motivation for increasing the ETL to collect more data without incurring any additional blurring in the resulting reconstruction. In addition, the use of LLR regularization in the reconstruction formulation Eq. (15) provides additional denoising.
Echo Train Ordering
In conventional proton-density 3D FSE acquisition, phase encodes along an echo train are ordered according to radial distance so that the k-space center is sampled first and the periphery is sampled last during each echo train. By using a center-out ordering, the k-space center is acquired early during the signal evolution, providing high SNR and producing apparent proton-density contrast. Figure 3a depicts the echo train ordering for center-out sampling. Because the signal decays during the echo train, k-space is apodized. The effect is equivalent to space-variant low-pass filtering in image space and leads to a blurring point spread function (PSF). Refocusing flip angle modulation reduces this blurring for tissues with a particular range of T2 values, but it does not fully compensate for this effect. Furthermore, tissues with short T2 remain affected and are blurred out.
Figure 3.
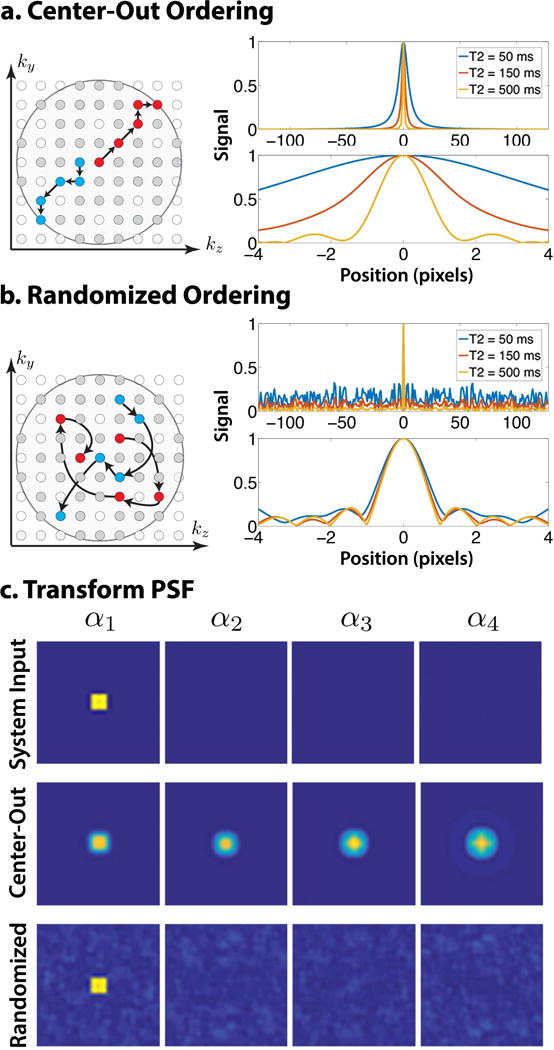
Comparison of center-out and randomly shuffled view ordering schemes (shown for exponential decay to emphasize effect). a. The echo trains in a center-out ordering start at central k-space and move outward in a radial fashion. The resulting normalized PSF for species with high T2 is sharp. For low T2, the normalized PSF has non-negligible width, indicating intrinsic image blur. b. The echo trains for a randomly shuffled ordering traverse k-space in a random fashion, and phase encodes may be repeatedly re-sampled. The PSF has a distinct sharp peak, indicating reduced blur, and incoherent artifacts. The peak remains sharp for low T2 values at the cost of larger incoherent artifacts. c. The system input and TPSF due to the first temporal coefficient (other coefficients show similar behavior). Center-out ordering (middle) blurs and spreads interference coherently, while randomized ordering (bottom) spreads interference incoherently.
Since the inverse problem defined in Eq. (15) uses ideas from compressed sensing to reduce sample complexity through the use of LLR regularization, the data space should be sampled incoherently with respect to the unknown (42). The forward model Eq. (7) represents the data in k-t space. In this view, a center-out ordering acquires low-frequency k-space samples at early echo times and high-frequency k-space samples at later echo times, which is not incoherent with respect to the temporal coefficients. An incoherent sampling approach that fits the signal distribution relies on randomized sampling in k-space and in time (41, 48). Figure 3b depicts an alternative view ordering scheme, in which echo trains are formed by randomly selecting phase encodes throughout k-space. This randomly shuffled ordering induces a PSF with a sharp peak, indicating reduced blur, and spreads artifacts incoherently. However, the peak-to-sidelobe ratio decreases as T2 decreases, highlighting the difficulty of recovering images with short T2.
The effect of randomly shuffled echo trains can also be observed in the subspace domain. Figure 3c shows a system input containing a uniform patch in the first temporal coefficient and the resulting transform PSF (TPSF). A uniform patch is used as it represents a single coefficient (point) in the LLR domain. The center-out ordering (top) leads to blurring and coherent interference. The coherent interference couples the coefficients, which demonstrates the deconvolution is ill-posed. The randomized ordering (bottom) spreads interference incoherently through space and time, and does not couple the coefficients. The LLR soft threshold operation on the randomized TPSF will reduce the incoherent artifacts. The computation of the TPSF is shown in the supporting information and described by Supporting Figures S-4 — S-7.
Methods
Subspace Selection
The subspace selection affects both the compression power and the modeling error. In this work we pre-computed the subspace by simulating an ensemble of signal evolutions that match the distribution of T2 values in the anatomy of interest. For each imaging protocol (e.g. knee, foot), we computed a single subspace offline once and stored it for future exams. Figure 4a shows a T2 map of a human foot and the corresponding histogram of T2 values. We sampled 256 T2 values from this distribution and EPG-simulated with a variable refocusing flip angle train to produce the ensemble of signal evolutions shown in Figure 4b. Because of the weak dependence of T1 on the signal evolution (5, 6), EPG simulations were repeated with T1 values of 500, 700, 1000, and 1800 ms., for a total of N = 1024 signal evolutions. The temporal subspace was generated by taking the first K = 4 principal components of the ensemble of signal evolutions through PCA. Four principal components are sufficient to represent each signal evolution with greater than 99% accuracy.
Figure 4.
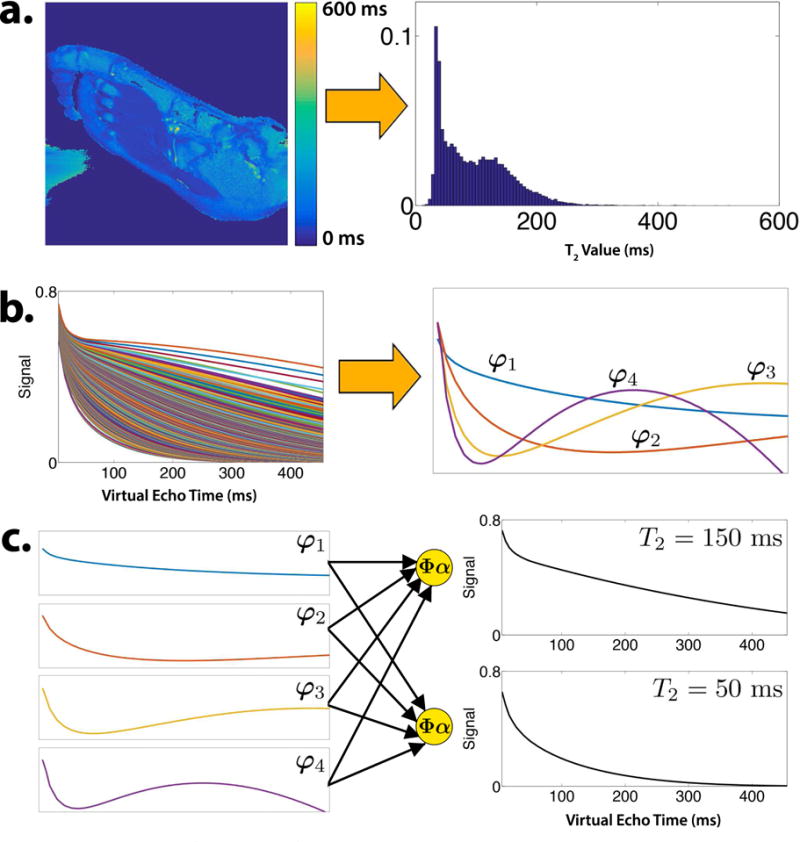
a. T2 map and histogram of the foot derived from a 2D multi-echo scan. b. Ensemble of EPG-simulated signal evolutions using values from the T2 histogram and the first four principal components that comprise the temporal subspace. c. Temporal subspace curves are linearly combined to form signal evolutions.
Figure 4c shows the subspace curves for K = 4 and an ETL of 78, and their use in forming signal evolutions corresponding to different tissue relaxation through Eq. (14). Since the subspace flexibly represents arbitrary signal evolutions, it need not precisely represent all relaxation values. In particular, if a voxel contains multiple tissue species, and each respective tissue’s signal evolution lives in the subspace ΦK, then the sum of the signal evolutions will also live in the subspace (19). For the FSE signal model, the subspace property also allows for mismatches between the simulated and actual refocusing flip angle trains, e.g. due to B1 inhomogeneity. Figure 5a shows a simulation of the impact of B1 inhomogeneity on the subspace model error. To simulate B1 homogeneity, EPG simulations were repeated by scaling the RF excitation and refocusing flip angles by up to 40% and the normalized model error was computed according to
| (16) |
where is the signal evolution generated with B1 inhomogeneity and ΦK was generated from the purely homogeneous B1 field. As expected, the model error is lowest at 100% scaling, with a maximal error of 0.5%. The worst-case model error increases to 3% at high B1 inhomogeneity, and remains at a tolerable level for most signal evolutions.
Figure 5.

a. Normalized subspace model error (K = 4 coefficients) in the presence of B1 inhomogeneity for a range of EPG-simulated signal evolutions. B1 inhomogeneity was simulated by scaling the RF excitation and refocusing flip angles during the echo train by a fixed percentage. The subspace was generated from a 100% homogeneous B1 field. b. Normalized subspace model error (top, Eq. (16)) and overall RMSE (bottom, vs. subspace size for short-T2 and long-T2 signal evolutions with T1 = 1000 ms. The dashed black line shows the RMSE due to noise for σ = 0.07. With K = 4 coefficients, a low model error is uniformly achieved with a reasonable noise penalty.
The subspace size presents a tradeoff between bias and noise. As K increases, the model error decreases and the noise amplification increases. Figure 5b shows the tradeoff for short-T2 and long-T2 signal evolutions with T1 = 1000 ms. The top plot shows normalized model error given by Eq. (16), and is less than 0.5% across all simulated signal evolutions for K = 4. The bottom plot shows the overall root mean-squared error (RMSE) derived from Eq. (31). The RMSE was calculated with σ = 0.7, which corresponds to an SNR of about 15 dB for T2 = 14 ms.
Data Acquisition
The CUBE 3D FSE pulse sequence (GE Healthcare, Waukesha, Wisconsin, USA) was previously modified to support Poisson disc sampling (4). We have extended the sequence to re-sample and store phase encodes at multiple echo times, enabling the prescription of arbitrary sampling patterns and echo trains. In a conventional 3D FSE scan, the operator first prescribes imaging parameters such as resolution, TR, and TE to meet a target image contrast, and next chooses a suitable spatial acceleration factor and ETL to meet a target scan time. Because T2 Shuffling resolves the full tissue dynamics at any virtual echo time during the echo train, it is no longer necessary to set a target TE. Instead, the operator chooses a target resolution, TR, and scan time. The TR and scan time provide an upper limit on Ntrains, the number of echo trains, independent of ETL:
| (17) |
The ETL is now a free parameter, and can be experimentally chosen for each protocol to account for SNR, T1 recovery, and specific absorption rate (SAR) limits.
Conventional spatial acceleration factor is no longer a scan parameter. Instead, we define the relative acceleration as the number of phase encode measurements acquired with respect to a fully sampled circular k-space coverage. Although this definition does not account for the ETL, it serves as a metric for the effective amount of data collected. In addition, since K temporal coefficient images are reconstructed with T2 Shuffling, we also define the apparent acceleration as K times the relative acceleration. The apparent acceleration represents the amount of data collected with respect to the number of degrees of freedom in the forward model.
One approach to incoherent sampling is to generate a unique variable-density Poisson disc mask with Ntrains samples for each echo time. An echo train is then formed by choosing one sample from each mask. However, since the ETL is on the order of 80, it is not practical to generate a new mask for each echo time. Additionally, naively chaining together samples from each mask could result in large gradient switching during the echo train and lead to eddy current artifacts. To overcome this limitation, we present an alternative sampling approach in the supporting information that reduces both the number of sampling patterns generated as well as the distance between points in the echo train.
Due to the variable refocusing flip angle scheme, the signal evolutions start in a transient decay before reaching pseudo steady state (6, 11). Thus traditional center-out 3D FSE may discard up to 15 initial echoes in each echo train. Since T2 Shuffling models the signal decay, data are acquired during the transient state, increasing scan efficiency. The first two echoes in the echo train are used to fully cover the center of k-space. This provides a time-consistent calibration region for estimating ESPIRiT coil sensitivity maps. All remaining echoes are used for reconstruction.
2D Retrospective Under-sampling and Anatomical Simulation
To test the forward model in Eq. (7) and the proposed sampling procedure, a fully sampled 2D multi-echo sequence was used to scan a sagittal slice of a volunteer’s foot at equispaced echo times at 3T (TR/TE = 3060/10 ms, 32 echoes, 32 coils, 180 degree refocusing flip angles) under an approved IRB study. To reduce computation time, the data were coil-compressed to 8 virtual channels (49) and used to estimate ESPIRiT coil sensitivity maps. We discarded the first echo time from the data and generated a T2 map by performing a pixel-wise mono-exponential fit (Figure 4a). From the T2 map, synthetic multi-echo data sets were generated through EPG simulation with variable refocusing flip angles and a fixed value of T1 = 1000 ms. The synthetic data were then multiplied by the ESPIRiT maps and Fourier transformed to produce k-t space. Figure 6a shows the first TE of the fully sampled, simulated data with an ETL of T = 80.
Figure 6.

Proton-density reconstructions on retrospectively undersampled data from (a) variable flip angle modulation simulation, and (b) actual acquisition data. From left to right: first TE of the fully sampled slice; L1-ESPIRiT reconstruction using a center-out echo train ordering; L1-ESPIRiT reconstruction using a randomly shuffled echo train ordering; First virtual TE of T2 Shuffling reconstruction with center-out echo train ordering; First virtual TE of T2 Shuffling reconstruction with randomly shuffled echo train ordering. c. Comparison of the 100 ms TEeff image for the fully sampled slices and the T2 Shuffling reconstructions (with randomly shuffled ordering) for both the simulation and the acquisition data. d. Representative signal evolution curves from the fully sampled slices and the reconstructions in (c).
To simulate the effects of a 3D FSE acquisition on a single slice in the readout direction, the coil-compressed, multi-echo data were retrospectively under-sampled using a center-out view ordering (Figure 2a). The data were also retrospectively under-sampled using the randomly shuffled view ordering scheme (Figure 2b). The two under-sampled data sets were each reconstructed with T2 Shuffling to produce a time series of images. The data were also summed along the time dimension to simulate 3D FSE with a spatial acceleration factor of 2 (40 in k-t space). These were then reconstructed using L1-ESPIRiT, a compressed sensing and parallel imaging method that does not compensate for signal decay (50). The retrospective experiments were also repeated on the original multi-echo data (no flip angle modulation, 32 time points) to investigate the performance of T2 Shuffling for constant flip angle schemes (approximately exponential decay).
In Vivo Data
Adult volunteers and pediatric patients were scanned under an approved IRB study and informed consent/assent using the modified CUBE pulse sequence for knee imaging with an 8-channel coil array at 3T. Table 1 lists the scan and imaging parameters used. The first scan (Scan 1a) matched the current pediatric knee protocol used at the Lucille Packard Children’s Hospital (Stanford, California) with a center-out view ordering and variable density Poisson disc sampling. The second scan (Scan 2a) used a randomly shuffled view ordering and sampling as discussed in the supporting information. The first scan was reconstructed into a single proton-density image using L1-ESPIRiT. The second scan was reconstructed into 78 virtual echo time images using T2 Shuffling. Both scans were 6 minutes and 30 seconds in duration. A second set of scans with scan times of 7 minutes and 30 seconds was also used to reduce the ETL for the center-out ordering (Scan 1b) and to reduce the acceleration for the randomly shuffled ordering (Scan 2b). We compared T2 Shuffling to L1-ESPIRiT because compressed sensing has shown great promise toward improving 3D FSE (4, 7, 8).
Table 1.
Scan and imaging parameters used for in vivo experiments.
| All Scans | |
|---|---|
|
| |
| TR (ms) | 1400 |
| Echo Spacing (ms) | 5.5 |
| Receive Bandwidth (kHz) | ±62.5 |
| Fat Saturation Efficiency | 0.85 |
| Acquisition Matrix | 288 × 260 × 240 |
| Reconstruction Matrix | 512 × 512 × 472 |
| Acquisition Voxel (mm3) | 0.6 × 0.6 × 0.7 |
| Reconstruction Voxel (mm3) | 0.3 × 0.3 × 0.4 |
| Reformat Slice Thickness (mm) | Axial: 0.3, Sagittal: 1.5, Coronal: 2.0 |
| Scan 1a | Scan 2a | Scan 1b | Scan 2b | |
|---|---|---|---|---|
| View Ordering | Center-out | Randomly Shuffled | Center-out | Randomly Shuffled |
| ETL | 33 | 80 | 28 | 82 |
| Ntrains | 278 | 278 | 321 | 321 |
| Initial Discarded Echoes | 5 | 2 | 5 | 2 |
| TEeff (ms) | 23 | - | 23 | – |
| Relative Accelerationa | 6.3 | 2.3 | 6.6 | 1.9 |
| Apparent Accelerationb | – | 9.2 | – | 7.6 |
|
| ||||
| Image Contrast | Proton | Proton, T2 (78 images) | Proton | Proton, T2 (80 images) |
|
| ||||
| Scan Time | 6 min. 30 sec. | 6 min. 30 sec. | 7 min. 30 sec. | 7 min. 30 sec. |
The acceleration with respect to a fully sampled circular k-space coverage.
The relative acceleration multiplied by the number of temporal coefficient images.
Reconstruction Implementation
The proposed T2 Shuffling reconstruction was implemented in C and CUDA using the Berkeley Advanced Reconstruction Toolbox (BART) (51, 52). MATLAB demonstration code is available for download at http://eecs.berkeley.edu/~mlustig/Software.html.
The reconstruction problem Eq. (15) is convex and is solved efficiently with ADMM (53). ADMM requires repeated application of the forward and adjoint operators described by the normal equations,
| (18) |
In this naive formulation, the run-time and memory requirements scale with the ETL. For an ETL of T = 80, K = 4 temporal coefficients, and 8 coils, the forward operator amounts to a 80 × 4 matrix multiplication per voxel, followed by 80 sensitivity map multiplications and 640 FFTs. The result is multiplied by the sampling mask and similar operations are applied in reverse order for the adjoint. Although some operations can be parallelized, they pose a large memory and computation bottleneck on the reconstruction.
To reduce computation, we follow a similar approach to Step 1 in (54). Since the temporal basis ΦK operates across time and the sensitivity map multiplication S and Fourier transform F operate across space, the operators commute:
| (19) |
Thus, the normal equations can be rewritten more compactly:
| (20) |
| (21) |
Here, is a K × K sampling kernel per voxel, and can be pre-computed prior to reconstruction. For K = 4, the forward operation now only requires the application of 4 sensitivity map multiplications and 32 FFTs, followed by a 4 × 4 matrix multiplication per voxel. The adjoint operation sees a similar reduction in computation. The data y and time series of images x are no longer explicitly stored, making the reconstruction’s memory and run-time requirements independent of the ETL. The complexity is roughly K = 4 times greater than that of an L1-ESPIRiT reconstruction.
Results
2D Retrospective Undersampling and Anatomical Simulation Results
The first experiment, carried out on the anatomical simulation, is shown in Figure 6a. The left image shows the first TE of the simulated, fully sampled data and serves as the gold-standard proton-density contrast. The middle-left shows the L1-ESPIRiT reconstruction with center-out ordering, and represents a conventional compressed sensing approach. The blurring due to T2 decay is evident, reaffirming the limitation of current FSE. After randomly shuffling the echo train ordering (middle image), the L1-ESPIRiT reconstruction shows incoherent artifacts, which are explained by the PSF in Figure 3b. There is also mixed contrast due to the k-space modulation induced by the random sampling. Despite the image artifacts, detailed structure remains, indicating the potential to “denoise” with T2 Shuffling. The first virtual echo time from the T2 Shuffling reconstruction applied to center-out ordering is shown in the middle-right image. The reconstruction does not successfully recover the time series of images because the sampling is coherent in k-t space (ill-posed deconvolution). The T2 Shuffling reconstruction in tandem with randomized view ordering (right image) is sharp, and the first virtual echo time image shows similar quality and contrast to that of the fully sampled image. There is a clear delineation of fine structure that is not afforded by the conventional 3D FSE pipeline. Figure 6b shows a similar trend on the acquisition data. Since the multi-echo sequence used a fixed 180-degree flip angle schedule, the blurring from center-out ordering is even more pronounced. The T2 Shuffling reconstruction with randomized view ordering is comparable to the fully sampled slice despite the approximate exponential signal decay.
The T2 Shuffling reconstruction recovers the full time series of virtual echo time images and provides various degrees of T2 contrast, all from the same data. Figure 6c shows a later virtual echo time image (approximately 100 ms) for both the fully sampled simulation and acquisition slices, and well as the T2 Shuffling reconstructions (with the randomly shuffled ordering). As suggested by (5), we show the effective contrast-equivalent TE (TEeff) for the variable flip angle modulation. The reconstructions closely match the fully sampled slices. Figure 6d shows representative temporal signal evolutions for the cases considered in Figure 6c. The signal curves for the variable flip angles show close agreement, indicating low model error and successful reconstruction. Note the deviation from the true signal evolution in the case of the constant flip angle; this is a result of the non-exponential behavior that was not modeled in the basis and indicates the importance of matching the temporal subspace to the pulse sequence design.
In Vivo Results
Figure 7a depicts axial reformatted images of modified Poisson disc CUBE with L1-ESPIRiT vs. T2 Shuffling reconstructions on a pediatric patient with bone marrow edema (Table 1, Scans 1a and 2a, respectively). The proton-density T2 Shuffling image shows increased delineation of the patellar tendon and other fine structures as compared to the L1-ESPIRiT reconstruction. The later virtual echo time images clearly show the edema due to the higher T2 value of the fluid relative to the surrounding tissue. Figure 7b shows sagittal and coronal reformatted T2 Shuffling images from a knee scan of a pediatric patient with a discoid meniscus (Table 1, Scan 2b). The early virtual echo time image points to intrasubstance degeneration, but the later virtual echo time clearly shows the tear and fluid.
Figure 7.
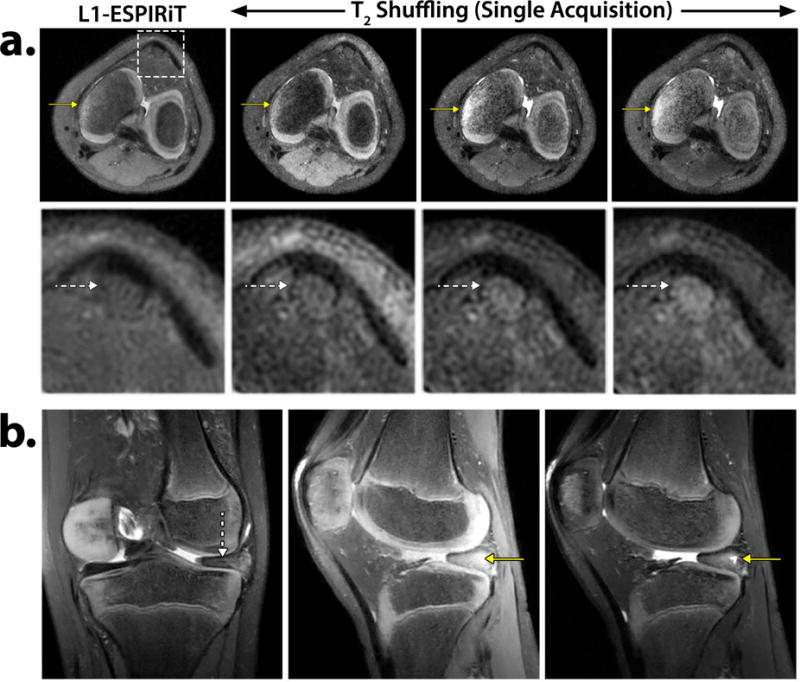
a. Axial reformatted reconstructions of L1-ESPIRiT using Poisson disc CUBE and T2 Shuffling at three virtual echo times. The solid yellow arrows depict increasingly improved contrast of the bone marrow edema. The dashed white arrows (zoomed-in region) show enhanced delineation of the patellar tendon in the T2 Shuffling images. Acquisition parameters are listed in Table 1, Scan 1a and Scan 2a. b. T2 Shuffling reconstruction of a pediatric patient scan with a discoid meniscus. The coronal reformat at 50 ms TEeff shows the discoid meniscus (dashed white arrow). The sagittal reformat at 20 ms TEeff shows potential intrasubstance degeneration. The same slice at 90 ms TEeff clearly depicts the meniscal tear and fluid (solid yellow arrow). Acquisition parameters are listed in Table 1, Scan 2b.
In some cases T2 Shuffling only afforded marginal qualitative improvement. Figure 8 presents such a case for a pediatric patient, comparing sagittal reformats of Poisson disc CUBE with L1-ESPIRiT and T2 Shuffling at two virtual echo times (Table 1, Scan 1a and 2a, respectively). Although there are some differences between the proton density images, it is not immediately clear if they are due to deblurring or due to residual aliasing artifacts. The solid yellow arrow shows increased apparent resolution in the muscle, while the dashed white arrow shows ringing in the bone only present in the T2 Shuffling images.
Figure 8.
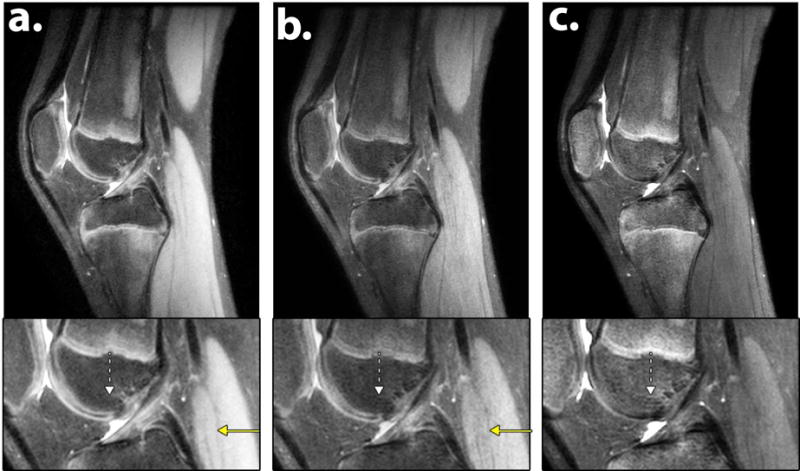
a. Sagittal reformatted reconstructions of (a) L1-ESPIRiT using Poisson disc CUBE and (b–c) T2 Shuffling at two virtual echo times. The solid yellow arrow shows increased apparent resolution in the muscle, while the dashed white arrow shows ringing in the bone signal of the T2 Shuffling images. Acquisition parameters are listed in Table 1, Scan 1a and Scan 2a.
Figure 9a shows an axial reformatted slice of the first virtual echo time image using T2 Shuffling for a volunteer. The image depicts the trabecular bone structure in the distal femur. This area is challenging in particular for parameter mapping methods because of the multi-compartmental nature of the bone structure. Since T2 Shuffling does not explicitly estimate the T2 value and instead flexibly represents the voxels by a linear subspace, the modeling error is low and the structure is preserved. The dimensionality reduction offered by LLR is depicted in Figure 9b; each voxel neighborhood is constrained to a smaller subspace within the global subspace. The local rank is determined by taking non-overlapping patches of the reconstructed temporal coefficient images, reshaping each patch into a matrix, and computing the number of non-zero singular values. Regions in the image containing a single tissue species are captured by a single coefficient. The regions at tissue boundaries require more coefficients to represent due to the diversity in T2. The correlation between tissues is naturally exploited by the subspace constraint; Figure 9c shows the result of applying k-means to the coefficient images. With little effort, the image is segmented into broad tissue classes based on the temporal coefficients of each voxel.
Figure 9.
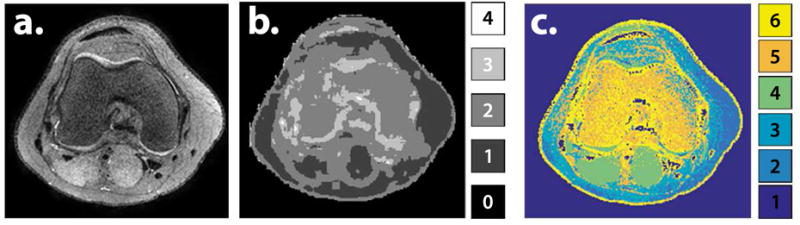
a. Axial reformatted slice of the T2 Shuffling reconstruction at the first virtual echo time. b. Number of degrees of freedom in each voxel after LLR reconstruction. c. K-means clustering applied to the coefficient images after reconstruction. Each color represents a broad tissue class.
The supporting information section includes additional examples of in vivo reconstructions. Supporting Figure S-1 compares Poisson disc CUBE with L1-ESPIRiT to the 5th and 30th virtual TE of T2 Shuffling on an adult volunteer (Table 1, Scan 1b and Scan 2b, respectively). In this comparison, a short ETL of 28 was used for the first scan to reduce intrinsic blur. The short ETL was compensated for by very high Poisson disc sampling acceleration with compressed sensing. At this scan time and ETL, the deblurring is negligible; however, both proton-density and T2 contrast are recovered by T2 Shuffling in the same scan time. Supporting Figure S-2 compares the first virtual TE of linear reconstructions without and with Tikhonov regularization (i.e. solving Eq. (15) without LLR regularization) to the T2 Shuffling reconstruction with LLR regularization. Because the linear system is under-determined, the linear reconstructions suffer from noise amplification and loss of detail, while the LLR-regularized reconstruction recovers the image. Supporting Figure S-3 shows preliminary results to applying T2 Shuffling to other anatomy for pediatric and adult MRI. Supporting Video S-1 shows the virtual echo time progression and depicts the changing T2 contrast over time. Supporting Video S-2 shows the same images, but rescales each image frame to the dynamic range of the first virtual TE to show the signal decay. The videos are included in the supporting information.
Discussion
Conventional FSE imaging methods must balance the tradeoffs between scan time, image sharpness, and image contrast. T2 Shuffling is able to break this dependency and resolve a time series of sharp images from a single acquisition. Instead, T2 Shuffling inherits similar benefits and challenges present with compressed sensing: the limited acquisition time manifests as incoherent artifacts in the images. Short T2 species impart larger artifacts, and these artifacts spread through the entire image volume. Thus successful recovery is tied to the sampling rate and distribution in k-t space. From this viewpoint, a center-out echo train ordering does not adequately sample the temporal signal evolution curve and leads to an ill-conditioned inverse problem. However, it is possible to sample k-t space incoherently by randomly shuffling the echo train ordering. The modification is straightforward and we have built this functionality into the CUBE pulse sequence. The signal modulation from randomized echo train orderings is no longer smooth, but we mitigate eddy current effects by assigning nearby phase encodes to the same echo train, as discussed in the supporting information.
The ability to reconstruct the time series of images from the limited data is due to the high degree of sparsity. We have built upon similar work (18–21) to produce a faithful low-dimensional representation of the temporal signal evolutions. This temporal basis can be computed offline once and stored for future exams. The temporal subspace constraint alone does not provide a sufficiently compact representation, as K ≈ 4 observations are required at each voxel. However, the use of LLR regularization further reduces the sample complexity by about a factor of 2. In addition, the added denoising offered by LLR enables the use of a larger subspace (to reduce model error) without a large increase in sample complexity. By constraining patches to be locally low rank, the spatio-temporal images are represented as a union of subspaces. It is possible to improve upon this representation through subspace clustering methods (55). Unlike LLR, subspace clustering can group voxels that are not spatially localized. We have begun to investigate the use of subspace clustering methods, but it is beyond the scope of this work.
A second consequence of the subspace constraint is that the intrinsic dimension of the image set does not grow with increasing ETLs. For feasible TRs, there remains observable signal throughout the TR due to tissue with high T2. This residual signal informs the entire reconstruction to reduce incoherent artifacts throughout the image volume. Nonetheless, the ETL cannot occupy the entire TR in order to retain sufficient time for longitudinal recovery. For a particular imaging metric, it may be possible to choose an optimal flip angle schedule and ETL given SAR constraints. In (56) and (57), the optimal TEs are chosen to maximize SNR and parameter estimation admissibility given a multi-exponential decay model. We are investigating a similar metric for the flip angle and ETL selection.
Throughout the design of the T2 Shuffling pulse sequence and reconstruction, we have emphasized the importance of maintaining a clinical workflow. The use of BART as a CPU-and GPU-accelerated iterative reconstruction platform has afforded 20-minute reconstruction times for the full time series of images. Others have noted it is not feasible to save and display all images along the signal relaxation curve (38, 58). As a proof-of-principle, we currently store and provide four virtual echo time images to the radiologist for examination. However, since the signal evolutions are fully derived from the temporal coefficients through Eq. (14), it is feasible to save the temporal coefficients only and compute arbitrary virtual echo time images in real-time. We envision the use of advanced image viewers to intuitively navigate the 4D data set in space and in time in a manner similar to the capabilities of the SyMRI software (SyntheticMR AB, Linkoping, Sweden). Further clinical validation is needed to motivate the selection and visualization of the data.
Despite the demonstrated benefits of T2 Shuffling, the linear relaxation through PCA comes at the cost of lower apparent SNR. In addition, if the temporal subspace does not suitably model the signal formation, e.g. due to motion, the model mismatch will lead to poor data fidelity and degrade the reconstruction. The bias vs. noise tradeoff presented in the Appendix only considered fully sampled signal evolutions. Even though the analysis does not directly extend to under-sampled acquisitions, it was used as a rule-of-thumb for the T2 Shuffling acquisition and reconstruction. Because the acquisition is highly accelerated, the reconstruction relies on a strong sparsity prior. In the absence of sparsity, longer scan times are necessary to fully suppress the incoherent aliasing artifacts. These drawbacks must be fully understood and addressed before wider clinical adoption.
Although this work focused on volumetric imaging, similar tradeoffs exist for 2D FSE. The signal decay that leads to blurring is partially mitigated by reducing ETLs and interleaving slices in multi-shot 2D FSE (1). Variable refocusing flip angles have also been used to reduce blurring in single-shot 2D FSE (59). We plan to explore the application of T2 Shuffling to 2D FSE to further reduce blurring due to long ETLs as well as resolve multiple image contrasts.
Conclusion
In this work we presented T2 Shuffling, a novel acquisition and reconstruction method for volumetric FSE imaging. Conventional 3D FSE trades off scan time and image quality, e.g. shorter scans incur more blurring. Additionally, current clinical methods separately acquire proton-density and T2-weighted image contrasts. T2 Shuffling addresses both issues by simultaneously reconstructing multi-contrast images with increased sharpness from a single 3D FSE acquisition. Each image in the time series exhibits T2 contrast corresponding to a particular virtual echo time. We have demonstrated the diagnostic utility of multiple image contrasts at isotropic resolution: the signal evolution of tissue microstructure provides additional information on pathology.
Supplementary Material
List of Supporting Information
1. Supporting Information attached under t2shuffling_support.pdf. The supporting information describes (1) additional in vivo results and comparisons; (2) the calculation of the transform point spread function; and (3) the algorithm used to generate randomly shuffled phase encode and view orderings.
List of Supporting Figures in t2shuffling_support.pdf
S-1 Reconstruction comparison of volunteer scans (see Table 1, Scan 1b and Scan 2b for acquisition parameters). a. Poisson disc CUBE acquisition and L1-ESPIRiT reconstruction. The short ETL of 28 was offset by a high Relative Acceleration of 6.6. b. T2 Shuffling at the 5th virtual echo time (TEeff = 21 ms). c. T2 Shuffling at the 30th virtual echo time (TEeff = 90 ms).
S-2 Comparison of linear reconstructions (a) without and (b) with Tikhonov regularization to (c) T2 Shuffling with LLR regularization at the first virtual TE. The linear reconstruction without regularization suffers from noise amplification. Tikhonov regularization reduces noise amplification, but detailed structure is lost. The LLR-regularized reconstruction recovers the image, indicating the reduced sample complexity. Scan parameters are given in Table 1, Scan 2b.
S-3 T2 Shuffling reconstructions of brain, ankle, wrist, and prostate scans at two virtual echo times.
S-4 Visualization of the block-wise matrix operator for LLR. Non-overlapping blocks from each temporal coefficient image are reshaped into columns to form small matrices. The transform components are the singular vectors of the matrices.
S-5 System input and ideal system response for TPSF calculation. Each row represents a system input. The center of the active temporal coefficient image contains a 7-by-7 uniform magnitude-one patch.
S-6 The TPSF for center-out echo train ordering shows coherent interference. The patch in the active coefficient leaks to adjacent coefficients and is blurred.
S-7 TPSF for randomly shuffled echo train ordering. The main patch remains sharp, and interference is spread incoherently to all transform coefficients.
Sha-1: d06cb9598fbad657e2e34e8daeb2a7f7540caf08
2. Supporting Video S-1 attached under t2shuffling.avi. A video showing the virtual echo time progression from a T2 Shuffling reconstruction. Each image frame is rescaled to occupy the full dynamic range. T2 contrast is enhanced over time.
Sha-1: 1c4cdd413167accf85d6bdd310cbbb0df2606497
3. Supporting Video S-2 attached under t2shuffling-noscale.avi. A video showing the virtual echo time progression from a T2 Shuffling reconstruction without rescaling each image frame.
Sha-1: cb8b0873f168a2f80f590d5662223dba0d602077
Acknowledgments
This work was supported by NIH Grants R01EB019241, R01EB009690, and P41RR09784, the Sloan Research Fellowship, the Okawa Research Grant, and by research support from GE Healthcare.
Appendix: Signal Evolution Noise Characteristics
In this section we show that the noise variance of a fully sampled, subspace-constrained linear reconstruction is equal to σ2K, where K is the dimension of the subspace (47). Consider a noisy signal evolution at voxel r, as described by Eq. (4) and Eq. (5):
| (22) |
| (23) |
where
| (24) |
Each noise observation wi(r) is an independent, zero-mean complex Gaussian random variable with variance σ2. Thus,
| (25) |
We can approximate y(r) by projecting it onto the temporal subspace spanned by the semi-unitary matrix . Let . The random vector α(r) has covariance matrix given by
| (26) |
| (27) |
| (28) |
i.e. the temporal coefficients remain independent and Gaussian, and the total variance is reduced to . After projecting back to the time series, we arrive at an estimate . Since the matrix ΦK has orthonormal columns, the total variance in is unchanged; however, the noise at each time point is no longer independent nor identically distributed. The covariance matrix of is . In general, earlier time points will have higher noise values after the projection since the vectors given by ΦK represent signal decay.
Bias vs. Noise
The distribution of the error is given by
| (29) |
From this, the mean-squared error is
| (30) |
| (31) |
There is an inherent tradeoff between model error and noise amplification with subspace size. As K increases, the model error decreases and the noise amplification increases. The SNR of the measured signal is T2-dependent, and is given by
| (32) |
The root mean-squared error (RMSE) is plotted in Figure 5b for σ = 0.07, which corresponds to an SNR of about 15 dB for T2 = 14 ms.
Footnotes
To achieve translation invariance, the temporal coefficient images are randomly shifted at each iteration prior to LLR regularization.
Part of this work has been presented at the ISMRM Annual Conference 2015.
References
- 1.Mugler JP. Optimized three-dimensional fast-spin-echo MRI. J Magn Reson Imaging. 2014;39:745–767. doi: 10.1002/jmri.24542. [DOI] [PubMed] [Google Scholar]
- 2.Gold GE, Busse RF, Beehler C, Han E, Brau ACS, Beatty PJ, Beaulieu CF. Isotropic MRI of the knee with 3D fast spin-echo extended echo-train acquisition (XETA): initial experience. AJR. 2007;188:1287–93. doi: 10.2214/AJR.06.1208. [DOI] [PubMed] [Google Scholar]
- 3.Kijowski R, Gold GE. Routine 3D magnetic resonance imaging of joints. J Magn Reson Imaging. 2011;33:758–71. doi: 10.1002/jmri.22342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tariq U, Lai P, Lustig M, Alley M, Zhang M, Gold G, Vasanawala SS. Proc Intl Soc Mag Reson Med. Vol. 21. Salt Lake City: 2013. Impact of sampling pattern on combined parallel imaging compressed sensing volumetric knee MRI; p. 1664. [Google Scholar]
- 5.Busse RF, Hariharan H, Vu A, Brittain JH. Fast spin echo sequences with very long echo trains: design of variable refocusing flip angle schedules and generation of clinical T2 contrast. Magn Reson Med. 2006;55:1030–7. doi: 10.1002/mrm.20863. [DOI] [PubMed] [Google Scholar]
- 6.Busse RF, Brau ACS, Vu A, Michelich CR, Bayram E, Kijowski R, Reeder SB, Rowley HA. Effects of refocusing flip angle modulation and view ordering in 3D fast spin echo. Magn Reson Med. 2008;60:640–9. doi: 10.1002/mrm.21680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Recht MP, Otazo R, Rybak L, Gyftopoulos S, Petchprapa C, Geppert C, Bruno M, Raithel E. Proc Intl Soc Mag Reson Med. Vol. 23. Toronto: 2015. 3D TSE imaging using sparse-SENSE acceleration: Comparison with conventional 2D TSE imaging for detection of internal derangement of the knee; p. 1198. [Google Scholar]
- 8.Reid SA, King KF, Lomas DJ, van der Wolf-deLijster FvdWL, Estkowski L, Graves MJ. Proc Intl Soc Mag Reson Med. Vol. 23. Toronto: 2015. Imaging of the knee using 3D fast spin echo with compressed sensing; p. 1197. [Google Scholar]
- 9.Zhou X, Liang ZP, Cofer GP, Beaulieu CF, Suddarth SA, Johnson GA. Reduction of ringing and blurring artifacts in fast spin-echo imaging. J Magn Reson Imaging. 1993;3:803–7. doi: 10.1002/jmri.1880030518. [DOI] [PubMed] [Google Scholar]
- 10.Oshio K, Singh M. Correction of T2 distortion in multi-excitation RARE sequence. IEEE Trans Med Imaging. 1992;11:123–8. doi: 10.1109/42.126919. [DOI] [PubMed] [Google Scholar]
- 11.Çukur T, Lustig M, Saritas EU, Nishimura DG. Signal compensation and compressed sensing for magnetization-prepared MR angiography. IEEE Trans Med Imaging. 2011;30:1017–27. doi: 10.1109/TMI.2011.2116123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Takahashi H, Ogawa K, Oshio K, Momoshima H. A proposal of removal method for T2 decay effects in RARE sequence. Nuclear Science, IEEE Transactions on. 1995;42:1343–1347. doi: 10.1109/23.467860. [DOI] [Google Scholar]
- 13.Santa-Marta C, Lafuente J, Vaquero JJ, Garcia-Barreno P, Desco M. Resolution recovery in turbo spin echo using segmented half fourier acquisition. Magn Reson Imaging. 2004;22:369–78. doi: 10.1016/j.mri.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 14.Block KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-echo MRI. IEEE Trans Med Imaging. 2009;28:1759–69. doi: 10.1109/TMI.2009.2023119. [DOI] [PubMed] [Google Scholar]
- 15.Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imaging. 2011;34:420–8. doi: 10.1002/jmri.22634. [DOI] [PubMed] [Google Scholar]
- 16.Sumpf TJ, Petrovic A, Uecker M, Knoll F, Frahm J. Fast T2 mapping with improved accuracy using undersampled spin-echo MRI and model-based reconstructions with a generating function. IEEE Trans Med Imaging. 2014;33:2213–22. doi: 10.1109/TMI.2014.2333370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ben-Eliezer N, Sodickson DK, Shepherd T, Wiggins GC, Block KT. Accelerated and motion-robust in vivo T2 mapping from radially undersampled data using bloch-simulation-based iterative reconstruction. Magn Reson Med. 2015 doi: 10.1002/mrm.25558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis. Magn Reson Med. 2011;66:706–16. doi: 10.1002/mrm.22826. [DOI] [PubMed] [Google Scholar]
- 19.Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly under-sampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn Reson Med. 2012;67:1355–66. doi: 10.1002/mrm.23128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Huang C, Bilgin A, Barr T, Altbach MI. T2 relaxometry with indirect echo compensation from highly undersampled data. Magn Reson Med. 2013;70:1026–1037. doi: 10.1002/mrm.24540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn Reson Med. 2015;74:489–498. doi: 10.1002/mrm.25421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Keerthivasan MB, Bilgin A, Martin DR, Altbach MI. Proc Intl Soc Mag Reson Med. Vol. 23. Toronto: 2015. Isotropic T2 mapping using a 3D radial FSE (or TSE) pulse sequence; p. 3237. [Google Scholar]
- 23.Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn Reson Med. 2010;64:1114–20. doi: 10.1002/mrm.22483. [DOI] [PubMed] [Google Scholar]
- 24.Hong M, Lin M, Liu F, Ge Y. Proc Intl Soc Mag Reson Med. Vol. 23. Toronto: 2015. MR image reconstruction from under-sampled measurements using local and global sparse representations; p. 3422. [Google Scholar]
- 25.Zhao B, Haldar JP, Christodoulou AG, Liang ZP. Image reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints. IEEE Trans Med Imaging. 2012;31:1809–20. doi: 10.1109/TMI.2012.2203921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Velikina JV, Samsonov AA. Reconstruction of dynamic image series from undersampled MRI data using data-driven model consistency condition (MOCCO) Magn Reson Med. 2015;74:1279–90. doi: 10.1002/mrm.25513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bhave S, Lingala SG, Johnson CP, Magnotta VA, Jacob M. Accelerated whole-brain multi-parameter mapping using blind compressed sensing. Magn Reson Med. 2015 doi: 10.1002/mrm.25722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Matzat SJ, McWalter EJ, Kogan F, Chen W, Gold GE. T2 relaxation time quantitation differs between pulse sequences in articular cartilage. J Magn Reson Imaging. 2015;42:105–113. doi: 10.1002/jmri.24757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013;495:187–92. doi: 10.1038/nature11971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ben-Eliezer N, Sodickson DK, Block KT. Rapid and accurate T2 mapping from multi-spin-echo data using bloch-simulation-based reconstruction. Magn Reson Med. 2015;73:809–817. doi: 10.1002/mrm.25156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pierre EY, Ma D, Chen Y, Badve C, Griswold M. Proc Int Symp Magn Reson Med. Vol. 23. Toronto: 2015. Multiscale image reconstruction for MR fingerprinting; p. 0084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tamir JI, Chen W, Lai P, Uecker M, Vasanawala SS, Lustig M. Proc Intl Soc Mag Reson Med. Vol. 23. Toronto: 2015. T2 shuffling: Multicontrast 3D fast spin echo imaging; p. 3399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Trzasko JD, Manduca A. Proc Int Symp Magn Reson Med. Vol. 19. Montreal: 2011. Local versus global low-rank promotion in dynamic MRI series reconstruction; p. 4371. [Google Scholar]
- 34.Trzasko JD, Manduca A. Calibrationless parallel MRI using CLEAR. Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR); 2011. pp. 75–79. [Google Scholar]
- 35.Zhang T, Cheng JY, Potnick AG, Barth RA, Alley MT, Uecker M, Lustig M, Pauly JM, Vasanawala SS. Fast pediatric 3D free-breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution. J Magn Reson Imaging. 2015;41:460–473. doi: 10.1002/jmri.24551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med. 2015;73:655–61. doi: 10.1002/mrm.25161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Li G, Weigel M, Meyer E, Paul D, Korvink J, Hennig J. Proc Intl Soc Mag Reson Med. Vol. 22. Milan: 2014. On the feasibility of hybrid acquisition in SPACE; p. 1467. [Google Scholar]
- 38.Kecskemeti S, Samsonov A, Hurley SA, Dean DC, Field A, Alexander AL. MPnRAGE: a technique to simultaneously acquire hundreds of differently contrasted mprage images with applications to quantitative T1 mapping. Magn Reson Med. 2015 doi: 10.1002/mrm.25674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Benkert T, Bartsch AJ, Blaimer M, Jakob PM, Breuer FA. Generating multiple contrasts using single-shot radial T1 sensitive and insensitive steady-state imaging. Magn Reson Med. 2015;73:2129–2141. doi: 10.1002/mrm.25337. [DOI] [PubMed] [Google Scholar]
- 40.Gouveia Ja, Parrilo PA, Thomas R. Lifts of convex sets and cone factorizations. Mathematics of Operations Research. 2011;38:248–264. doi: 10.1287/moor.1120.0575. [DOI] [Google Scholar]
- 41.Haldar JP, Hernando D, Liang ZP. Super-resolution reconstruction of MR image sequences with contrast modeling. Proc IEEE Int’l Symposium Biomedical Imaging. 2009:266–269. doi: 10.1109/ISBI.2009.5193035. [DOI] [Google Scholar]
- 42.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182–95. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 43.Lukzen NN, Savelov AA. Analytical derivation of multiple spin echo amplitudes with arbitrary refocusing angle. J Magn Reson. 2007;185:71–6. doi: 10.1016/j.jmr.2006.11.010. [DOI] [PubMed] [Google Scholar]
- 44.Tamir JI, Lai P, Uecker M, Lustig M. Proc Intl Soc Mag Reson Med. Vol. 22. Milan: 2014. Reduced blurring in 3D fast spin echo through joint temporal ESPIRiT reconstruction; p. 0616. [Google Scholar]
- 45.Kim K, Ye JC, Worstell W, Ouyang J, Rakvongthai Y, ElFakhri G, Li Q. Sparse-view spectral CT reconstruction using spectral patch-based low-rank penalty. Medical Imaging, IEEE Transactions on. 2015;34:748–760. doi: 10.1109/TMI.2014.2380993. [DOI] [PubMed] [Google Scholar]
- 46.Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity-promoting regularization in parametric dimension. Magn Reson Med. 2013;70:1263–73. doi: 10.1002/mrm.24577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tamir JI, Chen W, Lai P, Uecker M, Lustig M. Proc Intl Soc Mag Reson Med. Vol. 23. Toronto: 2015. Improved scan efficiency of 3D fast spin echo with subspace-constrained reconstruction; p. 2463. [Google Scholar]
- 48.Boesen ME, MaiorNeto LAS, Pulwicki A, Yerly J, Lebel RM, Frayne R. Fast spin echo imaging of carotid artery dynamics. Magn Reson Med. 2015;74:1103–9. doi: 10.1002/mrm.25494. [DOI] [PubMed] [Google Scholar]
- 49.Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn Reson Imaging. 2008;26:133–41. doi: 10.1016/j.mri.2007.04.010. [DOI] [PubMed] [Google Scholar]
- 50.Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Uecker M, Virtue P, Ong F, Murphy MJ, Alley MT, Vasanawala SS, Lustig M. ISMRM Scientific Workshop – Data Sampling and Image Reconstruction. Sedona: 2013. Software toolbox and programming library for compressed sensing and parallel imaging. [Google Scholar]
- 52.Uecker M, Zhang T, Ong F, Lustig M, Tamir JI, Bahri D, Virtue P, Cheng JY. BART version 0.2.08. 2015;5 doi: 10.5281/zenodo.18041. [DOI] [Google Scholar]
- 53.Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning. 2011;3:1–122. [Google Scholar]
- 54.Mani M, Jacob M, Magnotta V, Zhong J. Fast iterative algorithm for the reconstruction of multishot non-cartesian diffusion data. Magn Reson Med. 2015;74:1086–1094. doi: 10.1002/mrm.25486. [DOI] [PubMed] [Google Scholar]
- 55.Vidal R. Subspace clustering. IEEE Signal Processing Magazine. 2011;28:52–68. doi: 10.1109/MSP.2010.939739. [DOI] [Google Scholar]
- 56.Vidarsson L, Conolly SM, Lim KO, Gold GE, Pauly JM. Echo time optimization for linear combination myelin imaging. Magn Reson Med. 2005;53:398–407. doi: 10.1002/mrm.20360. [DOI] [PubMed] [Google Scholar]
- 57.Reiter DA, Lin PC, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magnetic Resonance in Medicine. 2009;61:803–809. doi: 10.1002/mrm.21926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Warntjes JBM, Leinhard OD, West J, Lundberg P. Rapid magnetic resonance quantification on the brain: Optimization for clinical usage. Magn Reson Med. 2008;60:320–9. doi: 10.1002/mrm.21635. [DOI] [PubMed] [Google Scholar]
- 59.Loening AM, Saranathan M, Ruangwattanapaisarn N, Litwiller DV, Shimakawa A, Vasanawala SS. Increased speed and image quality in single-shot fast spin echo imaging via variable refocusing flip angles. J Magn Reson Imaging. 2015;42:1747–1758. doi: 10.1002/jmri.24941. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
List of Supporting Information
1. Supporting Information attached under t2shuffling_support.pdf. The supporting information describes (1) additional in vivo results and comparisons; (2) the calculation of the transform point spread function; and (3) the algorithm used to generate randomly shuffled phase encode and view orderings.
List of Supporting Figures in t2shuffling_support.pdf
S-1 Reconstruction comparison of volunteer scans (see Table 1, Scan 1b and Scan 2b for acquisition parameters). a. Poisson disc CUBE acquisition and L1-ESPIRiT reconstruction. The short ETL of 28 was offset by a high Relative Acceleration of 6.6. b. T2 Shuffling at the 5th virtual echo time (TEeff = 21 ms). c. T2 Shuffling at the 30th virtual echo time (TEeff = 90 ms).
S-2 Comparison of linear reconstructions (a) without and (b) with Tikhonov regularization to (c) T2 Shuffling with LLR regularization at the first virtual TE. The linear reconstruction without regularization suffers from noise amplification. Tikhonov regularization reduces noise amplification, but detailed structure is lost. The LLR-regularized reconstruction recovers the image, indicating the reduced sample complexity. Scan parameters are given in Table 1, Scan 2b.
S-3 T2 Shuffling reconstructions of brain, ankle, wrist, and prostate scans at two virtual echo times.
S-4 Visualization of the block-wise matrix operator for LLR. Non-overlapping blocks from each temporal coefficient image are reshaped into columns to form small matrices. The transform components are the singular vectors of the matrices.
S-5 System input and ideal system response for TPSF calculation. Each row represents a system input. The center of the active temporal coefficient image contains a 7-by-7 uniform magnitude-one patch.
S-6 The TPSF for center-out echo train ordering shows coherent interference. The patch in the active coefficient leaks to adjacent coefficients and is blurred.
S-7 TPSF for randomly shuffled echo train ordering. The main patch remains sharp, and interference is spread incoherently to all transform coefficients.
Sha-1: d06cb9598fbad657e2e34e8daeb2a7f7540caf08
2. Supporting Video S-1 attached under t2shuffling.avi. A video showing the virtual echo time progression from a T2 Shuffling reconstruction. Each image frame is rescaled to occupy the full dynamic range. T2 contrast is enhanced over time.
Sha-1: 1c4cdd413167accf85d6bdd310cbbb0df2606497
3. Supporting Video S-2 attached under t2shuffling-noscale.avi. A video showing the virtual echo time progression from a T2 Shuffling reconstruction without rescaling each image frame.
Sha-1: cb8b0873f168a2f80f590d5662223dba0d602077


