A Method for Accurate Inference of Population Size from Serially Sampled Genealogies Distorted by Selection

Abstract

The serial coalescent extends traditional coalescent theory to include genealogies in which not all individuals were sampled at the same time. Inference in this framework is powerful because population size and evolutionary rate may be estimated independently. However, when the sequences in question are affected by selection acting at many sites, the genealogies may differ significantly from their neutral expectation, and inference of demographic parameters may become inaccurate. I demonstrate that this inaccuracy is severe when the mutation rate and strength of selection are jointly large, and I develop a new likelihood calculation that, while approximate, improves the accuracy of population size estimates. When used in a Bayesian parameter estimation context, the new calculation allows for estimation of the shape of the pairwise coalescent rate function and can be used to detect the presence of selection acting at many sites in a sequence. Using the new method, I investigate two sets of dengue virus sequences from Puerto Rico and Thailand, and show that both genealogies are likely to have been distorted by selection.

Introduction

Inferring population history from genetic data is a central focus of modern population genetics. The increasing availability of genetic data sampled from populations at multiple time points has facilitated this goal by allowing independent estimation of demographic and substitution rate parameters via the serial coalescent (Rodrigo and Felsenstein 1999; Drummond and Rodrigo 2000; Drummond et al. 2002). Although the serial coalescent and coalescent theory in general provide a powerful framework for inference of population parameters, they generally assume that the loci in question are evolving neutrally. However, recent research has suggested that selection may cause gene genealogies to differ from their neutral expectation (Barton and Navarro 2002; Williamson and Orive 2002; Barton and Etheridge 2004; O'Fallon et al. 2010; Seger et al. 2010), and this distortion may lead to biases in the inference of population parameters if not incorporated into the model. Despite growing awareness of the distorting effects of selection, the degree of inaccuracy that selection induces on demographic inference with the serial coalescent has not been examined, and few likelihood models explicitly include the effects of selection.

Appreciation of the effects of selection on genealogical structure has come relatively recently, with most earlier studies suggesting that selection has little effect. Although initial studies of strong “background” selection established that the time to most recent common ancestor (TMRCA) of a sample may be shortened considerably (Charlesworth et al. 1993), subsequent work using the Ancestral Selection Graph (Neuhauser and Krone 1997; Przeworski et al. 1999)indicated that selection did not greatly alter the shapes of genealogies. This belief was reinforced by the subsequent studies of Williamson and Orive (2002) and Barton and Etheridge (2004), who employed simulations and analytic studies, respectively, and also found that selection had little effect on genealogical structure. Investigating conditional genealogies in which samples could be assigned to allelic states, Wakeley (2008) found that strong negative selection also had no effect on genealogies, provided multiple deleterious types were not present in the sample.

More recently, however, studies have established that some selective conditions may cause genealogies to differ significantly from neutral expectations. In particular, purifying selection at many closely linked sites may produce a characteristic distortion of genealogies that affects both branch lengths and tree topology (Maia et al. 2004; O'Fallon et al. 2010; Seger et al. 2010). The distortions found in these models are due in part to alterations in the rate at which lineages coalesce, which is an increasing function of (backwards) time. The rate increase follows from the fact that selection is less effective at purging deleterious mutations from the population in the absence of recombination, an effect known as Hill–Robertson interference (Hill and Robertson 1966; Felsenstein 1974; Comeron et al. 2008). The preponderance of segregating polymorphisms that arises in this situation generates variability in heritable fitness, and lineages sampled under these conditions perform a random walk in backward time over fitness states (e.g., Rouzine and Coffin 2006; Seger et al. 2010). The random walk is biased toward high fitness states, and when multiple lineages “arrive” at such states, the chance that they coalesce may be significantly higher than the neutral expectation. The approach to this level may be slow, however, and the coalescent rate is a function of time that increases from the neutral expectation (often the reciprocal of the effective size) near the tips to a higher rate near the root. The magnitude of the distortion is maximized at intermediate selection coefficients because very strong selection reduces population-wide fitness variability, and the coalescent rate becomes similar to that expected under neutrality. The amount of selection that maximizes coalescent rate is an increasing function of the mutation rate, such that if mutation and selection are jointly large, coalescent rate may be greatly increased.

Less well understood is the structure of gene genealogies under selection when samples are taken at different times. Because the coalescent rate of lineages increases with time prior to the time at which lineages are sampled, the lineages present at a particular depth may have different propensities to coalesce. Although overall coalescent rate will increase with genealogical depth, the rate may fluctuate in a complex manner depending on the strength of selection as well as the times at which samples were taken. These fluctuations are likely to obscure traditional methods of population size estimation, which often assume that coalescent rate is affected only by population size. In particular, by increasing coalescent rate, selection may cause reconstruction methods to infer population sizes that are much lower than the true size. If all sequences are sampled at the same time, the population may appear to be growing, since coalescent rate increases with backward time. However, when samples are taken at different times, selection is likely to induce distortions that are distinct from population growth because coalescent rate may decrease as well as increase depending on the the times at which samples were taken.

In this work, I develop an approximate method for calculating the likelihood of observing a genealogy with noncontemporaneous samples given arbitrary population size and a model that describes how coalescent rate is affected by selection at many sites. The new likelihood calculation is used in a Bayesian Markov chain Monte Carlo (MCMC) inference context to estimate the posterior distributions of model parameters such as population size. Initially, I examine how current methods of demographic inference using the serial coalescent perform when the sequences are under selection, and then demonstrate that the new method corrects for the observed biases while allowing for an estimate of a selection-induced distortion parameter. Two important approximations are involved. First, I assume that coalescent propensity of a branch increases in a simple linear fashion with the distance to the tips of the genealogy. Second, all lineages with equal distances to the tips are assumed to be exchangeable with respect to coalescent rate, regardless of the number of coalescent events in which they have participated. Both approximations are investigated using forward simulation.

To demonstrate the method on empirical data, I re-examine two serially sampled data sets of dengue virus (DENV), a single-stranded positive sense RNA virus transmitted by the mosquito vector Aedes aegypti. Dengue virus is the etiologic agent of dengue fever and the more severe conditions dengue hemorrhagic fever and dengue shock syndrome, illnesses which affect an estimated 50–100 million people globally each year. Several recent studies have examined selective pressures in DENV, and instances of both positive and purifying selection have been detected (Bennett et al. 2003, 2006; Zhang et al. 2006). The relatively high substitution rate of the virus (5×10 ^{− 4} to 10 ^{− 3} substitutions/year; Twiddy et al. 2003) and compact, nonsegmented genome make DENV a likely candidate for selection-related genealogical distortion.

Methods

I begin by demonstrating that current methods of estimating population size using the serial coalescent become significantly biased if the sequences are linked to multiple sites experiencing selection. I then investigate the manner in which selection distorts the distribution of pairwise coalescent times when sequences are sampled at different times. Finally, I introduce modifications to the serial coalescent likelihood calculation that correct for the population size bias and allow for estimation of parameters affecting pairwise coalescent rate. The goal is not to infer the actual magnitude of the selection coefficients or the properties of the distribution of coefficients, but instead to detect selection indirectly, through the genealogical distortions it is predicted to induce.

Bias of Current Methods in the Presence of Selection

To investigate the effect of selection at multiple linked sites on population size estimates, the Bayesian genealogy sampler BEAST (Drummond and Rambaut 2007) was used with serially sampled data simulated from populations of known size. Data were generated using the forward simulator TreesimJ (O'Fallon 2010a), which assumes a haploid population of size N evolving via discrete nonoverlapping generations, where N ranged from 200 to 8,000. The source code was modified to allow for arbitrary serial-sampling strategies. The Kimura 2-parameter mutation model was employed with a selection model in which 1,000 neutral sites were completely linked to 1,000 sites with selection coefficient s. In this model, each site mutates with independent probability μ each generation, and when in the mutated state selected sites independently reduce fitness by fraction 1 − e ^{− s}. Fitness effects multiply across sites, such that the absolute fitness of an individual with n mutated sites is e ^{− ns}. Mutation is independent of selection and mutational state, hence back mutations are possible and lineages may increase in fitness in forward time. Genealogies were sampled from this population by sampling ten individuals every N/2 generations for five total sampling periods. This scheme creates trees with 50 tips with sampling periods spanning 2.5N total generations.

Population parameters were estimated using only the 1,000 neutral sites as input data. Including selected sites in the analysis may bias tree reconstruction and lead to inaccuracies that are not a product of genealogical distortion, the phenomenon I investigate here. BEAST runs were conducted for at least 5×10⁶ MCMC steps, with the (constant) population size, mutation rate, base frequencies, and transition to transversion ratio estimated from the data. Effective sample sizes were over 1,000 for nearly all parameters in all runs.

The Pairwise Coalescent Rate for Tips Sampled atDifferent Times

Kingman (1982a, 1982b) demonstrated that when the size of a population is substantially larger than the number of individuals sampled from it (N > > n), the probability that more than two lineages coalesce per unit time becomes vanishingly small, and the shape of a genealogy is described entirely by the number of samples (n) and the rate at which two lineages coalesce, which I refer to as the “pairwise coalescent rate.” In a neutrally evolving haploid population with constant size N, the pairwise coalescent rate is 1/N for all t. Previous studies have shown that when selection acts at many closely linked sites, this rate increases gradually with (backward) time (O'Fallon et al. 2010; Seger et al. 2010), reducing the mean time to coalescence and producing a characteristic bulge in the distribution of coalescence times. Few analytic results exist to describe how the rate changes as a function of time, and advances so far have been obtained using simulation. Here, I expand on previous simulation results to explore how the pairwise coalescent rate function depends not only on time but on the amount of time between sampling events.

Consider a haploid population of constant effective size N. When two individuals are sampled from this population at times t₁ and t₂, let the probability that they share a common ancestor t generations in the past, conditional on not having previously coalesced, be described by the function φ(t;t₁,t₂). As argued above, under neutrality

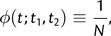(1)

for t > Max(t₁,t₂). The probability that two individuals first share a common ancestor at time t is described by the density

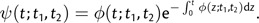(2)

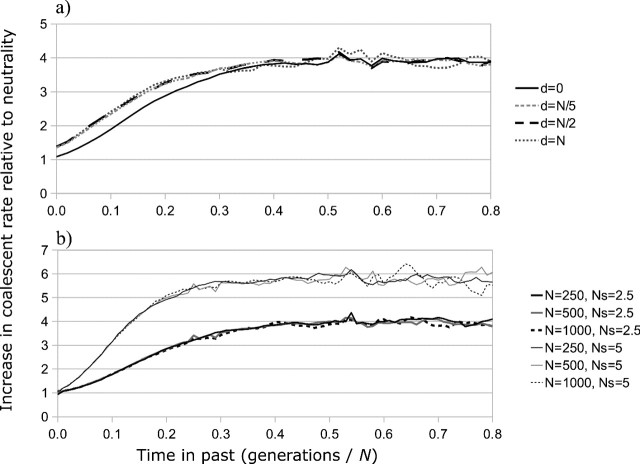
Under neutrality, ψ(t;t₁,t₂) is the probability density of an exponentially distributed random variable with mean N. However, little theory exists regarding the form of φ(t;t₁,t₂) for sequences under selection, and I turn to simulations to investigate the shape of the pairwise coalescent rate function. As above, simulations were performed with TreesimJ (O'Fallon 2010a), using constant population size, Kimura 2-parameter mutation, 1,000 selected sites with identical selection coefficients, and several mutation rates and selection coefficients. Investigation of the resulting rate functions demonstrates that, although coalescent rate may be substantially increased by selection, relatively little change is brought about by sampling sequences at different times (fig. 1a). When sequences are sampled d generations apart, pairwise coalescent rate curves are nearly identical for d = N/5 and d = N. In general, coalescent rate is increased moderately for a short period immediately following the second sampling event, but, as intuition suggests, the maximal coalescent rate reached is identical to that found when sequences are sampled at the same time. In addition, the curves appear to obey expectations from diffusion theory and are insensitive to changes in population size if Θ and Ns are held constant (fig. 1b).

FIG. 1.

Pairwise coalescent rate inferred from forward simulation. (a) Pairs where individuals were sampled “d” generations apart. In all curves, N = 250, Θ = 0.1, Ns = 2.5, and 1,000 sites experienced selection. (b) Two sets of curves in which population size was varied but Θ and Ns were held constant.

A Likelihood Calculation for Serially SampledGenealogies under Selection

In this section, I propose a new method of calculating the likelihood of observing a genealogy with noncontemporaneous tips, conditional on population size (N) and a single new parameter ρ that characterizes the increase in pairwise coalescent rate brought about by selection. The calculation involves several approximations regarding the manner in which coalescent rate varies over time and across lineages. First, it is assumed that the pairwise coalescent rate is unaffected by the time difference between samples, such that φ(t;t₁,t₂)≡φ(t;t_max,t_max), where t_max = max(t₁,t₂).

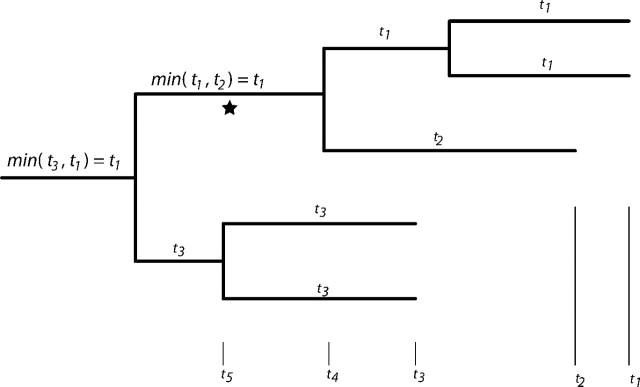
Second, a means of resolving instances in which a lineage is ancestral to samples taken at multiple different times is required. For instance, consider the lineage indicated by the asterisk (☆) in figure 2, which is ancestral to two samples taken at time t₁ and one taken at time t₂. To compute the probability of a coalescent event between ☆ and the lineages sampled at time t₃, I assume that there is a function g(t₁,t₂) that depends only on the depths of lineages that coalesced to create the lineage in question. That is, no account is made of the fact that there are two t₁ lineages and one t₂ lineage; only the times associated with the two coalescing lineages are examined. Intuitively, g(t₁,t₂) should return a result between t₁ and t₂, and the following reasoning suggests that the value should be closer to min(t₁,t₂) (where smaller times correspond to more tipward values). As mentioned above, the high coalescence rates associated with selection are due to the fact that, when traced backward in time, lineages occupy progressively higher fitness states. Two lineages are more likely to share a parent when they have similar fitnesses and when their fitness is high. Therefore, when two lineages coalesce, the probability that both were in a relatively high fitness state is much greater than the probability that they were both close to the mean population fitness. Thus, immediately rootward of a coalescence event, a lineage in question is likely to have a relatively high fitness, a state which is also induced by relatively long times since the sampling event. Without a more rigorous theory to guide the choice, I assume that g(t₁,t₂)≡min(t₁,t₂). Using this strategy, a “sampling height” can be assigned to each branch in the tree by starting from the tips and assigning heights as one progresses toward the root of the tree, always favoring the minimum height encountered when coalescent events occur.

FIG. 2.

Diagram demonstrating the technique used to assign sampling height to lineages when a lineage is ancestral to tips sampled at multiple times. See text for explanation.

Finally, to describe the effects of selection on the pairwise coalescent rate, I introduce a modification to the coalescent rate function as follows:

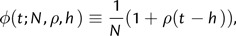(3)

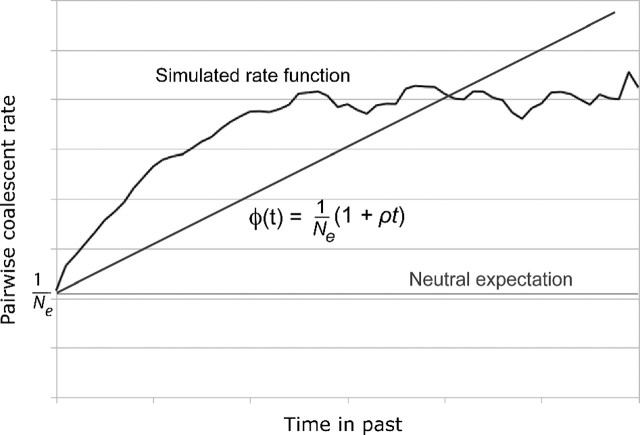
where h is the sampling height of the lineage in question. This new function depends on the sampling times t₁ and t₂ only through their effects on the sampling height h, and assumes that coalescent rate increases linearly in sampling height with slope ρ. At first, such a function may seem implausible since it implies that the coalescent rate increases without bound in t. Additionally, it is a poor fit for the pairwise rate functions observed from simulation data, which appear to approach an asymptote with large t (fig. 3). However, the linear function enjoys distinct advantages that form a compelling argument for its use. First, it introduces only a single additional parameter, ρ. Previous work with more complicated functions involving several parameters yielded biased and imprecise results. Although part of the inaccuracy is likely due to the greater number of parameters estimated, investigations revealed that most coalescent events occur at very low sampling heights, where the rate function is approximately linear (fig. 1). Hence, at least for the sampling schemes investigated here, little power may exist to infer higher-order components of the rate function. An additional advantage of the linear function is that its integral may be evaluated analytically and expressed without transcendental functions, aiding computational performance.

FIG. 3.

Diagram comparing the assumed rate function to an arbitrary simulated pairwise coalescent rate. See text for explanation.

In a manner similar to the neutral case, I compute the likelihood of a genealogy given N and ρ independently for each coalescent interval, where intervals are bounded by either sampling or coalescent events. Consider an interval bounded by tipward time t_a and rootward time t_b, with m total lineages categorized by their sampling height into i groups, where all n_i members of group i share sampling height h_i. Calculate first the probability that no coalescences occur between groups or within any group between the times t_a and t_b. Within group i, the pairwise coalescent rate is φ(t;N,ρ,h_i) and there are n_i2 possible pairings. The probability that no coalescent event occurred is then 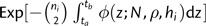. For pairs in which individuals are taken from different groups, say group j and group k, the sampling heights will differ. In this case, the maximum sampling height, here denoted h_j,k, is used to modify t. Since there are n_j individuals in group j and n_k individuals in k, there are n_jn_k possible pairings involving one individual from j and one from k. The probability that there is no coalescent event between j and k individuals is then . Multiplying these probabilities within each group and then between each pair of groups then yields the probability that no coalescent event occurred between the times t_a and t_b.

If the interval in question ends with a sampling event, there is nothing more to compute. However, if the interval ends in a coalescent event, the probability that a coalescence of the observed type occurred must be included. This term is the instantaneous rate of coalescence of lineages of the type that was observed to coalesce, either (n_i2)φ(t;N,ρ,h_i) if the coalescent event involved two individuals in group i, or n_jn_kφ(t;N,ρ,h_j,k) if two individuals from groups j and k coalesced.

All computations are performed using time scaled in units of population size (the current population size value in the MCMC chain). Therefore, the inferred posterior distributions do not depend explicitly on population size, only the compound parameters Θ and σ = Ns.

The approach described above makes an important assumption regarding the exchangeability of lineages under selection. In particular, the method ignores the fact that coalescences alter the expected fitness of a lineage, and hence the propensity of that lineage to coalesce further. The fact that a lineage's coalescent rate may be altered by factors other than the sampling height of the lineage implies that lineages with equal sampling heights are not exchangeable, and a more exact treatment would take into account two additional effects. First, because lineages that coalesce at a certain point are more likely to participate in additional coalescences, tree topologies are more likely to be unbalanced or skewed than under neutrality (Maia et al. 2004; Seger et al. 2010). By ignoring this factor, the new calculation produces trees that are more balanced than expected under selection, an effect likely to be most prominent in cases where the data are relatively uninformative.

Second, because interval length is influenced by the fitness of the lineages in the interval, the lengths of adjacent intervals are likely to covary to an extent that depends on the rate at which lineages change fitness over time. If lineages traverse fitness states relatively slowly, then a short interval predicts that adjacent intervals are likely to be short since the lineages involved would have a high fitness and, therefore, high coalescent rate. Such covariation could generate misleading estimates of parameters since successive short (or long) intervals are regarded as very unlikely by the method unless selection is very strong (or very weak). To investigate the accuracy of the independence assumption, I collected all coalescent interval lengths for groups of genealogies simulated under several combinations of Θ and Ns (table 1). For each parameter combination, I calculated Pearson correlation coefficients between interval lengths of adjacent intervals for all genealogies. While the correlation coefficient varied considerably over intervals, the mean coefficient across intervals was close to zero for all parameter combinations assessed. Additionally, no trend in the amount of correlation, either with genealogical depth or increasing selection coefficient, was apparent. Thus, the independence approximation appears to be justified, at least for the parameter combinations examined in this study.

Table 1.

Correlation coefficients for adjacent interval lengths from genealogies simulated under selection.

Θ	Ns	ρ (min, max)
0.025	5	-0.015 (-0.22, 0.28)
0.025	20	-0.008 (-0.21, 0.22)
0.025	50	-0.002 (-0.23, 0.35)
0.25	5	-0.05 (-0.32, 0.25)
0.25	25	-0.01 (-0.31, 0.45)
0.25	50	-0.012 (-0.34, 0.44)

ρ is the mean coefficient across all intervals for 50 genealogies. Min and max are extrema for intervals computed across all genealogies.

Analysis of Dengue Virus Isolates from Puerto Rico and Thailand

The virus is a single-stranded positive sense RNA virus in the family Flaviviridae, with a genome approximately 11kb in length encoding ten proteins. DENV exists as four distinct serotypes labeled DENV-1 to DENV-4.

To assess the performance of the new likelihood calculation on empirical data, I examine two serially sampled data sets of dengue virus. The first is a series of dengue virus type 4 (DENV-4) isolates sampled from 1981 to 1998 in Puerto Rico. Subsequent to the re-introduction of the mosquito vector in the 1970s, all four types of dengue virus have appeared in Puerto Rico, with type 4 first noted in 1981 (Gubler 1998). In 1982, type 4 accounted for nearly 90% of all cases, but since has maintained a frequency of 10–40% (Bennett et al. 2010), despite substantial year-to-year fluctuations in the total number of reported infections. The data comprised of 82 isolates, each consisting of 2,552 base pairs of the DENV-4 polyprotein precursor, encompassing the coding region for the Core (C), Matrix (M), and Envelope (E) proteins. Isolates were sampled and sequenced as described in Bennett et al. (2010). Because previous studies have suggested that inclusion of selected sites in data used to reconstruct genealogies may bias branch length estimates (O'Fallon 2010b), the analysis included only sites in the third codon position.

The second data set consists of 95 DENV-2 isolates sampled from Thailand between 1974 and 2001, as previously described in Zhang et al. (2006). The sequences used were from E gene only, and as above only sites in the third codon position were used. As in the DENV-4 case, a generation time of 2 weeks was assumed.

The data sets were analyzed using both the new likelihood calculation as well as the neutral coalescent likelihood model that is the default implementation in BEAST. All runs were conducted with an Hasegawa–Kishino–Yano (HKY)+Γ₄ model of nucleotide evolution, with N, μ, the gamma shape parameter α, base frequencies, transition to transversion ratio, and the new model parameter ρ estimated from the data. The MCMC chain was run for 10,000,000 steps, which was sufficient to achieve effective sample sizes of greater than 1,000 for most parameters. As for the simulation cases, an exponential prior with mean 10 was used for the distortion parameter ρ, and uniform priors were used for all parameters except the transition to transversion ratio, where a Jeffreys prior was employed.

Results

Bias in Population Size Estimates Using Current Methods

Using Bayesian genealogy sampler BEAST (Drummond and Rambaut 2007), I estimated the posterior distributions of population size for data sets with several different selection coefficients. In all cases, the true population size was 1,000 individuals and the mutation rate was 10 ^{− 4} per site per generation. All posteriors shown are the averages over at least 30 independent data sets. As mentioned above, the simulated “genome” consisted of 1,000 sites at which mutations had no selective effect completely linked to 1,000 selected sites, and only the neutral sites were used as input. In general, inference of population size requires knowing the generation time. In this analysis, I ignore this potential source of error and assume that the generation time is known exactly.

In the neutral case, the default BEAST method recovers the correct population size admirably, with a mean posterior value across data sets of 1057.6 (fig. 3a). However, as the intensity of selection increases, population size estimates decrease substantially. When the selection intensity Ns = 5, the mean inferred population size is 511, a 2-fold decrease from the true value. Similarly, at Ns = 25, the mean is 284. This bias is not accompanied by an increase in confidence intervals. Instead, apparent precision increases with the strength of selection, potentially creating a misleading impression of confidence.

When the mutation rate and strength of selection are held constant, increasing the population size results in an increasing degree of downward bias in the inferred population size (fig. 3b). At larger sizes, the amount of bias may be significant. For instance, when N = 8,000, the mean estimated population size is 1,481 and the standard deviation 274, thus the inferred value is some 23 standard deviations less than the true value.

This bias is consistent with the genealogy-distorting effects of selection, which increases coalescent rate and therefore decrease tree depth. Current models include only a single parameter that influences coalescent rate, population size, and therefore an increased rate can only be interpreted as evidence for a reduced size. Whereas the biases identified here are considerable, some evidence suggests that they may be even more severe in populations with very large size, such that Θ and Ns are both large. Seger et al. (2010) found instances in which the coalescent rate was increased by a factor of 30 or more from the neutral expectation (at N≈65,000, μ = 10 ^{− 6}, s≈0.001 with 2048 selected sites), suggesting that effective size estimates may be more than an order of magnitude below their true value in when inferred from data sets with similar parameters.

Likelihood Inference Using a Time-dependent Pairwise Coalescent Rate

The new likelihood calculation, implemented in BEAST, allows for estimation of population size and a new parameter that affects the shape of the coalescent rate function, ρ. Values of ρ near zero indicate neutrality, whereas values greater than zero suggest that the coalescent rate has increased with the sampling height of lineages (not the total depth of the tree), in a manner consistent with purifying selection at linked sites among the sequences.

To assess the accuracy of the new method, data were generated using forward simulation in the manner described above. Briefly, population size was held constant in all cases, and individual genomes consisted of 1,000 selected sites which all shared the same selection coefficient s. Serial samples were collected every N/2 generations, and in all cases ten individuals were sampled over five total sampling periods to yield trees with 50 total tips. These “true” genealogies were used directly as input to BEAST, thus the results reported in this section do not incorporate error in estimation of the genealogy.

A uniform prior was used for the population size parameter N, but experimentation indicated that accuracy of the procedure improved when an exponential prior was used for the distortion parameter ρ. Such a prior discounts very large values of ρ, which can lead to poor MCMC mixing and estimates of population size that are biased upward. The exponential prior also favors small values of ρ, therefore producing “conservative” estimates of distortion and improving performance when the true value of ρ is zero.

The new likelihood calculation allows for significantly more accurate estimation of population sizes when selection is influencing the genealogy (fig. 5). However, the new method is less precise, yielding confidence intervals somewhat larger than those produced by the old method, possibly due to the additional parameter that must be estimated from the data. In addition, the posterior distributions exhibit some rightward skew that caused the mean to overestimate the true value in some cases. The upward biasing results in part from the chosen parameterization. Under neutrality, the true value of ρ is equal to its lower bound (0), hence any error in estimation leads to an overestimate ρ and therefore inflated population size estimates. In general, the region of highest posterior probability (the maximum a posteriori region) is closer to the true value than the mean of the posterior.

FIG. 5.

Inferred posterior densities of population size using the new likelihood calculation for several different strengths of selection. (a) N = 1,000 and Θ = 0.01. (b) Population size as shown, Θ = 0.01, Ns = 10. 1,000 selected sites in all cases.

Results for additional combinations of N, μ, and s are presented in table 2. Reported values are means of 50 genealogies for each combination of N, μ, and s. Maximum a posteriori estimates of N demonstrate that the new method yields more accurate results in a variety of cases. When both θ and s are large, estimates of N are biased toward smaller values, but less so when using the new method than in the default BEAST implementation. In addition, the fraction of runs in which the 95% central posterior density (CPD) contained the true value was tabulated. Under neutrality, both methods perform well by this metric, with the 95% CPD containing the true value in approximately 95% of all cases in the default BEAST method, and in 87% of cases under the new method. When selection influences genealogical shape, however, the default method performs very poorly, with few or no runs containing the true value in the 95% CPD. In contrast, the new method performs well, with 95% CPD interval containing the true value in a high proportion of runs in all cases.

Table 2.

Performance of old and new likelihood calculations for several combinations of N, μ, and s.

			Default Method		New Method
Population size (N)	θ	Ns	MPE	Fraction containing true value	MPE	Fraction containing true value
500	0.01	0	470 (93)	0.98	537 (185)	0.87
500	0.01	10	317 (65)	0.14	475 (192)	0.96
500	0.05	20	187 (38)	0.0	387 (116)	0.94
1000	0.01	0	980 (233)	0.95	1088 (343)	0.87
1000	0.01	10	647 (137)	0.2	1019 (356)	0.97
1000	0.025	20	486 (104)	0.0	922 (280)	0.95
1000	0.05	25	365 (68)	0.0	804 (225)	0.9
2500	0.025	0	2578 (515)	0.95	2880 (830)	0.87
2500	0.025	10	1270 (283)	0.0	2443 (884)	0.96
2500	0.025	25	1315 (243)	0.0	1902 (701)	1
5000	0.05	10	2635 (557)	0.0	5055 (1711)	0.97
5000	0.025	25	2467 (501)	0.0	4221 (1481)	0.98

MPE, Maximum a posteriori estimate. Fraction containing true value indicates the fraction of data sets in which the 95% CPD contained the true population size.

An additional feature of the method is that it permits a visualization of the inferred pairwise coalescent rate function φ(t;N,ρ) and hence a way to validate the new method by comparing MCMC output to pairwise rate functions estimated directly from simulations (fig. 6). Because a rate function is determined entirely by N and ρ , multiple rate functions may be constructed by collecting N, ρ pairs from MCMC output, and investigating the density of many such functions. In figure 6, densities were computed and averaged over 50 MCMC runs for each strength of selection (Ns = 20, Ns = 2, and Ns = 0). The resulting plots demonstrated close correspondence between the functions inferred from MCMC and the rate function computed directly from simulations, suggesting that the rate functions inferred using the new method are, on average, accurate reconstructions of the underlying distortion process.

FIG. 6.

Comparison of pairwise coalescent rate function (φ(t;N,ρ)) inferred from MCMC output to rate functions computed directly from simulation data (black lines, for Ns = 0 the analytic expectation was used) for several strengths of selection. Lighter regions indicate greater posterior density. Top: Ns = 20, middle: Ns = 2, bottom Ns = 0. N = 1,000 and μ = 2.5×10 ^{− 5} in all cases.

Analysis of Dengue Virus Samples

When genetic data are sampled from obligate pathogens collected across hosts reconstruction of the genealogies reflects the transmission network of the pathogens, and therefore estimates of effective population size are in fact estimates of the “effective” number of infected hosts (Grenfell et al. 2004). Similarly, assessments of selection parameters based on genealogical structure, such as the ρ parameter introduced here, reflect the between-host process of transmission and infection and not, for instance, antigenic escape within hosts. In terms of the model introduced here, selection is defined as heritable variation in reproductive success, and at the between-host level this implies heritable differences in the number of new infections produced by a particular lineage.

Analysis using the default BEAST implementation (assuming a constant population size) suggests that the two dengue serotypes share similar demographic properties. Assuming a generation time of 2 weeks, the effective number of infections among the DENV-4 samples from Puerto Rico was approximately 18 compared with 21 in the DENV-2 samples from Thailand. The long-term effective size estimates appear roughly compatible with the demographic inference performed in Bennett et al. (2010), which found that the infection size varied from < 10 to nearly 100 among the Puerto Rico samples.

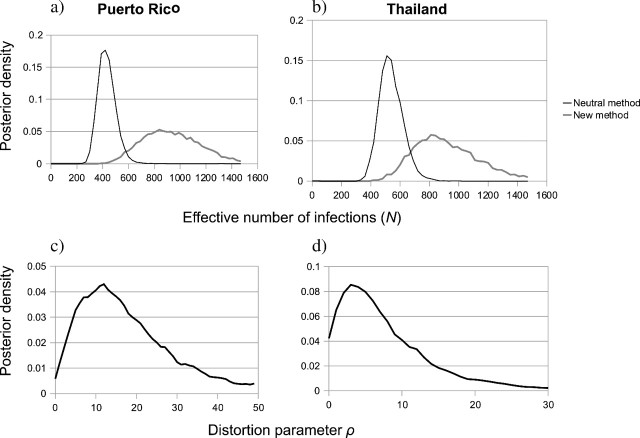
Performing the same analysis with the new method yielded a strong signal of selection-induced genealogical distortion and substantially higher infection size estimates for both data sets (figure 7). The mean effective number of infections was nearly identical for both data sets, roughly 36 and 37 for the Puerto Rico and Thailand data sets, respectively; 95% CPD intervals were also very similar, about 20–54 in both cases. Despite the difference in effective infection size produced by the new method, other model parameter estimates appear very similar. For instance, the TMRCA among the Puerto Rico samples for the default and new models is 38.3 (95% CPD 35.75–41.41) and 40 (95% CPD 36.6–43.0) years, respectively. Similarly, TMRCAs for the Thailand samples were 116.25 (96.3–137) and 113.75 (95.3–133.91) years for the default and new models.

FIG. 7.

(a,b) Posterior distributions of effective number of infections using both the standard and the new likelihood calculation, for Puerto Rico and Thailand data sets, respectively (c,d) Posterior distribution of genealogical distortion parameter ρ for the Puerto Rico and Thailand data sets.

Discussion

The analysis presented here demonstrates that selection of moderate strength at many linked sites can significantly bias common genealogy-based methods of inferring population size, and a modified likelihood calculation that corrects for the bias while allowing for estimation of a new parameter describing the degree of selection-induced distortion is presented. The new likelihood calculation assumes that selection at many sites affects genealogical structure primarily through a time-dependent alteration of the pairwise rate of coalescence and ignores the nonexchangeability of lineages with the same sampling height. Despite these simplifying assumptions, the new calculation yields significantly more accurate estimates of population size, and coalescent rate functions inferred from MCMC output appear to closely match the pattern of rate increase observed in simulations (fig. 6). Estimation of population size is made possible by use of the serial coalescent framework, in which demographic and mutation rate parameters are separable (Rodrigo and Felsenstein 1999; Drummond and Rodrigo 2000; Drummond et al. 2002).

The analysis is consistent with previous work documenting insensitivity of mitochondrial diversity with population size (Bazin et al. 2006), and calls into question studies that seek to infer population size from genetic data linked to selected sites. Inferences made using mitochondrial data are particularly concerning since recombination is absent or very infrequent, and mitochondria mutate rapidly and have many selected sites. If the degree of selective constraint and the mutation rate of mitochondria are similar across populations and species, then inferred sizes and measures of diversity may display little sensitivity to population size differences (fig. 4b). When selected sites are included in the data set, distortions are likely to be exaggerated even beyond those demonstrated in figure 4 because inferred basal branch lengths will be shorter than the true branch lengths (O'Fallon 2010b).

FIG. 4.

Posterior distributions of population size estimated using BEAST, for several intensities of selection. (a) The true population size is 1,000 individuals, μ = 10 ^{− 4}, 1,000 sites under selection, selection intensity as shown. (b) μ = 10 ^{− 4}, s = 0.0025, 1,000 sites under selection, true population size as shown.

The two dengue virus data sets examined reveal very similar stories of selection at the between-host level. When the long-term effective number of infections is estimated using standard techniques, both populations yield values of approximately 20. However, when the new likelihood calculation is employed, infection size estimates are increased nearly 100%, to near 36. In addition, the new likelihood calculation yields estimates of the distortion parameter ρ suggestive of selection, with posterior means of 9.2 and 18.4 for the Thailand and Puerto Rico populations, respectively. Together, these results suggest that Dengue virus exhibits moderate heritable variation in transmission and infection success, and that these factors should be included when reconstructing the demographic history of the virus.

The approach described here differs from other examinations of the effect of selection on genealogies in that no specific description of the selection model is proposed. Other studies have, for instance, examined inference procedures in a one-locus two-allele framework (e.g., Coop and Griffiths 2004; Slatkin et al. 2008), with precise descriptions of forward and backward mutation rates, selection intensities, etc. However, models that seek to describe selection coefficients and mutation rates for empirical DNA sequences are likely to be intractable analytically. As an alternative, the procedure described here searches for the particular distortions to the coalescent rate that are believed to be the products of selection at many linked sites. Both approaches have advantages and disadvantages; the method presented here is best applied to loci with multiple segregating mutations affecting fitness, as may be the case with the mitochondrion or RNA viruses with relatively high mutation rates. However, if mutation rates are low and population sizes modest, models that assume only a small number of segregating alleles (such as two) are likely to be more appropriate.

Although this work has not addressed the possibility of inferring complex population size changes simultaneously with genealogical distortion, such calculations would be feasible using the framework described here. However, in the absence of informative priors regarding population size, little power may exist to discriminate fluctuations in size and selection-induced rate variation since both may produce similar effects. In addition, computation of the likelihoods would likely require repeated numerical integration of the coalescent rate function (of the form φ(t;N,ρ)/N_e(t)), and therefore efficient computation may be a significant challenge.