Fast Diffusion Imaging with High Angular Resolution

Abstract

Purpose

High angular resolution diffusion imaging (HARDI) is a well-established method to help reveal the architecture of nerve bundles, but long scan times and geometric distortions inherent to echo planar imaging (EPI) have limited its integration into clinical protocols.

Methods

A fast imaging method is proposed here that combines Accelerated Multi-shot Diffusion Imaging (AMDI), Multiplexed Sensitivity Encoding (MUSE) and Crossing Fiber Angular Resolution of Intravoxel Structure (CFARI) to reduce spatial distortions and reduce total scan time. A multi-shot EPI sequence was used to improve geometrical fidelity as compared to a single-shot EPI acquisition, and acceleration in both k-space and diffusion sampling enabled reductions in scan time. The method is regularized and self-navigated for motion correction. Seven volunteers were scanned in this study, including four with volumetric whole brain acquisitions.

Results

The average similarity of microstructural orientations between under-sampled datasets and their fully sampled counterparts was above 85%, with scan times below 5 minutes for whole brain acquisitions. Up to 2.7-fold scan time acceleration along with four-fold distortion reduction was achieved.

Conclusion

The proposed imaging strategy can generate HARDI results with relatively good geometrical fidelity and low scan duration, which may help facilitate the transition of HARDI from a successful research tool to a practical clinical one.

Introduction

High angular resolution diffusion imaging (HARDI) has grown into a useful research tool for probing the complex microstructure of the nervous system and the architecture of white matter bundles (1,2). Integrating HARDI into clinical protocols might provide considerable added value, especially for neurosurgical planning and treatment monitoring (3,4). However, technical limitations such as long scan times and pronounced spatial distortions appear to have limited clinical adoption. The goal of the present work was to develop a HARDI implementation with reduced scan time and improve geometric fidelity to meet the demands of clinical environments.

The main characteristic of the HARDI scheme is the large number of diffusion encoding directions, typically hundreds, in sharp contrast with more basic schemes that may sample only a few. Because so many directions get probed, HARDI can help resolve fiber crossings, but requires relatively long scan times to do so. Strategies have been proposed to help reduce the number of directions and total scan time, such as utilizing spatial symmetries in the diffusion signal (5). Algorithms based on compressed sensing to exploit sparse features in the orientation distribution of white matter bundles have also been investigated. One such method, ‘Crossing Fiber Angular Resolution of Intravoxel Structure’ (CFARI), subsamples the data in the diffusion encoding space and identifies crossing fibers through an l1-norm regularization strategy similar to the recovery of compressed sensing data (6,7). An algorithm similar to CFARI was employed here to help reduce the number of sampled directions and total scan time.

Furthermore, HARDI is typically built upon the single-shot echo planar imaging (EPI) pulse sequence and for this reason proves vulnerable to geometric distortions in the presence of magnetic field inhomogeneities, especially at higher field strengths. Compared to single-shot EPI, multi-shot EPI can very much reduce distortion: k-space is divided into several interleaved segments acquired one at a time, increasing the sampling bandwidth in the blip-encoded direction and decreasing distortion accordingly (8). On the other hand, multi-shot EPI requires a longer scan time to accomplish the sampling of the entire k-space and is more susceptible to motion. Methods such as parallel imaging have been proposed to accelerate segmented EPI (9,10) and typically the acceleration factor is chosen to equal the number of interleaves, i.e., a single interleave is sampled. Such an accelerated single-shot EPI method combines the improved spatial fidelity of multi-shot sequences with the short acquisition time of a single-shot sequence. However reconstruction noise from parallel imaging will become significant as the acceleration increases. Regularization can be employed to help limit the noise amplification and associated SNR cost (11,12). In the present work, a regularized, self-navigated parallel imaging method was employed to accelerate EPI acquisitions by four-fold, combining improved geometric fidelity with relatively-short scan time.

The purpose of the present work was to introduce a fast HARDI method with good geometrical fidelity by accelerating the acquisition both in k-space (to reduce distortion) and in the diffusion-encoding space (to reduce acquisition time). Novelty emerges from the combination of regularization and k-space sampling ideas from the ‘accelerated multi-shot diffusion imaging’ (AMDI) method in (12), self-referencing ideas from the ‘multiplexed sensitivity encoding’ (MUSE) method in (13,14), and compressed sensing ideas from the CFARI method (6,7). The resulting approach for faster and less-distorted HARDI imaging was used here to image seven healthy volunteers. The acquisition for a whole-brain 3D coverage can be achieved in less than 5 minutes.

Methods

Ordering and subsampling scheme in diffusion space and k-space

In general, diffusion-encoded images can be characterized by the direction being probed and by the strength of the diffusion encoding. Diffusion-weighted imaging (DWI) schemes have been proposed over the years that call for different combinations of directions and b-values to be collected: For example, the HARDI scheme calls for a single non-zero b-value to be sampled for a large number of different directions, along with a b = 0 (b₀) reference. In contrast the AMDI method from (12) employed a diffusion encoding scheme that might be best described as Cartesian in the sense that a given set of b-values is collected for each one of several different diffusion encoding directions. In order to increase acquisition efficiency, the AMDI method prescribed how the choice of interleaves should be adjusted from one diffusion encoding to the next. The present implementation involved converting ideas originally developed for a Cartesian diffusion sampling scheme in (12) to the HARDI one, and required changes to the way k-space interleaves are picked for given diffusion images.

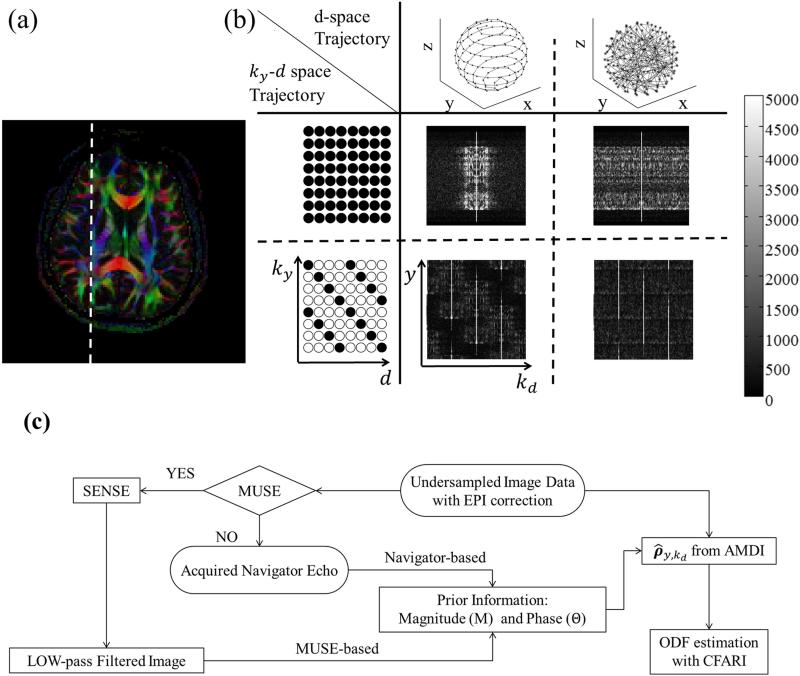
In Fig. 1, a regular, fully-sampled HARDI dataset was employed to help illustrate different subsampling schemes. A color fractional anisotropy (FA) slice is shown in Fig. 1a, along with a dashed white line indicating the 1D array of pixels further employed in Fig. 1b. The left-most column in Fig. 1b depicts the sampling scheme in k_y – d space: Fully sampled (middle row) or subsampled by R_k = 4 (bottom row). The top row in Fig. 1b depicts two extreme choices in the ordering of directions d: A smooth ordering along a spherical spiral path (central column) or a randomized ordering (right-most column). Magnitude results in y – k_d space, which is the Fourier dual of k_y – d space, are shown for all combinations of full vs. R_k = 4 sampling along k_y and of smooth vs. randomized ordering along d.

Fig. 1.

(a,b) A fully-sampled HARDI dataset is used to illustrate the proposed sampling and ordering scheme in k_y – d space. The present implementation sampled one out of every four k_y lines, as shown in the lower row in (b), and employed a smooth ordering along d, as shown in the middle column in (b). (c) The undersampled data were then reconstructed using the proposed algorithm, depicted here with a block diagram. See text for more details.

The sampling scheme implemented here optimized smoothness in d space, as depicted in the central column of Fig. 1b. The main purpose of Fig. 1b was to help justify this choice by contrasting data in the central (smooth ordering) and right-most column (randomized ordering). With smooth ordering along d, signals tended to concentrate around the k_d = 0 region, as seen in Fig. 1b. Even when R_k = 4 aliased replicas were created due to k_y subsampling (lower row in Fig. 1b), the amount of signal overlap among these replicas remained minimal in the ‘smooth’ case, as these replicas had limited extent along k_d. The subsampled k_y – d sampling scheme as shown in the left-most column of Fig. 1b, ensured that these replicas were shifted with respect to each other in y – k_d space, again to minimize signal overlap. While in the ‘smooth’ case replicas had a tendency to fall mostly side-by-side in y – k_d space, signals in the ‘randomized’ case tended to spread over the entire k_d axis and a full R_k = 4 overlap might have to be handled at most locations in y – k_d space. Any remaining overlap among replicas can be handled by a regularized and motion-corrected parallel imaging implementation as described below. However, minimizing the amount of signal overlap the algorithm must handle, as in the central column of Fig. 1b, can improve the odds of reconstructing good-quality images with the present processing. A k-space acceleration setting of R_k = 4 was employed here, as depicted in Fig. 1b (lower row), with the smooth sampling scheme in d-space (central column, Fig. 1b) to ensure that, at the very least, the stronger signals from different replicas do not overlap. Subsequently, the 4-fold signal overlap in y – k_d space was handled by the algorithm as depicted in Fig. 1c and described in the next section.

As opposed to the k-space acceleration factor R_k, the d acceleration factor R_d was not as well defined, since the concept of a fully-sampled d axis is open to interpretation: The more directions one samples, the better HARDI might resolve crossings, but no single widely-accepted number of directions can be clearly labeled as fully-sampled. In the present work, reference HARDI results were obtained using 128 directions and d acceleration was defined in comparison with this reference, i.e., R_d = (128 / N_d) where N_d is the number of sampled directions. Results were obtained here with N_d values of 64, and 48, i.e., for R_d acceleration factors of 2 and 2.7, respectively. In all cases the N_d sampled directions were evenly distributed along a smooth double spherical spiral path, as illustrated in Fig. 1b top row, central column.

k-space acceleration

The k-space signal s_ky,d associated with the d-th diffusion direction was modeled as:

$${\mathit{S}}_{k_y,d}={\mathbf{F}}_y\mathbf{C}ϴ{\mathbf{F}}_d^H{\rho }_{y,k_d}={\mathbf{E}}_yϴ{\mathbf{F}}_d^H{\rho }_{y,k_d},$$ (1)

where F_y and F_d perform Fourier transforms along y and d, respectively, H represents a conjugate transpose operator, C and Θ are diagonal matrices that represent the coil sensitivity and motion-induced phase errors, respectively, and ρ_y,kd is a vertical vector representing the imaged object in y – k_d space. EPI Nyquist ghost corrections are assumed to have already been applied to ρ_y,kd and are not explicitly included in the model from Eq. 1. For compactness, a spatial encoding operator E_y = F_yC was also defined in Eq. 1. Images ${\widehat{\rho }}_{y,k_d}$ were obtained by solving Eq. 1 subject to a least-square error minimization:

$${\widehat{\rho }}_{y,k_d}={\min }_{\widehat{\rho }}{\mid {\mathit{s}}_{k_y,d}-{\mathbf{E}}_yϴ{\mathbf{F}}_d^{\mathrm{H}}{\widehat{\rho }}_{y,k_d}\mid }_2^2+\lambda {\mid {\mathbf{M}}^{-1}{\widehat{\rho }}_{y,k_d}\mid }_2^2,$$ (2)

where the first term is for data consistency and the second term for regularization. The regularization matrix M is diagonal and λ is a scaling factor (15-18); both will be further discussed later in the text. The solution is expressed as:

$${\widehat{\rho }}_{y,k_d}={\left({\mathbf{F}}_d{ϴ}^{\mathrm{H}}{\mathbf{E}}_y^{\mathrm{H}}{\mathbf{E}}_yϴ{\mathbf{F}}_d^{\mathrm{H}}+\lambda {\mathbf{M}}^{-2}\right)}^{-1}{\mathbf{F}}_d{ϴ}^{\mathrm{H}}{\mathbf{E}}_y^{\mathrm{H}}(\mathbf{I}+\lambda {\mathbf{M}}^{-2}){\mathit{s}}_{k_y,d}.$$ (3)

Equation 3 is of a form widely employed for acceleration methods. In addition to a conventional pseudo-inverse computation, Eq. 3 further employs a scaling term (I + λM⁻²) where I is the identity matrix, as employed in (19) to partly compensate for regularization-related signal scaling. When using zeroth-order Tikhonov regularization, with M = I, such term might be unnecessary as it would merely amount to global scaling. But when M differs from I and different locations in the solution space are regularized differently as done here, the (I + λM⁻²) term may help obtain a more faithful reconstruction.

To solve Eq. 3, prior information including motion-induced phase errors Θ and a regularization matrix M was needed. In our prior work (12), such information was obtained from low spatial resolution navigator echoes. The requisite for an additional echo potentially reduced the number of slices N_z sampled during a given TR. For this reason, to increase N_z for greater volumetric coverage, a self-referenced approach that did not require navigator signals was sought here instead. An algorithm similar to MUSE (13,14) was implemented which essentially involved reconstructing data in two iterations: In a first step, image data were reconstructed without phase correction or object based regularization, in other words with λ=0. The resulting low quality images were then blurred to generate low-resolution images that can serve as navigators. In a second step the image data were reconstructed once more, this time using the ‘navigator’ data from the first step to populate the motion-compensation Θ and regularization M terms (12).

More specifically, the acquired data first underwent standard EPI correction, including Nyquist-ghost correction. The fully-sampled b₀ data were motion-corrected and reconstructed as in (20) and averaged; the multi-coil b₀ images obtained as a result images were then employed to generate B₁ sensitivity maps and the matrix C in Eq. 1. From this initial point on, the reconstruction then proceeded as described in the block diagram from Fig. 1c and in Eqs 1-3 above. The motion-related phase correction and the regularization information were retrieved from navigator data; these data can either be acquired directly or emulated from image data using MUSE. In the latter case, with MUSE, the image data were reconstructed a first time by parallel imaging alone, a low pass 64×64 Hamming filter was applied in k_x – k_y space to create a low-resolution dataset, which was then used in place of navigator signals. The matrices Θ and M were populated using actual or emulated navigator data and Eq. 3 was solved. The trace ADC, fractional anisotropy and principal diffusion direction were then evaluated from the diffusion-weighted data, ${\widehat{\rho }}_{y,k_d}$. The regularization factor λ in Eq. 3 was empirically set, within the range from 10⁻² to 10⁻⁴, as described in the Results section.

Diffusion-space acceleration

The diffusion-weighted data ${\widehat{\rho }}_{y,k_d}$ obtained from Eq. 3 were then transformed from y – k_d space to the more conventional y – d space:

$${\mathit{o}}_{y,d}={\mathbf{F}}_d^{\mathrm{H}}{\widehat{\rho }}_{y,k_d}.$$ (4)

While subsampling along k_y improved geometrical fidelity, sampling only a limited number of directions N_d was meant to reduce the acquisition time. To help evaluate the orientation density function (ODF) from only a reduced N_d, a CFARI algorithm was employed to help resolve intravoxel structures, associated with an l₁ – minimization formulation. CFARI models the diffusion weighted signals as linear combinations of several different anisotropic diffusion tensors. With g_d a 3-component vector that gives the 3D orientation of the diffusion encoding direction d, the diffusion weighed signal o(g_d) is modeled as:

$$\mathbf{o}\left({\mathbf{g}}_d\right)=s_0{\sum }_{i=1}^{N_m}{w}_i\exp (-b\ast {\mathit{g}}_d^T{\mathbf{D}}_i{\mathit{g}}_d),$$ (5)

where b is the b-factor, D_i represents the i^th prolate-shaped diffusion tensor being modeled, and w_i is the mixture weighting associated with it. For example, for crossings involving only two different fiber orientations, one would expect to find only two larger-valued w_i weights, while all others should have smaller values. In the present work 512 uniformly separate prolate-shaped tensors were modeled, assuming a 2:1:1 ratio for their diffusion coefficients along principal axes (6,7). Equation 5 can be expressed in matrix form:

$${\mathit{o}}_d=s_0\mathbf{B}\mathit{w},$$ (6)

where B contains the diffusion encoding elements and w the weights. The following l₁ – minimization problem was solved for w, where w was assumed sparse with only a small number of significant entries:

$$\mathit{w}={\min }_{\mathit{w}}{\mid {\mathit{o}}_d-s_0\mathbf{B}\mathit{w}\mid }_2^2+\beta {\mid \mathit{w}\mid }_1.$$ (7)

The regularization factor β was fixed here at 10⁻³. Once the non-negligible elements w_i from w have been identified, the ODF ψ(θ, φ) can be generated from the associated diffusion tensors D_i:

$$\Psi (\theta ,\phi )={\sum }_{i=1}^{N_m}{w}_i\frac{{\left({\mathit{r}}^{\mathrm{T}}{\mathbf{D}}_{\mathbf{i}}^{-1}\mathit{r}\right)}^{-\frac{3}{2}}}{4\pi \sqrt{\det \left({\mathbf{D}}_{\mathbf{i}}\right)}}$$ (8)

where (θ, φ) represent an orientation in spherical coordinates, and T stands for the transpose operation.

Evaluation Metrics

The main purpose of HARDI methods is to reveal the orientation of fiber tracks. As acceleration was performed in k_y and/or d space, metrics were needed to help evaluate the effect of acceleration on the ODF. Two such metrics were developed provided here: a similarity index and an angular dispersion index. The similarity index assessed, on a pixel-by-pixel basis, the overall changes in ODF that might have occurred between two different acceleration scenarios, R₁ = [R_k,1 R_d,1] and R₂ = [R_k,2 R_d,2]:

$$S_{1,2}=\frac{{\sum }_{\theta ,\phi }\left({\Psi }_{R_1}(\theta ,\phi )-\overline{{\Psi }_{R_1}(\theta ,\phi )}\right)\left({\Psi }_{R_2}(\theta ,\phi )-\overline{{\Psi }_{R_2}(\theta ,\phi )}\right)}{\sqrt{\left({\sum }_{\theta ,\phi }{\left({\Psi }_{R_1}(\theta ,\phi )-\overline{{\Psi }_{R_1}(\theta ,\phi )}\right)}^2\right)\left({\sum }_{\theta ,\phi }{\left({\Psi }_{R_2}(\theta ,\phi )-\overline{{\Psi }_{R_2}(\theta ,\phi )}\right)}^2\right)}}$$ (9)

Equation 9 can be understood as a cross correlation between the ODF Ψ_R1 (θ, φ) and Ψ_R2 (θ, φ) for acceleration scenarios R₁ and R₂, respectively. In practice, the summations in Eq. 9 were performed over 1024 different combinations of θ and φ, homegenously spread over a sphere using an electrostatic repulsion algorithm. Because orientation becomes meaningless as FA approaches zero, a threshold of FA > 0.1 was employed. The output of Eq. 9 is a percentage, with 100% denoting perfectly identical ODFs and 0% perfectly different ones. Intermediate values were helpful mostly in relative terms: For example, when compared to a gold standard case, a larger 80% similarity value would be preferable over a smaller 70% one, but in absolute terms it is unclear whether either or both cases might be sufficient for a given task.

The second metric employed here, the angular dispersion index, is related to angular differences in peak ODF diffusion directions. On a pixel-by-pixel basis, one or more angle θ_n was found, where n stands for the number of the ODF peak being probed and where θ_n = 0° would mean no change in the diffusion direction of ODF peak number n. In the present work, only voxels containing at most two significant peak directions were included for analysis, which include about 85% of all voxels in the ROIs analyzed here. The actual angular dispersion index, ${\stackrel{‒}{\theta }}_n$, was defined as the median of θ_n over the assessed volume, and represents the overall angular change in peak ODF diffusion direction as caused by acceleration.

Pulse sequence and scanning

Seven healthy volunteers (male/female = 5/2) were recruited and scanned following informed consent using an IRB-approved protocol. The scans were performed on a 3 T GE Discovery MR750 using a product 8-channel head coil. Scan parameters common to all seven sessions were: Matrix size = 128×128, FOV = 22 cm, and b-value = 1500 s/mm². Other parameters are listed in Table 1: The number of acquired slices N_slice thickness, slice gap, the k-space acceleration factor R_k, the number of EPI shots N_shot, TE, TR, presence/absence of a navigator echo, number of sampled directions N_d, and scan duration. For the accelerated acquisitions, with R_k = 4, the scan duration was equal to (N_d + 12)×TR: A single k-space interleaf was obtained for each diffusion-weighted image, and 12 extra TR periods were required to fully sample the b₀ data (8 TRs for 2 averages of 4 interleaves) and to gather reference information toward Nyquist ghost correction (4 TRs). In contrast, in cases without acceleration (i.e., Subjects 1-3), all interleaves were sampled for all diffusion images including the navigator data; these non-accelerated data were acquired for validation purposes.

Table 1.

Imaging Parameters. All scans were performed with matrix size = 128×128, FOV = 22 cm, and b-value = 1500 s/mm².

Subject No.	Nslice	Slice Thickness/Gap (mm)	Rk	Rd	Nshot	TE (ms)	TR (ms)	Navigator	Nd	Scan time (min:s)
#1 - 3	5	3.0 / 7.0	1	1	4	69.1	3000	YES	128	28:00
#4, 5	40	3.0 / 0.0	4	1	1	73.3	4000	NO	128	9:20
				2			6000	YES	64	7:36
				2.7			4000	NO	48	4:00
#6, 7	40	3.0 / 0.0	4	1	1	73.3	4000	NO	128	9:20
				2					64	5:04
				2.7					48	4:00

For Subjects #4-7, a fast-spin echo acquisition was performed with same FOV and slice setting as the diffusion-weighted acquisition, for comparison purposes. The parameters for the fast fast-spin echo scan were: TR = 7.8s, TE = 102ms, Echo Train Length = 24 and matrix size = 256×256.

Effect of regularization parameters

The parameter λ in Eq. 3 determines how much regularization gets applied during image reconstruction. Reconstructions were performed with λ settings spanning 8 orders of magnitude. While the main purpose of regularization is generally to help keep noise under control, too strong a regularization setting can lead to inaccurate reconstructions. As a rule of thumb, one tries to find the largest possible setting for λ that does not introduce appreciable errors in the reconstruction. Reconstructed FA results were used to help choose a reasonable setting for λ; more specifically, the mean and standard deviation of FA values, for all voxels in a representative image slice (excluding voxels outside the head and voxels with FA < 0.1), were calculated and plotted as a function of λ. The point of inflexion in these curves was used to help choose a reasonable setting for λ. It should be noted that if protocols were changed in ways that deeply impact SNR, such as changes in coil array and/or voxel size for example, one might need to readjust λ accordingly.

Simulated undersampling, from fully-sampled data

Subjects #1-3 were scanned using a fully-sampled 4-shot EPI sequence (R_k = 1), with navigator echo and 128 directions (R_d = 1). Scan time in this case was quite long, about 30 min, as all k-space data for all diffusion directions were acquired. For validation purposes, an R_k = 4 acceleration could be simulated from this dataset by discarding three out of four shots for each diffusion-weighted image; four independent subsampled datasets with R_k = 4 were generated from each fully-sampled R_k = 1 acquisition, and these four datasets were reconstructed separately as a form of repeatability test. Reductions in the number of sampled directions by R_d = 2, 3 or 4 were also simulated by discarding the appropriate number of diffusion-encoding directions. Fully sampled and subsampled datasets were reconstructed using Eq. 3, and comparisons were performed between the fully-sampled case [R_k R_d] = [1 1] and subsampled cases [R_k R_d] = [4 1], [4 2], [4 3] and [4 4]. Furthermore, each one of these comparisons could be performed either with or without using the acquired navigator signal as part of the reconstruction process.

Accelerated HARDI acquisition

Four human subjects, #4-7, were imaged with the fully-implemented version of the proposed method, to achieve multi-slice volumetric coverage with reduced distortion and reduced scan time. As seen from Table 1, forty-slice datasets were obtained with little geometrical distortion in as little as 4 min worth of scan time. These scans included varying numbers of sampled directions, with and without navigator signals.

Results

Effect of regularization parameters

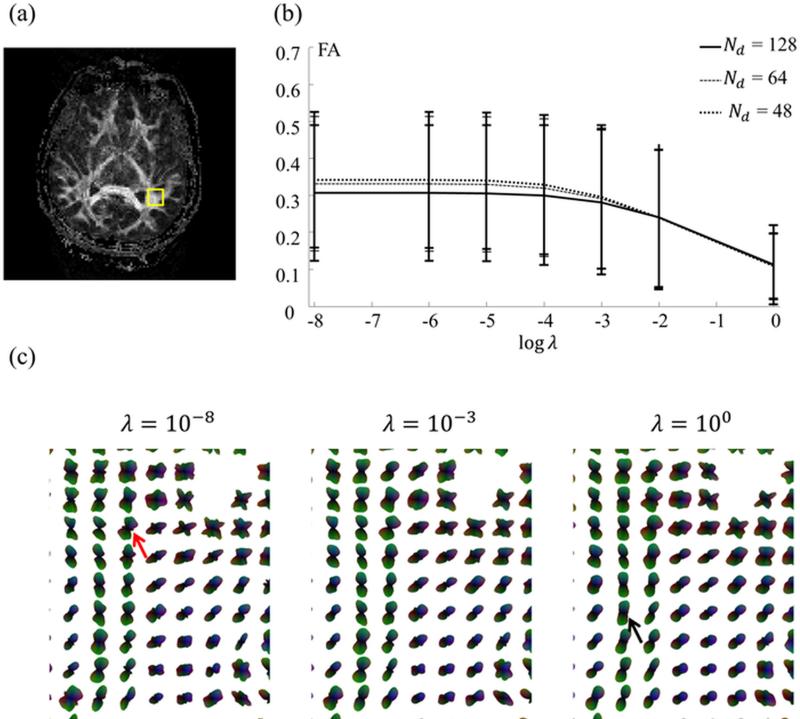
One representative slice (subject #6, slice #19 out of 40) was reconstructed for several different λ settings, and the mean as well as standard deviation for the FA value was computed for the ROI shown in Fig. 2a. These computed values were plotted in Fig. 2b, as a function of λ, for the 48-, 64- and 128-direction cases. Figure 2c further shows regional ODF values. Results from Fig. 2, as further confirmed from other slices and subjects, suggest that in the present implementation a setting in the range of 10⁻⁴ to 10⁻² might be appropriate. A setting of λ = 5×10⁻³ was selected here, for all reconstructed results presented below.

Fig. 2.

Images were reconstructed while varying λ in Eq. 3 (Subject #6, 64 directions). The mean as well as standard deviation of the FA value, calculated over the ROI shown in (a), is plotted in (b) as a function of λ. (c) Similarly, choices in λ also affected the shape of the ODFs. Although changes in 3D objects such as an ODF may be difficult to visualize, distortions at low / high λ values can be seen here, for example the red arrow in (c) pointing to a noise-induced secondary peak in the 10⁻⁸ case, and the black arrow pointing to a swollen ODF in the 10° case. A setting near the point of inflexion in (b) was chosen, λ = 5 × 10⁻³, and adopted for all results presented below.

Simulating undersampling from fully-sampled data

The fully sampled R_k = 1 data from Subject #1 gave rise to four independent R_k = 4 reconstructions, which were compared pair-wise as a measure of repeatability. The mean ODF similarity values were 97.4±2.4%, 93.0±5.5%, 87.6±9.4%, 85.6±10.5% for N_d = 128, 64, 48 and 32, respectively, as averaged over the ROI shown in Fig. 3a and over all 6 possible pair-wise combinations.

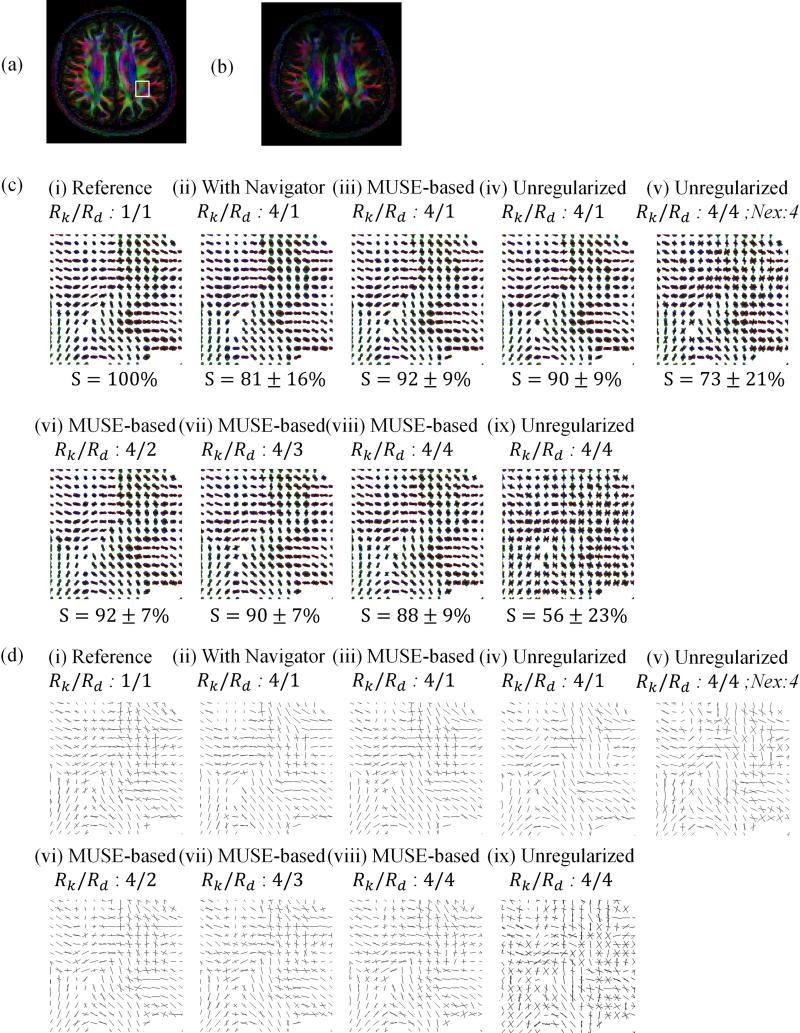
Fig. 3.

Color-coded FA maps are shown for the fully-sampled case (a), as well as an accelerated and navigated reconstruction (b). ODF maps and the similarity metrics within the ROI (c) and ODF peak directions maps (d) are shown, for the ROI indicated in (a), for 9 different acquisition/reconstruction scenarios. The fully-sampled reference is shown in column (i), and columns (ii-ix) involve 4-fold k-space accelerated results. More specifically: (ii) 128 directions, with navigator signal, (iii) 128 direction, MUSE-based self-navigation, (iv) 128 directions and regularization turned off, (v) 32 directions, 4-fold averaging, and regularization turned off, (vi) 64 directions, self-navigated, (vii) 42 directions, self-navigated, (viii) 32 directions, self-navigated, (ix) 32 directions, and regularization turned off.

The data from Subject #1 were further reconstructed in 9 different ways, as explained below. Cases reconstructed with all 128 acquired directions were displayed in Fig. 3c i-iv and Fig. 3d i-iv; cases with 64 and 48 directions in Fig. 3c vi-vii and Fig. 3d vi-vii, respectively; cases with 32 directions in Fig. 3c v, viii and ix, and Fig. 3d v, viii, and ix. The resulting diffusion-weighted images were processed to generate ODF maps (Fig. 3c) as well as maps of the peak directions of the ODF (Fig. 3d), for the ROI indicated in Fig. 3a. This particular anatomical region was selected because it featured an interesting mix of unidirectional fibers and fiber crossings. The similarity indices indicated for each ODF map in Fig. 3c are calculated based on the data inside the ROI using case (i) as the reference. The FA map in Fig. 3a was obtained for case (i), i.e., for [R_k R_d] = [1 1] and navigator, but similar FA maps were also obtained in all cases involving our reconstruction method and MUSE (not shown). Degraded FA maps were obtained in cases with R_k > 1 and navigator (e.g., Fig. 3b and case ii above), and when the proposed regularization scheme was turned off without averaging (case ix above).

Maps of the similarity metric of 6 reconstruction scenarios are shown in Fig. 4a for the same slice and subject as in Fig 3. Results for the other metric employed here, the angular dispersion index, were tabulated in Fig. 4a. In Fig. 4b, examples of ODFs were depicted to help illustrate how ODF shape and similarity index were connected: Similarity values in the 80% range tended to correspond to ODFs with main peaks pointing in similar directions but with visible shape differences, and with possible addition/omission of smaller side peaks. In the 70% range, more errors in shape but also in peak diffusion directions were typically observed.

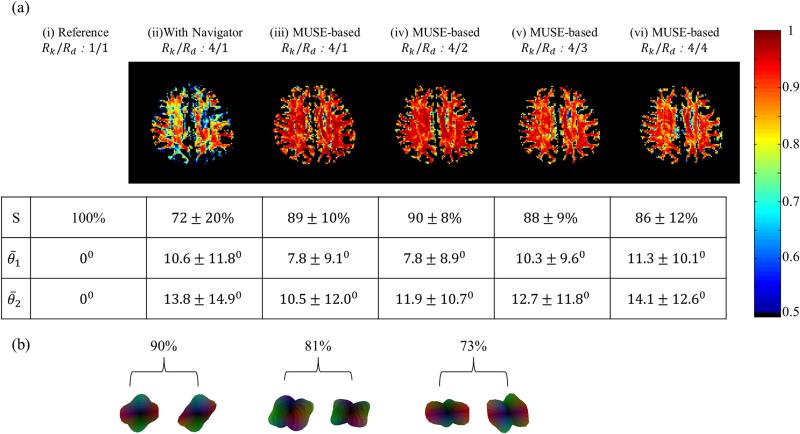
Fig. 4.

a) Six of the reconstruction scenarios from Fig. 3 are compared here as well, this time in terms of ODF. The similarity and the angular dispersion indices were calculated using the fully-sampled case as a reference standard. The similarity index is both mapped and tabulated, and its mean value varied from 100% (reference case compared to itself) down to 72% (navigated case). The self-navigated algorithm performed better than the navigated one; a mean similarity index of 86% was obtained with R_k and R_d both equal to 4-fold. The mean angular dispersion index is tabulated for cases without and with fiber crossings, with values of 11.3° and 14.1 °, respectively, again for R_k and R_d equal to 4-fold. (b) Examples of ODF shapes and their relation to the similarity index are depicted, see text for more details.

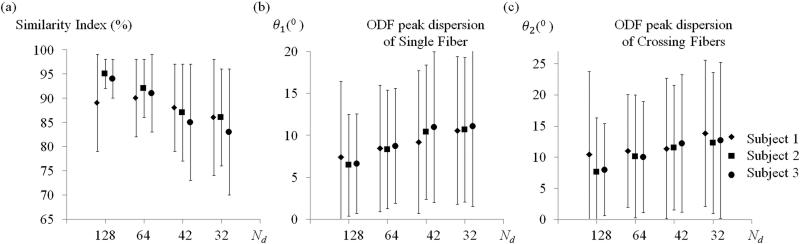
Results tabulated in Fig. 4a for subject #1 were plotted in Fig. 5, along with results for subjects #2 and #3. Results in all three subjects had similar numerical values. For example, in the maximum acceleration case (R_d and R_k = 4-fold), in all three subjects the mean similarity index was ~85% and the mean angular dispersion index was ~10° and ~13° for single-fiber and fiber-crossing voxels, respectively.

Fig. 5.

The similarity index and the angular dispersion index are plotted here for three different subjects for our proposed self-referenced reconstruction, for varying numbers of diffusion directions, N_d. Both mean and standard deviation values are shown. (a) Similarity index values decreased as the number of directions decreased, but remained high (~85%) even for the lowest number of direction, N_d = 32. (b,c) The mean angular dispersion index remained below about 13 ° even for the maximum-acceleration scenario considered here, and even in voxels featuring fiber crossings.

Accelerated HARDI acquisition

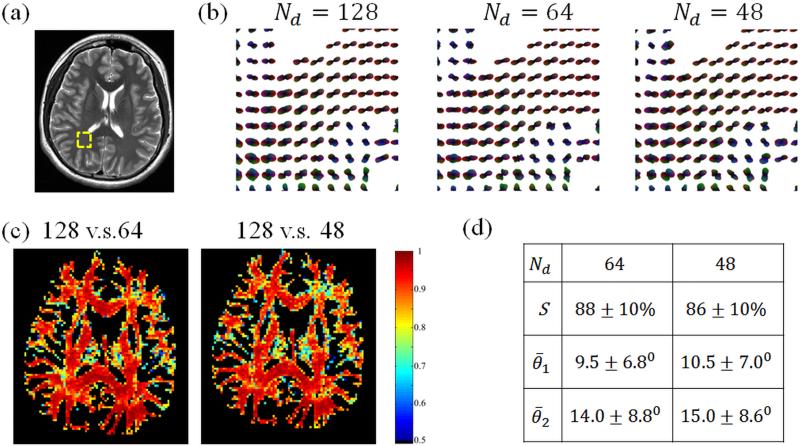
All three scans performed with Subject #6, with R_k = 4 and 128, 64 or 48 diffusion encoding directions are shown in Fig. 6. ODF maps (Fig. 6b), similarity maps (Fig. 6c) and tabulated values for mean indices (Fig. 6d) are displayed. The square ROI used for ODF displays is shown in Fig. 6a, overlaid on a T₂-weighted acquisition. While it is impossible to differentiate losses in similarity caused by motion from those caused by noise or other imperfections, motion in-between scans likely contributed, as indicated by the fact that similarity tended to be highest within white-matter regions and reduced near tissue boundaries, where motion might have most impact.

Fig. 6.

ODF maps (b) and similarity maps (c) are shown for all 3 scans performed with Subject #6. Visually-good geometrical fidelity was achieved compared to the T₂-weighted image in (a). The similarity and the angular dispersion indices for peak directions of the slice are shown in the table (d) using the 128-direction data as the reference. The ODF maps in (b) correspond to the ROI shown in (a) as on overlay to the T₂-weighted image.

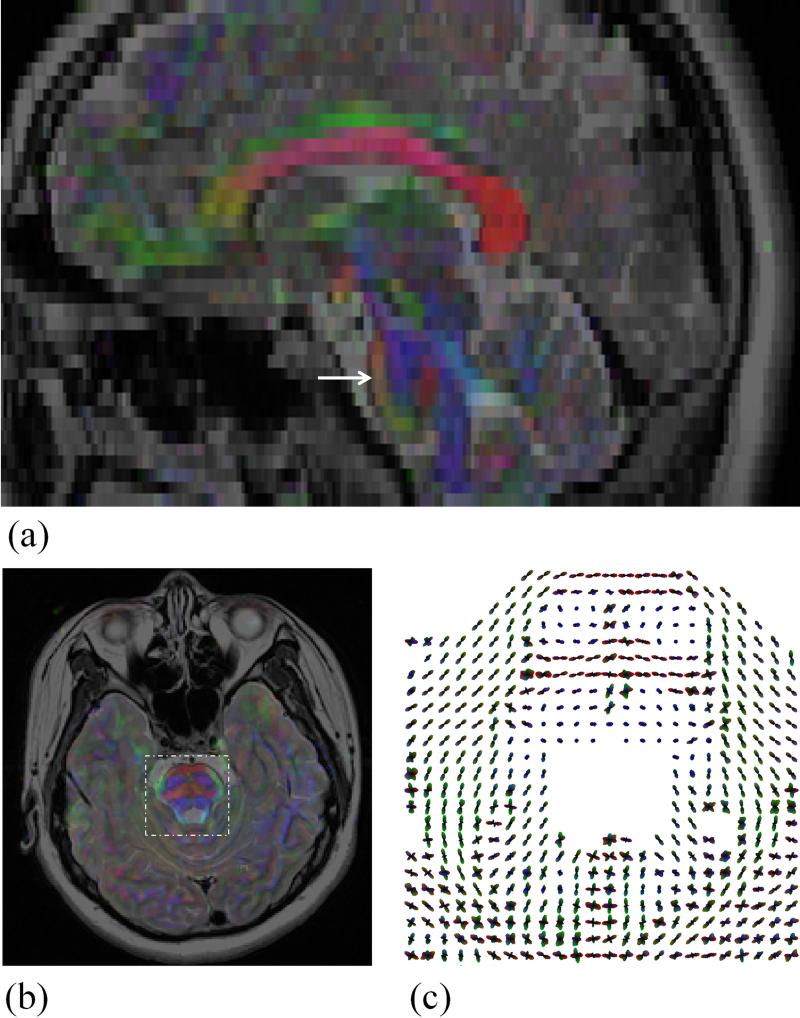
The geometrical fidelity of diffusion results was assessed in Fig. 7, as compared to a T₂-weighted acquisition. The color FA maps were overlaid on the T₂-weighted results, to help visually assess geometrical fidelity, both for the axial and the reformatted sagittal planes. An ODF map was also shown, as computed from 48 diffusion encoding directions, for an ROI indicated in Fig. 7b.

Fig. 7.

The color FA maps are overlaid on the corresponding T₂-weighted images both in a reformatted sagittal plane and an axial plane for visual comparisons to indicate the good geometrical fidelity for the DWI results (Subject #6, 48 directions). An arrow in the sagittal slice marks the location of the axial slice, and a dashed box in the axial slice depicts the ROI used for the ODF display.

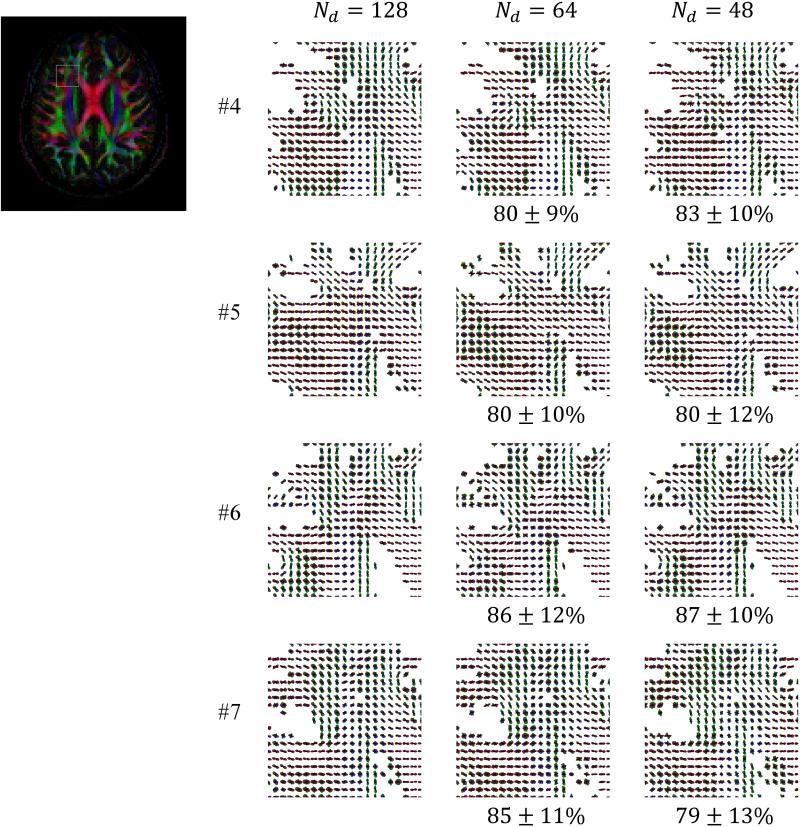
In Fig. 8, ODF maps are shown for all accelerated scans performed with the proposed method and protocol, i.e., for all scans performed for Subjects #4-7 (see Table 1). The displayed ROI was selected to cover the Anterior Corona Radiata (ACR), Corpus Callosum (CC) and some short association tracts (SAT) as this anatomical region is known to feature an interesting mix of unidirectional fibers and fiber crossings. Mean similarity index values were provided in Fig. 8 for the N_d = 64 and 48 cases, using the N_d = 128 case as a gold standard.

Fig. 8.

ODF maps are shown for the indicated ROI for all four subjects imaged with acceleration, i.e., not fully sampled: The k-space acceleration R_k was equal to 4, and the number of diffusion directions varied from 128 down to 48. The selected ROI contained white matter fibers from the Anterior Corona Radiata (ACR), Corpus Callosum (CC) and short association tracts (SAT). Results obtained with 128 sampled directions were used as a reference standard for similarity index measurements. The overall mean ODF similarity measure inside the ROI remained near or above 80%.

Discussion and Conclusion

A method was proposed to help improve geometric fidelity and reduce total scan time in HARDI acquisitions, by accelerating the data sampling process both in k-space and in d space. The method combined ideas from prior publications such as the CFARI (7), MUSE (13) and AMDI (12) methods. As a result an accelerated, regularized, motion-compensated and self-navigated HARDI implementation was obtained. Using our preferred setting, only about 9.3% of a full dataset was actually acquired, i.e., 1 / (R_k × R_d) with R_k = 4-fold acceleration in k-space and R_d = 2.7-fold reduction in the number of diffusion directions. With this setting, whole-brain 3D coverage with high geometric fidelity and 40 slices was achieved in 4 minutes of acquisition time.

DWI with good geometrical fidelity is typically difficult to achieve in the area around the brainstem, but results from Fig. 7 suggest that the proposed method performed well in this regard. More specifically, fiber tracts visible in the ODF results around the pons, such as the pontocerebellar tract and the corticospinal tract, appear well aligned with the anatomy. One possibly-surprising observation from the present work was that reconstructions involving navigator-echo signal provided lower quality than self-referenced ones, as seen in Fig. 3. Navigator signals were more heavily T₂-weighted and had lower spatial resolution that the imaging data, which may have had a role to play in the finding.

Decreasing the number of sampled directions and the number of k-space interleaves allowed good geometrical fidelity to be achieved in clinically-relevant scan times, but there were also, of course, negative impacts on image quality. Much of the presented method and of its regularization schemes were geared toward handling the extra noise and the less-favorable conditioning associated with the accelerated datasets. Even with only 32 directions (instead of 128) and a single k-space interleaf (instead of 4) the mean similarity index compared to the fully-sampled case remained relatively high at 86%, see Fig. 4a. More specifically, the shape of the ODF for voxels with unidirectional fibers varied very little from fully-sampled to accelerated cases, unlike voxels that included fiber crossings where subtle changes were observed. For this reason, results for single- and crossing-fiber voxels were presented separately in Fig. 5, and the mean angular dispersion index for crossing-fiber voxels was evaluated at ~13° for the case N_d = 32, in three subjects (Fig. 5c). In Fig. 3, for accelerated acquisitions, turning regularization off led to poor ODF results (Fig. 3c ix), which helped justify the regularized approach employed here. While averaging datasets, not surprisingly, did improve results (Fig. 3c v) acquiring different directions instead proved preferable, presumably because extra directions helped both in terms of noise and conditioning.

Limitations included a fairly limited number of subjects, seven here, and the fact that these subjects were healthy volunteers. Furthermore, while ODF maps are presented, no tractography results were explicitly generated, even though fast non-distorted tractography could ultimately prove the main application for the present imaging and reconstruction scheme. While they tend to be visually impressive, tractography results are notoriously difficult to compare and to quantitatively evaluate. Based on ODF maps metrics, were devised here to help measure and judge to some degree the effect of acceleration on data quality; in contrast, comparing tractography results instead of ODF maps would have proved a much more daunting and arguably less informative task.

As a further limitation, some acquisition parameters held constant in this study might ultimately benefit from optimization, such as the k-space acceleration factor R_k, the choice of receive coil array, and basic sequence-related parameters such as TR or spatial resolution. The setting R_k = 4 was selected here as a trade-off, as this value is higher than the two- or three-fold acceleration routinely obtained with parallel imaging alone, but yet small enough so that good-quality results could be confidently obtained in seven consecutive volunteers. Furthermore, small variations in imaging parameters among subjects were mostly unavoidable, as the fully-sampled reference-standard acquisitions performed in Subjects 1-3 required larger slice gaps to keep scan time within reason. The larger slice gap for Subjects 1-3, as compared to Subjects 4-7, may be associated with slightly increased SNR, although this effect was mitigated here by the use of a long TR period and the sequential acquisition of odd and even slices. Lastly, reconstruction time may also be considered a limitation of the proposed approach. For the present Matlab-based implementation, about 16 hours were required to reconstruct a 40-slice volumetric dataset with 48 diffusion-encoding directions. Reconstruction was performed in Matlab on the CPU of a single off-the-shelf computer, and reconstruction times could undoubtedly be much reduced through a more involved implementation involving lower-level programming, multi-threads, GPU processing and/or better hardware, so that reconstruction time is not expected to ultimately represent a major limitation of the approach.

In conclusion, HARDI results with good geometrical fidelity and clinically-realistic scan times were achieved, which may hopefully help further facilitate the transition of this very successful research tool to clinical practice.