MetMaxStruct: A Tversky-Similarity-Based Strategy for Analysing the (Sub)Structural Similarities of Drugs and Endogenous Metabolites

Abstract

Background: Previous studies compared the molecular similarity of marketed drugs and endogenous human metabolites (endogenites), using a series of fingerprint-type encodings, variously ranked and clustered using the Tanimoto (Jaccard) similarity coefficient (TS). Because this gives equal weight to all parts of the encoding (thence to different substructures in the molecule) it may not be optimal, since in many cases not all parts of the molecule will bind to their macromolecular targets. Unsupervised methods cannot alone uncover this. We here explore the kinds of differences that may be observed when the TS is replaced—in a manner more equivalent to semi-supervised learning—by variants of the asymmetric Tversky (TV) similarity, that includes α and β parameters.

Results: Dramatic differences are observed in (i) the drug-endogenite similarity heatmaps, (ii) the cumulative “greatest similarity” curves, and (iii) the fraction of drugs with a Tversky similarity to a metabolite exceeding a given value when the Tversky α and β parameters are varied from their Tanimoto values. The same is true when the sum of the α and β parameters is varied. A clear trend toward increased endogenite-likeness of marketed drugs is observed when α or β adopt values nearer the extremes of their range, and when their sum is smaller. The kinds of molecules exhibiting the greatest similarity to two interrogating drug molecules (chlorpromazine and clozapine) also vary in both nature and the values of their similarity as α and β are varied. The same is true for the converse, when drugs are interrogated with an endogenite. The fraction of drugs with a Tversky similarity to a molecule in a library exceeding a given value depends on the contents of that library, and α and β may be “tuned” accordingly, in a semi-supervised manner. At some values of α and β drug discovery library candidates or natural products can “look” much more like (i.e., have a numerical similarity much closer to) drugs than do even endogenites.

Conclusions: Overall, the Tversky similarity metrics provide a more useful range of examples of molecular similarity than does the simpler Tanimoto similarity, and help to draw attention to molecular similarities that would not be recognized if Tanimoto alone were used. Hence, the Tversky similarity metrics are likely to be of significant value in many general problems in cheminformatics.

Introduction

It is widely recognized that drugs exploit or “hitchhike on” protein transporters in order to be taken up into cells (e.g., Ecker and Chiba, 2009; Giacomini et al., 2010; Fromm and Kim, 2011; Giacomini and Huang, 2013; Ishikawa et al., 2013; Sugiyama and Steffansen, 2013; Ecker, 2014; You and Morris, 2014). However, it is not at all easy to predict which transporters are used simply by looking at the chemical structures of the drugs. As part of a series of studies of the transporter-mediated uptake of pharmaceutical drugs into biological cells (e.g., Dobson and Kell, 2008; Dobson P. et al., 2009; Kell and Dobson, 2009; Kell et al., 2011, 2013, 2015; Lanthaler et al., 2011; Kell, 2013, 2015a,b, 2016a,b; Kell and Goodacre, 2014; Mendes et al., 2015; Kell and Oliver, 2014; O'Hagan and Kell, 2015a), and driven by the availability of principled metabolic network reconstructions (Herrgård et al., 2008; Swainston et al., 2013; Thiele et al., 2013; Sahoo et al., 2014; Nigam, 2015; Palsson, 2015) (in which approximately one third of the enzymes are transporters), we have been developing the consequent idea that drugs do indeed share structural similarities with endogenous metabolites (“endogenites”; Dobson P. D. et al., 2009; O'Hagan and Kell, 2015c; O'Hagan et al., 2015). The implication would be that the natural (endogenite) substrates are those with which the drugs share the more significant molecular similarities. These latter studies, comparing drug-endogenite structures were purely “unsupervised,” and thus based on clustering-type comparisons. This was because (i) we wished to avoid any dangers of overtraining using a supervised method, and (ii) in relatively few cases do we in fact know the natural (endogeneous) substrates of those “SLC” (SoLute Carrier) transporters (Hediger et al., 2013; César-Razquin et al., 2015) that can be shown to transport drug molecules. A recent example of this latter is SLC35F2, that is responsible for rather more than 99% of the transport of the anti-cancer drug candidate YM155 (Winter et al., 2014), but whose endogenous substrate is unknown. In a related vein, it has been argued (with evidence) that the “natural” substrate of the OCTN1/SLC22A4 transporter (Koepsell, 2013) is not (as was widely believed) carnitine but instead the dietary and/or microbial product ergothioneine (Gründemann et al., 2005; Gründemann, 2012).

In some cases the structural similarities between drugs and endogenites are sufficiently close that it is clear which transporters are the most likely candidates, but this is not always the case. Although empirical (experimental) methods are coming forward that can help us find the relevant transporters more or less systematically (e.g., Lanthaler et al., 2011; Winter et al., 2014; César-Razquin et al., 2015), mostly we lack the means to generate good hypotheses for which transporters transport which drugs. The basic problem is that the purely unsupervised structural comparisons using Tanimoto similarities are based on the whole molecule, and substructures that are irrelevant (or not directly bound to the transporter protein when being transported) serve to act as skillful decoys. Specifically, and rather obviously, in the cases of proteins binding small molecules, any part of the small molecule that does not actually bind to the protein is unlikely to contribute much to its biological activity.

Supervised methods—that in cheminformatics amount to Quantitative Structure-Activity Relationships (QSARs; Sedykh et al., 2013; Cherkasov et al., 2014; Ruusmann et al., 2014)—are much more powerful than are unsupervised methods, but can hardly be applied when we do not know the relevant substrates nor (thus) have any assay data. However, besides strictly unsupervised and supervised learning, there is a third class of computational analysis, known as semi-supervised learning (e.g., Demiriz et al., 1999; Handl and Knowles, 2006; Zhu and Goldberg, 2009; Balcan and Blum, 2010; Chapelle et al., 2010; Kingma et al., 2014), in which one uses a surrogate objective function for unlabeled data where they are available, even when one does not know the true class membership (here, for instance substrate or inhibitor activity) that one is actually seeking in order to improve one's understanding of a system. Here, we recognize that the “surrogate” objective function may simply be a greater (or different) similarity coefficient when something is varied. Although not necessarily new in this context (Broomhead and Lowe, 1988; Moody and Darken, 1989), these “mixed” strategies have recently come to the fore in cases (e.g., Hinton and Salakhutdinov, 2006; Hinton et al., 2006; Hinton, 2007) where one uses an unsupervised method as (a preparatory) part of the training of a supervised system, in particular a deep neural learning system (Bengio, 2009; Erhan et al., 2010; Lecun et al., 2015).

A similar question relates to the choice of which kinds of molecules one might use in an experimental QSAR study given an initial hit or lead, and one answer must include molecules that bear at least some structural similarities to the initial hit/lead. Again, just basing the choice on an overall similarity is likely to mean that some molecules that contain a similar scaffold may appear to have a TS that is quite different from that of the initial hit and thus are not chosen. We clearly need “better” and more general methods for assessing “similarity,” where we recognize that the concept of “better” implies an objective function (and we give an example below).

As mentioned, the inevitable flaw in purely unsupervised methods is that they (can) have no knowledge of which parts of an input (e.g., substructures of a molecular structure) are “important” to (or correlate with) an output (process) of interest and which parts are not, because that is not the question being asked (Broadhurst and Kell, 2006; Hastie et al., 2009). The equivalent comparison in linear multivariate statistics is between principal components analysis (unsupervised) and partial least squares analysis (supervised; Wold et al., 2001). For the former, various kinds of normalization can be used to upweight or downweight particular features (e.g., Hotelling, 1933; Neal et al., 1994). This issue is particularly acute in standard cheminformatics, where the Tanimoto (Jaccard) coefficient is commonly used as an index of molecular similarity following fingerprints encoding, and where the numerical similarity returned is dominated by the number of bits set to 1 in the output comparator string (and hence is also a reflection of molecular size; Flower, 1998; Willett et al., 1998; Dixon and Koehler, 1999; Salim et al., 2003; Willett, 2006; Wang et al., 2007; Wang and Bajorath, 2008; Senger, 2009; O'Hagan and Kell, 2015c). In the case of drug-endogenite similarity measurements, this can often tend to favor particular endogenites that happen to share many chemical groupings with the drugs of interest; CoA derivatives fall (and fell O'Hagan et al., 2015) into this category, at least for certain cheminformatics encodings. We note, as pointed out by a referee, that the MACSS encoding was originally devised for cataloging chemicals; this said, it has been widely used for providing a computer-readable encoding for both similarity searches and even QSARs.

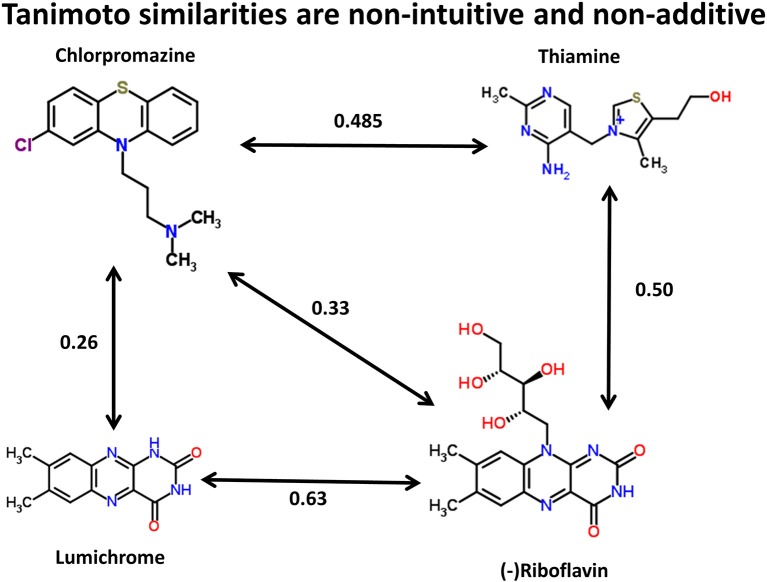
We can illustrate the basic principle (using the data available in the Supplementary Materials to (O'Hagan et al., 2015), and the kind of comparison illustrated for propranolol vs. endogenites in Figure 3 of that paper) by three of the structures in Figure 1. Thus, using the MACCS166 encoding (Durant et al., 2002), and chlorpromazine as the interrogatory drug, the top endogenite returned is thiamine. However, visual inspection of the structure of riboflavin (vitamin B₂), for instance, suggests that its tricyclic core is actually rather more similar to that of chlorpromazine (as has indeed occasionally been noted functionally Gabay and Harris, 1965; Pinto et al., 1981; Pelliccione et al., 1983; Tomei et al., 2001; Iwana et al., 2008; Caldinelli et al., 2010; Iwasa et al., 2011), but the Tanimoto similarity is both lower and potentially depressed by the ribitol sidechain. Nonetheless, removing the ribitol sidechain (to give lumichrome) actually lowers the Tanimoto similarity to chlorpromazine, consistent with the comments above regarding molecular size and Tanimoto similarity. In other words, (i) visual appearance can be a poor guide to calculated chemical similarity, (ii) one would here desire a method or methods that can pick up on a large change in a (small) part of a molecule that it otherwise still recognizes as being similar, and (iii) as pointed out by a referee the similarity coefficient necessarily depends on the encoding chosen (for reasons of space we use solely the MACCS166 encoding here).

Figure 1.

Tanimoto similarities between chlorpromazine and three other molecules (using the MACCS166 encoding).

Molecular similarity necessarily depends on context (Bender and Glen, 2004), and as we detailed earlier could differ quite widely for the same pairs of molecules as the encoding was varied. Given that our fundamental question (O'Hagan and Kell, 2015c; O'Hagan et al., 2015) is “which is the endogenite that is closest in molecular structure, in some sense, to a given drug molecule X?,” it is clear that what is needed is some kind of an automated analysis of this type. This would exploit information on selected parts of the molecule that might, when assessed “correctly,” be found to be more endogenite-like than when the assessment is made using the entire molecules. Thus, in general terms, it could look for substructures of drugs that increase the (Tanimoto or other) similarity of at least some metabolites relative to that based on their overall structure. These would thereby generate hypotheses that return those endogenous metabolites that are more likely (than the “overall most similar molecules” returned) to represent good suggestions for particular purposes, even if, during the computational analyses, we do not have measures of (i.e., the values for) those purposes. Holliday et al. (2002) provide a list of 22 similarity measures that have been used in cheminformatics, although they do not include the Tversky similarities on which we concentrate below.

The Tanimoto (Jaccard) similarity of a set of (typically binary) attributes is a true metric, defined as their intersection divided by their union, and is given (for simple bitstrings of the same length) as:

$$\begin{array}{l}\frac{M_{11}}{M_{10}+M_{01}+M_{11}}\end{array}$$ (1)

where M₁₁ is the number of positions in which both bits are set to 1 while the sum of M₁₀ plus M₀₁ together represent the number of positions in the reciprocal cases in which they are different.

Equivalently, if the number of bits set to 1 in A but to 0 in B is a, the number of those in B set to 1 but not in A is b, and those both set to 1 is c, the Tanimoto similarity TS between two bitstrings A and B is given by:

$$\begin{array}{l}\text{TS}(\text{A},\text{B})=\frac{c}{a+b+c}\end{array}$$ (2)

Simple inspection indicates that the Tanimoto similarity ranges from 0 (complete lack of similarity) to 1 (identity). However, a more general method of similarity assessment is that due to Tversky (1977).

The Tversky similarity coefficient (Tversky, 1977; Senger, 2009; Geitmann et al., 2011; Gan et al., 2014; or, more accurately, sets of similarity coefficients) represent, in a sense, a more discriminating and asymmetric variant of the Tanimoto similarity in which we might not wish to make the comparison over the whole molecule. This is done by introducing additional parameters α and β. The Tversky similarity coefficient Tv(A,B) is then defined as:

$$\begin{array}{l}\text{Tv}(\text{A},\text{B})=\text{c}/(\alpha \text{a}+\beta \text{b}+\text{c})\end{array}$$ (3)

where again a and b are the number of bits that are set to be “on” (1 bits) only in molecular fingerprints A or B, respectively, and c is the number of on bits shared by both A and B. For these purposes, A is an interrogatory molecule while B is the molecule being interrogated as to its similarity. It is common, but not necessary, to vary α and β such that α + β = 1. The smaller the value of α, the larger the contribution of B as a substructure of A (and hence to its similarity with A). The larger the value of α, the larger the contribution of B as a superstructure of A (equivalently A as a substructure of B). For α = β = 1 the coefficient is numerically equivalent to the Tanimoto similarity, while the coefficient when α (= β) = 0.5 is known as the Dice coefficient. Clearly, then, and as a simple extension of our previous Tanimoto-based analyses (O'Hagan and Kell, 2015c; O'Hagan et al., 2015), it is likely to be worth studying the effects of substituting the Tanimoto coefficient by various values of the Tversky coefficient to understand which kinds of drug molecules may begin to appear more similar to endogenites when α ≠ 1. This is the purpose of the present paper.

We note that there have been comparatively few systematic studies of this general topic, and none at all comparing marketed drugs and endogenites. An extension of this is also precisely the motivation (Riniker and Landrum, 2013) behind the “fraggle” algorithm, for which we cannot find a published reference, but which is explained at https://github.com/rdkit/UGM_2013/blob/master/Presentations/Hussain.Fraggle.pdf. Here, our desire for “good suggestions” hinges on what are, in fact, the endogenous substrates of relevant transporters. It turns out that one can use this general strategy to improve the similarity to at least one endogenite for a great many marketed drugs. This obviously might have a substantial and useful effect on the endogeneous metabolites (or other molecules) one might seek to test for their role as substrates (or indeed inhibitors) of the drug transporter activity of specific proteins.

Materials and methods

The list of endogenites derive from Recon2 (Thiele et al., 2013) and the full list of marketed drugs taken from DrugBank (Law et al., 2014) are those that were given previously (O'Hagan et al., 2015) and are all available in the Supplementary Materials to O'Hagan et al. (2015). In a similar vein, as before (O'Hagan and Kell, 2015b,c; O'Hagan et al., 2015), we used the KNIME software (see http://knime.org/ and e.g., Berthold et al., 2008; Mazanetz et al., 2012; Beisken et al., 2013) to create workflows for our analyses. In particular, substantial use was made of the RDKit nodes (see http://rdkit.org/ and e.g., Landrum et al., 2011; Landrum and Stiefl, 2012; Riniker and Landrum, 2013; Riniker et al., 2013, 2014; O'Hagan and Kell, 2015b), noting the very useful “fraggle” (http://www.rdkit.org/Python_Docs/rdkit.Chem.Fraggle-module.html). The Tv similarity calculations were obtained using a node from the Indigo library (see Saubern et al., 2011).

Results

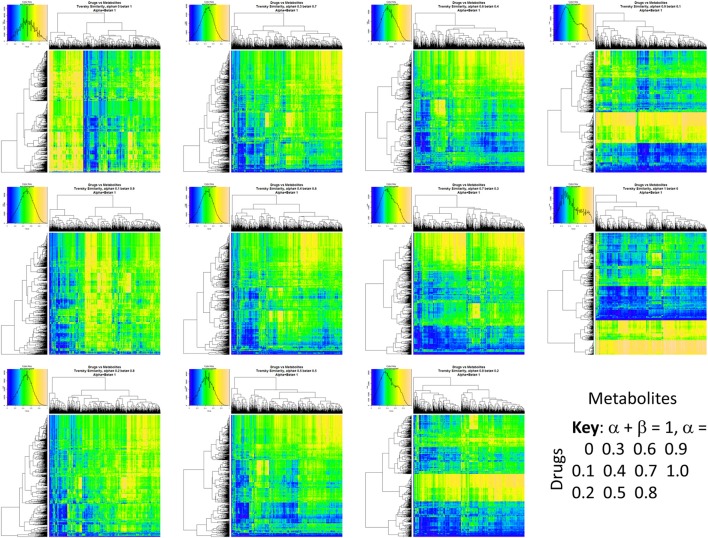
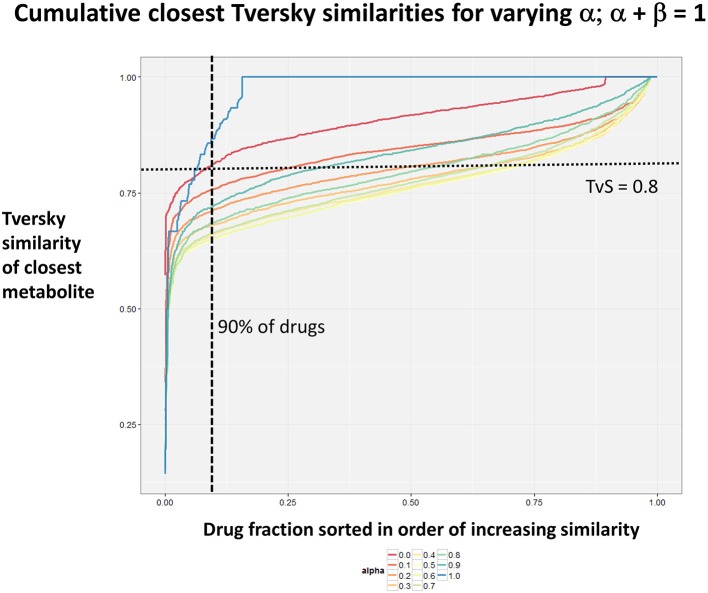
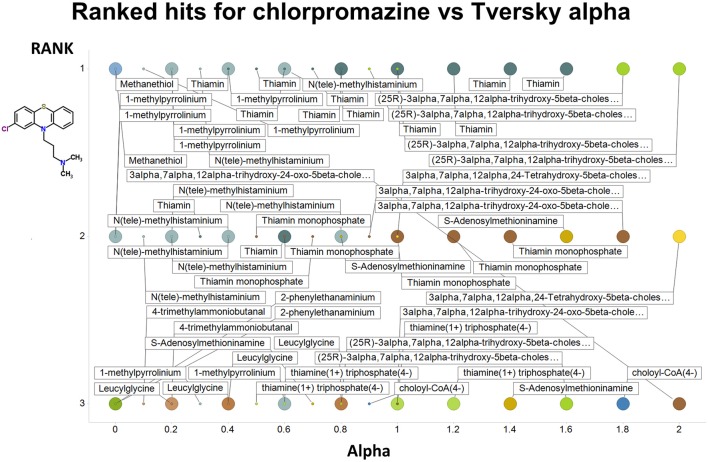
Figure 2 summarizes visually, via a series of 11 heatmaps, the effects of varying the Tversky α parameter in a comparison of drugs (vertical axes) and endogenites (horizontal axes), using the MACCS166 encoding (Durant et al., 2002), under conditions in which α + β = 1. Obviously there is a very substantial change in the apparent overall similarities of drugs and endogenites, with a strong tendency for greater overall similarities when alpha is closest to zero or 1, and with the similarities in general being considerably greater than the Tanimoto similarities described previously for the MACCS encoding (O'Hagan and Kell, 2015c; O'Hagan et al., 2015; which is the only one we use here). Figure 3 shows the cumulative effect of varying α using the data in Figure 2, which makes even more clear the fact that similarities can be much greater than those observed when Tanimoto is used. Also marked is the fraction of drugs whose largest Tversky similarity to an endogenite exceeds 0.8 (these will appear, with other data, in a secondary plot in Figure 10), where it is obvious that again this is a very strong function of α. There is also a clear tendency for the endogenites that are chosen simply to be more complex as α is increased, with (as implied above) CoA derivatives featuring much more than in the cases when α is lower. To this end, Figure 4 shows the similarities of the top 3 metabolites to chlorpromazine at different values of α, while Figure 5 provides similar data to those of Figure 2 for a number of cases of α for conditions in which α + β = 2 (as occurs for the Tanimoto similarity where α = β = 1), and with the cumulative plots equivalent to those for α + β = 1, shown now for α + β = 2, in Figure 6. As for the case in which α + β = 1, the trend is similar, with overall similarities being greatest when α is nearer its extreme values. However, the similarity values are generally much lower than when α + β = 1 (see the much greater extent of blue in the heatmaps in Figure 5, and the ordinate values in Figure 6); indeed it is seen that the Tanimoto coefficient (α = β = 1, α + β = 2), with 90% of drugs showing a TS > 0.5 as before (O'Hagan and Kell, 2015c; O'Hagan et al., 2015), is a poor choice if one is seeking to maximize the apparent similarity between two molecules. Similarly, the nature of the molecules whose similarity to a different interrogatory molecule is greatest also changes significantly with α. This is again illustrated, now for clozapine, in Figure 7. The data for the “top 20” similarities for chlorpromazine and for clozapine are given as Tables S1, S2.

Figure 2.

Eleven heatmaps showing color-encoded drug-endogenite Tversky similarities for Tversky α + β = 1. The figure is intended to give an easy overview, with similarities ranging from 0 in dark blue to 1 in buff orange as per the color map inserts. The key for the varying values of α is given in the lower right-hand corner of the figure.

Figure 3.

Cumulative plot of drug-endogenite likenesses using varying values of the Tversky similarity coefficient α with the constraint α + β = 1. For each curve, the maximum Tversky similarity to any metabolite for each drug is plotted in rank order, starting from the right. It is obvious that, especially for values of α closest to 0 or 1, there is an endogenite that is really very similar to the interrogating drug, and much more similar than those found (O'Hagan et al., 2015) when the metric is the Tanimoto similarity.

Figure 4.

Top 3 ranked hits for the closest endogenites to chlorpromazine at different values of the Tversky α for both α + β = 1 and α + β = 2. Two example points are given for α = 0, 0.2, 0.4, 0.6 0.8, and 1.0; the smaller circle is for α + β = 1. It is clear (as expected) that the top-ranked hits become more complex as α increases.

Figure 5.

Eleven heatmaps showing color-encoded drug-endogenite Tversky similarities for Tversky α + β = 2. The figure is intended to give an easy overview, with similarities ranging from 0 in dark blue to 1 in buff orange as per the color map inserts. The key for the varying values of α is given in the lower right-hand corner of the figure. The basic experiment is otherwise exactly the same as that in Figure 2.

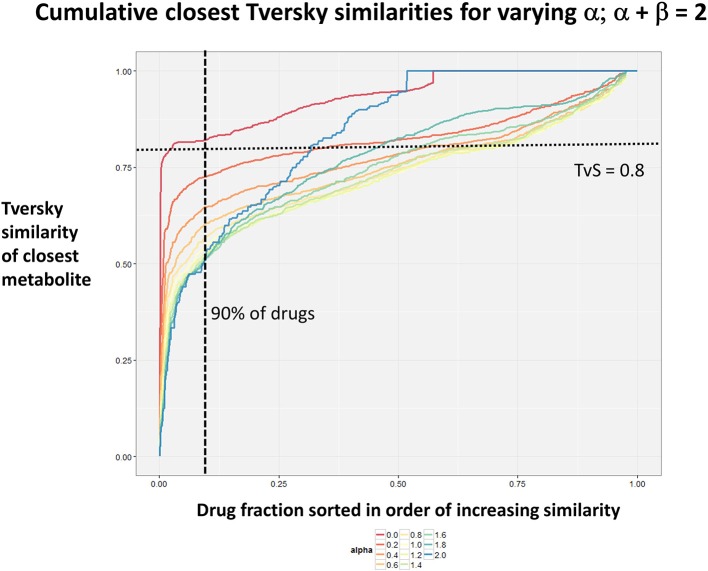
Figure 6.

Cumulative plot of drug-endogenite likenesses using varying values of the Tversky similarity coefficient for α + β = 2. For each curve, the maximum Tversky similarity to any metabolite for each drug is plotted in rank order, starting from the right. It is obvious that, especially for values of α closest to 0 or 2, there is an endogenite that is really very similar to the interrogating drug, and more similar than those found (O'Hagan et al., 2015) when the metric is the Tanimoto similarity. However, the similarities are always greater when α + β = 1 (Figure 2).

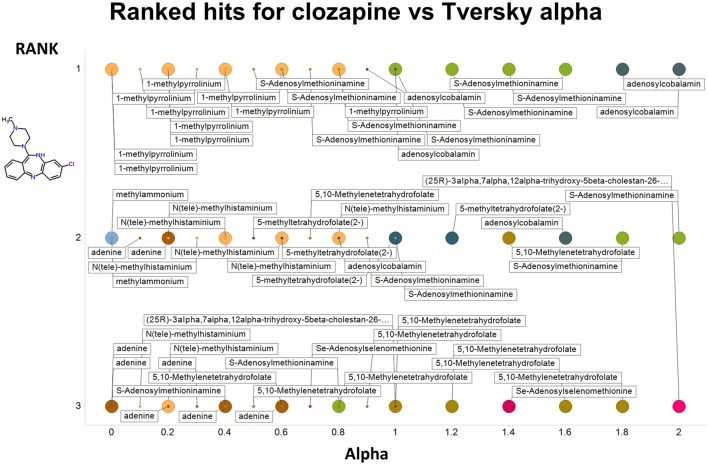
Figure 7.

As Figure 4, save the interrogating molecule is clozapine.

To illustrate that this improved variation in apparent molecular similarity works “both ways,” we use an endogenite, riboflavin, as the interrogating molecule, and assess its similarity to marketed drugs. Figures 8, 9 show the top hits for α = 0.1, β = 0.9, and α = 0.5, β = 0.5, respectively. Obviously, again, not only the typical magnitudes of the Tversky similarity change significantly but so does the rank order of molecules.

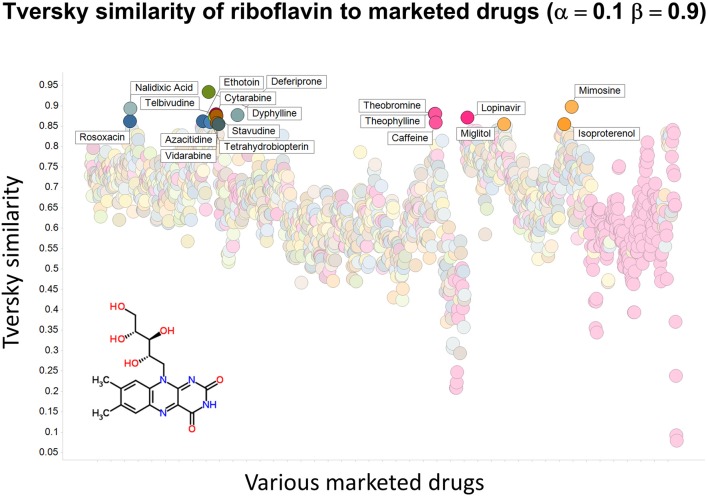
Figure 8.

Tversky similarity (α = 0.1, β = 0.9) of riboflavin to marketed drugs. Names are given for those with values of 0.85 or greater.

Figure 9.

Tversky similarity (α = 0.5, β = 0.5) of riboflavin to marketed drugs. Names are given for those with values of 0.85 or greater.

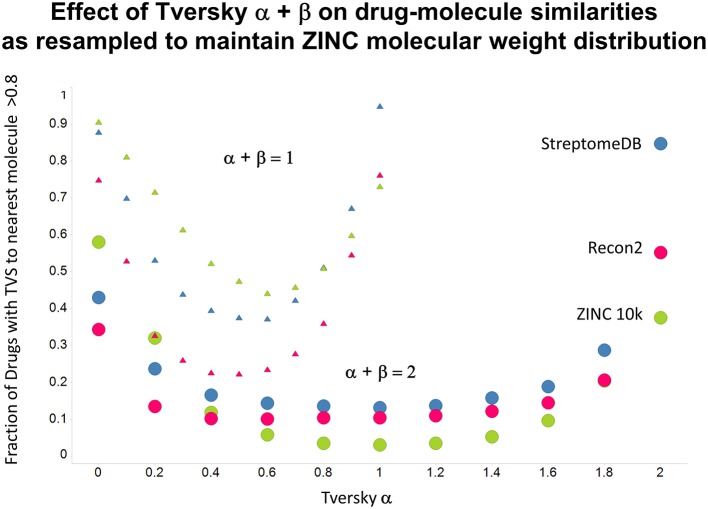
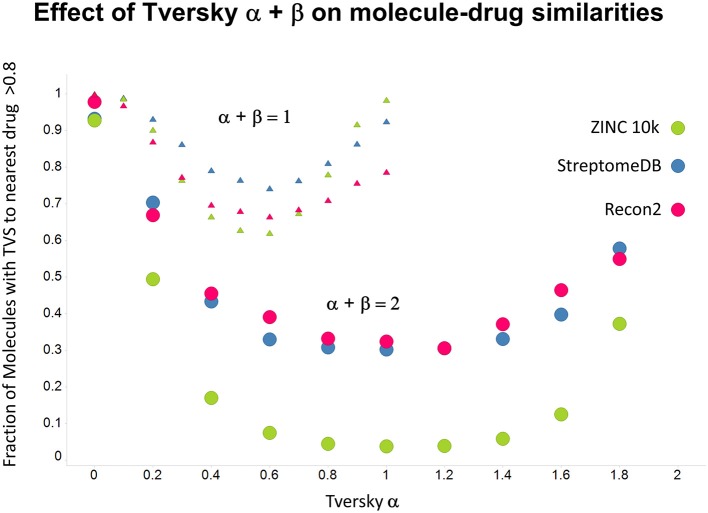
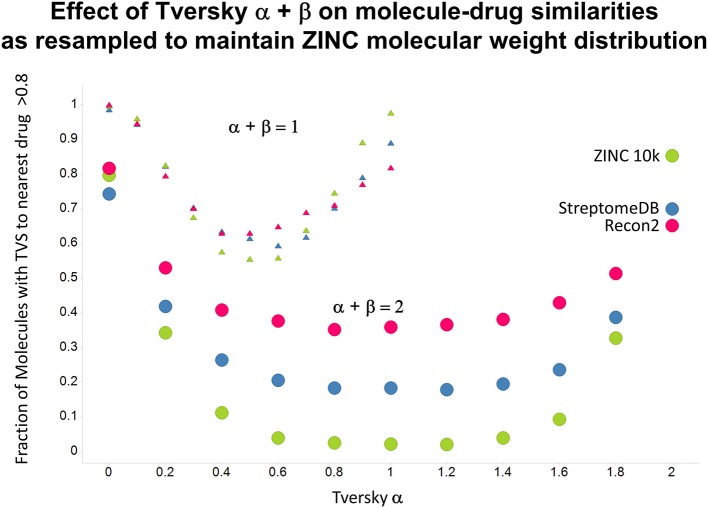
As shown before (O'Hagan and Kell, 2015c; O'Hagan et al., 2015), the shape of these cumulative plots (Figures 3, 6) of the similarities of marketed drugs to other molecules also depends on the nature of those other molecules. Thus, the overall similarities to marketed drugs were in the order endogenites > natural product library > synthetic chemical library. The question then arises, and this allows a semi-supervised analysis, as to whether there are values of α and β that minimize or maximize these differences. Figure 10 provides a secondary plot of the data shown in Figures 3, 6 for the fraction of drugs exceeding a (somewhat arbitrary) Tversky similarity of 0.8 as a function of α for both α + β = 1 (small symbols) and α + β = 2 (larger symbols). It is clear that both the magnitude and the apparent ranking of classes change as a function of the type of library. As before, when α = β = 1 (i.e., Tanimoto similarity), Recon2 metabolites are more like drugs than are natural products and ZINC library members. Figure 10 also shows the same secondary plot for 2400 molecules from StreptomeDB (Lucas et al., 2013; as representative of natural products) and from a subset of 10,000 molecules taken from the ZINC database (Irwin and Shoichet, 2005; Irwin, 2008; Irwin et al., 2012; Sterling and Irwin, 2015). Data for α = β = 1 (Tanimoto similarity) are essentially as previously published (O'Hagan et al., 2015; note that we take random subsets). However, extraordinarily striking differences are seen in the percentage of drugs exceeding a Tversky similarity of 0.8 to the different classes as α and β are varied. Thus, if one wishes to favor the druglikeness of natural products over molecules in ZINC then α + β = 2 is to be preferred, whereas α + β = 1 favors ZINC. We note (as before, O'Hagan et al., 2015) that the molecular weight distributions are not the same for the three classes, with those for ZINC being lowest, and that this could potentially be an issue in that TS favors larger molecules (see above). It is obvious that the varying ranking order of the classes at different values of α and β means that this is not a dominant issue. However, some differences were obtained when we sampled randomly from the classes in a manner that normalized the samples to have the same MW distribution, albeit that this also “clips” those endogenites with high molecular weights (not shown), and these are shown in Figure 11. We also ran the converse query, where the various classes of non-drugs are used to interrogate the list of marketed drugs for apparently similarity, with broadly converse findings (Figures 12, 13).

Figure 10.

Fraction of marketed drugs with a Tversky similarity >0.8 to at least one molecule in the stated collections. The comparison was against Recon2 (1112 molecules), streptome DB (Lucas et al., 2013) (2400 molecules) and a random subset of 10,000 molecules drawn from the ZINC (Irwin and Shoichet, 2005) database. Colors in this and the following three figures are labeled by the points for α = 2.

Figure 11.

As Figure 10, but data are subsampled to retain the same MW distrubtion for each class (which is effectively that of ZINC).

Figure 12.

Fraction of molecules with a Tversky similarity >0.8 to at least one marketed drug in the stated collections. The comparison was against Recon2 (1112 molecules), streptome DB (Lucas et al., 2013) (2400 molecules) and a random subset of 10,000 molecules drawn from the ZINC (Irwin and Shoichet, 2005) database.

Figure 13.

As Figure 12, but data are subsampled to retain the same MW distrubtion for each class (which is effectively that of ZINC).

Discussion

The general notion of the “similarity” between two or more objects, or their “closeness,” is a complex one (e.g., Johnson and Maggiora, 1990; Rouvray, 1992; Everitt, 1993; Bunke, 1997; Handl et al., 2005; Handl and Knowles, 2007), and this is no less true of molecular similarity (e.g., Hall et al., 1995; Willett et al., 1998; Gasteiger, 2003; Bender and Glen, 2004; Bender et al., 2006; Maldonado et al., 2006; Eckert and Bajorath, 2007; Gallegos-Saliner et al., 2008; Marín et al., 2008; Baldi and Nasr, 2010; Maggiora and Shanmugasundaram, 2011; Maggiora et al., 2014; Medina-Franco and Maggiora, 2014). Here, we confine ourselves to systems in which all the features used are transformed to simple bitstrings that may then be compared. Classical numerical (including chemo) taxonomy (Sneath and Sokal, 1973) gave equal weightings to each binary character, and this is clearly the most unbiased means by which one can make assessments of overall similarity. By contrast, a different tradition (e.g., Everitt, 1993; Petrone et al., 2012) asserts that any measurement of a similarity or clustering should be judged solely on its utility, in other words there are usually benefits to the use of a what in statistics is called a “biased estimator” (Hastie et al., 2009).

Our previous work comparing endogenites and successful (marketed) drugs showed that they did indeed share similarities, and more so than with the kinds of non-natural molecules common in drug discovery libraries (Dobson P. D. et al., 2009; O'Hagan and Kell, 2015c; O'Hagan et al., 2015). It was also noted that the nature and extent of these similarities could vary significantly with the type of (2D) molecular encoding used. However, in all of that work, the actual bitstring comparisons were based on the use of the Jaccard/Tanimoto similarity coefficient, as is indeed most common in cheminformatics (Willett, 2014). As a single metric, this admits only an unsupervised comparison.

However, the Tanimoto similarity is actually but one member of a larger family of similarity coefficients introduced by Tversky (1977), and it was of interest to see whether the use of a Tversky similarity coefficient Tv(A,B) might provide further information or utility. The Tversky similarity coefficient is indeed occasionally used in cheminformatics (Willett et al., 1998; Chen et al., 2005; Swamidass and Baldi, 2007; Ebalunode et al., 2008; Nasr et al., 2009; Rupp et al., 2009; Senger, 2009; Nicholls et al., 2010; Backman et al., 2011; Geitmann et al., 2011; Berenger et al., 2014; Gan et al., 2014; and also Wang et al., 2007; Wang and Bajorath, 2008), though that used in those papers seems to be based on a different definition from ours, but does not seem to enjoy widespread cheminformatics use. The attraction of Tversky similarities is that they effectively give different weightings to different molecular features, and some of these are likely to be more, and some less, important for understanding the bioactivity or other property of interest. Here we used it in a large-scale comparison of the structures of endogenous human metabolites and marketed drugs. It turned out that variants of the Tversky similarity do indeed provide a much richer harvest of “similar” molecules than do those provided (O'Hagan and Kell, 2015c; O'Hagan et al., 2015) by the standard Tanimoto similarity. The similarities differ both in magnitude and in rank order as α and β and their sum are varied, and thus provide a much broader range of candidate molecules to consider for experimental studies of interest. Being able to incorporate the similarity as part of a surrogate objective function thus allows the use of what amounts to a semi-supervised strategy.

We and others have written before about the potential utility of understanding the “likeness” of individual molecules to those considered representative of particular classes, such as drug-likeness (e.g., Karakoc et al., 2006; Paolini et al., 2006; Bickerton et al., 2012), natural-product-likeness (Ertl et al., 2008; Jayaseelan et al., 2012), or indeed metabolite-likeness (e.g., Cherkasov, 2006; Gupta and Aires-De-Sousa, 2007; Dobson P. D. et al., 2009; Peironcely et al., 2011; Walters, 2012; O'Hagan and Kell, 2015c; O'Hagan et al., 2015). Clearly this depends on the nature of the encoding used, but, as we see here, it can also depend markedly on the metric of similarity, that can be varied via the Tversky α and β parameters.

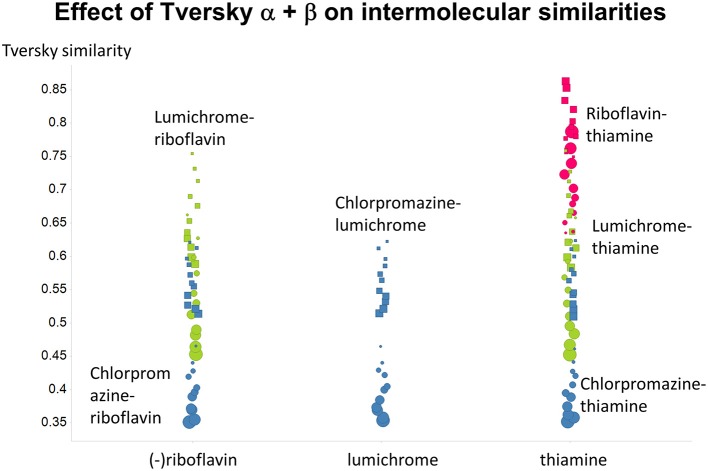
Previously, we found that the shapes of these curves of cumulative similarity differed markedly for different classes of compounds, e.g., when the comparison was made between marketed drugs and natural products or marketed drugs and subsets from drug discovery libraries rather than between drugs and Recon2 (O'Hagan and Kell, 2015c; O'Hagan et al., 2015). It was thus of considerable interest to see how this changed when we used Tversky instead of Taniomoto similarities. Most interestingly, it was not at all the case that the values of α and β favoring drug-likeness were always the greatest for endogenites (as they were for the Tanimoto similarity); particular values could make natural products libraries and ZINC compounds overtake them (Figures 10, 11). Thus it is possible to “tune” the Tversky parameters to favor the kinds of molecules that are most similar to marketed drugs. In a similar vein, the converse can be observed when we run the system “backwards,” interrogating the list of drugs serially with compounds in the three classes (Figures 12–14). Overall, for individual comparisons, the Tversky similarities could easily vary by as much as 0.3 over the ranges of α and β over the range examined here.

Figure 14.

Variance of Tversky similarities for the molecules that were depicted in Figure 1, as a function of α and β. Size proportional to α. Squares α + β = 1; circles α + β = 2.

Much as our earlier studies (Dobson P. D. et al., 2009; O'Hagan and Kell, 2015c; O'Hagan et al., 2015) had indicated, the more things one varies in even quite an elementary molecular comparison, and even using standard methods, the greater the range of molecular similarities that can become apparent. The present work extends this, by including variants of the comparison metric itself, spreading the Tanimoto similarity to the family of Tversky similarities. The much increased richness of molecular similarity space thereby uncovered, even for just a few interrogations, implies that the Tversky similarities will be of much more use in cheminformatics than their comparatively sparse use to date might imply. We are not yet in a position to recommend specific values of the Tversky parameters; rather we recognize that they simply increase the richness of the molecular space one should take into account when evaluating similarity. As more data emerge it is entirely possible that preferred values of α and β will emerge with them. An obvious extension is to compare the utility of Tversky α and β when different molecular encodings are used.

Authors information

DK is a Research Professor at the University of Manchester, a role to which he returned full time following a 0.8FTE 5-year secondment at Chief Executive of the Biotechnology and Biological Sciences Research Council. He was previously Director of the Manchester Centre for Integrative Systems Biology (www.mcisb.org). His interests include systems biology, chemical biology, pharmaceutical drug transporters, synthetic biology, cheminformatics, bacterial dormancy, machine learning and iron metabolism. His website is http://dbkgroup.org and he tweets as @dbkell. At Google Scholar his work has been cited more than 33,000 times, with an H-index of 91. SO has a Ph.D. in Chemistry from Warwick University, and following a period in industry is now a Computer Officer at the University of Manchester, specializing in cheminformatics, chemometrics, machine learning and the closed-loop automation of scientific instrumentation.

Author contributions

DK and SO conceived of the study, participated in its design and coordination and helped to draft the manuscript. SO wrote the workflows. All authors read and approved the final manuscript.

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphar.2016.00266

Table S1

“Top 20” hits for chlorpromazine cpz_hits_new.xlsx.

Table S2

“Top 20” hits for clozapine clozapine_hits_new.xlsx for various values of α.