Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Aug 22;6:30819. doi: 10.1038/srep30819

Probing the Spatial Organization of Molecular Complexes Using Triple-Pair-Correlation

Yandong Yin 1, Eli Rothenberg 1,a
PMCID: PMC4992864  PMID: 27545293

Abstract

Super-resolution microscopy coupled with multiplexing techniques can resolve specific spatial arrangements of different components within molecular complexes. However, reliable quantification and analysis of such specific organization is extremely problematic because it is frequently obstructed by random co-localization incidents between crowded molecular species and the intrinsic heterogeneity of molecular complexes. To address this, we present a Triple-Pair-Correlation (TPC) analysis approach for unbiased interpretation of the spatial organization of molecular assemblies in crowded three-color super-resolution (SR) images. We validate this approach using simulated data, as well as SR images of DNA replication foci in human cells. This demonstrates the applicability of TPC in deciphering the specific spatial organization of molecular complexes hidden in dense multi-color super-resolution images.

Optical super-resolution (SR) imaging techniques greatly surpass diffraction-limited microscopy, enabling the visualization of subcellular architectures with an accuracy of tens of nanometers1,2,3,4. In particular, when extended to multicolor imaging, SR can potentially resolve individual morphologies, as well as the specific internal spatial arrangement of molecular complexes5,6,7. However, the enhanced detection sensitivity of SR imaging and the resulting highly detailed information imposes serious challenges for accurate and unbiased quantification of the specific features of molecular complexes. This is especially critical for analysis of images containing particularly dense and abundant molecular species that are subjected to heterogeneous distribution, various orientations, and random co-localization incidents8,9. The recent advent of local-density and temporal-stochastic based segmentation methods10,11,12 has improved the quantification of single-color SR images with high molecular densities. In these methods the geometric center of molecular clusters is identified from their local spatial descriptive statistics, which can then be applied for analysis of Nearest-Neighboring-Distances (NND) between molecules labeled with different colors. However, in the case of multicolor molecular clusters, NND analysis cannot distinguish truly correlated species from randomly colocalized ones, and as a result, non-specific and random co-localization events inevitably dominate the NND distribution. Alternatively, Cross-Pair-Correlation analysis of SR images is capable of recognizing correlated molecules and calculating their correlation distances13, but such distance information between two components ultimately cannot be used for quantification of complicated molecular complexes, especially complexes composed of more than two components that are nonlinearly arranged.

Here, we report a Triple-Pair-Correlation (TPC) approach14 for unbiased analysis of the organization of molecular complexes in three-color SR images. The TPC approach generates a correlation profile derived from three independent geometric features, providing accurate quantification of the spatial arrangements of three different species labeled with different colors within a specific molecular assembly.

Results and Discussion

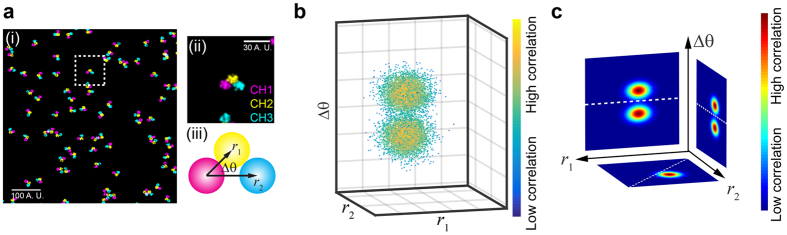
For simplicity, we annotate the three different color channels as Channels 1–3, as shown in the simulated data in Fig. 1a. The TPC algorithm calculates the probability of simultaneously finding three different molecules, each in a different channel, as a function of their relative displacement. Specifically, for each molecule located at vector coordinates R in channel 1 (CH1), the average probability of finding a molecule located at R + r1 in channel 2 (CH2), and another molecule located at R + r2 in channel 3 (CH3) is given by the TPC function (equation (1) and Fig. 1a(iii)):

Figure 1. Conceptual illustration of Triple-Pair-Correlation function.

Figure 1

Open in a new tab

(a) Simulated molecular complex randomly orientated and localized in a three-color image (i), with each complex composed of three different colored elements (ii) and its internal spatial organization defined by (r1, r2, Δθ) (iii). (b) Schematic illustration of the 3D Triple-Correlation g(r1, r2, Δθ) corresponding to the geometric properties shown in (a). (c) Three 2D correlation maps obtained through one dimensional integration of (b).

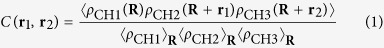graphic file with name srep30819-m1.jpg

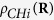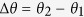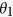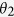where Inline graphic is the molecular density detected at position R = (R, θ) in channel i. Since the molecular complexes can be randomly orientated Inline graphic and Inline graphic, their internal correlation is derived from their relative orientation Inline graphic rather than an absolute one (Inline graphic and Inline graphic). Hence, the TPC only relies on three variables, and is written as: 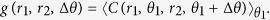Inline graphic Figure 1b shows an illustrative TPC 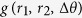Inline graphic plot of the molecules shown in Fig. 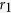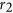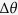1a, reaching the highest response at a specific combination of Inline graphic, Inline graphic, and Inline graphic which represents the internal spatial arrangement of the three molecules. Note that the molecular pattern can be imaged as a pair of reflectional symmetries in 2D (facing up and down), and therefore 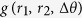Inline graphic has an equal response in the 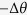Inline graphic region (Fig. 1b). 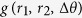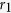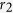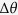To generate a more comprehensive mapping in the TPC cube, we integrated Inline graphic through each dimension, Inline graphic, Inline graphic, and Inline graphic, resulting in a combination of three 2D correlation maps (Fig. 1c).

Similar to the Pair Correlation function15, the TPC function can be represented as equation (2) (see Supplementary Note 1 for derivation):

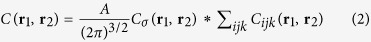graphic file with name srep30819-m19.jpg

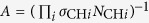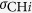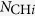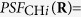
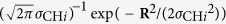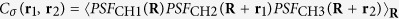where Inline graphic with Inline graphic and Inline graphic denote the localization uncertainty and number of fluorophores in channel i, respectively; the effective point spread function of fluorophores in CHi is described as Inline graphicInline graphic, and Inline graphic is their triple correlation, representing how localization uncertainties contribute to the whole TPC function; 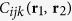Inline graphic quantifies the spatial correlation among the ith fluorophore from CH1, the jth fluorophore from CH2, and the kth fluorophore from CH3; and *denotes convolution.

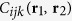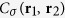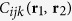When the fluorophores from different channels randomly distribute relative to each other (Fig. 2a), Inline graphic is constantly equal to 1, and consequently the TPC function, as a result of the convolution between Inline graphic and Inline graphic, represents a constant (Fig. 2b(i–iii)). 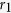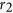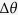On the other hand, when the fluorophores are arranged into certain molecular patterns, the whole TPC function quantifies the internal spatial organization of the molecular patterns as a function of Inline graphic, Inline graphic, and Inline graphic (Fig. 1). Figure 2c shows simulated molecular patterns each composed of three fluorophores of different colors (designated as M, Y, and C), and their TPC maps (Fig. 2d (i–iii)), which display a unique response at 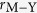Inline graphic = ~8.3 (A.U.), rM−C = ~19 (A.U.), and Δθ = ~0 (deg.) according to a Gaussian fit (Supplementary Figure S1), in good agreement with the pre-assigned geometry (Fig. 2c). We note that the localization uncertainty does not affect the position of the TPC profile within the g(r1, r2, Δθ) cube (or maps), but that an increasing localization uncertainty will widen the TPC profile (Supplementary Figure S2). Meanwhile, if the fluorophores of the same color accumulate into a cluster, and the clusters of different colors are then arranged into certain patterns, an increasing size of clusters will also widen the TPC profiles (Supplementary Figure S3). We also simulated molecular patterns that have non-linear internal organizations, and their non-zero Δθ are well resolved by the TPC function (Supplementary Figure S4).

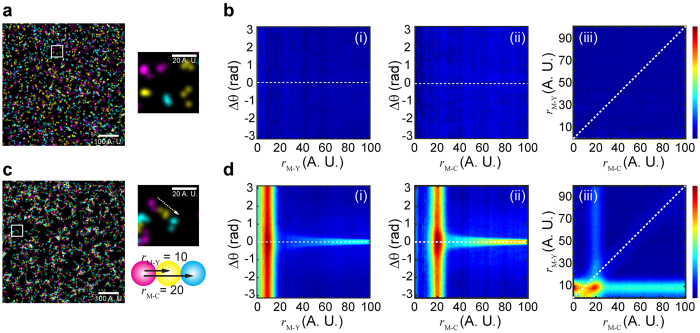
Figure 2. Triple-Pair-Correlation resolves simulated molecular pattern in highly dense SR image.

Figure 2

Open in a new tab

(a) Simulated molecules that randomly distribute in all the three channels. (b) Triple-Pair-Correlation maps of simulated images of (a) displays no spatial correlation between molecules from all the three channels. (c) Simulated molecules that linearly arrange into a certain sequential pattern. (d) Triple-Pair-Correlation analysis well resolved the internal spatial organization of molecular complex in (c) (Supplementary Figure S1). The feature appearing at 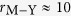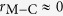Inline graphic, Inline graphic is a residual signal arising from the indirect bispectrum calculation (Supplementary Note 2), and accordingly can be subtracted as such. Color bar from blue to red represents low to high correlation amplitude, respectively. Images shown in (a,c) were Gaussian blurred for display purpose.

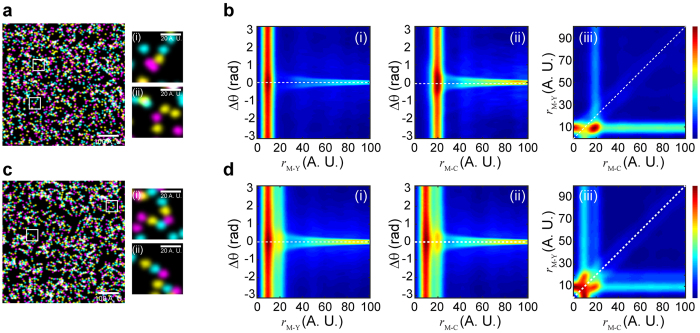
To further test if this approach is capable of resolving the heterogeneity of molecular patterns present in the same image, we carried out TPC analysis on simulated images with molecular patterns that have heterogeneous distributions. We first simulated a scenario where only functional molecules can form a specific pattern that is shown in Fig. 2c (Fig. 3a(i)), while non-functional molecules are randomly distributed (Fig. 3a(ii)). Figure 3b(i–iii) shows the TPC analysis of this scenario, where functional molecular patterns can be well distinguished from those randomly distributed molecules. We also tested the TPC approach by analyzing two different patterns present in the same image (Fig. 3c). In this scenario, half of the molecules form a Magenta-Yellow-Cyan (M-Y-C, Fig. 3c(i)) pattern and the other half form a Magenta-Cyan-Yellow (M-C-Y, Fig. 3c(ii)) pattern (i.e. 50% M-Y-C vs. 50% M-C-Y). While the resulting TPC profiles (Fig. 3d(i–iii)) show both populations peaking at r = ~9 and r = ~19 (A.U.) as a function of either rM−Y or rM−C, the two different patterns are well resolved in Fig. 2f(iii), with two distinct populations peaking at rM−Y = ~9 & rM−C = ~19 and rM−Y = ~20 & rM−C = ~9 (A.U.) (Supplementary Figure S5). This demonstrates the advantage of TPC analysis over other methods, especially since the Cross-Pair-Correlation between M and Y and between M and C is the same, so that the two patterns cannot be resolved by a Cross-Pair-Correlation approach.

Figure 3. Two scenarios of simulated SR images that contain heterogeneous molecular complex.

Figure 3

Open in a new tab

(a) Simulated SR image that contains ~49% spatially arranged molecular complex (i) and ~51% randomly distributed molecules (ii). (b) Triple-Pair-Correlation maps of simulated images of (a), succeeding in resolving the spatial organization of the molecular complex from randomly distributed molecules. (c) Simulated SR image that contains ~50% M-Y-C pattern (i) and ~50% M-C-Y pattern (ii). (d) The Triple-Pair-Correlation analysis well resolved the heterogeneity of molecular complex with different internal organization (Supplementary Figure S5). Color bar from blue to red represents low to high correlation amplitude, respectively. Images shown in (a,c) were Gaussian blurred for display purpose.

Next, we tested the TPC approach by analyzing three-color SR imaging data examining DNA replication in human U2OS cells. DNA replication is performed by the replisome, a multifunctional protein machine that orchestrates parental DNA unwinding, single-stranded DNA stabilization, and nascent DNA synthesis. As viewed by diffraction-limited microscopy, replisome proteins form bright replication foci where the different replication factors co-localize with nascent chromatin16. Both nascent DNA and replisome proteins are highly abundant in the nucleus during S-phase, resulting in random overlap of the different replisome components17. To examine whether the TPC approach can distinguish the arrangements of the active replisomes subpopulation from random species, we carried out three-color imaging of cells where nascent DNA and the replication proteins PCNA and RPA were labeled (Methods). We note that RPA specifically binds to single-stranded DNA at replication forks and at other locations, further increasing the difficulty of resolving and quantifying individual replications units within such data.

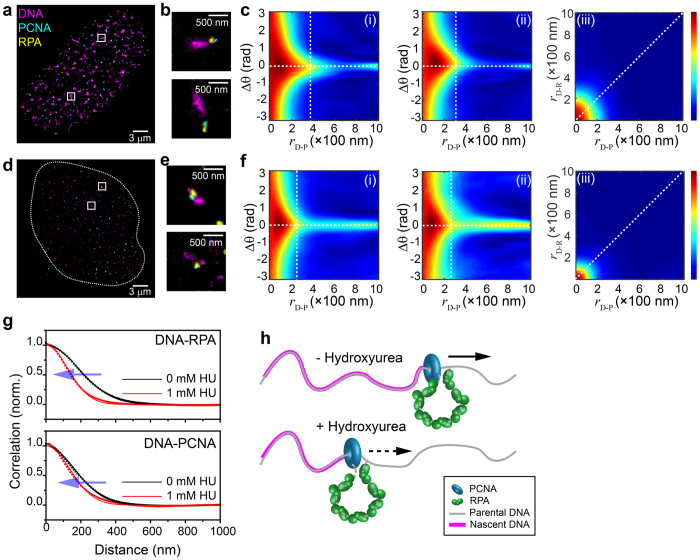
Figure 4a shows a SR image of a U2OS cell nucleus with labeled nascent DNA (magenta), RPA (yellow) and PCNA (cyan). While repetitive features can be seen in individual foci (Fig. 4b), due to the abundance of the different factors, their specific spatial arrangement with respect to nascent DNA is barely discernable. By applying TPC analysis (Fig. 4c(i–iii), Supplementary Figure S6) we identified a clear correlation (triple-colocalization) of PCNA, RPA, and nascent DNA, which otherwise cannot be quantitatively distinguished from random colocalization incidents in such high-density images when interpreted via non-correlation methods. The TPC analyses enabled us to derive the average correlation distances of PCNA and RPA from nascent DNA as ~132 and ~150 nm, respectively. These metrics are significant as the observed patterns are anticipated based on current models describing replisome assembly18. We note that correlation distances are convolved with a number of factors that are intrinsic to single-molecule localization microscopy, such as the experimental localization accuracy (~15 nm, 37 nm, and 44 nm for Alexa Fluor 647, Alexa Fluor 568, and Alexa Fluor 488, respectively), volume of the antibodies used for immunofluorescence19,20, and the projection of 3D data to a 2D image. As such, the correlation distances cannot be used as absolute distance measurements, but rather provide an accurate description of the relative placement of molecules for analysis of their spatial arrangement. TPC analysis also revealed that the angle between DNA-PCNA and DNA-RPA axis is ~0 deg. (Fig. 4c(i,ii)). In addition to the fact that the observed cluster size is comparable with their correlation distance, we reasoned that the broad distribution of the correlation profile can arise from its 3D nature. To further test our analysis, we also imaged U2OS cells where nascent DNA, RPA, and the replicative helicase MCM were labeled. TPC analysis applied to these images yielded the same pattern, except that the correlation distance of MCM from nascent DNA was ~164 nm, which is further than PCNA and RPA (Supplementary Figure S8). This organization is in agreement with the prevailing replication fork model where the replicative DNA helicase is located at the front of the replication fork18.

Figure 4. Triple-Pair-Correlation analysis of the SR resolved spatial arrangement of replisomes in cells.

Figure 4

Open in a new tab

(a) Mutlicolor SR image of a U2OS cell nucleus in early S-phase with nascent DNA, PCNA, and RPA stained in magenta, cyan, and yellow, respectively. (b) Two magnified images showing examples of the internal spatial organization of a replication focus. The experimental localization accuracies for the different colors used in these measurements are: 15 nm, 37 nm, and 44 nm for magenta (Alexa Fluor 647), yellow (Alexa Fluor 568), and cyan (Alexa Fluor 488), respectively (see Data Analysis in Methods section). (c) Triple-Pair-Correlation maps obtained by averaging the Triple-Correlation of 13 nuclei. Distances from DNA to RPA (rD−R) and from DNA to PCNA (rD−P) are ~149.7 ± 0.6 and 132.0 ± 0.7 nm, respectively; angles in between rD−R and rD−P follows a Gaussian distribution centering at 0 with standard deviation of ~29 deg. (Supplementary Figure S6). (d) Mutlicolor SR image of a U2OS cell nucleus treated with 1 mM HU in early S-phase. (e) Two magnified images showing examples of the internal spatial organization of a replication focus under replication stress. (f) Triple-Pair-Correlation maps obtained by averaging the Triple-Pair-Correlation of 18 nuclei. Distances from DNA to RPA (rD−R) and from DNA to PCNA (rD−P) are ~100 ± 1 and 109 ± 1 nm, respectively. Angles in between rD−R and rD−P follows a Gaussian distribution centering at 0 with standard deviation of ~20 deg. (Supplementary Figure S8, all errors are propagated fitting errors). (g) 1D correlation of rD−R (top) and rD−P (bottom) obtained via integration of rD−R − rD−P correlation map (c(iii),f(iii)) along rD−P and rD−R, respectively. Both graphs display a decrease of correlation distances when cells treated with 1 mM HU. Dots and lines represent the raw data and modified Gaussian fit, respectively (Supplementary Note 3). 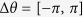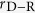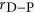We note that the overlapped portion between nascent DNA and replisome proteins resulted in a high Triple-Correlation response at rD−R (or rD−P) of ~0 nm covering all Inline graphic, which further resulted in a high correlation at Inline graphic (or Inline graphic) of ~0 nm after integration through 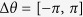Inline graphic in (c(iii),f(iii),g) (Supplementary Note 3 and Supplementary Figure S7). (h) Schematic illustration of the internal organization of a single replication fork obtained from the TPC analysis. Straight and Dashed arrows represent regular and stalled replication processing, respectively.

Finally, we tested the ability of TPC to resolve perturbations in the arrangements of replisomes. To this end, we imaged S-phase U2OS cells that were treated with hydroxyurea (HU), which suppresses DNA replication by depleting dNTP pools21. Figure 4d shows the nucleus of a cell treated with 1 mM HU during replication, where a sharp decrease in the amount of nascent DNA (magenta) is observed. TPC analysis of HU-treated cells identified individual replication forks containing nascent DNA, PCNA, and RPA where PCNA and RPA are localized at the edge of nascent DNA clusters (Fig. 4f). The analysis revealed smaller nascent DNA clusters along with shorter DNA-PCNA and DNA-RPA distances of ~109 nm, and ~100 nm, respectively as compared to control cells (Fig. 4g,h, and Supplementary Figure S9).

In summary, we have demonstrated that TPC analysis is a robust approach, capable of unbiased identification of the spatial arrangement of distinct subpopulations of molecular complexes contained in noisy multicolor SR images. The fundamental strength of TPC analysis is its ability to distinguish every correlated three-component species from randomly distributed and uncorrelated populations, which would otherwise prevent quantitative analysis of the molecular complex of interest. As compared to Cross-Pair-Correlation analysis, TPC provides far more topological information by extending the measurable geometric properties from distance-only to distances together with their angular distributions and directionalities. We also note that the correlation algorithm presented in this study can be extended for unbiased analysis of 3D SR images. Consequently, the TPC approach is widely applicable for the comprehensive quantitative analysis of the spatial organization of molecular complexes in biological SR imaging, as well as other fields applying multiplexed high-resolution imaging.

Methods

Cell culture, cell synchronization, and in vivo EdU labeling

U2OS cells (ATCC HTB-96) were passaged onto glass coverslips and cultured in Modified McCoy’s 5A medium (ThermoFisher 16600) with 10% FBS (Germini Bio. 100–106) and 100 U/mL Penicillin-Streptomysin (ThermoFisher 15140) for 24 hours. The cells were then synchronized to early S-phase via 72 hours Serum withdrawal followed by 15 hours incubation in full medium22. The cells were incubated in full medium with 0 or 1 mM HU for another 2 hours, and during the last hour of HU treatment, EdU was added to a final concentration of 10 μM for nascent DNA labeling23.

Imaging sample preparation

Cells were immediately permeablized and fixed after EdU labeling. In brief, cells were extracted with CSK buffer (10 mM Hepes, 300 mM Sucrose, 100 mM NaCl, 2 mM MgCl2, and 0.5% Triton X-100, pH = 7.4) for 10 minutes to remove replisome proteins that are unbound to chromatin, followed by fixation with paraformaldehyde (PFA, 4% in PBS) for 30 minutes24,25. Cells were then washed twice with blocking buffer (2% glycine, 2% BSA, 0.2% geltin, and 50 mM NH4Cl in PBS) and blocked for 1 hour at room temperature or overnight at 4 °C for further immunofluorescence staining.

Nascent DNA staining was performed by tagging Alexa Fluor 647 picolyl azide onto EdU via the ‘click’ reaction26 (Click-iT chemistry, thermoFisher C10640). RPA, PCNA, and MCM were stained with validated monoclonal antibodies27,28,29. In detail, RPA was immunostained with a rabbit monoclonal against RPA70 (Abcam, ab79398) followed by secondary immunostaining with goat-anti-rabbit conjugated with Alexa Fluor 568 (ThermoFisher, A11036); PCNA and MCM were immunostained with Mouse monoclonal against PCNA (Abcam, Ab29) and MCM5 (Abcam, ab6154), respectively, followed by secondary immunostaining with goat-anti-mouse conjugated with alexa Fluor 488 (ThermoFisher, A11029).

Coverslips were mounted onto a microscope microfluidics chamber for SR imaging.

Microscope and Super-resolution imaging

We used a custom-built optical imaging platform based on a Leica DMI 300 inverted microscope equipped with three laser lines: 473 nm laser line (Opto Engine LLC, MBL-473-300 mW), 532 nm laser line (OEM Laser Systems, MLL-III 200 mW), and 640 nm laser line (OEM Laser Systems, MLL-III 150 mW). All three laser lines were collimated and reflected into an HCX PL APO 100X NA = 1.47 OIL CORR TIRF objective by a multi-band dichroic (Chroma, zt405/488/532/640rpc-XT). Cell samples were excited in Highly inclined and Laminated Optical sheet (HILO) illumination mode30, and a 405 nm laser line (Applied Scientific Pro., SL-405 nm-300 mW) was employed to enhance photoswitching of fluorophores.

The emitted fluorescence was sequentially recorded. In brief, fluorescence of Alexa Fluor 568 and Alexa Fluor 647 were simultaneously collected through a dual-band bandpass filter (Chroma, CY3/CY5, 59007m) and subsequently split into two channels using a dichroic mirror (Semrock, FF660-Di02) in conjugation within a dual-view cube (Photometrics, DV2); fluorescence of Alexa Fluor 488 was afterwards recorded with the dual-band bandpass filter replaced by a narrow single-band filter (Semrock, FF01-531/40) via a filter wheel (ThorLabs, FW102C), and then was reflected onto one half side of the camera by the FF660 dichroic. All three colors were recorded at 512 × 512 pixels (~with configured pixel size of 160 × 160 nm2) using an Andor iXon+ 897 EMCCD camera at 33 Hz for 2000 frames31. The three channels were calibrated by matching the same fluorescent beads (ThermoFisher, T7279) observed in different channels via a polynominal morph-type mapping algorithm.

Super-resolution imaging buffer was composed of an oxygen scavenging system (1 mg/mL glucose oxidase, 0.02 mg/mL catalase, and 0.8% glucose in PBS) and 100 mM cycteamine (MEA)4. The oxygen scavenging solution was freshly mixed before injection into the sample chamber.

Data analysis

Single-molecule localization was performed by QuickPalm with previously described parameter sets32. Specifically, single-molecule localization was determined with the QuickPalm parameter minimum SNR = 4, and the maximum FWHM = 4. The obtained (x, y) coordinates list of all the localization events was then written into a new image with pixel sizes of 10 × 10 nm2. The localization uncertainty 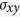Inline graphic was evaluated through equation33 (3):

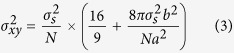graphic file with name srep30819-m35.jpg

where 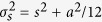Inline graphic, s is the standard deviation of the PSF of each single molecule events, a is the pixel dimension; N is the number of photons and b is the background. The frequency counts of all uncertainties were then generated and the peak position given by a skew Gaussian fit of the frequency distribution was considered as the average uncertainty. For correlation analysis, the central region of each nucleus was cropped to avoid the heterogenic edge distribution effect34. The cropped region had a minimum dimension of 8 μm, substantially bigger than the scales of the complexes of interest (correlation distance ~100–200 nm).

Triple-Correlation was calculated using its Fourier Transforms known as bispectrum (equation (4)):

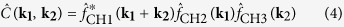graphic file with name srep30819-m37.jpg

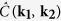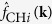where Inline graphic and Inline graphic are the Fourier Transforms of C(r1, r2) and ρChi(r), respectively, with ki the corresponding spatial frequency of ri. Considering the computing difficulty for a direct 4D Inverse Fourier Transform with each dimension of ~800 pixels (or sampled frequency), we instead 2D scanned r1 (or r2), and accordingly performed 2D Fast Fourier Transform (FFT) and inverse FFT over r2 (or r1) at each fixed r1 (or r2) (Supplementary Note 2). The 4D Triple Correlation was then integrated through θ1 as mentioned in the main text and finally yielded the 3D correlation g(r1, r2, Δθ). We integrated through each parameter of g(r1, r2, Δθ) to yield a combination of three 2D correlation maps. For more precise quantification of each parameter, we integrated the 3D correlation data through the other two parameters and performed 1D fit via a modified Gaussian model (Supplementary Note 3).

Additional Information

How to cite this article: Yin, Y. and Rothenberg, E. Probing the Spatial Organization of Molecular Complexes Using Triple-Pair-Correlation. Sci. Rep. 6, 30819; doi: 10.1038/srep30819 (2016).

Supplementary Material

Supplementary Information
srep30819-s1.pdf (1.4MB, pdf)

Acknowledgments

We would like to thank members of the Rothenberg lab and Dr. Nick Cowan for helpful suggestions and thoughtful discussions. Work in E.R.’s laboratory is supported by National Institutes of Health Grants GM057691, CA187612, and GM108119; and a Shifrin–Meyer Breast Cancer Discovery award.

Footnotes

Author Contributions Y.Y. and E.R. conceived the project and designed algorithm. Y.Y. performed the simulations and experiments. Y.Y. and E.R. analyzed the simulated and experimental data. Y.Y. and E.R. wrote the manuscript.

References

  1. Rust M. J., Bates M. & Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat Methods 3, 793–795, doi: 10.1038/nmeth929 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Hell S. W. Far-Field Optical Nanoscopy. Science 316, 1153–1158, doi: 10.1126/science.1137395 (2007). [DOI] [PubMed] [Google Scholar]
  3. Shroff H., Galbraith C. G., Galbraith J. A. & Betzig E. Live-cell photoactivated localization microscopy of nanoscale adhesion dynamics. Nat Methods 5, 417–423, doi: 10.1038/nmeth.1202 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Heilemann M., van de Linde S., Mukherjee A. & Sauer M. Super-resolution imaging with small organic fluorophores. Angew Chem Int Ed Engl 48, 6903–6908, doi: 10.1002/anie.200902073 (2009). [DOI] [PubMed] [Google Scholar]
  5. Xu K., Zhong G. & Zhuang X. Actin, Spectrin, and Associated Proteins Form a Periodic Cytoskeletal Structure in Axons. Science 339, 462–465, doi: 10.1126/science.1232251 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bossi M. et al. Multicolor Far-Field Fluorescence Nanoscopy through Isolated Detection of Distinct Molecular Species. Nano Letters 8, 2463–2468, doi: 10.1021/nl801471d (2008). [DOI] [PubMed] [Google Scholar]
  7. Jungmann R. et al. Multiplexed 3D cellular super-resolution imaging with DNDNA-PAINT and Exchange-PAINT. Nature Methods 11, 313–318, doi: 10.1038/nmeth.2835 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Zhao Z. W. et al. Spatial organization of RNA polymerase II inside a mammalian cell nucleus revealed by reflected light-sheet superresolution microscopy. Proc Natl Acad Sci USA 111, 681–686, doi: 10.1073/pnas.1318496111 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Coltharp C., Yang X. & Xiao J. Quantitative analysis of single-molecule superresolution images. Current Opinion in Structural Biology 28, 112–121, doi: 10.1016/j.sbi.2014.08.008 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Owen D. M. et al. PALM imaging and cluster analysis of protein heterogeneity at the cell surface. J Biophotonics 3, 446–454, doi: 10.1002/jbio.200900089 (2010). [DOI] [PubMed] [Google Scholar]
  11. Bar-On D. et al. Super-resolution imaging reveals the internal architecture of nano-sized syntaxin clusters. J Biol Chem 287, 27158–27167, doi: 10.1074/jbc.M112.353250 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Rubin-Delanchy P. et al. Bayesian cluster identification in single-molecule localization microscopy data. Nat Methods 12, 1072–1076, doi: 10.1038/nmeth.3612 (2015). [DOI] [PubMed] [Google Scholar]
  13. Sengupta P. et al. Probing protein heterogeneity in the plasma membrane using PALM and pair correlation analysis. Nat Methods 8, 969–975, doi: 10.1038/nmeth.1704 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ridgeway W. K., Millar D. P. & Williamson J. R. The spectroscopic basis of fluorescence triple correlation spectroscopy. J Phys Chem B 116, 1908–1919, doi: 10.1021/jp208605z (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Veatch S. L. et al. Correlation functions quantify super-resolution images and estimate apparent clustering due to over-counting. PloS one 7, e31457, doi: 10.1371/journal.pone.0031457 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Masai H., Matsumoto S., You Z., Yoshizawa-Sugata N. & Oda M. Eukaryotic Chromosome DNA Replication: Where, When, and How? Annual Review of Biochemistry 79, 89–130, doi: 10.1146/annurev.biochem.052308.103205 (2010). [DOI] [PubMed] [Google Scholar]
  17. Saner N. et al. Stochastic association of neighboring replicons creates replication factories in budding yeast. The Journal of cell biology 202, 1001–1012, doi: 10.1083/jcb.201306143 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Yeeles J. T., Deegan T. D., Janska A., Early A. & Diffley J. F. Regulated eukaryotic DNA replication origin firing with purified proteins. Nature 519, 431–435, doi: 10.1038/nature14285 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Szymborska A. et al. Nuclear Pore Scaffold Structure Analyzed by Super-Resolution Microscopy and Particle Averaging. Science 341, 655–658, doi: 10.1126/science.1240672 (2013). [DOI] [PubMed] [Google Scholar]
  20. Nieuwenhuizen R. P. et al. Quantitative localization microscopy: effects of photophysics and labeling stoichiometry. PloS one 10, e0127989, doi: 10.1371/journal.pone.0127989 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Chen Y. H. et al. ATR-mediated phosphorylation of FANCI regulates dormant origin firing in response to replication stress. Mol Cell 58, 323–338, doi: 10.1016/j.molcel.2015.02.031 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Khammanit R., Chantakru S., Kitiyanant Y. & Saikhun J. Effect of serum starvation and chemical inhibitors on cell cycle synchronization of canine dermal fibroblasts. Theriogenology 70, 27–34, doi: 10.1016/j.theriogenology.2008.02.015 (2008). [DOI] [PubMed] [Google Scholar]
  23. Yokochi T. & Gilbert D. M. Replication Labeling with Halogenated Thymidine Analogs. Curr Protoc Cell Biol 35, 22.10.01–22.10.14, doi: 10.1002/0471143030.cb2210s35 (2007). [DOI] [PubMed] [Google Scholar]
  24. Britton S., Coates J. & Jackson S. P. A new method for high-resolution imaging of Ku foci to decipher mechanisms of DNA double-strand break repair. The Journal of cell biology 202, 579–595, doi: 10.1083/jcb.201303073 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Cseresnyes Z., Schwarz U. & Green C. M. Analysis of replication factories in human cells by super-resolution light microscopy. BMC cell biology 10, 88, doi: 10.1186/1471-2121-10-88 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kolb H. C., Finn M. G. & Sharpless K. B. Click Chemistry: Diverse Chemical Function from a Few Good Reactions. Angew. Chem. Int. Ed. Engl. 40, 2004–2021, doi: (2001). [DOI] [PubMed] [Google Scholar]
  27. Rakotomalala L. et al. Hepatitis B virus X protein increases the Cdt1-to-geminin ratio inducing DNA re-replication and polyploidy. J Biol Chem 283, 28729–28740, doi: 10.1074/jbc.M802751200 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. McQueen J. et al. Restoration of oligodendrocyte pools in a mouse model of chronic cerebral hypoperfusion. PloS one 9, e87227, doi: 10.1371/journal.pone.0087227 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Toledo L. I. et al. ATR prohibits replication catastrophe by preventing global exhaustion of RPA. Cell 155, 1088–1103, doi: 10.1016/j.cell.2013.10.043 (2013). [DOI] [PubMed] [Google Scholar]
  30. Tokunaga M., Imamoto N. & Sakata-Sogawa K. Highly inclined thin illumination enables clear single-molecule imaging in cells. Nat Methods 5, 159–161, doi: 10.1038/nmeth1171 (2008). [DOI] [PubMed] [Google Scholar]
  31. Zhu L., Zhang W., Elnatan D. & Huang B. Faster STORM using compressed sensing. Nat Methods 9, 721–723, doi: 10.1038/nmeth.1978 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Henriques R. et al. QuickPALM: 3D real-time photoactivation nanoscopy image processing in ImageJ. Nat Methods 7, 339–340, doi: 10.1038/nmeth0510-339 (2010). [DOI] [PubMed] [Google Scholar]
  33. Mortensen K. I., Churchman L. S., Spudich J. A. & Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat Methods 7, 377–381, doi: 10.1038/nmeth.1447 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Coltharp C., Yang X. & Xiao J. Quantitative analysis of single-molecule superresolution images. Current opinion in structural biology 28, 112–121, doi: 10.1016/j.sbi.2014.08.008 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep30819-s1.pdf (1.4MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES