Survival Impact Index and Ultrahigh-dimensional Model-free Screening with Survival Outcomes

Summary

Motivated by ultrahigh-dimensional biomarkers screening studies, we propose a model-free screening approach tailored to censored lifetime outcomes. Our proposal is built upon the introduction of a new measure, survival impact index (SII). By its design, SII sensibly captures the overall influence of a covariate on the outcome distribution, and can be estimated with familiar nonparametric procedures that do not require smoothing and are readily adaptable to handle lifetime outcomes under various censoring and truncation mechanisms. We provide large sample distributional results that facilitate the inference on SII in classical multivariate settings. More importantly, we investigate SII as an effective screener for ultrahigh dimensional data, not relying on rigid regression model assumptions for real applications. We establish the sure screening property of the proposed SII-based screener. Extensive numerical studies are carried out to assess the performance of our method compared with other existing screening methods. A lung cancer microarray data is analyzed to demonstrate the practical utility of our proposals.

1. Introduction

This paper addresses the ultrahigh-dimensional screening problem encountered in bio-medical data analysis. For example, in an ultrahigh-dimensional gene expression setting, the first step of data analysis is usually to rank the importance of genes based on their marginal associations with the outcome variable and remove unimportant genes from the bottom of an ordered list. Many ad hoc screeners were implemented in published studies. Recent statistical literature has favored the marginal regression-based screening measures owing to their desirable theoretical properties (Fan and Lv, 2008; Fan et al., 2009; Li et al., 2012; Cheng et al., 2014). It may be more appealing to consider a robust approach that can be resistant against model misspecification; see (Zhu et al., 2011; Li et al., 2012) for related discussions.

We consider censored lifetime outcomes in this paper. Though variable screening and variable selection methods for continuous and binary outcomes are abundant, the related development in survival analysis has been relatively sparse and most existing approaches focus on Cox proportional hazards model (Fan and Li, 2002; Fan et al., 2010; Bradic et al., 2011; Zhao and Li, 2012) or other regression methods (Huang et al., 2006; Johnson et al., 2008). These methods may be problematic when the assumed data generating mechanism is not adequate for the actual failure process.

To overcome this limitation, several authors have proposed non-model based screening methods. For example, He et al. (2013) introduced a novel model-free screener, named as the quantile adaptive sure independence screening (QaSIS) procedure. They proposed to perform screening based on the disparity between unconditional and conditional quantiles given each covariate under investigation. QaSIS abandons the specification of a statistical model by utilizing nonparametric estimators of distribution quantiles and can be flexibly applied to different quantiles. More recently, Song et al. (2014) studied the use of Kendall’s τ as a variable screening criterion for randomly censored data. Their method is robust to outliers and can well capture nonlinear covariate-response relationships. The technique of inverse probability of censoring weighting (IPCW) was adopted by these approaches to handle the random censoring of outcomes.

Motivated by He et al. (2013)’s work while intending to develop a screening device with better generalizability and estimability with survival outcomes, we propose a new and sensible measure, called survival impact index (SII). By the definition, SII characterizes the impact of a covariate on the outcome distribution by evaluating the absolute deviation of the covariate-stratified survival distribution from the unstratified survival distribution.

The proposed SII renders multi-fold potential advantages of SII-based screener over QaSIS. First, SII works on the probability scale and is naturally bounded. This largely reduces the variability of the screening procedure while the estimated quantiles for QaSIS are not necessarily bounded and could be extrapolated to extreme values from the fitted model for certain covariates. Secondly, SII integrates the absolute survival differences across a meaningful range of the failure time. In contrast, QaSIS only focuses on a single quantile level and therefore may lack sufficient capacity to capture the full-range covariate impact on the overall survival experiences. Thirdly, as we shall elaborate in Section 2, the definition of SII naturally entails smoothing-free estimation and thus avoids the complexity involved in smoothing parameter specification. Further, compared to IPCW, the proposed technique for handling random censoring enables easier adaptations to different censoring and truncation mechanisms which may emerge in various survival studies.

In Section 2, we introduce the concept of SII and develop an inferential framework for the classical multivariate setting. In Section 3, we investigate the utility of SII as a screener for ultrahigh dimensional data. In Section 4, we carry out extensive numerical simulations to assess the performance of the proposed SII screener and make comparisons with other existing approaches. In Section 5, a lung cancer data is analyzed as an illustration.

2. Survival impact index

Let T be the failure time subject to random right censoring by C, and X = (X₁,⋯, X_p)^T be the corresponding p-dimensional covariate vector. For a random sample of size n, we can only observe {(Y_i, δ_i, X_i) : i = 1,⋯, n}, where Y_i = min(T_i, C_i) and δ_i = I(T_i ≤ C_i).

We define the survival impact index (SII) for each marker X_j, j = 1,⋯, p by

$$\begin{array}{c}{\xi }_j={\int }_{t\in \mathcal{T},x\in \mathcal{X}}{W}_{\xi }\left(t,x\right)|P(T>t|X_j>x)-P\left(T>t\right)|\mathit{dxdt}\\ ={\int }_{t\in \mathcal{T},x\in \mathcal{X}}{W}_{\xi }\left(t,x\right)|S(t|X_j>x)-S\left(t\right)|\mathit{dxdt},\end{array}$$ (1)

where S(t|X_j > x) is a covariate-stratified survival function defined as the conditional survival function of T given X_j > x, and S(t) is the unconditional (or unstratified) survival function of T. The integration is over a range of values of interest for T and X_j, namely $\mathcal{T}$ and $\mathcal{X}$ respectively. Here W_ξ(t, x) is a pre-determined weight function, which offers additional flexibility for capturing the impact of X_j. For example, one may emphasize the covariate impact on early (or late) survival by letting W_ξ(t, x) be a decreasing (or increasing) function of t. Without loss of generality, we assume ${\int }_{t\in \mathcal{T},x\in \mathcal{X}}{W}_{\xi }(t,x)\mathit{dxdt}=1.$

The proposed survival impact index ξ_j may be interpreted as the weighted average absolute difference between the survival function assessment with and without considering X_j. If for at least one t and one x the survival function stratified on X_j > x differs from the unstratified survival function at t, the value of ξ_j will be non-degenerate under mild distributional smoothness assumption. On the other hand, ξ_j = 0 would result from T and X_j being independent. Therefore ξ_j is a sensible index for characterizing the importance of X_j in affecting the distribution of T.

The definition of SII also entails a good estimability. We can naturally estimate the unknown ξ_j by

$${\widehat{\xi }}_j={\int }_{t\in \mathcal{T},x\in \mathcal{X}}{W}_{\xi }\left(t,x\right)|\widehat{S}(t|X_j>x)-\widehat{S}\left(t\right)|\mathit{dxdt},$$

where Ŝ(t|X_j > x) is the Kaplan-Meier (KM) estimator for the conditional survival function of T given X_j > x and Ŝ(t) is the KM estimator for the survival function of T, respectively. The KM estimator is implemented in most statistical software and can be easily adopted to calculate ${\widehat{\xi }}_j$. Note that, Ŝ(t|X_j > x) can be obtained simply as the KM estimator based on the sub-sample where X_j > x.

By adopting KM estimators in ${\widehat{\xi }}_j$, we implicitly impose a random censoring assumption, which requires that T and C are independent given X_j > x for each $x\in \mathcal{X}$. This is not stronger than the assumption usually required by model-based method (Fan and Lv, 2008; Fan et al., 2009, among others). It is clear that the computation of ${\widehat{\xi }}_j$ does not involve smoothing. When T is subject to more complex censoring or truncation, we may readily evaluate ${\widehat{\xi }}_j$ by replacing Ŝ(t|X_j > x) and Ŝ(t) with suitable survival estimators for the covariate stratified sample and the unstratified sample respectively. See Turnbull (1976); Vardi (1982); Wang et al. (1986), among others for examples.

Note that ${\widehat{\xi }}_j$ offers a nonparametric test statistic for evaluating the effect of covariate X_j on the survival outcome T. For this type of testing problems, Peng and Fine (2008) exploited a similar idea of utilizing stratification by covariates. However they only investigated test statistics that capture the weighted average difference (rather than the weighted average absolute difference used by ${\widehat{\xi }}_j$) between survival functions. As a test statistic, ${\widehat{\xi }}_j$ is then expected to have superior power compared to Peng and Fine (2008)’s test statistics, particularly in the presence of cross-over effects. As a summary statistic, ${\widehat{\xi }}_j$ may provide a more appropriate characterization for the overall impact from a variable on the survival outcome.

The consideration of weighted average absolute difference between covariate-stratified survival functions and the unstratified survival function, nevertheless, poses complications for the asymptotic studies for ${\widehat{\xi }}_j$. The common linearization technique (Kosorok, 2008), though working for Peng and Fine (2008), is not applicable for studying ${\widehat{\xi }}_j$. To spell it out, though a uniform i.i.d. summation representation for {Ŝ_j(t; x)−Ŝ(t)}−{S_j(t; x)−S(t)} can follow from rather standard arguments, it cannot be extended to help derive the limit distribution of ${\widehat{\xi }}_j-{\xi }_j$ ,which equals to ${\int }_{t\in \mathcal{T},x\in \mathcal{X}}{W}_{\xi }(t,x)\{|\widehat{S}(t|X_j>x)-\widehat{S}(t)|-|S(t|X_j>x)-S(t)|\}\mathit{dxdt}.$

To tackle this challenge, we resort to other statistical techniques including the functional delta method (Van Der Vaart and Wellner, 2000) and establish the large sample properties of ${\widehat{\xi }}_j$ in the following theorem.

Theorem 1

As n → ∞, we have ${\widehat{\xi }}_j\to {\xi }_j$ in probability, and furthermore,

1. if ξ_j = 0, then

   $$\sqrt{n}{\widehat{\xi }}_j\stackrel{d}{\to }{\int }_{(t,x)\in \mathcal{T}\times \mathcal{X}}{W}_{\xi }(t,x)|{\mathbb{X}}_j(t,x)|\mathit{dxdt};$$ (2)
2. if ξ_j ≠ 0, and there exists a positive constant κ_j such that the Lebesgue measure of $\mathrm{\Omega }({\kappa }_j):=\{(t,x):|S(t|X_j>x)-S(t)|<{\kappa }_j,(t,x)\in \mathcal{T}\times \mathcal{X}\}$ is 0, then

   $$\sqrt{n}({\widehat{\xi }}_j-{\xi }_j)\stackrel{d}{\to }{\int }_{(t,x)\in \mathcal{T}\times \mathcal{X}}{W}_{\xi }(t,x)\mathit{sgn}(S_j(t;x)-S(t)){\mathbb{X}}_j(t,x)\mathit{dxdt};$$ (3)

where ${\mathbb{X}}_j(t,x)$ is a mean-zero Gaussian process defined in (8) in Appendix.

Theorem 1 indicates that the asymptotic distribution of ${\widehat{\xi }}_j$ warrants separate discussions as in (a) and (b), depending on the value of ξ_j as well as the measure of $\{(t,x):|S(t|X_j>x)-S(t)|=0,(t,x)\in \mathcal{T}\times \mathcal{X}\}$. The restriction on the latter is primarily owing to the fact that, though the absolute value function is not differentiable at zero, Hadamard-differentiability of the functional ${\int }_{{\mathrm{\Omega }}^c({\kappa }_j)}{W}_{\xi }(t,x)|\cdot |\mathit{dtdx}$ can be achieved when the measure of $\{(t,x):|S(t|X_j>x)-S(t)|=0,(t,x)\in \mathcal{T}\times \mathcal{X}\}$ equals zero. It is clear that the condition in (a) is satisfied when X_j is independent of T, and hence the asymptotic result in (2) is useful for characterizing the SII of noise variables. In case (b), a zero measure of $\{(t,x):|S(t|X_j>x)-S(t)|<{\kappa }_j,(t,x)\in \mathcal{T}\times \mathcal{X}\}$ does not pose an unrealistic data assumption. Under most typical regression modeling of X_j and T, such as the Cox proportional hazards model, the condition in (b) would hold when X_j has a non-zero coefficient given that κ_j can be arbitrarily small. The proof of Theorem 1 is given in the Appendix.

The asymptotic results in Theorem 1 can be applied to construct confidence intervals for ξ_j. The unknown covariance functions may be hard to estimate. In practice, we may adopt a nonparametric bootstrap procedure to resample {Y, δ, X_j} and construct confidence intervals from the bootstrap empirical distributions. The construction of confidence intervals can be readily converted to a testing procedure for the null hypothesis, ξ_j = 0.

When the interest lies in the comparison of the survival impact of two markers, say ξ_j and ${\xi }_{j^{\prime }}$, j ≠ j′, we may test the following hypothesis:

$$H_0:{\xi }_j={\xi }_{j^{\prime }},\mathrm{v}\text{.s}.H_1:{\xi }_j\ne {\xi }_{j^{\prime }}.$$ (4)

A two-sided test may be constructed based on $\mathrm{Q}=|{\widehat{\mathrm{\xi }}}_j-{\widehat{\xi }}_{j^{\prime }}|$. However, similar to Theorem 1, we can show that the limit distribution of Q could involve even more complicated stochastic integrals. Therefore we suggest using a permutation test for (4). Specifically a permutation sample is constructed as $\{(Y_i,{\delta }_i,X_{ji}^{\ast },X_{j\prime i}^{\ast }):i=1,\cdots ,n\}$, where Y_i and δ_i are the sample observations and $X_{ji}^{\ast }$, $X_{j\prime i}^{\ast }$ are independently drawn from a discrete uniform with atoms {X_ji, X_j′i}. A large number of permutation samples are obtained and we evaluate ${\mathrm{Q}}^{\ast }=|{\widehat{\xi }}_j^{\ast }-{\widehat{\xi }}_{j^{\prime }}^{\ast }|$ for each permutation. The test p-value is the empirical proportion that Q* > Q. Our extensive simulation studies indicate satisfactory performance of the permutation test.

3. Variable screening

The preceding section addresses estimation and inference of SII in the classical setting with a finite number of covariates. A more important goal of this work is to investigate the utility of SII as a screening device for ultrahigh dimensional data. To this end, we assume the total number of covariates p satisfying p = O(exp(n^c)) for a positive c < 1. We adopt the common sparsity assumption and believe that only a small subset of these p covariates are indeed related to the survival outcome. Directly applying any penalty-based estimation with p markers is infeasible in most statistical programs. It is necessary to first implement a screening procedure and cut the number p from the non-polynomial order to a much smaller (polynomial) order. For the survival-based screening, we intend to recover a sparse subset

$${\text{ℳ}}_{\ast }=\{1\le j\le p:{\xi }_j>0\}$$ (5)

with nonsparsity size s_* = |ℳ_*|. The set defined in (5) is indeed model free and the dependence of ξ_j on the covariates is only via the conditional distribution of survival time. While the data in the simulation settings are generated from certain known parametric models, our estimation and screening procedures do not require a pre-specified model and hence do not utilize any distribution information from the true model.

We propose to compute the estimated survival impact index ${\widehat{\xi }}_j$ for each X_j using the methods introduced in the preceding section and then select the subset of variables

$$\widehat{\text{ℳ}}=\{1\le j\le p:{\widehat{\xi }}_j\ge {\nu }_n\},$$ (6)

where ν_n is a pre-defined threshold value. In practice, we often rank the markers by ${\widehat{\xi }}_j$ and keep the top [n/log(n)] markers, where [a] denotes the integer part of a. Our screening procedure does not involve any model-fitting and is thus immune to model misspecification.

To justify the proposed screener based on SII, we need to show $P({\text{ℳ}}_{\ast }\subset \widehat{\text{ℳ}})$ has a high probability. We impose the following regularity conditions to facilitate our technical derivations.

1. Let S_j(·) and S_C(·) be the marginal survival functions of X_j and C, respectively. Given $t_0\in \mathcal{T}$, $x_0\in \mathcal{X}$, there exist constants γ, τ and λ, such that 0 < γ ≤ S(t₀)S_C(t₀), 0 < τ ≤ S_j(x₀) and 0 < λ ≤ Pr (Y > t₀, X_j > x₀), for all 1 ≤ j ≤ p.

2. p = O(exp(n^c)) for some 0 < c < 1, and ${min}_{j\in {\text{ℳ}}_{\ast }}{\xi }_j>c_0{n}^{-\alpha }$ for some positive constant c₀ and 0 ≤ α < (1 − c)/2.

Condition (C1) ensures that the information collected from the region $\mathcal{T}\times \mathcal{X}$ can produce a rather stable estimation of X_j’s impact on the distribution of T. Condition (C2) assumes that the variables in the signal set ℳ_* have strong enough influences upon T ; a smaller α represents a higher impact. The constraint, 0 ≤ α < (1 − c)/2, in (C2) then indicates that a larger p (corresponding to a larger c) would demand a greater minimal “signal strength”, given by c₀n^−α.

The following theorem characterizes the finite sample behavior of ${\widehat{\xi }}_j$, j = 1,⋯, p.

Theorem 2

Under the condition (C1), given 24/(nτγ⁴) < ε < 1,

$$\mathit{Pr}(\underset{1\le j\le p}{\text{max}}|{\widehat{\xi }}_j-{\xi }_j|>\epsilon )\le c_3\text{exp}(-n{c}_4{\epsilon }^2-c_5\text{log}\epsilon ).$$

where c₃, c₄ and c₅ are some positive constants only depending on τ, γ, and λ, and n is sufficiently large.

Theorem 2 indicates that ${\widehat{\xi }}_j$’s are uniformly consistent to ξ_j’s with an exponential rate error bound. This sharp bound allows us to obtain the desirable sure screening property immediately:

Corollary 1

(Sure screening property). Under the conditions (C1) and (C2), if ν_n is chosen to be bn^−α with b ≤ c₀/2, then

$$Pr\left({\text{ℳ}}_{\ast }\subset \widehat{\text{ℳ}}\right)\ge 1-c_3|{\text{ℳ}}_{\ast }|\text{exp}(-n{c}_4{(c_0-b)}^2{n}^{-2\alpha }-c_5\text{log}((c_0-b)n^{-\alpha })),$$

where positive constants c₃, c₄ and c₅ are specified in Theorem 2. In particular, $Pr\left({\text{ℳ}}_{\ast }\subset \widehat{\text{ℳ}}\right)\to 1$ as n → ∞.

Another interesting question is how many noise variables are retained after the screening. The following corollary provides a bound on the size of incorrect selection from the screening.

Corollary 2

(False positive control). Under the condition (C1) and (C2), if ν_n is chosen to be no less than $\sqrt{(\text{log}p+c_5\text{log}n/2)/(c_{4}n)}$,

$$\mathit{Pr}\left(|\widehat{\text{ℳ}}\backslash {\text{ℳ}}_{\ast }|<n^c\right)\ge 1-2c_{3}p\text{exp}(-n{c}_4{\nu }_n^2-c_5\text{log}{\nu }_n),$$

where c₃, c₄, c₅ are specified in Theorem 2 and c is specified in the condition (C2). In particular $\mathit{Pr}\left(|\widehat{\text{ℳ}}\backslash {\text{ℳ}}_{\ast }|<n^c\right)\to 1$ as n → ∞.

The above corollary is analogous to Theorem 3.4 in He et al. (2013). It indicates that if the screening threshold, ν_n is no less than $\sqrt{(\text{log}p+c_5\text{log}n/2)/(c_{4}n)}$, the number of noise variables (false positives) retained after screening is of polynomial rate with high probability. In practice, since the constants c₄ and c₅ are unknown, we may choose ν_n of rate $\sqrt{\text{log}p\text{log}n/n}$. Notice that $\sqrt{\text{log}p\text{log}n/n}\le \sqrt{n^c\text{log}n/n}=o(n^{-\alpha })$ according to the condition (C2). This choice of threshold satisfies the conditions in Corollary 1, and thus still guarantees the sure screening property. The proof of Theorem 2 is provided in the Appendix, and the proofs of Corollaries 1 and 2 are relegated to Supplementary Web Material.

4. Simulation

4.1 Estimation and inference for SII

We first evaluate the proposed estimation and inference for SII in the classical multivariate setting with finite p. We consider two cases with different error distributions. The sample sizes are set as n = 200 or 400 in the following. The sample sizes considered in this paper are comparable to most medical studies where usually hundreds of subjects are screened for a disease. In the real case study of this paper, the sample size is slightly larger and is above 400. The large sample condition may be better satisfied for such an example and the desired theoretical properties established in this paper may follow. Our simulation provides further empirical support for practitioners facing moderate sample sizes. Investigators may also use numerical results in this section to decide the sample size when designing a screening study with a pre-fixed error margin.

Case A

We consider model log(T) = 2X₁ + 2X₂ + 4X₃ + 8X₄ + ε. The vector of covariates X = (X₁,…, X_p) is generated from the multivariate normal distribution with mean 0 and the covariance matrix Σ = (σ_ij)_p×p with number of covariates p = 4, σ_ii = 1 and σ_ij = ρ, i ≠ j, ε ~ N(0, 1) is independent of X. In this case, we consider different correlation ρ = 0, 0.4, and 0.8. The logarithm of censoring time C is generated from a 3-component normal mixture distribution N(0, 4) − N(5, 1) + 0.5N(20, 1). The censoring rate is about 30%.

Case B

The setting is the same as that in Case A except that ε ~ logit(2, 2) is independent of X, where logit(a, b) is logistic distribution with location a and scale b and the logarithm of censoring time C is generated from N(0, 4) − N(5, 1) + 0.5N(25, 1). The censoring rate is also about 30%.

The number of repetitions is 500. For the bootstrap confidence intervals, we set the size of bootstrap resamples to be 500. For the permutation tests, we set the number of permutations to be 1000. The true ξ for each covariate is evaluated from a sample of size 50,000. To compute ${\widehat{\xi }}_j$, we used the uniform weight W (t, x) = 1 over the observation range for all cases. The results on point estimation, bootstrap confident intervals and permutation tests for Cases A and B are shown in Table 1. The means of the estimates for SII are reported under different settings. For the bootstrap 95% confidence intervals, we report the coverage probabilities. For the permutation tests, we examine the rejection rates for testing H₀ : ξ₁ = ξ_j.

Table 1.

Simulation results on estimation and inference in finite p cases

Case	n	ρ		ξ1	ξ2	ξ3	ξ4
A		0	True	0.062	0.062	0.124	0.255
	200		Estimate	0.066	0.062	0.123	0.251
			Coverage	0.980	0.960	0.940	0.900
			Rejection		0.06	0.69	1
	400		Estimate	0.064	0.063	0.124	0.254
			Coverage	0.950	0.940	0.940	0.950
			Rejection		0.05	0.92	1
		0.4	True	0.181	0.181	0.209	0.270
	200		Estimate	0.182	0.183	0.212	0.271
			Coverage	0.930	0.960	0.960	0.960
			Rejection		0.05	0.46	1
	400		Estimate	0.182	0.182	0.211	0.272
			Coverage	0.930	0.970	0.960	0.950
			Rejection		0.04	0.63	1
		0.8	True	0.265	0.265	0.272	0.289
	200		Estimate	0.269	0.270	0.278	0.295
			Coverage	0.960	0.940	0.950	0.950
			Rejection		0.05	0.30	0.85
	400		Estimate	0.268	0.267	0.275	0.292
			Coverage	0.970	0.990	0.980	0.970
			Rejection		0.03	0.34	0.97
B		0	True	0.058	0.058	0.116	0.239
	200		Estimate	0.060	0.059	0.117	0.236
			Coverage	0.970	0.980	0.910	0.930
			Rejection		0.07	0.69	1
	400		Estimate	0.060	0.059	0.117	0.236
			Coverage	0.950	0.940	0.950	0.940
			Rejection		0.03	0.89	1
		0.4	True	0.174	0.174	0.202	0.259
	200		Estimate	0.176	0.176	0.203	0.260
			Coverage	0.940	0.940	0.920	0.960
			Rejection		0.08	0.46	1
	400		Estimate	0.174	0.175	0.202	0.262
			Coverage	0.940	0.950	0.960	0.950
			Rejection		0.04	0.59	1
		0.8	True	0.258	0.258	0.264	0.281
	200		Estimate	0.262	0.261	0.271	0.287
			Coverage	0.930	0.940	0.950	0.960
			Rejection		0.10	0.30	0.86
	400		Estimate	0.261	0.260	0.268	0.284
			Coverage	0.950	0.970	0.940	0.980
			Rejection		0.04	0.26	0.95

True: true value of ξ; Estimate: average of the estimated SII; Coverage: coverage rate of the 95% bootstrap confidence intervals; Rejection: average rejection rate for the permutation test comparing ξ_j to ξ₁

In all scenarios, the nonparametric KM-based estimates for SIIs are close to the true SIIs. The bootstrap confidence intervals provide satisfactory coverage for the true parameters as the observed coverage rate is close to the nominal confidence level. The permutation tests also work very well. We note that ξ₁ = ξ₂ in both case A and B, and thus the average rejection rates reported in the column of ξ₂ represent the empirical sizes of the proposed permutation tests for H₀ : ξ₁ = ξ_j. Table 1 suggests that our tests achieve the correct size, with average rejection rates close to the nominal significance level. As the difference between ξ₁ and ξ_j (j = 3, 4) becomes larger, the test for the hypothesis H₀ : ξ₁ = ξ_j becomes more powerful with an increasing rejection rate.

4.2 Screening performance

We now consider different screening methods with simulated random samples. The proposed SII screening method, the model-based (MB) screening method and the quantile-adaptive screening (QaSIS) method were compared across all scenarios. In the MB method, we simply fit a Cox PH regression model to the data for each covariate and rank the covariates by the Wald test P-value. For the QaSIS method, we consider the first and second quartiles (corresponding to α = 0.25 and α = 0.5, respectively) of the distribution. In addition, we also include a practical screening approach based on Harrell’s C-statistic (Harrell et al. (1996)). We note that Harrell’s C-statistic is usually interpreted as a survival concordance measure or the integrated time-dependent area under ROC curve (Li and Ma (2011)). Similar to SII, a greater value of C-statistic may suggest a stronger association between the failure outcome and the marker. We consider a large number of covariates in this section with p = 200. The purpose is to screen from this set to identify important markers. Simulation results with other choices of p are available from the authors upon request.

The following data generation mechanisms represent various types of covariate functions with different degree of nonlinearity, different correlation structures among the covariates, different numbers of important predictors and multiple failure and censoring distributions.

Case I

Let g₁(x) = 5x, g₂(x) = −4x(1−x), g₃(x) = 10(exp(−(3x−1)²)+exp(−4(x−3)²))−1.5, g₄(x) = 4 sin(2πx). We consider the following model: log(T) = g₁(X₁)+g₂(X₂)+g₃(X₃)+ g₄(X₄) + ε, where the vector of covariates X = (X₁,…, X_p) is generated from the multivariate normal distribution with mean 0 and the covariance matrix Σ = (σ_ij)_p×p,σ_ii = 1 and σ_ij = ρ^|i−j| for i ≠ j, ε ~ N(0, 1) is independent of X, where ρ = 0, 0.4, and 0.8. The censoring time C is generated from a 3-component normal mixture distribution N(0, 4) − N(5, 1) + 0.5N(25, 1).

Case II

The setting and estimation are the same as those in Case I except that log(T) = X₁ + X₂ + X₃ + 2X₁X₂ + 2.5X₁X₃ + 3X₂X₃ + 2ε.

Case III

Let g₁(x) = 5 cos(2πx), g₂(x) = 5 exp(1.2x − 1) − 3, g₃(x) = −0.5(x − 1)³, g₄(x) = 3 arctan(3x − 2). We consider fitting log(T) = g₁(X₁) + g₂(X₂) + g₃(X₃) + g₄(X₄) + ε. The generation of X is the same as that in Case I. We let ε ~ logit(2, 2). The censoring time C is generated from N(0, 4) − N(5, 1) + 0.5N(20, 1).

Case IV

Let g₁(x) = 5(2x−1)², β₁ = 8, β₂ = 9, β₃ = 7. We consider fitting $\text{log}(T)=g_1(X_1)+X_2{\beta }_1+X_3{\beta }_2+X_4{\beta }_3+\sqrt{1.74}\epsilon$. The covariates are simulated according to the random-effect model $X_j=\frac{W_j+\rho U}{1+\rho }$, j = 1,…, p, where W₁,…, W_p and U are i.i.d Unif(0,1) random variables, and ε ~ N(0, 1). The censoring time C is generated from N(0, 4) − N(5, 1) + 0.5N(45, 1). In this case, we consider ρ = 0, 0.5, and 1. The other settings remain the same as that in Case I.

Case V

Let g₁(x) = 4 cos(2πx), g₂(x) = 4 exp(1.2x)−8, g₃(x) = 5x, g₄(x) = 3 arctan(3x−2). We consider fitting log(T) = g₁(X₁)+g₂(X₂)+g₃(X₃)+g₄(X₄)+ε. The generation of covariates are the same as that in Case IV. The censoring time C is generated from N(0, 4) − N(5, 1) + 0.5N(15, 1). In this case, we consider ρ = 0, 0.5, and 1.

Case VI

Let g₁(x) = 3 cos(2πx), g₂(x) = 2 exp(1.2x − 1) − 4, g₂(x) = −0.3(x − 1)³, g₃(x) = 2 arctan(3x − 2), β₁ = 2.5, β₂ = −2, β₃ = 3, β₄ = −1.5. We consider fitting log(T) = g₁(X₁) + g₂(X₂) + g₃(X₃) + g₄(X₄) + X₅β₁ + X₆β₂ + X₇β₃ + X₈β₄ + ε. The censoring time C is generated from N(0, 4) − N(5, 1) + 0.5N(10, 1). The other settings are identical to that in Case I.

The simulation results of all cases over 500 simulations are shown in Table 2. Two main performance criteria were computed: (i) ℛ and IQR, median and inter-quartile range of the minimum model size that covers all important markers; (ii) $\mathcal{S}$, coverage probability that the set of top [n/log(n)] markers after screening includes all important markers. A good screener should achieve a small ℛ and a large $\mathcal{S}$.

Table 2.

Simulation results on screening performance in ultra-high dimensional cases

				SII		MB		C Index		QaSIS (α = 0.25)		QaSIS (α = 0.5)
Case	n	ρ	p*	ℛ (IQR)	$\mathcal{S}$	ℛ (IQR)	$\mathcal{S}$	ℛ (IQR)	$\mathcal{S}$	ℛ (IQR)	$\mathcal{S}$	ℛ (IQR)	$\mathcal{S}$
I	200	0	4	92.5 (84.75)	0.16	118.5 (86)	0.09	122 (86.5)	0.14	195.5 (30.5)	0	129 (72.25)	0.02
		0.4	4	93 (71.5)	0.12	143.5 (64.75)	0.01	136 (97.75)	0.08	187 (37)	0	133 (84.5)	0.10
		0.8	4	18.5 (41.25)	0.63	73.5 (125.25)	0.28	72 (108.5)	0.29	183.5 (76)	0.03	61 (90.5)	0.39
	400	0	4	71.5 (69.5)	0.44	110.5 (94)	0.27	99 (101.75)	0.36	199 (17)	0.02	119 (95)	0.22
		0.4	4	60 (75.75)	0.56	136 (81.75)	0.14	135 (89.5)	0.17	194.5 (36.5)	0.01	126.5 (79)	0.14
		0.8	4	6 (10)	1	60 (113.5)	0.52	26 (92.5)	0.67	184.5 (65.75)	0.07	35 (74.25)	0.63
II	200	0	3	4.5 (8)	0.95	15 (46.25)	0.70	101 (72.5)	0.07	53.5 (112.25)	0.45	26 (43.5)	0.67
		0.4	3	3 (1)	1	14 (36.75)	0.69	76.5 (92.5)	0.26	189 (65.25)	0.09	28.5 (53)	0.59
		0.8	3	3 (0)	1	12.5 (30.5)	0.76	13 (40.25)	0.72	200 (0)	0	4 (2)	0.99
	400	0	3	3 (0)	1	3 (4)	0.97	108.5 (96)	0.30	20 (72.5)	0.68	10.5 (18.25)	0.92
		0.4	3	3 (0)	1	4 (7)	0.97	41.5 (91.25)	0.61	199 (27.75)	0.10	14 (19)	0.91
		0.8	3	3 (0)	1	5 (5.75)	0.98	5 (5)	0.96	200 (0)	0.01	3 (0.25)	1
III	200	0	4	53.5 (54.25)	0.33	96.5 (99.75)	0.20	93 (107.25)	0.21	183 (57.25)	0.02	108 (91.75)	0.14
		0.4	4	42.5 (61.25)	0.45	82.5 (90.75)	0.21	109 (90.5)	0.18	170 (51.75)	0.01	86 (94.75)	0.18
		0.8	4	4 (1)	0.99	6 (6.25)	0.94	7 (10.25)	0.88	188 (50)	0.01	13 (32.25)	0.75
	400	0	4	48 (44.25)	0.67	86 (100.75)	0.40	113.5 (98)	0.28	174 (52)	0.03	102 (99)	0.31
		0.4	4	14 (25.75)	0.91	48.5 (108.5)	0.55	75 (106.5)	0.47	179.5 (54.75)	0.08	68 (86)	0.49
		0.8	4	4 (1)	1	6 (2)	0.99	5 (1)	1	197 (27.25)	0.02	7 (6.25)	0.98
IV	200	0	4	6.5 (9)	0.93	108 (86.75)	0.10	107 (103)	0.17	186.5 (58.25)	0.01	16 (28.25)	0.76
		0.5	4	21 (43.5)	0.64	100 (82)	0.10	135 (75.75)	0.07	179.5 (36.5)	0.01	45.5 (84.5)	0.42
		1	4	17 (37.25)	0.67	98 (89.5)	0.13	149 (72.75)	0.06	187 (29.25)	0	48 (68.5)	0.40
	400	0	4	4 (0.25)	1	122 (116)	0.32	(101.5) (94.25)	0.31	189.5 (56.25)	0.08	4 (2)	0.99
		0.5	4	7 (15.25)	0.95	86.5 (90.5)	0.35	144 (85.25)	0.16	182 (47.75)	0.01	18.5 (40.25)	0.83
		1	4	6 (12.25)	0.95	93.5 (85.5)	0.34	154.5 (78)	0.12	186.5 (23.5)	0	41.5 (84.25)	0.63
V	200	0	4	4 (1)	0.98	125.5 (100.25)	0.10	104 (87.5)	0.11	190 (41)	0.01	49 (61.25)	0.37
		0.5	4	5 (3)	0.96	136 (71.75)	0.05	183.5 (47.75)	0.01	183 (42.25)	0	24.5 (27.5)	0.72
		1	4	11 (19.25)	0.79	172.5 (52.25)	0	197 (21.25)	0	168.5 (53.25)	0	42 (42.25)	0.43
	400	0	4	4 (0)	1	96 (96.25)	0.31	105.5 (98.25)	0.34	192.5 (33)	0.01	17.5 (33)	0.83
		0.5	4	4 (0)	1	144.5 (79.5)	0.17	190 (30.25)	0	176 (72.25)	0.05	10 (12.25)	0.99
		1	4	5 (4)	0.98	178.5 (43.5)	0.01	199 (4.25)	0	164 (61.5)	0.05	30.5 (33)	0.87
VI	200	0	8	82 (82.5)	0.18	103 (85.75)	0.15	114 (96.25)	0.12	197 (14)	0	142.5 (70)	0
		0.4	8	149 (71)	0.01	160 (57.75)	0.01	155 (93)	0.01	193 (20)	0	161 (52.75)	0
		0.8	8	8 (2)	0.95	8 (4)	0.95	8.5 (2)	0.95	199 (5)	0	43.5 (67.25)	0.45
	400	0	8	67.5 (71.25)	0.49	103 (94.25)	0.30	106.5 (108)	0.30	198.5 (9)	0	124.5 (62.5)	0.11
		0.4	8	135 (59.25)	0.14	160 (59.75)	0.07	136.5 (88.75)	0.14	195.5 (19.25)	0	147 (65.25)	0.06
		0.8	8	8 (0)	1	8 (0)	1	8 (0)	1	200 (2)	0	36 (45.75)	0.76

p*: number of truly important markers; ℛ: median of minimum model size that covers all important markers; IQR: inter-quartile range of minimum model size that covers all important markers; $\mathcal{S}$: empirical probability that the set of top [n/log(n)] markers after screening includes all important markers.

When PH assumptions do not hold and marker effects are nonlinear (all six cases), MB performs worse than SII. MB may include too many unimportant markers than SII in all scenarios with unacceptably high ℛ values. When PH assumptions do not hold but marker effects are approximately linear (Case II), MB may perform well but still not as well as SII, judging from ℛ and $\mathcal{S}$ values.

We observe that QaSIS with α = 0.5 works better than QaSIS with α = 0.25 in all cases. QaSIS with α = 0.25 may even have poorer performance compared to MB. This indicates that the choice of α matters for the success of this approach in identifying relevant important markers. Among all methods compared in simulations, QaSIS, Harrell’s C and MB perform less satisfactorily than SII. A strong supporting example is Case IV, where the minimum coverage numbers from SII are much smaller than those from median QaSIS and MB, while SII’s coverage rates are substantially higher than both median QaSIS and MB. In this example, the median QaSIS achieves better performance than MB but not QaSIS with α = 0.25. All methods improve with increasing sample sizes.

In summary, the simulation results demonstrate that the proposed nonparametric screener is clearly more robust than model-based screener. Compared to QaSIS, which focuses on a local outcome region reflected by the selection of quantile level α, the proposed SII-based screening procedure can better capture the global influences of covariates on the survival outcome.

5. Example: Lung Cancer

Lung cancer represents the leading cause of cancer death for both men and women in the United States and many Western countries. Accurate early detection is thus crucial for lung cancer treatment. Prognostic gene expression signatures for survival in early-stage lung cancer have been proposed for clinical applications (Lu et al., 2006; Chen et al., 2007).

Our example comes from a large retrospective, multi-site, blinded study (Shedden et al., 2008), which involved 442 lung adenocarcinomas, the specific type of lung cancer that is increasing in incidence. Gene expression data were generated by four different laboratories under a common protocol. The same data set has been used in Xie et al. (2011) as a validation sample for a separate analysis. A total of 437 subjects are included in the downstream analysis. The median follow-up time is 46 months. The overall censoring rate is 46.22%. For each subject, the expressions of 22283 genes are available. A screening is necessary prior to any meaningful model construction.

The number of selected covariates is [n/log(n)] = 72 after the screening. For MB screening under Cox PH model, we display the ID of selected genes in the following:

20612	4051	14544	7951	20022	4260	4313	149	8236	19150	2875	9847
9311	9835	4809	10999	17303	778	5145	14581	19536	2821	12536	17369
831	6546	21478	1525	4835	265	3406	816	18244	14073	10238	12334
17872	13085	11626	8934	9558	2330	10223	14525	15885	13290	9451	1418
15746	17558	16748	4024	19151	21901	4647	8223	5715	21948	3263	14103
12471	5758	5069	21441	8539	17229	11759	9987	3495	5448	17521	6681

The above screening procedure requires that data follow the Cox PH model. One important assumption for Cox model is the proportionality of hazard functions across time. To check the PH assumption, a test based on martingale residuals was carried out for each selected marker, implemented by cox.zph in R. The proportion of significant p-values (< 0.05) is 29/72 = 0.40. This raises concerns over the applicability of the MB approach given that the key assumption appears to be invalid for a large portion of the models.

We then considered using the proposed model-free SII method. The genes after screening (listed below) are now completely different from those obtained from the MB approach with 0 overlap.

6253	20336	7426	6312	4078	3949	5347	6361	19167	6781	5703	6283
15402	9769	7446	7651	10376	6974	10043	14915	9464	3977	5419	14212
16986	16877	6078	6743	9340	5	5752	10975	4110	6168	19053	4799
7449	20323	5960	5948	4109	7040	14243	6478	6165	6796	10797	13794
7273	5282	18829	5556	5527	19187	20787	5398	5904	6692	5385	9818
6524	6132	9853	16933	6687	4913	16442	5704	7227	15243	5580	7464

In Table 3, we compare the screening results for the top 9 genes obtained by SII with those from MB and QsSIS with α = 0.25 and α = 0.50. The survival impacting values ξ for the top 9 genes selected by the SII indicate an average of over 40% change in survival probabilities after covariate stratification, while most top genes selected by the model-based method only change the survival probability < 10%. This comparison clearly indicates that the SII method identifies markers with more relevant information to calibrate the survival probability. The correlation between ξ and the Wald test p-value from Cox model is −0.098, affirming a very weak agreement between SII and the Cox model-based screening. Harrel’s C statistics are reported for all genes in this table. Except those identified from the MB method, the C statistics are all very close to 50%, suggesting very low concordance. Such a discrimination statistic may not work well for the purpose of screening in this example.

Table 3.

Summary of the top 9 selected genes from different screening methods for the lung cancer data

		MB				QaSIS (α = 0.25)				QaSIS (α = 0.5)		SII
rank	ID	p-value	C Index	ξ	ID	QaSIS	C Index	ξ	ID	QaSIS	C Index	ξ	ID	ξ	p-value	C Index
1	20612	1.42e-10	0.647	0.054	6253	1.02e+06	0.505	0.463	6253	3.69e+06	0.505	0.463	6253	0.463	0.339	0.505
2	4051	5.07e-09	0.616	0.143	7426	6.34e+04	0.545	0.433	7426	7.40e+04	0.545	0.433	20336	0.438	0.621	0.515
3	14544	9.27e-09	0.593	0.117	20336	4.91e+04	0.515	0.438	6312	6.55e+04	0.539	0.430	7426	0.433	0.541	0.545
4	7951	4.74e-08	0.618	0.044	4078	1.54e+04	0.520	0.423	20336	4.59e+04	0.515	0.438	6312	0.430	0.755	0.539
5	20022	6.61e-08	0.630	0.086	6312	1.01e+04	0.539	0.430	4078	1.60e+04	0.520	0.423	4078	0.423	0.121	0.520
6	4260	8.49e-08	0.567	0.206	5347	8.94e+03	0.505	0.413	16877	1.12e+04	0.525	0.367	3949	0.416	0.583	0.517
7	4313	1.23e-07	0.612	0.089	5703	7.94e+03	0.535	0.403	6974	1.05e+04	0.532	0.378	5347	0.413	0.175	0.505
8	149	2.33e-07	0.606	0.051	6781	5.68e+03	0.510	0.403	15402	9.78e+03	0.533	0.386	6361	0.413	0.293	0.517
9	8236	2.81e-07	0.603	0.067	5948	4.23e+03	0.538	0.344	5347	8.06e+03	0.505	0.413	19167	0.412	0.326	0.504

ID: gene ID; p-value: p values from the Wald tests in Cox regression; C Index: Harrell’s C-statistics; ξ: SII values.

We note that the genes selected by the QaSIS at the first (α = 0.25) and the second (α = 0.5) quartiles are only slightly different from those obtained under the SII method in Table 3. These model-free approaches enjoy better agreement, with an overall sample correlation in ξ around 0.40. However, the estimated screening criterion values resulted from QaSIS are extremely large (> 10³) and may not be easy to interpret in practice. To provide further insight on the two approaches, we display in Figure 1 the rankings for top 20 genes obtained from SII and QaSIS at 8 different percentiles (α = 0.1,…, 0.8). Almost all the top genes identified by the SII are also identified by the QaSIS at some but often different quantile levels. Using QaSIS at a single quantile level may not be very desirable since by construction it is restricted to a local probability and may not select genes causing large modification to the survival distribution. Nonetheless, combining the QaSIS results at different percentiles could lead to very similar screening results as the SII. In fact, the correlation between QaSIS and SII for all of the top 20 genes selected by the pooled QaSIS across τ = 0.1,…, 0.8 is 0.77, showing a strong correspondence between the two model-free screening approaches.

Figure 1.

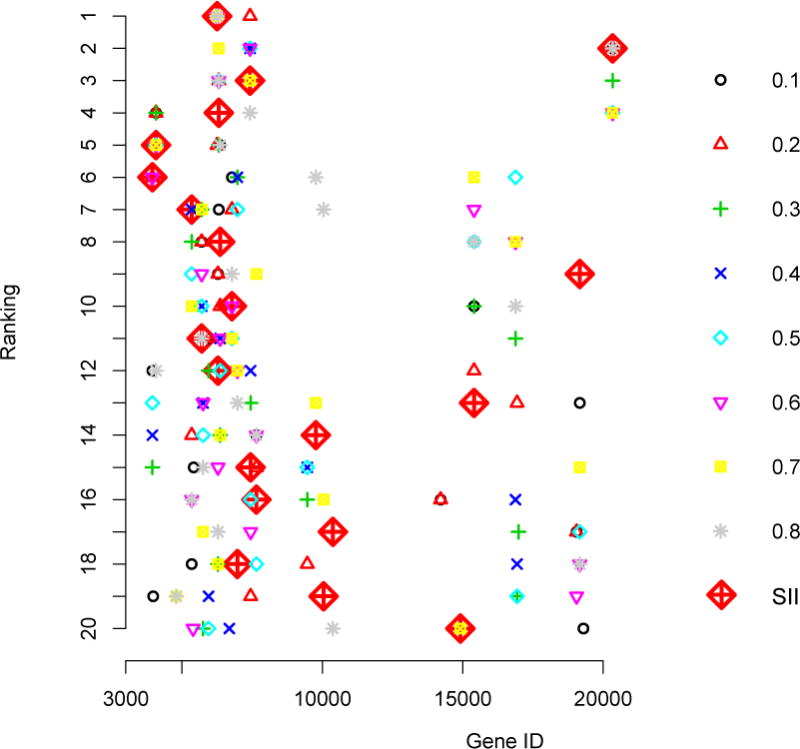
The top 20 genes screened from SII and QaSIS at quantiles 0.1 through 0.8 for the lung cancer data.

We next consider making inferences for the ξ’s. Specifically, we consider comparing the two genes selected as the No. 1 by SII and MB, respectively. The estimated ξ for the top genes selected by the two methods are 0.463 (bootstrap confidence interval [0.442, 0.485]) and 0.054 (bootstrap confidence interval [0.025, 0.044]). The permutation test for comparing these two genes gives a p-value 0.011, suggesting that the top gene selected by our method is associated with a significantly higher SII measure than the top gene selected by MB approach. Other inference results can be similarly obtained.

6. Discussion

Recent vast expansion of research efforts on ultrahigh dimensional data produced effective screening procedures under various assumptions. When there is little information to support a model or clear empirical evidence against certain class of models, it may be safer to consider model-free approaches. Both QaSIS and SII are easy to implement, built on existing nonparametric estimation programs. By their designs, QaSIS inquires into a specified segment of outcome distribution, while SII targets global covariate effects. SII being bounded in the probability scale makes it more straightforward to interpret and compare. The numerical examples in this paper evince that these methods may lead to meaningful discovery that otherwise is unattainable. More experiments on different data sets may be necessary before these approaches are fully accepted by practitioners.

Fan and Lv (2008) and Fan et al. (2010) showed that an iterative screening procedure may perform better than non-iterative procedure, especially for complicated designs. It is possible to conduct iterative SII screening and further refine the screening results attained in this paper. Such an iterative procedure may also be helpful to resolve the dependent censoring issue for survival data and reduce the false positive rate. More detailed development is beyond the scope of this paper and will be studied in our forthcoming work.

Appendix

We first introduce some notations. Let a ˄ b = min(a, b). Denote S(t|X_j > x) by S_j(t; x). Let N_+,i(t) = 1{Y_i ≤ t, δ_i = 1}, N_+,i,j(t, x) = 1{Y_i ≤ t, δ_i = 1, X_ji > x} and R_+,j,i(t, x) = 1{Y_i ≥ t, X_ji > x}. Let λ(·) and λ_j(·|X_j > x) denote the hazard function of T and T given X_j > x respectively. Given a 0 < ε < 1, $0={\eta }_0^{(j)}<{\eta }_1^{(j)}<\cdots <{\eta }_{L(\epsilon )}^{(j)}=x_0$ is a partition for X_j satisfying (a) $S_j({\eta }_{k-1}^{(j)})-S_j({\eta }_k^{(j)})\le \epsilon /3$, (b) L(ε) ≤ 6/ε. Let $M_{jn}(x)={\sum }_{i=1}^{n}1\{X_{ji}>x\}$ and $V_{ji}(u)={\sum }_{k=1}^{n}1\{Y_k>Y_i,X_{jk}>u\}/({\sum }_{k=1}^{n}1\{Y_k\text{>}{Y}_i,X_{jk}\text{>}u\}+1)$. If there is no tie at any observed time points, then $\widehat{S}(t|X_j>x)={{\prod }_{i=1}^n{V}_{ji}(x)}^{1\{Y_i\le t,X_{ji}>x,{\delta }_i)=1\}}$. The following fact (Foldes and Rejto (1981)) will be used in the proof, for some universal constants c₁ and c_2, and 12/(nγ⁴) < ε < 1.

$$Pr\left(\underset{t\in \mathcal{T}}{\text{sup}}|\widehat{S}(t)-S(t)|>\epsilon \right)\le c_1\text{exp}(-n{\gamma }^6{\epsilon }^2/c_2-\text{log}\epsilon ).$$ (7)

Proof of Theorem 1

${\widehat{\xi }}_j\to {\xi }_j$ in probability will be shown in Theorem 2. Following the definition of KM estimator, we are able to show that $n^{1/2}\left[({\widehat{S}}_j(t;x)-\widehat{S}(t))-(S_j(t;x)-S(t))\right]\stackrel{a}{=}{n}^{-1/2}{\sum }_{i=1}^{n}IC(Y_i,{\delta }_i,X_{ji},t,x):=n^{-1/2}{\sum }_{i=1}^n(I{C}_1(Y_i,{\delta }_i,X_{ji},t,x)+I{C}_2(Y_i,{\delta }_i,t))$ ,where $\stackrel{a}{=}$ means “asymptotically equivalent” and

$$\begin{array}{l}I{C}_1(Y_i,{\delta }_i,X_{ji},t,x):=-S_j(t;x)\frac{1\{X_{ji}>x\}}{S_j(x)}\left[{\int }_0^t\frac{1}{Pr(Y>u|X_j>x)}{N}_{+,j,i}(du,x)-{\int }_0^t\frac{R_{+,j,i}(u,x)}{Pr(Y>u|X_j>x)}{\text{λ}}_j(u|X_j>x)du\right]\\ I{C}_2(Y_i,{\delta }_i,t):=-S(t)\left[{\int }_0^t\frac{1}{Pr(Y>u)}{N}_{+,i}(du)-{\int }_0^t\frac{1(Y_i\ge u)}{Pr(Y>u)}\lambda (u)du\right].\end{array}$$

Since the class of indicator functions is Donsker and the sum of Donsker classes is also Donsker, $\{I{C}_1(Y_i,{\delta }_i,X_{ji},t,x),(t,x)\in \mathcal{T}\times \mathcal{X}\}$, $\{{\mathit{IC}}_2(Y_i,{\delta }_i,t),t\in \mathcal{T}\}$ and $\{IC(Y_i,{\delta }_i,X_{ji},t,x),(t,x)\in \mathcal{T}\times \mathcal{X}\}$ are all Donsker. By Donsker Theorem,

$$\sqrt{n}\left[({\widehat{S}}_j(t;x)-\widehat{S}(t))-(S_j(t;x)-S(t))\right]\stackrel{w}{⇝}{\mathbb{X}}_j(t,x),$$ (8)

in $l^{\text{∞}}(\mathcal{T}\times \mathcal{X})$, where $l^{\text{∞}}(\mathcal{T}\times \mathcal{X})$ is the collection of all bounded functions $\psi :\mathcal{T}\times \mathcal{X}\to \text{ℝ}$. Here, $\stackrel{w}{⇝}$ denotes “converge weakly”. The process ${\mathbb{X}}_j(t,x)$ has mean zero and covariance matrix $\text{cov}({\mathbb{X}}_j(t_1,x_1),{\mathbb{X}}_j(t_2,x_2))=E\left[IC(Y_i,{\delta }_i,X_{ji},t_1,x_1)IC(Y_i,{\delta }_i,X_{ji},t_2,x_2)\right]$.

Let h_n(t, x) be any sequence uniformly converging to h(t, x) on $\mathcal{T}\times \mathcal{X}$, where h(·,·) is a function with total variation bounded. If ξ_j = 0, the Lesbegue measure of $\{(t,x):|S(t|X_j>x)-S(t)|\ne 0,(t,x)\in \mathcal{T}\times \mathcal{X}\}$ is 0. Equation (8) becomes $\sqrt{n}({\widehat{S}}_j(t;x)-\widehat{S}(t))\stackrel{w}{⇝}{\mathbb{X}}_j(t,x)$. By the continuous mapping theorem [Theorem 1.11.1 in Van Der Vaart and Wellner (2000)],

$$\sqrt{n}{\widehat{\xi }}_j=\sqrt{n}{\int }_{\mathcal{T}\times \mathcal{X}}{W}_{\xi }(t,x)|{\widehat{S}}_{\mathrm{j}}(t;x)-\widehat{S}(t)|\mathit{dtdx}\stackrel{d}{\to }{\int }_{\mathcal{T}\times \mathcal{X}}{W}_{\xi }(t,x)|{\mathbb{X}}_j(t,x)|\mathit{dtdx}$$

If ξ_j ≠ 0 and the Lebesgue measure of $\mathrm{\Omega }({\kappa }_j):=\{(t,x):|S(t|X_j>x)-S(t)|<{\kappa }_j,(t,x)\in \mathcal{T}\times \mathcal{X}\}$ is 0, we argue that the functional ${\int }_{{\mathrm{\Omega }}^c({\kappa }_j)}{W}_{\xi }(t,x)|·|\mathit{dtdx}$ is Hadamard-differentiable at S_j(·;·)−S(·), where Ω^c(κ_j) is the complementary set of Ω(κ_j) on $\mathcal{T}\times \mathcal{X}$. The detailed arguments can be found in Supplementary Web Material. For the definition of Hadamard-differentiability, we refer to page 372 of Van Der Vaart and Wellner (2000). Applying the functional Delta method [Theorem 3.9.4 in Van Der Vaart and Wellner (2000)] yields

$$\sqrt{\mathrm{n}}({\widehat{\xi }}_j-{\xi }_j)=\sqrt{n}{\int }_{\mathcal{T}\times \mathcal{X}}{W}_{\xi }(t,x)\left[|{\widehat{S}}_j(t;x)-\widehat{S}(t)|-|S_j(t;x)-S(t)|\right]\mathit{\text{dtdx}}\stackrel{d}{\to }{\int }_{\mathcal{T}\times \mathcal{X}}{W}_{\xi }(t,x)\text{sgn}(S_j(t;x)-S(t)){\mathbb{X}}_j(t,x)\mathit{\text{dtdx}}.$$

This completes the proof of Theorem 1.