Enabling Privacy-Preserving GWAS in Heterogeneous Human Populations

Summary

The proliferation of large genomic databases offers the potential to perform increasingly larger-scale genome-wide association studies (GWAS). Due to privacy concerns, however, access to these data is limited, greatly reducing their usefulness for research. Here, we introduce a computational framework for performing GWAS that adapts principles of differential privacy—a cryptographic theory that facilitates secure analysis of sensitive data—to, for the first time, both protect private phenotype information (e.g., disease status) and correct for population stratification. This framework enables us to produce privacy-preserving GWAS results based on EIGENSTRAT and linear mixed model (LMM)-based statistics, both of which correct for population stratification. We test our differentially private statistics, PrivSTRAT and PrivLMM, on simulated and real GWAS datasets and find they are able to protect privacy while returning meaningful results. Our framework can be used to securely query private genomic datasets to discover which specific genomic alterations may be associated with a disease, thus increasing the availability of these valuable datasets.

Graphical abstract

Introduction

We are experiencing an unprecedented growth in the amount of personal and clinical genotype data in large repositories (Lowe et al., 2009). However, accessing this growing pool of data poses major privacy concerns for individuals (Murphy et al., 2011). At the same time, making this data more widely available could lead to novel biomedical insights that could inform medical research (Weber et al., 2009; Lowe et al., 2009). As such, there is hope that the privacy challenges posed in analyzing such data might not simply require tighter regulations over who can use the data—which is often limited to individuals who have gone through a time-consuming and burdensome application process—but instead may benefit from the development of cryptographic tools that allow secure access while also ensuring accurate analyses. In particular, there has been increased interest in the usefulness of a cryptographic technique known as differential privacy (Dwork, 2011) to allow researchers access to genomic data (Jiang et al., 2014; Johnson and Shmatikov, 2013; Uhler et al., 2013; Yu et al., 2014; Yu and Ji, 2014; Chen et al., 2014; Zhao et al, 2015; Zhang et al, 2013) while preserving every patient’s privacy. Unlike alternative methods for achieving privacy, differential privacy is able to provide formal guarantees of privacy while making minimal assumptions.

Here, we focus on privacy in the context of genome-wide association studies (GWAS) (Weber et al., 2009; Lowe et al., 2009), which are commonly used to identify single nucleotide polymorphisms (SNPs) associated with a given disease. Numerous works (Homer et al., 2008; Lumley and Rice, 2010; Im et al., 2012; Zhou et al., 2011.; Sankararaman et al., 2009) have shown that aggregate genomic data, including GWAS statistics, can leak private information about participants. These findings have led the NIH, among others, to place much of their aggregate genomic data into repositories and require researchers to apply for access (Erlich and Narayanan, 2014). Recent work (Shringarpure and Bustamante, 2015) has also shown that a popular method for sharing genomic data, “Genomic Data-Sharing Beacons,” actually leaks potentially private information about participants. Their results illustrate the need for new methods that allow privacy-preserving access to genomic data.

Differential privacy (Dwork et al., 2006; Dwork, 2011) (Box 1) has been proposed as one promising solution to the privacy conundrum (Jiang et al., 2014; Yu et al., 2014; Johnson and Shmatikov, 2013; Uhler et al., 2013; Yu and Ji, 2014; Chen et al., 2014; Zhao et al, 2015; Zhang et al, 2013; Tramer et al., 2015). The main advantage of differential privacy is that it gives a mathematical guarantee of privacy to all participants in a study. These guarantees make it possible to share genomic data without risking participant privacy. Interest in differential privacy has inspired development of improved methods for performing differentially private GWAS (Jiang et al., 2014), as well as numerous novel applications of differential privacy to other types of research data, including the Privacy Tools for Sharing Research Data project at Harvard University and the Enabling Medical Research with Differential Privacy project at the University of Illinois. Although the initial results of this research have been encouraging, there remain major limitations on the type of genomic analyses that can be performed accurately and efficiently (Fredrikson et al, 2014).

Box 1. Phenotypic differential privacy.

The cryptographic community introduced ε-differential privacy as a formal definition of privacy about a decade ago (Dwork et al., 2006). Intuitively, it ensures that the results of an analysis are almost equally likely whether or not any one individual participates in the study (more specifically, the probability differs by a factor of ≤ exp(ε), where ε is a positive real number). This helps insure that there is negligible private information being leaked.

Here we introduce ‘phenotypic differential privacy’, a formal definition of privacy that attempts to preserve private information about individuals (in this case disease status). As with all forms of differential privacy, phenotypic differential privacy requires the choice of a privacy parameter (also known as the privacy budget). This parameter, denoted by ε, controls the level of privacy guaranteed to all participants in the study: the closer to zero it is the more privacy is ensured, while the larger it is the weaker the privacy guarantee. This means we would like to set ε as small as possible; unfortunately, this comes at the cost of less accurate outputs (Dwork, 2011).

It is difficult to reach an intuitive understanding of ε. Informally, taking the frequentist’s perspective (Wasserman and Zhou, 2010), one can think of exp(ε) as bounding the power-to-significance ratio of any statistical test the adversary might use to determine a participant’s disease status based on ε-phenotypically differentially private data.

More formally, assume there is an adversary who would like to determine the i^th individual’s disease status. This can be thought of as performing a hypothesis test to distinguish between H₀: y_i = 1 and H₁: y_i = 0 based on the output of a ε-phenotypically differentially private statistic. The power of such a test (where the power equals the probability of rejecting H₀ given that H₁ is true) is bounded above by exp(ε) times that significance level of the test (where the significance level equals the probability of rejecting H₀ given that H₀ is true).

One can also look at exp(ε) from a more Bayesian perspective (Hsu et al., 2014). If an individual in the study is worried about some negative effect due to participating in the study (such as someone concluding they have a certain disease based on the study results), ε-phenotypic differential privacy guarantees the probability of that negative event occurring differs by at most a factor of exp(ε), based on whether or not they have the disease.

For example, ε ≤2 implies that, for any participant with the disease under investigation, releasing F (D, y) does not increase the adversary certainty in the participant’s disease status by more than a (multiplicative) factor of exp(2) < 7.5 compared to the case when the participant does not have the disease. In agreement with previous work (Vinterbo et al., 2012), we consider ε ≤2 to be a realistic level of privacy, though exact thresholds differ from application to application.

Note that the privacy guarantee decreases as the number of queries increases: If the user makes k queries, where the ith query is ε_i - phenotypic differentially private, the result is (ε₁ + ⋯ + ε_k)- phenotypic differentially private.

In practice, anyone who wants privacy-preserving access to a database begins by signing up for an account. Note that, unlike in the controlled access model, no time consuming application is necessary. All that is needed is to ensure a given individual has not signed up for an account before (you could, for example, have a system based off academic email addresses or PubMed author IDs). Upon registering, each user is given a privacy budget, ε. They can use that privacy budget to query the database in a differentially private way, until their privacy budget is used up (for example, the user may make k queries, where each query is $\frac{\epsilon }{k}$-differentially private). After the privacy budget is used up, the user must than apply for an increase in their privacy budget. More details are given in the Supplemental Experimental Procedure.

Privacy concerns are not the only hurdles facing modern GWAS. Such analyses are complicated by systematic differences between different human populations (Yang et al., 2014). Biologically meaningful mutations are often inherited jointly with unrelated mutations, leading to false GWAS associations. For example, the lactase gene is responsible for the ability to digest lactose (such as in milk), and is more common in people of Northern European ancestry than in those of East Asian ancestry. People from Northern Europe are also, on average, taller than those from East Asia. This observation would lead a naive statistical method to erroneously suggest that the lactase gene is related to height. Such confounding effects are a major problem that can render the results of a GWAS (particularly one with a large sample size) nearly nonsensical (Marchini et al., 2004). In order to avoid this common problem, known as population stratification, various methods have been employed, including EIGENSTRAT (Price et al., 2006), linear mixed models (LMMs) (Yang et al., 2014), genomic control (GC) (Devlin and Roeder, 1999), etc. In recent years, there has been a growing interest in using LMMs for this task, thanks to improved algorithms (Kang et al, 2010; Lippert et al., 2011; Tucker et al., 2014; Loh et al., 2015; Furlotte and Eskin, 2015). Even still, EIGENSTRAT remains a common approach for correcting for population stratification. However, previous works on differentially private GWAS have not addressed population stratification, greatly limiting their real-world applicability.

Here, we jointly address the population stratification and privacy issues that arise when using private data to answer GWAS queries. We focus on two types of queries: (i) GWAS statistics at SNPs of interest, and (ii) lists of SNPs highly associated with diseases of interest. We develop a differential privacy framework that can transform GWAS statistics commonly used to answer these queries into tools for privacy-preserving GWAS. We demonstrate this approach on two state-of-the-art statistics, EIGENSTRAT (Price et al., 2006) and linear mixed model (LMM)-based statistics (Yang et al., 2014), through our PrivSTRAT and PrivLMM methods, respectively. We test these methods on real and synthetic data, and show that they perform well both in terms of accuracy and runtime; indeed their accuracy improves as sample sizes increase.

Results

Motivating Scenario

We begin with a massive database, consisting of phenotype and genotype data from a large number of individuals—for example, from the database of Genotypes and Phenotypes (dbGaP) or EHRs. The curators of the database would like to make the data available to as many individuals as possible, with the hope of supporting new research. At the same time, the database curator is also responsible for protecting the privacy of the individuals in the database.

Our aim is to allow researchers access to this data while preserving privacy using a technique known as differential privacy. In our case, since we are focusing on protecting phenotype data, we introduce a slightly modified definition known as phenotypic differential privacy (See Box 1 for an overview and the Experimental Procedures for technical details). Intuitively, phenotypic differential privacy guarantees that an analysis performed on any dataset is statistically indistinguishable from the same analysis performed on any dataset that differs in any one individual’s disease status. This helps prevent the use of genotype information to learn about private phenotype information, and vice versa.

The exact definition of indistinguishability depends on a user-defined privacy parameter, ε (see Box 1 for details about this parameter). Note that the closer to zero this ε parameter, the greater the privacy. This indistinguishability ensures that our database offers negligible information about the participants’ private phenotype information. The current work focuses on developing methods to return answers to common genomic queries that are phenotypically differentially private.

Privately Estimating EIGENSTRAT Statistics

As privacy methods do not produce correct results on typical GWAS studies without population stratification (Supplemental Experimental Procedures, “No Stratification”), we start by looking at the most basic queries in GWAS, namely the calculation of the GWAS statistic for a given SNP. In particular, we are interested in calculating a χ² distributed statistic, known as the EIGENSTRAT statistic, for a given SNP in our database (Supplemental Experimental Procedures) while preserving privacy. As detailed in the Experimental Procedures, this is achieved using a modified version of the Laplacian mechanism (Dwork, 2011).

We studied the tradeoff between privacy (the ε parameter) and accuracy on real GWAS data for a rheumatoid arthritis dataset (Plenge et al., 2007) (Figure 1A), as well as on simulated data with two subpopulations (Figure 1B) (Experimental Procedures). As expected, our method quickly increases in accuracy as privacy decreases (i.e, as ε increases). Note that, for reasonable values of ε (ε around 1 or 2 [Vinterbo et al., 2012]) the median error introduced by our method is around .1 or .2. This is fairly small, corresponding to about a 5–10% error in the EIGENSTRAT statistic, an amount that is unlikely to affect the final conclusions of an analysis (Case Study).

Figure 1.

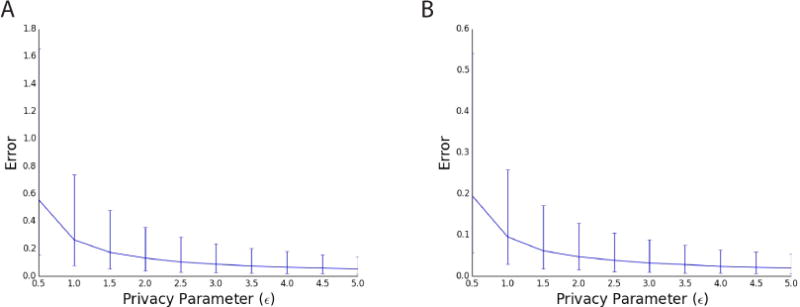
The accuracy of our mechanisms for approximating the EIGENSTRAT statistic on real (a) and simulated (b) GWAS data for various privacy parameters, ε. Median error over all SNPs, with error bars representing the 25% and 75% quantiles. As expected, the accuracy increases as ε increases (a.k.a. as privacy decreases).

Note that we can also calculate a phenotypically differentially private p-value for a given SNP using this returned statistic (Supplementary Experimental Procedures.)

Privately Selecting Highly Associated SNPs

Besides calculating χ² statistics, users may also be interested in determining which SNPs are most highly correlated with a given disease. A simple way to do this identification would be to use the above method to estimate the EIGENSTRAT statistic for all SNPs and returning the highest-scoring SNPs. The large number of queries required to do this, however, necessitates a small ε parameter for each query, resulting in poor accuracy. Much more accurate methods have been proposed for identification of high-scoring SNPs while also preserving privacy (Uhler et al., 2013; Johnson and Shmatikov, 2013; Yu et al., 2014). We focus on one of these methods, known as the distance-based method (Johnson and Shmatikov, 2013; Simmons and Berger, 2016). We compare the distance-based method with other methods in the Supplemental Experimental Procedure, showing that it performs the best in practice, a result that is consistent with previous work (Simmons and Berger, 2016).

The distance-based method has previously been used with simple statistics such as the Pearson or allelic test statistics. Here we show that, with a few algorithmic insights, we are able modify this approach to work for the much more complicated EIGENSTRAT statistic. This result is notable, given that it was only recently shown that this approach could be made computationally tractable even for the relatively simple allelic test statistic (Yu and Ji, 2014; Simmons and Berger, 2016).

Our algorithm for selecting highly associative SNPs takes a privacy parameter (ε, see Box 1 for details) and the number of SNPs to be returned (m_ret). The algorithm returns m_ret SNPs in a way that ensures that the returned SNPs are almost equally likely to have been produced (more specifically, the likelihood differs by at most a multiplicative factor of exp(ε)) if we changed one individuals disease status in our dataset (which we denote as ε - phenotypic differential privacy, see Box 1 and the Experimental Procedure), while maximizing the number of returned high-scoring SNPs.

We tested the accuracy of PrivSTRAT for selecting high-scoring SNPs and found we can obtain high accuracy for reasonable levels of privacy (ε around 1 or 2, Figure 2). More specifically, we used the algorithm to return the top m_ret SNPs, where m_ret∈ {3, 5} (this choice is based off previous work (Yu et al., 2014). Other values are explored in the Supplemental Experimental Procedures), for various values of the privacy parameter, ε. The accuracy of the returned results (averaged over 20 trials) is measured by the percentage overlap between the returned results and the true results (Yu et al., 2014). For both the rheumatoid arthritis (Figure 2A) and simulated (Figure 2B) data sets, accuracy increases as ε increases (privacy decreases), as expected. Moreover, near perfect accuracy is obtained for realistic values of ε (values around 1 or 2 (Vinterbo et al., 2012)) on real GWAS data, which will only increase as datasets grow (Supplemental Experimental Procedure). We also performed experiments on datasets with higher levels of population stratification (Figure S3, Supplemental Experimental Procedures). In particular, we took data from the HapMap project (consisting of 880 individuals of different ancestries) and simulated corresponding phenotype data. We see that our method for picking high scoring SNPs has lower accuracy, but this is consistent with the decrease in sample size (Supplemental Experimental Procedures, “Sample Size vs Accuracy”)

Figure 2.

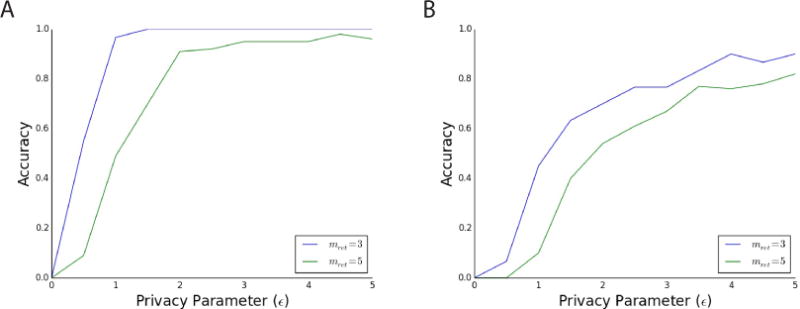
Measurement of the accuracy (percentage of the top SNPs correctly returned) of the PrivSTRAT algorithms for selecting top SNPs with m_ret (the number of returned SNPs) equal to 3 and 5 for the (a) rheumatoid arthritis GWAS dataset and (b) our simulated dataset, with varying values of the privacy parameter, ε. In all four cases, the accuracy increases as privacy decreases (as ε increases). More importantly, in three of the four cases, high accuracy is achieved for reasonable choice of privacy (ε around 2), which should increase with sample size. These results are averaged over 20 iterations.

Our method requires the user to specify the number of returned SNPs ahead of time (the m_ret parameter). This differs from the traditional GWAS approach, in which the researcher sets a p-value threshold and returns all SNPs with p-values below that threshold. Our framework can be modified to work in this way. In particular, it is possible to estimate the number of SNPs with scores below a certain p-value threshold in a privacy-preserving way using neighbor distance (Supplemental Experimental Procedures). We do not, however, envision this as the main use of our method–it is not meant to return all possible hits, but only the most promising handful (see the Case Study).

By running our algorithm on subsets of the rheumatoid arthritis dataset (with n=200, 400, 600, 800, and 1000 participants), we see that accuracy increases as sample size increases (Table S2), which suggests that the utility of our method will increase as genomic databases become larger.

Runtime

To assess the effects of the privacy-preserving nature of PrivSTRAT on runtime, we ran PrivSTRAT on the RA dataset described in the Experimental Procedure with m_ret = 3, and measured the amount of time taken by each step of the algorithm: calculate the SVD (using either the smartpca algorithm included in EIGENSTRAT (134.16 seconds) or an approximate method (14.37 seconds), see the Supplemental Experimental Procedures), calculating the μ vectors (8.6 seconds), calculating the neighbor distance (26.23 seconds), and picking the SNPs (.25 seconds). The results are an average over 10 trials. The calculation of the exact SVD is the slowest of these steps by a factor of >5, while even the approximate SVD calculation is only a factor of 2 faster than the slowest step in the privacy-preserving algorithm. Since calculating the SVD is required by the standard EIGENSTRAT statistic, the overhead required to preserve privacy is minimal.

Extending to LMMs: PrivLMM

We have thus far focused on performing privacy-preserving GWAS based on the EIGENSTRAT statistic. In recent years, however, there has been growing interest in using statistics based on LMMs to perform GWAS studies. The same framework introduced above can also be used to perform privacy-preserving LMM-based analysis (Supplemental Experimental Procedures), a method we denote PrivLMM.

To demonstrate this application, we tested PrivLMM for returning high-scoring SNPs on the rheumatoid arthritis GWAS dataset. We used the same set-up that we used for PrivSTRAT. As expected, privacy decreases as accuracy increases (Figure 3). High accuracy can be obtained for reasonable levels of privacy (ε around 1 or 2) (Figure 3). Note that we used values for the variance parameters (σ_e and σ_g) calculated using the FaST-LMM (Lippert et al., 2011) software. In theory, it is preferable to use a differentially private approach to calculate these parameters. A method to do this, based on previous work (Abowd et al., 2013), is described in Supplemental Experimental Procedures.

Figure 3.

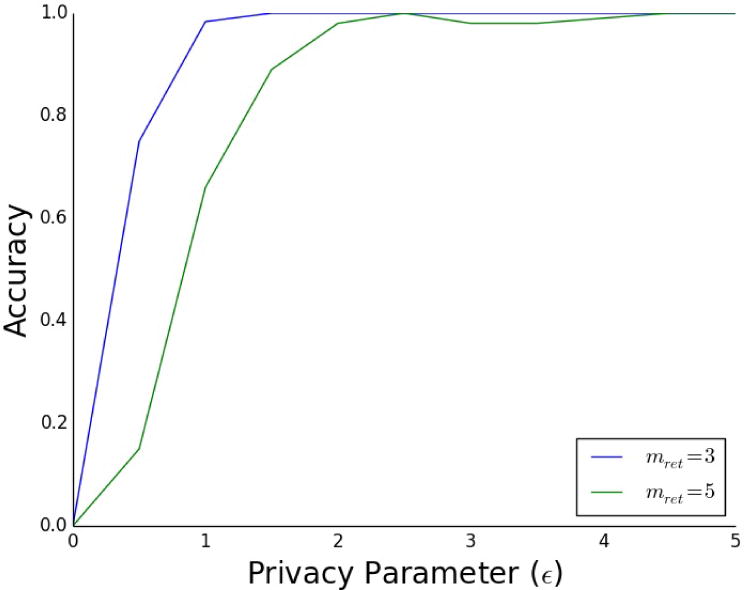
The accuracy (percentage of top SNPs correctly returned) of the PrivLMM method for selection of top SNPs with m_ret (the number of SNPs being returned) equal to 3 and 5 for our rheumatoid arthritis GWAS dataset, with varying values of the privacy parameter, ε. We see that, in both cases, high accuracy is achieved for reasonable privacy levels (ε around 2). These results are averaged over 20 iterations.

Case Study

Next, we provide a case study to illustrate one possible way PrivLMM and PrivSTRAT might be used in practice.

Consider a lab with limited resources that wants to run a GWAS study on a group of individuals. The study will result in a list of high-scoring SNPs, many of which are significant. There may, however, be many SNPs that are close to the threshold of being significant. Some of these close calls are due to chance, while some may be SNPs weakly associated with the disease, a concern particularly in smaller studies. The researchers might be interested in assessing several of these SNPs close to the significance boundary for significance on a new, larger dataset as validation. Unfortunately, they may not have direct access to such datasets due to privacy concerns. Our method, however, could allow these researchers access to the databases necessary to validate their results. Such validation is of particular interest in light of the large number of false positive results that appear in the biomedical literature (Kohane et al., 2012; Ioannidis, 2005).

To demonstrate this utility on a test dataset, we divided the rheumatoid arthritis dataset into two subsets of 450 cases and 450 controls (dataset 1), and the remaining 435 cases and 780 controls (dataset 2). We ran a GWAS on dataset 1, to obtain several significant SNPs below the p-value cut off of 10⁻⁶ (corresponding to a Bonferroni corrected p-value of .05). Two additional SNPs, rs498422 (P= 2.10 × 10⁻⁶) and rs9419011 (P= 1.19 × 10⁻⁶), do not quite reach the p-value cutoff. Since they are close to reaching statistical significance, we would like to test them both on dataset 2 to see if they might be worth further follow-up studies. Due to privacy concerns, however, we are not given direct access to this database. We can, however, apply PrivSTRAT with a total privacy budget of ε = 2. This gives us an estimate of the EIGENSTRAT statistic for both of these SNPs, with scores of 25.79 and 1.66 (estimated 95% CI 4.21–95.60 and 0–13.75), respectively (corresponding to p-values of ~5 × 10⁻⁷ and ~0.19).

Since we are only testing two SNPs, even after correcting for multiple hypothesis testing this is enough to suggest that rs498422 might be worth further investigation. Note that this result is consistent with previous findings on rheumatoid arthritis: rs498422 is close to the HLA locus in the human genome, a region known to be highly associated with rheumatoid arthritis risk. We see that, on the other hand, this result does not support further study of rs9419011, saving us possible wasted time and effort. Note that, in both cases, the PrivSTRAT statistics are very close to the actual EIGENSTRAT statistics (which equal 26.18 and 1.69, respectively). Note that we obtain similar accuracy when repeating this experiment (Supplemental Experimental Procedure, “Validation”).

Discussion

Here we introduce three key advances that make differential privacy useful for real-world GWAS statistics. First, we offer a modified, yet practical form of differential privacy, termed ‘phenotypic differential privacy’ (Box 1), with the aim of efficiently protecting private disease status information from being leaked while also accurately answering various common queries on genomic data. Notably, this definition does not guarantee that information about whether or not someone participated in our study is hidden (though it also does not guarantee that such information will be leaked). Instead, it prevents the release of private information that can be used to compromise a patient’s disease status using genotype information, or used to compromise a patient’s genotype data using disease information. With electronic health record (EHR) or large genomic databases (such as 23andMe), knowing that someone participated is equivalent to knowing they have their genotype on record, a fact that is unlikely to be private. As such, it makes sense to use phenotypic differential privacy in such settings.

Second, we introduce decompositions of EIGENSTRAT and LMM-based statistics that allow us to use a tool from differential privacy, the Laplacian mechanism (Dwork, 2011), to obtain accurate and fast estimations of the statistical significance of specific SNPs while also preserving patient privacy.

Third, we develop a greedy algorithm that allows us to return lists of SNPs highly associated with a disease while ensuring high levels of both accuracy and privacy. This result is particularly noteworthy since analogous methods for much simpler statistics have only recently been devised (Johnson and Shmatikov, 2013; Simmons and Berger, 2016). Combined, our tools demonstrate that it is possible to correct for population stratification while also preserving privacy in GWAS results, thus offering the possibility of applying a differentially private framework to large, genetically diverse groups of individuals and patients, such as those present in large genomic databases.

The major computational bottleneck in our methods comes not from the privacy-preserving component, but instead from the original statistics (calculating the eigenvectors in EIGENSTRAT or calculating the variance parameters in the LMM-based statistic). As such, our methods are well positioned to exploit computational advances in GWAS analysis. In particular, we are interested in modifying our method to take advantage of the computational advances introduced recently (Loh et al., 2015) for LMM-based association. (See Supplementary Materials for other potential directions.”

Note that we are not advocating privacy-preserving methods for all situations in which one might want to conduct a GWAS, but only when privacy concerns would make alternative approaches cumbersome or impossible. It is our hope that our Priv suite of tools will be used to improve access to private genomics data. This access will offer researchers new tools that can be used to produce novel hypotheses or validate previous findings in ways that are not currently possible due to privacy concerns.

As with any set of tools, it is important to understand the limitations of the Priv suite. Although our tools are useful for answering questions about large databases while preserving privacy, they are much less accurate on small databases (discussed in Experimental Procedure). Even on large databases, while our approach performs well in many circumstances, greater accuracy is desirable. Understanding exactly where our method is most useful will require tests on a large variety of datasets in numerous application domains. Moreover, our use of phenotypic differential privacy cannot guarantee privacy in databases with large levels of case ascertainment (that is, when the percentage of individuals with the disease in the study is much larger than the percentage in the background population), but is instead focused on databases that are representative of the background population (such as in 23andme or similar databases). It is our hope that future work will build upon our results to overcome these limitations.

In the long term, it is even possible that differential privacy techniques will no longer be needed, as we come to understand exactly how much privacy is lost after releasing aggregate genomic data (Simmons and Berger, 2015). Currently, however, we are far from this understanding. Thus, differential privacy provides us with the possibility of granting wider access to genomic data now, with immediate benefits for the research community.

Availability: An implementation of our results and simulated data is available on our website, http://groups.csail.mit.edu/cb/PrivGWAS, and on the Cell Systems website (Data S1).

Experimental Procedures

Notation

In the below, we use |v| to denote the length of the vector v. Moreover, for vectors u and v, we let u · v denote the dot product of u with v.

GWAS Revisited

The aim of genome-wide association studies (GWAS) is to link SNPs in a study cohort to a phenotype (e.g. disease) of interest. In a GWAS, the researcher begins with a group of n individuals genotyped at m SNPs. Let D be an n by m genotype matrix, where the ith entry in the jth row of D is equal to the number of times the minor allele occurs in the jth individual at the ith SNP (for autosomal SNPs this number is equal to either 0, 1, or 2). Details on how to handle missing genotypes are provided in Supplemental Experimental Procedure. Let X be the n by m matrix obtained by mean centering and variance normalizing each column of the genotype matrix D. Let x_i be the column of X corresponding to SNP i. Similarly, let y = (y₁, …, y_n) ∈ {0,1}ⁿ be a vector of phenotypes, where y_j = 1 if the jth individual has the disease, y_j = 0 otherwise.

Given X and y, we would like to determine which SNPs are associated with the disease phenotype. Here we will mainly focus on two statistics that allow us to test for these associations: EIGENSTRAT (Price et al., 2006) and LMM-based association statistics (Kang et al., 2010).

Phenotypic Differential Privacy

Below we give a formal definition of phenotypic differential privacy. See Box 1 for a more informal discussion.

Definition 1

Let F be a random function that takes in a n by m genotype matrix, D, and an n dimensional phenotype vector, y, and outputs F (D, y), where the output is in some set Ω. We say that F is ε-phenotypic differential privacy for some privacy parameter ε >0 if, for all genotype matrices D, all phenotype vectors y, y′ ∈ {0, 1} such that y and y′ differ in exactly one coordinate, and for all sets S ⊂ Ω, we have that

$$\mathrm{P}\left(\mathrm{F}\right(\mathrm{D},\mathrm{y})\in \mathrm{S})\le \text{exp}\left(\mathrm{\epsilon }\right)\mathrm{P}\left(\mathrm{F}\right(\mathrm{D},\mathrm{y}\prime )\in \mathrm{S})$$

Note that this definition of privacy can be viewed as a specific instantiation of both induced differential privacy (Kifer and Machanavajjhala, 2011) and of the Blowfish framework (Kifer and Machanavajjhala, 2014; He et al., 2014).

PrivSTRAT: Privacy-Preserving EIGENSTRAT

The differentially private GWAS literature has largely focused on three tasks: identifying highly-associated SNPs, estimating association statistics, and estimating the number of significantly-associated SNPs in a study. We consider all three tasks, focusing mainly on the first two (the third is addressed in the Supplemental Experimental Procedure).

Estimating χ²

We would like to estimate the χ² -statistic from EIGENSTRAT (Supplemental Experimental Procedure). In particular, assume we want an estimate of the EIGENSTRAT statistic, ${\mathit{\chi }}_{\mathit{i}}^2$, for a given SNP i. In order to do this, note that if we let ${\mu }_i=x_i^{\ast }/|x_i^{\ast }|$, then:

$${\chi }_i^2=\frac{\left(n-k-1\right){\left({\mu }_i\cdot y^{\ast }\right)}^2}{{|y^{\ast }|}^2}=\frac{\left(n-k-1\right){\left({\mu }_i\cdot y\right)}^2}{{|y^{\ast }|}^2}$$

so it suffices to get estimates of both μ_i · y and |y^∗| that are $\frac{\epsilon }{2}$-phynotypic differential privacy and combine the results (the fact that μ_i · y = μ_i · y^∗ follows since y^∗ is the projection of y onto a linear subspace containing μ_i). This can be done easily, however, using the Laplacian mechanism (Dwork, 2011). More details are in the Supplementary Experimental Procedure.

Selecting High-Scoring SNPs

Another task we consider is returning a list of the top m_ret-scoring SNPs for some user defined parameter m_ret while achieving ε-phenotypic differential privacy–in other words, we want to return the locations of the m_ret SNPs with largest χ² values. This is equivalent to picking the m_ret SNPs with largest |μ_i · y| values. In order to do this in a privacy-preserving way we use a modified version of the approach known as the distance based method (Johnson and Shmatikov, 2013). This works as follows: the user chooses a threshold c>0. The ith SNP is considered significant if |μ_i · y| > c, not significant otherwise (for example, c might correspond to a p-value of .05 or 10⁻⁸. In practice, instead of having the user choose c, we use a previous approach to automatically choose c (Simmons and Berger, 2016). Details are given in the Supplemental Experimental Procedure). The neighbor distance for the ith SNP, denoted b_i, is the minimum number of individuals whose phenotypes need to be changed to change SNP i from significant to not or vice versa. Formally:

$$b_i=b_i\left(c\right)=mi{n}_{y^{\prime }\in {\left[0,1\right]}^n,c=|{\mu }_i\cdot y^{\prime }|}{|y-y^{\prime }|}_0$$

where |v|₀ denotes the number of nonzero entries in the vector v. Note that b_i = min{d_i(c), d_i(−c)}, where

$$d_i(c)=mi{n}_{y^{\prime }\in {\left[0,1\right]}^n,c=|{\mu }_i\cdot y^{\prime }|}{|y-y^{\prime }|}_0$$

In order to use this neighbor distance to select high-scoring SNPs, we let $d_i^{\ast }=b_i$ for significant SNPs and $d_i^{\ast }=1-b_i$ for all other SNPs. The distance-based method picks m_ret SNPs without repetition, where the probability of picking the ith SNP is proportional to $\text{exp}(\frac{d_i^{\ast }}{2\epsilon m_{\mathit{ret}}})$ It is easy to see from previous work (Johnson and Shmatikov, 2013) that this mechanism is ε –phenotypic differential privacy. The difficult part is calculating d_i(c). Our significant algorithmic development is to show that this can be done using the greedy algorithm presented in Algorithm 1.

Algorithm 1: Calculates the neighbor distance

Require: y; μi; c

Ensure: Returns the neighbor distance, di(c).

Let i1, …, in be a permutation on 1, …, n such that, if

$u_r=\mathit{max}\left\{{\mu }_{i,i_r}\left(1-y_{i_r}\right),{\mu }_{i,i_r}\left(0-y_{i_r}\right)\right\}$

then u1 ≥ u2 ≥ ⋯ ≥ un.

Let j1, …, jn be a permutation on 1, …, n such that, if

$l_r=\mathit{min}\left\{{\mu }_{i,j_r}\left(1-y_{j_r}\right),{\mu }_{i,j_r}\left(0-y_{j_r}\right)\right\}$

then l1 ≤ l2 ≤ ⋯ ≤ ln.

Let $U_r={\sum }_{j=1}^k$ uj and $L_r={\sum }_{j=1}^k$ lj for k = 1, ⋯, n

Return r such that c − μi · y ∈ [Lr+1, Lr) ∪ (Ur, Ur+1]

Data

We test PrivSTRAT and PrivLMM on a rheumatoid arthritis dataset, NARAC-1 (Plenge et al., 2007). After quality control filtering, the dataset contained 893 cases and 1,243 controls, and a total of 67,623 SNPs. Note that this dataset includes some closely related individuals. Although LMM can handle such cryptic relatedness, EIGENSTRAT is not designed to do so. As such, before applying PrivSTRAT to this dataset, we used PLINK to remove relatives with estimated IBD greater than 0.2. Thus, the final dataset contained 885 cases and 1,230 controls. Since this dataset has relatively little population stratification, we also used PrivSTRAT on a simulated dataset with two subpopulations. This dataset and the associated code (based on Plink tools (Purcell et al., 2007)) are available online.