Significance
Massive stars, which terminate their evolution in a cataclysmic explosion called a type-II supernova, are the nuclear engines of galactic nucleosynthesis. Among the elemental species known to be produced in these stars, the radioisotope 60Fe stands out: This radioisotope has no natural, terrestrial production mechanisms; thus, a detection of 60Fe atoms within terrestrial reservoirs is proof for the direct deposition of supernova material within our solar system. We report, in this work, the direct detection of live 60Fe atoms in biologically produced nanocrystals of magnetite, which we selectively extracted from two Pacific Ocean sediment cores. We find that the arrival of supernova material on Earth coincides with the lower Pleistocene boundary (2.7 Ma) and that it terminates around 1.7 Ma.
Keywords: accelerator mass spectrometry, magnetofossils, supernova
Abstract
Massive stars (), which terminate their evolution as core-collapse supernovae, are theoretically predicted to eject of the radioisotope 60Fe (half-life 2.61 Ma). If such an event occurs sufficiently close to our solar system, traces of the supernova debris could be deposited on Earth. Herein, we report a time-resolved 60Fe signal residing, at least partially, in a biogenic reservoir. Using accelerator mass spectrometry, this signal was found through the direct detection of live 60Fe atoms contained within secondary iron oxides, among which are magnetofossils, the fossilized chains of magnetite crystals produced by magnetotactic bacteria. The magnetofossils were chemically extracted from two Pacific Ocean sediment drill cores. Our results show that the 60Fe signal onset occurs around 2.6 Ma to 2.8 Ma, near the lower Pleistocene boundary, terminates around 1.7 Ma, and peaks at about 2.2 Ma.
The isotope 60Fe is mostly produced during the evolution of massive stars () in two steps along the course of their evolution. In the first step, during their quiescent helium and carbon shell burning phases, 60Fe is synthesized at the base of these shells by a slow neutron capture process on preexisting stable seed nuclei, mostly by two successive neutron captures starting on stable 58Fe (1). In the second step, shock heating within the carbon shell, driven by the passage of the supernova (SN) blast wave, allows for the synthesis of a modest amount of 60Fe just before the subsequent disruption of the star and the concomitant explosive ejection of these shell mass zones, and the 60Fe within them, into the interstellar medium. The subsequent beta-decay of 60Fe, which has a half-life of Ma (weighted average of refs. 2 and 3), gives rise to two characteristic gamma-ray lines, which have been detected in the central part of the galactic plane (4), known to be a site of massive stars, confirming the association of 60Fe formation with regions of ongoing massive star nucleosynthesis.
If a core-collapse SN (CCSN) occurs sufficiently close to our solar system, part of the ejected matter should arrive in our solar system. The best candidate mechanism for overcoming the solar wind pressure and penetrating to Earth’s orbit is dust transport (5, 6). Recent investigations with far-infrared to submillimeter telescopes suggest that CCSN ejecta are efficient dust sources (7). For instance, copious amounts of dust with a large mass fraction contained in grains of above m size (and up to m) have recently been observed in the ejecta of SN 2010jl (8). During atmospheric entry, dust grains are expected to be partially or totally ablated, depending on composition, incident velocity, and angle of entry (9). The 60Fe released in the ablated fraction will enter the terrestrial iron cycle (10) and become deposited into geological reservoirs such as marine sediments.
An excess of 60Fe was already observed in -Ma-old layers of a ferromanganese (FeMn) crust retrieved from the Pacific Ocean (5, 11, 12) and, recently, in lunar samples (13). However, due to the slow growth rate of the FeMn crust, the 60Fe signal had a poor temporal resolution. This 60Fe has been attributed to a deposition of SN ejecta; however, this interpretation has been challenged by an alternate hypothesis attributing the 60Fe excess to micrometeorites (ref. 14, and references therein). An independent indication of a 2-Ma-old SN interaction with our solar system was recently deduced from the spectra of cosmic ray particles (15). In our work herein, we aimed at the analysis of the entire temporal structure of the 60Fe signature in terrestrial samples. This requires a geological reservoir with an excellent stratigraphic resolution and high 60Fe sequestration and low Fe mobility, which preserves 60Fe fluxes as they were (or nearly so) at the time of deposition, apart from radioactive decay. Both conditions were fulfilled in the carefully selected marine sediments used in this study.
One particularly interesting mechanism by which Fe is sequestered within sediments is through biomineralization, e.g., by dissimilatory metal-reducing bacteria (DMRB) (16), and by magnetotactic bacteria (MTB) (17). MTB are single-cell prokaryotes, which produce intracellular chains of magnetite (Fe3O4) nanocrystals called magnetosomes (18, 19). These bacteria achieve their highest population densities near the so-called oxic−anoxic transition zone (20), where the oxygen concentration drops, producing a well-defined redox boundary. In pelagic sediments, this boundary occurs within a few centimeters below the sediment−water interface (21), forcing the MTB populations to move upward as the sediment column grows, with dead cells being left behind. After decomposition of the dead cells, the magnetosomes remain embedded within the sediment bulk and are subsequently called magnetofossils (22).
The ablated Fe fraction of SN dust grains arriving in the oceans is expected to undergo dissolution and reprecipitation upon reaching the sediment in the form of nanominerals, such as poorly crystalline ferric hydroxides (10). The poor solubility of Fe(III) minerals at circumneutral pH values ( nmol/L) means that Fe is hardly mobilizable under oxygenated conditions. Many microorganisms, including DMRB and MTB, get around this problem by excreting organic compounds known as siderophores, which specifically complex Fe(III). DMRB reduce Fe(III) to highly soluble Fe(II), which, in turn, leads to the precipitation of new minerals, among which is magnetite (Fe3O4) (16). Other bacteria perform Fe(II) oxidation (23). The Fe uptake capability of DMRB from particulate sources depends on the type of source mineral and particle size. Poorly crystalline hydroxides, such as ferrihydrite (FeOOH), are preferred over goethite (α-FeOOH) and hematite (α-Fe2O3), and Fe reduction rates are proportional to the specific surface area of particles (24–26). In particular, surface normalized bacterial Fe-reducing reaction rates are ∼1.5 to 2 orders faster (26) for nano-sized ferrihydrite particles compared with grains with sizes comparable to bulk detrital grains. The Fe uptake capability of MTB has been investigated less extensively. Common constituents of the DMRB iron metabolism, such as genes for ferrous and ferric iron uptake, siderophore synthesis, and iron reductases, as well as iron-regulatory elements, are present in MTB (19). MTB are therefore able to take up ferric and ferrous iron from various sources (27) with similar capabilities as for DMRB. This is also supported by the fact that MTB are the main source of one reduction product—magnetite—in many types of sediments (28–31). The combination of Fe-reducing and Fe-oxidizing reactions supports the Fe cycle in sediments, yielding ultrafine ( nm) secondary Fe minerals (32, 33) (Supporting Information).
MTB extant at the time of SN 60Fe input to the ocean floor are expected, therefore, to have incorporated 60Fe into their magnetosomes, biogenically recording the SN signal (34). Unlike other Fe minerals and biomineralization products, magnetofossils have unique magnetic signatures enabling their detection down to mass concentrations in sediment of the order of few parts per million (29). As an essential point for this work, magnetofossil preservation ensures that the 60Fe signal is not altered, because the very existence of these microfossils means that postdepositional Fe mobilization through reductive diagenesis (28, 35) did not occur.
In general, Fe(III) sources accessible to bacterial reduction can be extracted with buffered solutions of reducing agents such as citrate−bicarbonate−dithionite (CBD) and, to a lesser extent, ammonium oxalate (36). The CBD protocol (37) has been specially conceived to selectively dissolve fine-grained ( nm) secondary oxides in soils, but not larger particles of lithogenic origin (38, 39) (see Supporting Information). Therefore, CBD can be used to selectively extract Fe from magnetofossils and other secondary minerals along with 60Fe, thereby minimizing any dilution from large-grained, 60Fe-free primary mineral phases.
Materials and Methods
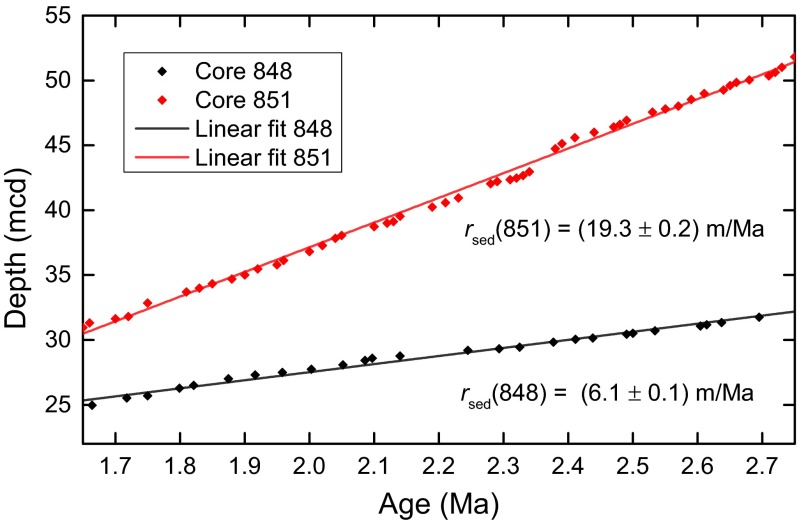
In our search for a biogenic SN signal, we selected two sediment cores, core 848 and core 851, from the equatorial Pacific (2°59.6’S, 110°29’W, 3.87 km water depth), recovered by the Ocean Drilling Program (ODP) during Leg 138 (40). The sediment of both cores is a pelagic carbonate (60% to 80% CaCO3, 20% to 30% SiO2) with a total iron content of 1.5 wt% to 3.5 wt% (41). Both cores are characterized by an excellent biostratigraphic and magnetostratigraphic record and almost constant sedimentation rates of () m/Ma and () m/Ma for cores 848 and 851, respectively, over the 1.7- to 2.7-Ma age range of interest (42), as shown in Fig. 1.
Fig. 1.
Age model data of ODP drill cores 848 and 851 with linear fits overlaid. The x axis represents the depth in the respective drill cores in meters core depth (mcd). The slopes of the fits yield sedimentation rates as shown. No significant departure from linearity is observed across the displayed time range, indicating that both cores had constant sedimentation rates. The errors represent 1σ SDs. Data courtesy of ref. 42.
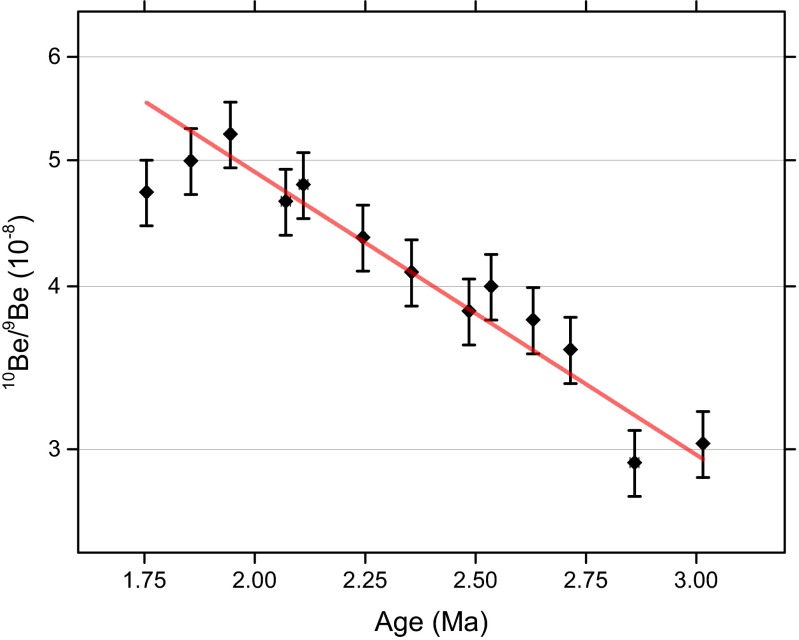
The presence of magnetofossils in these cores was confirmed by electron microscopy and magnetic analysis techniques based on first-order reversal curve (FORC) measurements (29, 34) (see Supporting Information and Figs. S1–S4). The average magnetofossil Fe concentration over the 1.7-Ma to 3.4-Ma interval was determined to be 25 μg/g to 30 μg/g for core 848, and 15 μg/g to 20 μg/g for core 851. Along with a constant sedimentation rate (Fig. 1) and sediment composition (43), the lack of significant magnetofossil concentration variations (see Supporting Information and Fig. S1), both absolute and relative to other magnetic Fe minerals, indicates that the depositional environment was stable during the period under investigation. An additional confirmation of stable sedimentation conditions was obtained by measurements of the 10Be/9Be ratio in representative samples of core 851, which show no significant deviation from exponential radioactive decay (see Supporting Information).
Fig. S1.
The /IRM vs. sediment age for core 851 composed from two different measurements. The systematic offset between the black and the red curve is due to the maximum field used to impart the IRM, which was 0.1 T for the red curve and 1 T for the black curve. IRM acquired in the larger field includes the contribution of high-coercivity minerals that are not magnetized during the measurement of , therefore yielding lower values of /IRM. Overall, /IRM displays minor variations and is consistently compatible with values expected for magnetofossil-rich sediments.
Fig. S4.
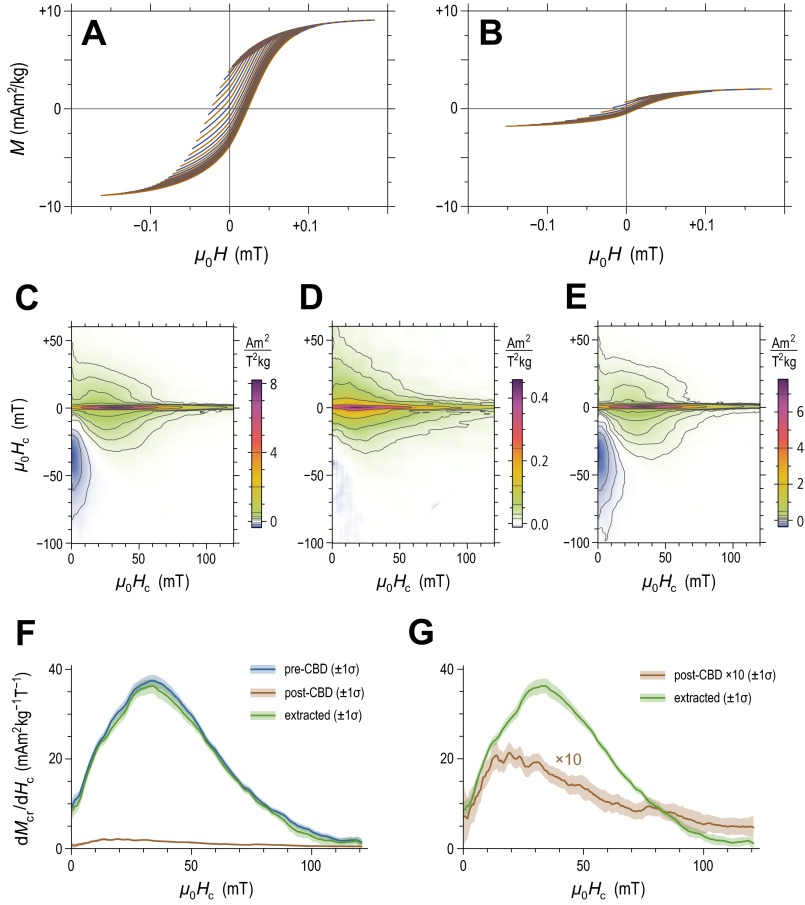
Magnetic analyses of a representative sample from core 841. (A) FORC measurements of the untreated sediment (every eighth curve shown for clarity). (B) Same as A for the residue of CBD extraction. (C) FORC diagram calculated from measurements in A. (D) FORC diagram calculated from measurements in B. Notice the -times-smaller amplitudes in comparison with C. (E) Difference between C and D, which can be identified with the magnetic signature of CBD-extractable particles. (F) Coercivity distributions associated with the central ridges in C−E (i.e., the ridges along ). Almost all SD particles responsible for these ridges can be extracted with the CBD procedure. (G) Same as F, but with the central ridge coercivity distribution of the CBD residue multiplied by 10 to show the fundamentally different distribution shape with respect to that of extractable particles.
To maximize the 60Fe/Fe atom ratio, a highly selective version of the CBD protocol (37) was developed (see Supporting Information); it is a very mild chemical leaching technique, able to completely dissolve secondary iron oxides such as magnetofossils, while leaving larger grains, which may not contain 60Fe, essentially intact (29). At least 27% of the total Fe extracted with this technique is contained in magnetofossils (29), which therefore represent a significant contribution to the analyzed Fe pool. Even with this carefully designed extraction protocol, the expected 60Fe concentrations are so low that the only viable measurement technique is ultrasensitive accelerator mass spectrometry (AMS), which has been carried out at the Gas-filled Analyzing Magnet System (GAMS) setup (44) at the Maier-Leibnitz-Laboratory (MLL) in Garching, Germany, over several beamtimes. The MLL features a 14-MV MP Tandem accelerator with an energy stability of . For AMS measurements of 60Fe, the samples are prepared as Fe2O3 powder mixed 50/50 by volume with Ag powder (120 mesh, lot J07W011; Alfa Aesar), which is subsequently hammered into a 1.5-mm-wide hole, drilled into a silver sample holder.
Fe was extracted as FeO− from a single-cathode, cesium sputter ion source, and was injected into the accelerator after a preacceleration to 178 keV. The tandem terminal voltage for the experiments described here ranged between 11 MV and 12 MV, which favored selection of the charge state 10+ for the radioisotope 60Fe after passing through a 4-μm-thick carbon stripper foil at the accelerator terminal. A charge state of 9+ was selected for the stable beam of 54Fe, because it has nearly the same magnetic rigidity as 60Fe10+ at nearly the same terminal voltage. After acceleration to 110 MeV to 130 MeV (depending on the available terminal voltage), the ions exit the accelerator and pass through a 90 degree dipole magnet for selection of the correct magnetic rigidity, and subsequently pass through two Wien velocity filters. Finally, the ions are directed toward the dedicated GAMS beamline by way of a switching magnet. Through use of the GAMS magnet, the challenging suppression of the stable isobar 60Ni is achieved.
The GAMS magnet chamber is filled with 4 mbar to 7 mbar of N2 gas. Through electron exchange reactions with the N2 gas, each ion species adopts an equilibrium charge state distribution that depends on its atomic number Z. Thus, isobars will be forced on different trajectories if a magnetic field is applied. Because 60Fe and 60Ni have , their trajectories on the exit side of the magnet can be spatially separated by 10 cm. The GAMS magnetic field can then be adjusted to make 60Fe enter the particle identification detector, while most 60Ni is blocked using a suitable aperture in front of the detector entrance. The detector itself is an ionization chamber featuring a Frisch grid and a fivefold split anode and is filled with 30 mbar to 50 mbar of isobutane as an ionization medium. Individual 60Fe ions can thus be identified by their energy deposition (Bragg curve), which is described in more detail in Supporting Information.
For measurements of the atom ratio 60Fe/Fe, the stable beam of 54Fe9+ is tuned into a Faraday cup in front of the GAMS, where the typical electrical current is 30 nA to 150 nA (sample-dependent). Then, the tandem terminal voltage and the injector magnet are switched to allow 60Fe10+ to pass, and the Faraday cup is retracted. The 60Fe ions are then individually identified and counted in the ionization chamber, while the 60Ni background count rate is only about 10 Hz to 100 Hz. In this manner, a highly selective discrimination of 60Fe against 60Ni and other background sources is achieved, as demonstrated by the extremely low blank levels obtained with different blank materials, such as processing blanks and environmental samples. The concentration of 60Fe/Fe is calculated from the number of 60Fe events counted by the detector, the measurement time, and the average current of 54Fe9+ in front of the GAMS. The transmission efficiency between the Faraday cup and the ionization chamber is canceled out by relating the measured concentration to the known concentration of a standard sample, which is measured periodically during a beamtime. For this work, the standard sample PSI-12, with a concentration , was used (see Supporting Information). The transmission efficiency of the entire system (including ion source yield, stripping yield, ion optical transmissions, and software cuts) during 60Fe measurements is in the range (1–4) × 10−4.
Results
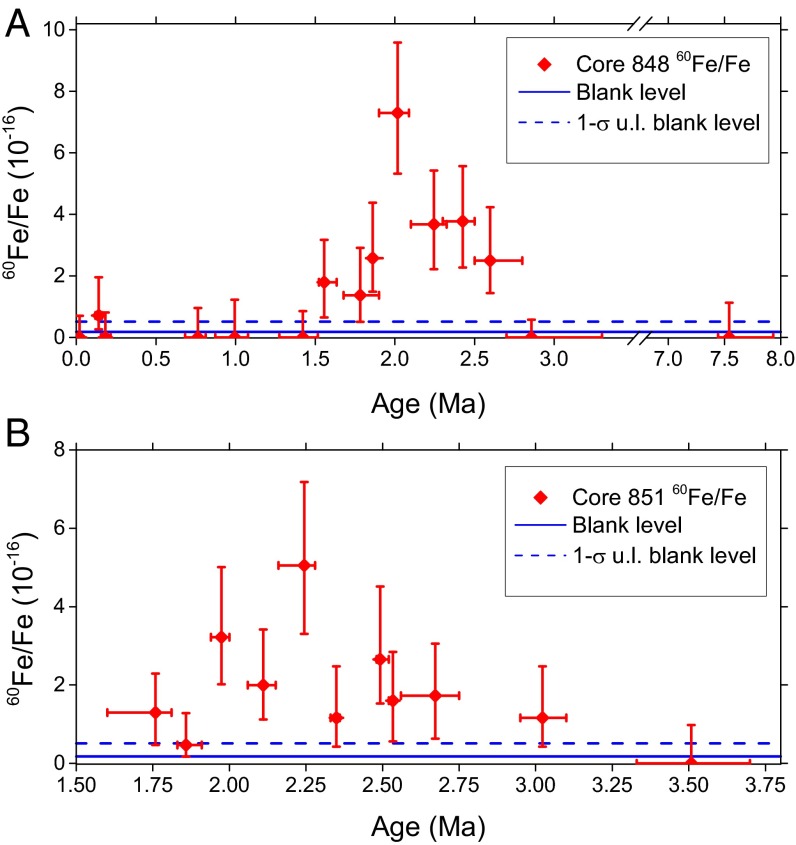
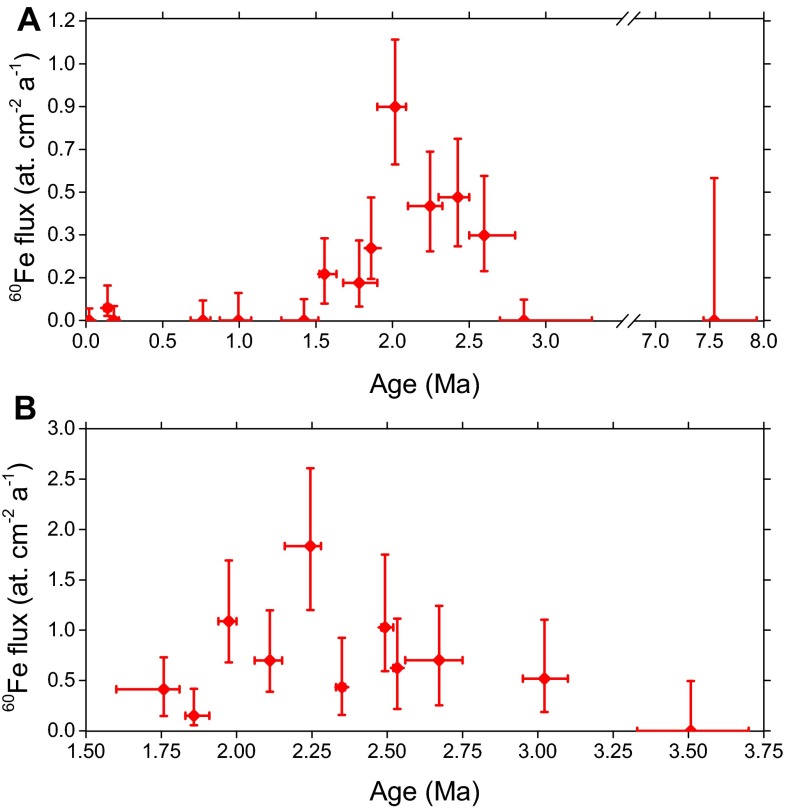
A total of 111 sediment samples (67 from core 848 and 44 from core 851), each with a mass of g, were treated with our CBD protocol, yielding mg AMS samples consisting of Fe2O3. Each AMS sample was measured for an average of 4 h until the sample material was exhausted, yielding one 60Fe event, on average, and a total of 86 events integrated over both cores (42 in core 848 and 47 in core 851). Details of the 60Fe event selection analysis can be found in Supporting Information and Figs. S5 and S6. Thus, several AMS samples have been grouped together to increase counting statistics, and our 60Fe/Fe results are displayed in Fig. 2. Owing to the availability of several near-surface (0 Ma to 1 Ma) and very deep (7 Ma to 8 Ma) samples in core 848, the presence of a distinct 60Fe signal could be clearly identified (Fig. 2A). The data are complemented by the observation of a similar signal in core 851 (Fig. 2B), which is characterized by a 1.5 times lower 60Fe/Fe ratio. The onset of the 60Fe signal occurs at Ma and is centered at () Ma. The signal termination is not as clear, because it remains slightly above the 1σ blank level until around 1.5 Ma, according to the data grouping used in Fig. 2A. A detailed analysis averaging over both sediment cores and several data groupings yields a more conservative estimate for the termination time of () Ma; this results in a () Ma long exposure of the Earth to the influx of 60Fe. The 60Fe flux, concomitant with the data of Fig. 2, is shown in Fig. S7 (see Supporting Information for its derivation).
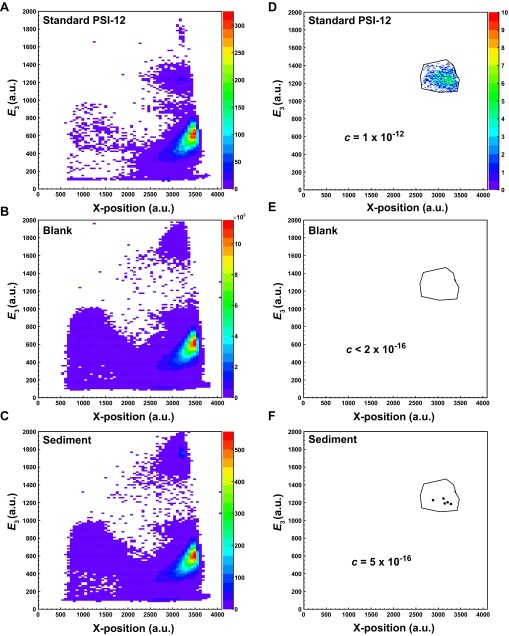
Fig. S5.
Illustration of the event selection process for 60Fe data analysis with representative data from sediment core 851, 2.35−2.36 Ma. Energy loss in anode 3, E3, and X-position spectra from (A) a standard sample, (B) a blank sample, and (C) the representative sediment sample are compared. Spectra in D−F are produced by applying 1D cuts on all energy signals except E3 and the incident x and y angles. If necessary, a final 2D cut is applied to one of the energy loss signals (in this case, E3) and the X-position, as indicated in D. This results in a final, 9D region of interest for 60Fe events, which can be applied to (E) the blank and (F) the sediment sample, yielding the number of events and thus the concentration of 60Fe/Fe.
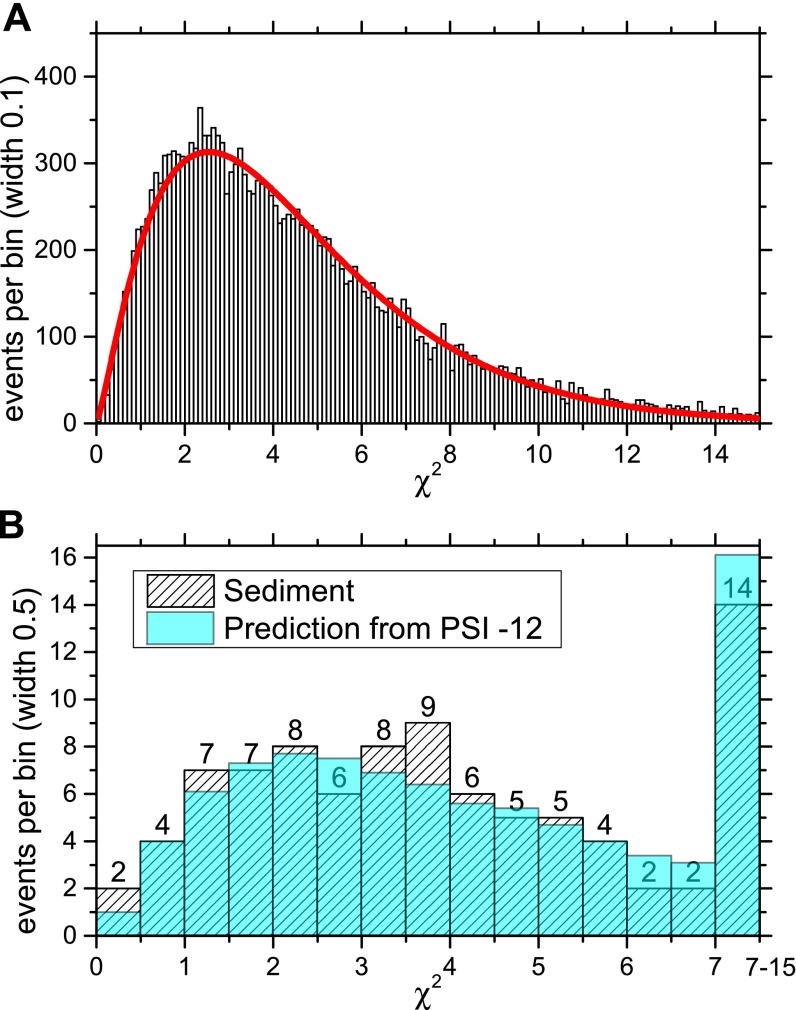
Fig. S6.
(A) The distribution of all () 60Fe events collected from standard samples over all beamtimes (black histogram) is fitted with a density function of variable amplitude and number of degrees of freedom (NDF). The best fit is produced using NDF = 4.5 (red line). The fit has a /NDF value of 1.7. (B) A comparison between the distribution of all 89 60Fe events in the sediment samples with the expected distribution obtained from the events in the standard sample (scaled from A). The last bin of B sums up all events in the range .
Fig. 2.
The 60Fe/Fe atom ratio determined in all sediment samples of cores (A) 848 and (B) 851. The y error bars indicate 1σ statistical uncertainties. The x axis ranges were chosen according to the availability of sample material. The x error bars represent core depth of sample material used for each data point. Each data point contains three to six adjacent individual AMS samples grouped together. The blank level and its 1σ upper limit (u.l.) are shown for a chemical processing blank. Note that A has a broken time axis relative to B.
Fig. S7.
Flux of 60Fe into the sediment cores deduced from the decay and blank corrected 60Fe/Fe ratios determined in all sediment samples of cores (A) 848 and (B) 851. The data use constant sedimentation rate and assume constant influx of CBD extractable Fe. The y error bars indicate 1σ statistical uncertainties; x error bars represent core depth of sample material used for data point. Each data point contains three to six adjacent individual samples grouped together. These data are representative of the temporal structure of the SN 60Fe signal. Note that A has a broken time axis relative to B.
An overview of the collected AMS data split into three age regions ( Ma, 1.8 Ma to 2.6 Ma, Ma) is shown in Table 1. An estimate for the significance of the 60Fe signal in the peak region can be obtained by applying the procedure suggested by ref. 45 for the superposition of two Poisson processes (i.e., signal and background). As a control region (no expected signal), we selected (i) the processing blank and, for comparison, (ii) the -Ma age interval of each respective sediment core. The second choice is rather conservative, because this overestimates the background signal. In the case of i, the procedure yields a significance (in multiples of σ) of 5.2 and 3.9 for cores 848 and 851, respectively. In the case of ii, these values become 7.2 and 2.0 (after subtraction of the blank level). The significance for core 851 is low in the case of ii, because only little data were collected in the control region.
Table 1.
Summary of all 60Fe data presented in this work
| Sample | Age range, Ma | Number of samples | 60Fe events | 60Fe/Fe AMS, | 60Fe/Fe corr., | Deposition rate, at 60Fe⋅a−1⋅cm−2 | Terrestrial fluence , at60Fe⋅cm−2 |
| Core 848 | 25 | 4 | |||||
| Core 848 | 27 | 38 | |||||
| Core 848 | 15 | 0 | |||||
| Core 851 | 3 | 2 | |||||
| Core 851 | 22 | 40 | |||||
| Core 851 | 19 | 5 | |||||
| Blank | 18 | 1 |
Rows indicate separation of the sediment cores into three intervals. The last row represents data obtained from processing blank material. The corrected (corr.) 60Fe/Fe concentrations are corrected for radioactive decay and the blank level. Fluence is in units of atoms (at) per square centimeter. All errors are given as 1σ uncertainties.
A useful measure for the intensity of the total 60Fe exposure is given by the terrestrial () fluence of 60Fe. represents the time-integrated, decay-corrected flux of 60Fe into a given terrestrial reservoir over the entire exposure time. To sum up the contributions of all sediment layers in the signal range, the following integral is computed to calculate the average concentration of 60Fe/Fe in the signal range:
| [1] |
The average terrestrial 60Fe fluence, , is then given by
| [2] |
where ρ is the dry sediment density, is the sedimentation rate, is the efficiency-corrected CBD yield of extracted iron per unit mass of dry sediment, is Avogadro’s number, and is the molecular weight of iron. Using Ma as a nominal signal duration results in a terrestrial fluence into our sediments of atoms per square centimeter (at/cm2) and at/cm2 for cores 848 and 851, respectively. The slightly different values and larger errors compared with Table 1 result from an averaging over different exposure times , whereas the fluences in Table 1 were calculated for a fixed Ma. For the following discussion, we use the error-weighted mean of the fluences determined in both sediment cores, which is at/cm2 (taking into account an additional 10% uncertainty for the signal duration).
To compare this result with the fluence obtained by ref. 11 for the Pacific Ocean FeMn crust, several correction factors must first be applied. Since those results were published, the half-life of 60Fe has undergone a revision (2, 3); the half-life of 10Be, which was used to convert the crust growth rate to geological time, has also been redetermined (46, 47). A correction for the different 60Fe standard samples used (which became available due to advanced cross-calibration measurements) must also be taken into account. The resulting, decay-corrected, terrestrial fluence derived from the FeMn crust now becomes at/cm2, which is about a factor of 4 to 5 higher than our result and does not take an uptake efficiency for Fe of the FeMn crust into account. Interestingly, another recently reported fluence value deduced from Indian Ocean sediments (48) ( at/cm2) is one to two orders of magnitude higher than the value reported in this work. Possible explanations for such differences are (i) a nonuniform 60Fe deposition at the respective locations of the geological reservoirs (see, e.g., ref. 49) and (ii) a selective chemical Fe uptake from bottom water currents at certain locations leading to fluence values above those related to the depositional flux.
Conclusions
In summary, we have extracted magnetofossils and other iron-bearing secondary minerals from two Pacific Ocean sediment cores, 848 and 851 of the ODP Leg 138. Using AMS on samples derived from these mineral phases, we have detected a time-resolved 60Fe signal, and this signal coincides with independently observed ones in a deep ocean FeMn crust (11, 12). In view of our results here, we would also note that the North Atlantic sediment results of ref. 12 possibly show a weak 60Fe signal in the same time range as ours. More recently, two other studies have found a compatible 60Fe signature in lunar samples (13) and in Indian Ocean marine sediments (48), with high statistical significance. Our results derive from two independent Pacific Ocean sediment cores, each possessing a continuous time record spanning the entire time window of the 60Fe signal and with no detectable changes in sedimentation rate (Fig. 1 and Fig. S8), no detectable changes of the depositional environment, and a relatively constant concentration of magnetofossils (Fig. S1 and ref. 34) across the time span of the 60Fe signal. For these reasons, our cores 848 and 851 data should be faithful recorders of the temporal profile of the SN material during its arrival on Earth. Fig. S7 (see Supporting Information) shows the half-life corrected flux of 60Fe into the sediments and, thus, represents the intrinsic temporal structure of the 60Fe signal. Because our Fe extraction protocol specifically targets authigenic Fe oxides including magnetofossils, rather than the total Fe mineral pool (which is ∼3% of dry sediment mass), as would aggressive leaching procedures, we potentially avoided a 60Fe dilution by up to approximately two orders of magnitude, because the majority of the total Fe mass is of detrital origin. This conclusion is supported by the fact that only ∼1% of the total Fe mineral pool is extracted by the CBD procedure (see Supporting Information), which, as seen with magnetic minerals, does not leach lithogenic minerals. Such a strong dilution would have placed our 60Fe/Fe ratio below the blank level, and thereby beyond detectability.
Fig. S8.
AMS results of 10Be from core 851 sediment samples. Horizontal error bars (almost negligible) represent the sampling range, and vertical error bars correspond to 1σ confidence intervals. The red line is a least-squares (/NDF = 1.25) fit obtained using a fixed 10Be half-life of 1.387 Ma.
We attribute this 60Fe signal to SN provenance, rather than to micrometeorites, for the following reasons: First, MTB are expected to obtain their iron budget from poorly crystalline hydroxides (see Supporting Information), and not from silicate and magnetite micrometeorite grains of >20 μm diameter (14); second, our CBD protocol was designed to selectively dissolve only fine-grained magnetite less than 200 nm in size, thereby avoiding dissolution of any large-scale micrometeorites. Thus, the we have extracted cannot be from such micrometeorites.
The Local Bubble (50) is a low-density cavity parsecs (pc; 1 pc = 3.09 × 1016 m) in diameter, within the interstellar medium of our galactic arm, in which the solar system presently finds itself. It has been carved out by a succession of SNs over the course of the last Ma, likely having originated from progenitors in the Scorpius−Centaurus OB star association (50, 51), a gravitationally unbound cluster of stars pc in radius. Analyses (51, 52) of the relative motion of this star association have shown that, around 2.3 Ma, it was located at a minimum distance of ∼100 pc from the solar system, making it the most plausible host for any SN responsible for our signal. The geological time span covered by our signal is intriguing, in that there is an established and overlapping marine extinction event of mollusks (53, 54), marine snails (55), and bivalve fauna (56, 57), in addition to a coeval global cooling period (56–58). The question whether this SN could have contributed to this extinction has been previously raised (51), where it is considered that a SN-induced UV-B catastrophe (59), and its concomitant knock-on effects in the marine biosphere via phytoplankton die off, could have been a proximate factor in this extinction. However, consensus now indicates that a canonical CCSN would need to be within 10 pc of our solar system for there to be a significant and lasting depletion of the ozone layer strong enough to give rise to sudden extinction events (60–62), disfavoring a direct and sudden causal connection, such as a UV-B catastrophe, between a Scorpius−Centaurus CCSN and the Plio-Pleistocene marine extinction.
Sedimentary Fe Cycle and Fe-Reducing Bacteria: Core Selection
Sediment cores suitable for an 60Fe search should contain the maximum possible 60Fe/Fe atom ratio. Assuming a homogeneous 60Fe flux over Earth’s surface, a maximum 60Fe/Fe atom ratio corresponds to a minimum of terrestrial Fe inputs. Because such inputs originate mainly from continents in the forms of river discharge and dust (63), pelagic sediments with a continuous sedimentation record over the time of interest (e.g., 1.7 Ma to 2.7 Ma) represent the preferred source. Furthermore, selected cores must not have been subjected to major Fe mobilization events, e.g., by reductive diagenesis (35), because such events would redistribute Fe over a much larger depth range, causing (i) 60Fe dilution, possibly below the detection limit, and (ii) incorrect deductions about the event dating and timing. Magnetic iron minerals, and, in particular, the most strongly magnetic one, magnetite (Fe3O4), are ideally suited for a systematic characterization of whole core sections to check the above-mentioned requirements. In particular, a distinction can be made between coarse primary magnetite crystals originating from rock erosion, on one hand, and fine secondary magnetite crystals forming in the water column and the topmost sediment layers, on the other hand (e.g., refs. 64–66). The latter crystals grow in aqueous solution, inorganically and/or by bacterial mediation, from easily mobilizable Fe sources (23, 33, 67, 68), which include 60Fe.
The magnetic properties of magnetite crystals depend on their magnetic domain configuration, which is mainly controlled by the crystal size with the following approximate ranges at room temperature: (i) nm unstable (superparamagnetic) single domain (SD), (ii) 20 nm stable SD to 100 nm stable SD, (iii) 0.1 μm to 1 μm pseudo-SD, and (iv) >1 μm multidomain (69, 70). Because the grain size distribution of secondary magnetite extends almost exclusively over ranges i and ii (71–74) the origin of sedimentary magnetite can be verified with magnetic measurements. Such measurements have allowed us to characterize and quantify the secondary and biogenic magnetite of our sediment cores. A precise but time-consuming characterization method is described in Magnetofossil Detection and Quantification.
A much faster technique suitable for characterizing the magnetic mineralogy of whole core sections consists in imparting, in the laboratory, a so-called anhysteretic remanent magnetization (ARM), which is very selective toward stable-single domain crystals (75), and normalizing it with a so-called isothermal remanent magnetization (IRM), which magnetizes all grain size ranges except those of previously mentioned category i (e.g., refs. 66 and 76). ARM is acquired in a slowly decaying alternating magnetic field superimposed to a small constant bias field. We used alternating fields with an initial amplitude of 0.1 T and a bias field mT, which correspond to typical settings reported in the literature (75). On the other hand, IRM was acquired applying a field of 0.1 T or 1 T using an electromagnet. ARM and IRM imparted to dried sediment powder pressed into plastic containers have been measured with a 2G Enterprises 755 SRM (superconducting rock magnetometer) at the paleomagnetic laboratory (77) of the Ludwig-Maximilians-Universität München. This magnetometer has a sensitivity of 10 pAm2, which is fully sufficient for measuring the magnetic moment ( nAm2) of the imparted magnetizations.
Because ARM intensity is proportional to , the ARM/IRM ratio is usually expressed through the so-called ARM susceptibility , which is the ARM divided by . Accordingly, /IRM is a grain-size-sensitive parameter with values 3 mA/m characteristic for well-dispersed, inorganic SD magnetite crystals (75) and magnetofossils (78). Magnetofossil-bearing sediments are systematically characterized by /IRM > 1 mA/m (31). ODP cores 848 and 851 considered in this work fulfill this condition over the whole age range under consideration, 1.7 Ma to 2.7 Ma (34) (see also Fig. S1).
Magnetofossil Detection and Quantification
Reliable magnetofossil detection requires a combination of at least two techniques: (i) TEM observation of magnetic extracts, which serves as a proof for the presence of magnetite crystals with the proper morphology and chemical purity, and (ii) magnetic characterization of the bulk sediment for a semiquantitative assessment of magnetofossil abundance. For better quantification of secondary Fe sources and, in particular, magnetofossils, we also relied on selective chemical extraction as explained in the following.
SEM and TEM Observations.
Because of the extremely low concentration of magnetofossils in the sediment samples (15 μg/g to 35 μg/g), their observation with the electron microscope is only possible after proper magnetic extraction. The magnetic extraction apparatus was built according to the design of ref. 79, which is, in turn, similar to other devices used for the same purpose (80). The extraction procedure starts with the dispersion of 7 g of sediment in 2 L of distilled and deionized water with an ultrasonic rod. After this step, the sediment suspension is constantly circulated by a peristaltic pump through a glass extraction vessel with a watertight opening in which a magnetic finger, covered by a teflon sleeve, is inserted. The strong magnetic field gradient in the proximity of the fingertip attracts suspended magnetic particles so that they adhere to the Teflon surface. After 24 h of continuous circulation of the sediment suspension, the magnetic finger is removed, and the collected material (1 mg to 2 mg) is easily harvested once the Teflon sleeve is removed from the magnetic fingertip. The iron concentration in the magnetic extract is low (a few percent), due to electrostatic adhesion of magnetite crystals to sediment particles (e.g., ref. 81) and incomplete extraction, but is sufficient for electron microscope observations.
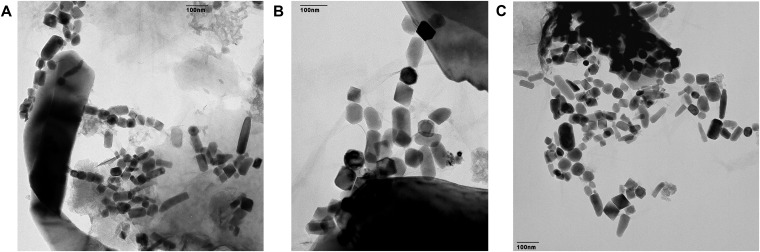
Scanning electron microscope (SEM) analyses, including energy-dispersive X-ray spectroscopy (EDX) and transmission electron microscope (TEM) analyses, were performed at the Chemistry Department of Technische Universität München for three samples of core 851 in the 2.41-Ma to 2.62-Ma age interval where 60Fe has been found. SEM images (Fig. S2) reveal the presence of large (>5 μm) grains of CaCO3 and SiO2, as well as diatom skeletons, which reflect the typical composition of these pelagic carbonates (82, 83). Large magnetic minerals of lithogenic origin (e.g., titanomagnetite) can also be recognized. TEM images, on the other hand, show abundant iron oxide crystals whose size and shape match those of equidimensional, prismatic, and tooth-shaped magnetosomes (Fig. S3) (22, 73, 84, 85). EDX mapping of Fe and O matches with these crystals, making them compatible with a magnetite (Fe3O4) composition. Few fragments of the original chain structure can be recognized; however, the original structures are not likely to be preserved by the magnetic extraction procedure, as seen from the comparison of magnetic signatures of extracts (86) with respect to that of chemically extractable single-domain magnetite as explained in Detailed Magnetic Characterization. The observed magnetofossil crystals are extremely well preserved, completely lacking corrosion signs indicative of incipient reductive diagenesis (87).
Fig. S2.
Scanning electron microscopy images of magnetic extracts obtained from representative sediment samples of core 848 over the 2.41-Ma to 2.62-Ma age interval. (A) Overview of the extract showing prominent features including (i) the copper sample-holding grid, (ii) large grains consisting mainly of CaCO3 and SiO2, and (iii) diatoms. (B) Image of a titanomagnetite grain (dark gray octahedron in the center) of most likely lithogenic origin. (C) Image of an octahedral titanomagnetite (dark, in the center) with small-grained Fe-bearing minerals adhering on its surface (bright spots). All images have been obtained with a JSM5900LV SEM (Jeol).
Fig. S3.
(A–C) Transmission electron microscopy images of magnetic extracts obtained from representative sediment samples of core 848 over the 2.41-Ma to 2.62-Ma age interval showing abundant magnetofossils. All images have been obtained with a JEM2011 (Jeol).
Detailed Magnetic Characterization.
Electron microscopy of magnetic extracts does not enable quantitative assessments of magnetofossil concentration, especially in relation to lithogenic minerals, nor is it possible to obtain information about the structural integrity of chains, due to the necessity of a possibly disruptive magnetic extraction for sample preparation. Therefore, our electron microscopy observations have been integrated with the most advanced magnetic characterization techniques based on the measurement of partial magnetic hysteresis, in the form of so-called FORC (88, 89). These curves sweep the whole area enclosed by the major hysteresis loop, thereby enabling a systematic investigation of irreversible magnetic processes, which can be represented as a 2D function (90) called a FORC distribution. In the context of the Preisach theory (91), each value of the FORC distribution represents the contribution of an elemental rectangular hysteresis loop (hysteron) with coercivity and horizontal bias field . In case of uniaxial SD particles, hysterons approximate the hysteresis loops of individual crystals (92). Hysterons no longer have a physical meaning in the case of other magnetic systems; however, natural particle assemblages have typical FORC signatures that reflect their domain state (93) and, to a certain extent, mineralogical composition (94).
The advantage of FORC distributions over other magnetic measurements resides in the fact that the signatures of specific magnetic mineral components remain recognizable also in the case of complex mixtures (95). This is particularly true for SD magnetite particles and magnetosome chains that are well dispersed in a sediment matrix. In this case, their signature consists of a sharp horizontal ridge at (31, 96), which can be separated from other contributions using appropriate numerical procedures (97). The separated central ridge is a pure coercivity distribution from which the total saturation magnetization of SD particles contributing to it can be calculated (31), obtaining a direct estimate of their mass concentration in sediment. This technique has become a standard method for magnetofossil detection, revealing magnetofossils’ widespread occurrence in marine and freshwater sediments (28, 98, 99). A detailed FORC investigation of sediment material from the 1.7-Ma to 3.8-Ma age interval of core 848 has been reported in ref. 29. Here, the FORC analysis protocol of ref. 97 has been applied to the untreated sediment material, and to the same material after selective dissolution of ultrafine magnetite particles with a CBD solution. Because this treatment removes most secondary Fe minerals while leaving large lithogenic crystals intact (38, 39), it provides an independent manner for identifying magnetofossils and other secondary magnetite crystals, thereby excluding possible contributions from SD magnetite particles enclosed in primary silicate minerals, which would not contain 60Fe. A summary of FORC analysis results from ref. 29 is provided in Fig. S4. The main outcomes of such analysis are summarized in the following.
-
i)
The sediment contains SD particles and chains of such particles, which are directly dispersed in the sediment matrix and not hosted inside lithogenic minerals; this proves their secondary origin as inorganic or biologically mediated precipitate, and as magnetofossils. The presence of magnetofossils is confirmed by TEM observations, whereas few irregularly shaped magnetite crystals compatible with a nonmagnetofossil origin could be found. The saturation magnetization of these particles, as deduced from the central ridge of the FORC function, corresponds to an Fe mass concentration of , which represents at least 27% of our CBD-extractable iron. Details about the calculation of Fe mass concentrations from SD magnetite particles are reported in ref. 19.
-
ii)
The difference between FORC diagrams measured before and after CBD treatment reveals a second contribution to the FORC function, which is also attributable to ultrafine (SD) magnetic particles. This contribution bears the signature of magnetostatic interactions and might be attributed to particle clusters, whose origin is not clear. They might be the product of chemical precipitation, as well as the result of magnetofossil chain collapse (100). Nevertheless, their secondary origin is supported by the fact that such particles are not located inside lithogenic minerals (e.g., silicates), and that application of the same chemical treatment to volcanic ash, which represents one of the major lithogenic sources of equatorial Pacific sediment (e.g., ref. 101), did not remove a significant amount of magnetic minerals (29). The saturation magnetization of these particles corresponds to an Fe mass concentration of , i.e., 15% of our CBD-extractable iron.
-
iii)
From the above-mentioned estimates, the total mass concentration of Fe from secondary magnetite crystals is , totaling 42% of CBD-extractable iron; this also represents an upper limit for the contribution of magnetofossils.
-
iv)
The FORC signature of sedimentary greigite (Fe3S4) (28), an iron sulphide produced exclusively during reductive diagenesis (102), is completely absent from the investigated sediment; this is also confirmed by the lack of magnetosomes with signs of corrosion in TEM images of magnetic extracts. Magnetofossil preservation implies that no major Fe transport or diagenesis occurred after the formation of magnetosomes, i.e., after their permanence in the so-called benthic mixed layer (BML), i.e., the topmost layer of the sediment column that is permanently mixed by benthic organisms.
-
v)
Assuming 7 cm for the typical thickness of the surface mixed layer in pelagic carbonates, along with an estimated sedimentation rate cm/ka for core 848 over the 1.7-Ma to 2.7-Ma age interval (Fig. 1 and ref. 103), we obtain a mean residence time ka for magnetofossils in the BML. Variations in L and/or over time produce an age uncertainty related to the change of . If maximum variations in total Fe concentration and /IRM over the time range of interest, which correspond to a factor of ∼2, are attributed to environmental changes that have a similar effect on , the maximum age uncertainty of Fe in secondary magnetite can be set to 26 ka, i.e., a negligible fraction of the total duration of the 60Fe signal ( Ma).
60Fe AMS Sample Preparation
The main goal of the chemical extraction and purification procedure was the production of AMS samples with a 60Fe/Fe ratio being as close as possible to the ratio in the targeted minerals, namely, secondary iron oxides such as magnetofossils. This requires that dilution with stable Fe from other sources be minimized, and that no contaminations with 60Fe from other sources can occur. The following procedure has been shown to accomplish these goals remarkably well, as described in ref. 29, where a more detailed description can be found.
For the preparation of the CBD procedure, ∼35 g of dry sediment were crushed in an agate mortar and then added to 200 mL of distilled and deionized H2O. Under constant stirring, the temperature was brought to () °C on a hot plate while adding 3.4 g of sodium bicarbonate and 12.6 g of sodium citrate. The reaction is then started by adding 5.0 g of sodium dithionite, a strong reducing agent. This corresponds to the concentrations suggested by ref. 38. The main extraction mechanism relies on Fe(III) reduction to Fe(II) by sodium dithionite on mineral surfaces. Fe(II) is then chelated by sodium citrate, while the pH is kept stable at 7.3 by the sodium bicarbonate.
The procedure was fine-tuned to selectively dissolve nm Fe3O4 crystals. This ensures that secondary iron oxides are completely dissolved, while primary ones are left essentially intact. To this end, an extraction temperature of 50 °C and an extraction time of 1 h were chosen.
After the extraction, the remaining undissolved sediment material was separated from the Fe(II) solution using filter paper of 0.1-μm pore size. The Fe(II) solution [clear yellow in color due to the presence of dissolved Fe(II)] was then evaporated to dryness. To destroy the sodium citrate chelation, the sample was then heated for 1 h at 300 °C, decomposing the citrate, until a black, carbon-rich solid was obtained. Fe(II) was then oxidized by adding 50 mL of HNO3 (65%). After another heating step for 1 h at 400 °C, all carbon was oxidized, and the sample became a colorless liquid that solidified upon cooling to room temperature. Fe(III) was then extracted using 30 mL of HCl (7.1 M), which was evaporated to dryness. Another 20 mL of HCl were added, and much of the organic residuals could be removed by centrifugation. This step was repeated by dissolving in another 20 mL of HCl, evaporating again, adding another 20 mL of HCl, and centrifugation. From the final HCl solution containing Fe(III), iron hydroxide was precipitated by adding NH3(aq) (25%). The precipitate was washed 3 times with slightly alkaline solution (pH 8 to 9) and then redissolved in 1.5 mL of HCl (10.2 M). To remove unwanted contaminations by other metals that might have coprecipitated, an anion exchange (DOWEX 1 × 8) step followed; this was done similarly to the procedure described in ref. 104. After reprecipitating the iron hydroxide and another three washing steps with deionized water, the samples were transferred to quartz crucibles and heated at 600 °C for 3 h, resulting in samples of Fe2O3 with a typical mass of 3 mg to 5 mg, sufficient to fill one AMS sample holder.
The recovery efficiency of this procedure was determined using commercial magnetite grains (40 nm to 60 nm, lot E08T027; Alfa Aesar) to be ()%. Contamination with stable Fe from the chemical reagents of this entire procedure was found to be less than 0.05 mg per sample.
60Fe Measurements at the GAMS Setup at the MLL
Ion Source.
The ion source used for the experiments described here is a homemade (105), single-cathode, Middleton-type (106) cesium sputter ion source with a spherical ionizer (107) optimized for optimum mass resolution. The Cs vapor is ionized on the tantalum ionizer and accelerated toward the sample using a 5-kV sputtering voltage. The negative ion beam is then extracted by applying an additional voltage of 23 kV. After preliminary mass separation by a dipole magnet, a beam of 54FeO− is selected and directed toward the accelerator entrance with several electrostatic lenses. After a further preacceleration to 178 keV, this beam is injected into the accelerator, at which point the typical electrical current of 54FeO− is 30 nA to 150 nA.
Ionization Chamber.
The particle identification detector is an ionization chamber filled with 40 mbar to 60 mbar of isobutane, featuring a fivefold split anode. The first two anodes sections are additionally split diagonally, to provide the horizontal entrance position (henceforth, X-position) and horizontal entrance angle of the incoming particles by comparing the left and right energy loss signals. Particle discrimination is possible using the five Ei anode signals, the Frisch grid signal (proportional to the sum of all Ei signals), and the X-position along with the horizontal and vertical entrance angles of the incident particles. The discrimination between the detector signals, from each anode, arising from the passage of ions of different atomic charge is possible on the basis of differential ionization energy loss (Bragg curve spectroscopy) of the ions passing through the detector gas; this also provides additional discrimination between the isobars 60Fe and 60Ni because they differ in their proton number, but also between different isotopes of the same element and other background.
Standard Sample.
For all measurements discussed in this work, 60Fe was measured relative to the standard sample PSI-12. The starting point for the production of this standard was material extracted from a beam-dump at the Paul Scherrer Institute that was later used for the half-life measurement of 60Fe in ref. 2. The high concentration of 60Fe/Fe was precisely measured by inductively coupled plasma mass spectrometry. This material was diluted, by introducing stable Fe, to a ratio of 60Fe/Fe and referred to as PSI-12 for clarity. To avoid cross-talk in the ion source, during each standard run (about every 3 h), only about 200 events of 60Fe are recorded, because the exposure of the ion source to a highly concentrated sample (in this case, four to five orders of magnitude above the blank level) must be minimized. The possibility of cross-talk was examined by first sputtering a sample with a concentration of 60Fe/Fe for 20 min (typical time for a standard measurement) and subsequently measuring a blank. This way, cross-talk from one sample to the next could be determined to be .
60Fe Event Selection.
The 60Fe events from the standard sample PSI-12 allow for empirically constructing, for each anode and the Frisch grid, their respective distribution/histogram of collected ionization charge from the transit of 60Fe in the ionization chamber. Knowing these distributions/histograms then allows for the identification of 60Fe from the actual sediment samples, which are of much lower 60Fe concentration. This procedure is illustrated in Fig. S5. Qualitatively, the distribution of collected ionization charge on each anode (Frisch grid), arising from 60Fe events from the PSI-12 standard sample, is very similar in shape to a normal distribution. As such, they are each characterized by their own centroid μi and width σi, both of which are determined from a Gaussian fit. To reduce the 6D space of the energy signals of an event in the ionization chamber, it is useful to introduce a value defined as the sum of squared deviations of a candidate 60Fe event’s charge signal in a given anode (or Frisch grid) from the known centroid value of actual 60Fe charge signals, μi, in that same anode (or Frisch grid), normalized to the known corresponding characteristic width, σi, of 60Fe charge signals in that anode; namely,
| [S1] |
Here, represent the six energy signals from the detector (with E0 corresponding to the Frisch grid signal) for the candidate event of 60Fe under consideration. The maximum of the χ2 distribution for the standard sample is not (as would be expected for a distribution with six degrees of freedom) about 4, but rather around 2.5, as shown in Fig. S6A. This discrepancy can be explained by taking into account that the energy signals are not completely independent and that, for some parameters, the tails of the distributions are not in the accepted signal range. Nonetheless, the value of a candidate event has high predictive power, i.e., a low favors a real 60Fe event. In most cases of 60Fe measurements, a 1D cut on the (accepting only events with ), combined with a 2D cut on the X-position and one of the energy signals (choosing the one with best separation—typically E3) was sufficient for event discrimination. The distributions obtained from the 60Fe events from both the standard sample and all sediment samples can be seen in Fig. S6B. Both distributions agree extremely well, confirming the authenticity of the observed 60Fe signal.
Discussion of AMS Uncertainties.
All AMS results in this work are presented with 1σ confidence intervals. Owing to the measurements relative to a standard sample, all systematic uncertainties related to transmissions and efficiencies cancel. The only systematic uncertainty that cannot be avoided is the uncertainty of the concentration of the standard sample itself (4.8%). This would, however, only shift all of the AMS 60Fe/Fe data up or down and was thus omitted.
The statistical errors that were included in all AMS results have several origins. The low count rate of 60Fe events is the main source of uncertainty; this was treated by using the confidence intervals suggested by ref. 108 for zero background. The uncertainty in the ion current reading was estimated to be 15% in each data run. Additionally, the fluctuation of the atom ratio 60Fe/Fe measured in the standard sample was typically 15%. Another 20% uncertainty is added due to the unknown behavior of the ion current during runs. With an average of four data runs per sample, the quadratic summation yields a statistical uncertainty of 15% for each sample, which is a rather conservative estimate. For each data point (e.g., grouped samples in Fig. 2), this number is divided by the square root of the number of samples used to produce the grouped data point. This result is then added in quadrature to the relative uncertainty of the confidence intervals given by ref. 108, except in the case of zero events, where the 1σ upper limit of 1.29 events is conservatively increased in all cases by 0.15 (corresponding to 15% at one event) to yield 1.44 events.
The horizontal error bar associated with each data point in the 60Fe/Fe plots (Fig. 2 and Fig. S7) represents the timespan interval over which raw sediment material was used in our CBD protocol to obtain a sufficiently large mass of Fe2O3 extract suitable for an AMS sample (at least 3 mg). The abscissa of each data point results from an averaging over the ages of the individual samples used in the grouping, where each sample's age is correspondingly weighted by the collected statistics of that sample (i.e., the product of average beam current and measuring time). The systematic uncertainty in core dating is not included in these error bars. One possible data grouping is shown in Fig. S7, after correction for radioactive decay of 60Fe.
Temporal Structure of the60Fe Signal
To extract the temporal structure of the 60Fe input into the sediment samples, the obtained 60Fe/Fe AMS data have to be corrected for the blank level and the radioactive decay of 60Fe. Using the established constant sedimentation rates (Fig. 1), this ratio is directly proportional to the deposition rate of 60Fe atoms, as shown in Table 1 for representative time intervals. The deposition rates corresponding to the data grouping of Fig. 2 are shown in Fig. S7 and take into account variations in the CBD-extracted Fe yield of every AMS sample.
Sample Preparation and 10Be Measurements at Dresden Accelerator Mass Spectrometry Facility
To further independently establish the constancy of the sedimentation rate, 13 sediment samples of core 851, in the depth (age) range 1.7 Ma to 3.0 Ma, were analyzed for 10Be [ Ma (46, 47)]. The 10Be is mainly produced in atmospheric spallation reactions and can be transported to Earth’s surface by dust, rain, and snow. Once 10Be is deposited into geological reservoirs such as ice cores and marine sediments, it can be used for dating over several million years (109).
From each depth, 3 g of sediment were subjected to a hydroxylamine-based leaching technique, described in ref. 110. The AMS measurements of 10Be were performed at the Dresden Accelerator Mass Spectrometry facility at the Helmholtz-Zentrum Dresden-Rossendorf, using the procedure described in ref. 111. The determined concentrations of 10Be/9Be follow the general trend of the exponential decay, which is expected for an undisturbed core of constant sedimentation rate; this is shown in Fig. S8. The exponential fit to the data using the known half-life produces a reduced of 1.25, and no significant deviation from an exponential decay as a function of age is evident, demonstrating again that our cores are characterized by constant sedimentation rates across the time window spanning 1.7 Ma to 3.0 Ma, consistent with the magnetostratigraphic models of ref. 42 and Fig. 1.
Acknowledgments
We are grateful to three anonymous reviewers for their constructive comments, which helped improve the original manuscript, and to the operators of the MLL and the Ion Beam Center at Helmholtz-Zentrum Dresden-Rossendorf for their help during beamtimes. The search for 60Fe supernova signatures is supported by the German Research Foundation (DFG), Grant DFG-Bi1492/1-1, and by the DFG Cluster of Excellence “Origin and Structure of the Universe” (www.universe-cluster.de).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. E.B. is a Guest Editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1601040113/-/DCSupplemental.
References
- 1.Limongi M, Chieffi A. The nucleosynthesis of 26Al and 60Fe in solar metallicity stars extending in mass from 11 to 120 M⊙: The hydrostatic and explosive contributions. Astrophys J. 2006;647(1):483–500. [Google Scholar]
- 2.Rugel G, et al. New measurement of the 60Fe half-life. Phys Rev Lett. 2009;103(7):072502. doi: 10.1103/PhysRevLett.103.072502. [DOI] [PubMed] [Google Scholar]
- 3.Wallner A, et al. Settling the half-life of 60Fe: Fundamental for a versatile astrophysical chronometer. Phys Rev Lett. 2015;114(4):041101. doi: 10.1103/PhysRevLett.114.041101. [DOI] [PubMed] [Google Scholar]
- 4.Wang W, et al. SPI observations of the diffuse 60Fe emission in the Galaxy. Astron Astrophys. 2007;469(3):1005–1012. [Google Scholar]
- 5.Knie K, et al. Indication for supernova produced 60Fe activity on Earth. Phys Rev Lett. 1999;83(1):18–21. [Google Scholar]
- 6.Athanassiadou T, Fields B. Penetration of nearby supernova dust in the inner solar system. New Astron. 2011;16(4):229–241. [Google Scholar]
- 7.Gomez H. Astrophysics: Survival of the largest. Nature. 2014;511(7509):296–297. doi: 10.1038/nature13640. [DOI] [PubMed] [Google Scholar]
- 8.Gall C, et al. Rapid formation of large dust grains in the luminous supernova 2010jl. Nature. 2014;511(7509):326–329. doi: 10.1038/nature13558. [DOI] [PubMed] [Google Scholar]
- 9.Plane JM. Cosmic dust in the earth’s atmosphere. Chem Soc Rev. 2012;41(19):6507–6518. doi: 10.1039/c2cs35132c. [DOI] [PubMed] [Google Scholar]
- 10.Jickells TD, et al. Global iron connections between desert dust, ocean biogeochemistry, and climate. Science. 2005;308(5718):67–71. doi: 10.1126/science.1105959. [DOI] [PubMed] [Google Scholar]
- 11.Knie K, et al. 60Fe anomaly in a deep-sea manganese crust and implications for a nearby supernova source. Phys Rev Lett. 2004;93(17):171103. doi: 10.1103/PhysRevLett.93.171103. [DOI] [PubMed] [Google Scholar]
- 12.Fitoussi C, et al. Search for supernova-produced 60Fe in a marine sediment. Phys Rev Lett. 2008;101(12):121101. doi: 10.1103/PhysRevLett.101.121101. [DOI] [PubMed] [Google Scholar]
- 13.Fimiani L, et al. Interstellar 60Fe on the surface of the Moon. Phys Rev Lett. 2016;116(15):151104. doi: 10.1103/PhysRevLett.116.151104. [DOI] [PubMed] [Google Scholar]
- 14.Stuart F, Lee M. Micrometeorites and extraterrestrial He in a ferromanganese crust from the Pacific Ocean. Chem Geol. 2012;322–323:209–214. [Google Scholar]
- 15.Kachelrieβ M, Neronov A, Semikov DV. Signatures of a two million year old supernova in the spectra of cosmic ray protons, antiprotons, and positrons. Phys Rev Lett. 2015;115(18):181103. doi: 10.1103/PhysRevLett.115.181103. [DOI] [PubMed] [Google Scholar]
- 16.Zachara J, Kukkadapu R, Fredrichson J, Groby Y, Smith S. Biomineralization of poorly crystalline Fe(III) oxides by dissimilatory metal reduncing bacteria (DMRB) Geomicrobiol J. 2002;19(2):179–207. [Google Scholar]
- 17.Bellini S. On a unique behaviour of freshwater bacteria. Chin J Oceanol Limnol. 2009;27(1):3–5. [Google Scholar]
- 18.Blakemore R. Magnetotactic bacteria. Science. 1975;190(4212):377–379. doi: 10.1126/science.170679. [DOI] [PubMed] [Google Scholar]
- 19.Faivre D, Schüler D. Magnetotactic bacteria and magnetosomes. Chem Rev. 2008;108(11):4875–4898. doi: 10.1021/cr078258w. [DOI] [PubMed] [Google Scholar]
- 20.Bazylinski DA, Frankel RB. Magnetosome formation in prokaryotes. Nat Rev Microbiol. 2004;2(3):217–230. doi: 10.1038/nrmicro842. [DOI] [PubMed] [Google Scholar]
- 21.Petermann H, Bleil U. Detection of live magnetotactic bacteria in South Atlantic deep-sea sediments. Earth Planet Sci Lett. 1993;117(1-2):223–228. [Google Scholar]
- 22.Kopp R, Kirschvink J. The identification and biogeochemical interpretation of fossil magnetotactic bacteria. Earth Sci Rev. 2008;86(1):42–61. [Google Scholar]
- 23.Konhauser K, Kappler A, Roden E. Iron in microbial metabolism. Elements. 2011;7(2):89–93. [Google Scholar]
- 24.Roden E, Zachara J. Microbial reduction of crystalline iron(III) oxides: influence of oxide surface area and potential for cell growth. Environ Sci Technol. 1996;30(5):1618–1628. [Google Scholar]
- 25.Zachara J, et al. Bacterial reduction of crystalline Fe(III) oxides in single phase suspensions and subsurface materials. Am Mineral. 1998;83(11):1426–1443. [Google Scholar]
- 26.Bosch J, Heister K, Hofmann T, Meckenstock RU. Nanosized iron oxide colloids strongly enhance microbial iron reduction. Appl Environ Microbiol. 2010;76(1):184–189. doi: 10.1128/AEM.00417-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yan L, et al. Magnetotactic bacteria, magnetosomes and their application. Microbiol Res. 2012;167(9):507–519. doi: 10.1016/j.micres.2012.04.002. [DOI] [PubMed] [Google Scholar]
- 28.Roberts A, Chang L, Heslop D, Florindo F, Larrasoaña J. Searching for single domain magnetite in the ‘pseudo-single-domain’ sedimentary haystack: Implications of biogenic magnetite preservation for sediment magnetism and relative paleointensity determinations. J Geophys Res. 2012;117(B8):B08104. [Google Scholar]
- 29.Ludwig P, et al. Characterization of primary and secondary magnetite in marine sediment by combining chemical and magnetic unmixing techniques. Global Planet Change. 2013;110(Part C):321–339. [Google Scholar]
- 30.Egli R. Characterization of individual rock magnetic components by analysis of remanence curves, 1. Unmixing natural sediments. Stud Geophys Geod. 2004;48(2):391–446. [Google Scholar]
- 31.Egli R, Chen A, Winkelhofer M, Kodama K, Horng C. Detection of noninteracting single domain particles using first-order reveral curve diagrams. Geochem Geophys Geosyst. 2010;11(1):Q01Z11. [Google Scholar]
- 32.Sobolev D, Roden EE. Evidence for rapid microscale bacterial redox cycling of iron in circumneutral environments. Antonie van Leeuwenhoek. 2002;81(1-4):587–597. doi: 10.1023/a:1020569908536. [DOI] [PubMed] [Google Scholar]
- 33.Taylor K, Macquaker J. Iron minerals in marine sediments record chemical environments. Elements. 2011;7(2):113–118. [Google Scholar]
- 34.Bishop S, Egli R. Discovery prospects for a supernova signature of biogenic origin. Icarus. 2011;212(2):960–962. [Google Scholar]
- 35.Rowan C, Roberts A, Broadbent T. Reductive diagenesis, magnetic dissolution, greigite growth and paleomagnetic smoothing in marine sediments: A new review. Earth Planet Sci Lett. 2009;277(1):223–235. [Google Scholar]
- 36.Roden E. Analysis of long-term bacterial vs chemical Fe(III) oxide reduction kinetics. Geochim Cosmochim Acta. 2004;68(15):3205–3216. [Google Scholar]
- 37.Mehra O, Jackson M. Iron oxide removal from soils and clays by a dithionite-citrate system buffered with sodium bicarbonate. Clays Clay Miner. 1958;7(1):317–327. [Google Scholar]
- 38.Hunt C, Singer M, Kletetschka G, TenPas J, Verosub K. Effect of citrate-bicarbonate-dithionite treatment on fine-grained magnetite and maghemite. Earth Planet Sci Lett. 1995;130(1):87–94. [Google Scholar]
- 39.Vidic N, TenPas J, Verosub K, Singer M. Separation of pedogenic and lithogenic components of magnetic susceptibility in the Chinese loess/paleosol sequence as determined by the CBD procedure and a mixing analysis. Geophys J Int. 2000;142(2):551–562. [Google Scholar]
- 40.Mayer L, et al. Shipboard Scientific Party, 1992: Site 848. Proc Ocean Drill Program Initial Rep. 1992;138:677–734. [Google Scholar]
- 41.Billeaud L, Lewis Pratson E, Broglia C, Lyle M, Dadey K. Data report: Geochemical logging results from three lithospheric plates; Cocos, Nazca, and Pacific: Leg 138, sites 844 through 852. Proc Ocean Drill Program Sci Results. 1995;138:857–884. [Google Scholar]
- 42.Shackleton N, Crowhurst S, Hagelberg T, Pisias N, Schneider D. A new late neogene time scale: Application to leg 138 sites. Proc Ocean Drill Program Sci Results. 1995;138:73–101. [Google Scholar]
- 43.Farrell J, et al. Late Neogene sedimentation patterns in the Eastern Equatorial Pacific Ocean. Proc Ocean Drill Program Sci Results. 1995;138:717–756. [Google Scholar]
- 44.Knie K, et al. High-sensitivity AMS for heavy nuclides at the Munich Tandem Accelerator. Nucl Instrum Methods Phys Res B. 2000;172(1-4):717–720. [Google Scholar]
- 45.Cousins R, Linnemann J, Tucker J. Evaluation of three methods for calculating statistical significance when incorporating a systematic uncertainty into a test of the background-only hypothesis for a Poisson process. Nucl Instrum Methods Phys Res A. 2008;595(2):480–501. [Google Scholar]
- 46.Chmeleff J, Blanckenburg FV, Kossert K, Jakob D. Determination of the 10Be half-life by multicollector ICP-MS and liquid scintillation counting. Nucl Instrum Methods Phys Res B. 2010;268(2):192–199. [Google Scholar]
- 47.Korschinek G, et al. A new value for the half-life of 10Be by heavy-ion elastic recoil detection and liquid scintillation counting. Nucl Instrum Methods Phys Res B. 2010;268(2):187–191. [Google Scholar]
- 48.Wallner A, et al. Recent near-Earth supernovae probed by global deposition of interstellar radioactive 60Fe. Nature. 2016;532(7597):69–72. doi: 10.1038/nature17196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fry B, Fields B, Ellis J. 2016. Radioactive iron rain: Transporting 60Fe in supernova dust to the ocean floor. arXiv:1604.00958.
- 50.Maíz Appelíniz J. The origin of the local bubble. Astrophys J. 2001;560:L83–L86. [Google Scholar]
- 51.Benítez N, Maíz-Apellániz J, Canelles M. Evidence for nearby supernova explosions. Phys Rev Lett. 2002;88(8):081101. doi: 10.1103/PhysRevLett.88.081101. [DOI] [PubMed] [Google Scholar]
- 52.Breitschwerdt D, et al. The locations of recent supernovae near the Sun from modelling 60Fe transport. Nature. 2016;532(7597):73–76. doi: 10.1038/nature17424. [DOI] [PubMed] [Google Scholar]
- 53.Allmon WD, Rosenberg G, Portell RW, Schindler KS. Diversity of Atlantic coastal plain mollusks since the Pliocene. Science. 1993;260(5114):1626–1629. doi: 10.1126/science.260.5114.1626. [DOI] [PubMed] [Google Scholar]
- 54.Petuch EJ. Molluscan diversity in the late neogene of Florida: Evidence for a two-staged mass extinction. Science. 1995;270(5234):275–277. [Google Scholar]
- 55.Dietl GP, Herbert GS, Vermeij GJ. Reduced competition and altered feeding behavior among marine snails after a mass extinction. Science. 2004;306(5705):2229–2231. doi: 10.1126/science.1106182. [DOI] [PubMed] [Google Scholar]
- 56.Raffi S, Stanley SM, Marasti R. Biogeographic patterns and Plio-Pleistocene extinction of Bivalvia in the Mediterranean and southern North Sea. Paleobiology. 1985;11(4):368–388. [Google Scholar]
- 57.Stanley SM. Anatomy of a regional mass extinction: Plio-Pleistocene decimation of the western Atlantic bivalve fauna. Palaios. 1986;1(1):17–36. [Google Scholar]
- 58.Berkman PA, Prentice ML. Pliocene extinction of Antarctic pectinid mollusks. Science. 1996;271(5255):1606–1607. [Google Scholar]
- 59.Cockell CS. Crises and extinction in the fossil record—A role for ultraviolet radiation? Paleobiology. 1999;25(2):212–225. [Google Scholar]
- 60.Gehrels N, et al. Ozone depletion from nearby supernovae. Astrophys J. 2003;585(2):1169–1176. [Google Scholar]
- 61.Beech M. The past, present and future supernova threat to Earth’s biosphere. Astrophys Space Sci. 2011;336(2):287–302. [Google Scholar]
- 62.Melott A, Thomas BC. 2016. Brief review and census of intermittent intense sources. arXiv:1605.04926v1.
- 63.Raiswell R. Iron transport from the continents to the open ocean: The aging-rejuvination cycle. Elements. 2011;7(2):101–106. [Google Scholar]
- 64.Watkins S, Maher B. Magnetic characterization of present-day deep-sea sediments and sources in the North Atlantic. Earth Planet Sci Lett. 2003;214(3-4):379–394. [Google Scholar]
- 65.Franke C, Dobeneck TV, Drury M, Meeldijk J. Magnetic petrology of equatorial Atlantic sediments: Electron microscopy results and their implications for environmental magnetic interpretation. Paleoceanography. 2007;22(4):PA4207. [Google Scholar]
- 66.Yamazaki T. Environmental magnetism of Pleistocene sediments in the North Pacific and Ontong-Java Plateau: Temporal variations of detrital and biogenic components. Geochem Geophys Geosyst. 2009;10(7):Q07Z04. [Google Scholar]
- 67.Canfield DE. Reactive iron in marine sediments. Geochim Cosmochim Acta. 1989;53(3):619–632. doi: 10.1016/0016-7037(89)90005-7. [DOI] [PubMed] [Google Scholar]
- 68.Fortin D, Langley S. Formation and occurrence of biogenic iron-rich minerals. Earth Sci Rev. 2005;72(1-2):1–19. [Google Scholar]
- 69.Butler R, Banerjee S. Theoretical single-domain grain-size range in magnetite and titatomagnetite. J Geophys Res. 1975;80(29):4049–4058. [Google Scholar]
- 70.Dunlop D, Özdemir Ö. Rock Magnetism. Cambridge Univ Press; Cambridge, UK: 1997. [Google Scholar]
- 71.Lovley D, Stolz J, Nord GL, Jr, Phillips EJP. Anaerobic production of magnetite by a dissimilatory iron-reducing microorganism. Nature. 1987;330(6145):252–254. [Google Scholar]
- 72.Maher B. Magnetic properties of some synthetic sub-micron magnetites. Geophys J. 1988;94(1):83–96. [Google Scholar]
- 73.Devourad B, et al. Magnetite from magnetotactic bacteria: Size distribution and twinning. Am Mineral. 1998;83:1387–1398. [Google Scholar]
- 74.Fairve D, et al. Mineralogical and isotopic properties of inorganic nanocrystalline magnetites. Geochim Cosmochim Acta. 2004;68(21):4395–4403. [Google Scholar]
- 75.Egli R, Lowrie W. Anhysteretic remanent magnetization of fine magnetic particles. J Geophys Res. 2002;107(B10):2209. [Google Scholar]
- 76.Snowball I, Zillén L, Sandgren P. Bacterial magnetite in Swedish varved lake-sediments: A potential bio-marker of environmental change. Quat Int. 2002;88(1):13–19. [Google Scholar]
- 77.Wack M, Gilder S. The SushiBar: An automated system for paleomagnetic investigations. Geochem Geophys Geosyst. 2012;13(3):Q12Z38. [Google Scholar]
- 78.Moskowitz B, Frankel R, Bazylinski D. Rock magnetic criteria for the detection of biogenic magnetite. Earth Planet Sci Lett. 1993;120(3-4):283–300. [Google Scholar]
- 79.Dobeneck T, Petersen N, Vali H. Bakterielle Magnetofossilien. Geowiss Unserer Z. 1987;1:25–27. German. [Google Scholar]
- 80.Hounslow M, Maher B. Quantitative extraction and analysis of carriers of magnetization in sediments. Geophys J Int. 1996;124(1):57–74. [Google Scholar]
- 81.Galindo-González C, et al. Magnetic and microscopic characterization of magnetite nanoparticles adhered to clay surfaces. Am Mineral. 2009;94(8-9):1120–1129. [Google Scholar]
- 82.Baldaug J, Iwai M. Neogene diatom biostratigraphy for the eastern equatorial Pacific Ocean, Leg 138. Proc Ocean Drill Program Sci Results. 1995;138:105–128. [Google Scholar]
- 83.Gurvich E, Levitan M, Kuzmina T. Chemical composition of Leg 138 sediments and history of hydrothermal activity. Proc Ocean Drill Program Sci Results. 1995;138:769–778. [Google Scholar]
- 84.Mann S, Sparks N, Blakermore R. Structure, morphology, and crystal growth of anisotropic crystals in magnetotactic bacteria. Proc R Soc Lond B Biol Sci. 1987;231:477–487. [Google Scholar]
- 85.Arató B, et al. Crystal-size and shape distributions of magnetite from uncultured magnetotactic bacteria as a potential biomarker. Am Mineral. 2005;90(8-9):1233–1241. [Google Scholar]
- 86.Chen A, Egli R, Moskowitz B. First-order reversal curve (FORC) diagrams of natural and cultured biogenic magnetic particles. J Geophys Res. 2007;112(B8):B08S90. [Google Scholar]
- 87.Vali H, Förster O, Amarantidis G, Petersen N. Magnetotactic bacteria and their magnetofossils in sediments. Earth Planet Sci Lett. 1987;86(2-4):389–400. [Google Scholar]
- 88.Hejda P, Zelinka T. Modelling of hysteresis processes in magnetic rock samples using the Preisach diagram. Phys Earth Planet Inter. 1990;63(1-2):32–40. [Google Scholar]
- 89.Pike C, Fernandez A. An investigation of magnetic reversal in submicron-scale Co dots using first order reversal curve diagrams. J Appl Phys. 1999;85(9):6668–6676. [Google Scholar]
- 90.Mayergoyz ID. Mathematical models of hysteresis. Phys Rev Lett. 1986;56(15):1518–1521. doi: 10.1103/PhysRevLett.56.1518. [DOI] [PubMed] [Google Scholar]
- 91.Preisach F. Über die magnetische Nachwirkung. Z Phys. 1935;94(5):277–302. German. [Google Scholar]
- 92.Néel L. Sur les effets d’un couplage entre grains ferromagnétiques doués d’hystérésis. Acad Sci Seance. 1958;24(4):2313–2319. French. [Google Scholar]
- 93.Roberts A, Pike C, Verosub K. First-order reversal curve diagrams: A new tool for characterizing the magnetic properties of natural samples. J Geophys Res. 2000;105(B12):28461–28475. [Google Scholar]
- 94.Roberts A, et al. Characterization of hematite (alpha-Fe2O3), geothite (alpha-FeOOH), greigite (Fe3S4), and pyrrhotite (Fe7S8) using first-order reversal curve diagrams. J Geophys Res. 2006;111(B12):B12S35. [Google Scholar]
- 95.Muxworthy A, Williams W. Magnetostatic interaction fields in first-order-reversal-curve diagrams. J Appl Phys. 2005;97(6):063905. [Google Scholar]
- 96.Newell A. A high-precision model of first-order reversal curve (FORC) functions for single-domain ferromagnets with uniaxial anisotropy. Geochem Geophys Geosyst. 2005;6(5):Q05010. [Google Scholar]
- 97.Egli R. VARIFORC: An optimized protocol for the calculating non-regular first-order reversal curves (FORC) diagrams. Global Planet Change. 2013;110(Part C):302–320. [Google Scholar]
- 98.Heslop D, et al. Quantifying magnetite magnetofossil contributions to sedimentary magnetizations. Earth Planet Sci Lett. 2013;382:58–65. [Google Scholar]
- 99.Heslop D, Roberts A, Chang L. Characterizing magnetofossils from first-order reversal curve (FORC) central ridge signatures. Geochem Geophys Geosyst. 2014;15(6):2170–2179. [Google Scholar]
- 100.Kobayashi A, et al. Experimental observation of magnetosome chain collapse in magnetotactic bacteria: Sedimentological, paleomagnetic, and evolutionary implications. Earth Planet Sci Lett. 2006;245:538–550. [Google Scholar]
- 101.Straub S, Schmincke H. Evaluating the tephra input into Pacific Ocean sediments: Distribution in space and time. Geol Rundsch. 1998;87(3):461–476. [Google Scholar]
- 102.Fu Y, Von Dobeneck T, Franke C, Heslop D, Kasten S. Rock magnetic identification and geochemical process models of greigite formation in Quaternary marine sediments from the Gulf of Mexico, (IODP Hole U1319A) Earth Planet Sci Lett. 2008;275:233–245. [Google Scholar]
- 103.Pisias N, Mayer L, Mix A. Paleoceanography of the eastern equatorial Pacific during the Neogene: synthesis of Leg 138 drilling results. Proc Ocean Drill Program Sci Results. 1995;138:5–21. [Google Scholar]
- 104.Merchel S, Herpers U. An update on radiochemical separation techniques for the determination of long-lived radionuclides via accelerator mass spectrometry. Radiochim Acta. 1999;84(4):215–219. [Google Scholar]
- 105.Schubert M. 2007. Radioaktive implantate für medizinische anwendungen. PhD thesis (Ludwig-Maximilians-Universität, Munich)
- 106.Middleton R. A versatile high intensity negative ion source. Nucl Instrum Methods Phys Res. 1983;214(2-3):139–150. [Google Scholar]
- 107.Urban A. 1986. Beschleunigermassenspektrometrie mit 41Ca. Diploma thesis (Tech Univ München, Munich)
- 108.Feldmann G, Cousins R. A unified approach to the classical statistical analysis of small signals. Phys Rev D Part Fields. 1998;57(7):3873–3889. [Google Scholar]
- 109.Bourlès D, Raisbeck G, Yiou F. 10Be and 9Be in marine sediments and their potential for dating. Geochim Cosmochim Acta. 1989;53(2):443–452. [Google Scholar]
- 110.Feige J, et al. 2013. AMS measurements of cosmogenic and supernova-ejected radionuclides in deep-sea sediment cores. arXiv.1311.3481.
- 111.Akhmadaliev S, Heller R, Hanf D, Rugel G, Merchel S. The new 6 MV AMS-facility DREAMS at Dresden. Nucl Instrum Methods Phys Res B. 2013;294:5–10. [Google Scholar]