A New Flexible Dependence Measure for Semi-competing Risks

Summary

Semi-competing risks data are often encountered in chronic disease follow-up studies that record both nonterminal events (eg. disease landmark events) and terminal events (eg. death). Studying the relationship between the nonterminal event and the terminal event can provide insightful information on disease progression. In this paper, we propose a new sensible dependence measure tailored to addressing such an interest. We develop a nonparametric estimator, which is general enough to handle both independent right censoring and left truncation. Our strategy of connecting the new dependence measure with quantile regression enables a natural extension to adjust for covariates with minor additional assumptions imposed. We establish the asymptotic properties of the proposed estimators and develop inferences accordingly. Simulation studies suggest good finite-sample performance of the proposed methods. Our proposals are illustrated via an application to Denmark diabetes registry data.

1. Introduction

In chronic disease follow-up studies, in addition to a terminal survival outcome of primary interest, nonterminal disease landmark events are often recorded to provide extra information on disease progression. This naturally postulates a semi-competing risks setting (Fine et al., 2001), where time to a nonterminal event (T₁) can be censored by time to a terminal event (T₂) but not vice versa. The underlying disease mechanism often implicates the dependence between the nonterminal event and the terminal event. While considerably complicating the inference on T₁, such a dependency itself can offer valuable insight on disease prognosis and thus poses an important problem to study.

Statistical methods tailored to semi-competing risks data have been developed in settings without covariates (Fine et al., 2001; Wang, 2003; Peng and Fine, 2006b; Lakhal et al., 2008, among others) and with covariates (Lin et al., 1996; Peng and Fine, 2006a; Ghosh, 2006; Peng and Fine, 2007; Hsieh et al., 2008; Chen, 2012; Li and Peng, 2015, among others). In most of existing work, the dependence between the nonterminal event and the terminal event is captured by a copula model assumed for the joint distribution of (T₁, T₂). For example, without considering covariates, Fine et al. (2001) derived a closed-form estimator for the constant cross-ratio measure under the Clayton copula model (Clayton, 1978). Wang (2003) and Lakhal et al. (2008) studied the estimation of the association parameter for the general class of Archimedean copulas. With regression models assumed for T₁ and T₂, Hsieh et al. (2008) developed an estimator for the Archimedean copula parameter when covariates are discrete. More recently, Chen (2012) studied a nonparametric maximum likelihood approach under a general specification of the copula model.

While modeling the dependence structure between T₁ and T₂ based on a copula model is intuitive and useful, such an approach can impose some implicit limitations that may often be ignored. For example, under the Clayton's copula model, the cross ratio function (Oakes, 1989) is confined to be constant over time. Peng and Fine (2007) investigated a time-dependent copula model, which allows for a time-varying association structure between T₁ and T₂. Their empirical results evidenced that a constant association between T₁ and T₂ can be inadequate in practical settings. When this occurs, a numerical example provided in Web Appendix B shows that the classical copula modeling approach assuming a constant associate parameter can lead to misleading conclusions. In addition, the interpretation of a copula parameter, constant or time-dependent, relies on the selection of the copula function. When there are covariates involved, a copula based approach is further prone to issues due to potential misspecifications of the marginal regression models for T₁ and T₂.

In this work, we propose an alternative perspective for characterizing the relation between the nonterminal event and the terminal event. The new perspective enables the accommodation of time-varying dependence without involving strong model assumptions. Our proposals are built upon a comparison of the quantile residual time to the terminal event with the occurrence of the nonterminal event versus that without the occurrence of the nonterminal event. The basic idea bears a similar flavor to that of the cross-ratio function(Oakes, 1989), which compares the hazards of the terminal event regarding the timing of the nonterminal event. In contrast to a hazard function, a quantile residual time can offer straightforward physical interpretations and usually does not require smoothing for nonparametric estimation. Quantile residual lifetime has been investigated mostly in univariate survival settings (Gelfand and Kottas, 2003; Jeong et al., 2008; Jung et al., 2009; Ma and Yin, 2010, for example); but its utility as a device to study the dependence between semi-competing risks has not been exploited.

The rest of the paper is organized as follows. In Section 2, we first introduce a new dependence measure defined on quantile residual times, well tailored to the special structure of semi-competing risks. In Section 3. We fit the new measure into a quantile regression framework, and develop a simple nonparametric estimator, which can also account for left truncation, a common complication in observational studies. We present asymptotic studies of the proposed estimator as well as inference procedures. An extension to adjust for covariates is discussed in Section 4. We conduct extensive simulation studies to evaluate the performance of our proposal. The proposed method is illustrated by an application to a Denmark diabetic registry dataset. The numerical results are presented in Section 5, followed by a few concluding remarks in Section 6.

2. The Proposed Measure

Let Q_τ(Y|A) ≡ inf{t : Pr(Y ≤ t|A) ≥ τ} denote the τ-th quantile of Y given condition A holds. For the terminal event of interest, the quantile residual time at a given time point t₀ is defined as Q_τ(T₂ – t₀|T₂ > t₀).

Our basic idea is to compare the quantile residual time to the terminal event given the nonterminal event having occurred and that without the past occurrence of the nonterminal event. That is, we consider the cross quantile residual ratio (CQRR) defined as

$$\mathit{\text{CQRR}}(\tau ;t_0)=\frac{Q_{\tau }(T_2-t_0|T_2>t_0,T_1>t_0)}{Q_{\tau }(T_2-t_0|T_2>t_0,T_1\le t_0)},\tau \in (0,1),t_0>0.$$

It is clear that a larger CQRR(τ; t₀), which reflects a larger difference in Q_τ(T₂ – t₀|T₂ > t₀, T₁ > t₀) and Q_τ(T₂ – t₀|T₂ > t₀, T₁ ≤ t₀), indicates a larger impact of having T₁ > t₀ (versus T₁ ≤ t₀) on the subsequent progression of T₂. Note that CQRR(τ; t₀) bears some similarity with the cross-ratio function in the semi-competing risks setting,

$$\frac{\lambda (t_2|T_1=t_1)}{\lambda (t_2|T_1>t_1)},t_1\le t_2,$$

where $\lambda (t_2|·)=\frac{d}{d\epsilon }P(T_2<t_2+\epsilon |T_2\ge t_2,·){|}_{\epsilon =0}$. Both of them assess the difference in the terminal event progression according to the timing of the nonterminating event. The distinction lies in that the cross-ratio function uses hazard functions to evaluate the progression of the terminating event, while the proposed CQRR(τ,; t₀) adopts quantile residual time, which can be directly interpreted in the time scale. Like the cross-ratio function defined above, CQRR(τ; t₀) only concerns the joint distribution of (T₁, T₂) at the upper wedge (i.e. T₁ ≤ T₂) and hence is nonparametrically identifiable with semi-competing risks data.

We further take a log transformation on CQRR(τ; t₀). Our proposed measure for the dependence of semi-competing risks events is given by

$$\mathit{\text{LCQRR}}(\tau ;t_0)=log\left\{\frac{Q_{\tau }(T_2-t_0|T_2>t_0,T_1>t_0)}{Q_{\tau }(T_2-t_0|T_2>t_0,T_1\le t_0)}\right\},\tau \in (0,1),t_0>0.$$

It is easy to interpret LCQRR(τ; t₀). For example, LCQRR(τ; t₀) > 0 (< 0) suggests that the nonterminating event occurring before t0 may be associated with a faster (or slower) progression to subsequent terminating event. The larger the magnitude of LCQRR(τ; t₀), the bigger the impact of having T₁ ≤ t₀ on the residual lifetime for T₂. When T₁ and T₂ are independent, LCQRR(τ; t₀) = 0 for any τ ∈ (0, 1) and t₀ > 0. Examining LCQRR(τ; t₀) with different t₀'s may help understand how the dependence between the nonterminal event and the terminal event evolves time. One may also vary the value of τ to evaluate the influence of T₁ on multiple segments of the residual time distribution of T₂.

To use LCQRR(τ; t₀) in practice, we recommend specifying τ and t₀ beforehand according to scientific interests. For example, t₀ may be chosen as time points that landmark the development of the nonterminal event. Some common choices of τ are τ = 0.25, 0.5 and 0.75, which can be used to reflect below average, average, and above average progression to the terminating event. In addition to assigning discrete values to τ and t₀, one can also evaluate LCQRR(τ; t₀) over a prespecified τ-interval or t₀-interval. Doing so would permit assessing the changing pattern of the semi-competing risks dependence structure, which may shed useful scientific insight but cannot be accommodated by many traditional methods

3. The Proposed Estimation and Inference Procedures

3.1 Data and notation

We begin with a formal introduction of data and notation. Let T₁ denote time to nonterminal event, T₂ denote time to terminal event, and C denote time to censoring, which is independent of (T₁, T₂). Without considering left truncation, the observed semi-competing risks data are X = T₁ ∧ T₂ ∧ C, Y = T₂ ∧ C, δ = I(T₁ < Y) and η = I(T₂ < C), where ∧ is the minimum operator.

With truncation, the observed data consist of n independent and identically distributed replicates of (X*, Y*, δ*, η*, L*), denoted by ${(X_i^{\ast },Y_i^{\ast },{\delta }_i^{\ast },{\eta }_i^{\ast },L_i^{\ast })}_{i=1}^n$, where (X*, Y*, δ*, η*, L*) follows the conditional distribution of (X, Y, δ, η, L) given Y > L. We restrict L to be always less than C, meaning that censoring only occurs after sampling time. Such assumption has been imposed in much previous work, for example, Wang (1991), Asgharian et al. (2002) and Li and Peng (2011). In addition, we assume that L is independent of (T₁, T₂) and D = C – L.

To simplify the presentation hereafter, we define additional notation, A*(t₀) = (1, I(X* > t₀))^T, ${\stackrel{\sim }{\mathit{A}}}^{\ast }(t_0)={(1,I(T_1^{\ast }>t_0))}^T$, A(t₀) = (1, I(X > t₀))^T and Ã(t₀) = (1, I(T₁ > t₀))^T. For a vector ν, we use ν^(l) to denote the lth component of ν.

3.2 The proposed estimator

We first study the standard semi-competing risks setting without left truncation. To estimate LCQRR(τ; t₀), we consider a working quantile residual lifetime regression model, which takes the form,

$$Q_{\tau }(T_2-t_0|T_2>t_0,I(T_1>t_0))=exp\{\stackrel{\sim }{\mathit{A}}{(t_0)}^T{\mathit{\beta }}_0(\tau ,t_0)\},$$ (1)

where β₀(τ, t₀) is a 2 × 1 vector of unknown coefficients. In model (1), I(T₁ > t₀) serves as the only covariate, which is binary. Consequently, model (1) essentially does not impose any parametric assumptions. The coefficients, ${\mathit{\beta }}_0^{(1)}(\tau ,t_0)$ and ${\mathit{\beta }}_0^{(2)}(\tau ,t_0)$, correspond to log Q_τ(T₂ – t₀|T₂ > t₀, T₁ ≤ t₀) and log Q_τ(T₂ – t₀|T₂ > t₀, T₁ > t₀) – log Q_τ(T₂ – t₀|T₂ > t₀, T₁ ≤ t₀) respectively. This indicates the equivalence between LCQRR(τ; t₀) and ${\mathit{\beta }}_0^{(2)}(\tau ,t_0)$. Therefore, estimating ${\mathit{\beta }}_0^{(2)}(\tau ,t_0)$ in the quantile regression framework leads to an estimator of LCQRR(τ; t₀).

A main challenge with fitting model (1) is that the covariate I(T₁ > t₀) is not always observed because T₁ is subject to censoring by both T₂ and C. Suppose there is no independent censoring by C, and then T₂ is fully observed. In this case, we see that I(T₁ > t₀) is observed and equals I(X > t₀) as long as Y > t₀. This suggests estimating β₀(τ, t₀) by a stratified quantile regression analysis, which solves the following estimating equation for b ∈ R²:

$$n^{-1/2}\sum _{i=1}^{n}I(Y_i>t_0)\mathit{A}(t_0)\{I[log(Y_i-t_0)\le \mathit{A}{(t_0)}^T\mathit{b}]-\tau \}=\mathbf{0}.$$ (2)

When T₂ is subject to independent censoring by C, we still have I(T₁ > t₀) = I(X > t₀) given Y > t₀. This nice feature allows us to adapt existing methods for quantile residual lifetime model to handle the effect of censoring. Specifically, we can use a stratified version of Ma and Yin (2010)'s estimating equation, which takes the form,

$$n^{-1/2}\sum _{i=1}^n\frac{I(Y_i>t_0){\eta }_i}{{\widehat{G}}_c(Y_i)}{\mathit{A}}_i(t_0)\{I[log(Y_i-t_0)\le {\mathit{A}}_i^T(t_0)\mathit{b}]-\tau \}=\mathbf{0},$$

where Ĝ_c(·) is the Kaplan-Meier estimate of the survival function of C.

When left truncation is present, we need to further modify the estimating equation (2) because I(T₁ > t₀) may be missing and if observed, may not be randomly sampled. Our strategy is to weigh the observed data in an appropriate way such that the bias induced by truncation and censoring is corrected in the estimation of β₀(τ, t₀). Let D* = C* – L*. It is critical to note that under the independence between D and (T₁, T₂, L), the distributions of D and D* are equivalent, and D* is also independent of $(T_1^{\ast },T_2^{\ast },L^{\ast })$. This fact greatly facilitates the application of the inverse probability of censoring weighting (IPCW) in the present problem with truncated data. As elaborated in Web Appendix A, we show that $G(Y_i^{\ast }-L_i^{\ast })$ can serve as an appropriate weight, where G(t) = Pr(D > t). More specifically, we prove that $E\{\frac{I(L^{\ast }\le t_0)I(Y^{\ast }>t_0){\eta }^{\ast }}{G(Y^{\ast }-L^{\ast })}{\mathit{A}}^{\ast }(t_0)\{I[log(Y^{\ast }-t_0)\le {\mathit{A}}^{\ast T}(t_0){\mathit{\beta }}_0(\tau ,t_0)]-\tau \}\}=0$.

We propose to estimate β₀(τ, t₀) by solving the following estimating equation for b:

$${\mathit{S}}_n(\mathit{b},\tau ,t_0)=\mathbf{0},$$ (3)

Where

$${\mathit{S}}_n(\mathit{b},\tau ,t_0)=n^{-1/2}\sum _{i=1}^n\frac{I(L_i^{\ast }\le t_0)I(Y_i^{\ast }>t_0){\eta }_i^{\ast }}{\widehat{G}(Y_i^{\ast }-L_i^{\ast })}{\mathit{A}}_i^{\ast }(t_0)\{I[log(Y_i^{\ast }-t_0)\le {\mathit{A}}_i^{\ast T}(t_0)\mathit{b}]-\tau \}.$$

The resulting estimator is denoted by β̂(τ, t₀). Here Ĝ(t) is the Kaplan-Meier estimator of G(t) obtained from ${(Y_i^{\ast }-L_i^{\ast },1-{\eta }_i^{\ast })}_{i=1}^n$,

$$\widehat{G}(t)=\prod _{Y_i^{\ast }-L_i^{\ast }\le t}\{1-\frac{{\sum }_{j=1}^{n}I(Y_j^{\ast }-L_j^{\ast }=Y_i^{\ast }-L_i^{\ast },{\eta }_j^{\ast }=0)}{{\sum }_{j=1}^{n}I(Y_i^{\ast }-L_i^{\ast }\le Y_j^{\ast }-L_j^{\ast })}\}.$$

Equation (3) can be easily solved given that it is a monotone estimating equation (Fygenson and Ritov, 1994). Specifically, following similar lines of Peng and Fine (2009), we can transform the solution finding to equation (3) to locating the minimizer of the convex function U_n(b, τ, t₀) given by

$$U_n(\mathit{b},\tau ,t_0)=\sum _{i=1}^{n}I(L_i^{\ast }\le t_0)I(Y_i^{\ast }>t_0){\eta }_i^{\ast }|\frac{log(Y_i^{\ast }-t_0)}{\widehat{G}(Y_i^{\ast }-L_i^{\ast })}-{\mathit{b}}^T\frac{{\mathit{A}}_i^{\ast }(t_0)}{\widehat{G}(Y_i^{\ast }-L_i^{\ast })}|+|M-(2\tau -1){\mathit{b}}^T\sum _{i=1}^{n}I(L_i^{\ast }\le t_0)I(Y_i^{\ast }>t_0){\eta }_i^{\ast }\frac{{\mathit{A}}_i^{\ast }(t_0)}{\widehat{G}(Y_i^{\ast }-L_i^{\ast })}|$$

where M is a sufficiently large positive number that can bound $|(2\tau -1){\mathit{b}}^T{\sum }_{i=1}^{n}I(L_i^{\ast }\le t_0)I(Y_i^{\ast }>t_0){\eta }_i^{\ast }\frac{{\mathit{A}}_i^{\ast }(t_0)}{\widehat{G}(Y_i^{\ast }-L_i^{\ast })}|$. Minimization of the L₁-type function U_n(b, τ, t₀) can be solved by using standard software, like the rq() function in the contributed R package quantreg.

3.3 Asymptotic results

Given that the proposed estimator of LCQRR(τ; t₀) is the second element of β̂(τ, t₀), it suffices to derive the asymptotic properties of β̂(τ, t₀).

We assume the following regularity conditions:

• C1. There exists ν > 0 such that P(D = ν) > 0 and P(D > ν) = 0.

• C2. (i) 0 < τ_L ≤ τ_U ≤ 1; (ii) t_L and t_U are interior points of the support of X*.

• C3. (i) β₀(τ, t₀) is Lipschitz continuous for τ ∈ [τ_L, τ_U] and t₀ ∈ [t_L, t_U]; (ii) f(t|Ã(t₀)) is continuous and bounded above uniformly in t, t₀ and Ã(t₀), where f(t|Ã(t₀)) = dF(t|Ã(t₀))/dt and F(t|Ã(t₀)) = E{I(T₂ ≤ t)|Ã(t₀)}.

• C4. For some ρ₀ > 0 and c₀ > 0, inf_{b∈B(ρ0),t0∈[tL,tU]} eigminH(b, t₀) ≥ c₀, where B(ρ) = {b ∈ R² : inf_{τ∈[τL, τU],t0∈[tL, tU]} ‖b – β₀(τ, t₀) ≤ ρ}‖ and H(b, t₀) = E[c(t₀)Ã(t₀)^⊗2 f(t₀ + exp(Ã^T(t₀)b)|Ã^T(t₀))exp(Ã^T(t₀)b)]. Here ‖ · ‖ is the Euclidean norm and u^⊗2 = uu^T for a vector u.

Define $N_i^G(t)=I(Y_i^{\ast }-L_i^{\ast }\le t,{\eta }_i^{\ast }=0)$, $Y_i(t)=I(Y_i^{\ast }-L_i^{\ast }\ge t)$, y(t) = P(Y* – L* ≥ t), λ^G(t) = lim_Δ→0P(Y* – L* ∈ (t, t + Δ)|Y* – L* ≥ t)/Δ, ${\mathrm{\Lambda }}^G(t)={\int }_0^t{\lambda }^G(s)\mathit{\text{ds}}$, and $M_i^G(t)=N_i^G(t)-{\int }_0^{\infty }{Y}_i(s)d{\mathrm{\Lambda }}^G(s)$. Let w(b, τ, t₀, t) = E{A*(t₀)Y(t)I(L* ≤ t₀)I(Y* > t₀)η*{I[log(Y* – t₀) ≤ A*^T(t₀)b] – τ}G(Y* – L*)⁻¹}, ζ_i(τ, t₀) = ξ_1,i(τ, t₀) – ξ_2,i(τ, t₀), where ${\mathit{\xi }}_{1,i}(\tau ,t_0)=I(L_i^{\ast }\le t_0)I(Y_i^{\ast }\le t_0){\eta }_i^{\ast }{\mathit{A}}_i^{\ast }(t_0)\{I[log(Y_i^{\ast }-t_0)\le {\mathit{A}}_i^{\ast T}(t_0){\mathit{\beta }}_0(\tau ,t_0)]-\tau \}G{(Y_i^{\ast }-L_i^{\ast })}^{-1}$ and ${\mathit{\xi }}_{2,i}(\tau ,t_0)={\int }_0^{\infty }\mathit{w}({\mathit{\beta }}_0(\tau ,t_0),\tau ,t_0,s)\frac{d{M}_i^G(s)}{y(s)}$, i = 1, …, n.

We have following theorems:

Theorem 3.1: Under conditions C1–C4,

$$\underset{n\to \infty }{lim}\underset{\tau \in [{\tau }_L,{\tau }_U],t_0\in [t_L,t_U]}{sup}\Vert \widehat{\mathit{\beta }}(\tau ,{\tau }_0)-{\mathit{\beta }}_0(\tau ,{\tau }_0)\Vert {\to }_{p}0.$$

Theorem 3.2: Under conditions C1–C4, √n{β̂(τ, t₀) – β₀(τ, t₀)} weakly converge to a mean zero Gaussian process G(τ, t₀) with covariance matrix $E\{\mathit{G}({\tau }^{\prime },t_0^{\prime })\mathit{G}{(\tau ,t_0)}^T\}$ given by

$$\mathbf{\Phi }({\tau }^{\prime },t_0^{\prime },\tau ,t_0)=\mathit{H}{\{{\mathit{\beta }}_0({\tau }^{\prime },t_0^{\prime }),t_0^{\prime }\}}^{-1}E\{{\mathit{\zeta }}_{\mathbf{1}}({\tau }^{\prime },t_0^{\prime }){\mathit{\zeta }}_{\mathbf{1}}{(\tau ,t_0)}^T\}{[\mathit{H}{\{{\mathit{\beta }}_0(\tau ,t_0),t_0\}}^{-1}]}^T,$$

where τ, τ′ ∈ [τ_L, τ_U] and $t_0,t_0^{\prime }\in [t_L,t_U]$.

Theorem 3.1 implies that the proposed estimator of LCQRR(τ; t₀) is uniformly consistent in τ ∈ [τ_L, τ_U] and t₀ ∈ [t_L, t_U]. Theorem 3.2 presents a closed form expression for the asymptotic distribution of the proposed estimator of LCQRR(τ; t₀). Detailed proofs of Theorem 3.1 and 3.2 are provided in Web Appendix A.

3.4 Inference procedures

The asymptotic covariance matrix of √n{β̂(τ, t₀) – β₀(τ, t₀)} involves unknown density functions. It is straightforward to use bootstrapping procedures or adapt resampling approaches, such as Parzen, Wei, and Ying (1994) and Jin, Ying, and Wei (2001), to estimate the asymptotic covariance without requiring density estimation. Alternatively, we can also derive a consistent plug-in estimate for the covariance matrix following the lines of Peng and Fine (2009). The specific procedure follows.

1. Calculate $\widehat{\sum }(\tau ,t_0,\tau ,t_0)=n^{-1}{\sum }_{i=1}^n{\widehat{\mathit{\zeta }}}_i{(\tau ,t_0)}^{\otimes 2}$, where

   $$\begin{array}{c}{\widehat{\mathit{\zeta }}}_i(\tau ,t_0)=\frac{I(L_i^{\ast }\le t_0,Y_i^{\ast }>t_0){\eta }_i^{\ast }}{\widehat{G}(Y_i^{\ast }-L_i^{\ast })}{\mathit{A}}_i^{\ast }(t_0)\{I[log(Y_i^{\ast }-t_0)\le {\mathit{A}}_i^{\ast T}(t_0)\widehat{\mathit{\beta }}(\tau ,t_0)]-\tau \}\\ -I({\eta }_i^{\ast }=0)(\sum _{j=1}^n{\mathit{A}}_i^{\ast }(t_0)I(Y_j^{\ast }-L_j^{\ast }\ge Y_i^{\ast }-L_i^{\ast })I(L_j^{\ast }\le t_0,Y_j^{\ast }>t_0){\eta }_j^{\ast }\times \{I[log(Y_j^{\ast }-t_0)\le {\mathit{A}}_j^{\ast T}(t_0)\widehat{\mathit{\beta }}(\tau ,t_0)]-\tau \}{\{\widehat{G}(Y_j^{\ast }-L_j^{\ast })\}}^{-1}/\sum _{j=1}^{n}I(Y_j^{\ast }-L_j^{\ast }\ge Y_i^{\ast }-L_i^{\ast }).\end{array}$$

2. Use spectral decomposition to find a symmetric matrix E_n(τ, t₀) such that $\widehat{\sum }(\tau ,t_0,\tau ,t_0)={\mathit{E}}_n^2(\tau ,t_0)$.

3. Calculate ${\mathit{D}}_n(\tau ,t_0)=[{\mathit{S}}_n^{-1}\{{\mathit{e}}_{n,1}(\tau ,t_0),\tau ,t_0\}-\widehat{\mathit{\beta }}(\tau ,t_0),{\mathit{S}}_n^{-1}\{{\mathit{e}}_{n,2}(\tau ,t_0),\tau ,t_0\}-\widehat{\mathit{\beta }}(\tau ,t_0)]$, where e_n,j is the jth column of E_n(τ, t₀), and ${\mathit{S}}_n^{-1}(\mathit{e},\tau ,t_0)$ is defined as the solution to S_n(b, τ, t₀) – e = 0.

4. A consistent estimate for the asymptotic covariance matrix of √n{β̂(τ, t₀) – β₀(τ, t₀)}is given by

   $$n{\mathit{D}}_n({\tau }^{\prime },t_0^{\prime }){\mathit{E}}_n^{-1}({\tau }^{\prime },t_0^{\prime })\widehat{\sum }({\tau }^{\prime },t_0^{\prime },\tau ,t_0){\mathit{E}}_n^{-1}(\tau ,t_0){\mathit{D}}_n^T(\tau ,t_0).$$

In the special case that τ′ = τ and $t_0^{\prime }=t_0$, a consistent estimate for the asymptotic variance matrix is simplified as $n\{{\mathit{D}}_n^{\otimes 2}(\tau ,t_0)\}$.

We can also develop second-stage inferences following the lines of Li and Peng (2011). For example, we can summarize LCQRR(τ; t₀) over t₀ ∈ [t_L, t_U] by ${\mathrm{\Omega }}_{\tau }=\frac{1}{t_U-t_L}{\int }_{t_L}^{t_U}{\mathit{\beta }}_0^{(2)}(\tau ,t_0)d{t}_0$, which may be consistently estimated by ${\widehat{\mathrm{\Omega }}}_{\tau }=\frac{1}{t_U-t_L}{\int }_{t_L}^{t_U}{\widehat{\mathit{\beta }}}_0^{(2)}(\tau ,t_0)d{t}_0$. We can show that the limiting distribution of √n(Ω̂_τ – Ω_τ) is a mean zero normal distribution, the variance of which may be consistently estimated by $n{\widehat{\sigma }}_{{\mathrm{\Omega }}_{\tau }}^2$, where ${\widehat{\sigma }}_{{\mathrm{\Omega }}_{\tau }}^2$ equals the (2,2) element of $\frac{1}{n^2}{\sum }_{i=1}^n{\{\frac{1}{t_U-t_L}{\int }_{t_L}^{t_U}\sqrt{n}{\mathit{D}}_n(\tau ,t_0){\mathit{E}}_n^{-1}(\tau ,t_0){\widehat{\mathit{\zeta }}}_i(\tau ,t_0)d{t}_0\}}^{\otimes 2}$. This result naturally renders a Wald-type test, T_Ωτ = Ω̂_τ/σ̂_Ωτ, for the null hypothesis H₀₁ : LCQRR(τ; t₀) = 0, t₀ ∈ [t_L, t_U]. That is, we reject H₀₁ when |T_Ωτ| > 100(1 – α/2)th percentile of N(0, 1) distribution, where α is the desired significance level. Similar results can be obtained for the overall summary and testing of LCQRR(τ; t₀) over τ ∈ [τ_L, τ_U], corresponding to ${\mathrm{\Omega }}_{t_0}=\frac{1}{{\tau }_U-{\tau }_L}{\int }_{{\tau }_L}^{{\tau }_U}{\mathit{\beta }}_0^{(2)}(\tau ,t_0)d\tau$, and H₀₃ : LCQRR(τ; t₀) = 0, τ ∈ [τ_L, τ_U] respectively.

We can also test the constancy of LCQRR(τ; t₀) over t₀ or τ. For example, a null hypothesis of interest may take the form, H₀₂ : LCQRR(τ; t₀) = C_τ, t₀ ∈ [t_L, t_U], where C_τ is an unspecified constant and may change with τ. Let Ξ(τ, t₀) denote a known weight function satisfying Ξ(τ, t₀) ≥ 0 and ${\int }_{t_L}^{t_U}\mathrm{\Xi }(\tau ,t_0)d{t}_0=1$. If H₀₂ holds, then ${\int }_{t_L}^{t_U}\mathrm{\Xi }(\tau ,t_0){\mathit{\beta }}_0^{(2)}(\tau ,t_0)d{t}_0-{\mathrm{\Omega }}_{\tau }=[{\int }_{t_L}^{t_U}\mathrm{\Xi }(\tau ,t_0)d{t}_0-1]C_{\tau }=0$. This motivates us to construct a test statistic for H₀₂ based on ${\mathrm{\Gamma }}_{\tau }=\sqrt{n}\{{\int }_{t_L}^{t_U}\mathrm{\Xi }(\tau ,t_0){\widehat{\mathit{\beta }}}^{(2)}(\tau ,t_0)d{t}_0-{\widehat{\mathrm{\Omega }}}_{\tau }\}$. Following the same line for proving Theorem 3.2, we can show that the limiting distribution of Γ_τ under H₀₂ is normal with mean 0. A consistent variance estimate for Γ_τ may be given by ${\widehat{\sigma }}_{{\mathrm{\Gamma }}_{\tau }}^2$, which is the (2,2) element of $n^{-1}{\sum }_{i=1}^n{[{\int }_{t_L}^{t_U}\{\mathrm{\Xi }(\tau ,t_0)-\frac{1}{t_U-t_L}\}\sqrt{n}{\mathit{D}}_n(\tau ,t_0){\mathit{E}}_n^{-1}(\tau ,t_0){\widehat{\mathit{\zeta }}}_i(\tau ,t_0)d{t}_0]}^{\otimes 2}$. A Wald-type test for H₀₂ is then given by T_Γτ = Γ_τ/σ̂_Γτ. A similar testing procedure can be developed for testing the constancy over t₀ ∈ [t_L, t_U], H₀₄ : LCQRR(τ; t₀) = C_t0, τ ∈ [τ_L, τ_U].

4. An Extension to Adjusting for Covariates

Exploiting population heterogeneity in semi-competing risks dependence is often scientifically meaningful, and for example, can help uncover uncommon disease mechanisms in subgroups. To this end, we propose an extension, which adjusts for covariates (captured by Z̃ ∈ R^p) in the assessment of the dependence between the nonterminal event and the terminal event.

First, we define the covariate-adjusted log cross quantile residual ratio as

$$\mathit{\text{LCQRR}}(\tau ,t_0|\stackrel{\sim }{\mathit{Z}})=log[\frac{Q_{\tau }(T_2-t_0|T_2>t_0,T_1>t_0,\stackrel{\sim }{\mathit{Z}})}{Q_{\tau }(T_2-t_0|T_2>t_0,T_1\le t_0,\stackrel{\sim }{\mathit{Z}})}].$$

When all covariates of interest are discrete, one may conduct stratified analyses based on the methods in Section 3 to estimate and make inference on LCQRR(τ; t₀|Z̃).

In many practical settings, covariates of interest can be continuous. Thus we investigate a general scenario where Z̃ can include both continuous and discrete covariates. Specifically, we are interested in formulating linear covariate effects on LCQRR, which may be expressed as

$$\mathit{\text{LCQRR}}(\tau ,t_0|\stackrel{\sim }{\mathit{Z}})={Ž}^T{\mathit{\alpha }}_0(\tau ,t_0),$$ (4)

where Ž = (1, Z̃^T)^T. The non-intercept coefficients in α₀(τ, t₀) depict how LCQRR changes per unit change in the corresponding covariate.

To address the interest in the linear effects of covariates on LCQRR, we consider the following quantile residual lifetime model:

$$Q_{\tau }(T_2-t_0|T_2>t_0,I(T_1>t_0),\stackrel{\sim }{\mathit{Z}})=exp\{{\mathit{Z}}^T(t_0){\mathit{\gamma }}_0(\tau ,t_0)\}\equiv exp[{\mathit{\gamma }}_0^{(1)}(\tau ,t_0)+I(T_1>t_0){\mathit{\gamma }}_0^{(2)}(\tau ,t_0)+{\stackrel{\sim }{\mathit{Z}}}^T{\mathit{\gamma }}_0^{3:(2+p)}(\tau ,t_0)+{\stackrel{\sim }{\mathit{Z}}}^{T}I(T_1>t_0){\mathit{\gamma }}_0^{(3+p):(2+2p)}(\tau ,t_0)],$$ (5)

where Z(t₀) = (1, I(T₁ > t₀), Z̃^T, Z̃^TI(T₁ > t₀))^T, and v^a:b denotes the vector that includes the ath to bth components of vector v. It is important to note that (5) implies

$$\mathit{\text{LCQRR}}(\tau ;t_0|\stackrel{\sim }{\mathit{Z}})={\mathit{\gamma }}_0^{(2)}(\tau ,t_0)+{\stackrel{\sim }{\mathit{Z}}}^T{\mathit{\gamma }}_0^{(3+p):(2+2p)}(\tau ,t_0).$$

When there are only discrete covariates, model (5) and model (4) can be equivalent. These suggest that under slightly stronger assumptions regarding the effects of continuous covariates, model (5) defines the same linear relationship between covariates and LCQRR as does model (4). Compared to model (4), model (5) is more convenient to tackle. This is because model (5) takes the same form as the working quantile residual lifetime model (1) considered for the one-sample case. As shown below, this fact greatly facilitates an extension to the general case with covariates. By these considerations, we adopt model (5) as the vehicle to explore the linear covariate effects on LCQRR.

Suppose the observed data include n i.i.d. replicates, ${(X_i^{\ast },Y_i^{\ast },{\delta }_i^{\ast },{\eta }_i^{\ast },L_i^{\ast },{\stackrel{\sim }{\mathit{Z}}}_i^{\ast })}_{i=1}^n$, where ${\stackrel{\sim }{\mathit{Z}}}_i^{\ast }$ is the truncated counterpart of Z̃_i following the conditional distribution of Z̃ given Y > L. We assume that D is independent of (T₁, T₂, L, Z̃) and L is independent of T₂ given (T₁, Z̃). Define ${\mathit{K}}^{\ast }(t_0)={(1,I(X_i^{\ast }>t_0),{\stackrel{\sim }{\mathit{Z}}}_i^{\ast T},{\stackrel{\sim }{\mathit{Z}}}_i^{\ast T}I(X_i^{\ast }>t_0))}^T$. Adapting the idea presented for the one-sample case, we propose to estimate γ₀(τ, t₀) by solving the following estimating equation for r ∈ R^2+2p:

$${\mathit{S}}_n(\mathit{r},\tau ,t_0)=\mathbf{0},$$

where

$${\mathit{S}}_n(\mathit{r},\tau ,t_0)=n^{-1/2}\sum _{i=1}^n\frac{I(L_i^{\ast }\le t_0)I(Y_i^{\ast }>t_0){\eta }_i^{\ast }}{\widehat{G}(Y_i^{\ast }-L_i^{\ast })}{\mathit{K}}_i^{\ast }(t_0)\{I[log(Y_i^{\ast }-t_0)\le {\mathit{K}}_i^{\ast T}(t_0)\mathit{r}]-\tau \}.$$

The resulting estimator is denoted by γ̂(τ, t₀). It is easy to see that the subvector, γ̂^(3+p):(2+2p)(τ, t₀), can be used to describe the linear effect of Z̃ on LCQRR. With an additional assumption that Z̃ is uniformly bounded (i.e. sup_i‖Z̃_i‖ ≤ M₁ < ∞), we can established the same asymptotic properties and inference procedures for γ̂(τ, t₀) as those presented in Section 3.

5. Numerical Studies

5.1 Simulations

Simulation studies are conducted to examine the finite-sample performance of the proposed methods in the left-truncated semi-competing risks setting. Specifically, we generate (T₁, T₂) from a gamma frailty model, in which

$$P(T_1>x,T_2>y)={[P{(T_1>x)}^{1-\theta }+P{(T_2>x)}^{1-\theta }-1]}^{1/(1-\theta )},$$

with T_i following a Weibull(α_i, λ_i) distribution and P(T_i > x) = exp(−λ_ix^αi), i = 1, 2. The truncation time L is generated from a mixture of a point mass at zero and a positive-valued random variable L̃. The proportion of zero truncation time is set as 20%.

The simulations are conducted under two scenarios,

Scenario 1: T₁ ∼ Weibull(1.4, 0.6), T₂ ∼ Weibull(3.5, 0.5), L̃ and D following uniform distributions.

Scenario 2: T₁ ∼ Weibull(3, 0.85), T₂ ∼ Weibull(3, 0.4), L̃ and D following Weibull distributions.

For Scenario 1, there is a low truncation level with P(Y < L) = 0.3, and a high dependent censoring rate with P(δ = 0, η = 1|L ≤ Y) close to 0.4. For Scenario 2, there is a high truncation level of 0.5 and a low dependent censoring rate around 0.15. In each scenario, we consider three different θ values, 1, 2 and 3, corresponding to independence, moderate positive association, and high positive association respectively. The detailed specifications of the marginal distributions of L̃ and D as well as censoring and truncation proportions are shown in Table 1.

Table 1.

Summary statistics for different simulation scenarios. All % are conditional on L ≤ Y.

θ	L̃	D	P(Y < L)	%(δ = 0)	%(η = 0)	%(δ = 0, η = 1)	%(X < L)
Scenario 1
1	Un(0,1.67)	Un(0.05,3.2)	30	52	21	39	20
2	Un(0,1.67)	Un(0.17,2.6)	30	59	22	42	15
3	Un(0,1.67)	Un(0.15,2.55)	30	63	23	44	13
Scenario 2
1	Wei(2.6,0.35)	Wei(1.1,0.38)	50	26	20	16	40
2	Wei(1.2,0.49)	Wei(1.3,0.3)	50	27	20	15	20
3	Wei(0.5,0.55)	Wei(1.5,0.22)	50	27	20	15	9

We perform the proposed methods on 1000 simulated datasets with sample size n = 200 or 400 for each simulation setup, where M is set as 10⁷. For Scenario 1, Figure 1 presents the empirical bias (EmpBias), empirical standard error (EmpSE) and average estimated standard error (EstSE) for the proposed estimator of LCQRR(τ; t₀) under different combinations of (θ, τ, t₀), where τ = 0.25, 0.5, 0.75, t₀ = 0.55, 0.84, 1.1 and circles denote corresponding values. It is observed that the proposed estimator of LCQRR(τ; t₀), performs well with moderate sample size. The point estimates have small biases. The corresponding standard error estimates agree well with empirical standard errors, and the agreement generally improves as sample size increases. We have very similar observations from Figure 1 in Web Appendix B, which presents the simulation results for Scenario 2.

Figure 1.

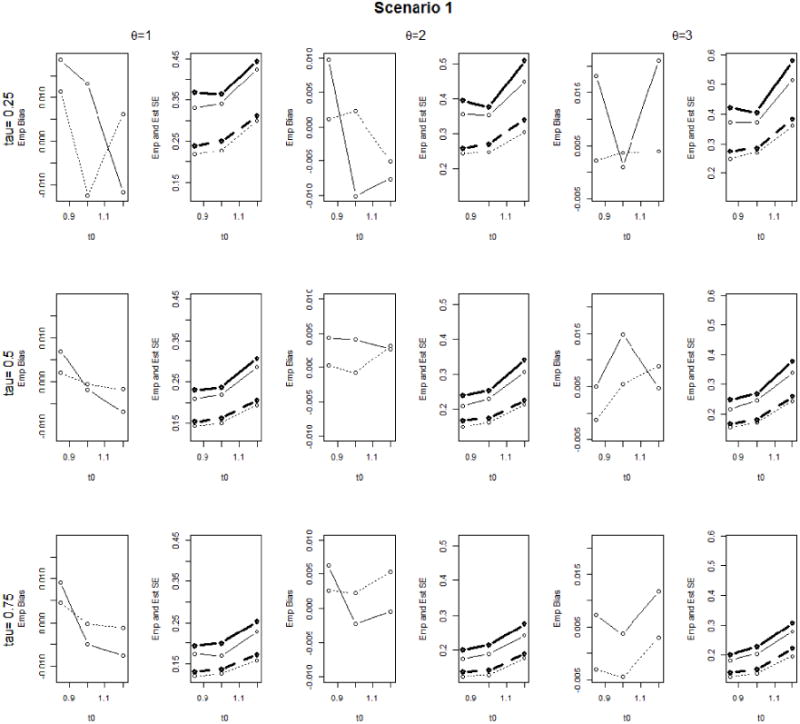
Simulation results for Scenario 1: Empirical bias (EmpBias), empirical standard error (EmpSE) and average estimated standard error (EstSE) of the proposed estimator of LCQRR. EmpBias for n = 200 and EmpBias for n = 400 are plotted in solid lines and dotted lines respectively. EmpSE and EstSE for n = 200 are plotted in solid lines and bold solid lines respectively. EmpSE and EstSE for n = 200 are plotted in dotted lines and bold dashed lines respectively.

We also examine the proposed second-stage inferences. With fixed τ, we evaluate the average of LCQRR over t ∈ [t_L, t_U], and test whether LCQRR(τ; t₀) equals 0 for t ∈ [t_L, t_U] and whether LCQRR(τ; t₀) is constant over t ∈ [t_L, t_U]. We consider three τ values, 0.25, 0.5, and 0.75. For Scenario 1, we set t_L = 0.42 and t_U = 1.20. For Scenario 2, we set t_L = 0.68 and t_U = 1.28. We compute integrals using left Riemann sums on intervals of equal length 0.001 and choose the weight function Ξ(τ, t₀) = 2I[t₀ ≤ (t_L + t_U)/2]/(t_U – t_L). In Table 2, we summarize the EmpBias, EmpSE and EstSE of Ω̂_τ, and the empirical rejection rates (EmpRR) for the proposed Wald tests for H₀₁ and H₀₂. Note that for both H₀₁ and H₀₂, the EmpRR gives empirical sizes when θ = 1 and empirical power when θ = 2, 3. Table 2 shows that for both scenarios, the empirical biases of Ω̂_τ are small and the estimated standard errors match the empirical standard errors very well. The test for either H₀₁ or H₀₂ appear to have empirical sizes close to the nominal levels. The power for testing H₀₁ is good, while the constancy tests appear to be conservative. The empirical power increases considerably as sample size and θ value increase for both tests.

Table 2. Empirical biases, empirical standard errors and average standard errors estimates of Ω̂_τ and empirical rejection rates for H₀₁ and H₀₂.

			Ω̂τ			H01	H02
θ	τ	n	EmpBias	EmpSE	EstSE	EmpRR	EmpRR
Scenario 1
t0 ∈ [0.42, 1.20]
1	0.25	200	0.008	0.181	0.191	0.041	0.051
		400	0.003	0.128	0.132	0.053	0.046
	0.50	200	0.006	0.153	0.160	0.056	0.043
		400	0.005	0.112	0.110	0.052	0.046
	0.75	200	0.008	0.143	0.149	0.065	0.037
		400	0.001	0.101	0.104	0.054	0.048
2	0.25	200	0.006	0.172	0.188	0.927	0.102
		400	0.003	0.119	0.127	1.000	0.149
	0.50	200	0.007	0.140	0.153	0.928	0.142
		400	0.003	0.102	0.107	0.995	0.215
	0.75	200	0.003	0.137	0.148	0.857	0.160
		400	0.005	0.099	0.104	0.988	0.234
3	0.25	200	0.014	0.166	0.182	0.999	0.118
		400	0.001	0.112	0.122	1.000	0.213
	0.50	200	0.011	0.143	0.149	0.999	0.184
		400	0.003	0.097	0.103	1.000	0.313
	0.75	200	0.010	0.143	0.147	0.981	0.200
		400	0.005	0.097	0.103	1.000	0.347
Scenario 2
t0 ∈ [0.68, 1.28]
1	0.25	200	-0.004	0.243	0.237	0.066	0.066
		400	0.001	0.168	0.164	0.053	0.059
	0.50	200	-0.004	0.193	0.198	0.065	0.049
		400	0.002	0.133	0.138	0.048	0.050
	0.75	200	-0.001	0.174	0.179	0.080	0.047
		400	0.003	0.119	0.127	0.056	0.039
2	0.25	200	0.003	0.172	0.176	0.984	0.117
		400	0.001	0.124	0.120	1.000	0.211
	0.50	200	-0.004	0.140	0.141	0.984	0.128
		400	-0.001	0.098	0.097	1.000	0.194
	0.75	200	-0.001	0.128	0.133	0.965	0.096
		400	0.000	0.087	0.093	1.000	0.144
3	0.25	200	-0.007	0.133	0.137	1.000	0.161
		400	0.002	0.087	0.093	1.000	0.259
	0.50	200	-0.002	0.113	0.116	1.000	0.125
		400	0.000	0.078	0.080	1.000	0.161
	0.75	200	0.000	0.108	0.117	1.000	0.100
		400	0.001	0.075	0.081	1.000	0.118

With fixed t₀, we assess the second-stage inferences over [τ_L, τ_U]. For Scenario 1, we consider t₀ = 0.55, 0.84, 1.10 and set [τ_L, τ_U] = [0.1, 0.87]. For Scenario 2, we consider t₀ = 0.85, 1.00, 1.20 and set [τ_L, τ_U] = [0.1, 0.9]. In both scenarios, Ξ(τ, t₀) = 2I[τ ≤ (τ_L + τ_U)/2]/(τ_U – τ_L). Table 1 in Web Appendix B presents the EmpBias, EmpSE and EstSE of Ω̂_t0 and the EmpRR for the proposed tests. Similarly, we observe small empirical biases, well-matched estimated and empirical standard errors, and pretty accurate empirical sizes. The power for the constancy tests is not high but increases as sample size increases.

5.2 Denmark Diabetes Registry Data Analysis

We apply the proposed method to a dataset from the Denmark diabetes registry study (Andersen et al., 1993). The Denmark diabetes registry study is a prospective cohort study on insulin-dependent diabetes patients referred to the Steno Memorial Hospital in Greater Copenhagen. Diabetic nephropathy (DN), an indicator of kidney failure, is a significant complication among patients with diabetes. From 1933 to 1981, 2727 patients who were diagnosed with insulin-dependent diabetes mellitus prior to age 31 and between 1933 and 1972 were accrued. At entry, patients' age at diabetes diagnosis and the presence of DN were recorded. All patients were then followed until death, emigration or December 31, 1984. In our analysis, the time origin is the age at diabetes diagnosis, with event times recorded in years since diagnosis. It is seen that time to DN and time to death naturally formed a semi-competing risks structure because death terminated the observation on time to DN, but remained observable after the occurrence of DN. Administrative left truncation on mortality was also involved. That is, patients who had died before study enrollment were excluded. Out of 2727 patients, there were 731(26.8%) experiencing DN, 718(26.3%) dead in the end and 652(24%) with diabetic onset at entry. Summary statistics for the data are presented in Table 3.

Table 3. Summary statistics for diabetes registry data.

	n(%)
(δ, η) = (0, 0)	1729(63.4%)
(δ, η) = (0, 1)	267(9.8%)
(δ, η) = (1, 0)	280(10.3%)
(δ, η) = (1, 1)	451(16.5%)
L = 0	652(24%)
X < L	116(4.25%)

Our focus is first to quantify the relationship between DN and death by using the proposed measure LCQRR(τ; t₀). We fit model (1) to the data and adopt M = 10⁷ as in the simulations. We restrict t0 to be within [6,40] to ensure reasonable sample sizes accumulated for strata defined by I(X* > t₀). In Figure 2, we display the results for τ = 0.25, 0.5, 0.75 and t₀ values at an equally space grid on [6, 40] with step size=0.1. Estimated LCQRR(τ; t₀) are plotted in bold solid lines. The corresponding 95% pointwise confidence intervals are in dotted lines and the 95% pointwise Wald-type bootstrapping confidence intervals are in long-dashed lines. In Figure 2, we see that for all three τ values, the estimated LCQRR(τ; t₀) is generally positive; the lower bounds of confidence intervals are above 0 for t₀ less than 30, which is roughly the third quartile of X*. This observation is consistent with the common belief that DN is positively associated with mortality. Our formal test for H₀₁ yields p-values, < 0.001, 0.002, < 0.001, respectively, for τ = 0.25, 0.5, 0.75, confirming that DN is a significant prognostic factor for mortality.

Figure 2.

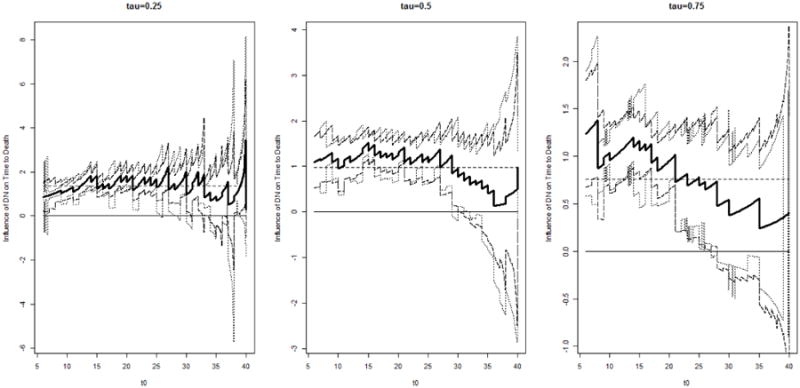
Denmark Diabetes Registry Study: Estimated LCQRR(τ; t₀) (bold solid lines), and the corresponding 95% pointwise confidence intervals (dotted lines) and 95% pointwise Wald-type bootstrapping confidence intervals (long-dashed lines).

We note that the confidence intervals for LCQRR(τ; t₀) with t₀ > 30 become wider and mostly cover 0. This may be partly due to the reduced power/efficiency as t₀ approaches the upper tail of X, resulting in smaller effective sample sizes for the proposed estimator. The insignificant difference between LCQRR(τ; t₀) and 0 with t₀ > 30 may also have the implication that the occurrence of DN has diminished prognostic power for mortality among patients who had lived long since diabetes diagnosis. In addition, we observe that the estimated LCQRR(τ; t₀) appears rather constant for τ = 0.25 and τ = 0.5, but the decreasing trend in the estimated LCQRR(τ; t₀) with τ = 0.75 is quite apparent. This observation is confirmed by the constancy tests for H₀₂, which yield p-values, 0.95, 0.23, and 0.01 for τ = 0.25, 0.5, 0.75 respectively. The significant changing pattern of LCQRR(τ; t₀) may second the previously conjectured inhomogeneous prognostic ability of DN on mortality.

We also choose three t₀ values, t₀ = 15, 21, 29, which stand for the 25th, 50th and 75th quantile of X*, respectively, to explore the patterns of LCQRR(τ; t₀) over τ ∈ [0.1, 0.82]. Figure 2 of Web Appendix B displays estimated LCQ̂RR_l(τ; t₀) in bold solid lines at equally spaced τ-grids with step size 0.001, with the corresponding 95% pointwise confidence intervals in dotted lines and 95% pointwise Wald-type bootstrapping confidence intervals in long-dashed lines. We observe that LCQRR(τ; t₀) may be significantly different from 0 for all three t₀'s. This is confirmed by tests for H₀₃, which give p-values, < 0.001, < 0.001, and 0.002, respectively. For t₀ = 21 and 29, we observe a clear decreasing trend in the estimated LCQRR(τ; t₀). Constancy tests for H₀₄ yield p-values, 0.24, 0.004, 0.004, for t₀ = 15, 21, 29, respectively. The finding that LCQRR(τ; t₀) may decrease with τ aligns with previous results, manifesting a weak or negligible association between DN and mortality in long-term diabetes survivors.

Next, we study how diabetes onset age, a continuous covariate, affects the dependence between DN and mortality. We fit model (5) to the data and the coefficient ${\mathit{\gamma }}_0^{(4)}(\tau ,t_0)$ represent the change in LCQRR per one year increase in diabetes onset age. For τ = 0.25, 0.5, 0.75, we estimate ${\mathit{\gamma }}_0^{(4)}(\tau ,t_0)$ at an equally spaced grid on [8, 36] with step size 0.1 for t₀. In Figure 3, we display the estimates for ${\mathit{\gamma }}_0^{(4)}(\tau ,t_0)$ along with their 95% pointwise confidence intervals. We see from Figure 3 that with all selected τ's, ${\widehat{\mathit{\gamma }}}_0^{(4)}(\tau ,t_0)$ is generally significantly positive for t₀ belong to the first half of the time interval [8, 36], but loses significance from 0 for larger t₀. This suggests that for patients who were diagnosed with diabetes at older age, the occurrence of DN before t₀ may imply a bigger disadvantage in residual survival time. Such an effect of diabetes onset age may diminish for large t₀'s, which point to the groups of patients who had survived for a long time since diagnosis. Tests for H₀₁ over t₀ ∈ [8, 22) confirm our observation from Figure 3, yielding three nearly zero p-values. Constancy tests for H₀₂ gave p-values, 0.64,0.11,0.07, respectively, for τ = 0.25, 0.5, 0.75. This provides some evidence for the observed diminishing effect of diabetes onset age over t₀.

Figure 3.

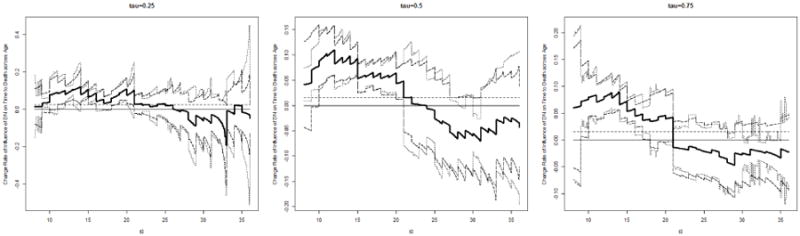
Denmark Diabetes Registry Study: ${\mathit{\gamma }}_0^{(4)}(\tau ,t_0)$ Estimated (bold solid lines), the corresponding 95% pointwise confidence intervals (dotted lines) and 95% pointwise Wald-type bootstrapping confidence intervals (long-dashed lines), and the overall influence of DN across time (horizontal dashed lines).

We also evaluate ${\widehat{\mathit{\gamma }}}_0^{(4)}(\tau ,t_0)$ over a τ-range [0.1, 0.82] for fixed t₀ values, 15, 21, 29. Results displayed in Figure 3 of Web Appendix B suggest similar findings. That is, DN may have a bigger influence on subsequent mortality for patients with later diabetes diagnosis compared to those with earlier diagnosis. Such an effect of diagnosis age may varnish when t₀ is large.

6. Remarks

In this paper, we propose a robust measure to assess the dependence of the nonterminal event and the terminal event in a semi-competing risks setting. Evaluating this measure at multiple t₀ and τ allows us to perform a comprehensive and robust evaluation of semi-competing risks dependence. It also offers the flexibility to explore the dynamic pattern of the dependence structure. The developed estimation and inference procedures well utilize the semi-competing risks structure with left truncation, and can be extended to adjust for covariates. Simulation studies show that the proposed estimation procedure performs well in finite sample cases.

Other approaches to obtaining a nonparametric estimator of LCQRR(τ; t₀) are available. For example, in the standard semi-competing risks setting without left truncation, note that T₁ ∧ T₂ is only subject to independent censoring by C and thus the joint survival function of (T₁, T₂) on the upper wedge can be consistently estimated by using methods, such as Lin and Ying (1993). Then we can estimate the two conditional residual quantiles in LCQRR(τ; t₀) by reversing their corresponding conditional distribution estimates. Our preference of adopting a quantile residual lifetime regression framework is primarily because of the resulting simple extension to accommodate covariates in the consideration of LCQRR(τ; t₀). Our strategy of connecting LCQRR with quantile residual lifetime regression models enables a unified approach to characterizing semi-competing risks dependence with or without covariates. Existing techniques for quantile regression can readily be applied to inferences and make our work neat.

In practice, the choices of τ and t₀ mainly depend on the interest of investigators. They may be adjusted according to the empirical observations of the data. For example, the estimation efficacy may be unsatisfactory at small or large values of t₀. This is because the number of observations satisfying X* ≤ t₀ (or X* > t₀) may be quite small when t₀ is small (or larger), making the estimate for Q_τ(T₂ – t₀|T₂ > t₀, T₁ ≤ t₀) (or Q_τ(T₂ – t₀|T₂ > t₀, T₁ > t₀)) inaccurate or unstable. Based on our numerical experiences, we find that our method works well for estimating both LCQRR(τ; t₀) and covariance matrix when n_t0,1 ∧ n_t0,2 > 15, where $n_{t_0,1}={\sum }_{i=1}^{n}I(L_i^{\ast }\le t_0,Y_i^{\ast }>t_0,X_i^{\ast }>t_0){\eta }_i^{\ast }$ and $n_{t_0,2}={\sum }_{i=1}^{n}I(L_i^{\ast }\le t_0,Y_i^{\ast }>t_0,X_i^{\ast }\le t_0){\eta }_i^{\ast }$. For a larger τ, we may need n_t0,1 and n_t0,2 to be larger. These can serve as useful empirical rules to guide the selection of τ and t₀ in real data analysis.