Protein Folding and Structure Prediction from the Ground Up: The Atomistic Associative Memory, Water Mediated, Structure and Energy Model

Abstract

The associative memory, water mediated, structure and energy model (AWSEM) is a coarse-grained force field with transferable tertiary interactions that incorporates local in sequence energetic biases using bioinformatically derived structural information about peptide fragments with locally similar sequence that we call memories. The memory information from the protein data bank (PDB) database guides proper protein folding. The structural information about available sequences in the database varies in quality and can sometimes lead to frustrated free energy landscapes locally. One way out of this difficulty is to construct the input fragment memory information from all-atom simulations of portions of the complete polypeptide chain. In this paper, we investigate this approach first put forward by Kwac and Wolynes in a more complete way by studying the structure prediction capabilities of this approach for six alpha-helical proteins. This scheme which we call the atomistic associative memory, water mediated, structure and energy model (AAWSEM) amounts to an ab initio protein structure prediction method that starts from the ground-up without using bioinformatic input. The free energy profiles from AAWSEM show that atomistic fragment memories are sufficient to guide the correct folding when tertiary forces are included. AAWSEM combines the efficiency of coarse-grained simulations on the full protein level with the local structural accuracy achievable from all-atom simulations of only parts of a large protein. The results suggest that a hybrid use of atomistic fragment memory and database memory in structural predictions may well be optimal for many practical applications.

Introduction

Protein folding is a spontaneous physicochemical process, a consequence of the motions of the atoms making up a protein along with those in its environment; as such, it should be accessible to simulation from the ground up.¹ Protein folding, however, is also an essential biological process that translates the information encoded by evolution in a protein sequence into functional dynamic form. Molecular physics, evolution and abstract information processing ideas all therefore inform our current understanding of the folding process and our current methods of protein structure prediction. ²

The most practical method of protein structure prediction today relies on evolution: the construction of homology models. The need to retain an active three dimensional structure in the face of relentless mutational changes in sequence has selected those sequences whose physicochemical energy landscapes retain the ability to guide an unfolded protein to a functional three dimensional structure even when the sequence has been radically perturbed. Because of this, we can be pretty sure that two naturally evolved sequences with recognizably similar sequences will also have very similar three dimensional folded structures. Recognizing global sequence similarity reflecting evolution from a common ancestor, called “homology”, thus empowers us to predict the tertiary structures of a given protein if we know the structure of one of its relatives.

Nowadays, when many protein structures have become known and are conveniently catalogued in the Protein Data Bank³ this idea makes structure prediction by homology modeling a very powerful tool indeed. Still, basic homology modeling is not a completely universal tool for a variety of reasons. Sometimes we cannot recognize from the sequences alone that two sequences are in fact sufficiently closely related so as to have the same structure. This problem of there being a “Twilight Zone” of sequence identity⁴ was profound several decades ago when fewer sequences and structural data were available and when sequence comparison algorithms were weaker than they are now. Advances on both those fronts, while helping, have not yet completely vanquished the problem however. In addition while sometimes the main parts of two sequences can be recognized as being similar, major portions of the sequences, often parts of likely functional relevance, find no match in known homologues. Some of these local sequences bear the sequence signatures of being “intrinsically disordered proteins”, as isolated elements, and therefore often don’t show up in already determined monomeric protein structures. Also sequence homology, while often fine at the monomer level by itself, does not tell us enough to assemble larger protein complexes from the monomers, In that event, however, low resolution laboratory structural determination methods like Cryoelectron microscopy can provide additional constraints.

While the “top-down” homology modeling strategy based on the robustness of folding through evolution is powerful and practical, purely physicochemical approaches that start from the ground up have also met with some success. Refinement of atomistically detailed force fields over a period of decades, along with advances in sampling algorithms and computational power, have finally allowed all atom simulations of small and moderate size proteins to be carried out for sufficient time to fold proteins and thereby predict tertiary structure. ⁵ The scope of this direct approach for structure prediction will certainly continue to grow with time but presently full atomistic simulation of the complete folding process remains computationally expensive for very large systems and is not manageable for routine use by most people.

The very evolutionary robustness of protein folding, fortunately enables an approach to predicting protein structure using coarse-grained simulations of protein folding that can be informed by bioinformatic data. ⁶ A key idea behind these approaches is that the energy landscapes of proteins are funneled ⁷ . The funneled nature of an evolved protein folding landscape explains why the structures of a folded protein can be much less sensitive to details of sequence than would be the ground state structure of the rugged energy landscapes that are expected for sequences that have not had to run the gauntlet of evolutionary selection to fold. Robustness against sequence variation also implies there should be some robustness with respect to the level of modeling used to describe the protein. Since evolution changes sequences residue by residue not atom by atom, we expect a coarse-grained force field described at the residue level to do a reasonable job of capturing the funneled aspect of the folding energy landscape even when the model is lacking complete chemical details. In addition to justifying the use of coarse grained models, energy landscape theory provides a quantitative algorithm for learning from known examples the parameters in a coarse-grained force field^6,8,9 that will lead to optimally funneled folding landscapes.⁷ The minimal frustration principle of energy landscape theory that quantifies the idea of a folding funnel through a ratio of characteristic energy scales provides a machine learning algorithm to find the effective forces between residues. ⁹ These forces include both direct interactions between the residues and interactions that are mediated by the protein perturbing the aqueous solvent¹⁰ or the membrane environment.¹¹

Energy landscape analysis also suggests that a large fraction (roughly a third) of the specificity of folding arises from local signals, interactions along the backbone involving residues close in sequence. ^12,13 This observation justifies the use of information about the forces shaping the structures of local fragments of the protein chain in order to build a globally funneled landscape when the tertiary interactions are included. A short cut to doing this is to use known structures of locally similar sequences to construct the forces that stabilize those configurations. Mathematically finding such forces resembles schemes for associating clues or prompts with specific memorized examples. ¹⁴ When such interactions are incorporated in the force field we call the resulting model an “Associative Memory Hamiltonian”. ^8,15

Associative Memory force fields can be used in many ways. If in fact the local structures are already known with even modest precision, high accuracy structures of the entire protein or larger protein complexes can be constructed. ¹⁶ For studying complexes, such an algorithm amounts to a flexible docking scheme; for studying monomers, employing the algorithm based on the associative memory hamiltonian with local information from homologues amounts to a sophisticated homology modeling tool. In this mode also associative memory models can be used to study structural aspects of kinetic pathways and mechanisms of folding and functional events that other methods of structure prediction such as fragment assembly that do not employ the Boltzmann principle of statistical mechanics cannot address.

The associative memory hamiltonian augmented by water-mediated interactions can also be used for de novo structure prediction in the absence of any reliable structural homolog information. ^9,10,15,17 In this latter mode the memories used in the Hamiltonian are chosen by finding correspondences using various measures of sequence matching either in a purely local manner when local peptide sequences are directly compared (a method we call finding “fragment memories”) or in a way that does take into account the global context of a sequence fragment by doing a preliminary sequence-structure alignment of the entire protein. The global method of choice makes some sense since occasionally the same local sequence shows up in different proteins having different secondary structures. Both approaches of choosing memories do quite well at moderate resolution but sometimes prediction entirely without homology input fails to pick up important structural features. ¹⁷ This problem usually shows up only in part of protein; typically when none of the local fragments that have been identified as input memories for that region, in fact, have similar structures to the protein at that location. Because of this, completely de novo structure prediction using AWSEM may sometimes miss important details. While the wisdom of the database can successfully inform many predictions, that wisdom is sometimes limited just when you most need it.

One possible way around the limitations of using the structural database as the sole source of information about local in sequence forces, is to create the memory database yourself through fully atomistic simulation of fragments of the protein in their environment. Kwac and Wolynes made a preliminary exploration of this approach several years ago by simulating fragments of the 434 repressor in water and then using the sampled fragment structures as the input memories to an associative memory hamiltonian. The associative memory hamiltonian they used was less sophisticated than the current one. The older hamiltonian employed only direct contact energies for the tertiary interactions. ¹⁸ While the results were encouraging, the study revealed also some of the difficulties of such a ground up approach. Paramount among these at the time was that the all atom simulations of the fragments, while considerably less computationally expensive than full all atom simulations of folding the entire protein in water, were nevertheless very time consuming.

While the computational set up cost of constructing a fragment memory by atomistic simulation remains high, even today, it is now much less of a problem because of improved multiprocessor computers. Also we know that the direct contact energies that were used in the Kwac-Wolynes study do not lead to as funneled a global landscape as the currently available coarse-grained force fields that also have water mediated interactions. For these reasons, we therefore decided to re-examine the approach of constructing memories from the ground up via atomistic fragment simulations. In this paper, we chose for study several examples of proteins whose structures had previously been predicted using the AWSEM code based on memories that were chosen by sequence similarity criteria alone using only non homologuous structures in the database. For each of these proteins we divided the sequence up into shorter segments typically comprising about two elements of secondary structure and simulated those segments with an all atom force field in explicit water. By simulating all of the fragments in parallel, significant speed-ups can be achieved over simulating the entire protein at the all atom level. After clustering the structures sampled in these runs, we used representative structures from the simulated clusters as memories in AWSEM structure prediction simulations to predict the complete tertiary structure. This divide and conquer strategy thus amounts to a prediction scheme from the ground up, avoiding the use of database input entirely. We call this protocol AAWSEM, the atomistic associative memory water mediated structure and energy model.

After describing the protocol we detail the results and discuss the pros and cons of using the ab initio fragment strategy for studying protein folding dynamics and structure prediction.

Methods

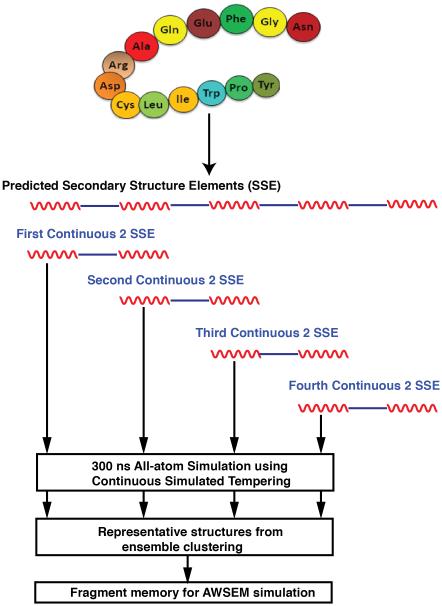
The prediction protocol is divided into several steps. A flow chart is shown in Fig 1. First, the entire protein is divided into overlapping segments using a preliminary secondary structure prediction as a guide, with each segment similar in size (each having around 20 residues). Typically, each segment was comprised of approximately two elements of secondary structures (here alpha helices) (Such a simulation will provide information especially about the conformations of the end of helices and then turn regions). Next the overlapping segments were simulated individually in an explicit-solvent environment (ESS) using a transferrable fully atomistic forcefield. Results from the all-atom sampling of the segments were then clustered. Members of these clusters were then used to construct the associative memory libraries. An AWSEM hamiltonian was then assembled for each protein and simulated annealing of 20 copies was carried out, resulting in structure predictions of each protein in its entirety.

Figure 1.

Protocol for structural prediction using AAWSEM. The secondary structure of 1R69 is used as an illustration.

1: Generating the atomistic fragment memory

In order to ensure the fragments constructed were likely to include the necessary start and stop signals to form stable capped helices, the secondary structure of the protein is first predicted using PsiPred (Psipred is a standard prediction tool with a high validated level of performance). ¹⁹ The protein is then divided up in sequence into shorter segments of around 20 residues in size. Each segment is comprised of two continuous predicted secondary structure elements (SSE). These segments are chosen so that each predicted element occurs in two fragment simulations in an overlapping fashion as shown in Fig 1. Fully atomistic simulations were carried out for these segments in water using the CHARMM27 parameter set for the protein molecules and 0.15M salt ions and TIP3P model for water in a dodecahedron box containing approximately 20000 to 40000 water molecules depending on the initially chosen structure of the polypeptide fragment.²⁰ This force field has been judged to have a somewhat stronger α helical bias than more recent versions (e.g. CHARMM36), but this should not be a problem for the current test set.^21–23 Each segment was simulated for 300 nanoseconds. Structures were sampled from the last 250 nanoseconds. The calculations were done with the GROMACS software package.²⁴

2: Explicit-solvent simulation (ESS) enhanced sampling protocol

We employed an enhanced sampling method for the atomistic simulation of the protein fragments in water. A thorough sampling of protein configurations guarantees a better characterization of the local fragment folding landscape. The largest clusters in such a sampling should correspond to minimal free energy structures on the landscape that can guide the global folding of protein when augmented with the water mediated interaction of the AWSEM force field. We used a single-copy continuous simulated tempering (CST) method. CST speeds up the search of protein configuration space. In this method along with conventional MD configurational simulation, the temperature of the ensemble undergoes a random walk by following a Langevin equation.

$$\frac{d(1∕\beta )}{dt}=E-\langle E\left(\beta \right)\rangle -\frac{\partial lnw\left(\beta \right)}{\partial \beta }+\frac{\sqrt{2}}{\beta }\xi$$ (1)

where ξ is a Gaussian white noise satisfying (ξ(t) · ξ(t^′)) = δ(t − t^′). β = 1/k_BT , with k_B the Boltzmann constant and T the temperature. E is the potential energy of the system at current configuration. (E(β)) is the ensemble averaged potential at a specific temperature. Using this Langevin equation ensures that the simulation will eventually settle down to a generalized canonical ensemble with a probability distribution

$$p(\beta ,X)\propto \frac{exp[-\beta E\left(X\right)]\cdot w\left(\beta \right)}{Z\left(\beta \right)}$$ (2)

where w(β) is a predefined temperature distribution of this generalized ensemble. While the choice of w(β) is flexible, we used w(β) = 1/β in our following simulations based on previous successful predictions. ^25,26 Details of the CST protocol are described in Ref 25.²⁵

3: The AWSEM force field

A detailed description of the AWSEM force field has been given in Davtyan et al.⁶ Briefly, AWSEM is a predictive coarse-grained protein folding forcefield constructed using ideas from energy landscape theory. The Hamiltonian is summarized in Eq. (3). It consists of a backbone term,V_backbone, which restricts the chain to polypeptide like conformations and is mostly sequence independent. The burial term, V_burial, attempts to sort each residue into its preferred burial environment - exposed, partially buried or completely buried. The contact term, V_contact, consists of a direct contact interaction and a water or protein mediated interaction. Depending on the instantaneous local density of an interacting residue pair, this term accounts for the water and protein mediated interactions, respectively. The hydrogen bonding term, V_HB , consists of two interactions which favor hydrogen bonding geometries. The first one is sequence independent, long range, and favors cooperative formation of β-sheets, and the other is sequence dependent and depends sensitively on the distance and relative orientation of the interacting groups. Finally, the local-in-sequence interactions (3 ≤ |i − j| ≤ 9, i, j are residue indices) are governed by the associative fragment memory term, V_{F M} .

$$V_{total}=V_{backbone}+V_{contact}+V_{burial}+V_{HB}+V_{FM}$$ (3)

The form of V_FMis given by the following equation.

$$V_{FM}=-{\lambda }_{FM}\sum \sum exp[-{(r_{ij}-r_{ij}^m)}^2∕2{\delta }_{ij}^2]$$ (4)

where the outer sum is over all the fragment memories and the inner sum is over possible pairs of C_α and C_β atoms within the fragment with a length separation by two or more residues. r_ij is the instantaneous distance between the atoms during a simulation, while the r^m are the fixed distances between residue i and j in the individual memories labeled by the index m. δ_ij = |i − j|^0.15 is a sequence separation dependent width. ⁶ λ_FM is the scaling factor to control the relative strength of different fragments, and is determined by the cluster size from atomistic simulations in our case. AWSEM has been proved to be a powerful tool in handling protein structure prediction, protein-protein association, ²⁷ and the initial stages of misfolding and aggregation. ^28,29 While in standard AWSEM, fragment memories are generated based on sequence similarity from the Protein Data Bank (PDB) database, here they are generated from clusters found in all-atom explicit-solvent simulations (ESS) of overlapping segments of the protein.

4: Clustering algorithm to select representative structures

Representative structures from simulation were clustered using a “single linkage” algorithm. The clusters were determined by progressively adding a structure to each cluster when its distance to each element of that cluster is smaller than a preset threshold. In our case, the distance employed is the backbone Root Mean Square Deviation (RMSD) between two structures after their structural alignment. We have adopted a threshold value of 0.25 nm.

5: Order parameter for umbrella sampling and free energy calculation

Q is used to compare the structural similarity of all snapshots. The form of Q is given by

$$Q=\frac{2}{(N-2)(N-3)}\sum _{j>i+2}exp[-{(r_{ij}-r_{ij}^N)}^2∕2{\delta }_{ij}^2]$$ (5)

where N is the total number of residues. To survey the energy landscapes of a protein, we use Q as an order parameter in umbrella sampling in which a harmonic bias has been added to the Hamiltonian:

$$V_{Q-bias}=1∕2k_{Q-bias}{(Q-Q_0)}^2$$ (6)

All free energy profiles were calculated using the Weighted Histogram Analysis Method (WHAM).

Results

1: Sructure prediction for six monomeric α -helical proteins

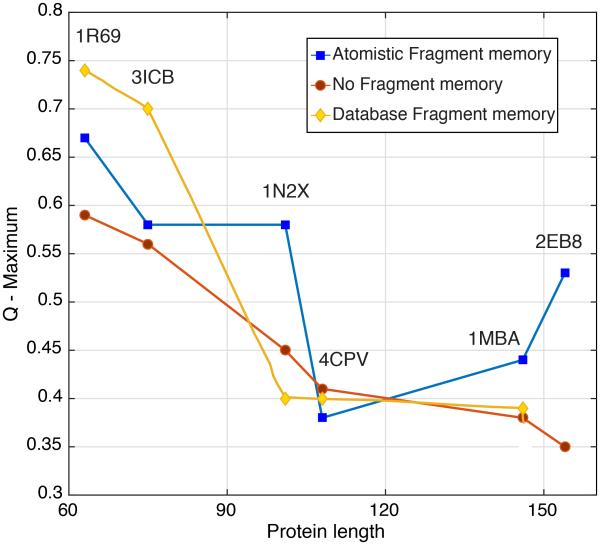
We summarize our structure prediction results in Figure 2. Here we have plotted the maximum Q (pairwise distance among residues between two structures) value achieved for a protein sequence versus its sequence length. These Q values generally are achieved near the end of a simulation run. The results for the “atomistic fragment” predictions are shown as blue squares, while those from simulations using no fragment memories as input are shown as red circles. We have also plotted the “homologues excluded” (yellow diamonds) results from earlier prediction studies for comparison. ⁶ As expected, the results from “atomistic fragment memory” predictions are better for 1N2X, 1MBA and 2EB8 than the results that used no fragment memory term whatsoever. Strangely, both the “atomistic fragment memory” and the “database fragment memory” predictions are worse than “no fragment memory” predictions for the 4CPV example. Predictions for 1R69 and for 3ICB using “atomistic fragment memory” are also overall improved compared to the predictions using “no fragment memory”, but here the “database fragment memory” predictions outperformed the other two models. The large amount of similar local structures for 1R69 and 3ICB apparently has allowed higher prediction Q values using “database fragment memory”. In 1N2X, 1MBA and 2EB8, the number of similar local structures in the database is smaller, so the “database fragment memory” predictions are limited.

Figure 2.

Maximum Q score versus sequence length for the “atomistic fragment memory” AWSEM (blue squares) and “no fragment memory” AWSEM (red circles). Maximum Q score for “homologues excluded” “database fragment memory” AWSEM (yellow diamonds) ⁶ are also shown where available.

To assess the consistency of the results from many annealing runs, we also display the final Q values for each of the 20 annealing runs (sorted in ascending order) in Fig 3. These figures show that, in 1R69, 3ICB, 1N2X, 1MBA and 2EB8, the predictions from the “atomistic fragment memory” runs are better and more consistent than those that employed “no fragment memories”. Strangely for 4CPV, the trend is different, suggesting that the atomistic fragment memories somehow actually hamper proper folding process.

Figure 3.

Prediction quality for 1R69 (a), 3ICB (b), 1N2X (c), 4CPV (d), 1MBA (e) and 2EB9 (f). Red diamonds correspond to “atomistic fragment memory” predictions, blue diamonds to “no fragment memory” predictions. In each case, 20 results from annealing simulations are shown in ascending order.

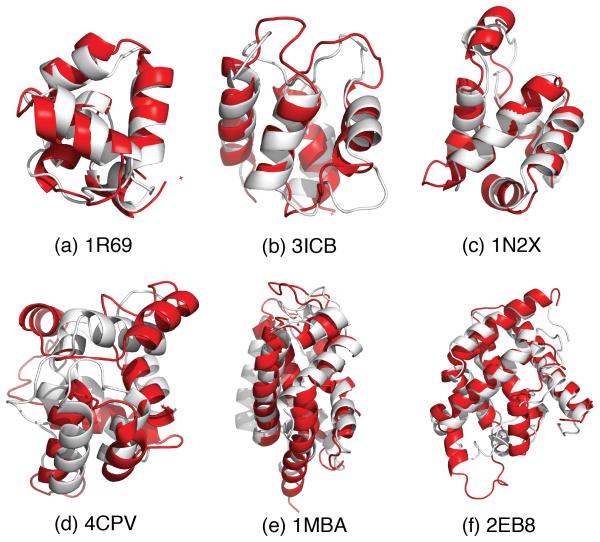
The alignments of the predicted and native structures are shown in Fig 4. For 1R69, 3ICB and 1N2X, the best predicted structures agree well with the native structures, with almost perfect secondary structure alignment. The major deviations arise from the loop regions. For 4CPV, which contains a 3-10 helix in its native structure with relative low stability, even the best predicted structure (Q ≈ 0.4) deviates rather far from the native form. This perhaps arises because the AAWSEM forcefield explicitly excludes the 3-10 helix hydrogen bonding pattern. We simulated two forms of myoglobin, one whose structure is determined without its cofactor heme (2EB8), one the holo form containing the cofactor(1MBA). The best structural alignments of the holoform 1MBA, myoglobin, and 2EB8, apomyoglobin, overlap quite well except for the C-terminal helix that shows the only significant deviations as we will discuss below.

Figure 4.

Alignments between structures obtained from “atomistic fragment memory” predictions shown in red, while the crystal structure is shown in white.

2: Myoglobin vs. apomyoglobin

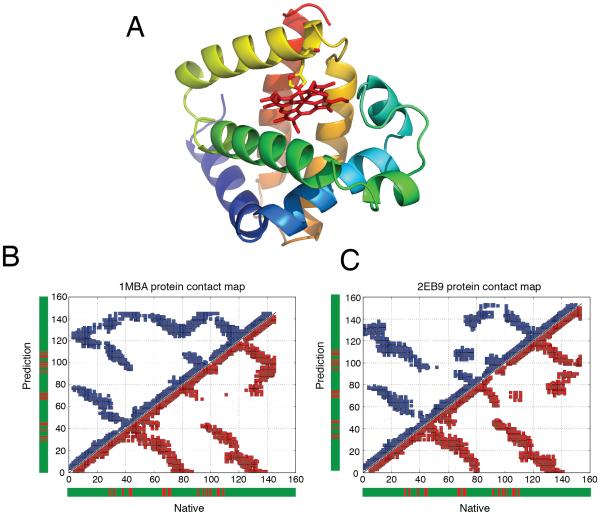
Many of the longer proteins (> 100 residues) simulated in our previous assessments of structure prediction protocols contain cofactors. In all previous studies as well as the present one, no cofactor constraints were included in the AWSEM simulations themselves. For myoglobin, structure prediction (1MBA) using AWSEM, achieved a Q of around 0.37, a generally recognizably correct structure but one having many flaws. In predictions using AAWSEM, the atomistic fragments improved the result to 0.44 with an RMSD of around 3.9 Å. We believe that in the model, the main challenge for structural prediction of myoglobin comes from the absence of the heme cofactor located on the C-terminal of the structure in the simulated annealing runs (Fig 5A). In the crystal structure, the heme is bound to His95. The heme provides extra stabilization energy and steric bulk that prevents over collapse. ³⁰ In the AAWSEM simulations of 1MBA, the absence of the heme near the C-terminal end makes it impossible to provide stabilizing contacts with the polypeptide chain, and thus leads to greater structural heterogeneity near the C-terminal region. In the contact map for 1MBA shown in Fig 5B, we see many additional contacts (nonnative ones) between parts of the polypeptide chain have been made compared to what is found in the native form.

Figure 5.

The apomyoglobin could fold properly. (A): The crystal structure of myoglobin with multiple α-helices colored from blue at the N-terminal to yellow at the C-terminal. The heme is also shown in red sticks attached to His95 on myoglobin. (B): Comparative contact maps of the maximum Q score structures obtained from “atomistic fragment memory” predictions for 1MBA and (C) 2EB8, the blue stands for contact maps for predicted structures and the red stands for native structures. The residues that are highlighted in red in the sidebars make contacts with the heme cofactor. We see that in 1MBA one of the contacting regions, the one near residue 40, makes non-native contacts with the region between 120 and 145.

The structure of an apoform natively lacking the co-factor has been experimentally determined, so we decided to see how the AAWSEM protocol fared for this system since both nature and simulations are missing the heme. The absence of the cofactor significantly influences the prediction results (Fig 5C). When we carry out the AAWSEM protocol for this sequence apomyglobin (2EB8) , the result is improved to an Q value of 0.53 with a very acceptable RMSD of around 3.1 Å. For the apoform, the major part of the deviations in the predictions arises from the loop regions (Fig 4F).

Discussion

1: Atomistic information encoded in fragment memories guides folding

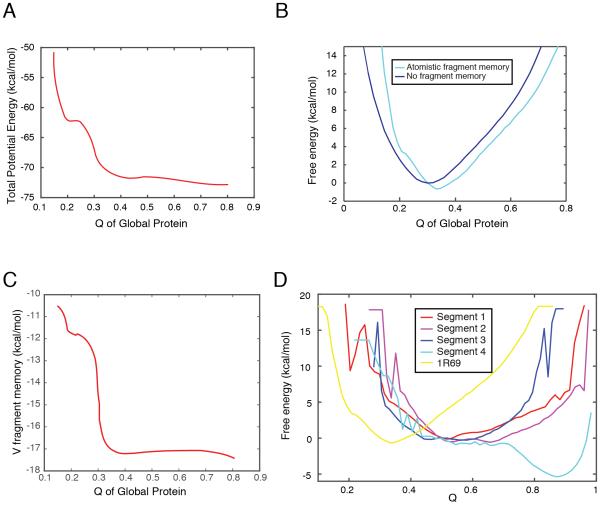
The standard AWSEM protocol uses a knowledge-based search to generate fragments that generate the local in sequence forces. In the AAWSEM protocol, the fragment memory input is obtained by using structures representative of clusters from explicit-solvent simulation of overlapping polypeptide segments. This short range in sequence information helps structure prediction. It does so by adding to the funneling of the landscape on short length scales. To assess this hypothesis, we computed free energy profiles for 1R69 using umbrella sampling with Q as the order parameter.

As shown in Fig 6A, the total solvent-averaged potential energy that guides tertiary structure formation falls as Q increases, indicating that the folding towards the native state is energetically favored. In addition, a comparison between the free energy profiles (Fig 6B) with (cyan) and without (blue) atomistic fragment memory demonstrates that atomistic fragment memories help guide the folding of protein towards its native state. The total fragment memory potential energy falls as Q increases (Fig 6C), indicating that the input fragment memories guide the correct folding. Further, we calculated the free energy profiles for the ordering by themselves of each of the four segments used in the atomistic inputs for folding this protein (Fig 6D). All of these free energy profiles favor a highly folded state in local terms for each fragment (Q ≥ 0.6 and especially Q = 0.9 for segment 4). The difference between these profiles and that of the entire protein order (Q ≈ 0.4) again signifies the important role of fragment energies in providing local sequence signals for finding the correct folded state.

Figure 6.

The atomistic fragment memories guide the folding of 1R69 towards a native-like state. (A): The total potential energy decreases as Q increases. (B): Free energy profiles of 1R69 as a function of Q using atomistic fragment memory (cyan) and without fragment memory (blue). (C): The fragment memory energy (Eq. (4)) decreases as Q increases. (D): Free energy profiles are shown of the segments as a function of the Q of the individual segments (red to blue) and the global Q (yellow) are shown.

2: AAWSEM reduces the sampling problem in traditional all-atom simulation

In conventional explicit-solvent simulations, considerable computer resources are currently needed to ensure sufficient sampling. The cost problem grows more severe when the size of the proteins is increased for several reasons. First even the timescale for the free motion of the polypeptide chain scales polynomially with the length. Also on the relatively rugged surfaces of present day atomistic force fields, the number of minima in which proteins may be trapped also increases significantly with protein size. Direct atomistic simulation as a means of structure prediction therefore scales poorly with protein size. In contrast, while the input to AAWSEM in the present protocol requires atomistic simulation in explicit solvent, finding the input data for the full simulation requires simulating only protein fragments with fixed sizes (usually around 20 residues), so the computational cost scaling with length of the complete prediction is much better. Breaking up the entire protein into several fragments leads to only a linear-scale increase in simulation time for finding the input fragment structures. The globally funneled nature of the AAWSEM tertiary structural landscape again ensures that there is only a polynomial scaling of the coarse-grained simulation itself with system size, as expected for minimally frustrated landscapes.

3: A hybrid assignment of fragment memories is probably optimal in structural predictions

The predictions using fragment memories generally are better than these found simply ignoring short range signals entirely as seen in Fig 2. Nevertheless the relative quality of the predictions using either database or atomistic inputs varies sporadically. Neither scheme is always superior to the other. The predictions from the database inputs were better for 1R69 and 3ICB, while predictions using atomistic fragment inputs were better for 1N2X, 1MBA and 2EB8. The database approach would eventually be ideal if we were to have a perfect library that contains all possible sequences, an unachievable goal. Yet the present database often shows sufficient coverage for most protein segments in natural proteins. The overhead of generating memories from the atomistic approach is much greater than simple database search, and indeed exceeds the cost of the tertiary coarse grained simulated annealing used finally to predict the structure. This upfront cost argues against using the atomistic approach universally but the atomistic input strategy should be quite effective as a complement to simple sequence matching especially when we know that only a particular small region of the entire protein sequence is unrepresented in the existing database, for example by being predicted to be an intrinsic disordered region. Employing a combination of the two different approaches of choosing fragments should greatly assist efficient prediction of large proteins, and protein assemblies and also will enable long time scale studies of functional dynamics of proteins.