Solvation Thermodynamics of Oligoglycine with Respect to Chain Length and Flexibility

Abstract

Oligoglycine is a backbone mimic for all proteins and is prevalent in the sequences of intrinsically disordered proteins. We have computed the absolute chemical potential of glycine oligomers at infinite dilution by simulation with the CHARMM36 and Amber ff12SB force fields. We performed a thermodynamic decomposition of the solvation free energy (ΔG^sol) of Gly_2–5 into enthalpic (ΔH^sol) and entropic (ΔS^sol) components as well as their van der Waals and electrostatic contributions. Gly_2–5 was either constrained to a rigid/extended conformation or allowed to be completely flexible during simulations to assess the effects of flexibility on these thermodynamic quantities. For both rigid and flexible oligoglycine models, the decrease in ΔG^sol with chain length is enthalpically driven with only weak entropic compensation. However, the apparent rates of decrease of ΔG^sol, ΔH^sol, ΔS^sol, and their elec and vdw components differ for the rigid and flexible models. Thus, we find solvation entropy does not drive aggregation for this system and may not explain the collapse of long oligoglycines. Additionally, both force fields yield very similar thermodynamic scaling relationships with respect to chain length despite both force fields generating different conformational ensembles of various oligoglycine chains.

Introduction

The protein trinity hypothesis says that proteins may exist in an ordered, collapsed-disordered (molten globule), or extended-disordered (random coil) conformational state, and that these states give rise to particular, biological functions (1, 2). Intrinsically disordered proteins (IDPs) or regions (IDRs) within proteins present a diverse ensemble of structures with a range of molecular dimensions. To capture this diversity, Uversky (3) proposed the addition of an intermediate premolten globule thermodynamic state characterized with a compactness and residual structure between that of the collapsed and extended states. An IDP or IDR’s occupancy in and interconversion between these states depends, in part, on sequence composition and chain length (2, 4), while other processes (e.g., binding, allostery, posttranslational modifications) shift the equilibrium between these states. Here we are interested in how the innate properties of a short, model IDP may affect the competition between intrapeptide and peptide-solvent interactions and thus result in extended or compact conformational ensembles of relevance to longer IDPs.

Extended IDPs tend to lack hydrophobic side chains and often have a large overall net charge (3, 4, 5, 6, 7). Many IDPs collapse or aggregate despite the absence of hydrophobic side chains and/or the presence of a large, net charge (8, 9, 10, 11). Oligoglycine (i.e., the common protein backbone) is a particularly interesting example, as it is found in many IDRs (12, 13), exhibits IDR qualities, and has been shown to collapse in a length-dependent manner (14, 15, 16, 17). High glycine content has also been associated with compact IDRs (5). Evidence suggests that as chain length increases, favorable protein backbone interactions out-compete backbone-solvent interactions resulting in oligoglycine collapse (15, 16). The fact that the solubility of oligoglycine decreases dramatically with chain length (N = 1–5) further supports this idea (18). However, whether favorable intrapeptide interactions are due to H-bonding, electrostatic (elec), and/or van der Waals (vdw) interactions, is a subject of debate (14, 15, 16, 19). Interestingly, the solvation free energy of fixed conformations of oligoglycine in infinite dilution is negative and continues to decrease with chain length (20, 21)—further suggesting that collapse may not be a consequence of unfavorable solvent interactions, but due to the availability of more potential intrapeptide interactions. Few studies have considered the entropic contributions to the solvation free energy of oligoglycines in particular—or IDPs in general—as a function of chain length. While the hydrophobic effect (i.e., solvation entropic penalty) is known to play a key role in protein folding, its importance to aggregation and collapse of IDPs is less clear.

Using computational free energy methods, we performed a decomposition of the solvation thermodynamics for successively longer oligoglycine polypeptides (Gly₂-Gly₅). We use multistage free energy perturbation (FEP) to calculate solvation free energy $\left(\Delta G^{\text{sol}}\right)$ and its vdw $\left(\Delta G^{\text{vdw}}\right)$ and elec $\left(\Delta G^{\text{elec}}\right)$ components. We further decomposed $\Delta G^{\text{sol}}$, $\Delta G^{\text{vdw}}$, and $\Delta G^{\text{elec}}$ into their entropic and enthalpic components. FEP simulations were performed with oligoglycine models either constrained to a rigid-extended conformation or completely flexible (i.e., without positional constraints) using both the CHARMM36 (C36) (22) and AMBER ff12SB (23) force fields. We consider rigid and flexible oligoglycine models because we have previously shown how $\Delta G^{\text{sol}}$ depends on flexibility and geometry (20, 24, 25). C36 and ff12SB are used to discriminate and control for force field effects and to investigate how the differences observed in the structural properties of oligoglycine predicted by these two force fields (17) affect the solvation thermodynamics.

We find that $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$ decrease with chain length but their magnitude and rate of decrease depends on conformational flexibility. Despite force-field-dependent structural properties of oligoglycine, both force fields yield very similar thermodynamic scaling profiles with respect to chain length. As chain length increases, $-T\Delta S^{\text{sol}}$ becomes more unfavorable but is offset by a more favorable $\Delta H^{\text{sol}}$ for both rigid and flexible oligoglycines. Differences in $-T\Delta S^{\text{sol}}$ and $\Delta H^{\text{sol}}$ between flexible and rigid oligoglycines is pronounced; however, due to their compensatory nature, they yield small differences in $\Delta G^{\text{sol}}$. Significant compaction of oligoglycine is predicted for chains containing >10 glycine residues (14, 15, 16). The question remains whether the solvation thermodynamics of short oligoglycines can predict (i.e., group-additivity) the solvation free energy of longer oligoglycine chains that can form complex, compact structures.

Both free energy error estimates and the necessary computational resources increase with chain length and limit this study to relatively short oligoglycines. However, our results help to provide mechanistic insight into the forces that may drive the collapse of longer oligoglycines.

Materials and Methods

FEP simulations were performed for a rigid-extended conformation of Gly₂, Gly₃, and Gly₄ as well as for completely flexible Gly_2–5 using NAMD 2.10 (26) with the CHARMM36 (C36) (22) and AMBER ff12SB force fields (23) at 300 and 320 K. Solvation free energy, $\Delta G^{\text{sol}}$, was calculated by first scaling the vdw interactions with the solvent followed by elec charging by means of a coupling parameter, λ. Below we describe the setup of the simulations, common simulation parameters, parameters specific to FEP, and the analysis methods.

System

For simulations with C36, oligoglycines were built in a fully extended state using the VMD plugin MoleFacture (27) and capped with neutral acetyl (ACE) and N-methylamide (NME) groups. They were similarly built using XLeap in AmberTools (23) for simulations with ff12SB. Systems were solvated with TIP3P water using either VMD’s Solvate plugin or XLeap ensuring at least a 10 Å padding between oligoglycine and the sides of the simulation box.

General simulation parameters

All simulations were performed at constant temperature (either 300 or 320 K) and pressure (1 atm) using a Langevin thermostat and barostat. NAMD’s default switching function at 1.0 nm was used to smoothly truncate nonbonded interactions at 1.2 nm. Electrostatic forces were calculated using particle mesh Ewald on a grid with a 1.0 Å spacing. The 1–4 scaling was set to 0.8333 for simulations with ff12SB to match AMBER’s nonbonded exclusion convention. The velocity Verlet algorithm with a 2 fs time step was used to integrate the equations of motion. Coordinates and energies were saved every 1 ps.

Free energy perturbation simulations

To set up the FEP simulations, we first performed a steepest descent minimization for each system, allowing only water coordinates to change for simulations with fixed oligoglycine. Configurations for FEP simulations of flexible oligoglycines were taken either from a short equilibration run or from the final configurations from long molecular dynamics (MD) simulations from previous studies in our lab at constant temperature and pressure. These configurations were used to initiate the FEP simulations at 300 K.

The process of solvating each oligoglycine was decomposed into two pathways following a protocol similar to that of Kokubo et al. (24). First, the vdw interactions between oligoglycine and the solvent are gradually turned on via a coupling parameter, ${\lambda }^{\text{vdw}}$, that takes on values between 0 (i.e., gas phase) and 1 (i.e., vdw interactions fully on). For intermediate ${\lambda }^{\text{vdw}}$ values, the vdw interactions are scaled according to a soft-core potential (28). Then, with ${\lambda }^{\text{vdw}}=1$, the elec interactions are linearly scaled with ${\lambda }^{\text{elec}}$ such that when ${\lambda }^{\text{elec}}=1$, oligoglycine is fully solvated. The interactions between atoms in oligoglycine were not scaled. For the vdw pathway, a $\Delta {\lambda }^{\text{vdw}}$ value of 0.02 (50 windows) was used for rigid/fixed and flexible Gly₂, Gly₃, and Gly₄ simulations, while a spacing of 0.04 was used for flexible Gly₅. A $\Delta {\lambda }^{\text{elec}}$ value of 0.0625 (16 windows) was used for all electrostatic pathways. Independent, concurrent MD simulations at 300 K were performed at each λ for 50 ns for fixed and flexible Gly_2–4 and 80 ns for flexible Gly₅. The change in free energy was computed from these simulations at each ${\lambda }^{\text{vdw}}$ and ${\lambda }^{\text{elec}}$ and is discussed in the following section. The simulations were then repeated at 320 K, using the final configuration from the simulations at 300 K, to measure the change in solvation entropy (29, 30). One nanosecond at each λ was attributed to equilibration. In total, 1748 simulations were performed for an aggregate simulation time of 92.3 μs. While the overall solvation free energy is a state function, its vdw and elec components, as defined here, are path/protocol-dependent.

Solvation free energy

The vdw and elec contributions to solvation free energy are computed separately according to the exponential form of the FEP formula (31, 32):

$$\Delta G^{\text{vdw}}=-\frac{1}{\beta }{\sum }_{i=1}^{n^{\text{vdw}}}ln{\langle \text{exp}\left(-\beta \Delta U_i^{\text{vdw}}\right)\rangle }_i,$$ (1)

$$\Delta G^{\text{elec}}=-\frac{1}{\beta }{\sum }_{i=1}^{n^{\text{elec}}}ln{\langle \text{exp}\left(-\beta \Delta U_i^{\text{elec}}\right)\rangle }_i,$$ (2)

$$\Delta G^{\text{sol}}=\Delta G^{\text{vdw}}+\Delta G^{\text{elec}},$$ (3)

where i is used to index a particular ${\lambda }_i^{\text{vdw}}$ or ${\lambda }_i^{\text{elec}}$ that take on values between 0 and 1; β is the inverse temperature; and $\Delta U_i=\Delta U\left({\lambda }_{i+1}\right)-\Delta U\left({\lambda }_i\right)$, which is the difference in either the vdw or elec potential energy for a configuration generated in the ${\lambda }_i^{\text{vdw}}$ or ${\lambda }_i^{\text{elec}}$ ensemble and those for the same configuration if it were in the ${\lambda }_{i+1}^{\text{vdw}}$ or ${\lambda }_{i+1}^{\text{elec}}$ ensemble, respectively. ${\langle \dots \rangle }_i$ is an ensemble average and the summation is either over the ${\lambda }^{\text{vdw}}$ or ${\lambda }^{\text{elec}}$ values. Simulations at each λ yield trajectories of $\Delta U_i^{\text{vdw}}$ or $\Delta U_i^{\text{elec}}$ values. Note that the small contributions from pressure and volume are not included in the estimates of $\Delta G$. For a detailed review on multistage FEP calculations, we refer the reader to Kokubo et al. (24) and Pohorille et al. (31). The total solvation free energy, $\Delta G^{\text{sol}}$, is the sum of $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$.

Solvation entropy and enthalpy

Two approaches were used to decompose $\Delta G^{\text{sol}}$ into its enthalpic and entropic components. In the first method, referred to as the finite difference (FD) approach, we further decompose $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$ into their enthalpic and entropic components. In this approach, the vdw and elec contributions to solvation entropy are given by a central finite difference approximation (29, 30):

$$\Delta S^{\text{vdw}}\left(310\text{K}\right)={-\frac{\partial \Delta G^{\text{vdw}}}{\partial T}|}_{310\text{K}}\approx -\frac{\Delta G^{\text{vdw}}\left(310\text{K}+\Delta T\right)-\Delta G^{\text{vdw}}\left(310\text{K}-\Delta T\right)}{2\Delta T},$$ (4)

$$\Delta S^{\text{elec}}\left(310\text{K}\right)={-\frac{\partial \Delta G^{\text{elec}}}{\partial T}|}_{310\text{K}}\approx -\frac{\Delta G^{\text{elec}}\left(310\text{K}+\Delta T\right)-\Delta G^{\text{elec}}\left(310\text{K}-\Delta T\right)}{2\Delta T},$$ (5)

where $\Delta T$ is 10 K. Similarly, $\Delta S^{\text{sol}}$ is the sum of $\Delta S^{\text{vdw}}$ and $\Delta S^{\text{elec}}$. To calculate solvation enthalpy and its components, we estimate $\Delta G^{\text{sol}}$, $\Delta G^{\text{vdw}}$, and $\Delta G^{\text{elec}}$ at 310 K as the average of those measured at 300 and 320 K, and use the fact that $\Delta G=\Delta H-T\Delta S$.

Alternatively, we directly calculate solvation enthalpy at 300 and 320 K as the difference in the average, total potential energy of the fully solvated state (aqueous), and the gas phase reference state (referred to as the end point energy (EP) approach):

$$\Delta H^{\text{sol}}\approx \Delta U^{\text{sol}}=\langle U^{\text{aq}}\rangle -\langle U^{\text{gas}}\rangle ,$$ (6)

$$\Delta H^{\text{sol}}\approx \langle U^{\text{total}}\left({\lambda }^{\text{vdw}}=1\cap {\lambda }^{\text{elec}}=1\right)\rangle -\langle U^{\text{total}}\left({\lambda }^{\text{vdw}}=0\cap {\lambda }^{\text{elec}}=0\right)\rangle .$$ (7)

Here, $U^{\text{total}}$ is the sum of all bonded and nonbonded peptide-peptide, peptide-solvent, and solvent-solvent potential energy terms. Whereas the solvation free energy depends only on the peptide-solvent potential energy, the solvation enthalpy and entropy include contributions from all bonded and nonbonded interactions in the system (33). $\Delta S^{\text{sol}}$ at 300 and 320 K is calculated as $T\Delta S=\Delta H-\Delta G$. Note that $\Delta S^{\text{sol}}$ was not further decomposed into its vdw and elec components as in the FD approach. To directly compare to the FD approach, $\Delta S^{\text{sol}}$ and $\Delta H^{\text{sol}}$ were approximated at 310 K as the average of those measured at 300 and 320 K. The change in the heat capacity of solvation is minor and indicates that both the FD approach and the averaging of the thermodynamic quantities to yield estimates at 310 K are reasonable approximations for the temperature range considered.

Error analysis

We use two independent methods to estimate errors (i.e., statistical uncertainties) in $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$ at 300 and 320 K. We briefly describe these methods but a more detailed description can be found in Appendix A. The first method involves estimating the correlation times from autocorrelation functions (ACFs) of $\text{exp}\left(-\beta \Delta U_i\left(t\right)\right)$ for each of the 1748 λ-simulations. We note that ACFs of $\Delta U_i\left(t\right)$ yielded very similar autocorrelation times. Error propagation, corrected for the number of independent observations using the correlation times, is applied to the exponential form of the FEP equation (31) to estimate errors, ${\sigma }_{\text{ACF}}^{\text{vdw}}$ and ${\sigma }_{\text{ACF}}^{\text{elec}}$, in $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$, respectively. In the second method, we use a blocking approach (34, 35) in which trajectories of $\Delta U_i^{\text{vdw}}$ and $\Delta U_i^{\text{elec}}$ are broken up into blocks that span λ-space. $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$ are calculated using Eq. 1 and Eq. 2, respectively, for each block and the variance of these block estimates is used to calculate the block standard error (BSE). The BSEs are calculated as a function of block length and the point at which the BSE stops varying with block length will yield error estimates, ${\sigma }_{\text{BSE}}^{\text{vdw}}$ and ${\sigma }_{\text{BSE}}^{\text{elec}}$, of $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$, respectively. The errors measured by these two methods are then propagated, separately, to estimate errors in $\Delta G^{\text{sol}}$.

For the FD approach, ACF and BSE errors in $\Delta G^{\text{sol}}$, $\Delta G^{\text{vdw}}$, and $\Delta G^{\text{elec}}$ are propagated to estimate errors in $\Delta S^{\text{sol}}$, $\Delta S^{\text{vdw}}$, $\Delta S^{\text{elec}}$, $\Delta H^{\text{sol}}$, $\Delta H^{\text{vdw}}$, and $\Delta H^{\text{elec}}$. For the EP approach, autocorrelation times of $U^{\text{aq}}\left(t\right)$ and $U^{\text{gas}}\left(t\right)$ were estimated from their respective ACFs similarly detailed in Appendix A. Errors in $\langle U^{\text{aq}}\rangle$ and $\langle U^{\text{gas}}\rangle$ were corrected for the number of independent observations and then propagated to estimate the error in $\Delta H^{\text{sol}}$. Additionally, BSEs were calculated in a similar manner detailed above but with $\langle U^{\text{aq}}\rangle$ or $\langle U^{\text{gas}}\rangle$ estimated within each block. The error in the endpoint energy estimate of $\Delta H^{\text{sol}}$ calculated via the ACF or BSE approaches were combined with the corresponding errors in $\Delta G^{\text{sol}}$, to estimate the errors in $\Delta S^{\text{sol}}$.

Results

Toward understanding the solvation thermodynamic mechanisms that dictate, in part, the structural properties of disordered oligoglycine chains, we have decomposed the solvation free energy $\left(\Delta G^{\text{sol}}\right)$ of oligoglycine into its vdw $\left(\Delta G^{\text{vdw}}\right)$ and elec $\left(\Delta G^{\text{elec}}\right)$ components as a function of chain length and force field using stratified FEP. The solvation free energy was further decomposed into its entropic $\left(\Delta S^{\text{sol}}\right)$ and enthalpic $\left(\Delta H^{\text{sol}}\right)$ contributions using two independent approaches (i.e., the FD and EP approaches as discussed in the Materials and Methods). The FD approach also yields the vdw and elec components of $\Delta S^{\text{sol}}$ and $\Delta H^{\text{sol}}$. Because the FD approach provides a more accurate estimate of $\Delta S$ at the midpoint (i.e., 310 K) and to compare results from both approaches, $\Delta S^{\text{sol}}$ and $\Delta H^{\text{sol}}$ calculated via the EP approach were approximated at 310 K as the average of those measured at 300 and 320 K. We also investigate the effects of conformational flexibility on these various thermodynamic quantities. Below we present the results for each quantity at 310 K, and provide the results at 300 and 320 K in the Supporting Material.

Solvation free energy

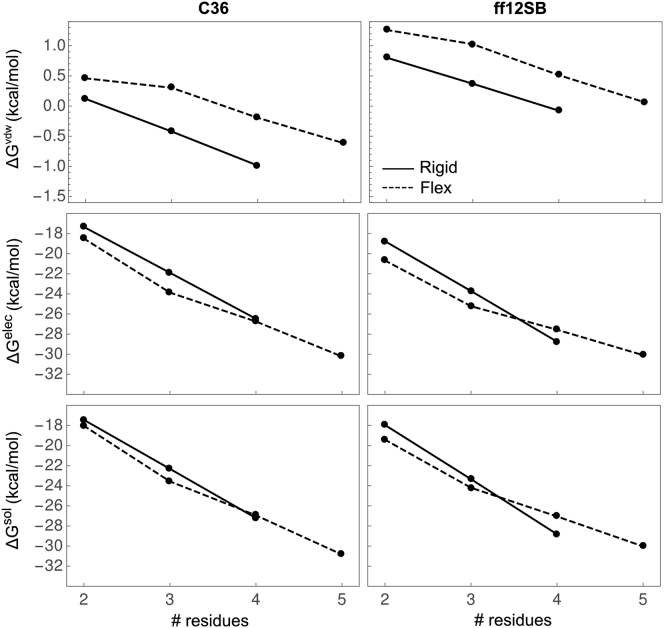
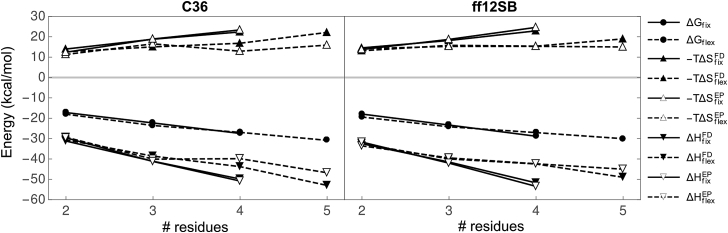
Fig. 1 depicts the scaling of $\Delta G^{\text{sol}}$, $\Delta G^{\text{vdw}}$, and $\Delta G^{\text{elec}}$ with chain length (N) for fixed, rigid-extended (solid line) and flexible (dashed line) oligoglycines from FEP simulations with C36 and ff12SB at 310 K. The subscripts “fix” and “flex” are used to denote solvation free energies from simulations in which oligoglycine is fixed in an extended, rigid conformation or allowed to freely explore conformation space, respectively. We used two independent approaches to estimate errors. These approaches are detailed in the Materials and Methods and Appendix A. Both methods yield errors ∼1 kcal/mol or less for the ΔG values, suggesting our estimates have converged to sufficiently high precision to infer mechanism. Table S1 in the Supporting Material provides $\Delta G^{\text{vdw}}$, $\Delta G^{\text{elec}}$, and $\Delta G^{\text{sol}}$ for each oligoglycine at 300 and 320 K, which were averaged to yield estimates of those at 310 K.

Figure 1.

Solvation free energy of rigid/extended (solid) and flexible (dashed) oligoglycines at 310 K as a function of chain length from simulations with the C36 (left) and ff12SB (right) force fields. The vdw, elec, and overall solvation free energy are shown in order from top to bottom. Errors associated with each quantity can be found in Table S1.

Both force fields yield similar trends in the scaling of $\Delta G_{\text{fix}}^{\text{sol}}$, $\Delta G_{\text{flex}}^{\text{sol}}$, and their vdw and elec components with N. For example, $\Delta G_{\text{fix}}^{\text{sol}}$ is negative and continues to decrease linearly as the number of residues increase. The average difference, or slope, in $\Delta G_{\text{fix}}^{\text{sol}}$ between $Gl{y}_n$ and $Gl{y}_{n+1}$ is −5.12 and −5.44 kcal/mol per peptide unit for C36 and ff12SB, respectively. This scaling is consistent with the −5.00 and −5.48 kcal/mol per peptide unit reported by Tomar et al. (36) and Hu et al. (21) using different force fields and conformations of oligoglycine. Compared to $\Delta G_{\text{fix}}^{\text{sol}}$, $\Delta G_{\text{flex}}^{\text{sol}}$ decreases at a slower rate with respect to N with an average contribution per peptide of −4.27 kcal/mol for C36 and −3.54 kcal/mol for ff12SB. There appears to be a transition occurring at Gly₃ that estimates the scaling of the longer oligoglycines. In terms of the free energy components, both $\Delta G^{\text{elec}}$ and $\Delta G^{\text{vdw}}$ are negative for rigid and flexible oligoglycines and also depend on conformational flexibility. $\Delta G_{\text{flex}}^{\text{vdw}}$ is consistently, slightly less favorable than $\Delta G_{\text{fix}}^{\text{vdw}}$, but their contributions to $\Delta G^{\text{sol}}$ are small in comparison to their dominant electrostatic counterparts. The differences in $\Delta G^{\text{elec}}$ between force fields (Fig. S1 in the Supporting Material) are ∼2 kcal/mol or less with those for $\Delta G^{\text{sol}}$ at ∼1 kcal/mol at both temperatures.

Solvation entropy

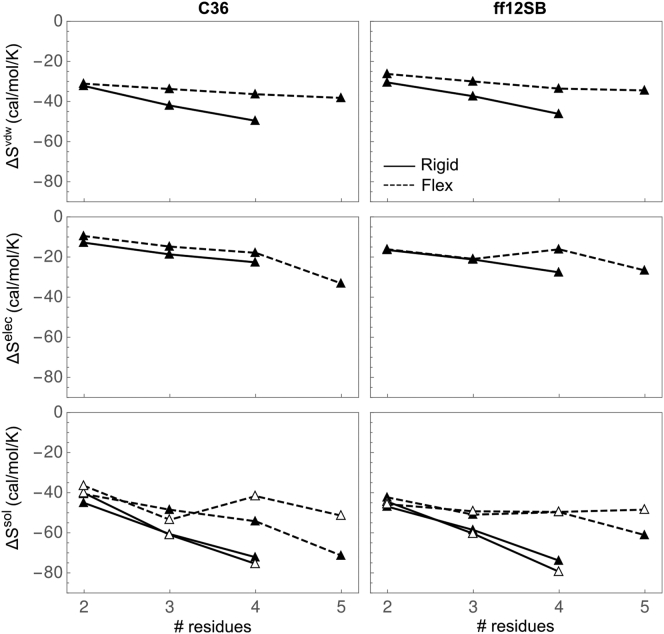
In the FD approach, solvation entropy was calculated from the numerical derivative with respect to temperature using the free energy at 300 and 320 K. Fig. 2 (solid triangles) shows the scaling of $\Delta S^{\text{sol}}$ and its elec $\left(\Delta S^{\text{elec}}\right)$ and vdw $\left(\Delta S^{\text{vdw}}\right)$ components for rigid and flexible oligoglycine. Data are provided in Table S2. Similar to the trends in solvation free energy, we find $\Delta S_{\text{fix}}^{\text{sol}}$, $\Delta S_{\text{fix}}^{\text{vdw}}$, and $\Delta S_{\text{fix}}^{\text{elec}}$ to be reasonably linear with respect to the number of residues with average contributions per peptide being −13.55, −8.68, and −4.90 cal/mol/K, respectively, for C36 and −13.48, −7.85, and −5.58 cal/mol/K for ff12SB. $\Delta S_{\text{flex}}^{\text{sol}}$, while still unfavorable, is more positive than $\Delta S_{\text{fix}}^{\text{sol}}$, indicating that conformational flexibility reduces the entropic penalty of solvating these short oligoglycines. The separation between $\Delta S_{\text{flex}}^{\text{sol}}$ and $\Delta S_{\text{fix}}^{\text{sol}}$ is largely due to the differences in the scaling of the vdw component, which contributes more to the overall solvation entropy than the elec component.

Figure 2.

Solvation entropy of rigid/extended (solid) and flexible (dashed) oligoglycine as a function of chain from simulations with the C36 (left) and ff12SB (right) force fields using the FD (solid triangle) and EP (open triangle) approaches. The vdw, elec, and overall solvation entropy are shown in order from top to bottom. Error estimates are provided in Tables S2 and S3.

In the EP approach, $\Delta S^{\text{sol}}$ at 300 and 320 K was calculated first by directly estimating $\Delta H^{\text{sol}}$ as the difference in the average potential energy of the system in the fully solvated state relative to the gas phase at both temperatures, then using $\Delta G^{\text{sol}}=\Delta H^{\text{sol}}-T\Delta S^{\text{sol}}$ to solve for $\Delta S^{\text{sol}}$ (Fig. S2; data provided in Table S3). To compare to the FD approach, $\Delta S^{\text{sol}}$ at 310 K was approximated as the average of $\Delta S^{\text{sol}}$ at 300 and 320 K. $\Delta S_{\text{fix}}^{\text{sol}}$ and $\Delta S_{\text{flex}}^{\text{sol}}$ calculated by the EP approach scale in a manner consistent with that observed from the FD approach (Fig. 2, open triangle). Again, both force fields yield a similar scaling of $\Delta S^{\text{sol}}$, $\Delta S^{\text{elec}}$, and $\Delta S^{\text{vdw}}$ for rigid and flexible oligoglycine with N (Fig. S3).

Solvation enthalpy

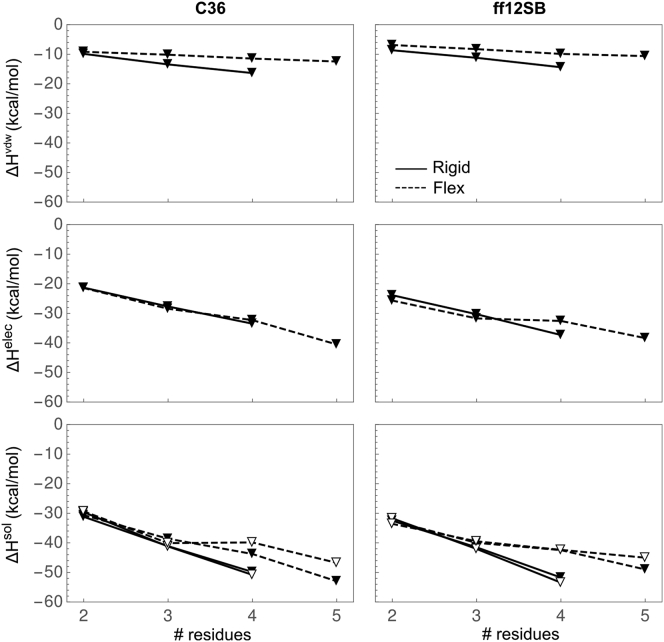
Next, for the FD approach, we calculated solvation enthalpy $\left(\Delta H^{\text{sol}}\right)$ and its components at 310 K using $\Delta H=\Delta G+T\Delta S$. We selected a temperature of 310 K because the finite difference used to approximate $\Delta S$ is more precise at the midpoint than at 300 or 320 K. $\Delta G$ at 310 K was estimated as the average of $\Delta G$ at 300 and 320 K. For the EP approach, $\Delta H^{\text{sol}}$ was directly calculated at 300 and 320 K, then averaged to give $\Delta H^{\text{sol}}$ at 310 K. Fig. 3 shows $\Delta H^{\text{vdw}}$, $\Delta H^{\text{elec}}$, and $\Delta H^{\text{sol}}$ as a function of chain length, force field, and approach for rigid and flexible oligoglycines. Data are provided in Tables S4 and S5. Both $\Delta H_{\text{fix}}^{\text{sol}}$ and $\Delta H_{\text{flex}}^{\text{sol}}$ are large and negative, but the rate of decrease with respect to length of $\Delta H_{\text{flex}}^{\text{sol}}$ is slightly less. The scaling of $\Delta H^{\text{sol}}$ with chain length is predominantly determined by $\Delta H^{\text{elec}}$. The average rate of decrease of $\Delta H_{\text{flex}}^{\text{vdw}}$ is −1.09 and −1.25 kcal/mol/unit for C36 and ff12SB, respectively, which is less than half of those observed for $\Delta H_{\text{fix}}^{\text{vdw}}$. Differences between force fields were slightly larger for $\Delta H$ than $\Delta S$ and $\Delta G$, with differences ranging between −4 and 4 kcal/mol (Fig. S5).

Figure 3.

Solvation enthalpy of rigid/extended (solid) and flexible (dashed) oligoglycine at 310 K as a function of chain from simulations with the C36 (left) and ff12SB (right) force fields calculated by the FD (solid triangle) and EP (open triangle) approaches. The vdw, elec, and overall solvation enthalpy are shown in order from top to bottom.

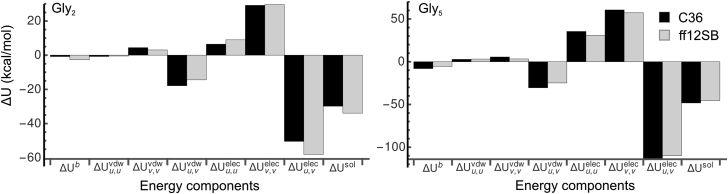
Whereas $\Delta G^{\text{sol}}$ depends only on peptide-solvent interaction energy, $\Delta H^{\text{sol}}$ and $\Delta S^{\text{sol}}$ include bonded and nonbonded intrapeptide contributions as well as a solvent reorganization energy (33). To parse out these contributions, we decomposed $\Delta U^{\text{sol}}$ (i.e., the EP approximation of $\Delta H^{\text{sol}}$) into its various peptide-peptide ($\Delta U_{u,u}^{\text{vdw}}$, $\Delta U_{u,u}^{\text{elec}}$), peptide-solvent ($\Delta U_{u,v}^{\text{vdw}}$, $\Delta U_{u,v}^{\text{elec}}$), solvent-solvent ($\Delta U_{v,v}^{\text{vdw}}$, $\Delta U_{v,v}^{\text{elec}}$), and intrapeptide-bonded $\left(\Delta U^b\right)$ average energies for flexible Gly₂ and Gly₅. Fig. 4 depicts this energetic breakdown. We find that $\Delta H^{\text{sol}}$ is favorable and continues to decrease with chain length due primarily to a favorable, decreasing change in the elec peptide-solvent interaction energy. As expected, this is slightly offset by a positive $\Delta U_{v,v}^{\text{vdw}}$ and much more so by $\Delta U_{v,v}^{\text{elec}}$, or a solvent reorganization penalty. For rigid oligoglycines, bonded and nonbonded intrapeptide energies cancel and favorable peptide-peptide interactions yield a favorable, decreasing $\Delta H^{\text{sol}}$ with chain length. However, for flexible oligoglycines, solvation has the effect of reducing intrapeptide electrostatic energy, resulting in a positive $\Delta U_{u,u}^{\text{elec}}$, and, to a lesser extent, $\Delta U_{u,u}^{\text{vdw}}$, in a length-dependent manner. The bonded, intrapeptide potential energy contributes little to the solvation enthalpy. That the electrostatics dictates the scaling of $\Delta H^{\text{sol}}$ with N is consistent with what we observe by the FD approach.

Figure 4.

Differences in the average energies of the components contributing to $\Delta H^{\text{sol}}\approx \Delta U^{\text{sol}}$ for flexible Gly₂ (left) and Gly₅ (right). The subscript u denotes the solute/peptide and v denotes the solvent. $\Delta U^b$ is the difference between the average bonded intrapeptide energies (e.g., dihedral, bond, angle energies) of oligoglycine in the final, solvated state and the gas phase.

Error analysis

Calculation of entropy differences from free energies requires strict control of errors. Accurately estimating errors in free energy calculations continues to be a challenging problem (31). Here, we used two independent methods to estimate errors, the details of which can be found in the Materials and Methods and Appendix A. Table S1 provides errors in the free energy and its components from the autocorrelation function (ACF) and the BSE approaches. Both approaches demonstrate that the error in $\Delta G_{\text{flex}}^{\text{sol}}$ is largely due to the error in $\Delta G_{\text{flex}}^{\text{elec}}$ whereas the errors in $\Delta G_{\text{fix}}^{\text{vdw}}$ and $\Delta G_{\text{fix}}^{\text{elec}}$ are of similar magnitudes. Errors also increase with chain length. However, the ACF errors are systematically larger than those calculated using the BSE approach. Two reasons may explain, in part, this observation.

First, the procedure used to fit the ACFs to estimate the correlation times appears to be sensitive to weak, long-time correlations (<5% self-similarity and oscillation), which are predominantly present in simulations of flexible oligoglycines in which the electrostatic interactions are turned on. The correlation times across the ${\lambda }^{\text{elec}}$ simulations for flexible oligoglycines ranged from 1 ps to 34 ns and increased with chain length. The BSE approach appears to be less sensitive to these weak, long-time correlations. To test this, we calculated the BSE at each ${\lambda }^{\text{vdw}}$ and ${\lambda }^{\text{elec}}$ at 300 and 320 K for flexible Gly₅ and calculated the correlation times using $BSE=\sigma \sqrt{\tau /N}$, where σ is the variance, τ is the correlation time, and N is the number of samples. While the profiles of correlation times across ${\lambda }^{\text{elec}}$ were similar for both approaches, the correlation times calculated with the BSE approach were orders-of-magnitude (data not shown) less than those reported by the ACF approach. Others have noted that this BSE approach typically underestimates the true correlation time of dynamic observables (34, 37). In contrast, the vdw correlation times differed, at most, by a factor of 2.

Second, we took a conservative approach in estimating the correlation times as four times the decay constant from a best fit of the ACFs to an exponentially decaying function. For these reasons, we interpret the errors from the BSE and ACF approaches as loose lower and upper bounds, respectively, on the true error. The ACF errors, although larger, still indicate that our estimates of $\Delta G^{\text{vdw}}$, $\Delta G^{\text{elec}}$, and $\Delta G^{\text{sol}}$ have converged to a precision <1 kcal/mol for rigid and flexible Gly_2–4 (Table S1) and slightly larger for flexible Gly₅. Due to the propagation of uncertainty and the fact that we are taking a finite derivative in the FD approach, the ACF and BSE errors are larger for $\Delta S^{\text{sol}}$, $\Delta H^{\text{sol}}$ and their vdw and elec components (Tables S2 and S4). Interestingly, persistent, weak correlations were not present in the ACFs of $U^{\text{aq}}\left(t\right)$ and $U^{\text{gas}}\left(t\right)$ as compared to the ACFs of $\text{exp}\left(-\beta \Delta U_i\left(t\right)\right)$. This led to errors (Tables S3 and S5) in $\Delta H^{\text{sol}}$ and $\Delta S^{\text{sol}}$ that were systematically less than those calculated via the FD approach. The BSEs reported by both approaches are more similar. We also do not observe as strong of a length dependence of the errors estimated by the EP approach.

Discussion

Scaling of solvation free energy, enthalpy, and entropy with chain length and the effects of flexibility

Computational free energy methods can be used to measure the thermodynamic properties of disordered polypeptides that are otherwise difficult to access with experiment. Here, we have performed a complete thermodynamic decomposition of the solvation free energy of oligoglycine as a function of chain length (N), force field, and positional constraints. Few studies have considered the scaling of solvation entropy of the protein backbone with the number of residues and the effects of flexibility on this scaling relationship. Accurately estimating the solvation free energy and entropy even for these short oligoglycine models required extensive sampling, particularly for flexible oligoglycines. This study required a total of 1748 simulations for an aggregate simulation time of 92.3 μs.

We find that both force fields yield very similar trends in the scaling of $\Delta G^{\text{sol}}$, $\Delta H^{\text{sol}}$, and $\Delta S^{\text{sol}}$ and their vdw and elec components with N (Figure 1, Figure 2, Figure 3). Fig. 5 shows $\Delta G^{\text{sol}}$, $\Delta H^{\text{sol}}$, and $-T\Delta S^{\text{sol}}$ for rigid-extended and flexible oligoglycines as a function of chain length and force field at 310 K (Tables S6 and S7) calculated by the FD and EP approaches. $\Delta G^{\text{sol}}$ is negative and continues to decrease at a rate similar to that observed in previous studies of oligoglycine fixed in various conformations (21, 36, 38). Unlike for successively larger alkanes (39), the scaling of $\Delta G^{\text{sol}}$ is enthalpically driven and only moderately compensated by unfavorable entropy changes. This is consistent with the transfer free energy of N-methylacetamide (NMA), a peptide group analog, from the gas to solvent phase (14, 40). However, $\Delta G^{\text{sol}}$ of NMA is −10 kcal/mol at 298 K, which is nearly twice as large as the glycine peptide contribution per monomer we find for rigid oligoglycines and larger yet for flexible oligoglycines.

Figure 5.

Thermodynamic decomposition of solvation free energy for rigid/extended (solid) and flexible (dashed) oligoglycines as a function of chain length and force field at 310 K calculated by the FD and EP approaches. (Solid circle) $\Delta G^{\text{sol}}$ calculated by free energy perturbation; (solid and open triangles) $\Delta H^{\text{sol}}$ and $-T\Delta S^{\text{sol}}$ calculated by the FD and EP approaches, respectively. Note that $\Delta H^{\text{sol}}$ and $-T\Delta S^{\text{sol}}$ at 310 K was approximated as their averages at 300 and 320 K.

When considering the effects of flexibility, we find that $-T\Delta S^{\text{sol}}$ increases and $\Delta H^{\text{sol}}$ decreases at a slower rate than their rigid counterparts. However, the increase in entropy associated with solvating flexible oligoglycines offsets the reduction in enthalpic interactions relative to that observed for rigid oligoglycines, and, as a result, differences in $\Delta G_{\text{flex}}^{\text{sol}}$ and $\Delta G_{\text{fix}}^{\text{sol}}$ are less pronounced. The FD and EP approaches predict very similar thermodynamic scaling profiles for the rigid and flexible oligoglycine models. However, the EP approach yields smaller statistical uncertainties and requires half as many FEP simulations to obtain $\Delta H^{\text{sol}}$ and $\Delta S^{\text{sol}}$ as the FD approach.

Given the trends in the scaling relationships established here for short oligoglycines, we expect the differences in $\Delta G_{\text{flex}}^{\text{sol}}$, and their entropic and enthalpic components, to be amplified for longer oligoglycines. As we will discuss below, this will have implications for the validity of group-additive models to predict the thermodynamics of long, disordered polypeptides from the thermodynamic properties of its isolated chemical groups. Future work will address the predictive capabilities of these scaling relationships for longer oligoglycines.

Decomposing $\Delta G^{\text{sol}}$, $\Delta H^{\text{sol}}$, and $\Delta S^{\text{sol}}$ into vdw and elec components provides insight into the mechanisms that yield their scaling relationships with N. $\Delta G^{\text{elec}}$ dominates $\Delta G^{\text{vdw}}$ and largely dictates the scaling of $\Delta G^{\text{sol}}$, as has been previously noted for various oligoglycine and oligoalanine chains (21, 24). On the other hand, $\Delta S^{\text{vdw}}$ is of the same order of magnitude of $\Delta S^{\text{elec}}$ but contributes more to $\Delta S^{\text{sol}}$. This is consistent with the idea that inserting a large vdw cavity in water reduces the translational entropy of the solvent and disrupts the water-water interaction network more so than the subsequent charging of the cavity (41, 42). The inverse relationship between enthalpy and entropy is also apparent in their vdw and elec components with $\Delta H^{\text{elec}}$ being ∼1.5–3 times more favorable than $\Delta H^{\text{vdw}}$ for rigid and flexible oligoglycines. In general, both the absolute value and the rate of decrease of the vdw and elec components of $\Delta G$, $\Delta H$, and $\Delta S$ change when positional constraints are not imposed on the oligoglycine chain. Most notably, $\Delta G_{\text{flex}}^{\text{vdw}}$, $\Delta H_{\text{flex}}^{\text{vdw}}$, and $\Delta S_{\text{flex}}^{\text{vdw}}$ are consistently more positive than their fixed counterparts. We note that in a previous study in which oligomers of alanine were decomposed in a similar fashion, vdw solvation free energies were found to be consistently more positive for flexible alanine polypeptides than their rigid-extended counterparts (24). Flexibility has the consequence of giving less instantaneous vdw exposure to the solvent for most conformations as favorable peptide-solvent interactions may be screened. This is understandable, given the range of vdw attractions to solvent. Note that, for flexible alanine chains, the slope of $\Delta G_{\text{flex}}^{\text{vdw}}$ turned positive. But just as in this study, the overall solvation free energy was dominated by the elec component.

Force-field comparison

Figs. S1, S3, and S5 show the differences in $\Delta G^{\text{sol}}$, $\Delta H^{\text{sol}}$, and $\Delta S^{\text{sol}}$ and their components between force fields. Differences in $\Delta G^{\text{sol}}$ between C36 and ff12SB are within 1–2 kcal/mol for rigid and flexible Gly_2–5. Interestingly, there appears to be a compensatory relationship between force fields in that ff12SB consistently underestimates $\Delta G^{\text{vdw}}$ relative to C36, but overestimates $\Delta G^{\text{elec}}$ for Gly_2–4, resulting in smaller differences in $\Delta G^{\text{sol}}$. These cancellations are also observed for flexible Gly₅, but do not follow the aforementioned trend. Hu et al. (21) previously measured $\Delta G^{\text{sol}}$ for various fixed conformations of Gly_2–5 using the CHARMM27 (C27) force field and found an average contribution per peptide of −5.48 kcal/mol, which is consistent with the −5.26 and −5.57 kcal/mol/unit we find with C36 and ff12SB, respectively. However, the absolute values of $\Delta G^{\text{sol}}$ were different. For example, they reported a $\Delta G^{\text{sol}}$ of Gly₅ that was roughly 10 kcal/mol less than what we find with C36 and ff12SB, which further highlights the effects of flexibility on solvation free energy.

While employing different strategies, C36 and ff12SB were parameterized to match experimental and theoretical structural and thermodynamic data (22, 23). We have previously shown that C36 generates structural ensembles of Gly₃ and Gly₁₀ to a greater extent, which are more extended and less compact than ff12SB with significant differences in individual dihedral angle populations (17). The small differences we observe in $\Delta G^{\text{sol}}$ between C36 and ff12SB may suggest either that the solvation thermodynamic properties of oligoglycine are robust to differences in force-field structural parameters or that the chain lengths considered here are too short to realize significant differences in structural ensembles generated by C36 and ff12SB. The former implies a degenerate relationship between the structural manifold of oligoglycine and its solvation thermodynamics. Even for Gly₅, differences in force fields are pronounced, with ff12SB sampling more compact conformations than C36 (data not shown). Given the striking differences in the structural ensemble of Gly₁₀ produced by these two force fields (17), we expect differences in the scaling of $\Delta G^{\text{sol}}$ to become more apparent for larger N. While this clearly needs to be tested, we note that caution should be exercised when attempting to connect structural ensembles to biological mechanisms from such potential models (i.e., force fields) even when those models are in thermodynamic agreement.

Implications for group-additivity

The notion of group-additivity posits that the solvation free energy of a macromolecule is the result of additive contributions of the chemical groups that comprise it. Additive principles have been applied to and observed in numerous studies of hydrocarbon and protein systems (18, 21, 43, 44, 45, 46, 47, 48, 49). However, evidence continues to mount that additivity is context-specific, and depends on local chemical environment and molecular conformation/geometry. While rough estimates are possible, the method may not accurately predict the solvation free energy of amino acids and proteins (20, 25, 36, 38, 50, 51, 52, 53, 54, 55). From a study of 50 conformations of decaglycine, we have shown that even an individual atom’s contribution to $\Delta G^{\text{vdw}}$ and its repulsive component are not well defined and vary with respect to conformation; the result depends on local chemical environment and force field, which is contrary to what one would expect if additivity held (20).

While chemical context and conformation matter, the apparent linear scaling of $\Delta G_{\text{fix}}^{\text{sol}}$ with N and the relatively small differences between $\Delta G_{\text{flex}}^{\text{sol}}$ and $\Delta G_{\text{fix}}^{\text{sol}}$ observed here are consistent with an additive contribution of the glycine peptide unit to the overall solvation free energy. However, our data also indicate different rates of decrease of $\Delta G_{\text{flex}}^{\text{sol}}$ and $\Delta G_{\text{fix}}^{\text{sol}}$ with N. A recent study (36) has shown that the binding energy of a glycine peptide with the solvent depends on or is correlated with that of its neighboring peptides for a series of extended, fixed oligoglycines. They note that correlated fluctuations can change the free energy of the solute and this effect occurs over spatially distant moieties. For longer, flexible oligoglycines, structural fluctuations and long-range peptide-peptide interactions alter the local solvent structure around any one glycine peptide in the chain from that of the linear peptide. As a result, the contribution of each glycine peptide to the overall solvation free energy of the entire chain is conditioned by both its near and spatially more distant neighbors. These correlations or cooperative effects could not have been predicted from the solvation free energy of an isolated glycine and, thus, leads to a departure from group-additivity. This may explain why $\Delta G_{\text{flex}}^{\text{sol}}$ and $\Delta G_{\text{fix}}^{\text{sol}}$ decrease at different rates initially for short oligoglycines and oligoalanines (24) and suggests that longer chain lengths will be needed to better resolve the effects of flexibility and structural correlations on the solvation free energy of each peptide unit.

Implications for aggregation of short oligoglycines and collapse of long oligoglycines

If the scaling relationships we establish here hold, then favorable enthalpic interactions with the solvent will continue to drive the decrease in $\Delta G^{\text{sol}}$ for long oligoglycines. However, long oligoglycines (N ≥ ∼15) collapse in relatively dilute or infinitely dilute solutions as observed in both experiment and simulation (14, 15, 16). In addition, short oligoglycines become exceedingly insoluble with visible aggregates forming for Gly₅ at finite (millimolar) concentrations (18, 19). Thus, solvation does not drive the aggregation of short oligoglycines and the collapse of long oligoglycines.

We previously investigated the hydrophobic effect as a potential force driving the collapse of decaglycine (20). $\Delta G^{\text{vdw}}$ is often defined as the hydrophobic solvation free energy, and, as seen for macromolecules and various alkanes (39), it is expected to increase roughly linearly with solvent-exposed surface area $\Delta G^{\text{vdw}}={\gamma }^{\text{vdw}}A$, where ${\gamma }^{\text{vdw}}$ is the implied surface tension, independent of the chemical properties of the solute and A is the exposed surface area (56, 57). Others have suggested that $\Delta G^{\text{vdw}}$ should be split into an attractive $\left(\Delta G^{\text{att}}\right)$ and repulsive $\left(\Delta G^{\text{rep}}\right)$ component and that $\Delta G^{\text{rep}}$ should increase linearly with $A\left(\Delta G^{\text{rep}}={\gamma }^{\text{rep}}A\right)$ (58, 59). For a detailed review on various theories of hydrophobicity, we refer to Harris and Pettitt (54) and Ben-Amotz (60). A solvation free energy that increases with A would favor the initial folding or collapse of proteins by limiting the surface area exposed to solvent. Interestingly, from our study of 50 conformations of decaglycine, we found that $\Delta G^{\text{vdw}}$ actually favors extended conformations with ${\gamma }^{\text{vdw}}<0$ because $-{\gamma }^{\text{att}}>{\gamma }^{\text{rep}}$ and that ${\gamma }^{\text{rep}}$ was weakly correlated, if at all, with A and depended on the conformation of decaglycine (20). Taking N as a proxy for A, in this study we also find that ${\gamma }^{\text{vdw}}<0$, but it depends both on force field and flexibility. While we did not further decompose $\Delta G^{\text{vdw}}$ here, it is reasonable to assume that the attractive component outweighs the repulsive component. Tomar et al. (61) similarly find that attractive peptide-solvent dispersion interactions can prevent the collapse of deca-alanine. This seemingly counterintuitive observation that water-mediated, hydrophobic interactions promotes chain expansion rather than collapse as the surface area (i.e., solute size or chain length) increases is discussed in detail in Ben-Amotz (62).

A reasonable explanation for the observed collapse of long oligoglycines and their insolubility is that peptide-peptide interactions outcompete the still favorable peptide-solvent interactions—an observation that could not have been predicted from the solvation free energies of short, isolated oligoglycines. Using single molecule fluorescence correlation spectroscopy, Teufel et al. (15) found the hydrodynamic radius of gyration (R_h) of Gly₂₀ to be significantly less than that of NME-Gly₂₀ (wherein the amide hydrogens of Gly₂₀ were replaced with methyl groups). They conjectured that the methyl groups preclude the formation of backbone H-bonds resulting in the observed increase in solubility and R_h of NME-Gly₂₀ relative to Gly₂₀. In another study using MD simulations, Karandur et al. (16) found that the collapse of Gly₁₅ and Gly₂₅ may be explained by nonhydrogen-bonding, intrapeptide dipole-dipole interactions. In a similar manner, these dipole-dipole correlations and charge layerings were also observed to stabilize clusters or aggregates of Gly₅ (19). It appears that as chain length or concentration increase, and subsequently the number of available intra- or interpeptide interactions increase, these interactions are favored over peptide-solvent interactions. Uversky et al. (4) has noted that the extent of collapse or compaction of IDPs is, in part, a length-dependent property and that “…weak, intramolecular interactions can be unspecifically amplified by an increase in protein size.”

Alternatively, if the thermodynamic scaling relationships presented here do not hold, then at some longer chain length, $T\Delta S^{\text{sol}}$ may overtake $\Delta H^{\text{sol}}$ and the initial collapse of long oligoglycines would be entropically driven, as others have noted (14). In this situation, collapsed states may be further favored via backbone interactions. So group-additive models would fail to predict the solvation thermodynamics of long oligoglycines from short ones. However, the scaling of $\Delta G^{\text{sol}}$, $\Delta H^{\text{sol}}$, and $\Delta S^{\text{sol}}$ with chain length for shorter oligoglycines may provide upper bounds on these quantities for longer oligoglycines by explicitly neglecting structural correlations between short segments that comprise the larger chain. Further work will need to assess the predictive capabilities of the scaling relationships we established, and whether a thermodynamic transition exists in which a negative entropic component to the free energy drives collapse of longer oligoglycines.

Conclusion

The structural ensemble of an IDP/IDR is the result of a complex competition between intrapeptide and peptide-solvent interactions (63, 64, 65). A number of determinants, like chain length (4), sequence composition (5), and charge patterning (66), influence the propensity of an IDP/IDR to adopt compact or extended structures. The protein trinity hypothesis (1, 2), and its variants (3), have been useful in classifying or characterizing the structural properties of IDPs/IDRs and relating those properties to biological function. Here, we sought to gain insight into the solvation thermodynamics of long chains by considering isolated, short oligoglycine chains more amenable to computational free energy methods. IDRs, especially those found in the disordered regulatory domains of nuclear transcription factors (13), are enriched with oligoglycine tracts and glycine content (5, 12).

We have performed a complete thermodynamic decomposition of the solvation free energy into its enthalpic and entropic components as well as each of their vdw and elec contributions as functions of chain length. For both rigid and flexible oligoglycine models, the decrease in $\Delta G^{\text{sol}}$ with chain length is enthalpically driven with only a weak entropic compensation. Solvation free energies of alkanes and polypeptides are often measured by imposing positional constraints on their structures. Here we have shown that the rate of decrease of $\Delta G^{\text{sol}}$, $\Delta S^{\text{sol}}$, $\Delta H^{\text{sol}}$, and their vdw and elec components with N depends on conformational flexibility; however, longer chain lengths may be needed to better resolve differences between $\Delta G_{\text{flex}}^{\text{sol}}$ and $\Delta G_{\text{fix}}^{\text{sol}}$. The differences in the initial rate of decrease of $\Delta G_{\text{flex}}^{\text{sol}}$ and $\Delta G_{\text{fix}}^{\text{sol}}$ for shorter oligoglycines may be due to local solvent reorganization around individual peptide groups brought on by correlated, structural fluctuations (i.e., near and spatially distant neighbor effects) as proposed by Tomar et al. (36). For these reasons, we anticipate differences $\Delta G_{\text{flex}}^{\text{sol}}$ and $\Delta G_{\text{fix}}^{\text{sol}}$ to become more pronounced for longer chain lengths where long-range interactions (e.g. excluded volume) are more prominent and weak peptide-peptide interactions are amplified.

Previously, we have shown that the C36 and ff12SB fields yield considerably different conformational ensembles of Gly₃ and Gly₁₀ with C36 sampling more extended oligoglycine structures (17). Even for Gly₅ we find ff12SB to sample more compact structures than C36 (data not published). Interestingly, these force fields, both of which were parameterized with different structural and thermodynamic target data, yield remarkably similar scaling relationships of $\Delta G_{\text{flex}}^{\text{sol}}$, $\Delta S_{\text{flex}}^{\text{sol}}$, and $\Delta H_{\text{flex}}^{\text{sol}}$ with chain length. This seems to imply a degenerate relationship between conformational ensemble and solvation thermodynamics, and complicates the ability to make consistent mechanistic inferences.

A favorable, enthalpically driven solvation free energy that continues to decrease with chain length (or surface area) does not account for the observed insolubility of Gly₅ (18, 19) or the preferred collapse of longer oligoglycines (14, 15, 16). Alternatively, our work supports the idea that peptide-peptide interactions outcompete favorable peptide-solvent interactions. Whether solvation entropy promotes the collapse of longer oligoglycines outside this scope of work remains to be seen. Attempting to predict the solvation thermodynamics of longer, disordered polypeptides from that observed for shorter chain segments where intrapeptide interactions are limited may be problematic and render group-additive models less useful.

While there is a tendency for long oligoglycines to collapse, they adopt a diverse set of conformations (14, 16, 17, 21, 67) with shorter chain segments assuming extended conformations more exposed to the solvent. This observation, in combination with the fact that we find short oligoglycine tracts to favorably interact with solvent, may suggest that the conformational ensemble of long oligoglycine chains could be shifted to favor more extended or collapsed states without the need to overcome excessively high free energy barriers. In this way, the protein backbone provides a scaffold amenable to both collapsed-disorder and extended-disorder and that evolutionary forces have selected unique combinations of side chains to alter the distribution of these two states.

Author Contributions

J.A.D. was responsible for performing the free energy calculations, error analysis, interpretation, and cowriting the article. R.C.H. was responsible for thermodynamic analysis and interpretation. B.M.P. was responsible for aspects of the project design, interpretation of the results, and cowriting the article.

Editor: Amedeo Caflisch.

Appendix A

The free energy change at a particular λ, $\Delta G_i$, is a nonlinear function of $\Delta U_i$ measured from an MD simulation and is given by Eq. A.1 below. We drop the vdw and elec superscripts as the following applies to both components. While the simulations were performed in the NPT ensemble, we are neglecting the small contributions of pressure and volume to the free energy.

$$\Delta G_i=-\frac{1}{\beta }\text{ln}\left[\frac{1}{N_i}{\sum }_{j=1}^{N_i}\text{exp}\left(-\beta \Delta U_{i,j}\right)\right],$$ (A.1)

where N_i is the number of observations or frames from a simulation with ${\lambda }_i$, j indexes each frame, and $\Delta U_{i,j}=U{\left({\lambda }_{i+1}\right)}_j-U{\left({\lambda }_i\right)}_j$. $\Delta G$ is then the sum of the contributions $\Delta G_i$:

$$\Delta G={\sum }_{i=1}^n\Delta G_i,$$ (A.2)

where n is the number of λ-values and will differ for the vdw and elec components.

Time correlation analysis

For a function $f\left(x_1,x_2\dots \right)$, that is a linear combination of independent, random variables $x_1,x_2\dots$, the variance of $f\left(x_1,x_2\dots \right)$ is given by Eq. A.3 (i.e. error propagation):

$${\sigma }_f^2={\left(\frac{\partial f}{\partial x_1}\right)}^2{\sigma }_{x_1}^2+{\left(\frac{\partial f}{\partial x_2}\right)}^2{\sigma }_{x_2}^2+\dots$$ (A.3)

To calculate the variance of $\Delta G_i$ at ${\lambda }_i$ $\left({\sigma }_{\Delta G_i}^2\right)$, we apply Eq. A.3 but with only one independent variable $\left(\Delta U_i\right)$, to Eq. A.1, which gives

$${\sigma }_{\Delta G_i}^2=\frac{1}{N_i^{\text{eff}}{\beta }^2}\frac{{\langle \text{exp}\left(-2\beta \Delta U_i\right)\rangle }_i}{{\langle \text{exp}\left(-\beta \Delta U_i\right)\rangle }_i^2}-\frac{1}{N_i^{\text{eff}}{\beta }^2},$$ (A.4)

$$N_i^{\text{eff}}=\frac{N_i}{\frac{2{\tau }_i}{\Delta t}+1}.$$ (A.5)

$N_i^{\text{eff}}$ is the effective number of independent observations from a simulation, ${\tau }_i$ is the correlation time, and $\Delta t$ is the time interval at which the $\Delta U_i$ values were saved. To determine ${\tau }_i$, we first generated the time ACF, $C\left(t\right)$, of $\text{exp}\left(-\beta \Delta U_i\left(t\right)\right)$ for each simulation. Visual inspection of the ACFs showed an initial, rapid decay in correlations, followed in many cases by a second, slower decay as the ACF approaches zero. Due to the large number of simulations and to capture the two-phase decay, we fit the ACFs with a double exponential function:

$$C_{\text{fit}}\left(t;{\gamma }_1,{\gamma }_2\right)=A_1\text{exp}\left(\frac{-t}{{\gamma }_1}\right)+A_2\text{exp}\left(\frac{-t}{{\gamma }_2}\right),$$ (A.6)

where ${\gamma }_1$ and ${\gamma }_2$ are the decay rate constants and ${\gamma }_1$ < ${\gamma }_2$. If the double exponential fit failed or A₂ < 0.01, the ACFs were fit with a single exponential. To improve the likelihood of capturing the true correlation time, the correlation times were conservatively estimated as ${\tau }_i=4{\gamma }_2$ or ${\tau }_i=4{\gamma }_1$ for the double or single exponential fits, respectively. In the situations where the fits yielded ${\tau }_i$ < 0, we took a conservative approach and set ${\tau }_i$ to 1 ps (i.e., $\Delta t$). These correlation times were used with Eq. A.4 to estimate the errors, ${\sigma }_{\text{ACF}}^{\text{vdw}}$ and ${\sigma }_{\text{ACF}}^{\text{elec}}$ (square root of the variance), in $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$ at 300 and 320 K. For the FD approach, Eq. A.3 was used to estimate errors in $\Delta G^{\text{sol}}$ at both temperatures, $\Delta S^{\text{sol}}$, $\Delta H^{\text{sol}}$, and their vdw and elec components. For the EP approach, ACFs of $U^{\text{aq}}\left(t\right)$ and $U^{\text{gas}}\left(t\right)$ were similarly fit to Eq. A.6 and their autocorrelation times estimated as described above. Variances of $\langle U^{\text{aq}}\rangle$ and $\langle U^{\text{gas}}\rangle$ were adjusted for the effective number of independent observations (Eq. A.5), and Eq. A.3 was used to estimate the error in $\Delta H^{\text{sol}}$ at 300 and 320 K. Equation A.3 was then used to estimate the error in $\Delta S^{\text{sol}}$ at both temperatures.

BSE analysis

Separately for the vdw and elec components, we construct a matrix of $\Delta U_i$ -values in which the columns are particular λ-values that span either ${\lambda }^{\text{vdw}}$ or ${\lambda }^{\text{elec}}$ and the rows are time points. The matrix has dimensions N × n, where N is the total number of frames and n is the number of λ-values—subscripts have been dropped because all simulations for the vdw and elec pathways, respectively, were simulated for the same length of time and number of λ-values. The matrix is then broken into blocks of a particular length such that N = M × b, where M is the number of submatrices of dimensions b × n and b is the block length. For a given b, $\Delta G$ values are calculated using Eq. 1 for each of the M blocks. The BSE is the standard deviation of these block free energies divided by the square root of the number of blocks, M. A series of BSE values are computed for a range of block lengths and the error is estimated at the point in which the BSE curve plateaus or BSE stops varying with block length. A maximum block length of 8 and 12 ns were used for fixed and flexible Gly_2-4 and flexible Gly₅, respectively. Taking a conservative approach, we estimate the errors ${\sigma }_{\text{BSE}}^{\text{vdw}}$ and ${\sigma }_{\text{BSE}}^{\text{elec}}$ in $\Delta G^{\text{vdw}}$ and $\Delta G^{\text{elec}}$ by taking the maximum BSE across the range of block lengths. Equation A.3 was used to estimate the errors in solvation free energy at 300 and 320 K, solvation entropy, solvation enthalpy, and their vdw and elec components. For the EP approach, BSEs were calculated in a similar manner except with $\langle U^{\text{aq}}\rangle$ or $\langle U^{\text{gas}}\rangle$ estimated within each block. Equation A.3 was then used to estimate the BSE of $\Delta H^{\text{sol}}\approx \langle U^{\text{aq}}\rangle -\langle U^{\text{gas}}\rangle$, which was further combined with the BSE of $\Delta G^{\text{sol}}$ to yield the BSE of $\Delta S^{\text{sol}}$ at both temperatures.