Critically evaluating the theory and performance of Bayesian analysis of macroevolutionary mixtures

Significance

We show that Bayesian analysis of macroevolutionary mixtures (BAMM)—a method for identifying lineage-specific diversification rates—is flawed. Exposing the problems with BAMM is important both to empiricists (to avoid making unreliable inferences using this method) and to theoreticians (to focus their efforts on solving the problems that we identify).

Abstract

Bayesian analysis of macroevolutionary mixtures (BAMM) has recently taken the study of lineage diversification by storm. BAMM estimates the diversification-rate parameters (speciation and extinction) for every branch of a study phylogeny and infers the number and location of diversification-rate shifts across branches of a tree. Our evaluation of BAMM reveals two major theoretical errors: (i) the likelihood function (which estimates the model parameters from the data) is incorrect, and (ii) the compound Poisson process prior model (which describes the prior distribution of diversification-rate shifts across branches) is incoherent. Using simulation, we demonstrate that these theoretical issues cause statistical pathologies; posterior estimates of the number of diversification-rate shifts are strongly influenced by the assumed prior, and estimates of diversification-rate parameters are unreliable. Moreover, the inability to correctly compute the likelihood or to correctly specify the prior for rate-variable trees precludes the use of Bayesian approaches for testing hypotheses regarding the number and location of diversification-rate shifts using BAMM.

Evolutionary biologists have long sought to detect patterns and understand the causes of variation in rates of lineage diversification (speciation $-$ extinction). This has motivated the development of several statistical methods for detecting whether (and where) diversification rates have changed across the branches of a phylogeny (1–4). A recent approach—Bayesian analysis of macroevolutionary mixtures (BAMM) (5)—promises to greatly enhance our ability to study this problem.

This important new method offers several key advantages. (i) BAMM is based on an explicit model that describes how diversification rates shift across the branches of a tree. (ii) The underlying branching process is more complex (and presumably more realistic) than those used in previous methods. Specifically, BAMM not only includes parameters for the rate of speciation and extinction, but also accommodates possible time-dependent effects (where the age of a lineage may affect its diversification rate). This is intended to approximate the phenomenon of diversity-dependent diversification (where the number of species in a lineage may affect its diversification rate), which is believed to be a prevalent feature of empirical phylogenies (6). (iii) By virtue of developing this method in a Bayesian statistical framework, BAMM allows us to gauge the uncertainty in our inferences by providing marginal posterior probability densities rather than point estimates of parameters. (iv) By averaging inferences over any number of diversification-rate shifts, BAMM both accommodates uncertainty in the choice of model and avoids potential complications associated with model selection.

BAMM provides estimates of the number and location of diversification-rate shifts across the branches of a tree and also estimates the diversification-rate parameters—speciation, extinction, and time dependence—on each branch of the tree. Because of these potential benefits, BAMM has been enthusiastically embraced by the biological community.

In this study, we critically evaluate this innovative approach. We first show that the theoretical foundation of BAMM is flawed (the likelihood function is incorrect and the prior model is problematic). We then demonstrate via simulation that these theoretical issues compromise the statistical behavior of BAMM (posterior estimates of the number of diversification-rate shifts are highly sensitive to the choice of prior and estimates of the diversification-rate parameters are unreliable). Critically, these theoretical and methodological concerns confound the ability of BAMM to provide valid hypothesis tests of the number and location of diversification-rate shifts.

Theoretical Issues

The objective is to estimate the joint posterior probability density of the BAMM model parameters—the number, k, and location, ξ, of diversification-rate shifts, and the rate parameters ($\lambda ,\mu$, and z describing the rates of speciation, extinction, and temporal dependence) for each branch of the phylogeny. Following Bayes’ theorem, this joint posterior probability density is proportional to the product of the joint prior probability density (which reflects our beliefs about the parameter values before evaluating the data at hand) and the likelihood function (which extracts the information in the data to update the prior to return the posterior probability, reflecting our beliefs about the parameter values after evaluating the data at hand). The joint posterior probability density of the BAMM model parameters is approximated numerically by means of Markov chain Monte Carlo (MCMC) simulation. In this section, we demonstrate that the likelihood function in BAMM is incorrect, and that the prior it uses to describe diversification-rate shifts across the tree is problematic.

The Likelihood Function in BAMM Is Incorrect.

The likelihood function is the heart of any likelihood-based inference method, because it is the vehicle that conveys the information in the data to estimate the parameters of interest. The likelihood function in BAMM extends the theory developed to assess the impact of a discrete binary trait on rates of lineage diversification under the binary state speciation and extinction (BiSSE) model (7). Briefly, the BiSSE model describes the evolution of a binary trait—with parameters $q_{01}$ and $q_{10}$ that specify the instantaneous rates of change between the two states, 0 and 1—where the rate of lineage diversification depends on the current state. When a lineage is in state 0, the stochastic-branching process has rate parameters ${\varphi }_0=\left\{{\lambda }_0,{\mu }_0\right\}$, and when it is in state 1, the process has rate parameters ${\varphi }_1=\left\{{\lambda }_1,{\mu }_1\right\}$.

There is no analytical solution for computing the probabilities of an observed phylogeny under this branching process, so probabilities are approximated using a numerical algorithm. In outline, this approach recursively solves a set of coupled ordinary differential equations (ODEs), traversing the tree from the tips (where the state of each species is observed) to the root, moving incrementally down the branches in small steps, $\mathrm{\Delta }t$. For each interval, we compute the probability of realizing the observed lineage, N, from some point in the past, t, to the present, given that it is in state $i\in \left\{\mathrm{0,1}\right\}$, which is denoted $D_{N,i}\left(t\right)$. Because this is a birth–death process, we must also compute the probability of unobserved (extinct or unsampled) lineages, which is denoted $E_i\left(t\right)$. These coupled probabilities simply enumerate all of the possible scenarios that could occur during each interval, $\mathrm{\Delta }t$; that is, an episode of speciation, extinction, or character-state change.

BAMM extends this BiSSE modeling framework in three ways: (i) in contrast to BiSSE, where there are two state-specific branching processes, ${\varphi }_0,{\varphi }_1$, BAMM allows the tree to diversify under a countably infinite number of branching processes, ${\varphi }_i$; (ii) in contrast to BiSSE, where the states (0 and 1) of the state-specific process are observed in the extant species, the processes modeled in BAMM are completely unobserved; and (iii) in contrast to BiSSE, where each state-specific process is time homogeneous (i.e., parameters ${\lambda }_0,{\mu }_0,{\lambda }_1,\hspace{0.17em}\text{and}\hspace{0.17em}{\mu }_1$ are constant through time), BAMM allows the speciation rate to vary through time. Specifically, the time dependence of the speciation rate is described by the function ${\lambda }_i\left(t\right)={\lambda }_i\exp \left(z_{i}t\right)$, such that the process is time homogeneous when $z_i=0$ or is time heterogeneous with either an increasing speciation rate when $z_i>0$, or with a decreasing speciation rate when $z_i<0$.

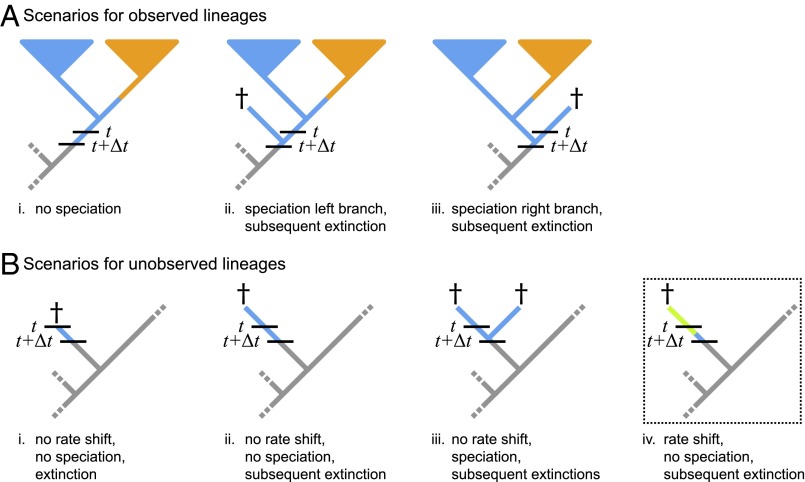
As with BiSSE, the likelihood of the data under the BAMM model is approximated numerically by recursively solving the coupled ODEs, $\text{d}{D}_{N,i}\left(t\right)/\text{d}t$ and $\text{d}{E}_i\left(t\right)/\text{d}t$ (Fig. 1). However, computation of the likelihood in BAMM is flawed. Unlike BiSSE, BAMM cannot enumerate all of the possible (infinite) processes, ${\varphi }_i=\left\{{\lambda }_i,{\mu }_i,z_i\right\}$, that could be realized at a given time on a given branch. Instead, BAMM numerically integrates over possible processes using “data augmentation.” Under this approach, the locations of diversification-rate shifts are first sampled from a prior model (described below); these events are then mapped onto branches of the study tree, and then the probability of the sampled event history is computed. Integration over all possible processes relies on MCMC (i.e., by repeatedly sampling, mapping, and computing probabilities of the realized histories). Although data augmentation provides a viable solution for computing the probabilities of events that occur along extant lineages, this scheme obviously cannot map diversification-rate shifts onto unobserved (extinct) branches of the study tree. Accordingly, computation of the extinction probabilities, $E_i\left(t\right)$, in BAMM ignores scenarios in which diversification-rate shifts occur on extinct lineages (Fig. 1). This is clearly problematic: The probability that a lineage goes extinct depends critically on its diversification-rate parameters, which can change through time under the BAMM model.

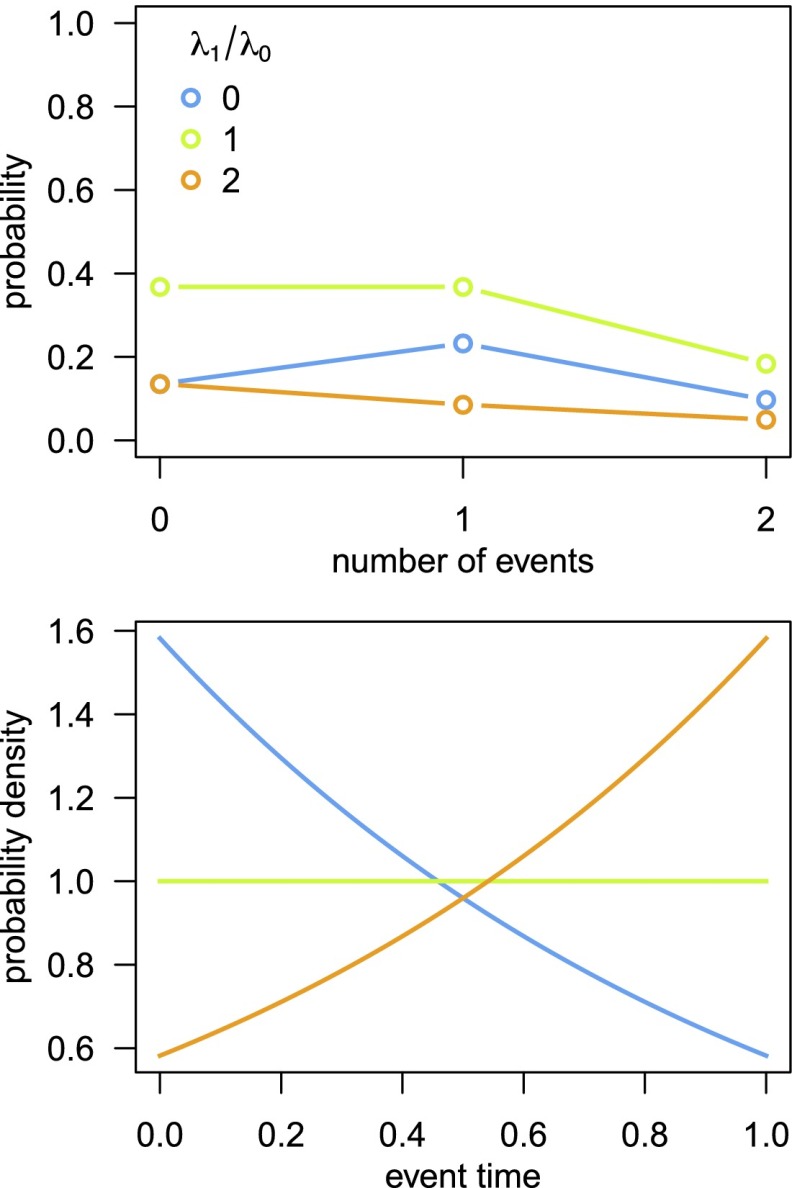
Fig. 1.

Approximation of the likelihood under the BAMM model ignores diversification-rate shifts on extinct lineages. In lieu of an analytical solution for the likelihood function, the probability of observing the data under the BAMM model is approximated by an algorithm that traverses the tree from the tips to the root in small time steps, $\mathrm{\Delta }t$. At each step, two terms are computed: (A) the probability of realizing the observed lineage, N, over time t, given that it is in process i—denoted $D_{N,i}\left(t\right)$—which simply sums over all of the possible scenarios that could occur in the instant $\mathrm{\Delta }t$, and; (B) the probability of unobserved (extinct or unsampled) lineages, $E_i\left(t\right)$, which is computed similarly. The last scenario—iv, where diversification-rate shifts occur on an extinct lineage—is not included in the likelihood computation, causing BAMM to incorrectly estimate the extinction probabilities (cf. Fig. 2).

For these reasons, BAMM can only correctly compute the likelihood when rates of speciation and extinction are constant. When diversification rates vary across lineages, the extinction probabilities estimated by BAMM are strongly biased (Fig. 2). Predictably, for a given frequency of diversification-rate shifts, the bias in extinction probabilities increases with the depth of nodes in the tree; more ancient unobserved lineages will have had more opportunity to experience diversification-rate shifts (Fig. 2B). Similarly, for a branch of a given age, the bias in extinction probabilities increases with the frequency of diversification-rate shifts. The severely biased estimates of the extinction probabilities, in turn, cause extremely biased estimates of the likelihood in BAMM: When diversification-rate shifts occur, the true likelihood of the data are up to 20 times the value computed by BAMM (Fig. 3). Because BAMM cannot correctly compute the likelihood of realizing the data under the model, the method cannot reliably infer the model parameters—the branch-specific diversification-rate parameters—and also confounds Bayesian hypothesis-testing procedures to infer the number and location of significant diversification-rate shifts (discussed below).

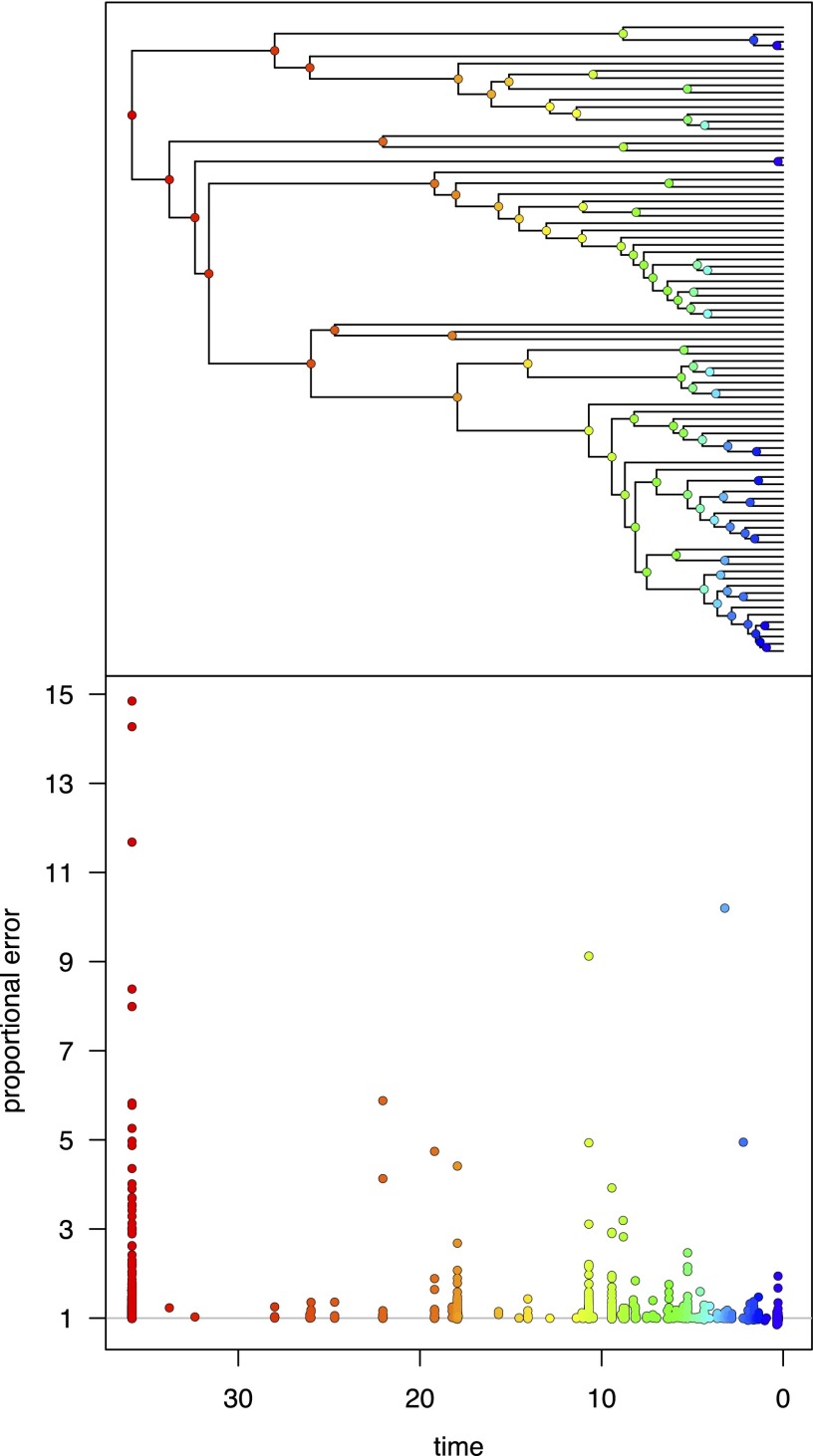
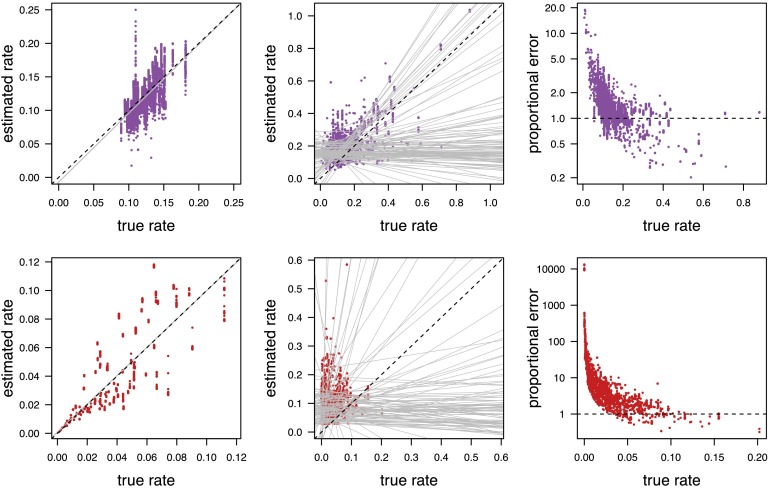
Fig. 2.

BAMM provides biased estimates of the extinction probabilities for individual nodes. We illustrate the bias in the extinction probabilities estimated for individual nodes of the whale phylogeny (Upper). (Lower) A plot of the proportional error in the extinction-probabilities estimates (y axis) for nodes in the tree as a function of node age (x-axis); each point represents an extinction-probability estimate for a single MCMC sample. Proportional error is simply the correct extinction probability (estimated by computationally intensive Monte Carlo simulation, Materials and Methods) divided by the extinction probability estimated by BAMM. (Note that we are concerned with the proportional error in estimates of extinction probabilities, not extinction rates.) Accordingly, if BAMM provided unbiased estimates of extinction probabilities, the proportional error (the ratio of the correct and estimated probabilities) would be 1 (gray line). The bias in the extinction-probability estimates increases predictably toward the root of the tree, where the probability of a diversification-rate shift along an extinct lineage is greater. Note that these results illustrate the bias in the estimated extinction probabilities for a single lineage at various node times in the tree. Bias in the extinction-probability estimates for individual branches has a very large cumulative effect on the likelihood when summed over all branches in the tree (cf. Fig. 3).

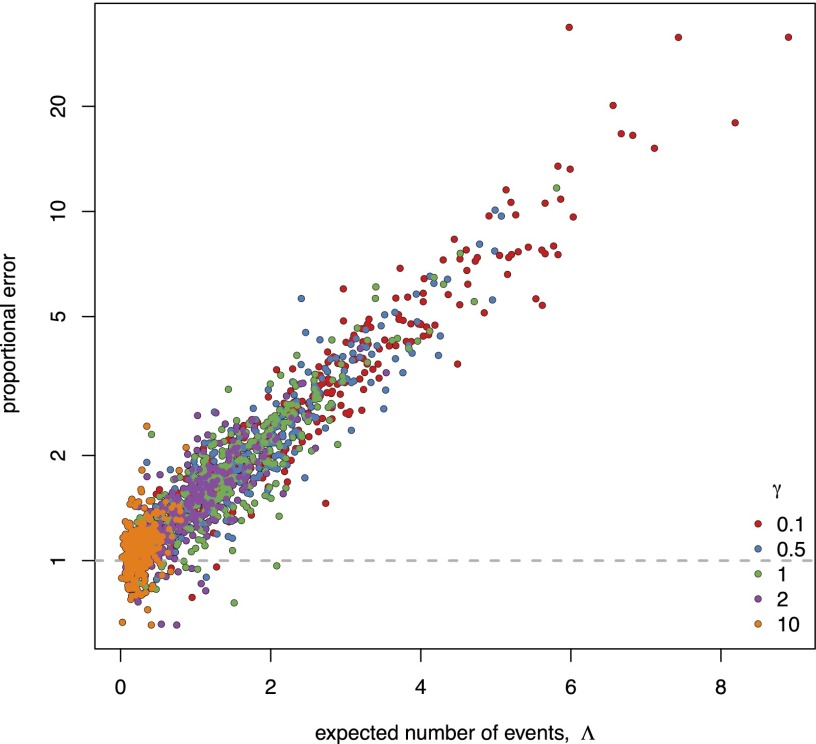
Fig. 3.

BAMM cannot correctly compute the likelihood of the data. When diversification rates vary across branches, the extinction probabilities estimated by BAMM are biased (Fig. 2), which causes the likelihood to be computed incorrectly. We illustrate this problem using the whale tree (Fig. 2, Upper) by computing the proportional error in the overall likelihood estimated by BAMM; this is simply the correct likelihood (estimated using computationally intensive Monte Carlo simulation; see SI Appendix, section S2.2) divided by the likelihood estimated by BAMM. Accordingly, if BAMM computed the likelihood correctly, the proportional error (the ratio of the correct and estimated likelihoods) would be one (dashed line). We plotted the proportional error in the likelihood estimated by BAMM (y axis) against the number of events (x axis) over a range of priors for the expected number of diversification-rate shifts, $\gamma =\left\{0.1,0.5,\mathrm{1,2,10}\right\}$ (indicated by the colors of the dots shown in the inset legend). When rates of diversification vary across branches, the likelihood of the data computed by BAMM is up to $\approx 20$ times lower than the true value.

The Prior Model for Diversification-Rate Shifts in BAMM Is Problematic.

The BAMM model is implemented in a Bayesian statistical framework, which treats parameters as random variables. Accordingly, this statistical inference framework requires that we specify a prior probability distribution for each parameter to explicitly describe the nature of its random variation. These distributions summarize our beliefs in the parameter values before evaluating the data. In BAMM, parameters for the rate of speciation, λ, and extinction, μ, are described using independent exponential prior probability distributions, and the time-dependence parameter, z, is described using a normal prior probability distribution.

To describe the prior distribution of diversification-rate shifts across the tree—including the number, k, and location, ξ, of events—BAMM draws upon theory developed to describe shifts in substitution rates across branches of a phylogeny under the “compound Poisson process (CPP) relaxed-molecular clock model” (8, 9). Under the CPP prior model, the waiting times between events (rate shifts) are exponentially distributed (where $\mathrm{\Lambda }$ is the rate of the exponential), the locations of rate shifts are uniformly distributed over the tree length (i.e., the sum of all branch lengths), and the prior mean (i.e., the expected number) of rate shifts is $E\left(k\right)=\gamma$. When an event occurs, we draw a new set of diversification-rate parameters from their corresponding prior probability densities, that is, the event gives rise to a new process with parameters ${\varphi }_i=\left\{{\lambda }_i,{\mu }_i,z_i\right\}$. Between rate-shift events, the lineage diversifies under a time-dependent birth–death stochastic-branching process, where the nature of the time dependence is described by the z parameter.

Prior sensitivity.

Adopting the CPP as a model to describe the prior distribution on diversification-rate shifts may be problematic, because it is known to be nonidentifiable, or weakly identifiable (10). For example, when used as a relaxed-clock model, the CPP model can explain patterns of substitution-rate variation across branches equally well by specifying relatively frequent rate shifts of small magnitude, or by specifying less frequent rate shifts of greater magnitude. In fact, there are an infinite number of CPP model parameterizations for which the data have an identical likelihood (i.e., for which the model is “nonidentifiable”). Because it is nonidentifiable, the CPP relaxed-clock model cannot estimate (i.e., “identify”) parameter values based on the likelihood (i.e., using the information in the data), which causes posterior estimates under the CPP relaxed-clock model to be very sensitive to the choice of priors specifying the frequency and magnitude of events (10, 11). Accordingly, this CPP model is said to exhibit “prior sensitivity.” It is possible that these issues may also apply to the CPP when it is used as a prior model to describe the distribution of diversification-rate shifts across branches.

To address this concern, Rabosky (5) explored the prior sensitivity of BAMM under simulation. To this end, trees were simulated under constant diversification rates (i.e., where the true number of diversification-rate shifts in each tree is zero). Each simulated tree was then analyzed using BAMM under a range of priors on the expected number of diversification-rate shifts, $\gamma \in \left\{\mathrm{1,5,10}\right\}$. The results of this simulation indicated that posterior estimates of the number of events using BAMM “…are robust to choice of γ,” in that “…the method is unlikely to yield strong support for models that are more complex than the generating [constant-rate] model.” This conclusion, however, is an artifact of how the results were summarized.

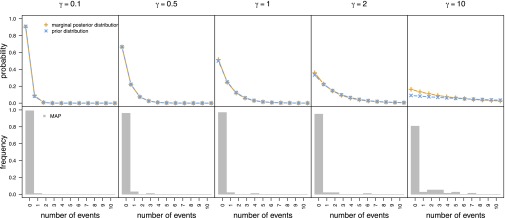
Specifically, the posterior probability distribution on the number of diversification-rate shifts, k, was summarized using the maximum a posteriori estimate (MAP; the mode of the posterior probability distribution). The MAP is an unfortunate choice of summary statistic in this case, however, because it is mathematically insensitive to the effect of the prior. Specifically, the geometric prior distribution on the number of events has a mode of zero, so the MAP (posterior mode) will indicate zero diversification-rate shifts (consistent with the constant-rate generating model), regardless of the prior mean on k (Fig. 4, Lower). Accordingly, the MAP summary uniquely conceals the extreme prior sensitivity of BAMM. Simple inspection makes it immediately obvious that the posterior distribution on the number of diversification-rate shifts is heavily influenced by the number of events assumed a priori (Fig. 4, Upper). The extreme prior sensitivity of BAMM is also manifest by empirical datasets (SI Appendix, Figs. S19–S32).

Fig. 4.

The posterior number of diversification-rate shifts inferred by BAMM is extremely sensitive to the assumed prior. We simulated 100 constant-rate trees and analyzed each using BAMM under a variety of priors for the expected number of diversification-rate shifts, γ (columns). (Upper) For each value of the γ prior, we combined the MCMC samples from analyses of the 100 trees and plotted the marginal posterior probability density of the number of rate shifts estimated by BAMM (dashed orange lines) and the corresponding prior density (dashed blue lines). For all values of the γ prior, the estimated posterior is virtually indistinguishable from the assumed prior, and the mode of the prior densities is zero (i.e., zero diversification-rate shifts). (Lower) We then summarized the results of our simulation following Rabosky (5). For each value of the γ prior, we recorded the mode of the posterior density (MAP) for each of the 100 trees and then summarized these 100 MAP values as a histogram. For all values of the γ prior, the most frequent MAP has a value of zero (simply because the mode of the geometric prior is always zero, and the estimated posterior density closely mirrors the assumed prior). Rabosky (5) misinterpreted the consistency of these MAP histograms for all values of the γ prior as evidence that BAMM is insensitive to the assumed prior. This erroneous conclusion is based on an erroneous summary of the results: simple visual inspection confirms that the (assumed) prior and (inferred) posterior distributions for the number of diversification-rate shifts are virtually identical (i.e., demonstrating the extreme prior sensitivity of inferences using BAMM).

These results indicate that posterior estimates on the number of diversification-rate shifts in BAMM are extremely sensitive to the prior (12). This is particularly problematic, because there is typically no biological information regarding the expected number of diversification-rate shifts in a given tree. Accordingly, any choice regarding the expected number of events in a particular tree will be biologically arbitrary, and these arbitrary choices will strongly influence the biological conclusions using BAMM.

Statistical incoherence.

Following Huelsenbeck et al. (8), BAMM adopts a CPP prior model to describe the distribution of events on the tree. These events involve shifts in substitution rate across branches under the CPP relaxed-clock model and shifts in the diversification rate across branches under the BAMM model. The two applications of the CPP prior model—describing changes in substitution or diversification rates across branches of the tree—therefore seem to be quite similar. However, these two processes differ in a fundamental way that invalidates use of the CPP prior model in BAMM: Substitution-rate shifts occur along the branches of an existing tree, whereas diversification-rate shifts are generating the tree itself.

Under the CPP prior model, events occur with a uniform probability over the tree length, and the number of events follows a Poisson distribution. Although this provides a valid prior model to describe events (substitution-rate shifts) across the branches of an existing tree, it does not provide a valid prior model to describe events (diversification-rate shifts) that are generating the tree. That is, diversification-rate shifts are not uniformly distributed over the tree length and the number of events does not follow a Poisson distribution (Fig. 5). Accordingly, the CPP prior model is said to be “statistically incoherent”; it cannot accurately describe the correct stochastic-branching process (we provide formal proofs in SI Appendix, sections 1.3.3 and 1.3.4).

Fig. 5.

The CPP prior model assumed by BAMM is incoherent. BAMM adopts a CPP prior model to describe the number and location of diversification-rate shifts over the tree. Under the CPP prior model, events are uniformly distributed through time (over the tree length) and the number of events is Poisson-distributed. Although this prior model provides a valid description of processes in which events occur along an existing tree, it does not provide a valid description of processes in which the events affect the generation of the tree. We illustrate this issue with a special case of the BAMM model: a pure-birth ($\mu =0$) process with two speciation-rates, ${\lambda }_0$ and ${\lambda }_1$, where the branching process switches between speciation rates at rate η. The probability distribution of the number of diversification-rate shifts (and no speciation events) does not follow a Poisson distribution (Upper), and the timing of a single event does not follow a uniform distribution (Lower), except in the special case where ${\lambda }_0={\lambda }_1$ (i.e., when diversification-rate shifts are disallowed, shown by the green line in both panels). Because it cannot describe the correct branching process, the CPP prior model assumed by BAMM is statistically incoherent.

In contrast to the problems identified with the likelihood function—for which we were able to develop computationally intensive numerical methods to estimate the correct extinction probabilities and likelihoods—the problems with the prior model on diversification-rate shifts are far more intractable. As conceived, the CPP prior model in BAMM describes a process that is assumed to be conditional on the phylogeny (i.e., it occurs independently on the study tree). This is clearly incorrect; the events involve changes in the birth–death process giving rise to the tree. Accordingly, a statistically coherent prior model must specify the joint prior probability distribution for the stochastic process that generates both the phylogeny (the topology and divergence times) and ${\varphi }_i$ (the number and location of changes in the diversification-rate process, and diversification-rate parameters of each process). Because we lack a means—even a computationally impractical means—for specifying this joint prior model, we cannot directly explore the consequences of this theoretical problem.

Hypothesis-Testing Procedures Using BAMM Are Untenable.

BAMM is intended to identify the number and location of significant diversification-rate shifts across the branches of a tree, which requires the use of a formal testing procedure to assess the relative support for two competing hypotheses (whether a shift did or did not occur). All formal Bayesian testing procedures require either: (i) the ability to compute the marginal likelihoods of the competing hypotheses (where the marginal likelihood is the likelihood of the data averaged over the prior); or (ii) the ability to compute the posterior probabilities of the competing hypotheses (where the posterior is proportional to the product of the likelihood and the prior). Unfortunately, BAMM does not correctly compute the likelihood (it is off by a large and variable factor), and the prior model is incoherent (it does not correctly describe the distribution of events over the tree). Consequently, it is not possible to perform formal hypothesis tests regarding the number or location of diversification-rate shifts using BAMM.

Statistical Behavior

In this section, we illustrate the repercussions of the theoretical problems—demonstrated in the previous section—on the statistical behavior of BAMM.

Diversification-Rate Estimates Using BAMM Are Unreliable.

We explored the ability of BAMM to accurately estimate diversification-rate parameters by simulating trees under a constant-rate birth–death process (where diversification-rate shifts do not occur), and under a variable-rate birth–death process (where the diversification rate varies across lineages). The results of our simulation study reveal that BAMM can reliably estimate the diversification-rate parameters when diversification rates are constant but cannot accurately estimate parameters when rates of speciation and extinction vary (Fig. 6). Predictably, the true and estimated branch-specific diversification-rate parameters are quite strongly correlated for constant-rate trees (Fig. 6, Left, gray line). This result is consistent with our theoretical characterization of the method; the likelihood function and prior model in BAMM are correct (and only correct) when rates of speciation and extinction are constant. Conversely, the true and estimated branch-specific diversification-rate parameters are uncorrelated when rates of speciation and extinction vary across the tree (Fig. 6, Middle, gray lines). (We present estimates of the speciation, extinction, net-diversification, and relative-extinction rates under a range of priors on the expected number of diversification-rate shifts in SI Appendix, Figs. S8–S12.) These results are consistent with the theoretical problems demonstrated earlier: Estimates of the diversification-rate parameters in BAMM are unreliable because the likelihood function is incorrect and the CPP prior model is incoherent when diversification rates are variable.

Fig. 6.

Branch-specific diversification-rate parameters estimated by BAMM are inaccurate when rates vary over the tree. We simulated 100 constant-rate trees (without diversification-rate shifts) and 100 rate-variable trees (with diversification-rate shifts) and analyzed each tree using BAMM. (Left) For the constant-rate trees, we plotted the posterior-mean estimates (the mean of the estimated marginal posterior distributions) of the speciation rate (purple, top row) and extinction rate (red, bottom row) for every branch of each tree (y axis) against the true speciation and extinction rates (x axis). Following Rabosky (5), we used linear regression to estimate the relationship between the true rate and the estimated rates (solid gray line). For constant-rate trees, the branch-specific rate estimates are approximately unbiased. (Middle) For the rate-variable trees, we similarly plotted the posterior-mean estimates for the speciation and extinction rates for every branch of each tree (y axis) against their true value (x axis). For each simulated tree, we used linear regression to estimate the relationship between the true rates and the estimated rates (solid gray lines). The average slope of the correlation coefficients is zero, indicating that estimated rates are, on average, uncorrelated with the true rates. (Right) For trees with diversification-rate shifts, we computed proportional error of the speciation-rate estimates (Upper) and extinction-rate estimates (Lower) for each branch in the tree, where the proportional error is simply the posterior-mean estimate of the rate divided by the true rate. (Note that the proportional error is plotted on a log scale.)

Summary

Understanding the history of events that have shaped the tree of life is a fundamental goal in evolutionary biology. We recognize the inherent benefits—and agree with the general approach—of pursuing this goal using explicitly model-based methods implemented in a Bayesian statistical framework. Accordingly, we appreciate both the motivation for and the general approach adopted by the BAMM method. Based on the enthusiastic response from the biological community, it seems clear that we are not alone in this regard. Unfortunately, as conceived and implemented, BAMM is a flawed method. First, the likelihood function is incorrect: It ignores diversification-rate shifts on extinct lineages, which biases estimates of the extinction probabilities—and therefore, the overall likelihood of the data—when speciation and extinction rates may vary. In principle, this issue can be solved: We developed a computationally intensive numerical solution that (although impractical) can correctly estimate extinction probabilities and likelihoods. Second, the CPP prior model used to describe the distribution of diversification-rate shifts over the tree further confounds the method: The weak identifiability of the CPP model causes the inferred number of diversification-rate shifts to be extremely sensitive to arbitrary prior assumptions. Moreover, the CPP prior model does not provide a statistically coherent description of the relevant branching process; solutions to the problems with the prior model are far more intractable. We have shown that these theoretical issues cause inferences using BAMM to be unreliable. We are hopeful that a reliable, model-based, Bayesian approach for detecting diversification-rate shifts can eventually be developed, but this remains a difficult and unsolved problem.

Materials and Methods

We augment the following synopsis with a complete description of the materials and methods in SI Appendix.

Monte Carlo Simulation of Extinction Probabilities.

The likelihood function in BAMM ignores scenarios where diversification-rate shifts occur on unobserved (extinct or unsampled) lineages, which will bias estimates of the extinction probabilities, $E_i\left(t\right)$. We illustrate this bias using an empirical dataset [the whale phylogeny presented in the original study (5)] by comparing the extinction probabilities estimated by BAMM to those estimated using Monte Carlo simulation. To this end, we first used BAMMtools to specify priors for the rates of speciation, λ, extinction, μ, and set the prior on the expected number of diversification-rate shifts, $\gamma =1$. To isolate potentially confounding factors, we assumed that species sampling was complete and that rates of speciation were not time-dependent (i.e., $z=0$).

Next, we performed an MCMC analysis under these priors using BAMM v.2.5. For each MCMC sample, we recorded: (i) the estimated extinction probabilities at the root node (reflecting the ancestral process) and at all nodes where the process was inferred to change (i.e., nodes immediately subtending diversification-rate shifts); and (ii) the rate parameters, ${\lambda }_i$ and ${\mu }_i$, for each of these i distinct processes. We then estimated the extinction probability for each of these i nodes by simulating 50,000 realizations of the episodic birth–death process that were initiated from the age of the node, $t_i$, under the speciation and extinction rates for that process, ${\lambda }_i$ and ${\mu }_i$. Next, we computed the fraction of simulations that went extinct before the present. We then compared the extinction probabilities estimated by BAMM to those estimated by Monte Carlo simulation (Fig. 2B). We performed simulations under a constant-rate birth–death process to validate the Monte Carlo estimated of extinction probabilities. Additional details regarding the Monte Carlo simulation—and the tests to validate the extinction probabilities estimated using this approach—are described in SI Appendix, section S2.

Simulation Study.

We explored the prior sensitivity and parameter estimation of BAMM by simulating trees under a constant-rate birth–death process (i.e., where the diversification rate does not vary across lineages) and under a variable-rate birth–death process (i.e., where the diversification rate varies across lineages). To ensure that our simulated trees are biologically realistic, we based our simulation on an empirical dataset; the whale tree presented in the original study (5). To this end, we first estimated the posterior probability distribution of the speciation and extinction rates for the whale tree under a constant-rate birth–death model using RevBayes (13). Each tree was simulated under speciation and extinction rates that were independently sampled from the corresponding marginal posterior probability distributions that were previously estimated from the empirical tree. We then simulated 100 trees with 87 species (equal in size to the whale tree) under a constant-rate birth–death model using the R package TESS (14, 15); we simulated trees under a variable-rate birth–death process where diversification-rate shifts entailed drawing new diversification-rate parameters from exponential distributions centered near their respective posterior means from the constant-rate analysis of the whale tree.

We analyzed each simulated tree using BAMM v.2.5. For each tree, we explored a range of values for the prior on the expected number of diversification-rate shifts, $\gamma =\left\{0.1,0.5,\mathrm{1,2,10}\right\}$. We inferred the joint posterior probability distribution for each simulated tree (under each γ prior) using the MCMC algorithm implemented in BAMM v.2.5, performing two replicate MCMC simulations for ${10}^7$ cycles, and thinned each chain by sampling every 1,000th state. We assessed the reliability of the MCMC simulations using the Tracer (16) and coda (17) packages. Finally, we computed mean diversification rates for each branch in each simulated tree using BAMMtools.

Data Availability.

All of the simulated data—as well as the code used to generate and analyze those data have been archived on the Dryad digital repository (doi: 10.5061/dryad.mb0sd).