Assessment of Protein Side-Chain Conformation Prediction Methods in Different Residue Environments

Abstract

Computational prediction of side-chain conformation is an important component of protein structure prediction. Accurate side-chain prediction is crucial for practical applications of protein structure models that need atomic detailed resolution such as protein and ligand design. We evaluated the accuracy of eight side-chain prediction methods in reproducing the side-chain conformations of experimentally solved structures deposited to the Protein Data Bank. Prediction accuracy was evaluated for a total of four different structural environments (buried, surface, interface, and membrane-spanning) in three different protein types (monomeric, multimeric, and membrane). Overall, the highest accuracy was observed for buried residues in monomeric and multimeric proteins. Notably, side-chains at protein interfaces and membrane-spanning regions were better predicted than surface residues even though the methods did not all use multimeric and membrane proteins for training. Thus, we conclude that the current methods are as practically useful for modeling protein docking interfaces and membrane-spanning regions as for modeling monomers.

Introduction

Proteins perform a wide variety of vital biological tasks, including catalysis, signaling, and maintenance of cellular structures. Protein tertiary structure provides crucial information for understanding the atomic details of these tasks. However, experimental methods for structure determination are resource-intensive and to date fewer than 0.1% of protein sequences have a solved structure¹. Furthermore, integral membrane proteins present difficulties in many steps of structural determination; consequently, structures of membrane proteins are underrepresented by an order of magnitude² in the Protein Data Bank (PDB)³. In part to improve structural coverage of sequence data, much effort has been dedicated to the development of accurate computational protein structure prediction methods⁴. In the protein structure prediction field, the accuracy of models has been mainly evaluated in terms of main-chain conformation as it has been done in the Critical Assessment of Structure Prediction (CASP), a biennial evaluation of the field^1;5. Although structure models with the correct fold but lacking atomic detail have several useful applications, including fitting structures to an electron microscopy map⁶, predicting function from structure⁷, and guiding and interpreting site-directed mutagenesis, full atom models are needed for many important applications of computational models. Notable examples include artificial design of proteins⁸ that fold into desired folds^9;10 or bind specifically to molecules such as proteins^11;12 and DNA¹³ as well as design of molecules that bind specifically to a protein¹⁴. Additionally, atomic-level accuracy is needed for using computational models for molecular replacement in X-ray crystallography¹⁵. Accurate side-chain prediction is becoming critically important for computational models used in recent applications, which are expanding the biological usefulness of modeled structures.

Side-chain prediction also has applications with structures that have already been solved, such as determining the docking conformation of a protein complex where the subunit structures were solved separately^16–18. Residues at a protein-protein interface exhibit a different conformation than the same residue in solution^19;20; thus, predicting the interface side-chain conformation of the complex improves the accuracy of the docked structure.

In the past decades, dozens of side-chain conformation prediction algorithms have been developed. Works from the 1970s investigated the distribution of side-chain conformations in known structures^21;22. Observation of side-chain distributions led to the idea of rotamers^23–26 and conformers²⁷, which are discrete sets of side-chain conformations for each amino acid often used by prediction programs. An advantage of using a library of rotamers is that the side-chain conformation prediction problem can be addressed as a combinatorial optimization problem, to which various optimization algorithms can be applied. Such algorithms include dead-end elimination²⁸, neural networks^29;30, the A* algorithm³¹, an evolutionary method³², an iterative optimization applying a mean field theory³³, and a graph decomposition of side-chain clusters^34;35. Alternatively, energy minimization may be applied without using a rotamer library^36–38.

In this work, we benchmarked eight available side-chain conformation prediction programs. Unlike previous works that have classified residues by environment but only as buried or non-buried^39;40, in our benchmark we further classify non-buried residues as protein interacting interface (protein-exposed), membrane-spanning (lipid-exposed), and surface (aqueous-exposed) for a total of four environments. Many methods were trained using only soluble monomeric proteins^35;38;39 and as a result are not necessarily expected to predict with high accuracy in protein interface and intramembrane environments. Nevertheless, given the particular importance of protein structure prediction for membrane proteins and protein-protein docking, we wanted to determine whether these methods retain high prediction accuracy for membrane and multimeric proteins. This would serve both to evaluate the validity of using monomer-trained side-chain prediction methods on non-monomer proteins and to highlight potential areas of improvement for these methods. It is also worth noting that almost all previous benchmarks have been performed by developers of side-chain conformation prediction methods; in contrast, we have no vested interest in the accuracy of any particular method.

For all methods except one, overall χ₁ angle accuracy exceeded 80%. Buried residues were best predicted. Contrary to expectation, side-chains at protein interfaces and membrane-spanning regions were better predicted than surface residues even though most of the methods did not use multimeric or membrane proteins for parameter optimization. Thus, we conclude that the current methods are as practically useful for modeling protein docking interfaces and membrane-spanning regions as for modeling monomers. Accuracies of each amino acid type relative to accessible surface area and conformational entropy are also discussed.

Materials and Methods

Selection of Software

Our search for software programs to predict side-chain conformations from backbones found nine options: FoldX³⁸, IRECS⁴¹, OPUS-Rota⁴², OSCAR^40;43, RASP⁴⁴, Rosetta-fixbb⁴⁵, Scap⁴⁶, Sccomp³⁹, and SCWRL4³⁵. Of these nine programs, we were unable to use three: IRECS, OPUS-Rota, and Scap. Neither IRECS nor Scap ran and while OPUS-Rota ran using complete PDB files, it produced invalid results given backbone coordinates only. This left six programs, two of which had slow and fast versions. In total, we compared eight algorithms for predicting side-chain conformations from backbones: FoldX, OSCAR-o and OSCAR-star, RASP, Rosetta-fixbb, Sccomp-S and Sccomp-I, and SCWRL4. The algorithms differ in three primary ways: rotamer library, scoring function, and search procedure.

FoldX

FoldX³⁸ is designed to predict the free energy change caused by single residue mutation. Thus, its primary purpose is not side-chain conformation but it models side-chains in the course of energy computation. FoldX models side-chains using the mutate function of WHAT IF⁴⁷. The FoldX scoring function is a linear combination of the following terms: solvent exposure, van der Waals, solvation, hydrogen bonds, electrostatics, backbone and side-chain entropy, and water bridges.

OSCAR

OSCAR^40;43 uses the backbone-dependent rotamer library by Dunbrack and Cohen⁴⁸. The OSCAR scoring function includes the following terms: backbone dependency, contact surface, overlapped volume, electrostatic interactions, and desolvation energy. OSCAR has two algorithm versions: OSCAR-o⁴⁰ (slow) and OSCAR-star⁴³ (fast). OSCAR-star is a speed-optimized version of OSCAR-o that uses a rigid rather than flexible rotamer model. For both versions, the distance-dependent energy function is represented as a power series and the side-chain dihedral angle potential energy function is represented as a Fourier series. Finally, the distance-dependent energy function is multiplied by an orientation-dependent function. To predict a protein conformation, twenty structures with random rotamers are initialized. Then, low energy side-chain conformations are exchanged using a genetic algorithm. Next, all twenty structures are optimized using Monte Carlo simulation. These two steps are repeated thirty times with decreasing temperature (simulated annealing), and the lowest energy structure is kept.

RASP

RASP⁴⁴ uses the backbone-dependent rotamer library by Dunbrack and Cohen⁴⁸. In addition to rotamer probability, the RASP scoring function calculates backbone/side-chain and side-chain/side-chain interaction energy with the following terms: attractive and repulsive van der Waals potential, disulfide bond energy, and hydrogen bond energy. The search function begins by reducing the search space with dead-end elimination. An interaction graph is then constructed. Interaction energies are only calculated between residues with C_β atoms within 5 Å. An edge is created between residues if the difference between the highest and lowest energy rotamer pair combinations is greater than 3 kcal/mol. Small graphs are solved with branch-and-terminate and large graphs are solved with Monte Carlo simulated annealing. Finally, residues in clash are relaxed.

Rosetta

Rosetta-fixbb⁴⁵ uses the backbone-dependent rotamer library by Dunbrack and Cohen⁴⁸. The scoring function uses the attractive and repulsive portions of the Lennard-Jones van der Waals energy, statistical energy of backbone-dependent rotamers, Lazaridis-Karplus solvation energy⁴⁹, distance-dependent residue pair potential, and energy of side-chain/backbone hydrogen bonds. The search function uses multiple Monte Carlo runs initialized with a different random structure.

Sccomp

Sccomp³⁹ uses a modified version of the backbone-dependent rotamer library by Dunbrack and Cohen⁴⁸ such that each rotamer of histidine, glutamic acid, and asparagine are split into two: one with the original values and the other with the terminal bond flipped 180°. The scoring function is based on surface complementarity (which reflects contact surface and binary chemical similarity), excluded volume, intra-residue energy (rotamer probability and residue size), and solvation (solvent-accessible surface area and atomic solvation). Sccomp has two algorithm versions, iterative (fast) and stochastic (slow). The iterative algorithm (Sccomp-I) builds the side-chains in descending order of neighbor count. Each side-chain is modeled one by one while holding the other side-chains fixed. After each iteration, the modeling order is reversed. The iterative algorithm stops when the side-chain conformation is the same in two successive runs or the maximum iteration number is reached. The stochastic algorithm (Sccomp-S) initializes all residues to a random rotamer, then chooses a given residue’s rotamer according to the Boltzmann distribution. Modeling starts with the residue having the most neighbors and on subsequent steps proceeds to a random neighbor. The probability a rotamer will be accepted at each step follows the Boltzmann distribution.

SCWRL4

SCWRL4³⁵ uses a backbone-dependent rotamer library that gives the rotamer probabilities, mean angles, and variances as a smooth, continuous function of Φ and Ψ main-chain angles using kernel density estimates⁵⁰. The scoring function consists of single rotamer and pairwise rotamer energies which use attractive and repulsive van der Waals and hydrogen bonding terms. Interactions of rotamers in a protein are represented as a graph. After removing edges that have virtually no interactions and applying dead-end elimination to remove rotamers from consideration, the graph is decomposed into subgraphs for final rotamer optimization.

Training Sets of the Methods

As the protein datasets used to derive the rotamer libraries and to train the algorithms are expected to impact the accuracy of side-chain conformation prediction, we summarized the types of proteins present in these datasets in Table II. The first two rows of Table II describe the protein datasets used by the rotamer libraries. OSCAR, RASP, Rosetta, and Sccomp used the rotamer library by Dunbrack and Cohen⁴⁸. SCWRL4 used the rotamer library by Shapovalov and Dunbrack⁵⁰. The Dunbrack and Cohen rotamer library has been superseded by the Shapovalov and Dunbrack rotamer library, so the details of the former are no longer available. However, as both rotamer library protein datasets were compiled with the PISCES server⁵¹ and no removal of multimeric or membrane proteins was described, it is likely that the datasets show similar composition (49% multimeric proteins and 0.3% membrane proteins).

Table II.

Number and Types of Proteins in Rotamer Library and Method Training Datasets.

Software	Source	Proteins
		Total	Multimer	Membrane
Rotamer Library by Dunbrack and Cohen48	PISCES 2.0 Å	518	?	?
Rotamer Library by Shapovalov and Dunbrack50	PISCES 1.8 Å	3985	1971	13
FoldX38	ProTherm66	9	0	0
OSCAR40	PISCES 2.0 Å	5279	?	?
RASP44	PISCES 1.8 Å	300	145	1
Rosetta-fixbb45	?	30	?	?
Sccomp39	PISCES 1.8 Å	15	0	0
SCWRL435	PISCES 1.8 Å	100	0	0

A question mark indicates that the information could not be found in the original paper.

For the method training datasets, many papers do not list the exact PDB codes in the dataset. However, almost all groups used the PISCES server⁵¹ to compile non-redundant lists of PDB files. RASP used a dataset from PISCES that contained 48% multimeric proteins and 0.3% membrane proteins (Table II). OSCAR also used a PISCES dataset without removing multimers or membrane proteins. By inference to the datasets used by RASP and the rotamer library by Shapovalov and Dunbrack, it is likely that the OSCAR dataset consists of half multimeric proteins and a small number of membrane proteins. Three methods were trained using only soluble monomeric proteins: FoldX, Sccomp, and SCWRL4. Importantly, none of the methods divided the training sets by protein type or residue environment.

Selection of Benchmark Proteins

In order to compare the accuracy of protein side-chain conformation prediction for different environments, we chose sets of proteins from three categories: monomeric, multimeric, and membrane. Proteins that did not run on all software methods were removed from the dataset. A total of ten proteins were removed for this reason. OSCAR-o, Sccomp-I, and Sccomp-S did not complete 1vtz or 1yce. OSCAR-o and OSCAR-star did not complete 2xfr. Sccomp-I and Sccomp-S did not complete 1yn3, 2qap, 3mjo, or 4ery. RASP did not complete 2wwx, 3ivv, or 4ate. Counts of the protein types in the datasets can be found in Table I. A full list of the proteins in the dataset can be found in Supplemental Table S1.

Table I.

Number of protein chains and residues by type and environment.

Type	Chains	Residues	Residues by environment
			Buried	Surface	Interface	Membrane
Monomer	231	33461	11009	22452	n/a	n/a
Multimer	132	13932	3632	7199	3101	n/a
Membrane	45	10847	3845	4305	n/a	2697

For monomers and multimers, we started with a non-redundant subset of the PDB from the PISCES⁵¹ server: resolution 1.6 Å or lower, maximum sequence identity 20%, and maximum R-factor 0.25 (2089 protein chains). As an additional quality control step, we removed all PDB files meeting any of the following criteria: missing main chain atoms, internal residue numbering skips, or residues other than the twenty canonical amino acids. We eliminated from the dataset PDB files with any ligand larger than five heavy atoms. This was to remove side-chains with conformations primarily influenced by large ligands. Proteins were classified as monomeric or multimeric using the biological unit annotation in the PDB, favoring author annotation over software annotation. Multimeric proteins with only one chain in the PDB file were removed to avoid applying crystallographic transformations, which can introduce atomic clashes as discussed by Krivov et al.³⁵. For any PDB file with more chains than the size of the biological unit, we checked if the duplicated chains in the file had sufficiently similar conformations. Such PDB files were included only if the copies had the same number of atoms and an RMSD of 1.5 Å or less.

Integral membrane proteins were poorly represented in the PISCES protein set. Therefore, we started with a list of crystallized membrane proteins compiled by Stephen White (http://blanco. biomol.uci.edu/mpstruc/; 766 PDB codes) and filtered the structures with the PISCES server. Very few membrane structures have resolution of 2 Å or lower²; therefore, we included structures up to 2.8 Å resolution. We also allowed ligands with more than five heavy atoms due to the frequent presence of lipid or lipid-analogue molecules. To finalize the dataset, each membrane structure was visually inspected to confirm the presence of membrane-embedded residues. The membrane protein dataset represents proteins with α-helical and β-barrel secondary structure, polytopic and monotopic proteins, and monomeric and multimeric proteins.

Environmental Classification of Residues

Residues in the three sets, monomeric, multimeric, and membrane proteins, were further classified into one of four environments: buried, surface, interface, or membrane-spanning. Protein and residue counts of the datasets are in Table I. Residues in monomeric proteins were classified as buried or surface. We calculated relative accessible surface area (ASA) of each residue by dividing ASA from DSSP⁵² by the theoretical maximum ASA of that residue in the tripeptide GXG⁵³. A residue with relative ASA was less than 10% was classified as buried. Other residues were classified as surface.

Residues in multimeric proteins were classified as buried, interface, or surface. Each multimer PDB file was separated into single chain files before the DSSP ASA calculation described previously. Interface regions were determined by finding residues with any heavy atom within 5 Å of a heavy atom in a different protein chain. Buried residues were classified as described above. A non-buried residue in an interface region was classified as interface. Other residues were classified as surface.

Residues in membrane proteins were classified as buried, membrane-spanning, or surface. Membrane PDB files were not separated by chain before DSSP ASA calculation. When available, transmembrane region information was obtained first from the MPtopo membrane topology database⁵⁴ or secondarily as determined by the depositor. Proteins lacking transmembrane region annotation were visually inspected, guided by topology images found in the structure references and anchoring aromatic residues (considered part of the membrane-spanning region). Buried residues were classified as described above. A non-buried residue in a membrane-spanning region was classified as membrane-spanning. Other residues were classified as surface.

Prediction Procedure

Prior to predicting side-chain conformations, each PDB file was reduced to backbone coordinates by removing side-chain and ligand atoms with PHENIX⁵⁵. While some of the software is able to use water and other ligand information as input, we removed all ligands in order to provide the same amount of input information to each algorithm.

Evaluating Prediction Accuracy

Prediction accuracy was evaluated in terms of predicted χ₁ and χ₂ side-chain torsion angles. χ₁ and χ₂ torsion angles were calculated for each residue using the PDB module⁵⁶ of the Biopython package⁵⁷. The χ₁ angle is the dihedral angle between the planes defined by the atoms N, C_α, C_β, and C_γ; the χ₂ angle is defined by C_α, C_β, C_γ, and C_δ. Each predicted torsion value was subtracted from the corresponding torsion value from the PDB file to obtain the torsion error. A predicted angle was considered correct if the torsion error was in the range of ±40°, as in previous works^35;39;40;44. This large window is due to the clustering of χ angles at −60°, 60°, and 180°⁵⁸. Some residues have symmetry at χ₁ (valine) or χ₂ (aspartic acid, leucine, phenylalanine, and tyrosine). For example, the δ position of aspartic acid has two different atoms (denoted in a PDB file as OD1 and OD2). In these cases, both possible predicted χ₂ angles were compared to the angle from the PDB file and the smallest error was kept. Mean χ_1&2 accuracy was defined as the proportion of residues with a defined χ₂ angle that were correctly predicted for both χ₁ and χ₂. Accuracy was averaged per protein chain to prevent large proteins from disproportionately influencing the results. For multimeric proteins, only the chain listed in the PISCES database was checked for accuracy.

Entropy of Rotamers

We used Shannon entropy (SE)^59;60 to characterize the distribution of rotamers in the experimentally solved structures in the dataset. An even distribution has a high SE while an uneven distribution (i.e. with a dominant state) has a low SE. SE was calculated using Equation 1. To apply SE to side-chains of amino acids in PDB files, we used a maximum likelihood estimator on the χ angle distribution binned by 10° (Equation 2, where c_i is the count in any bin)⁶¹.

$$\text{SE}=-{\displaystyle \sum _{i=1}^n{p}_i{\log }_2{p}_i}$$ (1)

$$p_i=\frac{c_i}{{\displaystyle \sum _i{c}_i}}$$ (2)

Results

We tested the side-chain prediction accuracy of eight software methods on a dataset of 408 proteins. The dataset includes monomeric, multimeric, and membrane proteins (Table I). The modeled proteins and raw accuracy data are made available at http://www.kiharalab.org/Side-Chain_Dataset1/.

Overall Accuracy

First, we examined overall accuracy for each method (Figure 1). Median per-protein χ₁ accuracy was above 80% for all methods except FoldX, which showed accuracy about 10 percentage points lower than other methods. OSCAR showed median accuracy close to 90%. χ_1&2 accuracies were 10–20 percentage points lower than χ₁ accuracies, with methods following the same rank as χ₁ accuracy. The observed χ₁ and χ_1&2 accuracies were consistent with previous benchmark studies^{35;39;40;43;44}. The lower accuracy for FoldX is likely because the original purpose of FoldX is not rotamer prediction but detailed energetic analysis of single residue mutation. Comparing the two versions of OSCAR, the median accuracy was similar but OSCAR-star had a higher minimum accuracy than OSCAR-o. Comparing the two versions of Sccomp, Sccomp-S showed median accuracy slightly higher than Sccomp-I for both χ₁ and χ_1&2. To compute average accuracy over different methods in subsequent discussion, we excluded FoldX due to its lower accuracy than the other methods as well as OSCAR-o and Sccomp-I because these versions had accuracy similar to their counterparts.

Figure 1.

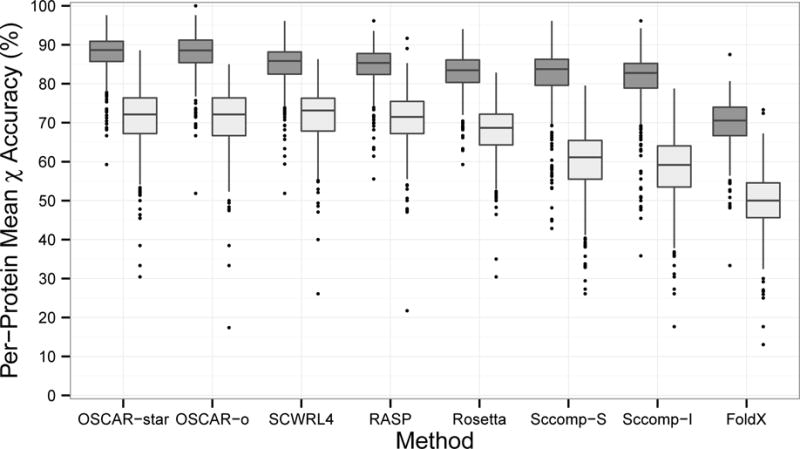
Prediction accuracy by method. Lower and upper hinges: 1st and 3rd quartile. Whisker length: 1.5 times the interquartile range. Dark grey: χ₁, Light grey: χ_1&2.

We also examined the proteins that were predicted poorly in Figure 1 by analyzing the lower outliers (more than 1.5 times the interquartile range below the 1st quartile). We compared the protein chain length distribution of the outliers and the whole set (Figure 2). The outlier distribution peaked at a shorter length (30–40 residues) than the whole set (70 to 90 residues). The outliers included a 27 residue short protein, fragment of rat tropomyosin (PDB ID: 3azd), which was below 63% accuracy for all methods.

Figure 2.

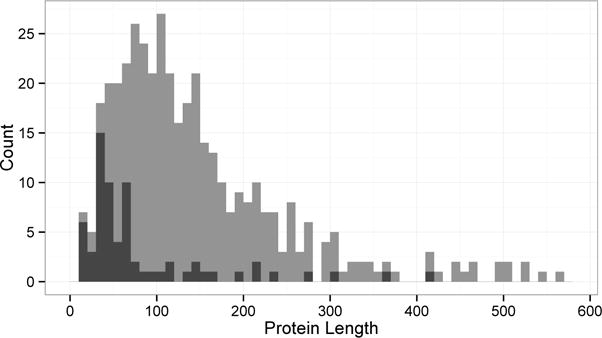
Protein chain length distribution of the entire dataset (gray) and low outliers in Figure 1 (black). The outliers are the protein chains with χ₁ and/or χ_1&2 prediction accuracy less than 1.5 times the interquartile range below the 1st quartile of the accuracy for each method. There are a total of 65 outliers.

Next, we compared accuracy divided by method and protein type. We performed statistical analysis on prediction accuracy, treating differences between software methods as the variable of interest and differences between proteins as secondary variability (blocks). Examination of the distributions of each method suggested possible deviations from normality, so we checked differences between methods using the nonparametric Friedman test and performed pairwise comparison using the Wilcoxon–Nemenyi–McDonald–Thompson test, both available in the R package coin⁶². OSCAR-star and OSCAR-o were not significantly different in any group, but they were more accurate than the other six methods for χ₁ accuracy in soluble proteins (Table III). FoldX was significantly less accurate than the other seven methods except for membrane χ_1&2 accuracy. The average accuracy did not drop substantially from monomer to multimer proteins (a mean difference in χ₁ accuracy of −0.9 percentage points). Thus, the absence of multimeric proteins in an algorithm’s training dataset did not have a sizable impact on prediction accuracy for multimeric proteins. A slightly larger difference was observed between monomer and membrane proteins (a mean difference in χ₁ accuracy of −2.5 percentage points). Both Sccomp algorithms showed relatively less variation by protein group. In contrast, the decreased accuracy for membrane proteins was more than 3 percentage points for RASP, Rosetta, and OSCAR-star.

Table III.

Mean prediction accuracy (percent) by protein type and method.

	Monomer		Multimer		Membrane
	χ1	χ1&2	χ1	χ1&2	χ1	χ1&2
OSCAR-star	88.3a	71.7a	87.3a	71.5a	85.0a	65.9ab
OSCAR-o	88.1a	71.7a	87.4a	71.1a	85.4a	66.0ab
SCWRL4	85.2b	72.0a	84.6b	72.3a	82.2b	68.6a
RASP	85.2b	71.0a	84.7b	71.5a	81.3b	67.4a
Rosetta	83.3c	68.2b	82.4c	68.3b	79.9b	63.3bc
Sccomp-S	82.3c	59.6c	80.6c	59.4c	81.3b	59.0cd
Sccomp-I	81.3c	57.7c	80.2c	58.4c	80.0b	57.5de
FoldX	70.4d	49.7d	69.5d	49.3d	68.7c	50.2e

Within each column, methods that share no letters are significantly different with p < 0.05.

Accuracy by Environment

We further compared the difference in accuracy by the residue environments in the three protein types (Figure 3). Residue environments showed larger differences than protein types. Median accuracy was highest for buried residues (90–95% for χ₁), lowest for surface residues (78–82% for χ₁), and intermediate for interface (87% for χ₁) and membrane-spanning (82% for χ₁). This order was consistent across protein types. χ_1&2 accuracy was about 8 percentage points lower than χ₁ for buried residues but over 16 percentage points lower for surface residues. Buried and surface residues showed very similar accuracy between monomeric and multimeric proteins. In contrast, buried and surface residues in membrane proteins had median χ₁ accuracy 4 to 5 percentage points lower. Therefore, the lower accuracy for membrane proteins compared to monomer proteins (Table III) was not solely due to the membrane-spanning residues. Surface and buried residues are expected to be in a similar environment regardless of protein type, so the lower accuracy in membrane proteins may have been due to the presence of lipid molecules in the input files. In general, surface residues have the fewest steric constraints; therefore, they can take on more conformations and are more difficult to predict^35;46. Furthermore, residues in an X-ray crystal structure that seem to be on the surface may exhibit a conformation influenced by crystal contacts that are not present in the raw PDB file⁶³.

Figure 3.

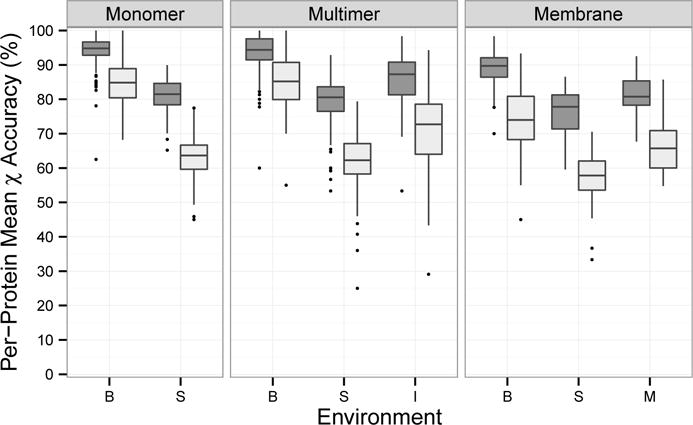
Prediction accuracy of proteins by protein type and environment. Values were averaged for OSCAR-star, RASP, Rosetta, Sccomp-S, and SCWRL4. B: buried, S: surface, I: interface, M: membrane-spanning; Dark grey: χ₁, Light grey: χ_1&2.

Accuracy by Residue Type

Next, we examined the prediction accuracy for each residue type (Figure 4). We combined monomeric and multimeric proteins in Figure 4a as they showed similar trends in Table III and Figure 3. Membrane proteins were analyzed separately in Figure 4b.

Figure 4.

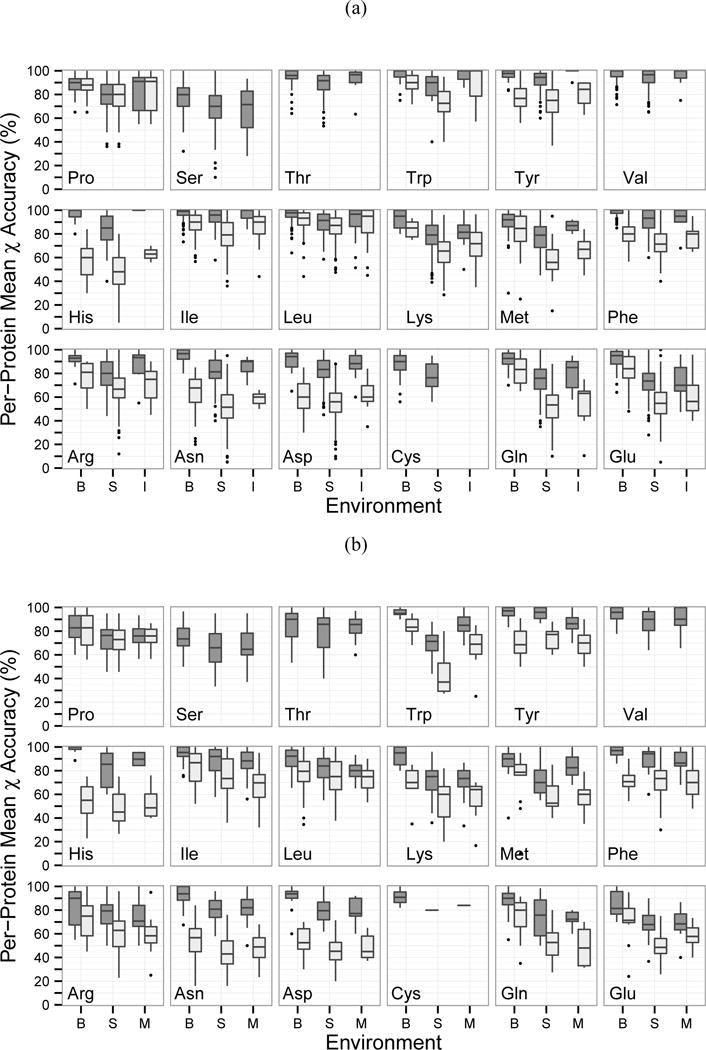
Prediction accuracy of proteins for each residue type and environment. Values were averaged for OSCAR-star, RASP, Rosetta, Sccomp-S, and SCWRL4. B: buried, S: surface, I: interface, M: membrane-spanning; Dark grey: χ₁, Light grey: χ_1&2. Cysteine, serine, threonine, and valine do not have δ heavy atoms to calculate the χ₂ angle. The dataset did not include any cysteine residues in an interface environment. (a): monomeric and multimeric proteins; (b): membrane proteins.

For monomeric and multimeric proteins, serine was the least accurate while valine and isoleucine were the most accurate (Figure 4a), agreeing with the overall trend of previous works^35;39;40. While accuracy was lower for interface residues compared to buried in most cases, seven residue types showed interface accuracy similar to buried accuracy (arginine, histidine, isoleucine, leucine, proline, tryptophan, and tyrosine). Two residue types had χ₁ and χ_1&2 accuracy within 5 percentage points (leucine and proline) while three showed differences of 20–40 percentage points (asparagine, glutamine, and histidine). The high accuracy of proline χ₂ is most likely due to its unique side-chain to backbone connection and consequent limited conformational space. The high accuracy of valine can also be attributed to its χ₁ symmetry. Rotamers only account for rotation around single bonds between sp³ hybridized atoms (e.g. a carbon with four single bonds). Rotations around single bonds with an sp² hybridized atom (e.g. a carbon with two single bonds and one double bond) are non-rotameric degrees of freedom and show broader distribution compared to rotamer angles⁵⁰. Among canonical amino acids, sp² atoms include C_γ of asparagine, aspartic acid, histidine, phenylalanine, tryptophan, and tyrosine as well as C_δ of glutamine and glutamic acid. Thus, the relatively larger drop in prediction accuracy from χ₁ to χ_1&2 of asparagine and histidine may be due in part to the non-rotameric degrees of freedom at the χ₂ position.

For membrane proteins, in general buried residues were predicted best, followed by surface and membrane-spanning; only histidine, methionine, and tryptophan showed membrane-spanning accuracy higher than surface (Figure 4b). It is surprising that membrane-spanning residues were not predicted more accurately than surface residues, as surface residues are less physically constrained than membrane-spanning residues, which is considered to be the primary reason for poor surface residue prediction accuracy⁴⁶. Compared to soluble proteins, lower accuracy was observed for all cases except buried histidine. The relative accuracy rank of residues was very similar between membrane and soluble proteins. In soluble proteins, tryptophan median χ₁ accuracy was above 90% for all environments; however, in membrane proteins, tryptophan surface residue accuracy decreased to 70%.

Correlation between Accessible Surface Area and Accuracy

We investigated the prediction accuracy of each amino acid relative to accessible surface area (Figure 5). We found an overall decrease in accuracy of about 17 percentage points from completely buried to completely exposed residues (the subplot “all”). This trend was consistent across all environments: buried, surface, interface, and membrane-spanning. However, the observed negative correlation was not as large as has been previously reported³⁵. At the residue level, leucine, isoleucine, threonine, serine, valine, and tyrosine showed only a marginal decrease of about 10 percentage points. In contrast, methionine showed a decrease of 40 percentage points. In most cases, interface residues have slightly higher accuracy than a surface residue at the same ASA.

Figure 5.

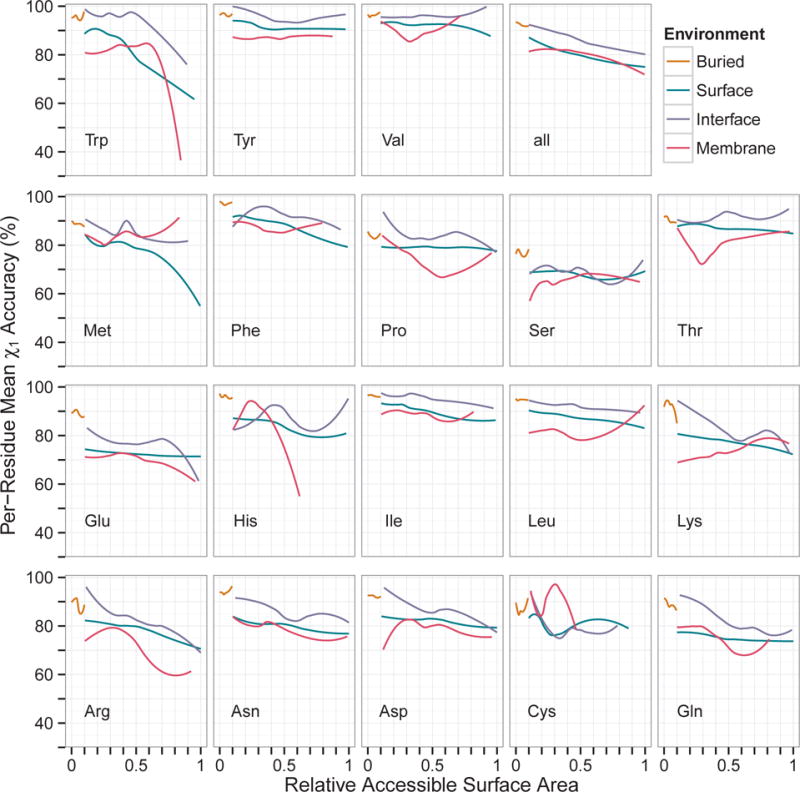
Prediction accuracy as a function of relative accessible surface area (RASA). Monomeric and multimeric proteins were combined. Residues with RASA above unity were excluded. The data were smoothed using local regression (loess). Values were averaged for OSCAR-star, RASP, Rosetta, Sccomp-S, and SCWRL4. B: buried, S: surface, I: interface, M: membrane-spanning.

Correlation between Rotamer Entropy and Accuracy

We further examined correlation of prediction accuracy to rotamer entropy. The rotamer entropy computed here quantified the randomness of rotamer distributions in specific protein environments. It has been observed that entropy does not correlate with solvent accessibility of residues³³. In this analysis, three environments (buried, surface, and interface) in soluble monomeric and multimeric proteins were used (Figure 6).

Figure 6.

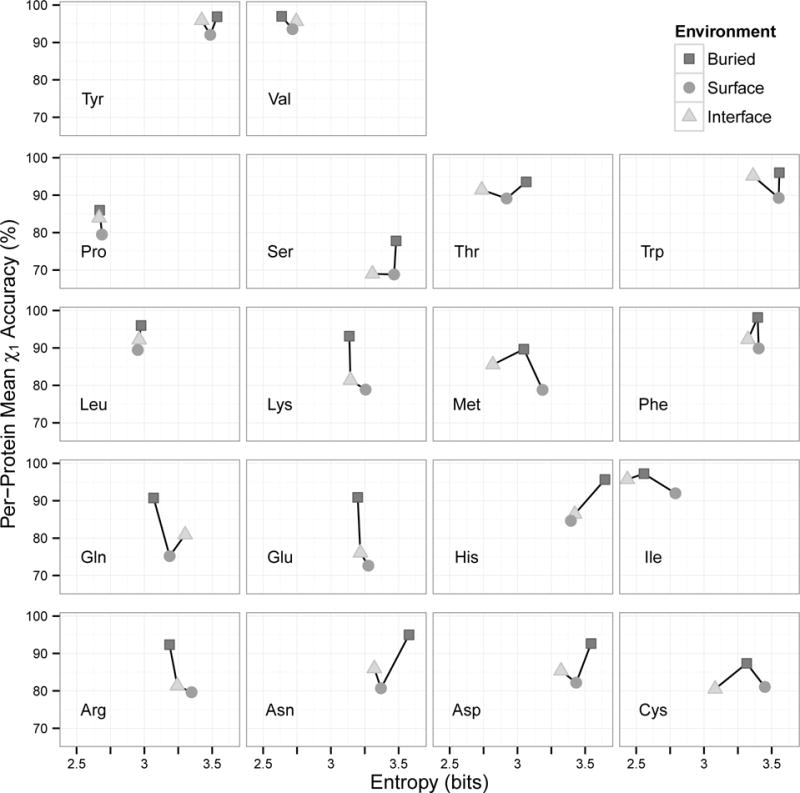
Prediction accuracy as a function of rotamer entropy. Monomeric and multimeric proteins were combined. Rotamer entropy was computed for residues in three environments: buried, surface, and interface. Values were averaged for OSCAR-star, RASP, Rosetta, Sccomp-S, and SCWRL4.

Contrary to our expectations, surface positions did not always have the highest entropy of the three environments. In fact, surface had the largest entropy for only eight residue types (serine, lysine, methionine, phenylalanine, isoleucine, cysteine, glutamic acid, and arginine). There were very small differences in entropy between residue environments for five residue types, all of which are hydrophobic (leucine, phenylalanine, proline, tyrosine, and valine). Comparing buried and interface environments, interface has lower entropy in eleven residue types. Buried residues had higher entropy than surface residues in four residue types (asparagine, aspartic acid, histidine, and threonine). Again unexpectedly, only three residue types showed negative correlation between entropy and prediction accuracy. Clear negative correlation was observed only for lysine, glutamic acid, and arginine, all of which are charged.

Consensus Accuracy

We explored whether the consensus prediction between methods increased accuracy. To create a consensus, the rotamer angles were divided into 10° bins. For each residue, the mode (most frequently predicted angle bin) was determined. If there were multiple modes and the range of the modes was greater than 40°, the residue was classified as having no consensus. However, if a residue had multiple modes but the range of the modes was less than 40°, the consensus was considered accurate if all modes were within 40° of the PDB torsion angle. Figure 7 shows cumulative accuracy and coverage at various consensus strength cutoffs. The consensus rotamer was more accurate than the best single method (OSCAR-star) with a consensus strength cutoff of 4 or higher at the expense of reduced coverage. The accuracy increased as the consensus strength grew. Particularly, accuracy of surface, interface, and membrane residues increased to approximately 10 percentage points higher than OSCAR-star.

Figure 7.

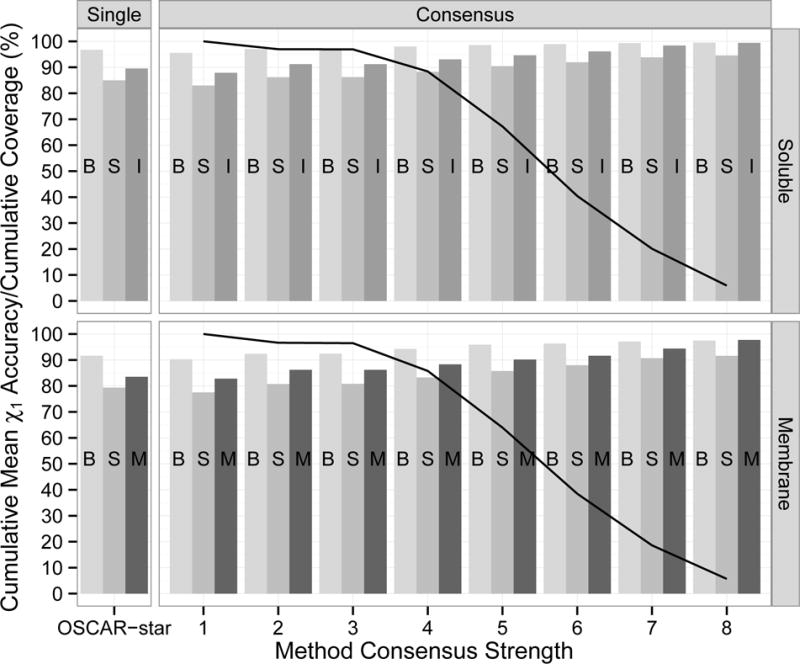
Cumulative mean χ₁ accuracy and coverage by consensus of eight prediction methods. The eight methods are listed in Table III. The soluble group consists of the monomeric and multimeric proteins. The consensus rotamer for each residue was computed as the most common rotamer using 10° bins. The consensus strength was the number of methods that predicted the consensus rotamer. At each strength cutoff, the bars indicate the mean accuracy for residues with that consensus strength or higher and the line shows the fraction of residues covered. For comparison, accuracy of the best performing single method (OSCAR-star) is shown.

Computational Time

Finally, we compared the computational time of the methods. For this test, we chose proteins between 36 and 341 residues in length (Supplemental Table S2), a range covering most of the proteins in the whole dataset (Figure 2). All times were measured on a machine with an Intel Core i7-3820 3.6 GHz processor and 24 GB RAM running Ubuntu Linux.

We can classify the eight methods into three groups according to computational time needed (Figure 8). OSCAR-o, FoldX, and Sccomp-S spent on the order of 100 to 1000 seconds; OSCAR-star, Sccomp-I, SCWRL4 and Rosetta-fixbb required on the order of 1 to 10 seconds; and RASP was the fastest, completing all proteins on the order of 0.01 to 1 second. Thus, considering the comparable accuracy shown by RASP, its algorithm is efficient. OSCAR-o showed the highest accuracy (Figure 1, Table III) but the computational time required grew quickly as the protein length increased. RASP and Rosetta had the smallest increase in computational time (1.4 and 2.0 seconds, respectively) for the proteins we tested.

Figure 8.

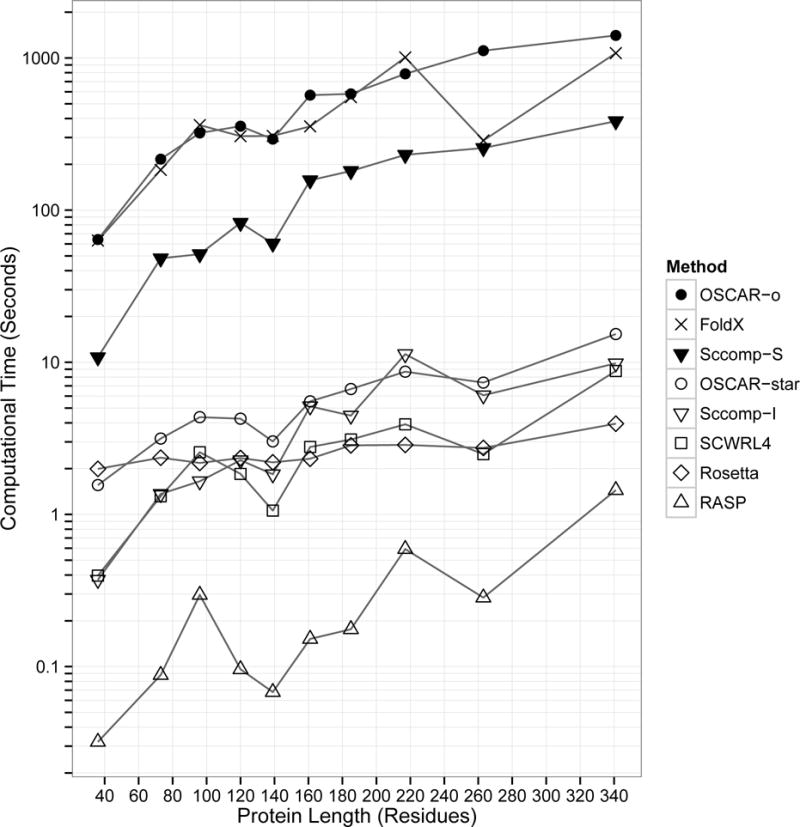
Computational time for proteins between 36 and 341 residues in length (Supplemental Table S2). The times were measured on a Linux machine with an Intel Core i7-3820 processor, 3.6 GHz.

Discussion

Accurate side-chain prediction is crucial for constructing protein models with atomic detail. The importance has been highlighted recently as more and more computational models are applied to protein design and drug development, where atomic level accuracy is essential. To understand the performance of current side-chain conformation prediction software, we benchmarked eight programs on a large dataset of 408 proteins and complexes, including 231 monomeric proteins, 132 chains from protein complexes, and 45 chains from membrane proteins. This is the first large scale benchmark study of side-chain prediction performed by a third party not involved in developing any of the methods tested. It is important to note that it is impossible to perform a completely fair performance comparison as each method is trained with a different dataset. Thus, this work is to be considered as a practical evaluation of the methods rather than a rigorous, competitive comparison between the methods.

To expand the usefulness of this benchmark study, we tested the methods on four residue environments (buried, surface, protein interaction surface, and membrane-spanning) from three protein types (monomeric, multimeric, and membrane). While none of the tested methods were specifically trained on membrane or multimeric proteins, we still wanted to test their accuracy on residues in different environments because protein-protein interfaces (docking) and membrane proteins have recently become important targets of structure modeling. Among the environments considered, protein surfaces were included as in many previous works. Residues at protein surfaces change their conformation in molecular dynamics simulations; thus, one might wonder if reproducing the conformations seen in crystal structures is meaningful. However, studies have shown that side-chains on surfaces adopt unambiguous conformations, often through salt bridges and hydrogen bonds^64;65. In Figure 6 we showed that surface residues did not always have higher conformational entropy than buried or interface residues. Therefore, prediction of surface side-chains is relevant.

To summarize the main conclusions of this work: (1) overall, monomeric and multimeric proteins had similar high accuracy of over 80% (Table III). (2) As expected, buried residues had the highest overall prediction accuracy. In multimeric proteins, interface residues were better predicted than surface residues (Figure 3). (3) Accuracy for membrane proteins was lower than for monomeric and multimeric proteins but still over 80% (Table III). Thus, very importantly, current methods predicted side-chain conformations of protein-protein interfaces and membrane proteins to a practically useful level. (4) Membrane proteins showed lower accuracy not solely due to low accuracy of membrane-spanning residues; buried and surface residues in membrane proteins also showed lower accuracy. (5) Small, hydrophobic residues showed higher accuracy than large, polar, and/or charged residues. (6) For all methods, χ₂ prediction accuracy left room for improvement.

In this work, we have focused on evaluating prediction accuracy given the correct main-chain conformation. However, in a practical structure prediction procedure, the main-chain would also be predicted and have a range of errors. Therefore, it is useful to analyze side-chain prediction accuracy in the case that the main-chain conformation is predicted with varying levels of accuracy. It should also be noted that the accuracy required of side-chain prediction depends on the application of the computational models, e.g. ligand-protein docking or protein-protein docking prediction. Ultimately, the practical usefulness of side-chain prediction and its required accuracy must be discussed in terms of the resulting accuracy of the applications of the structure models, which is left for future works.