Tensor decomposition for multi-tissue gene expression experiments

Abstract

Genome wide association studies of gene expression traits and other cellular phenotypes have been successful in revealing links between genetic variation and biological processes. The majority of discoveries have uncovered cis eQTL effects via mass univariate testing of SNPs against gene expression in single tissues. We present a Bayesian method for multi-tissue experiments focusing on uncovering gene networks linked to genetic variation. Our method decomposes the 3D array (or tensor) of gene expression measurements into a set of latent components. We identify sparse gene networks, which can then be tested for association against genetic variation genome-wide. We apply our method to a dataset of 845 individuals from the TwinsUK cohort with gene expression measured via RNA sequencing in adipose, LCLs and skin. We uncover several gene networks with a genetic basis and clear biological and statistical significance. Extensions of this approach will allow integration of multi-omic, environmental and phenotypic datasets.

Introduction

Studies of cellular phenotypes are transforming our understanding of the genetic influences on complex traits. Genomic screens of gene expression levels¹, chromatin accessibility², chromatin state³ and protein levels⁴ are all helping to elucidate how genetics is related to disease mechanisms. Over the last few years eQTL mapping has emerged as a key component in this research and has led to the identification of many genetic variants affecting gene expression. Typically, these studies involve assaying gene expression in a single tissue or cell type, though multi-tissue experiments are beginning to emerge as a way to uncover the principles of gene regulation.

The standard paradigm for single tissue eQTL studies involves testing the expression of each gene or transcript against SNP genotypes in a local region to identify cis eQTLs. This approach has been successful, with recent large eQTL studies suggesting that there will be at least one cis eQTL for almost all expressed genes⁵. Multi-tissue approaches can increase the power to find cis eQTLs⁶, however, as cis eQTLs are estimated to account for only 30-40% of the heritability of expression levels^7,8 there is a need to identify trans eQTLs to account for the remaining heritability.

The detection of trans eQTLs and networks of genes with related expression patterns is hard both computationally and statistically. Testing all genes against all SNPs via tens of thousands of genome-wide scans incurs a substantial penalty for multiple testing. In addition, trans eQTL effect sizes tend to be smaller than cis eQTLs making their detection harder⁹. For these reasons, scans for trans eQTLs usually work with a reduced set of genetic variants, such as those associated with disease traits^9,10. In general, the approach of carrying out very large numbers of marginal statistical tests (of one SNP versus one gene at a time) ignores the complex structure of these datasets. The expression levels of each gene will likely be due to a mixture of several different sources, related to underlying biology and also confounding factors.

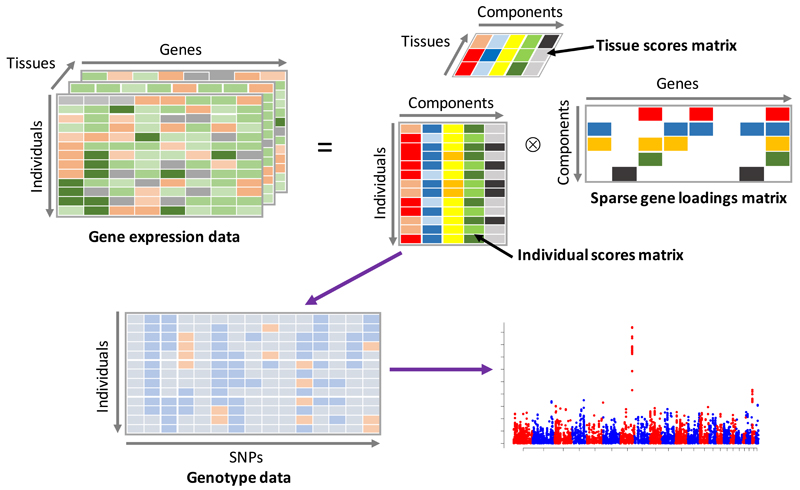
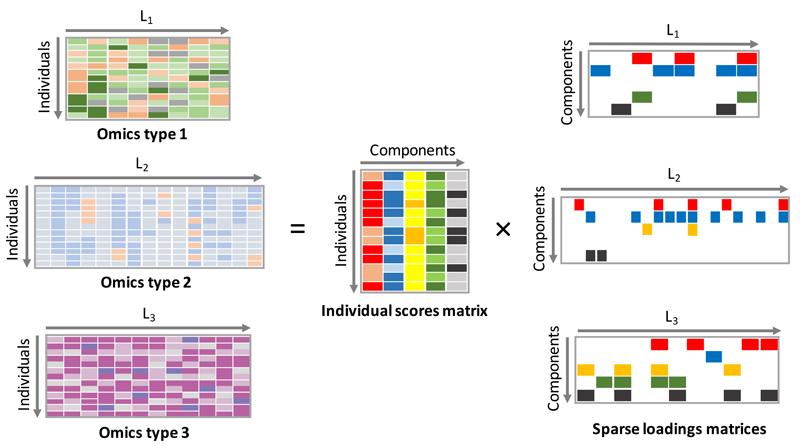
In this paper we present a novel method for the analysis of multi-tissue gene expression experiments, with a specific focus on identifying trans eQTLs and gene networks. The data from such experiments can be viewed as a ‘3D’ array, or tensor, with dimensions representing individual, gene and tissue (see Figure 1). Our method decomposes this tensor into a number of latent components (or factors) that represent major modes of variation in the dataset. Each of these components consists of three vectors of scores (or loadings) that indicate the relative contribution of each individual, gene and tissue. For example, if a consistent pattern of gene expression across a network of genes occurs in a subset of tissues, with a different magnitude in each individual, then our model aims to represent this in a single component. Such signals might naturally arise due to transcription factor genes that have multiple targets throughout the genome. If the expression level or function of a gene is altered by cis-acting genetic variants, then we would likely observe different magnitudes of effects across individuals.

Figure 1. Graphical representation of the method.

The gene expression data tensor (top left) is decomposed into the product of an individual scores matrix, a tissue scores matrix and a gene loadings matrix (top right). Columns of the individual scores matrix are then used as phenotypes in a GWAS using SNP genotypes (bottom left) in order to uncover genetic variation correlated with the latent components.

One useful way to think about the approach is as analogous to the use of principal components analysis (PCA) applied to ‘2D’ (individual by SNP) genetic datasets. PCA is routinely used to decompose genome-wide SNP datasets into components of variation that are then used to understand population structure (see ¹¹ for example). Here we aim to decompose higher dimensional datasets into components that uncover real biology.

Our method has several notable properties:

• Our approach is developed in a Bayesian framework, and we use a sparse ‘spike and slab’¹² prior to allow the gene loadings of each component to have a unique level of sparsity. This allows us to shrink gene effects to zero so that we can infer more clearly which genes are involved in gene networks.

• The individual scores represent the magnitude of the effect of each component across individuals, analogously to the individual scores that are usually plotted in a PCA analysis of genetic datasets. We use these scores as phenotypes in genome-wide SNP scans to identify genetic variants that drive each component. The number of components we test is typically much smaller (a few hundred) than the number of genes (tens of thousands), which substantially reduces the multiple testing burden when compared to approaches that test all genes against all genetic variants in all tissues.

• We do not claim that all genes identified in a network will reach genome-wide significance thresholds with the driving SNPs. However, when applied to real datasets we find that the majority of genes are nominally significant.

• The tissue scores vector indicates the ‘activity’ of the component for each tissue. By examining the entries of the tissue scores matrix across components we can make inferences about how many components are shared across tissues.

• Our model also allows for non-sparse components that might be expected to arise from confounding effects, such as batch effects or sequencing properties.

• In addition, the model can naturally accommodate missing data, such as samples without gene expression on subsets of tissues, which is a real and prevalent feature of multi-tissue experiments.

Our motivation for this work stemmed from similar approaches that have emerged in the field of neuroscience to uncover shared signals across different high-dimensional imaging modalities^13,14. Most tensor decomposition methods^15–17 are not able to handle missing data or invoke sparsity on the components, although there are some exceptions¹⁸. Our model is the first tensor decomposition method utilizing spike and slab priors with model fitting carried out using Variational Bayes (see Online Methods). Via extensive simulations (Supplementary Note) we show that our method has the best performance in terms of estimation of the component individual scores and recovery of sparsity patterns in the gene loadings when compared to other matrix and tensor decomposition methods, and is well powered to detect trans eQTL signals and gene networks. Our method is implemented in a software package called SDA (Sparse Decomposition of Arrays) (see URLs).

Results

We have validated our approach by applying it to RNA sequencing data from the TwinsUK cohort, which consists of gene expression measured on 845 related individuals in adipose, LCLs and skin^19,20. In order to focus on robustly identified components we applied our method 10 times to the TwinsUK RNA-seq dataset and combined results across runs via clustering (see Online Methods). After clustering, we identified 236 robust components for further investigation. Examination of the tissue scores matrix is informative about which tissues each component is active in (see Supplementary Figure 1). We found that the majority of the 236 components were active in a single tissue (57 in Adipose, 74 in LCLs and 70 in Skin). There were 20 components that were active in all 3 tissues, 14 components active in just Adipose and Skin and 1 component active in Adipose and LCLs. The full details of these 236 components are given in the Supplementary Data Set.

The individual scores vectors of these components were then used as phenotypes in genome-wide scans using SNP genotype data imputed using the 1000 Genomes Phase 1 reference panel. We used a threshold of 1×10^-10 to assign significance (see Online Methods). There were 26 components that reached this level of significance: 5 were active in just 1 tissue (1 in Adipose, 4 in LCLs), 20 components were active in all 3 tissues and 1 component was active in just Adipose and Skin. The majority of these components were clearly uncovering cis eQTLs. In all but two of these components we identified pairs of SNPs (significantly associated with our component scores) and genes (with a non-zero loading) that had previously been identified as a cis eQTLs in the MuTHER and GTEx studies^7,21. These components exhibited very sparse gene loadings, with a single localized cluster of high gene loadings and highly significant SNP associations in the flanking region (Supplementary Figures 2-21). Methodology for the detection of cis eQTLs is well established and is best carried out using focused analysis that looks for such effects at SNPs flanking each gene. Our main focus is on uncovering trans eQTLs and gene networks so we do not pursue the cis eQTLs that our method finds any further.

The remaining 6 components were less sparse in their gene loadings, and exhibited patterns of gene loadings and SNP associations that highlight gene expression networks with substantial biological significance. For these networks the majority of gene loadings tend to be unidirectional suggesting the components are identifying a directional effect on expression. These components are summarized in Figures 2-6 which show the gene loadings, SNP GWAS and tissue activation patterns. Supplementary Table 1 shows that the majority of genes identified in each of these networks have nominally significant p-values in the relevant tissues. At the suggestion of a reviewer, we also applied PCA and ICA to the Twins UK dataset. Neither of these approaches uncovered the gene networks reported here; more details are given in the Supplementary Note.

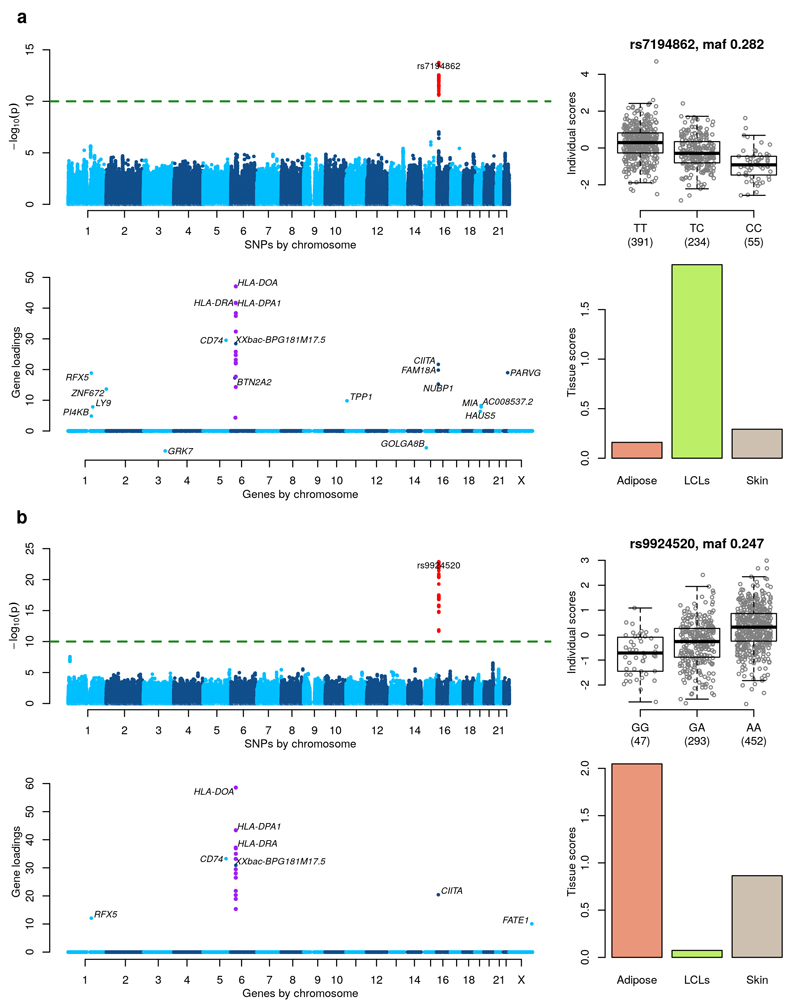
Figure 2. MHC Class II regulation.

Figures a and b shows two components identifying a similar network in different tissues. (Top left) GWAS with the component’s individual scores vector as a phenotype. (Top right) Boxplot of individual scores stratified by genotypes at the lead GWAS SNP. Boxplots show the median, upper and lower quartiles, with whiskers extending to either 1.5 times the interquartile range (IQR), or to the most extreme data point if this is within 1.5 times IQR. (Bottom left) Gene loadings for the component. Only gene loadings with a PIP>0.5 are shown. (Bottom right) Tissue scores vector for the component shown as a barplot.

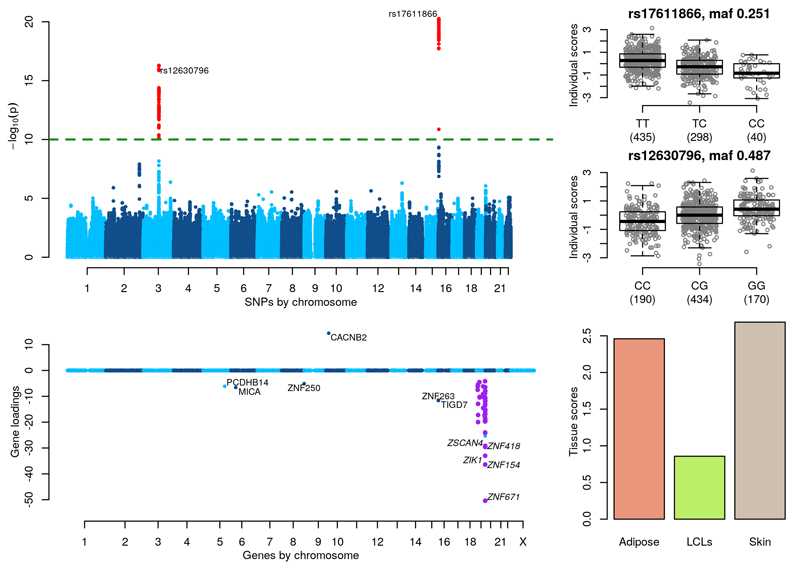
Figure 6. Zinc finger gene network.

(Top left) GWAS with the component’s individual scores vector as a phenotype. (Top right) Boxplots of individual scores stratified by genotypes at the lead GWAS SNPs, rs17611866 and rs12630796. (Bottom left) Gene loadings for the component, with zinc finger genes on chr 19 highlighted in purple. Only gene loadings with a PIP>0.5 are shown. (Bottom right) Tissue scores vector for the component shown as a barplot.

We found 2 clustered components (Figure 2) with individual scores that exhibit significant SNP associations in the gene CIITA on chromosome 16p13 (see also Supplementary Figure 22). The first component is active mostly in Adipose and Skin and has a lead SNP rs9924520 (p-value = 1.33×10^-23, MAF=0.247) that is an intronic variant of CIITA. The second component is active mostly in LCLs and has a lead SNP rs7194862 (p-value = 1.74×10^-14, MAF=0.282) that is 5’ of CIITA. The SNPs rs9924520 and rs7194862 are in strong LD (r² = 0.82). Both components show a cluster of MHC Class II genes on chromosome 6 with non-zero gene loadings. In addition, 2 other genes have significant gene loadings in both components (RFX5 on chromosome 1 and CD74 on chromosome 5). CIITA is known to be a master controller in the regulation of MHC Class II gene expression²². It is recruited to the proximal promoter regions of the classical MHC class II genes (HLA-DP, HLA-DR and HLA-DQ), and to HLA-DM, HLA-DO and the CD74 gene (encoding the molecular chaperone invariant chain which associates with the MHC class II complex) through protein-protein interactions with other components of the MHC class II enhanceosome, which includes RFX5. Supplementary Table 2 details the direct associations of SNPs rs9924520 and rs7194862 with the expression levels of all the genes identified in our components (in all three tissues) after correction for covariates and 15 PEER factors²³ (see Online Methods). Both SNPs are strongly associated with HLA-DOA and HLA-DMA in Adipose and Skin (p-values in the range [2.89×10^-8, 5.56×10^-19]) and with CIITA in Adipose (p-values = 2.08×10^-11, 1.44×10^-12). However, neither SNP reaches a strict Bonferroni threshold for a trans analysis of 9.05×10^-13 = 5×10^-8/(3×18409) (obtained by accounting for genome-wide testing across all genes in all tissues) with any of the other genes in the 3 tissues. These results suggest that while a trans eQTL association would have been found between SNPs in the CIITA region and expression at two MHC class II genes, the more extensive network of genes recovered by our components would not have been uncovered via a marginal trans analysis.

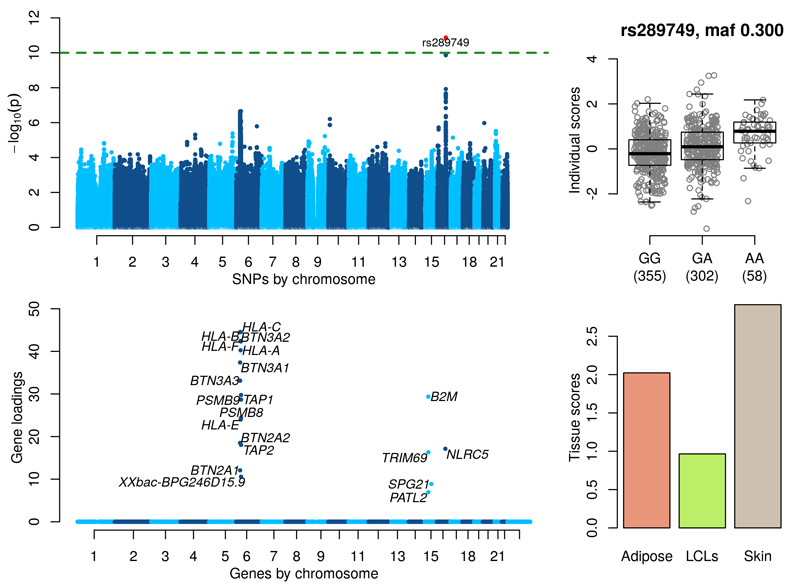
Figure 3 shows significant associations in the gene NLRC5/CITA on chromosome 16q13 (see also Supplementary Figure 23). The lead SNP rs289749 (p-value = 1.34×10^-11, MAF=0.3) is an intronic variant of NLRC5/CITA. The component shows a cluster of genes on chromosome 6 with non-zero gene loadings that include MHC Class I genes (HLA-O, HLA-B, HLA-F, HLA-A, HLA-E), BTN genes (BTN3A2, BTN3A1, BTN3A3, BTN2A2, BTN2A1), TAP1, TAP2, PSMB8 and PSMB9. Overexpression of NLRC5/CITA is known to increase mRNA levels of genes encoding human MHC Class I molecules and proteins functioning in the MHC Class I mediated antigen presentation pathway, including beta-2-microglobulin (B2M), transporter associated with antigen processing 1 (TAP1) and the proteasome subunit beta type-9 (PSMB9)²⁴. B2M, TAP1 and PSMB9 all have significant gene loadings in the component. Supplementary Table 3 details the direct associations of SNP rs289749 with the expression levels of all the genes in the component in all three tissues. In skin, rs289749 is strongly associated with NLRC5/CITA (p-value = 1.37×10^-28) and moderately associated with several MHC class I genes; HLA-F (p-value = 3.02×10^-12), HLA-A (p-value = 1.22×10^-9) an HLA-B (p-value 1.35×10^-10)); although none of these associations would pass a Bonferroni corrected significance level in a trans analysis (9.05×10^-13). p-values for association between rs289749 and other genes in this component suggest that the link between NLRC5/CITA and BTN, TAP and PSMB genes or the B2M gene would not have been recovered using a traditional trans analysis. In addition, these direct associations fail to provide evidence for the signal in either Adipose or LCLs.

Figure 3. MHC Class I regulation.

(Top left) GWAS with the component’s individual scores vector as a phenotype. (Top right) Boxplot of individual scores stratified by genotypes at the lead GWAS SNP rs289749. (Bottom left) Gene loadings for the component. Only gene loadings with a PIP>0.5 are shown. (Bottom right) Tissue scores vector for the component shown as a barplot.

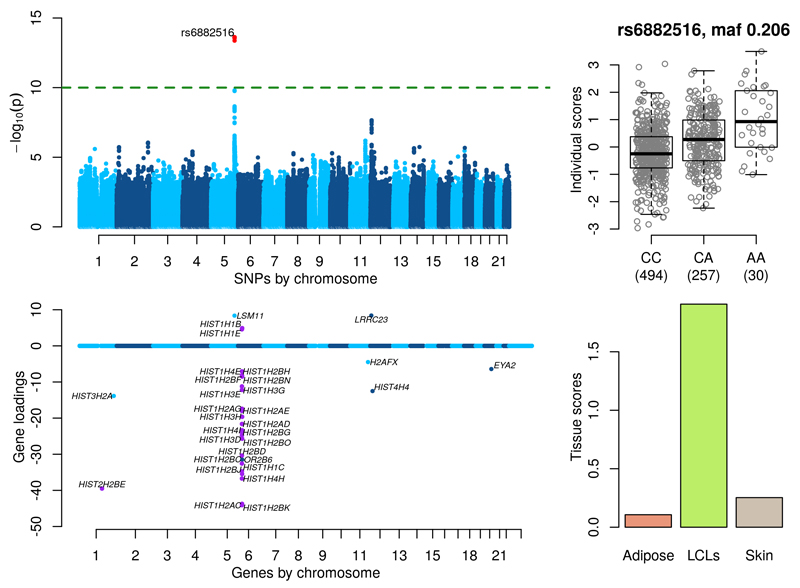
Figure 4 shows significant associations for a cluster of SNPs near LSM11 on chromosome 5q33.3 which is known to be involved in histone RNA processing²⁵ (see also Supplementary Figure 24). The gene loadings of our component show a striking cluster of 23 histone genes in the chromosome 6p21 cluster as well as the gene HIST2H2BE in the 1q21 cluster (Figure 4 purple points). There are also additional signals at other histone genes on chromosome 1q42 (HIST3H2A), 11q23 (H2AFX) and 12p12 (HIST4H4). SNP rs6882516 (p-value = 2.39×10^-15, MAF=0.206) is in the 3’ UTR of LSM11 and predicted to be a microRNA binding site using mirSNP²⁶. Key histone gene regulatory factors are organized in a limited number of subnuclear foci. It is known that cell cycle-dependent phosphorylation of p220^NPAT by cyclin E/CDK2, that induces histone gene transcription, occur at these intranuclear sites. p220^NPAT colocalizes with both (a) the histone gene clusters on chromosome 1q21 and 6p21, (b) the protein subunit LSM11¹³. A set of 31 significant genes (loadings with a PIP>0.5, see Online Methods) show Gene Ontology p-values of 1.91×10^-25 and 1.40×10^-24 for the terms ‘nucleosome organization’ and ‘chromatin assembly or disassembly’ respectively. The tissue scores indicate that this component is only active in LCLs. Supplementary Table 4 details the direct associations of SNP rs6882516 with expression levels of LSM11 and the other genes in this component in all three tissues. The SNP is significantly associated with LSM11 in LCLs (p-value = 5.57×10^-33), and has p-values in the range (2.65×10^-12, 1.17×10^-12) with three histone genes in our component with extreme gene loadings (HIST1H1C, HIST1H2BJ and HIST1H2BK). Although these associations are encouraging, they do not pass a strict trans analysis significance level and additionally, these direct associations do not uncover the link between LSM11 and the histone gene cluster on 1q21 (the p-value for rs6882516 and HIST2H2BE in LCLs is 5.40×10^-9).

Figure 4. Histone RNA processing.

(Top left) GWAS with the component’s individual scores vector as a phenotype. (Top right) Boxplot of individual scores stratified by genotypes at the lead GWAS SNP rs6882616. (Bottom left) Gene loadings for the component. Only gene loadings with a PIP>0.5 are shown. (Bottom right) Tissue scores vector for the component shown as a barplot.

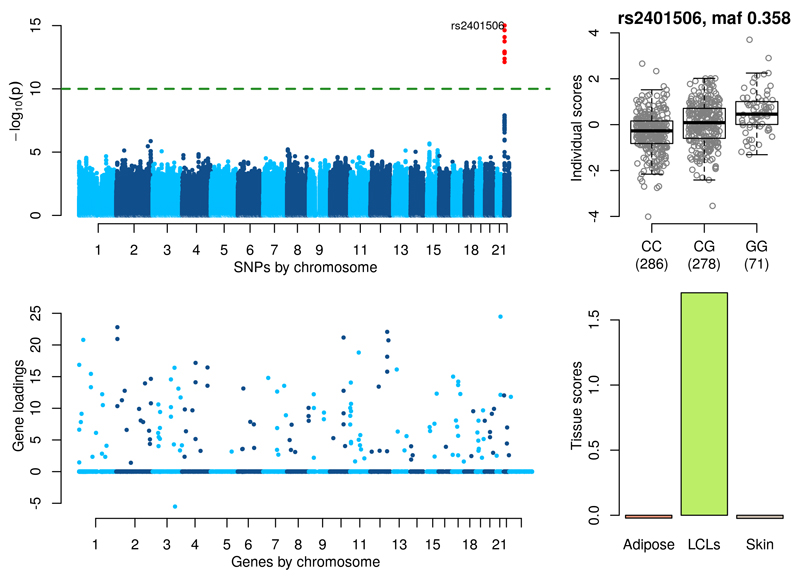
Figure 5 shows significant associations near the gene USP18 (see also Supplementary Figure 25). The lead SNP rs2401506 (p-value = 9.82×10^-16, MAF=0.358) is 5kb upstream of USP18. The set of 160 genes in the loadings with a PIP>0.5 show Gene Ontology p-values of 1.73×10^-42 and 1.23×10^-38 for the terms ‘defense response to virus’ and ‘response to type I interferon’ respectively. Of the 70 genes annotated by ‘response to type I interferon’ we find 28 with non-zero gene loadings (Supplementary Figure 26). These include all four of the 2′-5′ oligoadenylate synthetase (OAS) gene family (OAS1, OAS2, OAS3 and OASL) known to be actively induced by interferons²⁷, the genes STAT1 and STAT2 which are key mediators of type I and type III IFN signaling, several Interferon γ-inducible protein (IFI) genes (IFI6, IFI44L, IFI16, IFIH1, IFIT1, IFIT3, IFIT5, IFIT2, IFITM1, IFITM2, IFI35) and the genes MX1 and MX2 also related to IFN signaling. USP18, a type I IFN-induced protein that deconjugates the ubiquitin-like modifier ISG15 (which is also in our component) from target proteins²⁸, plays an important function in down regulation of interferon responses^29,30 and significantly inhibits tumour growth³¹. The tissue scores indicate that this component is only active in LCLs. Supplementary Table 5 details the direct associations of SNP rs2401506 with the 160 genes identified in this component across all three tissues. There is only evidence of association in LCLs, with several genes obtaining p-values smaller than 1×10^-8 (IFIT1, PLSCR1, STAT1, CMPK2, RSAD2 and EIF2AK2) but none are significant when accounting for genome-wide testing across all genes, suggesting that this network of genes would not have been uncovered by a scan of all SNPs versus all genes.

Figure 5. Type I Interferon Response.

(Top left) GWAS with the component’s individual scores vector as a phenotype. (Top right) Boxplot of individual scores stratified by genotypes at the lead GWAS SNP rs2401506. (Bottom left) Gene loadings for the component. Only gene loadings with a PIP>0.5 are shown. (Bottom right) Tissue scores vector for the component shown as a barplot.

Figure 6 shows two significant associations on separate chromosomes for a component with a striking cluster of non-zero gene loadings for zinc finger genes on chromosome 19. SNP rs17611866 (p-value = 5.40×10^-21, MAF = 0.251) on chromosome 16 is a mis-sense variant in ZNF75A, which is one of 6 ZNF genes in a local cluster. Flanking genes ZNF263 and TIGD7 have non-zero gene loadings (see Supplementary Figure 27). SNP rs12630796 (p-value = 5.10×10^-17, MAF = 0.487) on chromosome 3 is an intronic SNP in SENP7. A SNP in high LD with this SNP (rs13320918, p-value = 7.34×10¹⁵, MAF = 0.377) has been shown to be a microRNA QTL for miR-1270 (p-value=1.71×10^-10) which is located in a zinc finger cluster on chromosome 19p12³². In a separate study, 4 other intronic SNPs in SENP7 (rs2553419, rs2682386, rs9859077 and rs2141180), all in high LD with each other and with rs13320918, were shown to correlate with cis-acting regulation of SENP7 expression in CD4 and CD8 lymphocytes and trans-acting regulation of ZNF154, ZNF274 and ZNF814³³, which all reside within a ~250-kb region on chromosome 19q13.43 (see Supplementary Figure 28).

Supplementary Table 6 details the direct associations of SNPs rs12630796 and rs17611866 with SENP7 on chromosome 3 and genes with non-zero gene loadings in the component in all three tissues. This analysis partially recovers the signal that we find using our method, see the Supplementary Note for more details.

It can be challenging to interpret the large number of components that are produced by sparse matrix and tensor decomposition methods. By clustering components across independent runs of the method, and then selecting components with genetic associations, we have shown that it is possible to identify gene networks with clear biological significance. However, we have found evidence that the components without genetic associations are also capturing important variance in the data. Many components have individual scores vectors that are significantly associated with variables measuring properties of the sequencing; these components are mostly dense with several thousand non-zero gene loadings (see Supplementary Figures 29-31 and Supplementary Table 7). Similarly, we have identified several components that are significantly associated with measured phenotypes including age, BMI and cholesterol levels (Supplementary Figure 32). We find two components that show association with age. These components are shown in Supplementary Figures 33 and 34. The most significant molecular function ontology term for both components is ‘oxidoreductase activity’ with p-values of 1.9×10^-24 and 2.1×10^-22.

In addition, we have found that it can be useful to examine the components from a single run of the method. Specifically, we focus on the best run of 10 that produces the highest value of the model negative free energy (Online Methods). We identified all components highlighted in Figures 2-6 with significant or very close to significant GWAS p-values. In addition, we find several components that identify KLF14 as a master trans regulator³⁴ (for example, see Supplementary Figure 35). More details are given in the Supplementary Note and the Supplementary Data Set.

A previous analysis of a similar set of samples in the MuTHER study⁷ using a microarray based gene expression experiment called 518, 491 and 493 trans eQTLs SNPs at a normal GWAS threshold of 5×10^-8. They reported an FDR of < 10% at this threshold, however only ~5% of these signals replicated at a nominal significance threshold of 0.05 in at least one out of 5 other studies. The overlap with our results is (a) a SNP rs7714390 on chromosome 5 (near our lead SNP rs6882516) associated with two Histone genes (HIST1H2BK on chr 6 with a p-value = 8×10^-9 in LCLs and HIST2H2BE on chr1 with a p-value of 3.2×10^-8 in LCLs) (b) a SNP rs220377 on chr 16 (near our lead SNP rs17611866) associated with a Zinc finger gene (ZNF667 on chr 19 with a p-value = 2.9×10^-9 in LCLs), and (c) several associated SNPs near rs4731702 that overlap with the KLF14 network with p-values between 4.4×10^-8 and 2.2×10^-15). This analysis did not identify the Type I Interferon network or the MHC networks that we find in our analysis.

Discussion

We have described a new algorithm for efficient tensor decomposition for multi-tissue gene expression datasets, and have demonstrated its utility on a real, three tissue dataset to uncover sparse gene networks with clear biological and statistical significance. A marginal analysis of all SNPs versus all genes would not have uncovered these networks in the same way or with as much power. For example, no aspect of the Type I interferon component would have been identified. We have further shown in simulations that our method has good power to detect sparse gene networks correlated to genetic variants, and dense confounding factors.

This approach complements current eQTL analysis pipelines that tend to mainly focus on identifying cis eQTLs in one tissue at a time. Analysis of cross tissue effects usually proceeds in a subsequent step by comparing effect sizes across tissues. Our method focuses on decomposing the complete multi-tissue dataset into components of variance with varying levels of sparsity. We then test each component against genetic variation genome-wide to uncover underlying eQTL effects, ensuring robustness by only considering components that are consistently found across multiple runs. We view our approach as complementary to an association analysis of all SNPs versus all genes, since it requires 2 orders of magnitude fewer tests, and has more power to detect SNP associations with gene networks.

In general, we find that dense components uncovered by our method show high levels of significance with confounding variables and the method additionally uncovers many very sparse components that represent cis eQTLs. More interestingly, we find 6 components with intermediate levels of sparsity with gene loadings spread across multiple chromosomes that represent gene networks showing a highly significant association with genetic variants. In all 6 of these components, we are able to link the gene networks they describe to known biology. In the future it will be natural to apply this method to gene expression datasets with even more tissues, such as that being collected by the GTEx Project³⁷ or the Allen Institute for Brain Science (AIBS) human microarray data set³⁸.

There are several interesting ways in which this model can be extended or changed. The method can be naturally extended to higher dimensional datasets. For example, 4D multi-tissue gene expression experiments through time and/or under different experimental conditions (see Supplementary Figure 36).

One assumption of our model is that the gene loadings pattern of a component is constant across active tissues, which may or may not be true dependent upon the dataset being analyzed. One way to overcome this would be to develop a model that applies a matrix decomposition to the gene expression matrix for each tissue but with a linked individual scores matrix (see Supplementary Figure 37). A downside of such an approach is that it would significantly increase the number of unknown parameters in the factorization. However, this model would allow variation in the gene loadings between tissues if there were indeed clear differences, and might be a way of combining together components found by our tensor method (like those describing MHC class II regulation pathways) with clearly similar gene loadings. However, it may also be necessary to model the similarity between gene loadings to aid estimation, given the larger parameter space. This approach has strong connections to sparse canonical correlations analysis (CCA)³⁹ and unsupervised multi-view learning⁴⁰.

Such a linked matrix decomposition method could also be used to integrate different genomic datasets. The model has no constraint that the set of matrices being jointly decomposed have the same dimensions. So, for example, matrices of gene expression and epigenetic measurements could be jointly decomposed to uncover relevant shared biology (see Figure 7). Example applications might include joint decomposition of different omics datasets collected on cancer samples from the International Cancer Genome Consortium (ICGC) (see URLs). This model can further be extended to tensors of different data types (see Supplementary Figure 38).

Figure 7. Multi-omics data integration.

Graphical representation of a linked decomposition for several genomic assays. A matrix decomposition is applied to each data type. The matrix decompositions identify a different loadings matrix for each data type and a shared individual scores matrix.

Online Methods

Bayesian Sparse Tensor Decomposition Model

We use Y to denote the 3D array or tensor containing pre-processed gene expression measurements. Y has dimensions N × L × T where N is the number of individuals, L is the number of genes and T is the number of tissues. We model Y as follows

$$Y_{nlt}={\displaystyle \sum _{c=1}^c{A}_{nc}{B}_{tc}{X}_{cl}+{\epsilon }_{nlt}}$$

where C is the number of components (also called factors). A is an N × C matrix with the c^th column containing the individuals scores of the c^th component. B is a T × C matrix with the c^th column containing the tissue scores of the c^th component. X is a C × L matrix with the c^th row containing the gene loadings of the c^th component.

The error term is modeled as ${\epsilon }_{nlt}\sim N\left(0,{\lambda }_{lt}^{-1}\right)$ where λ_lt is the precision of the error term at the l^th gene in the t^th tissue.

We deal with missing samples for a given tissue by not including them in the model likelihood. We introduce an indicator variable I_nt that equals 1 when gene expression has been measured in tissue t for sample n and zero otherwise. The likelihood is then given by

$$P\left(Y|\text{Θ}\right)={{\displaystyle \prod _{n,l,t}P\left(Y_{nlt}|\text{Θ}\right)}}^{I_{nt}}$$

where Θ is the vector of model parameters.

We fit this model in a Bayesian framework, and place priors on the entries of the matrices A, B, X and also the precisions λ_lt. A key prior is the one we place on the elements of the gene loadings matrix X. We wish to encourage sparsity in the rows of this matrix, so we use a hierarchical ‘spike and slab’ prior⁴² of the form

$$\begin{array}{l}{X}_{cl}\sim p_{cl}N\left(0,{\beta }_c^{-1}\right)+\left(1-p_{cl}\right){\delta }_0\\ {\beta }_c\sim Gamma\left(e,f\right)\\ p_{cl}\sim {\rho }_{c}Beta\left(q,r\right)+\left(1-{\rho }_c\right){\delta }_0\\ {\rho }_c\sim Beta\left(s,z\right)\end{array}$$

For the purposes of making inference easier (see Supplementary Note) we use the equivalent factorization of the spike and slab distribution as X_cl = W_clS_cl where

$$\begin{array}{l}{W}_{cl}\sim N\left(0,{\beta }_c^{-1}\right)\\ S_{cl}\sim Bernoulli\left(p_{cl}\right)\end{array}$$

For the elements of A and B we use standard normal priors A_nc ∼ N(0,1) and B_tc ∼ N(0,1).

Model fitting

We fit this model using Variational Bayes (VB)⁴³, which approximates the posterior distribution $P\left(\text{Θ}|Y\right)\approx Q\left(\text{Θ}\right)$. The approach iteratively refines the estimate Q(Θ), by minimizing the Kullbeck-Lieber (KL) divergence between Q(θ) and P(Y｜θ), or equivalently maximize the negative free energy. Once converged, Q(θ) can be used to approximate properties of the posterior distribution. The full details of the parameter factorization we use, the resulting VB update equations and details of parameter initialization are given in the Supplementary Note. The resulting algorithm has complexity O(NLTC²) and can be run on a multi-core server. For the TwinsUK data analyzed in this paper the method took 20 hours for each of the 10 runs using 8 threads.

Our model has the ability to shrink an entire component to zero (ρ_c = 0) and effectively remove that component from the model. In this way our model can adaptively choose the number of components it needs. Just a small amount of experimentation is needed to find a large enough value of C so that components start being shrunk to 0. For the TwinsUK data we fit the model with 1,000 components and found that in all 10 runs of the method around 50 components would always be estimated as 0.

Summarizing the Variational Bayesian posterior approximation

The form of the VB posterior for every entry of the gene loadings matrix X_cl has the same spike and slab form as the prior. We use this distribution to calculate the expected value, denoted E_Q(X_cl). We also calculate a Posterior Inclusion Probability (PIP) that X_cl is not equal to zero, which is equal to E_Q(S_cl). We use the PIPs to infer a network of genes for each component consisting of the genes with a PIP > 0.5. We summarize the individual and tissue scores vectors in a similar way by using the expected values of the VB posterior, E_Q(A_cl) and E_Q(B_cl) respectively.

Identifying robust components

The model is complex and has a large number of parameters and there is no guarantee that the VB algorithm will find a global solution when optimizing the bound on the marginal likelihood. Running the method multiple times highlights this issue. Some components are found consistently across multiple runs, whereas other components only occur in a small number of runs. For example, our method often uncovers components that show strong cis eQTL signals when using the associated component scores as phenotypes. To identify robust components, we implemented a method that clusters similar components across different runs. We then focus on large clusters containing components from multiple different runs, and use these as the basis for our search for novel signals.

More specifically, we run our method 10 times and store the individual and tissue scores, gene loadings and PIPs. We calculate the absolute correlation between the individual scores for all pairs of components across the 10 runs. Hierarchical clustering is then used to group components into clusters, using one minus the absolute correlation as a dissimilarity measure. The clustering is terminated when no correlations between clusters are above 0.6.

The components within each cluster are then combined. We take the mean of the individual scores, tissue scores and gene loadings and the median PIPs. The individual scores for each component cluster are then used as a phenotype against a genome-wide dataset of SNPs on the same individuals to identify which components have a genetic basis. We apply quantile normalization to the individual scores before testing for association with SNPs. Tissue scores are thresholded to obtain tissue activity patterns. The distribution of tissue scores tends to be tri-modal with one, well defined mode centered on zero so a threshold can easily be picked to set small score values to zero. We only test averaged components calculated from clusters with a minimum (user-defined) membership size, in order to focus on components that are robustly and consistently identified across runs.

Analysis of the TwinsUK dataset

Gene expression levels were measured for 845 female twins from the TwinsUK cohort using whole transcriptome sequencing (RNA-seq), with data in three tissues (adipose, lymphoblastoid cell lines (LCLs) and skin) for the majority of the individuals^19,20. Experiments were performed using the Illumina TruSeq sample preparation kit and sequenced on a HiSeq2000 machine. Reads were mapped on to the GRCh37 reference genome using BWA v0.5.9⁴⁴. Only reads that map uniquely were used. We run the method using RPKMs (reads per kilobase per million) after performing the following pre-processing and normalization steps; (i) genes with >20% zeros in all three tissues are removed resulting in 18,409 genes, (ii) quantile normalization of expression data within each tissue, (iii) rank based transformation of each gene onto a standard normal.

Samples were genotyped on a combination of the HumanHap300, HumanHap610Q, 1M-Duo and 1.2MDuo Illumina arrays. Samples were imputed using the 1000 Genomes Project Phase 1 reference panel (data freeze 10 November 2010) using IMPUTE2⁴⁵ and filtered (minor allele frequency (MAF) < 0.01 and IMPUTE info value < 0.8). Imputed genotypes were available on 795 of the 845 individuals.

We also used 11 concurrently measured phenotypes that were available on the samples (age, BMI, weight, height, total cholesterol, HDL cholesterol, LDL cholesterol (calc), total triglycerides, adiponectin, insulin and glucose) and variables derived from the sequencing. Specifically, we used (a) the mode of the insert size calculated for each sample, which can vary between sequencing library preps, (b) GC-content of the reads from a sample, which can vary due to biochemical differences in library prep and lane effect, (c) date of sequencing and (d) primer index.

We ran our method 10 times on the dataset and combined components across runs via clustering (see above). Supplementary Figure 39 shows the resulting distribution of cluster size. Only those clusters with more than or equal to 5 components were then retained for GWAS.

We used a linear mixed model⁴⁶ to test an individual scores vector as a phenotype against the SNP genotypes. The scores vector was subset down to the 795 individuals for which imputed genotype data was available. We used a Bonferroni corrected significance threshold of 1×10⁻¹⁰, calculated by scaling a genome-wide significance threshold of 5×10⁻⁸ by 500 to account for the multiple GWAS we perform.

Testing associations between individual scores vectors and phenotypes and batch variables was also performed using a linear mixed model⁴⁶, again only using 795 individuals. Only one member of each twin pair was used in the associations with age. The categorical batch variables, date and primer index, were dealt with by creating binary vectors (one for each category) and individually using these as a fixed effect in the linear mixed model.

Gene Ontology analysis was carried out using the TopGO R package⁴⁷. Gene ontology analysis evaluates whether a particular set of genes are enriched for a GO term in comparison to a background gene set. TopGO uses Fisher's exact test to get a p-value for enrichment based on the expected and observed number of genes with a GO term. Of the 18,409 genes used in this analysis, 13,965 have GO annotations. To get a significance level for this analysis we randomly sampled 10,000 sets of genes of a random size and performed an enrichment analysis on each set. We take the smallest p-value from each gene set to create a null distribution and use this distribution to estimate a significant level of 1%.

We use a linear mixed model⁴⁶ to perform direct associations between the SNPs and the (normalized) expression levels of genes involved our components. In order to account for unmeasured confounding factors, we fit the PEER model²³ to each tissue’s expression data with 15 factors and use these as covariates in the mixed model. In addition to the PEER factors, we also include two phenotypes, (age and BMI) and two tissue-specific batch variables (GC mean and insert size mode) as covariates.

Application of fastICA

We used the R package fastICA to apply ICA to the TwinsUK dataset. We concatenated the normalized expression data from the 3 tissues into a single matrix. Only 618 out of 845 individuals had expression data on all 3 tissues, so this matrix had 618 rows and 3×18409 columns. We fit the maximum number of components possible (618). We selected the 200 components for the measure of kurtosis of the gene loadings was > 3.5 and ran a GWAS against all SNPs. We also tested the components individual scores against the known confounding variables from the sequencing. More details are given in the Supplementary Note.