Abstract
Whole-exome sequencing has enabled new approaches for discovering genes associated with monogenic disorders. One such approach is gene-based burden testing, in which the aggregate frequency of “qualifying variants” is compared between case and control subjects for each gene. Despite substantial successes of this approach, the genetic causes for many monogenic disorders remain unknown or only partially known. It is possible that particular genetic architectures lower rates of discovery, but the influence of these factors on power has not been rigorously evaluated. Here, we leverage large-scale exome-sequencing data to create an empirically based simulation framework to evaluate the impact of key parameters (background variation rates, locus heterogeneity, mode of inheritance, penetrance) on power in gene-based burden tests in the context of monogenic disorders. Our results demonstrate that across genes, there is a wide range in sample sizes needed to achieve power due to differences in the background rate of rare variants in each gene. Increasing locus heterogeneity results in rapid increases in sample sizes needed to achieve adequate power, particularly when individual genes contribute to less than 5% of cases under a dominant model. Interestingly, incomplete penetrance as low as 10% had little effect on power due to the low prevalence of monogenic disorders. Our results suggest that moderate incomplete penetrance is not an obstacle in this gene-based burden testing approach but that dominant disorders with high locus heterogeneity will require large sample sizes. Our simulations also provide guidance on sample size needs and inform study design under various genetic architectures.
Introduction
Many diseases are monogenic, meaning that in affected individuals within a family, a single gene contains pathogenic variation that has a predominant influence on their disease status. Monogenic disorders are commonly referred to as Mendelian disorders, although many monogenic disorders may not show strictly Mendelian patterns of inheritance, especially in the presence of incomplete penetrance. Traditionally, genes associated with monogenic disorders have been mapped by linkage approaches in families. The advent of whole-exome sequencing (and increasingly whole-genome sequencing) has motivated new approaches to mapping genes associated with disease and has spurred rapid discovery of genes underlying hundreds of monogenic disorders.1 However, for many monogenic disorders, the genetic causes have not yet been found or have been found for only a subset of cases.
Aspects of genetic architecture (such as frequency and penetrance of disease alleles) exist along a spectrum from rare monogenic disorders (e.g., cystic fibrosis) to polygenic disorders (e.g., type 2 diabetes). Even among monogenic diseases, there is variability in genetic architecture. However, individuals with monogenic disease can be distinguished from those with polygenic disease by requiring that pathogenic variants have penetrance substantially greater than disease prevalence. If this condition is satisfied, affected relatives are likely to have inherited the same pathogenic variant(s) (see Supplemental Note).2 Linkage analysis has been most successful at this monogenic end of this spectrum, because the excess sharing of alleles between affected relatives can be quite low for polygenic disorders.2, 3 However, there are several important limitations to linkage analysis even for monogenic diseases. Incomplete penetrance can greatly reduce power in linkage analyses, even at levels of penetrance much higher than typically seen for variants influencing polygenic disease.2, 4, 5 Critically, incomplete penetrance can greatly reduce the number of affected individuals in any given family, making large families difficult to ascertain and thereby requiring aggregation of evidence across multiple families with small numbers of affected individuals. In the presence of locus heterogeneity, the effects of incomplete penetrance will be magnified, because reduced penetrance will necessitate combining linkage evidence across families that mostly have different genes associated with disease.
With the advent of exome sequencing, gene-based burden tests have been increasingly applied to try to overcome these limitations, particularly for diseases where linkage analysis is not feasible or has been ineffective. Gene-based burden testing approaches are typically applied to cohorts of unrelated probands. In this approach, the burden of variants in each gene is compared between disease-affected case subjects and suitable control subjects. Various filters, such as allele frequency thresholds and predictions of functional consequence, are applied to enrich for variants that are more likely to be pathogenic from the otherwise high background of benign variants. In accordance with Cirulli et al., we refer to variants that meet these filters as “qualifying variants.”6 Once these filters are applied, the aggregate frequency (burden) of qualifying variants is compared between case and control subjects. This approach is highly comparable to gene-based burden testing strategies frequently applied in rare variant association studies in polygenic traits,7, 8 and so is in theory applicable across a range of genetic architectures. Although the power of this strategy is well characterized for polygenic disorders,9, 10, 11 the power under different genetic architectures for monogenic disorders has not been systematically characterized. Because there are wide differences across even monogenic diseases in terms of genetic architecture (i.e., rate of background variation in disease-associated genes, mode of inheritance, penetrance, locus heterogeneity), we hypothesized that the genetic architecture or the nature of the disease-associated genes makes some disorders less amenable to these exome-sequencing-based gene discovery approaches.
We sought to determine the power to detect genes associated with monogenic disorders under various genetic architectures and to examine whether certain genetic architectures are less amenable to gene-based burden approaches. Estimating the sample sizes needed to find genetic causes of disease is important, especially since individuals with rare monogenic disorders are often difficult to ascertain in large numbers. Previous studies have begun to address this question but have not been comprehensive in their analyses of power and have not utilized actual exome-sequencing data to guide simulations.12, 13 To more comprehensively evaluate power and sample size requirements, we created a simulation framework that leverages empirical large-scale exome-sequencing data to determine the effect of relevant parameters on power to detect disease-associated genes. Our simulation framework can also be used to help place bounds on genetic architectures of ongoing projects and to inform which genetic architectures are amenable to this gene-based burden testing approach.
Material and Methods
Framework
In our framework, we consider rare monogenic disorders for which the genetic causes are unknown. Each monogenic disorder can be caused by mutations in any number of disease-associated genes. We consider a simple two-class model, where variants are either pathogenic (they can cause disease) or benign (no effect on disease risk). We define a monogenic disorder to be a disorder in which pathogenic mutations in a single disease-associated gene are largely responsible for disease in any given individual with disease; specifically, we require that the penetrance of causal mutations be substantially greater than the prevalence of disease. When this is true, any two related individuals with a given disorder will have co-inherited the same underlying pathogenic variant(s), meaning that the pathogenic variants are the predominant genetic influence on individuals with disease (Supplemental Note).
In the typical study design, a cohort of individuals with a monogenic disorder and a suitable control cohort undergo exome sequencing. To improve power, criteria are set for enriching for pathogenic variants. Criteria usually include a minor allele frequency (MAF) threshold and a threshold for the predicted effect of the variant on protein function, under the assumption that rarer variants and variants with a greater effect at the protein level are more likely to be pathogenic for a monogenic disorder.14, 15, 16 We refer to variants that pass these thresholds as “qualifying variants.”6 For each gene, the frequency of qualifying variants is compared between case and control subjects using a typical 2 × 2 contingency table test or other applicable statistical test.
In an ideal situation, pathogenic variants could be readily distinguished from benign variants, but in most cases, some proportion of qualifying variants are actually benign and some proportion of non-qualifying variants are actually pathogenic. Furthermore, if there is incomplete penetrance, unaffected control individuals may in fact harbor pathogenic variants. Qualifying variants present in disease-free controls are therefore comprised of: (1) benign variants that are difficult to distinguish from pathogenic variants and (2) incompletely penetrant pathogenic variants. These qualifying variants in control subjects represent a background rate of variation for each gene. If one were able to perfectly distinguish between pathogenic and benign variants, then all qualifying variants in disease-free control subjects would represent incompletely penetrant variants. Conversely, if all pathogenic variants are fully penetrant, then all qualifying variants in disease-free control subjects would represent benign variants that are misclassified. Similar arguments hold for qualifying variants present in case subjects, except that the qualifying variants also include disease-manifesting pathogenic variants. We assume that for each gene, the background rate of variation not contributing to disease (comprised of incompletely penetrant pathogenic variants not manifesting as disease and benign variants that are misclassified) is the same between case and control subjects.
Parameters
In this framework, we consider two groups of parameters that influence the case sample sizes needed for power to detect genes associated with monogenic disorders. The first group of parameters encompasses aspects of the genetic architecture, which are intrinsic to a given disorder. These include the background rate of variation in disease-associated genes (β), the mode of inheritance (autosomal-dominant or -recessive), locus heterogeneity (modeled by fcase, or proportion of disease cases attributable to pathogenic variants in each disease-associated gene), and penetrance (π). Throughout, we use a bolded fcase to represent a summary parameter for the average contributions of genes to a given disorder, and unbolded fcase to represent the contribution of any given disease-associated gene. The second group of parameters is related to study design and analytical methods. These include the ability to distinguish pathogenic from benign variants and characteristics of the control cohort. Additional descriptions of these parameters are provided in the Supplemental Note.
Estimating Background Rate of Variation
In this study, we estimated the background rate of variation (β) in each gene based on a set of 2,597 exome-sequencing samples obtained from dbGaP under accession numbers phs000007, phs000179, phs000200, phs000209, phs000280, phs000286, phs000287, and phs000285 (see Supplemental Note for dbGaP acknowledgments). Ethical approval for the use of cohorts from dbGaP was obtained from the Institutional Review Board of both Boston Children’s Hospital and the Broad Institute of Harvard and MIT.
These exome-sequencing samples were jointly called by the ExAC Consortium along with approximately 85,000 additional exomes.17, 18 Samples were pruned to remove related individuals (IBS > 0.25). PCA outlier analyses were performed by projecting exome-sequencing samples onto HapMap3 samples using SMARTPCA.19, 20 A subset of 2,597 individuals of European ancestry as determined by the PCA analysis was used in all analyses. Effects of variants were annotated with Ensembl Variant Effect Predictor (VEP) v.77.21 Only variants within canonical transcripts of protein coding genes were analyzed. MAF filtering was based on the population maximum allele frequency from ExAC.18 To prevent circularity in calculating the MAF from ExAC, we excluded the subset of individuals in our samples for the MAF calculation (since some of the samples used are a part of ExAC).
This cohort is comprised of samples not ascertained on a specific monogenic disorder; thus, for any single rare monogenic disorder, the number of individuals in this cohort with that disorder is likely to be minimal. We estimate β as the proportion of individuals in the cohort who carry a qualifying variant (defined as below) in each gene.
To model thresholds for distinguishing pathogenic from benign variants, we used minor allele frequency (MAF) thresholds and predicted effect on protein function. MAF thresholds were set at 1%, 0.1%, 0.01%, or private (not seen elsewhere in ExAC). We set three levels of stringency for predicted effect on protein function. The least stringent threshold we evaluated included all nonsynonymous variants as qualifying variants. The most stringent level included only loss-of-function (LOF) variants: essential splice site, nonsense, and frameshift. We also set an intermediate threshold where we included LOF variants and missense variants predicted to be damaging by three of three different protein-prediction algorithms: PolyPhen-2, SIFT, and MutationTaster.22, 23, 24
Construction of Contingency Table
For any given set of parameters, we can construct a 2 × 2 contingency table for that gene, where the columns are case and control subjects and the rows are presence or absence of a qualifying variant for that gene (Figure S1).
We use the background rate of variation (β) for each gene (observed from our sample of exome-sequencing data from 2,597 individuals) to simulate the number of control subjects carrying (CONTROLQV) or not carrying (CONTROLNQV) a qualifying variant in that gene:
Qualifying variants in case subjects (CASEQV) represent the background rate of variation plus disease-manifesting pathogenic variants. For any given gene, the number of case subjects carrying disease-manifesting pathogenic variants is a function of locus heterogeneity (ƒcase for that gene) and the sensitivity (S) to detect pathogenic variants given the thresholds. At a given observed background rate of variation (β) and an assigned CASETOTAL, ƒcase, and S, we can calculate the expected number of case subjects carrying (CASEQV) and not carrying (CASENQV) qualifying variants for that gene.
In calculating CASEQV, the term CASETOTAL × ƒcase × S represents the number of case subjects who carry pathogenic variants that met the filters. The term (1 − ƒcase) × β represents background variation in the case subjects who do not carry pathogenic variants.
Simulating Sample Size Needs for Each Gene
To determine power to detect a specific gene, we used the background rate of variation for that gene (β, observed from the exome-sequencing data of 2,597 individuals) and specified the fcase and the sensitivity to detect pathogenic variants given the thresholds (S). At a given total case cohort size (CASETOTAL), we then perform 1,000 simulations. In each simulation, we simulate the number of pathogenic disease mutations observed in the case subjects (CASEPATH), where CASEPATH is distributed binomially as:
The number of case subjects carrying (CASEQV) and not carrying (CASENQV) qualifying mutations in cases for that simulation is then:
The number of control subjects carrying qualifying variants (CONTROLQV) is calculated based on the background variation β (see above). The number of case and control subjects carrying and not carrying qualifying variations are then compared using a two-sided Fisher’s exact test (non-integer values were rounded to integers for the Fisher’s exact test). p values less than 2.5 × 10−6 (α = 0.05 corrected for testing of approximately 20,000 genes) are considered to be significant (see Supplemental Note for additional information on p values). 80% power is determined as the minimum CASETOTAL that results in 80% of simulations achieving statistical significance.
Simulating Power to Detect Any Gene
To determine power to find at least one gene associated with a given disease (as opposed to a single, specified gene), we first model gene sets (sets of fractional contributions of disease-associated genes to disease cases) where each disease-associated gene contributes an equal proportion (ƒcase) to disease cases and there are 1/ƒcase genes. We iterate a total case sample size (CASETOTAL) upward with step size of 1. At each CASETOTAL, we perform 1,000 simulations. For each of these simulations, we draw a set of 1/ƒcase random genes, where the genes are selected randomly from the genome. For each gene in the set of disease-associated genes, the number of case subjects carrying pathogenic variants is simulated as described above.
For each set of random genes, using the simulated CASEQV and CONTROLQV, we calculate a p value for each gene in the set. At each CASETOTAL, we can then calculate the number of random sets of genes (out of 1,000 simulated sets) where at least one gene in the set resulted in a significant p value. The number of samples needed for 80% power is the minimum CASETOTAL for which more than 80% simulations had at least one gene reach statistical significance (p ≤ 2.5 × 10−6).
Power under Recessive Model
Simulations to calculate the samples needed for each gene and the samples needed for a gene set under the recessive model were performed similarly as above. The background rate of variation (β) in control subjects for the recessive model is based on the number of individuals carrying two or more qualifying variants in a given gene. It is important to note that individuals carrying two or more variants in a gene can be homozygous recessive, compound heterozygous, or carry two variants on the same haplotype (since we cannot readily resolve phase in our samples). Since some proportion of the individuals who carry two variants in a gene actually represent two variants on the same haplotype, the background rate under the recessive model is inflated, which would have the effect of slightly deflating power. Because phase is also unknown for most actual studies, our simulations should correspond closely to actual studies.
Simulation of Unequal Contributions of Disease-Associated Genes
Whereas throughout the majority of the manuscript, we modeled gene sets where there are 1/ƒcase genes, each of which contributes to ƒcase proportion of disease cases, in simulations related to Figures S9A–S9C, we modeled unequal contributions of disease-associated genes. We created three sample disease-associated gene sets. In set 1, there are 10 genes, each contributing to 10% of cases. In set 2, there are 6 genes: one gene contributing to 50% of cases and 5 genes each contributing to 10% of cases. In set 3, there are 51 genes: one gene contributing to 50% of cases and 50 genes each contributing to 1% of cases. For these simulations, we observe the number of gene sets (out of 1,000) that resulted in at least 1, 2, 3, 4, and 5 genes, and no genes reach statistical significance at increasing sample sizes. Simulations were performed as described above.
Simulation of Phenocopies
To simulate the effect of phenocopies or disease cases that have disease due to polygenic or non-genetic causes, we introduce a phenocopy rate parameter: ϕ. ϕ represents the proportion of case subjects who do not manifest disease due to a pathogenic mutation in one of the monogenic disease-associated genes, but rather due to a different cause. The fcase of the disease-associated genes sum to 1 − ϕ. We simulated power for ϕ ranging from 0.1 to 1.0. Simulations were performed as described above.
Effect of Penetrance
To examine the effect of penetrance, we make the simplifying assumption that the background rate of variation observed from the 2,597 individuals entirely represents benign variants. To simulate the effect of penetrance, we then add to this background rate of benign variants an additional factor to reflect incompletely penetrant pathogenic variants not manifesting as disease present in a disease-free control cohort. We represent this rate of these incompletely penetrant pathogenic variants as , which can be modeled given the penetrance (π), disease prevalence (P), sensitivity to detect pathogenic variants given a set of thresholds (S), and the locus heterogeneity parameter, ƒcase.
In this formula, the term represents the proportion of the population who would carry a detectable pathogenic variant in a given disease-associated gene. Since we are simulating a healthy control population, we must multiply by 1 − to obtain the proportion of healthy individuals in the control population who carry a pathogenic variant not manifesting as disease in a given disease-associated gene. To then calculate a total background rate of variation for each gene, we add to the background rate of qualifying variants observed from the 2,597 individuals. The number of control subjects carrying (CONTROLQV) and not carrying (CONTROLNQV) can then be calculated as above.
For case subjects, we again assumed that the background rate (representing benign variants and incompletely penetrant pathogenic variants not manifesting as disease) is the same in case subjects and in control subjects. We again spike in pathogenic variants and calculate the number of case subjects (CASEQV) carrying and not carrying (CASENQV) qualifying variants as described above.
Effect of Control Size and Population-Based Controls
To simulate the effect of control size, we used the same background rate of variation as above but scaled the CONTROLTOTAL to 1,000, 10,000, 100,000, and 1,000,000 total control subjects. To simulate the effect of using population-based control subjects rather than disease-free control subjects, we used the same simulation framework but modeled the additional effect of having disease-affected individuals in the control cohort as a function of the prevalence (P) of disease (modeled at 1%, 0.1%, 0.01%, and 0.001%). In this situation, there is additional background variation resulting from disease-manifesting individuals in the control subjects which equals . The background variation resulting from disease-manifesting individuals in the control cohort is added to the background variation observed from the data to generate a modified control background rate that was then used in the simulations.
Comparison of Known and Constrained Genes
For Gene Damaging Index (GDI) scores, we considered constrained genes to be those marked as “Low” for “Gene damage prediction (all disease-causing genes).”25 For Residual Variation Intolerance Scores (RVIS), we considered constrained genes to be genes in the lowest 25th percentile according to the “OEratio-percentile[ExAC]” metric.26 For analyses related to Figure S16, we used a set of 631 OMIM genes that reportedly act in a dominant fashion. Coding gene lengths were obtained from Gencode v.19; for each gene, the length of the longest transcript was used. Power calculations were performed as described above.
Software
All simulations were performed with R v.3.1.27 Code used for the simulations is available upon request. Processing of vcf files was performed with bcftools v.1.228 and custom Python scripts (v.2.7).
Results
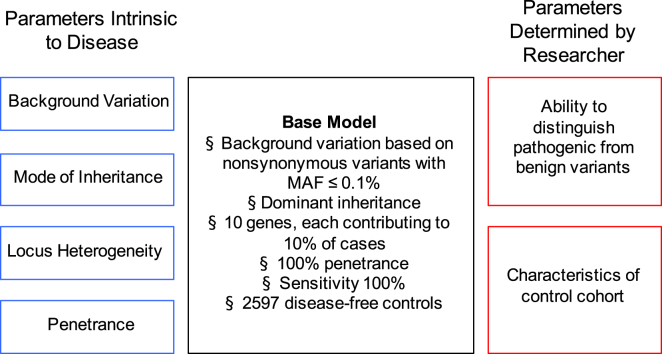
In this study, we developed a simulation framework to understand how multiple factors can influence power to detect genes underlying a monogenic disorder in an exome-sequencing gene-based burden testing strategy. We broadly classify these factors into: (1) components of the genetic architecture (background rate of variation in disease-associated genes, locus heterogeneity, mode of inheritance, and penetrance of causal variants) and (2) aspects of the study design and analytical methods (ability to distinguish pathogenic from benign variants and characteristics of the control cohort) (Figure 1A). Our simulation framework is based on empirically determined rates of background genetic variation (Figure S1). First, we use large-scale exome-sequencing data to tabulate the background rates of qualifying variants in each gene in the genome. Using these empirically derived background rates, we simulate power under a base model and then systematically alter each factor to evaluate its effect on power. Additional details regarding the framework and simulations are provided in the Material and Methods and the Supplemental Note. A listing and description of all the parameters used can be found in Table S1.
Figure 1.
Determinants of Power in Exome-Sequencing Studies for Monogenic Disorders
The black box (center) lists the values for each parameter under the “base model” monogenic disorder we consider. On the left (blue) are the parameters that are intrinsic to a given disorder (background rate of variation of disease-associated genes, mode of inheritance, locus heterogeneity, and penetrance). On the right (red) are parameters that are determined by the researcher (sensitivity to detect pathogenic variants and characteristics of control cohort). The values used in the paper are listed in Table S1.
Background Rate of Variation across Genes
In a typical study design, filters such as minor allele frequency (MAF) and computational predictions of whether a variant is damaging are applied to enrich for variants that are more likely to be pathogenic. We refer to the variants that pass these filters as “qualifying variants”6 and define the background rate of variation to be the proportion of individuals in a disease-free control cohort who carry qualifying variants.
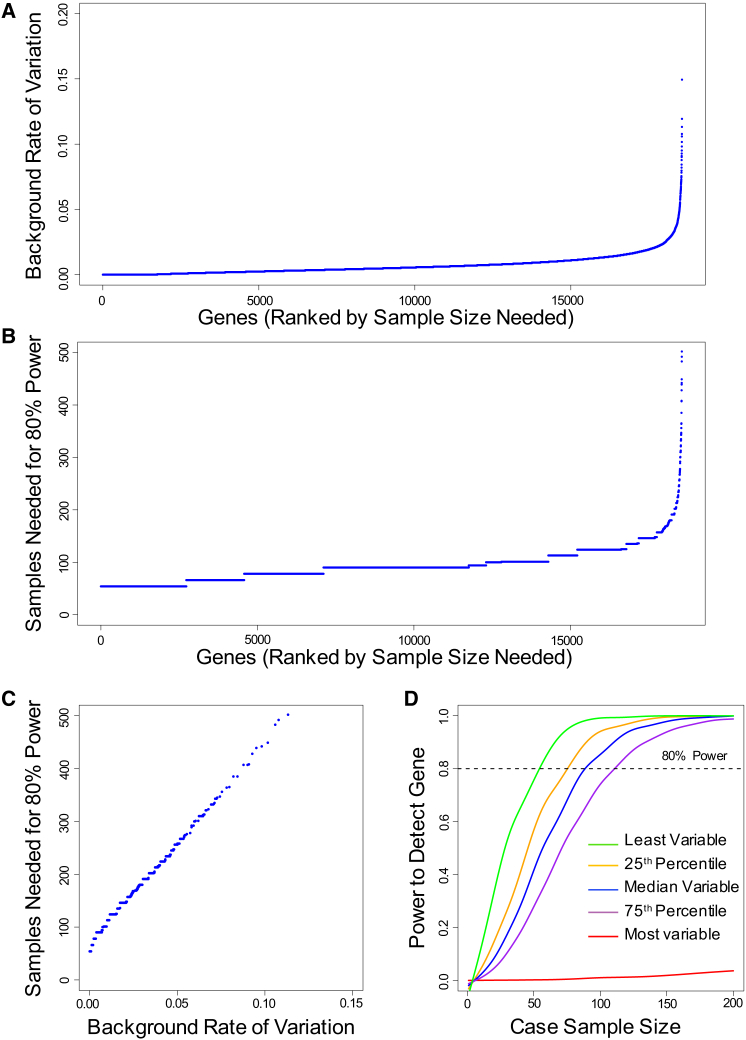
We first examined the distribution of background rate of variation across all genes, utilizing exome-sequencing data from 2,597 individuals (see Material and Methods). Because we are simulating an arbitrary rare disease, we for now make the assumption that the cohort under study is free of the disease. In this control cohort, we observed a wide range of background variation across genes. For example, if we define qualifying variants as all nonsynonymous variants with MAF ≤ 0.1%, then 1,744 genes have no individuals who carry a qualifying variant, whereas for the most variable gene (TTN), 38.2% of individuals carry at least one variant that meets these criteria (Figure 2A).
Figure 2.
Background Rate of Variation and Power to Detect Specific Genes
(A) Background rate of variation (proportion of control subjects carrying qualifying variants) in each gene considering all nonsynonymous variants at MAF ≤ 0.1%. Genes are ranked on the horizontal axis from the least variable to the most variable. Each point on the plot represents a single gene. Not shown: MUC16 (0.209) and TTN (0.382).
(B) Sample size needed to have 80% power to detect each gene in the genome under the base model (see Figure 1 for details of the base model). Genes are ranked from least to most samples needed for 80% power. Not shown: SYNE1 (502 samples), FLG (548), OBSCN (692), MUC16 (1,058), and TTN (3,740).
(C) Sample size needed to have 80% power to detect each gene in the genome as a function of background rate of variation. Simulations were performed under base model. Not shown: SYNE1 (0.113 background rate; 502 samples), FLG (0.119; 548), OBSCN (0.149; 692), MUC16 (0.209; 1,058), and TTN (0.382; 3,740).
(D) Power to detect a gene at increasing sample sizes, for the least variable gene (green), genes at 25th (orange), 50th (blue), 75th (purple) percentiles of variability, and most variable gene (red). Simulations performed under the base model. Curves were smoothed using smooth.spline function in R.
Distribution of Sample Sizes Needed across Genes
Having observed a wide range of background rates across gene, we next used these data to determine sample sizes needed for power to detect each gene, if it were a disease-associated gene. We first modeled a moderately favorable architecture, hereafter referred to as the “base model,” where each gene contributes a dominant, completely penetrant, rare (MAF ≤ 0.1%) nonsynonymous variant to 10% of disease-affected case subjects (Figure 1, Table S1). Note that the assumption of complete penetrance implies that all qualifying variants present in control subjects represent benign variants “misclassified” by using insufficiently stringent filters (see Material and Methods). Using this base model, for each gene in the genome, we determined sample sizes needed for 80% power to detect that specific gene at p ≤ 2.5 × 10−6 (see Supplemental Note for details on p value thresholds). We found a wide range of sample sizes needed to achieve 80% power (Figure 2B), which was linearly related to the background rate of variation in each gene (Figure 2C). As expected, genes with the most background variation are the most difficult to discover and may require intractably large numbers of case samples. For example, TTN, which has the highest background rate of variation, would require approximately 3,740 case subjects to achieve 80% power even under this moderately favorable scenario. At the other extreme, a gene with no observed background variation requires approximately 54 cases to achieve 80% power under the same scenario. The background rate of variation also influences power across a wide range of other criteria for defining qualifying variants (Figures S2–S7).
To further illustrate the relationship between background rate and power, we chose five representative genes: the least variable gene, genes at the 25th, 50th, and 75th percentiles of variability, and the most variable gene in the genome based on nonsynonymous variants with MAF ≤ 0.1%. Background rates of qualifying variants for these five genes were 0%, 0.23%, 0.50%, 0.90%, and 38.2%, respectively. For each of these five genes, we then determined power at increasing sample sizes if the gene contributes to 10% of disease-affected case subjects under a dominant model. We observed a sigmoidal relationship between power and sample sizes (Figure 2D); there is a “lag” in power gain before reaching a sample size at which power increases rapidly. At some point, the gains in power begin to level off with increasing sample size. For the most highly variable gene, there were no significant power gains even after 200 case samples are sequenced. These analyses demonstrate that differences in the rate of background variants across genes strongly influence the power to detect different genes for a given genetic architecture.
Power to Detect at Least One of a Set of Disease-Associated Genes
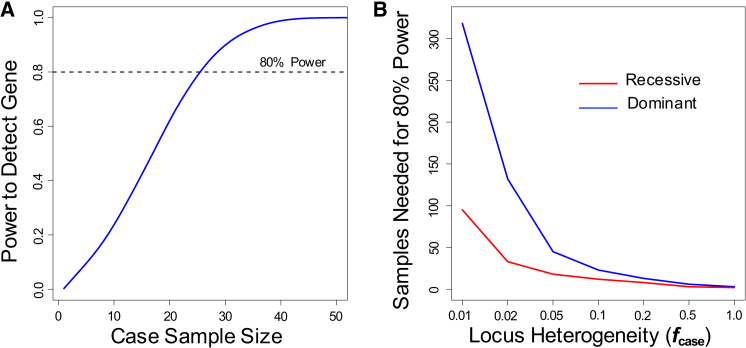
Having determined the sample size needed to detect a single disease-associated gene, we next evaluated the power of exome sequencing to detect at least one of any genes, given a set of genes that underlie a disease. We make the simplifying assumption that the disease-associated genes have background rates of variation equivalent to a random sample of genes drawn from the entire genome. We calculated the power to detect at least one gene using the base model described above. In this scenario, 25 samples provide 80% power to detect at least one of the ten disease-associated genes (Figure 3A).
Figure 3.
Power to Detect at Least One Gene Associated with Disease
(A) Power to detect at least one gene associated for a disease with ten disease-associated genes, each of which contributes to 10% of cases (fcase = 0.1). Analyses were performed at increasing case cohort sample sizes under a dominant model and considering nonsynonymous variants at MAF ≤ 0.1%.
(B) Sample sizes needed to have 80% power to detect at least one gene association for a disease under a dominant (blue) and recessive (red) model. Simulations were performed under base model at varying values of fcase (0.01 to 1.0)
In the analyses that follow, we continue to explore the sample sizes needed to achieve 80% power to detect at least one gene, varying each parameter in the base model individually and assessing the impact of each parameter on power under different scenarios.
Power under Recessive Model
The base model assumes a dominant model, in which only one qualifying variant is needed to manifest disease. To examine the impact of a recessive model on power, we consider only genes with two qualifying variants. As expected, using the same MAF threshold for defining a qualifying variant, the background rate of variation for each gene was smaller under the recessive model than under a dominant model (Figure S8A). For example, for nonsynonymous variants at MAF ≤ 0.1%, none of the 2,597 individuals carried qualifying variants for 15,311 genes under a recessive model (by comparison, none of the individuals carried qualifying variants for only 1,744 genes under the dominant model). This decreased background rate of variation under the recessive model results in a corresponding decrease in the sample sizes needed to achieve 80% power to detect each gene (Figure S8B). In later analyses, we determine the effect of changing the MAF threshold, which might often be appropriately higher for recessive disorders than for dominant disorders.
Impact of Locus Heterogeneity
To model locus heterogeneity, we assign a parameter ƒcase to represent the fraction of disease cases caused by qualifying variants in each disease-associated gene; this parameter is inversely related to degree of locus heterogeneity. We first analyzed power in scenarios where each disease-associated gene contributes equal proportions to disease cases, for values of ƒcase ranging from 0.01 to 1.0 (in the base model, ƒcase is 0.1). We found that locus heterogeneity had a strong effect on power (Figure 3B). Starting from the base model, as ƒcase increases from 0.1 to 1.0, typical sample sizes needed for 80% power decrease from 23 to 3 case subjects. Conversely, as ƒcase decreases, the sample sizes needed to detect a disease-associated gene rise sharply; this effect is particularly striking when ƒcase falls below 0.05, with 318 case subjects needed to detect at least one disease-associated gene under the base model when ƒcase is 0.01. As expected from the lower rate of background variation, the recessive model performs better at the same MAF threshold; when ƒcase is 0.01, 95 case samples are needed for 80% power for the recessive model.
For actual diseases, the contributions of each disease-associated gene probably differ across the genes. To simulate the impact of variable contributions of individual genes, we simulated three different sets of contributions to disease cases, all under a dominant model. In set 1, each of ten disease-associated genes contributes to 10% of cases (base model); in set 2, one gene contributes to 50% of cases and five genes each contribute to 10% of cases; in set 3, one gene contributes to 50% of cases and 50 additional genes each contribute to 1% of cases. We observed similar patterns of power across each of these three gene sets (Figures S9A–S9C) and that the power to detect at least N disease-associated genes is driven primarily by the genes with the ∼Nth largest ƒcase values. Specifically, the power to detect at least one gene is higher with larger maximum values of ƒcase for a given disease.
Finally, we note that in some situations, the contributions of the disease-associated genes might not sum to 100%. This may be due to phenocopies from other disorders, non-genetic causes, or polygenic causes of disease. We encapsulate these possibilities as a “phenocopy rate” and simulate scenarios where values of ƒcase sum to less than 1 due to this phenocopy rate. As expected, higher phenocopy rates increase the required sample sizes with sample sizes doubling at a 40% phenocopy rate (i.e., a genetic architecture in which exonic, monogenic variants contribute to 60% of disease cases) (Figure S10).
Effect of Penetrance
We next sought to evaluate the effect of incomplete penetrance on the power to detect disease-associated genes. Elsewhere in the manuscript we have assumed complete penetrance so that all qualifying variants present in disease-free control subjects are benign variants that are misclassified. To examine the effect of incomplete penetrance, we now modify our assumptions such that the background rate of variation observed in the 2,597 individuals represent benign variants and then add to this observed rate of background variation an additional factor representing the rate of incompletely pathogenic variants not manifesting as disease in a disease-free control cohort (see Material and Methods).
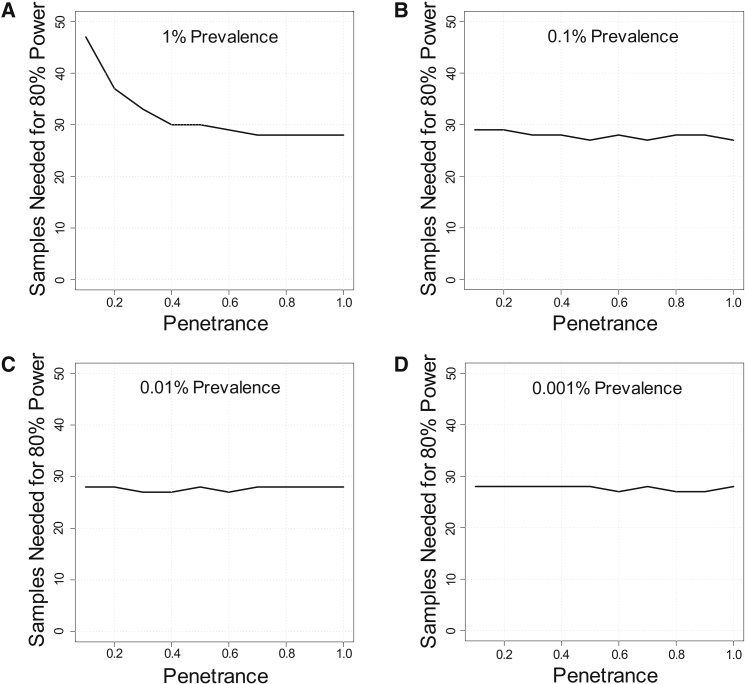
We simulate penetrance with the parameter π (probability of a variant causing disease in an individual) and assessed the impact of variable penetrance on power (π ranging from 10% to 100%). Importantly, in contrast to other analyses in this manuscript, the prevalence of disease now becomes an important consideration: the background rate of variation due to incomplete penetrance is related to the prevalence of disease, while the background rate of variation due to misclassification is independent of prevalence. We note that our working definition of a monogenic disorder is disease due to variants whose penetrance is substantially greater than the disease prevalence (see Supplemental Note); we therefore focus our analyses on scenarios where penetrance is at least 10-fold greater than prevalence.
Starting from the base model and evaluating a range of disease prevalence from 1% to 0.001%, we found that the effect of penetrance was relatively small, especially at low disease prevalence. For example, decreasing penetrance from 100% to 10% only substantially increased sample sizes when disease prevalence was 1% (Figures 4A–4D). These patterns hold at other values of locus heterogeneity (Figures S11 and S12). These simulations demonstrate that incomplete penetrance, in isolation, has little impact on power for this gene-based burden testing approach, especially if disease prevalence is low. Intuitively, the effect of moderately low penetrance (in the range of 10% or even lower) is small for rare monogenic diseases because the low disease prevalence, relative to penetrance, means that few disease-free control subjects will carry pathogenic mutations. This low rate of pathogenic variants in healthy control subjects corresponds to a small effect on background variation and limited dilution of power in the gene-based burden test. Moreover, because this strategy ascertains case subjects on affected status, reduced penetrance will have almost no effect on the variants observed in the case subjects.
Figure 4.
Effect of Penetrance
Effect of penetrance on sample sizes needed for 80% power to detect at least one gene associated with disease. Simulations were performed at varying disease prevalence of 1% (A), 0.1% (B), 0.01% (C), or 0.001% (D). Values of penetrance range from 0.1 to 1.0. Simulations were performed assuming a dominant disorder with ten disease-associated genes, each of which contributes to 10% of cases (fcase = 0.1).
Effect of Ability to Distinguish Pathogenic from Benign Variants
The analyses above assessed the impact of genetic architecture (background rate of variation, locus heterogeneity, mode of inheritance, and penetrance) on power to detect genes associated with a disease. We next analyzed the impact of aspects of study design on power. We first examined the choice of filters for selecting qualifying variants. For most genes and diseases, these filters are currently imperfect at distinguishing pathogenic from benign variants and thus have an associated sensitivity and specificity for each gene. The sensitivity is the proportion of truly pathogenic variants that are correctly classified as qualifying variants, whereas specificity is the proportion of benign variants that are correctly classified as non-qualifying variants.
To model the effect of increasing specificity (that is, decreasing in the number of truly benign mutations that are misclassified as qualifying), we examined the effect of increasingly stringent filters on power. Two commonly used filters are MAF and predicted effect of variant on protein function, with the assumption that rare variants and variants with a greater effect on protein function are more likely to be pathogenic for rare monogenic disorders. Different values of the MAF filter—1%, 0.1%, 0.01%, or private (not present elsewhere in cohort or in reference populations)—affected the observed background rate of variation (Figure S2), which led to a corresponding change in power (Figure S3). Likewise, varying the stringency of filters for the predicted effect of the variant on protein function (LOF only, LOF plus missense predicted to be damaging, or all nonsynonymous variants) affected the background rate of variation (Figure S4) and power (Figure S5).
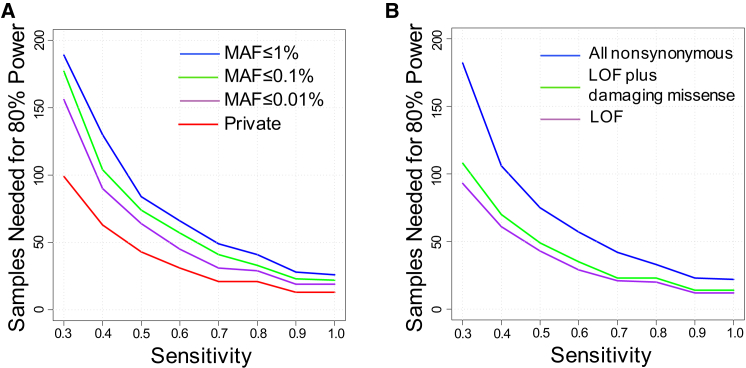
Although applying more stringent filters to increase specificity can improve power by decreasing the background variation rate, there may also be detrimental effects on power due to decreased sensitivity. For example, a MAF filter that is too stringent can decrease sensitivity if some truly pathogenic variants are more common than the MAF threshold being applied. To evaluate this trade-off between sensitivity and specificity, we determined power using filters with different stringency and modeling values of sensitivity (Figures 5A and 5B). For example, under our base model and MAF ≤ 1%, 26 samples are needed to obtain 80% power at 100% sensitivity to detect any gene associated with a given disease (Figure 5A). Tightening the MAF filter from 1% to considering only private variants would decrease sample sizes for 80% power from 26 to 13, assuming sensitivity of 100% is maintained. However, if this more stringent filter reduced sensitivity to 60% or below, then there would actually be a loss of power as compared to applying a MAF filter of 1% and retaining 100% sensitivity.
Figure 5.
Effect of Ability to Distinguish Pathogenic from Benign Variants
(A) Sample sizes needed to achieve 80% power to detect at least one disease-associated gene at varying MAF cutoffs (1%, 0.1%, 0.01%, or private) and sensitivities (0.3 to 1.0) to detect pathogenic variants. Simulations were performed assuming a dominant disorder with ten disease-associated genes, each of which contributes to 10% of cases (fcase = 0.1). Background rates of variation were calculated based on all nonsynonymous variants.
(B) Sample sizes needed to achieve 80% power to detect at least one disease-associated gene at varying protein-deleteriousness cutoffs and sensitivities (ranging from 0.3 to 1.0) to detect pathogenic variants. Protein-deleteriousness cutoffs include all nonynonymous (blue), LOF plus damaging missense (green), or LOF only (purple). Damaging missense assignments were based on three protein-prediction algorithms (see Material and Methods). LOF only includes only nonsense, splice site, and frameshift. Simulations were performed assuming a dominant disorder with ten disease-associated genes, each of which contributes to 10% of cases (fcase = 0.1). Background rates of variation were calculated based on MAF ≤ 0.1%
For both MAF threshold and protein-deleteriousness filters, we found that the sample sizes needed to achieve 80% power to detect at least one disease-associated gene rise exponentially with decreased sensitivity; every 30% reduction in sensitivity results in approximately a 2-fold increase in sample sizes needed (Figures 5A and 5B).
Impact of Control Cohort
We next considered the effect of changing parameters of the control cohort. We found that increasing control sample size has little effect on power to detect genes associated with disease as control cohort size increased past 10,000 control subjects (Figure S13A). There was also little impact of using a population-based control cohort rather than a disease-free control cohort at various disease prevalences, especially as the disease becomes increasingly rare (prevalence less than 0.1%; Figure S13B).
Bounds on Genetic Architecture
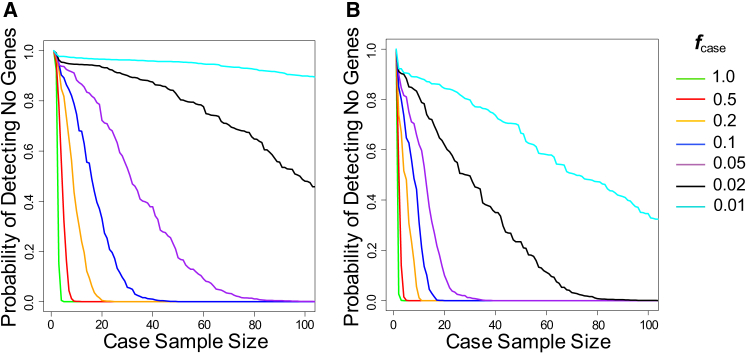
In most situations, the genetic architecture of a disease under study is not known a priori. Having determined that locus heterogeneity and mode of inheritance are the two most important drivers of power in a gene-based burden test for a monogenic disorder, we asked whether our simulation framework could be used to place bounds on the genetic architecture after a given number of case subjects have been sequenced and no gene has emerged as being associated with disease. We analyzed the probability of not detecting any gene at increasing sample sizes under different hypothesized values of locus heterogeneity (ƒcase ranging from 0.01 to 1.0) and modes of inheritance (dominant or recessive) (Figures 6A and 6B). As expected, there were rapid decreases in the likelihood of not finding any disease-associated genes with increasing sample sizes, especially when ƒcase was high or for recessive diseases. At a given case sample size where no gene has been implicated for a disease, a low likelihood of not detecting a disease-associated gene for a particular hypothesized ƒcase and mode of inheritance indicates that the genetic architecture is less favorable than hypothesized. For example, if 80 samples have been sequenced for a disease and no gene has reached statistical significance, the probability of any disease-associated gene contributing pathogenic variants to at least 5% to disease cases (ƒcase of 0.05) and acting in a dominant fashion is less than 1% (Figure 6A). This negative result would indicate that qualifying variants in any of the genes associated with disease most likely contribute to less than 5% of disease case subjects, suggesting either high locus heterogeneity, a large fraction of pathogenic variants that are not being captured as qualifying variants (such as noncoding variants or more common variants filtered out by the thresholds), or a substantial influence of phenocopies.
Figure 6.
Bounds on Genetic Architecture
Probability of not detecting any genes associated with a given disorder at increasing sample sizes. Analyses were performed at different hypothesized fcase ranging from 0.01 to 1.0 under a dominant model (A) or a recessive model (B). All nonsynonymous variants with MAF ≤ 0.1% were used in calculating background variation rates.
Power for Known and Predicted Disease-Associated Genes
Genes associated with disease may differ from the rest of the genome in characteristics such as background rates of variation. To assess how this would affect power, we first examined genes that have been demonstrated to display genic constraint by two metrics: GDI and RVIS.25, 26 As expected, genes showing constraint by either metric had lower background rates of variation as compared to the rest of the genome (Figures S14A and S15A) and required fewer samples to achieve power (Figures S14B, S14C, S15B, and S15C). However, genes associated with disease may not necessarily be easier to detect by this gene-based burden testing approach. In fact, known disease-associated genes cataloged by OMIM and reported to be dominant actually have higher background rates as compared to the rest of the genome (Figure S16A). This effect appears to be due to the correlation between gene length and background rate and the observation that these genes previously implicated in disease are systematically longer as compared to the rest of the genome (Figures S16B and S16C). Accordingly, the sample size needed to detect genes associated with disease was slightly higher (Figures S16D and S16E).
Discussion
We have applied a simulation framework to determine power in exome-sequencing studies that apply gene-based burden tests for discovery of genes associated with monogenic disorders. Our framework utilizes actual exome-sequencing data to understand how differences across a wide range of genetic architectures and realistic study designs affect power. To our knowledge, our work is the most comprehensive examination to date of the parameters that drive power in gene-based burden tests for monogenic disorders and is the first to incorporate empirical exome-sequencing data.
We demonstrated that background variation, which varies across genes, directly affects sample sizes needed to detect associations for that gene. The need for large sample size is particularly pronounced for genes such as TTN, where a large proportion of individuals in the population carry qualifying variants (Figures 2A and 2B). The number of case subjects needed to find associations for such genes can easily reach the hundreds or thousands depending on disease genetic architecture. These sample sizes may often exceed practical limits and implicating these genes in diseases will probably rely on additional lines of evidence, such as functional assays, analysis of specific subdomains (as has been done for TTN [MIM: 188840]), or segregation data in large pedigrees.29, 30
Our simulations demonstrated that locus heterogeneity and mode of inheritance are primary drivers of sample size needs for discovery of genes associated with monogenic disorders. As the contribution of any gene to a disease decreases (reflecting increased locus heterogeneity and/or “contamination” with phenocopies), the sample sizes needed to detect that gene rise rapidly; in a situation where any gene contributes to only a small fraction (e.g., 1%) of cases, hundreds of case subjects are needed to provide reasonable power to detect at least one gene associated with a disease under a dominant model. However, under a recessive model, the sample size needs are much smaller, even in the presence of high locus heterogeneity. A recent study illustrated the challenges that locus heterogeneity places in implicating genes associated as monogenic causes of rare disorders.6 After screening for genes known to be associated with amyotrophic lateral sclerosis (MIM: 105400), no gene was found to contribute more than 1% to disease case subjects. This study required 4,161 case subjects to implicate 2 new genes—TBK1 (MIM: 604834) and NEK1 (MIM: 604588)—which contributed to 0.9% and 0.7% of disease cases, respectively. Even known genes such as CHCHD10 (MIM: 615903) and ALS2 (MIM: 205100), which were originally implicated in segregation/linkage analyses in large kindreds,31, 32 had p values greater than 0.05 in a discovery cohort of 2,843 case subjects because the fractional contributions of these two genes were very small (estimated at 0.07% and 0.007%, respectively).
To our initial surprise, we found that decreased penetrance had a relatively small effect on power, at least for monogenic disorders with low prevalence. However, intuitively, this result is sensible in light of the high degree of penetrance relative to prevalence for monogenic disorders. For example, even if all pathogenic variants had a relatively low penetrance of 10% for a dominant disorder with a prevalence of 0.1%, only ∼1% of a disease-free control cohort would carry pathogenic variants. This low background rate of pathogenic mutations in control subjects has limited effect on power. Additionally, because the case cohort is ascertained on affected status, incomplete penetrance will have almost no effect on the number of variants observed in case subjects. By contrast, incomplete penetrance has strong negative effects on approaches relying on linkage in large multiplex families. Incomplete penetrance will obscure Mendelian patterns of inheritance, hindering the ascertainment of large families with multiple affected individuals that provide the power for an affecteds-only linkage approach. Moreover, in the presence of incomplete penetrance, linkage analysis incorporating unaffected family members into the analysis is unlikely to be effective. Thus, linkage analysis with low penetrance alleles will typically require aggregation of linkage evidence across multiple families, which is particularly problematic in the presence of significant locus heterogeneity.
Our study also evaluated the complex relationship between power and the filters used to enrich for variants that are more likely to be pathogenic. The precise nature of the trade-off between sensitivity and specificity is challenging to characterize empirically. This is because the true sensitivity or specificity of various filters at any given threshold is not known for any gene, and existing assignments of pathogenicity (e.g., ClinVar) can depend on MAF thresholds and protein predictions, introducing an inherent circularity to the pathogenicity assignments. Nonetheless, our simulations showed that the samples sizes needed to achieve power to detect a gene associated with disease rise exponentially with decreased sensitivity, suggesting that in some scenarios, application of less stringent filters might be advantageous. However, less stringent filters may also decrease the aggregate penetrance of qualifying variants. This decreased penetrance of qualifying variants would result in higher background rates and corresponding dilution of power. However, because penetrance has a limited effect on power, the adverse effect of decreased penetrance with increased sensitivity is likely to be minimal. Nonetheless, this relationship between choice of thresholds and power merits further study.
Under the wide range of genetic architectures we tested, our simulations demonstrated that the current size of publicly available control cohorts (such as the Exome Aggregation Consortium)18 is probably sufficient to maximize power (Figure S13A), although for populations with ancestries that are not yet as well represented in publicly available sequencing projects, additional sequencing data will be beneficial. Using population-based control subjects rather than disease-free control subjects also had negligible effects on power (Figure S13B). These data suggest that using large databases of shared control subjects is likely to be a resource-efficient approach to finding genes associated with rare monogenic disorders. Of course, to avoid false positives, the control cohort needs to be matched to the case samples for ancestry and for technical factors such as depth of coverage in each gene/region.
There are several important limitations of our study. First, we chose a simple gene-based burden testing approach, although there are more sophisticated methods that have been applied to both monogenic and polygenic diseases.7, 33 Second, our study focused on the use of unrelated individuals with the disease in the case cohort. Addition of linkage and segregation data can improve power in gene discovery efforts, as will be discussed below.33, 34 Third, we focused our analyses on whole-exome sequencing rather than whole-genome sequencing. However, the relative effects of each of the parameters we studied are applicable to a whole-genome sequencing project, although the filters to assess pathogenicity for noncoding variants are even less well established. As compared to exome sequencing, whole-genome sequencing will have gains in greater ability to ascertain all genes as well as potentially greater sensitivity to detect even coding pathogenic variants.35
In our study, we demonstrated that monogenic disorders with high locus heterogeneity and dominant modes of inheritance are less amenable to a gene-based burden testing approach. There are several potential ways to mitigate these limitations. First, although we assumed a simple model in which pathogenic variants in different genes each cause a form of disease that is indistinguishable at the phenotypic level, there may be clinically recognizable subgroups that are associated with distinct genes and/or that may help to distinguish monogenic from non-monogenic forms of disease. In this situation, examining each subgroup in isolation would increase power because the genes associated with that clinical subgroup will account for a larger fraction of disease cases, reducing the effective locus heterogeneity.
Second, although the gene-based burden approach is typically applied to unrelated probands, segregation data can be immensely useful. For example, for a dominant disorder, analyzing only variants that are shared among affected individuals in a family will greatly reduce the number of qualifying variants (assuming, as we have here, that penetrance is high enough relative to disease prevalence to greatly reduce the chance of phenocopy within a family). Emerging methods aim to calibrate this segregation data within families to properly compare with control subjects and incorporate into a burden-testing framework.33, 34 These methods will face challenges in the presence of incomplete penetrance and using both unaffected and affected family members in the analyses. Family data can also be immensely helpful in the context of de novo mutations, which can be identified with only one affected individual and their parents (rather than a larger pedigree). For a dominant disorder that is caused by moderately or highly penetrant mutations and greatly decreases reproductive fitness, it can be presumed that many pathogenic mutations will be de novo. As the rate of de novo mutations is very low in the exome (on average less than one nonsynonymous variant per individual exome), the background rate of variation across genes will be extremely low, greatly enhancing the power to detect a gene associated with disease.36
We demonstrated that power in these studies is highly dependent on the choice of thresholds for enriching for likely pathogenic variants and that the best threshold is usually not apparent a priori. Strategies that test multiple thresholds and select the best-performing threshold for each gene can help overcome this limitation, as demonstrated by Cirulli et al.6 However, this strategy incurs a penalty for multiple hypothesis testing.37 Emerging techniques in functional genomics may be able to assess a priori the functional consequences of each variant in a gene;38, 39 if the functional assay aligns well with pathogenicity, this information can dramatically improve the sensitivity and specificity of filters used to distinguish pathogenic from benign variants.
Our study on gene-based burden testing, in the context of much previous work on power in linkage analyses, suggest which situations are more amenable to each approach. In the setting of locus heterogeneity but high penetrance, large kindreds with multiple affected individuals should be available for ascertainment. In this circumstance, the traditional pedigree-based linkage approach should be feasible as an initial discovery phase and can be combined with evidence from burden testing in unrelated individuals. However, with incomplete penetrance, large recognizable pedigrees with multiple affected individuals will be infrequent and difficult to recognize and ascertain. Here, gene-based burden testing may represent the only feasible approach and is likely to remain a successful approach, whereas linkage/segregation approaches utilizing evidence from both affected and unaffected individuals within a family will be largely ineffective. We also note that gene-based burden testing, unlike linkage, is highly sensitive to the ability to distinguish pathogenic from benign variants, so this approach will benefit from a better understanding of which types of variants have phenotypically relevant functional consequences.
In actual study designs, the genetic architecture parameters are generally not known a priori, making it difficult to estimate power. However, our simulations can help place bounds on genetic architectures—in a study where no gene association has emerged after sequencing a given number of samples, our simulations can bound the likely modes of inheritance and locus heterogeneity of genes associated with disease, assuming that the filters used to define qualifying variants capture a reasonable fraction of the actual causal variants. This could in turn inform the minimum number of additional samples needed to discover genes associated with disease via this gene-based burden testing approach.
Acknowledgments
We thank members of the J.N.H. lab for insightful feedback. We thank Monkol Lek and Daniel MacArthur and the ExAC consortium for joint variant calling of the exome-sequencing data used throughout this paper. M.H.G. and J.N.H. are supported by NIH-NIDDK award R01DK075787. A.D. was supported by NIH-NICHD award K23HD073351. Y.-M.C. was supported by DDCF grant 2013110. M.F.L. was supported by NIH-NICHD award P50 HD028138. R.M.S. was support by NIH-NHLBI award 1K99HL122515-01A1.
Published: August 18, 2016
Footnotes
Supplemental Data include supplemental notes, 16 figures, and 1 table and can be found with this article online at http://dx.doi.org/10.1016/j.ajhg.2016.06.031.
Web Resources
Dominant OMIM gene list, https://github.com/macarthur-lab/gene_lists/blob/master/lists/berg_ad.tsv
ExAC Browser, http://exac.broadinstitute.org/
Human Gene Damaging Index (GDI) scores, lab.rockefeller.edu/casanova/assets/file/GDI_full_10282015.txt
OMIM, http://www.omim.org/
Residual Variation Intolerance Scores (RVIS), genic-intolerance.org/data/GenicIntolerance_v3_12Mar16.txt
Supplemental Data
References
- 1.Chong J.X., Buckingham K.J., Jhangiani S.N., Boehm C., Sobreira N., Smith J.D., Harrell T.M., McMillin M.J., Wiszniewski W., Gambin T., Centers for Mendelian Genomics The genetic basis of Mendelian phenotypes: discoveries, challenges, and opportunities. Am. J. Hum. Genet. 2015;97:199–215. doi: 10.1016/j.ajhg.2015.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Risch N. Linkage strategies for genetically complex traits. II. The power of affected relative pairs. Am. J. Hum. Genet. 1990;46:229–241. [PMC free article] [PubMed] [Google Scholar]
- 3.Risch N., Merikangas K. The future of genetic studies of complex human diseases. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
- 4.Greenberg D.A., Abreu P., Hodge S.E. The power to detect linkage in complex disease by means of simple LOD-score analyses. Am. J. Hum. Genet. 1998;63:870–879. doi: 10.1086/301997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ploughman L.M., Boehnke M. Estimating the power of a proposed linkage study for a complex genetic trait. Am. J. Hum. Genet. 1989;44:543–551. [PMC free article] [PubMed] [Google Scholar]
- 6.Cirulli E.T., Lasseigne B.N., Petrovski S., Sapp P.C., Dion P.A., Leblond C.S., Couthouis J., Lu Y.F., Wang Q., Krueger B.J., FALS Sequencing Consortium Exome sequencing in amyotrophic lateral sclerosis identifies risk genes and pathways. Science. 2015;347:1436–1441. doi: 10.1126/science.aaa3650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lee S., Abecasis G.R., Boehnke M., Lin X. Rare-variant association analysis: study designs and statistical tests. Am. J. Hum. Genet. 2014;95:5–23. doi: 10.1016/j.ajhg.2014.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Morgenthaler S., Thilly W.G. A strategy to discover genes that carry multi-allelic or mono-allelic risk for common diseases: a cohort allelic sums test (CAST) Mutat. Res. 2007;615:28–56. doi: 10.1016/j.mrfmmm.2006.09.003. [DOI] [PubMed] [Google Scholar]
- 9.Moutsianas L., Agarwala V., Fuchsberger C., Flannick J., Rivas M.A., Gaulton K.J., Albers P.K., McVean G., Boehnke M., Altshuler D., McCarthy M.I., GoT2D Consortium The power of gene-based rare variant methods to detect disease-associated variation and test hypotheses about complex disease. PLoS Genet. 2015;11:e1005165. doi: 10.1371/journal.pgen.1005165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zuk O., Schaffner S.F., Samocha K., Do R., Hechter E., Kathiresan S., Daly M.J., Neale B.M., Sunyaev S.R., Lander E.S. Searching for missing heritability: designing rare variant association studies. Proc. Natl. Acad. Sci. USA. 2014;111:E455–E464. doi: 10.1073/pnas.1322563111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Guey L.T., Kravic J., Melander O., Burtt N.P., Laramie J.M., Lyssenko V., Jonsson A., Lindholm E., Tuomi T., Isomaa B. Power in the phenotypic extremes: a simulation study of power in discovery and replication of rare variants. Genet. Epidemiol. 2011;35:236–246. doi: 10.1002/gepi.20572. [DOI] [PubMed] [Google Scholar]
- 12.Zhi D., Chen R. Statistical guidance for experimental design and data analysis of mutation detection in rare monogenic mendelian diseases by exome sequencing. PLoS ONE. 2012;7:e31358. doi: 10.1371/journal.pone.0031358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Krawitz P., Buske O., Zhu N., Brudno M., Robinson P.N. The genomic birthday paradox: how much is enough? Hum. Mutat. 2015;36:989–997. doi: 10.1002/humu.22848. [DOI] [PubMed] [Google Scholar]
- 14.Goldstein D.B., Allen A., Keebler J., Margulies E.H., Petrou S., Petrovski S., Sunyaev S. Sequencing studies in human genetics: design and interpretation. Nat. Rev. Genet. 2013;14:460–470. doi: 10.1038/nrg3455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li M.X., Gui H.S., Kwan J.S., Bao S.Y., Sham P.C. A comprehensive framework for prioritizing variants in exome sequencing studies of Mendelian diseases. Nucleic Acids Res. 2012;40:e53. doi: 10.1093/nar/gkr1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stitziel N.O., Kiezun A., Sunyaev S. Computational and statistical approaches to analyzing variants identified by exome sequencing. Genome Biol. 2011;12:227. doi: 10.1186/gb-2011-12-9-227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.DePristo M.A., Banks E., Poplin R., Garimella K.V., Maguire J.R., Hartl C., Philippakis A.A., del Angel G., Rivas M.A., Hanna M. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat. Genet. 2011;43:491–498. doi: 10.1038/ng.806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Exome Aggregation Consortium (ExAC) Analysis of protein-coding genetic variation in 60,706 humans. bioRxiv. 2016 doi: 10.1038/nature19057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Price A.L., Patterson N.J., Plenge R.M., Weinblatt M.E., Shadick N.A., Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 20.Altshuler D.M., Gibbs R.A., Peltonen L., Altshuler D.M., Gibbs R.A., Peltonen L., Dermitzakis E., Schaffner S.F., Yu F., Peltonen L., International HapMap 3 Consortium Integrating common and rare genetic variation in diverse human populations. Nature. 2010;467:52–58. doi: 10.1038/nature09298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McLaren W., Pritchard B., Rios D., Chen Y., Flicek P., Cunningham F. Deriving the consequences of genomic variants with the Ensembl API and SNP Effect Predictor. Bioinformatics. 2010;26:2069–2070. doi: 10.1093/bioinformatics/btq330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Adzhubei I.A., Schmidt S., Peshkin L., Ramensky V.E., Gerasimova A., Bork P., Kondrashov A.S., Sunyaev S.R. A method and server for predicting damaging missense mutations. Nat. Methods. 2010;7:248–249. doi: 10.1038/nmeth0410-248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schwarz J.M., Rödelsperger C., Schuelke M., Seelow D. MutationTaster evaluates disease-causing potential of sequence alterations. Nat. Methods. 2010;7:575–576. doi: 10.1038/nmeth0810-575. [DOI] [PubMed] [Google Scholar]
- 24.Kumar P., Henikoff S., Ng P.C. Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm. Nat. Protoc. 2009;4:1073–1081. doi: 10.1038/nprot.2009.86. [DOI] [PubMed] [Google Scholar]
- 25.Itan Y., Shang L., Boisson B., Patin E., Bolze A., Moncada-Vélez M., Scott E., Ciancanelli M.J., Lafaille F.G., Markle J.G. The human gene damage index as a gene-level approach to prioritizing exome variants. Proc. Natl. Acad. Sci. USA. 2015;112:13615–13620. doi: 10.1073/pnas.1518646112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Petrovski S., Gussow A.B., Wang Q., Halvorsen M., Han Y., Weir W.H., Allen A.S., Goldstein D.B. The intolerance of regulatory sequence to genetic variation predicts gene dosage sensitivity. PLoS Genet. 2015;11:e1005492. doi: 10.1371/journal.pgen.1005492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.R Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2014. R: A Language and Environment for Statistical Computing. [Google Scholar]
- 28.Li H., Handsaker B., Wysoker A., Fennell T., Ruan J., Homer N., Marth G., Abecasis G., Durbin R., 1000 Genome Project Data Processing Subgroup The Sequence Alignment/Map format and SAMtools. Bioinformatics. 2009;25:2078–2079. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.MacArthur D.G., Manolio T.A., Dimmock D.P., Rehm H.L., Shendure J., Abecasis G.R., Adams D.R., Altman R.B., Antonarakis S.E., Ashley E.A. Guidelines for investigating causality of sequence variants in human disease. Nature. 2014;508:469–476. doi: 10.1038/nature13127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Herman D.S., Lam L., Taylor M.R., Wang L., Teekakirikul P., Christodoulou D., Conner L., DePalma S.R., McDonough B., Sparks E. Truncations of titin causing dilated cardiomyopathy. N. Engl. J. Med. 2012;366:619–628. doi: 10.1056/NEJMoa1110186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hosler B.A., Sapp P.C., Berger R., O’Neill G., Bejaoui K., Hamida M.B., Hentati F., Chin W., McKenna-Yasek D., Haines J.L. Refined mapping and characterization of the recessive familial amyotrophic lateral sclerosis locus (ALS2) on chromosome 2q33. Neurogenetics. 1998;2:34–42. doi: 10.1007/s100480050049. [DOI] [PubMed] [Google Scholar]
- 32.Bannwarth S., Ait-El-Mkadem S., Chaussenot A., Genin E.C., Lacas-Gervais S., Fragaki K., Berg-Alonso L., Kageyama Y., Serre V., Moore D.G. A mitochondrial origin for frontotemporal dementia and amyotrophic lateral sclerosis through CHCHD10 involvement. Brain. 2014;137:2329–2345. doi: 10.1093/brain/awu138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hu H., Roach J.C., Coon H., Guthery S.L., Voelkerding K.V., Margraf R.L., Durtschi J.D., Tavtigian S.V., Shankaracharya, Wu W. A unified test of linkage analysis and rare-variant association for analysis of pedigree sequence data. Nat. Biotechnol. 2014;32:663–669. doi: 10.1038/nbt.2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ionita-Laza I., Lee S., Makarov V., Buxbaum J.D., Lin X. Family-based association tests for sequence data, and comparisons with population-based association tests. Eur. J. Hum. Genet. 2013;21:1158–1162. doi: 10.1038/ejhg.2012.308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Belkadi A., Bolze A., Itan Y., Cobat A., Vincent Q.B., Antipenko A., Shang L., Boisson B., Casanova J.L., Abel L. Whole-genome sequencing is more powerful than whole-exome sequencing for detecting exome variants. Proc. Natl. Acad. Sci. USA. 2015;112:5473–5478. doi: 10.1073/pnas.1418631112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.De Rubeis S., He X., Goldberg A.P., Poultney C.S., Samocha K., Cicek A.E., Kou Y., Liu L., Fromer M., Walker S., DDD Study. Homozygosity Mapping Collaborative for Autism. UK10K Consortium Synaptic, transcriptional and chromatin genes disrupted in autism. Nature. 2014;515:209–215. doi: 10.1038/nature13772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Price A.L., Kryukov G.V., de Bakker P.I., Purcell S.M., Staples J., Wei L.J., Sunyaev S.R. Pooled association tests for rare variants in exon-resequencing studies. Am. J. Hum. Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Starita L.M., Young D.L., Islam M., Kitzman J.O., Gullingsrud J., Hause R.J., Fowler D.M., Parvin J.D., Shendure J., Fields S. Massively parallel functional analysis of BRCA1 RING domain variants. Genetics. 2015;200:413–422. doi: 10.1534/genetics.115.175802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Majithia A.R., Flannick J., Shahinian P., Guo M., Bray M.A., Fontanillas P., Gabriel S.B., Rosen E.D., Altshuler D., GoT2D Consortium. NHGRI JHS/FHS Allelic Spectrum Project. SIGMA T2D Consortium. T2D-GENES Consortium Rare variants in PPARG with decreased activity in adipocyte differentiation are associated with increased risk of type 2 diabetes. Proc. Natl. Acad. Sci. USA. 2014;111:13127–13132. doi: 10.1073/pnas.1410428111. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.