Three Measures of Explained Variation for Correlated Survival Data under the Proportional Hazards Mixed-effects Model

Abstract

Measures of explained variation are useful in scientific research, as they quantify the amount of variation in an outcome variable of interest that is explained by one or more other variables. We develop such measures for correlated survival data, under the proportional hazards mixed-effects model (PHMM). Since different approaches have been studied in the literature outside the classical linear regression model, we investigate three measures R², R² and ρ² that quantify three different population coefficients. We show that although the three population measures are not the same, they reflect similar amounts of variation explained by the predictors. Among the three measures, we show that R², which is the simplest to compute, is also consistent for the first population measure under the usual asymptotic scenario when the number of clusters tends to infinity. The other two measures, on the other hand, all require that in addition the cluster sizes be large. We study the properties of the measures both analytically and through simulation studies. We illustrate their different usage on a multi-center clinical trial and a recurrent events data set.

1 Introduction

Correlated survival data arise in many areas of biomedical applications. They arise in multicenter clinical trials where, despite rigorously designed protocols, complex procedures and different clinical practices may lead to different treatment effects at different centers. Recurrent events are another type of correlated survival data, though with their specific chronological orders. Genetic studies, often by design, recruit groups of subjects who are family members and share the same genetic or environmental factors. As for independently and identically distributed (i.i.d.) data, often we would like to be able to quantify the amount of variation in the correlated outcomes that is explained by the predictors, which is an important attribute of any regression model.

The R² coefficient of determination in classical linear regression is the definitive solution to such a need. For correlated outcomes data, random effects models (sometimes called variance components models) are a natural way of decomposing the variation in the outcomes into different components [1]. As an example of application in genetic epidemiology, it is common to decompose the variation in a disease outcome into contributions from genetic, environmental, and residual components [2–4], all expressed as percentages that add up to one.

To date, much attention has been given to developing measures of explained variation in the presence of right-censored survival data. Many of the early proposals were based on extensions of different yet equivalent definitions of the R² coefficient of determination under the multiple linear regression model [5]. These extensions are not the same outside of the normal linear model. A comprehensive comparison of the early proposals can be found in Schemper and Stare [6]. Proposals have also been made in the literature based on computationally intensive methods such as multiple imputation of the censored observations [7]. More recently Heller [8] proposed a measure of explained risk (instead of variation) under the Cox model, and Preseley et al. [9] applied some of these measures to surrogate evaluation. Recent discussions of the related concepts and recommendations can be found in references [10–13], with [13] also considering applications to high dimensional data such as gene expression. While a lot of these recent discussions have required a good measure to be unaffected by an independent censoring mechanism, [14] make an interesting point that some measures have achieved this through implicit model extrapolation, and that an overemphasis on independence from censoring can lead to other important properties and interpretations being overlooked.

For analyzing correlated survival data, mixed-effects models have been proposed that specify the correlation structure within the outcomes, as well as to correlate with the predictors. In this paper we consider the proportional hazards mixed-effects model (PHMM) [15, 16]. This model encompasses the commonly known frailty model, which contains random intercepts but not random effects on arbitrary covariates. Under the PHMM we aim to define both population measures of explained variation, as well as their sample based estimates. We explore three commonly used approaches, which include a direct decomposition of the variance, a ratio of sums of squares, and an information theoretical measure that is easily computed by transforming the likelihood ratio statistic. These approaches have been developed both for the proportional hazards regression model, and for the linear mixed effects model, therefore they are natural candidates under the PHMM. In the following we will first recall details of the PHMM and related quantities that will be used to define the measures of explained variation.

1.1 Model and notation

The PHMM extends the Cox proportional hazards model by including a vector of random effects terms in the log relative risk:

$${\lambda }_{ij}(t\mid {\mathit{Z}}_{ij},{\mathit{b}}_i)={\lambda }_0\left(t\right)\exp ({\beta }^{\prime }{\mathit{Z}}_{ij}+{\mathit{b}}_i^{\prime }{\mathit{W}}_{ij}),i=1,\dots ,m;j=1,\dots ,n_i.$$ (1)

Here, λ_ij (t) is the hazard function of the j-th observation in the i-th cluster of size n_i, β is the vector of fixed effects, b_i is a vector of random effects associated with cluster i with E(b_i) = 0, and Z_ij and W_ij are covariate vectors corresponding to the fixed and random effects, respectively. The event time T_ij may be right-censored; we observe X_ij = min(T_ij, C_ij), where C_ij is the potential censoring time. Let δ_ij = 1{T_ij ≤ C_ij }, and Y_ij (t) = 1{X_ij ≥ t} be the “at-risk” indicator at time t. It is usually assumed that for every covariate with a random effect there is also a corresponding fixed effect, so that W_ij is a subset of Z_ij except possibly for a ‘1’ in the first entry that models the random cluster effect on the baseline hazard. For notational convenience we assume that W_ij consists of a ‘1’ followed by the first p coordinates of Z_ij ∈ ℝ^p+q. In general the random effects can be seen as cluster by covariate interactions [16]. Thus, the data consist of the triples (X_ij, δ_ij, Z_ij), i = 1, …, m, j = 1, …, n_i. The random effects b₁, …, b_m are independent of each other, and assumed to be N (0, Σ); they are also assumed to be independent of the covariates Z.

The following quantities under the PHMM are relevant to our development later. Conditional on the b_i’s, at each time t we have a probability distribution on the set of subjects at risk, given by:

$${\pi }_{ij}(t;\beta ,\mathit{b})=\frac{Y_{ij}\left(t\right)\exp ({\beta }^{\prime }{\mathit{Z}}_{ij}+{\mathit{b}}_i^{\prime }{\mathit{W}}_{ij})}{\sum _{k,l}{Y}_{kl}\left(t\right)\exp ({\beta }^{\prime }{\mathit{Z}}_{kl}+{\mathit{b}}_k^{\prime }{\mathit{W}}_{kl})}.$$ (2)

The term π_ij (t; β, b) can be interpreted as the probability that the j-th subject in cluster i fails at time t given the risk set and that exactly one failure occurs at that time. Evaluating π_ij at time t = X_ij and taking the product of such terms over the observed failure times (δ_ij = 1) forms the partial likelihood conditional on collection $\mathit{b}={({\mathit{b}}_1^{\prime },\cdots ,{\mathit{b}}_m^{\prime })}^{\prime }$ of random effects:

$$L_p(\beta ,\mathit{b})=\prod _{ij:{\delta }_{ij}=1}{\pi }_{ij}(X_{ij};\beta ,\mathit{b}).$$ (3)

The above was used in [15] to form the penalized partial likelihood under the PHMM. It is shown that the discrete probability distribution {π_ij (t; β, b)}^{i=1…m,j=1…ni} converges weakly to the conditional distribution of Z given T = t and the b_i’s, in the same way that an empirical distribution converges to the underlying distribution function [17]. Under the classic Cox model this conditional distribution has been used to construct time-dependent ROC curves [18].

The model parameters θ = (β, Σ, λ₀) can be consistently estimated by the nonparametric maximum likelihood estimator (NPMLE), which has been shown to have optimal asymptotic and numerical properties [19]. The NPMLE can be computed using an MCEM algorithm, and is available in the R package ‘phmm’. At convergence of the algorithm, the posterior distribution $p({\mathit{b}}_i\mid {\mathit{y}}_i,\widehat{\theta })$ of b_i, where y_i represents the observed data from cluster i, can be used to produce empirical Bayes “estimates” of the random effects. In doing so we are viewing the realized values of the b_i’s like parameters, estimated via a degree of shrinkage; this notion is closely related to the conditional inference discussed in references [20, 21]. We will make use of the empirical Bayes estimates ${\widehat{\mathit{b}}}_i=E\left({\mathit{b}}_i\mid {\mathit{y}}_i,\widehat{\theta }\right)$ when defining some of the measures below.

Finally, model (1) is known to be equivalent to the linear transformation mixed-effects model [17]

$$g\left(T_{ij}\right)=-({\beta }^{\prime }{\mathit{Z}}_{ij}+{\mathit{b}}_i^{\prime }{\mathit{W}}_{ij})+{ϵ}_{ij},$$ (4)

where g(·) = log Λ₀(·) is a monotone transformation, and E has the fixed (and known) extreme value distribution with variance π²/6. The general semiparametric transformation model with mixed effects in the form of (4) was considered in Zeng and Lin [22].

In the next section, we present measures of explained variation, both population and sample based, and discuss some of their properties. Simulation studies are carried out in Section 3, and the measures are applied to real data in Section 4. Section 5 contains some discussion and conclusion.

2 Measures of explained variation

In the context of the semiparametric regression models like (1) or (4), the specified part of the model only concerns the prediction of the ranks of the T ’s given the Z’s. The actual scale of the failure times as reflected in the observed data is not modeled, and is estimated by the nonparametric baseline hazard or the nonparametric transformation. In addition, in the presence of clustering in the data, the analysis is often concerned with how much variation is explained by the covariates or even the clustering itself.

2.1 First measure: direct decomposition of variation

The explained variation in a response A by its predictors Z can be defined based on the well-known formula Var(A) = E{Var(A|Z)} + Var{E(A|Z)} [10]. The first term in the decomposition can be seen as the expected residual variance in A after using Z to ‘explain’ A, and the second term as the variability explained by the conditional distribution of A given Z, often modeled by the regression. Under model (4) we consider A = g(T). The proportion of explained variation is then

$$\Omega =1-\frac{E\left\{\mathrm{Var}(g\left(T\right)\mid \mathit{Z})\right\}}{\mathrm{Var}\left(g\left(T\right)\right)}=1-\frac{{\pi }^2∕6}{\mathrm{Var}({\beta }^{\prime }\mathit{Z}+{\mathit{b}}^{\prime }\mathit{W})+{\pi }^2∕6},$$ (5)

where π²/6 is the error variance, and Z, b, W are generic versions of Z_ij, b_i, W_ij, i.e. random variables (or vectors) with the same distributions. While a version of (5) in the presence of only fixed effect was briefly mentioned in Kent and O’Quigley [23] those authors did not recommend its use in practice, although Choodari-Oskooei et al. [11] included it in their comparison study. We note that (5) has been used in the genetic epidemiology literature to quantify the genetic versus environmental contributions to disease onset [3, 4, 24].

Evidently, estimation of Ω² can be accomplished by estimating the variance of the so-called linear predictor η = β^′Z + b^′W. In the Appendix we derive the algebraic expression based on moments related to random vectors. This eventually leads to the following expression:

$${\Omega }^2=1-\frac{{\pi }^2∕6}{{\beta }^{\prime }\sum _Z\beta +{\tilde{\mu }}_{Z_1}^{\prime }\sum _b{\tilde{\mu }}_{Z_1}+\mathrm{tr}\left(\sum _{b_1}\sum _{Z_1}\right)+{\pi }^2∕6},$$ (6)

where µ and Σ with a subscript denote the expectation and covariance matrix of the random vector indicated, b₁ is defined by $\mathit{b}={(b_0,{\mathit{b}}_1^{\prime })}^{\prime }$, Z₁ is the first p components of Z that have both fixed and random effects, and ${\tilde{\mu }}_{Z_1}={(1,{\mu }_{z_1}^{\prime })}^{\prime }$. We can estimate β and Σ_b in (6) under the PHMM using the previously mentioned R package ‘phmm’, and estimate the mean and variance of Z using the corresponding sample moments. This leads to an estimate of Ω²:

$$R^2=1-\frac{{\pi }^2∕6}{{\widehat{\beta }}^{\prime }{\widehat{\Sigma }}_Z\widehat{\beta }+{\widehat{\tilde{\mu }}}_{Z_1}^{\prime }{\widehat{\Sigma }}_b{\widehat{\tilde{\mu }}}_{Z_1}^{\prime }+\mathrm{tr}\left({\widehat{\Sigma }}_{b_1}{\widehat{\Sigma }}_{Z_1}\right)+{\pi }^2∕6}.$$ (7)

2.2 Second measure: a sum of squares approach

The second approach was used in Q’Quigley and Flandre [26] and Q’Quigley and Xu [10] to define R² measures under the Cox model. The motivation is that in classical linear regression R² can be expressed as a ratio of sums of squared residuals. A well-known type of residual under the proportional hazards regression is the Schoenfeld residual [25]. O’Quigley and Xu [10] also extended the Schoenfeld residuals to ‘residuals’ of the prognostic index. Under the univariate Cox model, η has a one-to-one correspondence to the covariate Z, assuming that β ≠ 0. We now extend this method to the PHMM setting. Note that under model (1) or, equivalently model (4), the predicted ranks of T_ij ’s have a one-to-one correspondence to the prognostic indices ${\eta }_{ij}={\beta }^{\prime }{Z}_{ij}+{\mathit{b}}_i^{\prime }{\mathit{W}}_{ij},i=1,\cdots ,m,j=1,\cdots ,n_i$. In this sense η is like a ‘surrogate’ for the actual, possibly censored outcome T . This fact has been used in the prediction context by, for example Huang and Harrington [27], to select the penalty parameters.

In order to define the relevant residuals, we first need to define the expected prognostic index at a given failure time t, using the probability distribution defined in (2):

$${\mathrm{E}}_{\beta ,\mathit{b}}^{\pi }(\eta ;t)=\sum _{i,j}{\eta }_{ij}{\pi }_{ij}(t;\beta ,\mathit{b})=\sum _{i,j}\frac{Y_{ij}\left(t\right){\eta }_{ij}\exp \left\{{\eta }_{ij}\right\}}{\sum _{k,l}{Y}_{kl}\left(t\right)\exp \left\{{\eta }_{kl}\right\}}.$$ (8)

Here we view the realized values of b as parameters, to be estimated via the empirical Bayes shrinkage under the PHMM. At each failure time, we can then compare the value of η predicted by the model as in (8) with the one actually observed. Having estimated β and the b_i’s, the estimated prognostic index for the ij^th observation is ${\widehat{\eta }}_{ij}={\widehat{\beta }}^{\prime }{\mathit{Z}}_{ij}+{\widehat{\mathit{b}}}_i^{\prime }{\mathit{W}}_{ij}$. This gives the residuals

$$r_{ij}(\widehat{\beta },\widehat{\mathit{b}})={\widehat{\eta }}_{ij}-{\mathrm{E}}_{\widehat{\beta },\widehat{\mathit{b}}}^{\pi }(\widehat{\eta };X_{ij}),$$ (9)

whenever δ_ij = 1.

To form what is equivalent to a total sum of squares, we consider a ‘null’ model in order to contrast with the full model in question. When the interest lies in quantifying the amount of variation in the survival that is explained by both the covariates and the clustering itself, the latter modeled by the random intercept b₀, the corresponding null model is given by β = 0 and b = 0, and the hazard function is simply λ(t|Z, b) = λ₀(t). Let ℛ(t) be the risk set at time t and $\mid \mathcal{ℛ}\left(t\right)\mid ={\sum }_{i,j}{Y}_{ij}\left(t\right)$ its size. Under this null model all subjects in the risk set have the same probability for failure: ${\pi }_{ij}\left(t\right)=Y_{ij}\left(t\right)∕{\sum }_{k,l}{Y}_{kl}\left(t\right)=Y_{ij}∕\mid \mathcal{ℛ}\left(t\right)\mid$. The expected η at time t is then just the simple average over the risk set:

$${\mathrm{E}}_0^{\pi }(\eta ;t)=\stackrel{‒}{\eta }\left(t\right)=\frac{\sum _{i,j}{Y}_{ij}\left(t\right){\eta }_{ij}}{\mid \mathcal{ℛ}\left(t\right)\mid }.$$ (10)

We note that the β = 0 and b = 0 values only affect the probabilities π_ij (t) here, while the values of $\widehat{\eta }={\widehat{\beta }}^{\prime }{\mathit{Z}}_{ij}+{\widehat{\mathit{b}}}_i^{\prime }{\mathit{W}}_{ij}$ are still defined by $\widehat{\beta }$ and ${\widehat{\mathit{b}}}_i$ as they were under the full model. This is because the estimated prognostic index ${\widehat{\eta }}_{ij}$ serves as the ‘surrogate’ for the possibly censored failure time T_ij, whose variation we are trying to explain. The ‘null’ residuals are:

$$r_{ij}^0=r_{ij}(0,0)={\widehat{\eta }}_{ij}-\overline{\widehat{\eta }}\left(X_{ij}\right).$$ (11)

We can now define the coefficient of explained variation using the residual sum of squares under the full and the null models:

$$R_{res}^2=1-\frac{\sum _{{\delta }_{ij}=1}{r}_{ij}{(\widehat{\beta },\widehat{\mathit{b}})}^2}{\sum _{{\delta }_{ij}=1}{\left(r_{ij}^0\right)}^2}.$$

2.3 Third measure: explained randomness

The third approach is based on the notion of explained randomness using the Kullback-Leibler (KL) information gain [28], and it has been applied to the proportional hazards regression model [23, 29, 30]. A commonly encountered pitfall in the literature when defining such a measure, sometimes called the generalized R² [31], is ignoring the original definition based on the KL information and simply taking an ad hoc transformation of the likelihood ratio statistics; this in particular can lead to erroneous definitions in the presence of censored data [30]. Here we develop the explained randomness measure for the PHMM.

As discussed in Kent [28] when using the explained randomness to capture the dependence between two random variables, there is a certain degree of symmetry in using the conditional distribution of one variable given the other, or vice versa. In the special case of bivariate normal, no matter which way one conditions, the explained randomness is equal to the correlation coefficient squared. In the context of the semiparametric proportional hazards regression, predicting ranks of the T ’s given the Z’s is equivalent to predicting the Z’s given the T ’s [10]. In this way, it is natural to consider the conditional distribution of Z given T; this is also consistent with the partial likelihood inference procedure, as well as the residuals considered in the Section 2.2.

As before θ denotes the unknown parameters under the PHMM. The KL information is I(θ) = E (log{f (Z|T, b; θ)}), where f (·) is the conditional density or probability function of Z given T and b, and the expectation is taken with respect to the true underlying distribution. For two nested models indexed by θ ∈ Θ₀ ⊂ Θ₁, let θ_i = arg max{I(θ); θ ∈ Θ_i} (i = 0, 1), and Γ = 2{I(θ₁) − I(θ₀)}. If Θ₀ is the subset of model distributions for which T and Z are independent, we can think of Γ as measuring the information gained from modeling dependence. In that case Kent [28] called exp{−2I(θ₀)} the total randomness in Z, and exp{−2I(θ₁)} the residual randomness of Z given T . The proportion of explained randomness is then

$${\rho }^2=1-\frac{\exp \{-2I\left({\theta }_1\right)\}}{\exp \{-2I\left({\theta }_0\right)\}}=1-\exp (-\Gamma ).$$ (12)

The expectation in I(·) is typically unknown, but can be estimated by the empirical distribution of the data in general [28]. For a random sample of size n (without censoring) Γ can be estimated by 1/n times the likelihood ratio statistics for testing Θ₁ versus Θ₀. As described in the Introduction, under the PHMM the conditional distribution of Z given T and b is estimated by {π_ij (t; β, b)}_{i=1…m,j=1…ni}, and the log partial likelihood conditional on b is given by (3). Under the null model β = 0, b = 0, the log partial likelihood becomes $\log L_p^0=-{\sum }_{{\delta }_{ij}=1}\log \mid \mathcal{ℛ}\left(X_{ij}\right)\mid$. In the presence of right-censoring, the effective sample size is $K={\sum }_{i,j}{\delta }_{ij}$ which is the total number of events; K is also the number of terms in the log partial likelihood. Using an empirical distribution assigning mass 1/K to each observed failure to further approximate the expectation in I(·) [30], the estimated information gain is then

$$\widehat{\Gamma }=\frac{2}{K}\{\log L_p(\widehat{\beta },\widehat{\mathit{b}})-\log L_p^0\}.$$ (13)

Our measure of explained randomness is based on this information gain:

$${\widehat{\rho }}^2=1-\exp (-\widehat{\Gamma }).$$ (14)

2.4 Properties of the measures

As mentioned earlier the semiparametric PHMM only models explicitly the association between the covariates and the ranks of the failure times, beyond which the actual failure times as reflected via the baseline hazard function are not modeled. In this way it is natural to view the measures of explained variation under the PHMM as equivalent to a type of (squared) rank correlation. For rank correlations in general, Kendall and Gibbons [32] described their desirable properties, which include: (1) the value of the (squared) measure should lie between zero and one; (2) should increase with the strength of association, as reflected by the regression effects in a regression model; (3) the absence of such association should manifest itself in a value of the measure close to zero, and perfect association should manifest itself in a value close to one. In the following we briefly discuss the properties of the three approaches proposed in this section; further investigation is also carried out through simulations in the next section.

The simple form in our definition of Ω² makes a number of these properties apparent. From (6) we see that Ω² is between 0 and 1, and increases with each of the terms ${\beta }^{\prime }{\sum }_Z\beta ,{\tilde{\mu }}_{Z_1}^{\prime }{\sum }_b{\tilde{\mu }}_{Z_1}$, and $\mathrm{tr}\left({\sum }_{b_1}{\sum }_{Z_1}\right)$. The latter is best understood with a single covariate Z at first; in this case the three terms are, respectively, β²Var (Z), ${\beta }_2\mathrm{Var}\left(Z\right),{\mu }_Z^2\mathrm{Var}\left(b\right)$ (assuming b is the random effect for Z), and Var (Z) Var (b). We see that Ω² increases with the strength of the fixed regression effect |β| and the strength of the random effect as reflected by Var (b), together with |µ_Z | and Var (Z). It is well-known that the classic R² in linear regression increases with Var (Z), reflecting the confidence in the regression line when the covariate spread has a wide range. A bit more generally, if we assume that the covariates in Z₁ (those with both fixed and random effects) are uncorrelated and that the random effects are also uncorrelated, then ${\beta }^{\prime }{\sum }_Z\beta ={\beta }_1^2\mathrm{Var}\left(Z_1\right)+\cdots +{\beta }_p^2\mathrm{Var}\left(Z_p\right)$, ${\tilde{\mu }}_{Z_1}^{\prime }{\sum }_b{\tilde{\mu }}_{Z_1}=\mathrm{Var}\left(b_0\right)+{\mu }_1^2\mathrm{Var}\left(b_1\right)+\cdots +{\mu }_p^2\mathrm{Var}\left(b_p\right)$ and $\mathrm{tr}\left({\sum }_{b_1}{\sum }_{Z_1}\right)=\mathrm{Var}\left(Z_1\right)\mathrm{Var}\left(b_1\right)+\cdots +\mathrm{Var}\left(Z_q\right)\mathrm{Var}\left(b_q\right)$. This shows that Ω² is an increasing function of the strengths of the individual fixed effects |β_i|, the variances Var (Z_i), and the strengths of the individual random effects Var (b_i) together with |µ_i|. Finally, it is also immediately seen that in the absence of association, i.e β = 0 and Σ_b = 0, then Ω² = 0; and as any of the regression effects approaches infinity, fixed or random (as reflected by its variable), Ω² approaches one.

The measures $R_{res}^2$ and ${\widehat{\rho }}^2$ defined in Sections 2.2 and 2.3 are not intended to estimate Ω². While their population version can be written out as population limits or expectations that the sample quantities converge to as shown in [10], these expressions tend not to provide immediate insights into their properties. Certain analytical properties of $R_{res}^2$ and ρ² have been studied under the classic Cox model [10, 29, 30]. While some of these properties carry over under the PHMM, others do not. More specifically, for $R_{res}^2$ a sum of squares decomposition holds asymptotically, i.e. the total sum of squares ${\sum }_{i,j}{\delta }_{ij}{\left(r_{ij}^0\right)}^2$ is the residual sum of squares ${\sum }_{i,j}{\delta }_{ij}{r}_{ij}{(\widehat{\beta },\widehat{b})}^2$ plus a regression sum of squares given by ${\sum }_{i,j}{\delta }_{ij}{\{E_{\widehat{\beta },\widehat{b}}^{\pi }(\eta ;X_{ij})-E_0^{\pi }(\eta ;t)\}}^2$ when both m → ∞ and n_i → ∞, so that the b_i’s as well as β are consistently estimated [21]. On the other hand, with the b_i’s estimated by the ${\widehat{\mathit{b}}}_i’\mathrm{s}$ we cannot guarantee that $R_{res}^2$ or ρ² is always positive when both the true fixed effects and the true random effects are very close to zero, although in the simulation studies in the next section we show that they are almost always between zero and one, and increase with the strength of the fixed as well as the random effects.

Finally, all the measures are clearly not affected by any linear transformation of the covariates or monotonically increasing (i.e. rank preserving) transformation of the failure times. Asymptotically R² (as m → ∞) is consistent for Ω² which does not depend on censoring. Following the discussion in [10], $R_{res}^2$ should only depend weakly on censoring, and could be made completely independent of censoring if the squared residuals are weighted by the inverse probability of censoring. On the other hand, ρ² can be more affected by censoring due to the maximum follow-up time [30].

3 Numerical and simulation experiments

We now further investigate the performances of the measures through numerical simulation studies. In particular, we would like to know how well the analytical properties described in Section 2.4 hold in finite samples, how close the sample based measures are to their population equivalents, how the measures are affected by the variances of the random effects, and how they are affected when the covariates are correlated. In addition, we would also like to know in finite samples how the measures are affected by censoring, by the covariate distribution once the variance of the distribution is fixed, and by the baseline hazard function.

In general, the data were generated as follows. For a fixed value of β, the survival times T_ij were generated according to λ_ij (t) = exp(βZ_ij + b_0i + b_1iZ_ij), where Z_ij ~ N (0.5, 0.25), b_0i, b_1i ~ N (0, 0.25). Independent censoring times C_ij were generated from a uniform distribution on the interval (0, τ ), where τ was chosen so that there was about 25% censoring. The PHMM was then fit to the dataset using the phmm() function in the R package ‘phmm’. Simulations were carried out for 17 equally spaced values of β = 0, 0.25, 0.5, …, 4. For each scenario the simulation was repeated 100 times.

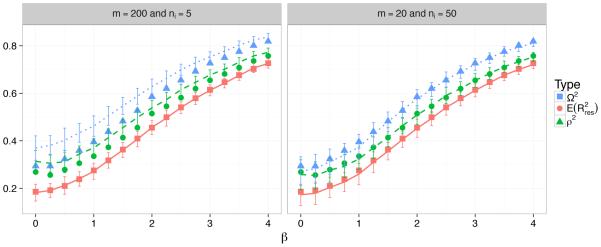
In Figure 1 we compare the three proposed measures and their population values. While the population value for R² is Ω² given in (5), the population value for $R_{res}^2$ as well as ρ² do not have closed-form expressions, and are obtained by using Monte Carlo simulation with a large sample size of 200 clusters with 50 observations in each cluster (200×50). These three population measures are marked by points with a square, circle, or triangle. The fact that they increase with |β| translates to improved predictive capability as |β| increases. Note that even when β = 0, the measures of explained variation are non-zero. This is because the model still retains the random effects, which explain part of the variation in the data: λ_ij (t) = λ₀(t)exp(b_0i + b_1iZ_ij).

Figure 1.

Squares, circles and triangles are the population measures; solid, dashed and dotted lines (of the same colors) are the corresponding sample measures R², $R_{res}^2$ and ${\widehat{\rho }}^2$, respectively.

From the figure it is clear that the three population measures are different quantities; they do, however, reflect similar strengths of predictability in our opinion, differing from each other by at most 10% in all cases. The sample-based measures are plotted using different line types, as noted in the figure caption. In comparing the left (200×5) versus the right (20×50) panels of Figure 1, we see how the sample sizes affect the accuracy of these measures in estimating their population equivalents. In particular, we see that in the left panel R² accurately estimates Ω², while the other two measures, both relying on the estimated ${\widehat{\mathit{b}}}_i’\mathrm{s}$, are not good estimates of their population equivalents due to the small cluster size of 5. On the other hand, in the right panel $R_{res}^2$ and ${\widehat{\rho }}^2$ are much closer to their population equivalents, while R² is a bit less accurate in estimating Ω² than in the left panel due to the smaller number of clusters 20. Note that the number of clusters is the sample size that affects the frequentist model parameters, while the cluster size affects the accuracy of ${\widehat{\mathit{b}}}_i’\mathrm{s}$.

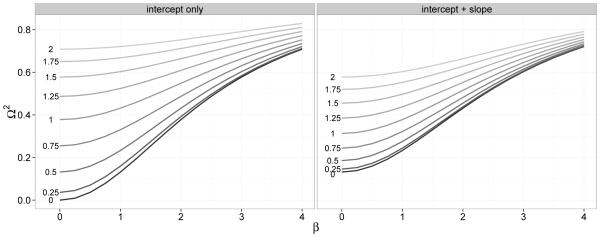
It was previously noted in Section 2.4 that the population coefficient Ω² is an increasing function of the variance components. In Figure 2 we set either Var(b_1i) = 0 (left panel) or Var(b_0i) = 0.25 (right panel). The other random effect then has standard deviation σ which varies between 0 and 2. We observe that for a fixed value of β, Ω² increases with σ and, even with β = 0, Ω² can be quite large if the variance component is large.

Figure 2.

Ω² increases with σ² = Var(b₀) (left) or σ² = Var(b₁) (right; Var(b₀) = 0.25).

Figure 3 illustrates Ω² with two covariates. The covariate vector Z has a bivariate normal distribution with mean µ_Z = (0.5, 0.5)^′, diag(Σ_Z) = (0.25, 0.25), and $\mathrm{corr}(Z_1,Z_2)=\sqrt{2}∕2$, 0, and $-\sqrt{2}∕2$, respectively. To enhance presentation we have also printed the values of Ω² in the plots as percentages; for example, ‘25’ means that Ω² = 0.25 for that particular configuration. The figure suggests that geometrically, as a function of β, the level curves of Ω² are concentric ellipses, so that Ω² increases with β along the principal axes of the ellipses; these axes correspond to the eigenvectors of Σ_Z.

Figure 3.

Ω² (as percentage) with two covariates.

Similar results to Figure 2 and Figure 3 have also been observed for the other two population measures (data not shown).

In supplement materials we also investigate the dependence of the measures on the amount of censoring, the covariate distribution once the variance of the distribution is fixed, and the baseline hazard function. Within the scope of our investigation it is seen that the covariate distribution (given fixed variance) and the baseline hazard function have little effect on the measures. Censoring also has little effect on all the measures except ${\widehat{\rho }}^2$, which increases noticeably if the amount of censoring is over 50%.

4 Applications

4.1 E1582 multi-center lung cancer trial

In Xu and Vaida [16] illustrated the application of the PHMM using a multi-center clinical trial in lung cancer conducted by the Eastern Cooperative Oncology Group (E1582). There were 579 patients from 31 institutions randomized to one of two chemotherapy regimens. The overall survival time was observed along with five relevant binary baseline covariates: treatment, presence of bone metastasis, presence of liver metastasis, ambulatory performance status, and weight loss prior to treatment. Gray [33] developed tests for variation across groups in survival data and showed that, for this dataset, there is significant variation by institution in the treatment effect. Xu and Vaida [16] and Xu et al. [34] fitted the PHMM to the data, and discovered random effects of bone metastases, which had even larger variance than the random effects for treatment. In the Bayesian variable selection context Dunson and Chen [35] concluded that after accounting for the random bone metastases effects, there was no direct evidence of institutional variation in treatment effects. This was then followed by a correspondence from Gray [36] and a further discussion in Lee et al. [37].

In the following we consider the explained variation for this data set, which can be seen as another angle of variable assessment in light of the earlier debates. We first consider univariate analyses allowing for random effects if necessary, taking into account the potential clustering structure in the data. In Table 1 we present the PHMM fits for treatment and bone metastases separately, each with a random effect. The initial fits of the PHMM to the other three covariates separately all had their variances of the random effects converging to zero during the EM iterations [16], and is hence presented with results from the regular Cox model fits without random effects. From the table we see that with or without the random effects, each covariate only explains a small percentage of variation in overall survival, indicating that each binary variable alone does not make a good predictor for survival, which is probably the case in reality. In comparing the three measures, we see that $R_{res}^2$ and ${\widehat{\rho }}^2$ gave slightly higher values than R², consistent with our numerical findings of the previous section.

Table 1.

Univariate fits of the lung cancer data; σ² is the variance of the random slope.

Covariate	β	σ 2	R 2	$R_{res}^2$	${\widehat{\rho }}^2$
Trt	−0.28 (0.10)	0.05 (0.03)	0.03	0.07	0.06
Bone	0.35 (0.14)	0.19 (0.12)	0.05	0.07	0.09
Liver	0.45 (0.09)	–	0.03	0.05	0.05
PS	−0.58 (0.10)	–	0.03	0.06	0.05
Wtlss	0.27 (0.09)	–	0.01	0.02	0.02

In the next step we incorporate all five covariates, as we typically would in a clinical analysis of prognostic variables. In terms of random effects we consider allowing none, treatment only, bone metastases only, or both treatment and bone metastases random effects (Table 2). For the ease of discussion here let us first focus on the R² values. It is seen that in terms of explained variation, the five fixed effects of the covariates together explain about 9% of the variation in overall survival, with allowing for random effects explaining a couple of percentage points. It is also seen that the random bone metastases effect explains 2% more variation than the random treatment effect, and that adding the random treatment effect to the random bone metastases effect does not appear to explain much additional variation. In Lee et al. [37] the authors also discussed the distinction between a relatively weak random effect (treatment) and a relatively strong random effect (bone metastases), and their impact on Bayesian variable selection. Our observation here appears consistent with those discussions.

Table 2.

Multivariate fits of the lung cancer data; all five fixed covariate effects are included.

Random effects	σ 2	R 2	$R_{res}^2$	${\widehat{\rho }}^2$
None	–	0.09	0.13	0.13
Treatment	0.07 (0.05)	0.11	0.16	0.17
Bone	0.14 (0.08)	0.13	0.17	0.18
Treatment + Bone	0.05 (0.08) 0.13 (0.12)	0.13	0.19	0.21

The two other measures $R_{res}^2$ and ${\widehat{\rho }}^2$ again have slightly higher values than R², although in our opinion all three measures reflect a somewhat similar degree of explained variation by the covariates. Note the data structure is such that each of the 31 institutions varies between a size of 1 to 50 patients, with an average of just under 20 patients per institution. In referencing to the discussion of the simulation section, 31 is effectively the sample size for R², and sample size for estimating the b_i’s used in $R_{res}^2$ and ${\widehat{\rho }}^2$ varies between 1 to 50 with the average just under 20. As with any real data we do not know the true values but in this case it may be reasonable to speculate that the truth lies somewhere between the R², and the $R_{res}^2$ and ${\widehat{\rho }}^2$ values.

4.2 CGD recurrent events data

The second application is from a placebo-controlled clinical trial in patients with Chronic Granulomatous Disease (CGD), and the data are available in the Appendix of Fleming and Harrington [38]. CGD is a genetic disorder in which the functioning of the immune system is impaired, leading to chronic and serious infections. In this trial, 128 patients were randomized to placebo or treatment with gamma interferon. For each patient the time to initial and any subsequent serious infections were recorded, for a total of 203 records. This gives an average of less than 2 observations per cluster, which is quite different from the lung cancer data structure above. For this reason in the following analyses we only consider R² and not the other proposed measures. In addition to treatment status, the covariates include pattern of inheritance (x-linked or autosomal recessive), age, height, weight, corticosteroid use at time of study entry (yes/no), antibiotic use at time of study entry (yes/no), hospital category (US - NIH, US - other, Europe - Amsterdam, or Europe - Other) and sex.

Following [16] we fit the PHMM with X_ij given by the j-th observed time since the last infection (or since study entry for the first infection) for patient i, and with a random effect on the baseline hazard to account for the correlation among the repeated infections. Table 3 displays the univariate fits for each covariate with a random intercept. For example, the treatment assignment has a log relative risk of −1.17 indicating that the gamma interferon group has lower risk of developing repeated infections, with the hazard of only exp(−1.17) = 0.31 times the placebo group. The other variables may increase or decrease the risk of repeated infections by itself though not necessarily statistically significant, when not adjusting for other variables since these are univariate analyses (the coefficients for hospital category are not shown since there are more than one). The variances of the random intercepts are substantial in all univariate models ranging from 1.09 to 1.45. The proportion of explained variation as reflected in R² values is about 46% in all cases, which is also quite high given that only a single fixed effect plus a random intercept is included in any of the models. For comparison purposes we also fit the classic univariate Cox model without the random intercept. The estimated fixed effect for each covariate does not change much with or without the random intercept (data not shown). However, for each covariate, without the random intercept the variation explained (R^2∗) is typically quite small, except for treatment which explains about 15% of the variation in the outcome. This indicates that the addition of the random intercept in the univariate models help to explain a relatively large portion of variation in the outcome.

Table 3.

Univariate fits of the CGD recurrent events data; σ² is the variance of the random intercept.

	Trtmt	Inherit	Age	Steroid	Antibio	Sex	Hosp (4 cat)
Coeff	−1.17 (0.35)	0.25 (0.38)	−0.03 (0.02)	1.12 (0.92)	−0.55 (0.51)	−0.25 (0.47)	–
σ 2	1.09 (0.45)	1.45 (0.58)	1.36 (0.45)	1.40 (0.49)	1.43 (0.61)	1.45 (0.59)	1.38 (0.45)
R 2 *	0.46	0.47	0.47	0.47	0.47	0.47	0.47
R 2	0.15	0.01	0.04	0.01	0.01	0.01	0.04

^*Without the random intercept.

Table 4 shows a set of nested PHMM fits to the data. The covariates become significant as they are added to the multivariate model, and the coefficients of the final model including all variables were given in Vaida and Xu [16]. From the table we see that as more covariates are added after treatment has been included in the model, the variance of the random intercept decreases while the R² value stays around 46-47%. This illustrates the fact that the random intercept captures the heterogeneity not reflected in the covariates that are included in the model, and that even after all the covariates have been included there still is additional individual heterogeneity, with the variance of the random intercept remains at 0.62. We also contrast the results with a set of nested Cox model fits without the random intercept (R^2∗). It is seen that with each additional covariate the R^2∗ increases, to a maximum of 31% when all the covariates are included. However compared to R² = 0.47 there is still variation that is captured by the random intercept term.

Table 4.

Nested model fits of the CGD recurrent events data; with (R²) or without (R²*) the random intercept.

Covariates	Random intercept	R 2	R2*
Treatment	1.09 (0.45)	0.46	0.15
Trtmt, Steroid	1.09 (1.52)	0.47	0.16
Trtmt, Steroid, Age	0.94 (0.94)	0.47	0.21
Trtmt, Steroid, Age, Antibio	0.90 (0.34)	0.47	0.22
Trtmt, Steroid, Age, Antibio, Inherit	0.85 (0.32)	0.46	0.23
Trtmt, Steroid, Age, Antibio, Inherit, Hosp	0.76 (0.41)	0.47	0.27
All**	0.62 (0.44)	0.47	0.31

^**All the fixed covariate effects are significant.

The above illustrates the application of the R² measure in clinical settings, both for quantifying the proportion of explained variation, and possibly as a method to aid in model selection.

5 Discussion

Measures of explained variation, as the name suggests, quantify the amount of variation in an outcome variable of interest that is explained by one or more other variables, i.e. covariates in a regression setting. Such quantification is useful in scientific research, as we have repeatedly experienced with our biomedical collaborators. Here we distinguish between measures of explained variation and measures of goodness-of-fit, and focus on the former in this paper. In other words, the measures proposed in this paper are not designed to be sensitive to departures from model assumptions; to the contrary, we believe that ideally such measures should be robust to model misspecification, provided that the model is not too far from the truth.

We have used a very simple definition of Ω² as a measure of explained variation, where consistent estimation of Ω² (i.e. R²) only requires consistent estimation of the usual parameters under the PHMM and the first two moments of the covariate vector. As a special case it can be used for the classic Cox regression model with no random effects. Heller [8] used a similar definition under the classic Cox model on the risk scale instead of the variance scale we consider here. Kent and O’Quigley [23] mentioned a similar definition but did not go on to recommend its use. In light of its straightforward definition and simple computation, as well as desirable properties as illustrated in this paper, we recommend it for general use under the Cox model, with or without random effects. A similar measure was recently used in [39] under the accelerated failure time model.

We have also considered other possible definitions for the same purposes, namely $R_{res}^2$ and ρ². These are generalizations of existing approaches in the literature to the PHMM. Our investigation here shows that for the sample based versions to be good approximations of their population equivalents, the cluster sizes need to be reasonably large, as they all require good ‘estimates’ of the realized random effects. Other than the sample size requirement, all measures considered in this paper have desirable properties including: 1) being consistent with the semiparametric nature of the PHMM, i.e. invariance under any monotonic transformation of the time scale, 2) increasing with the strength of association as reflected by the magnitudes of the fixed effects and variances of the random effects, 3) having interpretation as explained variation or explained randomness. In addition, while the three population measures (as illustrated in different colors in the figures) are not the same, they reflect, in our view, a similar amount of variation explained by the predictors.

We have also investigated a second estimator of Ω², but due to limitation of space it is included only in the supplemental materials. The idea is to use the estimated linear predictor ${\widehat{\eta }}_{ij}$ as in our second measure, and then use the sample variance of the ${\widehat{\eta }}_{ij}$’s to estimate Var (β^′Z + b^′W) in Ω². Since this measure makes use of the estimated b_i’s, its performance is similar to $R_{res}^2$ and ρ².

Sometimes we may be interested in the following question: having accounted for the clustering in the data using b₀, how much variation is explained by the covariates? A slightly different measure of explained variation than what we have focused on so far can be used to answer this question. For this purpose, we may define

$${\Omega }_0^2=1-\frac{\mathrm{Var}\left(b_0\right)+{\pi }^2∕6}{\mathrm{Var}({\beta }^{\prime }\mathit{Z}+{\mathit{b}}^{\prime }\mathit{W})+{\pi }^2∕6}.$$ (15)

In addition, partial coefficients of explained variation [10] often arise when one wants to know how much additional variation can be explained by some additional covariates, after a first set of covariates have already been included in a model. In general a partial coefficient can be defined as $R_{(1,2)}^2=1-\{1-R_{\left(1\right)}^2\}∕\{1-R_{\left(2\right)}^2\}$, where $R_{\left(1\right)}^2$ and $R_{\left(2\right)}^2$ are the measures already defined under the two models, with and without the additional covariates, respectively. Since each of our previously defined measures is of the form 1 − v/v₀, where v and v₀ are the estimated residual variation under the full and the null model, we can then write $R_{\left(1\right)}^2=1-v_1∕v_0$ and $R_{\left(2\right)}^2=1-v_2∕v_0$. This gives $R_{(1,2)}^2=1-v_1∕v_2$; in other words, this is equivalent to considering a new “null” model with the first set of covariates, and a full model with the additional covariates.

APPENDIX

In order to derive (6) we first express η as the inner product of two independent random vectors. Define the following vectors in ℝ^p+q+1:

$$\tilde{\beta }=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill \beta \hfill \end{array}\right),\tilde{\mathit{Z}}=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill \mathit{Z}\hfill \end{array}\right),\mathrm{and}\tilde{\mathit{b}}=\left(\begin{array}{c}\hfill \mathit{b}\hfill \\ \hfill 0\hfill \end{array}\right),$$

where 0 ∈ ℝ^q in the third expression is a vector of zeros. With $\mathit{U}=\tilde{\beta }+\tilde{\mathit{b}}$ and $\mathit{V}=\tilde{Z}$ we have η = U ^′V. The expectations of U and V are

$$\mathrm{E}\left(U\right)=\tilde{\beta }=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill \beta \hfill \end{array}\right),\mathrm{E}\left(\mathit{V}\right)=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill \mu Z\hfill \end{array}\right),$$

where µ_Z denotes the expectation of Z. The covariance matrices are

$$\mathrm{Var}\left(\mathit{U}\right)=\mathrm{Var}\left(\tilde{\mathit{b}}\right)=\left(\begin{array}{cc}\hfill \mathrm{b}\hfill & \hfill \hfill \\ \hfill \hfill & \hfill O_{q\times q}\hfill \end{array}\right),\mathrm{and}\mathrm{Var}\left(\mathit{V}\right)=\mathrm{Var}\left(\tilde{\mathit{Z}}\right)=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \hfill \\ \hfill \hfill & \hfill {\sum }_Z\hfill \end{array}\right)$$

where O_a×b is an a × b matrix of zeroes. Brown & Rutemiller [40] provide a formula for the variance of the inner product of two independent random vectors: $\mathrm{Var}\left({\mathit{U}}^{\prime }\mathit{V}\right)={\mu }_U^{\prime }{\sum }_V{\mu }_U+{\mu }_V^{\prime }{\sum }_U{\mu }_V+\mathrm{tr}\left({\sum }_U{\sum }_V\right)$. Thus the variance of η is $\mathrm{Var}\left(\eta \right)={\beta }^{\prime }{\sum }_Z\beta +{\mu }_{Z_1}^{\prime }{\sum }_b\tilde{\mu }{Z}_1+\mathrm{tr}\left({\sum }_{b_1}{\sum }_{Z_1}\right)$. This gives (6), where Ω² is a function of the population parameters β, µ_Z, Σ_Z, and Σ_b.