Combining dependent P-values with an empirical adaptation of Brown’s method

Abstract

Motivation: Combining P-values from multiple statistical tests is a common exercise in bioinformatics. However, this procedure is non-trivial for dependent P-values. Here, we discuss an empirical adaptation of Brown’s method (an extension of Fisher’s method) for combining dependent P-values which is appropriate for the large and correlated datasets found in high-throughput biology.

Results: We show that the Empirical Brown’s method (EBM) outperforms Fisher’s method as well as alternative approaches for combining dependent P-values using both noisy simulated data and gene expression data from The Cancer Genome Atlas.

Availability and Implementation: The Empirical Brown’s method is available in Python, R, and MATLAB and can be obtained from https://github.com/IlyaLab/CombiningDependentPvalues UsingEBM. The R code is also available as a Bioconductor package from https://www.bioconductor.org/packages/devel/bioc/html/EmpiricalBrownsMethod.html.

Contact: Theo.Knijnenburg@systemsbiology.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

In research studies where multiple sources of data are available, it is natural to ask whether the combined evidence of these sources supports a particular statistical hypothesis. Combining multiple P-values into a single unified P-value is a common meta-analysis in many research fields, including biology and more recently bioinformatics (Alves et al., 2014; Loughin, 2004).

The advent of high-throughput biology requires us to reconsider two important aspects of P-value combination schemes when applied in this field. First, biological samples can be described by thousands or even millions of data points representing a diverse array of information derived from sequencing, array-based, imaging, and other measurement techniques. Thus, researchers are potentially interested in combining a very large number of P-values. Second, the genome-wide biological data generated in these high-throughput experiments often show a high degree of internal correlation, i.e. strong statistical dependencies between the variables for which measurement data was obtained. For example, the intrinsic dimensionality of a complete gene expression dataset with thousands of genes is typically below 20 (Lähdesmäki et al., 2005). Similarly, principal components analysis of gene expression data shows that a handful of components can capture the large majority of variation in the data (Raychaudhuri et al., 2000; Ringnér, 2008). These examples illustrate the high internal correlation in gene expression data, which is at least partly due to the fact that many genes are involved in or influenced by the same biological processes. Other important sources of correlation include different data types that provide similar information about biological components and processes, and genome-wide measurements that show spatial correlation across the genome, such as DNA binding proteins and histone marks (Consortium et al., 2012b; Kundaje et al., 2015) and genetic variants due to linkage disequilibrium (Consortium et al., 2012a; Hartl et al., 1997).

Importantly, although many methods for combining P-values have been developed, most of them assume independent or weakly dependent P-values. Additionally, implementations of these methods in widely-used programming languages are often lacking, and it is unclear whether these methods will scale to combine many (hundreds or more) P-values.

The earliest method to combine independent P-values is seen in the work of Fisher (1948). Brown (1975) later extended Fisher’s method to the case where P-values were derived from data generated from a multivariate normal distribution with a known covariance matrix. Kost and McDermott (2002) further extended Brown’s method analytically for unknown covariance matrices and improved the numerical approximations used by Brown. Additional methods for combining P-values have been developed for specific purposes, e.g. combining differently weighted P-values (Whitlock, 2005), combining P-values across multiple heterogeneous data sources (Aerts et al., 2006), restricting analysis to the tail of the P-value distribution (Zaykin et al., 2002), and combining P-values using Simes approach, which is applicable for dependent P-values in specific conditions (Benjamini and Heller, 2008). Of these methods, Brown’s method using Kost’s improved polynomial fit (i.e. Kost’s method) most simply combines equally weighted dependent P-values assuming normally distributed underlying data. Additionally, in a recent comparison of methods for combining P-values, Kost’s method has been shown to be one of the best available (Alves et al., 2014).

In this work, we describe an adaptation of Brown’s method that uses the empirical cumulative distribution function derived directly from the data (Fig. 1). We show that this non-parametric version, which we call the Empirical Brown’s method (EBM), is accurate, more robust to noise compared to Kost’s method and can efficiently be applied to large intra-correlated biological datasets. We provide extensive comparisons to Fisher’s method and Kost’s method and we demonstrate EBM on gene expression data from The Cancer Genome Atlas (TCGA).

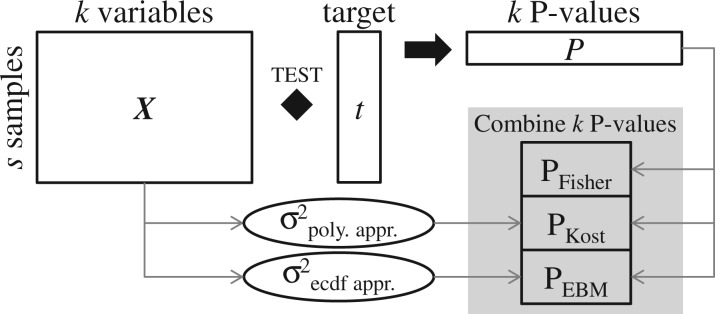
Fig. 1.

Simplified graphical overview of Fisher’s, Kost’s and Empirical Brown’s method (EBM) for combining P-values. Each of k variables in data matrix X is assessed for statistical association with target vector t using a statistical test resulting in k P-values. Fisher’s method combines these P-values assuming statistical independence between the k P-values. Kost’s method employs a polynomial approximation to calculate the covariance among the k variables based on the data in X. The covariance estimate is a measurement of statistical dependence between the k P-values and used to re-scale the ${\chi }^2$ distribution from which the combined P-value is calculated. Kost’s approximation assumes normally distributed underlying data. EBM does not assume any underlying distribution of the data, but instead uses an empirical cumulative distribution function (ecdf) on the (transformed) data in X to estimate the covariance. See Methods section and Supplementary information 1 for details

2 Methods

2.1 Fisher’s, Brown’s and Kost’s methods

Let there be k P-values, denoted P_i, generated from k statistical tests based on k normally distributed random variables, denoted X_i. Fisher showed that for independent P-values, the statistic $\Psi ={\displaystyle \sum _{i=1}^k-}2\log P_i$ follows a χ² distribution with 2k degrees of freedom, $\Psi \sim {\chi }_{2k}^2$. Brown extended Fisher’s method to the dependent case by using a re-scaled ${\chi }^2$ distribution

$$\Psi \sim c{\chi }_{2f}^2.$$ (1)

The constants represent a re-scaled number of degrees of freedom (f) and a scale factor (c) which is the ratio between the degrees of freedom of Fisher’s and Brown’s methods. Brown calculated these constants by equating the first two moments of $\Psi$ and $c{\chi }_{2f}^2$ resulting in

$$f=\frac{\text{E}{[\Psi ]}^2}{\text{var}[\Psi ]}\text{\hspace{1em}and\hspace{1em}}c=\frac{\text{var}[\Psi ]}{2\text{E}[\Psi ]}=\frac{k}{f}.$$ (2)

Furthermore, Brown showed that the expected value and variance of $\Psi$ can be calculated directly via numerical integration to find the covariance, respectively

$$\text{E}[\Psi ]=2k\text{\hspace{1em}and\hspace{1em}var}[\Psi ]=4k+2{\displaystyle \sum _{i<j}\text{cov}}(-2\log P_i,-2\log P_j).$$ (3)

Numerical integration is, however, not feasible for large datasets due to computational complexity (Supplementary information 3). Kost and McDermott fit a third-order polynomial to approximate this covariance

$$\text{cov}(-2\log P_i,-2\log P_j)\approx 3.263{\rho }_{ij}+0.710{\rho }_{ij}^2+0.027{\rho }_{ij}^3$$ (4)

where ρ_ij is the correlation between the random variables X_i and X_j. The combined P-value is then given by

$$P_{\text{combined}}=1.0-{\Phi }_{2f}(\psi /c)$$ (5)

where $\psi =-2{\displaystyle \sum _{i=1}^k\log }{P}_i$ and ${\Phi }_{2f}$ is the cumulative distribution function of ${\chi }_{2f}^2$.

2.2 Empirical Brown’s method

Our contribution is to calculate the covariance in Equation (3) empirically. In practice, each individual P-value, P_i, will be computed via a statistical test between a target variable and a vector of samples, ${\overrightarrow{x}}_i$, drawn from the random variable X_i. We define the transformed sample vector ${\overrightarrow{w}}_i=-2\log (1-\text{F}({\overrightarrow{x}}_i))$ where $\text{F}({\overrightarrow{x}}_i)$ denotes the right-sided empirical cumulative distribution function calculated from the sample ${\overrightarrow{x}}_i$. As a result, the covariance can also be computed empirically

$$\text{var}[\Psi ]=4k+2{\displaystyle \sum _{i<j}\text{cov}}({\overrightarrow{w}}_i,{\overrightarrow{w}}_j).$$ (6)

A more detailed explanation can be found in Supplementary information 1.

2.3 Generating null data

We compared EBM to Fisher’s method on generated null data. We generated these data by combining 20 P-values from the Pearson correlations between a sample of independent normal random variables with mean 0 and variance 1 (s = 200) and a sample (s = 200) of data generated from a 20-dimensional multivariate normal distribution centered around 0 with covariance matrix Σ; ${\sigma }_{ii}=1$ and ${\sigma }_{i\cancel{\ne }j}=a$, i.e. diagonal elements of 1 and off-diagonal elements of a. We calculated 100 000 combined P-values for each value of $a\in \{0.0,0.25,0.5,0.75\}$. Note that this methodology is equivalent to how we generated noisy intra-correlated data when b_j = 0 and ξ = 0 in Section 2.4.

2.4 Generating dependent normal data

We generated datasets with adjustable internal correlation structure and noise in order to compare Fishers’s method, Kost’s method and EBM. Let $Y=N_n(\mu ,\Sigma )$, where N_n is a n-dimensional normal distribution centered around μ = 0 with covariance matrix Σ; ${\sigma }_{ii}=1,{\sigma }_{1,i>1}={\sigma }_{i>1,1}=b_i$, and ${\sigma }_{i\cancel{\ne }j;i,j>1}=a$. Or, written as a matrix

$$\Sigma =\left[\begin{array}{cccccc}1& b_2& \cdots & b_j& \cdots & b_n\\ b_2& 1& \cdots & a& \cdots & a\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ b_j& a& \cdots & 1& \cdots & a\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ b_n& a& \cdots & a& \cdots & 1\end{array}\right].$$ (7)

In this model, the random variables $Y_{j>1}$ have a correlation structure governed by a and each Y_j is correlated to Y₁ via b_j. In our simulations, n = 4, a = 0.8 (the variables are highly correlated) and each b_j is randomly sampled from the uniform interval $[-0.5,0.5]$ to produce varying P-values, many of which are low because of non-zero covariance. Finally, given a sample $\overrightarrow{y}$ from Y (sample size s = 200), we added noise $\overrightarrow{x}=\overrightarrow{y}+\xi \overrightarrow{U}$, where ξ adjusts the magnitude of the noise and $\overrightarrow{U}$ are 200 samples from a four-dimensional uniform distribution on $[-1,1]$. We adjusted the parameter ξ between 0 and 2.5 in our simulations, which is equivalent to signal-to-noise ratios (SNRs) ranging from $\infty$ to 0.5. We computed sets of $n-1=3$ P-values estimated from the pairwise Pearson correlation between ${\overrightarrow{x}}_1$ and ${\overrightarrow{x}}_{i>1}$. These P-values were then combined using Fisher’s method, Kost’s method and EBM.

2.5 Combining P-values based on TCGA expression data

Fisher’s, Kost’s and EBMs were compared on the highly correlated gene expression data of glioblastomas (GBM) from TCGA (Brennan et al., 2013). We derived combined P-values by associating the expression levels of single genes with the expression levels of the genes that comprise each of the curated cancer signaling pathways from the Pathway Interaction Database (PID) (Schaefer et al., 2009), which consists of manually curated signaling pathways in cancer.

Specifically, let C_H be the set of pairwise correlation P-values between gene g and the genes in each pathway, $C_H=\{P_{\text{cor}}(g,h_i);h_i\in H,g\ne h_i\}$, where H is the set of genes in a pathway and $P_{\text{cor}}$ denotes the P-value from the Pearson correlation computed via a two-tailed test of the t-distribution. The P-values in each set C_H were combined using Fisher’s method, Kost’s method and EBM. This analysis was done for each of the genes in PID. For increased computational efficiency, we precomputed the entire covariance matrix of all genes in PID.

2.6 Calculating ground truth P-values using a permutation scheme

We employed a permutation scheme to compute ground truth combined P-values to gauge the accuracy of these methods. Every statistical test, where the P-value is derived from an analytical null distribution, has an equivalent permutation test. In the permutation test, the same test statistic is computed on the same data, yet with an appropriate permutation of the samples. This allows one to derive an empirical background distribution of permuted test statistics. A ground-truth P-value can be obtained by comparing the original test statistic (that is based on the non-permuted data) with this empirical background distribution. See our previous work (Knijnenburg et al., 2009), where we employed the same strategy.

Combining P-values using Fisher’s method, Kost’s method or EBM involves assessing the statistical significance of the statistic $\Psi$, the sum of the logarithm of P-values (defined in Section 2.1 and Equation (3) in the Supplementary information 1) against a ${\chi }^2$ distribution, i.e. the null distribution for this particular test. Importantly, all three methods compute the same test statistic $\Psi$. However, they evaluate this statistic against different ${\chi }^2$ distributions, i.e. different parameters f and c, that characterize this distribution. The different parameterizations derive from the different assumptions that underlie these tests. Specifically, Fisher’s method assumes independent P-values, whereas Kost’s method and EBM assume dependent P-values and estimate the covariance in the data to obtain f and c. Here, Kost’s method assumes normal data without noise and uses a third-order polynomial fit (Equation (4)), whereas EBM empirically computes the covariance.

Formally, to calculate the $\Psi$ (on non-permuted data), each of the P-values, P_i, is generated by some statistical test, T, to determine the statistical association between the target variable $\overrightarrow{t}$ with s data points and variable ${\overrightarrow{v}}_i$ also with s data points

$$P_i=T(\overrightarrow{t},{\overrightarrow{v}}_i)\text{\hspace{1em}and\hspace{1em}}\Psi ={\displaystyle \sum _{i=1}^k-}2\log P_i$$ (8)

The permutation scheme involves randomly permuting the values in $\overrightarrow{t}$ leading to ${\overrightarrow{t}}^{*}$, from which the permuted statistic ${\Psi }^{*}$ can be calculated

$$P_i^{*}=T({\overrightarrow{t}}^{*},{\overrightarrow{v}}_i)\text{\hspace{1em}and\hspace{1em}}{\Psi }^{*}={\displaystyle \sum _{i=1}^k-}2\log P_i^{*}$$ (9)

Importantly, this permutation scheme removes all statistical dependence between the target ($\overrightarrow{t}$) and the data in ${\overrightarrow{v}}_i$, yet retains the internal correlation structure amongst the variables ${\overrightarrow{v}}_i$.

For the normally generated data, target vector $\overrightarrow{t}$ corresponds to ${\overrightarrow{x}}_1$ and data vectors ${\overrightarrow{v}}_i$ to ${\overrightarrow{x}}_c$, where c is the column index ranging from 2 to k + 1 (see Section 2.4). For the TCGA GBM expression data, target vector $\overrightarrow{t}$ corresponds to $\overrightarrow{g}$, the gene expression of a single gene and data vectors ${\overrightarrow{v}}_i$ correspond to ${\overrightarrow{h}}_i$, the expression levels of all (k) genes in a pathway (see Section 2.5). In both these cases, T corresponds to a two-tailed t-test of the null hypothesis that the Pearson correlation coefficient is zero (no correlation).

Given test statistic $\Psi$ and M permuted statistics, ${\Psi }_1^{*},{\Psi }_2^{*},\dots ,{\Psi }_M^{*}$, the permutation test P-value is computed as

$$P_{perm}=\frac{{\displaystyle \sum _{m=1}^{M}I}({\Psi }_m^{*}\ge \Psi )}{M}$$ (10)

In case, the number of exceedances (${\displaystyle \sum _{m=1}^{M}I}({\Psi }_m^{*}\ge \Psi )$) is 10 or larger one can use the central limit theorem to show that this (Equation (10)) is an accurate P-value estimate (and provide confidence bounds) (Knijnenburg et al., 2009). Specifically, using M permutations allows one to compute permutation test P-values down to $10/M$. In our experiments, we set $M={10}^6$, which allowed to compute P-values of ${10}^{-5}$ and larger.

Once again, we note that the ground-truth P-values based on this permutation scheme are identical for Fisher’s method, Kost’s method and EBM.

3 Results and discussion

3.1 Empirical Brown’s method conservative on null data

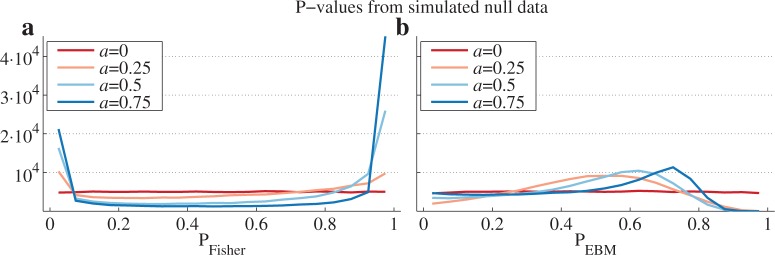
Combined P-values from randomly generated data should follow a uniform distribution. With Fisher’s method, there is a strong enrichment of extremely low and extremely high P-values as the intra-correlation of the normally distributed dataset is increased (Fig. 2a). The inflation of low P-values results in a high number of false positives even for modest coupling in the covariance matrix. With EBM, the distribution of P-values is slightly inflated in the middle of the interval $[0,1]$ and deflated towards the low and especially the high values (Fig. 2b). This suggests that our method provides a conservative estimate.

Fig. 2.

P-values from simulated data using Fisher’s method and EBM. (a) Line plot of histogram counts of P-values from Fisher’s method applied on simulated null data with varying degrees of covariance as represented by a. The histogram was created by binning the P-values in 20 bins of size 0.05 from 0 to 1. (b) Similar to (a) but for P-values derived with the Empirical Brown’s method

We note that at least 100 samples are needed for convergence of EBM (Supplementary information 2). Practically speaking, EBM requires large sample sizes because the data is used both to estimate the P-values (in this case derived from a correlation metric) and the covariance matrix of the P-value distribution.

3.2 EBM corrects Fisher’s bias on TCGA data

As an example of combining dependent P-values generated from real intra-correlated data, we compared Fisher’s method and EBM on associations between signaling pathways and EGFR using TCGA glioblastoma (GBM) gene expression data. EGFR is frequently amplified, mutated and overexpressed in GBM and is known to play an important functional role (Brennan et al., 2013). It is, therefore, unsurprising that we observed many statistically significant associations between EGFR and the signaling pathways (Fig. 3). However, Fisher’s method produced much lower P-values, especially for the pathways with a high degree of intra-correlation, as quantified with the scale factor c (Equation (5)). This is a clear indication that Fisher’s method produces spuriously low P-values when applied to correlated data. We also noted that Fisher’s method produced very similar sets of significant pathways when correlated against a variety of genes other than EGFR (see Section 3.3). We interpret this as further evidence to suggest that Fisher’s method is highly sensitive to the internal correlation structure of the data and detects falsely significant associations in highly correlated sets of P-values regardless of the actual association. As seen in Figure 3, EBM overcomes these biases.

Fig. 3.

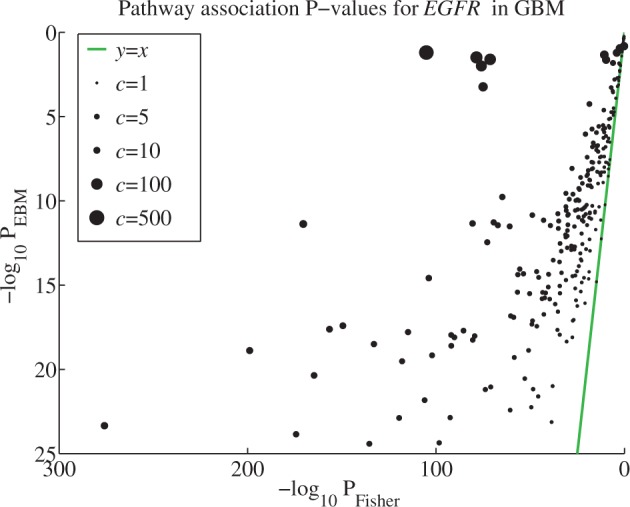
P-values from TCGA data using Fisher’s method and EBM scatter plot comparing pathway association P-values for the gene EGFR in the GBM dataset from TCGA. Each circle represents one pathway. The radius is proportional to c, which reflects the intra-pathway correlation

As a point of comparison between TCGA data and the simulated data, we can loosely equate the internal correlation parameter a to the mean of the absolute value of the pairwise gene expression correlations in TCGA data. The average Pearson correlation across all genes considered in this study is 0.18 ± 0.13 (5th–95th percentile: $[0.01,0.43]$).

3.3 The relation between combined P-values, scale parameter c and pathway size

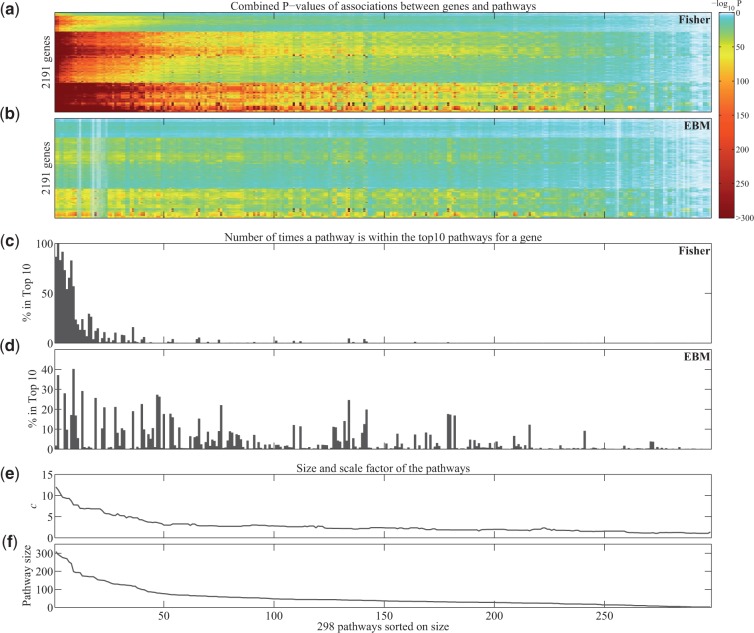
As shown above, Fisher’s method shows a strong bias towards more intra-correlated pathways, and produced dramatically more significant pathway P-value associations than EBM. The relative degrees of freedom between Fisher’s method and EBM, i.e. scale parameter c, provide a good measure of the correlation within a pathway. The scale parameter quantifies the percent change of degrees of freedom (in terms of variables), which are statistically redundant due to correlations with other variables. We investigated the relation between the combined P-values obtained with Fisher’s method and EBM, scale parameter c and the size of the pathways. For this analysis, we considered the combined P-values of all gene-pathway pairs, i.e. all pairwise combinations between 2191 genes and 298 pathways.

In concordance with the analysis of EGFR-pathway pairs, we observed that Fisher’s method produces much lower P-values overall (Fig. 4a and b). Importantly, the lowest P-values are obtained for the largest pathways, which were also found to have the largest values of scale parameter c (Fig. 4e and f). The association between scale parameter c and pathway size is not surprising. In Fisher’s method, the degrees of freedom (2k) are directly related to the number of genes in a pathway (k). Due to the high correlation among genes in a pathway, EBM estimates a much smaller number of degrees of freedom, subsequently leading to high values of scale parameter c.

Fig. 4.

Combined P-values for gene-pathway associations in TCGA GBM expression data. (a and b) Heatmap of combined P-values from Fisher’s method (a) and EBM (b) for gene-pathway pairs. The rows represent 2191 genes and are sorted based on hierarchical clustering (the same sorting for a and b). The columns represent 298 pathways and are sorted on the size of the pathway (with the largest pathway on the left). (c and d) Barplot indicating for each pathway the percentage of genes for which that pathway is within the gene’s top 10 of most strongly associated pathways according to the combined P-value as computed with Fisher’s method (c) and EBM (d). (e and f) Line plot of median-smoothed scale factor c (e) and size (f) across the pathways

Importantly, with Fisher’s method the large pathways produce the lowest P-values for the large majority of the genes and dominate the top of most statistically significant findings (Fig. 4c and d). For example, when using Fisher’s combined P-values the superpathway ‘Cell Adhesion Signaling Pathways’, which contains 428 genes, is found in the top 10 of most significant pathways for all 2191 genes. (This pathway has a bar that reaches to 100% in Fig. 4c.) On the contrary, when using EBM’s combined P-values, we observed that genes are associated with a variety of pathways of different sizes. (This can be seen by bars found across all pathways in Fig. 4d). For example, the top two pathways associated with tumor suppressor gene TP53 according to EBM P-values are ‘Aurora B Signaling’ (n =40 genes)—its connection to TP53 is described in many studies including (Gully et al., 2012)—and ’Direct P53 Effectors’ (n =129 genes). Both these pathways fall outside of the top 10 according to Fisher’s P-values, i.e. they are found on positions 66 and 13, respectively. These pathways are more relevant and plausible for GBM cancer biology than the large and highly intra-correlated pathways that are prioritized by Fisher’s method.

In summary, the number of P-values to be combined has a large effect on the combined P-value when using Fisher’s method on highly correlated data. P-value combination schemes that model the statistical dependence between the P-values, such as EBM, can compensate for this effect.

3.3.1 Note on transforming combined P-values to Q-values

A common way to correct for multiple testing other than the Bonferroni correction is by transforming the P-value to a Q-value (or false discovery rate). The two most common approaches to compute Q-values are Benjamini–Hochberg’s approach (Benjamini and Hochberg, 1995) and Storey’s approach (Storey, 2002). Importantly, we noted that Storey’s approach to compute Q-values (as implemented in the R and Python packages, Storey, 2015) is not directly appropriate for significance testing in this case due to complications in estimating the null hypothesis distribution. Specifically, the implementation of Storey’s approach assumes a particular distribution on the P-values and estimates parameters to fit this distribution. The EBM P-value distributions encountered in the gene expression data were problematic in terms of estimating these parameters, leading to non-sensical results. Benjamini–Hochberg’s non-parametric approach does not suffer from this limitation.

3.4 EBM more accurate on noisy generated data

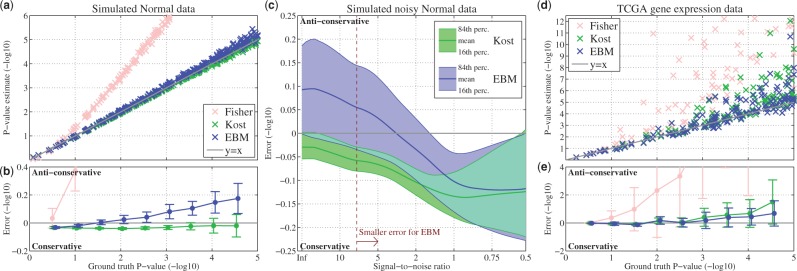
On generated normal data with no noise, EBM performs comparably with Kost’s method (Fig. 5a). The error of EBM increases slightly for smaller P-values producing marginally anti-conservative P-value estimates (Fig. 5b). Fisher’s method produces dramatically anti-conservative, i.e. too low, P-values, leading to many false positives. Importantly, Fisher’s method produces many low P-values even on null data (see Section 3.1). As noise is added to the normally generated data EBM begins to outperform Kost’s method, as evidenced by the smaller average error already for moderate levels of noise injection (SNR around 8) (Fig. 5c). Note that the errors in EBM before this point are comparable in magnitude with the errors in EBM on noiseless normal data. We, therefore, believe that these errors are largely due to the statistical effects implicit in sampling any distribution. As the noise component becomes very large, Kost’s method, EBM and Fisher’s method (not shown) all converge. This occurs because the large noise magnitude effectively destroys the underlying correlation structure in the data.

Fig. 5.

Estimated P-values and average error of the three combination methods on generated normal data and TCGA data. (a) Combined P-values from Fisher method, Kost method and EBM versus the ground-truth P-values for noiseless normal data. Each point is one simulation. The scatterplot shows only the simulations, where the ground-truth P-value is ${10}^{-5}$ or larger. (b) Error bars of the binned difference (error) between the estimated and ground-truth P-values. This error is defined as $-lo{g}_{10}(P_{estimate}/(P_{ground-truth})$. (c) The error as a function of the SNR for Kost and EBM. (d and e) Similar to (a and b) but each circle is a gene-pathway combined P-value based on TCGA gene expression data. These plots show the pathway associations for PTEN, PIK3CA, TP53 and CHD4, four genes known to be involved in GBM onset and progression

3.5 EBM more accurate on TCGA data

On one hand, the TCGA gene expression dataset is inherently interdependent and noisy. For relatively insignificant P-values, EBM and Kost perform comparably and both produce accurate P-values (Fig. 5d). Fisher’s method, on the other hand, produces many P-values that are very anti-conservative. As the P-values become more significant, EBM is more accurate and provides a more conservative estimate leading to fewer false positives than Kost’s method (Fig. 5e). Several studies have indicated that RNA-seq gene expression data are best modeled using a negative binomial distribution for both empirical and biophysical reasons (Anders and Huber, 2010; Friedman et al., 2006). This suggests that the Gaussian approximation explicit in Kost’s method is not appropriate. The fact that Kost’s method is less conservative may partially be explained by the following observation: approximating the cdf of a long-tailed distribution, such as a negative binomial, with a normal distribution will result in a lower (anti-conservative) P-value compared with the true cdf. This analysis shows that our empirical approach captures the underlying data well and can produce accurate P-values on a large and correlated biological dataset.

4 Conclusion

On generated and real data, we have shown that EBM performs well when combining P-values on noisy data with internal correlation structure. We observed that EBM corrects for correlation structure bias when compared with Fisher’s method and provides a conservative combined P-value when no correlations are present. When compared with Kost’s method, the non-parametric nature of EBM make it more robust to deviations from normality in the form of uniform noise and the method behaves comparably for idealized Gaussian data. As such, EBM is a highly useful P-value combination method when dealing with biological data which is often noisy, not necessarily Gaussian, and almost always has an internal correlation structure.

Future extensions include understanding how EBM behaves with other underlying distribution models (alternatives to the normal distribution as well as alternative noise models). Additionally, we believe EBM could be improved by using higher order approximations of the $\Psi$ distribution. We note that this approach is very general and need not be restricted to combining P-values derived from correlations but could be extended to many statistical tests and be applied to heterogeneous datasets. One shortcoming of the current method is that it cannot take external weights of different P-values being combined into account.

The non-parametric nature of EBM makes this P-value combination method an ideal candidate for combining P-values derived from discrete data, such as genetic variants. In particular, we will study the suitability of EBM as a so-called burden test to assess the statistical associations between groups of (rare) genetic variants and disease phenotypes (Lee et al., 2014). This will also allow us to investigate the usefulness of EBM in situations where statistical significance is more difficult to achieve, as is often the case for genome-wide association tests of complex diseases.

We have created efficient implementations of EBM in three widely used programming languages in bioinformatics: Python, R and Matlab, which are available through GitHub and Bioconductor (Supplementary information 4). These implementations can combine hundreds of P-values based on the data with thousands of samples in seconds (Supplementary information 3). Additionally, we have included Kost’s method and Fisher’s method within our code for increased functionality and comparisons. We believe that these implementations and evaluation of the method will provide a valuable tool for the bioinformatics community.