Abstract
Motivation: Both gene expression levels (GEs) and copy number alterations (CNAs) have important biological implications. GEs are partly regulated by CNAs, and much effort has been devoted to understanding their relations. The regulation analysis is challenging with one gene expression possibly regulated by multiple CNAs and one CNA potentially regulating the expressions of multiple genes. The correlations among GEs and among CNAs make the analysis even more complicated. The existing methods have limitations and cannot comprehensively describe the regulation.
Results: A sparse double Laplacian shrinkage method is developed. It jointly models the effects of multiple CNAs on multiple GEs. Penalization is adopted to achieve sparsity and identify the regulation relationships. Network adjacency is computed to describe the interconnections among GEs and among CNAs. Two Laplacian shrinkage penalties are imposed to accommodate the network adjacency measures. Simulation shows that the proposed method outperforms the competing alternatives with more accurate marker identification. The Cancer Genome Atlas data are analysed to further demonstrate advantages of the proposed method.
Availability and implementation: R code is available at http://works.bepress.com/shuangge/49/
Contact: shuangge.ma@yale.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Both gene expression levels (GEs) and copy number alterations (CNAs) have important biological implications. GEs are partly regulated by CNAs (Henrichsen et al., 2009). In the recent multidimensional studies, GE and CNA measurements have been collected on the same subjects, making it possible to study their regulation relationships (Shih et al., 2011; Wrzeszczynski et al., 2011; Wynes et al., 2014).
Analysing the regulation of GE by CNA is challenging. In general, a CNA is positively associated with the expression level of its corresponding gene. Multiple studies have conducted bivariate analysis and focused on the dependence between a GE and its corresponding CNA. For example, Schäfer et al. (2009) proposed a procedure based on a modified correlation coefficient to search for driver genes of which both GEs and CNAs display strong equally directed abnormalities. Salari et al. (2010) conducted supervised analysis and identified genes with significant GE-CNA correlations. Such ‘one GE against one CNA’ analysis has limitations. The expression level of one gene can be affected by multiple CNAs, and a CNA can induce altered expression levels of genes from unlinked regions (Stranger et al., 2007). Thus, if we consider a regression framework, it should be multiple GEs against multiple CNAs. As we need to search for the regulation relationships among a large number of GEs and CNAs, with the often low sample sizes, regularized estimation and marker selection are needed. The analysis gets more complicated with correlations among GEs and among CNAs. Specifically, high correlations among CNAs have been observed in both coding and non-coding regions (Stamoulis, 2011). Co-regulated genes can have highly correlated expression levels. Recent studies under simpler settings have shown that accounting for correlations is critical for analysing genetic data (Huang et al., 2011; Liu et al., 2013). A few studies have addressed the correlations among measurements. For example, Kim et al. (2009) developed the graph-guided fused Lasso method to address the dependency structure among responses. Peng et al. (2010) proposed the remMap method to identify master CNAs which affect most GEs. A common limitation of these studies is that correlation is only accounted for in one side of the regression model, and hence the analysis is not ‘complete’. In addition, ineffective estimation approaches have been adopted.
The goal of this study is to more effectively analyse GE and CNA data so as to better understand their relationships. To account for the fact that multiple CNAs can affect the expression level of a gene, we simultaneously model the joint effects of multiple CNAs. For the identification of important CNAs associated with a GE, an effective penalization approach is adopted. The most significant advancement is that networks are adopted to describe the correlations among GEs and among CNAs. When the correlations among GEs are taken into consideration, the analysis becomes a ‘multiple GEs against multiple CNAs’ regression problem. That is, both the responses and predictors are high-dimensional. To accommodate the network structures, we propose a sparse double Laplacian shrinkage (SDLS) approach, which combines the power of penalized variable selection and Laplacian shrinkage. To the best of our knowledge, this study is the first to effectively accommodate correlations in both sides of the GE-CNA regression. It is noted that although our analysis focuses on GEs and CNAs, the proposed method is potentially applicable to other types of genetic measurements.
2 Data and model settings
Consider a dataset with n iid samples, each with m GE and p CNA measurements. Let be the n × m matrix of GEs and be the n × p matrix of CNAs. We first process data so that the GEs are centered and the CNAs are centered and standardized with . Although it is possible that CNAs regulate GEs in a non-linear way, non-linear modeling incurs prohibitively high computational cost, and the dominating majority of existing studies have focused on linear modeling. Consider the multivariate regression model
| (1) |
where s are the error terms, and is the regression coefficient vector associated with the kth gene. The p × m regression coefficient matrix is . The expression level of a gene is regulated by at most a few CNAs, and one CNA affects at most a few GE levels. Thus, β is sparse.
2.1 Penalized identification
Under the sparsity condition, we use penalization for estimation and identification of important associations. Consider the estimate
| (2) |
where is the penalty function, and are parameters that define the penalty. A non-zero component of indicates an association between the corresponding CNA and GE. For the penalty function, first consider the MCP (minimax concave penalization; Zhang, 2010), where the penalty
| (3) |
with . λ is the tuning parameter, and γ is the regularization parameter. The MCP has been shown to have performance comparable to or better than many other penalties including Lasso, adaptive Lasso and SCAD (Breheny and Huang, 2011; Zhang, 2010). It conducts marker selection and regularized estimation but does not have a ‘built-in’ mechanism to accommodate correlations. Note that imposing P0 is equivalent to analysing each GE separately but with the same tuning parameter for all GEs to ensure comparability.
3 Sparse double Laplacian shrinkage
3.1 Construction of network adjacency measures
GEs (CNAs) are ‘connected’ to each other. In this study, we adopt a network approach to describe the interconnections among GEs and among CNAs. In a network, a node corresponds to a GE or a CNA. A network contains rich information. Of special importance to this study is the adjacency, which is one of the most important network measures and quantifies how ‘closely’ two nodes are connected to each other (Zhang et al., 2005).
Denote rij as the Pearson’s correlation coefficient between nodes i and j. Other similarity measures such as the Spearman’s correlation can also be used. Based on rij, Zhang et al. (2005) proposed several ways of constructing the adjacency matrix, whose (i, j)th element is aij, the adjacency between nodes i and j. Notable examples include (i) , where r is the cutoff calculated from the Fisher transformation (Huang et al., 2011); (ii) ; (iii) , and (iv) . In (iii) and (iv), α is determined using the scale-free topology criterion (Zhang et al., 2005). We acknowledge that other approaches, for example the Gaussian graphical model (Yuan et al., 2007), can also be used to construct the adjacency matrix. As our goal is to demonstrate the incorporation of adjacency not to compare different constructions of adjacency, we focus on (iii) with α = 5. Compared with the Gaussian graphical model and others, this construction has ignorable computational cost. The resulted adjacency matrix is sparse and easy to manipulate. α = 5 ensures that aij has the same sign as rij. Note that it is straightforward to implement other adjacency measures.
We compute the adjacency measures for GEs and CNAs in the same manner. Denote and as the adjacency matrices for CNAs and GEs respectively.
3.2 Penalized estimation and identification
Consider the penalized estimation framework specified in (2). We propose the SDLS penalty
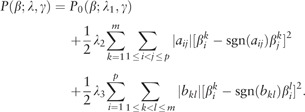 |
(4) |
is the vector of tuning parameters. is the sign function.
This penalty has been motivated by the following considerations. conducts selection using MCP, as described in Section 2.1. Two Laplacian type penalties (Liu et al., 2013) are introduced. Consider for example CNAs. If two CNAs are not connected with aij = 0, then the Laplacian penalty is equal to zero. If two CNAs have a large positive aij, then they are tightly connected and have highly correlated measurements. The Laplacian penalty encourages their regression coefficients to be similar, with the degree of similarity adjusted by the degree of adjacency . If two CNAs have a large negative aij, then the Laplacian penalty has a form similar to ridge penalty, which conducts regularized estimation and shrinks the magnitudes of both regression coefficients. Similar rationale holds for GEs. If two GEs are tightly connected in a network, then their regression coefficient profiles should be similar. The first Laplacian penalty corresponds to the rows of the coefficient matrix, and the second corresponds to the columns. Each element of the coefficient matrix is possibly included in multiple penalties. λ is adjusted data-dependently to avoid over-shrinkage.
The two Laplacian penalties take quadratic forms and can be associated with the Laplacians for undirected weighted graphs. Take the first Laplacian penalty as an example. Let , where . We can rewrite
| (5) |
where . The matrix L is associated with a labeled weighted graph with the vertex set and edge set . It has been referred to as the Laplacian of (Chung, 1997).
3.3 Computation
With the introduction of two Laplacian penalties, the existing algorithms are not directly applicable. We propose a two-layer coordinate descent (CD) algorithm. It optimizes with respect to one element of β at a time and cycles through all elements. Iterations are repeated until convergence. In this algorithm, the key is the update with respect to each element.
Consider the overall objective function defined in (2). For and , given the parameters () fixed at their current estimates, we seek to minimize the penalized objective function with respect to . Here only terms involving matter. This is equivalent to minimizing
| (6) |
where c is a term free of . The subscript ‘– i’ denotes the remaining elements after the ith is removed. Let . , and are defined as
| (7) |
It can be shown that the minimizer of in (6) is
| (8) |
With a fixed λ, the two-layer CD algorithm proceeds as follows.
Algorithm 1. the Two-layer Coordinate Descent Algorithm
1: Initialize s = 0 and component-wise. Compute .
2: repeat
3: for do
4: for do
5: Calculate and via (7);
6: Update via (8);
7: Update ;
8: end for
9: end for
10: ;
11: until the difference between two consecutive estimates is smaller than a predefined threshold.
12: return the estimate of β at convergence.
In the penalized objective function, the least squares loss function and two Laplacian penalties have quadratic forms. P0 is the sum of mp terms, with one for each component of β. Following Breheny and Huang (2011), the CD algorithm converges to the coordinate-wise minimum, which is also a stationary point. In our numerical study, convergence is achieved for all simulated and real data.
The SDLS method involves three tuning parameters and regularization parameter γ. For γ, Breheny and Huang (2011) and Zhang (2010) suggest examining a small number of values (for example, 1.8, 3, 6 and 10) or fixing its value. In our numeric study, we find that the results are not sensitive to γ and set γ = 6. In practice, one may need to experiment with multiple γ values, examine the sensitivity of estimates and select using data-dependent methods. The values of λ play a more important role. λ1 controls the sparsity of marker selection. λ2 and λ3 control the smoothness among coefficients. To reduce computational cost, one may set , imposing the same degree of shrinkage for CNAs and GEs. However, as the overall computational cost is affordable, we jointly search for the optimal λ1, λ2 and λ3 values using V-fold cross validation (V = 5). For λ1, we start with the smallest value under which all regression coefficients are zero. We then gradually reduce λ1 over a discrete grid of values. For λ2 and λ3, our experience suggests that the estimates can be relatively less sensitive to their values. We search over the discrete grid of .
4 Simulation
To mimic GE and CNA data in a pathway, we consider the scenario with . The proposed method is applicable to whole-genome data with a higher dimension. However, since the main objective is to accommodate interconnections among GEs and CNAs, it is reasonable to focus on a pathway, as genes within the same pathway are more likely to be co-regulated and have correlated measurements while genes in different pathways tend to be functionally and statistically uncorrelated. In the next section, we analyse The Cancer Genome Atlas (TCGA) data. In Supplementary Figure 3, we show the histograms of processed CNA values for two randomly chosen genes. Motivated by Figure 3, we simulate CNAs as a mixture of two normal distributions, one with a small and the other with a large variance. Both distributions have mean zero. For each normal distribution, we consider two correlation structures: (i) the block structure. CNAs belong to clusters. Those in different clusters are independent, while those in the same cluster have correlation coefficient ρ1; and (ii) the auto-regressive (AR) structure. CNAs i and j within the same cluster have correlation coefficient . For both structures, there are 40 clusters, with 5 CNAs per cluster. CNA measurements take discrete values, and for whole-genome data, they often have a block-wise constant structure. The simulated data have a continuous distribution, which has been motivated by the processed TCGA data (Supplementary Figure 3). In addition, the block-wise constant structure is not obvious when we focus on a pathway, as genes within the same pathway are not necessarily physically nearby.
We generate the sparse coefficient matrix β as having a block diagonal structure
where denotes the element-wise product. Wt and Kt have dimension 5 × 5 for . Kt has entries with independent Bernoulli draws with a success probability of 0.8. Wt is the effect size matrix with each entry independently drawn from a uniform distribution. Consider the following two examples.
Example 1 —
For , entries of odd columns in Wt are from , and those of even columns are from . For , entries of odd columns in Wt are from , and those of even columns are from . Entries in Wt are equal to 0 for t > 20. This example stresses the similarity among certain rows.
Example 2 —
For , entries of odd rows in Wt are from , and those of even rows are from . For , entries of odd rows in Wt are from , and those of even rows are from . For t > 20, Wt are equal to 0. This example stresses the similarity among certain columns.
For both examples, we expect that there are a total of true positives (20 clusters; elements per cluster; and 0.8 probability of being non-zero for each element). The random errors are generated independently from , reflecting the fact that GEs are also regulated by other mechanisms, for example methylation, which can lead to further correlation. The GE values are generated from the linear regression model (1). In addition, to examine whether performance of the proposed method depends on the number of true positives, we also simulate two examples with 40 true positives.
We analyse the simulated data using the SDLS method (which is also referred to as PGC, with Laplacian penalties on both ‘G’ and ‘C’). In addition, we also consider (i) a marginal approach. This approach conducts the regression of one GE on one CNA. The P-values from all pairs are pooled, and then an FDR (false discovery rate; Benjamini and Yekutieli (2001)) approach with target FDR = 0.05 is applied to identify important associations. (ii) P0, which is the proposed method with . (iii) PC, which is the proposed method with . It accommodates the network structure and so correlations among CNAs but not GEs. And (iv) PG, which is the proposed method with . It accommodates the network structure and so correlations among GEs but not CNAs. We acknowledge that multiple methods can be used to analyse the simulated data. The first approach conducts the popular ‘one GE against one CNA’ analysis, and the last three have a penalization framework closest to the proposed and can establish the value of accounting for correlations among both GEs and CNAs in the most direct way.
The identification performance is evaluated using the number of true positives (TP) and false positives (FP). In addition, we also measure prediction performance using the model error (ME), which is defined as . Note that the marginal approach does not generate model errors.
Simulation suggests the proposed method is computationally affordable. For example, for one data replicate under Example 1, PGC takes 445.3 seconds on a regular desktop. In comparison, P0, PC and PG take 50.0, 116.5 and 194.9 s, respectively. Summary statistics for Example 1 and 2 with 400 expected true positives are shown in Tables 1 and 2, respectively. Those with 40 expected true positives are shown in Supplementary Tables S4 and S5, respectively. Simulation suggests that the marginal approach is in general inferior. With weak correlations, it identifies fewer true positives. When there are strong correlations, it can have satisfactory performance in terms of true positives, however, at the price of a huge number of false positives. We have experimented with adjusting the target FDR value so that the number of true positives is comparable to that of the proposed method and found that the marginal approach has significantly more false positives (results omitted). For the penalization methods, when CNAs and GEs are only weakly correlated, performance of different methods is similar. For example, in Table 1 with the AR correlation structure and , the four penalization methods identify 385.6 (P0), 385.5 (PC), 388.2 (PG) and 388.3 (PGC) true positives, with 26.4, 25.9, 23.7 and 24.2 false positives, respectively. In addition, the prediction performance is also similar. However, when there exist moderate to strong correlations, the advantage of proposed method becomes obvious. For example in Table 1 with the AR correlation structure and , P0 identifies 384.2 true positives, whereas PCG identifies 396.9 true positives, at the price of a few more false positives. When , P0 only identifies 148.8 true positives, in comparison to 335.3 of PGC. In addition, PGC also has better prediction performance with ME equal to 8.00, compared to 38.13 of P0. The block correlation structure and Table 2 show similar patterns. Supplementary Tables S4 and S5 suggest that the proposed method also has superior performance when there are 40 expected true positives.
Table 1.
Simulation study of Example 1 with 400 true positives
| Correlation | AR |
Block |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| marginal | P0 | PC | PG | PGC | marginal | P0 | PC | PG | PGC | |
| (0.1, 0.1) | – | 10.5(0.9) | 10.4(0.9) | 8.9(1.0) | 8.9(1.0) | – | 7.48(0.93) | 7.39(0.85) | 6.32(0.85) | 6.28(0.85) |
| 198.4(18.8) | 385.6(9.3) | 385.5(8.7) | 388.2(8.8) | 388.3(8.7) | 261.5(18.0) | 391.0(9.0) | 391.2(9.1) | 393.9(9.1) | 393.9(9.1) | |
| 39.3(6.5) | 26.4(10.7) | 25.9(10.4) | 23.7(5.9) | 24.2(5.9) | 51.4(6.4) | 10.6(6.7) | 10.4(6.7) | 11.5(5.7) | 11.1(5.5) | |
| (0.1, 0.9) | – | 9.88(1.92) | 9.78(1.86) | 9.22(1.93) | 9.11(1.82) | – | 7.38(1.37) | 7.37(1.35) | 6.87(1.31) | 6.80(1.25) |
| 194.5(10.4) | 388.0(9.0) | 388.2(8.7) | 390.4(9.4) | 390.1(9.3) | 255.7(11.0) | 391.5(8.0) | 391.5(8.0) | 393.3(7.8) | 393.3(8.1) | |
| 38.5(6.3) | 23.5(9.2) | 23.1(6.7) | 29.6(11.2) | 27.4(10.1) | 50.1(6.9) | 11.0(4.8) | 10.9(5.6) | 14.1(6.3) | 13.9(6.1) | |
| (0.5, 0.1) | – | 8.25(1.10) | 5.98(0.68) | 6.22(0.77) | 5.54(0.66) | – | 5.69(0.55) | 4.70(0.33) | 5.07(0.41) | 4.66(0.33) |
| 353.6(16.6) | 384.2(7.7) | 394.9(7.9) | 393.8(7.4) | 396.9(7.8) | 396.9(12.4) | 391.2(9.6) | 397.2(8.9) | 395.1(9.5) | 397.3(8.8) | |
| 92.5(10.5) | 6.8(3.0) | 12.6(6.0) | 13.6(6.9) | 16.3(7.7) | 95.1(9.6) | 3.3(2.5) | 9.8(4.9) | 9.3(5.8) | 9.3(4.7) | |
| (0.5, 0.9) | – | 8.10(1.67) | 5.86(1.13) | 6.78(1.33) | 5.63(0.98) | – | 5.90(0.97) | 4.79(0.66) | 5.21(0.77) | 4.75(0.64) |
| 353.1(11.8) | 384.8(8.0) | 395.1(7.9) | 391.1(7.6) | 396.0(7.9) | 395.3(9.5) | 390.2(8.0) | 396.9(7.7) | 394.6(8.0) | 397.3(7.7) | |
| 91.8(7.9) | 8.5(4.2) | 13.4(6.6) | 15.3(6.3) | 16.0(7.0) | 96.7(8.8) | 3.2(2.2) | 9.4(5.3) | 9.9(5.6) | 10.7(6.1) | |
| (0.9, 0.1) | – | 38.53(2.16) | 7.88(0.69) | 10.92(1.57) | 7.67(0.61) | – | 50.71(1.99) | 6.51(0.63) | 30.66(2.94) | 6.54(0.62) |
| 398.4(10.1) | 147.0(10.2) | 333.1(10.5) | 308.0(13.4) | 336.9(10.6) | 398.4(10.0) | 99.1(3.0) | 351.4(10.3) | 210.5(14.0) | 350.4(10.1) | |
| 1575.5(161.1) | 96.8(45.8) | 48.8(20.3) | 94.3(15.6) | 51.2(13.4) | 102.5(9.5) | 4.2(14.4) | 36.8(6.0) | 45.5(34.6) | 36.3(5.6) | |
| (0.9, 0.9) | – | 38.13(2.95) | 8.07(0.99) | 11.32(1.37) | 8.00(1.01) | – | 50.17(2.61) | 6.75(1.04) | 30.34(3.23) | 6.78(1.10) |
| 400.4(9.9) | 148.8(10.9) | 332.2(14.2) | 309.5(12.7) | 335.3(15.6) | 400.5(9.9) | 99.1(4.4) | 345.8(11.0) | 205.0(18.0) | 345.0(10.9) | |
| 1571.9(116.4) | 98.2(46.7) | 49.5(19.2) | 90.5(18.1) | 57.5(13.7) | 99.9(10.0) | 6.0(15.6) | 38.2(5.9) | 29.8(17.9) | 35.7(6.1) | |
In each cell, the three rows are model error, number of true positives and number of false positives. The marginal approach does not generate model errors. Mean (standard deviation).
Table 2.
Simulation study of Example 2 with 400 true positives
| Correlation | AR |
Block |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| marginal | P0 | PC | PG | PGC | marginal | P0 | PC | PG | PGC | |
| (0.1, 0.1) | – | 18.66(2.66) | 18.66(2.66) | 16.59(2.57) | 16.60(2.56) | – | 16.96(1.79) | 16.91(1.72) | 14.71(1.72) | 14.72(1.74) |
| 94.8(9.7) | 378.9(10.6) | 378.9(10.6) | 381.7(10.6) | 381.7(10.6) | 120.7(14.7) | 380.4(8.3) | 380.2(8.4) | 384.3(9.8) | 384.3(9.8) | |
| 19.4(4.7) | 82.2(21.3) | 82.4(21.3) | 75.9(20.7) | 76.3(20.3) | 24.2(5.7) | 65.4(26.9) | 63.8(23.8) | 61.1(23.0) | 62.2(24.4) | |
| (0.1, 0.9) | – | 18.84(2.52) | 18.85(2.53) | 16.68(2.15) | 16.67(2.13) | – | 17.05(3.13) | 17.03(3.14) | 15.09(3.20) | 15.10(3.20) |
| 95.0(13.2) | 373.6(11.6) | 373.7(11.6) | 380.5(12.0) | 380.6(12.0) | 119.6(12.4) | 376.3(11.1) | 376.5(11.2) | 382.2(10.5) | 382.1(10.5) | |
| 18.5(5.6) | 70.2(21.9) | 70.6(21.9) | 87.4(32.8) | 87.6(32.1) | 23.5(5.7) | 60.7(26.8) | 61.4(26.6) | 74.7(29.4) | 74.8(30.4) | |
| (0.5, 0.1) | – | 52.71(2.37) | 52.61(2.39) | 51.99(2.36) | 51.94(2.42) | – | 53.80(2.88) | 53.34(2.72) | 51.05(3.07) | 50.97(3.03) |
| 68.7(10.1) | 169.3(18.4) | 170.4(18.4) | 177.5(18.5) | 178.3(18.5) | 136.3(16.1) | 237.8(34.9) | 234.4(27.7) | 267.6(35.0) | 263.8(38.4) | |
| 17.2(4.2) | 54.0(30.4) | 57.1(30.2) | 60.5(31.0) | 62.0(30.5) | 28.2(5.5) | 149.3(106.8) | 121.6(87.4) | 210.5(131.2) | 196.8(140.2) | |
| (0.5, 0.9) | – | 53.64(3.31) | 53.43(3.28) | 49.75(3.50) | 49.78(3.54) | – | 52.99(4.51) | 52.70(4.72) | 45.47(5.09) | 45.32(5.11) |
| 73.3(11.6) | 175.7(23.3) | 174.8(19.0) | 219.2(27.9) | 215.9(30.0) | 137.5(12.5) | 245.9(36.9) | 236.1(41.7) | 275.2(32.2) | 276.4(31.9) | |
| 18.2(4.5) | 63.7(49.2) | 59.3(38.1) | 115.8(64.6) | 108.7(64.7) | 31.4(6.2) | 167.3(99.8) | 127.0(102.3) | 168.2(91.0) | 171.3(93.2) | |
| (0.9, 0.1) | – | 17.41(0.92) | 15.35(0.93) | 15.72(0.94) | 15.25(0.89) | – | 17.84(0.65) | 12.06(0.88) | 16.81(0.73) | 12.03(0.78) |
| 214.4(24.5) | 71.5(7.3) | 117.2(16.8) | 97.3(10.4) | 118.8(15.6) | 232.0(21.2) | 68.6(5.0) | 219.4(20.1) | 84.7(8.1) | 220.5(18.4) | |
| 449.0(81.4) | 22.9(6.1) | 57.7(18.5) | 37.1(9.5) | 58.77(18.0) | 56.9(7.6) | 3.1(2.2) | 27.1(8.3) | 6.2(4.0) | 26.1(7.4) | |
| (0.9, 0.9) | – | 17.71(1.14) | 15.53(1.23) | 15.48(1.09) | 15.30(1.17) | – | 17.57(0.97) | 12.07(1.01) | 14.87(0.96) | 11.28(1.07) |
| 211.3(19.4) | 72.4(9.7) | 123.3(22.6) | 115.9(14.3) | 126.9(20.8) | 224.3(20.7) | 68.6(5.9) | 217.0(21.5) | 135.6(14.2) | 230.9(22.6) | |
| 439.7(64.6) | 22.7(8.0) | 65.8(26.9) | 63.3(19.0) | 69.1(25.7) | 57.3(7.7) | 3.1(2.4) | 27.0(8.8) | 18.4(6.6) | 26.9(7.6) | |
In each cell, the three rows are model error, number of true positives and number of false positives. The marginal approach does not generate model errors. Mean (standard deviation).
The inferior performance of the marginal approach is as expected, as a GE is jointly affected by multiple CNAs while the marginal approach analyses only one CNA at a time. It is interesting to note that the proposed PGC outperforms or is comparable to P0 across the whole spectrum of simulation with different correlation structures. Thus it can be ‘safe’ to use it in practice when the true correlation structure is unknown. With weak correlations, PGC and P0 perform similarly. PGC targets taking advantage of the interconnections among CNAs and GEs. When such interconnections are weak or do not exist, PGC cannot improve much over P0. It is also observed that after accounting for the network structure of CNAs, accounting for that of GEs leads to small improvement. This is also reasonable as in the simulated data, the interconnections among GEs are largely caused by those among CNAs. However, as we do observe moderate improvement of PGC over PC under multiple scenarios, it is sensible to account for both networks. PGC may lead to a few more false positives, as the newly added Laplacian penalties have a squared form, are dense penalties, and tend to ‘pull’ zero coefficients towards correlated important ones. In the simulated examples, the block sizes are equal. We have also experimented with unequal sizes and found comparable results (details omitted).
5 Data analysis
We first analyse the TCGA (http://cancergenome.nih.gov/) data on glioblastoma (GBM). GE and CNA measurements are available on 479 patients. We download and analyse the processed level 3 data. The GE measurements were originally generated using the custom Agilent 244K array platforms. The analysed data are the robust Z-scores, which are lowess-normalized, log-transformed, and median-centered version of gene expression data that take into account all of the gene expression arrays under consideration. The measurement determines whether a gene is up- or down-regulated relative to the reference population. The CNA measurements were originally generated using the Affymetrix SNP6.0 platforms. The loss and gain levels of copy number changes have been identified using the segmentation analysis and GISTIC algorithm and expressed in the form of log2 ratio of a sample versus the reference intensity. We analyse the apoptosis pathway. The set of genes is identified from Gene Ontology (GO) using the annotation package in GSEA (http://www.broadinstitute.org/gsea). Apoptosis is a regulated cellular suicide mechanism by which cells undergo death to control cell proliferation or in response to DNA damage. The apoptosis pathway is a hallmark of cancer (Khanna and Jackson, 2001). For the GBM data, there are 298 GEs and 338 CNAs in this pathway.
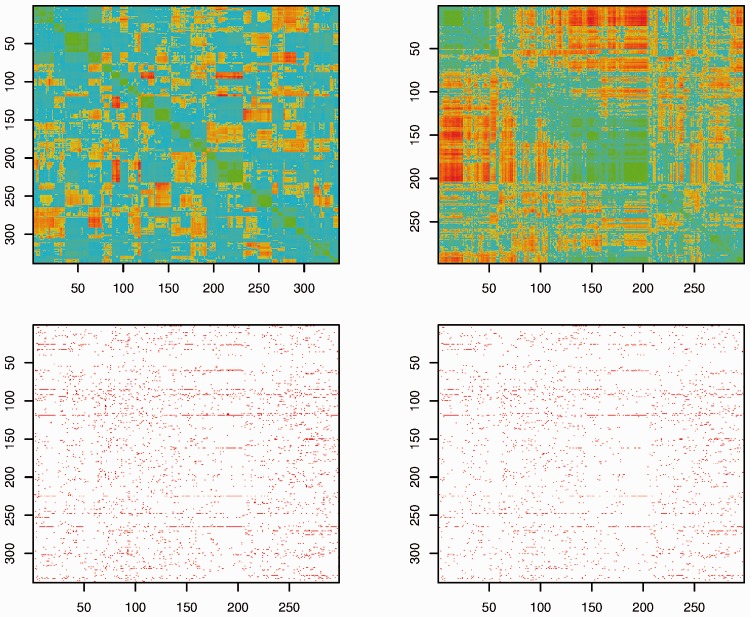
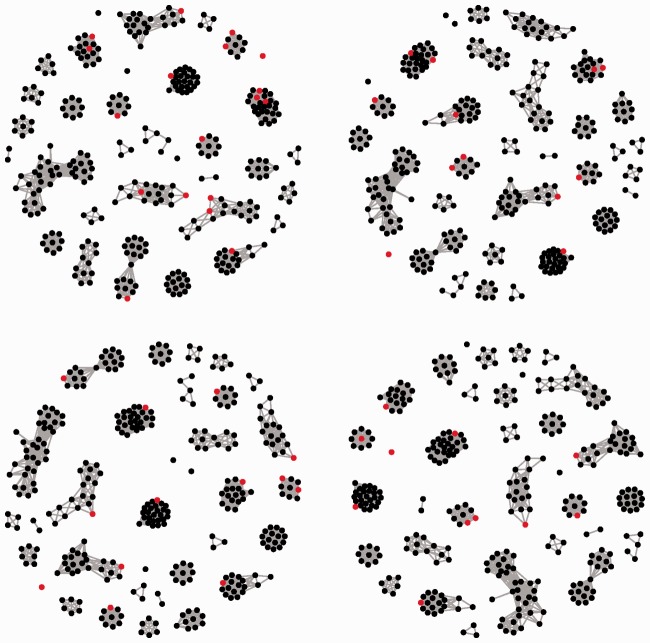
Figure 1 contains the heatmaps of the correlation coefficient matrices for both CNAs and GEs, after reordering the variables based on the hierarchical clustering so that highly correlated CNAs and GEs are clustered with block structures along the diagonal. The two plots show several blocks representing densely connected subgraphs for CNAs and GEs. The subgraphs for CNAs are further shown in Figure 2.
Fig. 1.
Analysis of the apoptosis pathway in GBM. Left-upper: heatmap for the correlation matrix of CNAs. Right-upper: heatmap for the correlation matrix of GEs. Left-lower: positions of the non-zero coefficients under PGC. Right-lower: positions of the non-zero coefficients under P0
Fig. 2.
Networks of CNAs in the apoptosis pathway in GBM. Red dots correspond to CNAs with non-zero coefficients for the expression of gene PTEN. Left-upper: PGC. Right-upper: PC. Left-lower: PG. Right-lower: P0
Beyond the marginal and four penalization methods as described in simulation, we also consider Puni, which regresses one GE on all CNAs at a time and applies penalized selection. For all penalization methods, the tuning parameters are selected using V-fold cross validation. For the 298 × 338 regression coefficient matrix β, 2747 (marginal), 3022 (Puni), 2662 (PGC), 1736 (P0), 2206 (PC) and 1917 (PG) non-zero elements are identified. Different methods identify different sets of associations. For example, there are only 104 overlaps between the marginal approach and PGC. For PGC and P0, we show in Figure 1 the positions of non-zero regression coefficients (represented by red pixels). The rows and columns have been rearranged corresponding to the upper panels of Figure 1. Corresponding results under Puni are provided in Supplementary Appendix. More details on the other methods are available from the authors. PGC identifies more non-zero elements than P0, PC and PG, which is in line with the observations made in simulation. When more closely examining the identified CNAs, we find that several critical genes, including IFNB1, HIPK3, CASP3, TIAL1, MAP3K10, VEGFA and CDKN2A, have been associated with quite a few GEs. PGC employs Laplacian penalties, which encourage the similarity of regression coefficients. We evaluate the similarity of columns of the regression coefficient matrix. We sum over the off-diagonal elements in the correlation matrices of regression coefficients, and obtain 399.2 for PGC, 357.7 for P0 and 177.5 for Puni, which suggests a higher level of similarity for PGC.
As a representative example, we also take a closer look at the PTEN gene. PTEN acts as a tumor suppressor through the action of its phosphatase protein product. This phosphatase is involved in the regulation of cell cycle, preventing cells from growing and dividing too rapidly. The identified CNAs and their estimated regression coefficients are shown in Table 3. Under the five penalization methods, CNA PTEN has positive regression coefficients, and their magnitudes are the largest. However, the marginal approach misses this CNA. PGC identifies the most CNAs. Our analysis suggests that the expression of PTEN is associated with not only its corresponding CNA but also a few others. In Figure 2, we also show the CNAs identified using different methods with respect to the subgraphs. For PGC, five subgraphs contain at least two identified CNAs. In contrast, P0 identifies one such subgraph, and Puni identifies none (Supplementary Appendix).
Table 3.
Regression coefficients for the expression of gene PTEN in the apoptosis pathway in GBM using different methods
| marginal | Puni | P0 | PC | PG | PGC | |
|---|---|---|---|---|---|---|
| ACVR1B | −0.231 | −0.264 | −0.282 | |||
| ALB | + | −0.261 | −0.349 | |||
| ANGPTL4 | + | 0.530 | 0.792 | 0.580 | 0.787 | 0.890 |
| ARHGDIA | + | |||||
| BBC3 | + | |||||
| HSP90B1 | + | |||||
| PMAIP1 | + | |||||
| SEMA4D | + | |||||
| TNFSF14 | + | |||||
| CASP3 | −0.174 | −0.178 | −0.155 | −0.174 | ||
| CD27 | −0.044 | |||||
| CD74 | −0.227 | −0.769 | −0.738 | |||
| DAPK2 | −0.096 | −0.428 | −0.476 | −0.402 | −0.510 | |
| HIPK3 | 0.277 | 0.214 | 0.260 | 0.281 | ||
| NUAK2 | −0.063 | −0.183 | −0.149 | −0.204 | −0.184 | |
| PTEN | 1.531 | 1.679 | 1.682 | 1.665 | 1.718 | |
| TIA1 | −0.520 | −0.991 | −1.107 | −0.935 | −1.016 | |
| TXNDC5 | 0.497 | 0.441 | 0.490 | 0.404 | ||
| CASP6 | −0.204 | |||||
| GLO1 | 0.144 | 0.060 | 0.227 | |||
| MAP3K10 | 0.318 | 0.424 | ||||
| TNFAIP8 | −0.826 | −0.915 | ||||
| GSK3B | −0.494 | −0.166 | ||||
| TIAF1 | 0.348 | 0.336 | ||||
| CALR | −0.394 | |||||
| IL12A | −0.098 | −0.432 | ||||
| SNCA | −0.492 | |||||
| STK3 | 0.217 | |||||
| TRIAP1 | 0.011 |
For the marginal approach, a ‘+’ represents an identified association.
The apoptosis pathway is cancer related. In Supplementary Appendix, we also conduct two additional analyses which may serve as ‘negative controls’. In the first set of analysis, we analyse the cellular localization pathway in the GBM data. The cellular localization pathway is biologically important. However, there is no evidence that it is associated with GBM or other cancers. In the second set of analysis, we analyse the gluconeogenesis pathway in the TCGA LIHC (liver hepatocellular carcinoma) data. The biological process regulated by this pathway is specific to liver and kidney in mammals. Detailed results are presented in Supplementary Appendix. The overall conclusions are similar to those drawn for the apoptosis pathway.
In our analyses, we focus on specific pathways, with the expectation that different pathways have different biological functions. Some genes belong to multiple pathways. For such genes, analysing them in different pathways will lead to different sets of identified CNAs. One way to solve this problem is to expand the proposed analysis to multiple pathways, which may lead to increased computational cost.
6 Discussion
Multiple types of genetic, epigenetic, and genomic changes can happen on the human genome. It is important to understand their relationships. Using GE and CNA as an example, we have developed a SDLS method. This method uses effective penalization for marker selection and regularized estimation. Significantly advancing from the existing studies, it adopts two Laplacian penalties to accommodate the interconnections among GEs and among CNAs. It has an intuitive formulation and can be realized using an efficient CD algorithm. Simulations show that it has comparable performance as the alternatives when there are only weak correlations among GEs and CNAs. However with moderate to strong correlations, as has been commonly observed in practical data, it has significantly better identification and prediction performance. In data analyses, it identifies associations different from those using the alternatives. The estimated regression coefficient matrix has a higher level of row and column similarity. Manually examining the analysis results for a few representative genes suggests reasonable analysis results.
To better accommodate finer data structures, the proposed method introduces new penalties with new tunings. The computational cost is thus higher than the alternatives, which is the price paid for better modeling data. However, as the Laplacian penalties are differentiable, the computational complexity is acceptable. To reduce computational cost, one may set , resulting in only two tunings. Our numerical experience suggests that three tuning parameters are also acceptable. As the main objective is to develop the new method, we have adopted only one adjacency measure. We acknowledge that there may exist other perhaps better adjacency measures. However, it is not our goal to compare and draw conclusions on the relative performance of different adjacency measures. Under multiple simulation settings, the proposed method has been shown to be superior. More extensive simulations may be conducted in the future. In data analyses, the proposed method identifies associations different from the alternatives. Simple examinations suggest that the results are reasonable. More extensive analyses are needed to fully validate the findings.
Supplementary Material
Acknowledgement
We thank the associate editor and three referees for careful review and insightful comments, which have led to a significant improvement of the article.
Funding
This work was supported by the National Institutes of Health (CA182984, CA142774, P50CA121974, and P30CA016359), the National Social Science Foundation of China (13CTJ001, 13&ZD148), the National Natural Science Foundation of China (71301162), and the VA Cooperative Studies Program of the Department of Veterans Affairs, Office of Research and Development.
Conflict of Interest: none declared.
References
- Benjamini Y., Yekutieli D. (2001) The control of the false discovery rate in multiple testing under dependency. Ann. Stat., 29, 1165–1188. [Google Scholar]
- Breheny P., Huang J. (2011) Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Ann. Appl. Stat., 5, 232–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung F.R. (1997) Spectral Graph Theory. Vol. 92 American Mathematical Society, Providence, RI. [Google Scholar]
- Henrichsen C.N., et al. (2009) Copy number variants, diseases and gene expression. Hum. Mol. Genet., 18, R1–R8. [DOI] [PubMed] [Google Scholar]
- Huang J., et al. (2011) The sparse Laplacian shrinkage estimator for high-dimensional regression. Ann. Stat., 39, 2021–2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khanna K.K., Jackson S.P. (2001) DNA double-strand breaks: signaling, repair and the cancer connection. Nat. Genet., 27, 247–254. [DOI] [PubMed] [Google Scholar]
- Kim S., et al. (2009) A multivariate regression approach to association analysis of a quantitative trait network. Bioinformatics, 25, 204–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J., et al. (2013) Incorporating network structure in integrative analysis of cancer prognosis data. Genet. Epidemiol., 37, 173–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J., et al. (2010) Regularized multivariate regression for identifying master predictors with application to integrative genomics study of breast cancer. Ann. Appl. Stat., 4, 53–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salari K., et al. (2010) Dr-integrator: a new analytic tool for integrating DNA copy number and gene expression data. Bioinformatics, 26, 414–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer M., et al. (2009) Integrated analysis of copy number alterations and gene expression: a bivariate assessment of equally directed abnormalities. Bioinformatics, 25, 3228–3235. [DOI] [PubMed] [Google Scholar]
- Shih I.-M., et al. (2011) Amplification of the ch19p13.2 nacc1 locus in ovarian high-grade serous carcinoma. Mod. Pathol., 24, 638–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamoulis C. (2011) Estimation of correlations between copy-number variants in non-coding DNA. In: Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE, pp. 5563–5566. IEEE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stranger B.E., et al. (2007) Relative impact of nucleotide and copy number variation on gene expression phenotypes. Science, 315, 848–853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wrzeszczynski K.O., et al. (2011) Identification of tumor suppressors and oncogenes from genomic and epigenetic features in ovarian cancer. PLoS ONE, 6, e28503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wynes M.W., et al. (2014) Fgfr1 mrna and protein expression, not gene copy number, predict fgfr tki sensitivity across all lung cancer histologies. Clin. Cancer Res., 20, 3299–3309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M., et al. (2007) Dimension reduction and coefficient estimation in multivariate linear regression. J. R. Stat. Soc. Ser. B (Statistical Methodology), 69, 329–346. [Google Scholar]
- Zhang B., et al. (2005) A general framework for weighted gene co-expression network analysis. Stat. Appl. Genet. Mol. Biol., 4, 1544–6115. [DOI] [PubMed] [Google Scholar]
- Zhang C.-H. (2010) Nearly unbiased variable selection under minimax concave penalty. Ann. Stat., 38, 894–942. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.