Abstract
The Chesapeake Bay plays an important role in transforming riverine nutrients before they are exported to the adjacent continental shelf. Although the mean nitrogen budget of the Chesapeake Bay has been previously estimated from observations, uncertainties associated with interannually varying hydrological conditions remain. In this study, a land‐estuarine‐ocean biogeochemical modeling system is developed to quantify Chesapeake riverine nitrogen inputs, within‐estuary nitrogen transformation processes and the ultimate export of nitrogen to the coastal ocean. Model skill was evaluated using extensive in situ and satellite‐derived data, and a simulation using environmental conditions for 2001–2005 was conducted to quantify the Chesapeake Bay nitrogen budget. The 5 year simulation was characterized by large riverine inputs of nitrogen (154 × 109 g N yr−1) split roughly 60:40 between inorganic:organic components. Much of this was denitrified (34 × 109 g N yr−1) and buried (46 × 109 g N yr−1) within the estuarine system. A positive net annual ecosystem production for the bay further contributed to a large advective export of organic nitrogen to the shelf (91 × 109 g N yr−1) and negligible inorganic nitrogen export. Interannual variability was strong, particularly for the riverine nitrogen fluxes. In years with higher than average riverine nitrogen inputs, most of this excess nitrogen (50–60%) was exported from the bay as organic nitrogen, with the remaining split between burial, denitrification, and inorganic export to the coastal ocean. In comparison to previous simulations using generic shelf biogeochemical model formulations inside the estuary, the estuarine biogeochemical model described here produced more realistic and significantly greater exports of organic nitrogen and lower exports of inorganic nitrogen to the shelf.
Keywords: Chesapeake Bay, nitrogen budget, interannual variability, modeling study
Key Points
A estuarine biogeochemical model was developed for Chesapeake Bay
Interannually varying nitrogen fluxes were computed for 2001–2005
N export to the shelf was mostly organic, even when DIN input was high
1. Introduction
Located at the intersection between land and ocean, estuaries play an important role in global carbon and biogeochemical cycles [Bauer et al., 2013; Bianchi and Bauer, 2011; Canuel et al., 2012]. Chesapeake Bay, the largest estuary in the United States, plays a particularly significant role in the transformation and burial of riverine terrestrial nitrogen [Bronk et al., 1998; Glibert et al., 1991 ; Horrigan et al., 1990; Kemp, 2005]. As a result, it significantly impacts the form and amount of nitrogen that is exported from riverine sources to the adjacent continental shelf.
The fate of riverine nutrients has been intensely studied in the Chesapeake Bay where available water quality data extend back to 1950 [Flemer et al., 1983]. Using five early years (1977–1982) of U.S. Environmental Protection Agency (EPA) data, Smullen et al. [1982] concluded that the Chesapeake Bay retained almost all the nutrients entering during this time period. Using the same data Nixon [1987] reassessed the nitrogen budget and concluded that the bay retained only a small amount (3–6%) of the nitrogen entering the system. In a third study, Fisher et al. [1988] developed a conceptual model suggesting roughly 50% of total nitrogen left the bay, primarily through phytoplankton sinking. In these early studies the relative amount of riverine total nitrogen loss in the bay and export to the open ocean were quite controversial, primarily because of the limited availability of observations and the different assumptions and approaches employed.
A more consistent Chesapeake Bay nitrogen budget came together in the 1990s, after additional measurements were available. Boynton et al. [1995] calculated that about 70% of the nitrogen entering the bay was lost to denitrification, burial, and fisheries harvest, and the remaining 30% was exported to the open ocean. However, these calculations did not include a separation of nitrogen between inorganic and organic forms. Furthermore, the nitrogen exchange between the bay and the adjacent shelf was calculated “by difference” from subtracting the bay internal sinks from riverine and atmospheric sources, rather than from direct measurements. An analysis of the estuarine‐ocean nitrogen exchange using a bay water quality model was additionally used to confirm the general magnitude and sign of the export flux.
A more detailed budget was described by Kemp et al. [1997]; however, this budget was limited to the main stem of the bay (Figure 1). In these calculations nitrogen was separated into dissolved inorganic and organic forms, and the nitrogen seaward transport was calculated from a model simulation. They concluded that roughly 75% of the nitrogen entering the main stem of the bay was exported to the open ocean. In addition, the ratio of dissolved inorganic nitrogen to total organic nitrogen at the bay mouth (0.04) was much smaller than that at the head of the bay (5.1). Overall, the net ecosystem production in the main stem of the bay was positive, leading Kemp et al. [1997] to conclude that this portion of the bay is net autotrophic.
Figure 1.
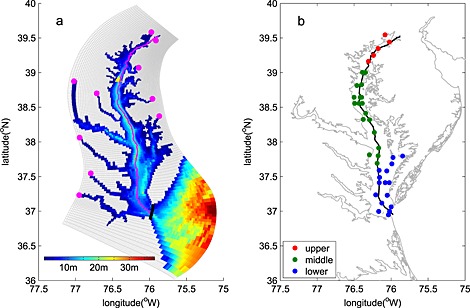
Chesapeake Bay (a) model grid, bathymetry, location of riverine inputs (magenta dots), and Thomas Point Light Buoy used for wind forcing (yellow triangle); (b) map illustrating location of EPA Chesapeake Bay Program Water Quality Monitoring Stations in the upper (red circles), middle (green circles), and lower (blue circles) bay. The black line in Figure 1a denotes the edge of the bay interior, over which the bay‐wide budget numbers are computed. The magenta line in Figure 1a and black line in Figure 1b show the stations along the trench of the bay used in Figures 3, 6, and 8.
Although nitrogen budget estimates from observational studies such as those described above have been becoming more consistent in recent decades, they are still associated with considerable uncertainties, largely resulting from relatively low temporal and spatial sampling frequency as well as the interannual variability associated with the observations. One issue with these previous nitrogen budget estimates, for example, is that due to data limitations, asynchronous observations had to be combined. In Kemp et al. [1997] nitrogen exchanges at the bay mouth were from the year 1986, but net ecosystem production (called net ecosystem metabolism in their paper) was from a multiple year average (1986–1993). In addition, to avoid variation of fluxes with different hydrological conditions, Kemp et al. [1997] remove years with extreme wet or dry conditions and used years with low to moderate river flow only.
In order to examine how interanually varying riverine inputs of nitrogen to Chesapeake Bay affect estuarine nitrogen fluxes, a land‐estuarine‐ocean biogeochemical modeling system is developed for this region. Riverine inputs of nitrogen to the bay are computed from a terrestrial ecosystem model that has been extensively validated with U.S. Geological Survey (USGS) river gauge data and resolves both gauged and ungauged riverine discharge variability on scales of days to years. This temporally varying discharge is then used as input to the estuarine‐biogeochemical model, which provides estimates of the nitrogen fluxes within the bay as well as advective exports from the bay to the adjacent Mid‐Atlantic Bight shelf. This coupled modeling system calculates the nitrogen budget of the Chesapeake Bay for a continuous 5 year period (2001–2005), of which the first two years (2001 and 2002) were dry‐flow years, the third year (2003) was a wet‐flow year, and the last two years (2004 and 2005) were intermediate‐flow years.
The content of this paper is organized as follows. Section 2 and the associated Appendix A present a complete description of our land‐estuarine‐biogeochemistry modeling system and the configuration implemented here. In section 3, model skill is evaluated relative to extensive data from the Chesapeake Bay Program as well as satellite ocean color data. In section 4, a simulated nitrogen budget for the bay is presented and compared to previous budgets derived using observational data as well as model results using a generic basin‐scale continental shelf model. A summary of our results and potential future work is provided in section 5.
2. Model Description
2.1. Hydrodynamic Model: Regional Ocean Modeling System
The physical component of the coupled model is based on the Regional Ocean Modeling System (ROMS) [Shchepetkin and McWilliams, 2005] version 3.6. The model domain and horizontal grid follows the Chesapeake Bay community implementation of the ROMS (ChesROMS) [Brown et al., 2013; Xu et al., 2012]. The domain spans the region from 77.2°W to 75.0°W and from 36°N to 40°N, covering the main stem and primary tributaries of the Chesapeake Bay, as well as part of the mid‐Atlantic Bight (Figure 1). The horizontal grid spacing varies with highest resolution (430 m) in the northern bay near the Chesapeake and Delaware Canal, lowest resolution (~10 km) in the southern end of the mid‐Atlantic Bight, and an average grid spacing within the Chesapeake Bay of 1.7 km. As in ChesROMS, the model has 20 terrain‐following vertical layers with higher resolution near the surface and bottom boundaries. However, unlike ChesROMS, the vertical s coordinate function follows Shchepetkin and McWilliams [2009], and stretching parameters at the surface and bottom are set to 6.0 and 4.0, respectively. The bottom topography is also slightly smoothed as in Scully [2013] to avoid pressure gradient errors caused by steep bathymetry.
The model is forced with spatially uniform but temporally varying winds, measured every hour at the Thomas Point Light Buoy (−76.4°W, 38.9°N). These observed winds are used rather than other wind products such as those derived from the North American Regional Reanalysis (NARR), since the latter underestimates the observed summer winds by roughly 30% and does not show the strong directional asymmetry that may play a key role in modulating the strength of vertical mixing [Scully, 2013]. Other atmospheric forcing, including air temperature, relative humidity, pressure, precipitation, longwave, and shortwave radiation were obtained from NARR with 3 h time resolution. The NARR shortwave radiation was found to be systematically higher than adjacent buoy observations, and therefore, it was reduced by 80% [Wang et al., 2012]. At the open boundary, the model is forced by open ocean tides and nontidal water levels as in ChesROMS [Xu et al., 2012].
The model is configured to use the recursive MPDATA 3‐D advection scheme for tracers, third‐order upstream advection scheme for 3‐D horizontal momentum and fourth‐order centered difference for 3‐D momentum in the vertical. The generic length‐scale vertical turbulent mixing scheme [Warner et al., 2005] is implemented with the stability functions of Kantha and Clayson [1994], and background mixing coefficients for both momentum and tracers are set to 10−5 m2 s−1 as in Scully [2010].
2.2. Estuarine Carbon Biogeochemistry Model
The estuarine carbon biogeochemistry (ECB) model implemented here includes a simplified nitrogen cycle with 11 state variables (Figure 2b): nitrate ([NO3]), ammonium ([NH4]), phytoplankton (P), zooplankton (Z), small and large detritus (DS and DL), semilabile and refractory dissolved organic nitrogen ([DON]SL and [DON]RF), inorganic suspended solids ([ISS]), chlorophyll ([Chl]), and oxygen ([O2]). Although analogous carbon state variables are included in the model as well (dissolved organic carbon, detrital carbon, and dissolved inorganic carbon), these will be described and analyzed in a separate publication. Phosphate is not included in this version of the model, but work toward this goal is planned for the near future (see section 5).
Figure 2.
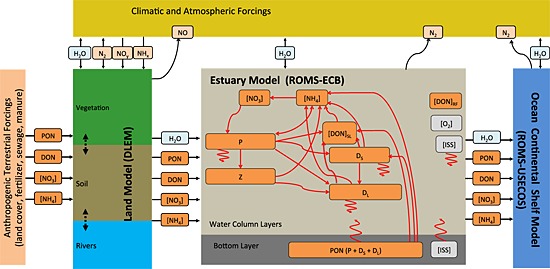
Schematic of the land‐estuarine ocean biogeochemical modeling system. The nitrogen cycle of the estuarine model was detailed illustrated.
A mathematical description of the biogeochemical source/sink terms for the ECB state variables that specifically pertain to the nitrogen cycle are summarized in the Appendix Tables A1 and A2. Model function symbols are defined in Appendix Table A3, and parameter definitions and values are provided in the Appendix Table A4. A complete set of equations for the nitrogen cycle is also provided in electronic form in the supporting information.
All state variables are horizontally and vertically advected and diffused along with the physical circulation variables. The model structure is based on Druon et al. [2010], which was originally derived from Fennel et al. [2006], with modifications similar to those described by Hofmann et al. [2008, 2011]. However, these models were all designed for coastal applications. To adapt the model to an estuarine application in the Chesapeake Bay, a number of model formulations were modified, as described below.
2.2.1. Refractory and Semilabile DON
Since dissolved organic nitrogen [DON] plays a critical role in estuarine nitrogen cycling processes [Keller and Hood, 2011], semilabile and refractory DON components are included as separate state variables in the model. Although [DON]RF does not participate actively in any biological processes, it is input from the rivers, and transported via advection and diffusion throughout the model domain and reduces the light intensity. The [DON]SL is derived from phytoplankton exudation ( ), sloppy feeding (+ (1 − β)λεgZ) and detrital solubilization ( ), and is remineralized into NH4( ).
2.2.2. Inorganic Suspended Solids
Similar to the refractory DON, inorganic suspended solids (ISS) do not participate in the nitrogen cycling directly but play an important role in reducing the light intensity in the northern Chesapeake Bay. The ISS formulation and related parameters follow Xu and Hood [2006]. Specifically, ISS is introduced as an additional state variable, which enters the bay through riverine input and sinks at a constant velocity (w ISS). After reaching the bottom, the ISS is instantly resuspended, based on a constant erosion rate (ξ), the bottom shear stress (Γ) and the critical shear stress (ΓC):
| (1) |
2.2.3. Light Attenuation
The photosynthetic available radiation decreases exponentially with water depth:
| (2) |
where I 0 is the light just below the sea surface, PARfrac is the fraction of light that is available for photosynthesis, KD is the diffuse attenuation coefficient, and z is depth. Xu et al. [2005] used chlorophyll, total suspended solids (TSS), and surface salinity to specify KD for the Chesapeake Bay, where salinity was used as a proxy for chromophoric dissolved organic matter (CDOM), since CDOM is generally inversely related to salinity. To avoid KD becoming negative in high‐salinity regimes, Xu et al. [2005] identified empirical relations for high (≥15 practical salinity unit (psu)) and low (≤15 psu) salinity regimes, respectively. They found that their model successfully explained 70% of the observed KD variability in the Chesapeake Bay. However, their empirical relationship was based on Chesapeake Bay Program observations from 1995 and 1996, which is outside the more recent study period used in this analysis. Therefore, as a part of this analysis their method was repeated using observations from 2000 to 2005 and resulted in the following empirical relationship:
| (3) |
where TSS (in mg L−1 represents total suspended solids, including both the inorganic suspended solids (section 2.2.2) and the organic suspended solids (defined here as particulate organic nitrogen including P, Z, DS, and DL). This relationship was found to explain 76% of the observed variability in KD. Chlorophyll was excluded from the relationship, as it did not successfully explain any significant additional variability. With this single relationship, KD is positive when salinity is less than ~24 psu, which covers almost the entire Chesapeake Bay. In high‐salinity regions of the model domain (close to the bay mouth and on the Mid‐Atlantic Bight shelf) it is possible for the right‐hand side of the above equation to become negative. To prevent this, the configuration of KD used for the U.S. East Coast shelf model (Hofmann et al., unpublished data, Old Dominion University, 2011), is used in high‐salinity regimes. If 1.4 + 0.063[TSS] − 0.057S < 0, then
| (4) |
where [DON] represents total DON, i.e., the sum of both refractory and semilabile components.
2.2.4. Phytoplankton Specific Growth Rate
A diverse assemblage of phytoplankton species is responsible for the high rates of primary production observed in the Chesapeake Bay. Although diatoms are abundant throughout the year, there are also typically large seasonal occurrences of dinoflagellates and cyanobacteria [Marshall et al., 2005; Marshall and Nesius, 1996]. Seasonal patterns of species composition vary throughout the bay, with diatom blooms routinely occurring as early as middle winter in the oligohaline section of the bay. In the higher‐salinity regions of the bay, dinoflagellate taxa are common in the summer months. In fall, a more diatom‐dominated assemblage is typically present throughout the bay. In general, the timing, position, and magnitude of the spring bloom is determined by the high fluxes of riverine dissolved inorganic nutrients entering the bay, whereas the mean and variability of summertime phytoplankton concentrations are determined more by the degree of nutrient regeneration [Fisher et al., 1988; Harding, 1994; Harding et al., 2002; Malone et al., 1988].
The growth rates of these phytoplankton communities have been measured over a wide range of different temperatures and nutrient conditions [Lomas and Glibert, 1999a, 1999b]. Here a constant temperature‐independent maximum growth rate is assumed, which is a simplification that has been successfully adopted by other modelers within the Chesapeake Bay and other surrounding regions. For example, Druon et al. [2010] found that using a temperature‐independent maximum specific growth rate (μ 0 = 1.6 day−1) substantially improved their model results in the Mid‐Atlantic Bight (their Table A2). In their Chesapeake Bay biogeochemical model, Xu and Hood [2006] also used constant (temperature‐independent) specific growth rates for phytoplankton but adjusted this rate for low salinity (μ 0 = 0.96 day−1) versus high‐salinity (μ 0 = 3.22 day−1) regions. Here a constant maximum specific growth rate (μ 0 = 2.15 day−1) is used for our single‐phytoplankton state variable, based on information provided by Li et al. [2009] for the Chesapeake Bay. Growth is furthermore limited by both nitrogen ( ) and light (L I). Phosphate limitation is not yet included in the model. Since phosphate limitation is known to be strongest temporally in the spring and spatially in the upper bay [Fisher et al., 1992, 1999], by neglecting this limiting nutrient one would expect that the model simulations might overestimate particulate organic nitrogen (PON) and chlorophyll in the spring and in the upper bay (see sections 3.4.3 and 3.4.5).
2.2.5. Water Column Denitrification
One of the most significant differences between the ECB model and model implementations for the continental shelf results from the fact that hypoxia can occur in estuarine subpycnocline waters when water column stratification prevents reaeration of deeper waters [Hagy et al., 2004; Bever et al., 2013]. During such periods, remineralization of organic matter in the water column transitions from an aerobic to an anaerobic process via facultative anaerobes that shift to suitable alternative electron acceptors such as nitrate or nitrite [King, 2005]. Water column denitrification has previously been considered in marine ecosystem models of other hypoxic systems, such as the Black Sea and Arabian Sea [Oguz, 2002; Resplandy et al., 2012]. The stoichiometric equation for oceanic denitrification first proposed by Richards [1965] follows
where organic matter is reduced and dinitrogen gas is released to the atmosphere, a process that has global N cycle implications [e.g., Codispoti et al., 2001].
Within the ROMS‐ECB implementation, onset of water column denitrification is associated with decreasing dissolved oxygen concentration, which reflects the known oxic repression of nitrogen oxide reductases that are needed to catalyze denitrification reactions [Hood et al., 2006]. With these issues in mind and following Oguz [2002], nitrate loss during water column denitrification is modeled as
| (5) |
where , and are the oxygen and nitrate limitation terms, respectively, for denitrification. The latter limitation is imposed to prevent generation of negative nitrate concentrations. In this way, water column denitrification depends on the stoichiometry for remineralization via denitrification (η DNF), the half‐saturation constant for water column denitrification (K DNF), as well as the half‐saturation constant for water column NO3 uptake shutting down (K WNO3).
2.2.6. Oxygen Limitation of Remineralization
In the water column, oxygen concentration also regulates the rate of nitrification, but in an inverse fashion as compared to its influence on denitrification: as denitrification is enhanced, nitrification is diminished. Thus, the nitrification limitation term in the ECB model takes the form
| (6) |
where K NTR is the half‐saturation constant for water column nitrification. The remineralization rate of organic matter is regulated by the combined rates of nitrification and denitrification; therefore, the summation of f NTR and f DNF is included for all terms associated with remineralization. The factors f NTR and f DNF are then used to partition aerobic and anaerobic bacterial processing of organic matter between consumption of oxygen and nitrate, respectively.
2.2.7. Burial and Resuspension of Organic Matter
Burial is an important pathway for particulate organic nitrogen removal from estuarine systems. Coupled biogeochemical‐circulation models often neglect this process by assuming that organic matter reaching the seabed is instantaneously remineralized [Fennel et al., 2006]. Although complex sediment biogeochemical models that include the potential of temporary storage of organic matter in the seabed exist [Soetaert et al., 2000], such models are rarely implemented in fully coupled hydrodynamic‐biogeochemical models largely due to computational constraints. ECB includes an intermediate approach following that of Druon et al. [2010], whereby a portion of the organic matter reaching the seabed is resuspended (ϕ 1, see Appendix A for symbol definitions), a fraction is permanently buried (ϕ 2 (1 − ϕ 1 )), and the remaining ((1 − ϕ 2 )(1 − ϕ 1 )) is instantaneously remineralized through coupled nitrification/denitrification. Specifically, the model formulations (see equations in Appendix A) assume that the instantaneously resuspended fraction of organic matter is a function of shear stress at the bottom.
2.3. Riverine Inputs
In this implementation, ROMS‐ECB is forced with daily riverine nutrient input derived from the Dynamic Land Ecosystem Model (DLEM), including NO3, NH4, DON, and PON as well as daily freshwater discharge (Figure 2a). DLEM is a grid‐based fully distributed model which couples major biogeochemical cycles, the water cycle, and vegetation dynamics to derive temporally and spatially explicit estimates of fluxes of water, greenhouse gases, and carbon and nitrogen storage in terrestrial ecosystems [Tian et al., 2010, 2014; Liu et al., 2013]. DLEM has been used to hindcast riverine discharge of freshwater [Yang et al., 2015a], nitrogen [Yang et al., 2015b], and organic matter [Tian et al., 2015] to the U.S. eastern continental shelf over the past century and forecast these fluxes over the 21st century. The model incorporates hydrological components to simulate lateral water flux from terrestrial ecosystems to river networks. Export of freshwater from land surface to coastal areas is simulated through three major processes: generation of surface runoff after rainfall events, the leaching of water from land to river networks in the form of overland flow and base flow, and the flow routing process along river channels from upstream areas to coastal regions.
The total export to the Chesapeake Bay computed by DLEM, including groundwater discharge, was apportioned to 10 tributaries and entered the model domain at these 10 locations (Figure 1a). In reality, freshwater inputs and nutrient loading occurs continuously along the Chesapeake coastline. The simplification of attributing these inputs to 10 distinct locations rather than continuously along the coastline is not likely to significantly affect the model results in the main stem of the bay or in the major tributaries, as our sensitivity experiments indicate that the model is more sensitive to the total amount of nutrients and freshwater entering the bay, than to the specific locations of these fluxes.
Because DON provided by DLEM was not separated into semilabile and refractory components, assumptions had to be made regarding the relative proportions of each component. Of the total DON entering the bay, 50% was assumed to be semilabile, and 20% was assumed to be refractory [Raymond and Bauer, 2001]. The remaining 30% of the DON leaving the rivers was assumed to flocculate and be buried before reaching the 5 psu isohaline [Bronk et al., 1998]. The PON provided by DLEM was assumed to enter the bay entirely as small particulate detritus.
In addition to the above nitrogen components, the river forcing of the model requires temperature and salinity, which was calculated from climatological USGS data (1980 to 2011), and oxygen, which was assumed to be at saturation and computed as a function of temperature and salinity [Weiss, 1970]. The concentration of other river variables, including phytoplankton (1.8 mmol N m−3), zooplankton (0.06 mmol N m−3), and chlorophyll (6.0 mg Chl m−3), were input to the model domain as uniform concentrations.
2.4. Model Implementation
At the open boundary, the Chapman [1985] condition is used for the free surface, the radiation condition is used for tracers and baroclinic 3‐D velocities and the Flather [1976] condition is used for barotropic 2‐D velocities. Temperature and salinity are nudged in and out of the model domain to climatological data fields generated from the 2001 World Ocean Atlas with time scales of 2 h and 2 day, respectively [Marchesiello et al., 2001]. The model is initialized with temperature and salinity fields that varied meridionally as in Xu et al. [2012]. The initial NO3 field is derived from fitting winter data from main stem stations with a power function [Xu and Hood, 2006]. The remaining biological variables are set to the following horizontally uniform values: [NH4] = 0.1 mmol N m−3, P = 6 mmol N m−3, Z = 1 mmol N m−3, DS = 6.66 mmol N m−3, DL = 3.33 mmol N m−3, [DON]SL = 13 mmol N m−3, [DON]R = 23 mmol N m−3, [Chl] = 15 mg Chl m−3, [O2] = 281.25 mmol O2 m−3, and ISS = 7 mg L−1 All initial fields are vertically uniform.
The model was first run starting with the above initial conditions from 1 January 2000 until 31 December 2005. The simulated distributions from 31 December 2005 were then used to restart the model on 1 January 2000 and the model was run until 31 December 2005 again. In total, this 6 year run was conducted 5 times to ensure the model was spun‐up adequately, i.e., there was no clear linear trend for any physical or biological variables and the fluctuations of each of the variables were nearly identical between the fourth and fifth simulations. The last 5 years of this simulation was used for analysis (2001–2005).
3. Model Skill Assessment
3.1. Model Skill Metrics
Quantitative model‐data comparisons using multiple skill metrics [Jolliff et al., 2009; Stow et al., 2009] are critical, as they reveal the advantages and potential limitations of a particular model, which must be carefully considered before using such a model as a tool for scientific study or decision‐making. In this analysis, multiple skill metrics were examined. For example, the correlation coefficient (r), which measures the tendency of the model and observed values to covary, was calculated as
| (7) |
where Oi is the observation at time ti, Mi is the model estimate at ti, is the mean of the observations, is the mean of the model estimates, and n is the total number of observations available for comparison with the model estimates. The bias, unbiased root‐mean‐squared difference (unbiased RMSD) and total root‐mean‐squared difference (RMSD) were calculated as
| (8) |
| (9) |
| (10) |
These three skill assessment statistics are particularly useful, as they are reported with the units of the quantity being assessed. The total RMSD is a particularly appropriate overall skill metric as it includes both a component for getting the mean correct (bias) and the variability correct (unbiased RMSD), i.e.,
| (11) |
Finally, the standard deviation of the model results (σ m) were also compared to that of the observations (σo) through the ratio (σr)
| (12) |
| (13) |
| (14) |
The Willmott skill score [Willmott, 1981], another widely used metric to quantify overall agreement between model and observations, was computed as
| (15) |
Specifically, W skill = 1 indicates perfect agreement between model results and observations, and W skill = 0 indicates that the model skill is equivalent to that of the observational mean [Willmott, 1981].
Here these model skill metrics are compactly visualized on Taylor [Taylor, 2001] and target diagrams [Jolliff et al., 2009; Friedrichs et al., 2009; Hofmann et al., 2008]. The Taylor diagram is plotted in a polar coordinate system and summarizes skill metrics including r, σr, and unbiased RMSD. In contrast, the target diagram is plotted in a Cartesian coordinate system and summarizes total RMSD, unbiased RMSD and bias. On both types of diagrams, skill statistics are typically normalized by the observational standard deviation (σo) to allow for the plotting of multiple different data sets on the same diagram. On the normalized Taylor diagram, the reference point sitting at (1, 0) represents a perfect skill score, whereas on the target diagram the center of the target (0, 0) represents a perfect skill score.
In this analysis, Taylor and target diagrams were used to visualize the model skill in reproducing both the spatial variability and the temporal variability of simulated distributions throughout the main stem of the bay (see Figure 1 for specific station locations). Spatial statistics were obtained by averaging the Chesapeake Bay Program (CBP) observations at each station over the 5 year simulation interval and reflects the ability of the model to reproduce the spatial variability of the climatological fields. Temporal statistics were obtained by calculating a bay time series by taking monthly averages of vertically integrated observations collected from all stations. This skill metric reflects the ability of the model to reproduce the temporal variability of the observed distributions.
3.2. Available Data for Model Evaluation
Using the skill metrics described above, the simulated physical fields (including temperature and salinity) and biogeochemical fields (including NO3, NH4, DON, PON, chlorophyll, and oxygen) were compared with available data from the EPA Chesapeake Bay Program (CBP) Water Quality Monitoring Program (data available from http://www.chesapeakebay.net/data). Model skill metrics were computed based on point‐to‐point comparisons by sampling the model results at the same horizontal, vertical, and temporal locations as the observations.
The Chesapeake Bay Program has been routinely monitoring the main stem of the Chesapeake Bay since June 1984. Specifically, throughout our analysis time period (2001–2005) many water quality parameters, including various forms of nitrogen as well as water temperature, salinity, and dissolved oxygen, were measured once each month during the colder late fall/winter/spring months, and twice each month during the warmer months. At each station (Figure 1b), vertical profiles of water temperature, salinity, and dissolved oxygen were measured at approximately 1 to 2 m intervals through the water column. Data on other variables such as NO3, NH4, DON, PON, and chlorophyll were collected in the surface and bottom layers, and at depths representing upper (above pycnocline) and lower (below pycnocline) layers in the deeper main stem stations where salinity stratification occurs.
In addition to comparing simulated fields with these in situ data, simulated surface chlorophyll fields were also compared with satellite‐derived surface chlorophyll concentrations from the Sea‐viewing Wide Field‐of‐view Sensor (SeaWiFS). For this purpose, monthly SeaWIFS data (available from http://oceancolor.gsfc.nasa.gov/cms/dataaccess) for the Chesapeake Bay were processed at a spatial resolution of 2 km using the OC4v6 chlorophyll algorithm (see http://oceancolor.gsfc.nasa.gov/REPROCESSING/R2009/ocv6/). Surface chlorophyll concentrations derived from this algorithm agree well with in situ CBP observations from the main stem of the bay. The correlation coefficient is high (0.76), the bias is low to (−0.58 µg/L), and the Willmott skill score is as high (0.81). Thus, the SeaWiFS‐derived chlorophyll concentrations are a useful additional source of information to which the model simulations can be compared, since the spatial resolution of these chlorophyll estimates (2 km) is much greater than that of the CBP data (Figure 1b).
3.3. Evaluation of Hydrodynamic Fields
Although the focus of this analysis is on the nitrogen budget of the Chesapeake Bay, reasonable nutrient distributions cannot be obtained without an adequate simulation of the observed hydrodynamic fields. Thus, simulated temperature and salinity fields were extensively compared to CBP observations.
3.3.1. Temperature
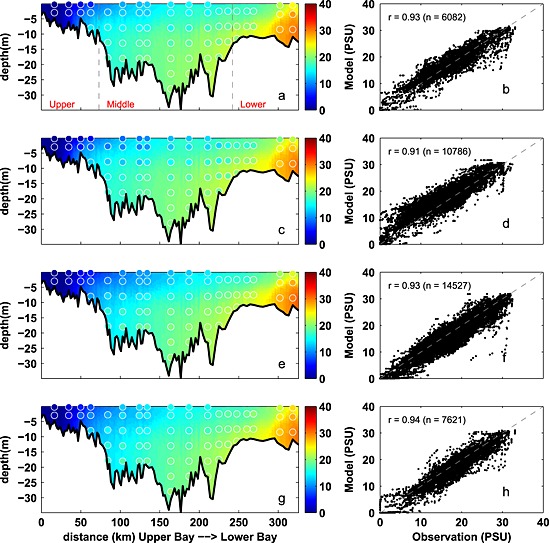
Seasonally averaged simulated temperature distributions are in very good agreement with CBP observations throughout the water column (Figure 3). Monthly depth‐averaged temperature in three bay subareas, the upper, middle, and lower bay (Figure 1), show comparable magnitude and fluctuations in both model and observations (Figure 4). Although the temperature field shows significant temporal variability, increasing from 0°C to 30°C between winter and summer (Figure 4), there is little horizontal or vertical variability within any given season, with average temperatures being nearly uniform throughout the water column and throughout the main stem of the bay (Figure 3). Model skill statistics for temperature (presented in Table 1 and summarized in Taylor and target diagrams (Figure 5)), indicate that correlations between the simulated and observed temperature fields are very high (>0.99) and the normalized unbiased RMSD (≤0.2) and bias (≤0.1) are both very small. Both temporal and spatial Willmott skill is close to 1.0, further demonstrating that the model has significant skill in reproducing the observed temperature field.
Figure 3.
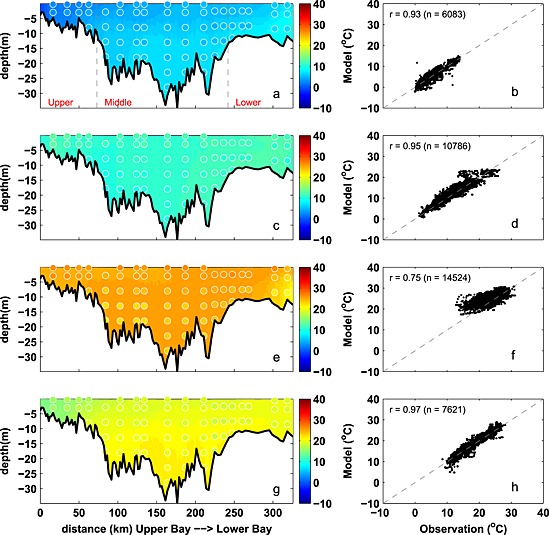
Observed and simulated seasonal temperature from 2001 to 2005. (a, c, e, and g) Temperature along the trench with background color representing the simulation and circles showing the observations. (b, d, f, and h) Modeled versus observed temperature at coincident times and locations, including correlation coefficient (r) and number of available data (n). Panels from top to bottom, winter (December–February), spring (March–May), summer (June–August), and fall (Septemebr–November). Gray dashed lines in Figure 3a denote the boundaries of the upper, middle, and lower bay. Stations from upper bay to lower bay are as follows: CB2.1, CB2.2, CB3.1, CB3.2, CB3.3C, CB4.1C, CB4.2C, CB4.3C, CB5.1, CB5.2, CB5.3, CB5.4, CB5.5, CB6.1, CB6.2, CB6.3, CB7.3, and CB7.4.
Figure 4.
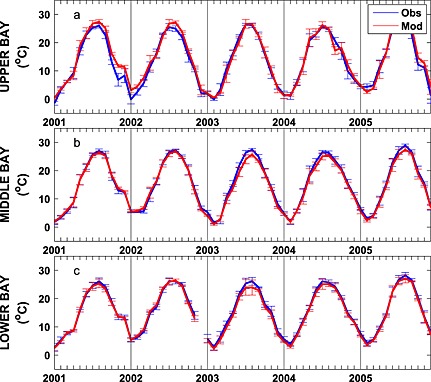
Observed and simulated mean monthly depth‐averaged temperature from 2001 to 2005 averaged over the (a) upper, (b) middle, and (c) lower bay stations illustrated in Figure 1. Vertical bars represent ±1 standard deviation.
Table 1.
Willmott Skill of Model Temperature, Salinity, NO3, NH4, PON, DON, Chlorophyll, and Dissolved Oxygen
| Upper Bay | Middle Bay | Lower Bay | All (Temporal) | All (Spatial) | |
|---|---|---|---|---|---|
| Temperature | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 |
| Salinity | 0.87 | 0.94 | 0.92 | 0.99 | 1.00 |
| NO3 | 0.84 | 0.74 | 0.40 | 0.77 | 0.99 |
| NH4 | 0.46 | 0.64 | 0.71 | 0.65 | 0.87 |
| PON | 0.32 | 0.39 | 0.54 | 0.52 | 0.88 |
| DON | 0.36 | 0.40 | 0.41 | 0.36 | 0.96 |
| Chlorophyll | 0.36 | 0.43 | 0.54 | 0.49 | 0.94 |
| DO | 0.93 | 0.98 | 0.96 | 0.97 | 0.97 |
Figure 5.
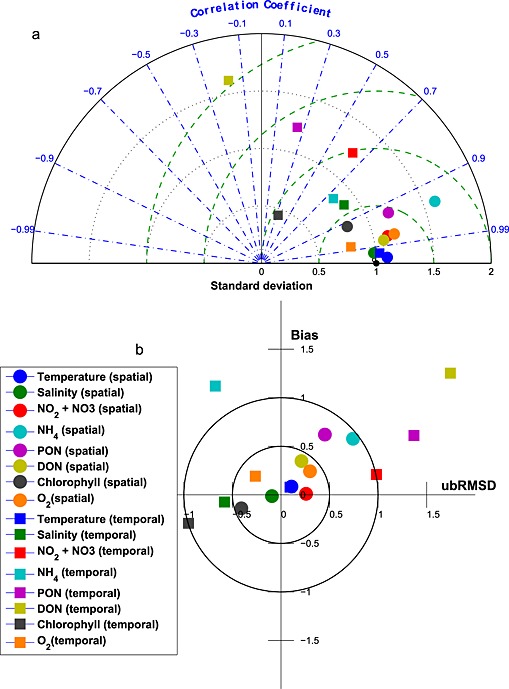
(a) Taylor and (b) Target diagrams illustrating model skill for hydrodynamic and biogeochemical fields [Taylor, 2001; Hofmann et al., 2008; Jolliff et al., 2009]. Squares represent temporal model skill, which was calculated by comparing time series of observational and model data. Circles represent spatial model skill, which was calculated by comparing the vertically integrated spatial series of observational and model data along the trench. Different colors represent different variables. In Figure 5a the solid lines represent lines of constant RMSD. In Figure 5b, the green dashed lines represent lines of constant unbiased RMSD, the blue dash‐dotted lines represent lines of constant correlation coefficient, and the black dotted lines represent lines of constant standard deviation. For a more detailed description of these diagrams and skill metrics, see section 3.1.
3.3.2. Salinity
Stratification is typically dominated by the salinity signal in the Chesapeake Bay, and thus, it is critical for the model to accurately represent the salinity field. Seasonally averaged simulated salinity distributions are in very good agreement with CBP observations throughout the water column (Figure 6), successfully capturing both the horizontal and the vertical gradients in salinity concentrations. In contrast to that of the temperature field, the spatial variability of the salinity field is much stronger than that of the temporal variability. Observed and simulated salinities vary from ≤ 5 psu in the upper bay to ≥ 25 psu in the lower bay where seawater intrudes into the bay mouth. Specifically, over this time period the observed (simulated) averaged salinity ± standard deviation in the upper bay is 3.5 ± 4.2 (4.1 ± 4.4) psu, in the middle bay is 15 ± 3.5 (14 ± 3.8) psu, and in the lower bay is 22 ± 3.7 psu (22 ± 4.3) psu. The simulated and observed salinity distributions also show significant interannual variability (Figure 7), which is strongly influenced by the variable riverine inputs. For example, average salinity was particularly low in late 2003 and 2004, which was an unusually wet period characterized by strong riverine inputs. Although the temporal model skill for salinity is not quite as high as for temperature (Figure 5 and Table 1), correlations between modeled and observed salinity are greater than 0.7 and Willmott skill is greater than 0.85.
Figure 6.
As in Figure 3 except for salinity.
Figure 7.
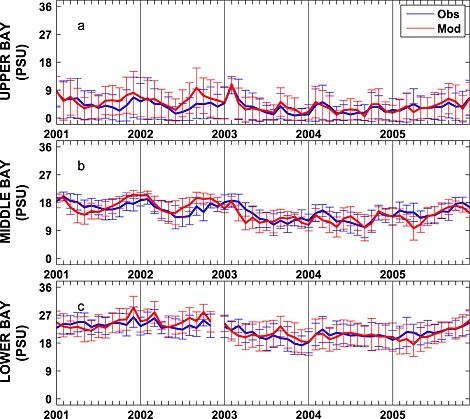
Observed and simulated mean monthly depth‐averaged salinity from 2001 to 2005 averaged over the (a) upper, (b) middle, and (c) lower bay stations illustrated in Figure 1. Error bars are ±1 standard deviations.
3.4. Evaluation of Biogeochemical Fields
Simulated nitrogen (NO3, NH4, PON, and DON), chlorophyll, and oxygen fields were also compared with CBP observations. A quantitative skill assessment analysis was performed on both the temporally averaged distributions and the spatially averaged distributions, in order to quantify how well the model captures both the spatial and the temporal (monthly) variability. Finally, the simulated surface chlorophyll concentrations were compared with those derived from SeaWIFS, in which case skill was assessed at each pixel.
3.4.1. NO3
The simulated NO3 field successfully captures the horizontal gradient of the observed CBP NO3 + NO2 field (Figures 8a and 8b). Nitrate concentration is about 60 mmol N m−3 in the upper bay throughout the water column, decreases rapidly to <15 mmol N m−3 in the middle bay, and is routinely lower than 5 mmol N m−3 in the lower bay. The observed and simulated nitrate fields show little vertical gradient throughout most of the bay, with the exception of the transition zone between the upper and middle bay (CBP station CB3.2, CB3.3C, and CB4.1C). The vertically integrated, simulated NO2 + NO3 field reproduces both the magnitude and the seasonal cycle of the observations in the upper bay (Figure 9a): the observed (simulated) values reach 1.3 ± 0.6 (1.5 ± 0.5) mol N m−2 in January, gradually decrease to 0.6 ± 0.5 (0.6 ± 0.3) mol N m−2 in August, and increase to 1.1 ± 0.5 (1.4 ± 0.7) mol N m−2 again in December. In the middle and lower bay, the model has more difficulty reproducing the observed seasonal variability: the simulated nitrate is in agreement with the observations for most of the year, but overestimates the observations in winter, though the observational variability is particularly large in these winter months. As a result, Wilmott skill of NO2 + NO3 is higher in the upper bay (0.84) than in the middle (0.74) or lower bay (0.34), since concentrations in the upper bay are primarily dependent on the riverine inputs and physical (advective/diffusive) processes which are well prescribed in this modeling system. Overall, as was the case for salinity and almost all biogeochemical variables, the model demonstrates a greater skill in reproducing the observed spatial mean and variability along the main stem of the bay, than the interannual mean and monthly variability. Correlations between the simulated and observed distributions are 0.98 (0.64) for the space (time) series. Similarly, the spatial model skill for NO3 was as high as 0.99, whereas the temporal model skill was somewhat lower (0.77).
Figure 8.
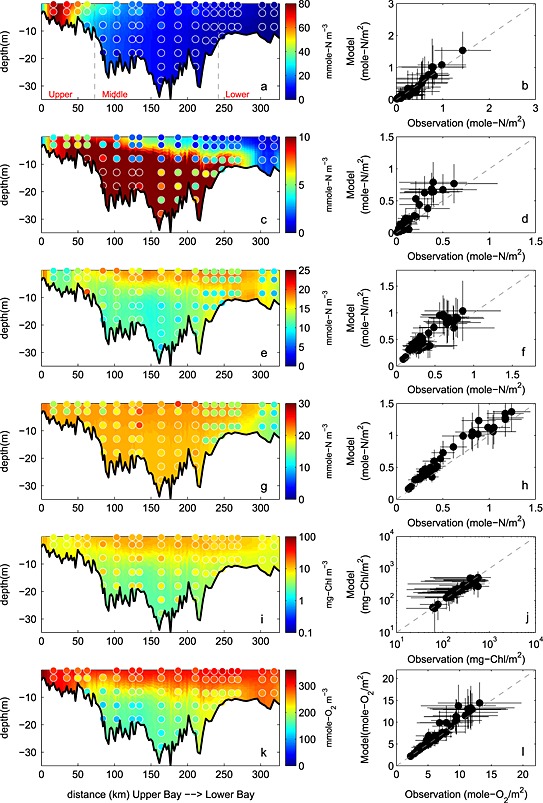
Observed and simulated climatological (average over 5 years) biogeochemical fields from 2001 to 2005. (a and b) NO2 + NO3, (c and d) NH4, (e and f) PON, (g and h) DON, (i and j) chlorophyll, and (k and l) oxygen. (Figures 8a, 8c, 8e, 8g, 8i, and 8k) concentrations along the trench with background color representing the simulation and circles showing the observations. (Figures 8b, 8d, 8f, 8h, 8j, and 8l) vertically integrated observed and simulated concentrations at stations shown in Figure 1b with error bars showing ±1 standard deviation relative to the 5 year mean. Gray dashed lines in Figure 8a denote the boundaries of the upper, middle, and lower bay.
Figure 9.
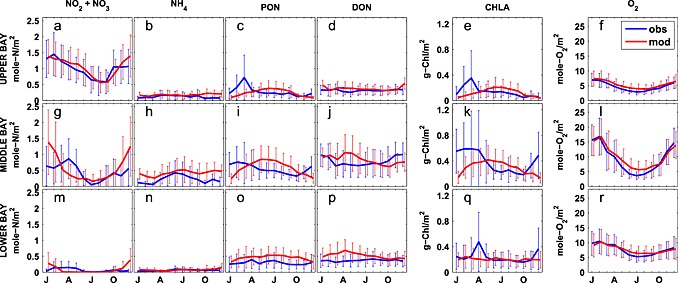
Observed and simulated vertically integrated monthly biogeochemical fields averaged over 2001–2005. Error bars are ±1 standard deviations. (a, g, and m) NO2 + NO3, (b, h, and n) NH4, (c, i, and o) PON, (d, j, and p) DON, (e, k, and q) chlorophyll, and (f, l, and r) oxygen. Panels from top to bottom, upper, middle, and lower bay.
3.4.2. NH4
Although the model reproduces the spatial variability of the ammonium field relatively well, the magnitude is overestimated, particularly in the upper and middle bay (Figures 8c and 8d). The depth of the strong vertical gradient of NH4 apparent in the observations (~10–15 m) was considerably deeper than that of the simulated NH4 fields (5–10 m). The bottom regeneration causing this vertical gradient may be overly strong in the model. Close to the mouth of the estuary (CBP station CB7.3 and CB7.4), the model successfully reproduces low ammonium concentrations throughout the water column. The model also reproduces the observed pattern of higher NH4 in the middle bay compared to other regions of the bay (Figures 9b, 9h, and 9n), but the model somewhat underestimates the magnitude of the seasonal cycle in this region, regenerating too much organic matter in the fall and winter months in this region (Figure 9h). The depth‐integrated annual average observed (modeled) NH4 concentrations in the upper bay are 0.12 ± 0.13 (0.18 ± .12) mol N m−2, in the middle bay are 0.25 ± 0.3 (0.43 ± 0.33) mol N m−2, and in the lower bay are 0.068 ± 0.064 (0.074 ± 0.083) mol N m−2, respectively. The quantitative skill of the simulated ammonium distributions are summarized in the Taylor and target diagrams (Figure 5). As is the case for NO3, the model has more skill in repeating the observed spatial variability than the temporal variability. Correlations between the simulated and observed distributions are 0.94 (0.74) for the space (time) series. Overall, the spatial model skill was 0.87, whereas the temporal model skill was again somewhat lower (0.65).
3.4.3. PON
The model reproduced the structure of the observed PON field throughout most of the upper and middle bay (stations CB2.1 to CB5.3) but overestimated PON in the lower portions of the bay (stations CB5.4 to CB7.4) (Figures 8e and 8f). At the upper bay stations, the observed (modeled) PON concentration was as low as 15 ± 8 mmol N m−3 (14 ± 10 mmol N m−3) throughout the water column. In the middle bay, the observed (modeled) PON was as high as 21 ± 9 mmol N m−3 (16 ± 8 mmol N m−3) above 10 m, but as low as 15 ± 6 mmol N m−3 (12 ± 9 mmol N m−3) below 10 m. This structure resulted from the fact that phytoplankton growth was not as light limited in the surface middle bay waters, as it was nearer the Susquehanna River, where high ISS and CDOM concentrations significantly decreased phytoplankton growth rates.
The annual cycle of depth‐integrated PON (Figures 9c, 9i, and 9o) illustrates that the PON in the middle bay is overestimated in the summer, primarily from May to September, when phytoplankton growth is overestimated. In the upper bay, observed PON shows a peak in March that is not captured by the model. Although this observed peak is associated with large interannual variability (0.72 ± 0.70 mol N m−2) and the modeled concentrations are within this range (0.25 ± 0.11 mol N m−2), future work will be devoted to improving this model‐data mismatch (see section 5). This is not likely caused by neglecting phosphate limitation, since adding phosphate limitation would further decrease upper bay spring organic matter concentrations. It is more likely caused by an overestimation of light attenuation due to ISS in the upper bay, and our simplifying assumption of a constant phytoplankton species composition in the bay. Because diatoms and dinoflagellates have differing C:Chl ratios and C:N ratios [Spilling et al., 2014], species composition differences may be responsible for the fact that spring blooms in both PON and chlorophyll observations are observed in the upper bay, whereas a spring bloom in chlorophyll and not PON is observed in the lower bay. As expected, correlations between simulated and observed PON concentrations (Figure 5) were higher for the spatial series (0.93) than the time series (0.25). Similarly, overall PON spatial model skill (Table 1) was as high as 0.88, whereas temporal model skill was lower (0.52).
3.4.4. DON
As is the case for ammonium, observed DON concentrations are highest in the middle bay, and somewhat lower in the upper and lower bay. The modeled DON concentrations are generally in agreement with the mean observed DON concentrations, but the model tends to overestimate DON in the upper bay and at some stations near the division between the middle and lower bay (Figures 8g and 8h). The mean observed (simulated) DON concentration in the upper bay is 21 ± 6 (17 ± 4) mmol N m−3, in the middle bay is 22 ± 4 (20 ± 4) mmol N m−3, and in the lower bay is 19 ± 4 (14 ± 3) mmol N m−3. The observed DON concentrations show only a slight seasonal signal, with higher concentrations from October through January; this is not well represented in the simulated distributions, which show relatively high concentrations from March to June in both the middle and the lower bay (Figures 9d, 9j, and 9p). Because the model reverses the observed temporal DON pattern, the temporal correlation between modeled and observed DON is negative (−0.17; Figure 5) and the temporal model skill is low (0.38; Table 1); however, the model has a high skill in reproducing the spatial variability (correlation = 0.98; spatial model skill = 0.96).
3.4.5. Chlorophyll
The model reproduces the structure of the observed chlorophyll field throughout most of the upper and lower bay. However, in the middle bay, the model is in agreement with the observations above 10 m but underestimates them in deeper waters (Figures 8i, and 8j). Not surprisingly, the annual cycle of chlorophyll (Figures 8e, 8k, and 8q) shows a pattern similar to that of PON in the upper and middle bay for both model and observations, since a significant component of PON is phytoplankton. As is the case for PON (see section 3.4.3), the model overestimates chlorophyll in the middle and upper bay from May to September, and underestimates chlorophyll in the late winter and spring (primarily at depth, Figures 8i and 8j). Observed chlorophyll also shows a peak in March in the upper bay; however, this peak is associated with large interannual variability (0.35 ± 0.43 g Chl m−2) and the modeled concentrations are within this range (0.11 ± 0.07 g Chl m−2). As discussed above for PON, overall correlation between model and observations (Figure 5) was higher for the spatial series (0.92) than for the time series (0.33). Similarly, overall spatial model skill for chlorophyll was as high as 0.94, whereas the temporal model skill was 0.49.
The averaged simulated surface chlorophyll fields were also compared with SeaWIFS‐derived chlorophyll concentrations (Figure 10). The model successfully captures the spatial along‐bay gradient of surface chlorophyll with an overestimation of the satellite‐derived estimates in the middle and lower bay. The 5 year mean surface chlorophyll distributions show very low RMSD and high Wilmott skill in the northern half of the bay but show some positive bias in the southern half of the bay. The median value of temporal model skill throughout the bay is 0.49 (Figure 10f). The 5 year mean vertically integrated primary production was also computed as 1321 mg C m−2 d−1, which is comparable to the mean net primary production (1357 mg C m−2 d−1) derived from Moderate Resolution Imaging Spectroradiometer‐Aqua [Son et al., 2014].
Figure 10.
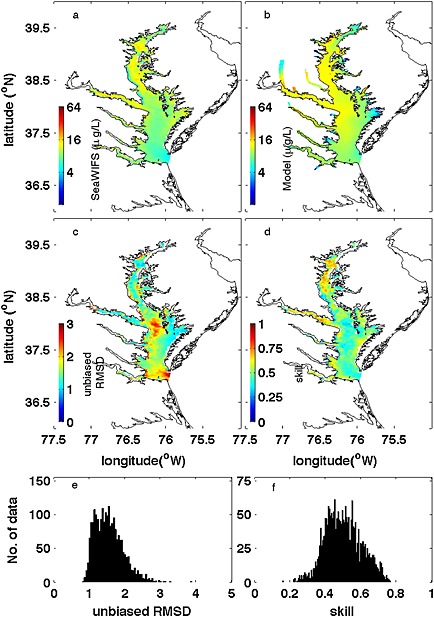
Comparison between 5 year (2001–2005) averaged sea surface chlorophyll from (a) SeaWiFS and (b) model simulation. Skill assessment is illustrated by (c) unbiased RMSD, and (d) Willmott skill together with histograms of (e) unbiased RMSD and (f) Willmott skill.
3.4.6. Dissolved Oxygen
The model reproduces the observed oxygen distributions in the bay very well. In the upper and lower bay, both simulated and observed oxygen concentrations are consistently high throughout the water column, whereas in the middle bay, both simulated and observed oxygen concentrations show a strong vertical gradient (Figures 8k and 8l). The model also successfully reproduces the observed vertically integrated dissolved oxygen seasonal cycle (Figures 9f, 9l, and 9r), which closely follows the seasonal cycle of temperature, largely due to the solubility effect of oxygen. Quantitatively, both spatial and temporal model skill are high for dissolved oxygen, with correlations between the simulated and observed fields reaching 0.98 in terms of both space and time (Figure 5) and overall spatial and temporal model skill both as high as 0.97.
4. Results and Discussion
A nitrogen budget for the Chesapeake Bay covering the time period 2001–2005 was computed from the simulated fields described above and is presented below. Because the model reproduced the annual mean nitrogen distributions (Figure 8) better than the seasonal variability of the nitrogen distributions (Figure 9), the focus of the nitrogen budget analysis described here is on the mean of the annual fluxes (Figure 11) and the interannual variability of these annual mean nitrogen fluxes (Figure 12). An analysis of the seasonal variability of these fluxes will be presented in a future paper, after the seasonal variability of simulated organic matter distributions is improved (see section 5).
Figure 11.
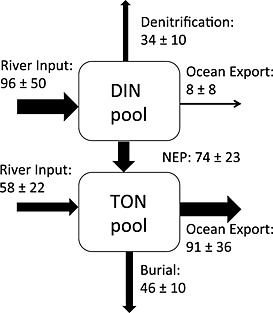
The nitrogen budget for 2001–2005 in the Chesapeake Bay from our modeling system (unit: 1 × 109 g N yr−1). The exchange of DIN/PON between the internal bay and exterior ocean was estimated using velocity and DIN/PON concentration at each time step at a cross section of the bay mouth (red line in Figure 1a). Net ecosystem production (NEP) was estimated as primary production minus phytoplankton and zooplankton respiration and TON remineralization. Error bars represent the standard deviations computed for the mean of the five annual values.
Figure 12.
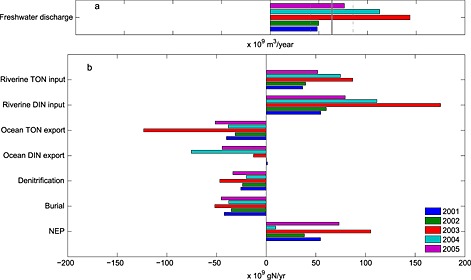
(a) Freshwater discharge for the 2001–2005 period. The long‐term (1980–2008) mean ± standard deviation of discharge computed from DLEM are included as the gray solid and dashed lines. (b) Interannual variability of nitrogen fluxes computed for the 2001–2005 analysis period.
4.1. Mean Nitrogen Fluxes
The mean nitrogen budget for the Chesapeake Bay (Figure 11) included a total riverine nitrogen (inorganic + organic) entering the Chesapeake Bay as computed from DLEM of 154 × 109 g N yr−1, with roughly 60% [Yang et al., 2015b] being present in the inorganic form (NO3 + NH4). Burial removed about 30% of the riverine nitrogen entering the bay (46 ± 10 × 109 g N yr−1), with less than half of this occurring in the main stem (Table 2). Water column and sediment denitrification removed roughly 20% of the riverine nitrogen entering the bay (34 ± 10 × 109 g N yr−1; Figure 11), with more than half of this occurring in the main stem. These percentages agree well with the results of Nixon et al. [1996], who estimated that burial and denitrification removed 40% and 25% of the total nitrogen entering the Chesapeake Bay.
Table 2.
Comparison of Chesapeake Bay Nitrogen Fluxes (109 g N yr−1)
| Historical Estimates (1975–1990) | DLEM‐ROMS‐ECB Modela (2001–2005) | ||
|---|---|---|---|
| Total nitrogen input from river | 134b | ||
| DIN | 84 ± 26c | 96 ± 50 | |
| TON | 38 ± 7c | 58 ± 22 | |
| Burial | stem + tributaries | 53b | 46 ± 10 |
| stem | 21d | 22 ± 4 | |
| Denitrificatione | stem + tributaries | 40b | 34 ± 10 |
| stem | 23d | 22 ± 9 | |
| Net ecosystem productionf | 54d | 74 ± 23 | |
| Total nitrogen export to ocean | |||
| DIN | 3d | 8 ± 8 | |
| TON | 78d | 91 ± 36 | |
The largest term representing loss of total nitrogen was advective export to the coastal ocean. Ocean export of inorganic nitrogen was small, whereas the export of organic nitrogen was the largest of the nitrogen loss terms (91 ± 36 × 109 g N yr−1). This value is likely an overestimate of the actual flux of organic nitrogen out of the bay, since simulated organic nitrogen concentrations near the bay mouth were overestimated (Figures 8e and 8g). However, since estuarine circulation is characterized by outflow at the surface and inflow at depth, the flux of organic nitrogen from the estuary to the ocean is primarily a function of the vertical gradient of organic nitrogen concentration (i.e., the difference between the surface and bottom concentrations, which the model simulates quite well), rather than the mean concentration. An error estimate associated with the export of organic nitrogen due to the model overestimating mean organic nitrogen at the bay mouth by 10 mmol N m−3 (or equivalently 0.14 × 109 g N km−3) is computed as follows: 0.14 × 109 g N km−3 × 100 km3 yr−1 = 14 × 109 g N yr−1, or roughly 15% of the total export of organic nitrogen to the ocean.
Together, the large amount of inorganic nitrogen entering the bay from the rivers coupled with the large amount of organic nitrogen exiting the bay through the bay mouth is indicative of a system characterized by a positive net ecosystem production (NEP = 74 ± 23 × 109 g N yr−1). This is consistent with other studies, which have similarly reported that the Chesapeake Bay acts as a net autotrophic estuary with production of organic nitrogen exceeding the loss of organic nitrogen due to remineralization processes [Fisher et al., 1988; Kemp et al., 1997, 2005].
Our simulated nitrogen budget for 2001–2005 is surprisingly comparable to earlier budgets derived from observations for both the whole bay [Boynton et al., 1995] and the main stem [Kemp et al., 1997], especially when considering that these estimates were based on different time periods. These previous observational estimates were based on data collected sporadically between 1975 and 1990 and thus represent a climatological estimate of the fluxes from this time period. In contrast, the model was implemented specifically for the years 2001–2005. Although year‐to‐year variability was very large during both of these time periods, estimates of freshwater discharge from DLEM and the CBP Watershed Model (Table 3) both indicate that the earlier time period had lower freshwater discharge [Yang et al., 2015a]. The DLEM estimates of riverine dissolved inorganic nitrogen (DIN) input for the earlier time period (84 × 109 g N yr−1) was also substantially smaller than that computed for the later time period (96 × 109 g N yr−1) [see also Yang et al., 2015b]. This is primarily a result of the anomalously high riverine discharge in 2003 caused by Hurricane Isabelle: the mean riverine DIN input computed without 2003 (including only 2001, 2002, 2004, and 2005) was only 77 × 109 g N yr−1, i.e., less than the DIN input computed for the earlier time period. Despite the differences in total riverine discharge between the earlier (1975–1990) and later (2001–2005) time periods, the percent DIN of total nitrogen entering the bay remained at roughly 60% [Boynton et al., 2008; Yang et al., 2015b].
Table 3.
Comparison of Freshwater Discharge (km3 yr−1), DIN Flux (109 g N yr−1) and TON Flux (109 g N yr−1) to Chesapeake Bay
| DLEM [Yang et al., 2015a] | CBP WMa [Shenk and Linker, 2013] | |
|---|---|---|
| Freshwater Discharge | ||
| 2001 | 48 | 55 |
| 2002 | 50 | 57 |
| 2003 | 144 | 138 |
| 2004 | 112 | 106 |
| 2005 | 76 | 81 |
| Mean 2001–2005 | 86 ± 41 | 87 ± 35 |
| Mean 1985–2005 | 63 ± 22 | 75 |
| DIN Flux | ||
| 2001 | 55 | 65 |
| 2002 | 61 | 73 |
| 2003 | 176 | 120 |
| 2004 | 112 | 88 |
| 2005 | 80 | 84 |
| Mean 2001–2005 | 96 ± 49 | 86 ± 21 |
| TON Flux | ||
| 2001 | 37 | 32 |
| 2002 | 40 | 33 |
| 2003 | 87 | 84 |
| 2004 | 75 | 67 |
| 2005 | 52 | 49 |
| Mean 2001–2005 | 58 ± 22 | 53 ± 21 |
G. Shenk and K. Hinson (personal communication, 2015).
Despite the different riverine inputs during these distinct analysis time periods, the observational‐based estimates of estuarine nitrogen fluxes still fall within the standard deviation of our simulation‐based estimates, demonstrating the robustness of the nitrogen budget derived from our modeling system. Simulated burial and denitrification rate estimates were very similar to the data‐derived estimates, with the latter falling within the standard deviation of the simulated estimates (Table 2) for both the main stem [Kemp et al., 1997] and the bay as a whole [Boynton et al., 1995]. The advective ocean export fluxes calculated using the two different methods (simulated versus climatologically data derived) were also surprisingly comparable, again especially when considering the significant interannual variability (standard deviations) in the simulated fluxes (Table 2). The net ecosystem production derived from our ROMS‐ECB simulation was calculated to be 5%–9% of total annual primary production, in excellent agreement with the 8% reported by Kemp et al. [1997]. Finally, although atmospheric nitrogen deposition and fisheries harvest have not been included in our analysis, these are estimated to represent relatively small source/sink terms, respectively [Boynton et al., 1995].
4.2. Interannual Variability of Annual Mean Nitrogen Fluxes
The simulated nitrogen fluxes in the bay vary considerably on interannual time scales, as quantified by the high standard deviations associated with the individual annual mean fluxes discussed above (Figure 11). Although some interannual variability exists in the wind, precipitation, and radiative forcing, the primary source of this variability is river discharge. For the 5 years analyzed, the DLEM freshwater river discharge varied by more than a factor of 2, from a mean of roughly 50 km3 yr−1 over the two lowest flow years (2001–2002) to a mean of nearly 128 km3 yr−1 over the two highest flow years (2003–2004; Figure 12a). This strong interannual variability in freshwater discharge estimated by DLEM [Yang et al., 2015a] closely matches (Table 3) that estimated by the regulatory EPA Chesapeake Bay Watershed Model (CBP WM), which has been well tuned to observations from USGS gauging stations [Shenk and Linker, 2013]: 2001–2002 = 56 km3 yr−1 and 2003–2004 = 122 km3 yr−1 (G. Shenk and K. Hinson, personal communication, 2015).
The strong interannual variability in freshwater discharge entering the bay leads to a similarly strong interannual variability in dissolved inorganic nitrogen (DIN) and total organic nitrogen (TON) inputs into the bay (Figures 12b and 13). Specifically, riverine inputs of TON for the high‐flow years of 2003–2004 (DLEM: 81 × 109 kg yr−1 and CBP WM: 75 × 109 kg yr−1) are more than twice those of 2001–2002 (DLEM: 38 × 109 kg yr−1 and CBP WM: 32 × 109 kg yr−1), with once again a similar magnitude for both the DLEM and the CBP WM estimates (Table 3). Both the DLEM and the CBP WM also indicate that the interannual variability of riverine DIN inputs is strong as well, though this interannual variability estimated by DLEM is somewhat stronger than that of the CBP WM (Table 3). Between 2001–2002 and 2003–2004, DLEM estimates a factor of ~2.5 increase in riverine DIN input (Figures 12b and 13).
Figure 13.
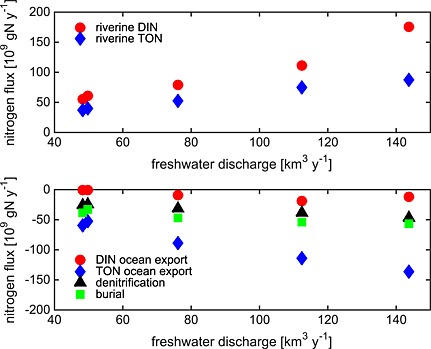
Nitrogen fluxes from Figure 12 plotted as a function of freshwater discharge.
The impact of interannually varying riverine freshwater discharge and associated nitrogen inputs on nitrogen fluxes within the bay is strong. Although the magnitude of NEP, denitrification, and burial were higher in high‐flow years and lower in low‐flow years, the magnitude of this interannual variability does not vary linearly with freshwater discharge (Figure 13). For example, DLEM estimated that the freshwater discharge increased 160% from the two lowest to the two highest flow years and was associated with a similarly large (150%) increase in riverine input of DIN; however, the resulting variability in the estuarine biogeochemical fluxes was considerably smaller. Burial, and denitrification increased by only about 50% (19 × 109 g N yr−1) and 70% (18 × 109 g N yr−1), respectively, between these pairs of years.
Interannually varying riverine inputs also impact the advective export of DIN and TON to the coastal ocean. The increase in TON export for the high‐flow versus low‐flow years was even greater in magnitude (69 × 109 g N yr−1) than the increase in TON riverine input (43 × 109 g N yr−1). This result, i.e., the fact that the export of TON increased more than the input of TON, can be explained by examining the inorganic nitrogen fluxes (Figure 13). Specifically, the increase in DIN export for the high‐flow versus low‐flow years was considerably smaller in magnitude (14 × 109 g N yr−1) than the increase in DIN riverine input (86 × 109 g N yr−1). The remaining excess DIN entering the estuary that was not exported to the coastal ocean was either denitrified or transformed into organic nitrogen prior to export to the continental shelf. In summary, roughly two thirds of the excess nitrogen entering the bay during the high‐flow years is exported to the continental shelf (mostly in the organic form), while the remaining third is either denitrified or buried.
4.3. Comparison of Simulated Fluxes With Those From a Continental Shelf Biogeochemical Model
The Chesapeake Bay nitrogen fluxes computed using the ROMS‐ECB estuarine model are significantly different (Table 4) from those computed using a regional biogeochemical shelf model configured for the mid‐Atlantic Bight [Druon et al., 2010; Hofmann et al., 2011; Xiao and Friedrichs, 2014a, 2014b]. The version of the regional shelf model used here for comparison (Table 4) did not include the estuarine‐specific processes developed for ROMS‐ECB (section 2.2) such as light attenuation due to inorganic suspended solids, estuarine‐specific phytoplankton growth rates, water column denitrification, and oxygen limitation of remineralization. Although the riverine fluxes to the Chesapeake Bay are generally comparable for the two models during the years examined, the burial and denitrification fluxes computed from the estuarine model removed nearly an order of magnitude more nitrogen from the bay than did the coastal model (Table 4). In addition, although the total ocean export of nitrogen was similar for the two models, the estuarine model exported almost entirely TON and very little DIN. In contrast, the regional shelf model exported nearly equal amounts of TON and DIN. The critical nitrogen transformations that occur within the estuary [Nixon et al., 1996] were not successfully represented in the regional model, and thus, this model overestimated the transport of riverine DIN to the coastal ocean.
Table 4.
Comparison of Chesapeake Bay Nitrogen Fluxes and Standard Deviations (109 g N yr−1) Obtained Using Estuarine Biogeochemical Model (ROMS‐ECB; This Study) and Regional Shelf Biogeochemical Model [Hofmann et al., 2011]
| ROMS‐ECB (2001–2005) | USECoS (2004–2008) | |
|---|---|---|
| River input DIN | 96 ± 50 | 82 ± 16 |
| River input TON | 58 ± 22 | 75 ± 16 |
| Burial | 46 ± 10 | 5 ± 1 |
| Denitrification3 | 34 ± 10 | 6 ± 1 |
| DIN export to ocean | 8 ± 8 | 49 ± 10 |
| TON export to ocean | 91 ± 36 | 56 ± 11 |
The above results demonstrate the importance of resolving estuarine‐specific processes in larger‐scale regional models that include estuarine domains. This is specifically critical for regions receiving considerable amounts of inorganic nutrients and organic matter from estuaries, such as the Mid‐Atlantic Bight [Nixon, 1987] and the Louisiana Shelf [Feng et al., 2012, 2014]. In these regions it will likely be necessary and will certainly be most efficient to have relatively high‐resolution models specifically developed for estuaries nested inside potentially coarser resolution regional shelf models. Fortunately, many of the critical estuarine biogeochemical formulations in ROMS‐ECB are active only in regions of low dissolved oxygen concentrations and high inorganic suspended solids. Since these conditions are not generally present in the mid‐Atlantic Bight shelf adjacent to the Chesapeake Bay, the ECB model is likely to successfully reproduce biogeochemical processes on the outer shelf as well as in the Chesapeake Bay. Research devoted to testing this hypothesis is currently underway.
5. Summary and Future Work
In this study the interannual variability associated with physical and biogeochemical nitrogen fluxes in the Chesapeake Bay has been quantified by means of an estuarine biogeochemistry model (ECB) coupled to a three‐dimensional hydrodynamic model (ROMS) and forced by a terrestrial ecosystem model (DLEM). The estuarine model was based on previous mid‐Atlantic Bight models [Druon et al., 2010; Hofmann et al., 2008, 2011] but was modified to include key estuarine processes including light attenuation due to inorganic suspended solids, estuarine‐specific phytoplankton growth rates, water column denitrification, and oxygen limitation of remineralization. The ROMS‐ECB‐DLEM implementation described here shows significant skill in reproducing the variability of both physical and biogeochemical fields of the bay when evaluating with in situ and satellite‐derived data for a contemporary period (2001–2005). In addition, the nitrogen fluxes computed with this modeling system closely match mean fluxes derived from historical Chesapeake Bay observations, which is particularly surprising given the strong interannual variability associated with these fluxes. Although a number of 3‐D coupled estuarine models have been previously implemented in the Chesapeake Bay [Cerco, 2000; Li et al., 2009; Testa et al., 2014; Xu and Hood, 2006; Scully, 2010, 2013; Luettich et al., 2013], these previous efforts have been limited to examining one or two specific aspects of estuarine biogeochemistry associated with nitrogen cycling, such as phytoplankton biomass, dissolved inorganic nutrients, or dissolved oxygen concentrations. To our knowledge, this is the first time both physical and biogeochemical components of the complete Chesapeake Bay nitrogen cycle have been investigated in detail using a coupled hydrodynamic‐biogeochemical model.
The continuous 5 year period selected for our analysis incorporated very different hydrological conditions: dry (2001 and 2002), wet (2003 and 2004), and intermediate (2005). The mean freshwater flow as well as the DIN and TON riverine fluxes were more than twice as high in these two wet years as compared to these two dry years. Approximately one third of the excess nitrogen entering the bay during the high‐flow years was denitrified and buried. The remaining two thirds of this excess nitrogen was exported to the continental shelf, with most of this being in the organic form. Thus, the increased DIN input to the bay during the high‐flow years was not exported directly as DIN to the coastal ocean but rather was primarily converted to TON through photosynthesis before being advected out of the bay.
Three‐dimensional (3‐D) coupled hydrodynamic‐biogeochemical models have been widely used in recent years for the study of marine biogeochemical cycling within ocean margins and provide a useful tool for examining the transformation of nutrients in coastal regions [Banas et al., 2009; Druon et al., 2010; Feng et al., 2014; Fennel et al., 2006, 2011; Friedland et al., 2012; Wakelin et al., 2012; Xue et al., 2013]. However, estuaries, which play an important role in global nutrient cycling, are often poorly represented in these types of models. Regional‐ and basin‐scale models typically either export riverine nutrients to coastal waters directly omitting the estuaries altogether or include estuarine regions but apply biogeochemical models derived for continental shelves to the estuarine domains [e.g., Fennel et al. [2006]; Druon et al. [2010]; Hofmann et al. [2008, 2011]]. Here nitrogen exported from the Chesapeake Bay computed from the estuarine‐specific ECB model was compared with a model developed for the U.S. eastern continental shelf. The significant resulting differences in DIN export (49 ± 10 × 109 g N yr−1 for the coastal model versus 8 ± 8 × 109 g N yr−1 for the estuarine model) highlight the importance of carefully resolving estuarine physical and biogeochemical processes in regional‐ and basin‐scale models.
Although the ROMS‐ECB‐DLEM simulations documented here closely replicated nitrogen fluxes derived from observations in the Chesapeake Bay, future efforts will be devoted to further improving the seasonal variability of organic matter in the bay. These future improvements are listed below, in the order from highest to lowest priority. First, a reassessment of ISS dynamics is required, as an overestimation of ISS in the upper bay is likely causing overly strong light attenuation, resulting in an underestimation of the spring bloom in the northern bay. Second, the incorporation of phosphate limitation, which is known to play an important role in limiting phytoplankton growth in the upper bay in the spring [Fisher et al., 1992], will improve our simulations of phytoplankton growth. Third, the ECB model currently includes only one type of phytoplankton and zooplankton, whereas in reality multiple distinct phytoplankton species are present in the bay [Marshall and Nesius, 1996]. Efforts are currently underway to expand the model to include two phytoplankton and two zooplankton components [Xiao and Friedrichs, 2014a, 2014b], which will also likely improve the model's ability to reproduce the correct seasonal variability of organic matter in the bay. Finally, future efforts will be directed toward refining our representation of pelagic‐benthic coupling processes by including a separate sediment digenetic model [e.g., Soetaert et al., 2000]. This will allow temporary storage of organic matter in the bay sediments, which will likely improve our simulations of chlorophyll and PON fields below 10 m depth.
Although ROMS‐ECB includes a full carbon cycle (not described here), the simulated carbon distributions have not been fully evaluated with available data within the bay. ROMS‐ECB currently uses a relationship derived from historical USGS Chesapeake river gauge data for the ratio of dissolved inorganic carbon (DIC) to alkalinity, and applies this to DIC riverine concentrations derived from a terrestrial ecosystem model; in the future, however, alkalinity will be available from the DLEM simulations directly. In addition, initial and open ocean boundary conditions for alkalinity and DIC are currently derived from regressions against temperature and salinity that have been developed for the North Atlantic. In the future initial conditions will be obtained from measurements of alkalinity and pH (from which DIC can be computed) from the EPA CBP Water Quality Monitoring Program, and alkalinity and DIC from recent cruises on the continental shelf [Wang et al., 2013] will be used to better represent outer boundary conditions. The resulting carbon budget in the bay will be compared to recent data‐derived estimates [Herrmann et al., 2015].
A significant difference between previous Chesapeake Bay model implementations and the modeling effort described here, is that our river forcing is provided by a process‐based terrestrial ecosystem model. An advantage of linking our estuarine biogeochemistry model directly to such a terrestrial ecosystem model is that the impacts on estuarine nutrient cycling processes of past and future changes in climate, land use, and land cover can be examined. Such past and future scenario simulations are currently being conducted and will be described in follow‐up studies. As a result, our linked modeling system will likely not only benefit future estuarine scientific studies but also support management applications and future high‐stakes decision‐making.
Supporting information
Supporting Information S1
Acknowledgments
This work was supported by the NASA Interdisciplinary Science Program (NNX11AD47G). The authors are grateful to the NASA U.S. Eastern Continental Shelf Carbon Cycling (USECoS) team for their useful comments. We thank Jeremy Werdell of NASA Goddard for providing the high‐resolution SeaWIFS chlorophyll level 3 data, and Kyle Hinson and Gary Shenk for providing us with phase 5.3.2 output from the Chesapeake Bay Program Watershed Model (http://www.chesapeakebay.net/). We particularly wish to thank Walter Boyton and two anonymous reviewers for their helpful suggestions to improve this manuscript. This is VIMS contribution 3483.
Appendix A. ECB Model Equations
A mathematical description of the biogeochemical source/sink terms for the ECB state variables that specifically pertain to the nitrogen cycle are summarized here in Tables A1 and A2. Model function symbols are defined in Appendix Table A3, and parameter definitions and values are provided in the Appendix Table A4. A complete set of equations for the nitrogen cycle is also provided in electronic form in the supporting information.
Table A1.
State Variable Equations Including All Biogeochemical Source and Sink Terms
| Variable (Symbol) | Processes | Time Rate of Change in Each Term |
|---|---|---|
| Phytoplankton (P) | Change per unit time = | ∂P/∂t = |
| + Primary production (← [NH4] + [NO3]) |
|
|
| − Exudation (→ [DON]SL) |
|
|
| − Exudation (→ [NH4]) |
|
|
| − Grazing assimilation (→ Z) | − βgZ | |
| − Fecal pellets from grazing on P (→ DL) | − (1 − β)(1 − λ)gZ | |
| − Sloppy feeding (→ [DON]SL) | − (1 − β)λεgZ | |
| − Sloppy feeding (→ [NH4]) | − (1 − β)λ(1 − ε)gZ | |
| − Mortality (→ DS) | − m P P | |
| − Aggregation (→ DL) | − τ(D S + P)P | |
| − Sinking (→ sediment) | − w P∂P/∂z | |
| Chlorophyll ([Chl]) | Change per unit time = | ∂[Chl]/∂t = |
| + Primary production ([NH4] + [NO3] → P) |
|
|
| − Exudation (P → [DON]SL) |
|
|
| − Exudation (P → [NH4]) |
|
|
| − Grazing (P → Z + DL + [DON]SL + [NH4]) | − gZ/P[Chl] | |
| − Mortality (P → DS) | − m P[Chl] | |
| − Aggregation (P → DL) | − τ(D S + P)[Chl] | |
| − Sinking (P → Sediment) | − ω P∂[Chl]/∂z | |
| Zooplankton (Z) | Change per unit time = | ∂Z/∂t = |
| + Grazing assimilation (← P) | + βgZ | |
| − Excretion (→ [NH4]) |
|
|
| − Mortality ((→ DL) | − m Z Z 2 | |
| Small Detritus (DS) | Change per unit time = | ∂D S/∂t = |
| + Mortality (← P) | + m P P | |
| − Aggregation (→ DL) | − τ(D S + P)D S | |
| − Solubilization (→ [DON]SL) |
|
|
| − Remineralization (→ [NH4]) |
|
|
| − Sinking (→ sediment) | − w S∂D S/∂z | |
| Large Detritus (DL) | Change per unit time = | ∂D L/∂t = |
| + Fecal pellets production (→ DL) | + (1 − β)(1 − λ)gZ | |
| + Mortality (← Z) | + m z Z 2 | |
| + Aggregation (← DS + P) | + τ(D S + P)2 | |
| − Solubilization (→ [DON]SL) |
|
|
| − Remineralization (→ [NH4]) |
|
|
| − Sinking (→ sediment) | − w L∂D L/∂z | |
| Semilabile Dissolved Organic Nitrogen [DON]SL | Change per unit time = | ∂[DON]SL/∂t = |
| + Exudation (← P) |
|
|
| + Sloppy feeding (← P) | + (1 − β)λεgZ | |
| + Solubilization (← DS + DL) |
|
|
| − Remineralization (→ [NH4]) |
|
|
| Ammonium [NH4] | Change per unit time = | ∂[NH4]/∂t = |
| ‐ Uptake (→ P) |
|
|
| ‐ Nitrification (→ [NO3]) | − nf NTR[NH4] | |
| + Exudation (← P) |
|
|
| + Sloppy feeding (← P) | + (1 − β)λ(1 − ε)gZ | |
| + Excretion (← Z) |
|
|
| + Remineralization (← DS + DL) |
|
|
| + Remineralization (← [DON]SL) |
|
|
| Nitrate [NO3] | Change per unit time = | ∂[NO3]/∂t = |
| − Uptake (→ P) |
|
|
| − Water column denitrification (→ N2) |
|
|
| + Nitrification (← [NH4]) | + nf NTR[NH4] | |
| Oxygen [O2] | Change per unit time = | ∂[O2]/∂t = |
| + Air‐sea flux |
|
|
| + Primary production ([NH4] + [NO3] → P) |
|
|
| + excess‐based production ([CO2]→ P) |
|
|
| − Nitrification ([NH4] → NO3]) | − 2f NTR n[NH4] | |
| − Exudation (P → [NH4]) |
|
|
| − Excretion (Z → [NH4]) |
|
|
| − Sloppy feeding (Z → [NH4]) |
|
|
| − Remineralization (DS → NH4]) |
|
|
| − Remineralization (DL → [NH4]) |
|
|
| − Remineralization ([DON]SL → [NH4]) |
|
|
| Inorganic suspended solid [ISS] | Change per unit time | ∂[ISS]/∂t = |
| − Sinking (→ sediment) | − w ISS∂[ISS]/∂z |
Table A2.
Biogeochemical Source/Sink Terms at the Bottom (Sediment) Boundary
| Variable | Processes | Time Rate of Change in Each Term |
|---|---|---|
| Small Detritus (DS) | Change per unit time = | ∂D S/∂t|z = H = |
| + total organic matter (DL + DS + P → DS) |
|
|
| Semilabile Dissolved Organic Nitrogen [DON]SL | Change per unit time = | ∂[DON]SL/∂t|z = H = |
| + Remineralization of unresuspended and unburied through coupled nitrification and denitrification (DL + DS + P → [DON]SL) |
|
|
| Ammonium [NH4] | Change per unit time = | ∂[NH4]/∂t|z = H = |
| + Remineralization of unresuspended and unburied through coupled nitrification and denitrification ((DL + DS + P → [NH4]) |
|
|
| Oxygen [O2] | Change per unit time = | ∂[O 2]/∂t|z = H = |
| + Remineralization of unresuspended and unburied through coupled nitrification and denitrification |
|
|
| Inorganic suspended solid [ISS] | Change per unit time = | ∂[ISS]/∂t|z = H = |
| + Resuspended inorganic matter | ξ(Γ|z = H − Γc) |
Table A3.
Definitions of Functions Used in State Variable Equations
| Symbol | Description | Equation | Units | ||
|---|---|---|---|---|---|
| F TON | Flux of total organic matter reaching to the bottom |
|
mmol N m−2 d−1 | ||
| F BC | Flux of total organic carbon in the sediment |
|
g C m−2 yr−1 | ||
| I | Photosynthesis available radiation |
|
W m−2 | ||
| KD | Light attenuation | 1.4 + 0.063[TSS] − 0.057S | m−1 | ||
| If 1.4 + .063[TSS] – 0.057S < 0, then | |||||
| 0.04 + 0.02486[Chl] + 0.003786{0, 6.625 ([DON]SL + [DON]RF) − 70.819}max | |||||
|
|
Bottom oxygen limitation factor |
|
dimensionless | ||
| L I | Photosynthesis‐light (P‐I) relationship |
|
dimensionless | ||
|
|
Nitrate uptake limitation with ammonium inhibitor |
|
dimensionless | ||
|
|
Ammonium uptake limitation |
|
dimensionless | ||
| TSS | Total suspended solid |
|
g m−3 | ||
| f NTF | Oxygen limitation for nitrification |
|
dimensionless | ||
| f DNF | Oxygen limitation for denitrification |
|
dimensionless | ||
| f WC | Nitrate limitation for nitrification |
|
dimensionless | ||
| g | Zooplankton grazing rate |
|
day−1 | ||
| n | Nitrification rate |
|
day−1 | ||
|
|
Gas exchange coefficient |
|
m/s | ||
| is the Schmidt number [Wanninkhof, 1992] | |||||
| u 10 is the wind speed 10 m above the sea surface | |||||
| Γ | Bottom shear stress |
|
Pa | ||
| ρ [Chl] | Fraction of phytoplankton growth devoted to chlorophyll synthesis |
|
dimensionless | ||
| ϕ 1 | Resuspension fraction |
|
dimensionless | ||
| ϕ 2 | Burial efficiency |
|
dimensionless |
Table A4.
Definitions of Biogeochemical Parameters Used in State Variable Equationsa
| Symbol | Description | Value | Units | |
|---|---|---|---|---|
| I NTR | Threshold for light inhibition of nitrification | 0.0095 | W m−2 | |
|
|
Half saturation for bottom denitrification switch | 26.5 | mmol O m−3 | |
| K DNF | Half‐saturation constant for water column denitrification | 1 | mmol N m−3 | |
| KI | Light intensity at which the inhibition of nitrification is half saturated | 0.1 | W m−2 | |
|
|
Half‐saturation constant for ammonium uptake | 0.5 | mmol N m−3 | |
|
|
Half‐saturation constant for nitrate update | 0.5 | mmol N m−3 | |
| K NTR | Half‐saturation constant for water column nitrification | 1 | mmol N m−3 | |
| KP | Half‐saturation concentration of phytoplankton ingestion | 2 | (mmol N m−3)2 | |
| K WNO3 | Half saturation for water column NO3 uptake shut down | 3 | mmol N m−3 | |
| PARfrac | fraction of light that is available for photosynthesis | 0.43 | dimensionless | |
| g max | Zooplankton maximum growth rate | 0.3 | day−1 | |
| l BM | Zooplankton basal metabolism | 0.1 | day−1 | |
| lE | Zooplankton specific excretion rate | 0.1 | day−1 | |
| mP | Phytoplankton mortality | 0.15 | day−1 | |
| mz | Zooplankton mortality | 0.025 | day−1 | |
| n max | Maximum rate of nitrification | 0.05 | day−1 | |
|
|
Remineralization of semilabile dissolved organic nitrogen | 0.00765 | day−1 | |
|
|
Remineralization of large detritus | 0.2 | day−1 | |
|
|
Remineralization of small detritus | 0.2 | day−1 | |
| w ISS | Inorganic suspended solid sinking velocity | 2.0 | m d−1 | |
| w L | Large detritus sinking velocity | 5 | m d−1 | |
| w P | Phytoplankton sinking velocity | 0.1 | m d−1 | |
| w S | Small detritus sinking velocity | 0.1 | m d−1 | |
| Γc | Critical stress | 0.05 | Pa | |
| α | Initial slope of the P‐I curve | 0.065 | W−1 m2 d−1 | |
| β | Zooplankton nitrogen assimilation efficiency | 0.75 | dimensionless | |
| γ | Phytoplankton exudation rate of semilabile DON | 0.04 | dimensionless | |
| γc | Parameter of carbon excess‐based DOC exudation | 0.2 | dimensionless | |
|
|
Fraction of bottom semilabile DON produced through coupled nitrification and denitrification | 0.01 | dimensionless | |
| δ N | Fraction of detritus solubilization to DON | 15% | dimensionless | |
| ε | Fraction of semilabile DON to total DON within the phytoplankton cell | 0.15 | dimensionless | |
| η C : N | Phytoplankton carbon:nitrogen ratio | 106/16 | mol C/mol N | |
|
|
Bottom small and large detritus carbon:nitrogen ratio | 9.3 | mol C/mol N | |
| η DNF | Stoichiometry for remineralization via denitrification | 84.8/16 | dimensionless | |
| η NF/DNF | Stoichiometry for remineralization via coupled nitrification and denitrification | 4/16 | dimensionless | |
|
|
Stoichiometry for O2 produced when consuming 1 more of nitrate | 138/16 | (mmol O m−3)(mmol N m−3)−1 | |
|
|
Stoichiometry for O2 produced when consuming 1 more of ammonium | 106/16 | (mmol O m−3)(mmol N m−3)−1 | |
|
|
Stoichiometry for O2 used when consuming 1 more of ammonium in coupled nitrification/denitrification process | 115/16 | (mmol O m−3)(mmol N m−3)−1 | |
| θ max | Maximum chlorophyll to phytoplankton ratio | 0.02675 | (mg Chl)(mg C)−1 | |
|
|
Temperature dependency remineralization of semilabile DON | 0.07 | (°C)−1 | |
| λ | Fraction of DON to TON [DON + PON] within the phytoplankton cell | 0.71 | dimensionless | |
| μ 0 | Phytoplankton growth rate | 2.15 | day−1 | |
| ξ | Erosion rate of ISS | 4320 | g m−2 d−1 Pa−1 | |
| τ | Aggregation parameter | 0.005 | day−1 | |
| ω | Phytoplankton exudation rate of labile DON | 0.03 | dimensionless |
DOC = dissolved organic carbon.
Feng, Y. , Friedrichs M. A. M., Wilkin J., Tian H., Yang Q., Hofmann E. E., Wiggert J. D., and Hood R. R. (2015), Chesapeake Bay nitrogen fluxes derived from a land‐estuarine ocean biogeochemical modeling system: Model description, evaluation, and nitrogen budgets, J. Geophys. Res. Biogeosci., 120, 1666–1695, doi:10.1002/2015JG002931.
References
- Banas, N. S. , Lessard E. J., Kudela R. M., MacCready P., Peterson T. D., Hickey B. M., and Frame E. (2009), Planktonic growth and grazing in the Columbia River plume region: A biophysical model study, J. Geophys. Res., 114, C00B06, doi:10.1029/2008JC004993. [Google Scholar]
- Bauer, J. E. , Cai W.‐J., Raymond P. A., Bianchi T. S., Hopkinson C. S., and Regnier P. A. G. (2013), The changing carbon cycle of the coastal ocean, Nature, 504, 61–70, doi:10.1038/nature12857. [DOI] [PubMed] [Google Scholar]
- Bever, A. J. , Friedrichs M. A. M., Friedrichs C. T., Scully M. E., and Lanerolle L. W. J. (2013), Combining observations and numerical model results to improve estimates of hypoxic volume within the Chesapeake Bay, USA, J. Geophys. Res. Oceans, 118, 4924–4944, doi:10.1002/jgrc.20331. [Google Scholar]
- Bianchi, T. S. , and Bauer J. E. (2011), Particulate organic carbon cycling and transformation, in Treatise on Estuarine and Coastal Science, edited by Wolanski E. and McLusky D. S., pp. 69–117, Academic Press, Waltham. [Google Scholar]
- Boynton, W. R. , Garber J. H., Summers R., and Kemp W. M. (1995), Inputs, transformations, and transport of nitrogen and phosphorus in Chesapeake Bay and selected tributaries, Estuaries, 18, 285–314, doi:10.2307/1352640. [Google Scholar]
- Boynton, W. R. , Hagy J. D., Cornwell J. C., Kemp W. M., Greene S. M., Owens M. S., Baker J. E., and Larsen R. K. (2008), Nutrient budgets and management actions in the Patuxent River Estuary, Maryland, Estuaries Coasts, 31, 623–651, doi:10.1007/s12237-008-9052-9. [Google Scholar]
- Bronk, D. A. , Gilbert P. M., Malone T. C., Banahan S., and Sahlsten E. (1998), Inorganic and organic nitrogen cycling in Chesapeake Bay: Autotrophic versus heterotrophic processes and relationships to carbon flux, Aquat. Microb. Ecol., 15, 177–189. [Google Scholar]
- Brown, C. W. , Hood R. R., Long W., Jacobs J., Ramers D. L., Wazniak C., Wiggert J. D., Wood R., and Xu J. (2013), Ecological forecasting in Chesapeake Bay: Using a mechanistic–empirical modeling approach, J. Mar. Syst., 125, 113–125, doi:10.1016/j.jmarsys.2012.12.007. [Google Scholar]
- Canuel, E. A. , Cammer S. S., McIntosh H. A., and Christina R. P. (2012), Climate change impacts on the organic carbon cycle at the land‐ocean interface, Annu. Rev. Earth Planet. Sci., 40, 685–711, doi:10.1146/annurev-earth-042711-105511. [Google Scholar]
- Cerco, C. F. (2000), Phytoplankton kinetics in the Chesapeake Bay eutrophication model, Water Qual. Ecosyst. Model., 1, 5–49. [Google Scholar]
- Chapman, D. C. (1985), Numerical treatment of cross‐shelf open boundaries in a barotropic coastal ocean model, J. Phys. Oceanogr., 15, 1060–1075, doi:10.1175/1520-0485(1985)015<1060:ntocso>2.0.co;2. [Google Scholar]
- Codispoti, L. A. , Brandes J. A., Christensen J. P., Devol A. H., Naqvi S. W. A., Paerl H. W., and Yoshinari T. (2001), The oceanic fixed nitrogen and nitrous oxide budgets: Moving targets as we enter the anthropocene?, Sci. Mar., 65, 85–105, doi:10.3989/scimar.2001.65s285. [Google Scholar]
- Druon, J. N. , Mannino A., Signorini S., McClain C., Friedrichs M., Wilkin J., and Fennel K. (2010), Modeling the dynamics and export of dissolved organic matter in the Northeastern U.S. continental shelf, Estuarine Coastal Shelf Sci., 88, 488–507, doi:10.1016/j.ecss.2010.05.010. [Google Scholar]
- Feng, Y. , DiMarco S. F., and Jackson G. A. (2012), Relative role of wind forcing and riverine nutrient input on the extent of hypoxia in the northern Gulf of Mexico, Geophys. Res. Lett., 39, L09601, doi:10.1029/2012GL051192. [Google Scholar]
- Feng, Y. , Fennel K., Jackson G. A., DiMarco S. F., and Hetland R. D. (2014), A model study of the response of hypoxia to upwelling‐favorable wind on the northern Gulf of Mexico shelf, J. Mar. Syst., 131, 63–73, doi:10.1016/j.jmarsys.2013.11.009. [Google Scholar]
- Fennel, K. , Wilkin J., Levin J., Moisan J., O'Reilly J., and Haidvogel D. (2006), Nitrogen cycling in the Mid Atlantic Bight and implications for the North Atlantic nitrogen budget: Results from a three‐dimensional model, Global Biogeochem. Cycles, 20, GB3007, doi:10.1029/2005GB002456. [Google Scholar]
- Fennel, K. , Hetland R., Feng Y., and DiMarco S. F. (2011), A coupled physical‐biological model of the northern Gulf of Mexico shelf: Model description, validation and analysis of phytoplankton variability, Biogeosciences, 8, 1881–1899, doi:10.5194/bg-8-1881-201. [Google Scholar]
- Fisher, T. R. , Harding L. W. Jr., Stanley D. W., and Ward L. G. (1988), Phytoplankton, nutrients, and turbidity in the Chesapeake, Delaware and Hudson Estuaries, Estuarine Coastal Shelf Sci., 27, 61–93, doi:10.1016/0272-7714(88)90032-7. [Google Scholar]
- Fisher, T. R. , Peele E. R., Ammerman J. W., and Harding L. W. Jr. (1992), Nutrient limitation of phytoplankton in Chesapeake Bay, Mar. Ecol. Prog. Ser., 82, 51–63, doi:10.3354/meps082051. [Google Scholar]
- Fisher, T. R. , Gustafson A. B., Sellner K., Lacouture R., Hass L. W., Wetzel R. L., Magnien R., Everitt D., Michaels B., and Karrh R. (1999), Spatial and temporal variation of resource limitation in Chesapeake Bay, Mar. Biol., 133, 763–778. [Google Scholar]
- Flather, R. A. (1976), A tidal model of the northwest European continental shelf, Mem. Soc. R. Sci. Liege, 10, 141–164. [Google Scholar]
- Flemer, D. A. , et al. (1983), Chesapeake Bay: A Profile of Environmental Change, U.S. Environmental Protection Agency, Chesapeake Bay Program, Annapolis, Md. [Google Scholar]
- Friedland, R. , Neumann T., and Schernewski G. (2012), Climate change and the Baltic Sea action plan: Model simulations on the future of the western Baltic Sea, J. Mar. Syst., 105–108, 175–186, doi:10.1016/j.jmarsys.2012.08.002. [Google Scholar]
- Friedrichs, M. A. M. , et al. (2009), Assessing the uncertainties of model estimates of primary productivity in the tropical Pacific Ocean, J. Mar. Syst., 76, doi:10.1016/j.jmarsys.2008.05.010. [Google Scholar]
- Glibert, P. M. , Garside C., Fuhrman J. A., and Roman M. R. (1991), Time‐dependent coupling of inorganic and organic nitrogen uptake and regeneration in the plume of the Chesapeake Bay estuary and its regulation by large heterotrophs, Limnol. Oceanogr., 36(5), 895–909. [Google Scholar]
- Hagy, J. D. , Boynton W. R., Keefe C. W., and Wood K. V. (2004), Hypoxia in Chesapeake Bay, 1950–2001: Long‐term change in relation to nutrient loading and river flow, Estuaries, 27(4), 634–658. [Google Scholar]
- Harding, L. W., Jr. (1994), Long‐term trends in the distribution of phytoplankton in Chesapeake Bay: Roles of light, nutrients, and streamflow, Mar. Ecol. Prog. Ser., 104, 267–291. [Google Scholar]
- Harding, L. W., Jr. , Mallonee M. E., and Perry E. S. (2002), Toward a predictive understanding of primary productivity in a temperate, partially stratified estuary, Estuarine Coastal Shelf Sci., 55, 437–463. [Google Scholar]
- Herrmann, M. , Najjar R. G., Kemp W. M., Alexander R. B., Boyer E. W., Cai W.‐J., Griffith P. C., Kroeger K. D., McCallister S. L., and Smith R. A. (2015), Net ecosystem production and organic carbon balance of U.S. East Coast estuaries: A synthesis approach, Global Biogeochem. Cycles, 29, 96–111, doi:10.1002/2013GB004736. [Google Scholar]
- Hofmann, E. E. , et al. (2008), Eastern U.S. continental shelf carbon budget: Integrating models, data assimilation, and analysis, Oceanography, 21(1), 86–104. [Google Scholar]
- Hofmann, E. E. , et al. (2011), Modeling the dynamics of continental shelf carbon, Annu. Rev. Mar. Sci., 3, 93–122, doi:10.1146/annurev-marine-120709-142740. [DOI] [PubMed] [Google Scholar]
- Hood, R. , et al. (2006), Functional group modeling: Progress, challenges and prospects, Deep Sea Res., Part II, 53, 459–512. [Google Scholar]
- Horrigan, S. G. , Montoya J. P., Nevins J. L., and McCarthy J. J. (1990), Natural isotopic composition of dissolved inorganic nitrogen in the Chesapeake Bay, Estuarine Coastal Shelf Sci., 30(4), 393–410, doi:10.1016/0272-7714(90)90005-C. [Google Scholar]
- Jolliff, J. K. , Kindle J. C., Shulman I., Penta B., Friedrichs M. A. M., Helber R., and Arnone R. A. (2009), Summary diagrams for coupled hydrodynamic‐ecosystem model skill assessment, J. Mar. Syst., 76, 64–82, doi:10.1016/J.Jmarsys.2008.05.014. [Google Scholar]
- Kantha, L. H. , and Clayson C. A. (1994), An improved mixed layer model for geophysical applications, J. Geophys. Res., 99, 25,235–25,266, doi:10.1029/94JC02257. [Google Scholar]
- Keller, D. P. , and Hood R. R. (2011), Modeling the seasonal autochthonous sources of dissolved organic carbon and nitrogen in the upper Chesapeake Bay, Ecol. Modell., 222, 1139–1162, doi:10.1016/j.ecolmodel.2010.12.014. [Google Scholar]
- Kemp, W. M. (2005), Eutrophication of Chesapeake Bay: Historical trends and ecological interactions, Mar. Ecol. Prog. Ser., 303, 1–29, doi:10.3354/meps303001. [Google Scholar]
- Kemp, W. M. , Smith E. M., Marvin‐DiPasquale M. M., and Boynton W. R. (1997), Organic carbon balance and net ecosystem metabolism in Chesapeake Bay, Mar. Ecol. Prog. Ser., 150, 229–248. [Google Scholar]
- King, G. M. (2005), Ecophysiology of microbial respiration, in Respiration in Aquatic Ecosystems, edited by Del Giorgio P. A. and Williams P. J. l. B., pp. 18–35, Oxford Univ. Press, New York. [Google Scholar]
- Li, M. , Zhong L., and Harding L. W. Jr. (2009), Sensitivity of plankton biomass and productivity to variations in physical forcing and biological parameters in Chesapeake Bay, J. Mar. Res., 67, 667–700, doi:10.1357/00222400979121887. [Google Scholar]
- Liu, M. , Tian H., Yang Q., Yang J., Song X., Lohrenz S. E., and Cai W.‐J. (2013), Long‐term trends in evapotranspiration and runoff over the drainage basins of the Gulf of Mexico during 1901–2008, Water Resour. Res., 49, 1988–2012, doi:10.1002/wrcr.20180. [Google Scholar]
- Lomas, M. W. , and Glibert P. M. (1999a), Interaction between NH4 and NO3 uptake and assimilation: Comparison of diatoms and dinoflagellates at several growth temperatures, Mar. Biol., 133, 541–551. [Google Scholar]
- Lomas, M. W. , and Glibert P. M. (1999b), Temperature regulation of nitrate uptake: A novel hypothesis about nitrate uptake and reduction in cool‐water diatoms, Limnol. Oceanogr., 44(3), 556–572. [Google Scholar]
- Luettich, R. A. , et al. (2013), The U.S. IOOS coastal and ocean modeling testbed, J. Geophys. Res. Oceans, 118, 6319–6328, doi:10.1002/2013JC008939. [Google Scholar]
- Malone, T. C. , Crocker L. H., Pike S. E., and Wendler B. W. (1988), Influences of river flow on the dynamics of phytoplankton production in a partially stratified estuary, Mar. Ecol. Prog. Ser., 48, 235–249. [Google Scholar]
- Marchesiello, P. , McWilliams J. C., and Shchepetkin A. F. (2001), Open boundary conditions for long‐term integration of regional oceanic models, Ocean Model., 3, 1–20, doi:10.1016/S1463-5003(00)00013-5. [Google Scholar]
- Marshall, H. G. , and Nesius K. K. (1996), Phytoplankton composition in relation to primary production in Chesapeake Bay, Mar. Biol., 125, 611–617, doi:10.1007/BF00353272. [Google Scholar]
- Marshall, H. G. , Burchardt L., and Lacouture R. (2005), A review of phytoplankton composition within Chesapeake Bay and its tidal estuaries, J. Plankton Res., 27(11), 1083–1102, doi:10.1093/plankt/fbi079. [Google Scholar]
- Nixon, S. W. (1987), Chesapeake Bay nutrient budgets: A reassessment, Biogeochemistry, 4, 77–90. [Google Scholar]
- Nixon, S. W. , et al. (1996), The fate of nitrogen and phosphorus at the land‐sea margin of the North Atlantic Ocean, Biogeochemistry, 35, 141–180. [Google Scholar]
- Oguz, T. (2002), Role of physical processes controlling oxycline and suboxic layer structures in the Black Sea, Global Biogeochem. Cycles, 16(2), 1019, doi:10.1029/2001GB001465. [Google Scholar]
- Raymond, P. A. , and Bauer J. E. (2001), Riverine export of aged terrestrial organic matter to the North Atlantic Ocean, Nature, 409, 497–500, doi:10.1038/35054034. [DOI] [PubMed] [Google Scholar]
- Resplandy, L. , et al. (2012), Controlling factors of the oxygen balance in the Arabian Sea's OMZ, Biogeosciences, 9, 5095–5109, doi:10.5194/bg-9-5095-2012. [Google Scholar]
- Richards, F. A. (1965), Anoxic basins and fjords, in A Treatise on Chemical Oceanography, edited by Riley J. P. and Shirrow G., pp. 611–645, Academic Press, London. [Google Scholar]
- Scully, M. E. (2010), Wind modulation of dissolved oxygen in Chesapeake Bay, Estuarine Coastal Shelf Sci., 33, 1164–1175, doi:10.1007/s12237-010-9319-9. [Google Scholar]
- Scully, M. E. (2013), Physical controls on hypoxia in Chesapeake Bay: A numerical modeling study, J. Geophys. Res. Oceans, 118, 1–18, doi:10.1002/jgrc.20138. [Google Scholar]
- Shchepetkin, A. F. , and McWilliams J. C. (2005), The regional oceanic modeling system (ROMS): A split‐explicit, free‐surface, topography‐following‐coordinate oceanic model, Ocean Model., 9, 347–404, doi:10.1016/J.Ocemod.2004.08.002. [Google Scholar]
- Shchepetkin, A. F. , and McWilliams J. C. (2009), Correction and commentary for “Ocean forecasting in terrain‐following coordinates: Formulation and skill assessment of the regional ocean modeling system” by Haidvogel et al., J. Comp. Phys. 227, pp. 3595–3624, J. Comput. Phys., 228, 8985–9000, doi:10.1016/j.jcp.2009.09.002. [Google Scholar]
- Shenk, G. W. , and Linker L. C. (2013), Development and application of the 2010 Chesapeake Bay watershed total maximum daily load model, J. Am. Water Resour. Assoc., 49, 1042–1056. [Google Scholar]
- Smullen, J. T. , Taft J., and Macknis J. (1982), Nutrient and sediment loads to the tidal Chesapeake Bay system, in Chesapeake Bay Program Technical Studies: A Synthesis, edited by Macalaster E. G., Barker D. A., and Kasper M., pp. 147–262, U.S. Environmental Protection Agency, Washington, D. C. [Google Scholar]
- Soetaert, K. , Middelburg J. J., Herman P. M. J., and Buis K. (2000), On the coupling of benthic and pelagic biogeochemical models, Earth Sci. Rev., 51(1–4), 173–201. [Google Scholar]
- Son, S. , Wang M., and Jr L. W. H. (2014), Satellite‐measured net primary production in the Chesapeake Bay, Remote Sens. Environ., 144(25), 109–119, doi:10.1016/j.rse.2014.01.018. [Google Scholar]
- Spilling, K. , Kremp A., Klais R., Olli K., and Tamminen T. (2014), Spring bloom community change modifies carbon pathways and C:N:P:Chl a stoichiometry of coastal material fluxes, Biogeosciences, 11, 7275–7289, doi:10.5194/bg-11-7275-2014. [Google Scholar]
- Stow, C. A. , Jolliff J., McGillicuddy D. J., Doney S. C., Allen J. I., Friedrichs M. A. M., Rose K. A., and Wallhead P. (2009), Skill assessment for coupled biological/physical models of marine systems, J. Mar. Syst., 76, 4–15, doi:10.1016/J.Jmarsys.2008.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor, K. E. (2001), Summarizing multiple aspects of model performance in a single diagram, J. Geophys. Res., 106(D7), 7183–7192, doi:10.1029/2000JD900719. [Google Scholar]
- Testa, J. M. , Li Y., Lee Y. J., Li M., Brady D. C., Toro D. M. D., Kemp W. M., and Fitzpatrick J. J. (2014), Quantifying the effects of nutrient loading on dissolved O2 cycling and hypoxia in Chesapeake Bay using a coupled hydrodynamic–biogeochemical model, J. Mar. Syst., 139, 139–158, doi:10.1016/j.jmarsys.2014.05.018. [Google Scholar]
- Tian, H. , Chen G., Liu M., Zhang C., Sun G., Lu C., Xu X., Ren W., Pan S., and Chappelka A. (2010), Model estimates of ecosystem net primary productivity, evapotranspiration, and water use efficiency in the southern United States during 1895–2007, For. Ecol. Manage., 259, 1311–1327. [Google Scholar]
- Tian, H. , Chen G., Lu C., Xu X., Hayes D. J., Ren W., Pan S., Huntzinger D. N., and Wofsy S. C. (2014), North American terrestrial CO2 uptake largely offset by CH4 and N2O emissions: Toward a full accounting of the greenhouse gas budget, Clim. Change, doi:10.1007/s10584-014-1072-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian, H. , Yang Q., Najjar R. G., Ren W., Friedrichs M. A. M., Hopkinson C. S., and Pan S. (2015), Anthropogenic and climatic influences on carbon fluxes from eastern North America to the Atlantic Ocean: A process‐based modeling study, J. Geophys. Res. Biogeosci., 120, 752–772, doi:10.1002/2014JG002760. [Google Scholar]
- Wakelin, S. L. , Holt J. T., Blackford J. C., Allen J. I., Butenschön M., and Artioli Y. (2012), Modeling the carbon fluxes of the northwest European continental shelf: Validation and budgets, J. Geophys. Res., 117, C05020, doi:10.1029/2011JC007402. [Google Scholar]
- Wang, Z. , Haidvogel D. B., Bushek D., Ford S. E., Hofmann E. E., Powell E. N., and Wilkin J. (2012), Circulation and water properties and their relationship to the oyster disease MSX in Delaware Bay, J. Mar. Res., 70, 279–308. [Google Scholar]
- Wang, Z. A. , Wanninkhof R., Cai W.‐J., Byrne R., Hu X., Peng T.‐H., and Huang W.‐J. (2013), The marine inorganic carbon system along the Gulf of Mexico and Atlantic coasts of the United States: Insights from a transregional coastal carbon study, Limnol. Oceanogr., 58, 325–342. [Google Scholar]
- Wanninkhof, R. (1992), Relationship between wind speed and gas exchange, J. Geophys. Res., 97, 7373–7382, doi:10.1029/92JC00188. [Google Scholar]
- Warner, J. C. , Sherwood C. R., Arango H. G., and Signell R. P. (2005), Performance of four turbulence closure models implemented using a generic length scale method, Ocean Model., 8, 81–113, doi:10.1016/j.ocemod.2003.12.003. [Google Scholar]
- Weiss, R. (1970), The solubility of nitrogen, oxygen, and argon in water and sea water, Deep Sea Res., 17, 721–735. [Google Scholar]
- Willmott, C. J. (1981), On the validation of models, Phys. Geogr., 2, 184–194, doi:10.1080/02723646.1981.10642213. [Google Scholar]
- Xiao, Y. , and Friedrichs M. A. M. (2014a), Using biogeochemical data assimilation to assess the relative skill of multiple ecosystem models: Effects of increasing the complexity of the planktonic food web, Biogeosciences, 11, 3015–3030, doi:10.5194/bg-11-3015-2014. [Google Scholar]
- Xiao, Y. , and Friedrichs M. A. M. (2014b), The assimilation of satellite‐derived data into a one‐dimensional lower trophic level marine ecosystem model, J. Geophys. Res. Oceans, 119, 2691–2712, doi:10.1002/2013JC009433. [Google Scholar]
- Xu, J. , and Hood R. R. (2006), Modeling biogeochemical cycles in Chesapeake Bay with a coupled physical‐biological model, Estuarine Coastal Shelf Sci., 69, 19–46, doi:10.1016/j.ecss.2006.03.021. [Google Scholar]
- Xu, J. , Hood R. R., and Chao S. Y. (2005), A simple empirical optical model for simulating light attenuation variability in a partially mixed estuary, Estuaries, 28, 572–580, doi:10.1007/BF02696068. [Google Scholar]
- Xu, J. , Long W., Wiggert J. D., Lanerolle L. W. J., Brown C. W., Murtugudde R., and Hood R. R. (2012), Climate forcing and salinity variability in Chesapeake Bay, USA, Estuarine Coastal Shelf Sci., 35, 237–261, doi:10.1007/s12237-011-9423-5. [Google Scholar]
- Xue, Z. , He R., Fennel K., Cai W.‐J., Lorhenz S., and Hopkinson C. (2013), Modeling seasonal and interannual variability of circulation and biogeochemical processes in the Gulf of Mexico, Biogeosciences, 10, 7219–7234, doi:10.5194/bg-10-7219-2013. [Google Scholar]
- Yang, Q. , Tian H., Friedrichs M. A. M., Liu M., Li X., and Yang J. (2015a), Hydrological responses to climate and land‐use changes along the North American east coast: A 110‐Year historical reconstruction, J. Am. Water Resour. Assoc., 51(1), 47–67, doi:10.1111/jawr.12232. [Google Scholar]
- Yang, Q. , Tian H., Friedrichs M. A. M., Hopkinson C., Lu C., and Najjar R. G. (2015b), Increased nitrogen export from eastern North America to the Atlantic Ocean due to climatic and anthropogenic changes during 1901–2008, J. Geophys. Res. Biogeosci., 120, 1046–1068, doi:10.1002/2014JG002763. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information S1


